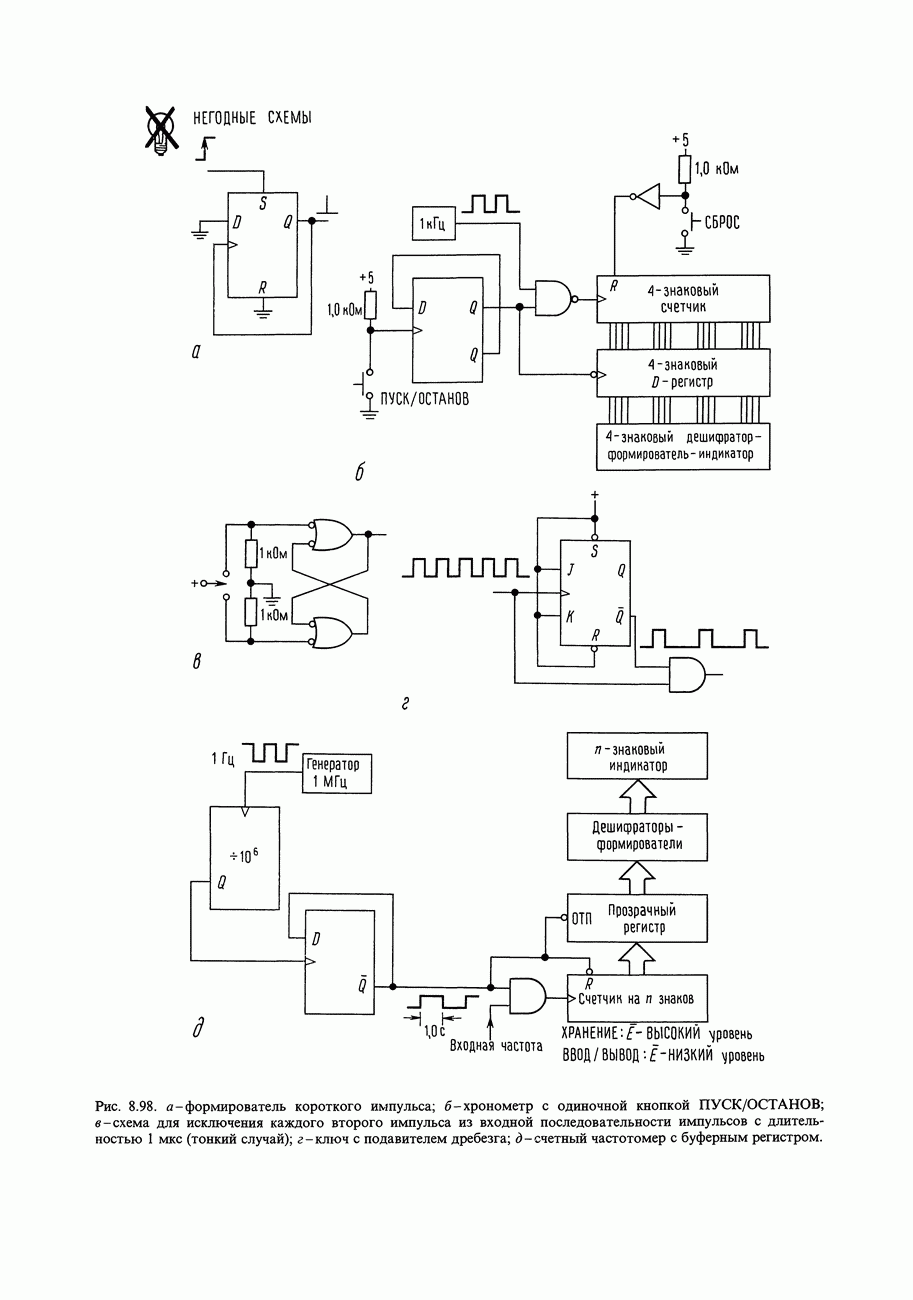
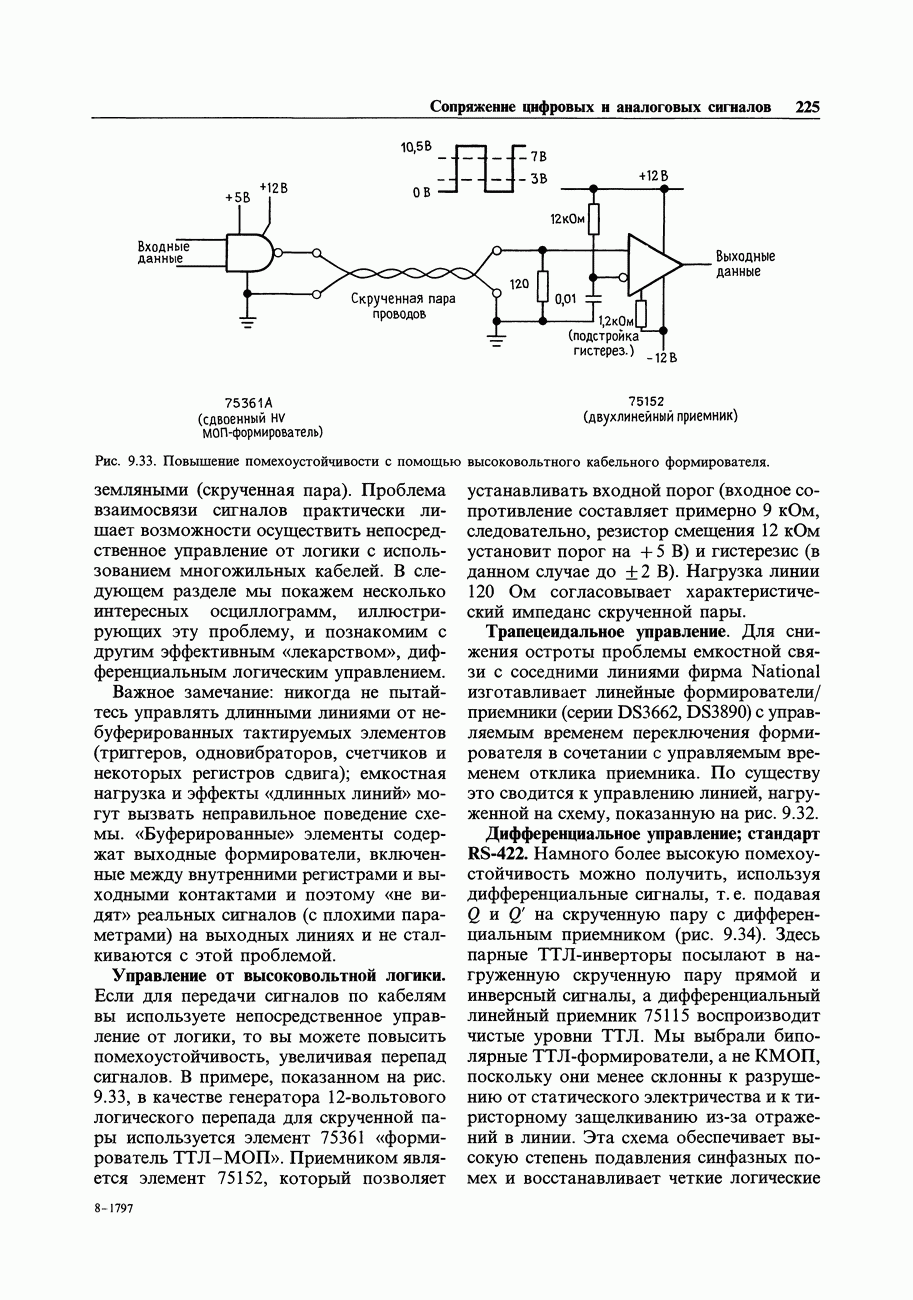
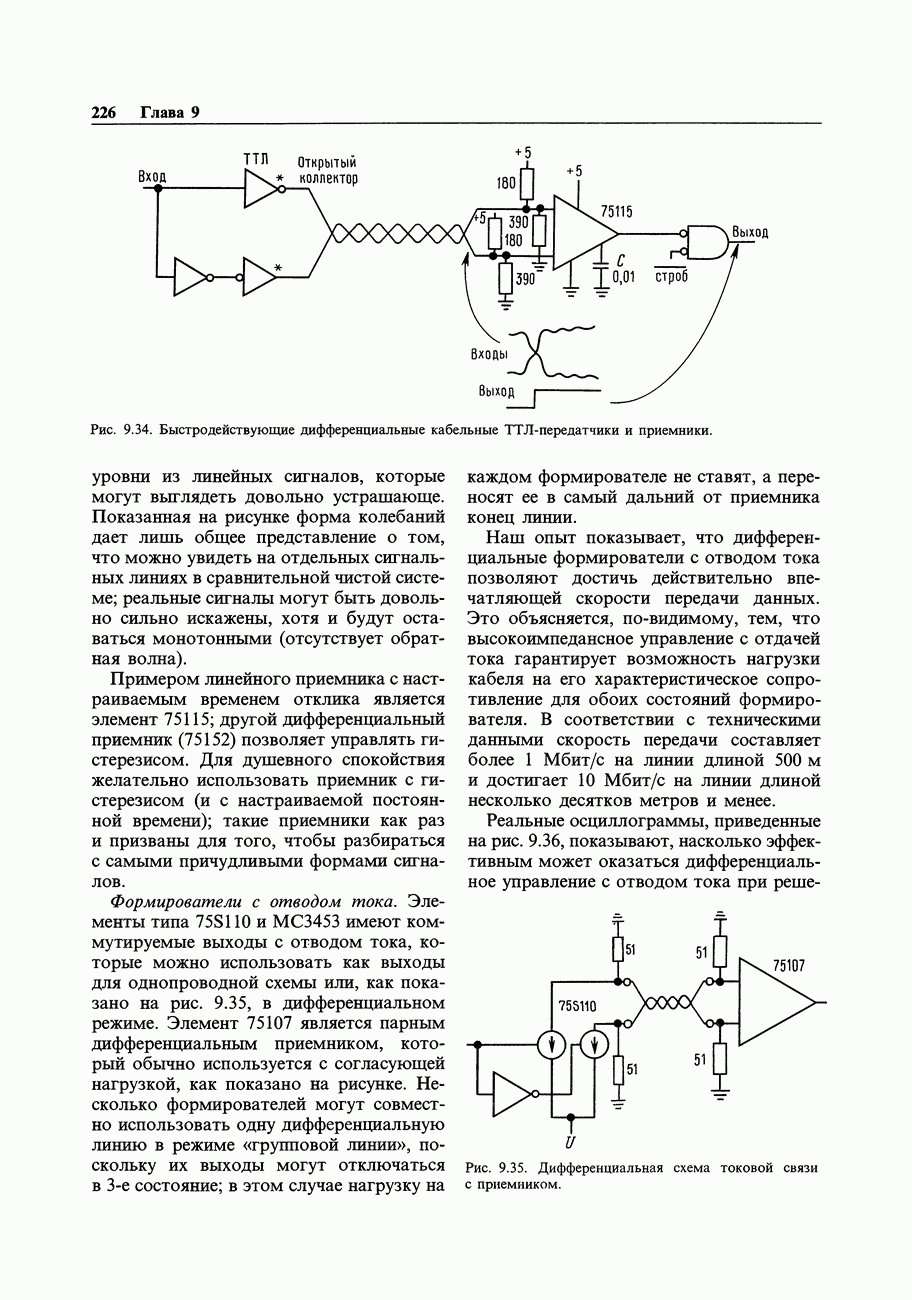
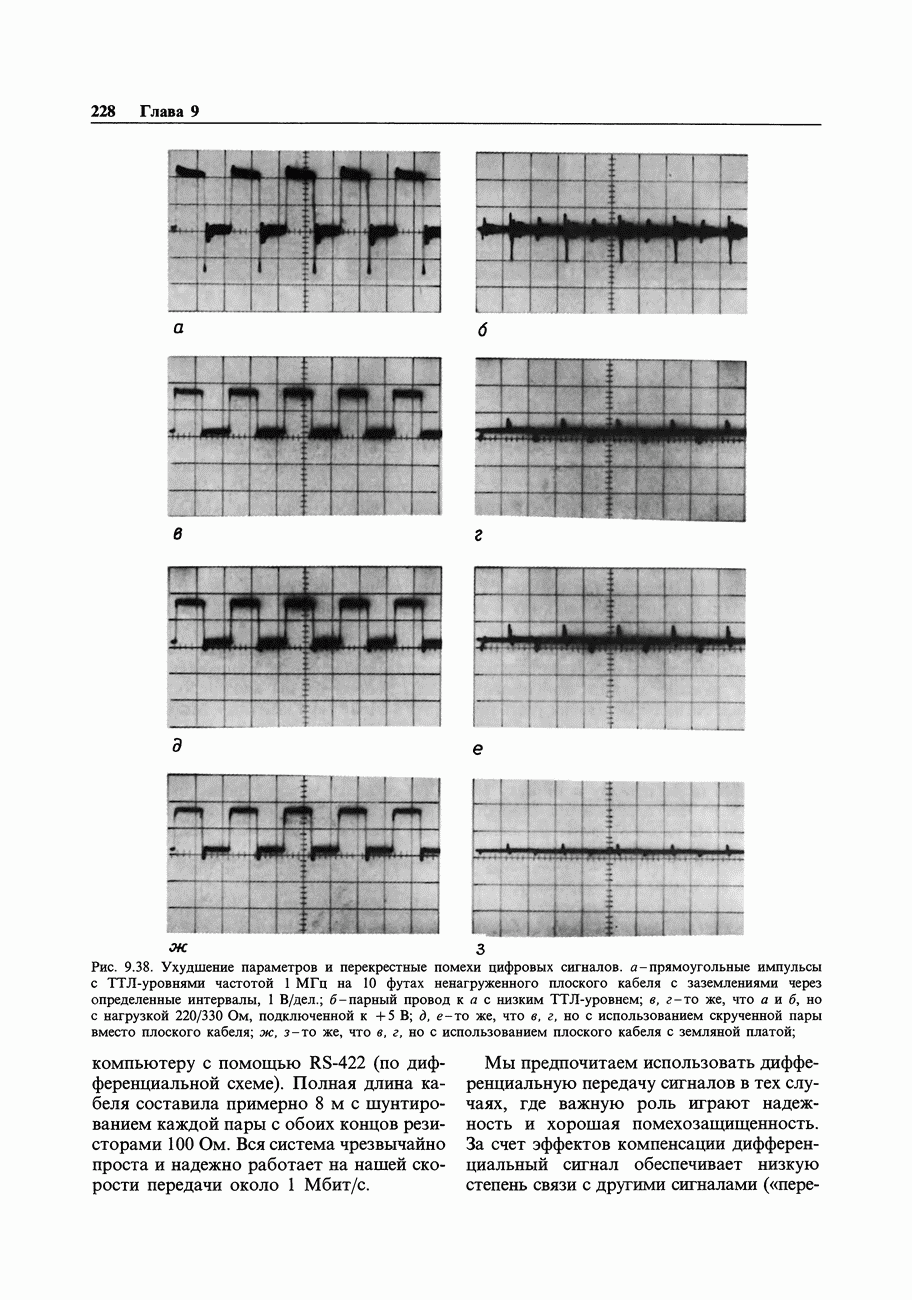
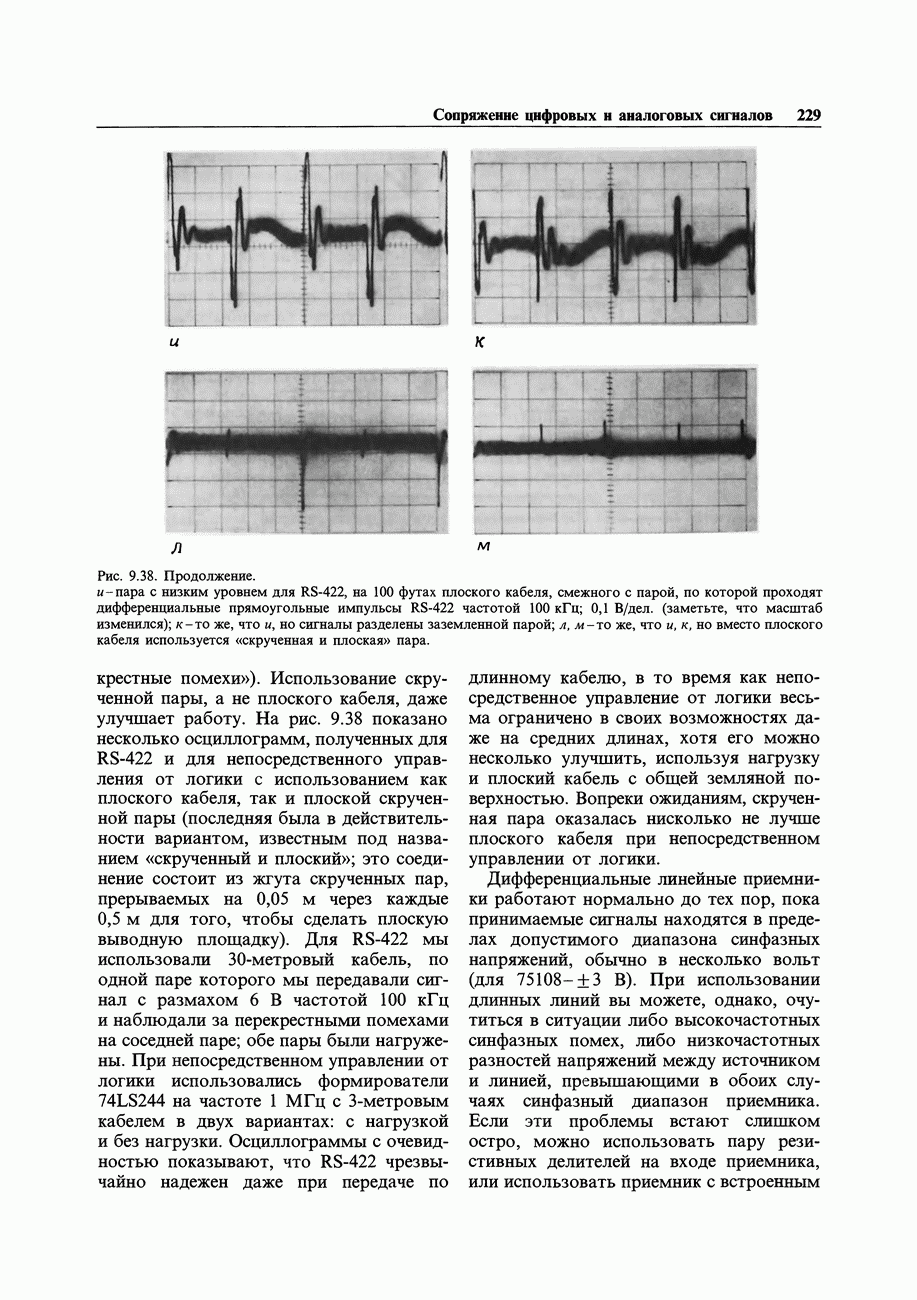
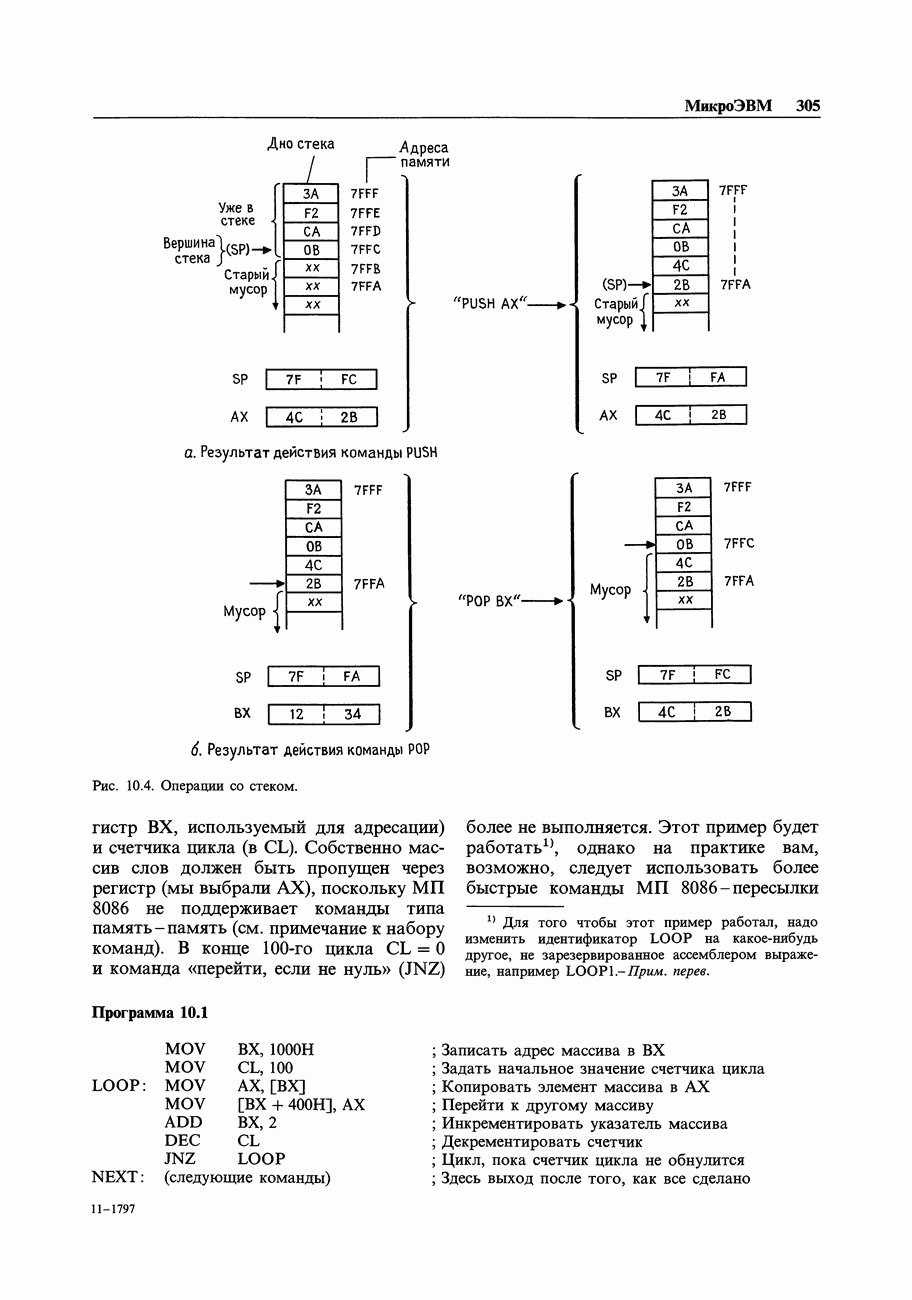
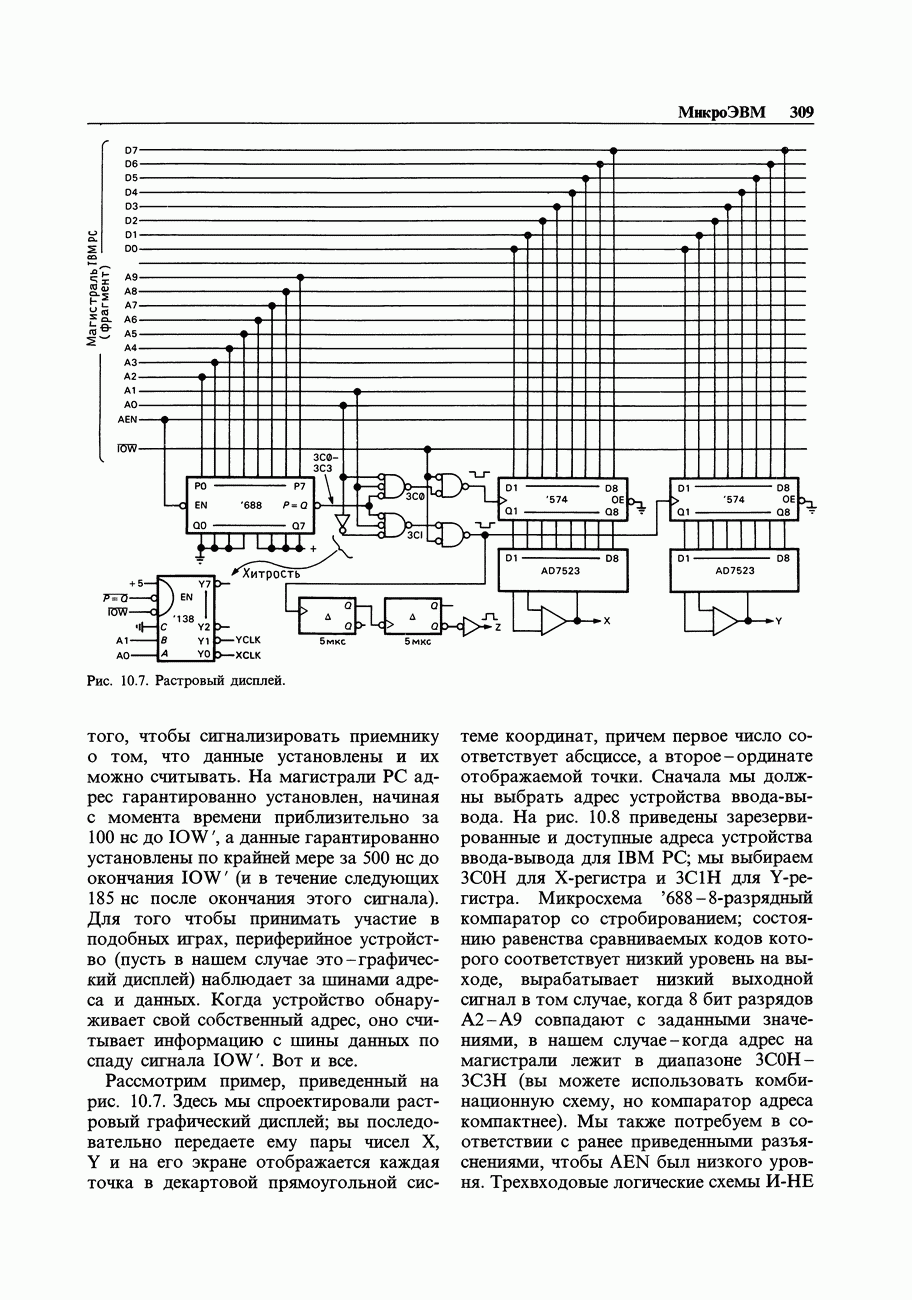
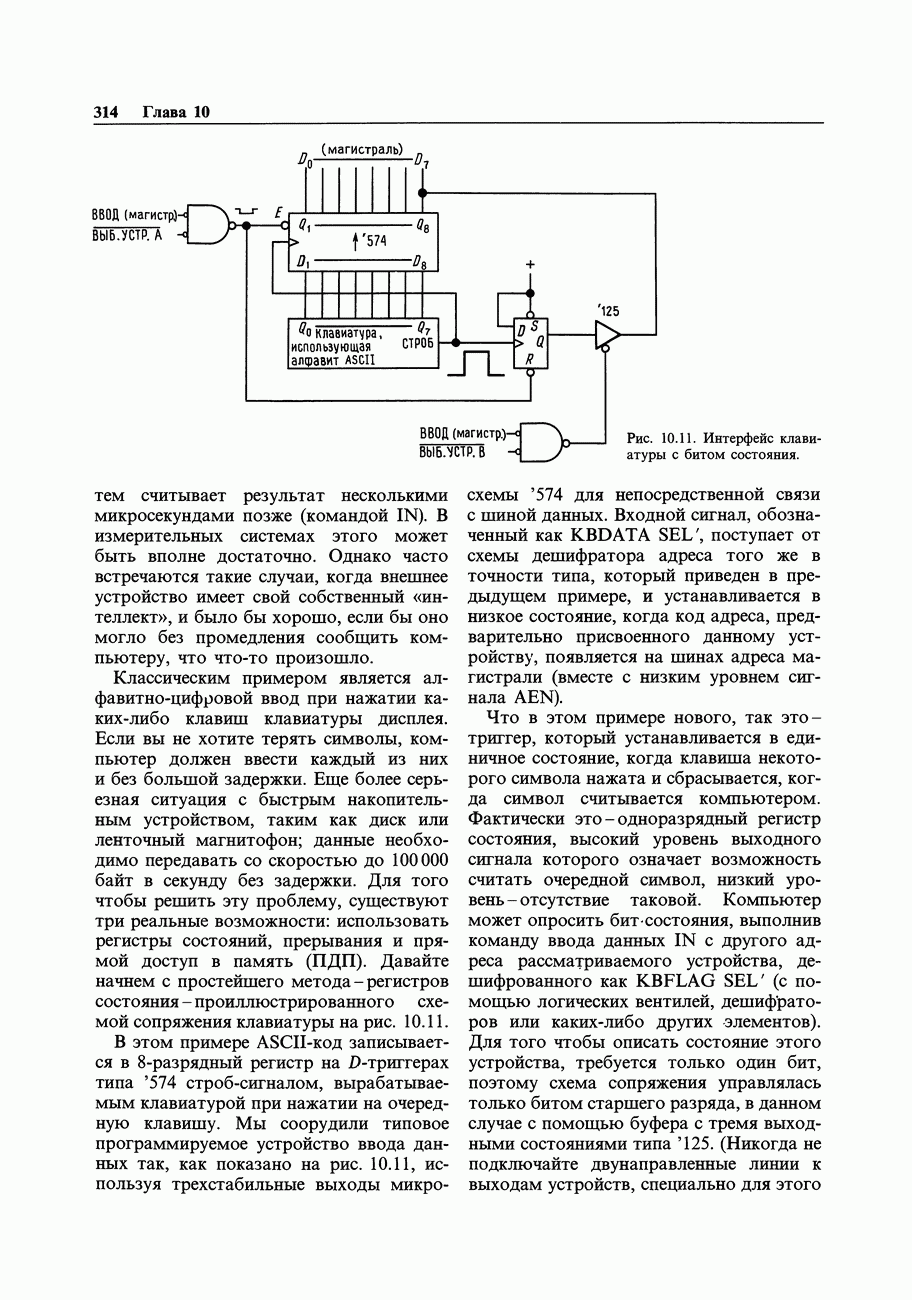
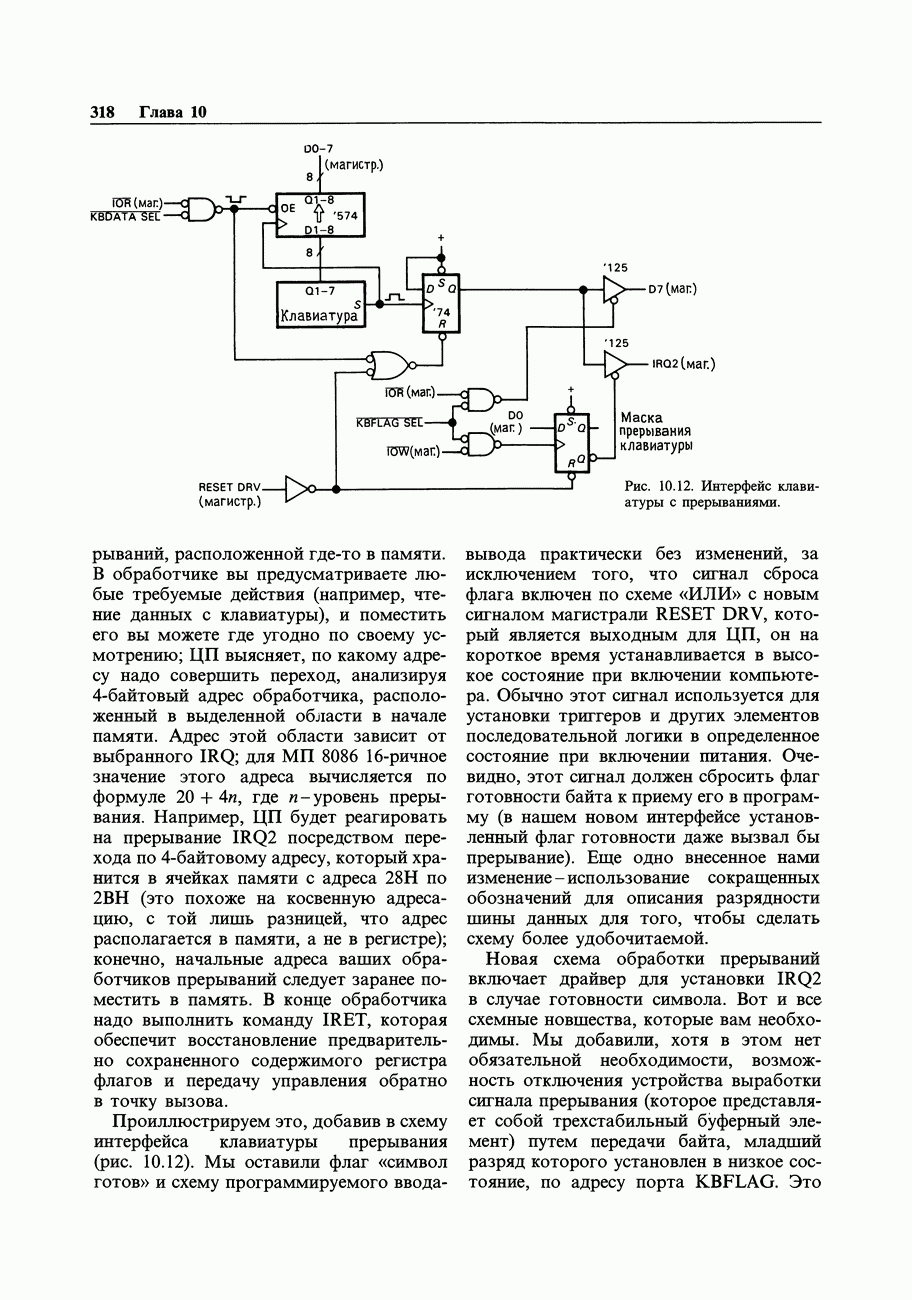
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
8.13. Минимизация и карты Карно
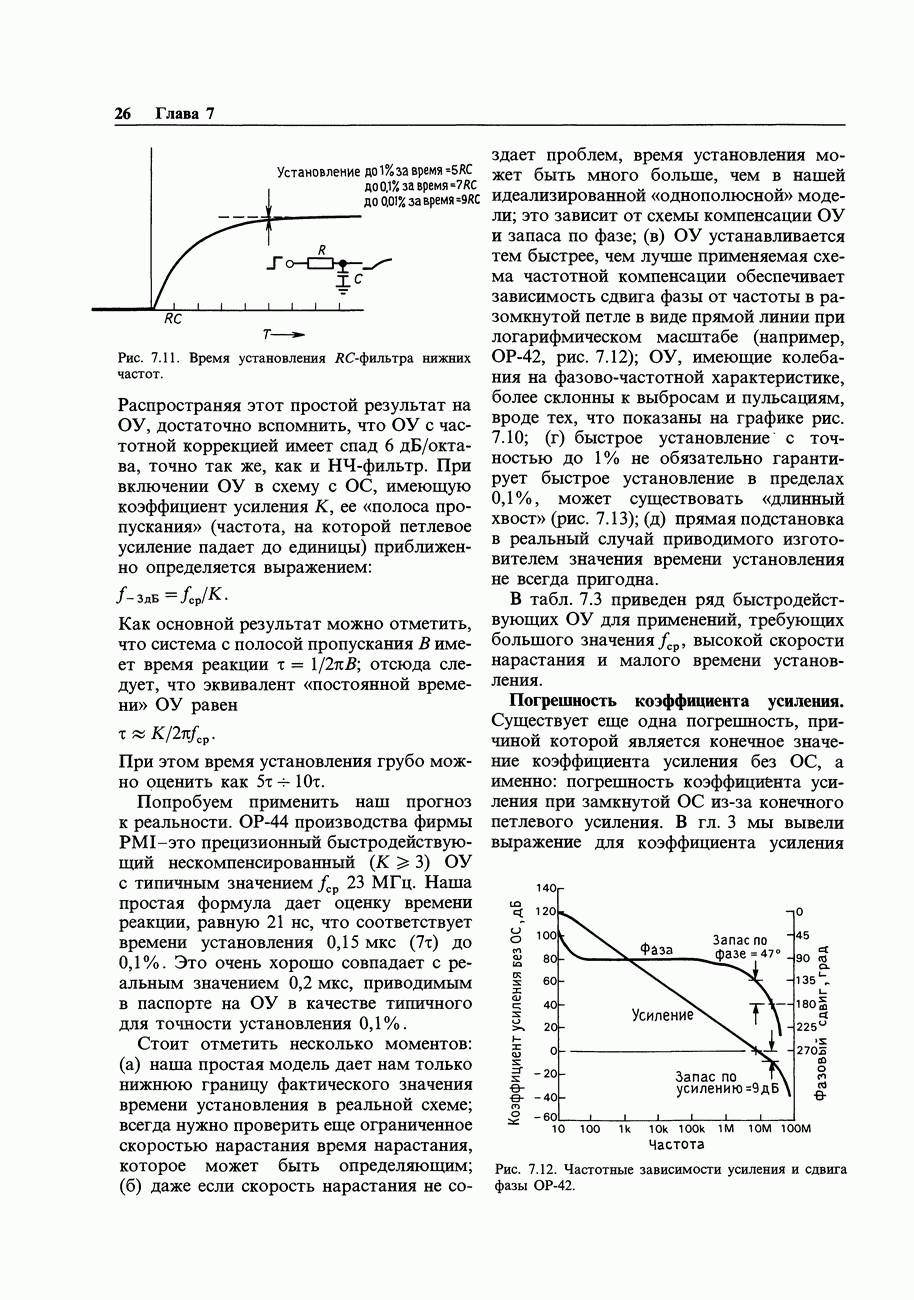
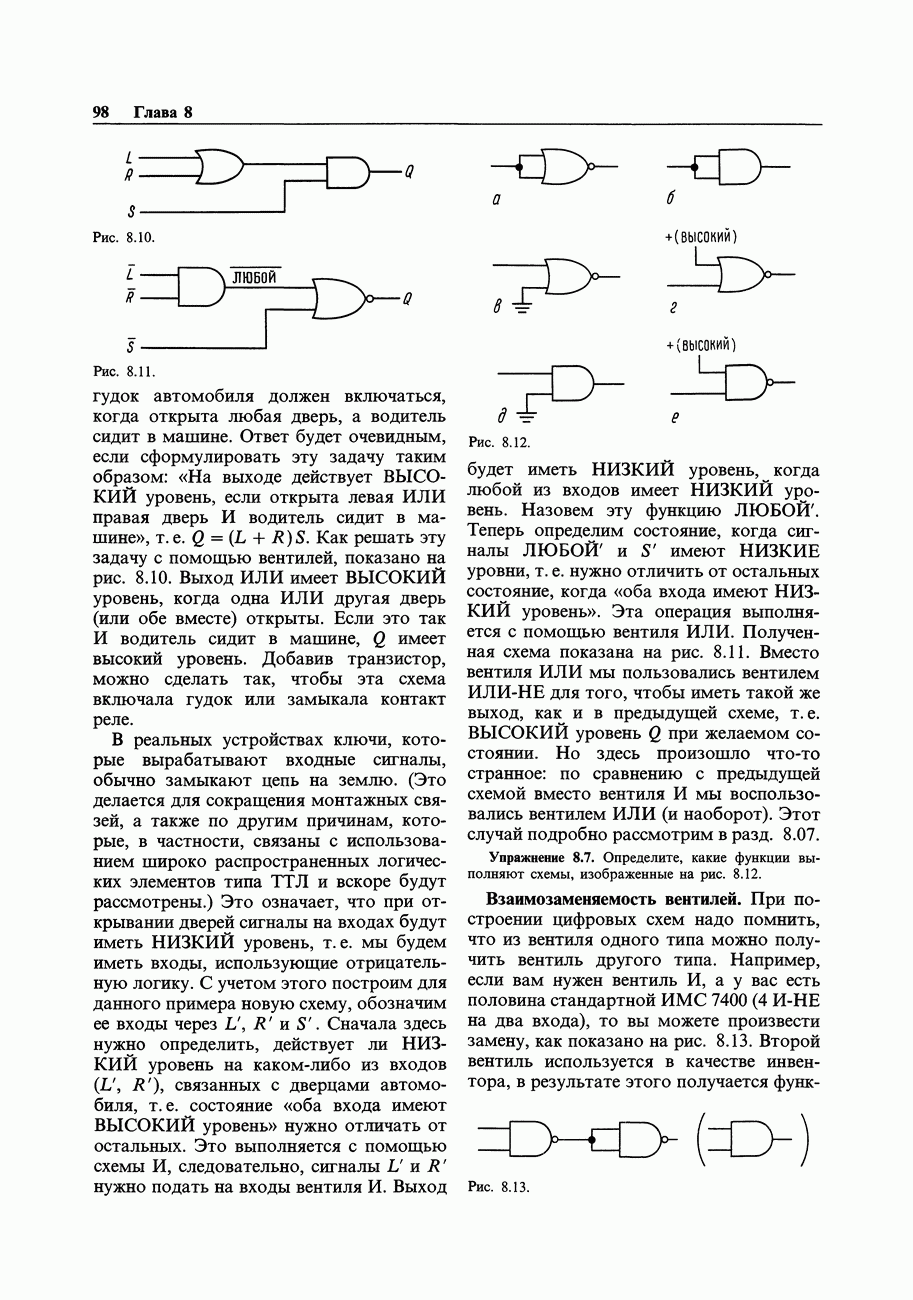
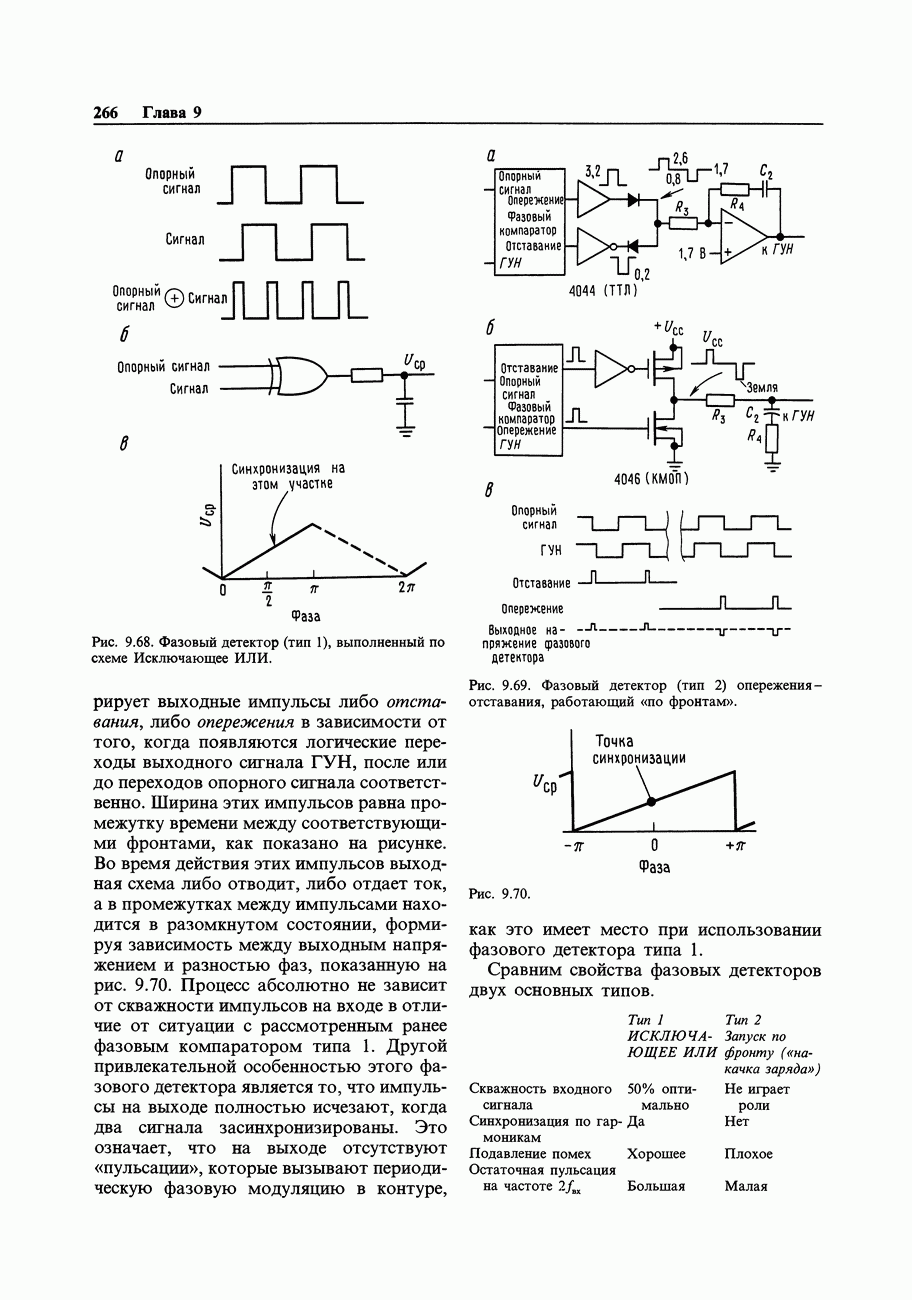
Поскольку логическую функцию, даже такую простую, как Исключающее ИЛИ, можно реализовать различными способами, часто бывает нужно найти для нее самое простое решение, или, возможно, наиболее удобное схемное решение. Над этой проблемой бились многие светлые умы и в настоящее время существует несколько способов ее разрешения, включая алгебраические методы, реализуемые с помощью ЭВМ. При числе входов, не превышающем четырех, наилучшим методом является составление карты Карно. Этот метод позволяет также найти логическое выражение (если оно заранее неизвестно) по таблице истинности. Проиллюстрируем этот метод с помощью примера. Предположим, что требуется построить схему для мажоритарного подсчета голосов при баллотировке. Будем считать, что имеются три входа, работающие в положительной логике (на любом из них может быть 1 или 0) и выход (0 или 1). Выход равен 1, если 1 присутствует не менее чем на двух входах.
Шаг 1. Составим таблицу истинности

Здесь должны быть представлены все возможные сочетания и соответствующие им состояния выхода (или выходов). В том случае, когда состояние входа не оказывает влияния на выход, ставится X (любое значение).

Рис. 8.27. Карта Карно.
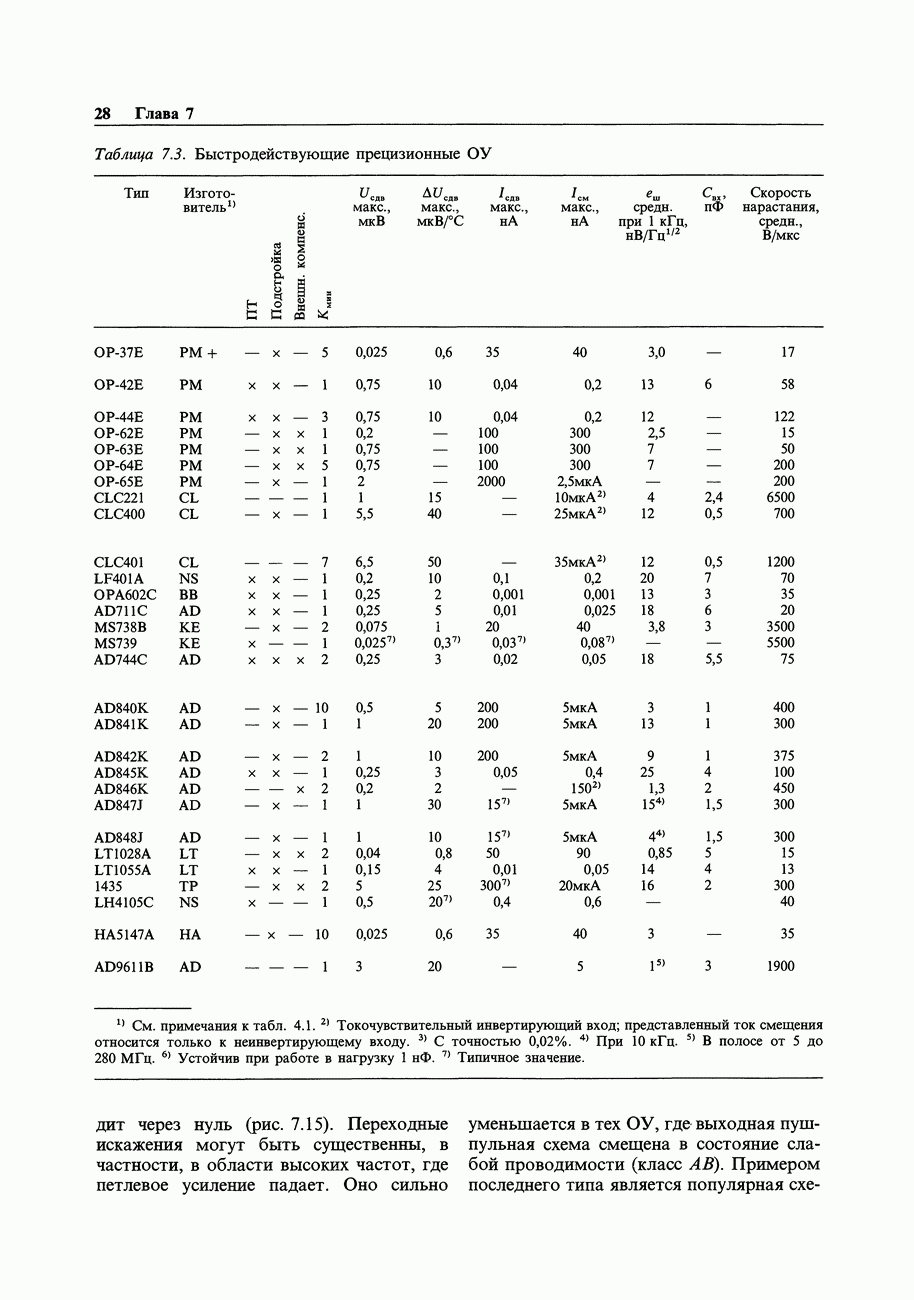
Шаг 2. Составим карту Карно. Она представляет собой нечто очень близкое к таблице истинности, но содержит переменные, которые расположены по двум осям. Переменные должны быть расположены таким образом, чтобы при переходе от каждого квадрата к соседнему менялось бы состояние только одного входа (рис. 8.27).
Шаг 3. Отметим на карте группы, содержащие 1 (можно также использовать и группы, содержащие 0). Три овала на рис. 8.27 определяют логические выражения АВ, АС и ВС.

Рис. 8.28.
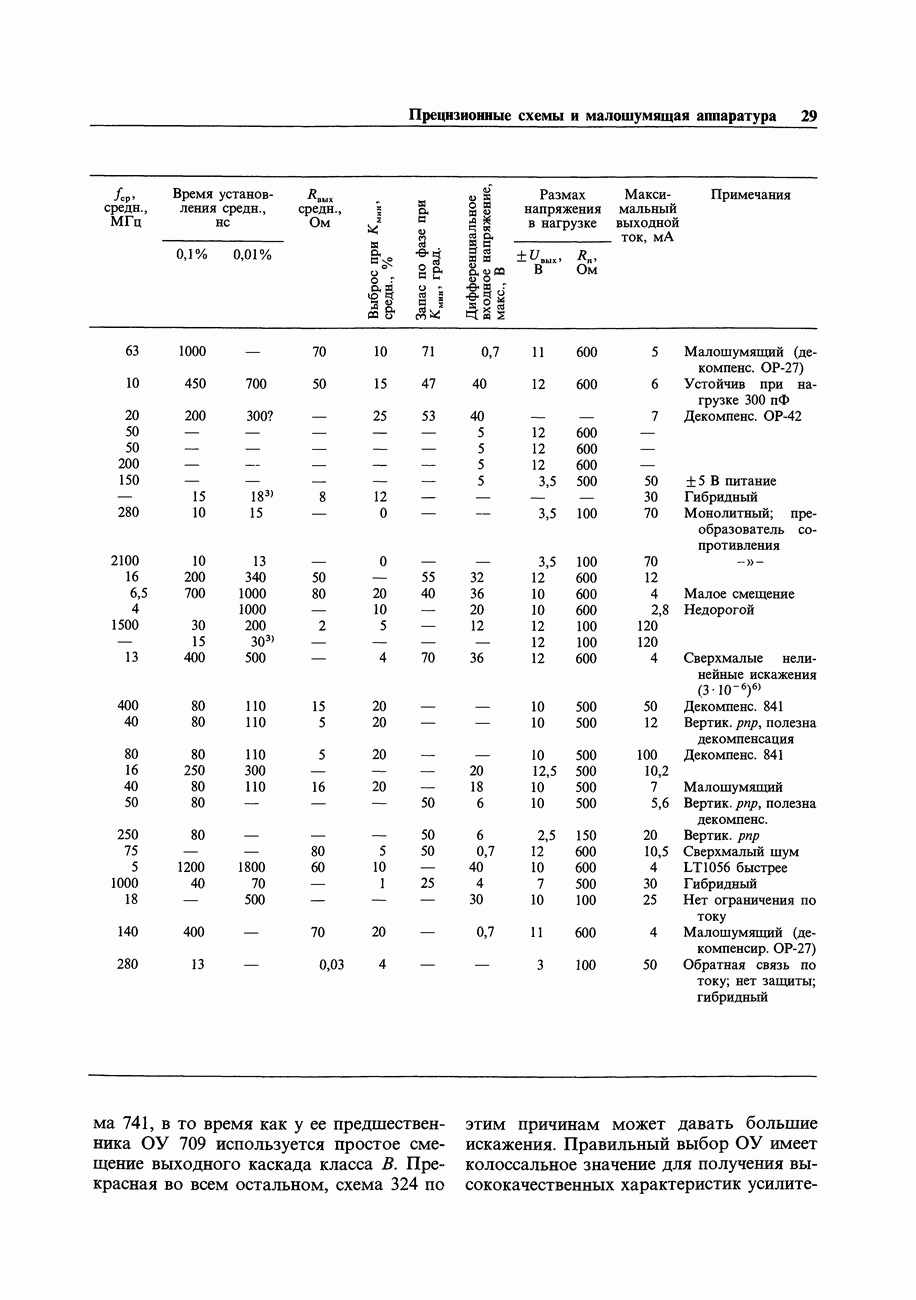
Далее получим требуемую функцию

схемная реализация ее показана на рис. 8.28. Этот результат кажется очевидным, когда он уже получен. Можно было бы составить выражение для нулей и вместо этого получить

Это выражение может оказаться полезным для случая, когда в каких-либо точках схемы имеются дополнения А, В и С.
Некоторые комментарии к картам Карно.
1. Ищите группы, содержащие 2, 4, 8 и т.д. квадратов. Они имеют простые логические выражения.
2. Логика будет тем проще, чем крупнее блок вы опишете.
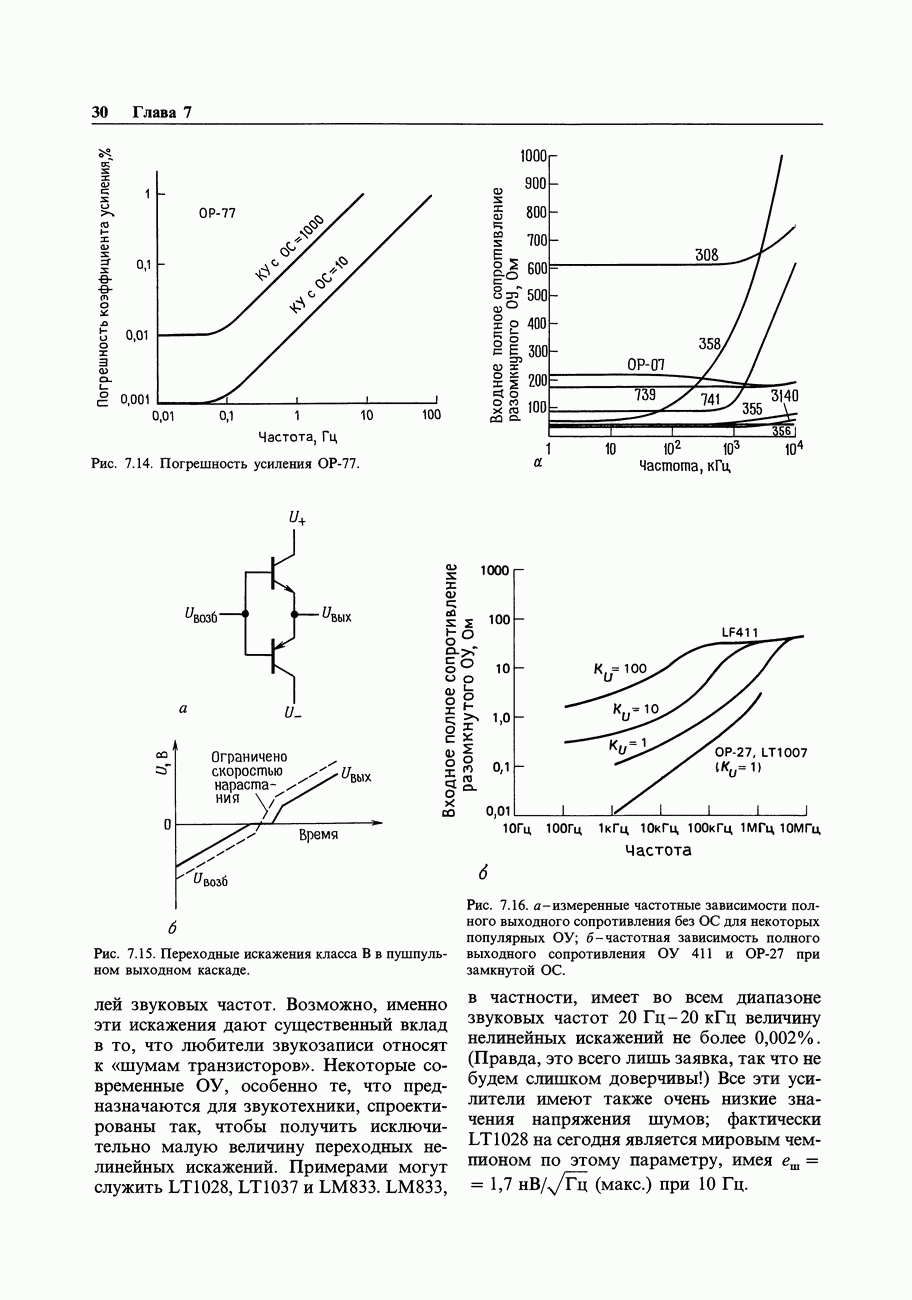
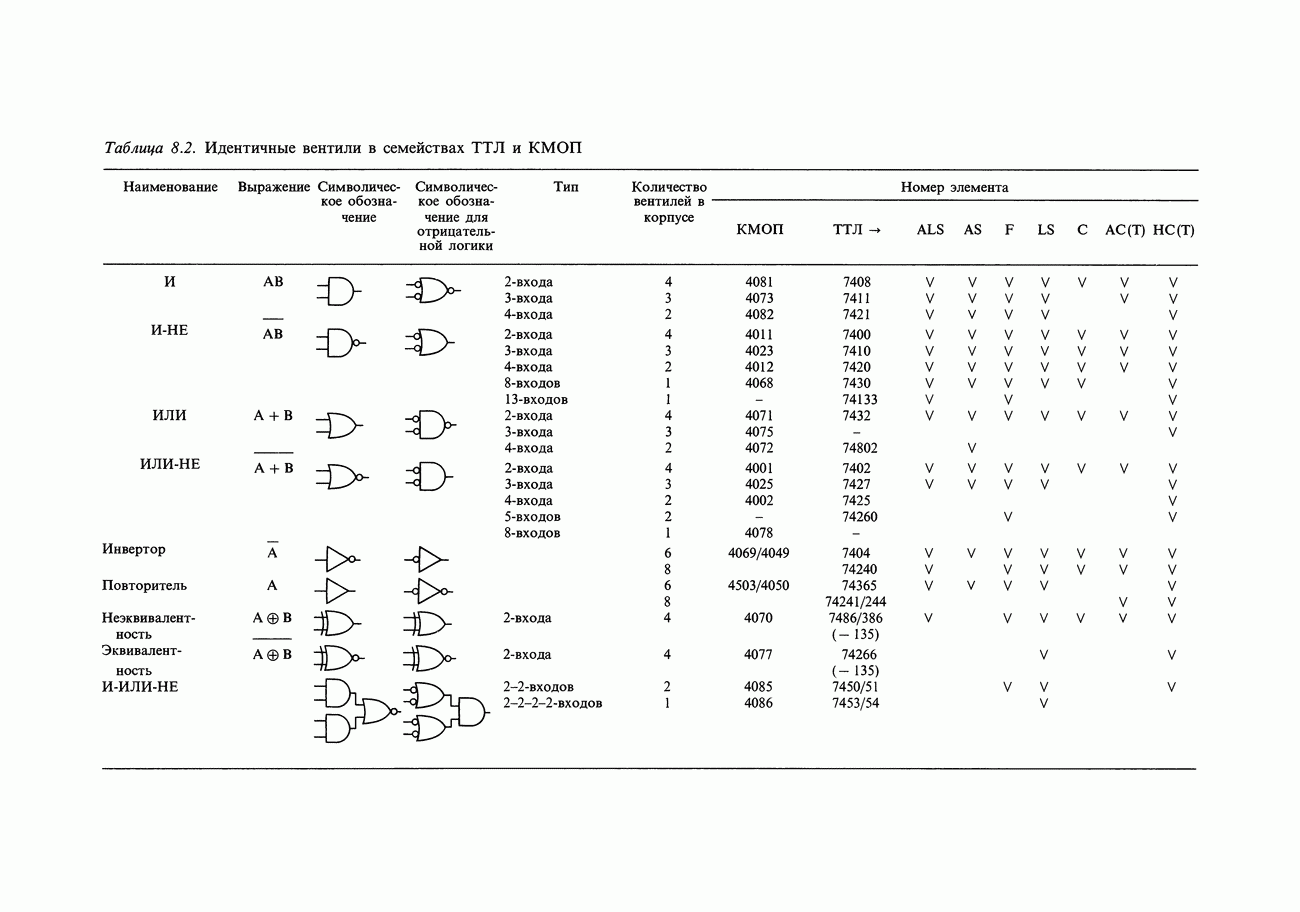
3. Состыкуйте края карты Карно. Например, карта на рис. 8.29 описывается выражением  С.
С.
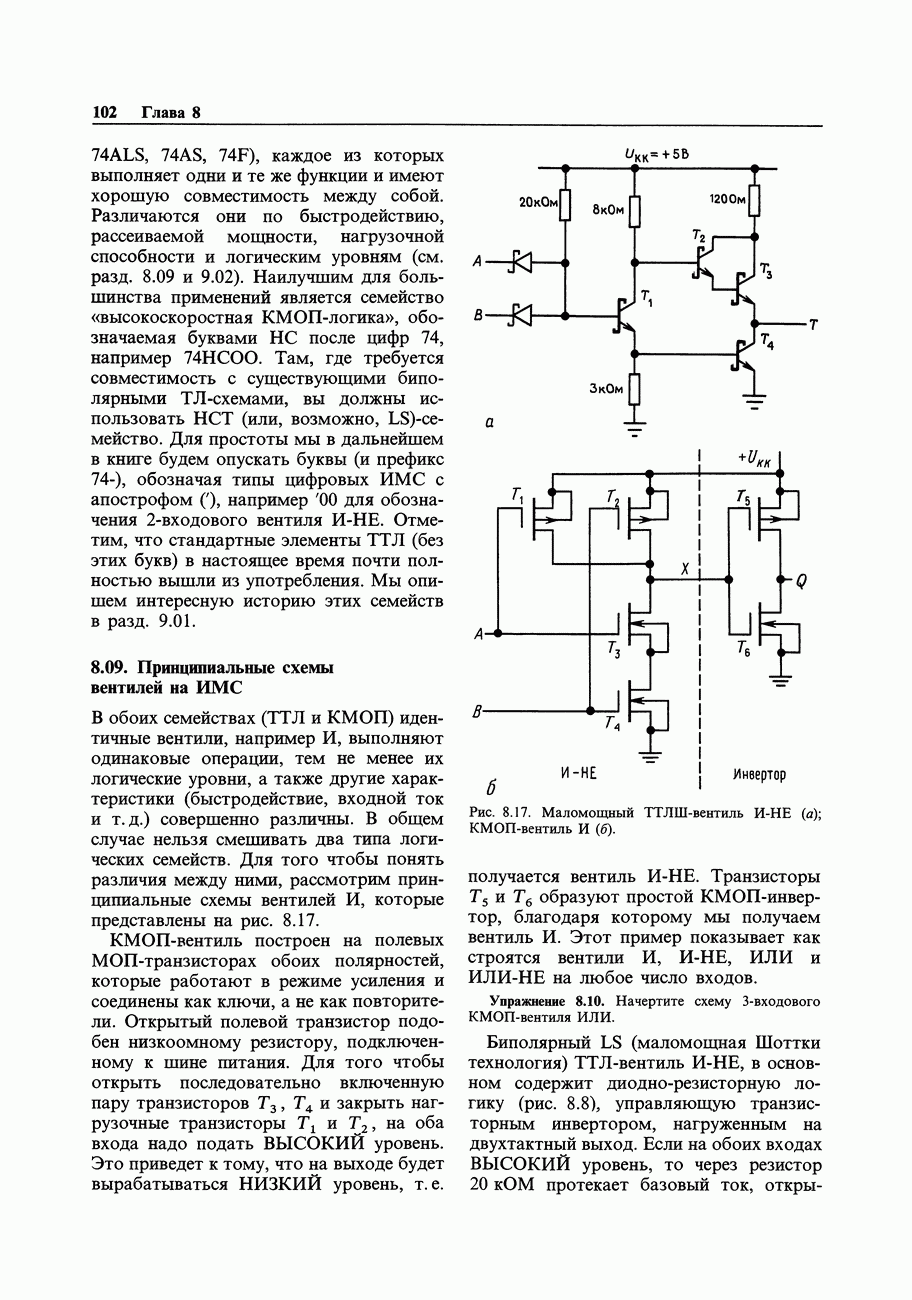
4. Блок «единиц», содержащий один или два «нуля», лучше всего описывается с помощью группировки, показанной на рис. 8.30. Этому блоку соответствует логическое выражение  .
.
5. Места, содержащие X (любое значение), представляют собой «карт-бланш». Записывайте в них «нули» или «единицы» так, чтобы можно было получить простейшую логику.

Рис. 8.29.

Рис. 8.30.
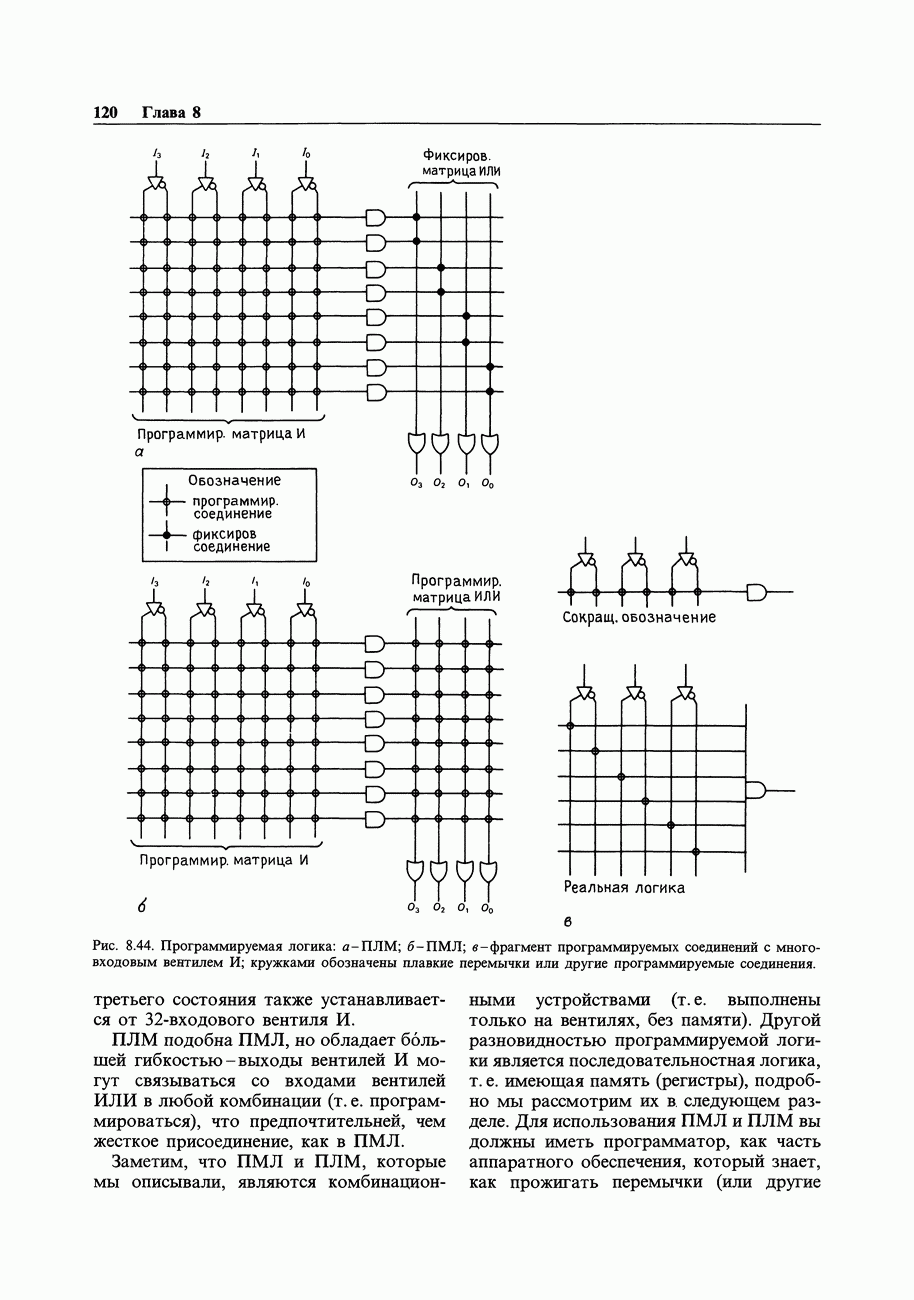
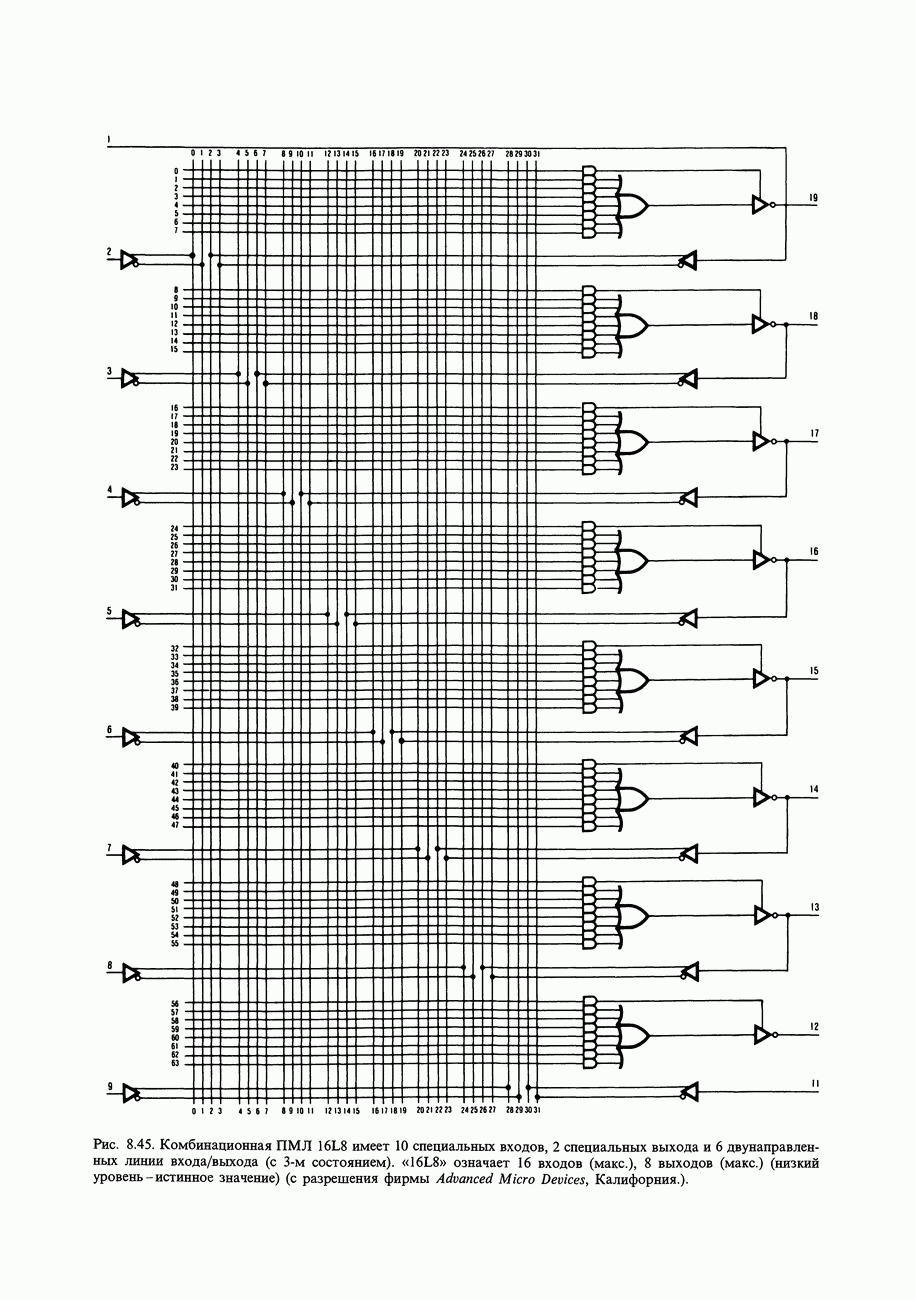
6. Карта Карно может и не привести к лучшему решению. Иногда более сложное логическое выражение имеет более простую схемную реализацию, например в случае, когда некоторые члены выражения уже сформированы схемой в виде логических сигналов, которые можно использовать в качестве входных. Кроме того, реализации Исключающего ИЛИ не очевидны из карты Карно. Наконец, при выборе логической структуры схемы определенную роль играют ограничения, связанные с конструкцией ИМС (например, когда в одном корпусе содержатся четыре  -входовых вентиля). Когда используются такие программируемые логические устройства как ПМЛ для конструирования логических функций, внутренняя структура (программируемые вентили И и фиксированные вентили ИЛИ) сдерживает реализацию, которая могла бы быть применена.
-входовых вентиля). Когда используются такие программируемые логические устройства как ПМЛ для конструирования логических функций, внутренняя структура (программируемые вентили И и фиксированные вентили ИЛИ) сдерживает реализацию, которая могла бы быть применена.
Упражнение 8.13. Нарисуйте карту Карно для логики, которая позволит определить, является ли  -разрядное двоичное число «главным», считая при этом, что главными не являются числа 0, 1 и 2. Дайте схемную реализацию на
-разрядное двоичное число «главным», считая при этом, что главными не являются числа 0, 1 и 2. Дайте схемную реализацию на  -входовых вентилях.
-входовых вентилях.
Упражнение  . Найдите логическое выражение, с помощью которого можно было бы умножить два
. Найдите логическое выражение, с помощью которого можно было бы умножить два  -разрядных двоичных числа и получить
-разрядных двоичных числа и получить  -разрядный результат. Рекомендации: для каждого выходного бита пользуйтесь отдельными картами Карно.
-разрядный результат. Рекомендации: для каждого выходного бита пользуйтесь отдельными картами Карно.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
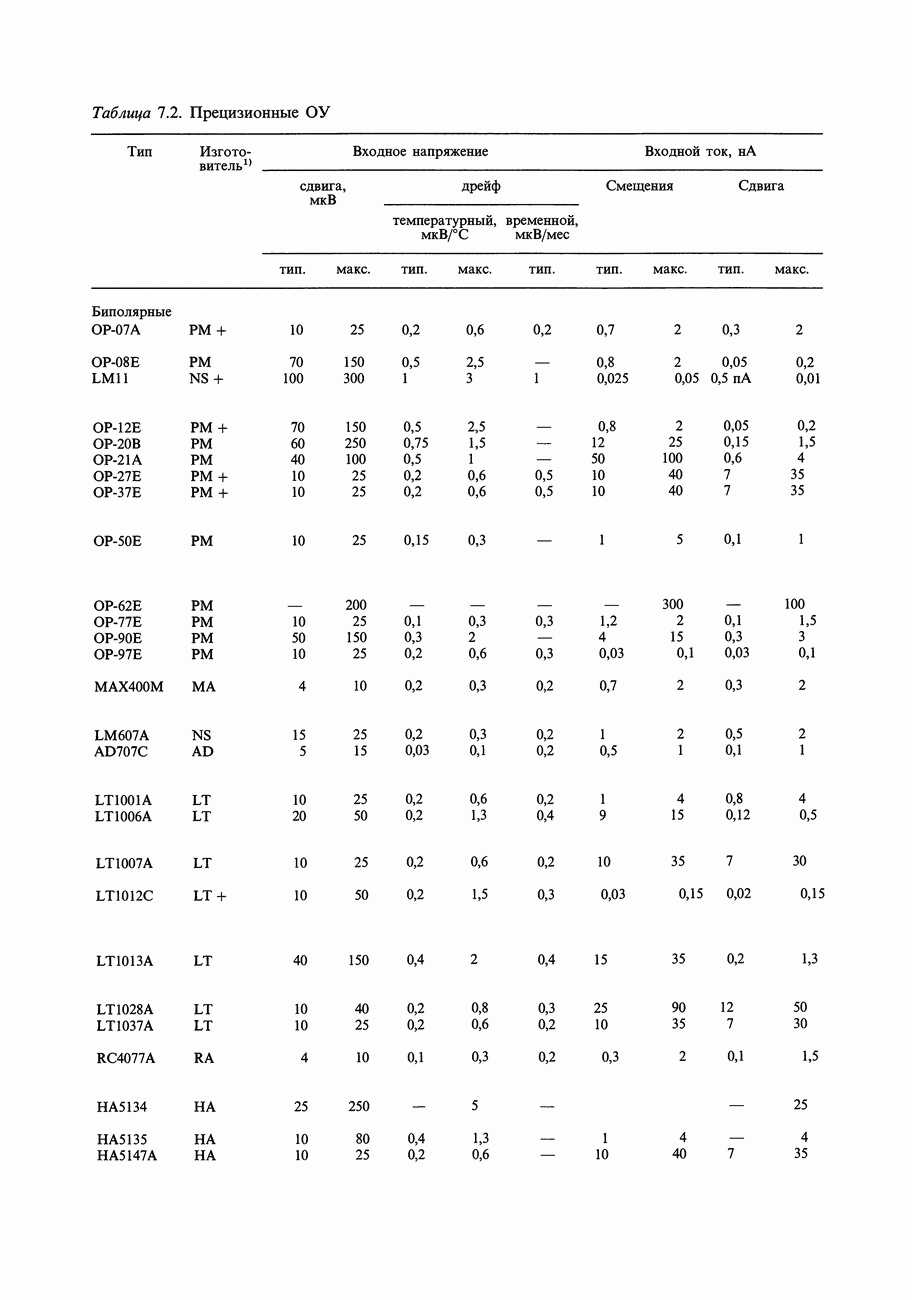
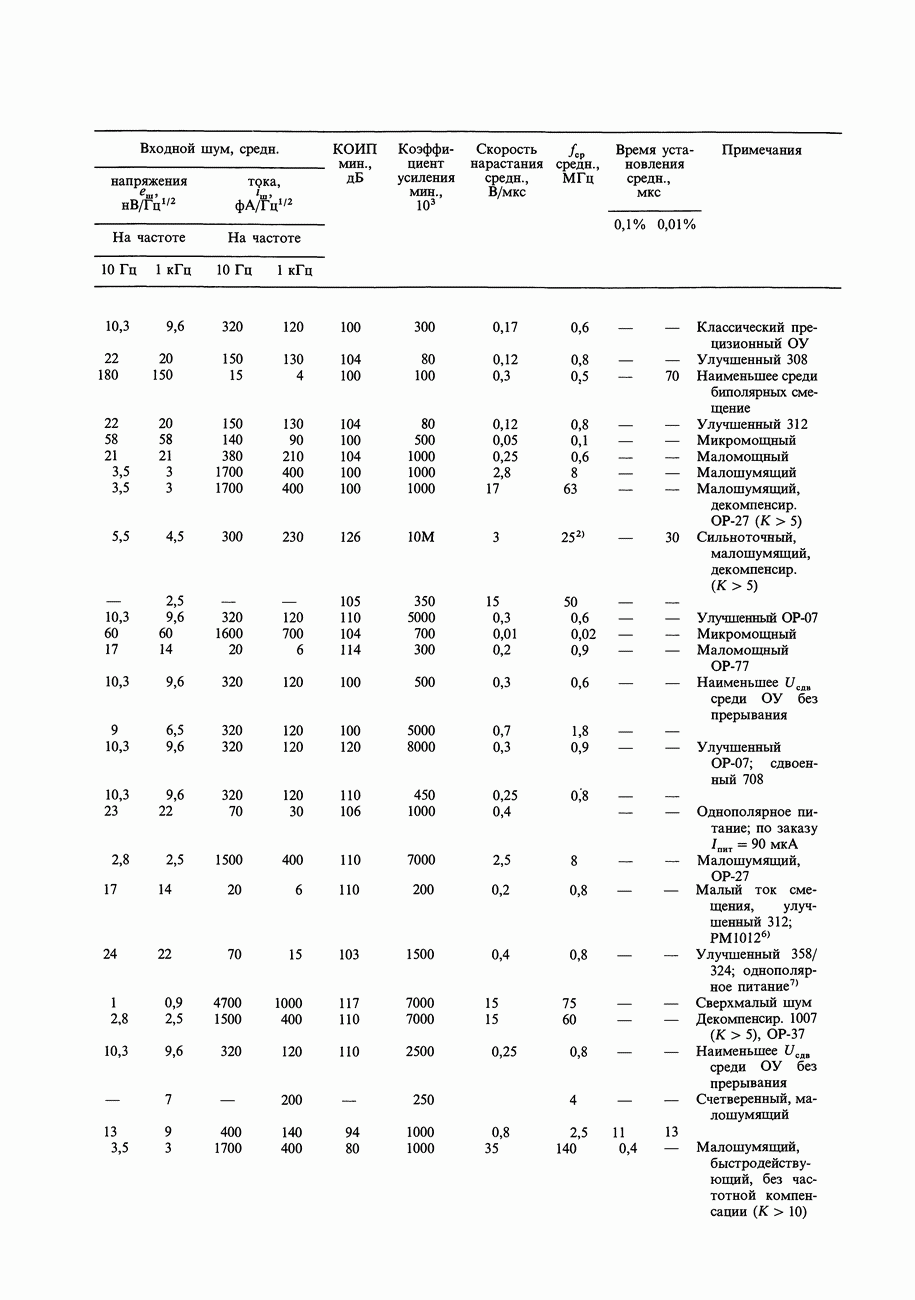
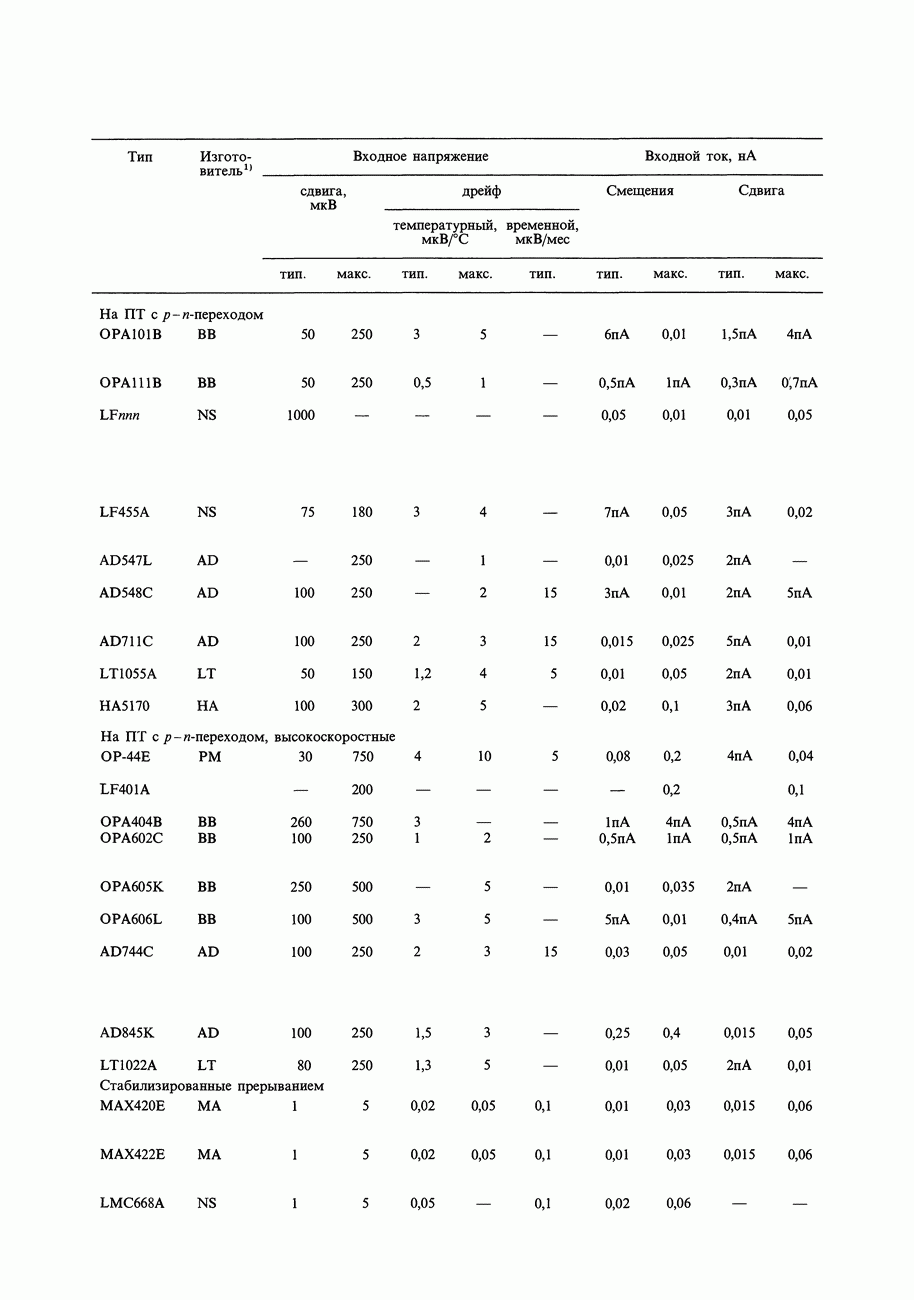
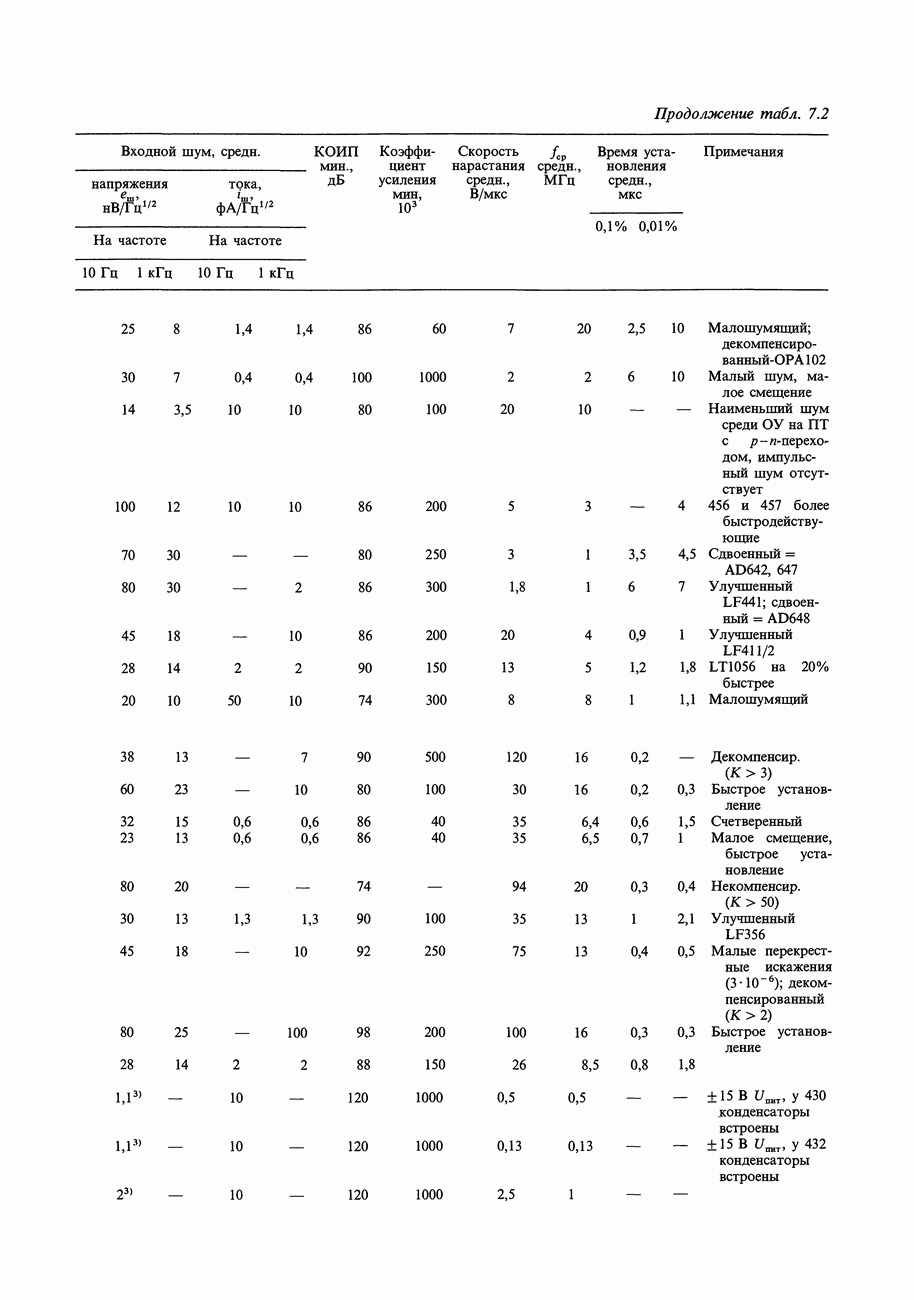
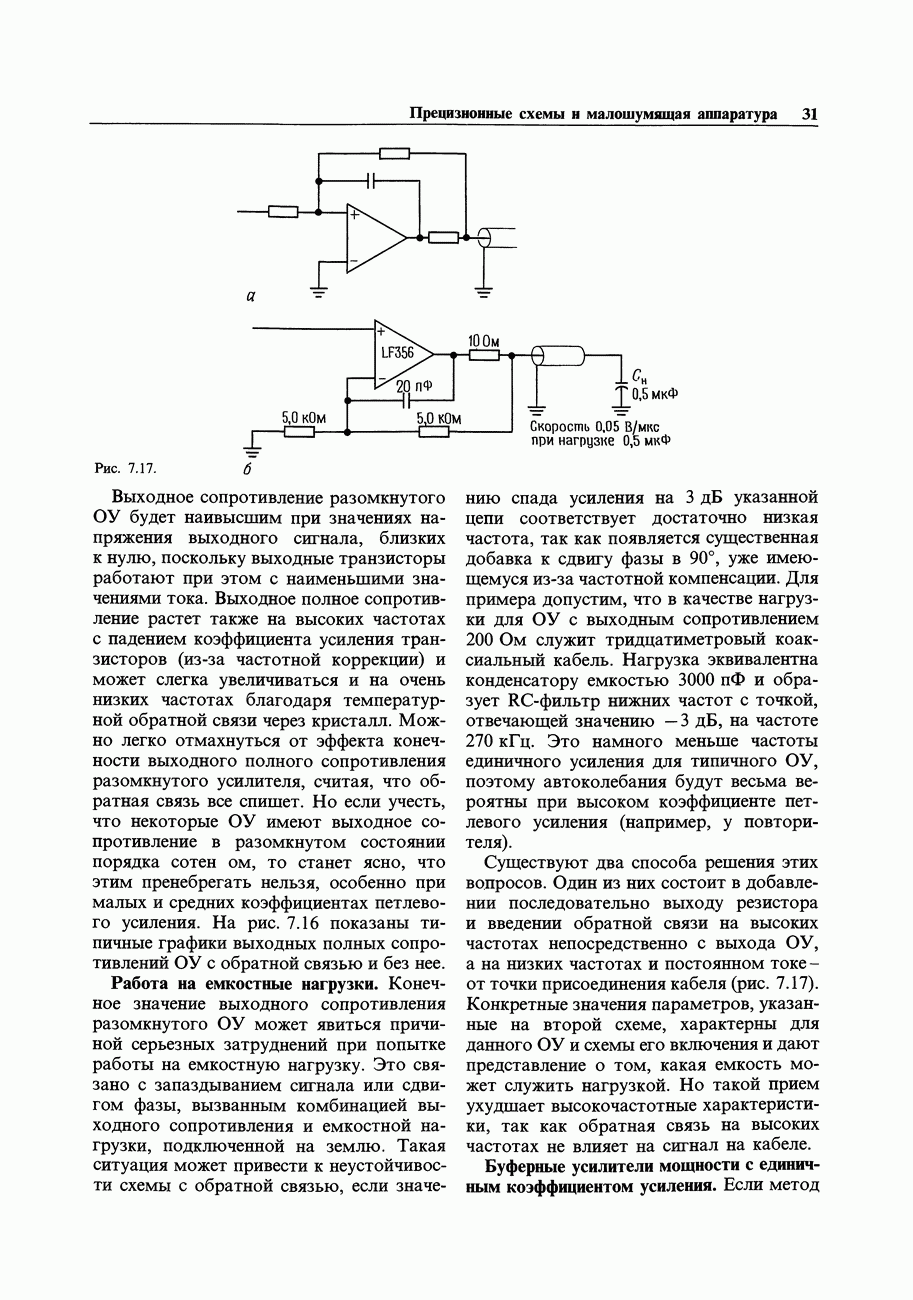
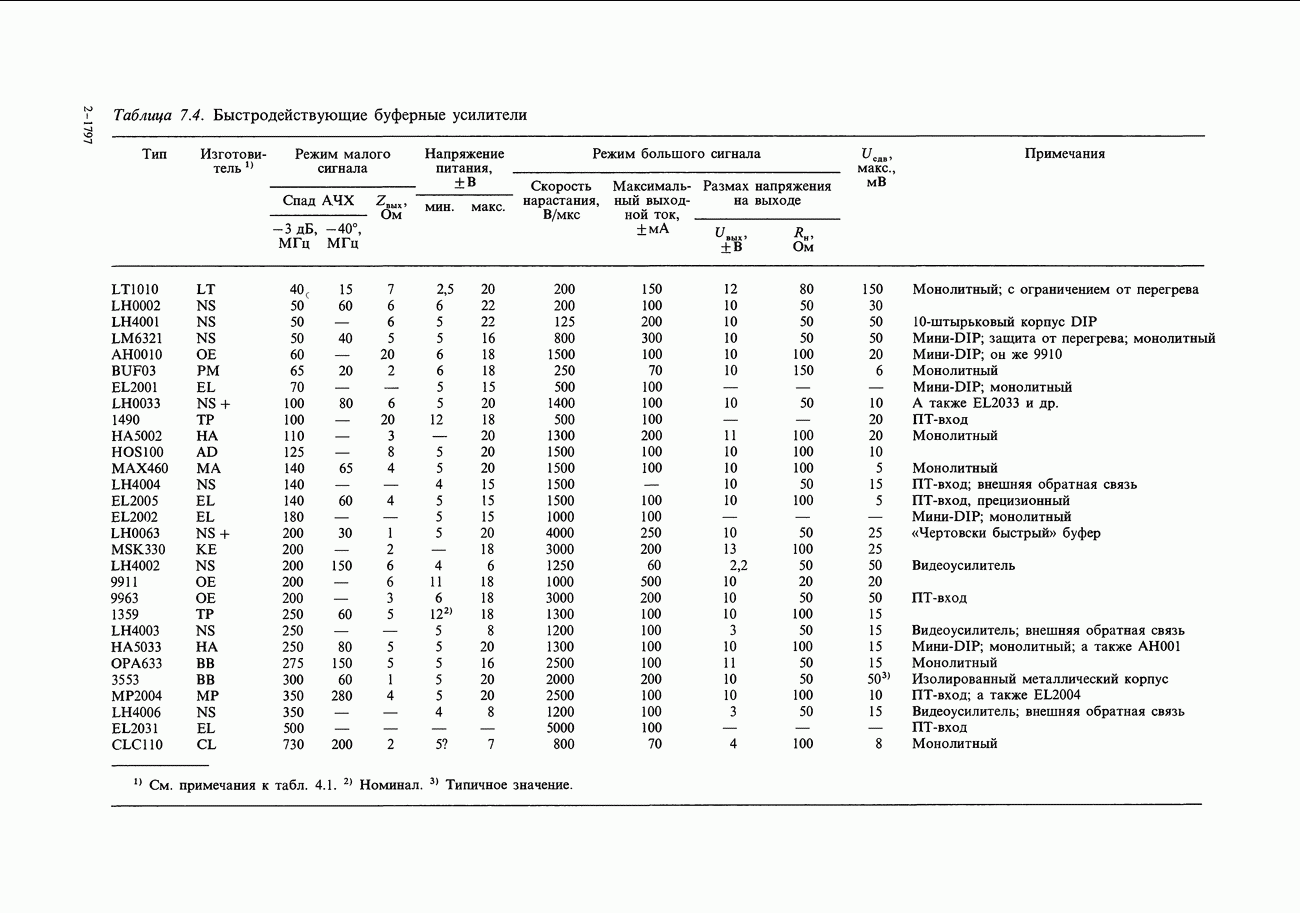
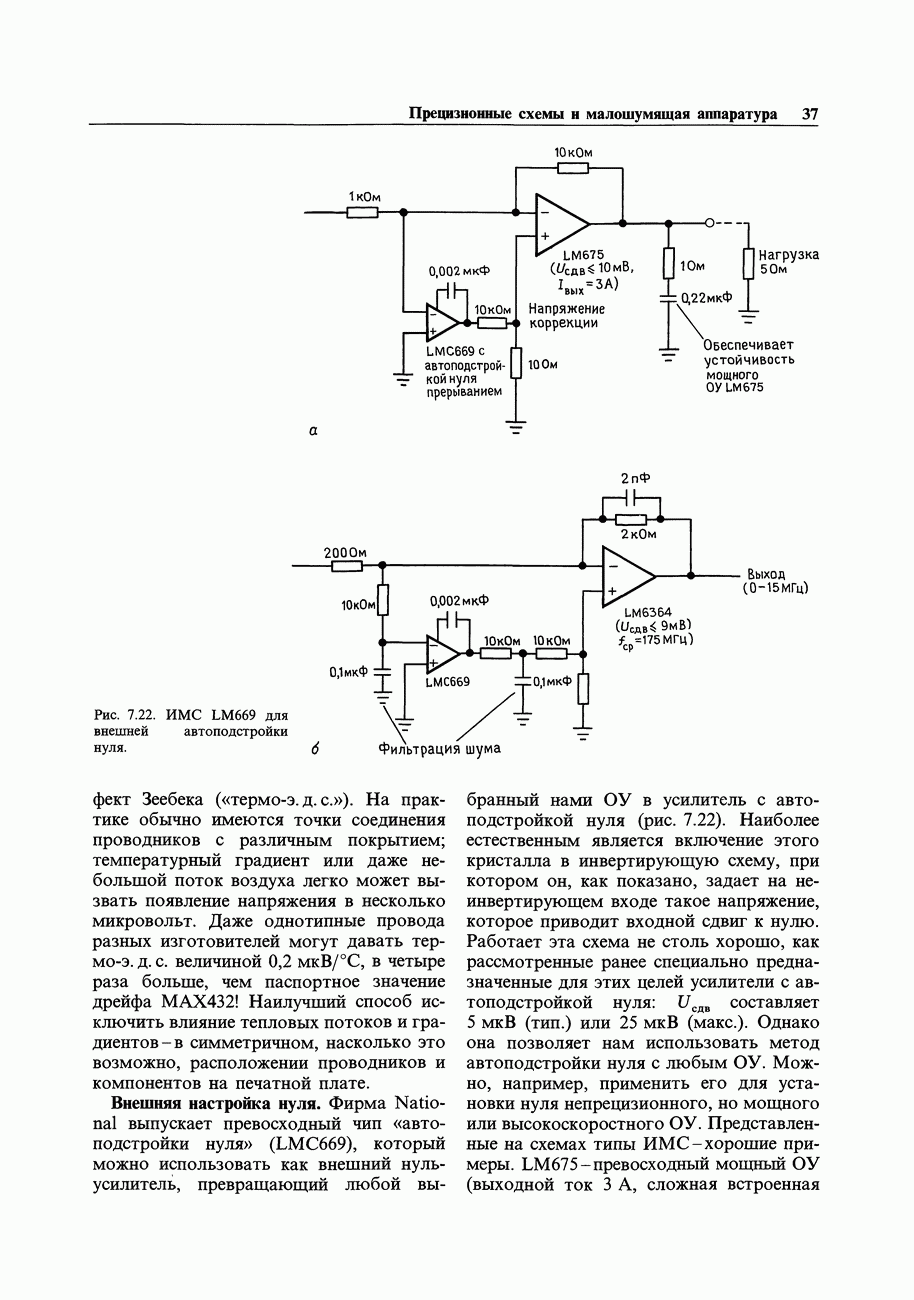
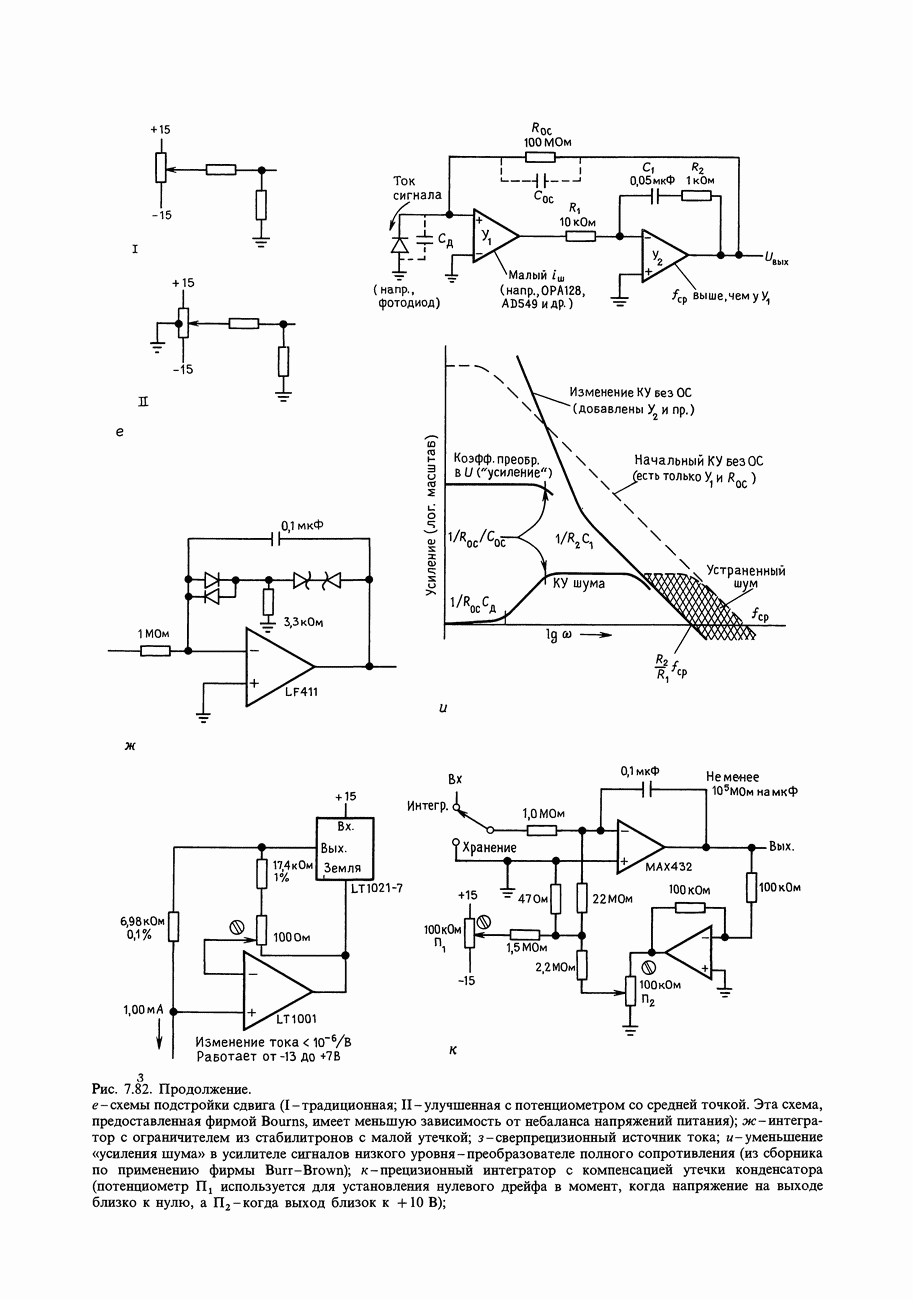
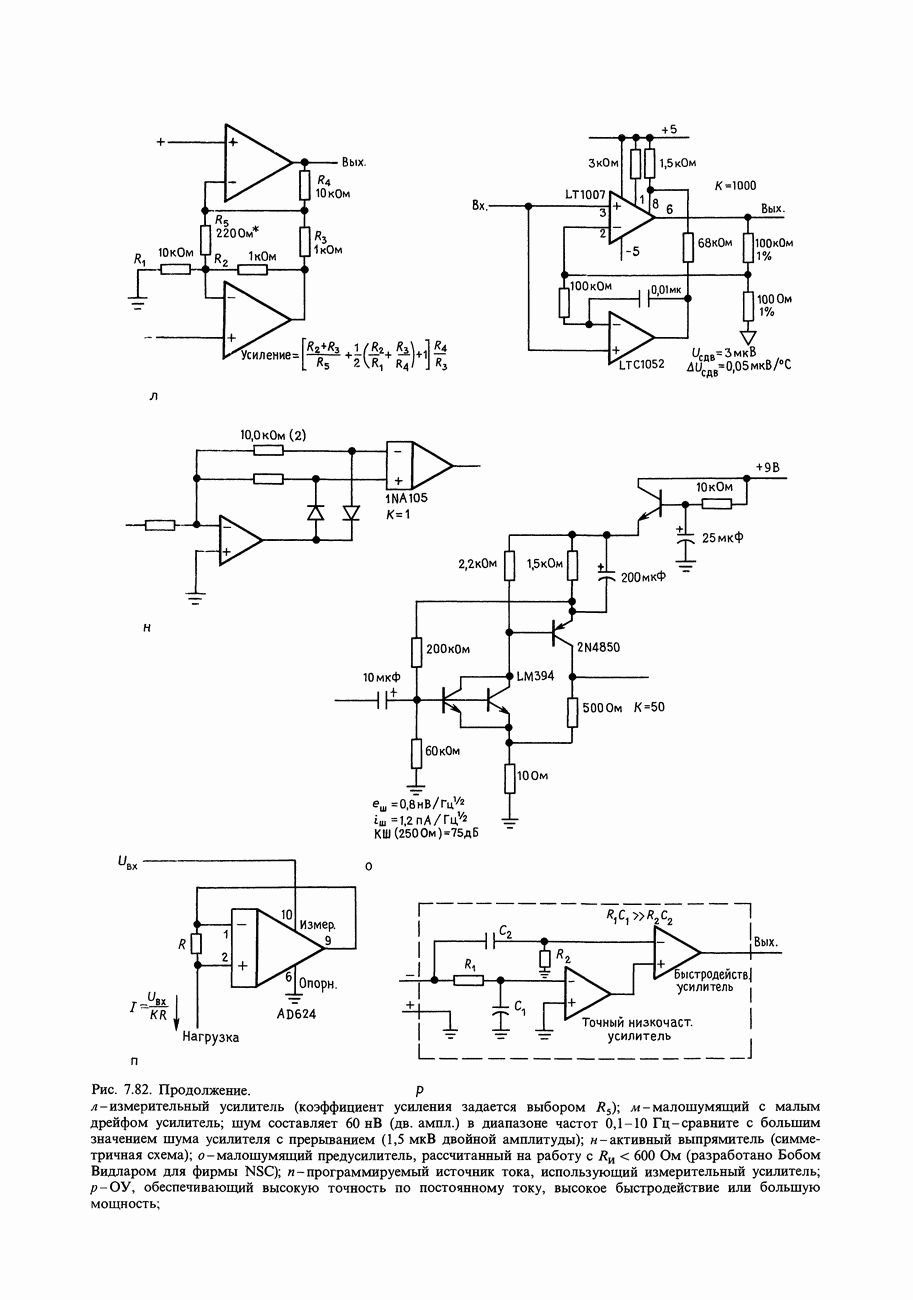
- ГЛАВА 7. ПРЕЦИЗИОННЫЕ СХЕМЫ И МАЛОШУМЯЩАЯ АППАРАТУРА
- 7.01. Соотношение точности и динамического диапазона
- 7.02. Бюджет погрешностей схемы
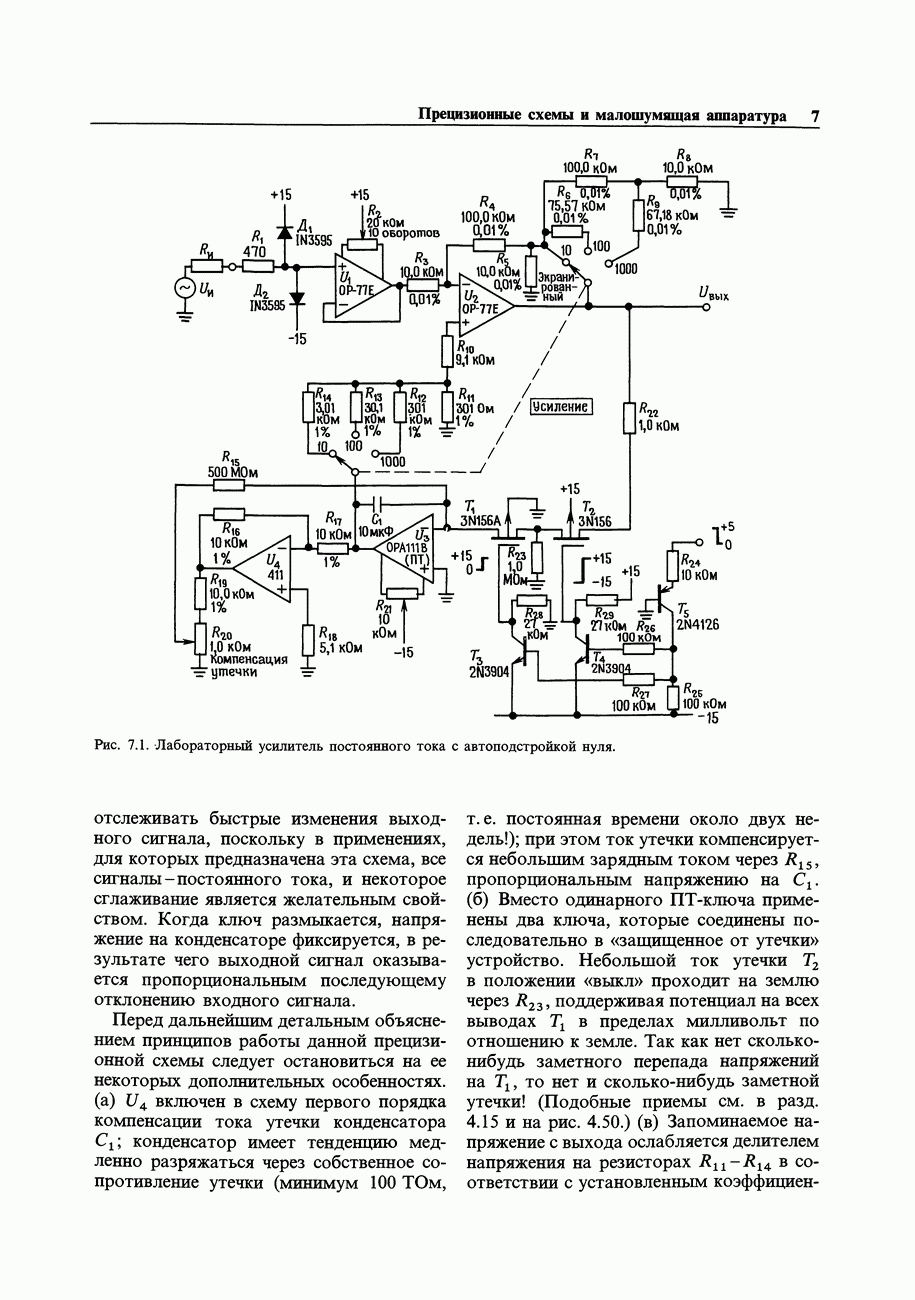
- 7.03. Пример схемы: прецизионный усилитель с автоматическим выбором нуля
- 7.04. «Бюджет погрешностей» при проектировании прецизионной схемы
- 7.05. Погрешности внешних цепей
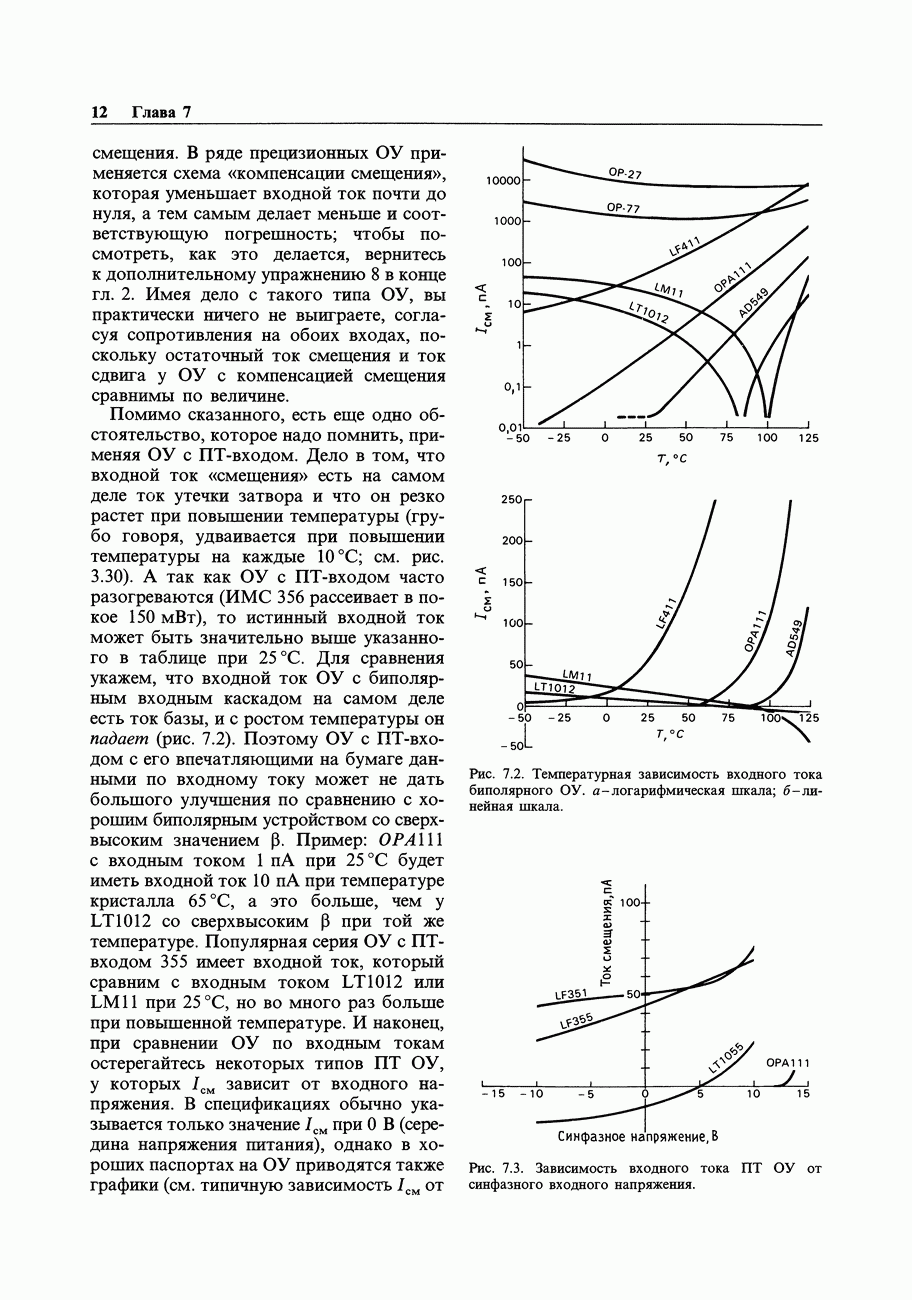
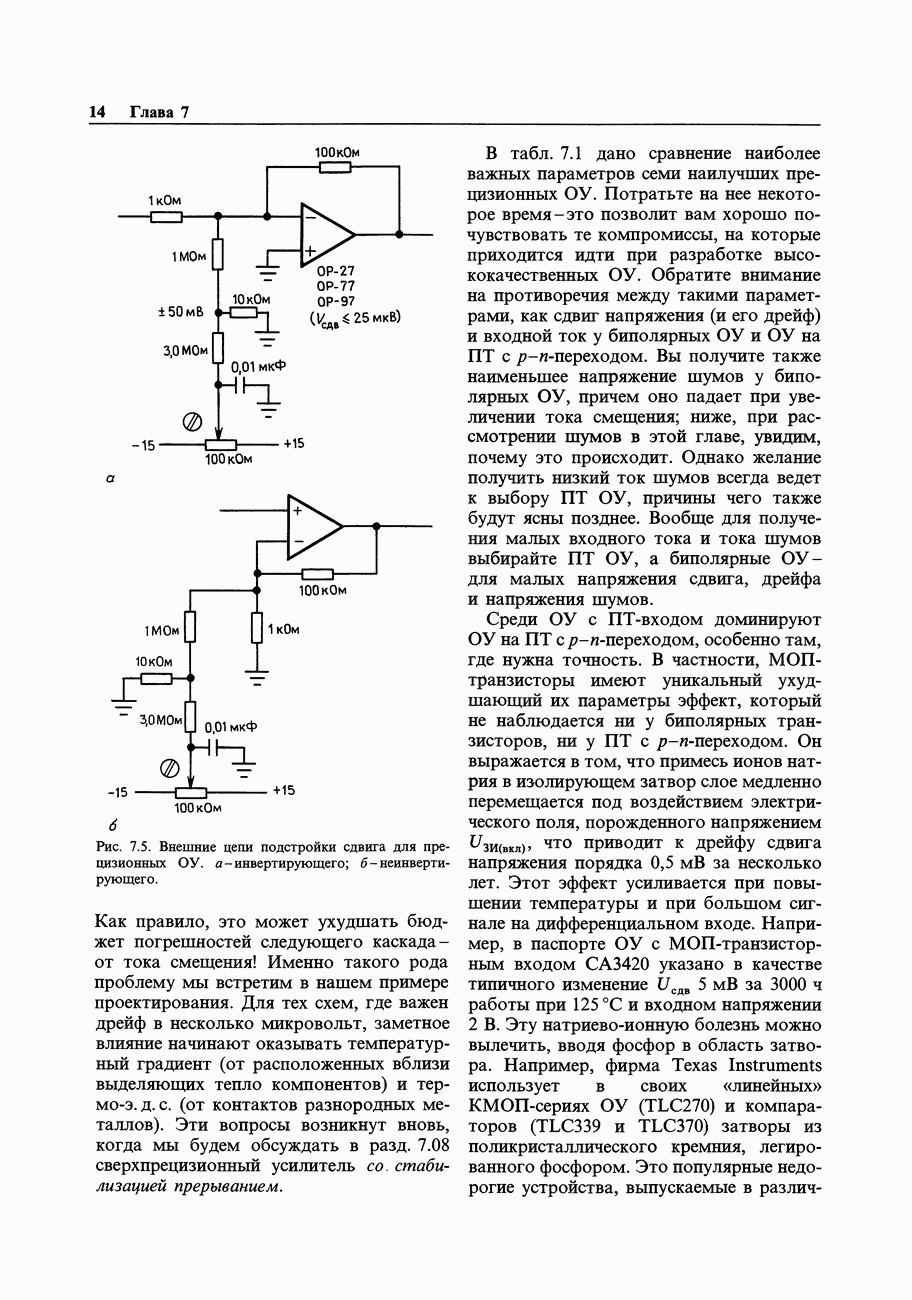
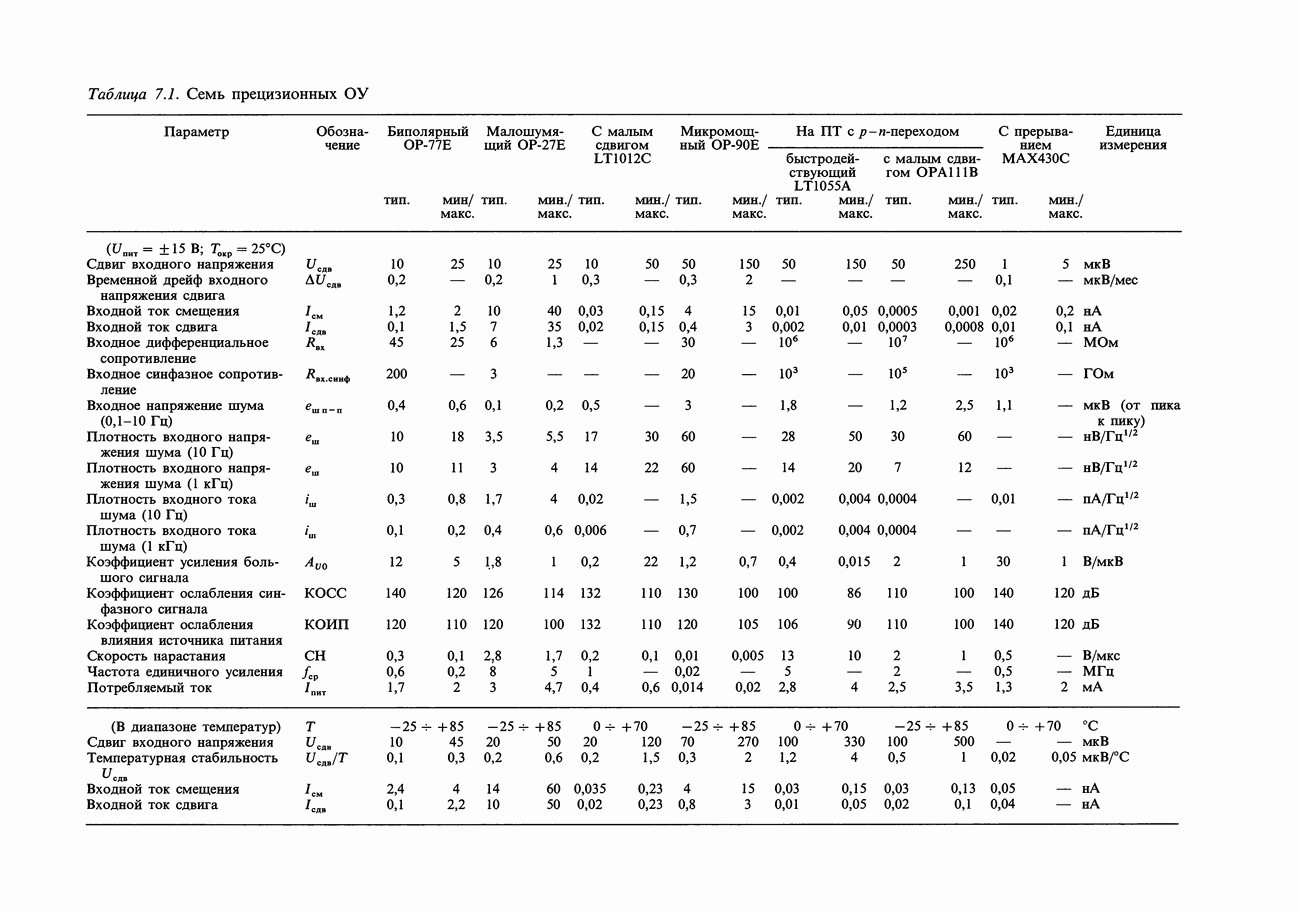
- 7.06. Входные погрешности усилителя
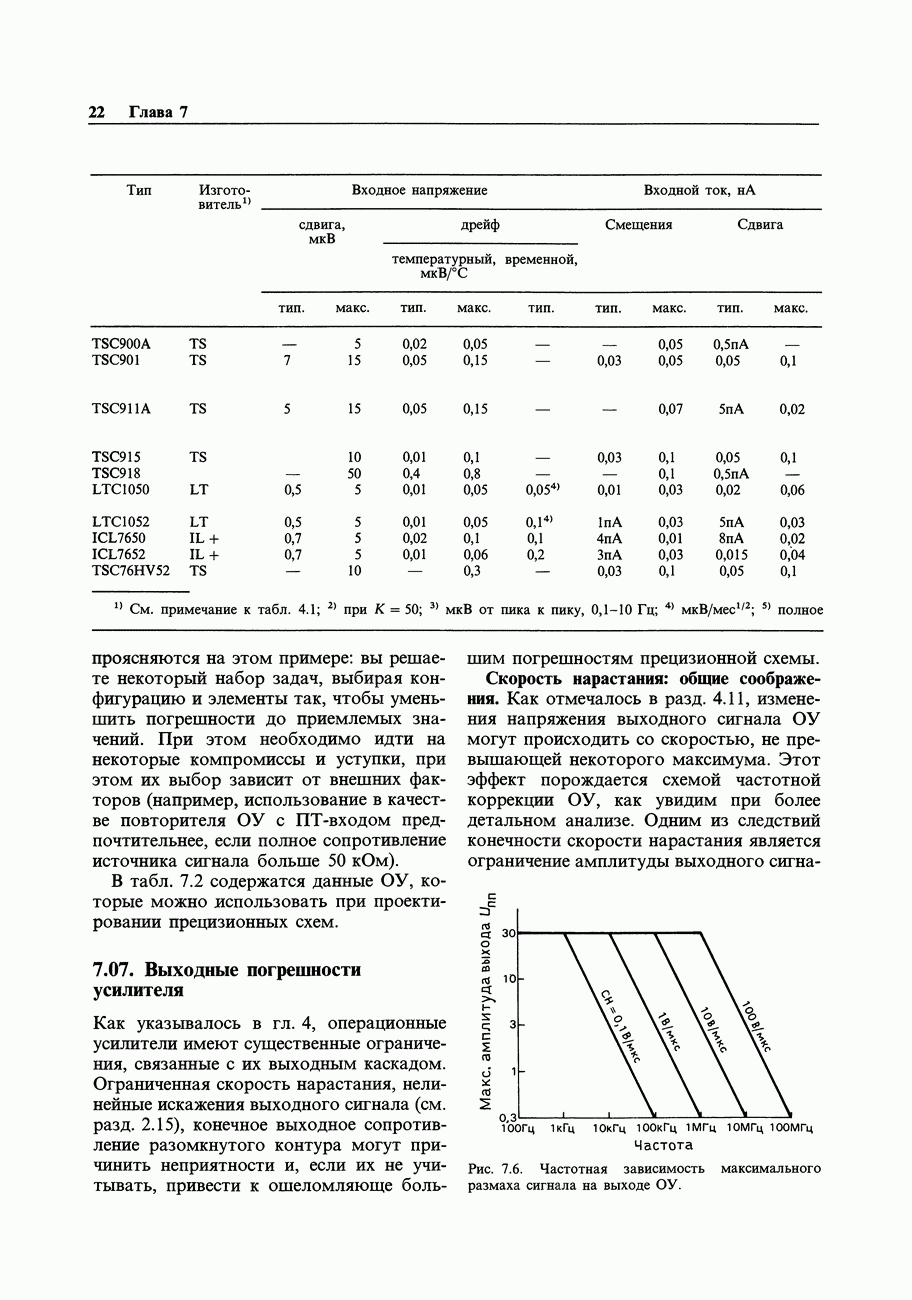
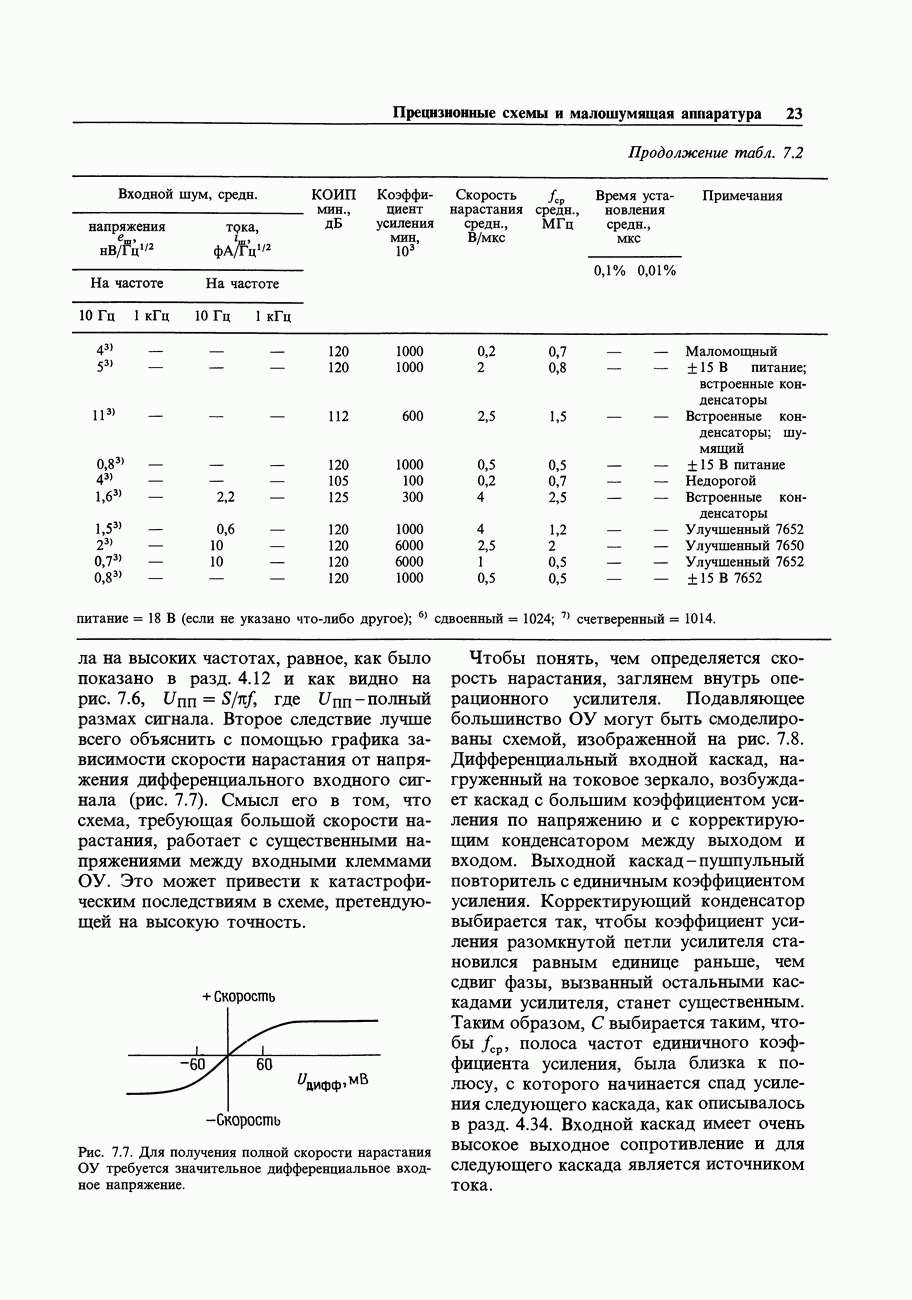
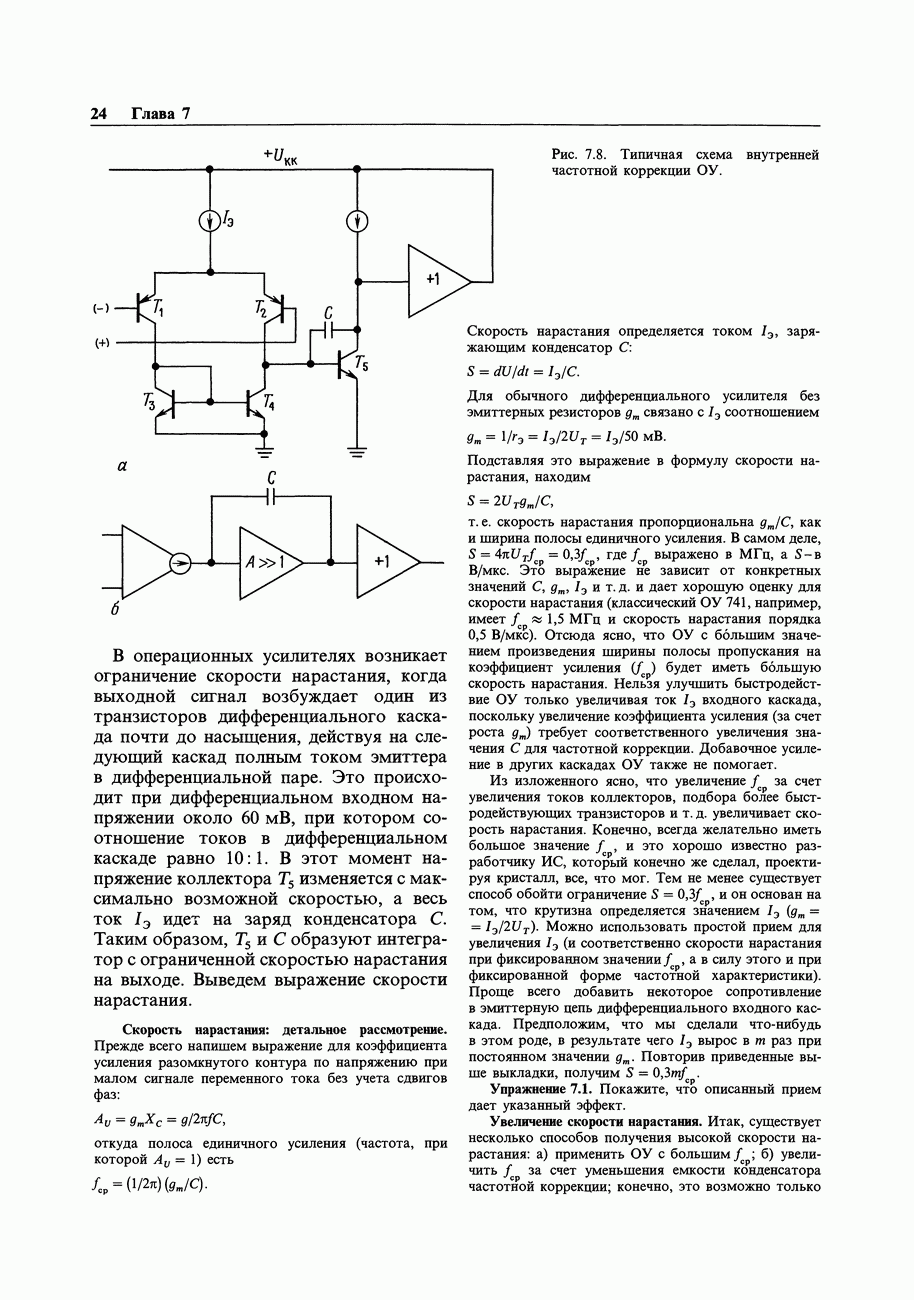
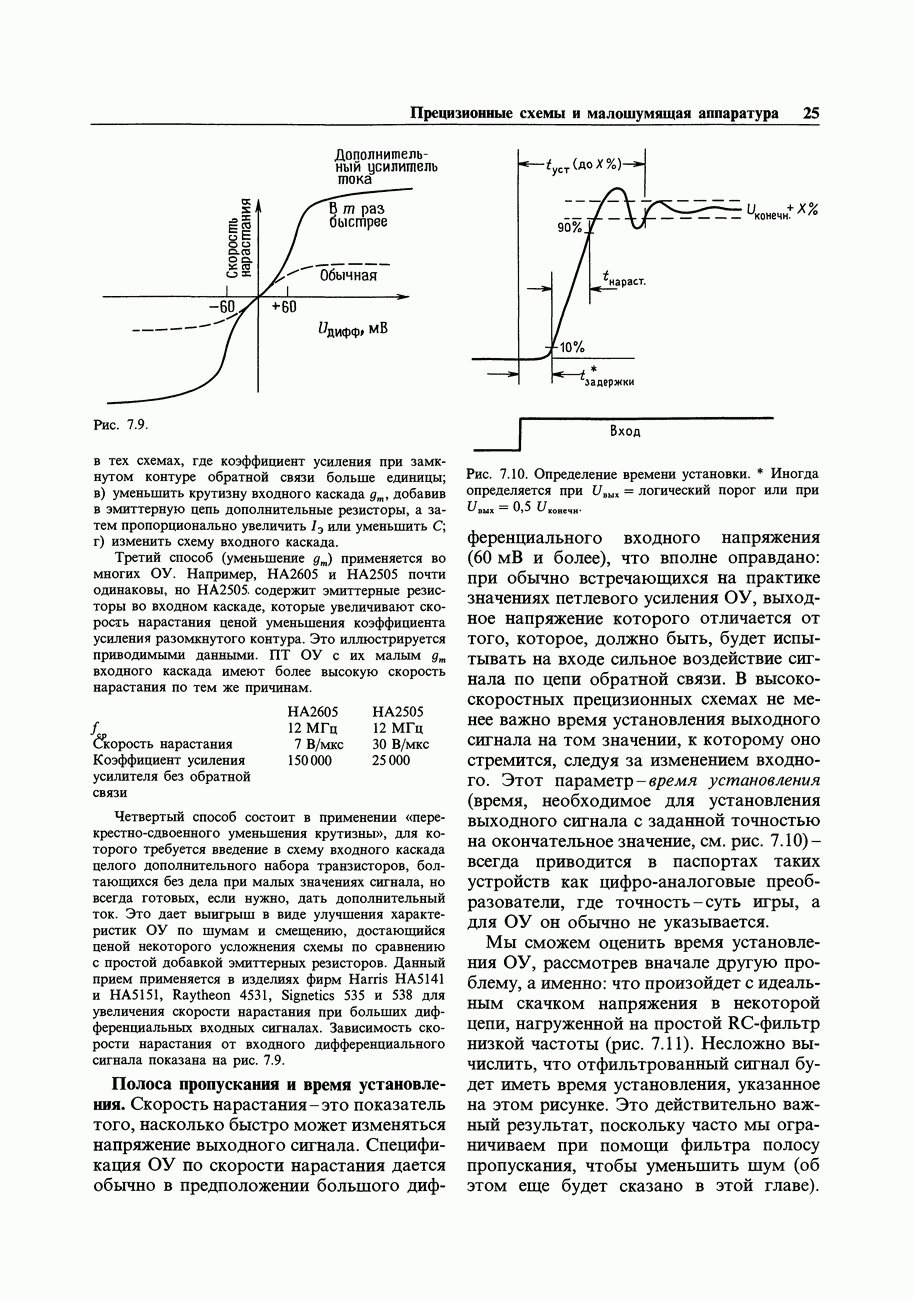
- 7.07. Выходные погрешности усилителя
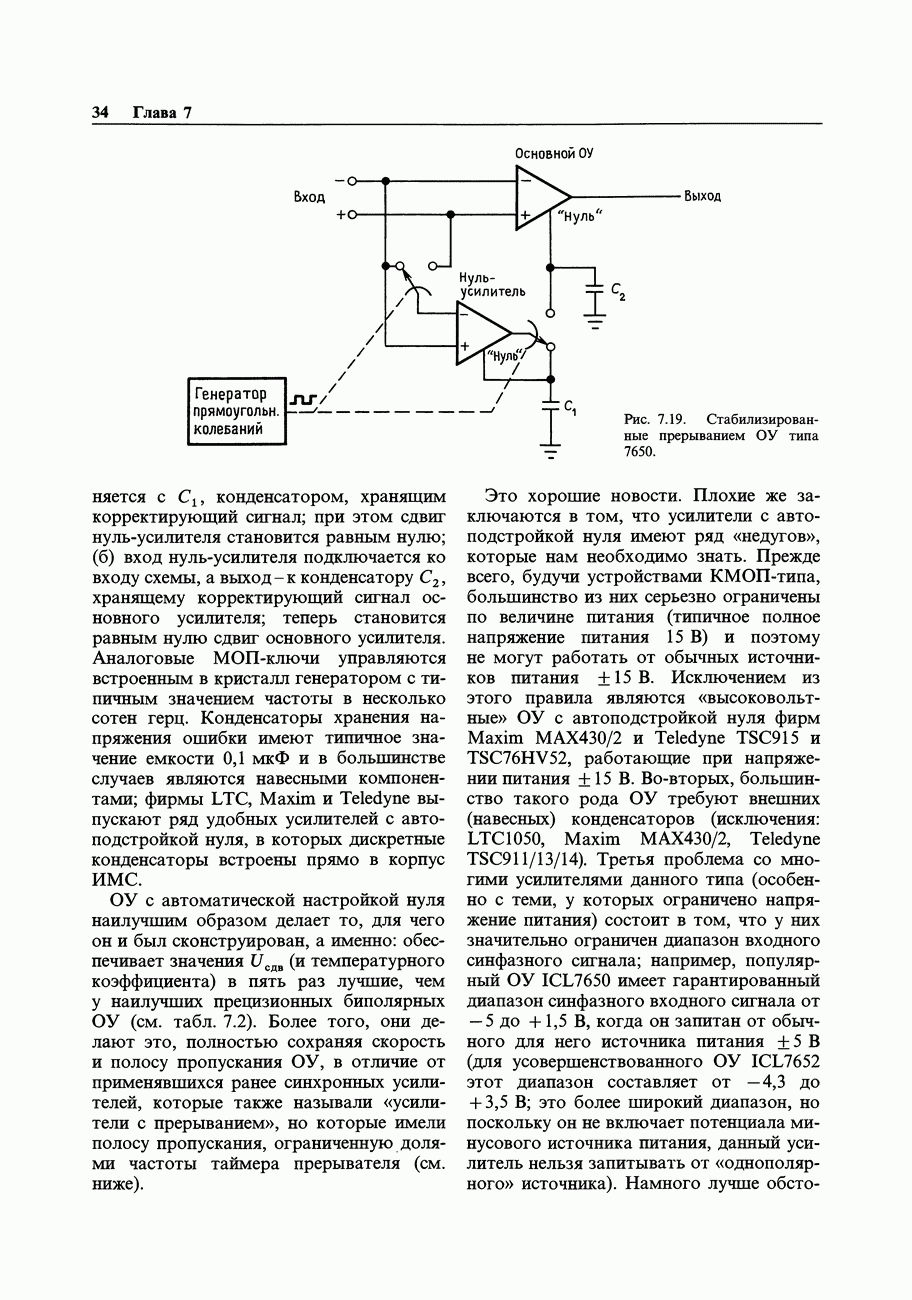
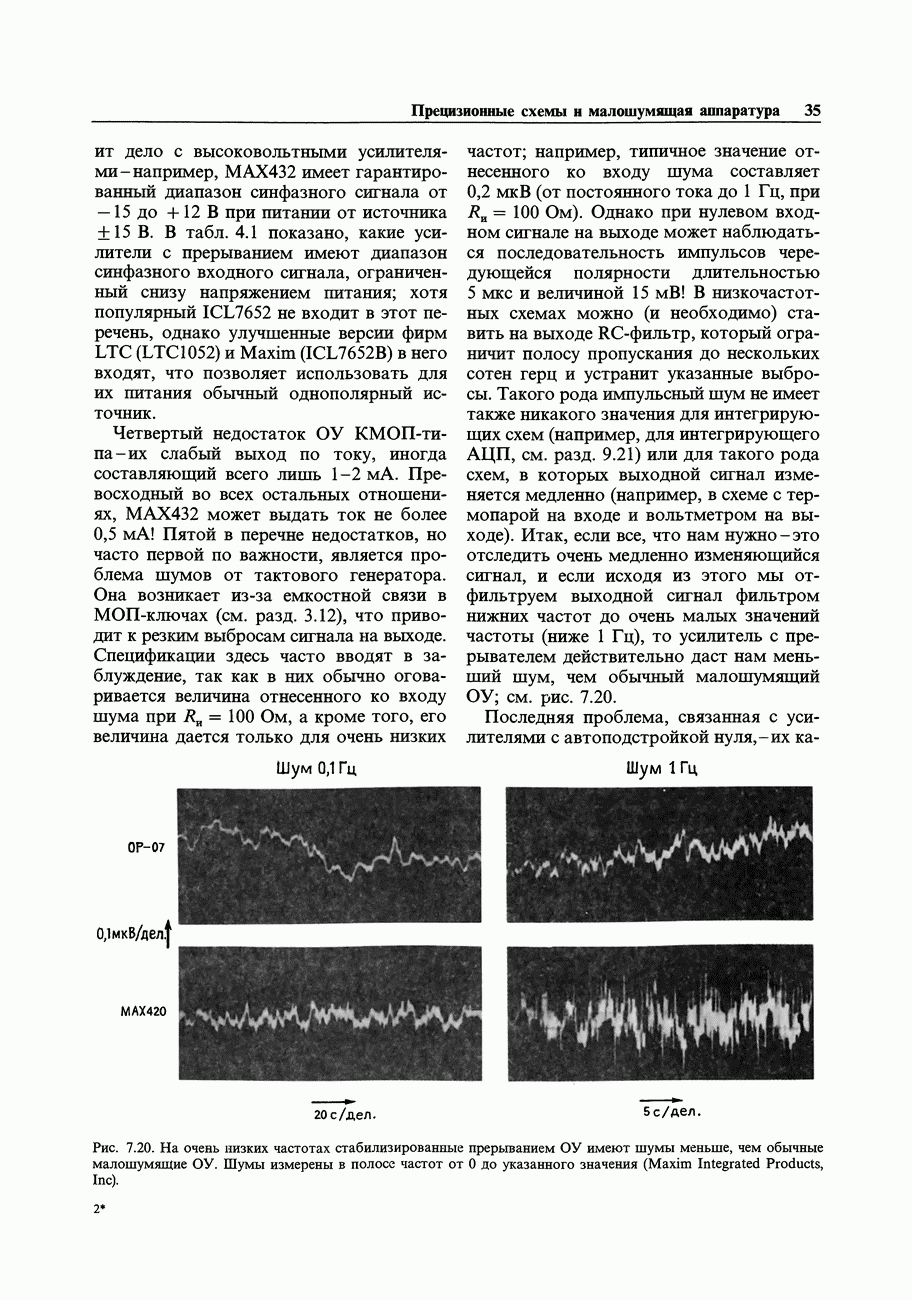
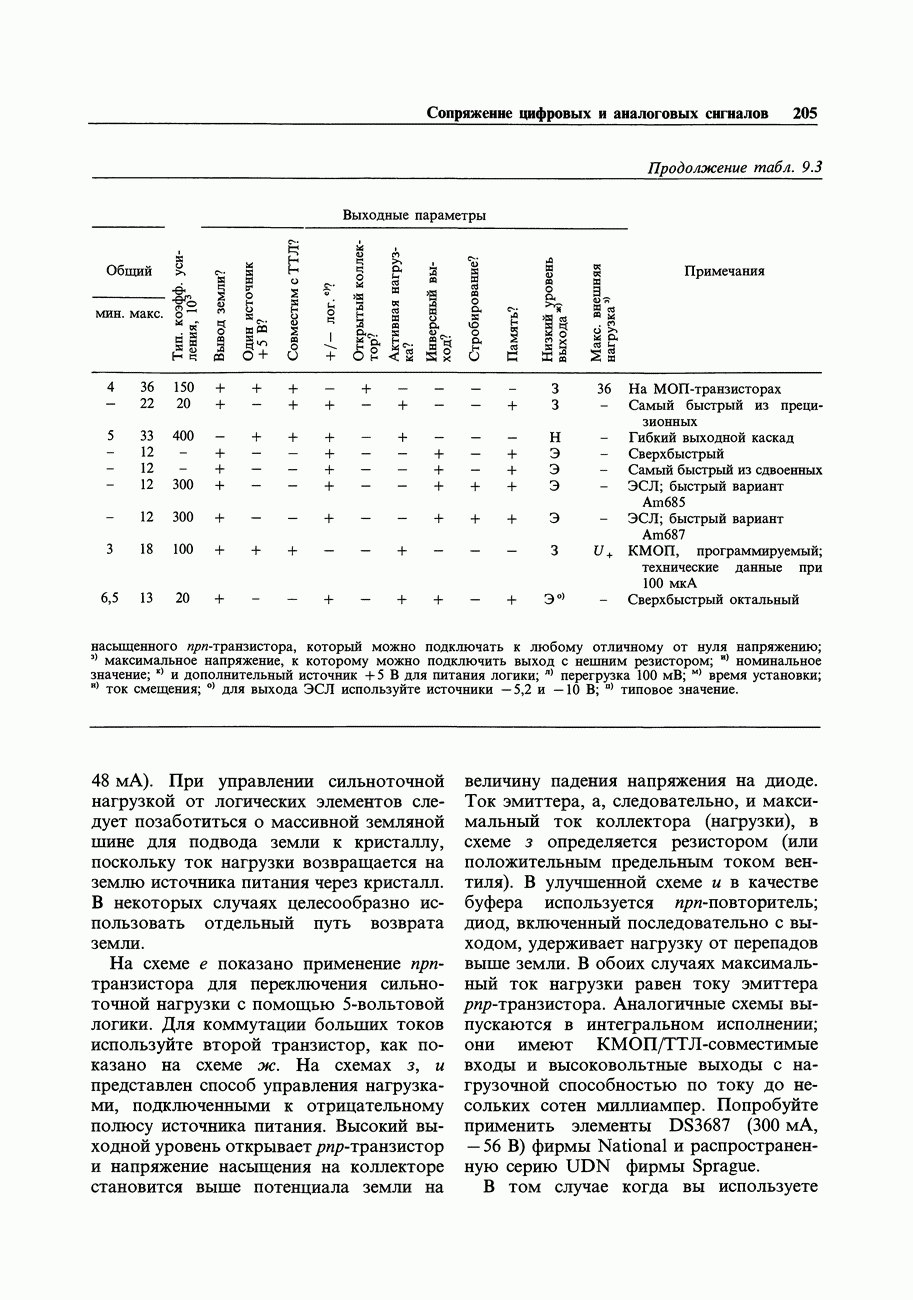
- 7.08. Усилители с автоподстройкой нуля (стабилизированные прерыванием)
- Кое-что еще о схемах с прерыванием
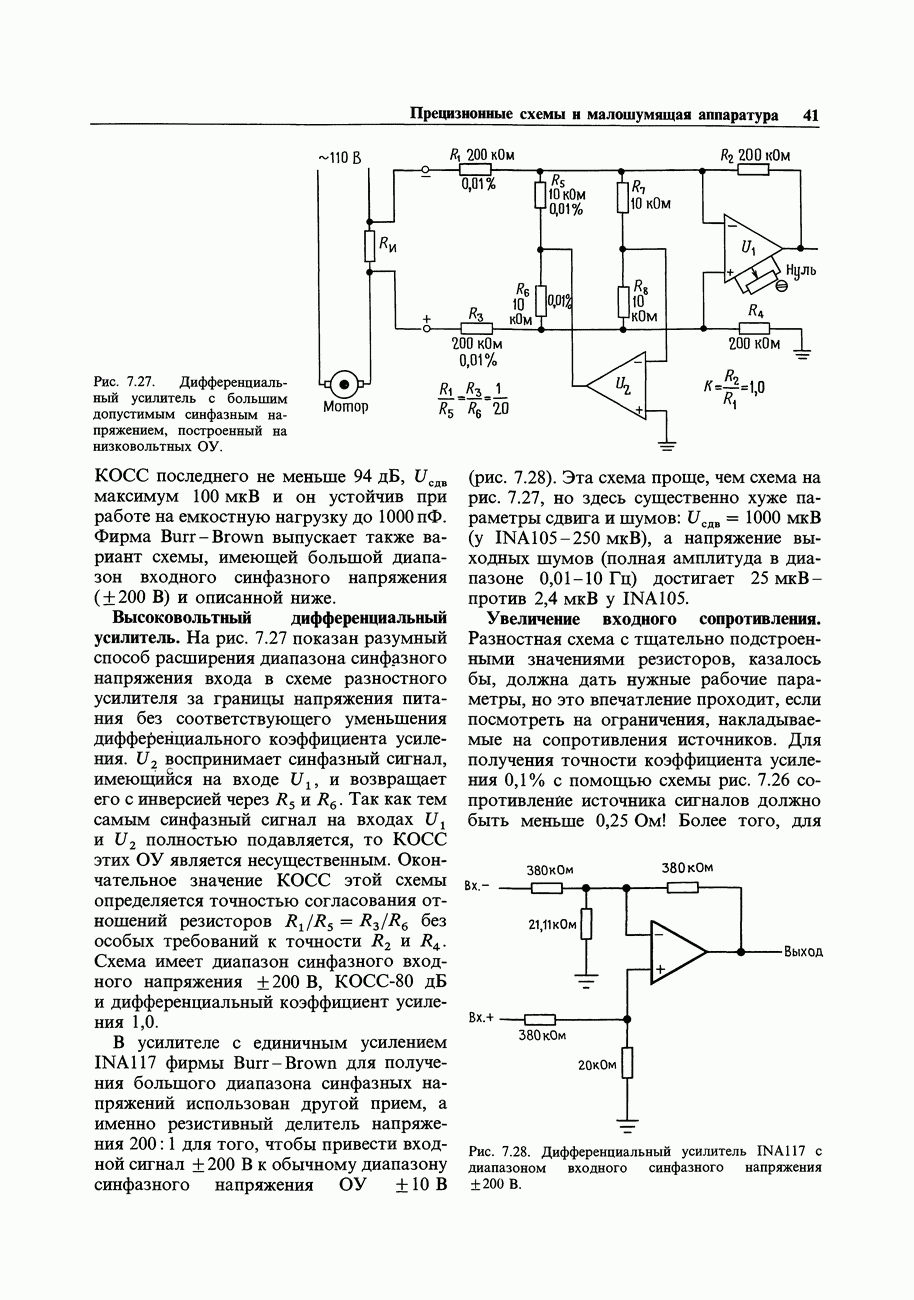
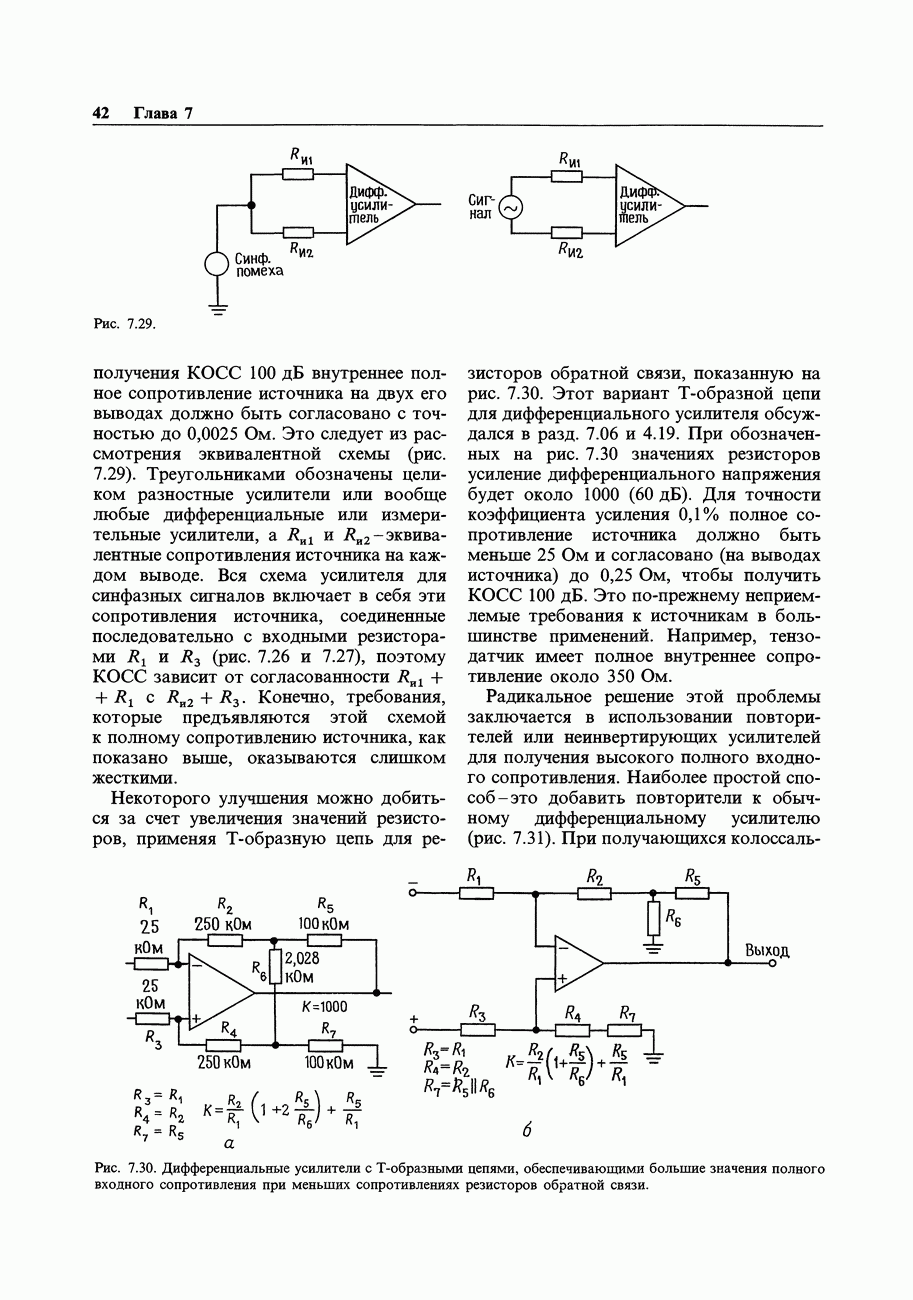
- ДИФФЕРЕНЦИАЛЬНЫЕ И ИЗМЕРИТЕЛЬНЫЕ УСИЛИТЕЛИ
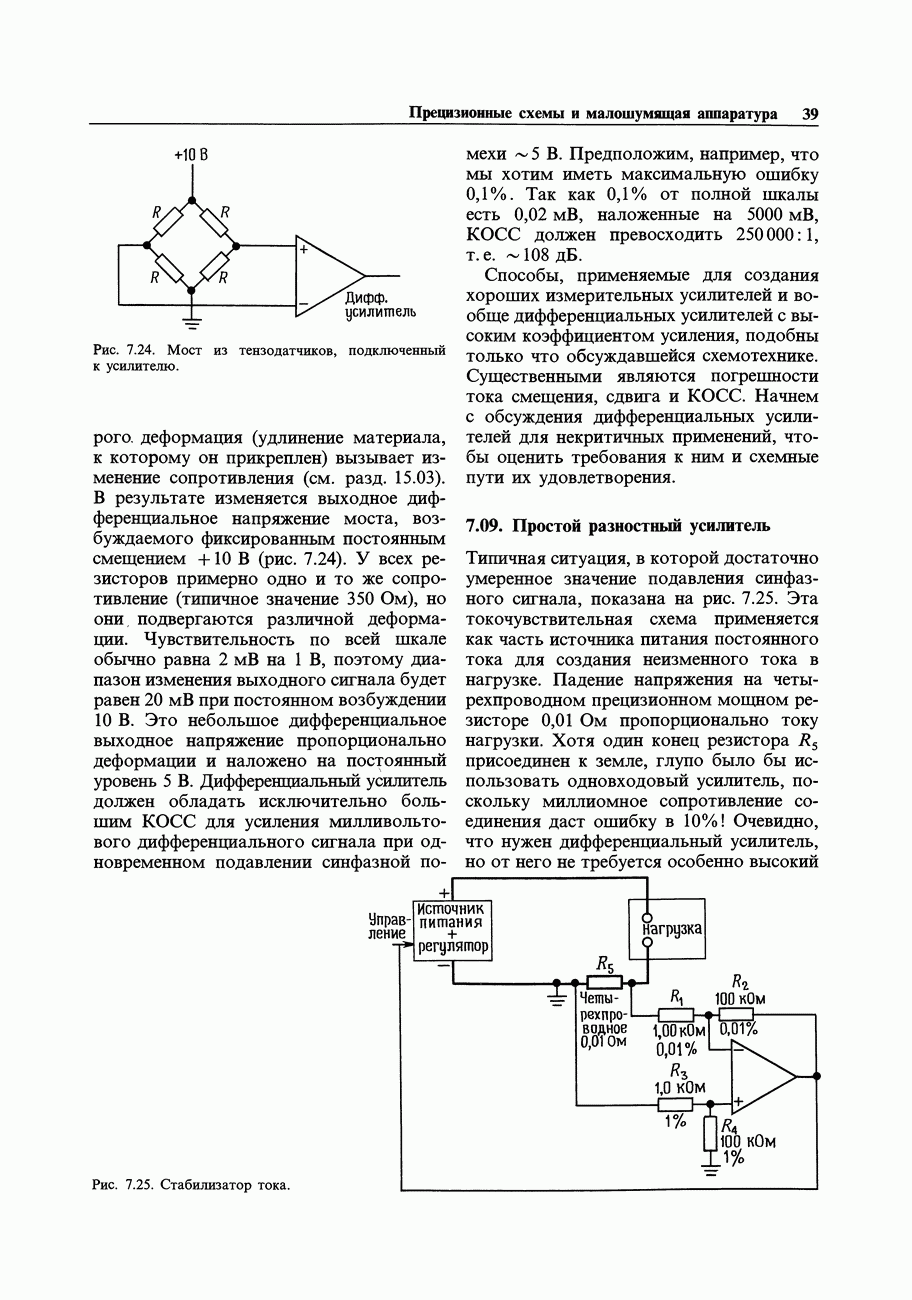
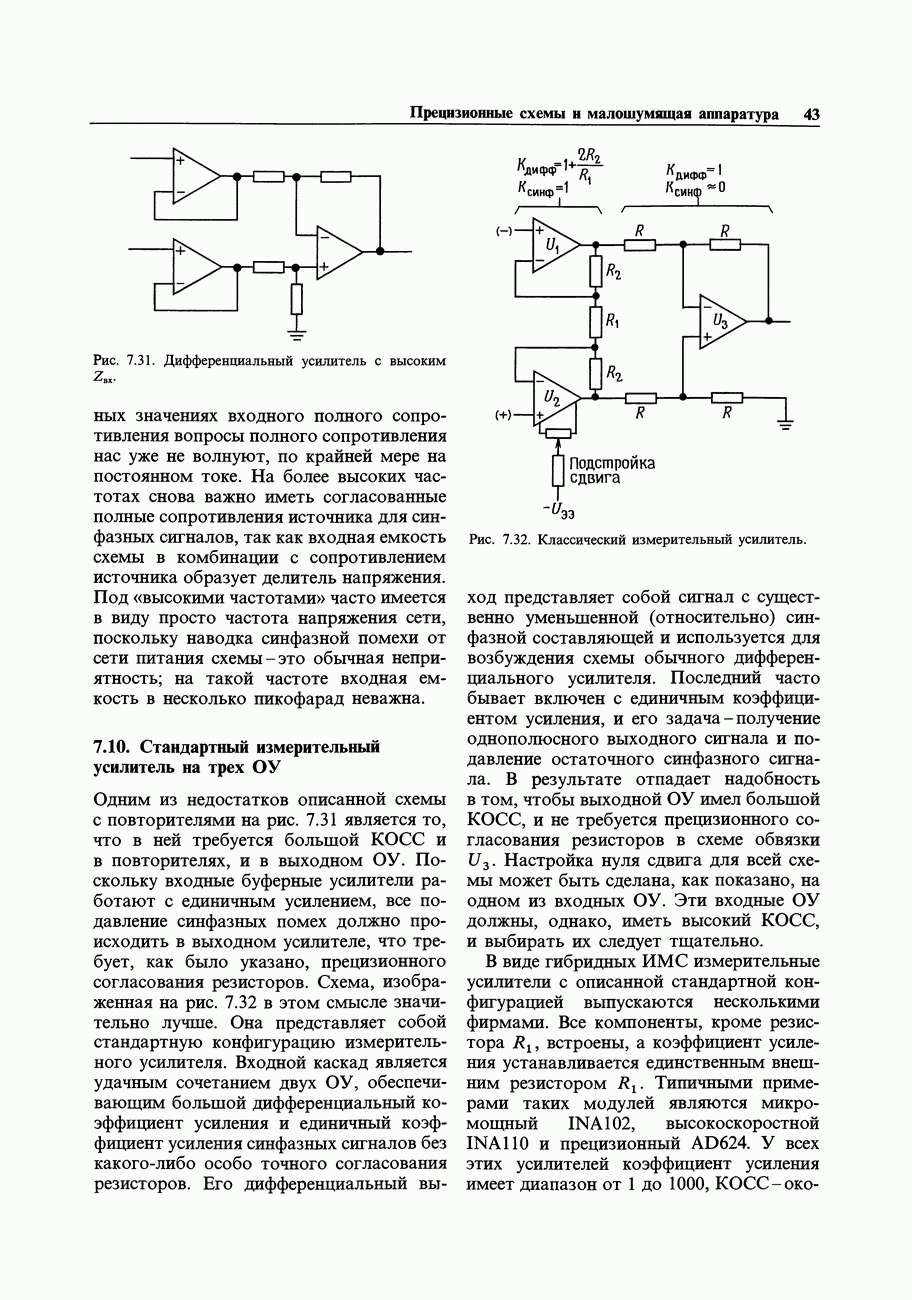
- 7.09. Простой разностный усилитель
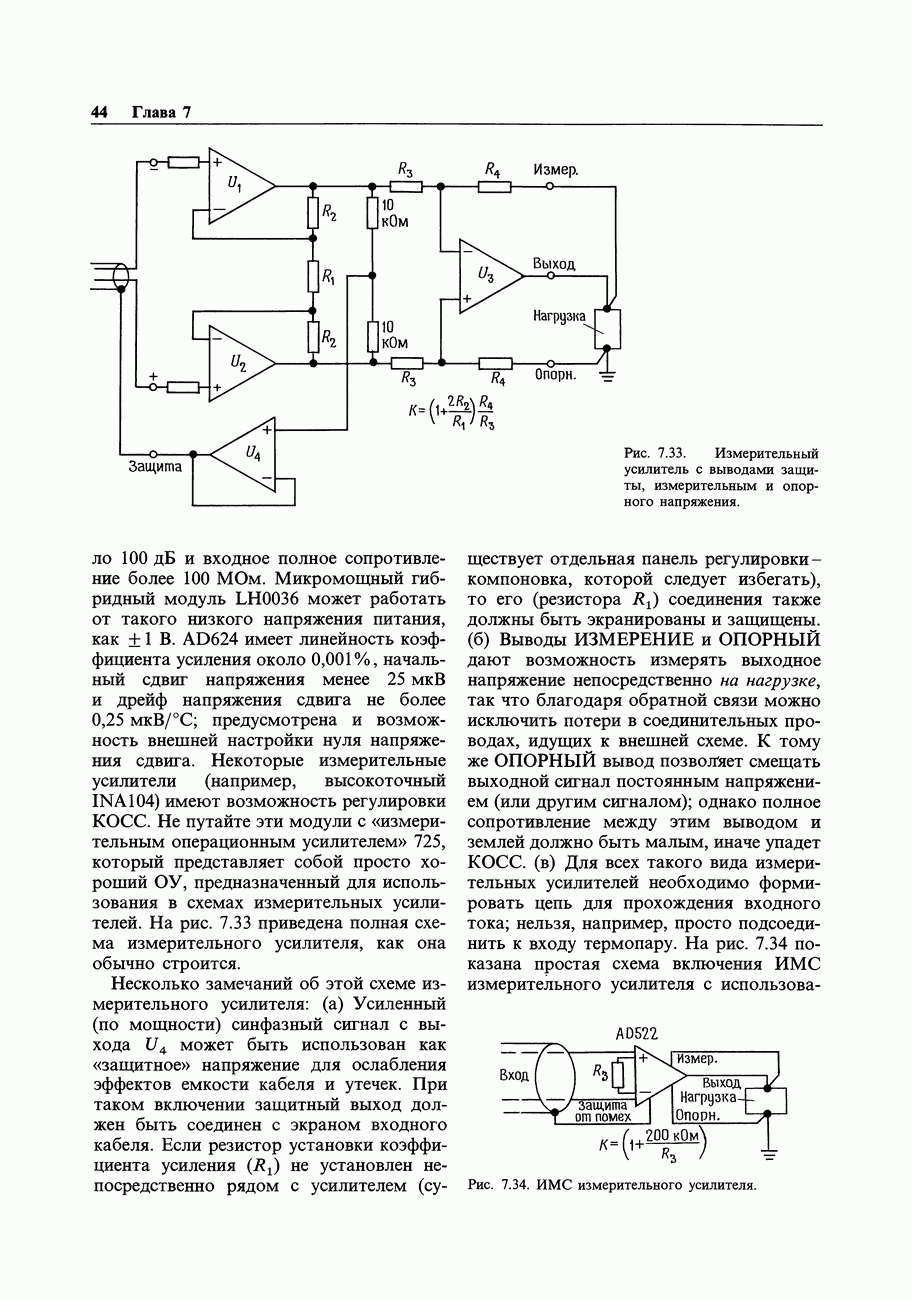
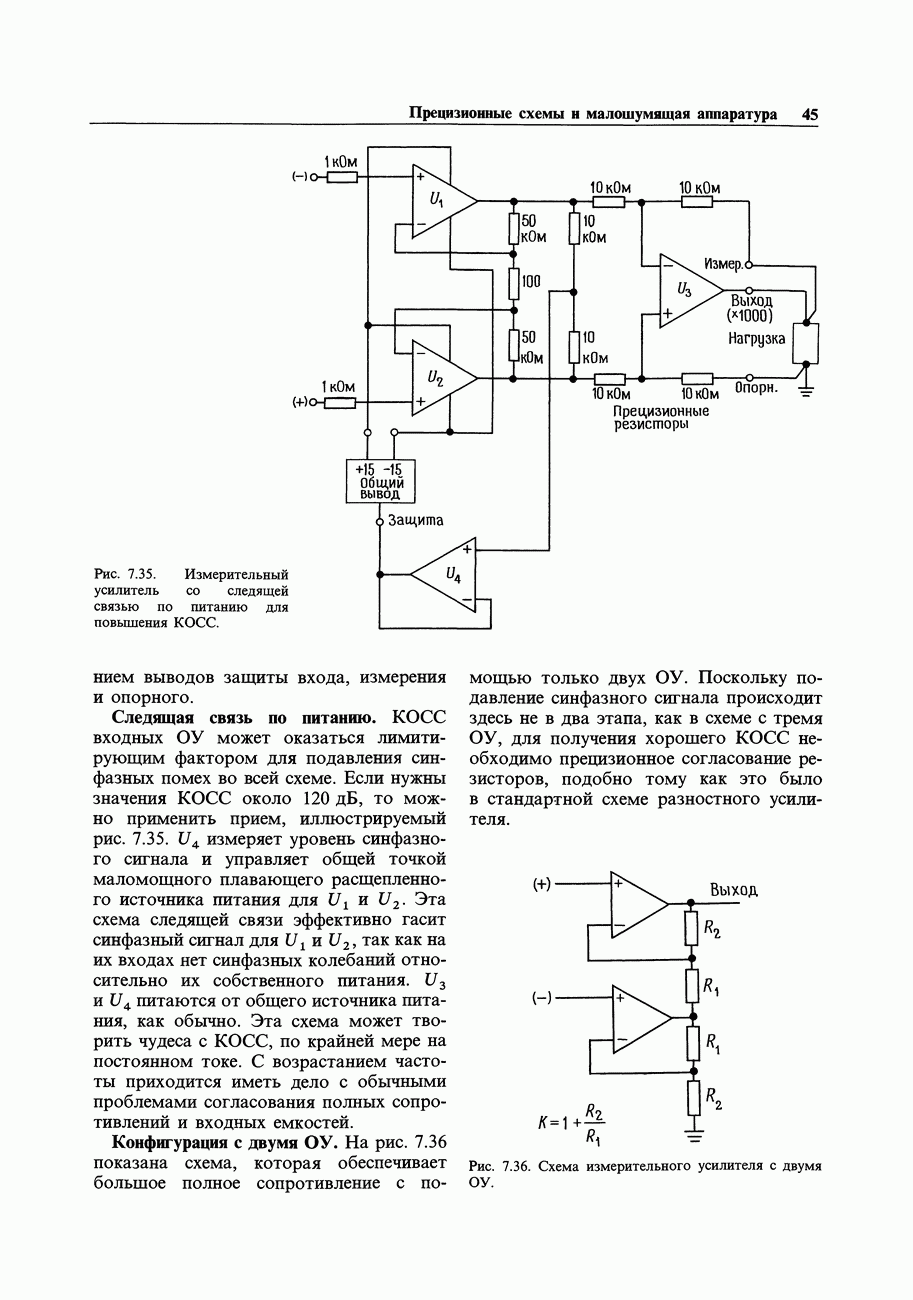
- 7.10. Стандартный измерительный усилитель на трех ОУ
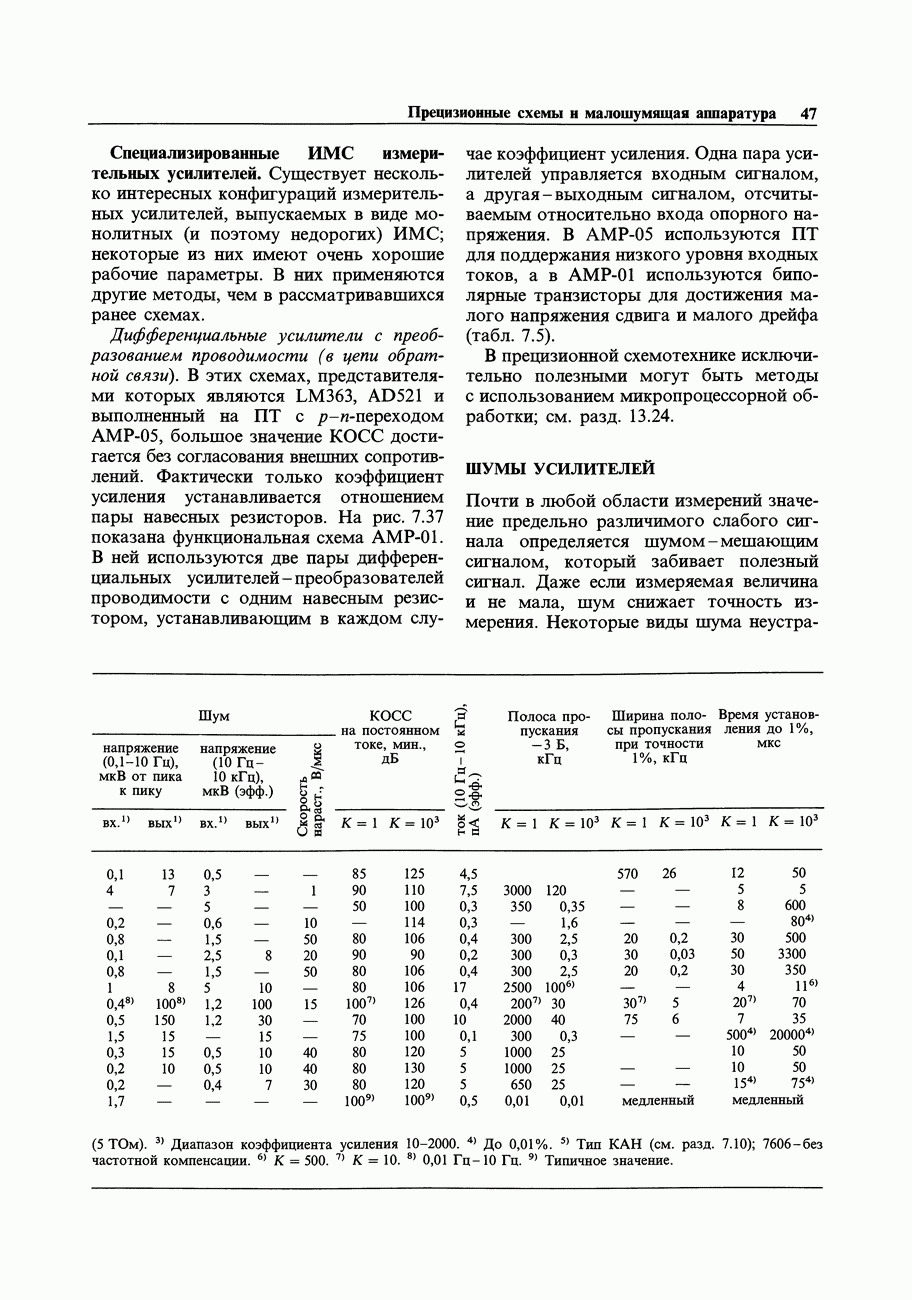
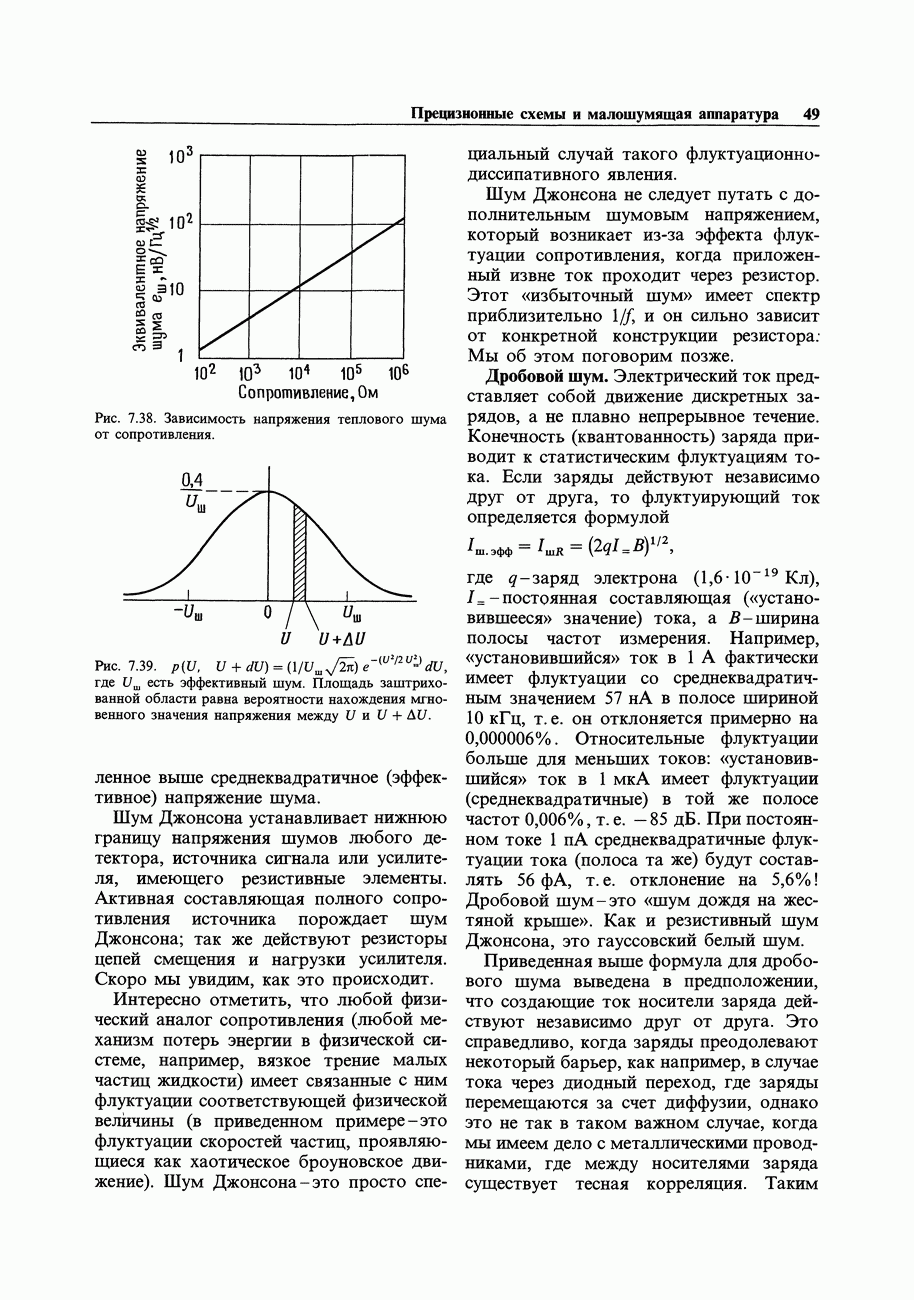
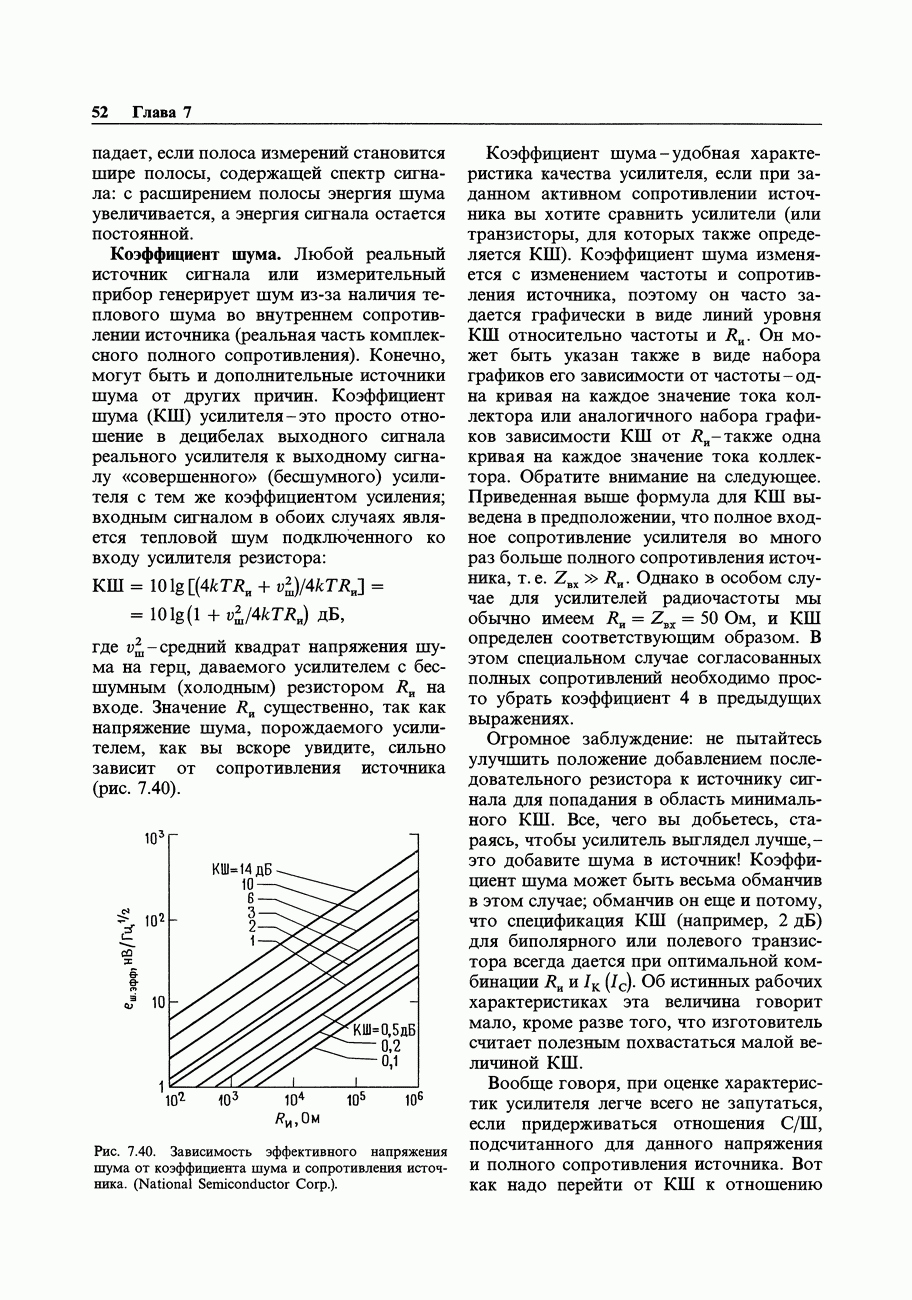
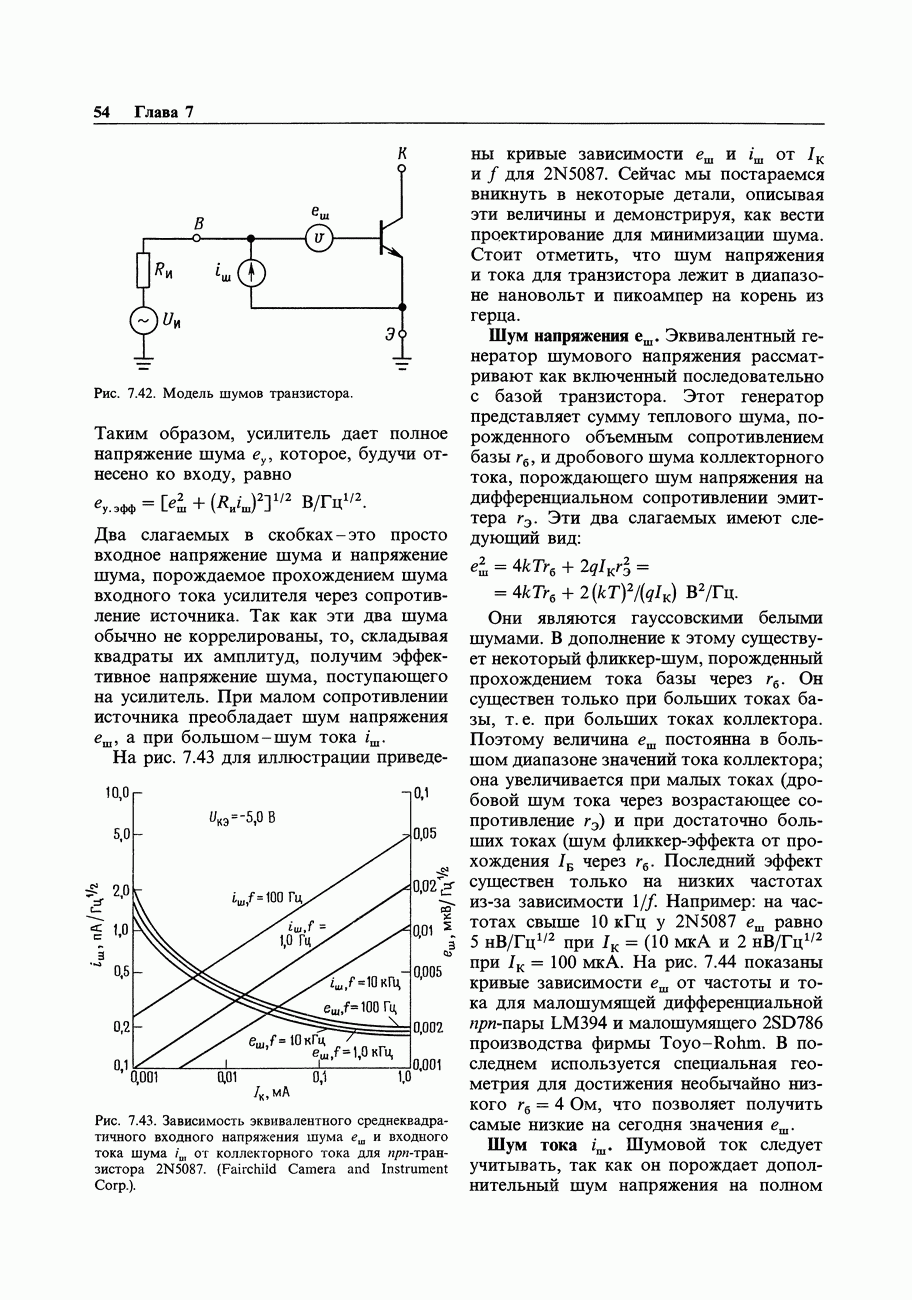
- ШУМЫ УСИЛИТЕЛЕЙ
- 7.11. Происхождение и виды шумов
- 7.12. Отношение сигнал/шум и коэффициент шума
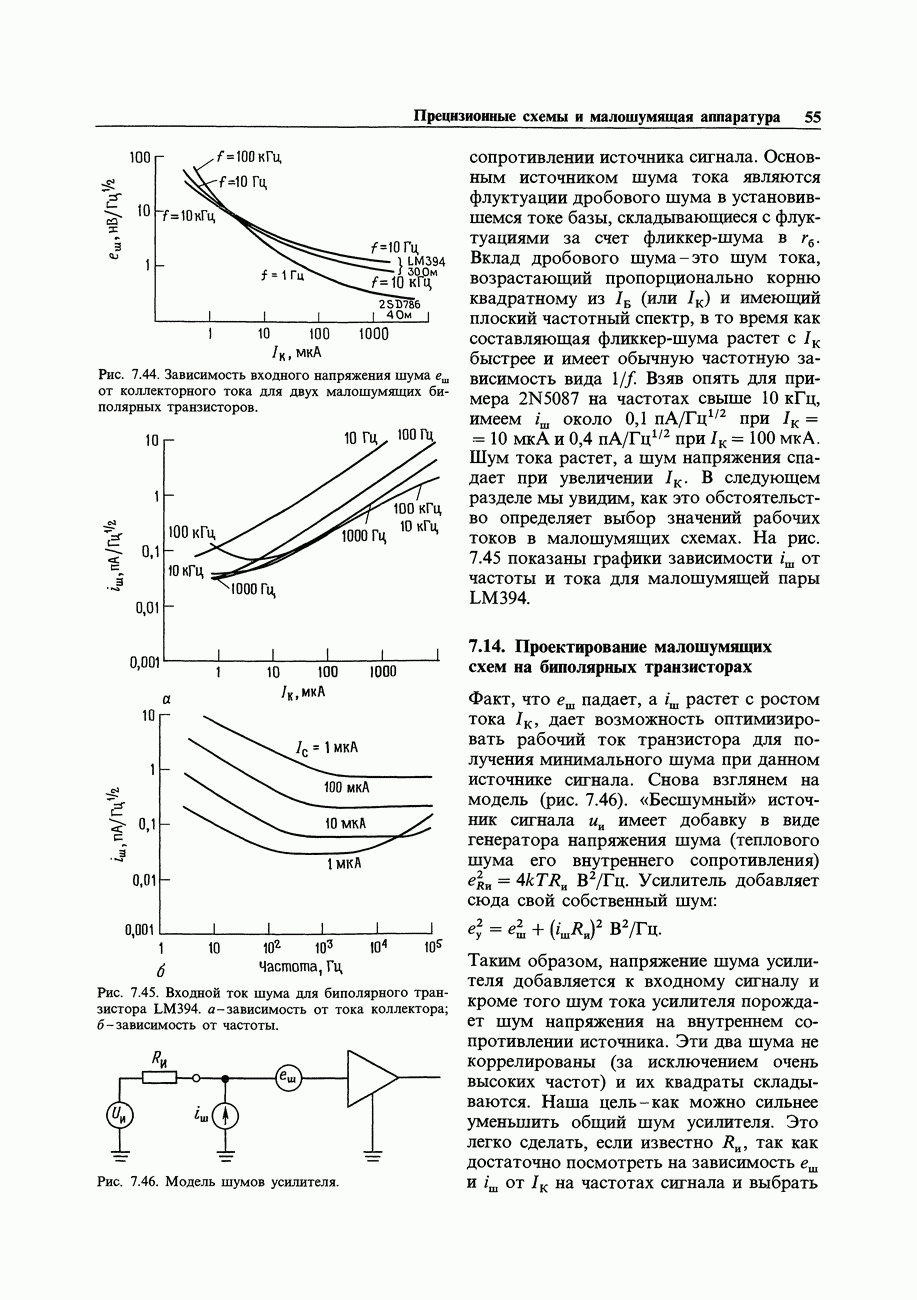
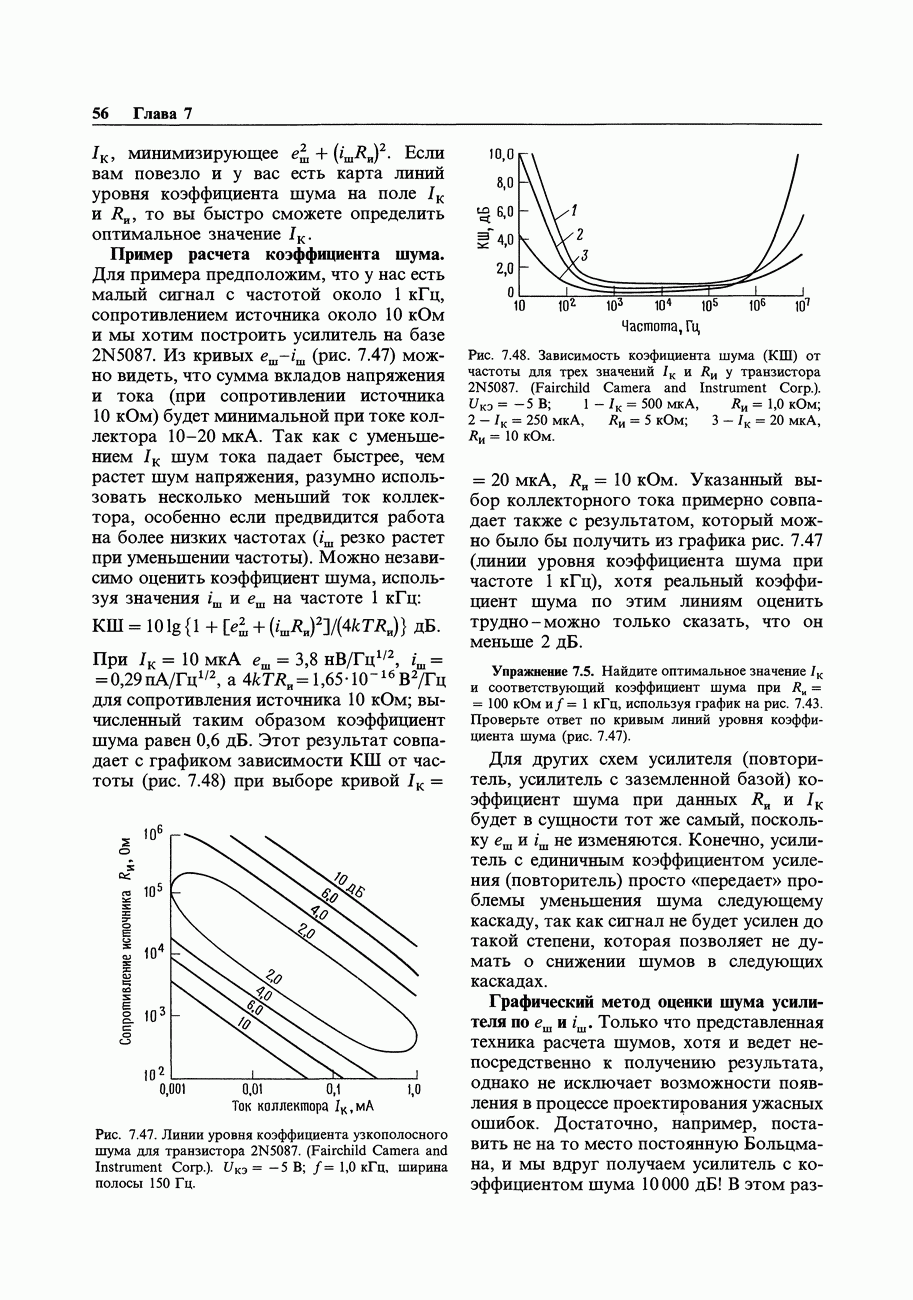
- 7.13. Шум тока и напряжения транзисторного усилителя
- 7.14. Проектирование малошумящих схем на биполярных транзисторах
- 7.15. Шум ПТ
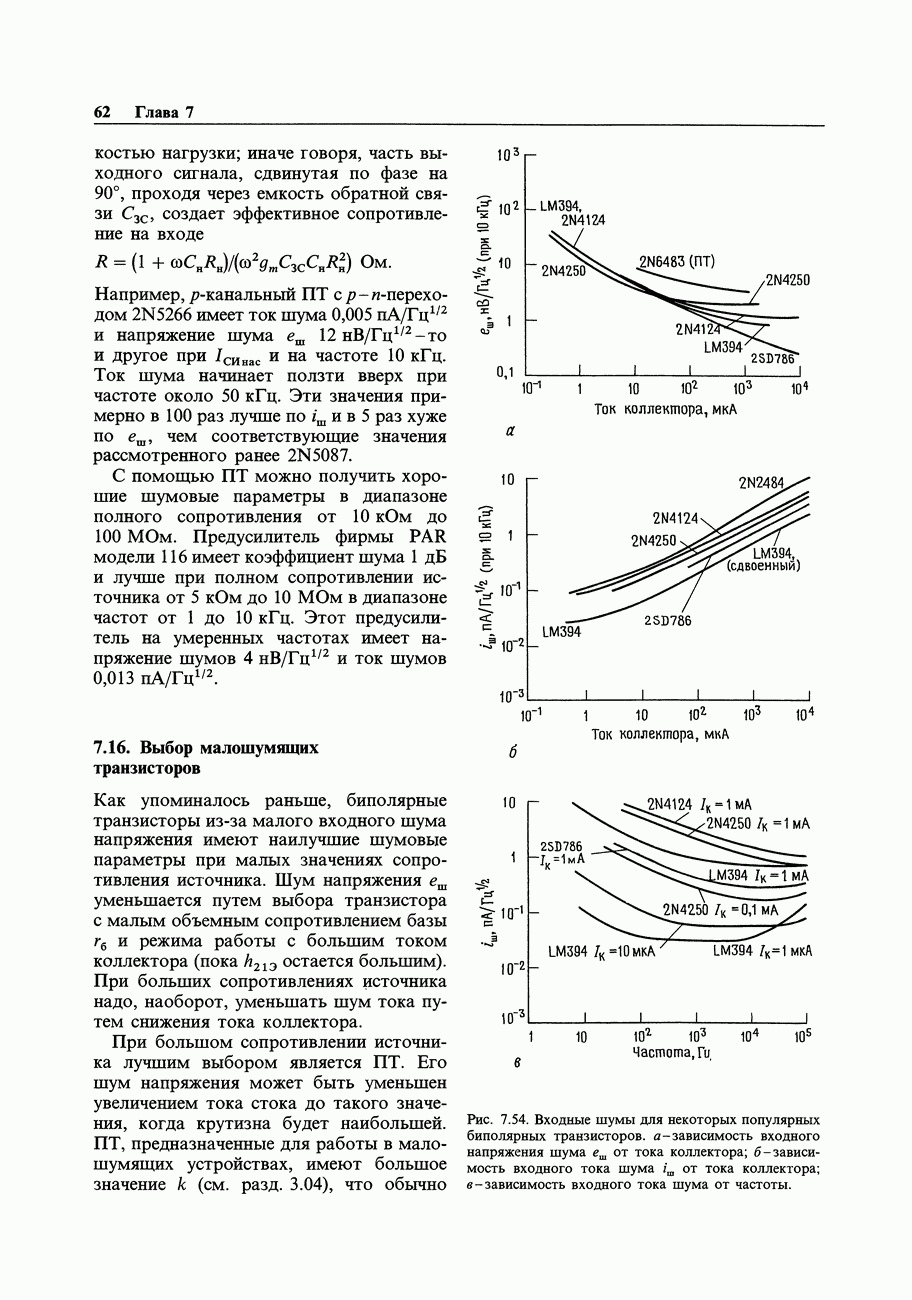
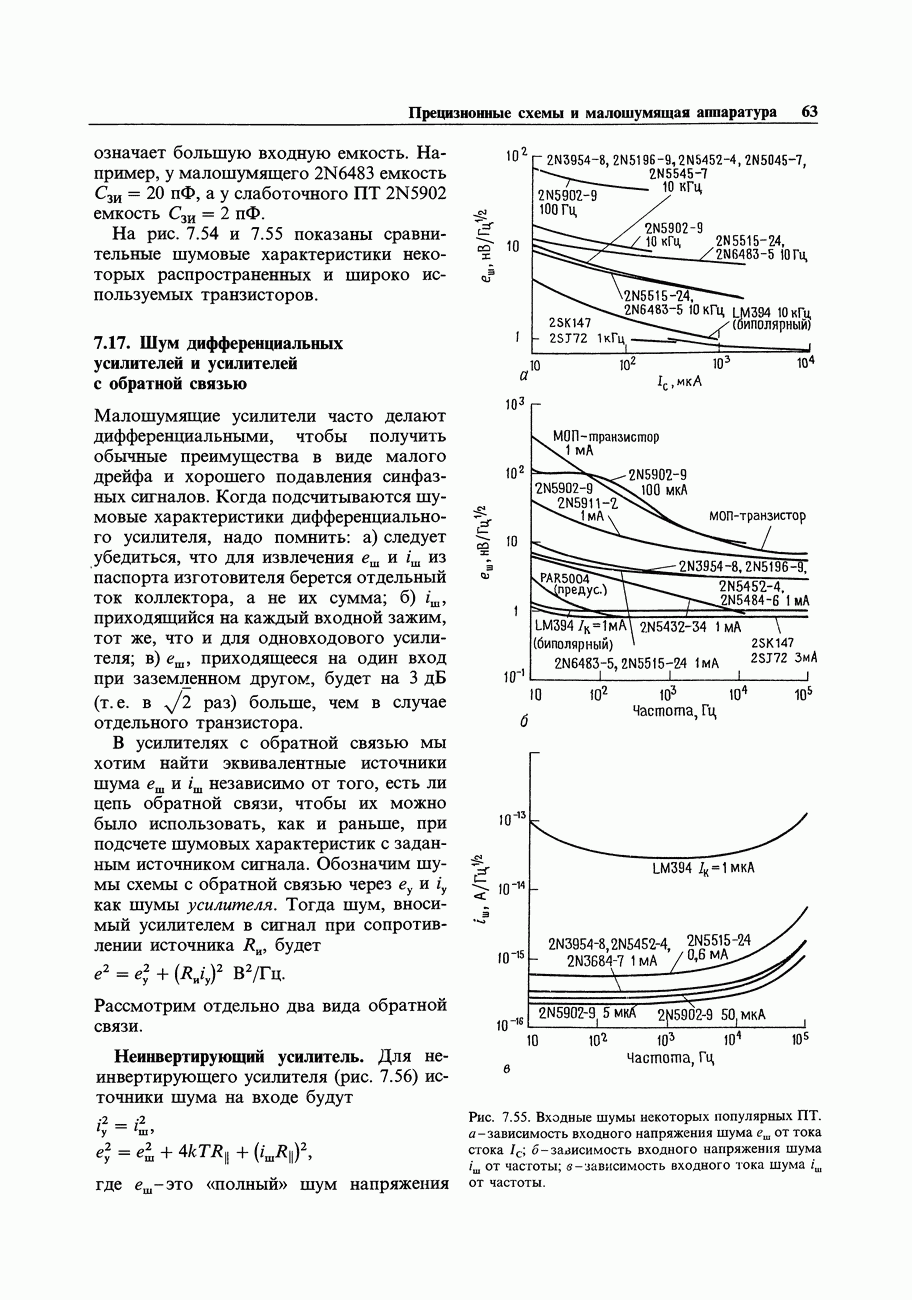
- 7.16. Выбор малошумящих транзисторов
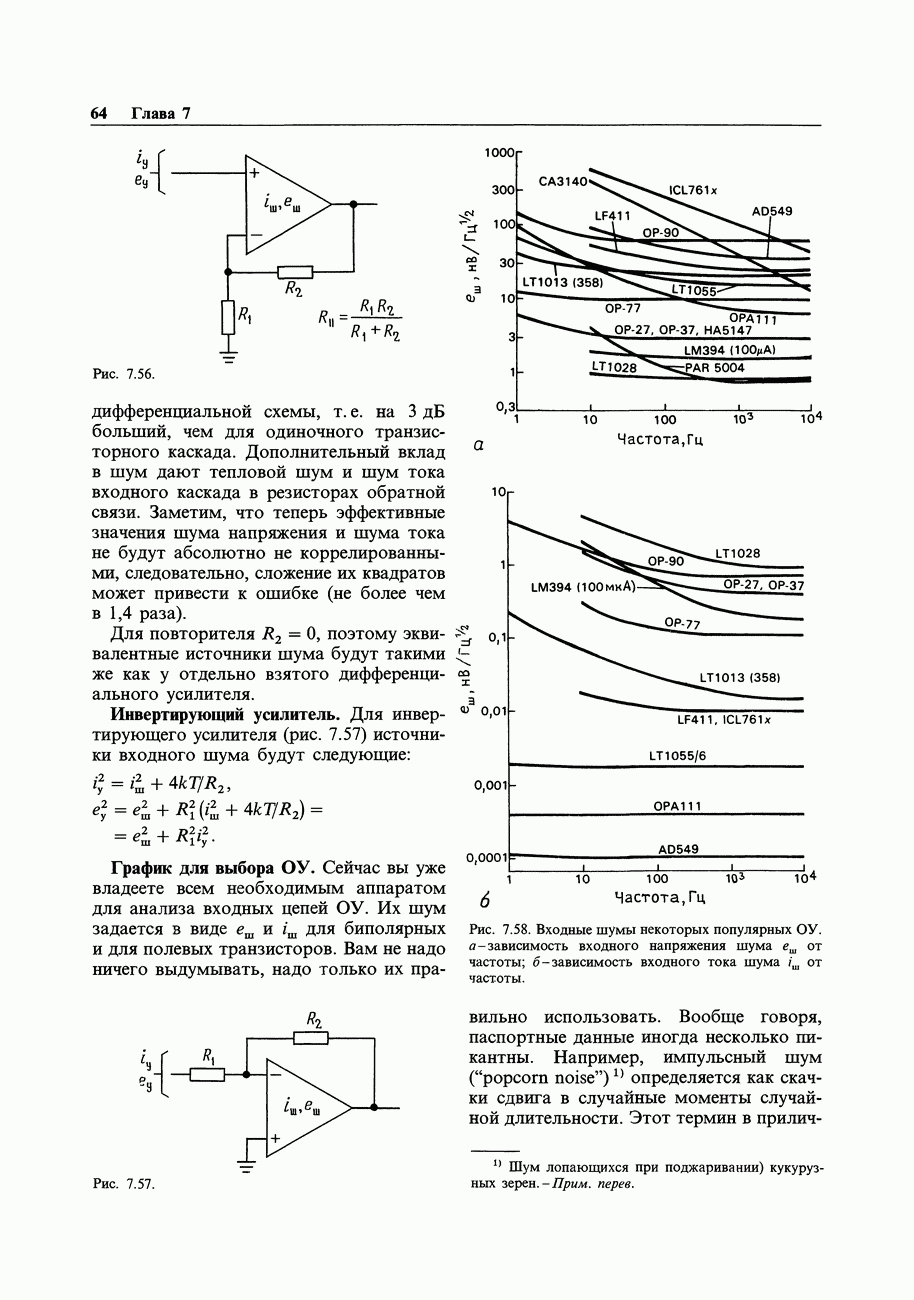
- 7.17. Шум дифференциальных усилителей и усилителей с обратной связью
- ИЗМЕРЕНИЕ ШУМА И ИСТОЧНИКИ ШУМА
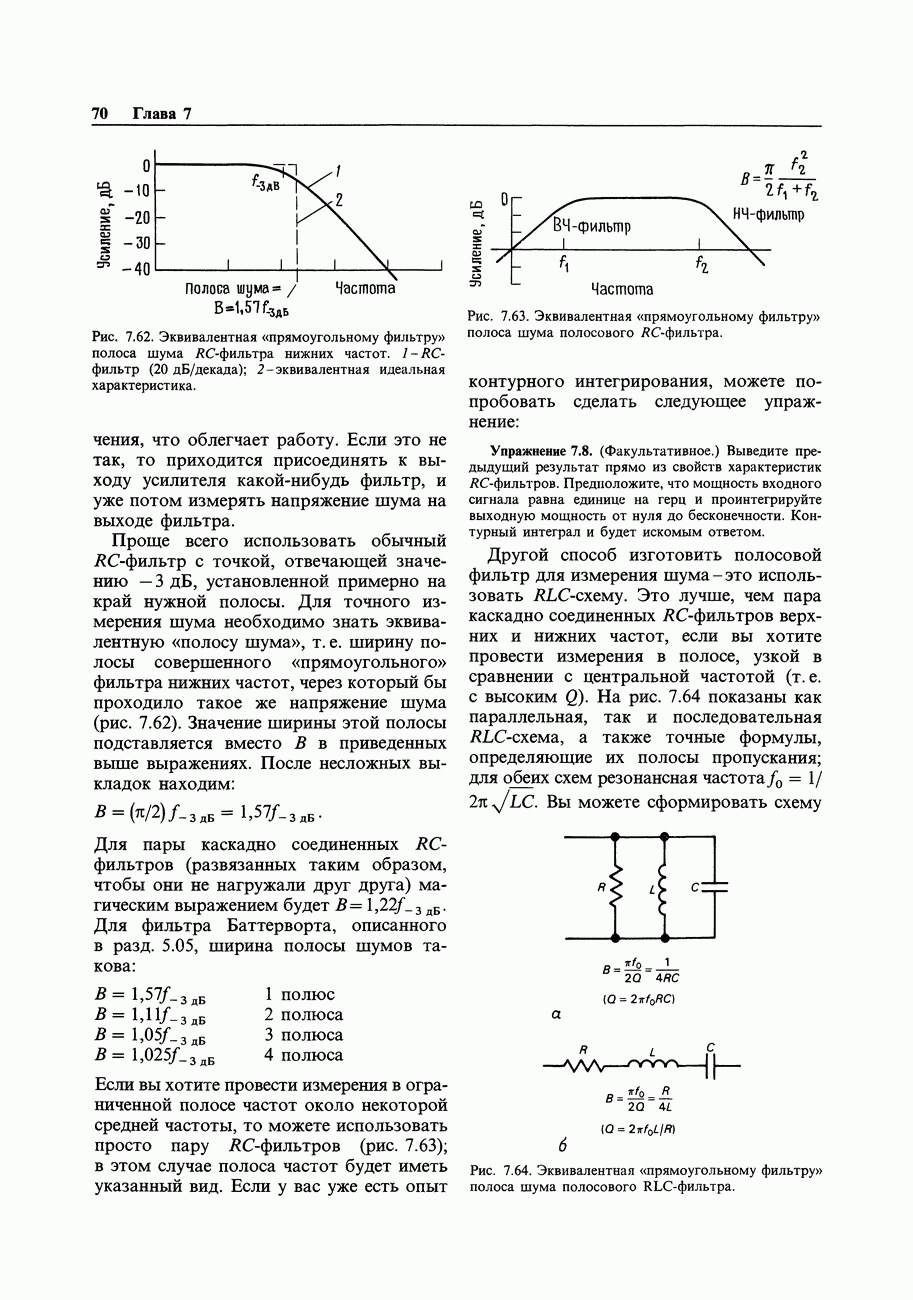
- 7.18. Измерение без источника шума
- 7.19. Измерение с источником шума
- 7.20. Генераторы шумов и сигналов
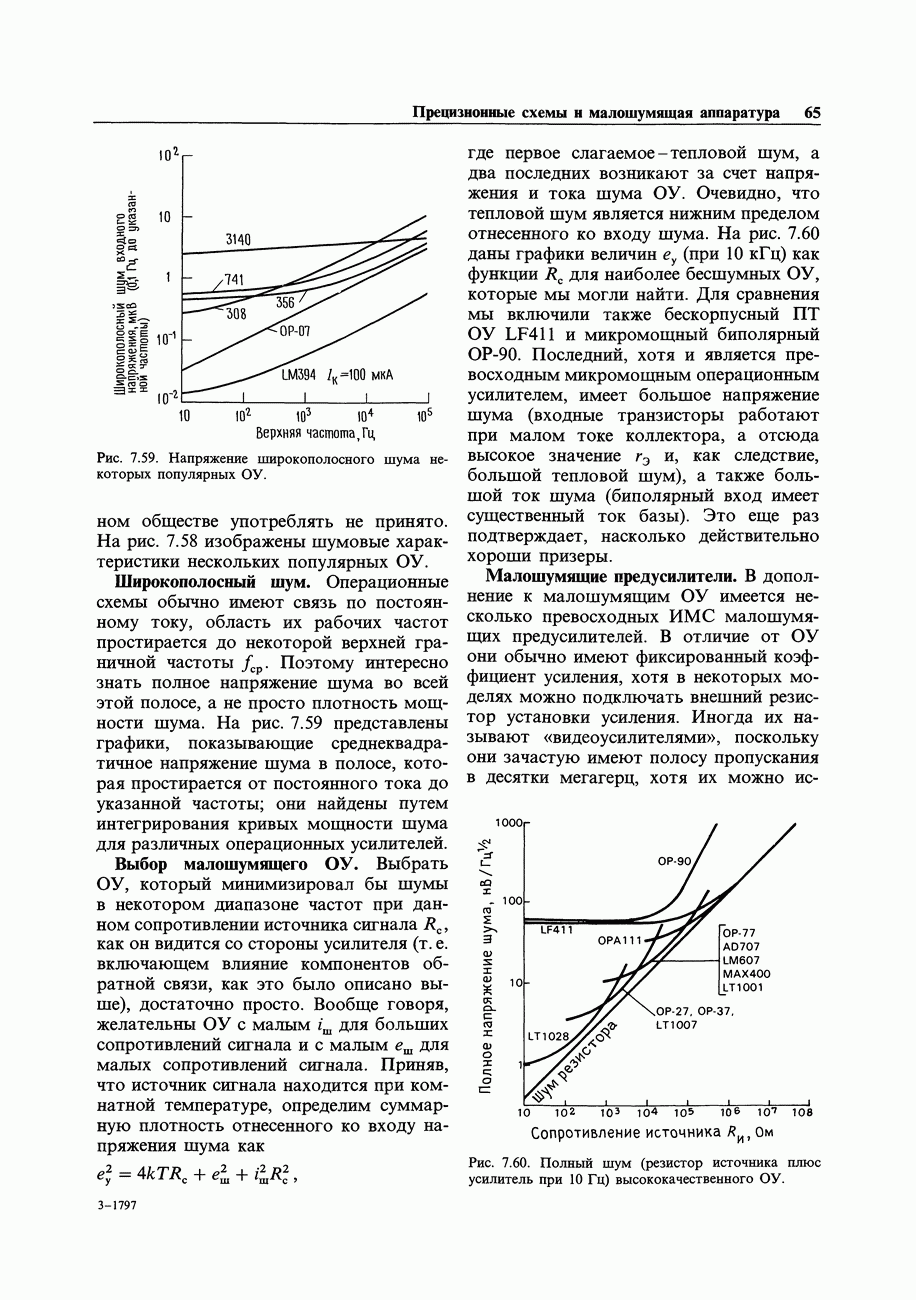
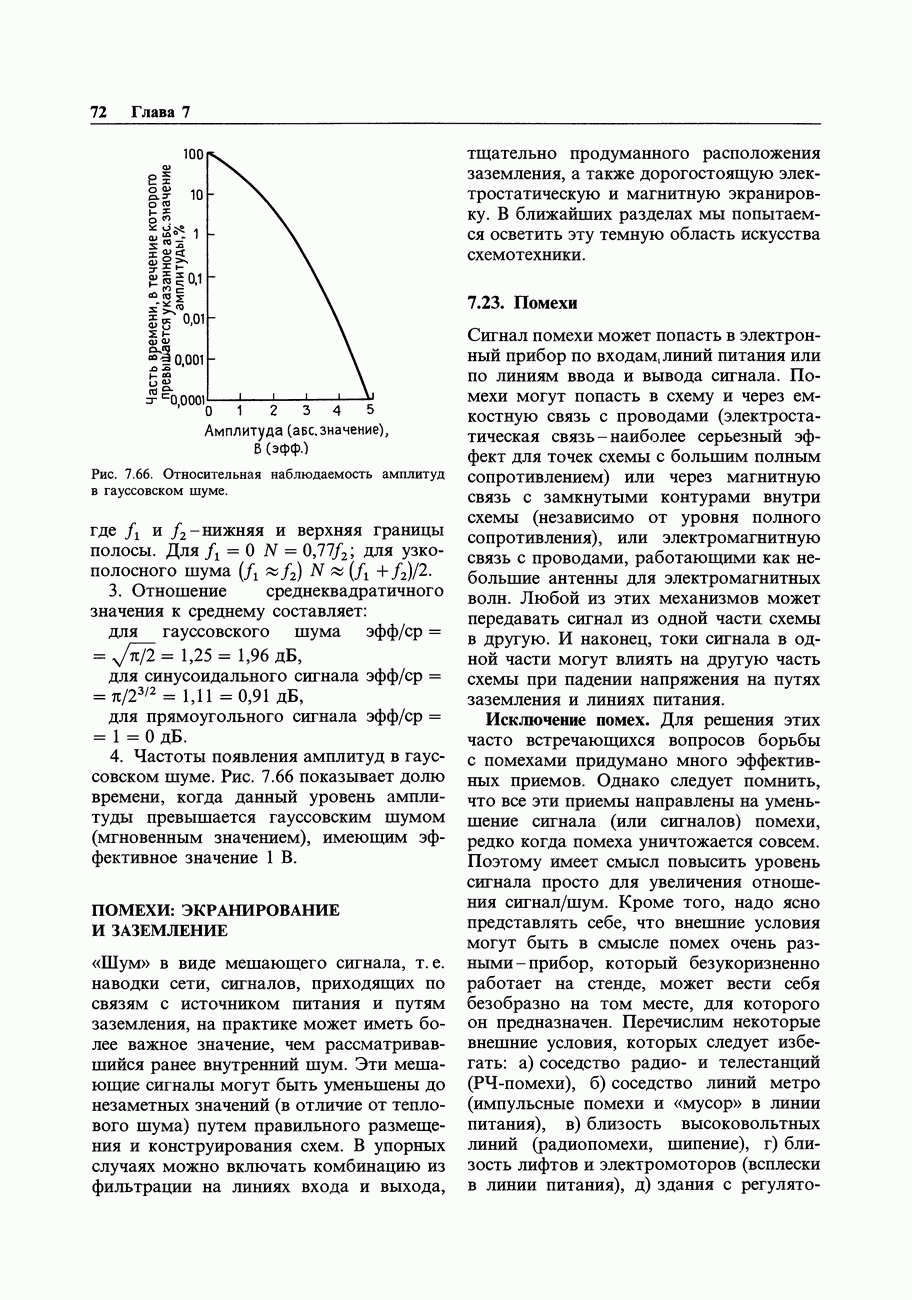
- 7.21. Ограничение полосы частот и измерение среднеквадратичного (эффективного) напряжения
- 7.22. Попурри на тему шумов
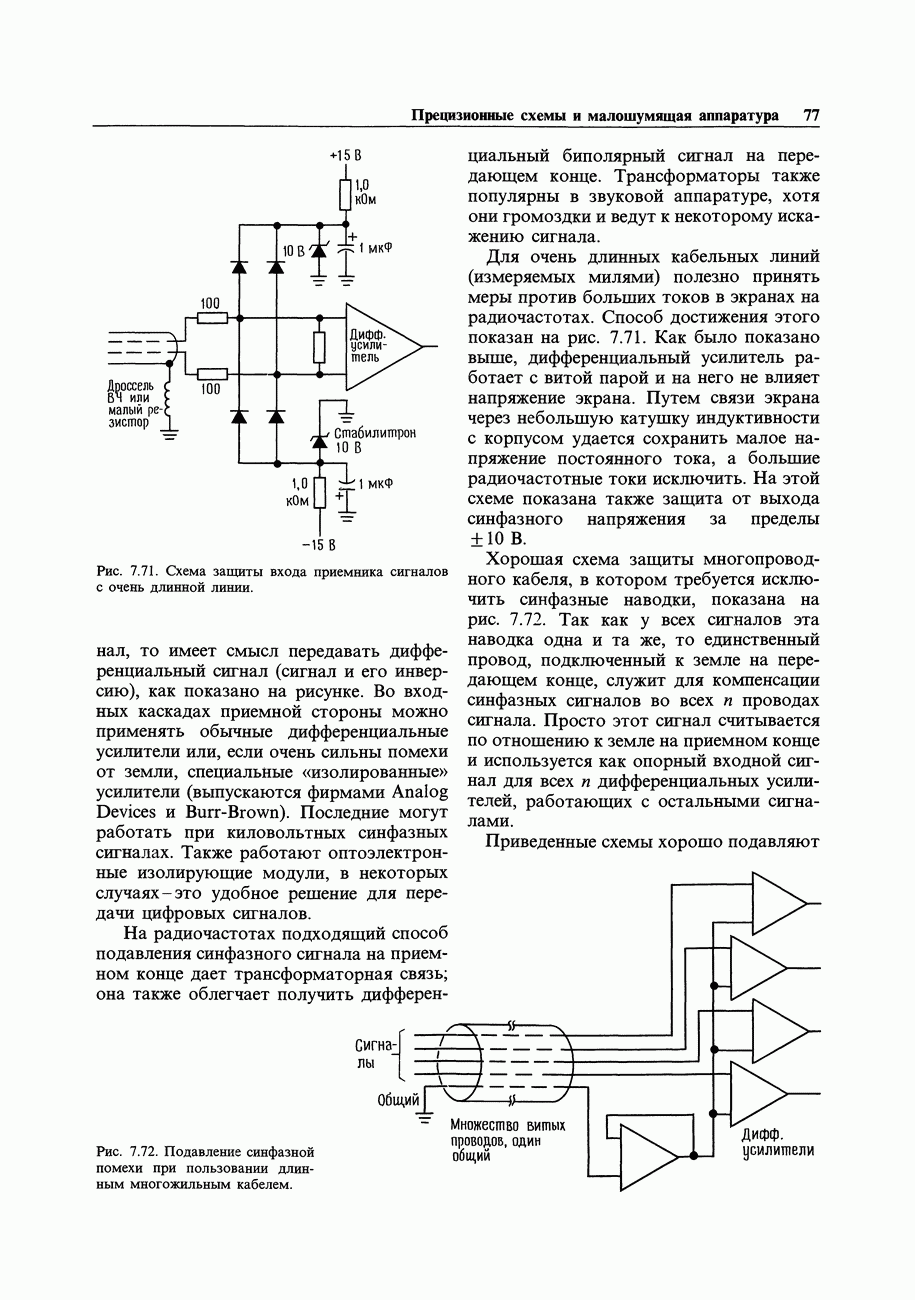
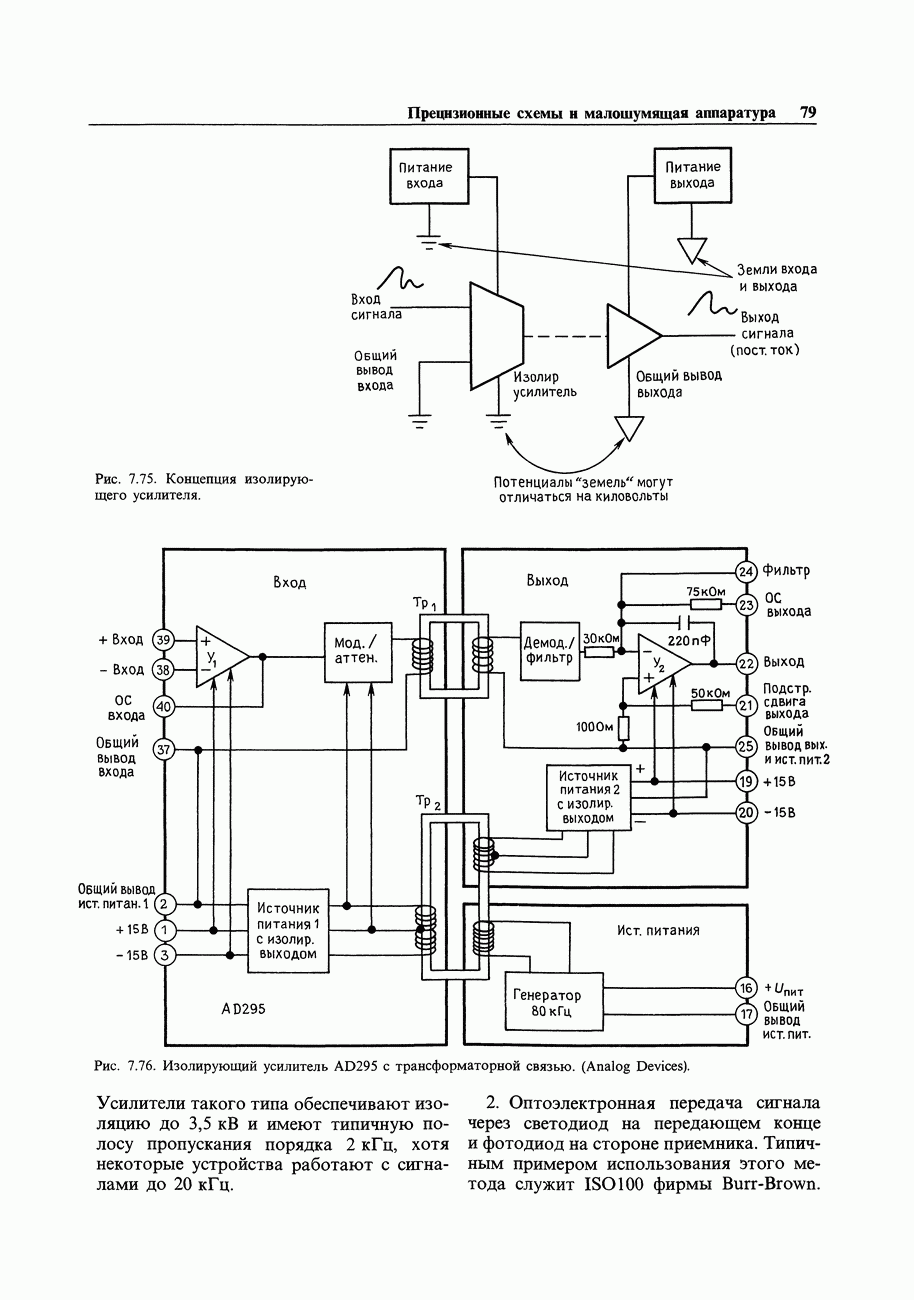
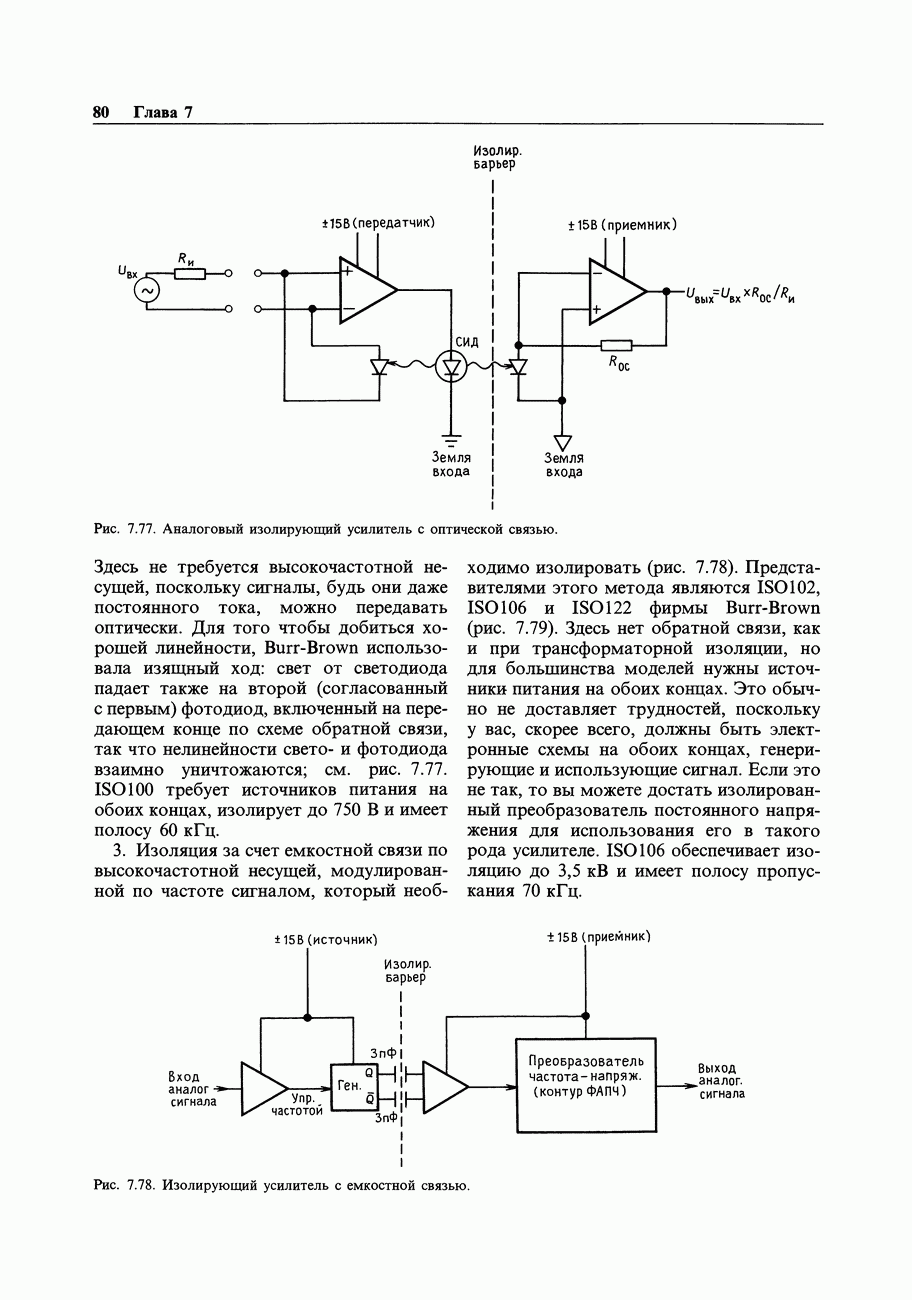
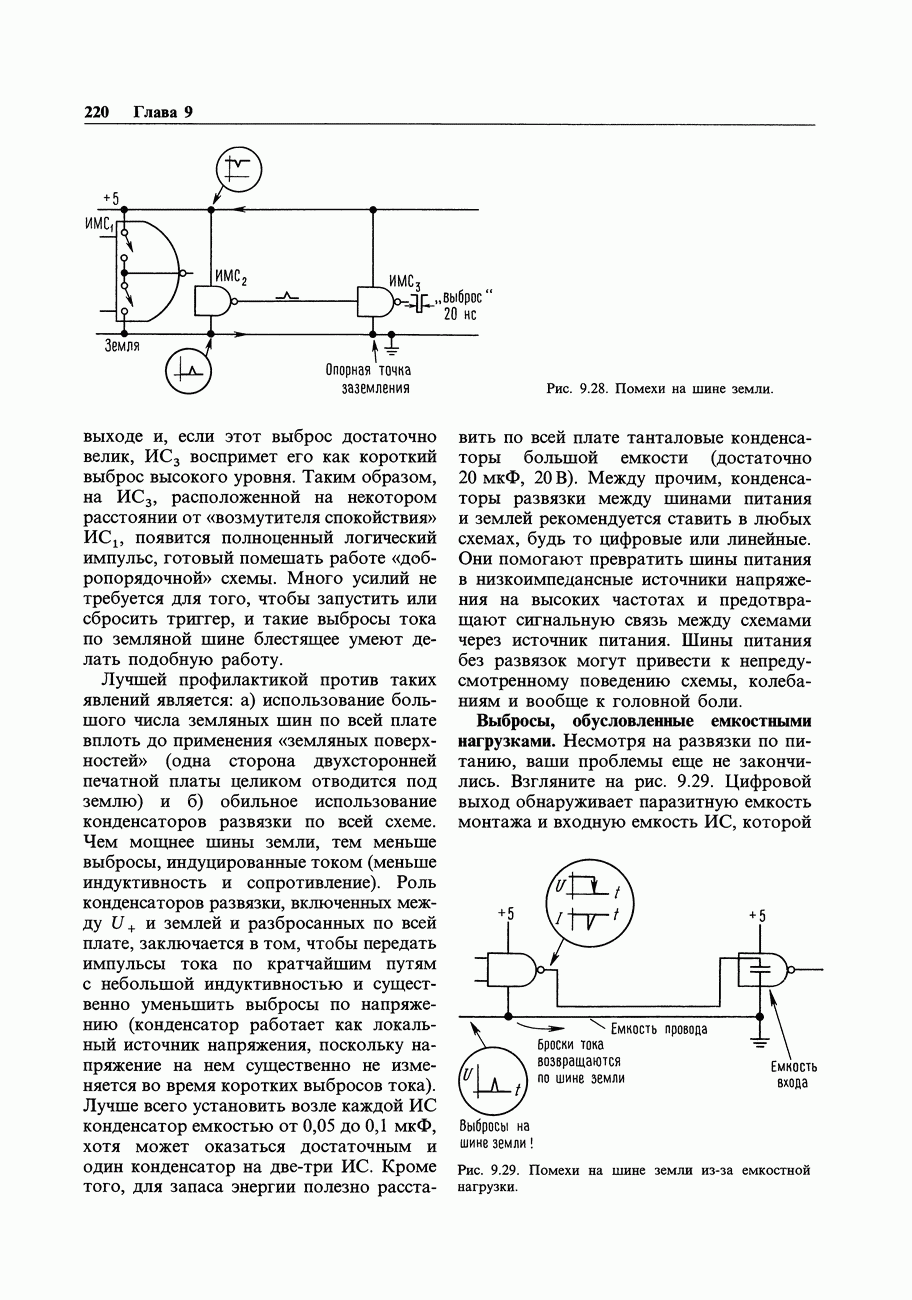
- ПОМЕХИ: ЭКРАНИРОВАНИЕ И ЗАЗЕМЛЕНИЕ
- 7.23. Помехи
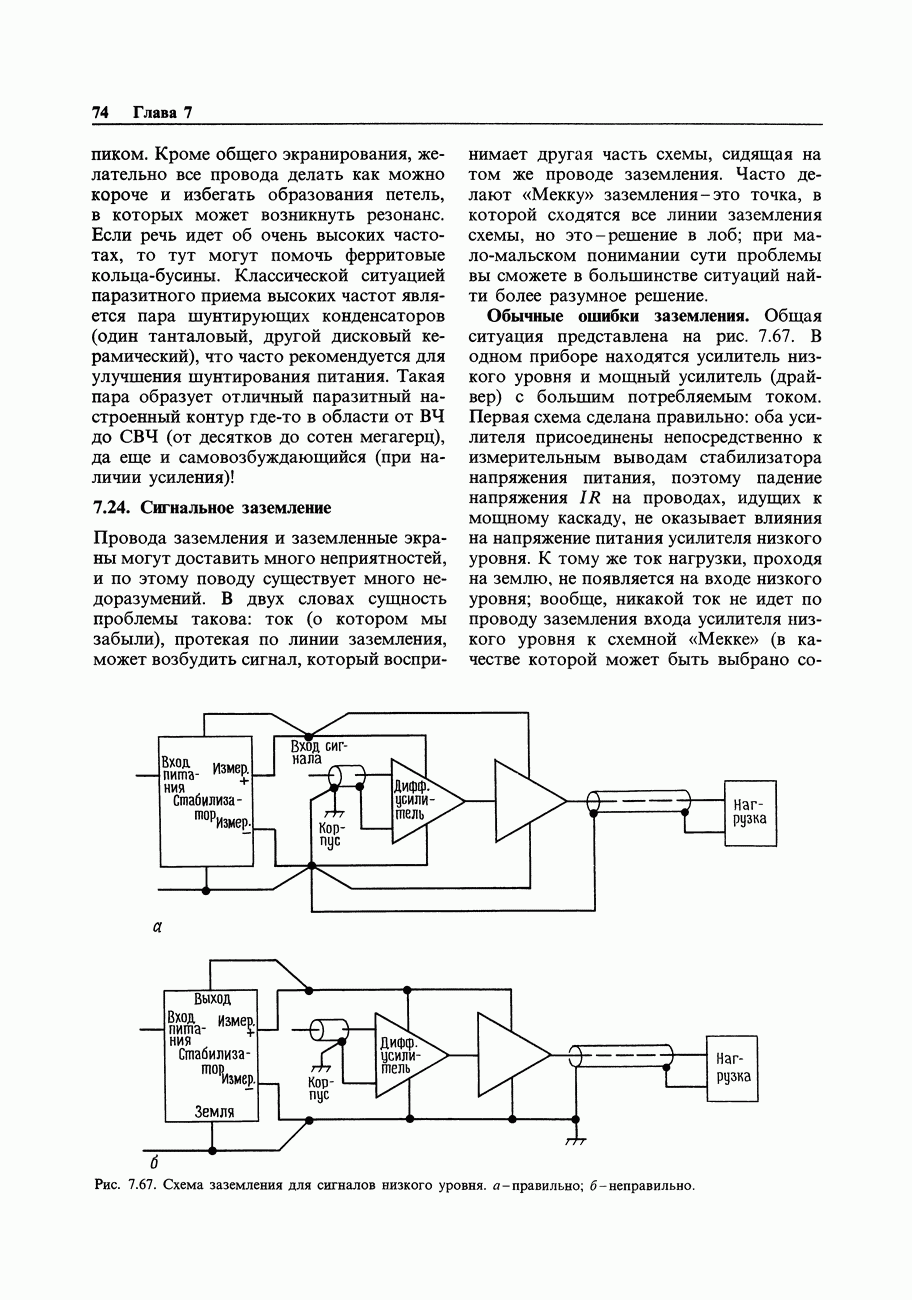
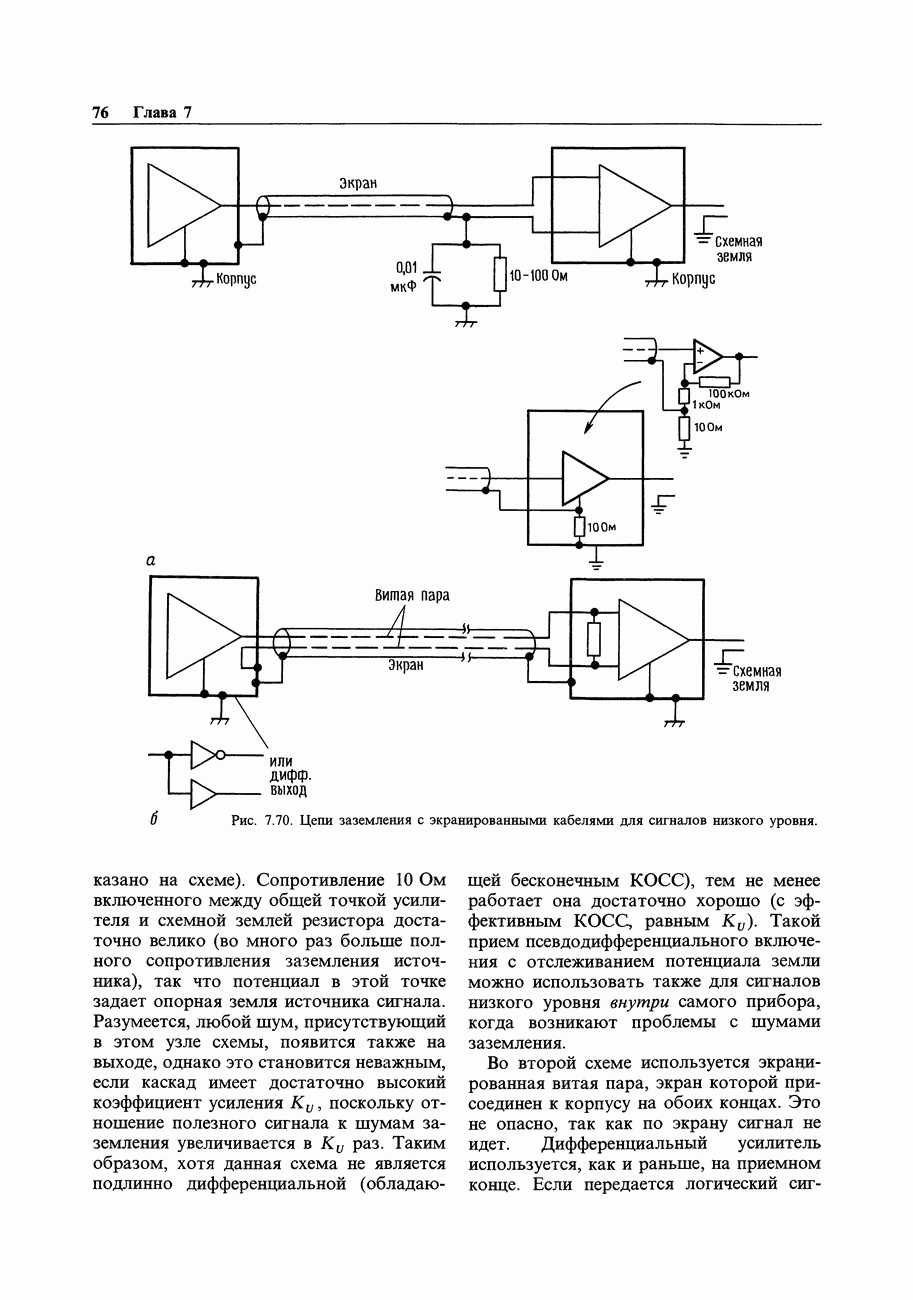
- 7.24. Сигнальное заземление
- 7.25. Межприборное заземление
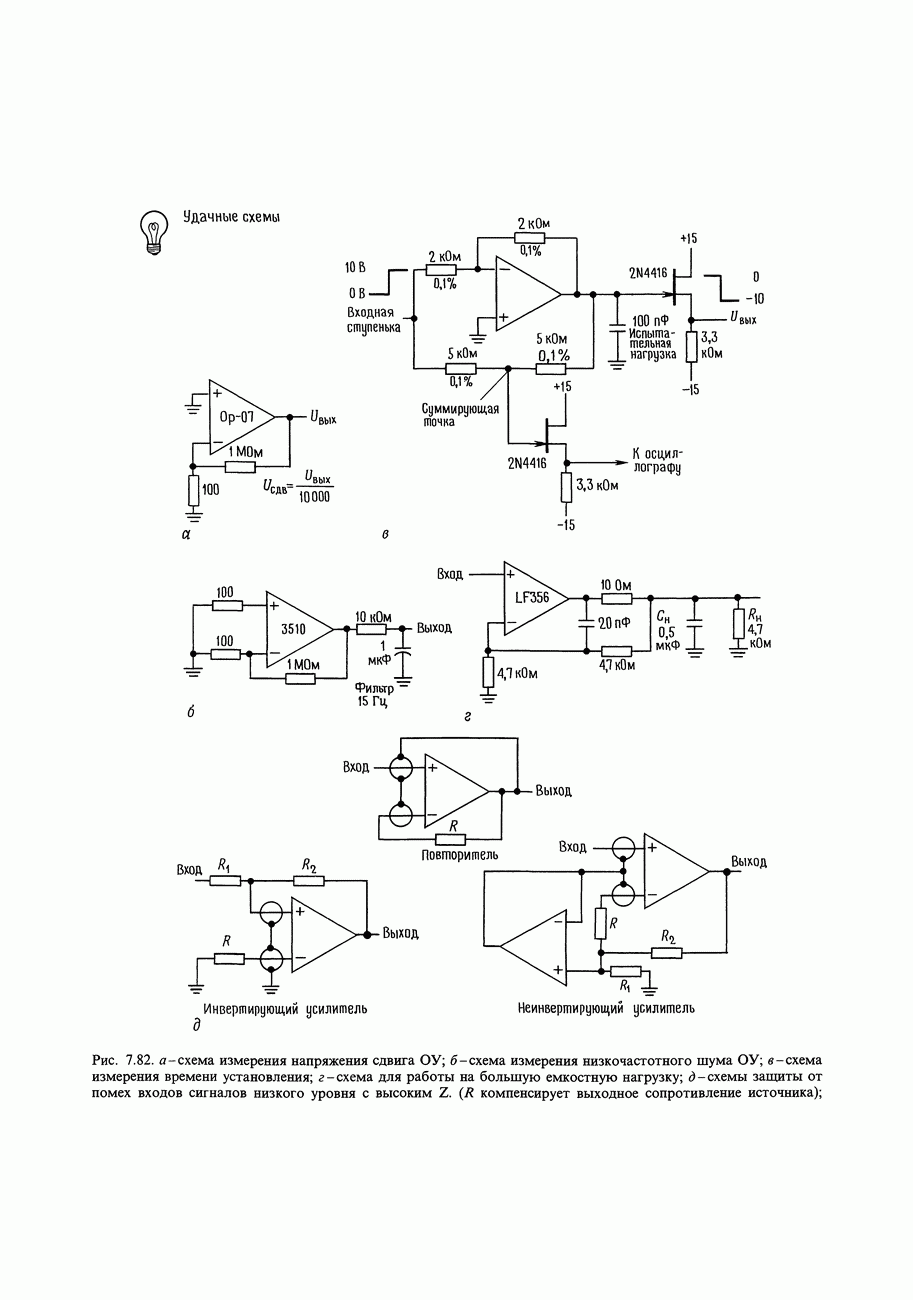
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
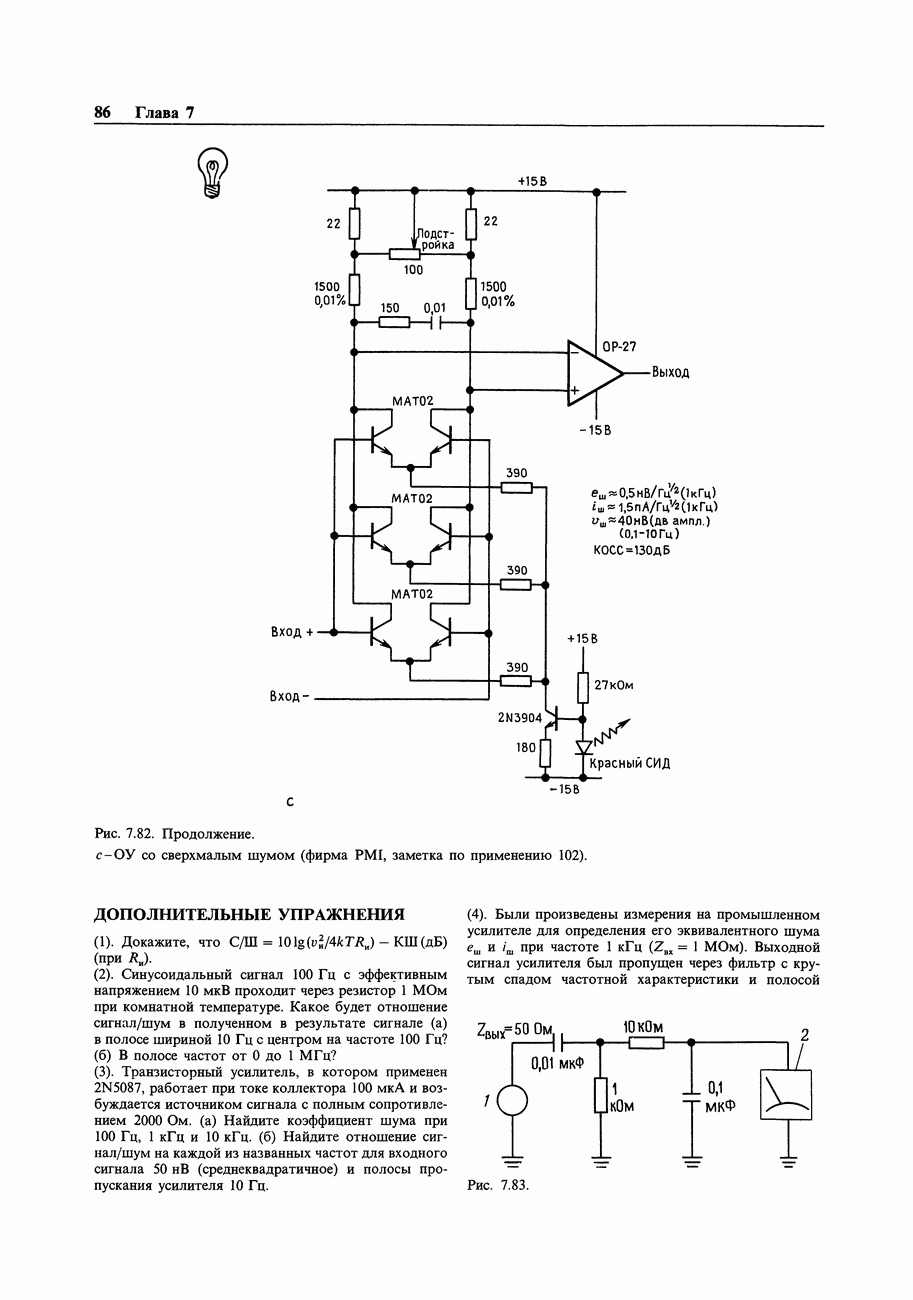
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 8. ЦИФРОВЫЕ СХЕМЫ
- 8.01. Цифровые и аналоговые сигналы
- 8.02. Логические состояния
- ЛОГИЧЕСКИЕ УРОВНИ
- 8.03. Числовые коды
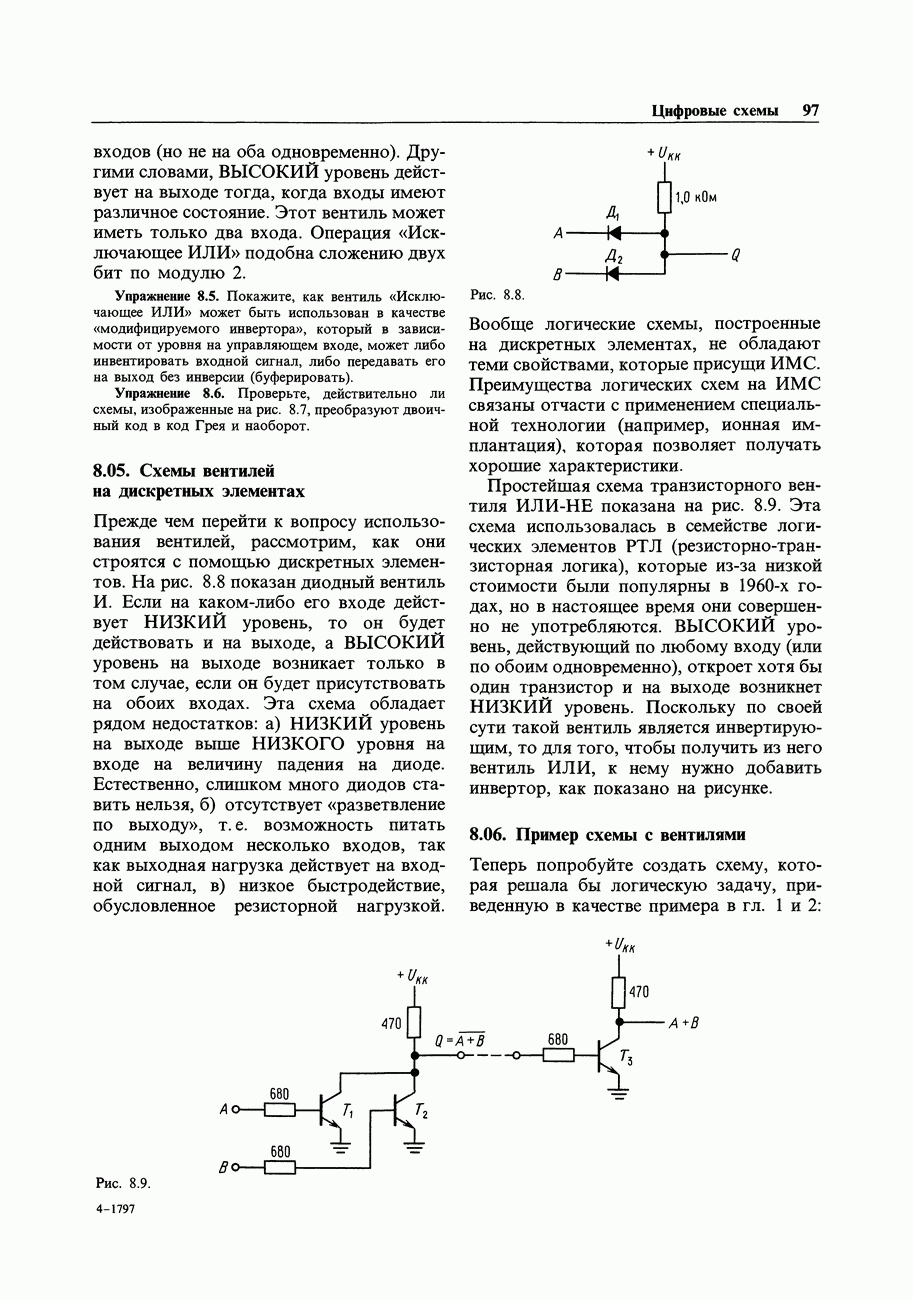
- 8.04. Вентили и таблицы истинности
- 8.05. Схемы вентилей на дискретных элементах
- 8.06. Пример схемы с вентилями
- 8.07. Логические обозначения при заданных уровнях
- 8.08. Каталог идентичных вентилей
- 8.09. Принципиальные схемы вентилей на ИМС
- 8.10. Характеристики ТТЛ и КМОП
- 8.11. Элементы с тремя состояниями и с открытым коллектором
- КОМБИНАЦИОННАЯ ЛОГИКА
- 8.12. Логические тождества
- 8.13. Минимизация и карты Карно
- 8.14. Комбинационные функциональные схемы, реализованные на стандартных ИМС
- 8.15. Реализация произвольных таблиц истины
- ПОСЛЕДОВАТЕЛЬНОСТНАЯ ЛОГИКА
- 8.16. Устройства с памятью: триггеры
- 8.17. Тактируемые триггеры
- 8.18. Последовательностная логика-объединение памяти и вентилей
- 8.19. Синхронизатор
- МОНОСТАБИЛЬНЫЕ МУЛЬТИВИБРАТОРЫ
- 8.20. Характеристики одновибраторов
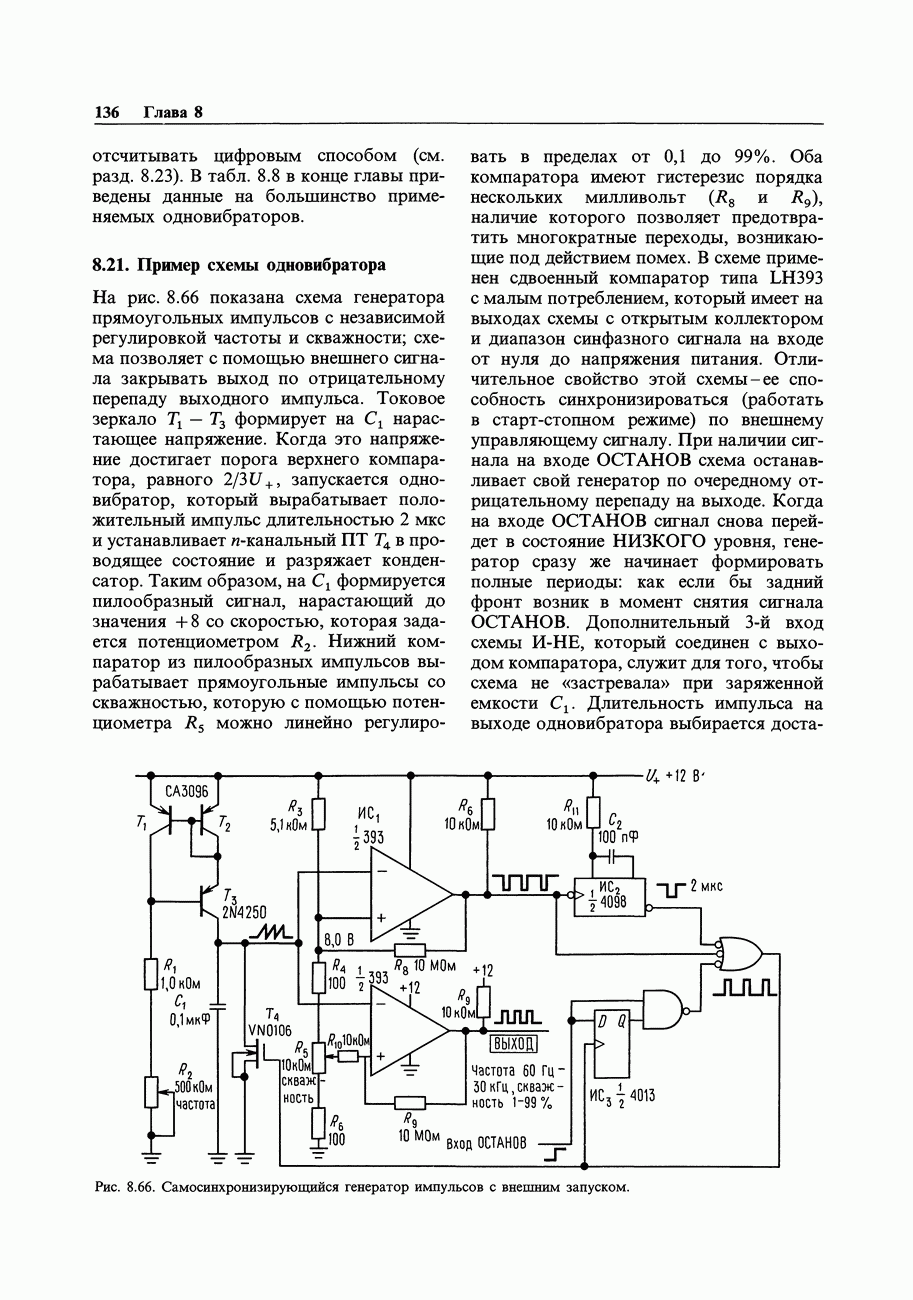
- 8.21. Пример схемы одновибратора
- 8.22. Предостережения относительно одновибраторов
- 8.23. Получение выдержки времени с помощью счетчиков
- ПОСЛЕДОВАТЕЛЬНОСТНЫЕ ФУНКЦИИ, РЕАЛИЗУЕМЫЕ НА СТАНДАРТНЫХ ИМС
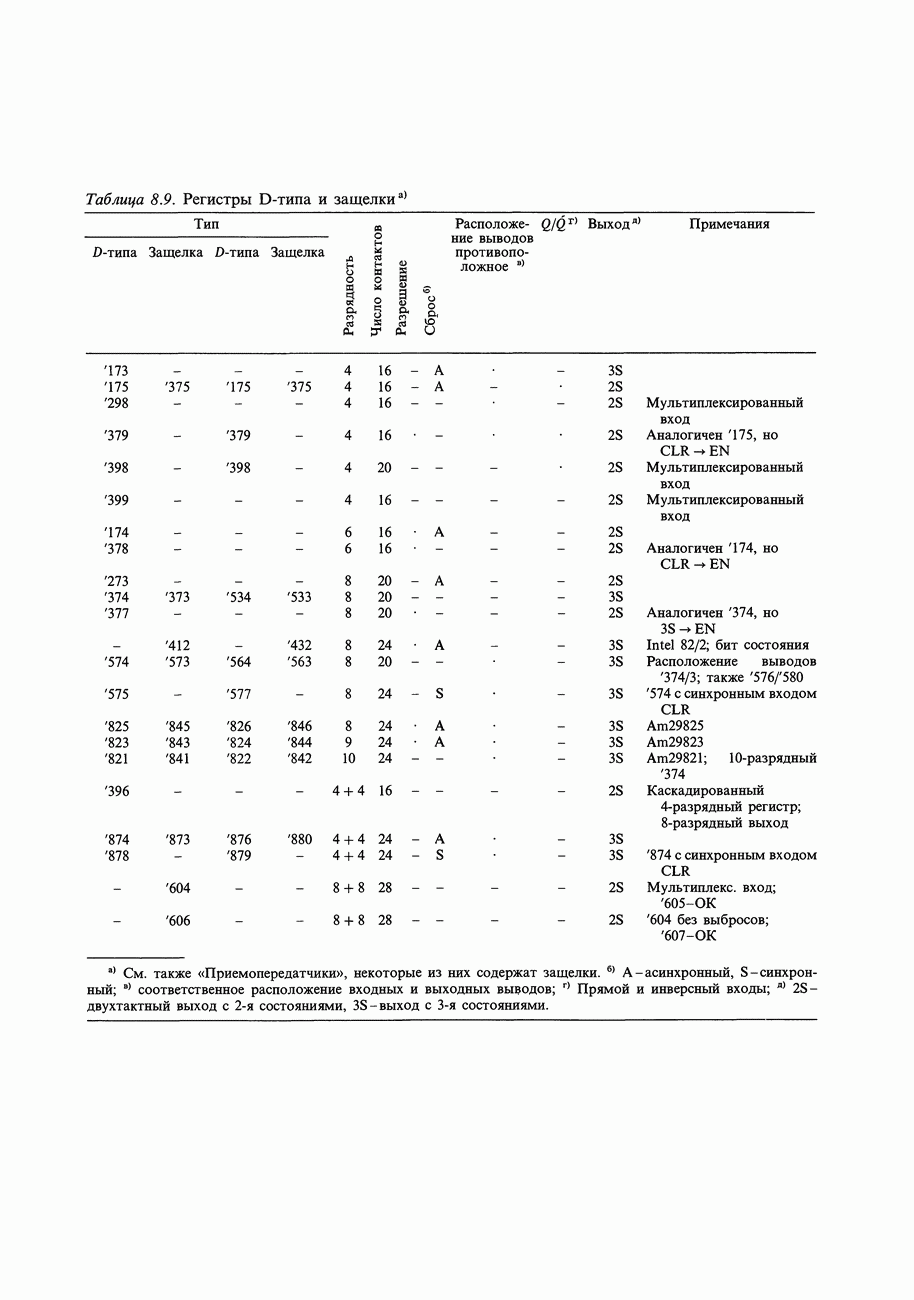
- 8.24. Фиксирующие схемы-защелки и регистры
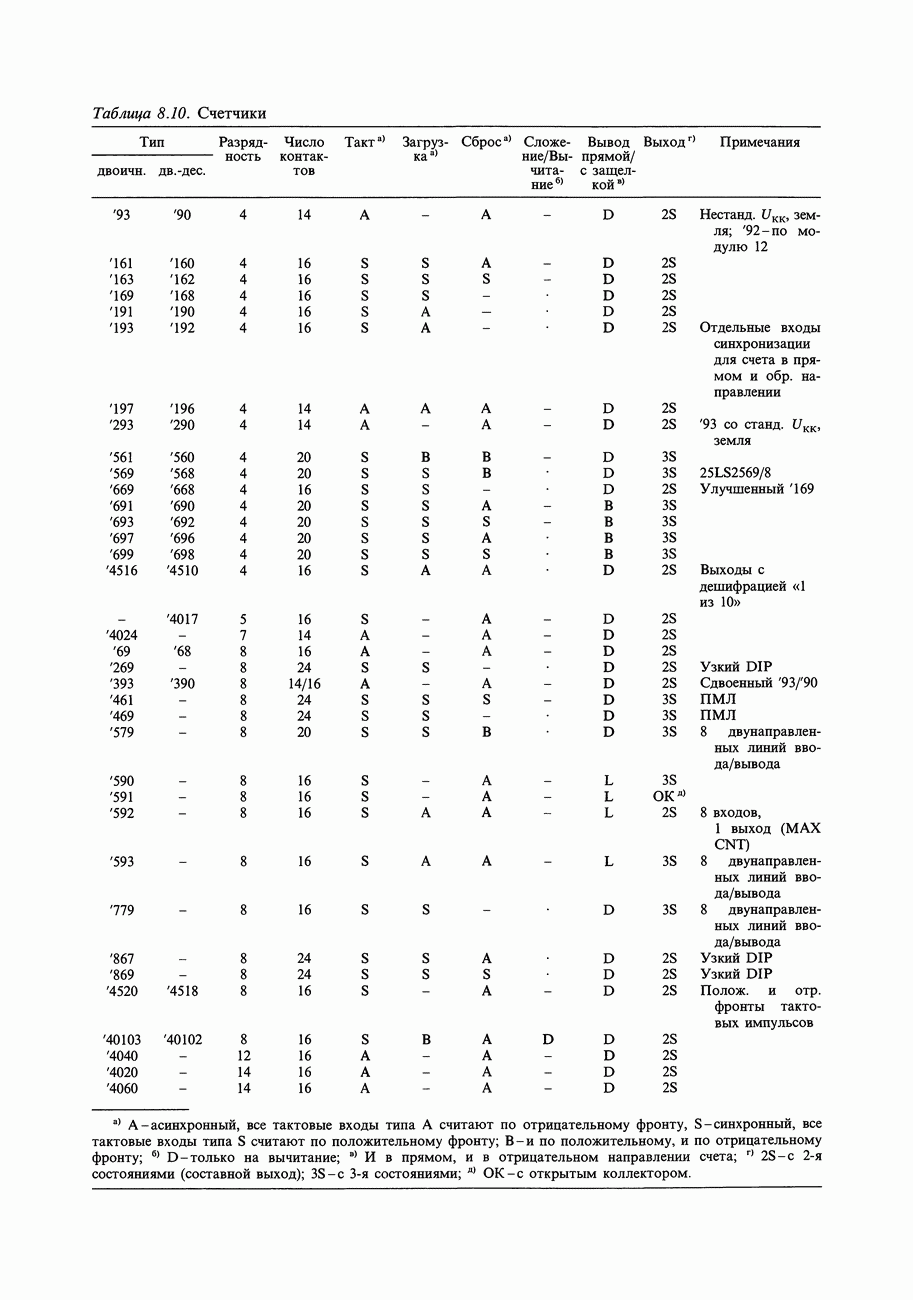
- 8.25. Счетчики
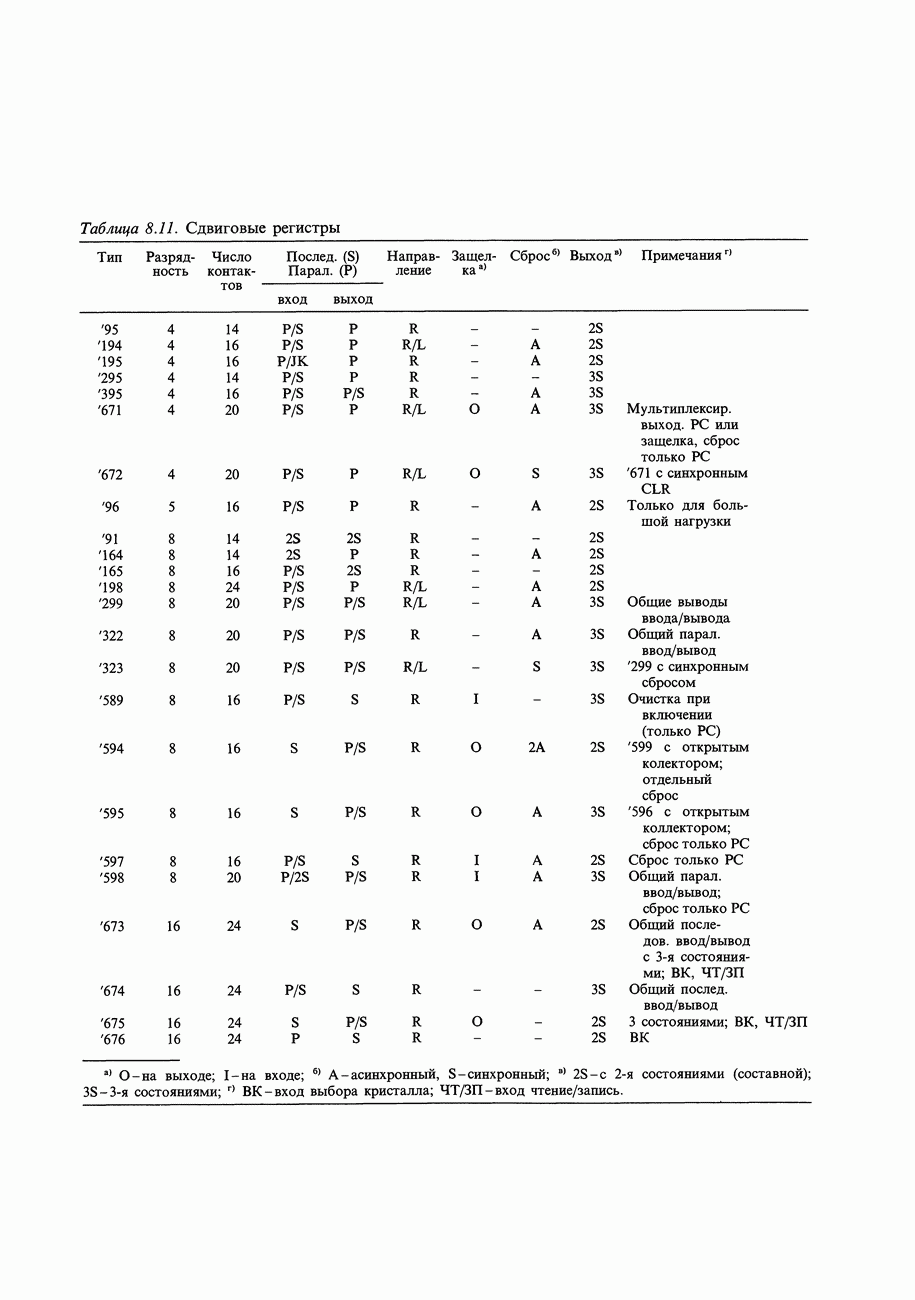
- 8.26. Регистры сдвига
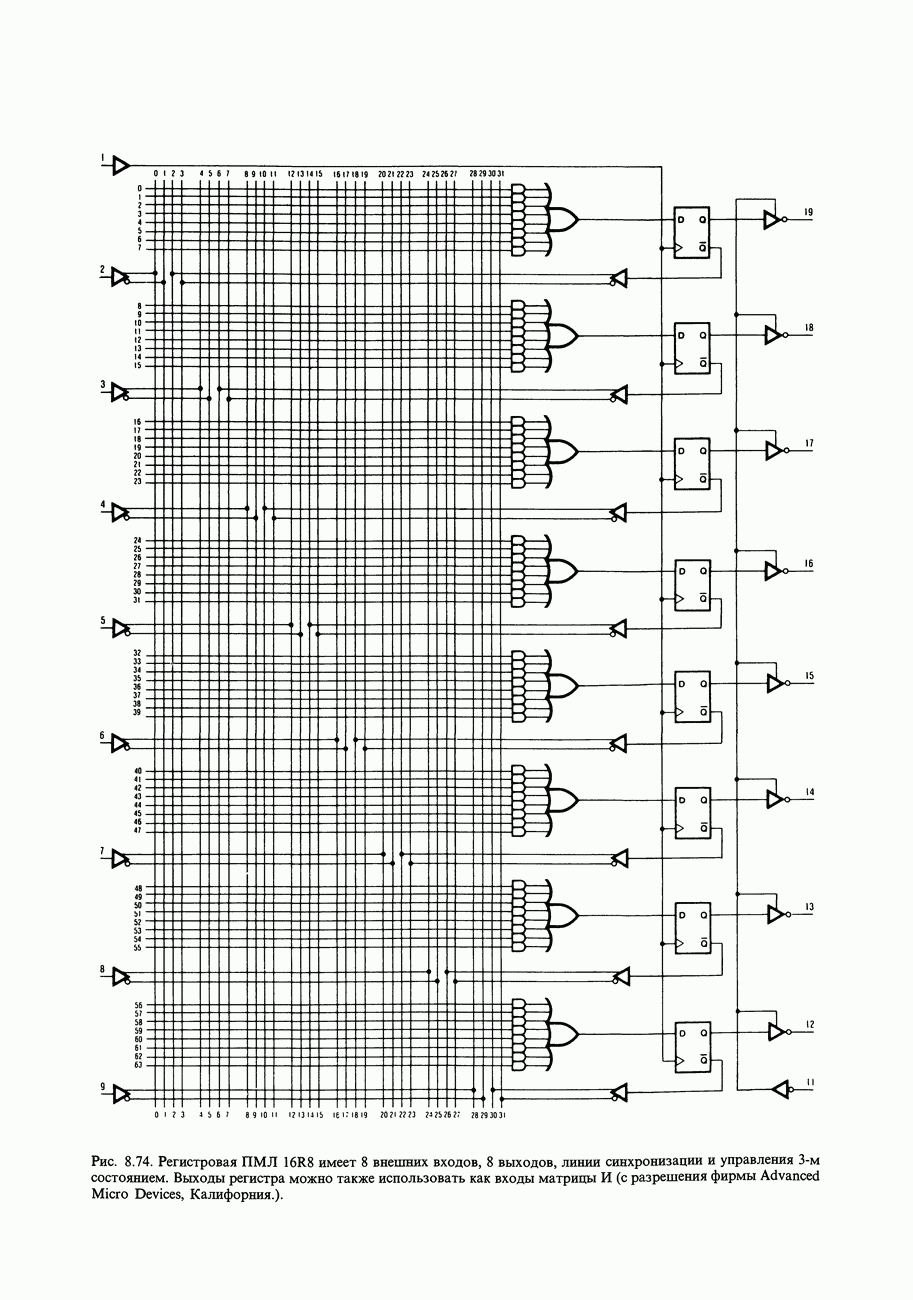
- 8.27. Последовательностные ПМЛ
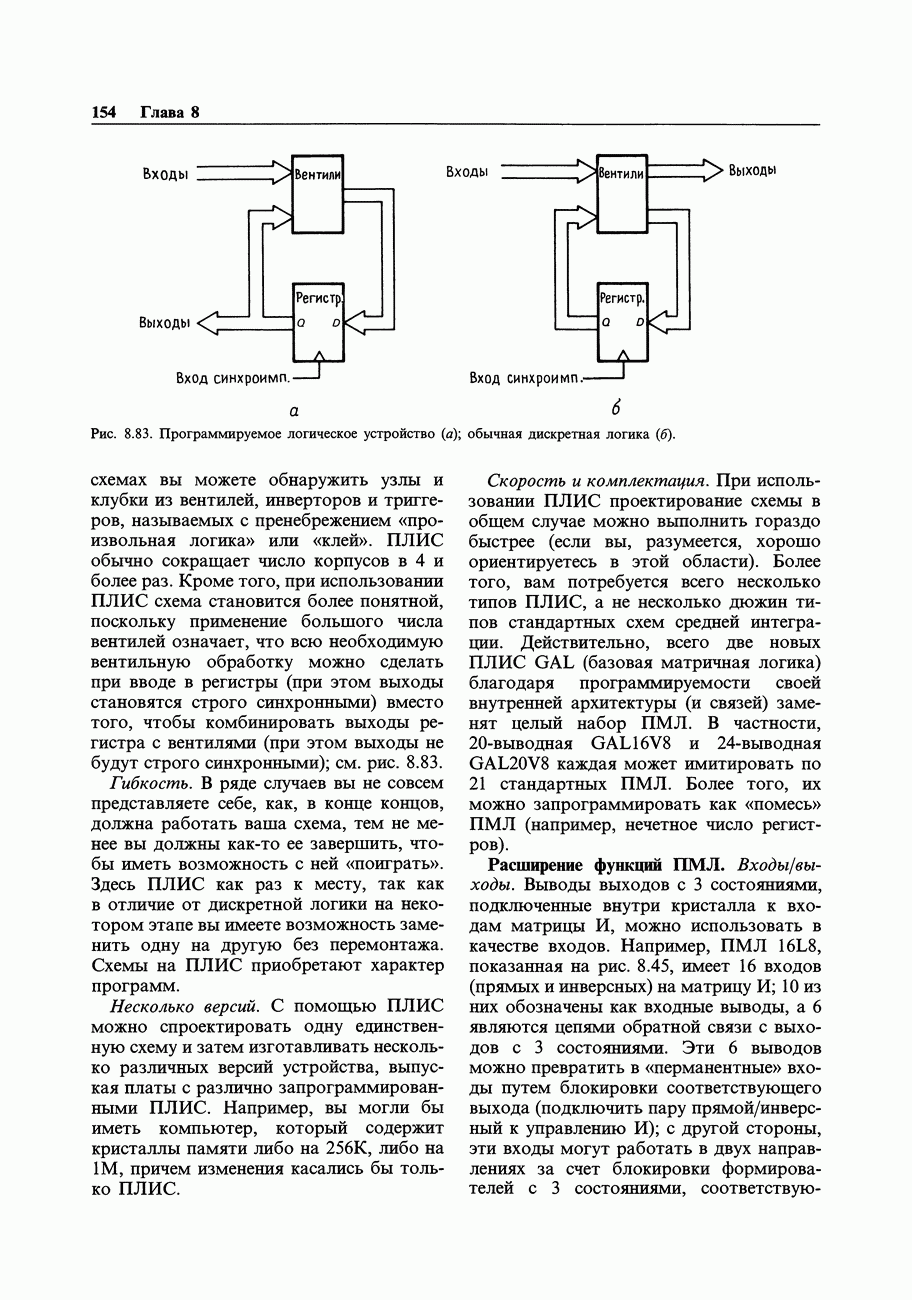
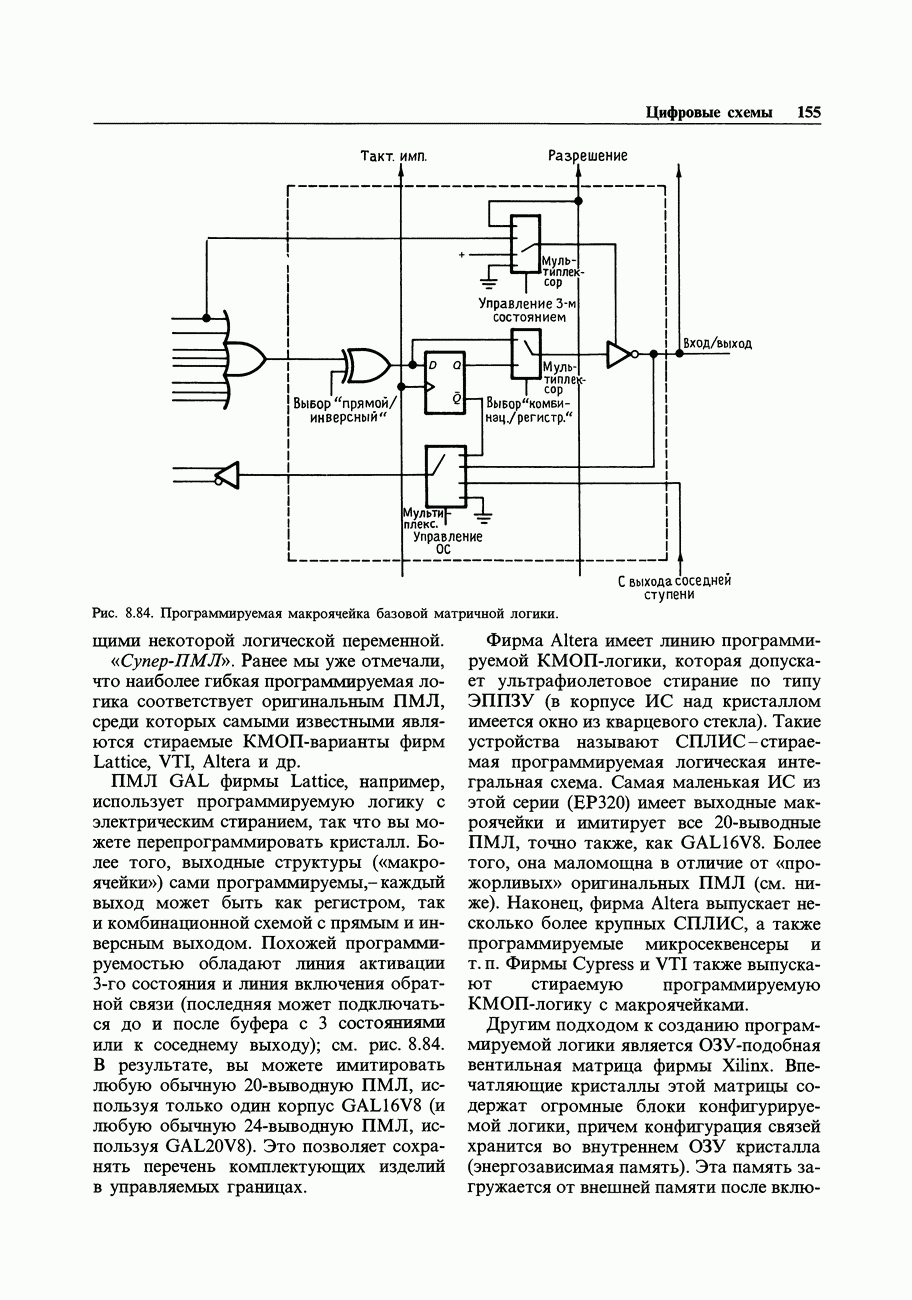
- Возможные применения программируемых логических интегральных схем (ПЛИС)
- 8.28. Разнообразные последовательностные схемы
- НЕКОТОРЫЕ ТИПОВЫЕ ЦИФРОВЫЕ СХЕМЫ
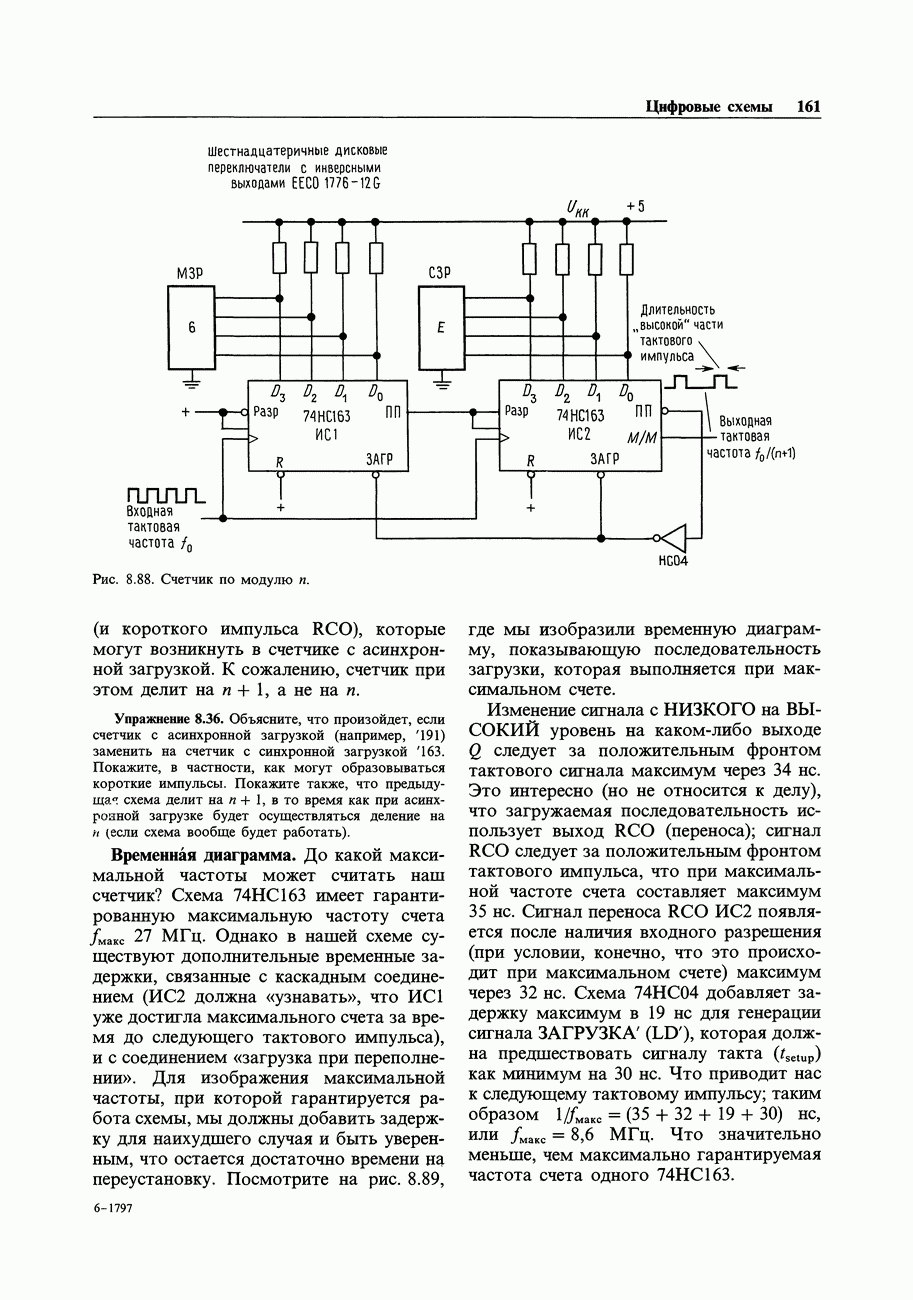
- 8.29. Счетчик по модулю n
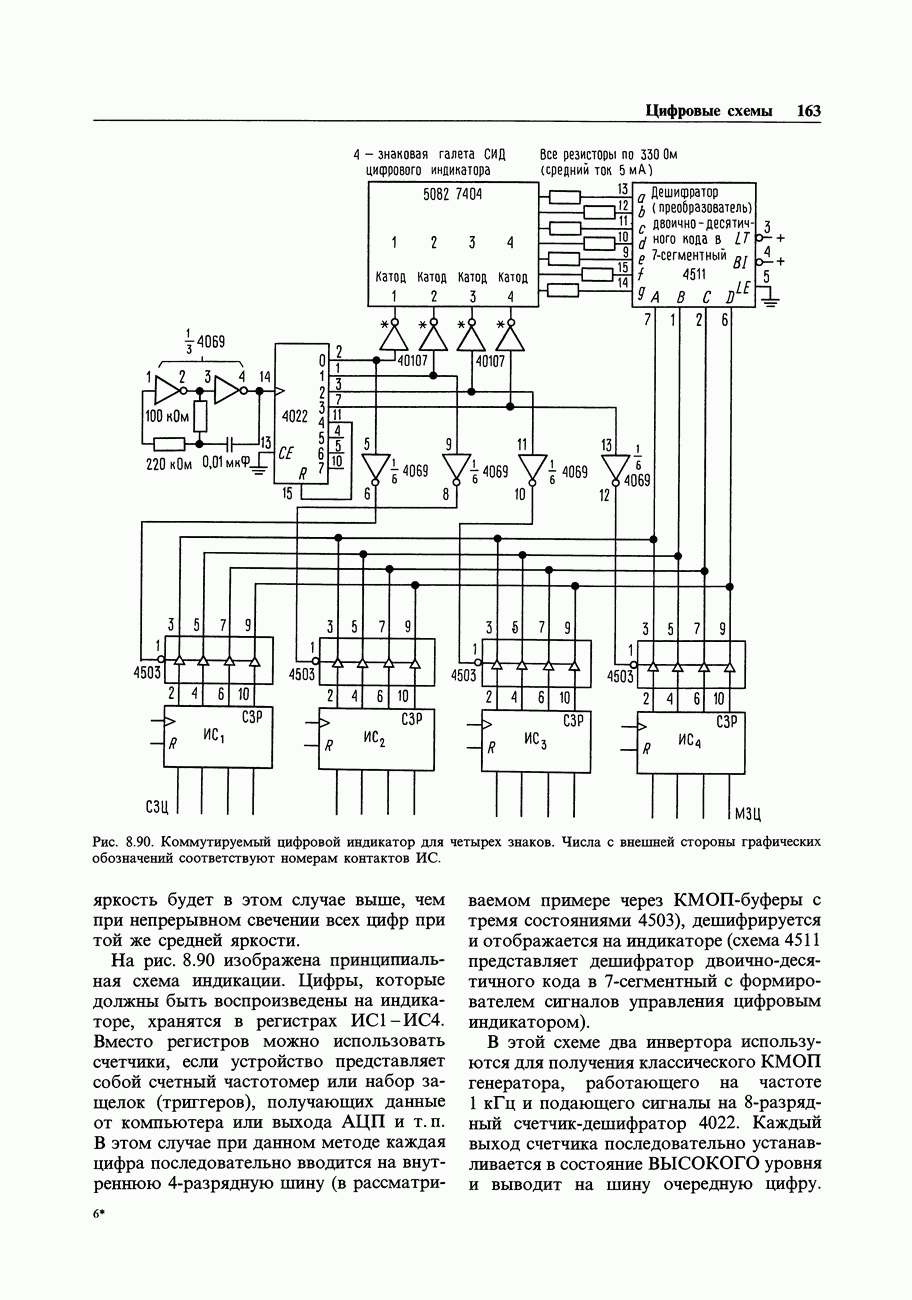
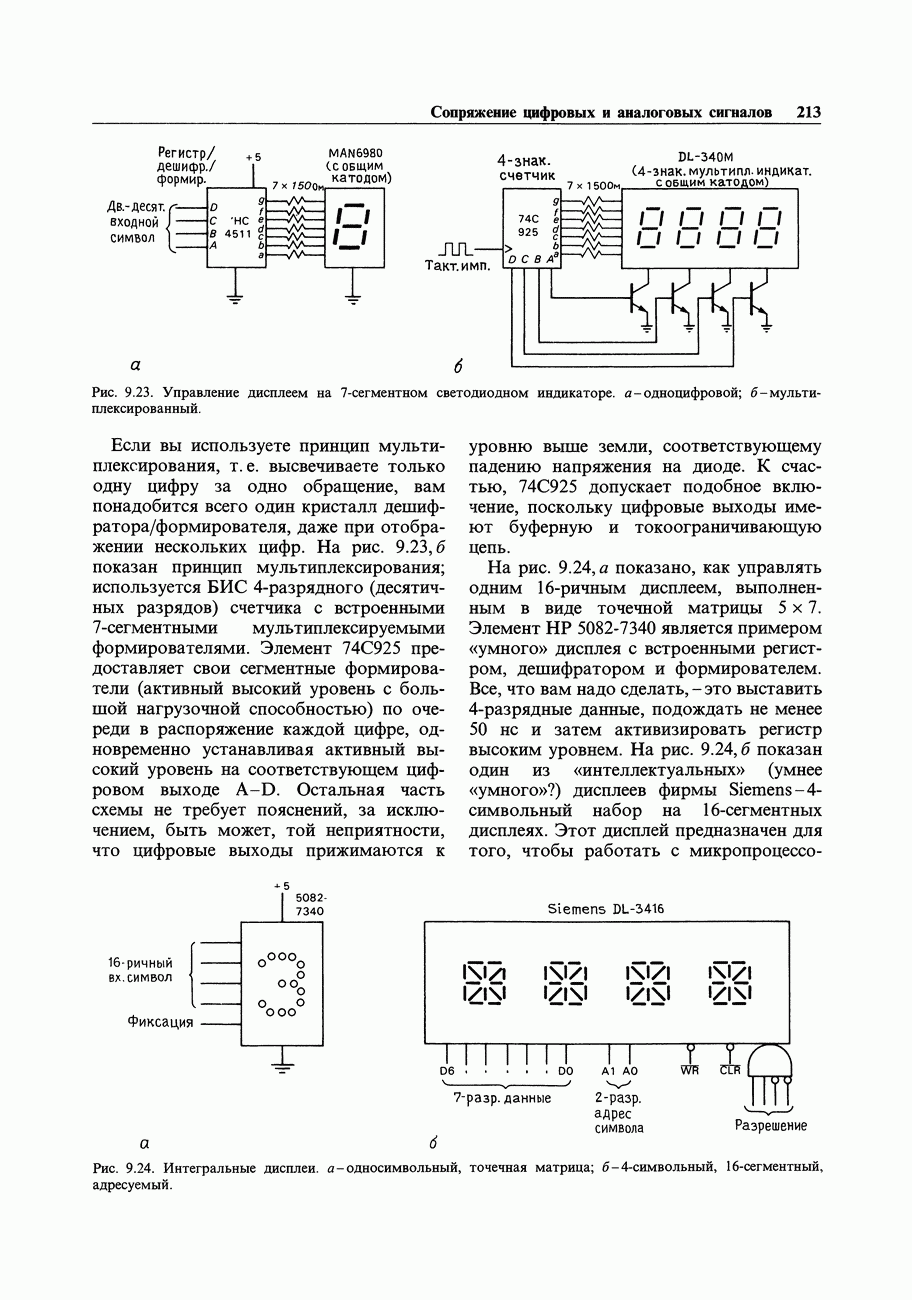
- 8.30. Мультиплексируемый цифровой индикатор на светодиодах
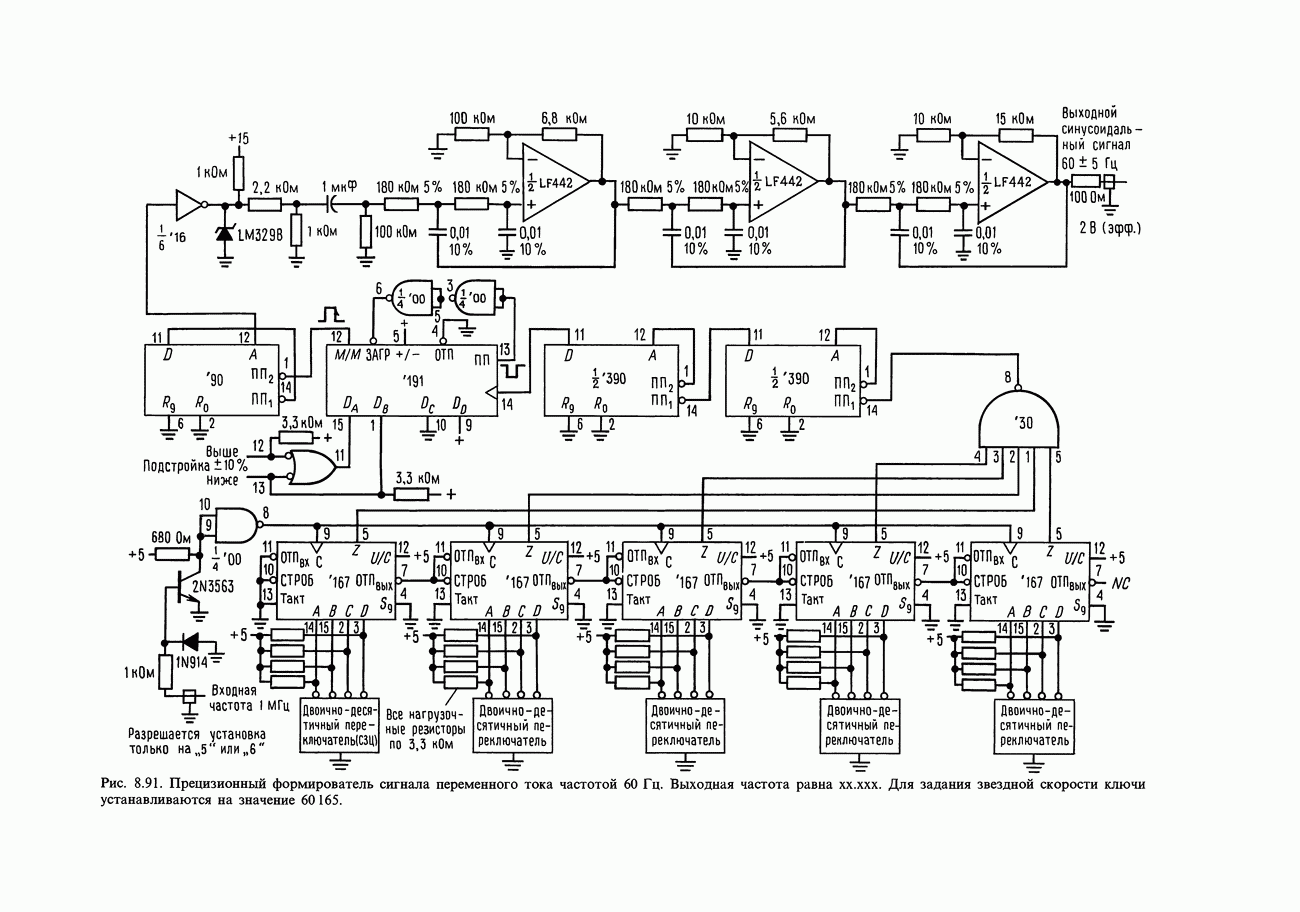
- 8.31. Привод звездного телескопа
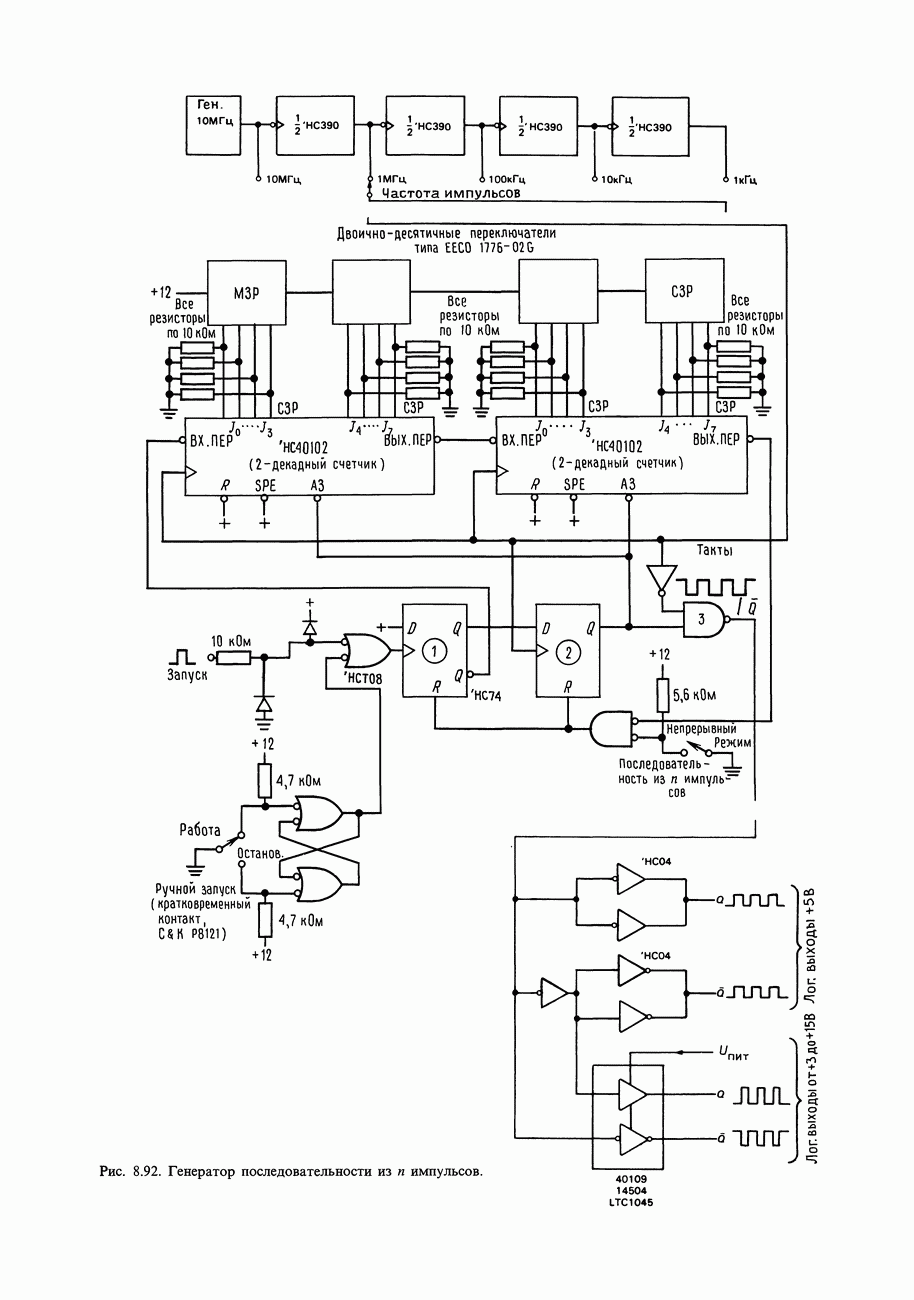
- 8.32. Генератор последовательности из n импульсов
- ПАТОЛОГИЯ В ЛОГИЧЕСКИХ СХЕМАХ
- 8.33. Проблемы статических режимов
- 8.34. Проблемы при переключениях
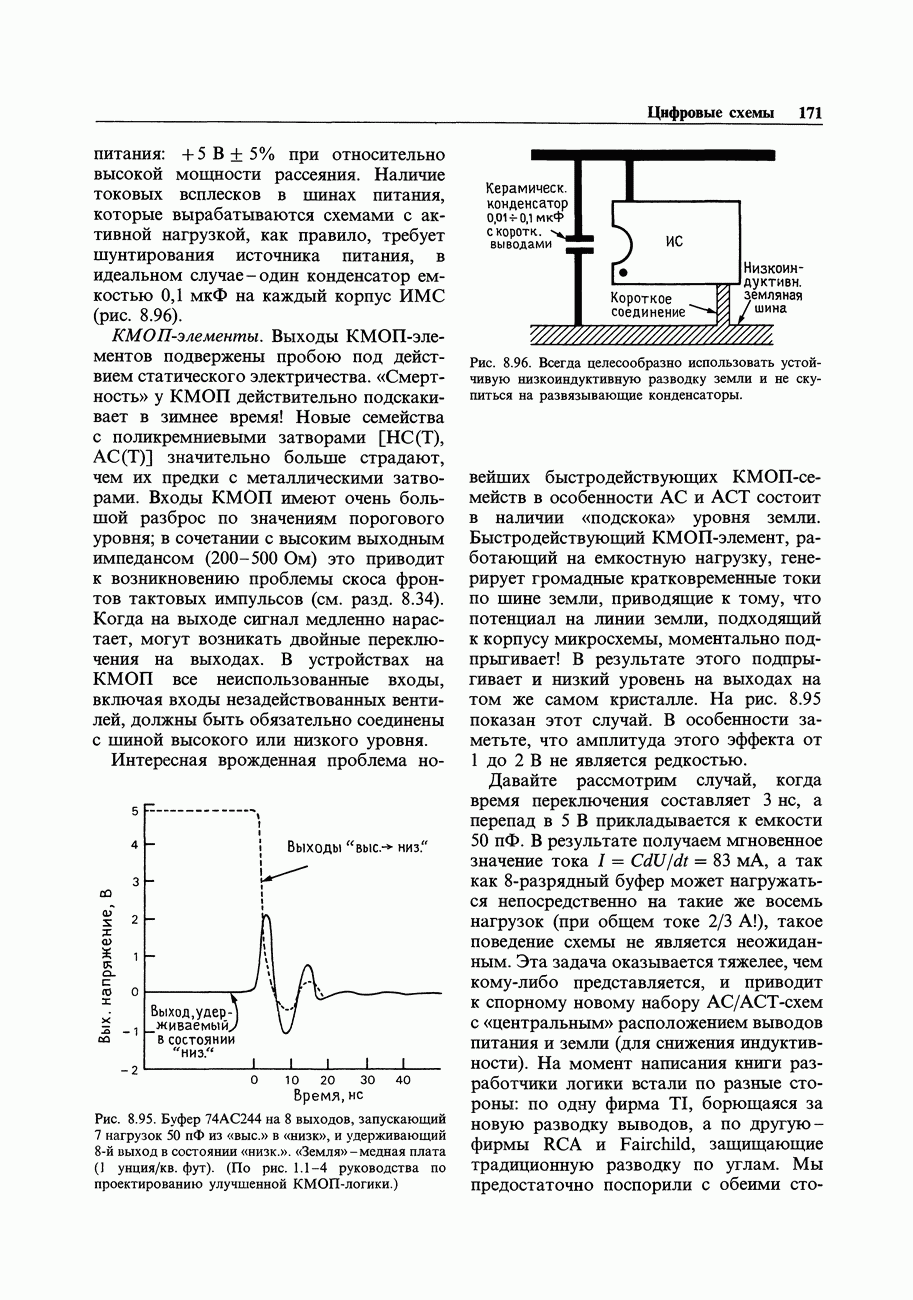
- 8.35. Прирожденные недостатки ТТЛ и КМОП
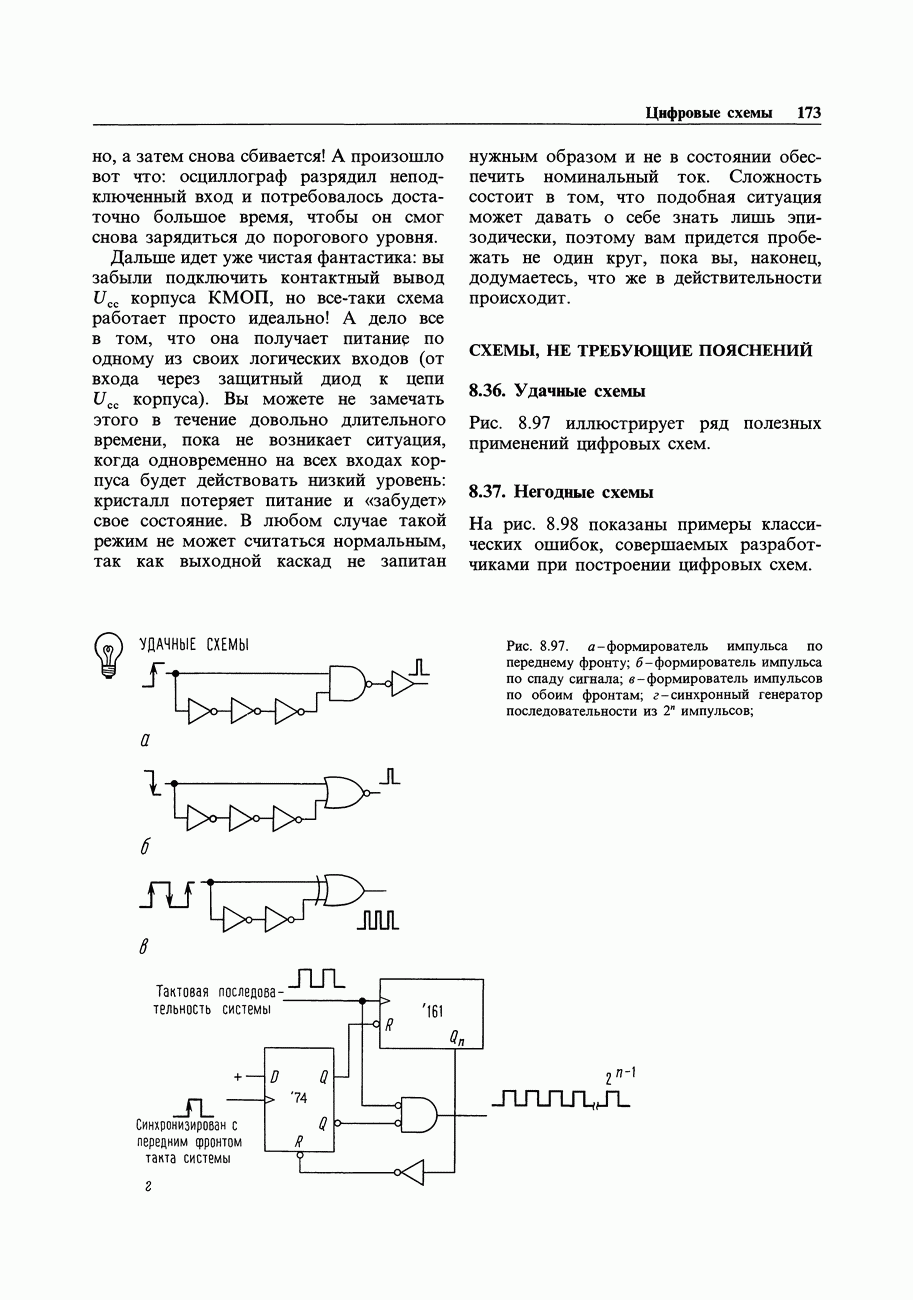
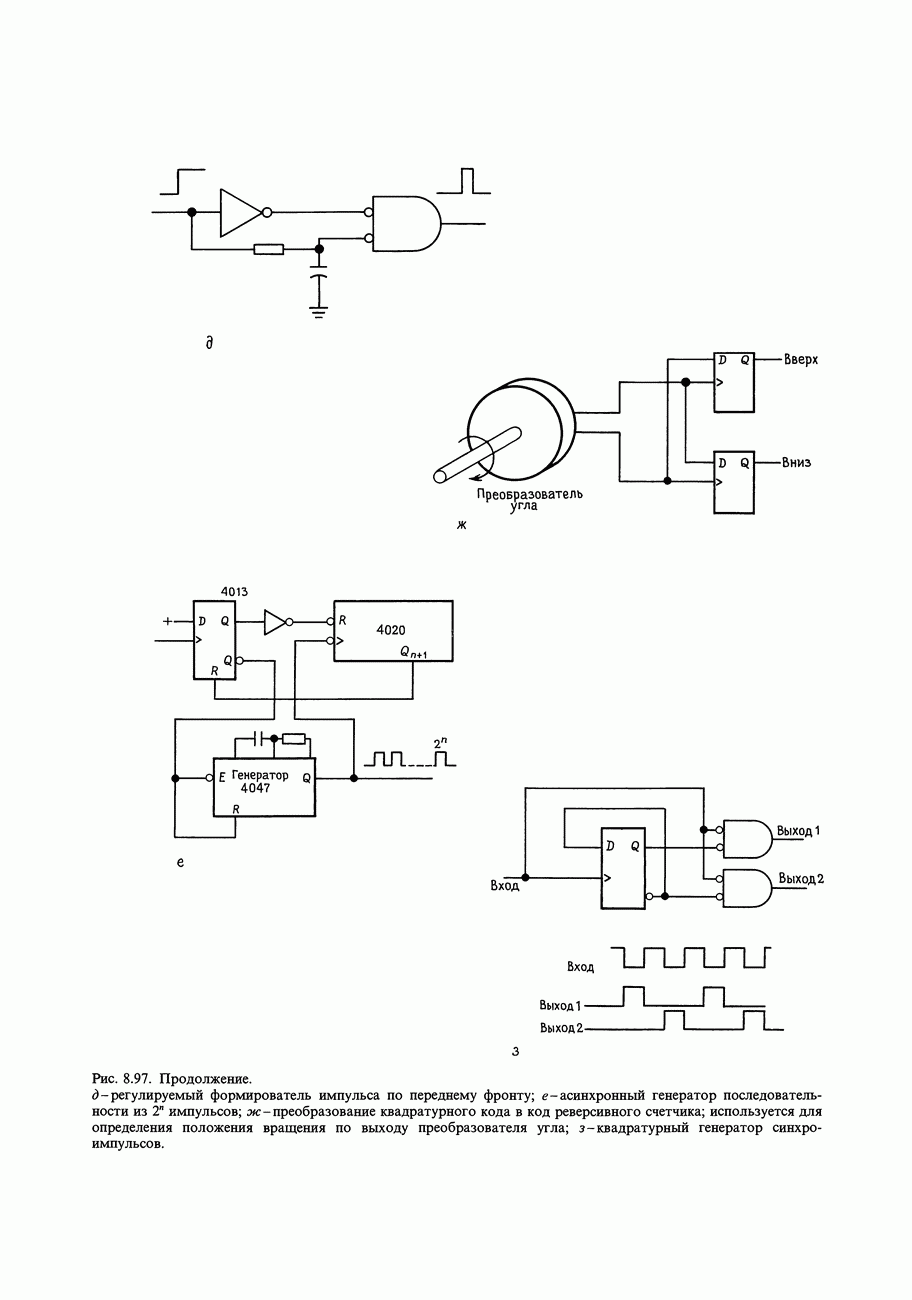
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
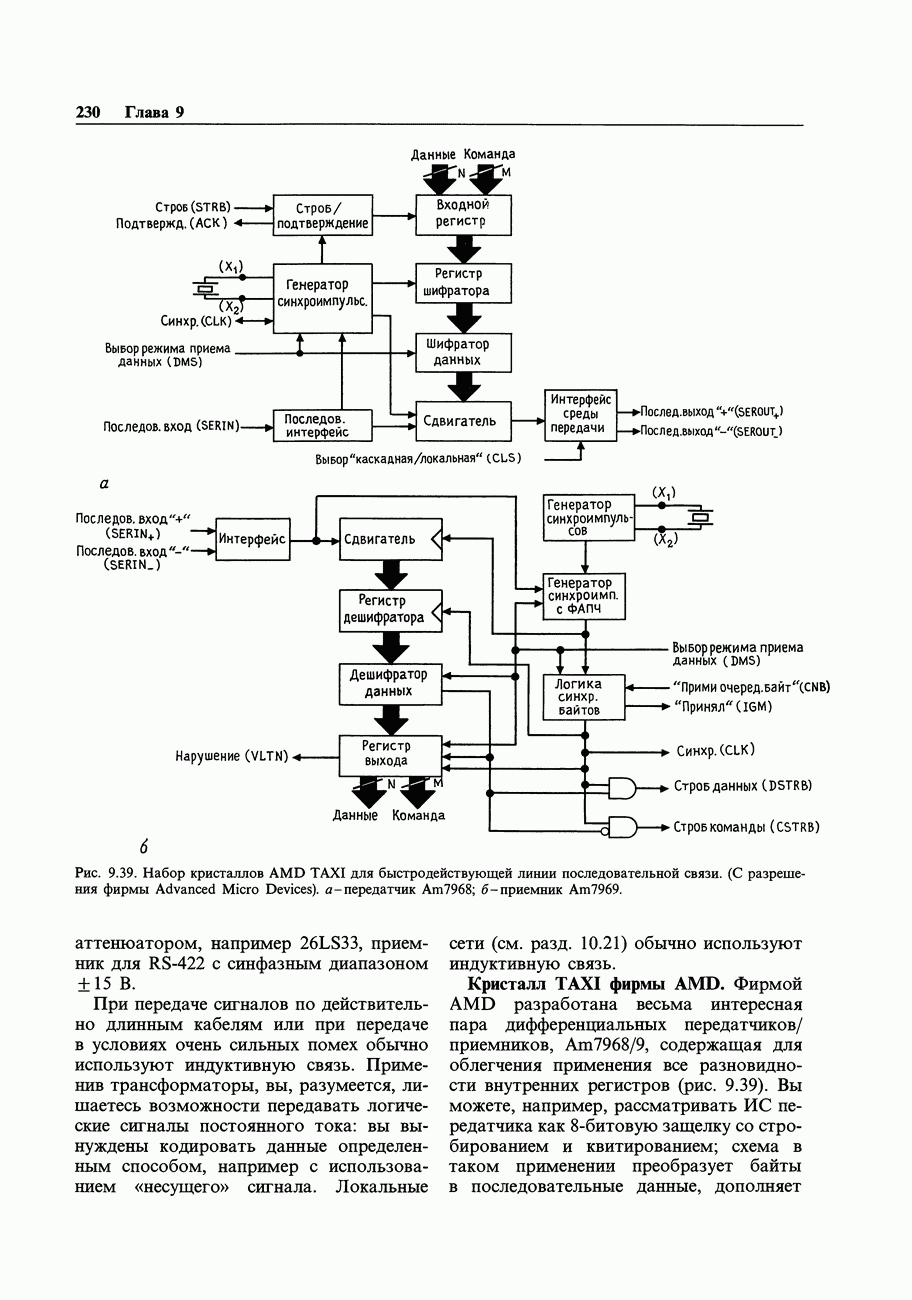
- ГЛАВА 9. СОПРЯЖЕНИЕ ЦИФРОВЫХ И АНАЛОГОВЫХ СИГНАЛОВ
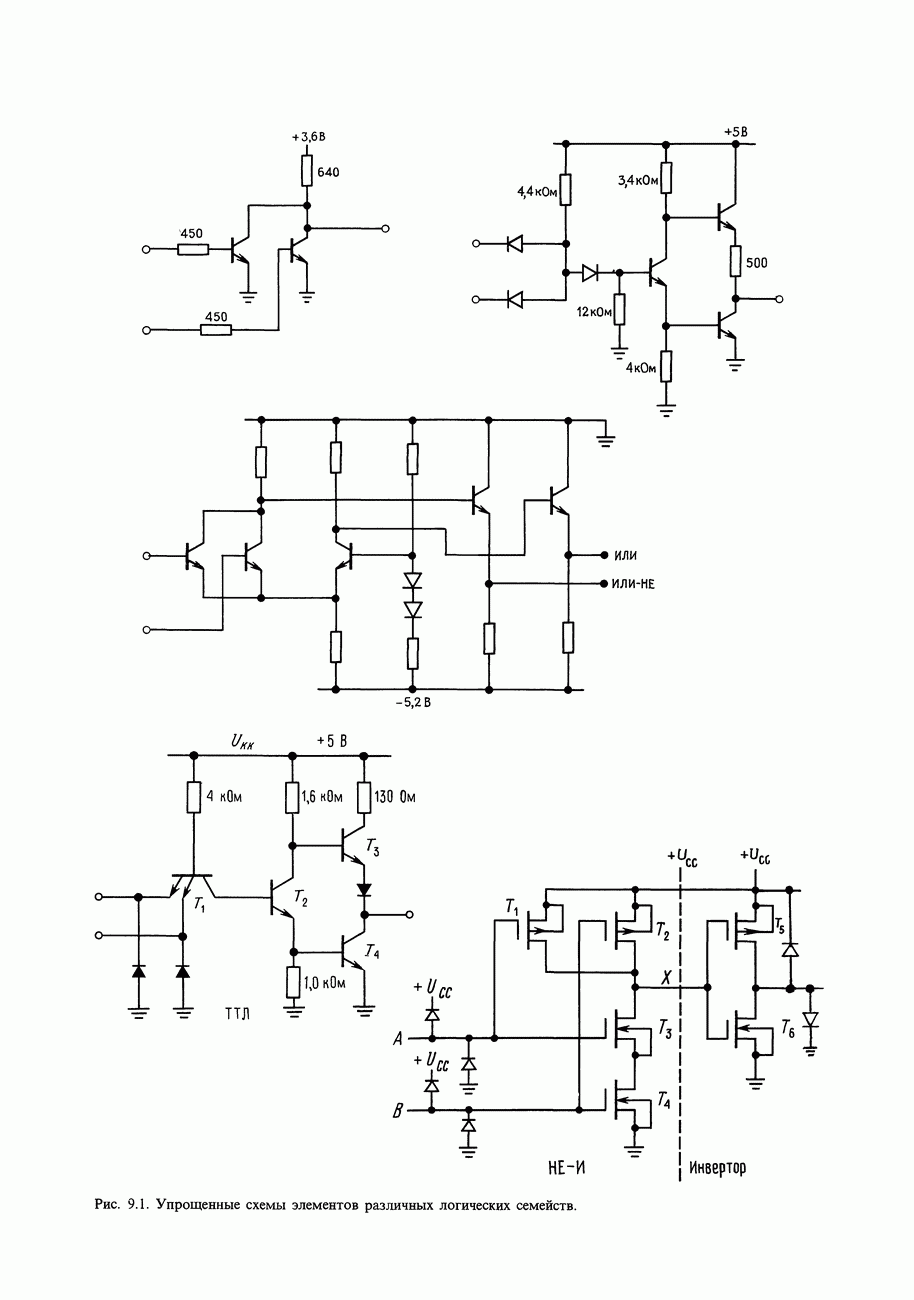
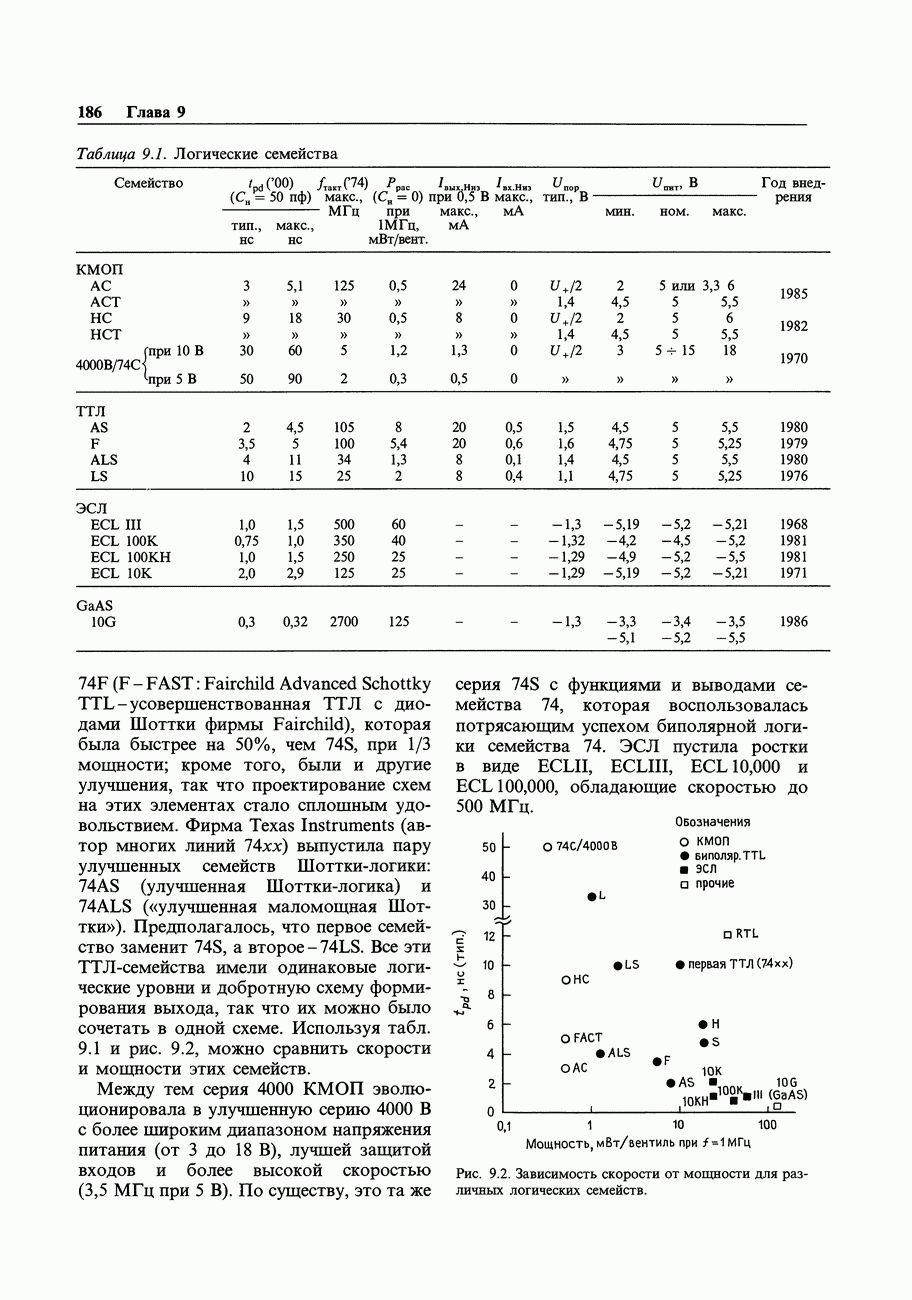
- 9.01. Хронология логических семейств
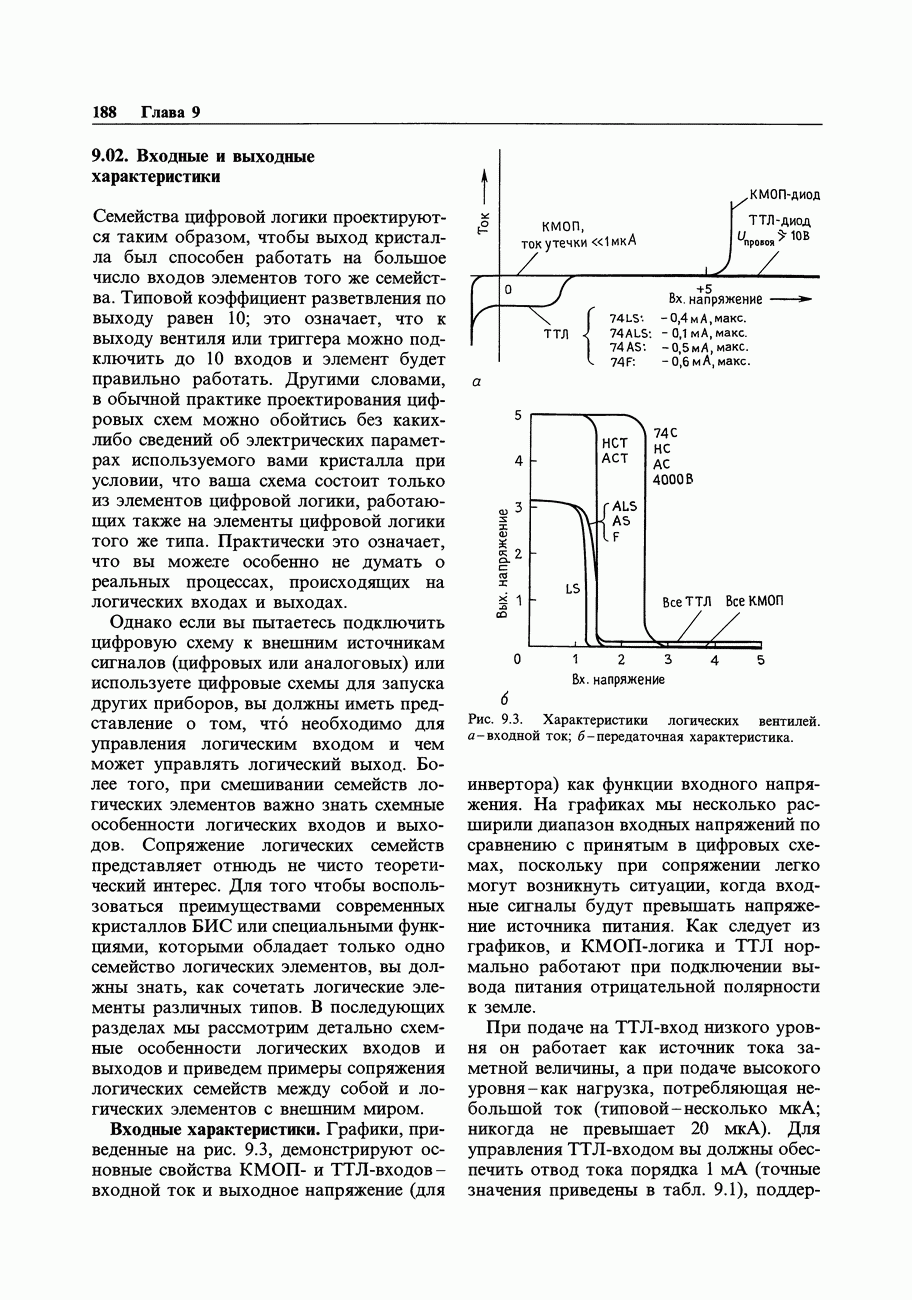
- 9.02. Входные и выходные характеристики
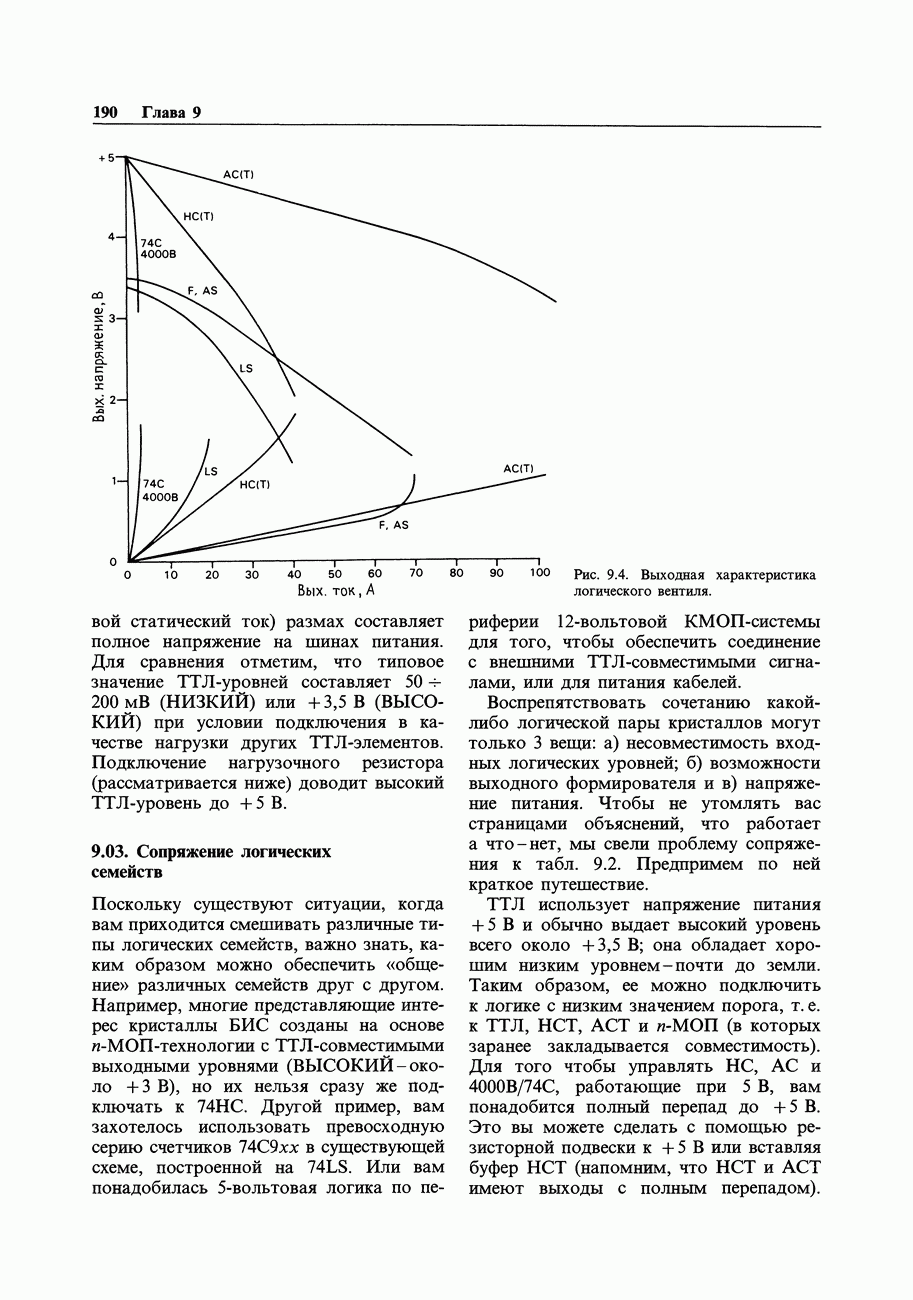
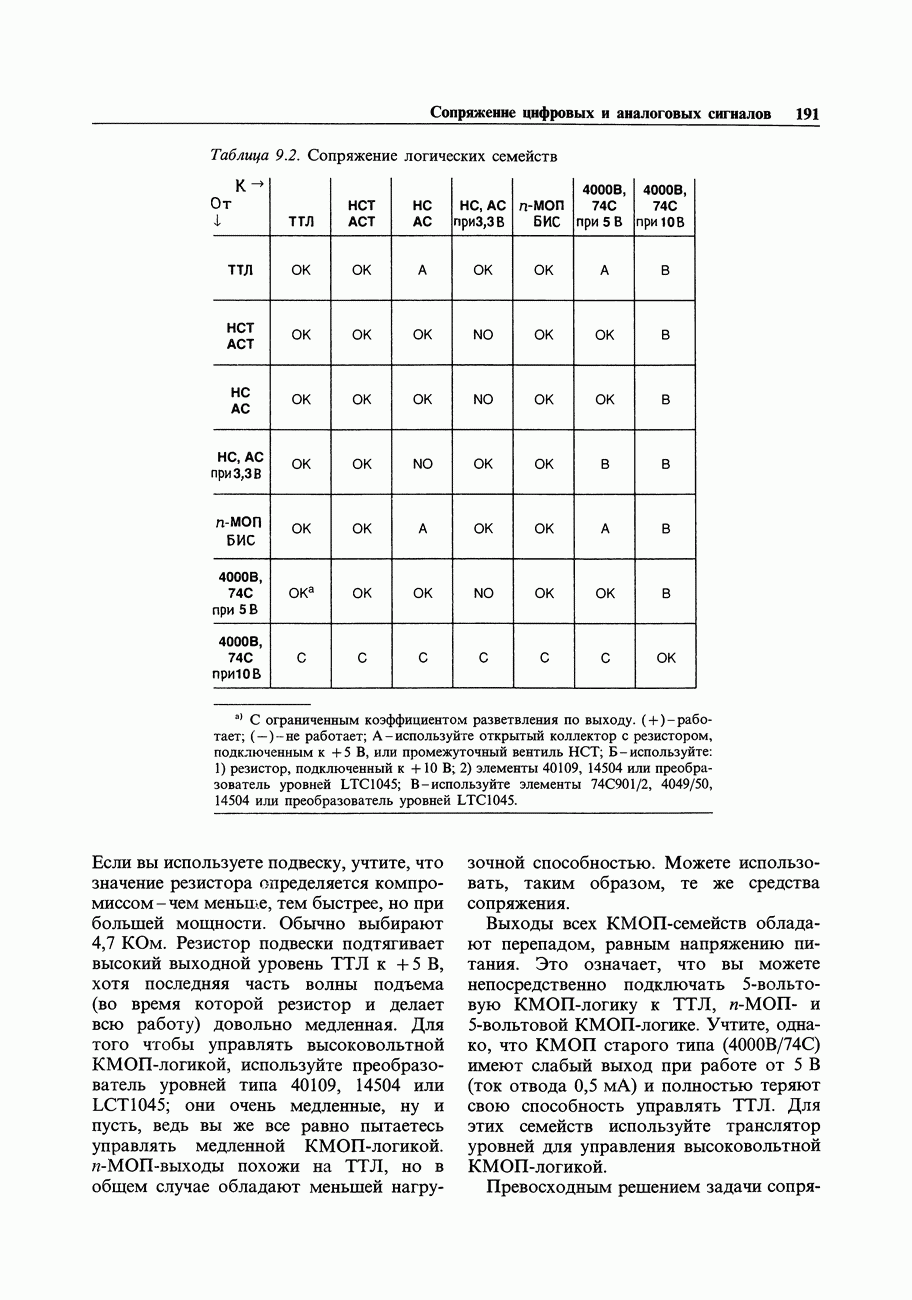
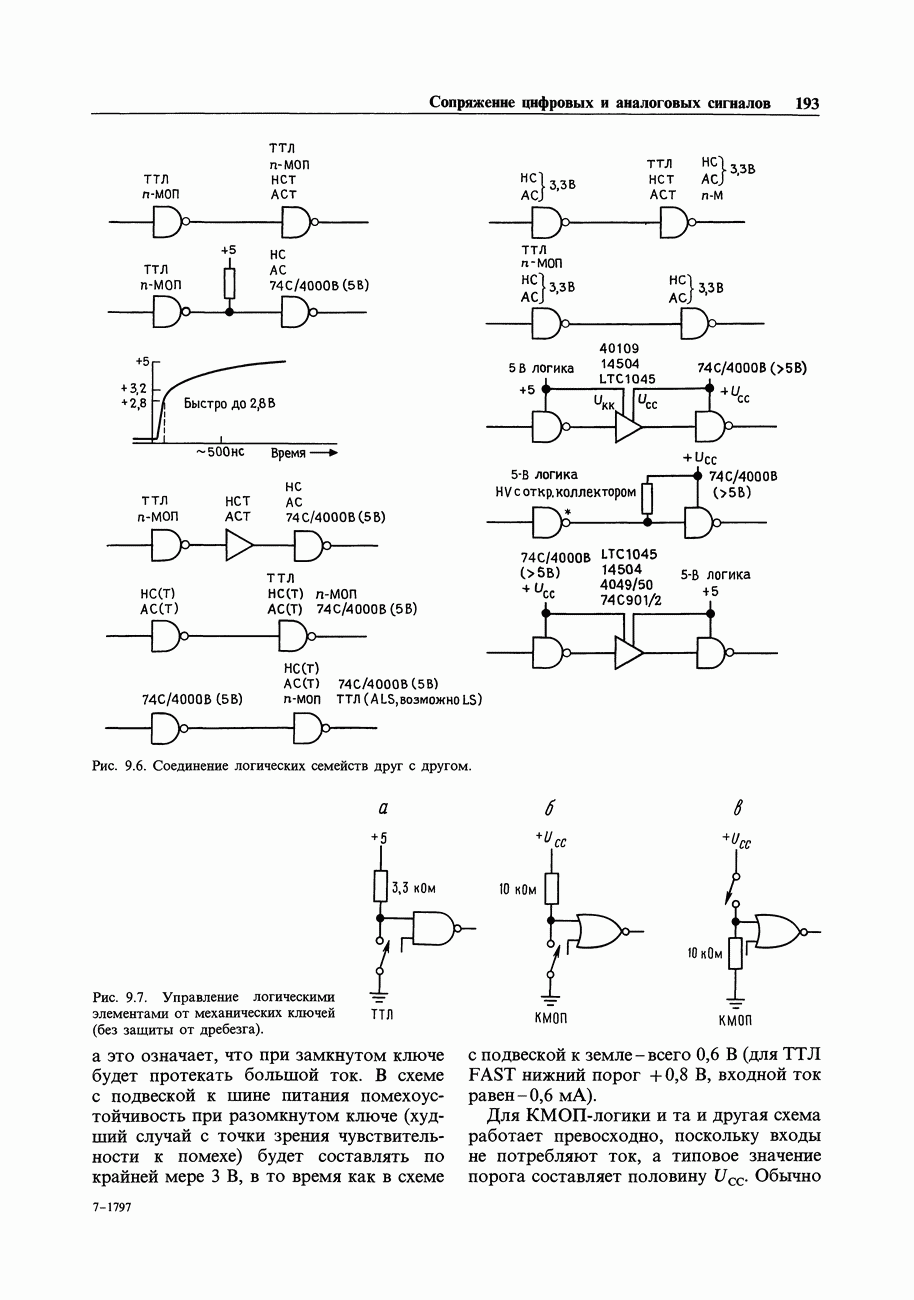
- 9.03. Сопряжение логических семейств
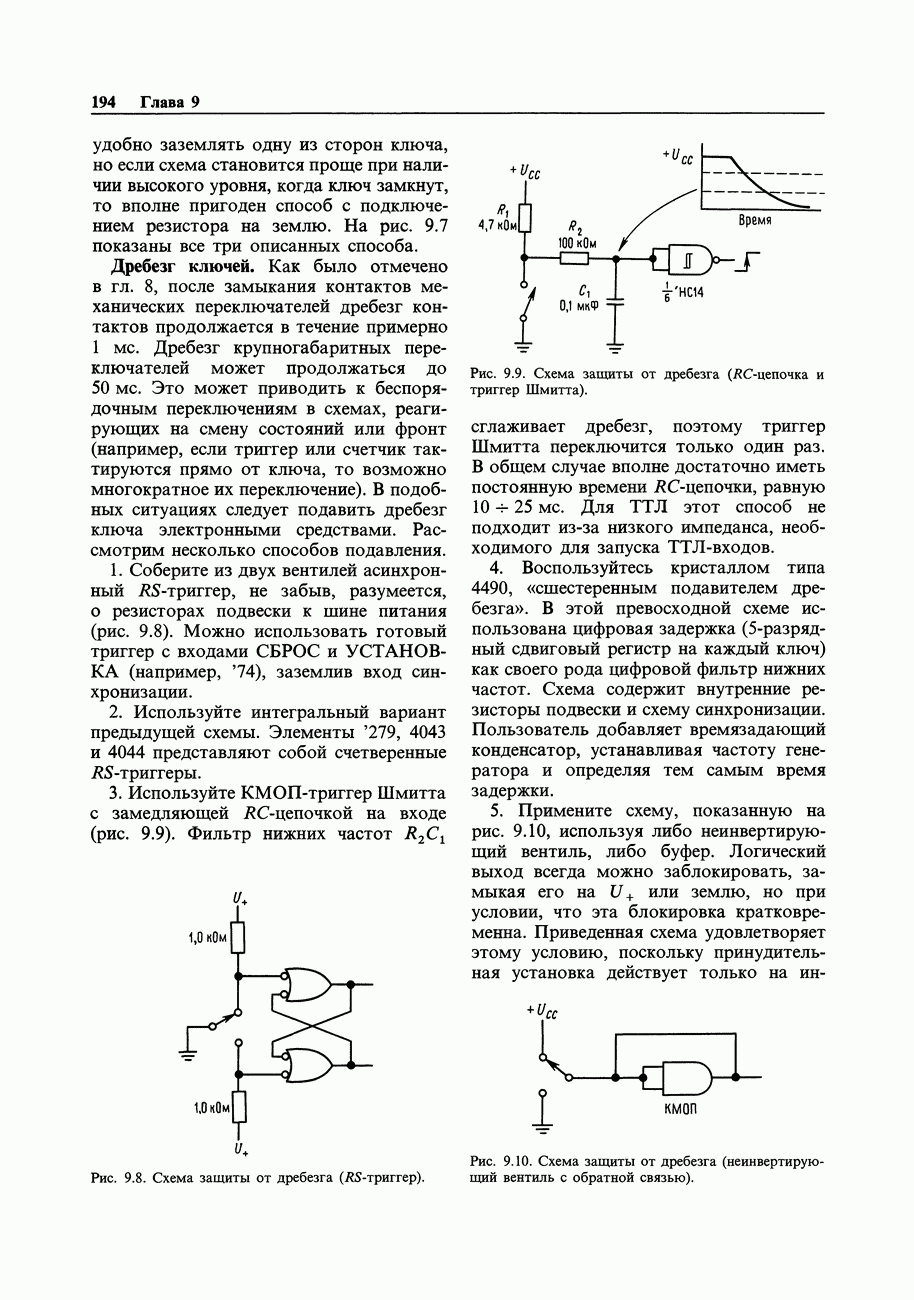
- 9.04. Управление КМОП-и ТТЛ-входами
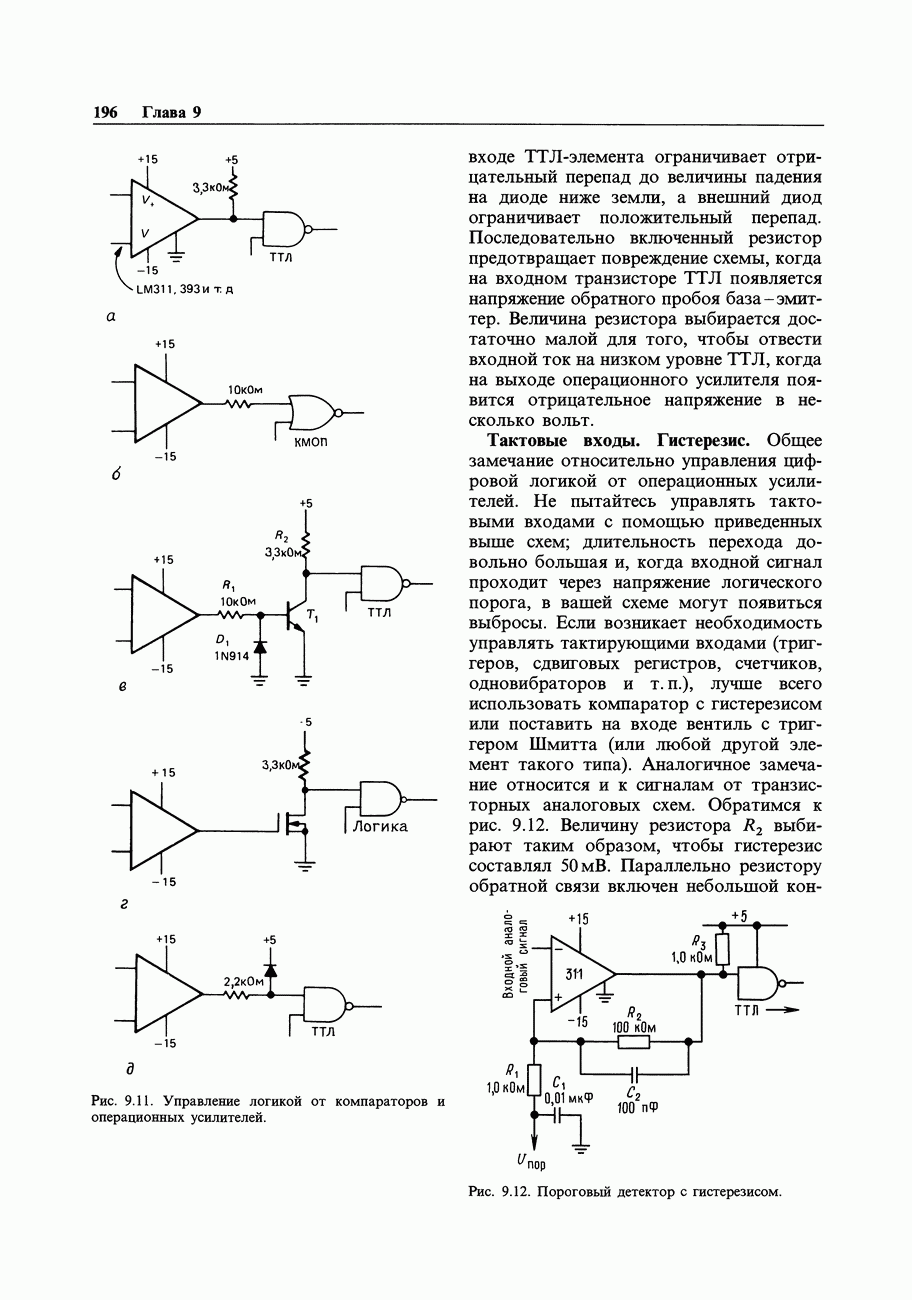
- 9.05. Управление цифровой логикой от компараторов и операционных усилителей
- 9.06. Некоторые замечания, касающиеся логических входов
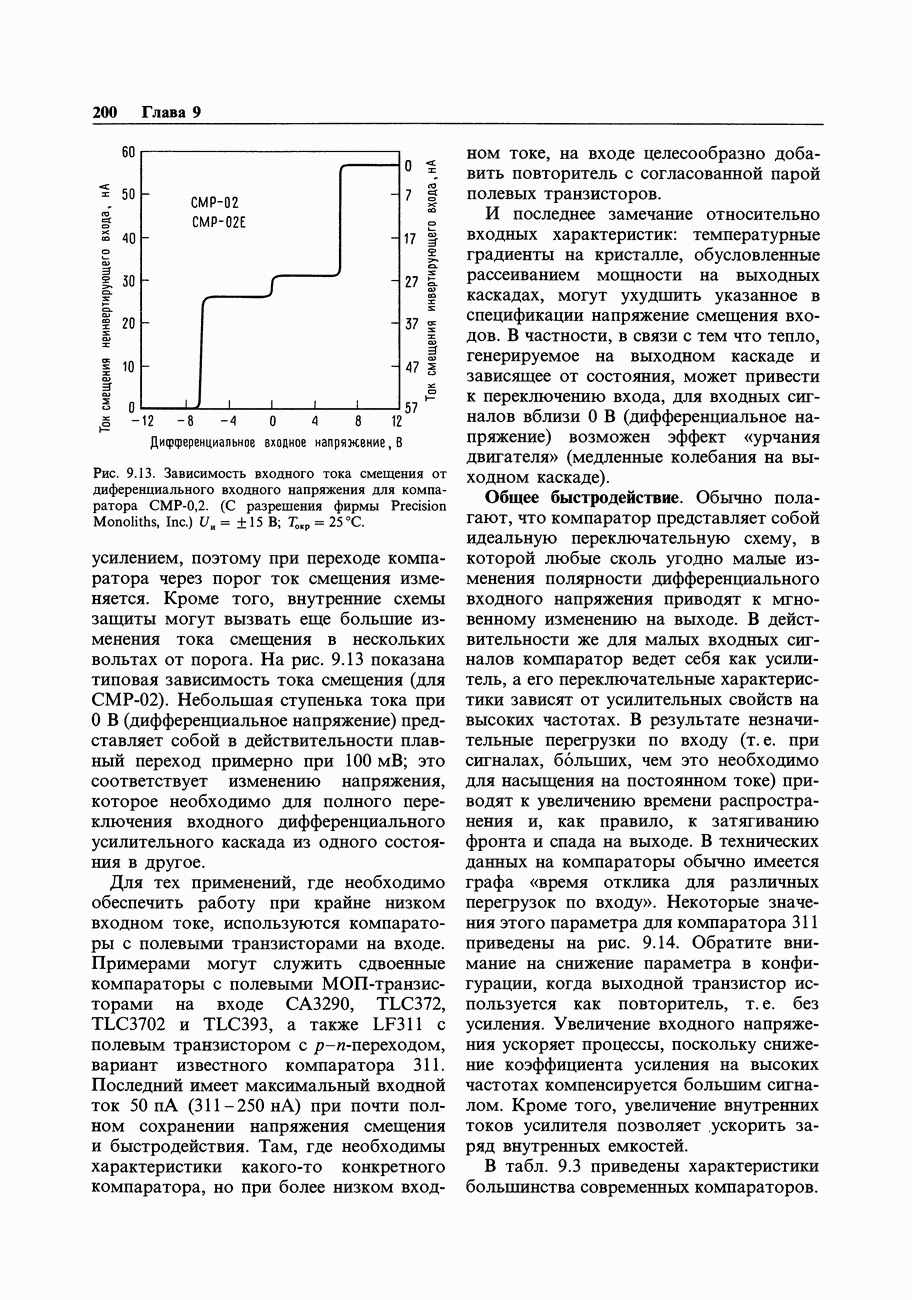
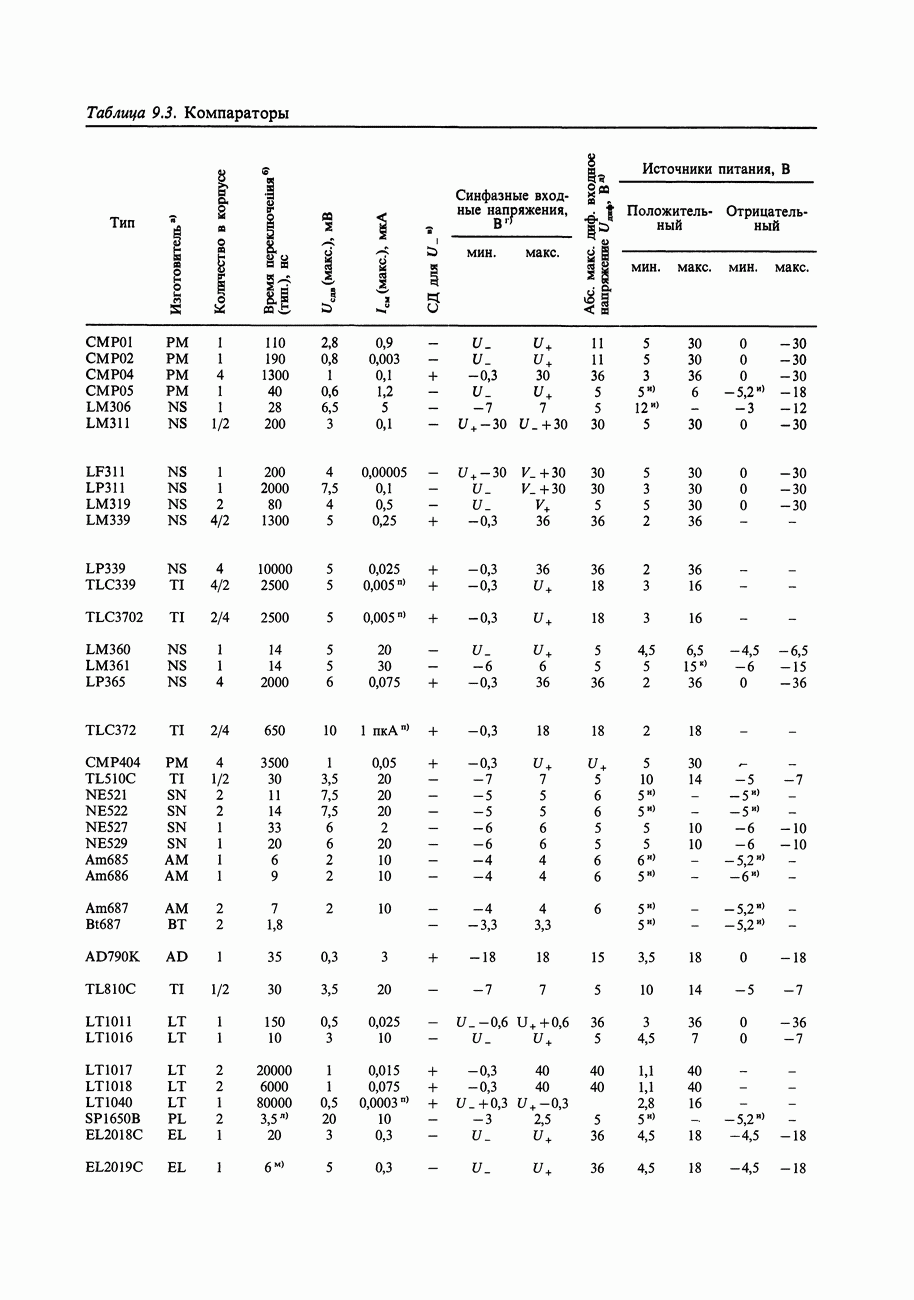
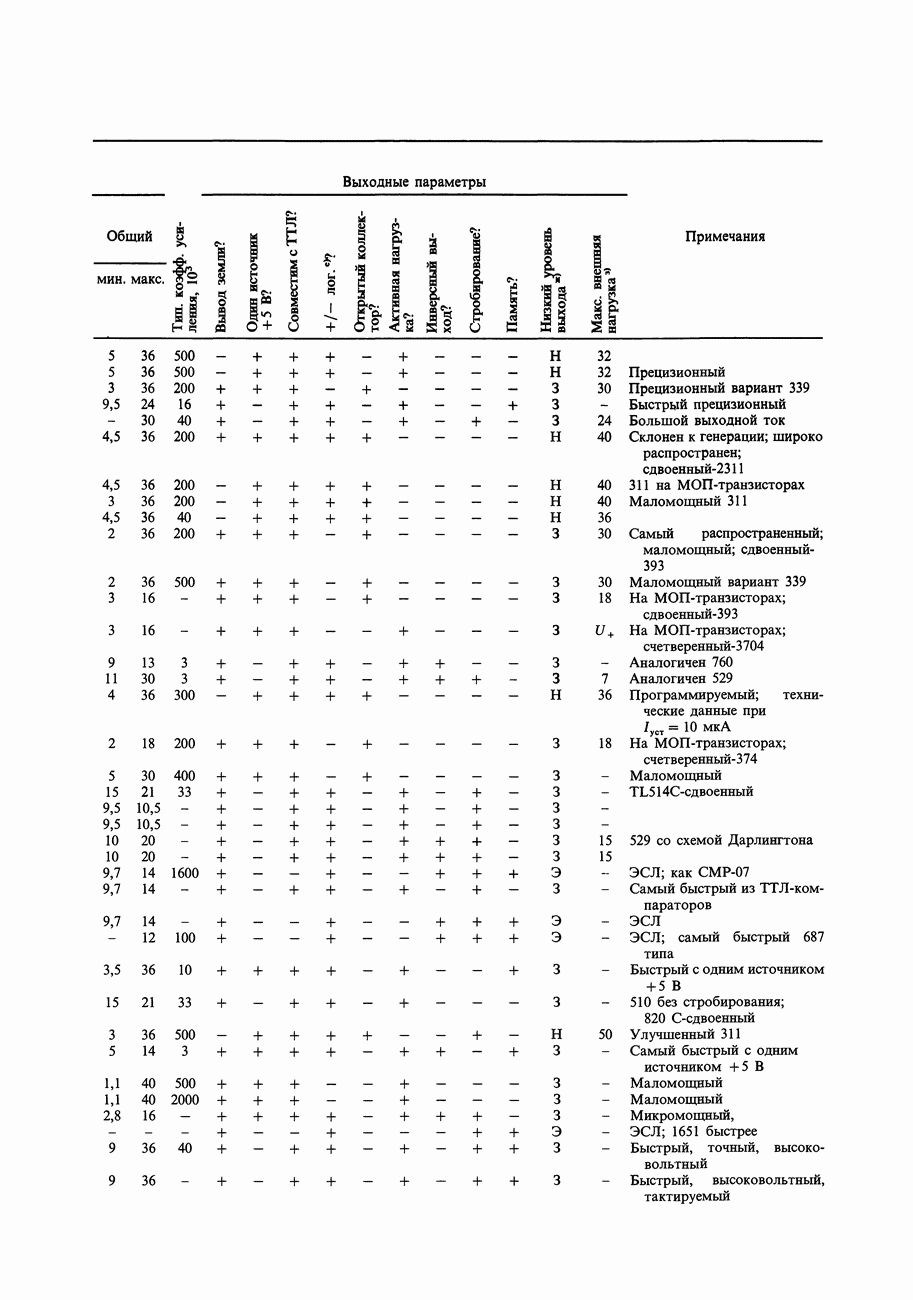
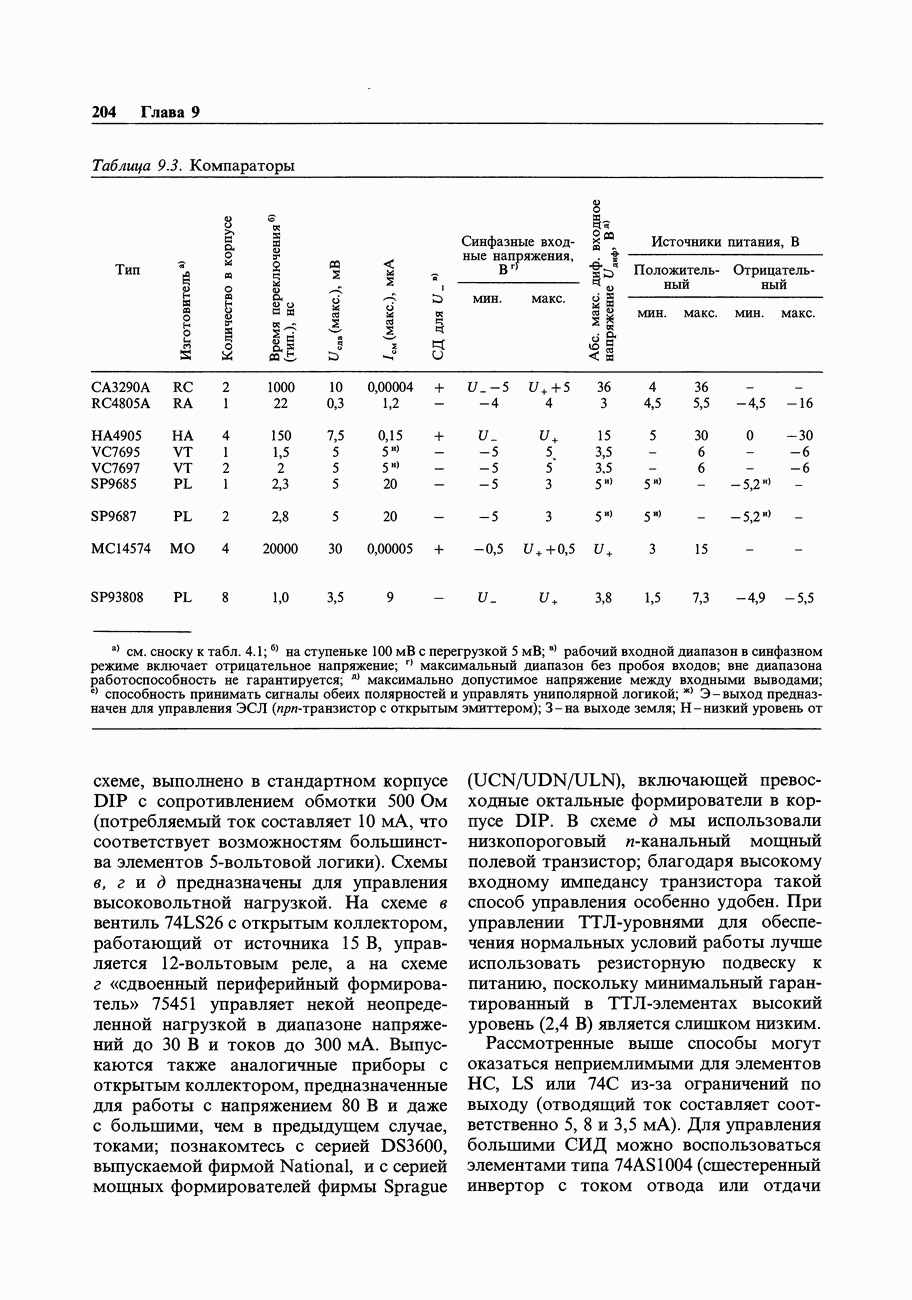
- 9.07. Компараторы
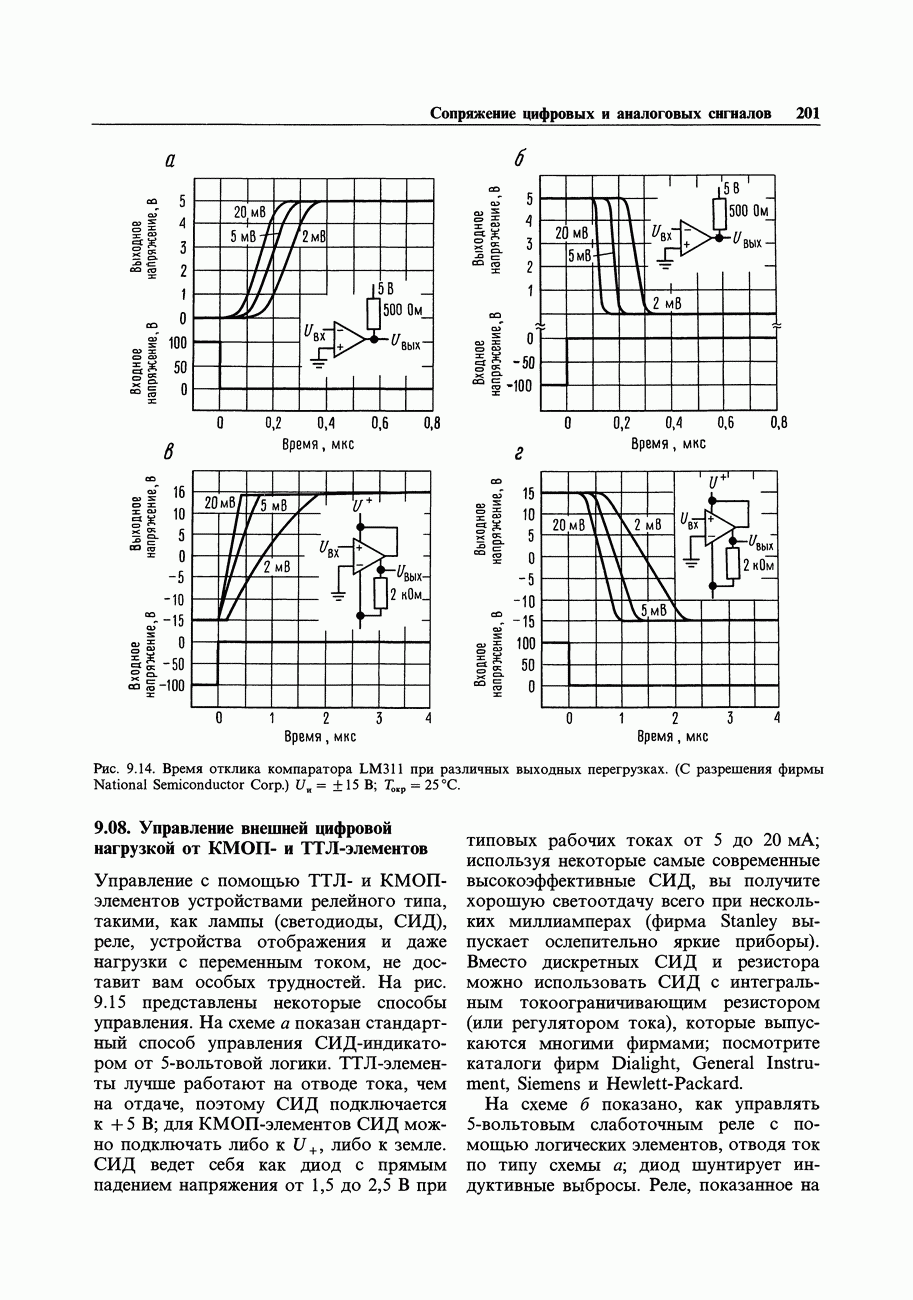
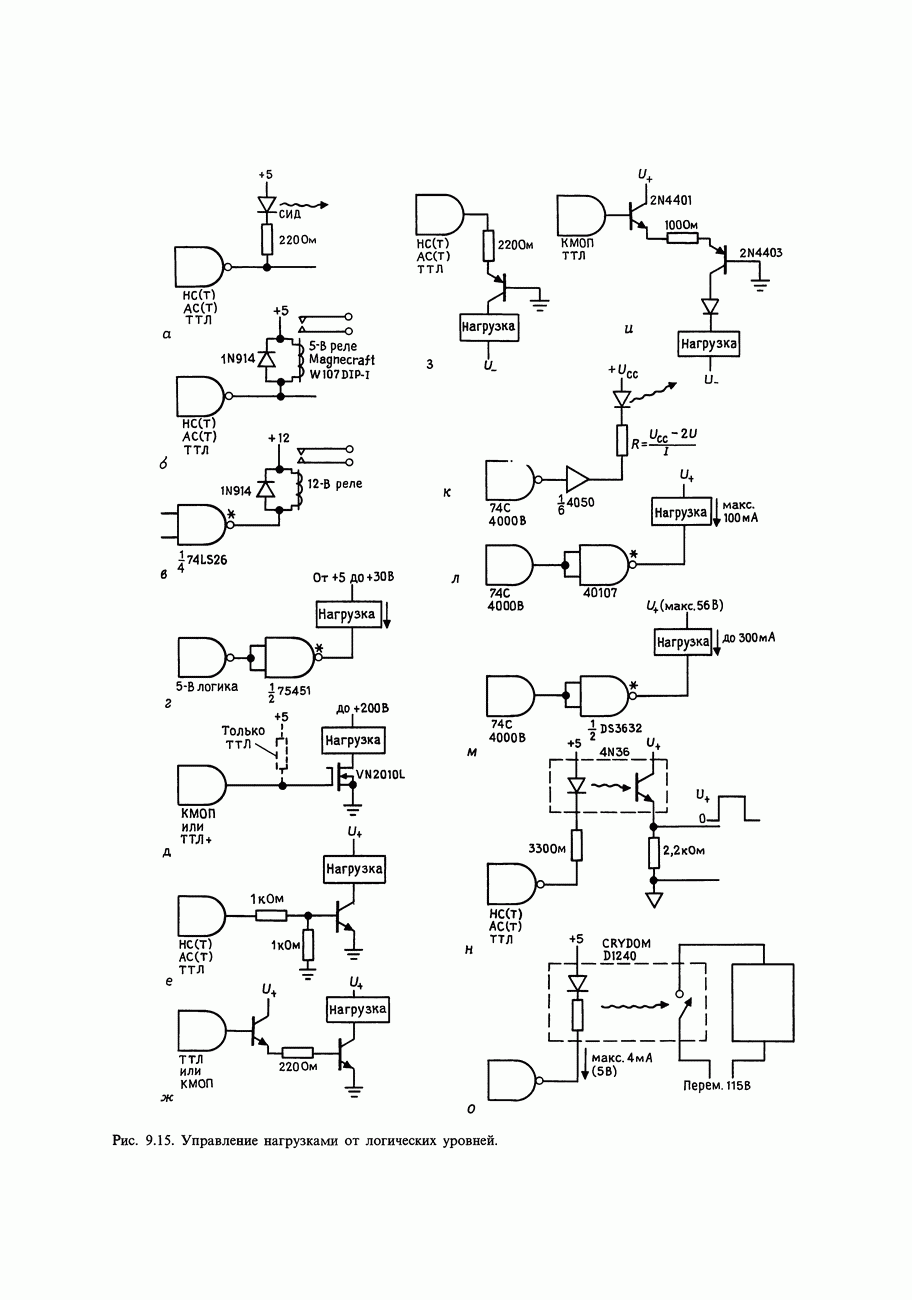
- 9.08. Управление внешней цифровой нагрузкой от КМОП- и ТТЛ-элементов
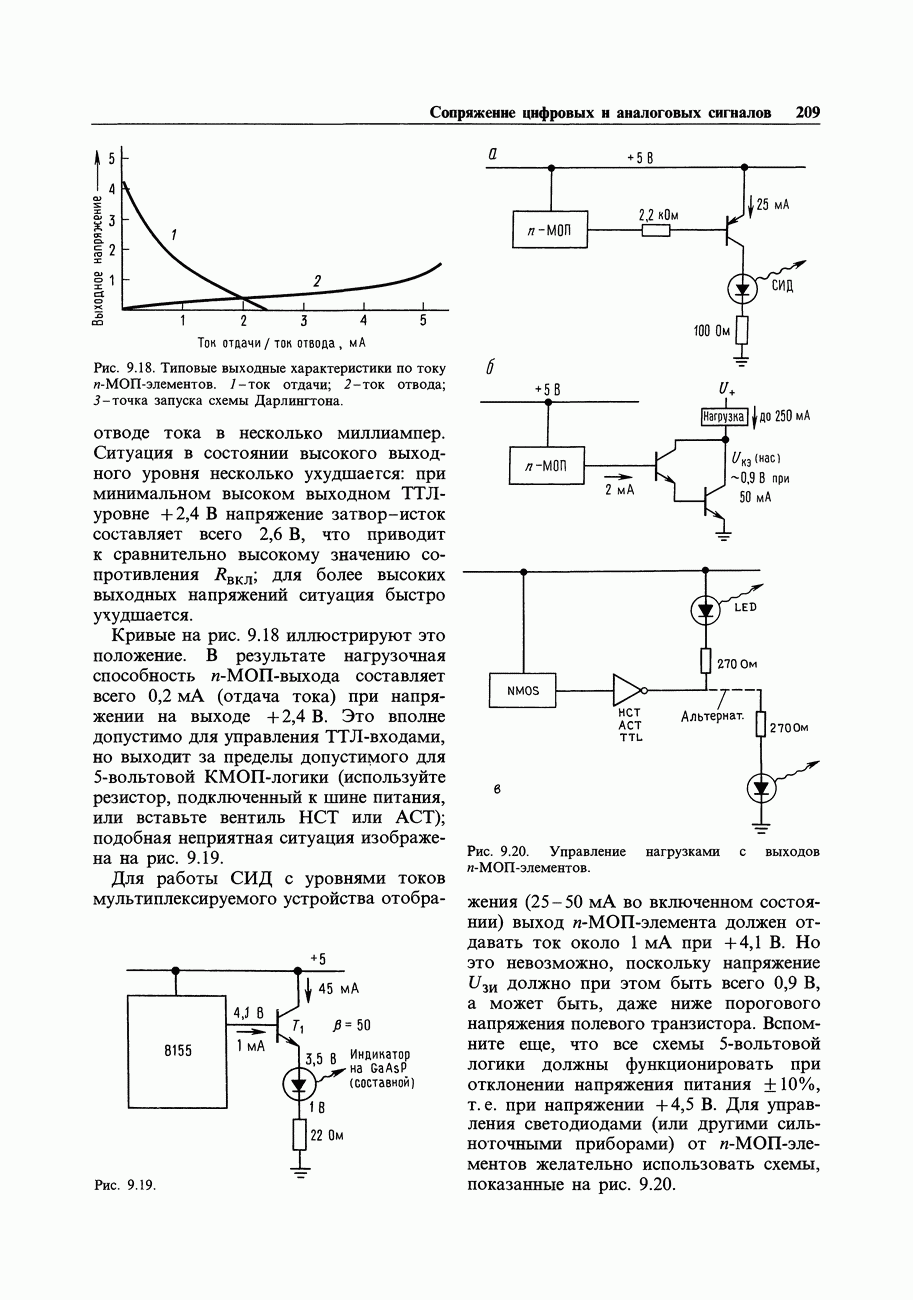
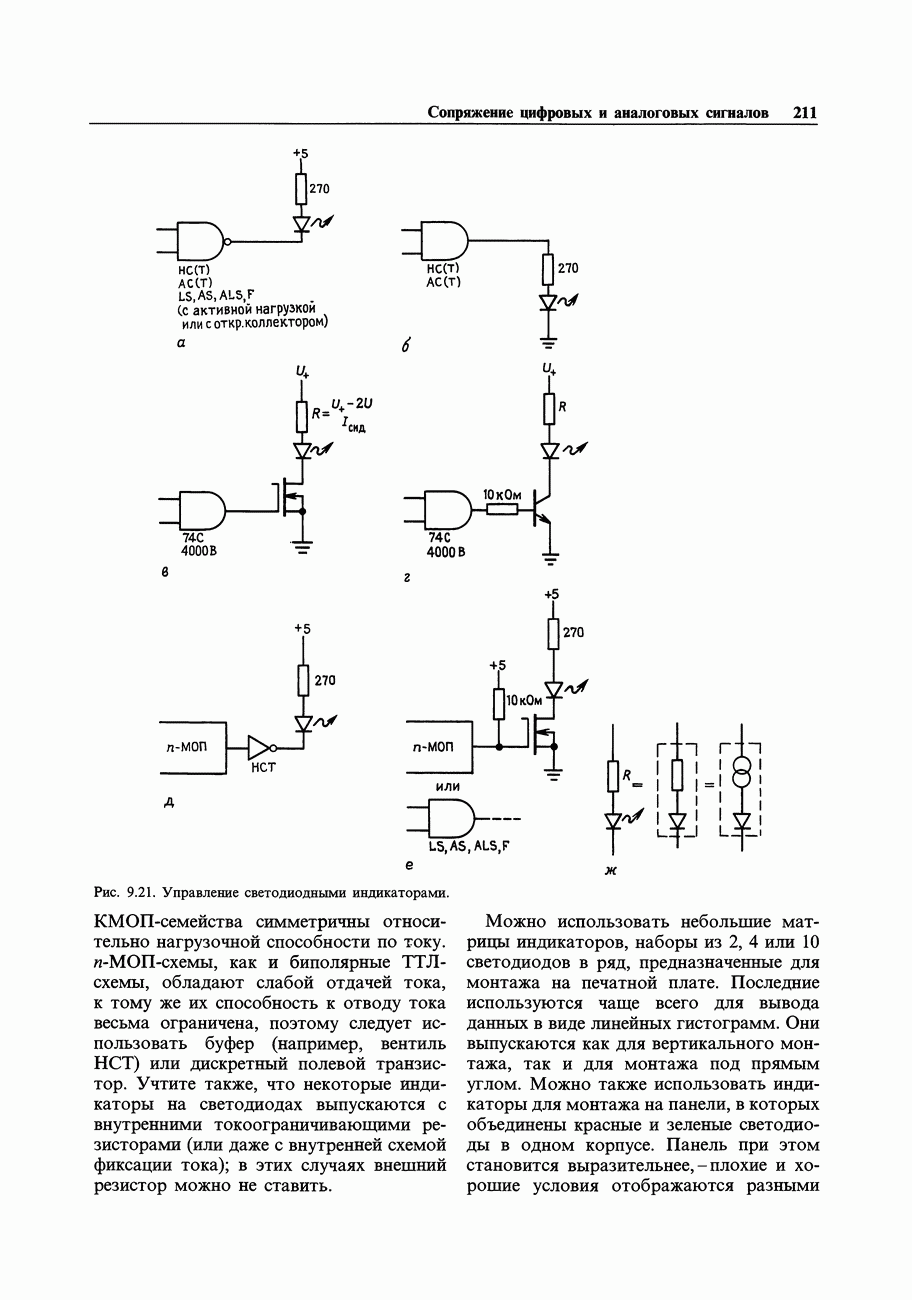
- 9.09. Сопряжение n-МОП БИС
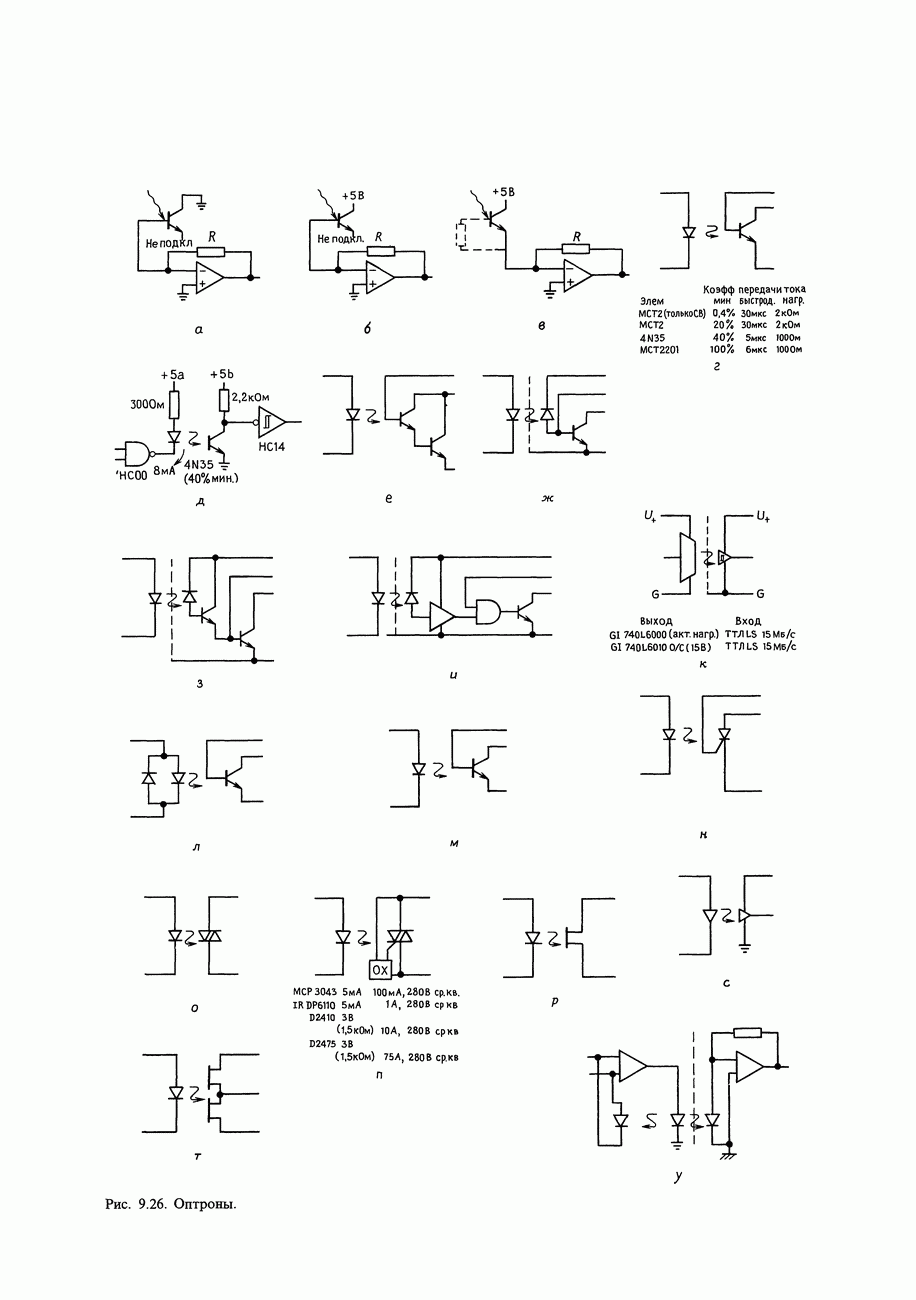
- 9.10. Оптоэлектроника
- ЦИФРОВЫЕ СИГНАЛЫ И ДЛИННЫЕ ЛИНИИ
- 9.11. Внутриплатные соединения
- 9.12. Межплатные соединения
- 9.13. Шины данных
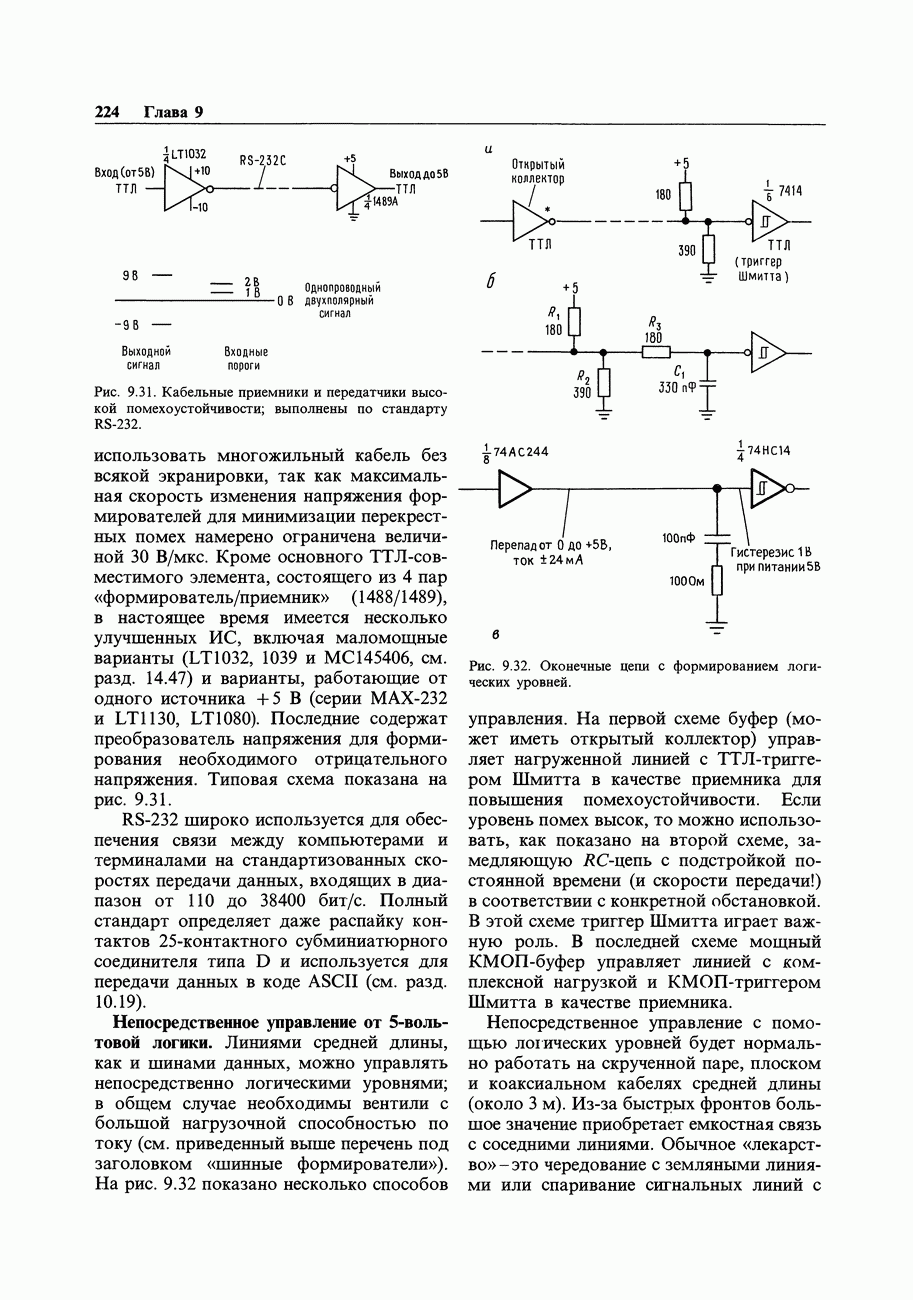
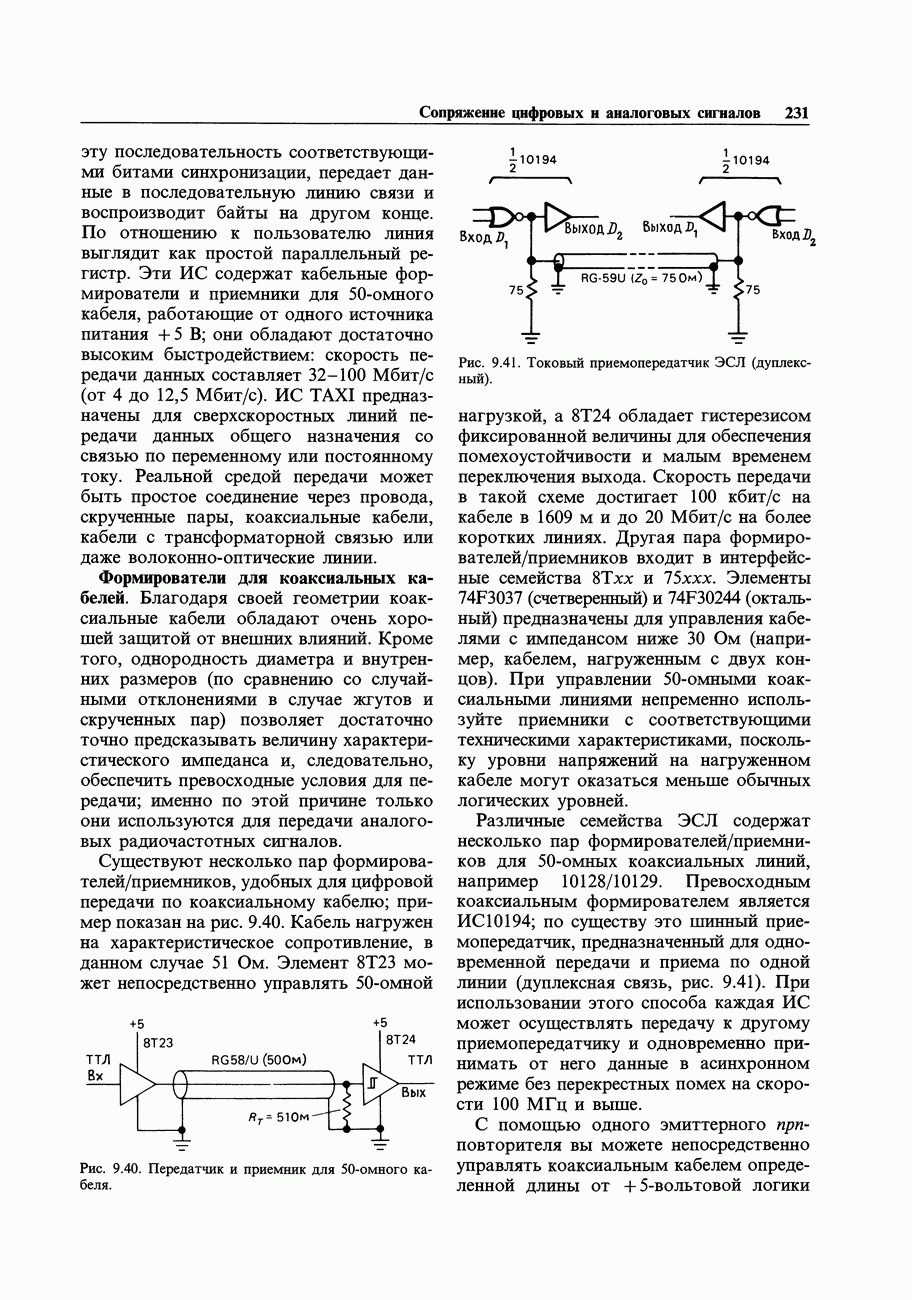
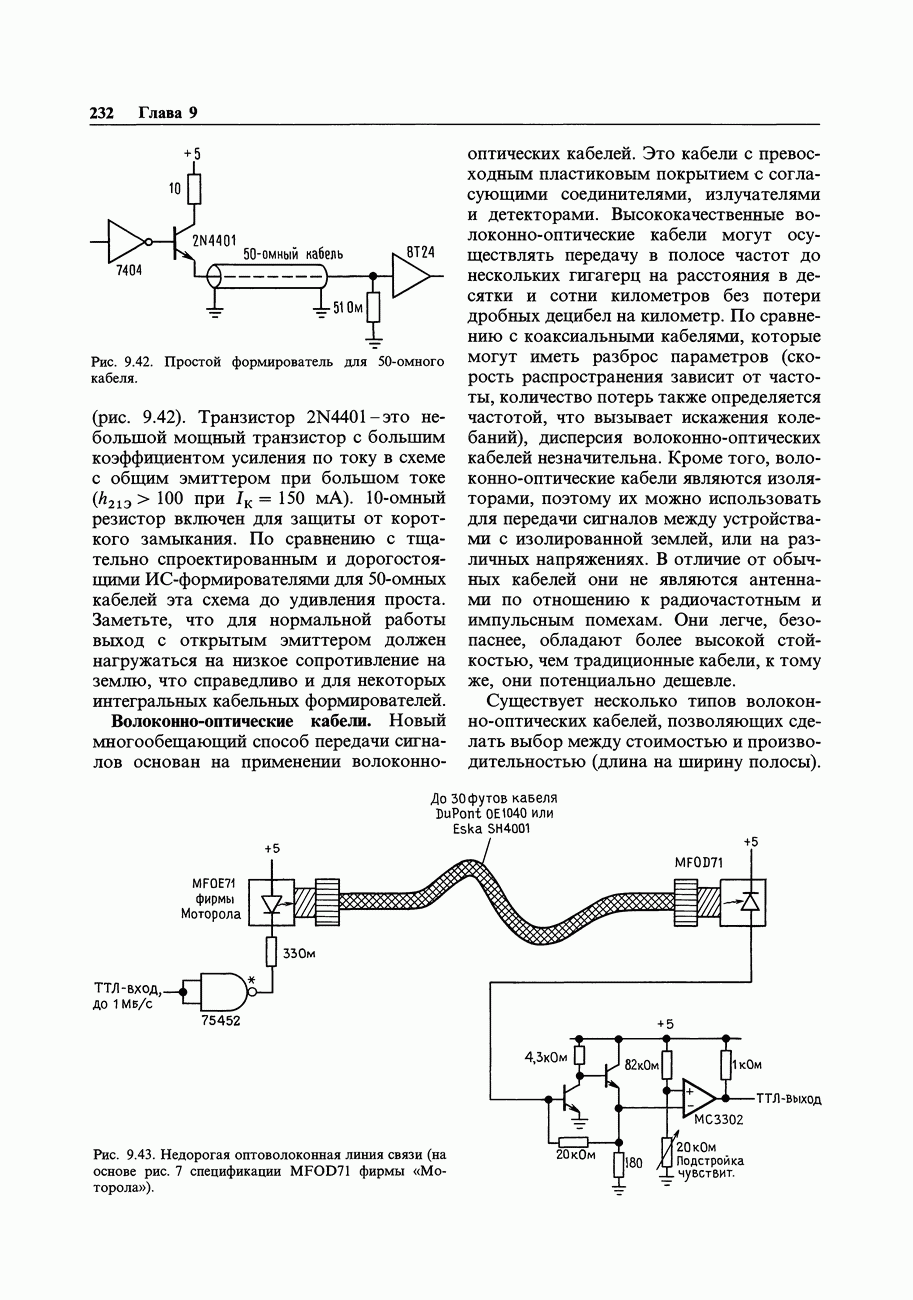
- 9.14. Кабельные связи
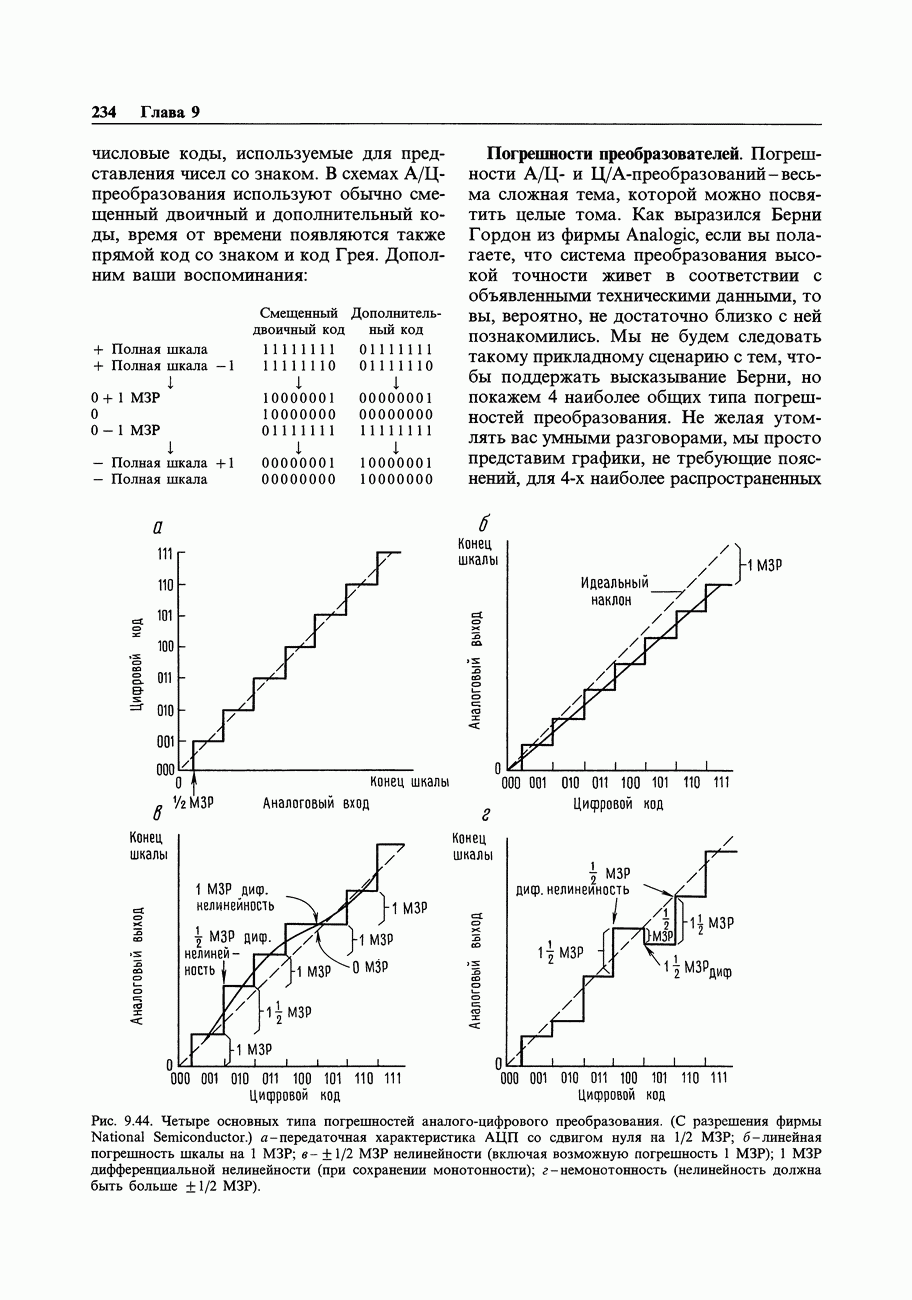
- АНАЛОГО-ЦИФРОВОЕ ПРЕОБРАЗОВАНИЕ
- 9.15. Введение в аналого-цифровое преобразование
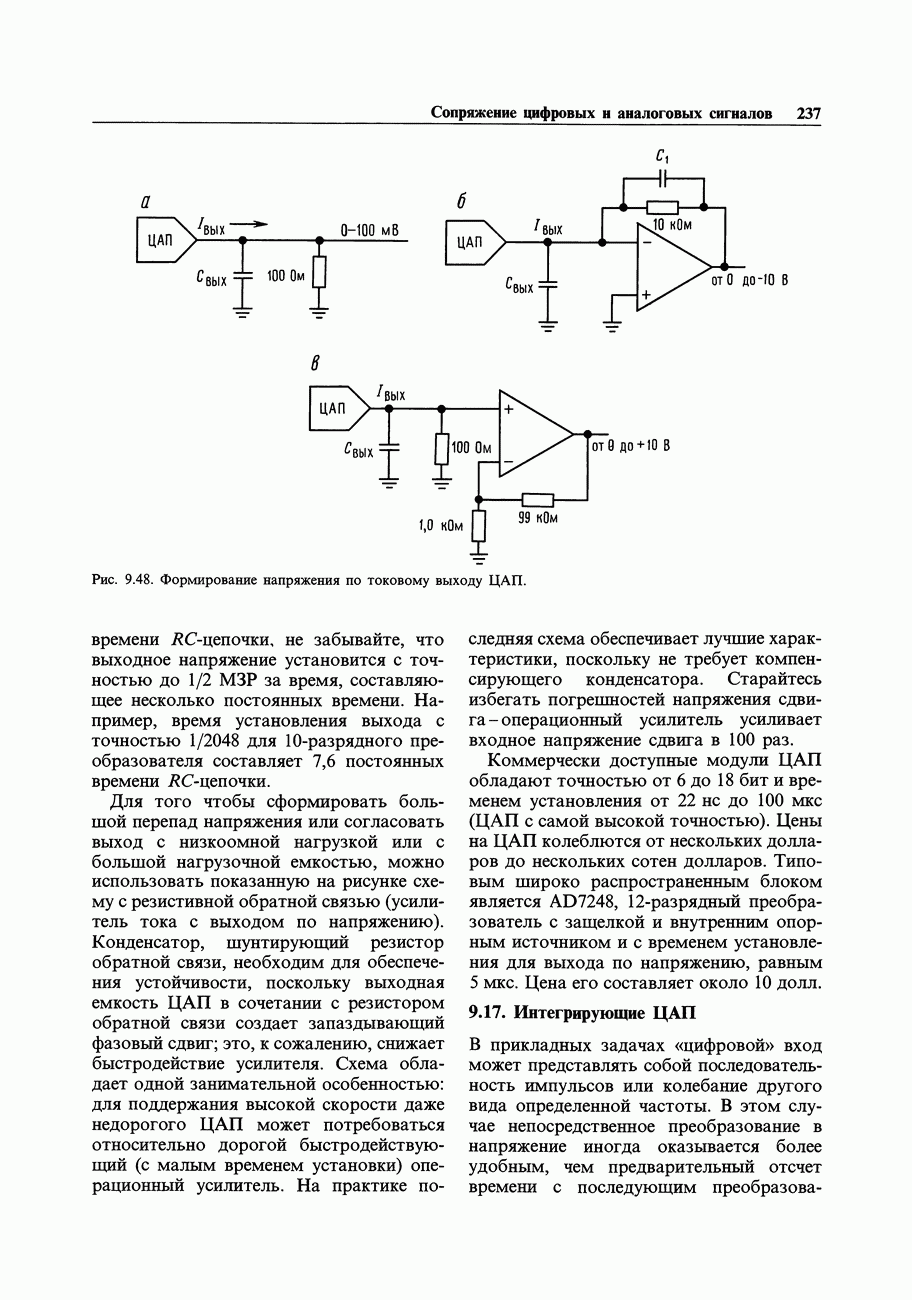
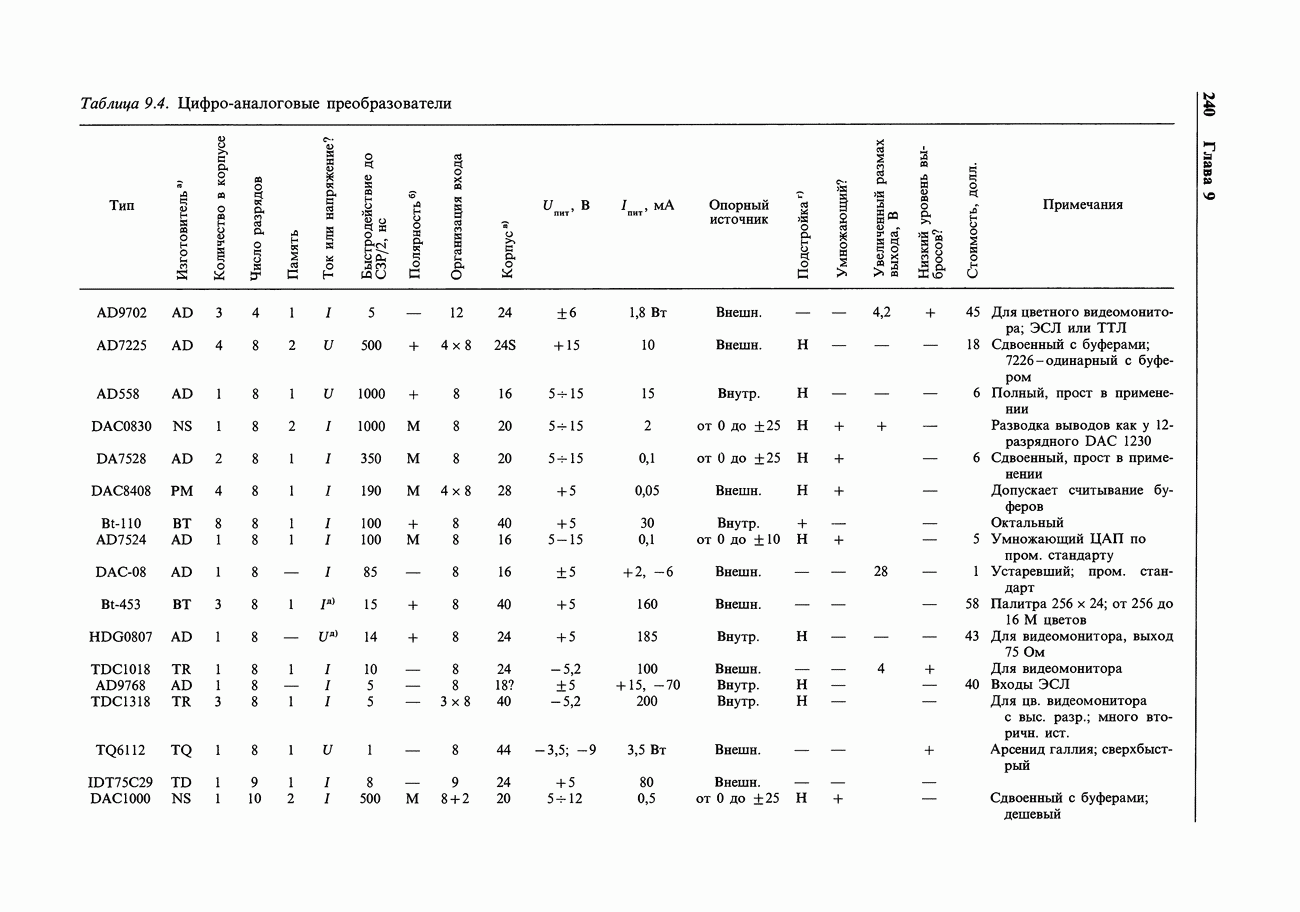
- 9.16. Цифро-аналоговые преобразователи (ЦАП)
- 9.17. Интегрирующие ЦАП
- 9.18. ЦАП с умножением
- 9.19. Выбор ЦАП
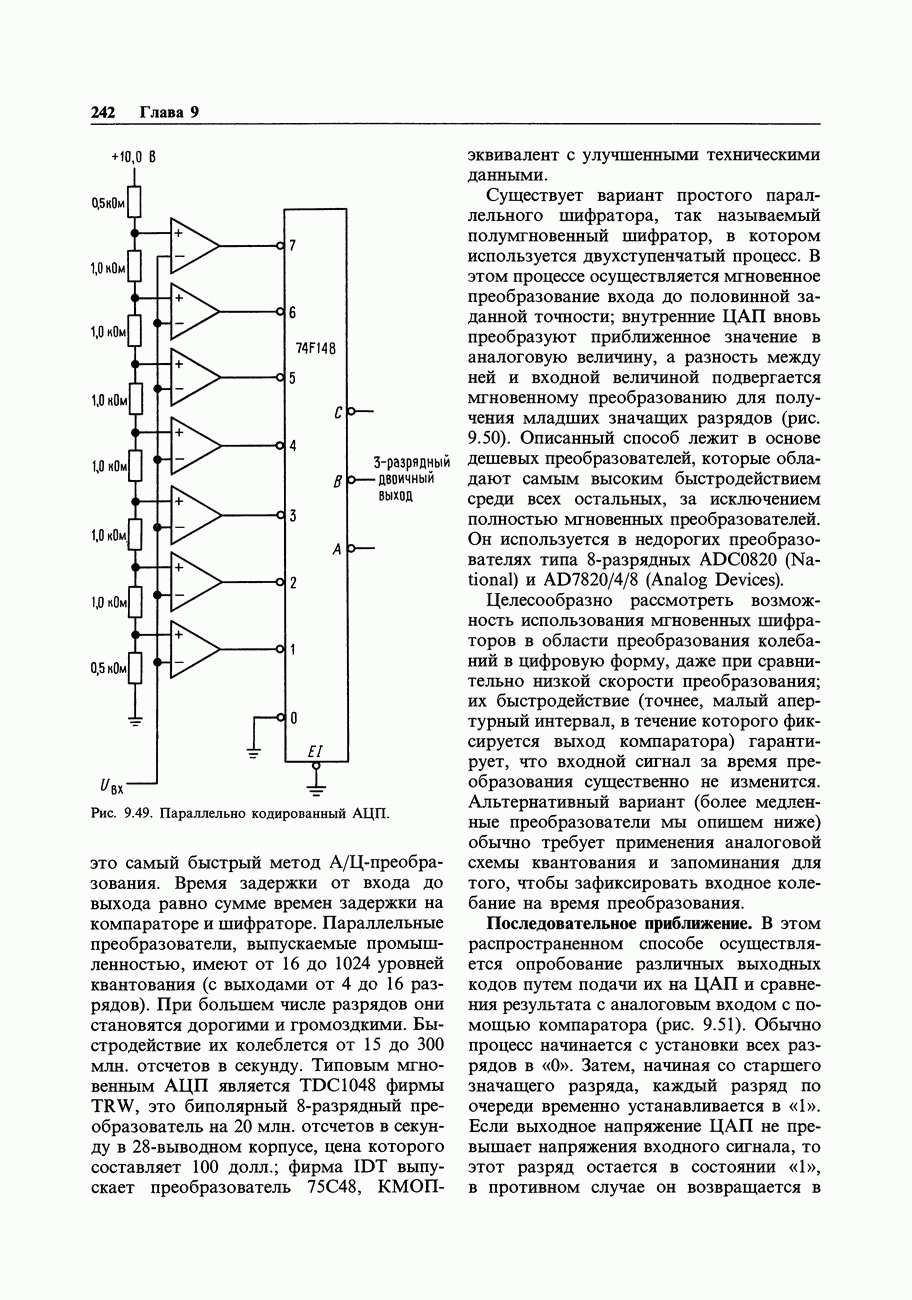
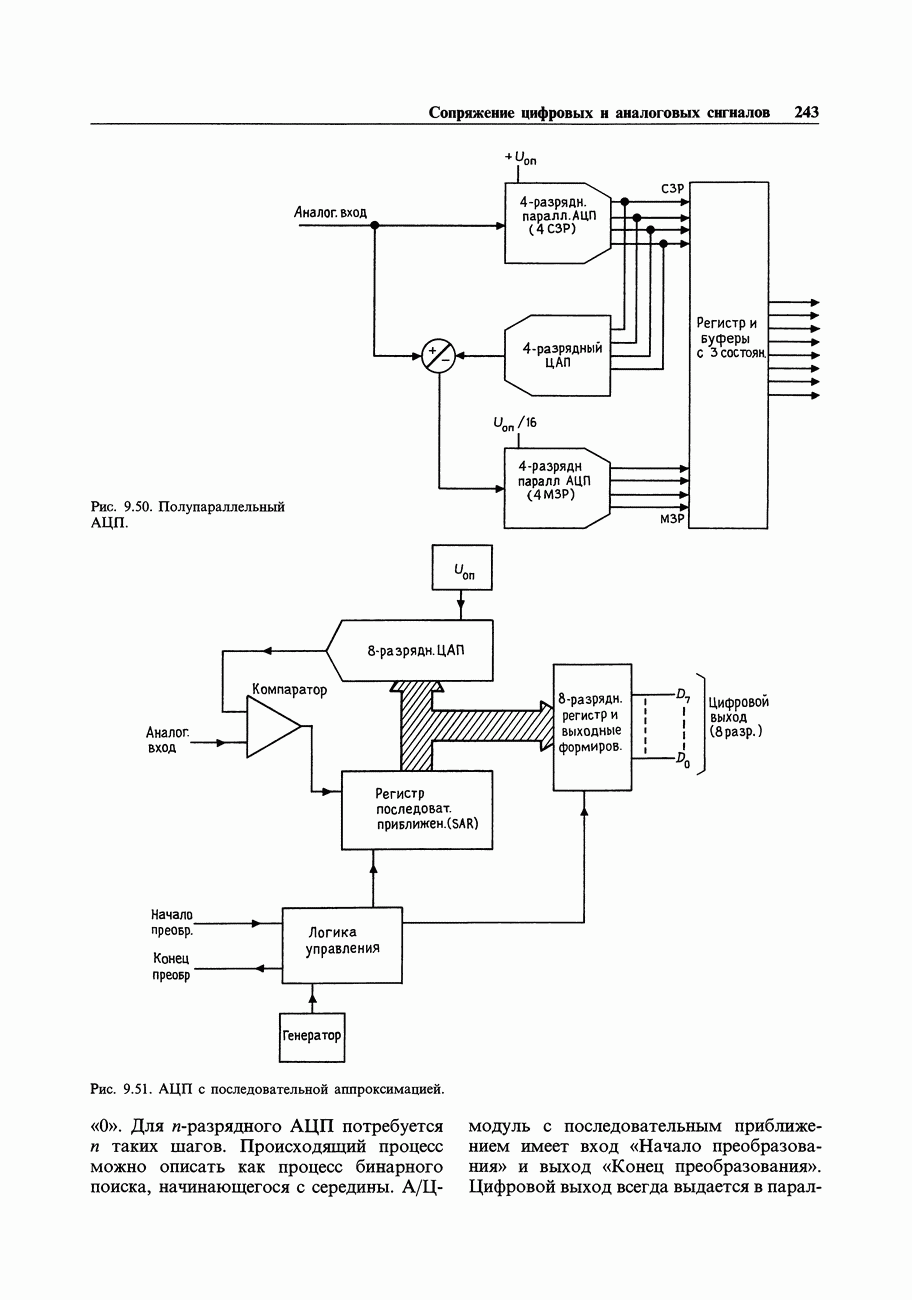
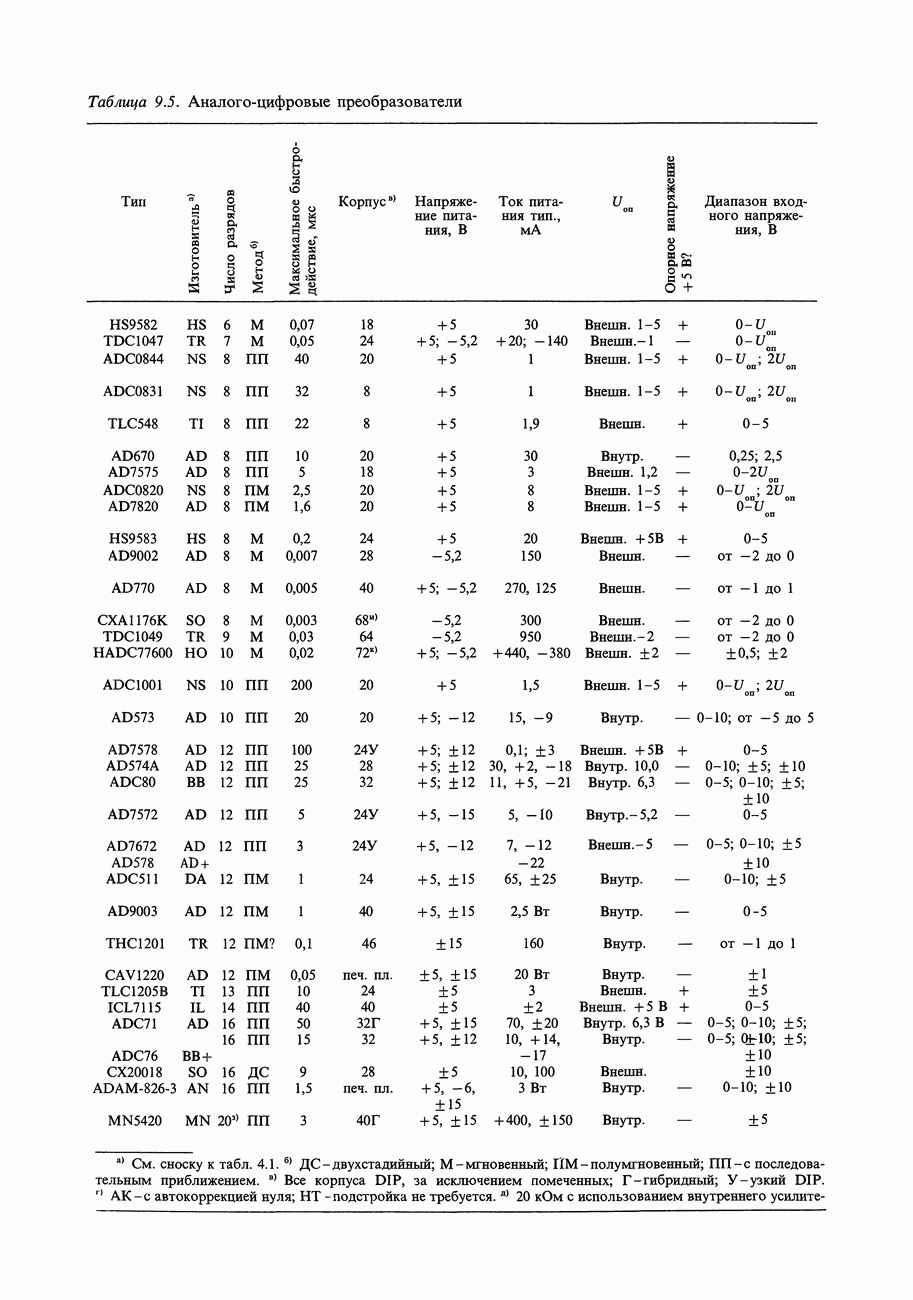
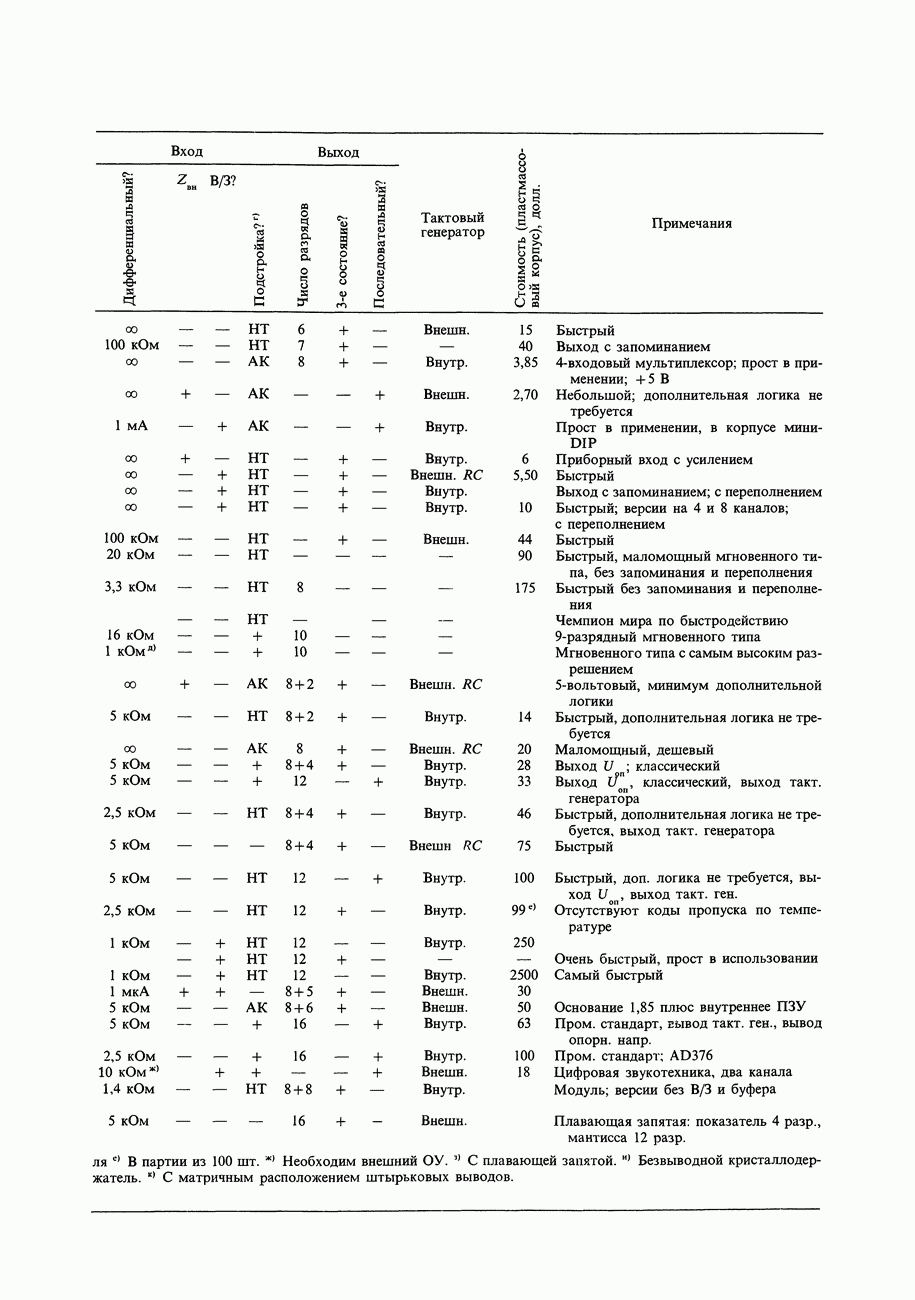
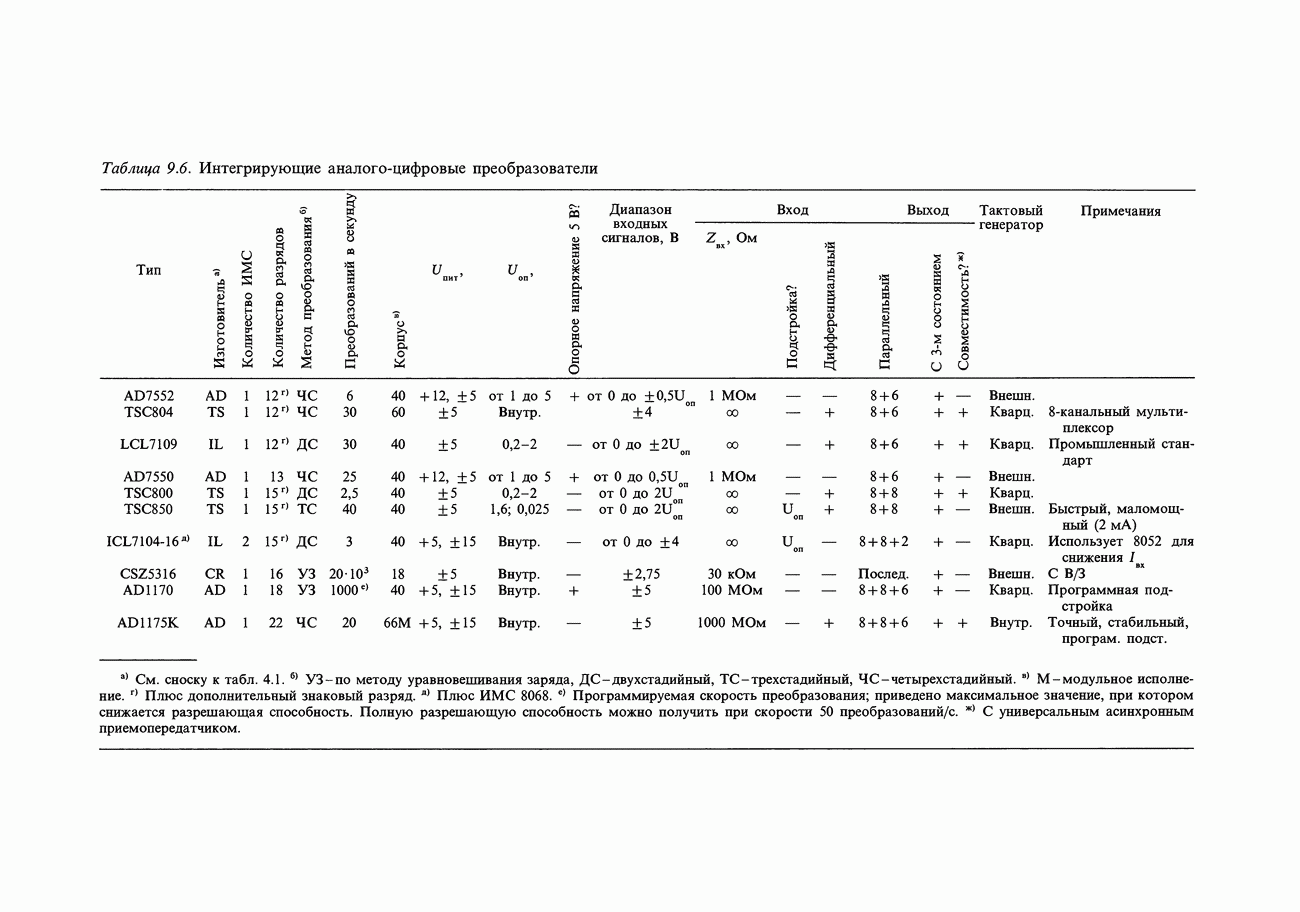
- 9.20. Аналого-цифровые преобразователи
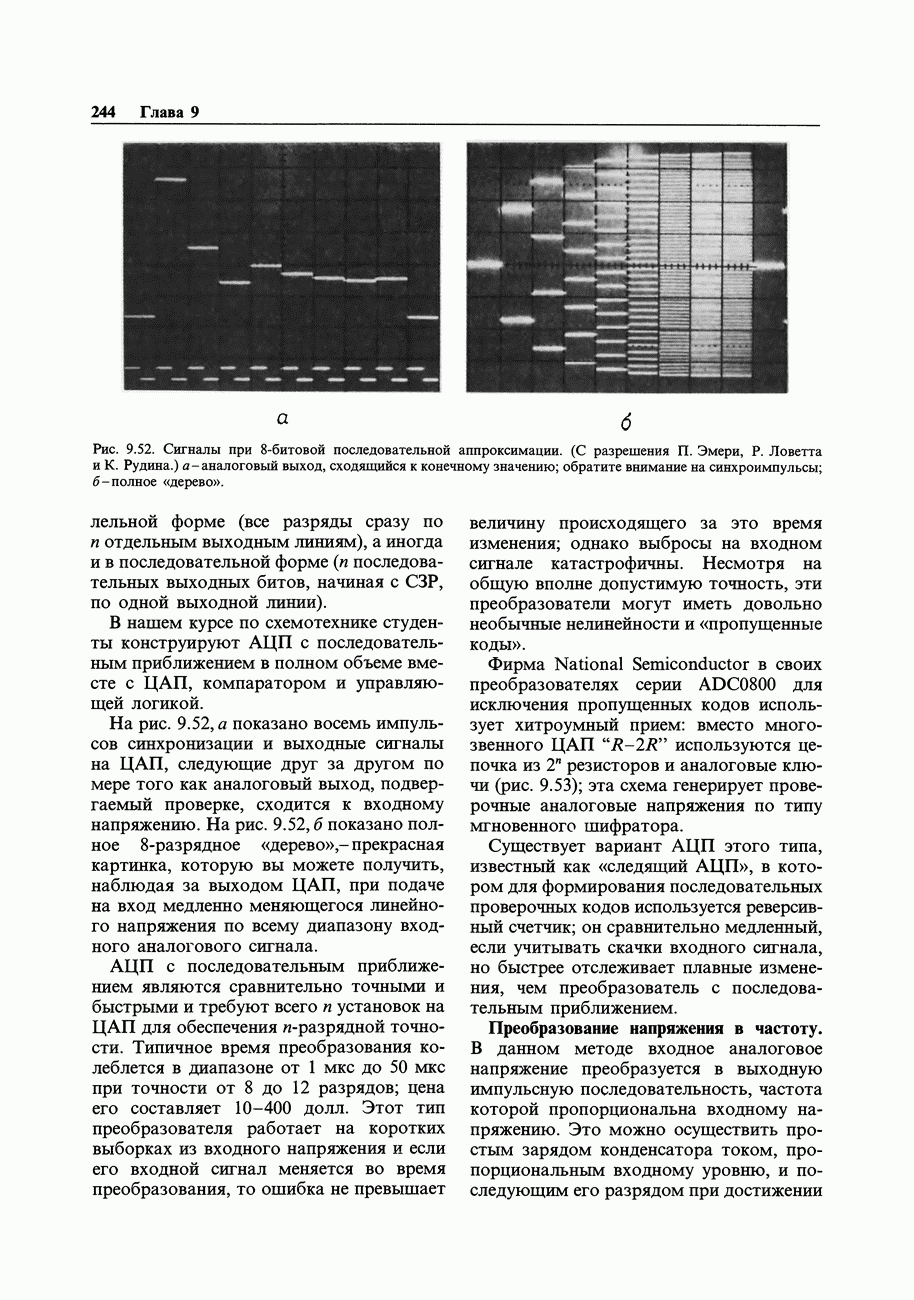
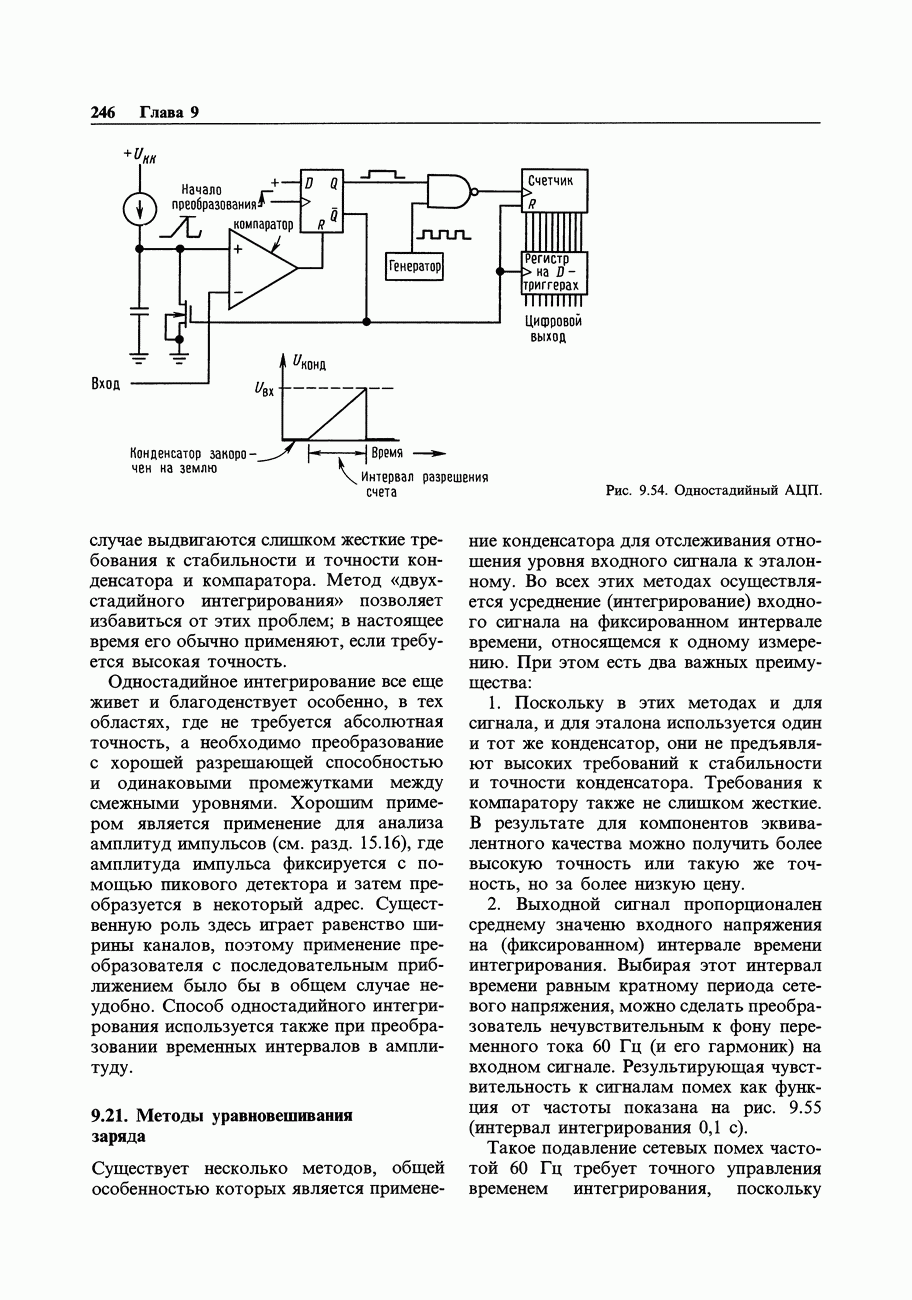
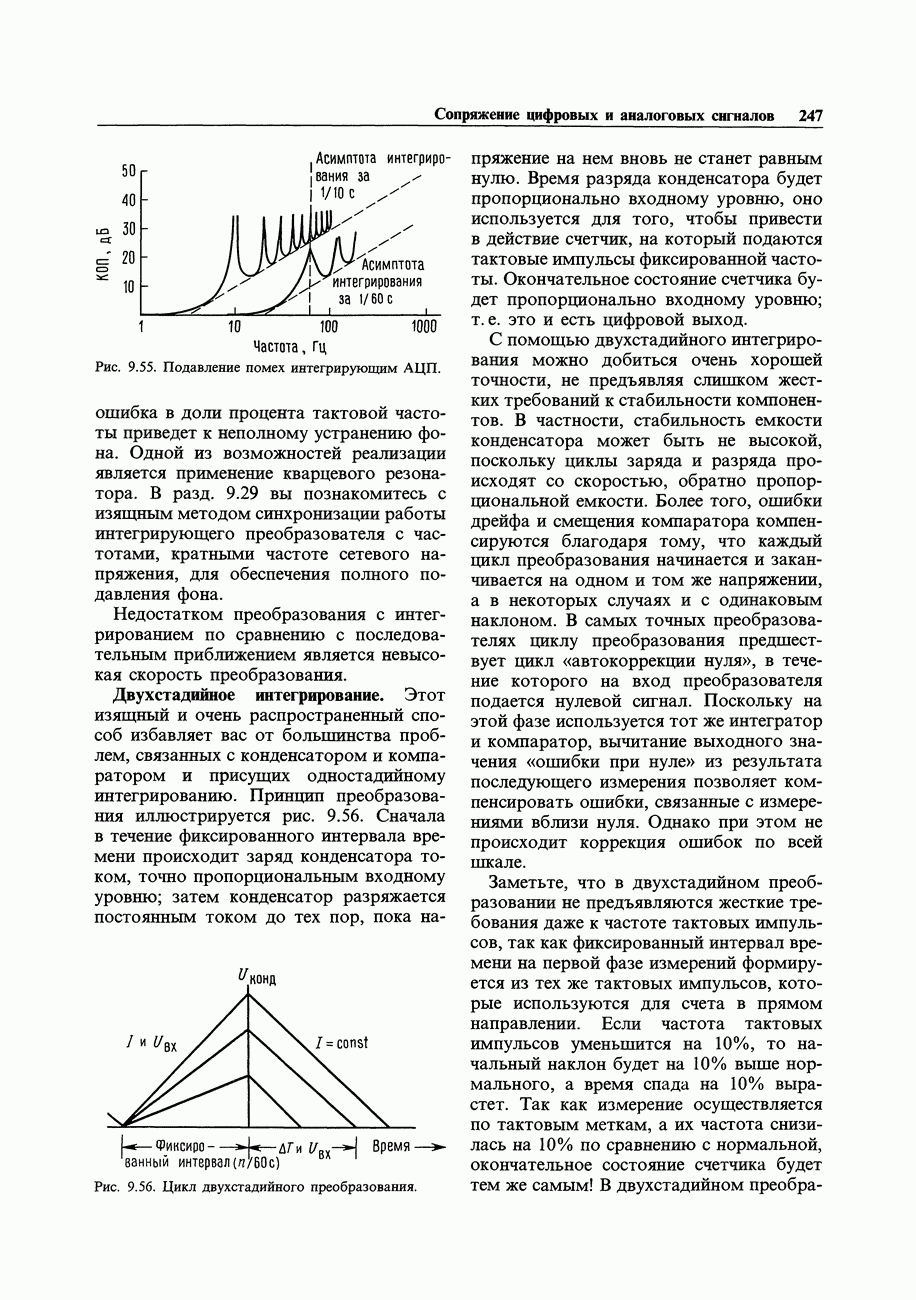
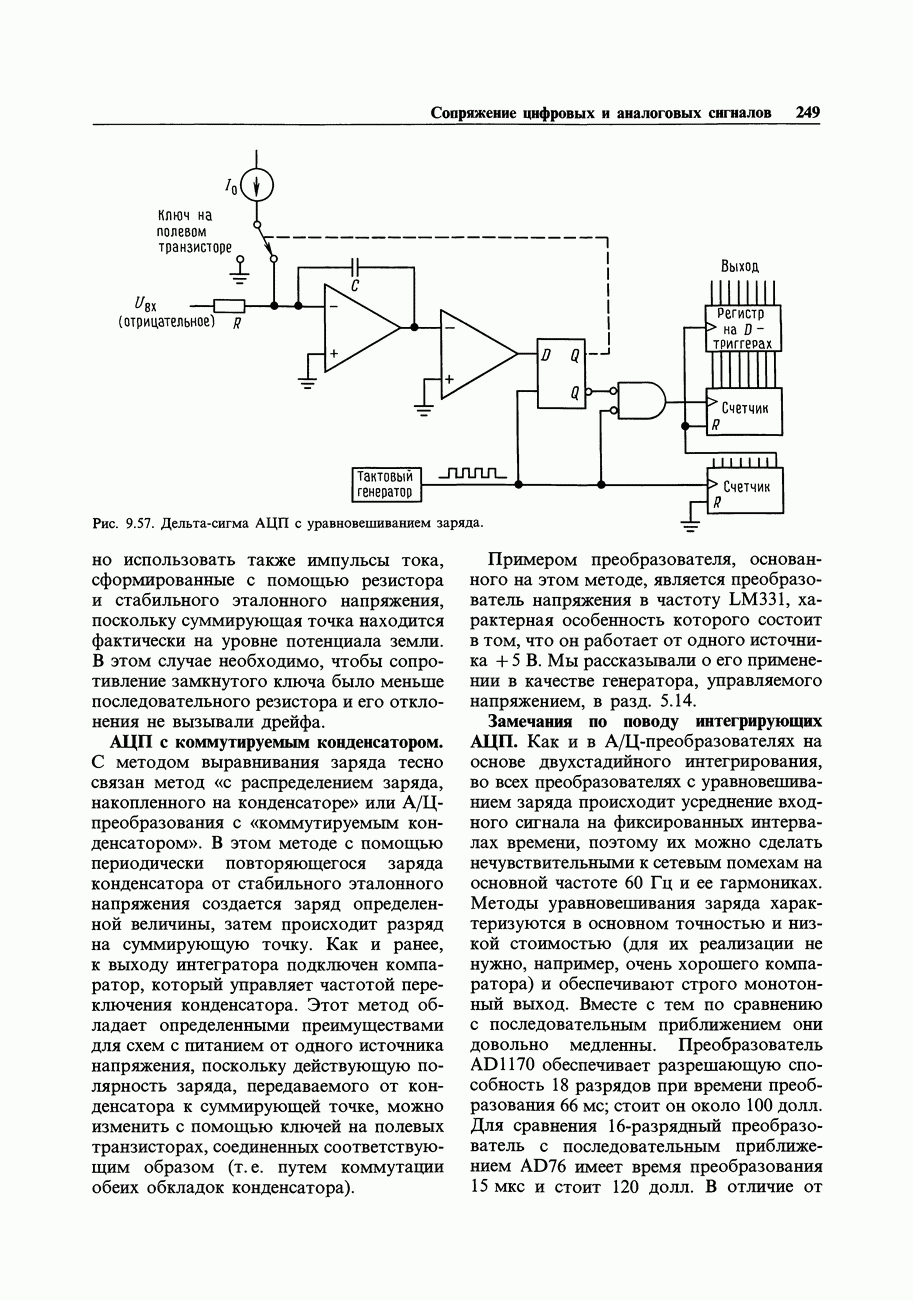
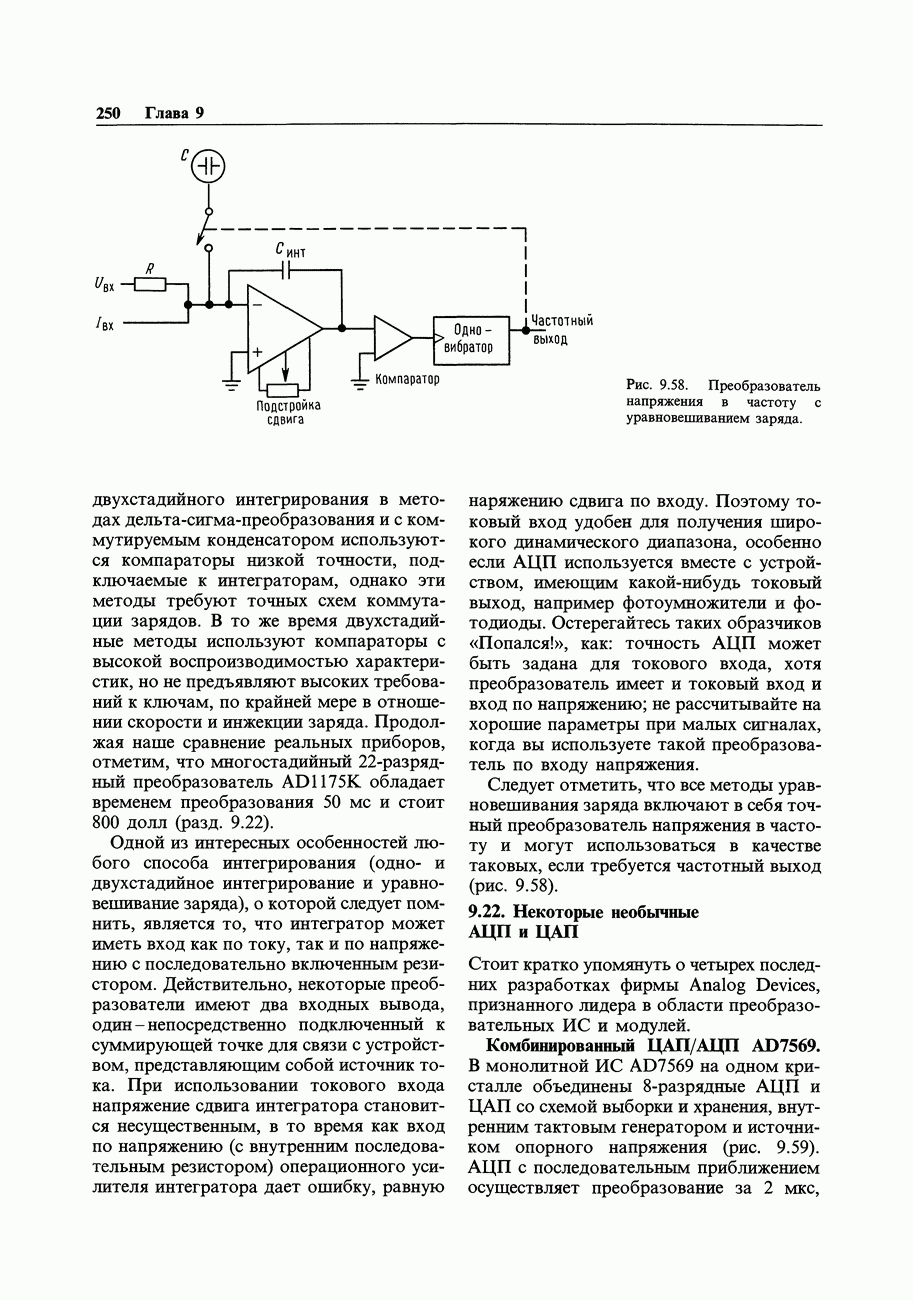
- 9.21. Методы уравновешивания заряда
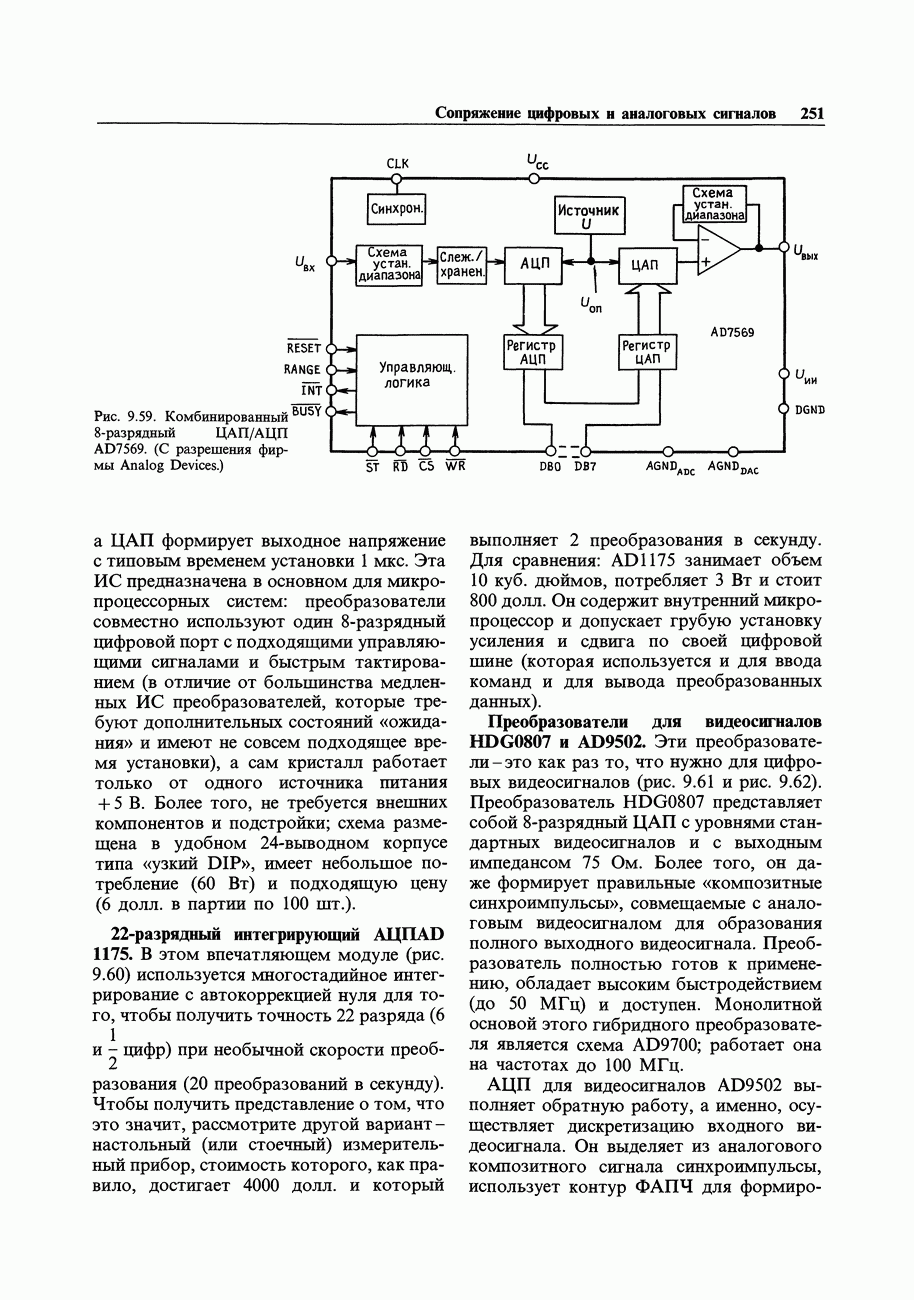
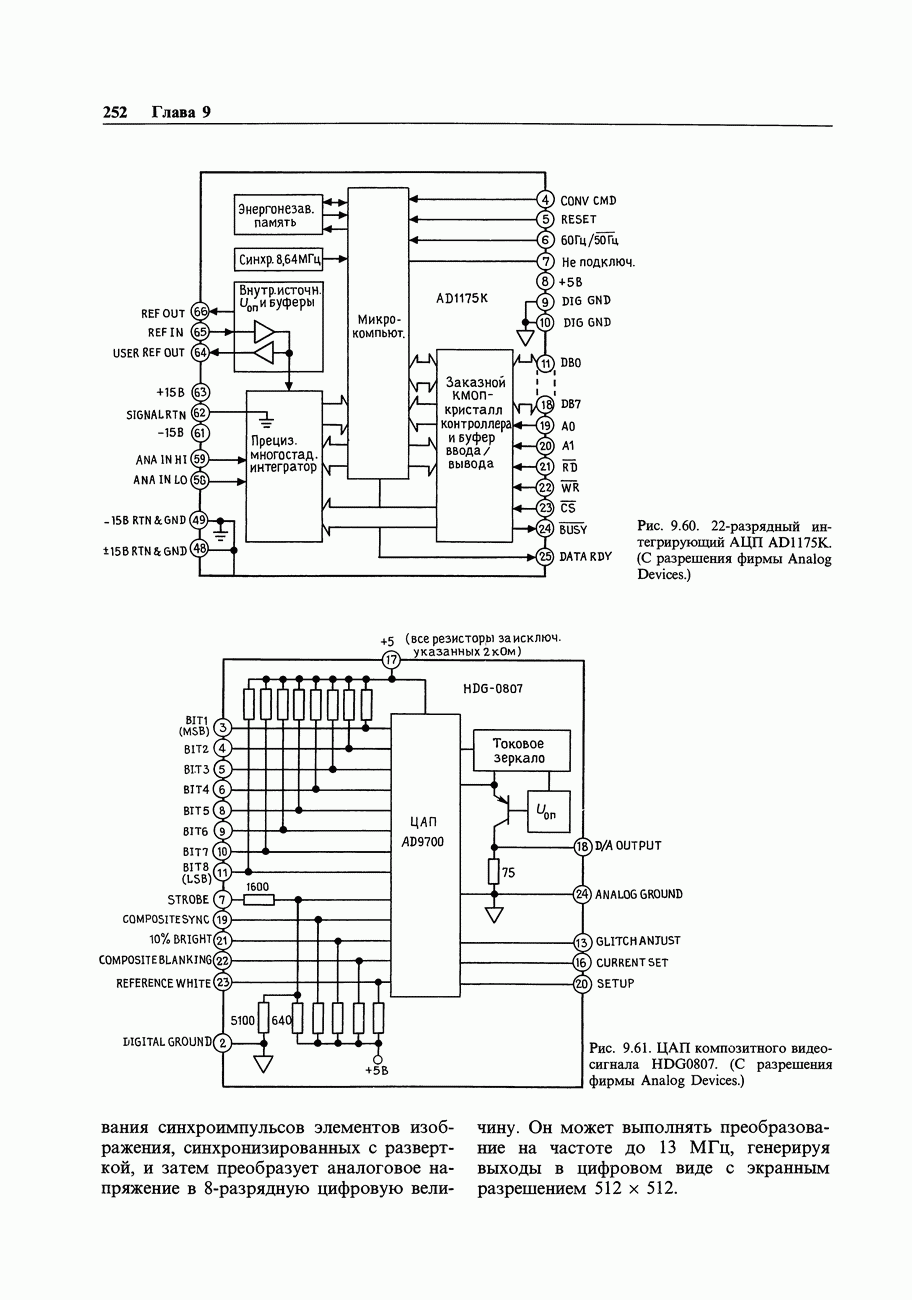
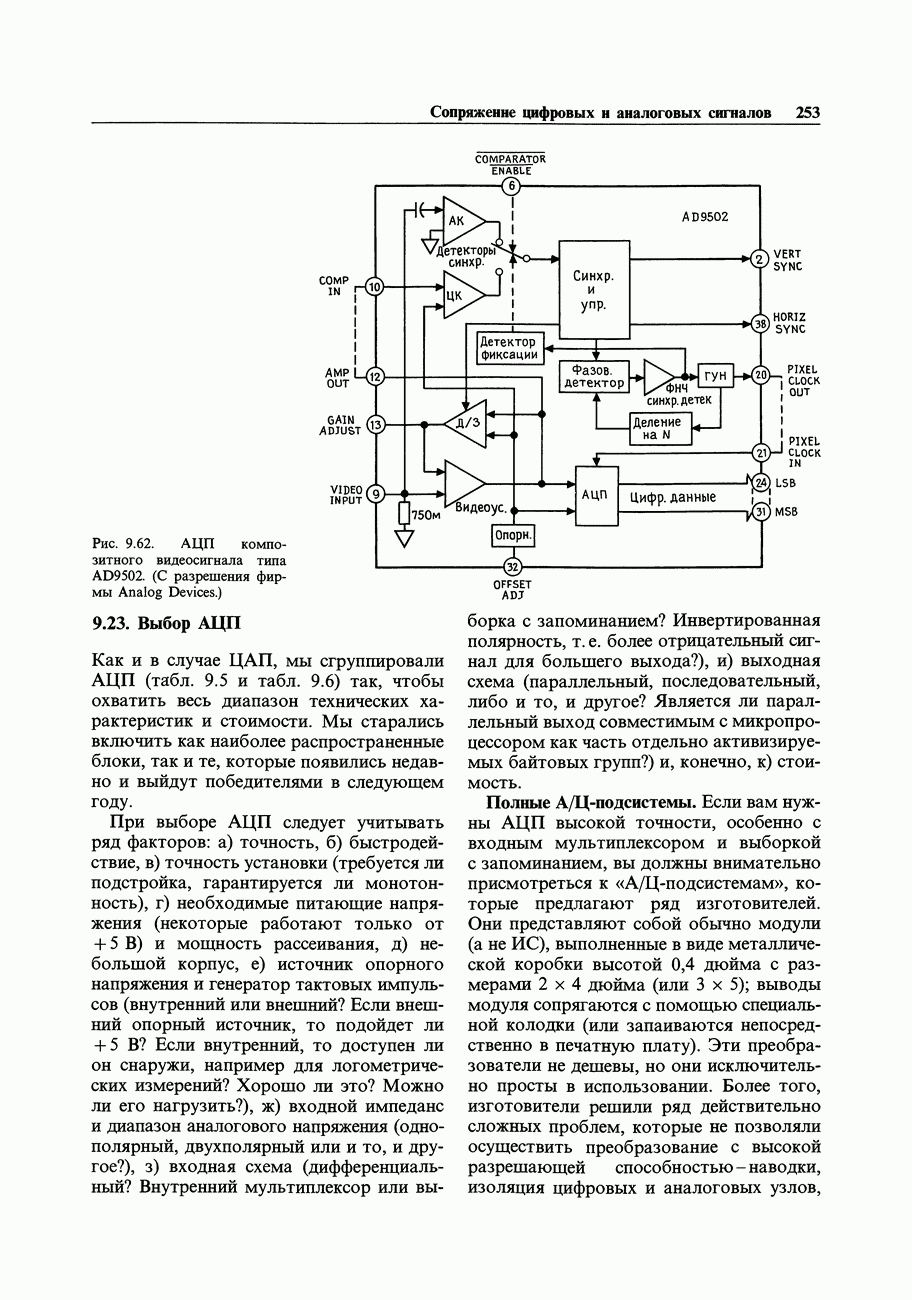
- 9.22. Некоторые необычные АЦП и ЦАП
- 9.23. Выбор АЦП
- ПРИМЕРЫ А/Ц-ПРЕОБРАЗОВАНИЯ
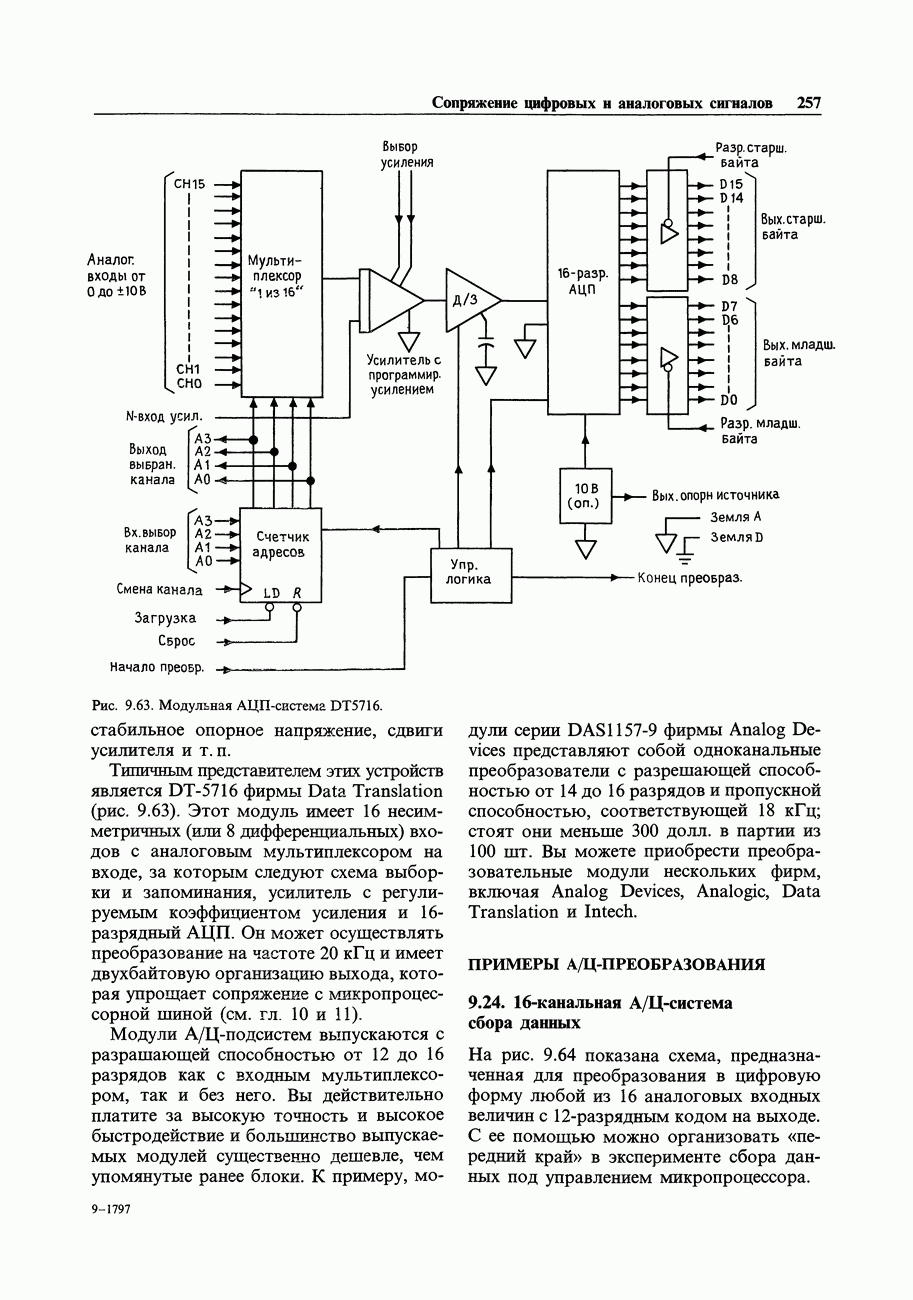
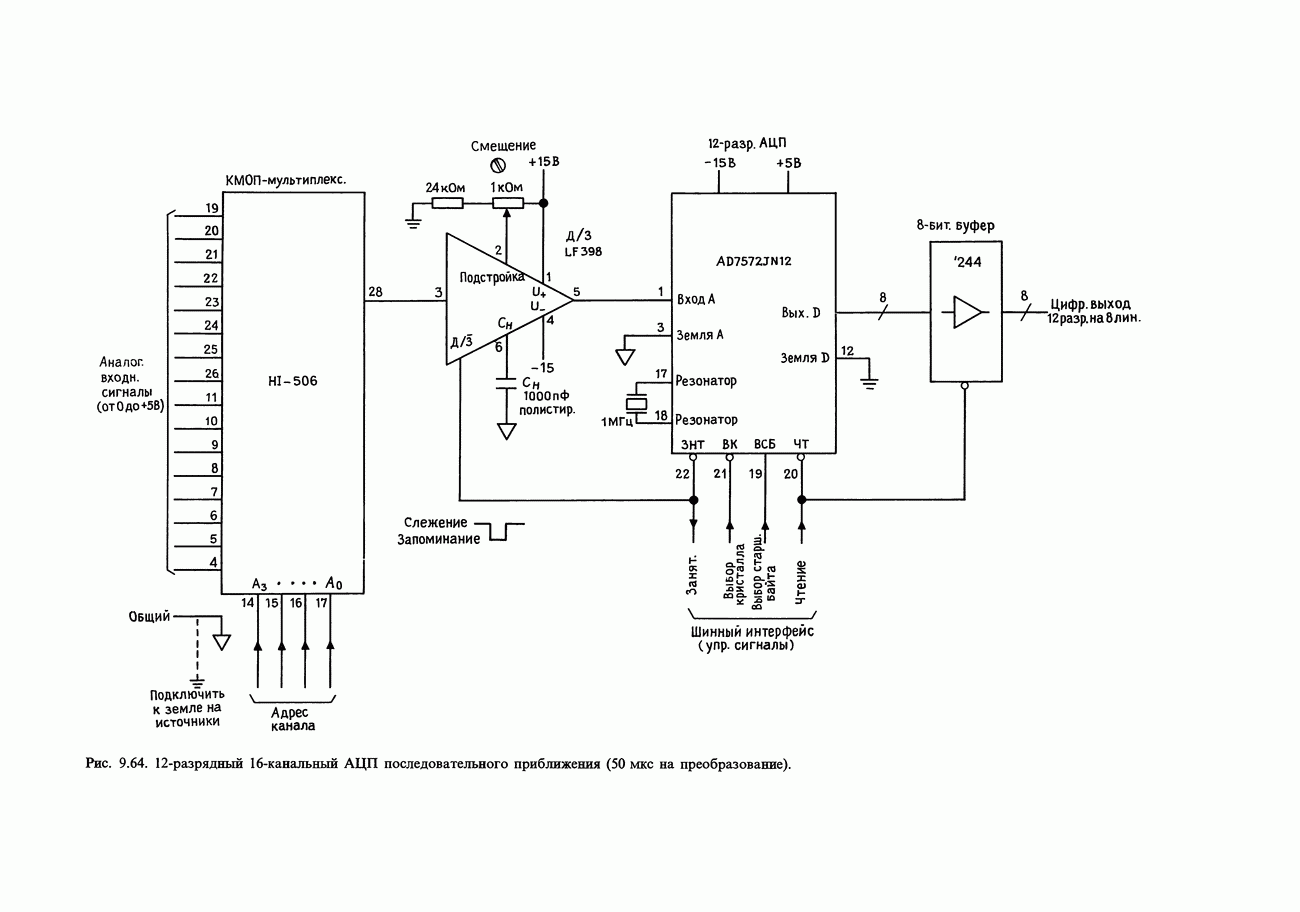
- 9.24. 16-канальная А/Ц-система сбора данных
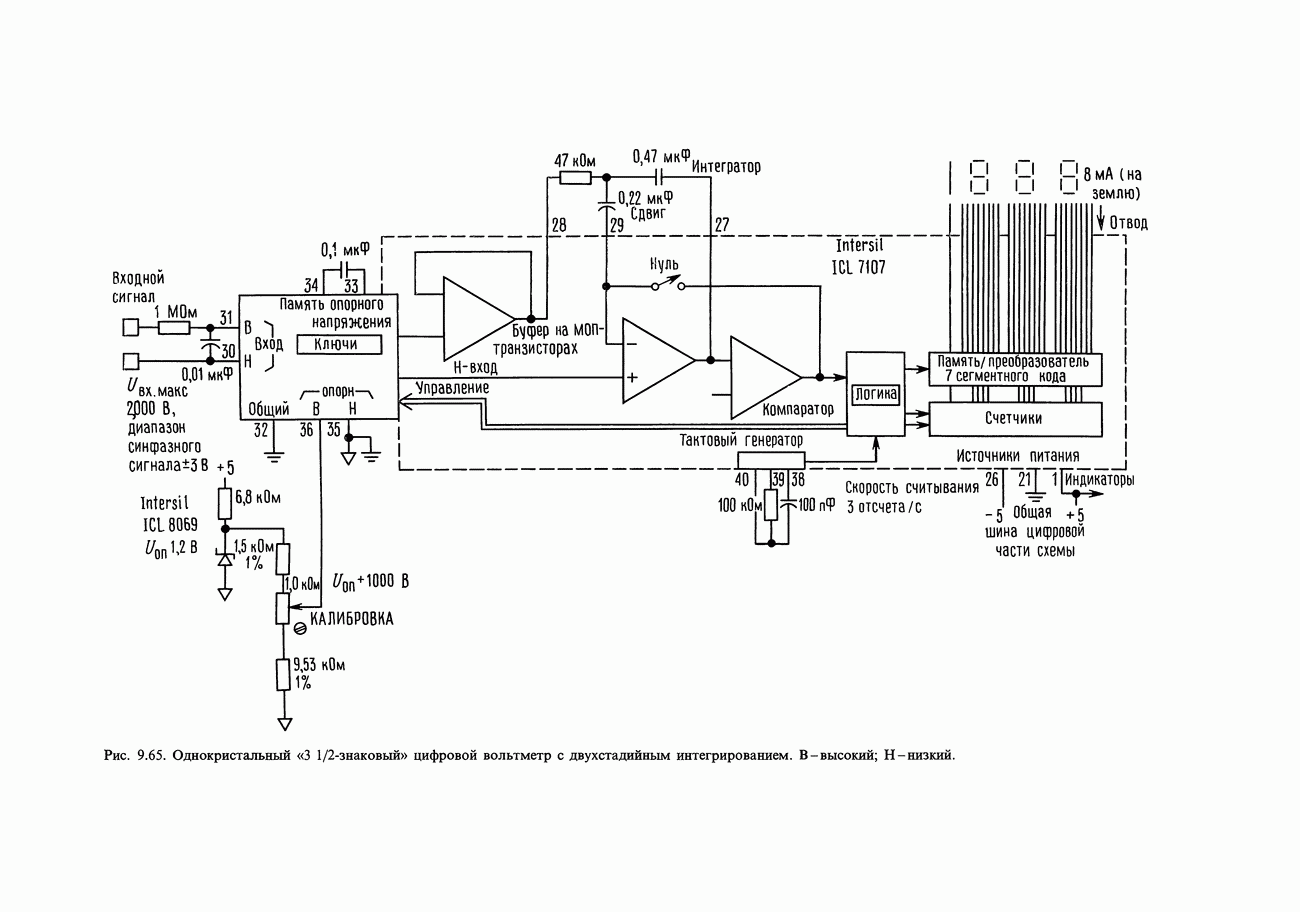
- 9.25. 3 1/2 — знаковый цифровой вольтметр
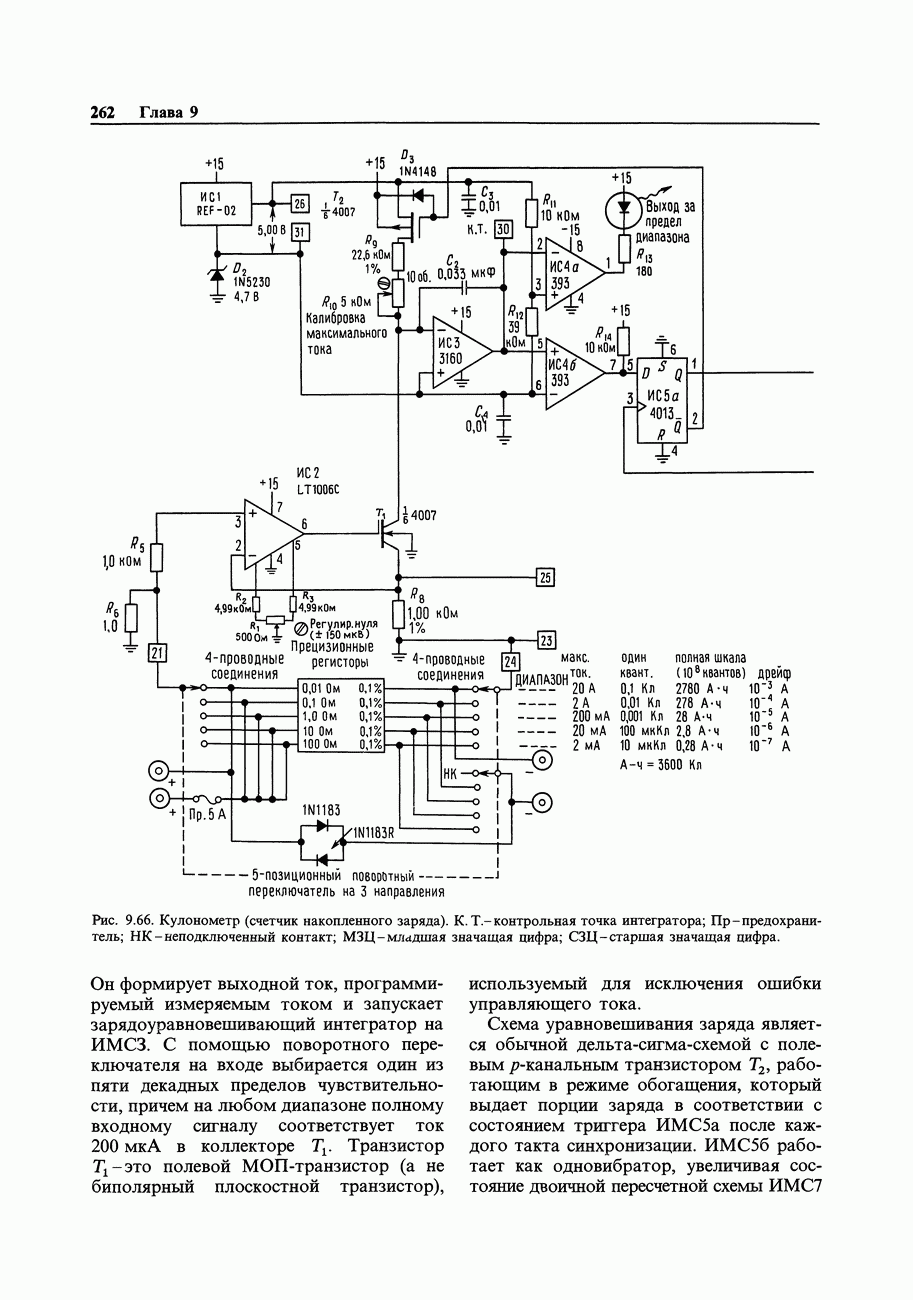
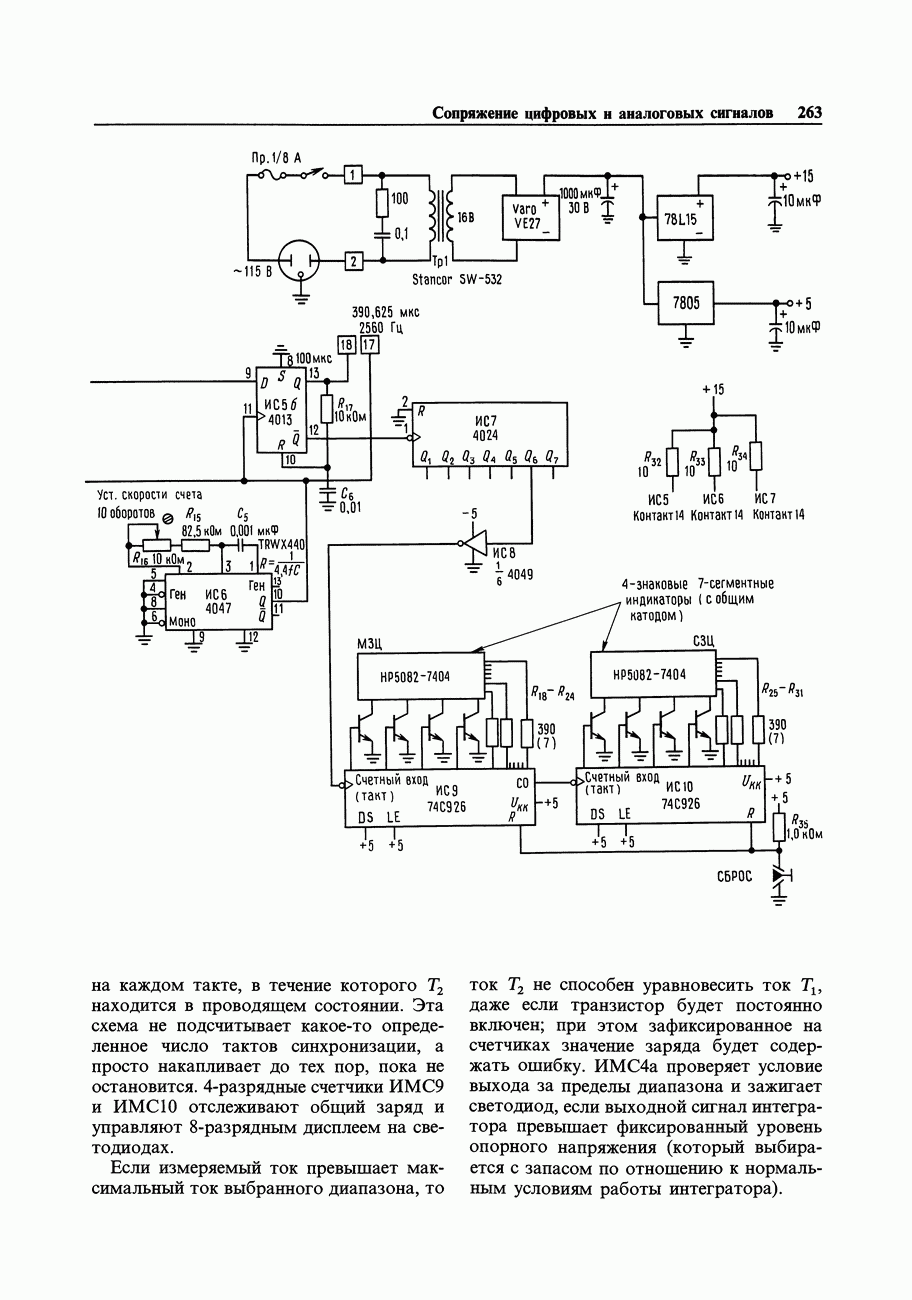
- 9.26. Кулонометр
- СХЕМЫ ФАЗОВОЙ АВТОПОДСТРОЙКИ ЧАСТОТЫ
- 9.28. Проектирование ФАПЧ
- 9.29. Пример разработки: умножитель частоты
- 9.30. Захват и слежение в системе ФАПЧ
- 9.31. Некоторые примеры применения систем ФАПЧ
- ПСЕВДОСЛУЧАЙНЫЕ ДВОИЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ГЕНЕРАТОРЫ ШУМА
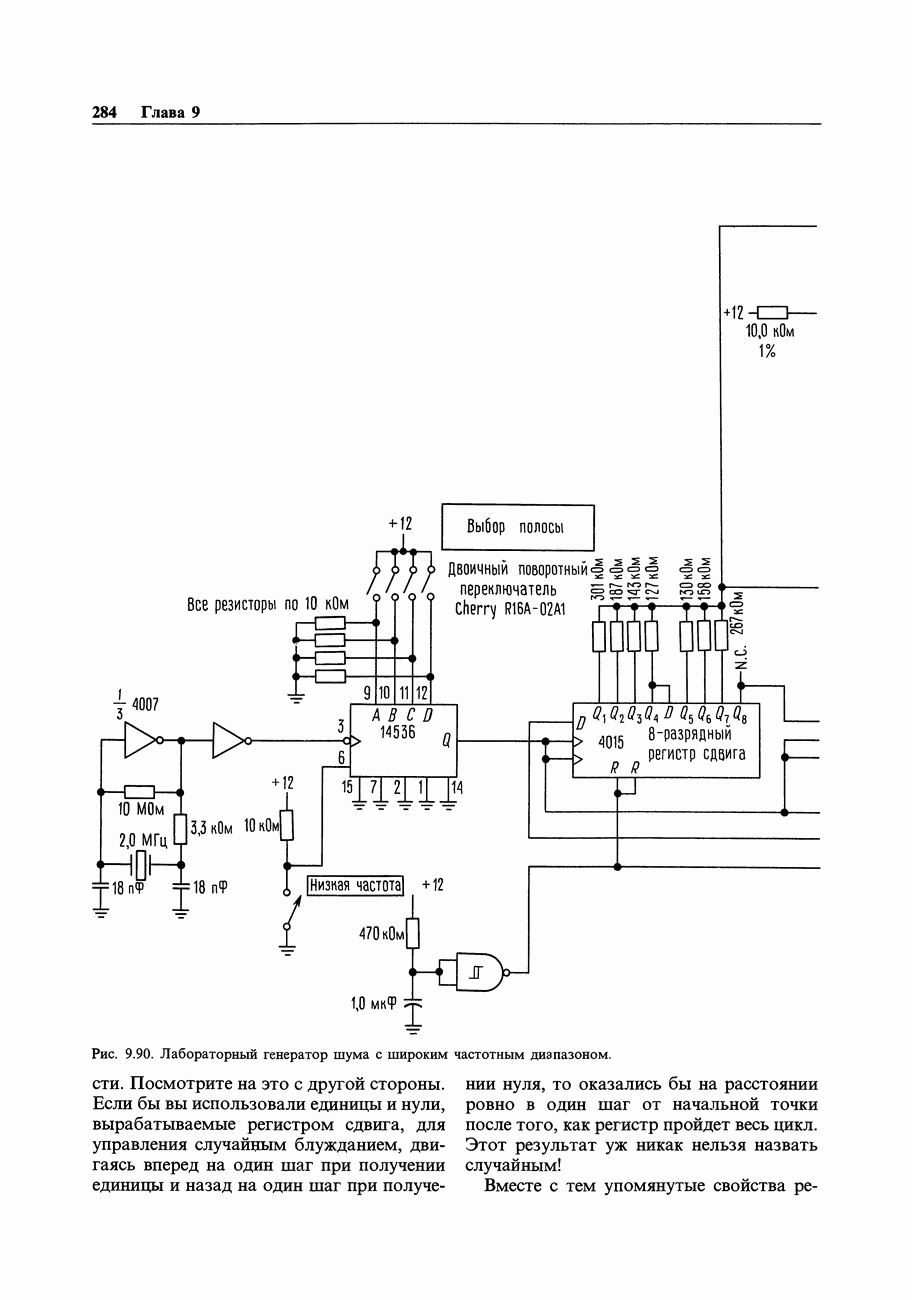
- 9.32. Цифровые методы генерации шума
- 9.33. Последовательности, генерируемые регистрами сдвига с обратными связями
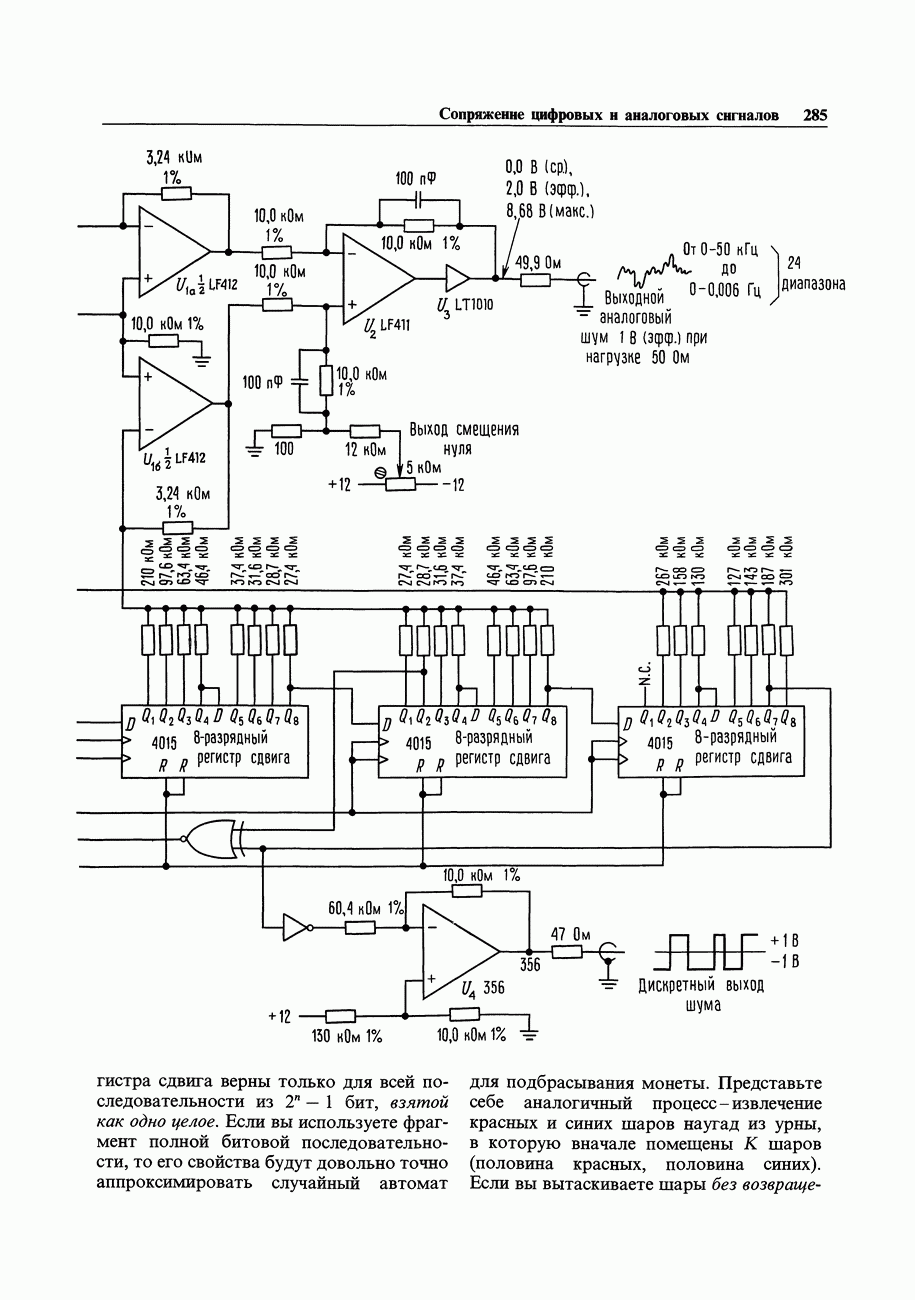
- 9.34. Формирование аналогового шума с использованием последовательностей максимальной длины
- 9.35. Энергетический спектр последовательности, сформированной при помощи регистра сдвига
- 9.36. Низкочастотная фильтрация
- 9.37. Краткое заключение
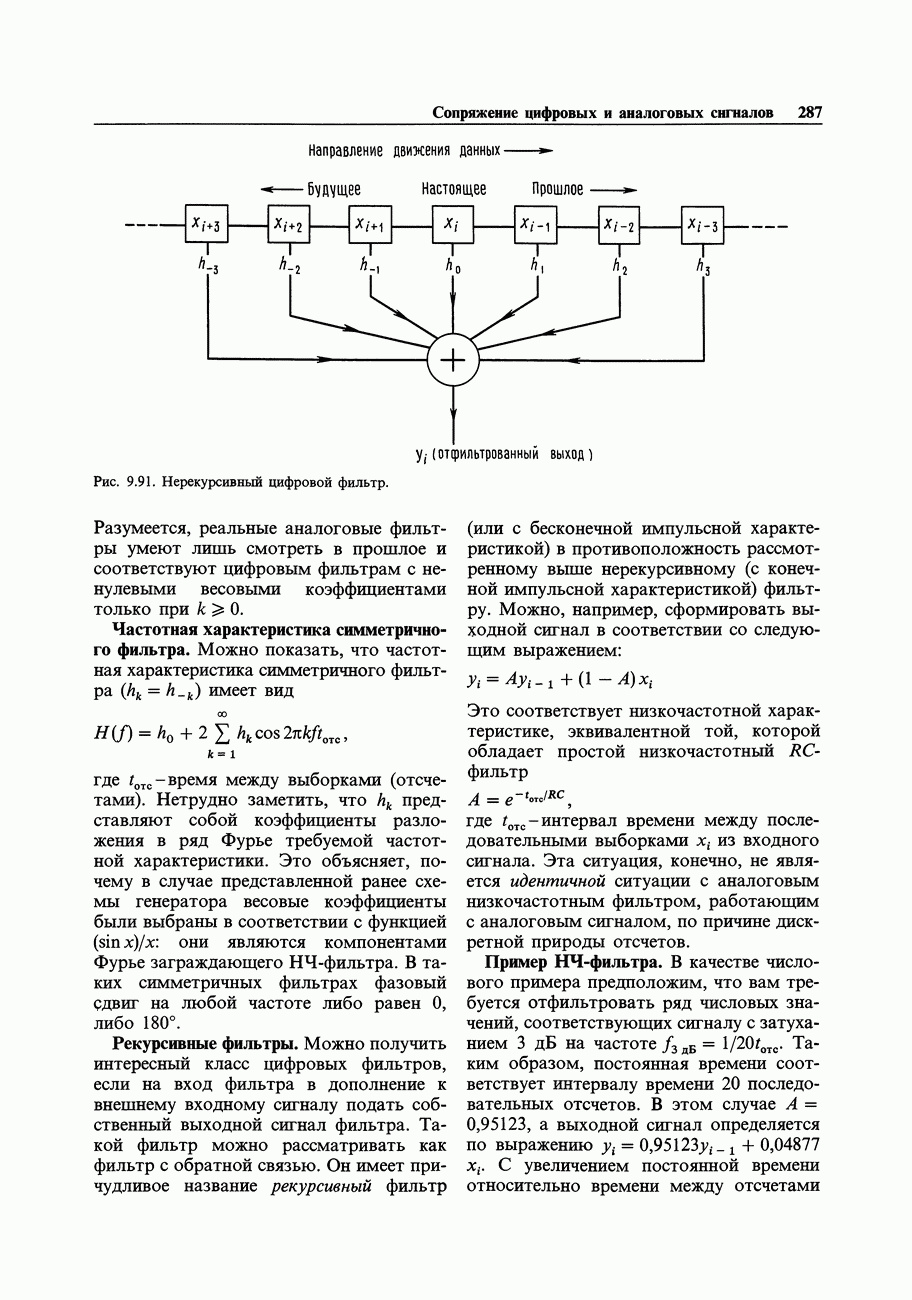
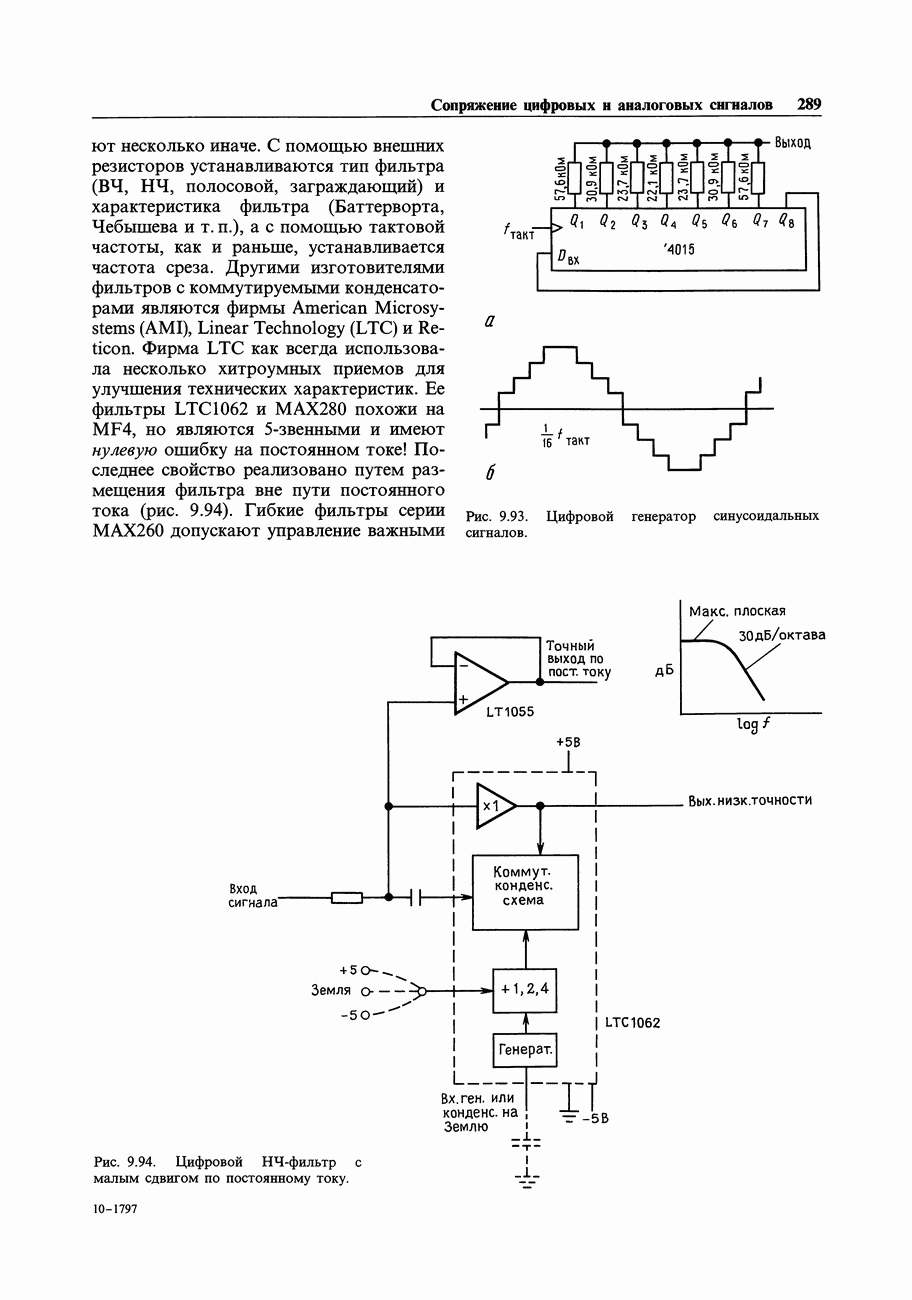
- 9.38. Цифровые фильтры
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 10. МИКРОЭВМ
- МИНИ-ЭВМ, МИКРОЭВМ И МИКРОПРОЦЕССОРЫ
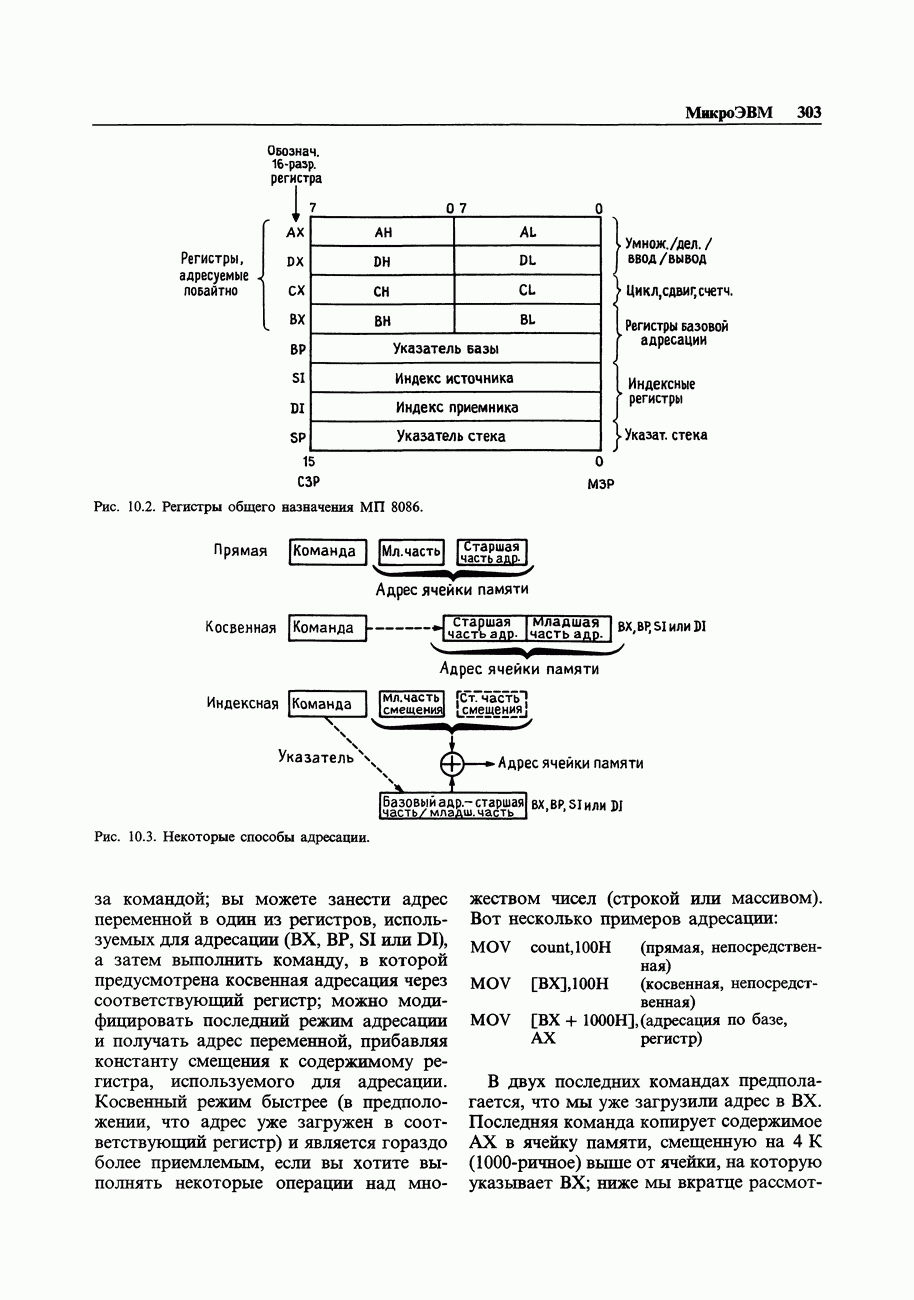
- 10.01. Архитектура микроЭВМ
- НАБОР КОМАНД КОМПЬЮТЕРА
- 10.02. Язык ассемблера и язык машинных кодов
- 10.03. Упрощенный набор команд процессора Intel 8086/8
- 10.04. Программный пример
- СИГНАЛЫ МАГИСТРАЛИ И ЕЕ ФУНКЦИОНИРОВАНИЕ
- 10.05. Основные сигналы магистрали: данные, адрес, синхронизация
- 10.06. Программируемый ввод-вывод: вывод данных
- 10.07. Программируемый ввод-вывод: ввод данных
- 10.08. Программируемый ввод-вывод: регистры состояний
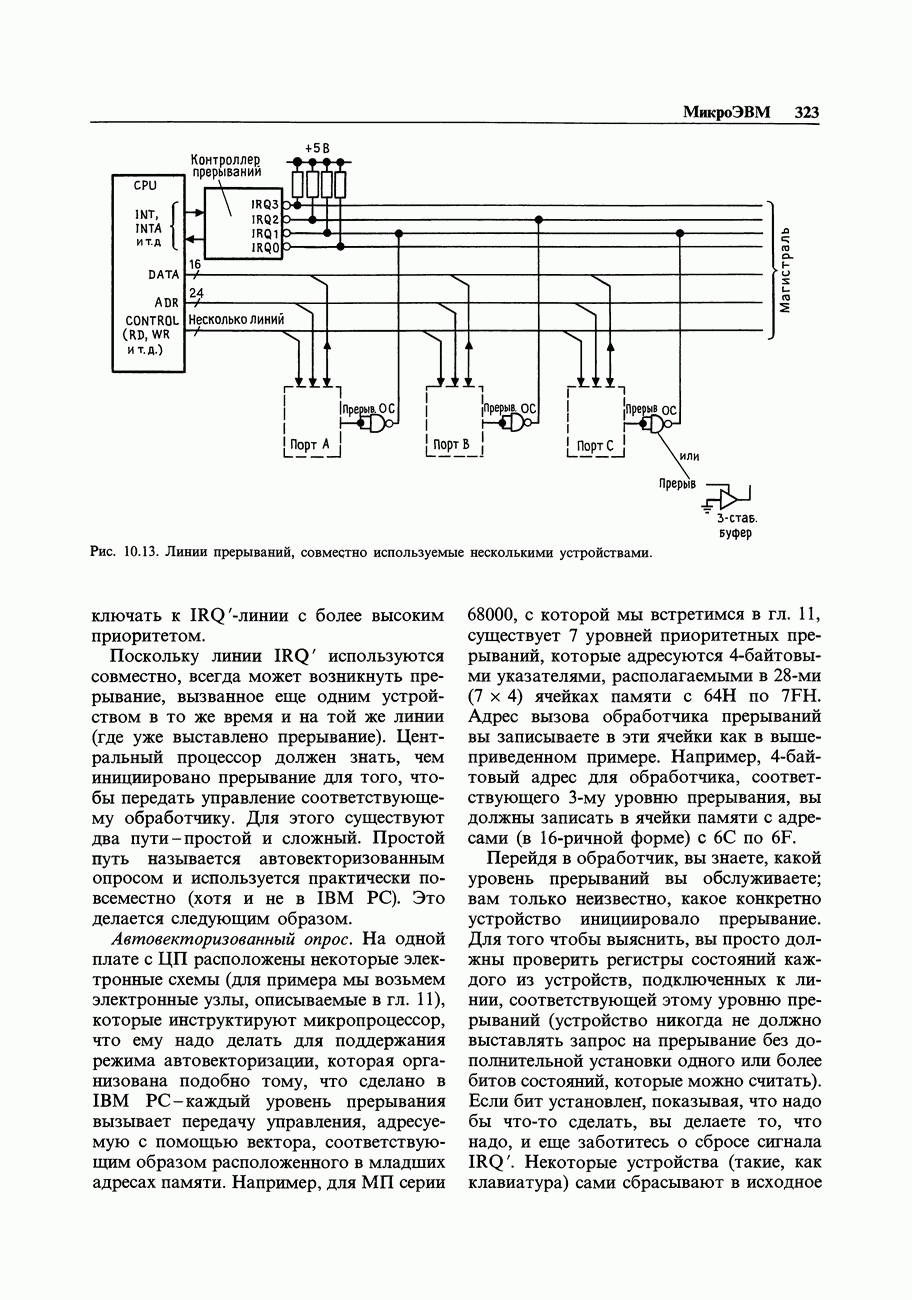
- 10.09. Прерывания
- 10.10. Обработка прерываний
- 10.11. Прерывания в целом
- 10.12. Прямой доступ в память
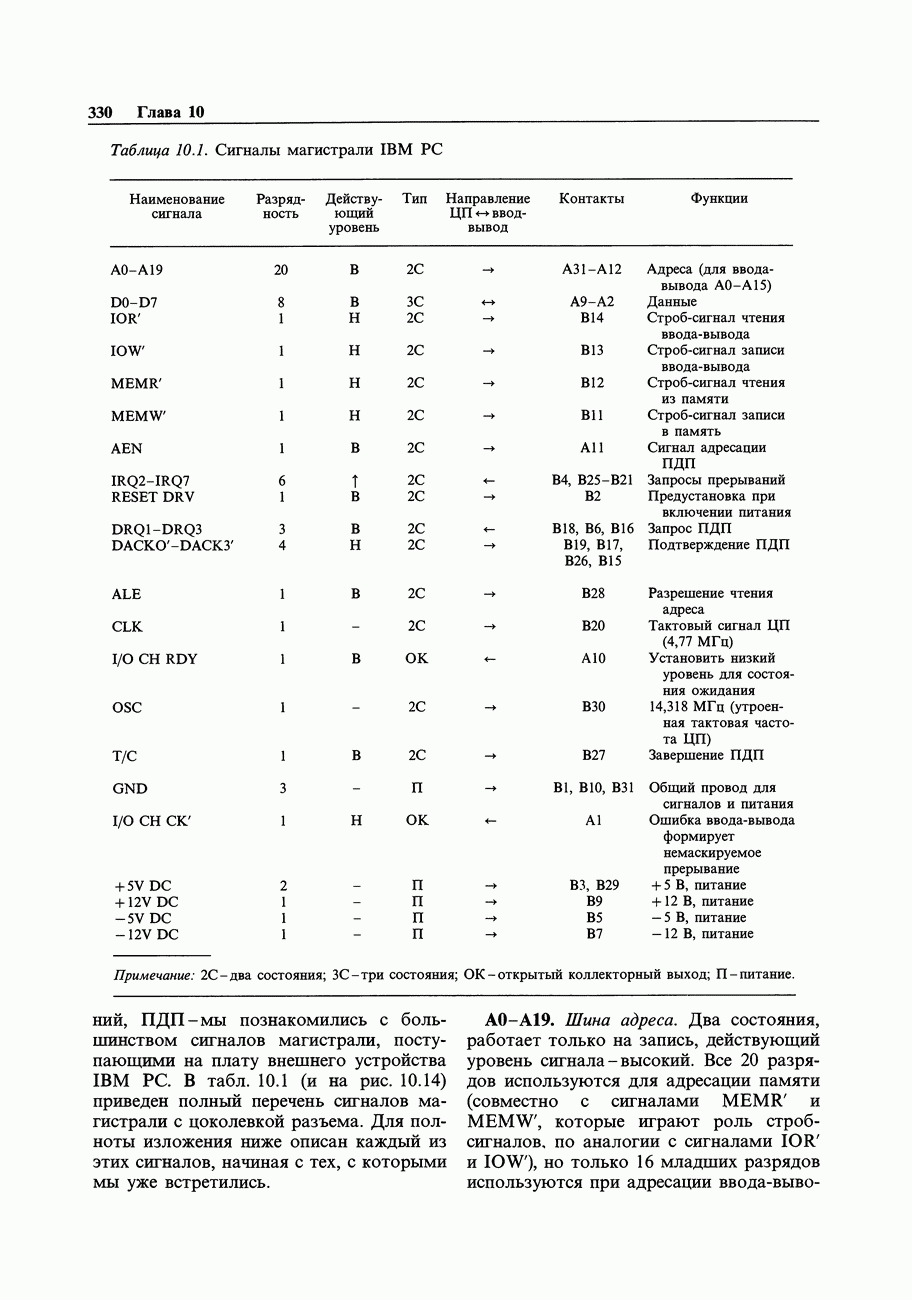
- 10.13. Сводный перечень сигналов магистрали IBM PC
- 10.14. Синхронный и асинхронный протоколы магистрали
- 10.15. Магистрали других микрокомпьютеров
- 10.16. Подключение к компьютеру периферийных устройств
- СИСТЕМНЫЕ КОНЦЕПЦИИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- 10.17. Программирование
- 10.18. Операционные системы, файлы и использование памяти
- ПРИНЦИПЫ ПЕРЕДАЧИ ДАННЫХ
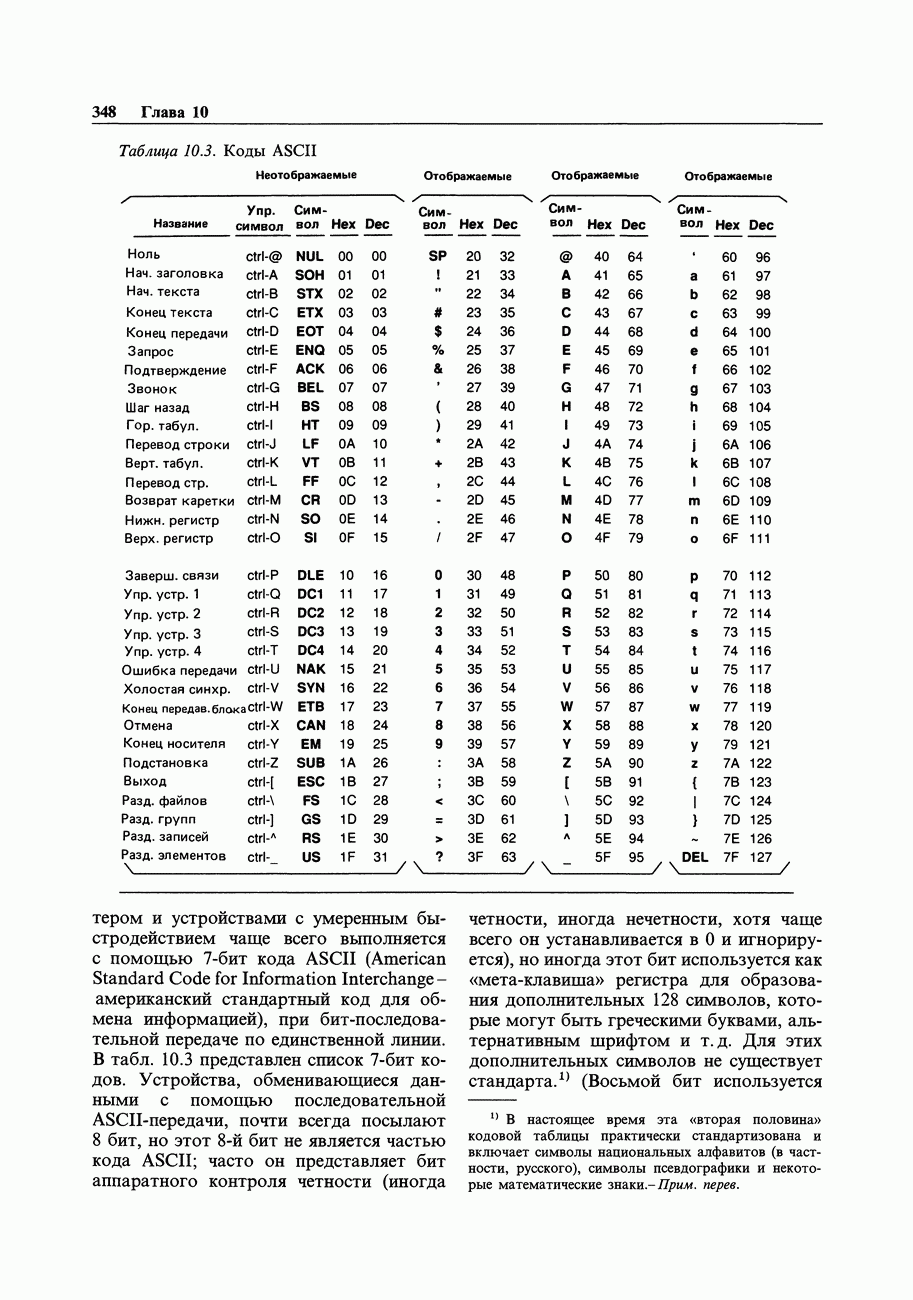
- 10.19. Последовательная связь и коды ASCII
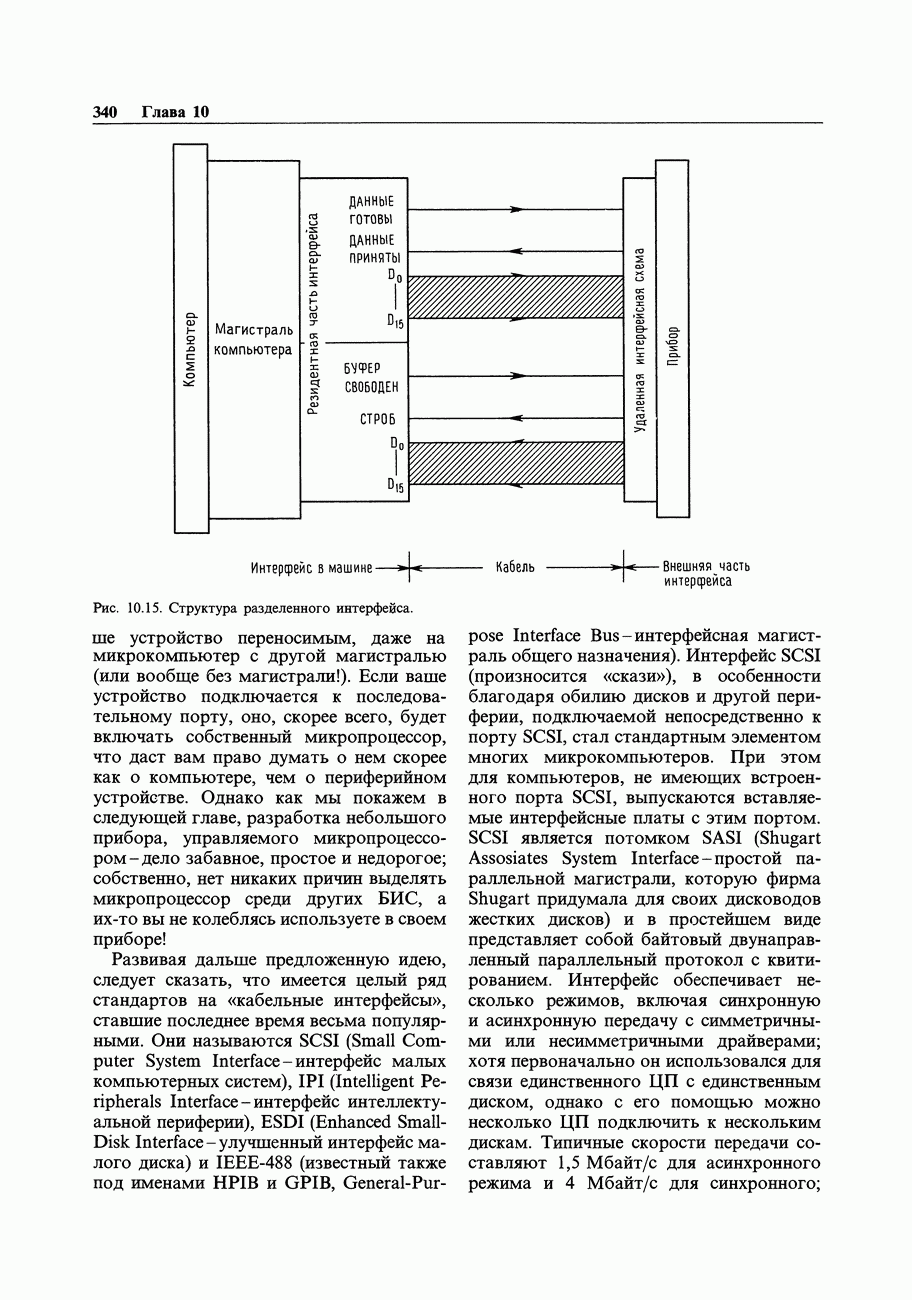
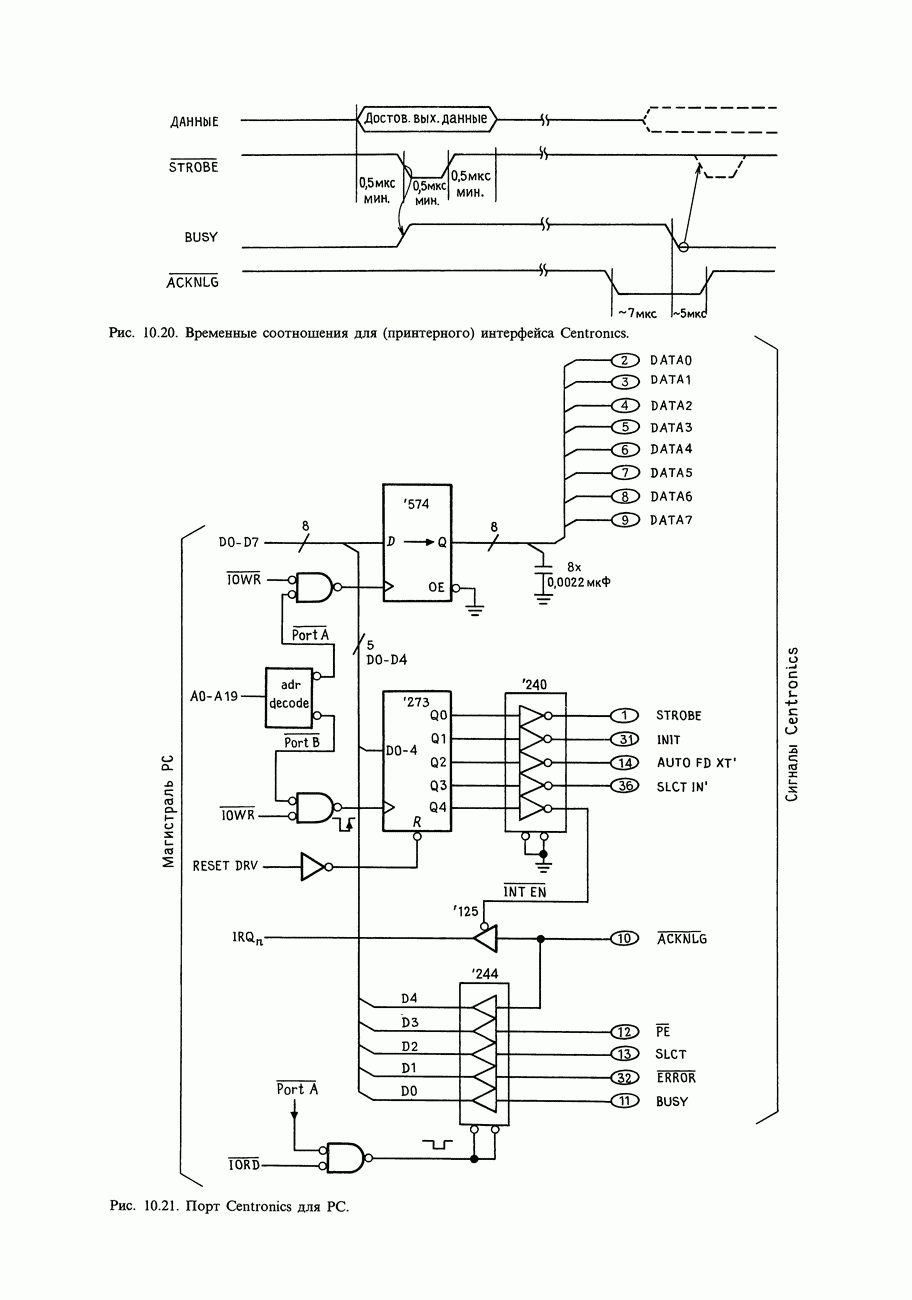
- 10.20. Параллельная связь
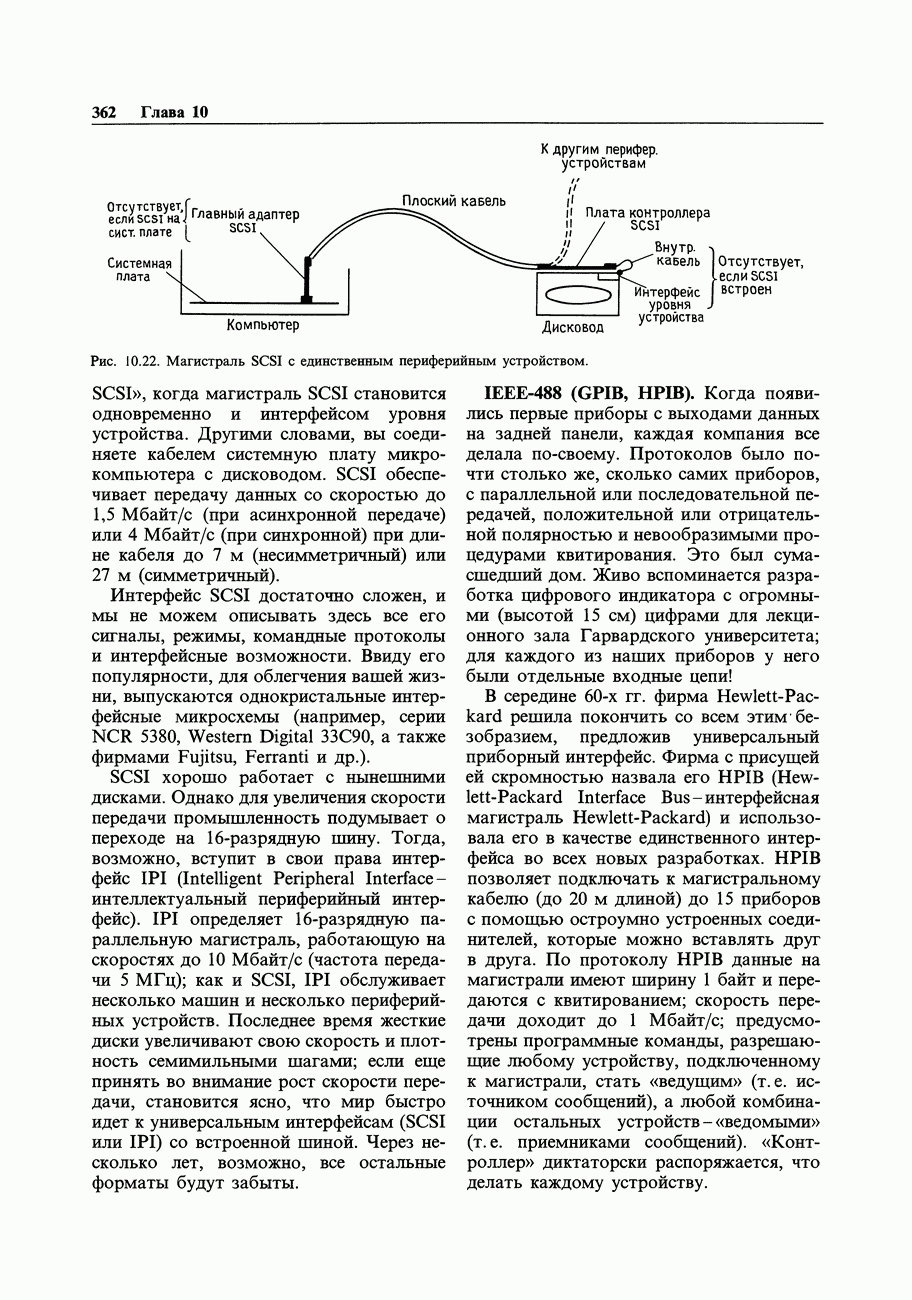
- 10.21. Локальные вычислительные цепи
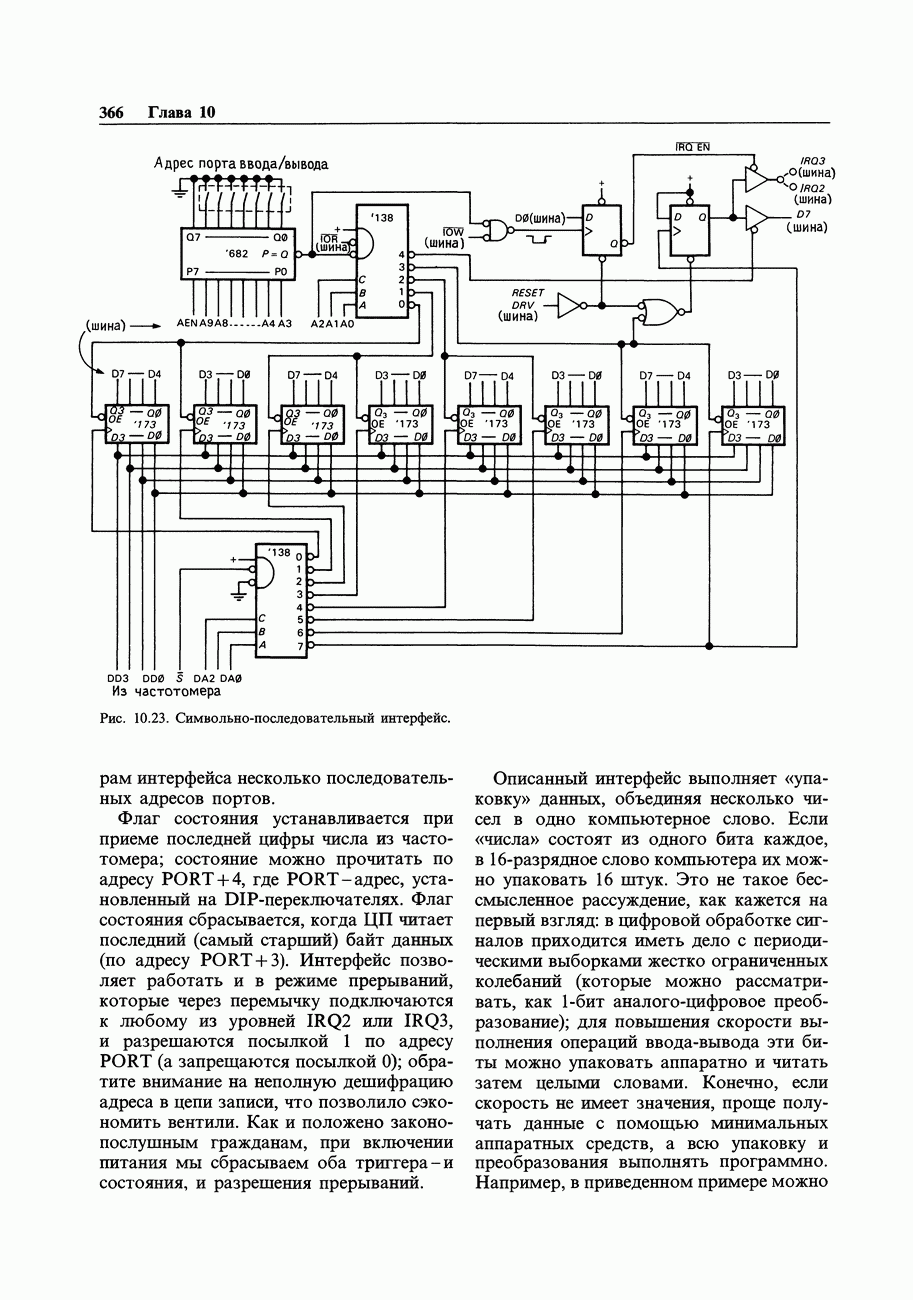
- 10.22. Пример интерфейса: аппаратная упаковка данных
- 10.23. Форматы чисел