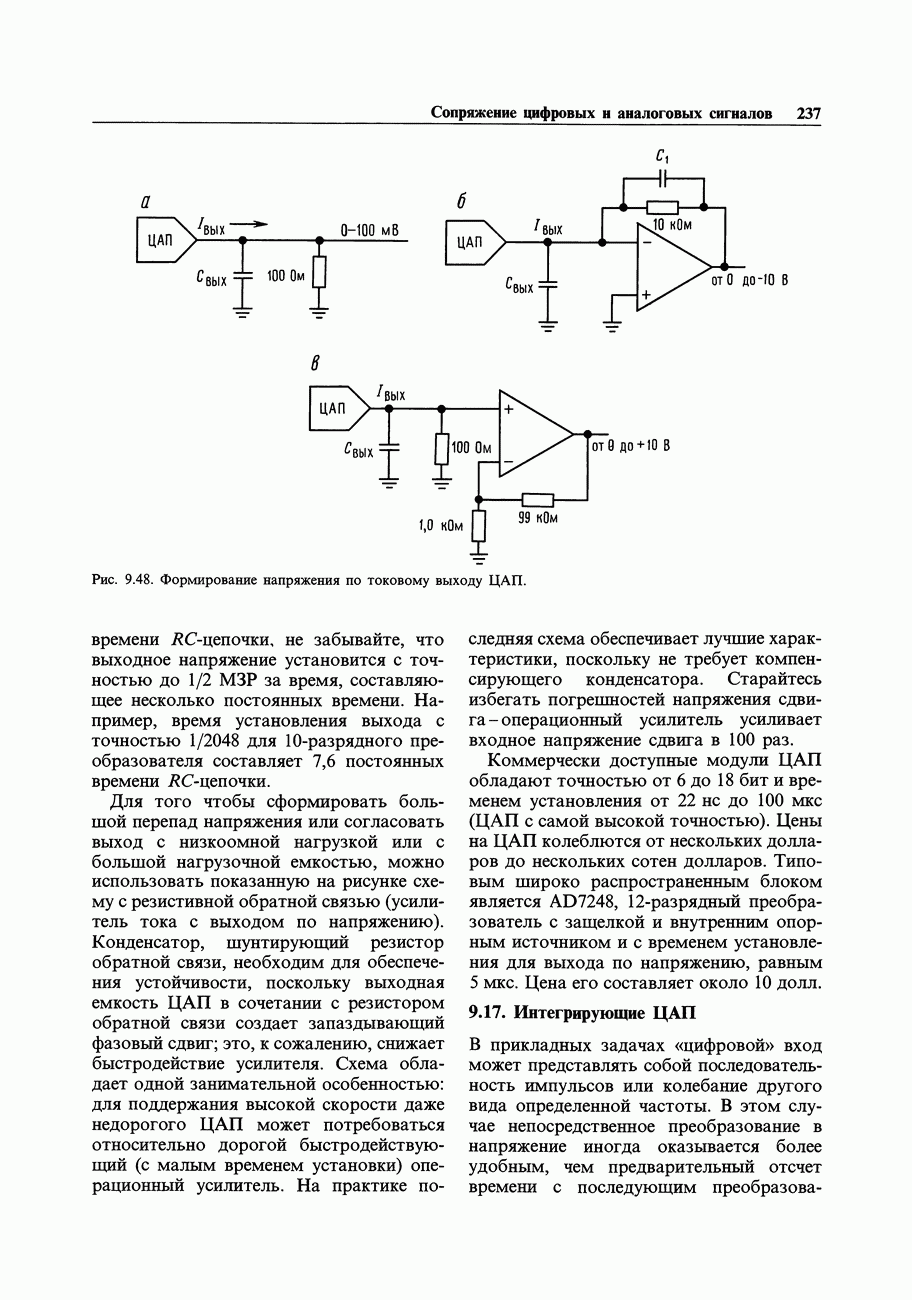
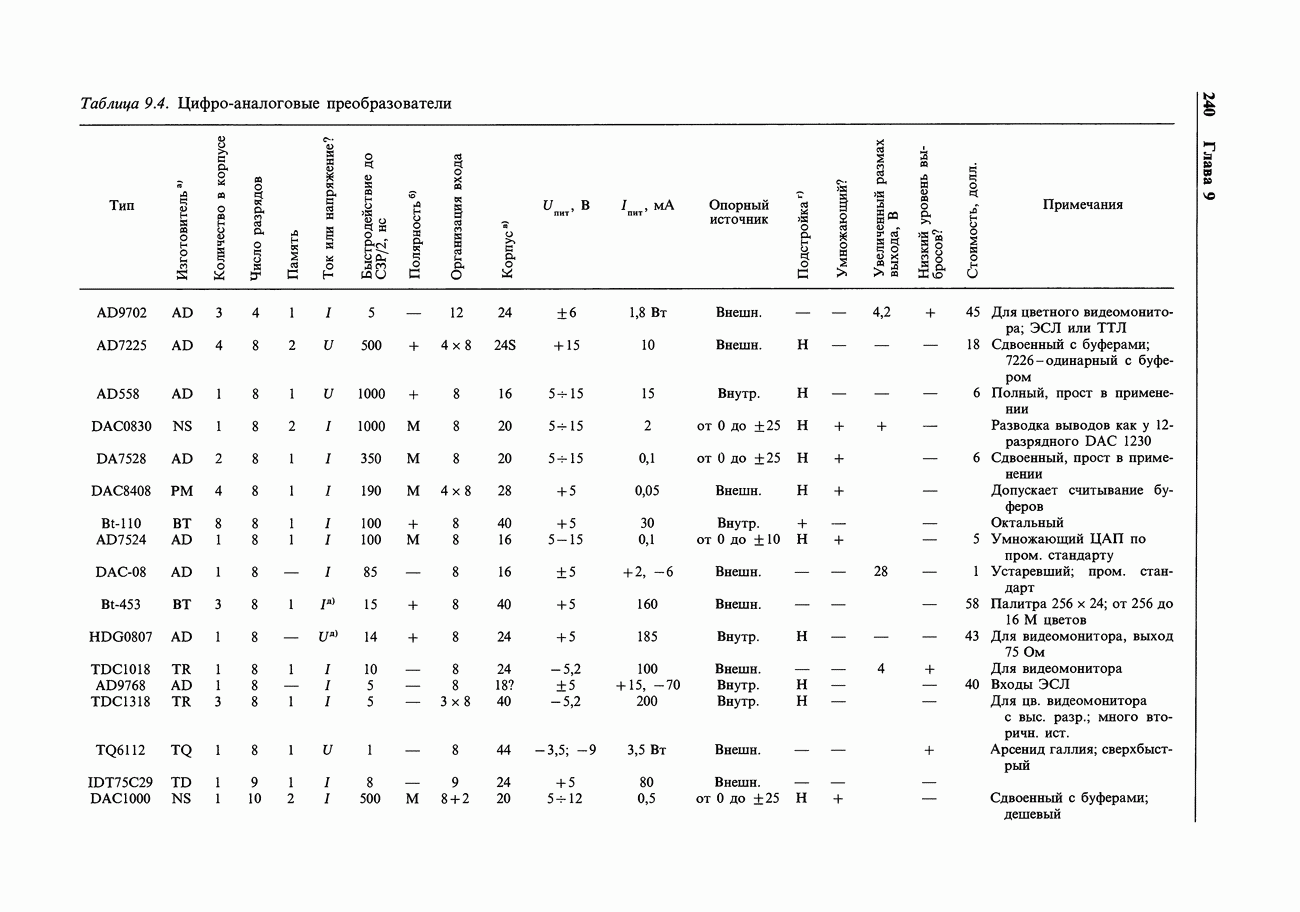
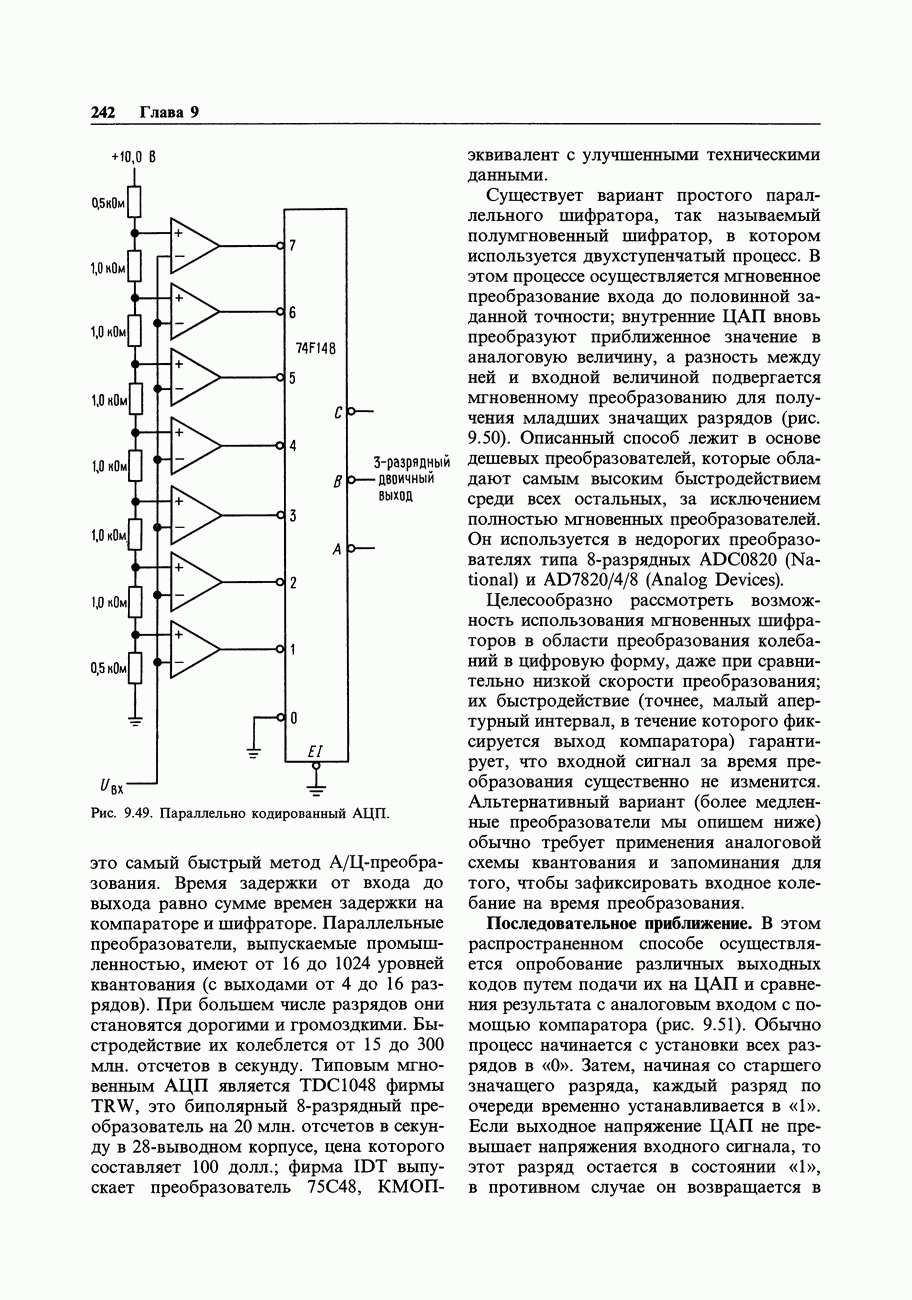
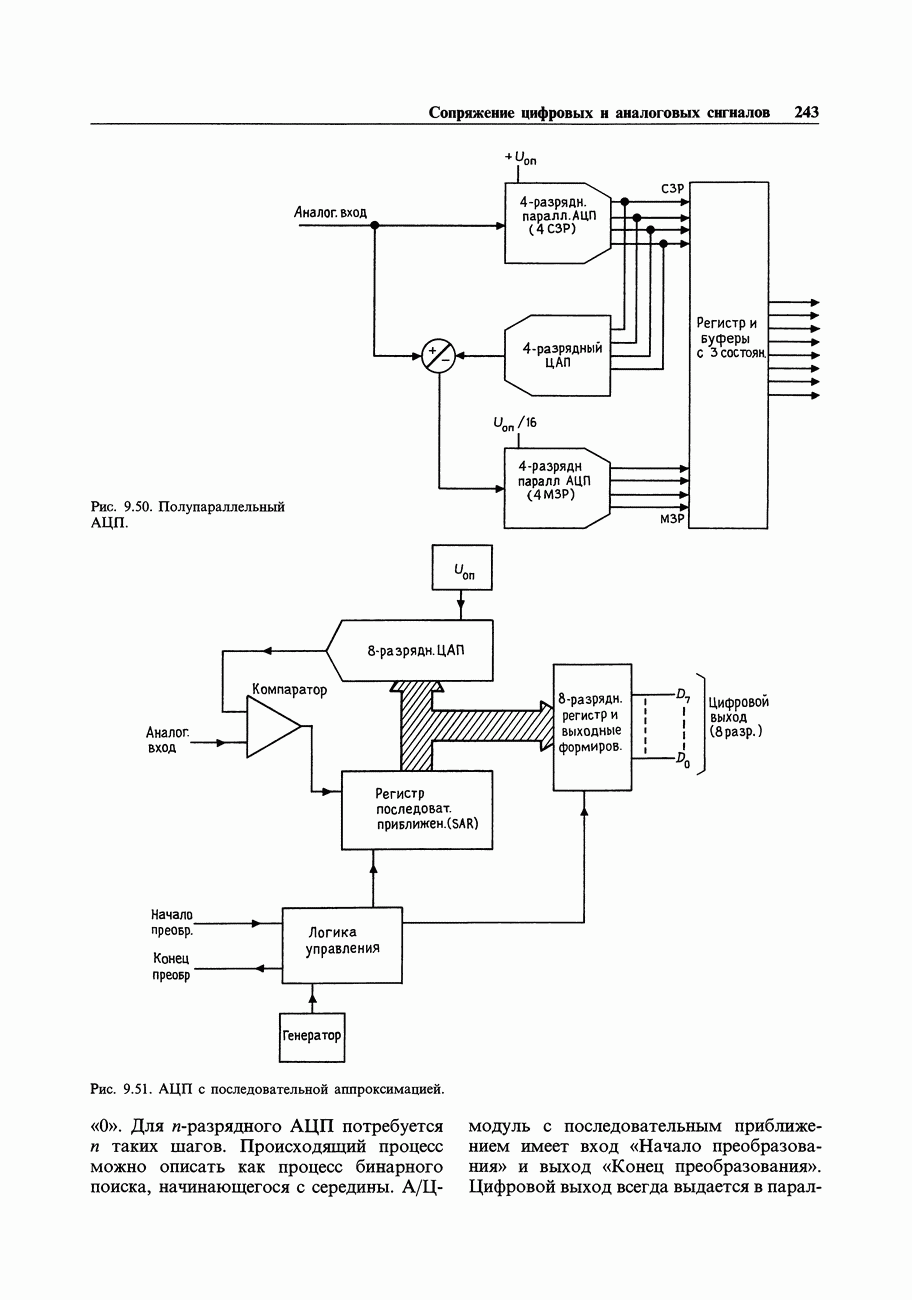
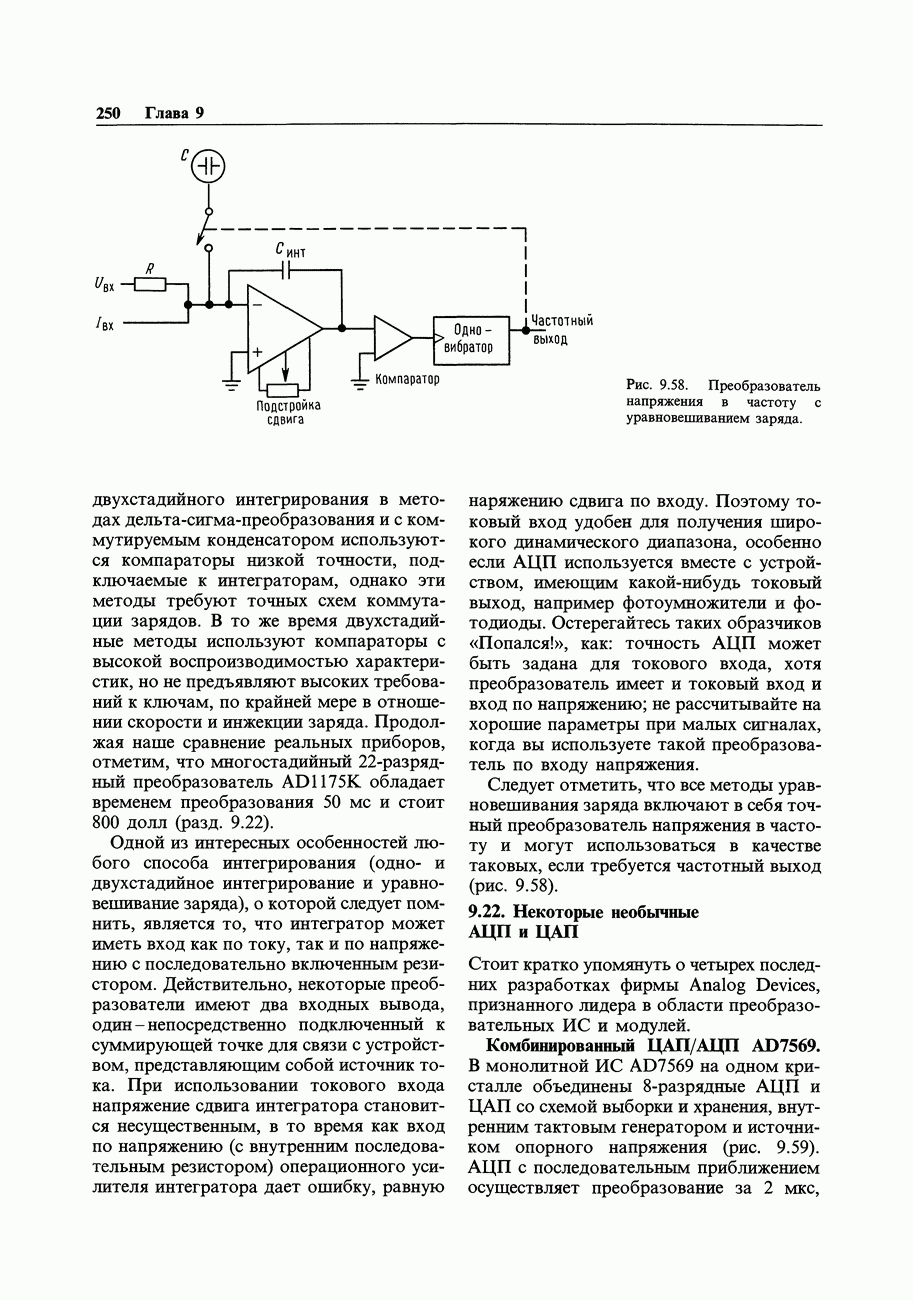
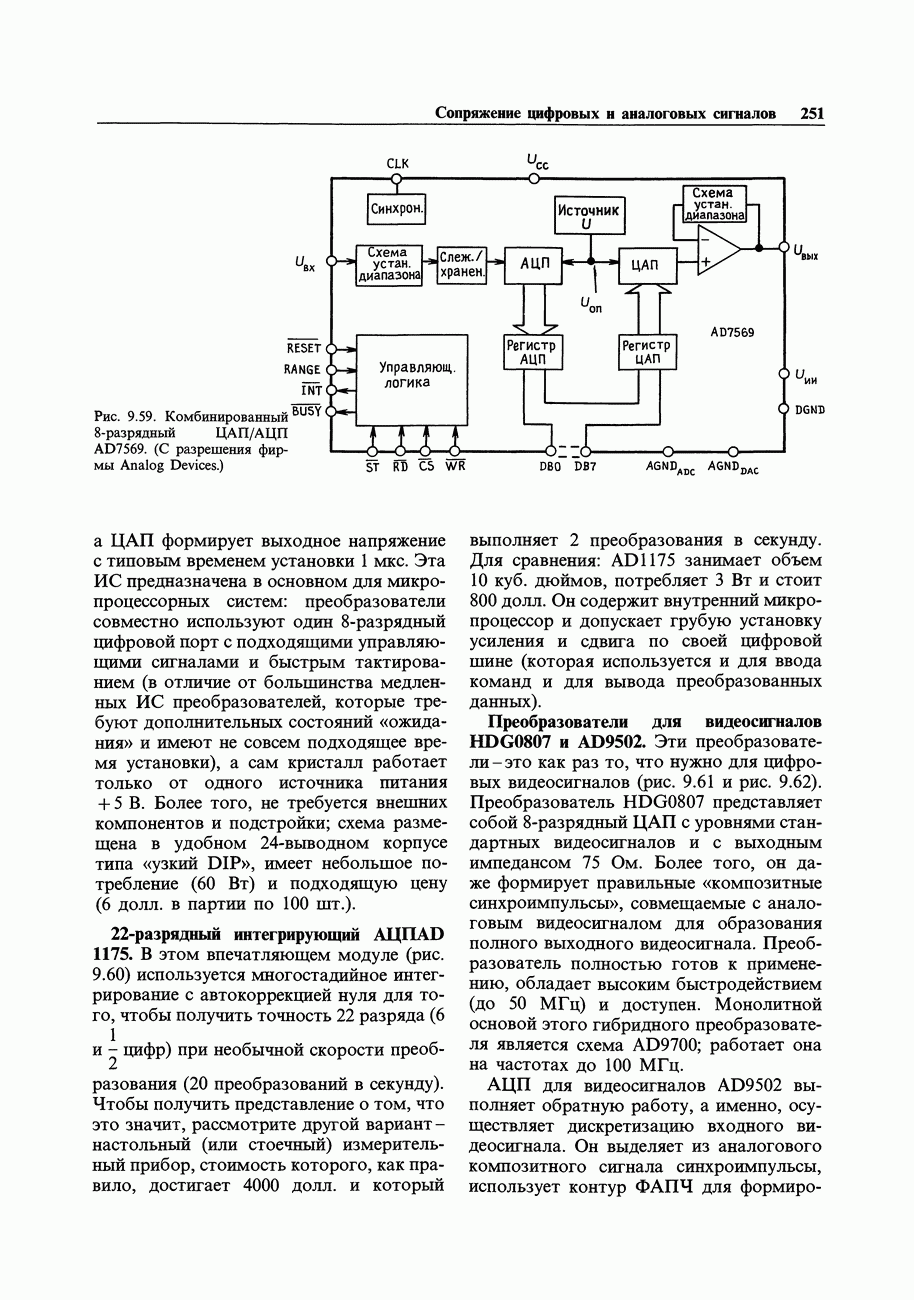
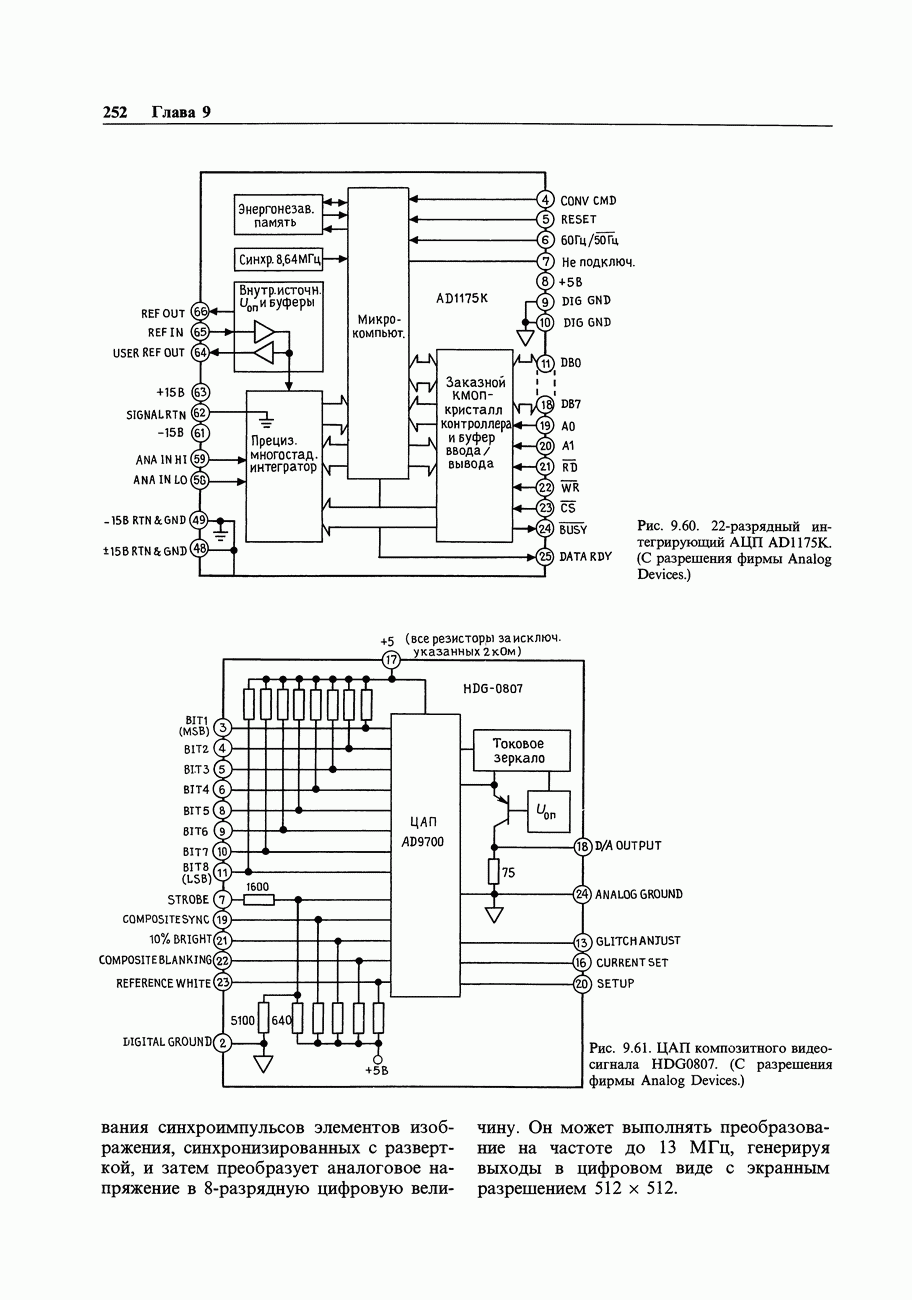
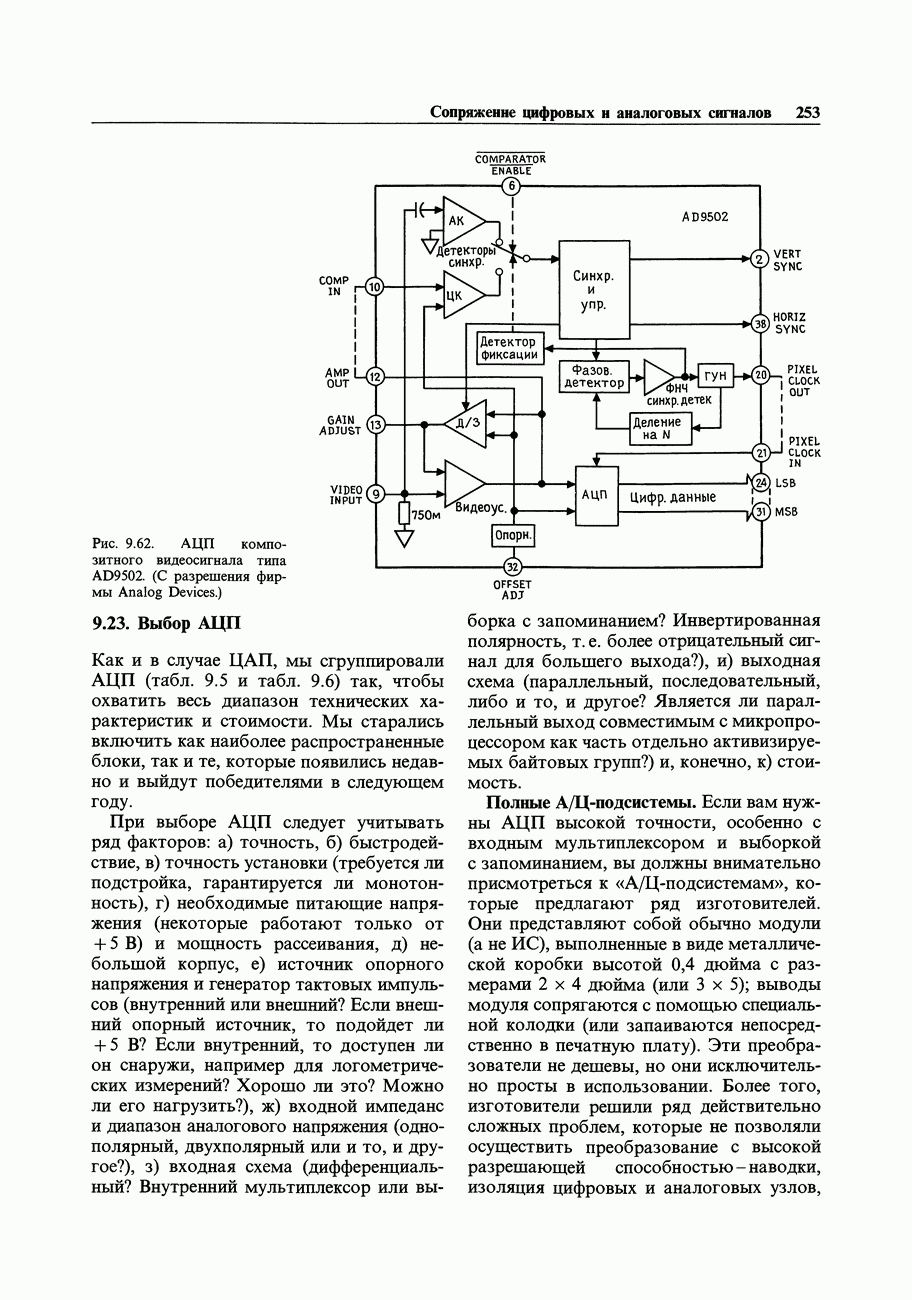
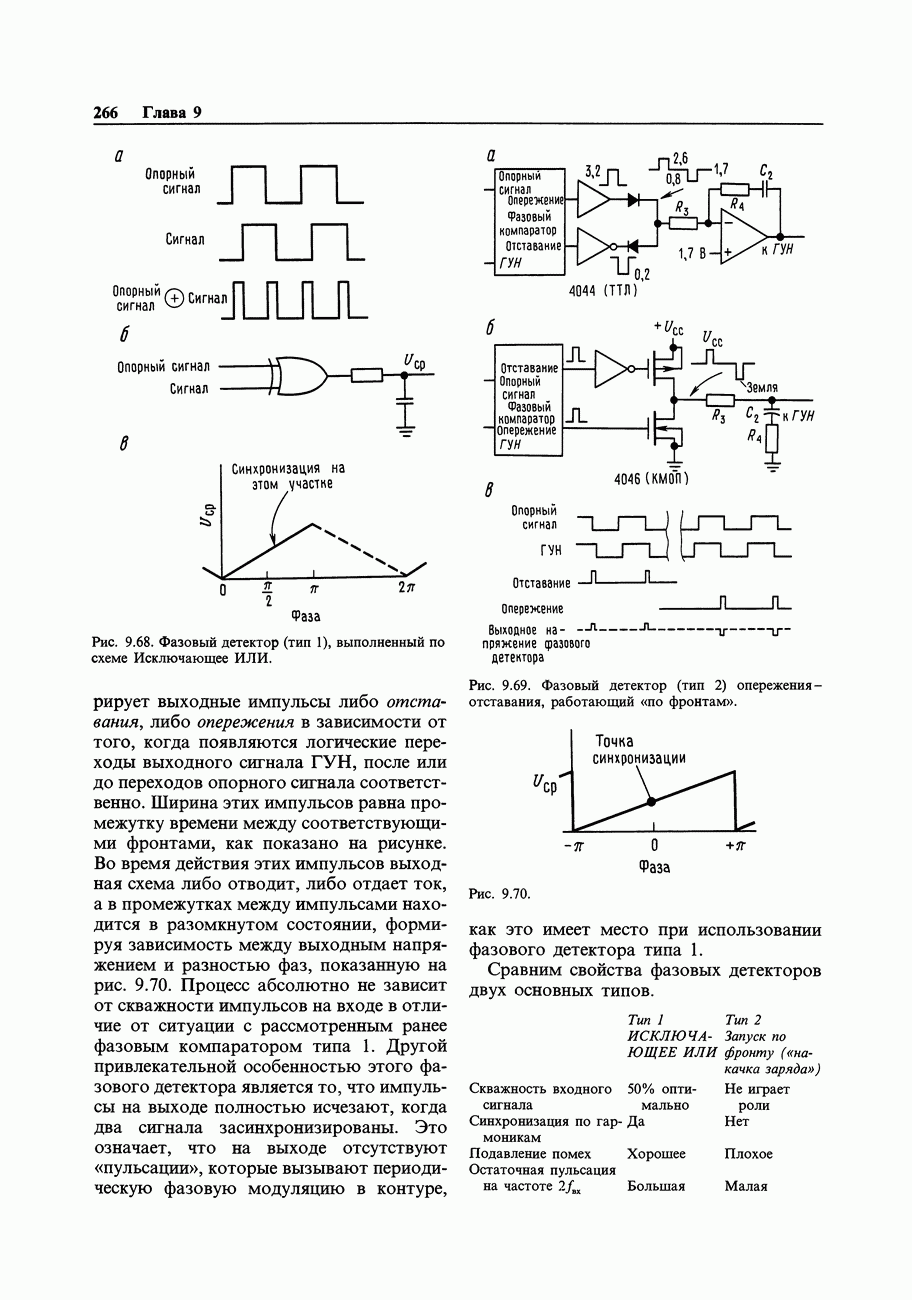
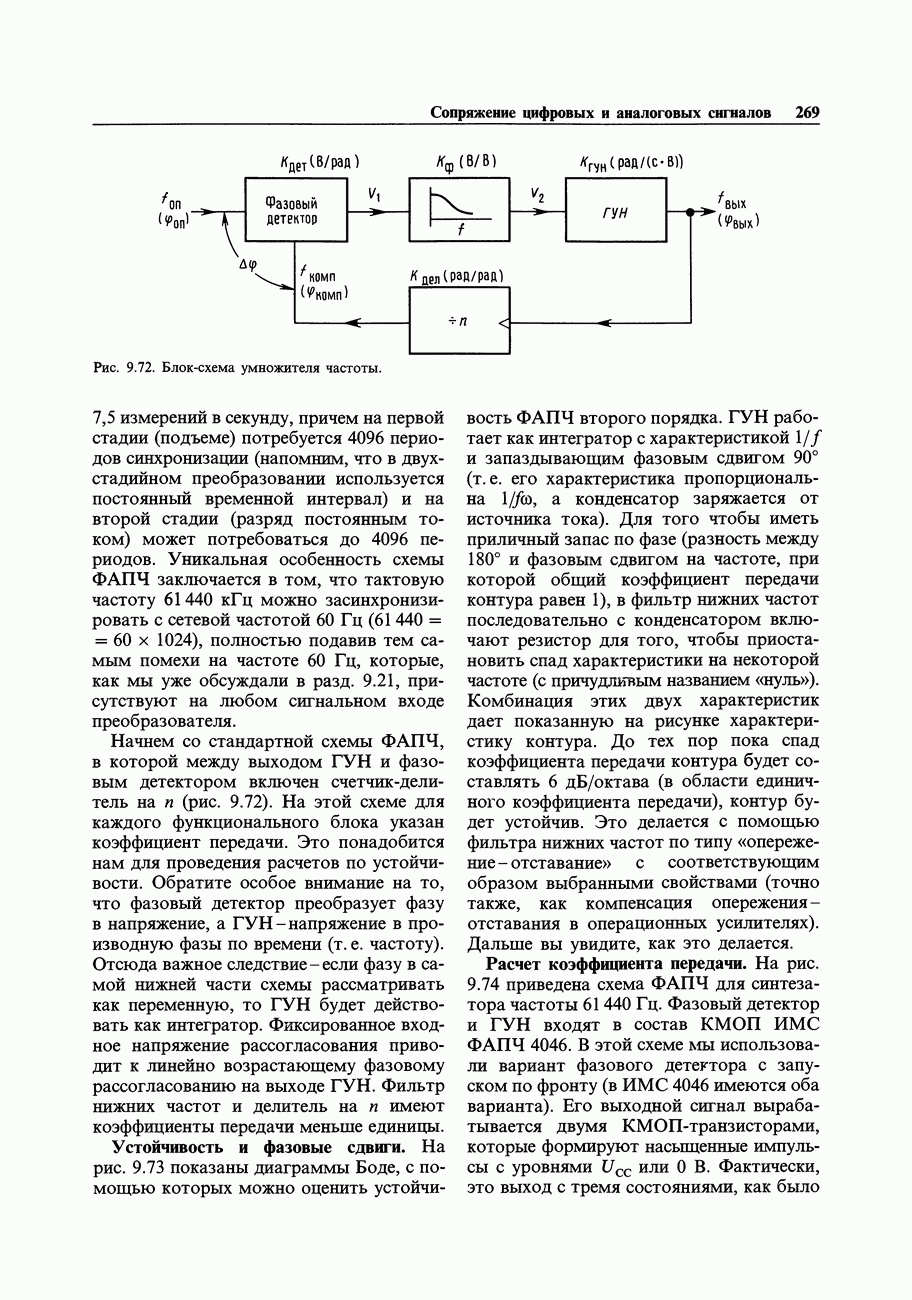
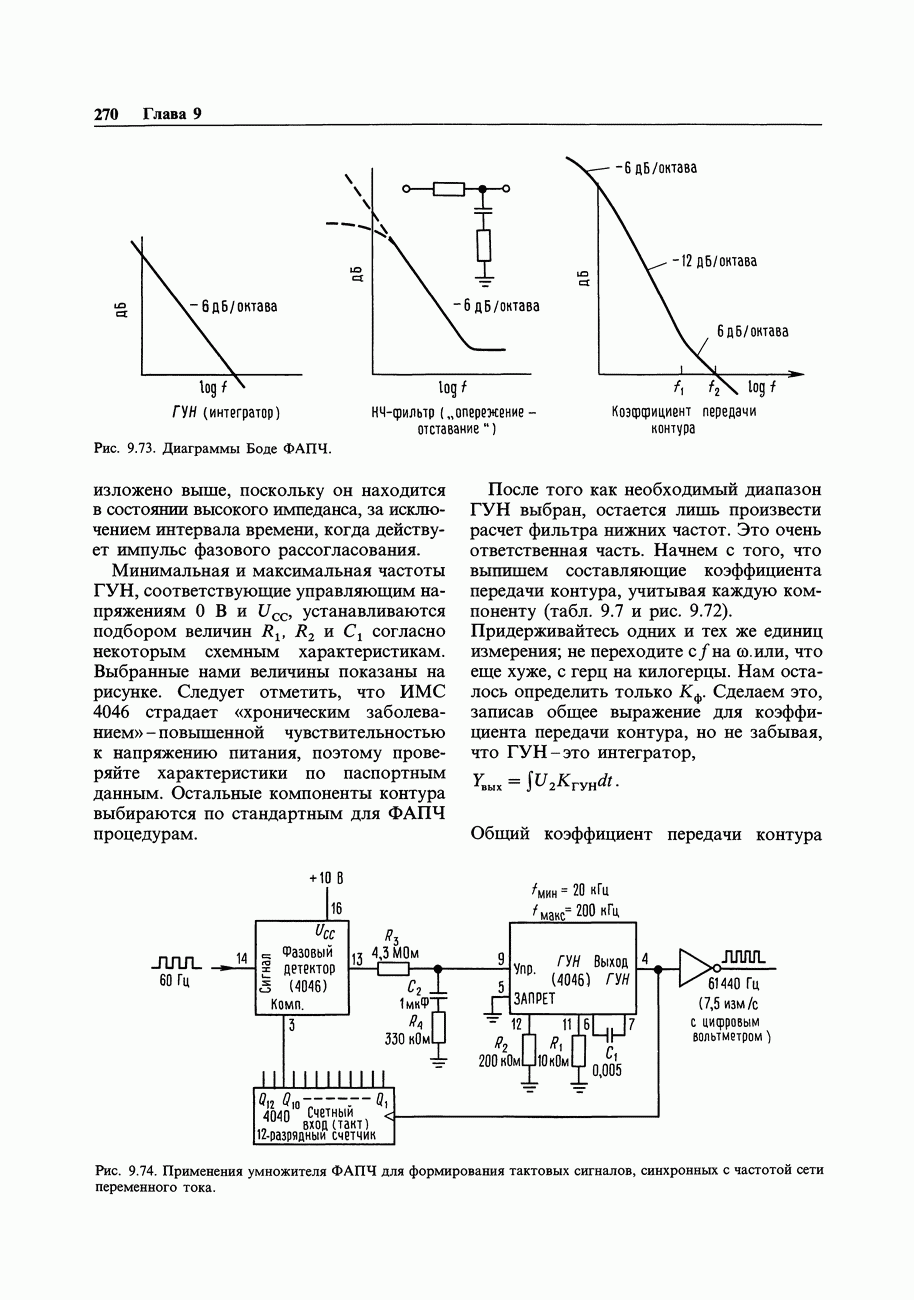
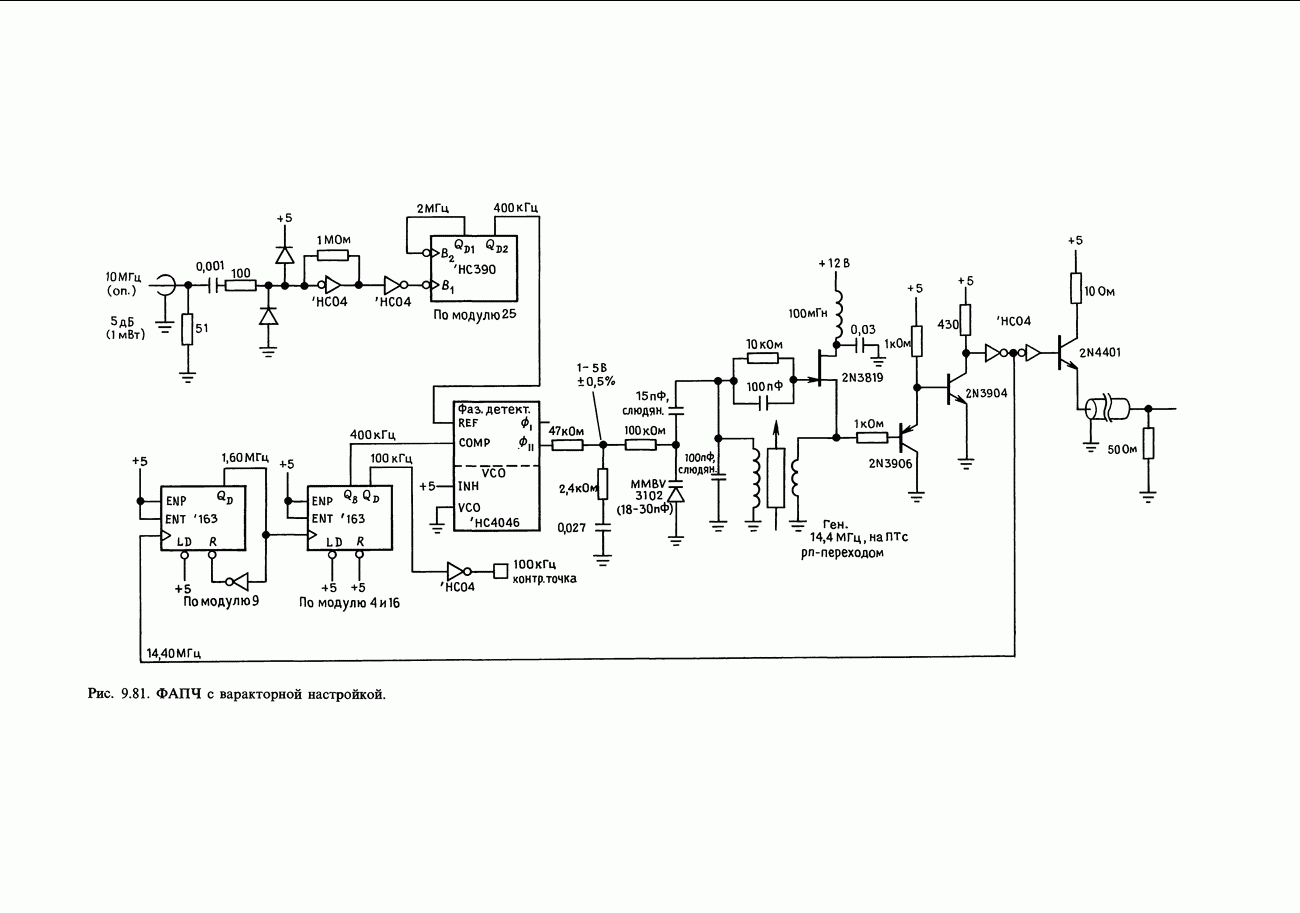
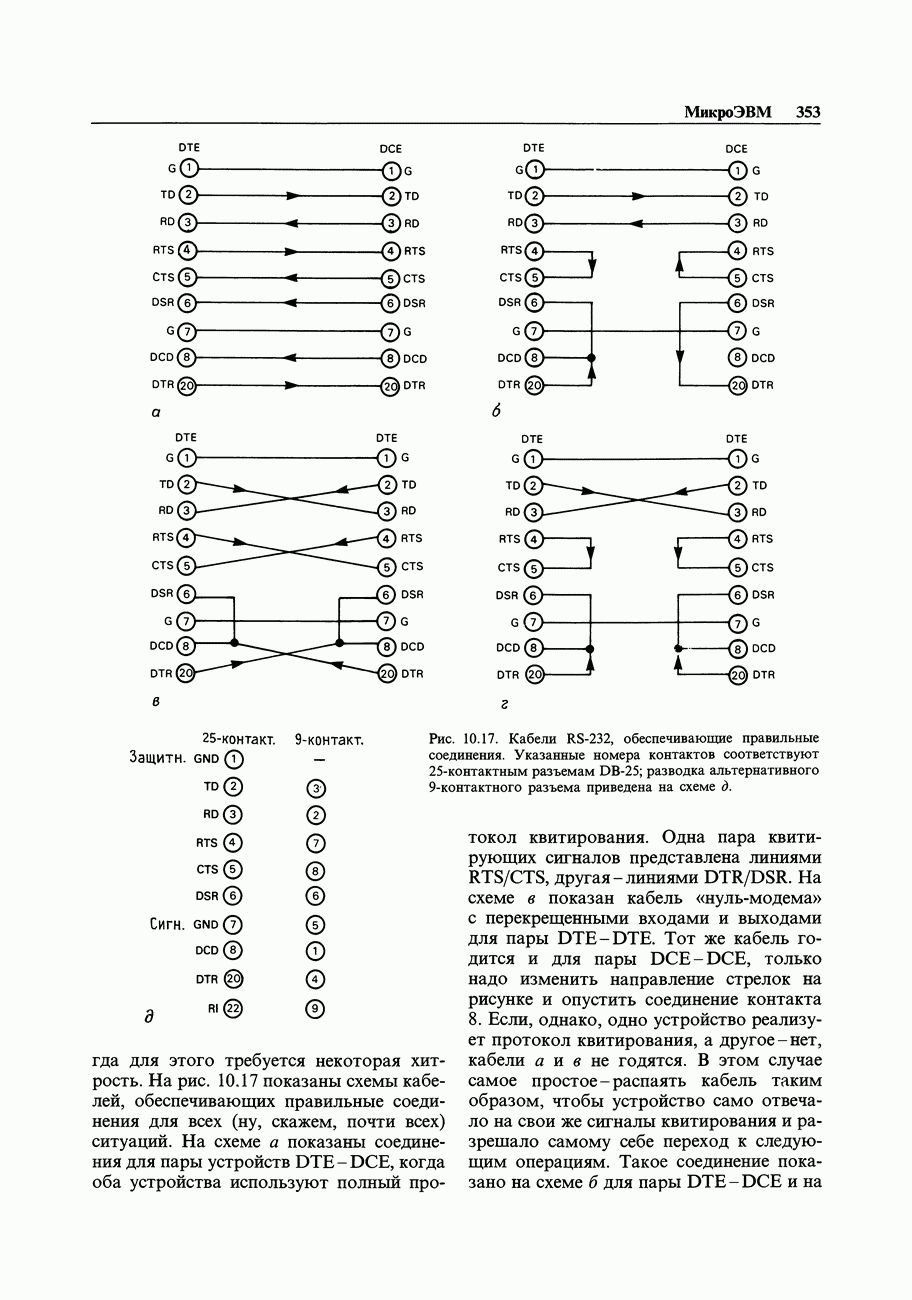
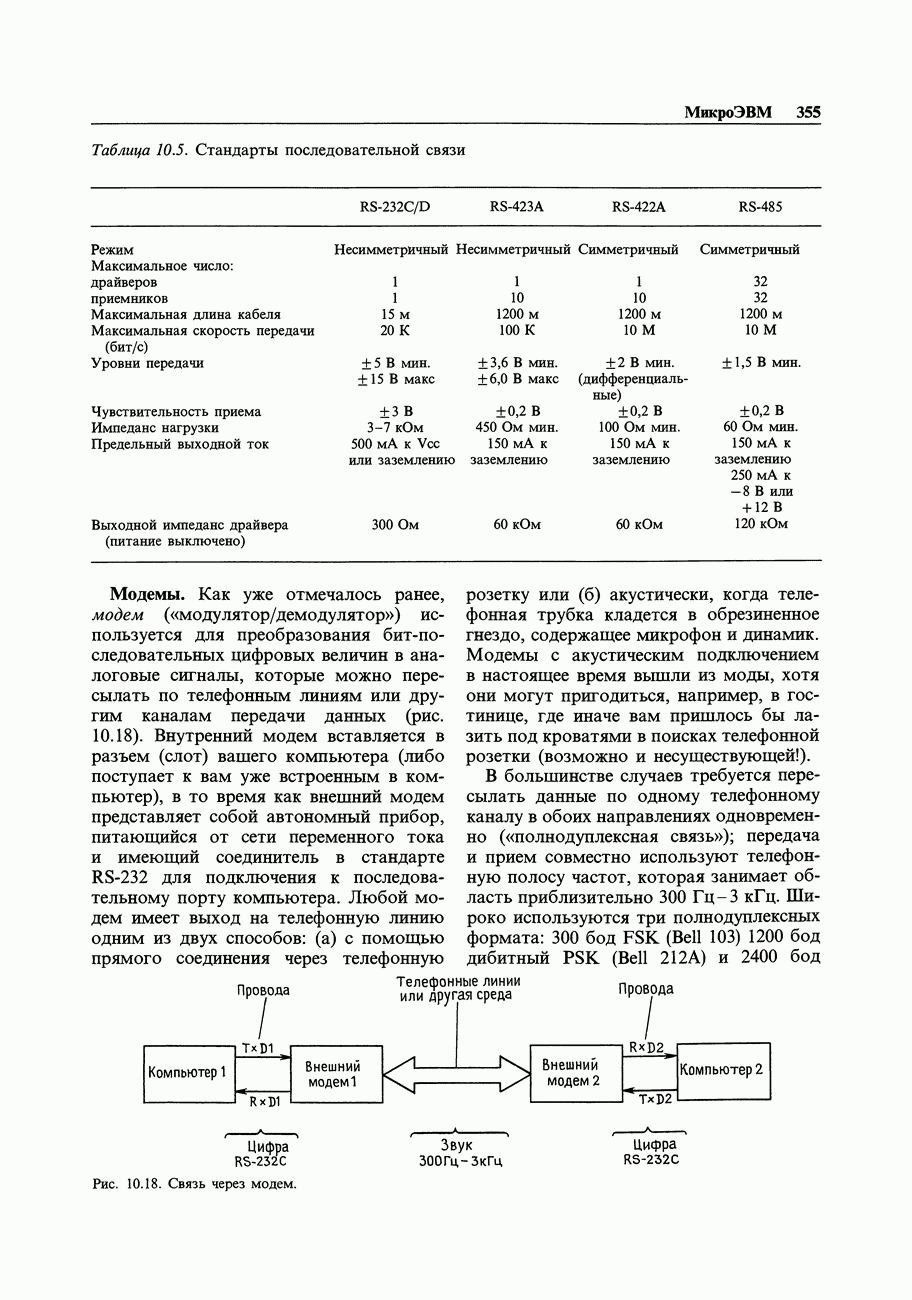
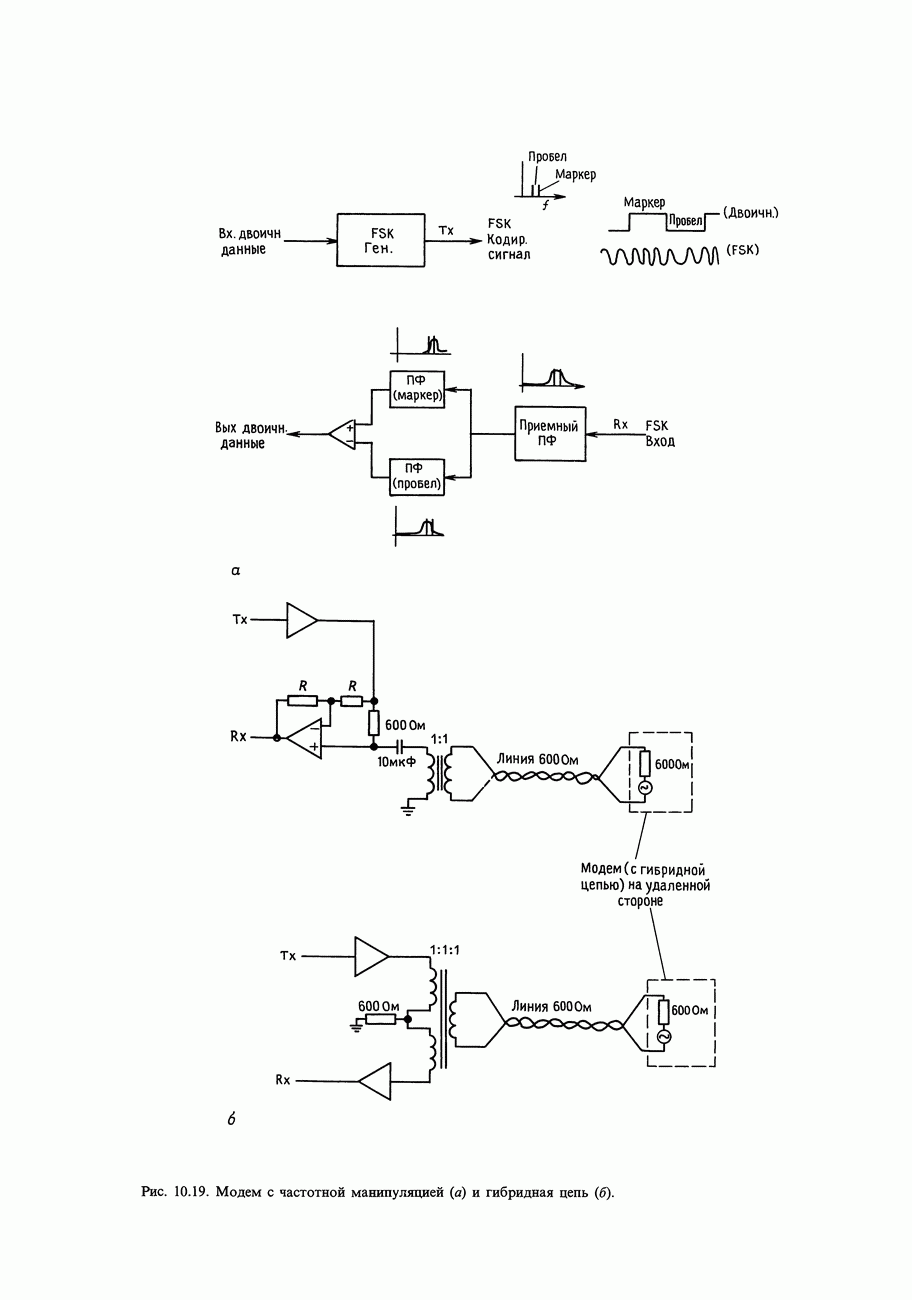
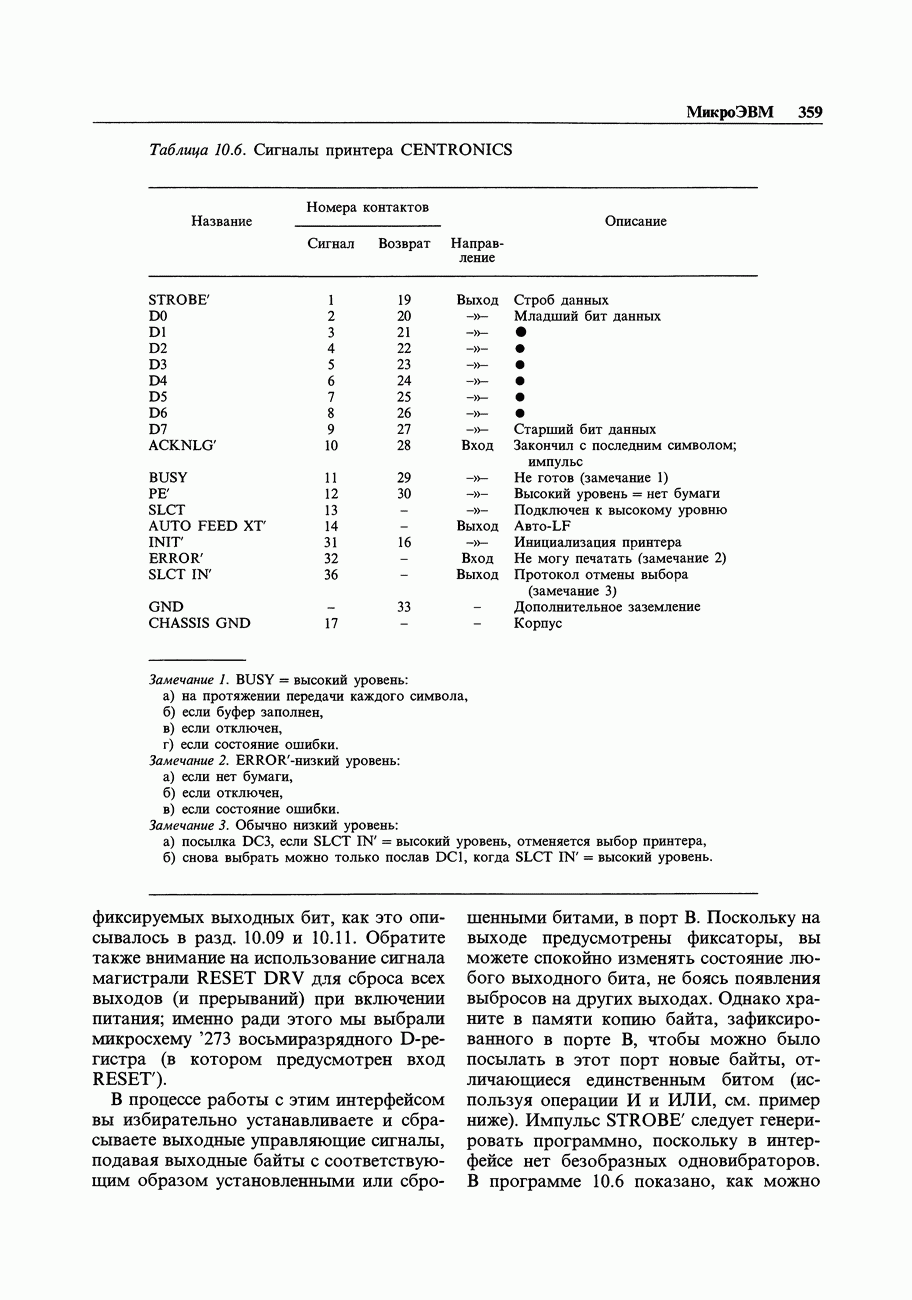
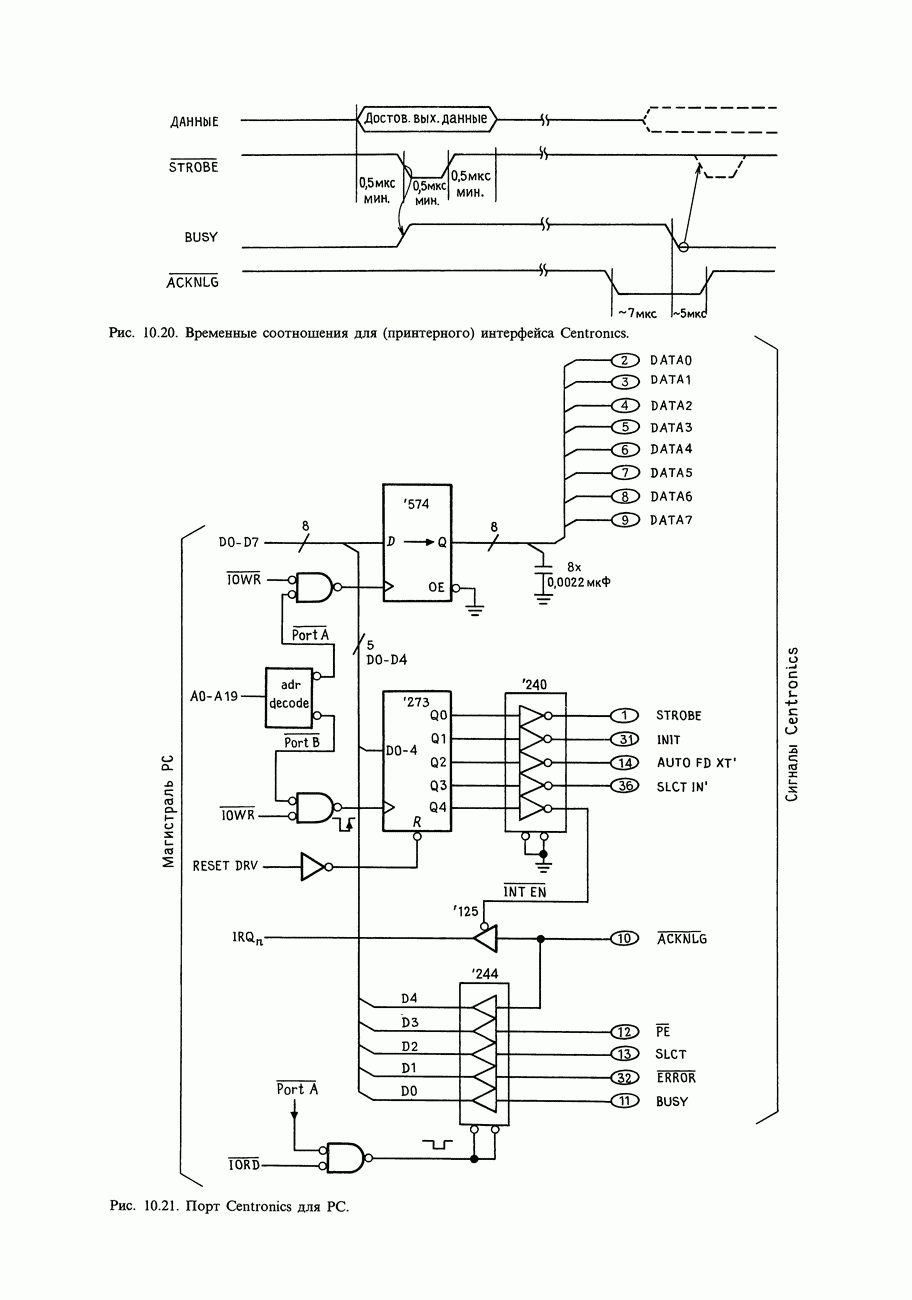
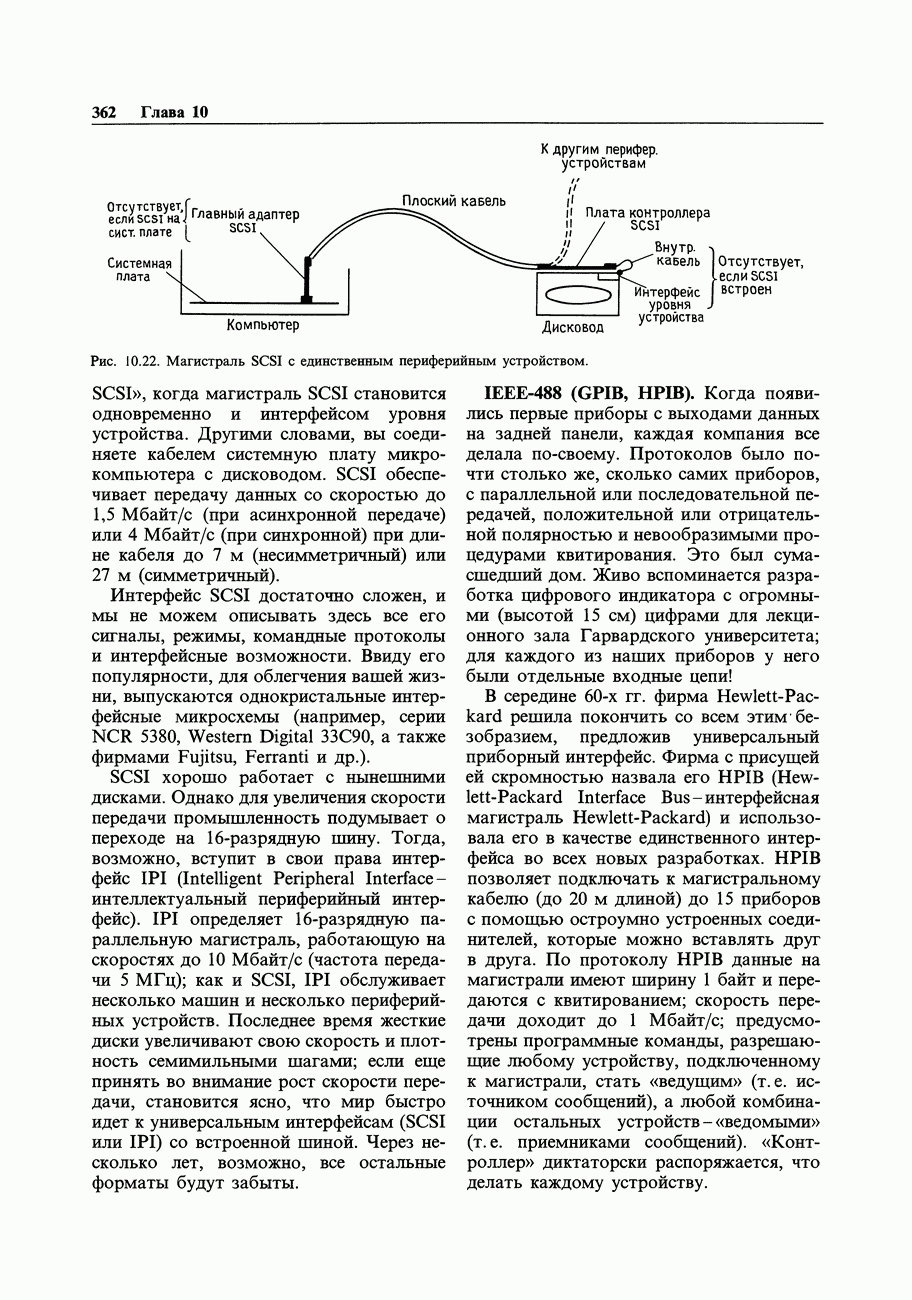
| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
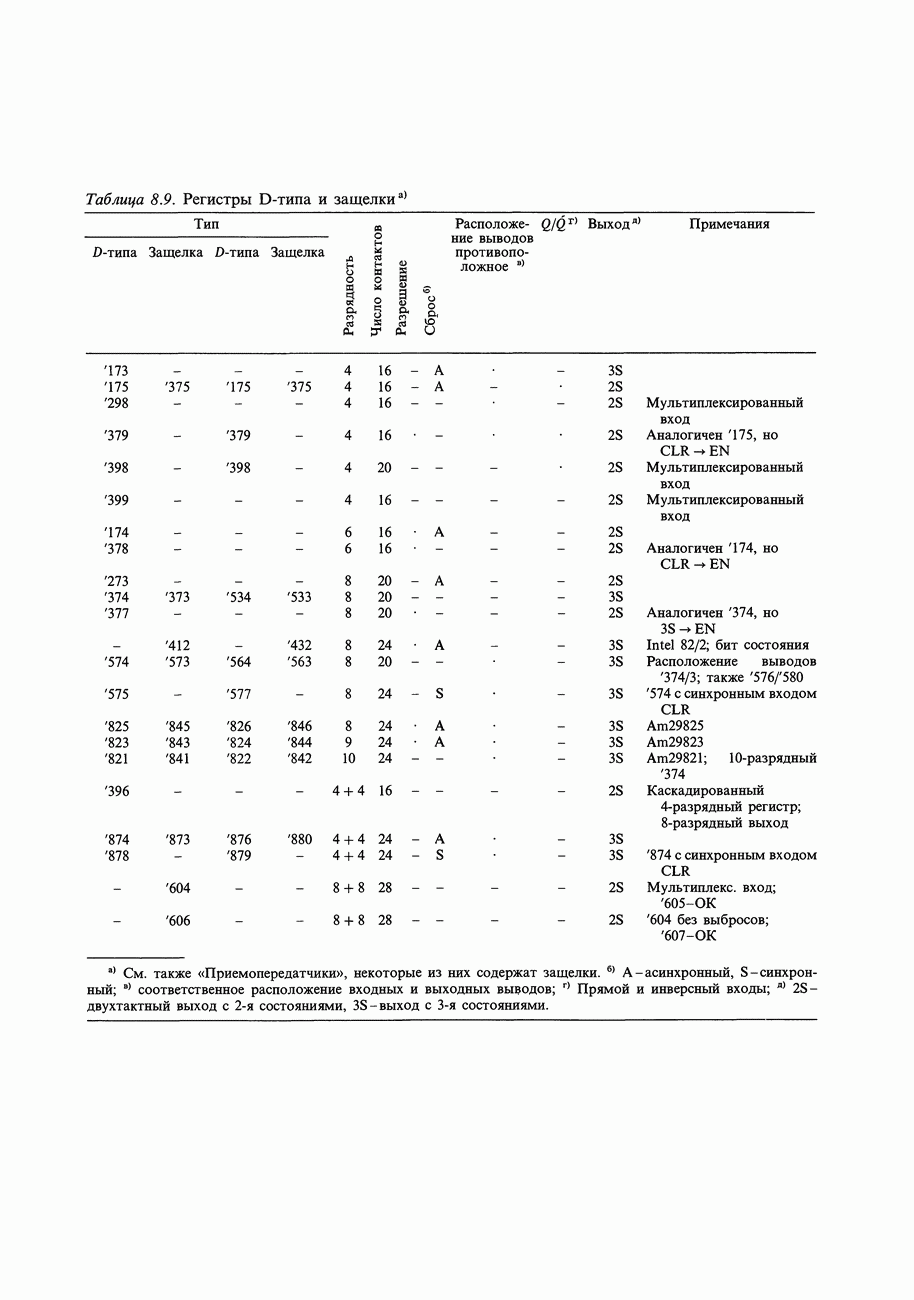
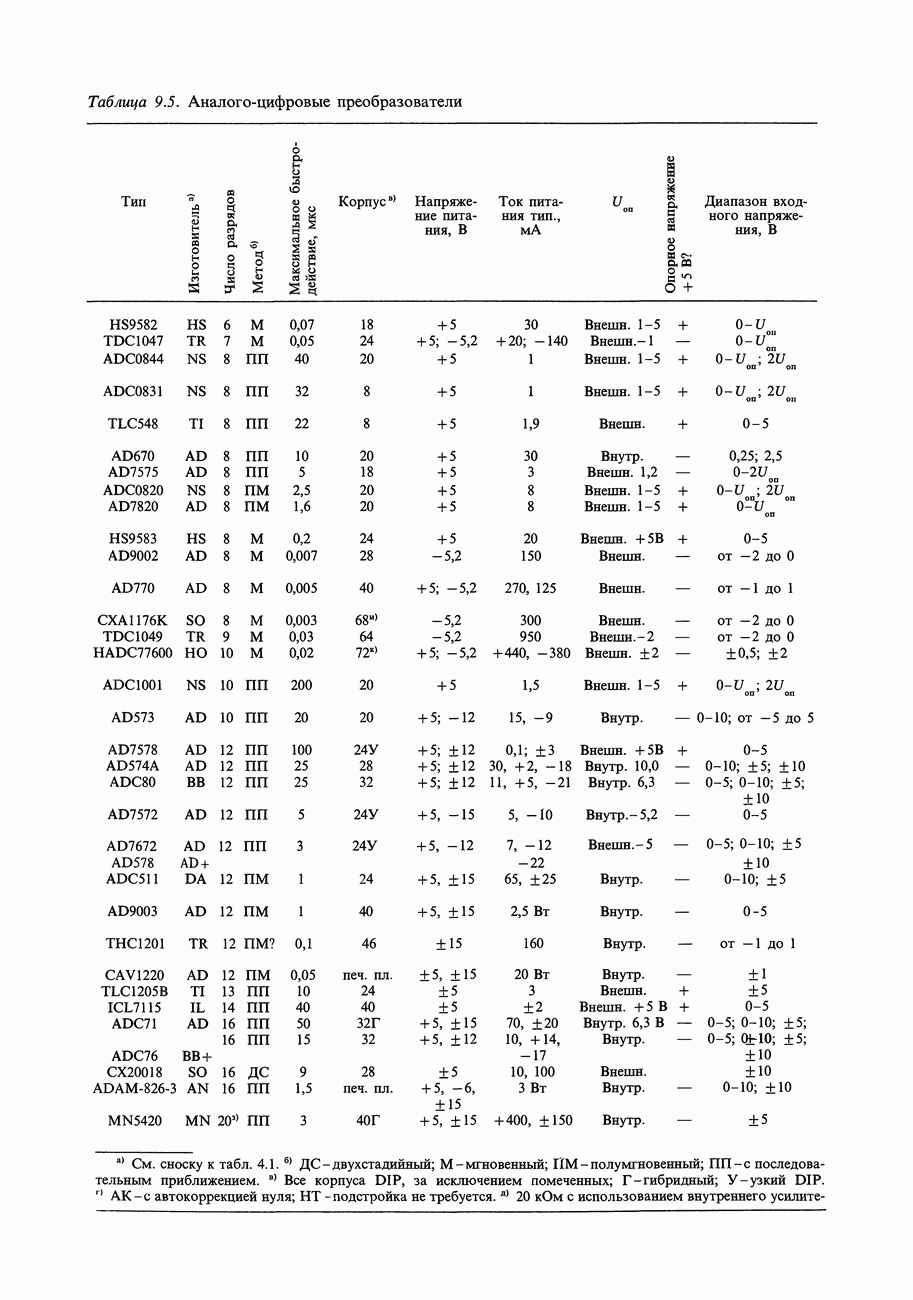
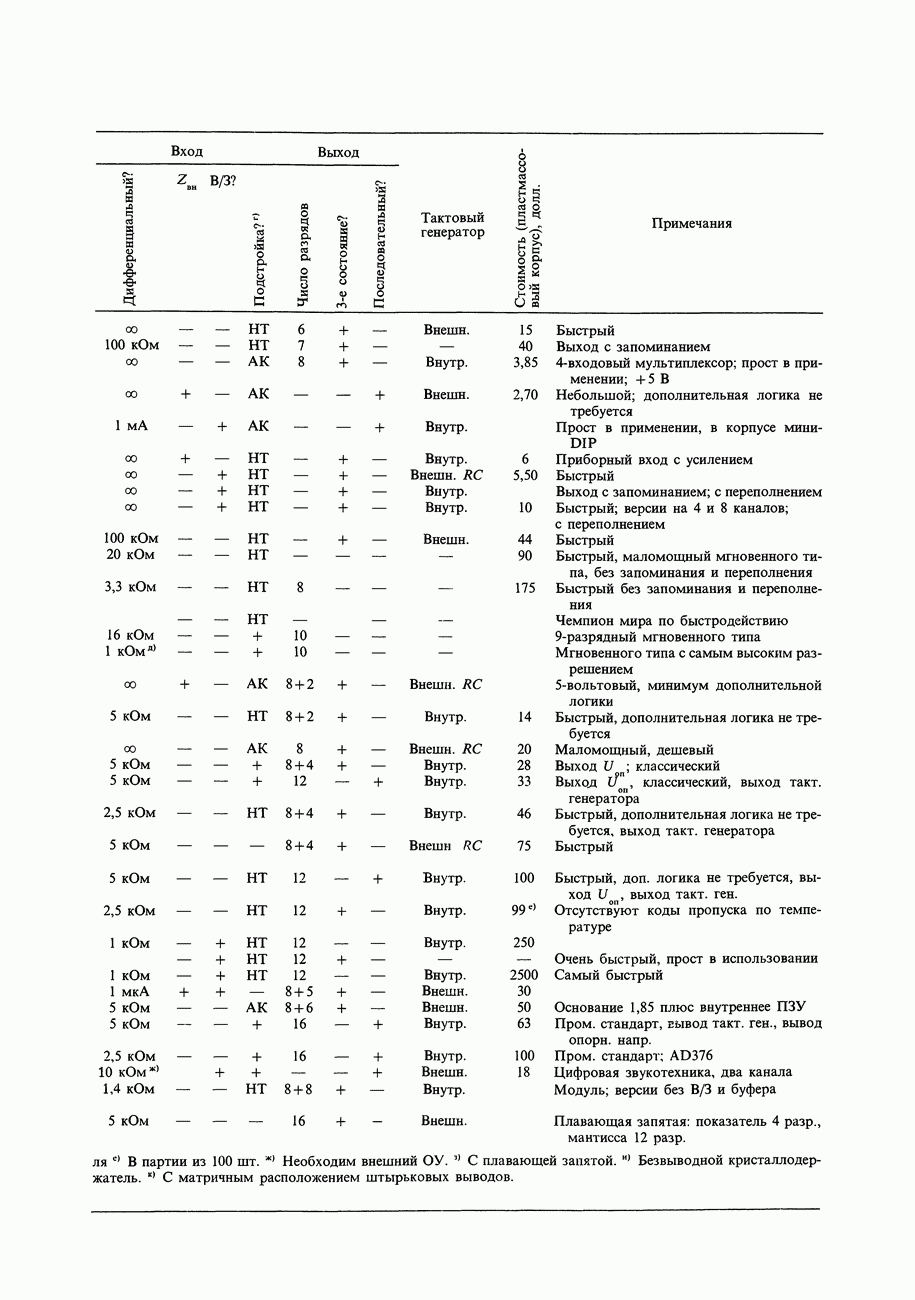
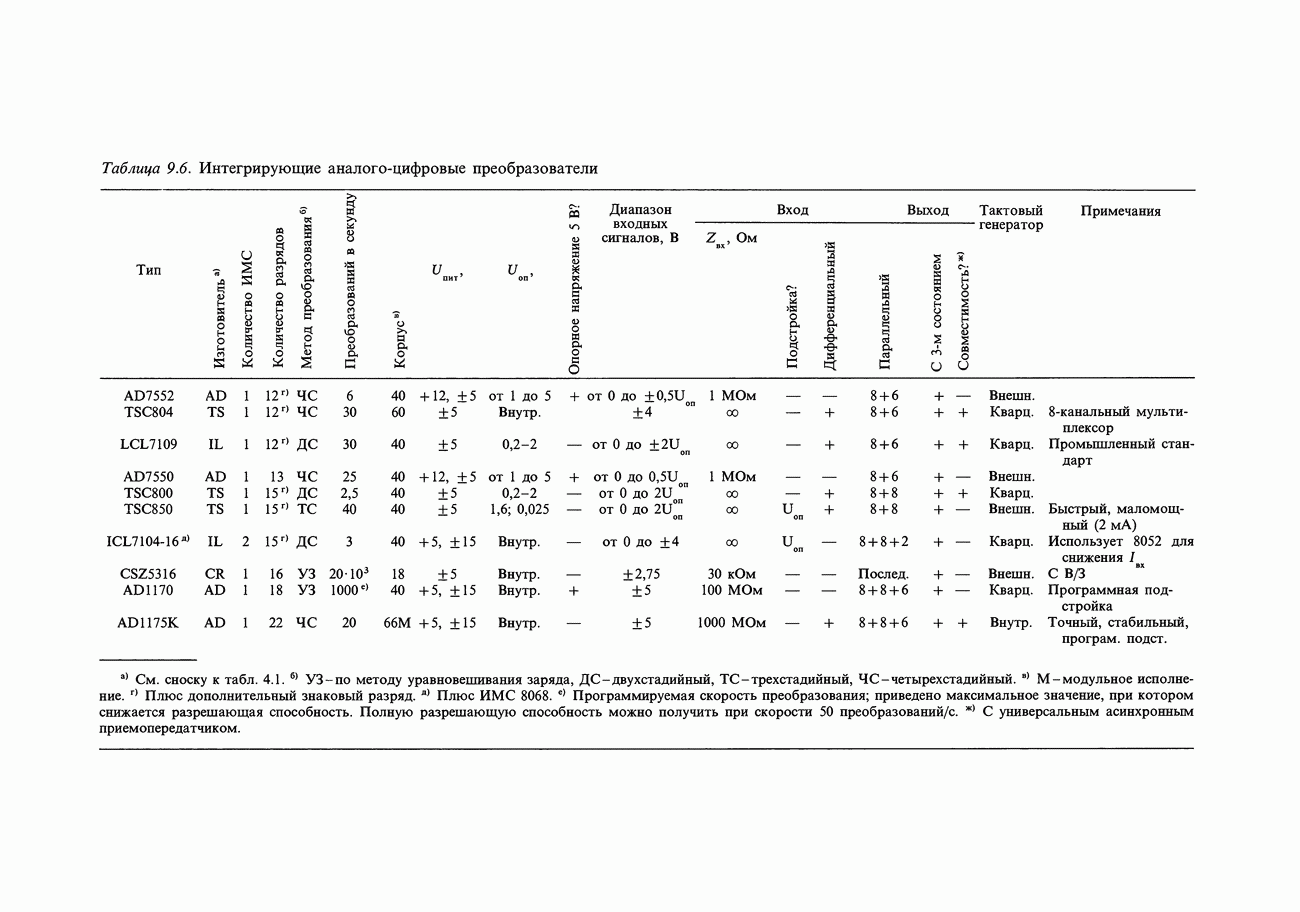
10.23. Форматы чисел
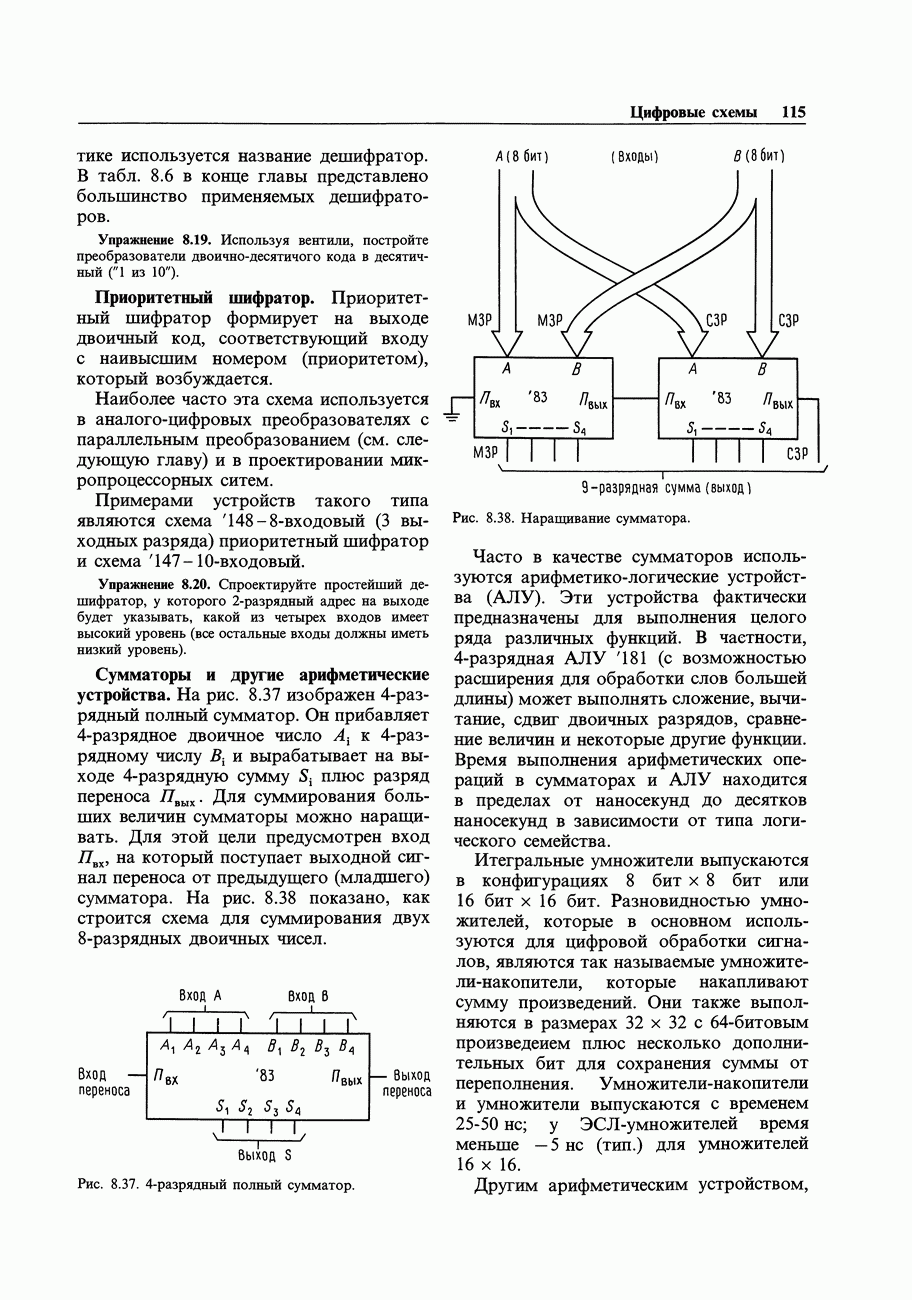
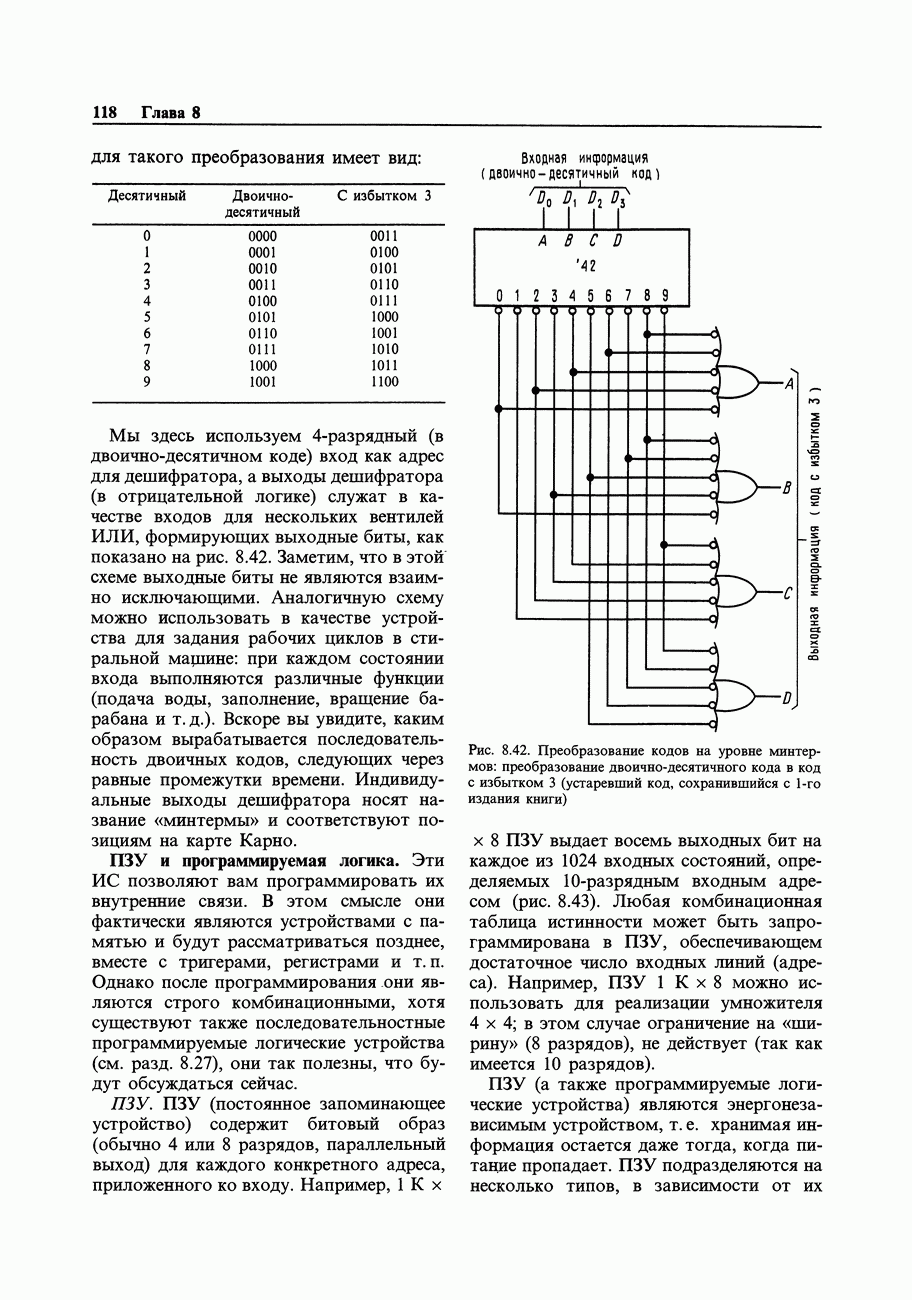
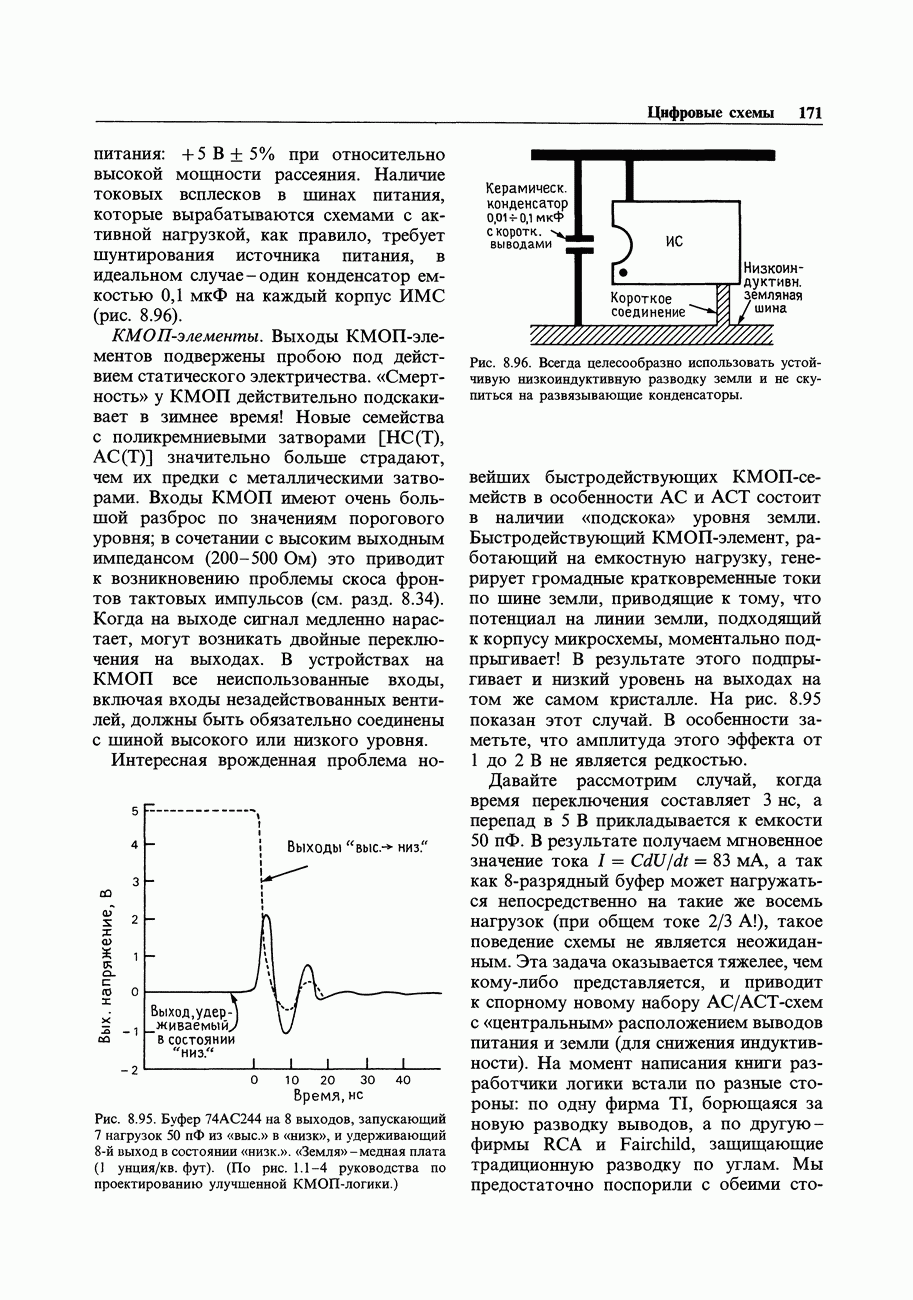
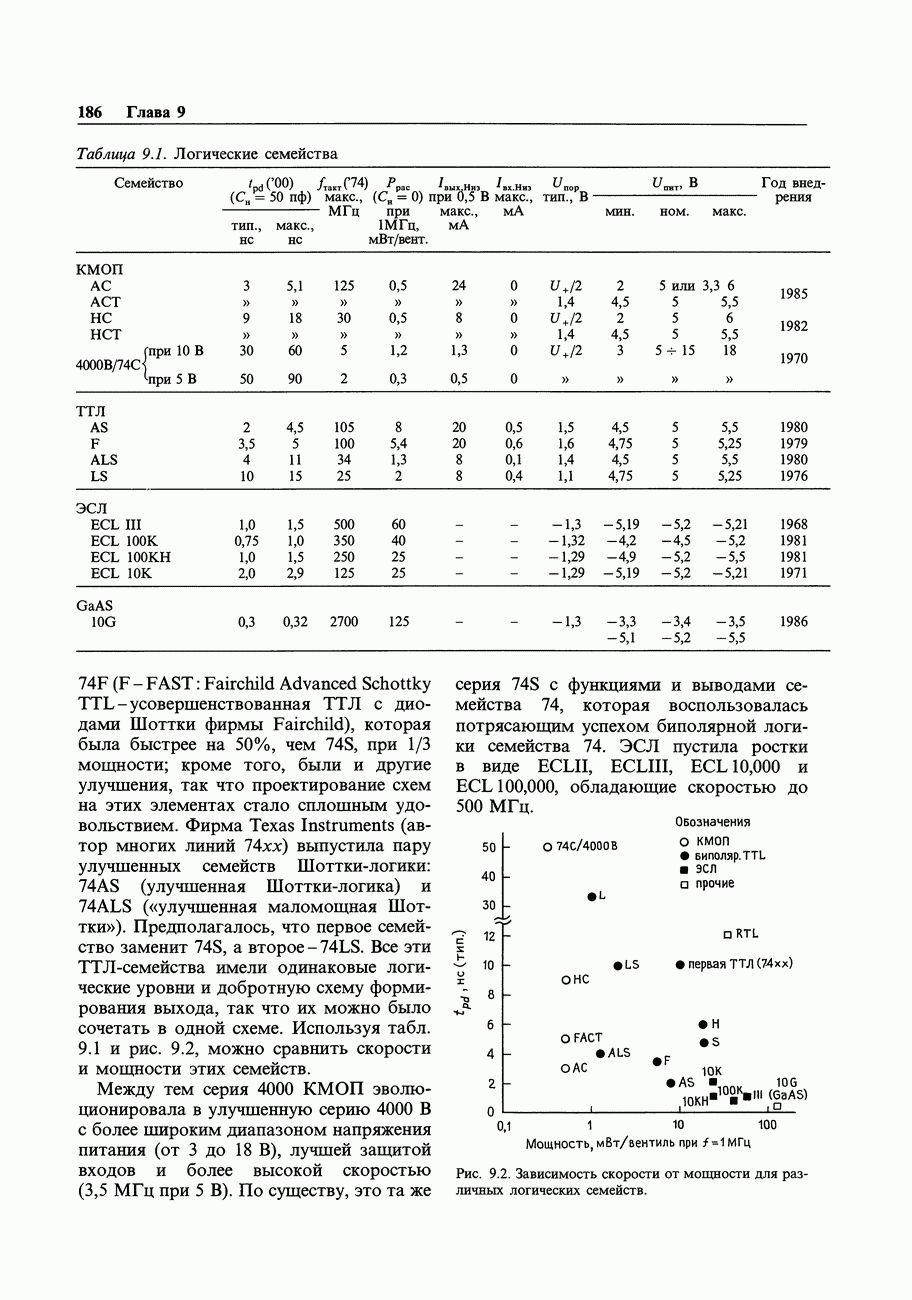
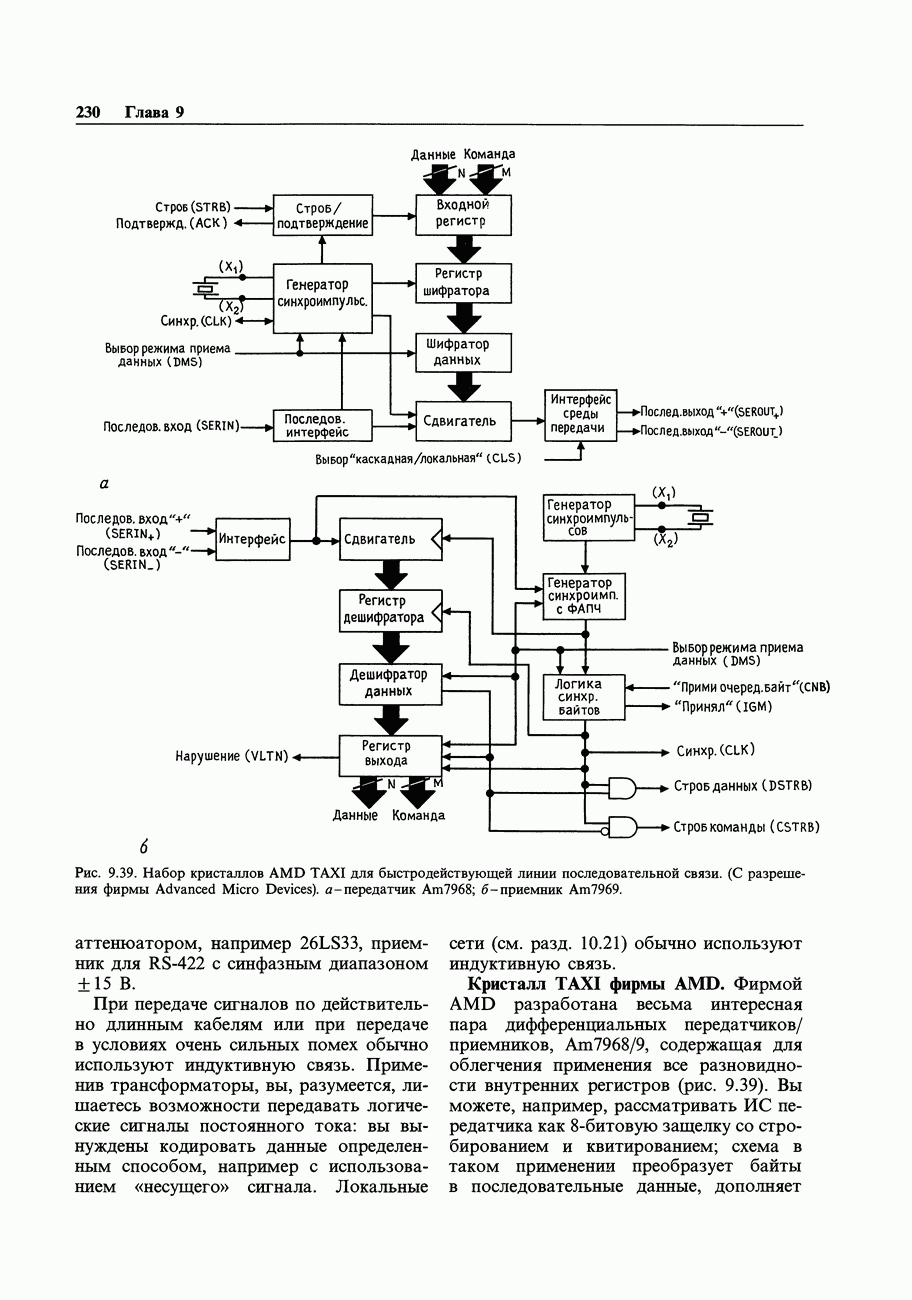
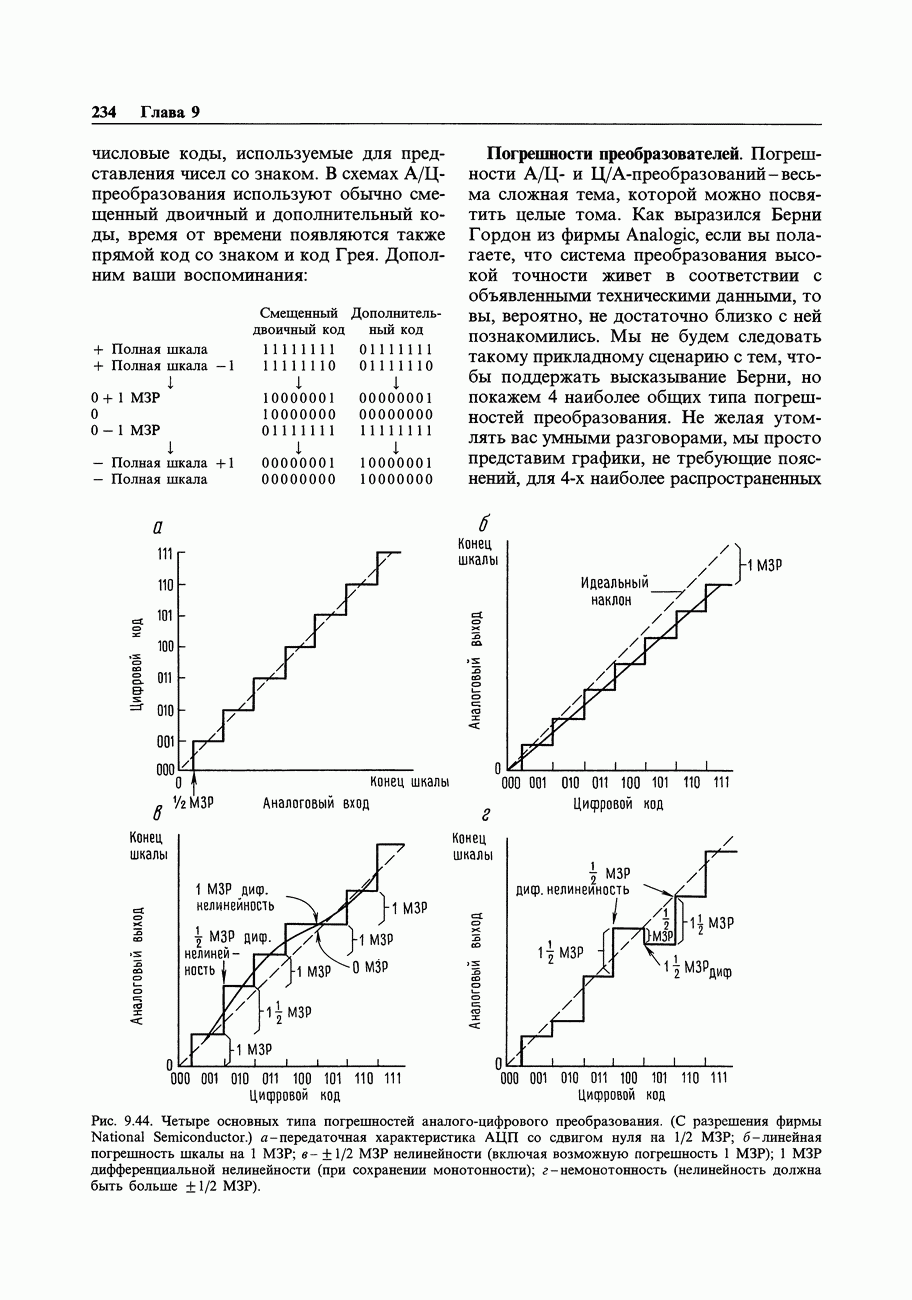
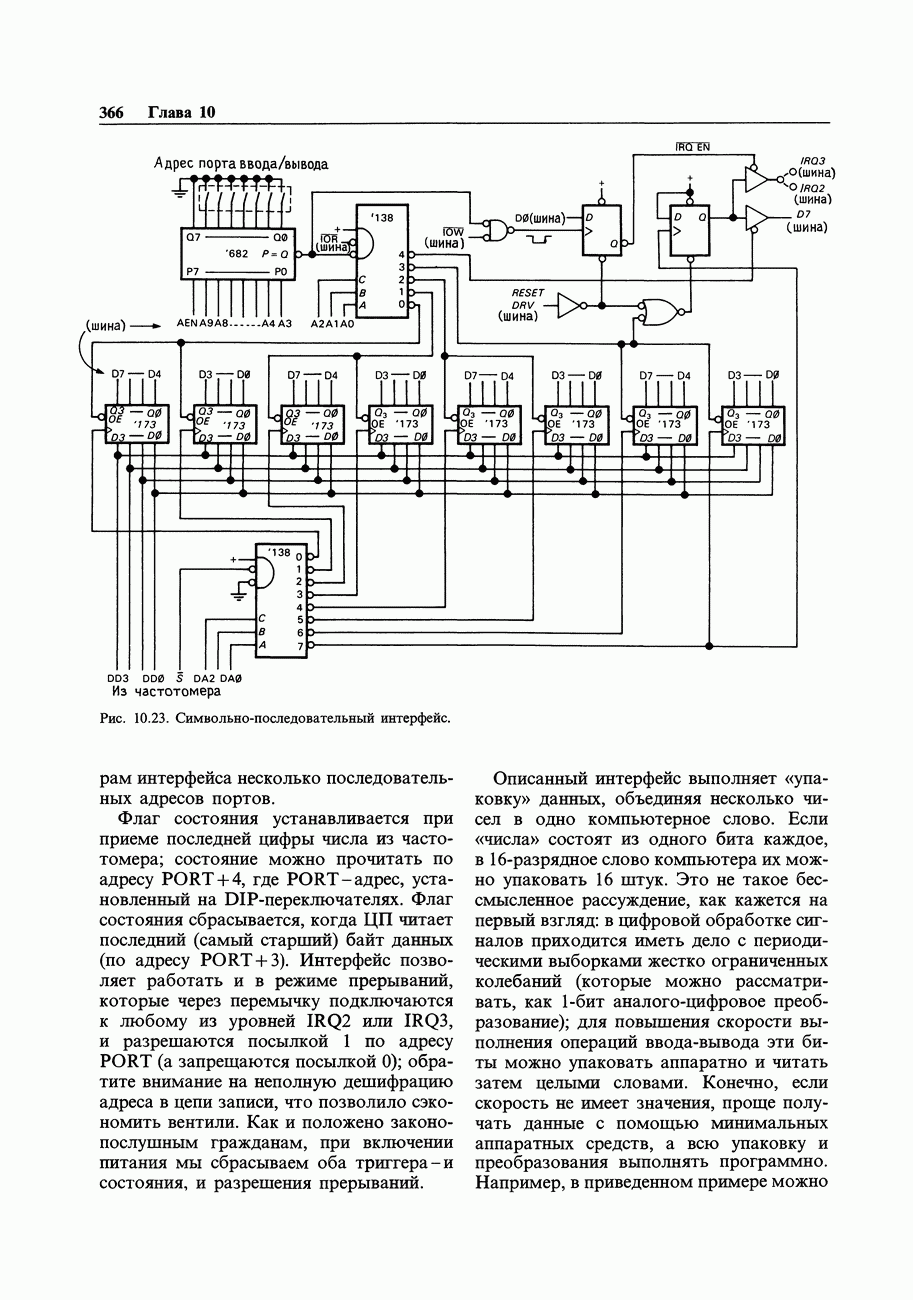
Формат байтов (или слов), получаемых из частотомера в рассмотренном примере, отличается от внутримашинного двоичного формата; частотомер образует двоично-кодированные десятичные коды, упакованные по две цифры в байте (или четыре цифры в слове). Чтобы с этими числами можно было выполнять какие-то вычисления, их следует преобразовать в целые числа или в числа с плавающей точкой (хотя в системе команд микропроцессора предусмотрены и команды с «десятичной коррекцией», позволяющие выполнять арифметические операции непосредственно над упакованными двоично-кодированными десятичными числами). Рассмотрим форматы чисел, обычно используемые в компьютерах (рис. 10.24), предмет, кратко затронутый нами в начале гл. 8.
Целые числа. Целые числа (integer) со знаком всегда представляются, как дополнение до 2 и занимают 1,2 или 4 байт (см. рис. 10.24). Старший бит является знаковым, хотя дополнение до двух не совпадает с представлением в виде знака и числа (т. е. — 1 записывается, как 11111111, а не 10000001; см. разд. 8.03). Дополнение до 2 можно представить себе, как «смещенное» двоичноес инвертированным старшим битом; но можно рассматривать его и как целое число со значением бит, указанным на рис. 10.24. Многие компьютеры позволяют объявлять переменные, как целые без знака в дополнение к объявлению целых со знаком в виде дополнения до 2. Двухбайтовое беззнаковое целое может иметь значение от 0 до 65535.
Числа с плавающей точкой.
Числа с плавающей точкой, называемые также действительными числами (real), обычно занимают 32 бит («одинарная точность») или 64 бит («двойная точность), однако иногда для промежуточных результатов вычислений используется дополнительный -бит формат. К сожалению, имеется несколько употребительных представлений этих чисел. Наиболее распространен формат IEEE (официальное название ANSI/IEEE
-бит формат. К сожалению, имеется несколько употребительных представлений этих чисел. Наиболее распространен формат IEEE (официальное название ANSI/IEEE  который реализован почти во всех микропроцессорных наборах с плавающей точкой (включая Intel 8087/287/287, Motorola 68881, а также наборы фирм AMD, Weitek и др.) и по этой причине является стандартным для микрокомпьютеров, использующих эти наборы (в том числе
который реализован почти во всех микропроцессорных наборах с плавающей точкой (включая Intel 8087/287/287, Motorola 68881, а также наборы фирм AMD, Weitek и др.) и по этой причине является стандартным для микрокомпьютеров, использующих эти наборы (в том числе  ).
).
На рис. 10.24 показаны  -бит и
-бит и  -бит форматы IEEE.
-бит форматы IEEE.  -бит формат одинарной точности предусматривает 1 знаковый бит, 8 бит порядка и 23 бит мантиссы. Порядок определяет степень 2, на которую следует умножить мантиссу (см. ниже). Порядок «смещен» путем прибавления 127, так что поле порядка 01111111 соответствует порядку 0; в результате диапазон порядка составляет от —127 до + 128.
-бит формат одинарной точности предусматривает 1 знаковый бит, 8 бит порядка и 23 бит мантиссы. Порядок определяет степень 2, на которую следует умножить мантиссу (см. ниже). Порядок «смещен» путем прибавления 127, так что поле порядка 01111111 соответствует порядку 0; в результате диапазон порядка составляет от —127 до + 128.

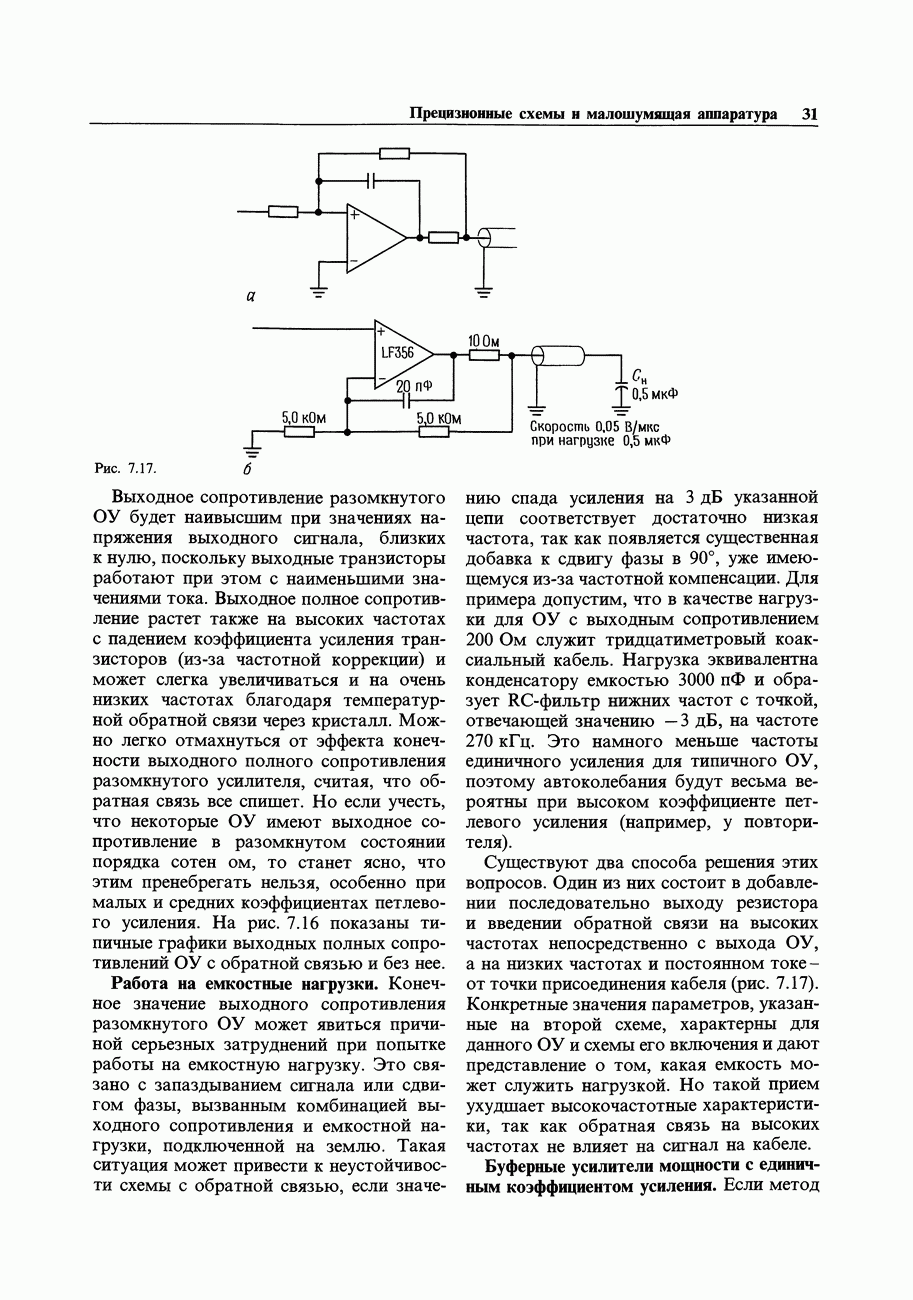
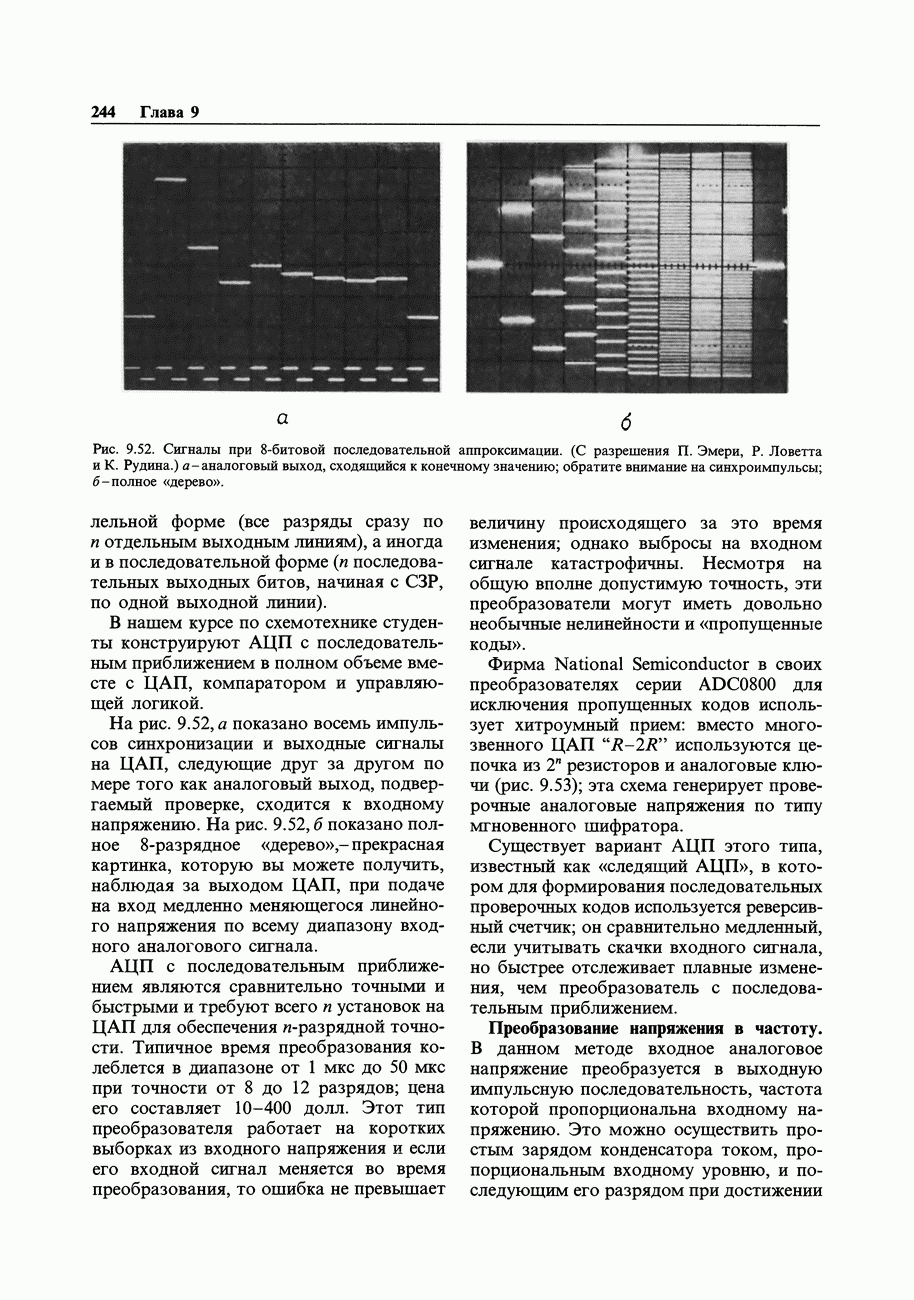
Рис. 10.24. Форматы чисел. S-знак.
Мантисса также записывается любопытным способом, который был впервые использован фирмой DEC в своем формате с плавающей точкой. Двоичное число с плавающей точкой всегда можно записать в виде  , где
, где  мантисса (по основанию 2) («значащая
мантисса (по основанию 2) («значащая  ), а е - порядок (степень 2). Для того чтобы получить при заданном числе бит мантиссы максимальную точность, она «нормализуется» путем сдвига влево (с соответствующим декрементом порядка), пока лидирующий бит не станет равен 1, в результате чего мантисса представляется в виде
), а е - порядок (степень 2). Для того чтобы получить при заданном числе бит мантиссы максимальную точность, она «нормализуется» путем сдвига влево (с соответствующим декрементом порядка), пока лидирующий бит не станет равен 1, в результате чего мантисса представляется в виде  . Далее, используется прием «скрытого бита». Поскольку результирующая значащая часть мантиссы всегда имеет ненулевой старший бит, хранить его в памяти было бы избыточно; вместо lfff можно записать просто
. Далее, используется прием «скрытого бита». Поскольку результирующая значащая часть мантиссы всегда имеет ненулевой старший бит, хранить его в памяти было бы избыточно; вместо lfff можно записать просто  , где лидирующая 1 подразумевается. В результате точность числа возрастает, так как его представление увеличивается на 1 бит, образуя диапазон от
, где лидирующая 1 подразумевается. В результате точность числа возрастает, так как его представление увеличивается на 1 бит, образуя диапазон от  до
до 
Упражнение 10.9. Сконструируйте на бумаге минимальное и максимальное нормализованные числа с плавающей точкой и убедитесь, что приведенные выше предельные значения соответствуют истине.
Формат IEEE с двойной точностью образуется аналогично, но точность мантиссы более чем удваивается (увеличиваясь на 29 бит), а порядок получает дополнительные 3 бит. Диапазон чисел указан на рисунке.
Формат IEEE допускает также хранение ненормализованных чисел, что несколько увеличивает диапазон со стороны маленьких чисел (за счет уменьшения точности); «денормализованные» числа могут доходить до величины  . Стандарт также определяет нуль
. Стандарт также определяет нуль  таким образом, есть 2 нуля,
таким образом, есть 2 нуля,  и —0), бесконечность
и —0), бесконечность  все единицы,
все единицы,  поэтому оба знака), а также любопытный класс зарезервированных величин, имеющих официальное название «не число»
поэтому оба знака), а также любопытный класс зарезервированных величин, имеющих официальное название «не число»  Number).
Number).
Другой важный микрокомпьютерный формат чисел с плавающей точкой принадлежит фирме DEC и используется в компьютерах  (а также в их предках, мини-ЭВМ VAX и
(а также в их предках, мини-ЭВМ VAX и  ). Он почти совпадает со стандартом IEEE, имея то же число бит в порядке и мантиссе (включая использование скрытого бита) чисел с одинарной точностью. Отличия заключаются в другом значении смещения (128 вместо 127), а также в отсутствии лидирующих бит в мантиссе, которая представляется в виде ,lfff (со скрытой 1). DEC определяет только один нуль (все биты которого равны 0); и не допускает ненормализованных чисел и бесконечности; имеются, однако, величины, аналогичные «не числам» IEEE. DEC также определяет
). Он почти совпадает со стандартом IEEE, имея то же число бит в порядке и мантиссе (включая использование скрытого бита) чисел с одинарной точностью. Отличия заключаются в другом значении смещения (128 вместо 127), а также в отсутствии лидирующих бит в мантиссе, которая представляется в виде ,lfff (со скрытой 1). DEC определяет только один нуль (все биты которого равны 0); и не допускает ненормализованных чисел и бесконечности; имеются, однако, величины, аналогичные «не числам» IEEE. DEC также определяет  -бит формат удвоенной точности.
-бит формат удвоенной точности.
Последние два формата, приведенные на рис. 10.24, используются не в микрокомпьютерах, а в больших ЭВМ или в машинах специального назначения. Формат  в течение некоторого времени использовался в универсальных ЭВМ фирмы IBM и даже в некоторых мини-ЭВМ, например, Nova фирмы Data General.
в течение некоторого времени использовался в универсальных ЭВМ фирмы IBM и даже в некоторых мини-ЭВМ, например, Nova фирмы Data General.
 -бит смещенный порядок определяет степень 16, а не 2, увеличивая диапазон чисел. Мантисса в результате может иметь до трех лидирующих нулей, т. е. нормализованная часть содержит ненулевую старшую шестнадцатеричную цифру.
-бит смещенный порядок определяет степень 16, а не 2, увеличивая диапазон чисел. Мантисса в результате может иметь до трех лидирующих нулей, т. е. нормализованная часть содержит ненулевую старшую шестнадцатеричную цифру.
Упражнение 10.10. Чтобы понять смысл последней фразы, напишите представление числа 1.0 в формате IBM. После этого напишите следующее меньшее число в том же формате.
Использование в формате IBM числа 16 в качестве основания увеличивает динамический диапазон, но уменьшает точность. Более того, точность несколько изменяется от числа к числу из-за переменного количества лидирующих двоичных нулей; это явление известно, как «качание» (wobble). В формате IBM отсутствуют «не числа» и бесконечность, и имеется только один нуль (все биты нули); не нормализованные числа не допускаются. Имеется формат IBM и для чисел с двойной точностью (64 бит).
Последний формат на рис.  , используется в военных системах. Он необычен в том отношении, что вместо знака и величины числа в нем записывается мантисса в форме дополнения до двух и порядок тоже в форме дополнения до двух (строго говоря, предыдущие форматы характеризуются записью мантиссы в форме знак/величина, а порядка в форме смещенного двоичного). В формате отсутствуют бесконечности, «не числа» и не нормализованные числа; имеется вариант для чисел с удвоенной точностью.
, используется в военных системах. Он необычен в том отношении, что вместо знака и величины числа в нем записывается мантисса в форме дополнения до двух и порядок тоже в форме дополнения до двух (строго говоря, предыдущие форматы характеризуются записью мантиссы в форме знак/величина, а порядка в форме смещенного двоичного). В формате отсутствуют бесконечности, «не числа» и не нормализованные числа; имеется вариант для чисел с удвоенной точностью.
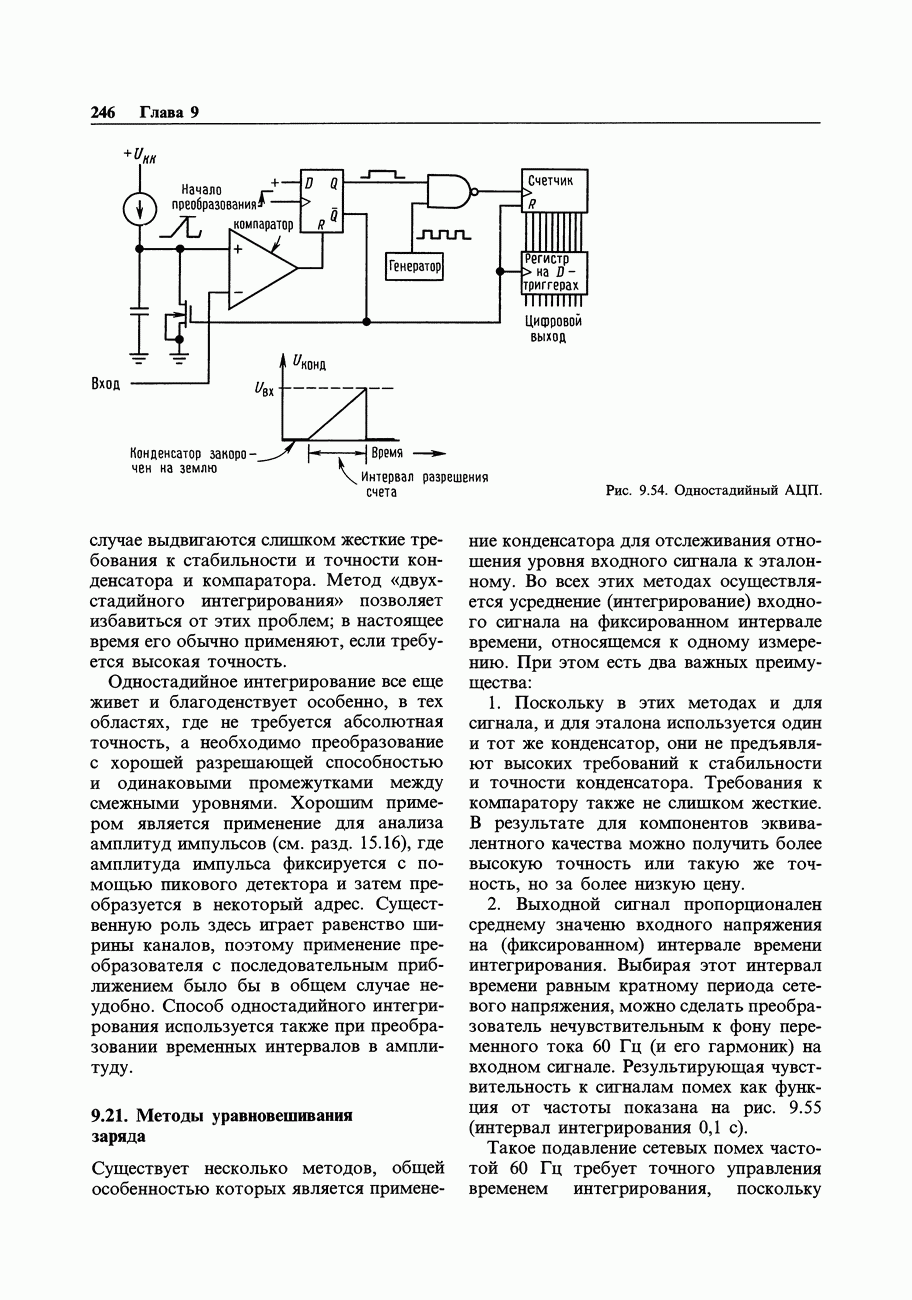
Хранение чисел в памяти.
Разработчики микропроцессоров любят выражать свою индивидуальность, предусматривая хранение чисел в памяти в своеобразном порядке. Микропроцессоры , следовательно, и компьютеры IBM PC и совместимые с ними) записывают числа в память, начиная с самого младшего байта, который располагается в байте памяти с наименьшим номером; для семейства 68000 характерен обратный порядок. Вот счастье-то!
, следовательно, и компьютеры IBM PC и совместимые с ними) записывают числа в память, начиная с самого младшего байта, который располагается в байте памяти с наименьшим номером; для семейства 68000 характерен обратный порядок. Вот счастье-то!
Преобразование данных в процессе ввода-вывода.
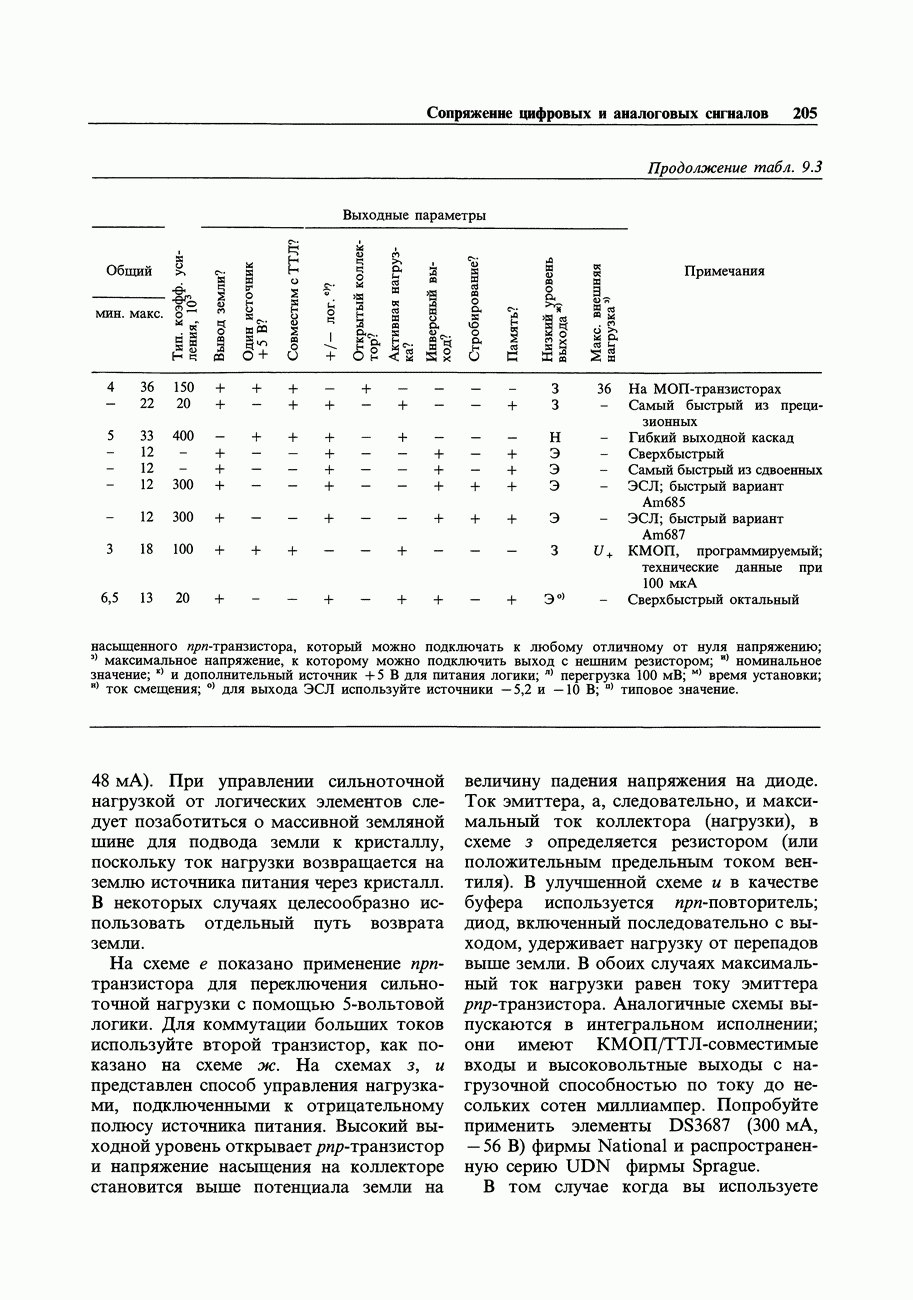
Нам пришлось уже обсуждать форматы данных в контексте аппаратного интерфейса, который выдавал упакованные двоично-десятичные числа. Каков наиболее оптимальный способ работы с -разрядными данными, получаемыми из такого интерфейса?
-разрядными данными, получаемыми из такого интерфейса?
В зависимости от типа входных данных, числа значащих цифр, диапазона их изменения и проч. может оказаться удобным преобразовывать входные данные в числа с плавающей точкой (для получения максимального динамического диапазона), или в целые числа (для получения максимального разрешения), или выполнить какие-то другие числовые процедуры (например, вычисление отклонений от среднего значения или разностей последующих отсчетов). Все это можно делать в программном «драйвере» конкретного устройства, т. е. в программном модуле, который управляет вводом данных. Мы видим, таким образом, что оптимизация программного обеспечения не может быть выполнена без понимания особенностей аппаратуры и смысла принимаемых данных. Еще одна причина, по которой столь важно освоиться в этом чудесном мире электронной аппаратуры!
| << Предыдущий параграф |
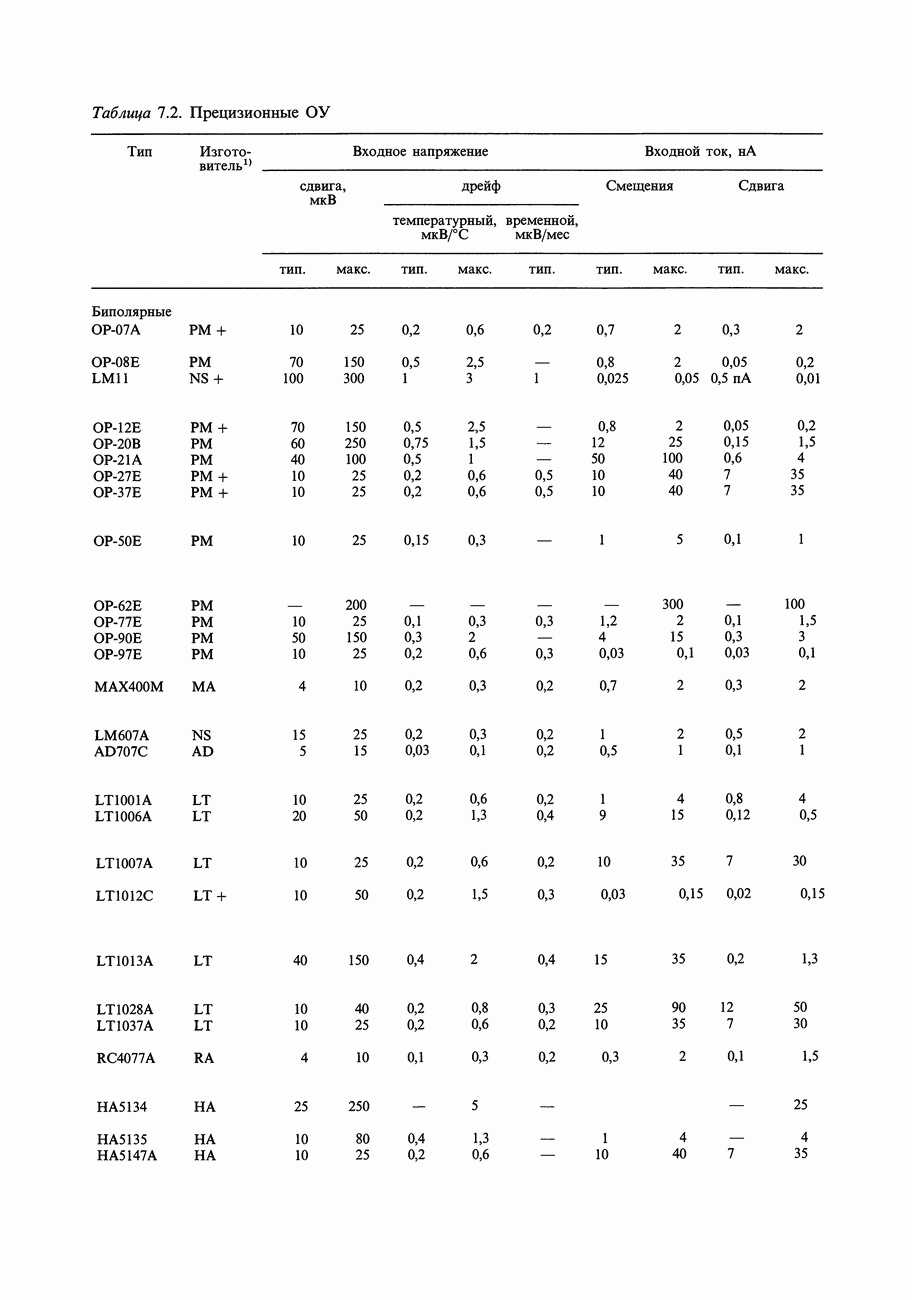
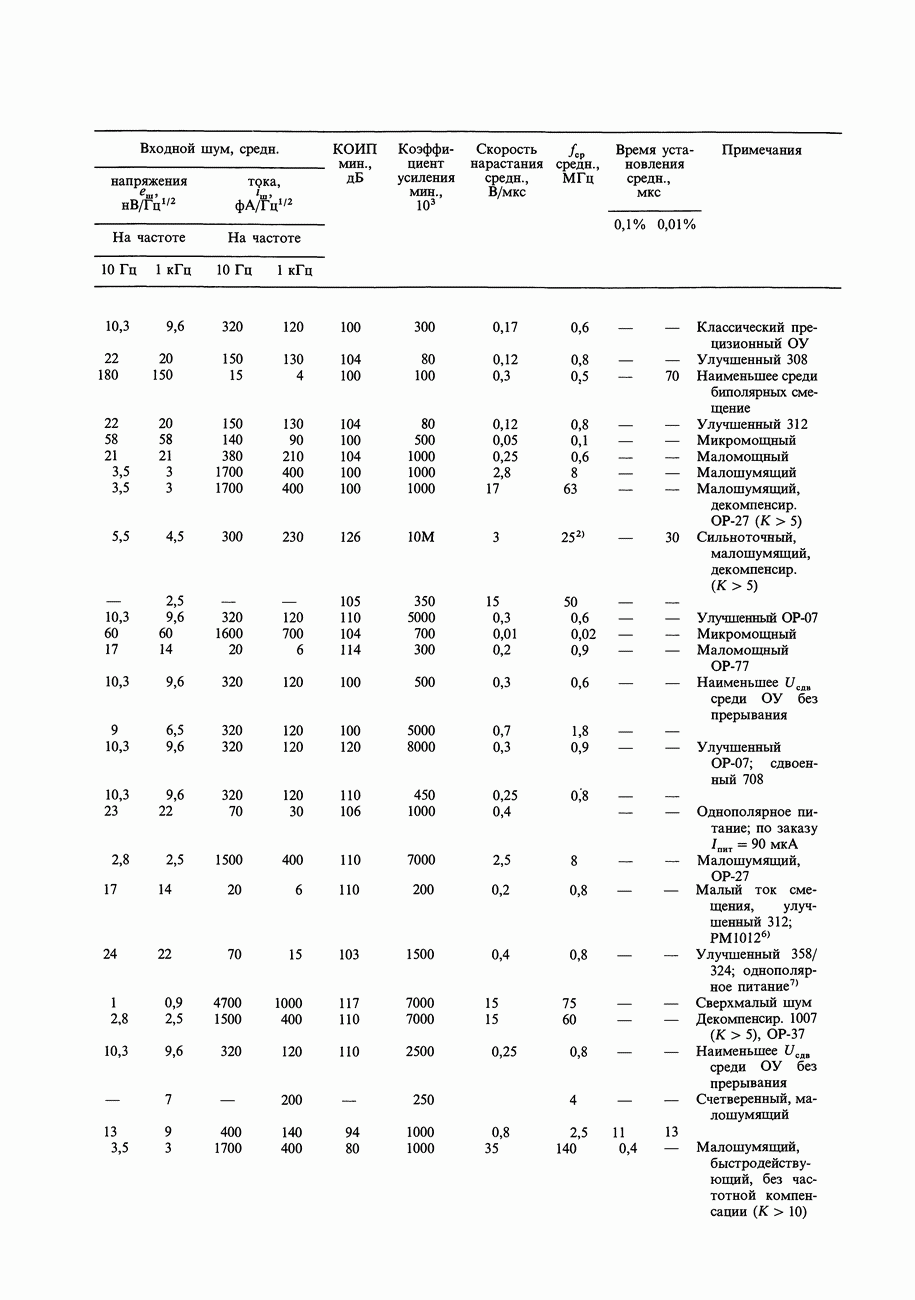
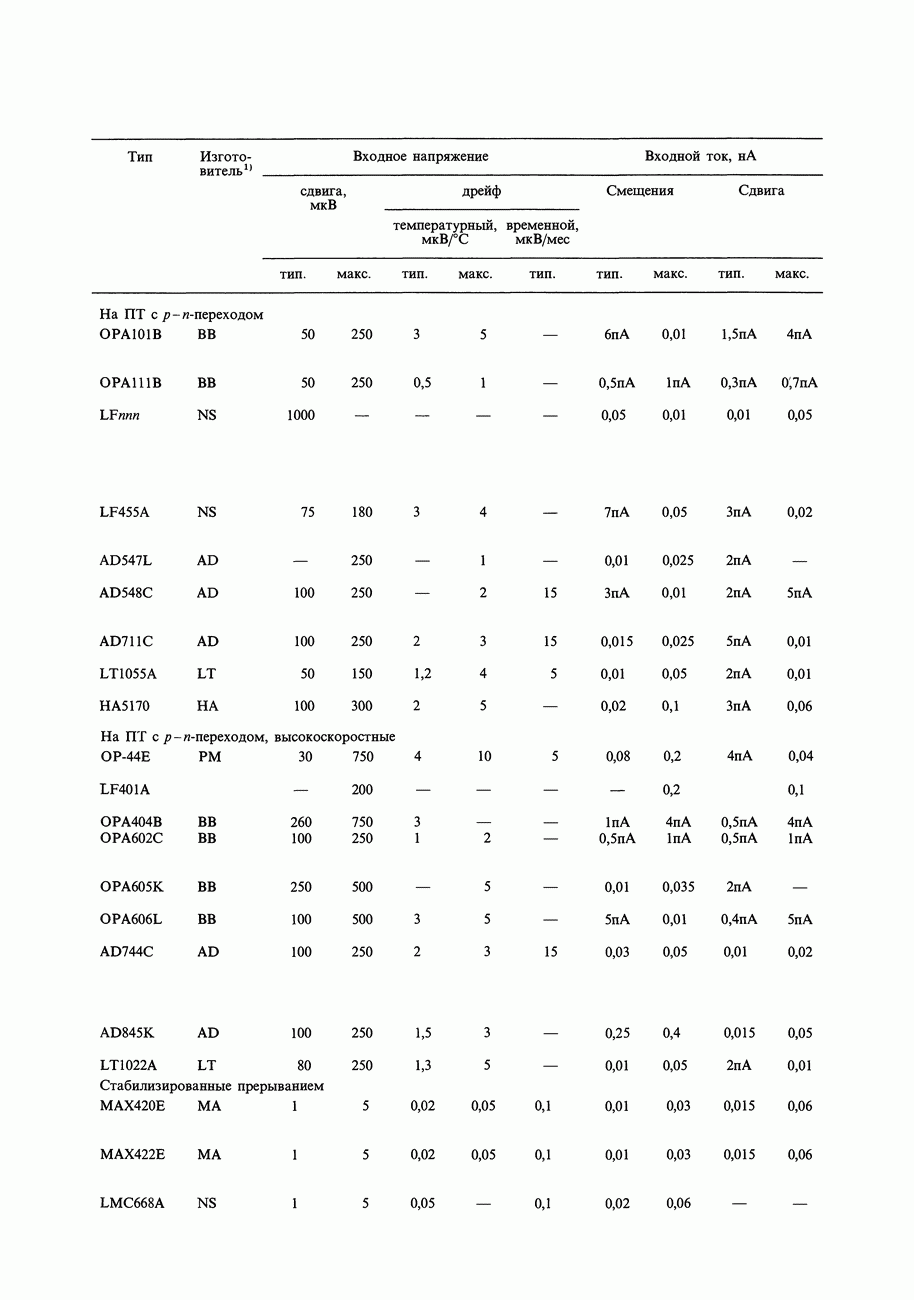
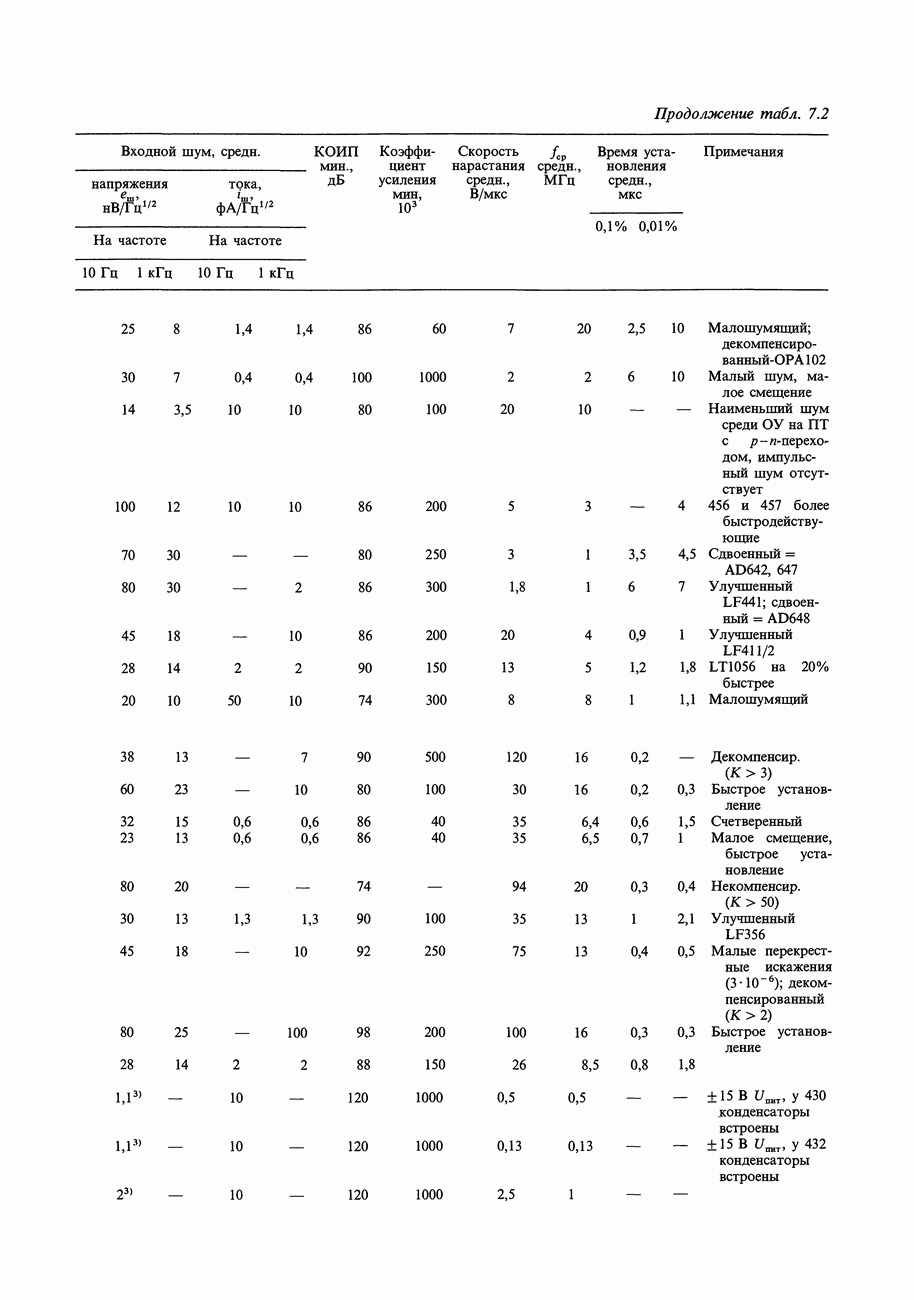
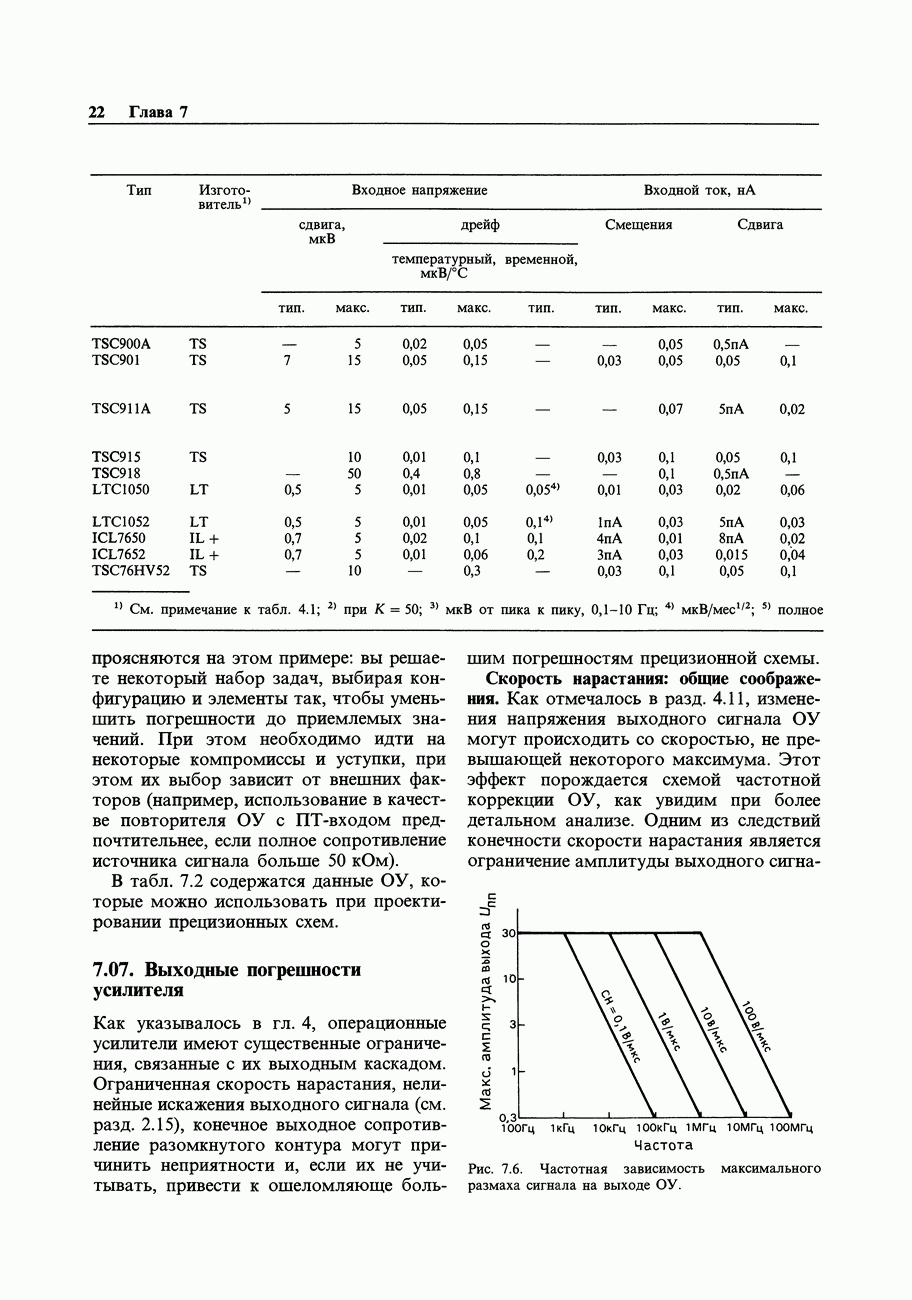
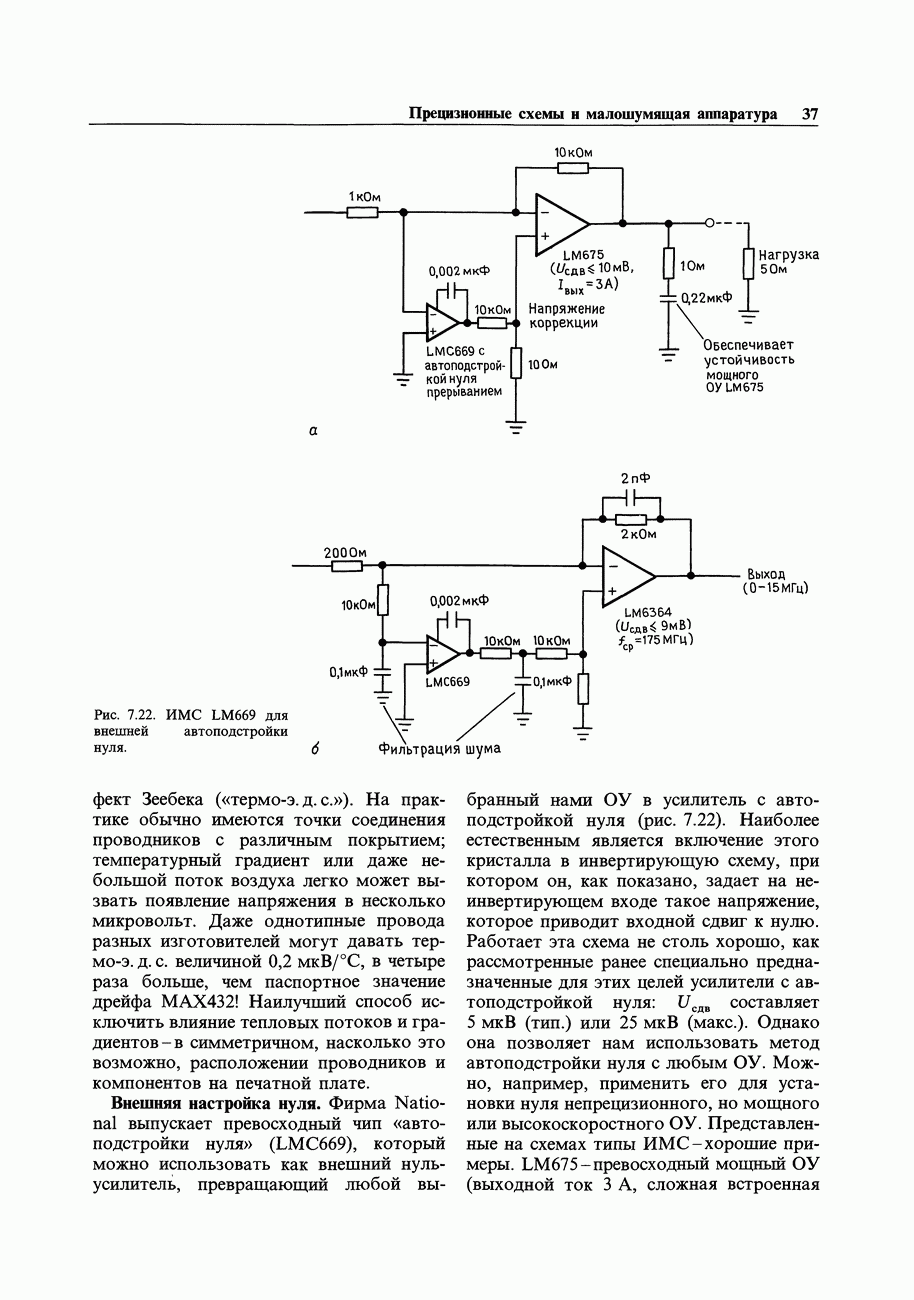
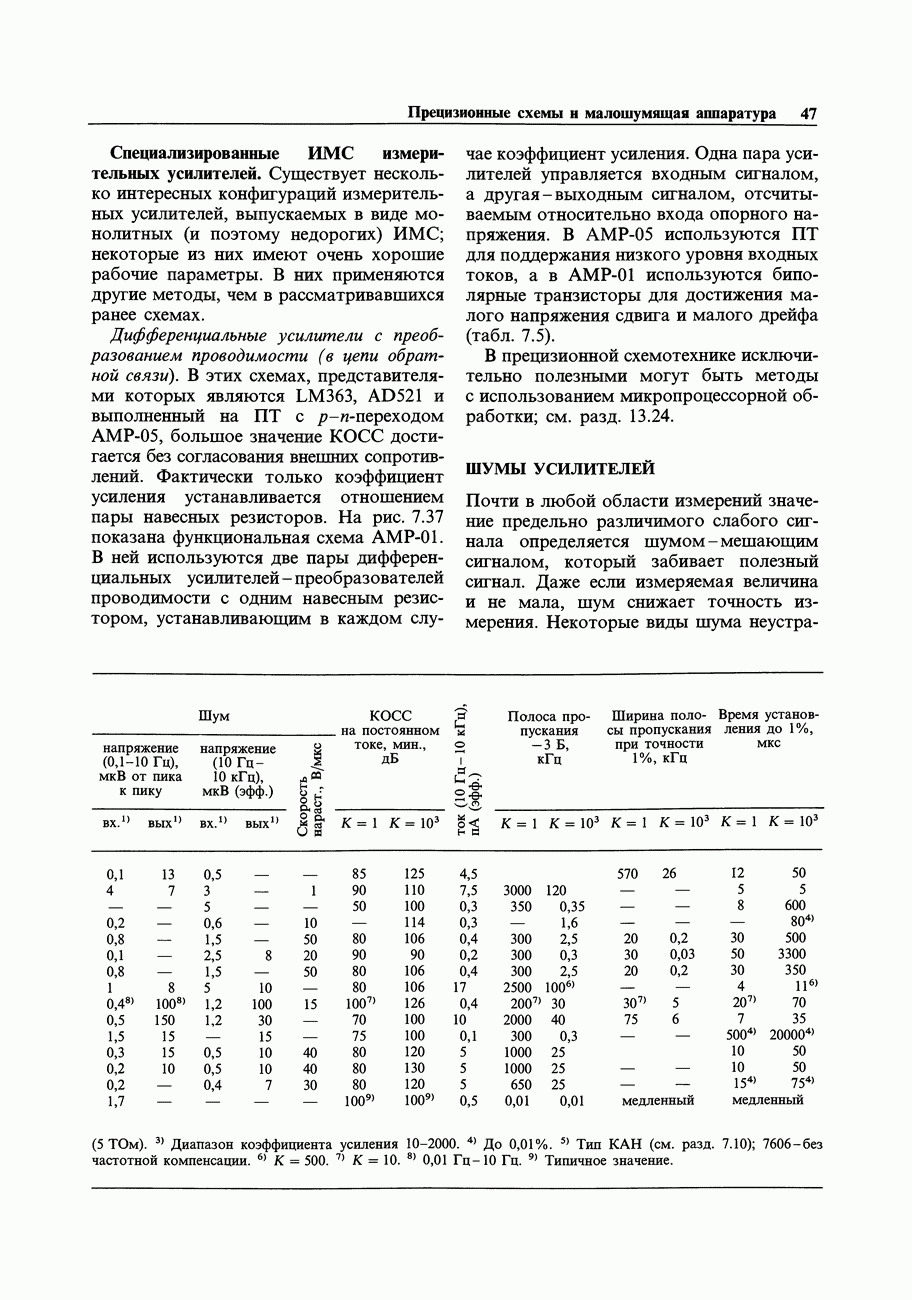
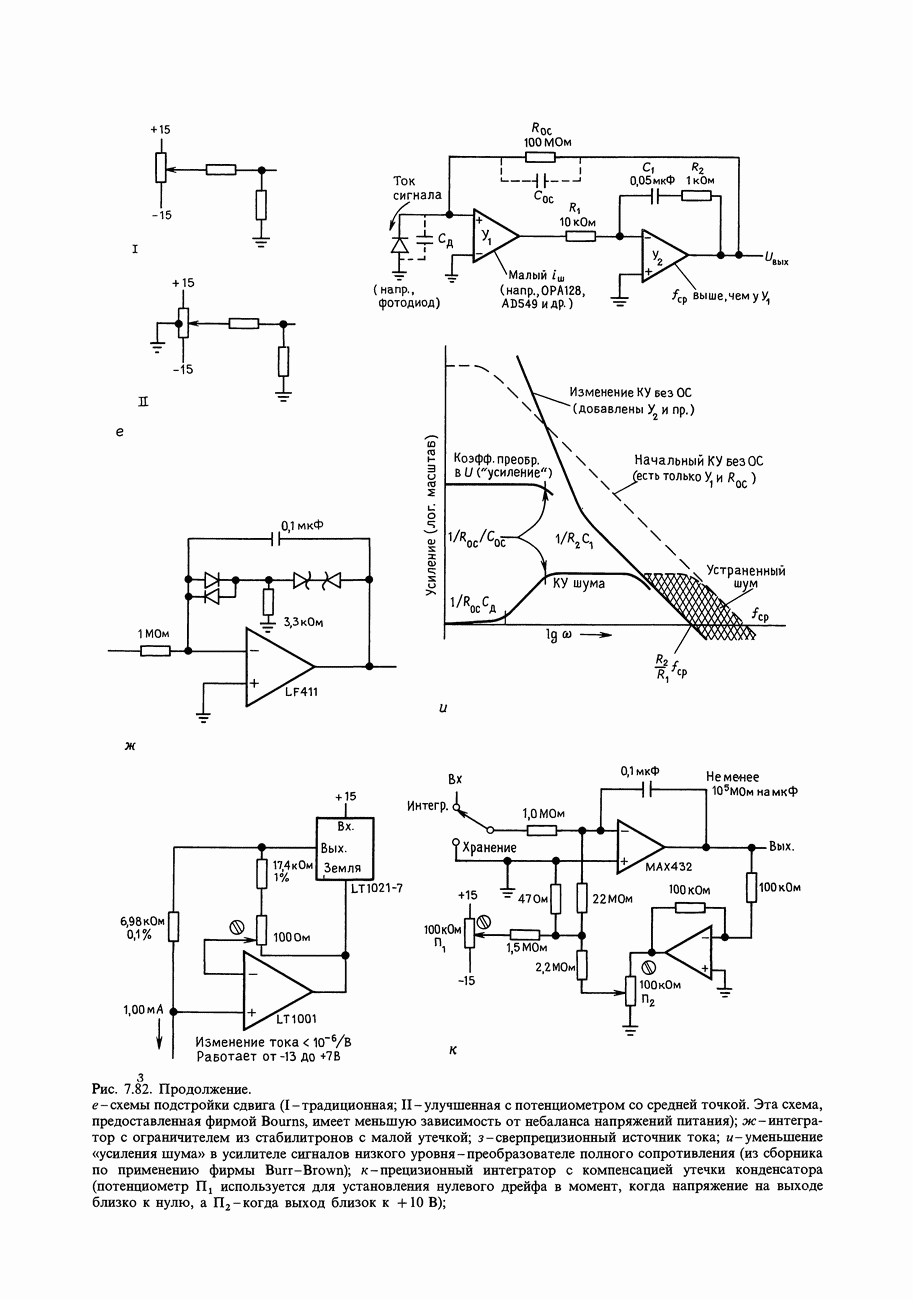
- ГЛАВА 7. ПРЕЦИЗИОННЫЕ СХЕМЫ И МАЛОШУМЯЩАЯ АППАРАТУРА
- 7.01. Соотношение точности и динамического диапазона
- 7.02. Бюджет погрешностей схемы
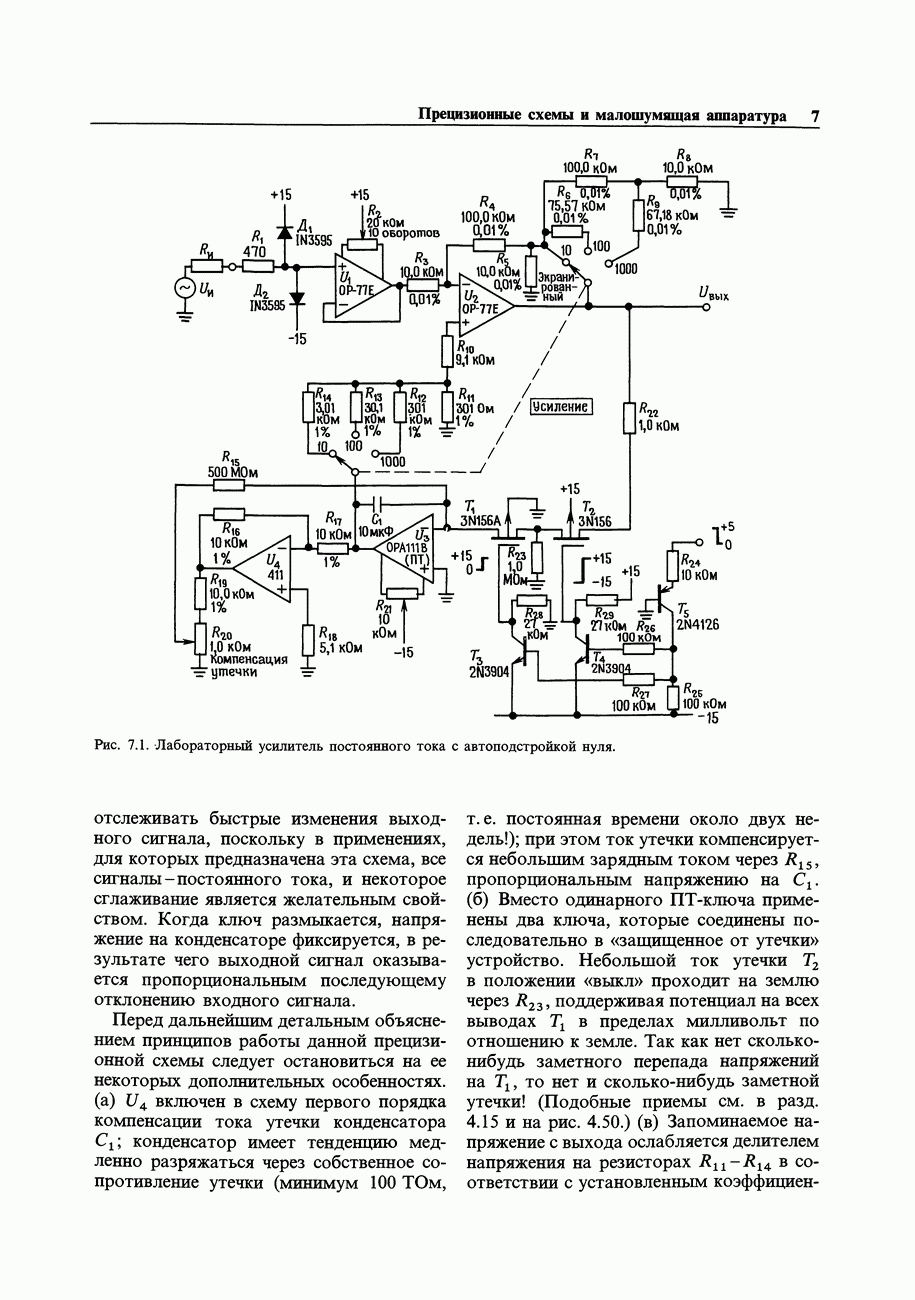
- 7.03. Пример схемы: прецизионный усилитель с автоматическим выбором нуля
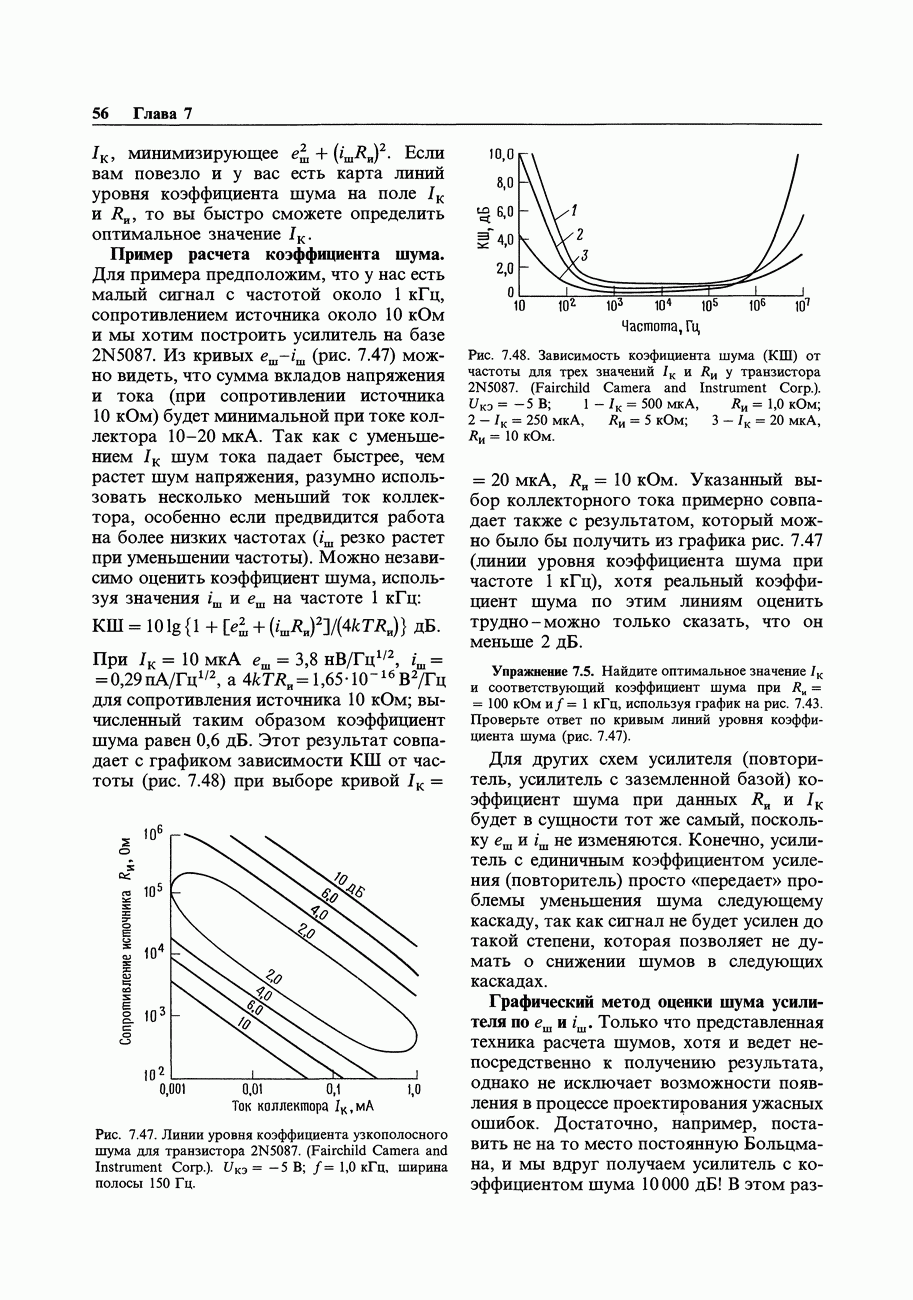
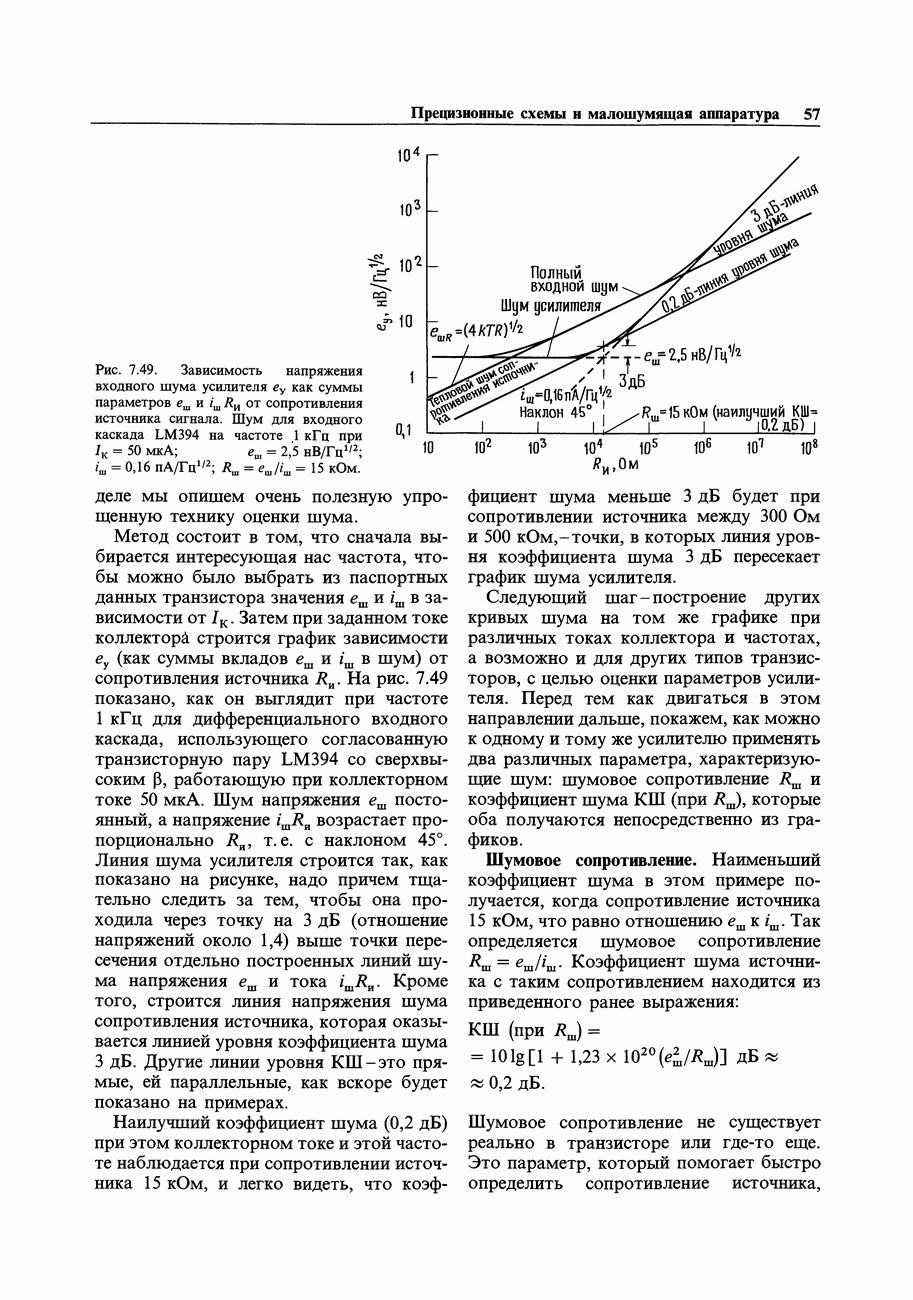
- 7.04. «Бюджет погрешностей» при проектировании прецизионной схемы
- 7.05. Погрешности внешних цепей
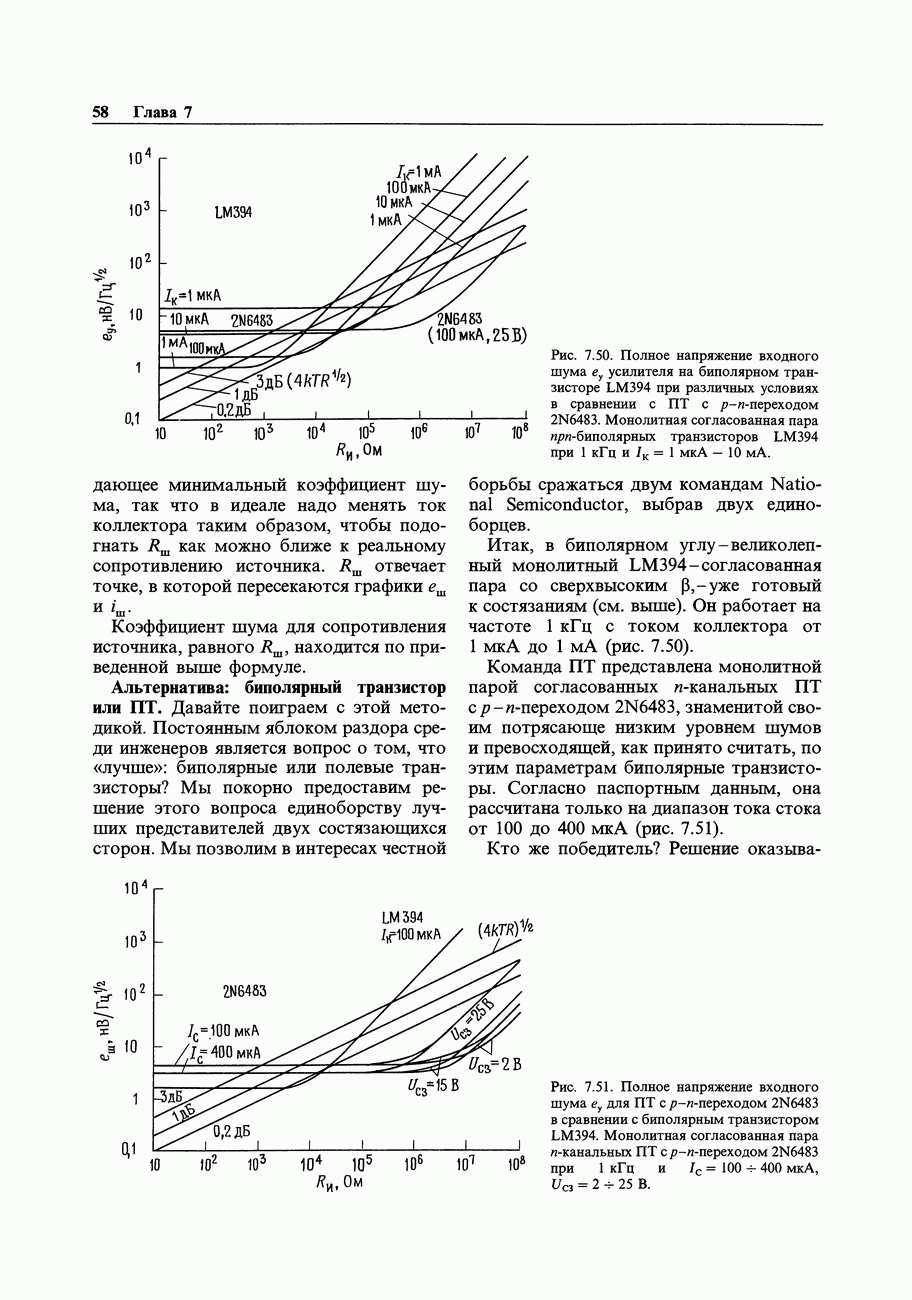
- 7.06. Входные погрешности усилителя
- 7.07. Выходные погрешности усилителя
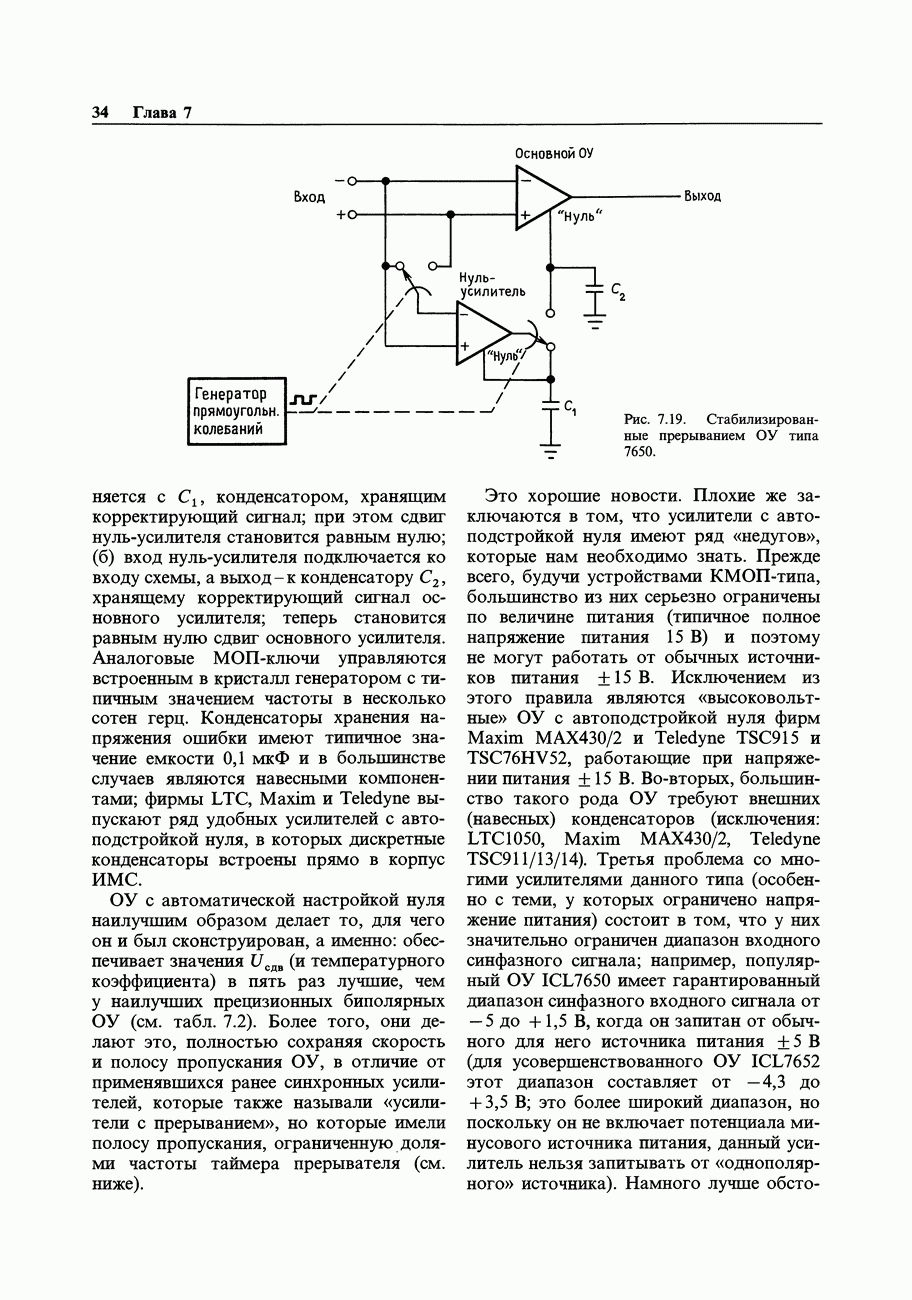
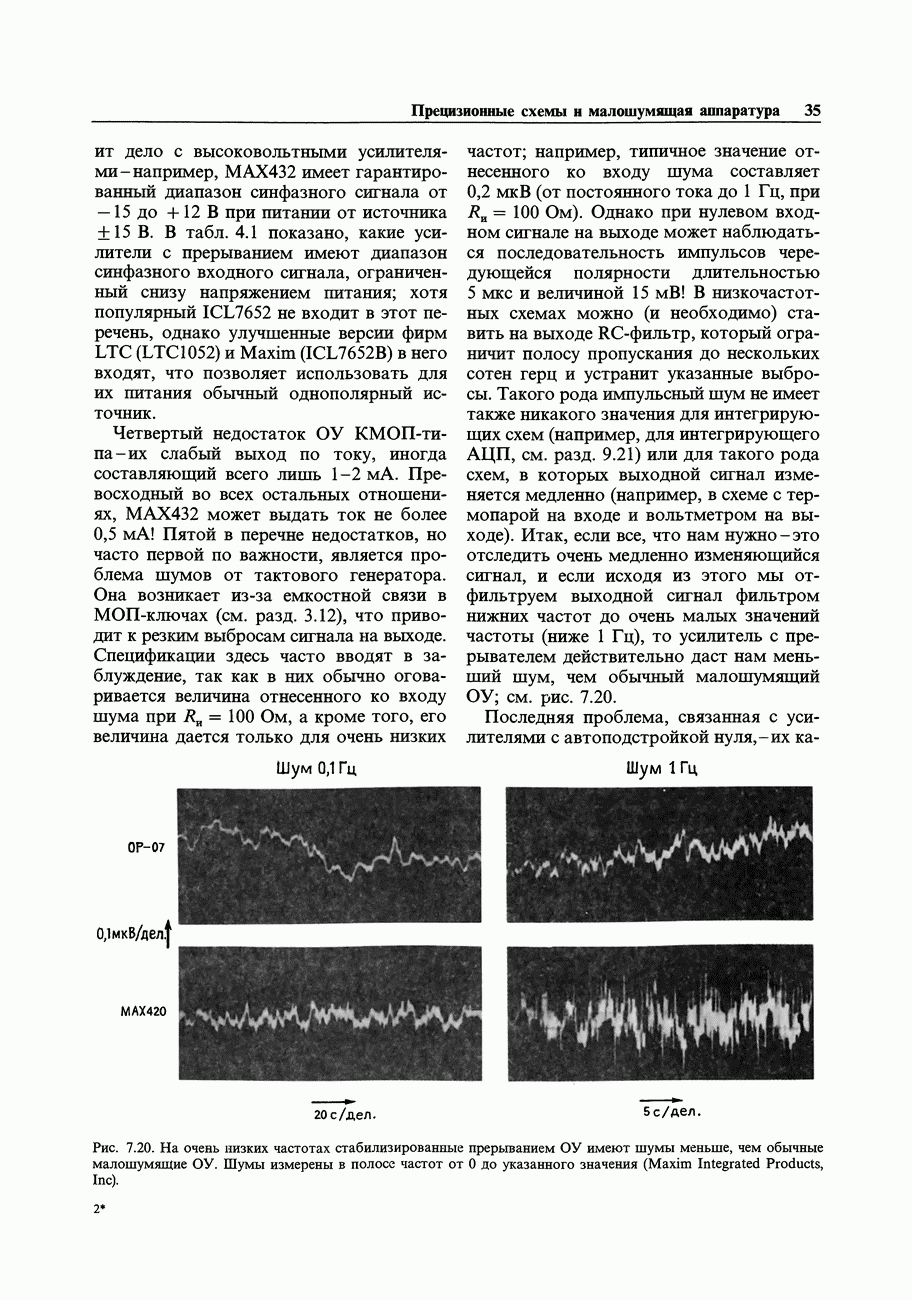
- 7.08. Усилители с автоподстройкой нуля (стабилизированные прерыванием)
- Кое-что еще о схемах с прерыванием
- ДИФФЕРЕНЦИАЛЬНЫЕ И ИЗМЕРИТЕЛЬНЫЕ УСИЛИТЕЛИ
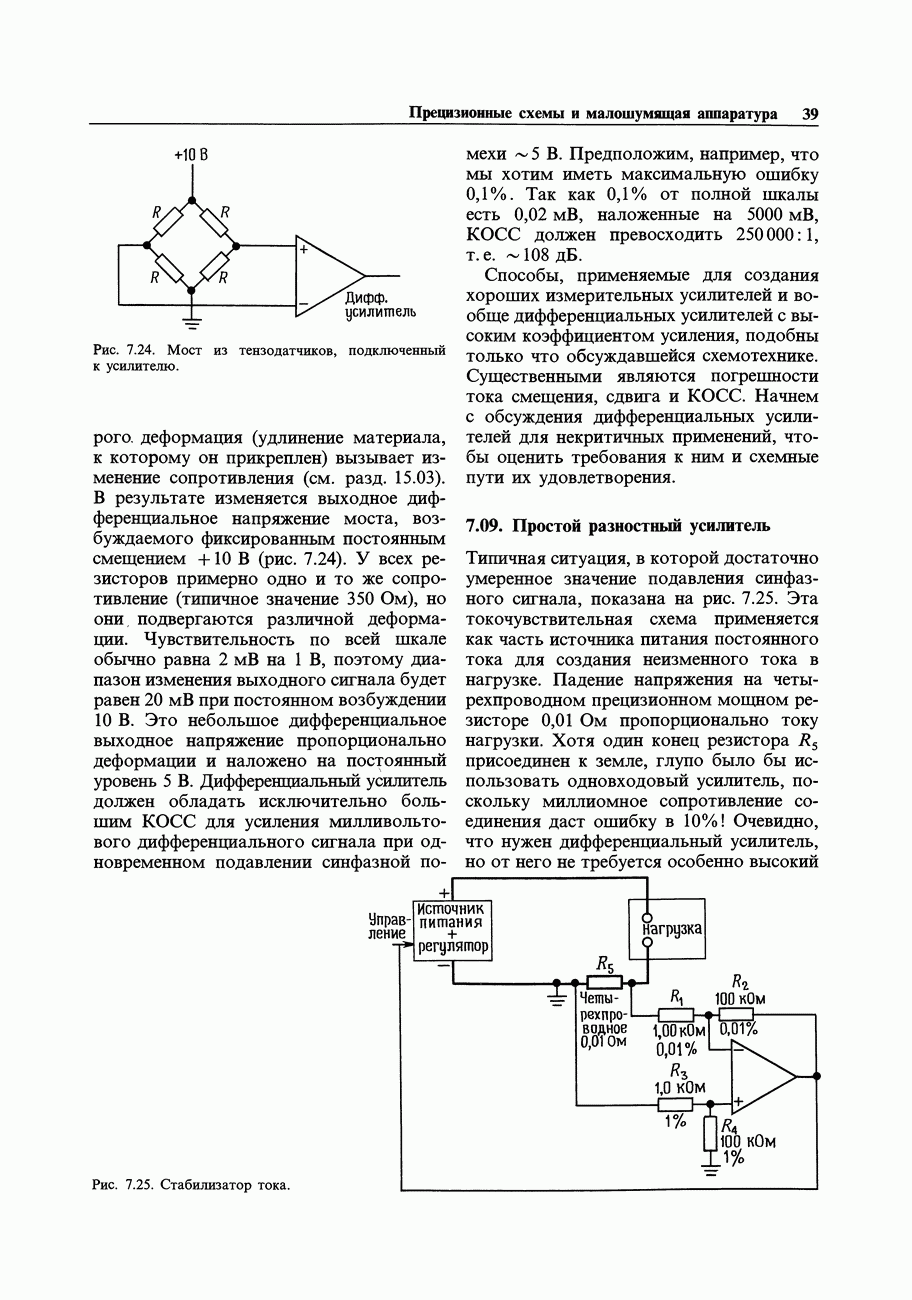
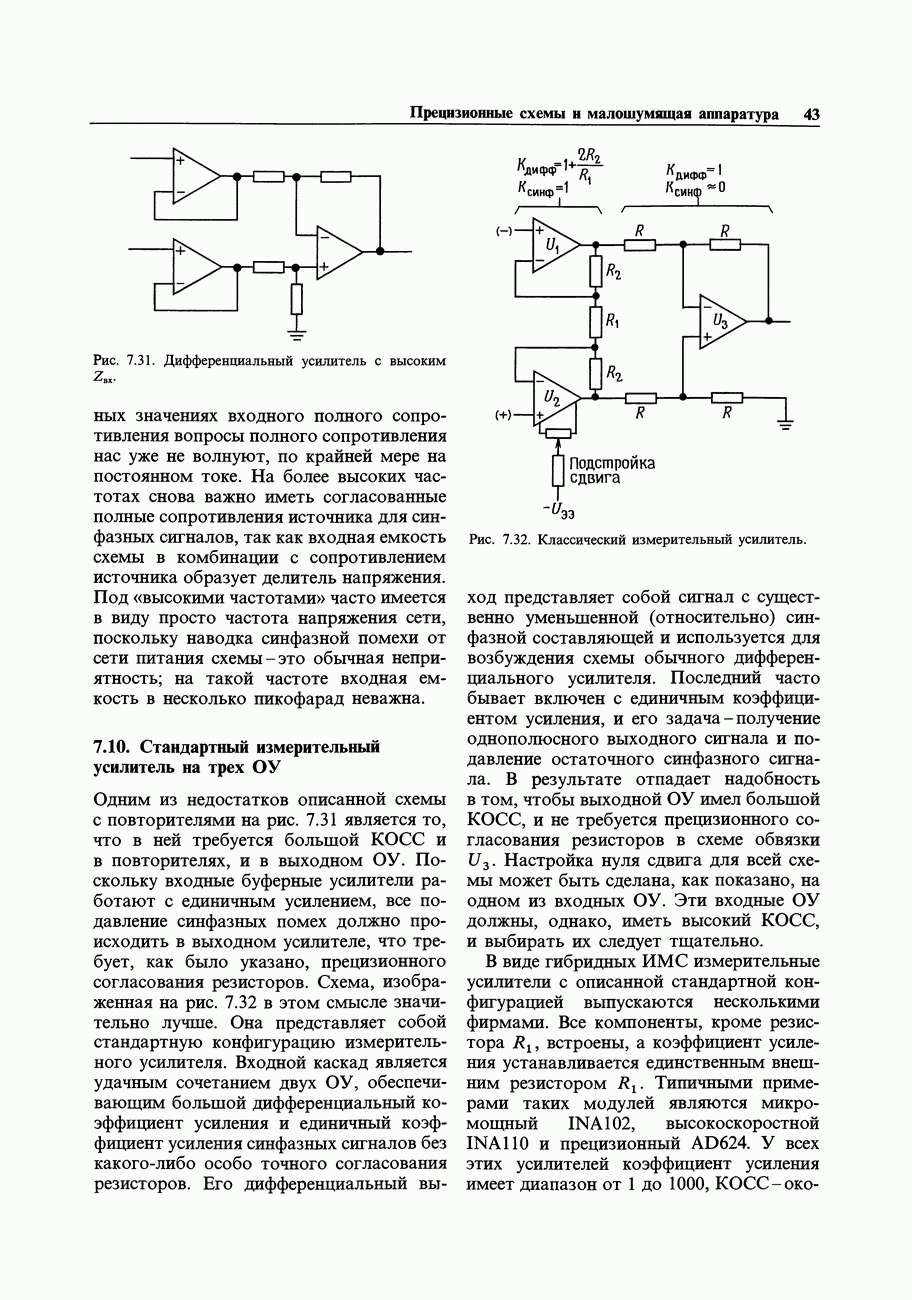
- 7.09. Простой разностный усилитель
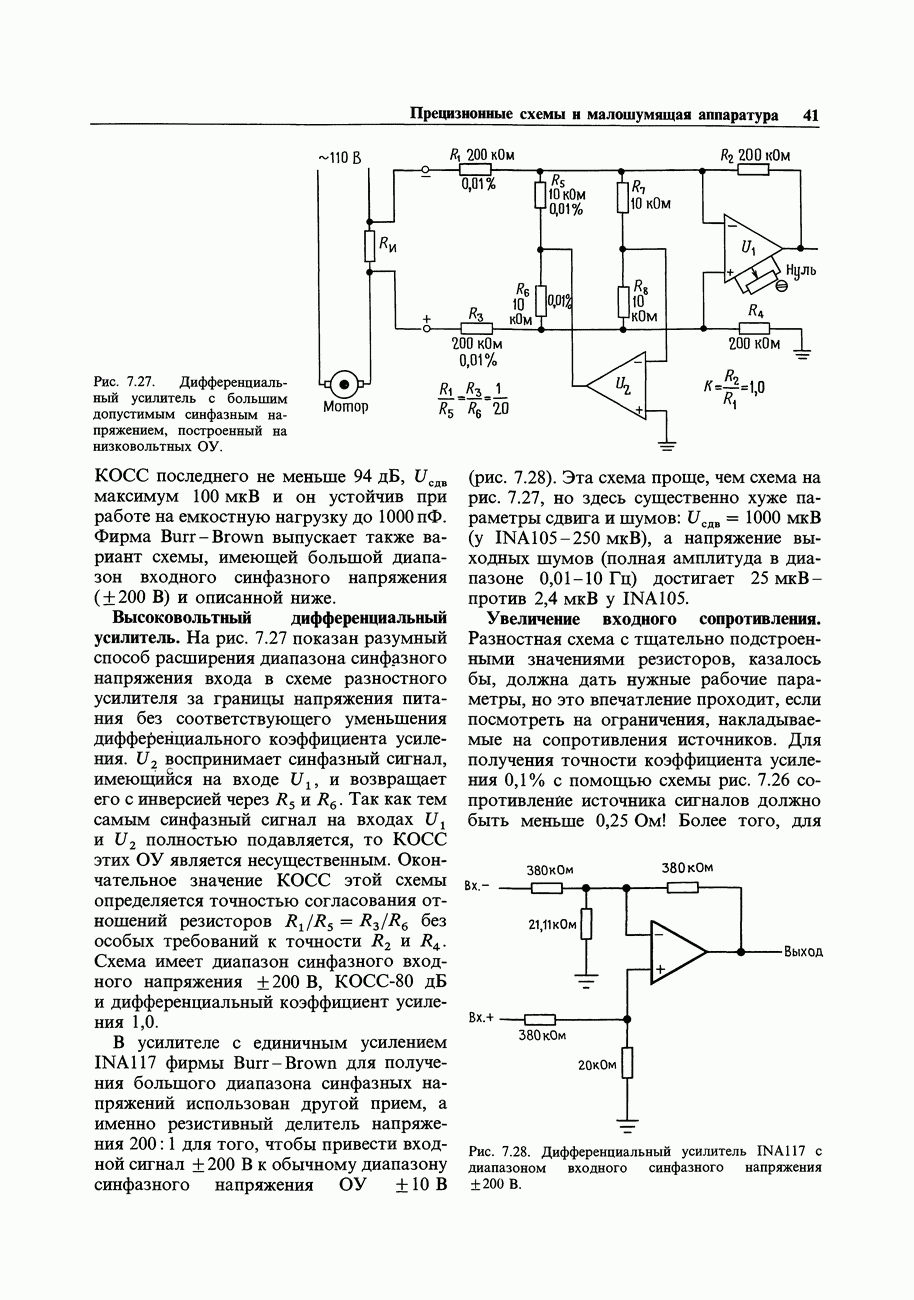
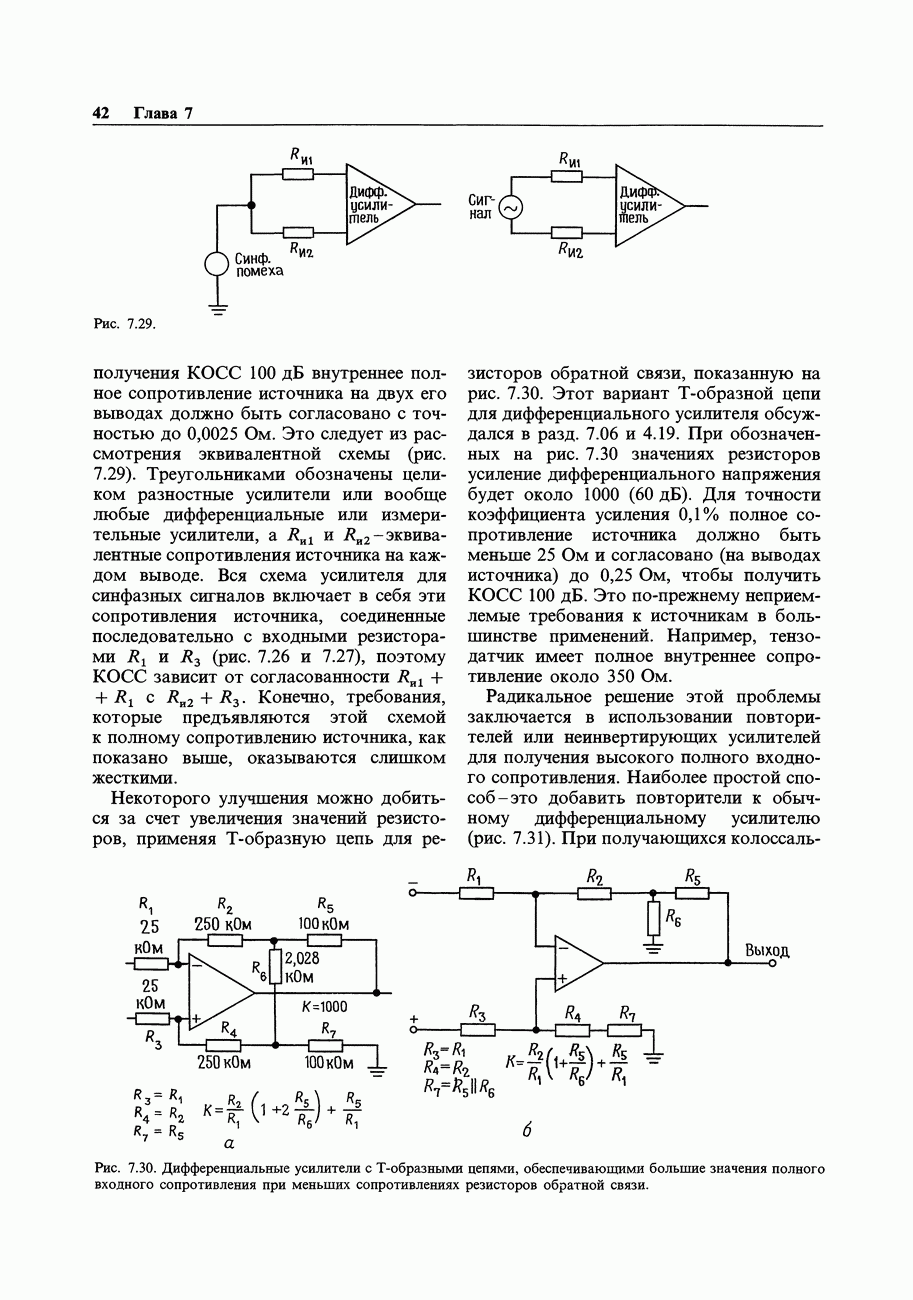
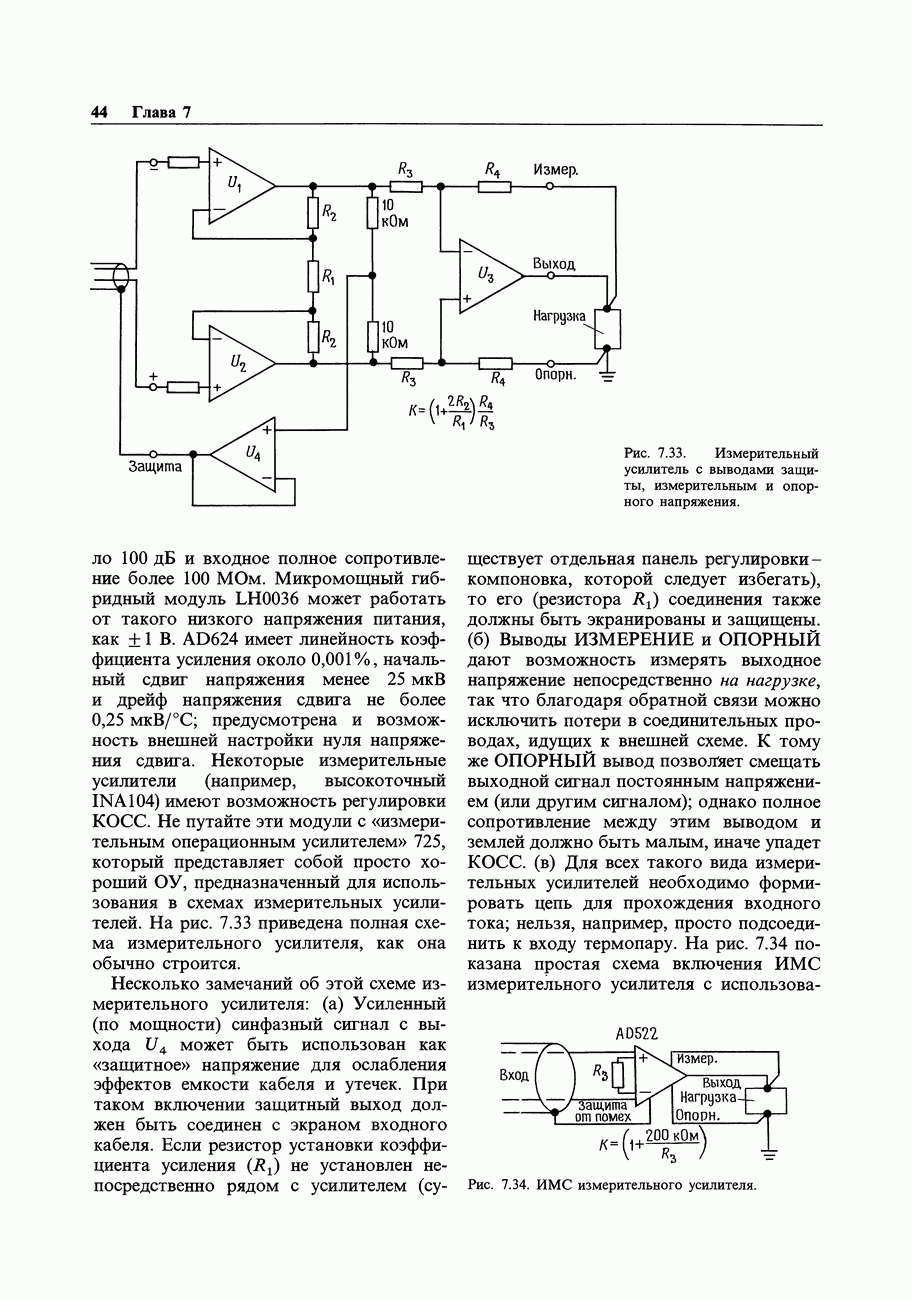
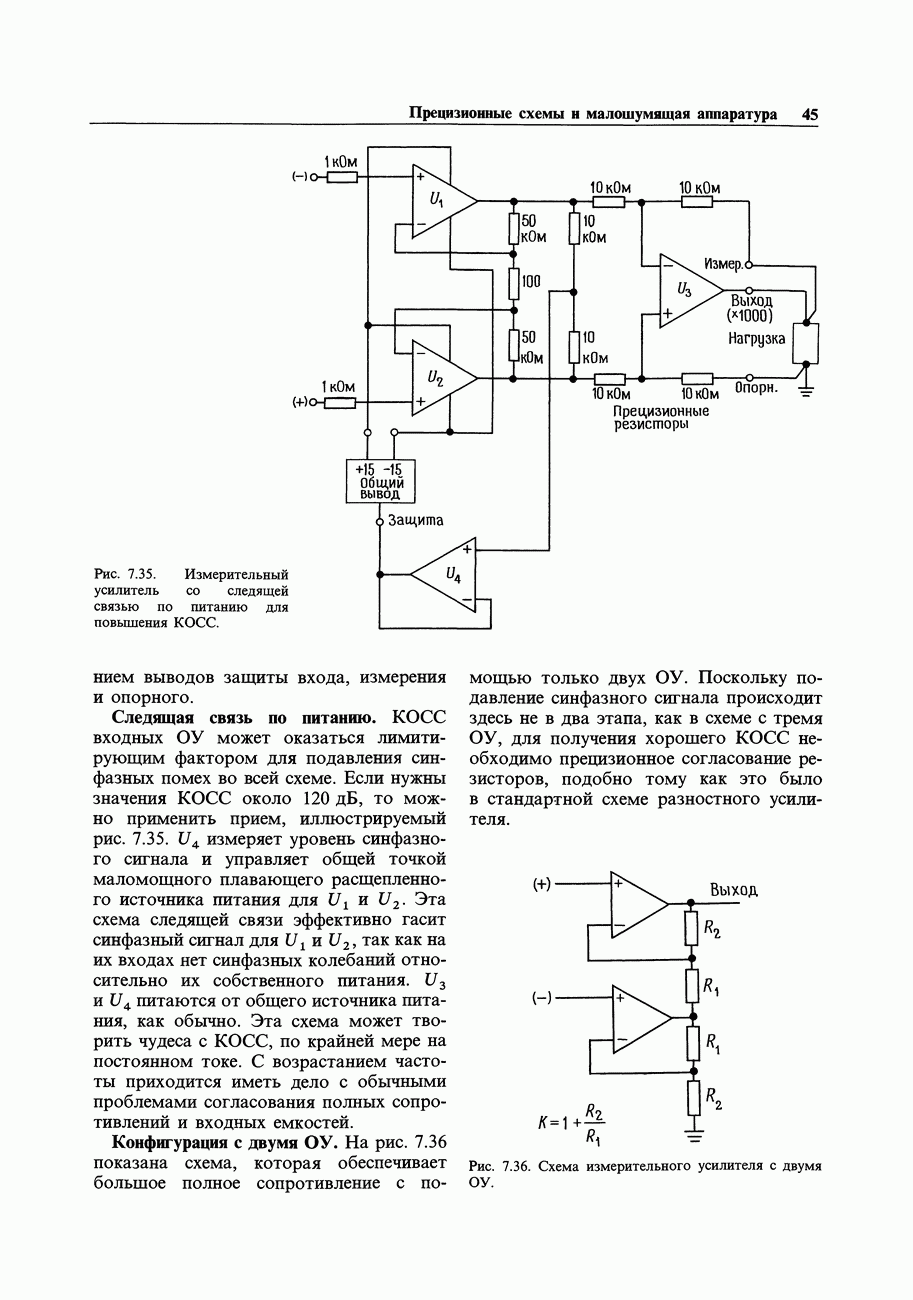
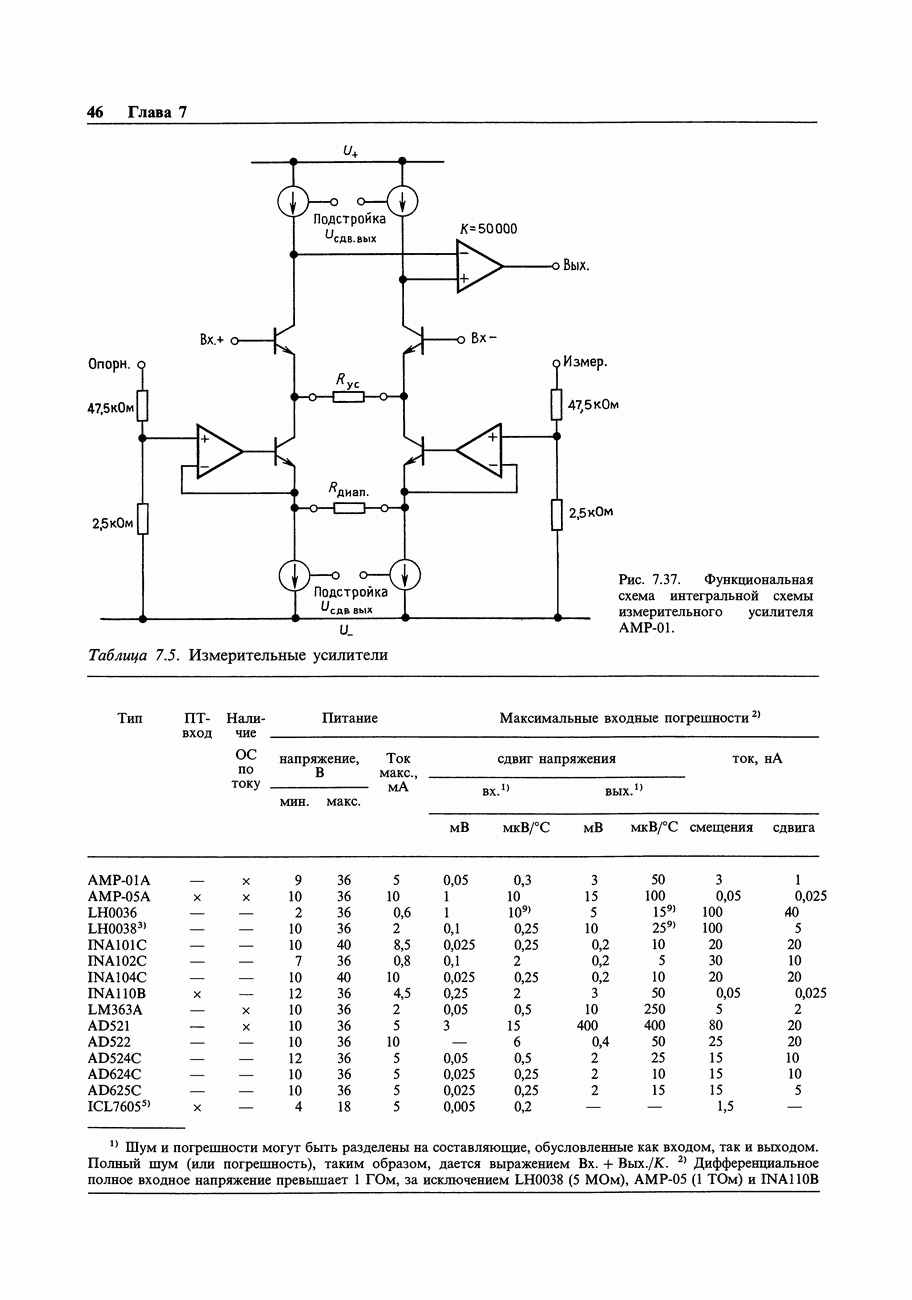
- 7.10. Стандартный измерительный усилитель на трех ОУ
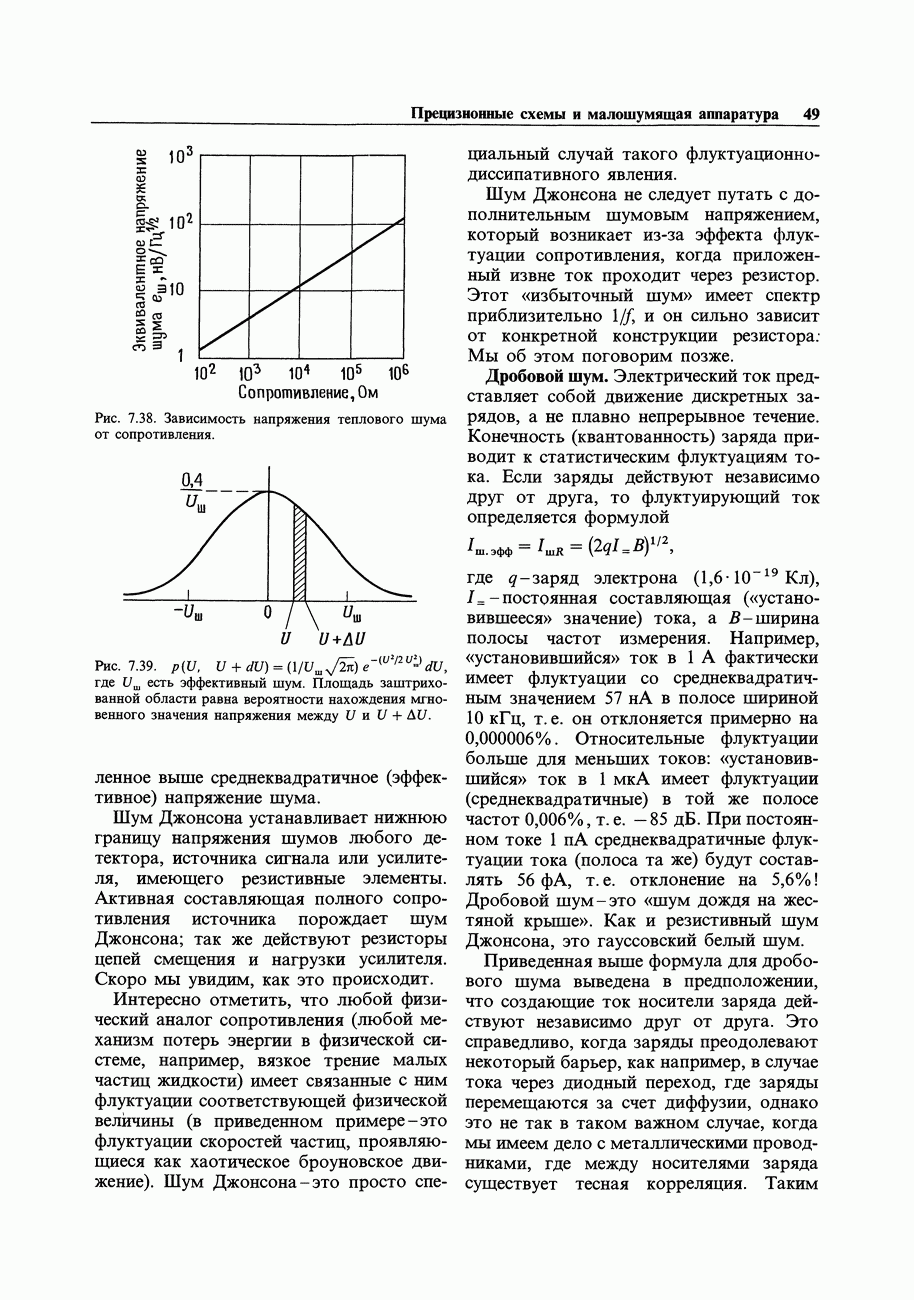
- ШУМЫ УСИЛИТЕЛЕЙ
- 7.11. Происхождение и виды шумов
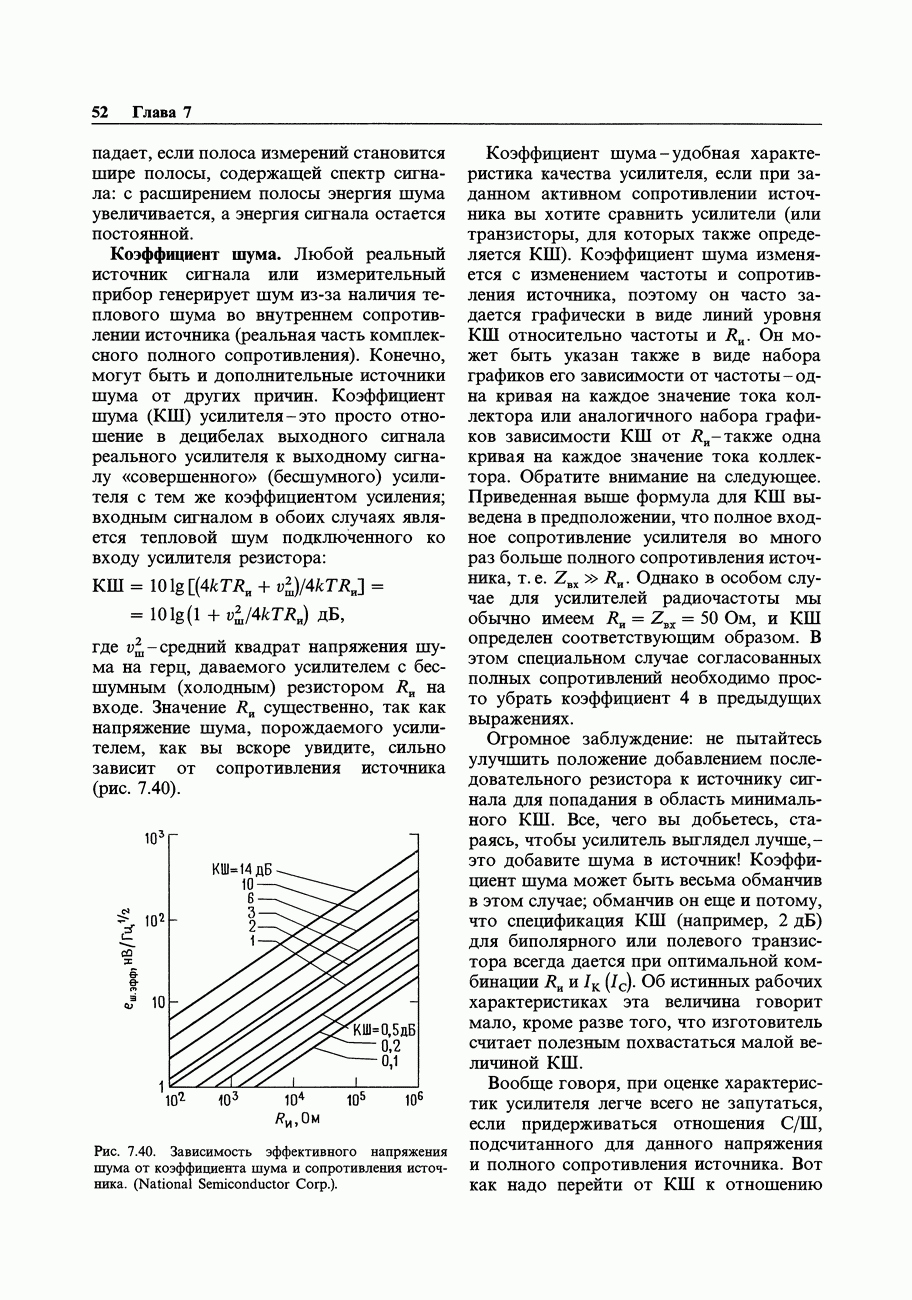
- 7.12. Отношение сигнал/шум и коэффициент шума
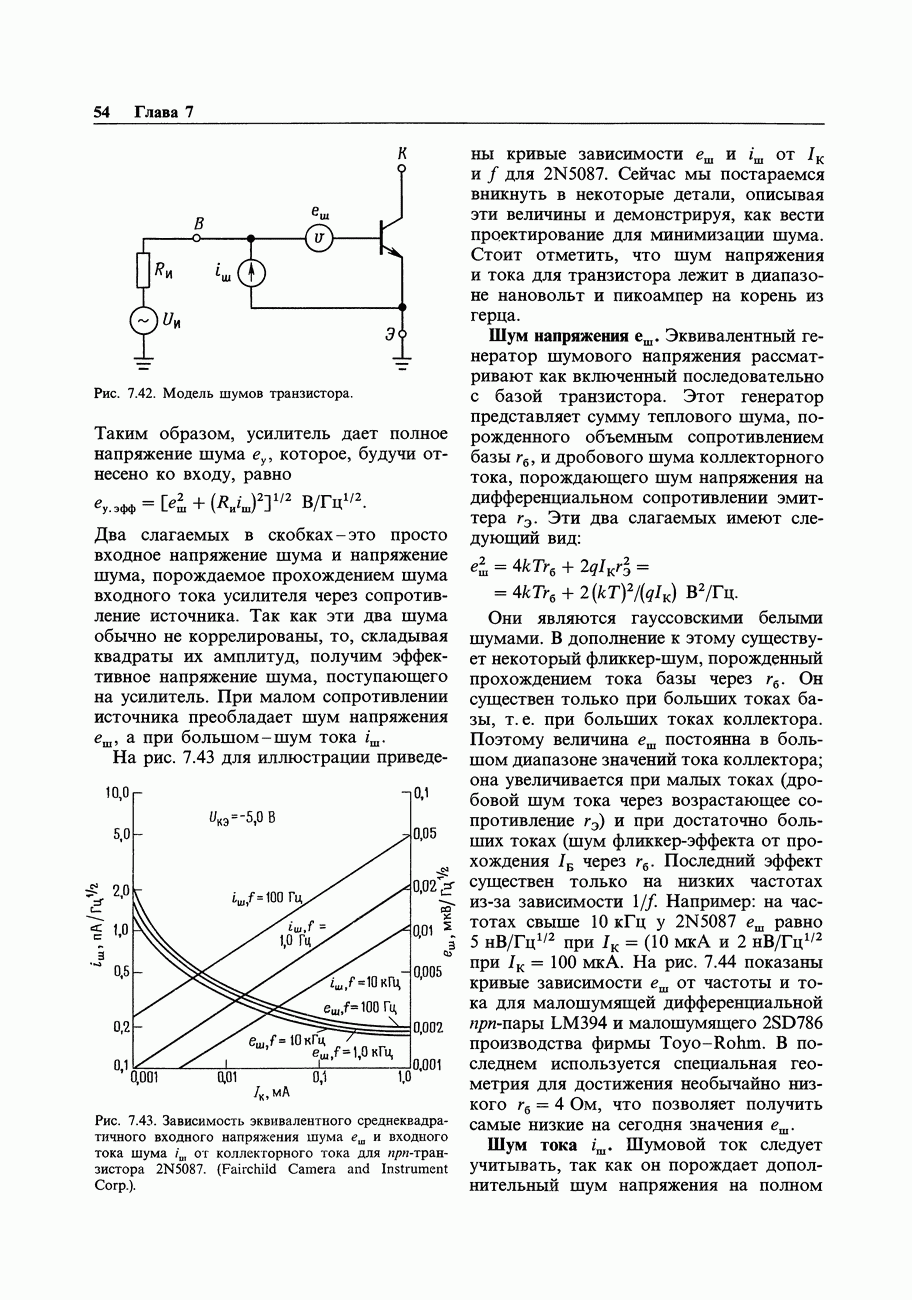
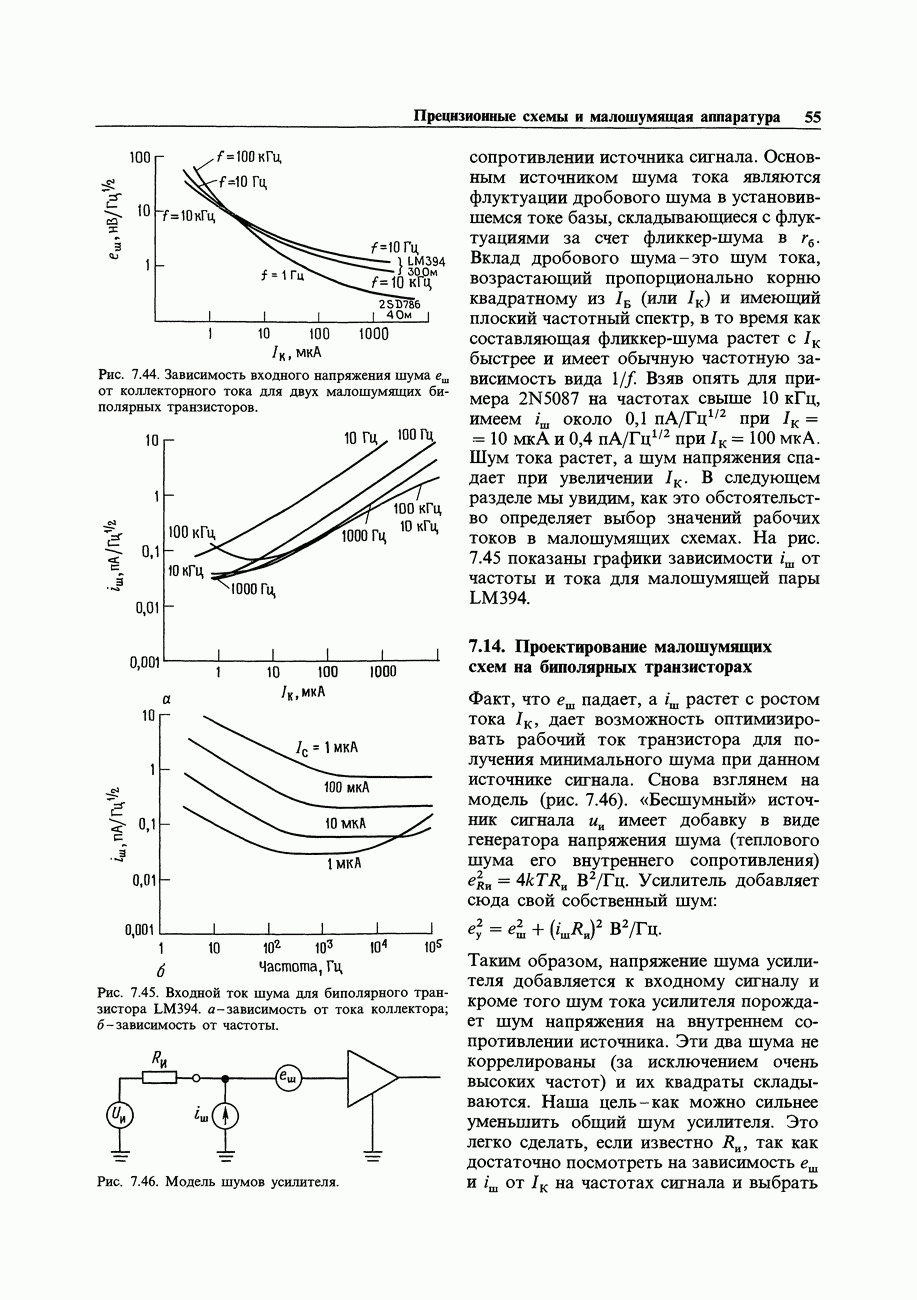
- 7.13. Шум тока и напряжения транзисторного усилителя
- 7.14. Проектирование малошумящих схем на биполярных транзисторах
- 7.15. Шум ПТ
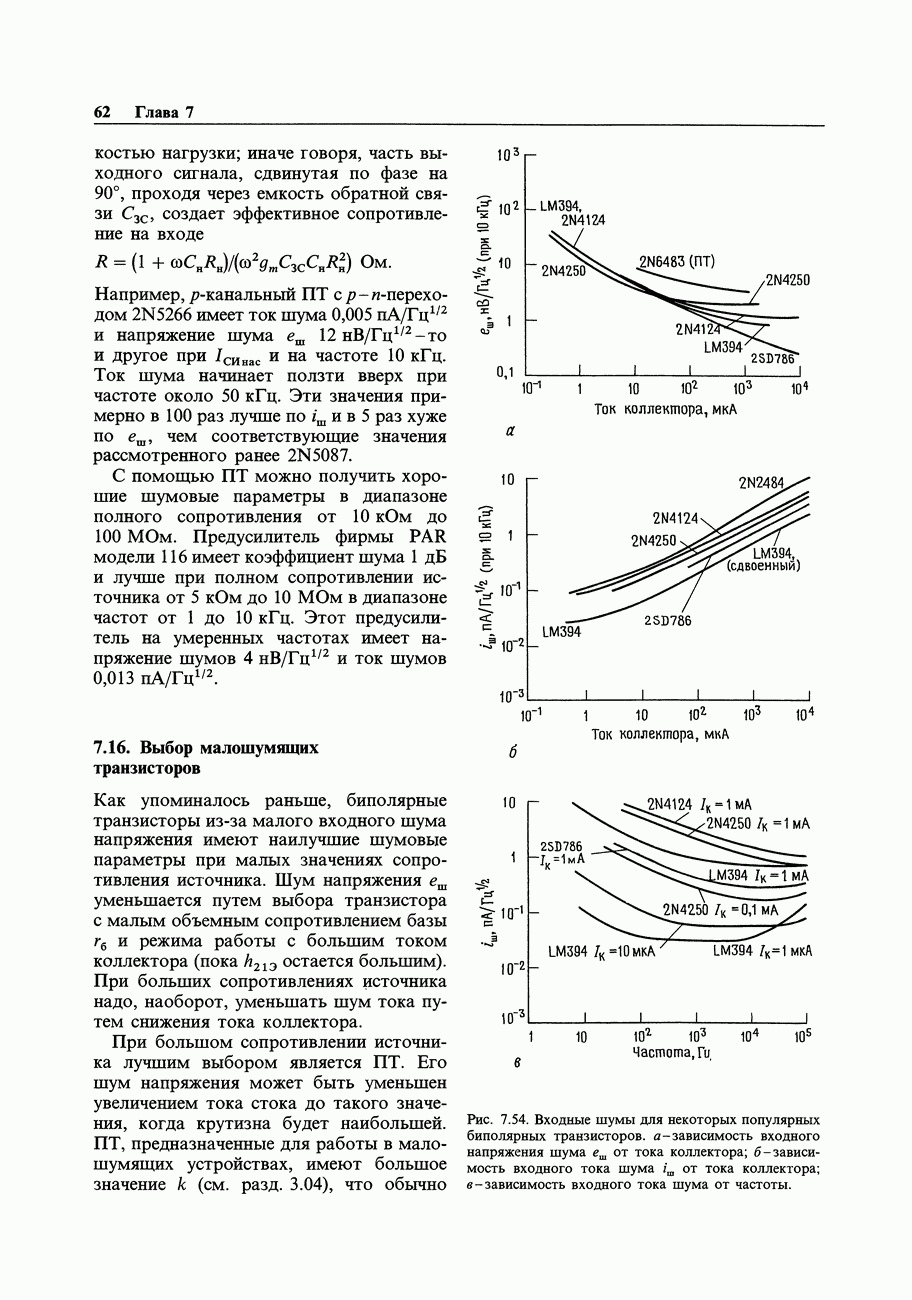
- 7.16. Выбор малошумящих транзисторов
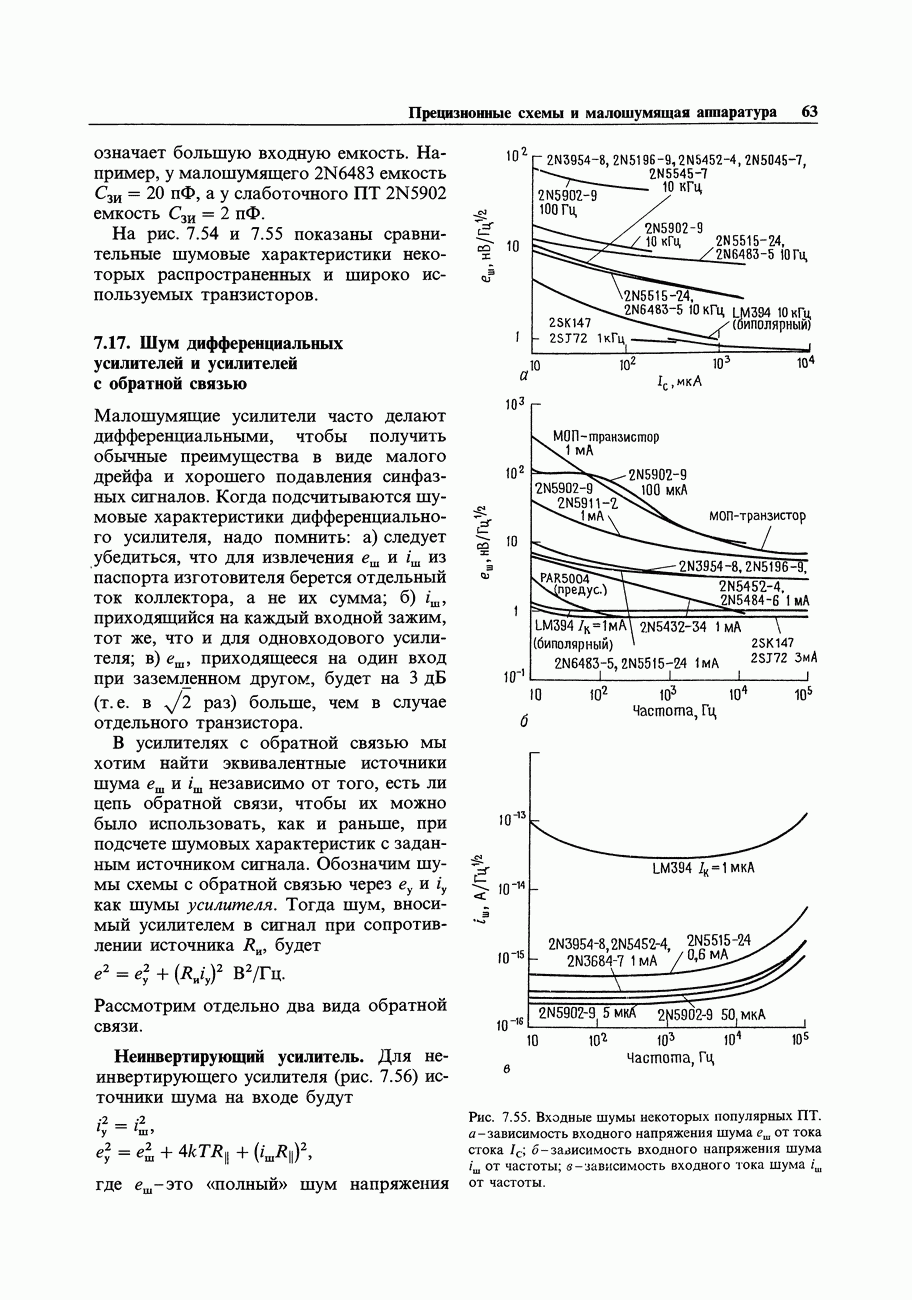
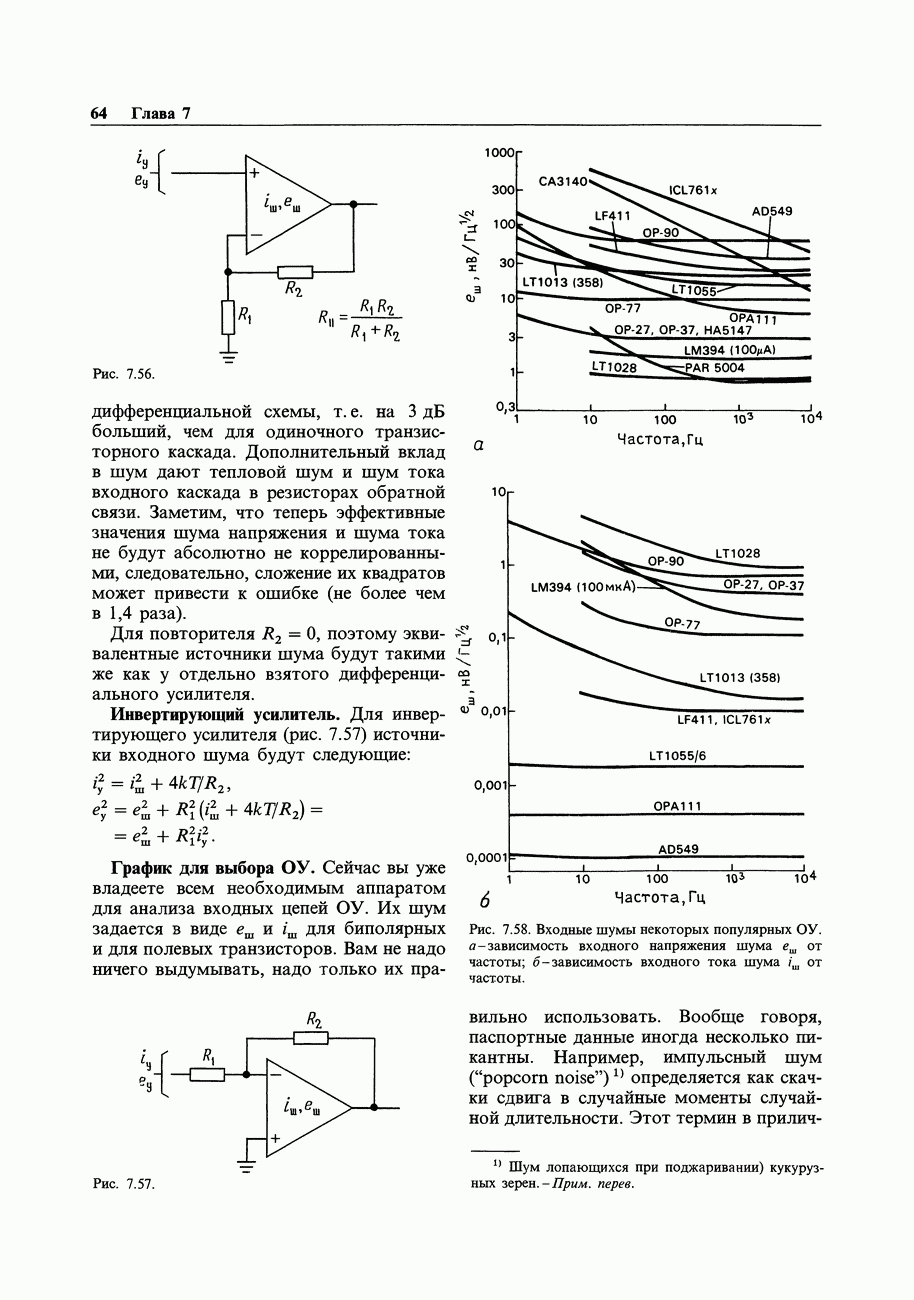
- 7.17. Шум дифференциальных усилителей и усилителей с обратной связью
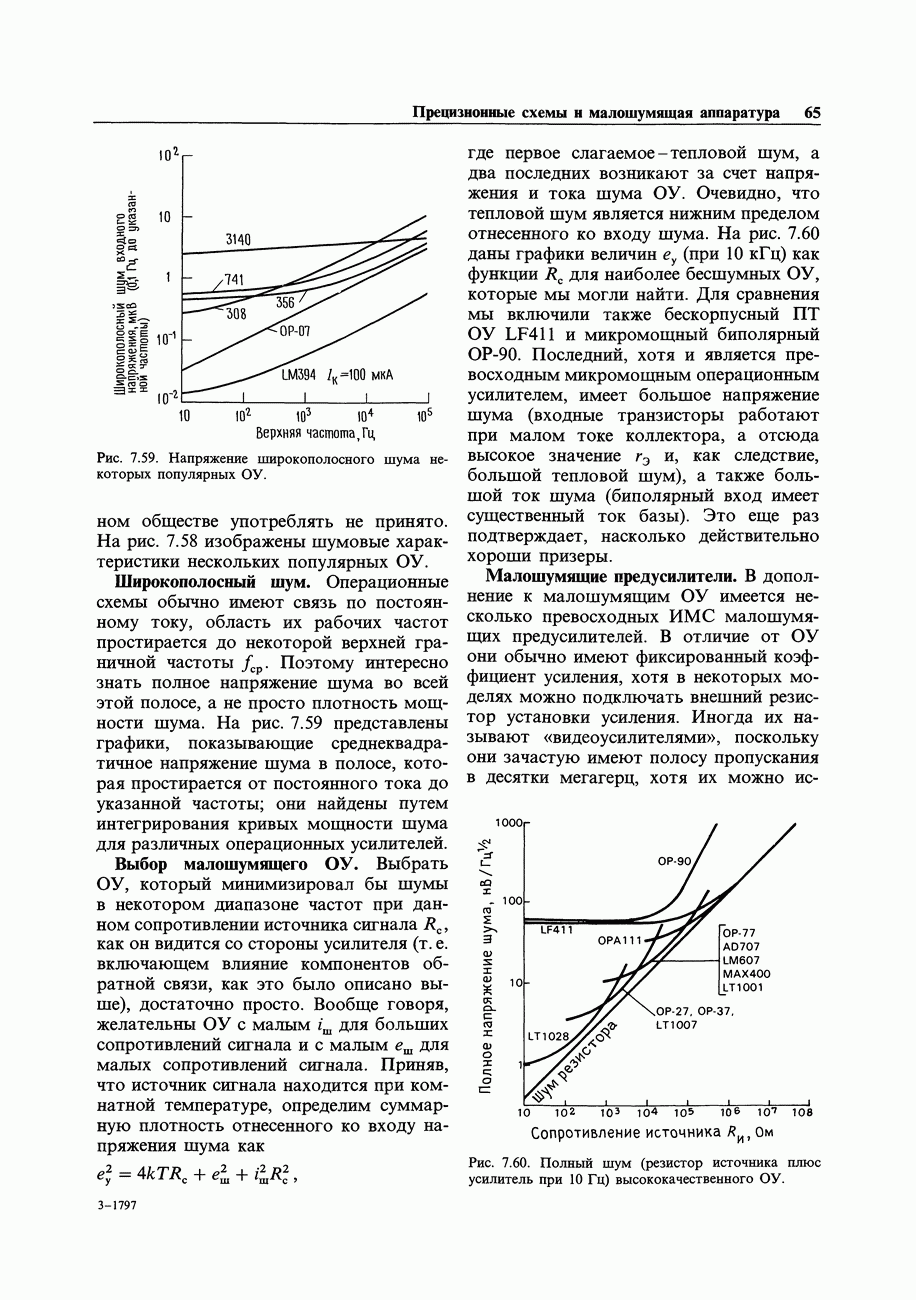
- ИЗМЕРЕНИЕ ШУМА И ИСТОЧНИКИ ШУМА
- 7.18. Измерение без источника шума
- 7.19. Измерение с источником шума
- 7.20. Генераторы шумов и сигналов
- 7.21. Ограничение полосы частот и измерение среднеквадратичного (эффективного) напряжения
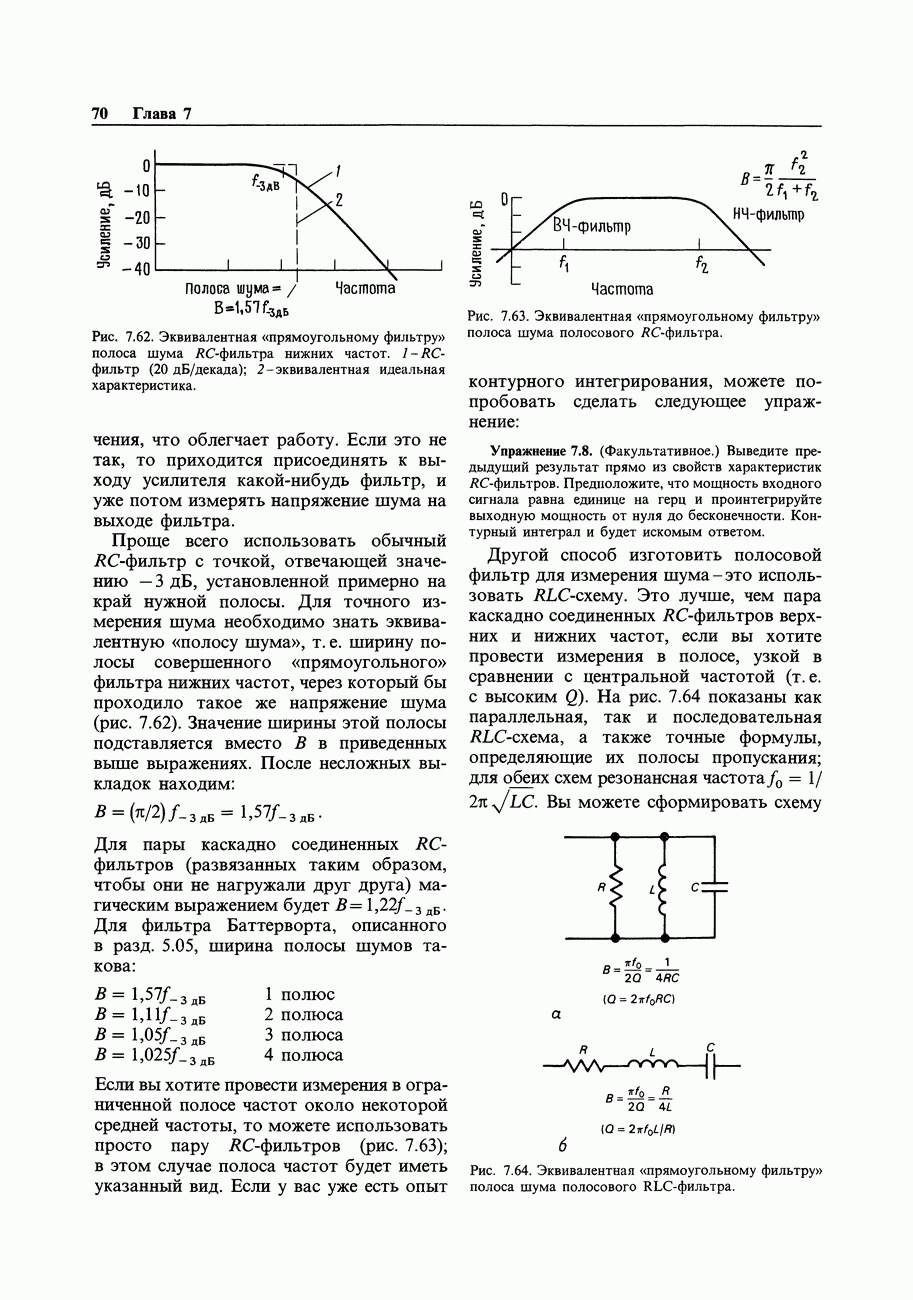
- 7.22. Попурри на тему шумов
- ПОМЕХИ: ЭКРАНИРОВАНИЕ И ЗАЗЕМЛЕНИЕ
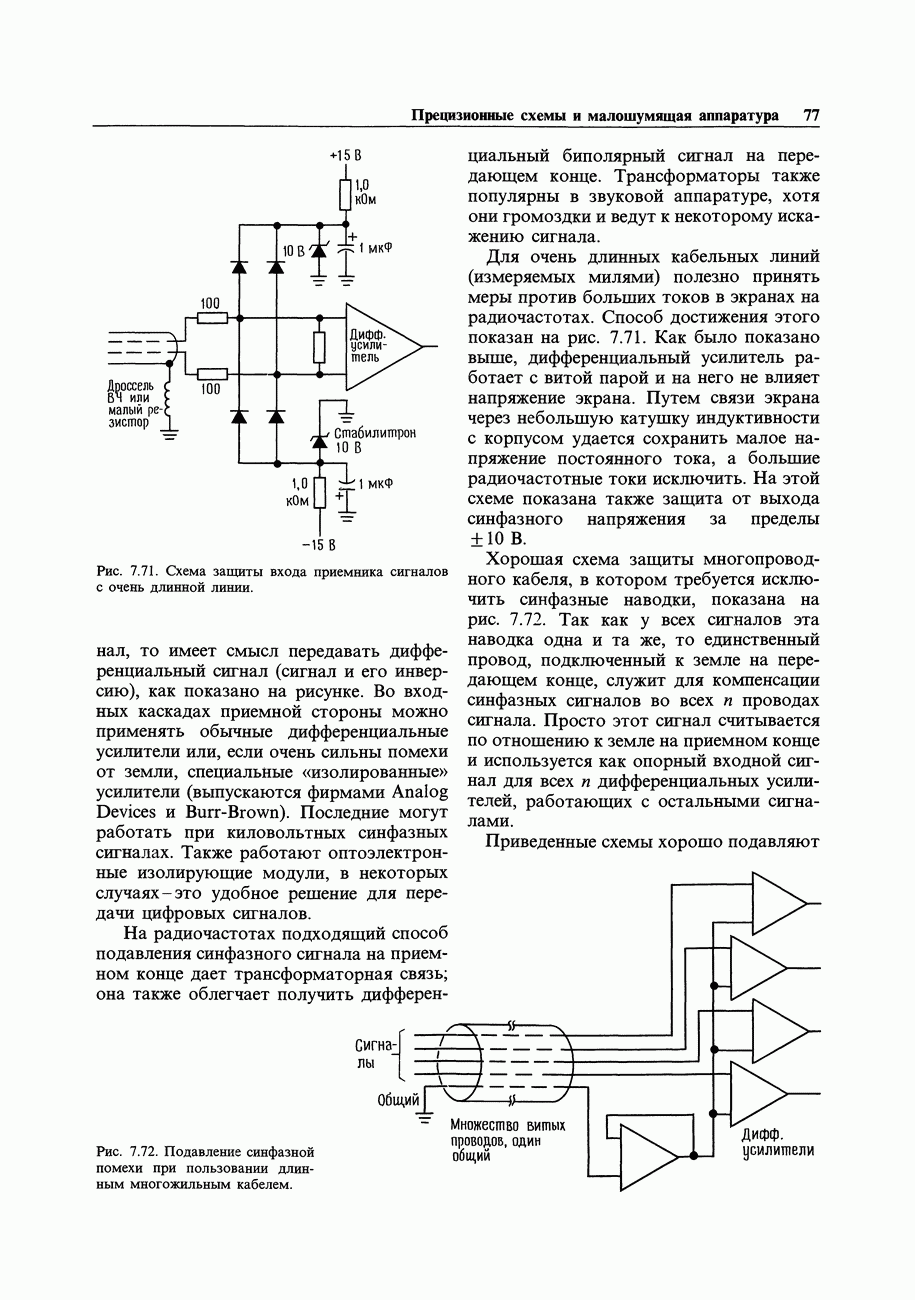
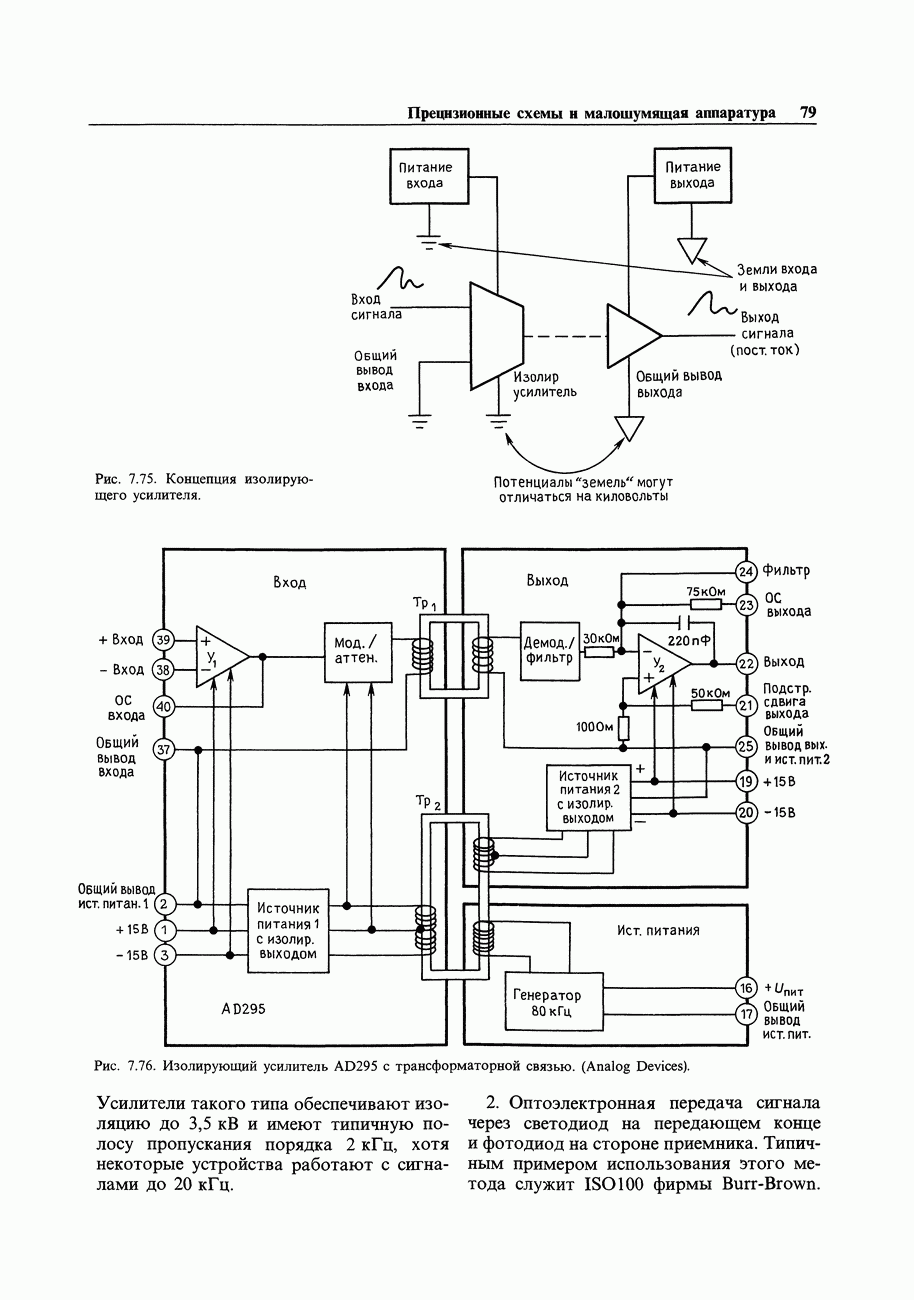
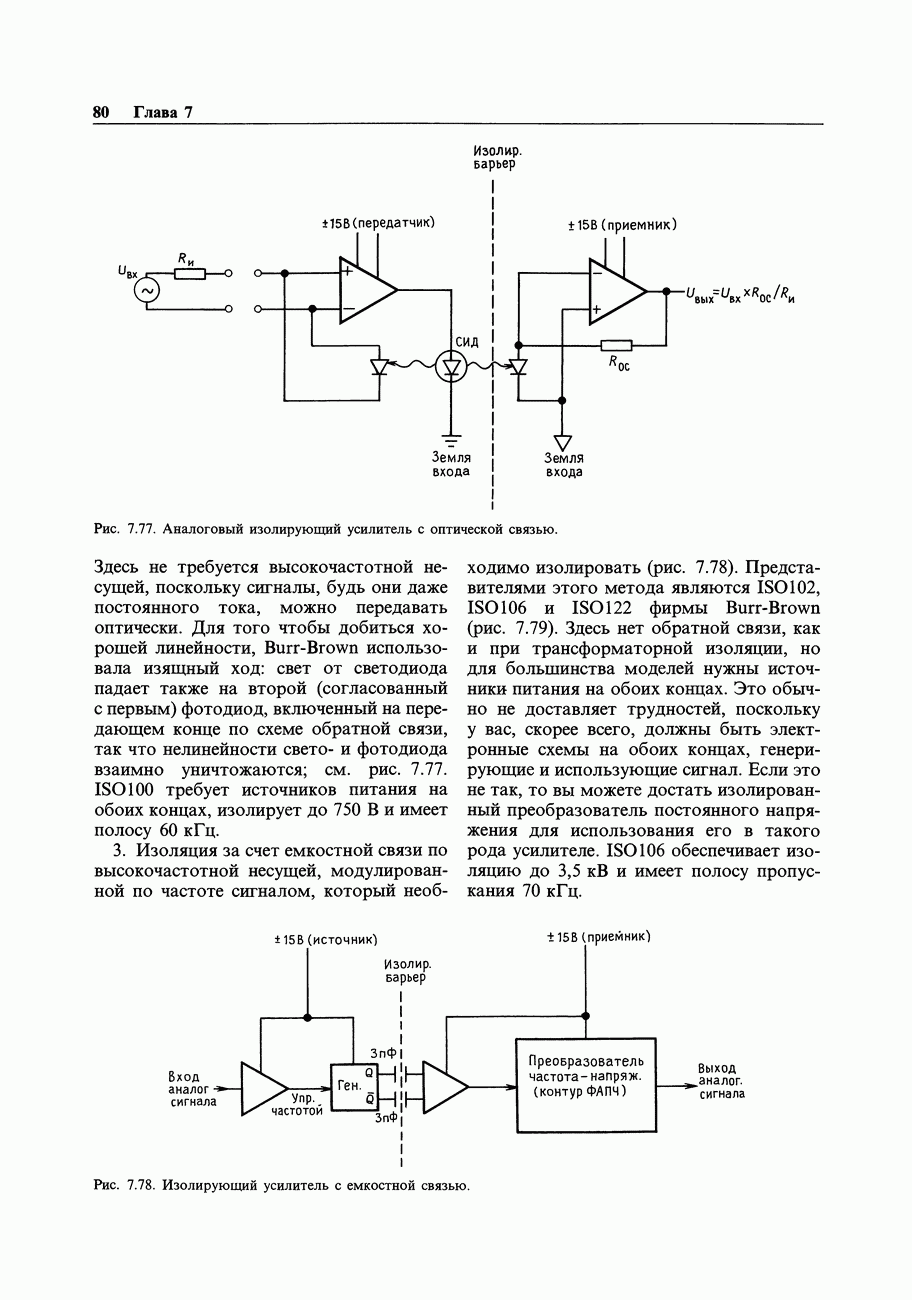
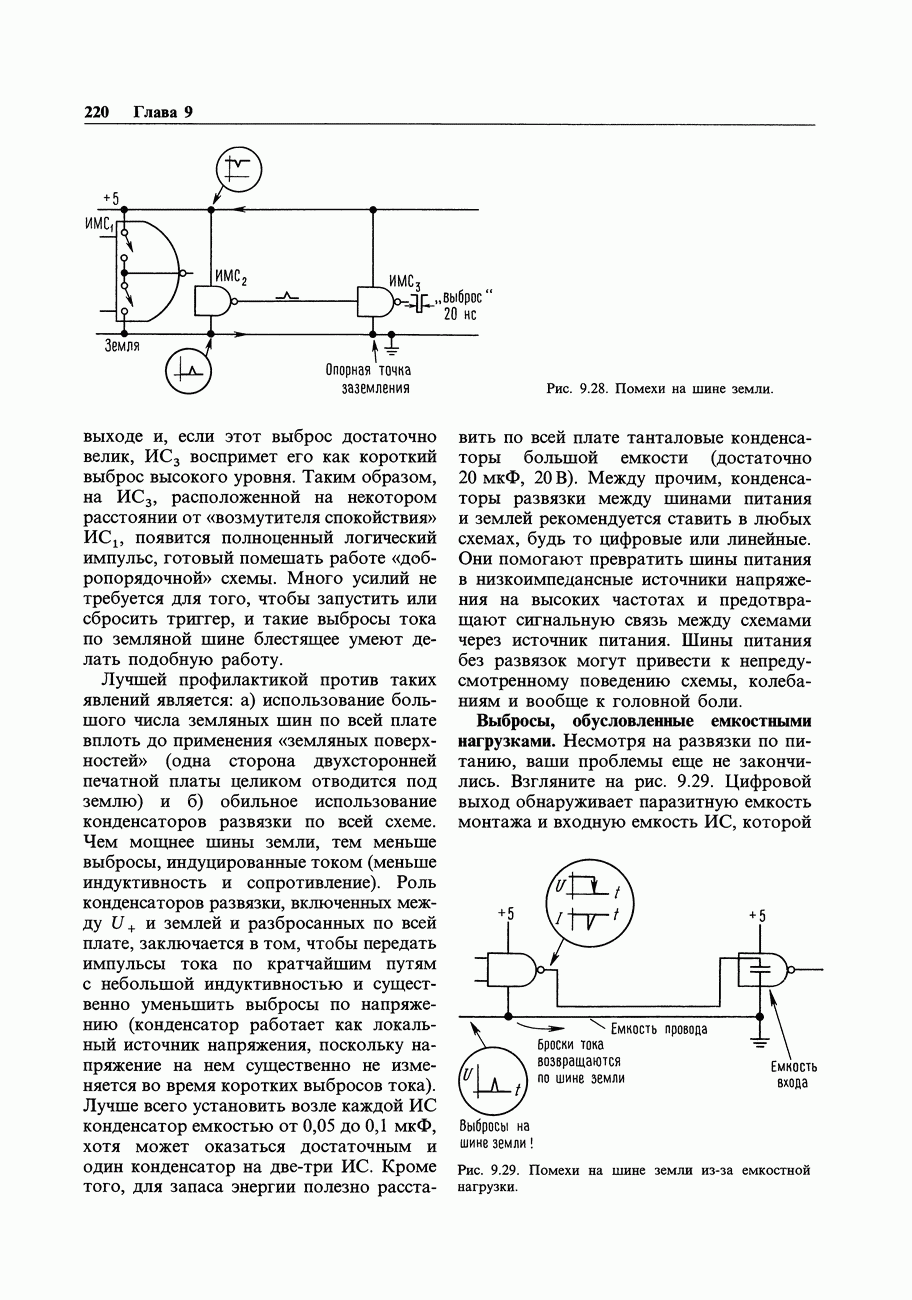
- 7.23. Помехи
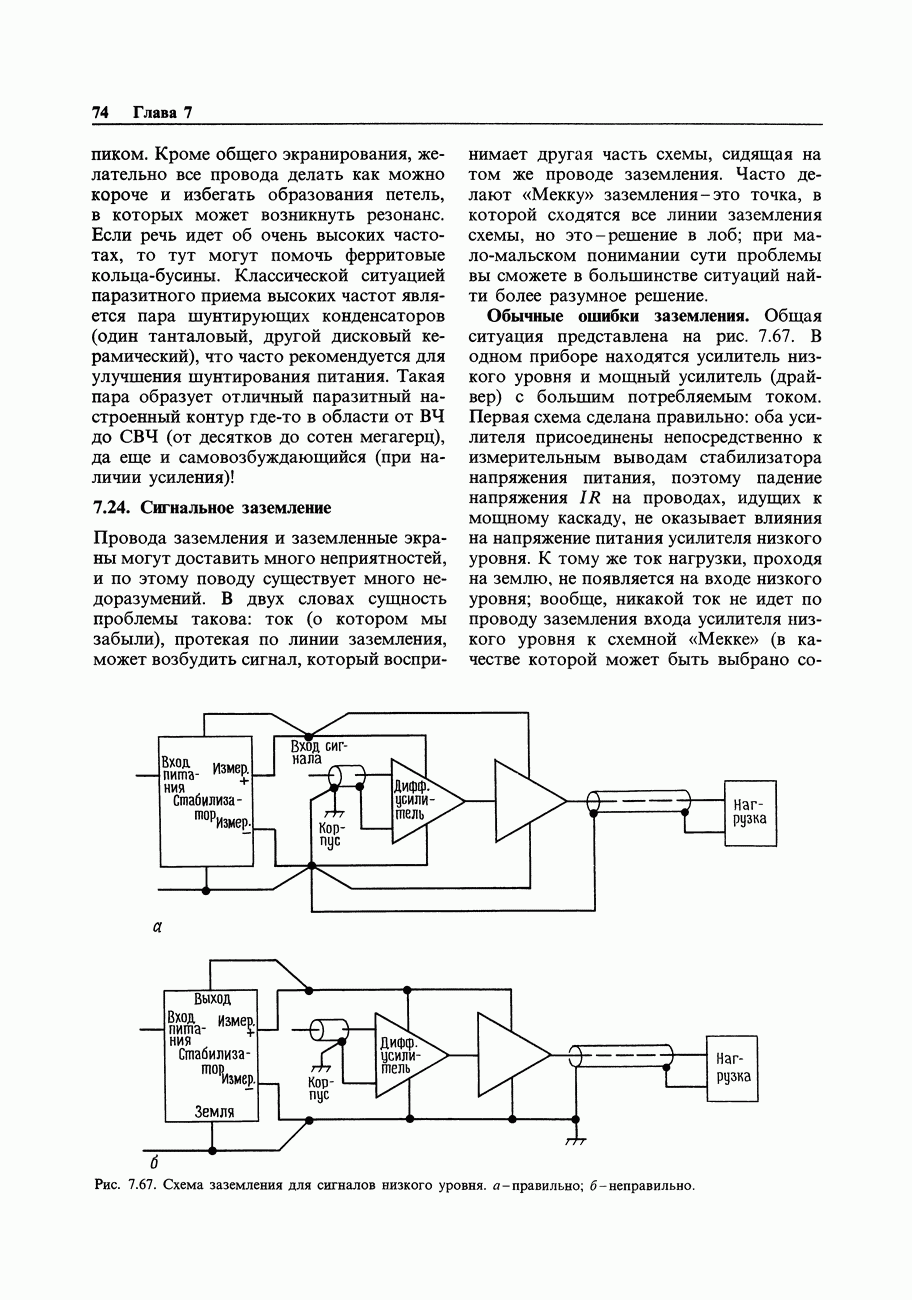
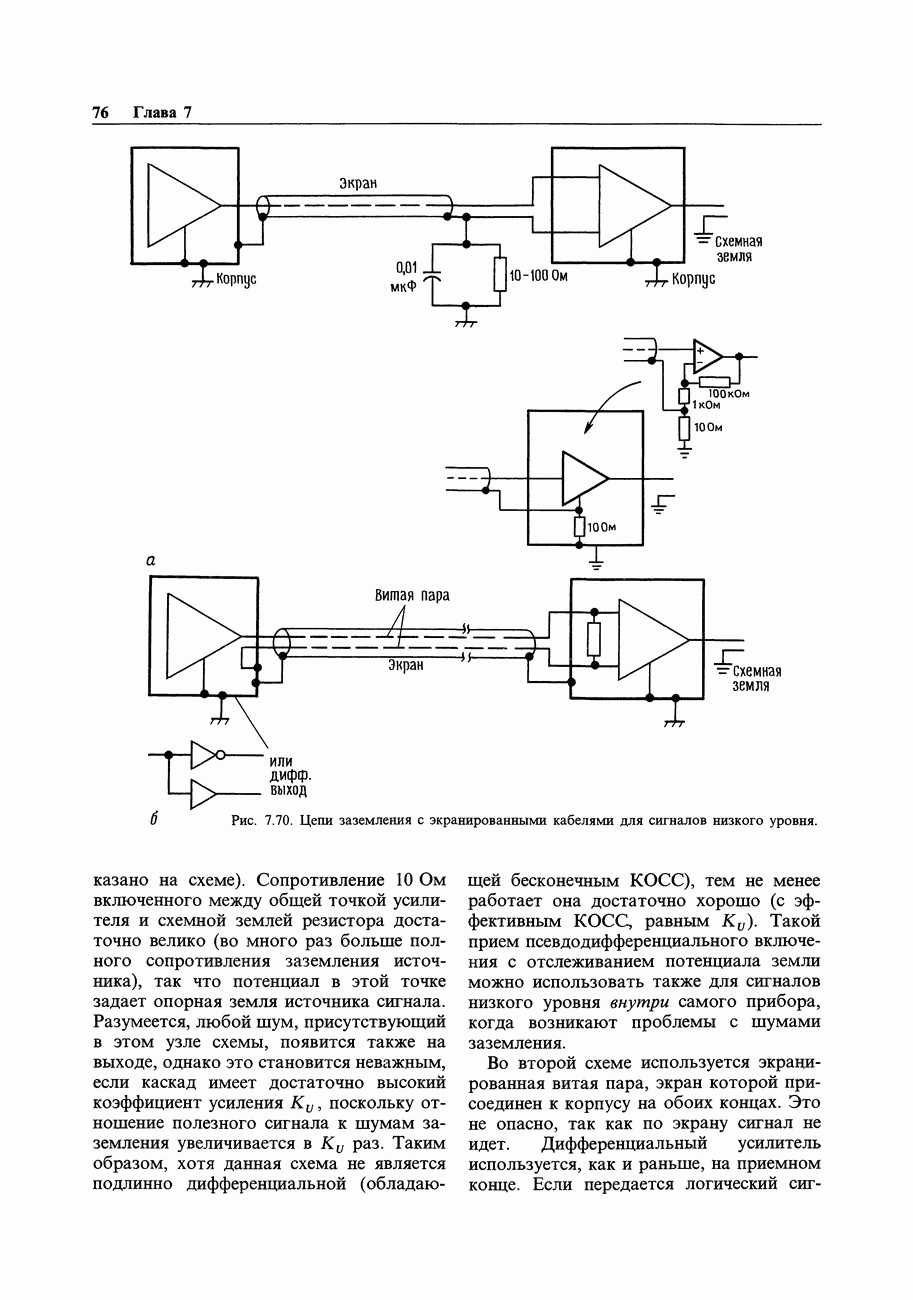
- 7.24. Сигнальное заземление
- 7.25. Межприборное заземление
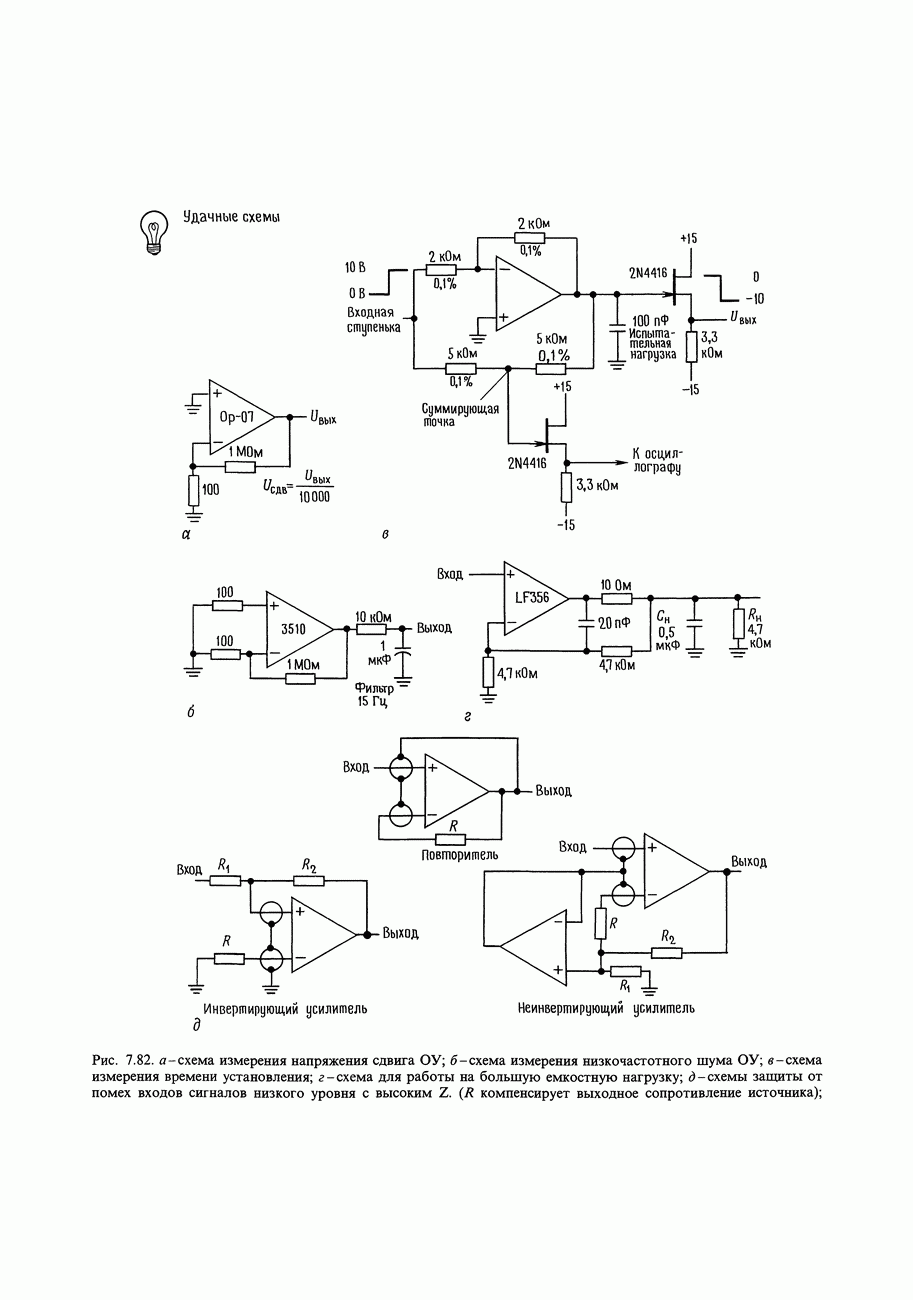
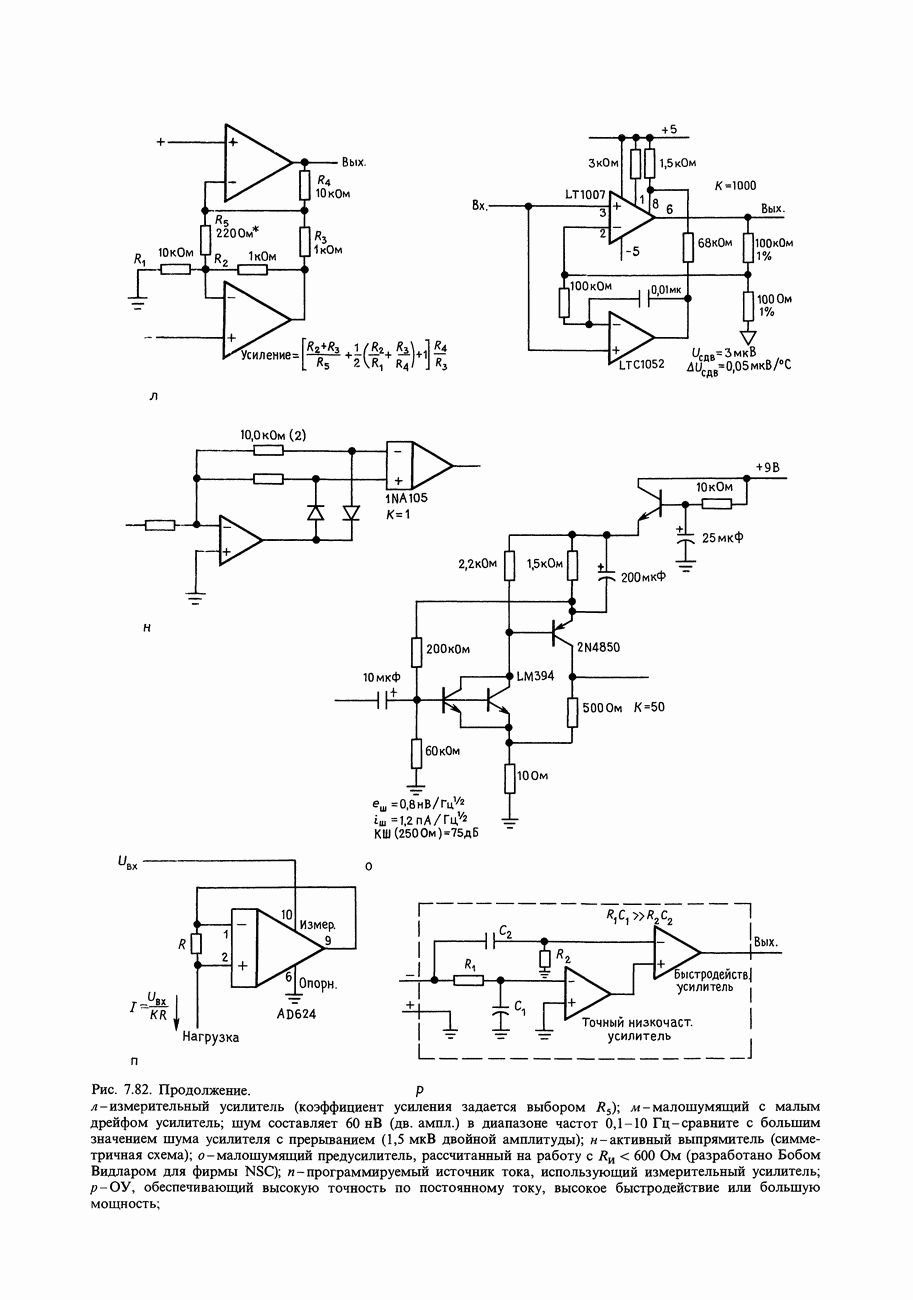
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 8. ЦИФРОВЫЕ СХЕМЫ
- 8.01. Цифровые и аналоговые сигналы
- 8.02. Логические состояния
- ЛОГИЧЕСКИЕ УРОВНИ
- 8.03. Числовые коды
- 8.04. Вентили и таблицы истинности
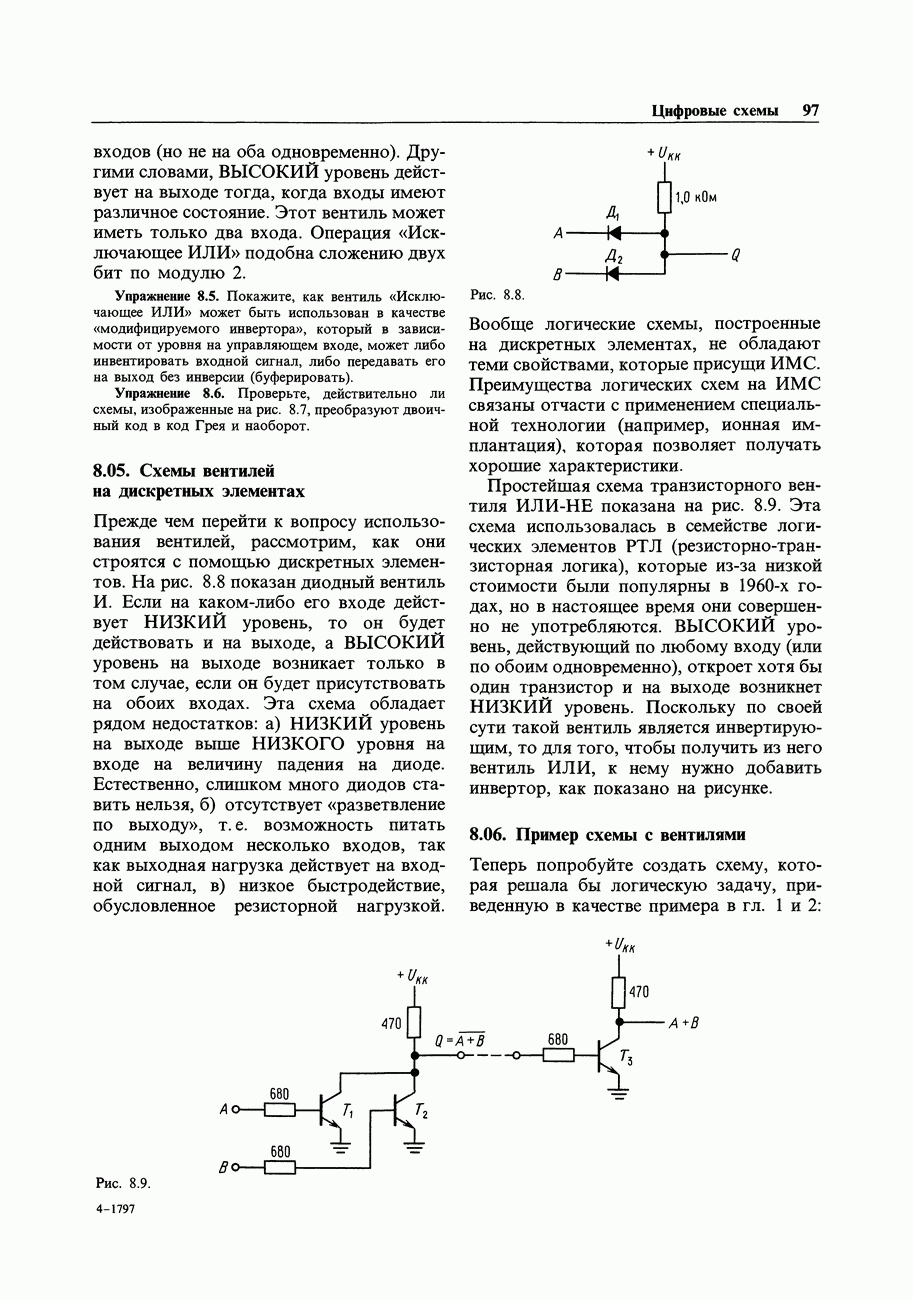
- 8.05. Схемы вентилей на дискретных элементах
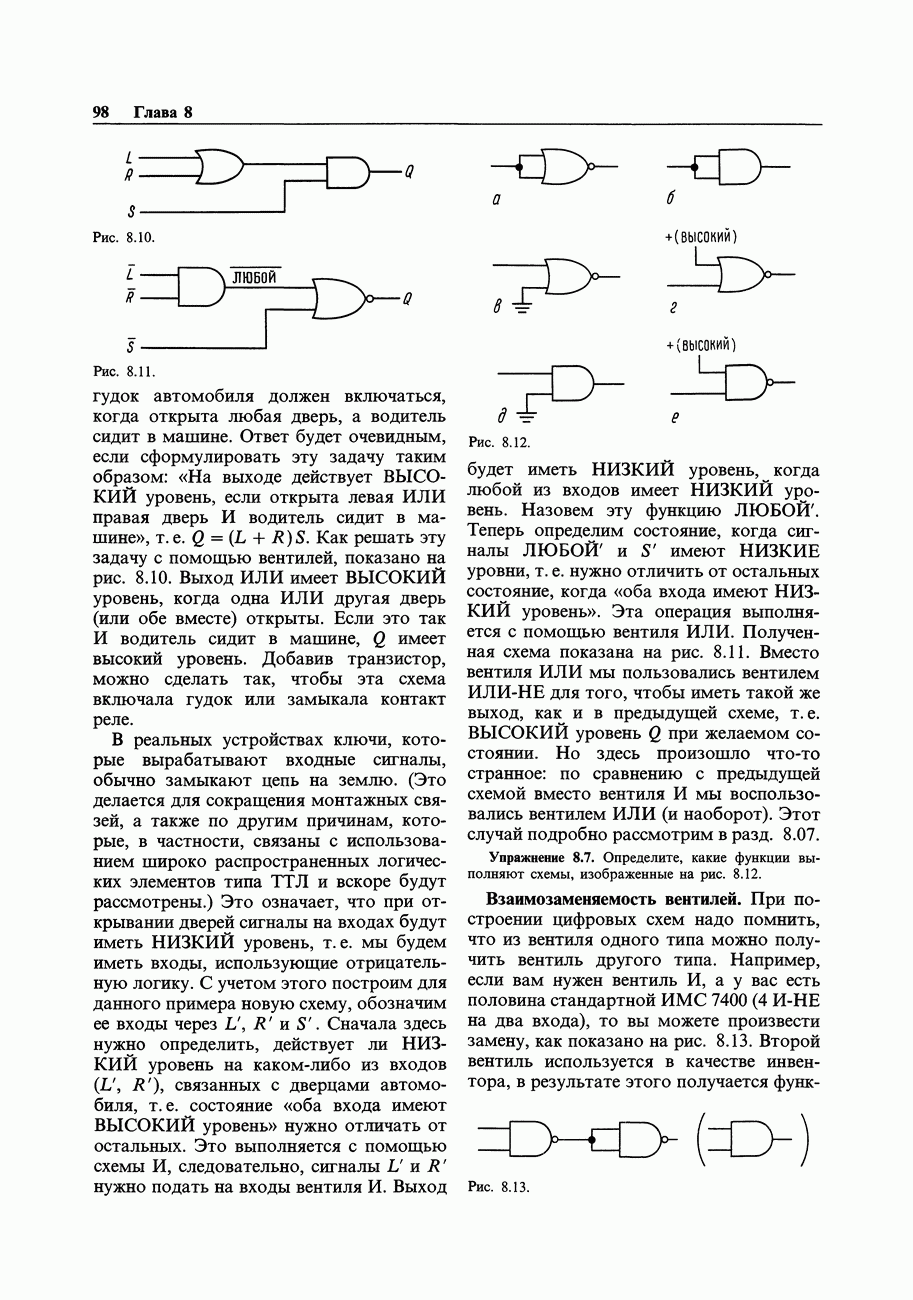
- 8.06. Пример схемы с вентилями
- 8.07. Логические обозначения при заданных уровнях
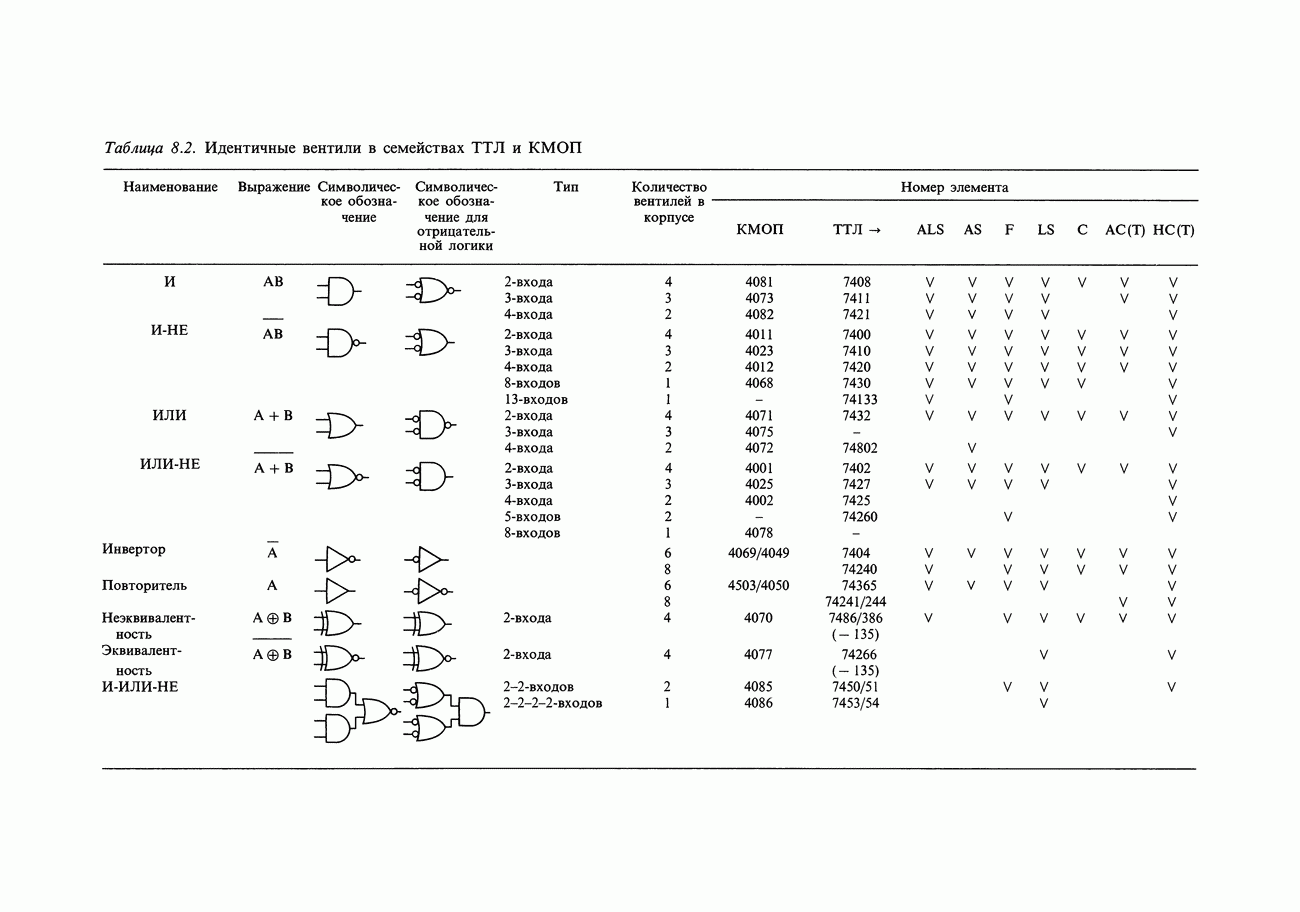
- 8.08. Каталог идентичных вентилей
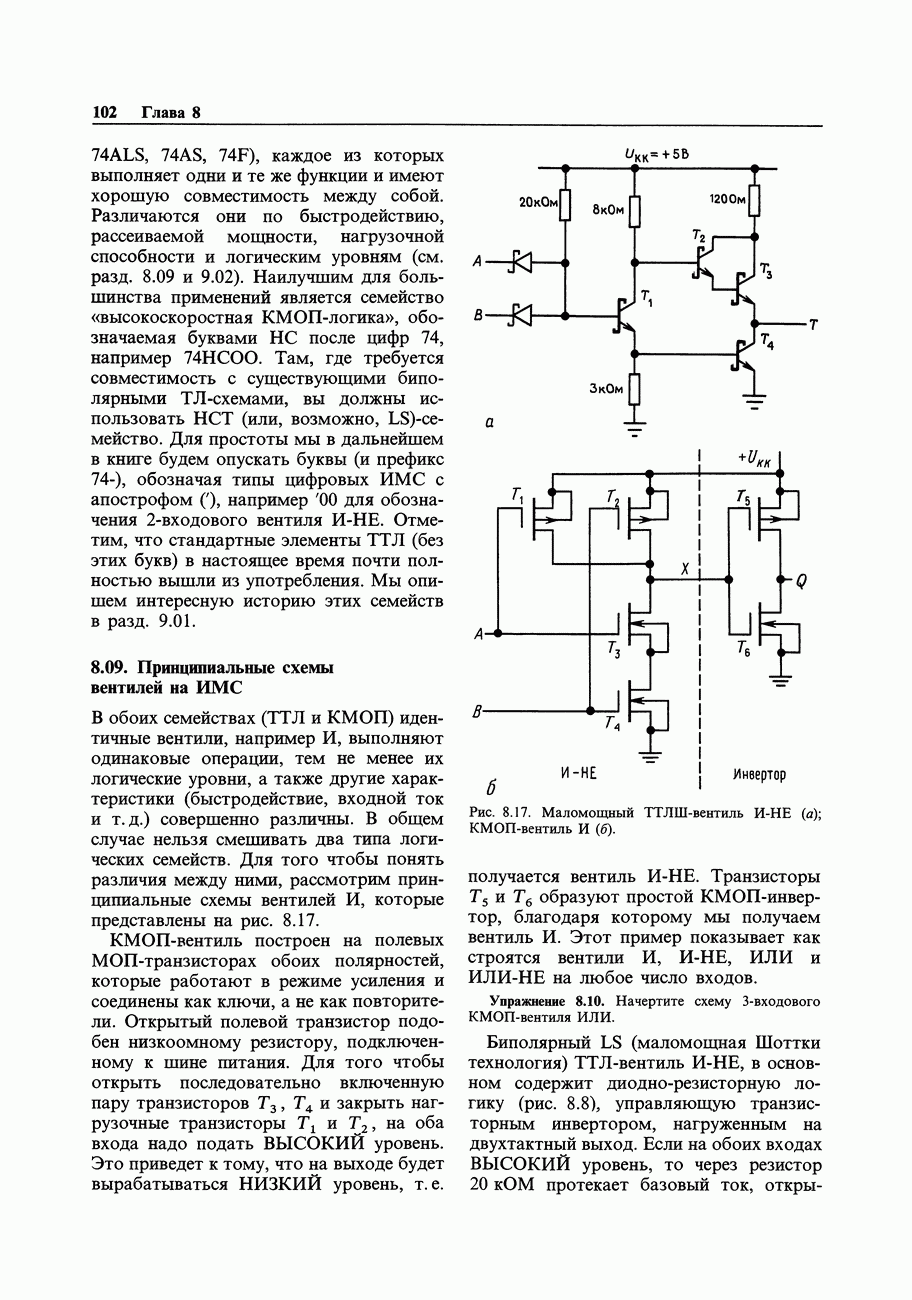
- 8.09. Принципиальные схемы вентилей на ИМС
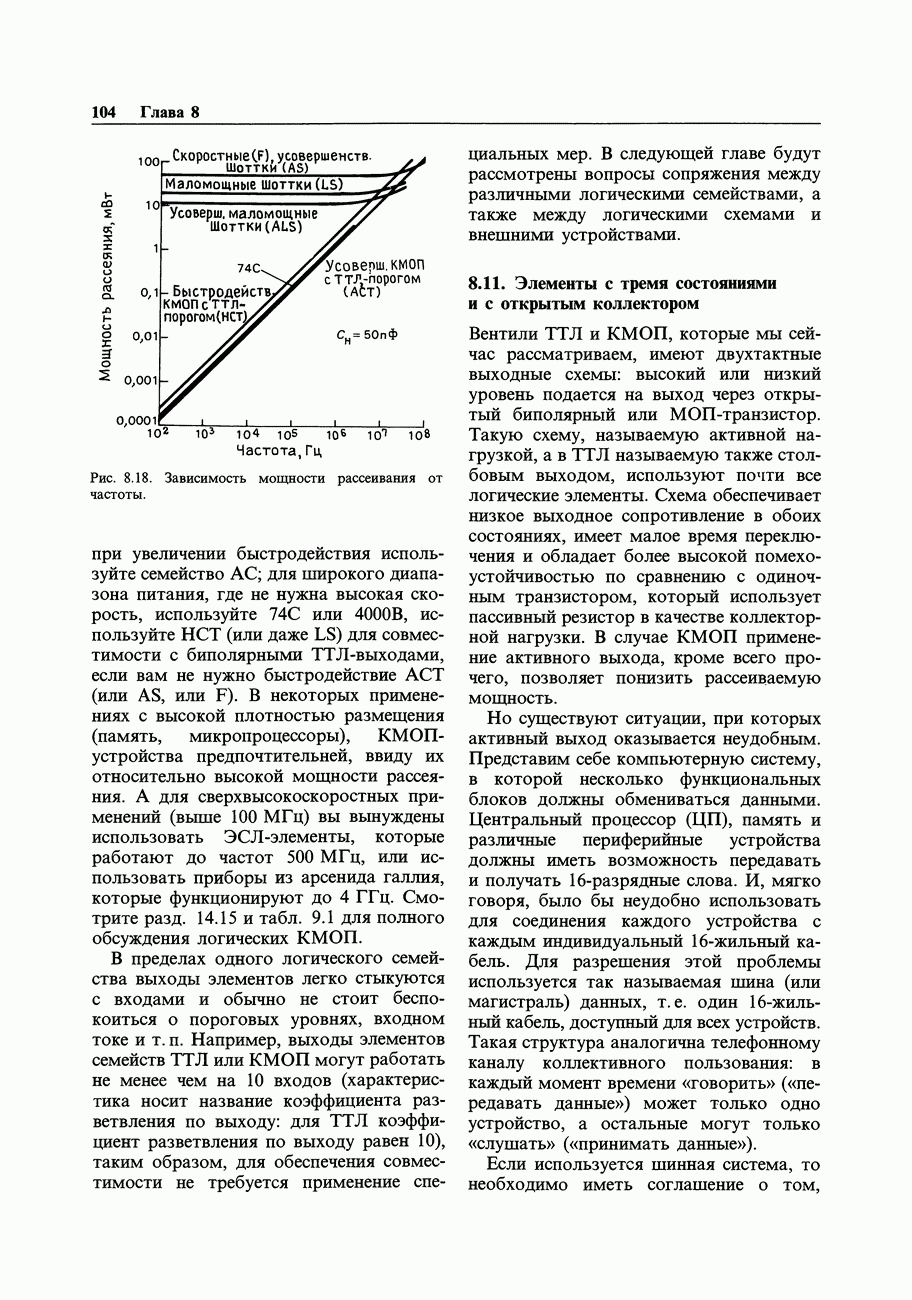
- 8.10. Характеристики ТТЛ и КМОП
- 8.11. Элементы с тремя состояниями и с открытым коллектором
- КОМБИНАЦИОННАЯ ЛОГИКА
- 8.12. Логические тождества
- 8.13. Минимизация и карты Карно
- 8.14. Комбинационные функциональные схемы, реализованные на стандартных ИМС
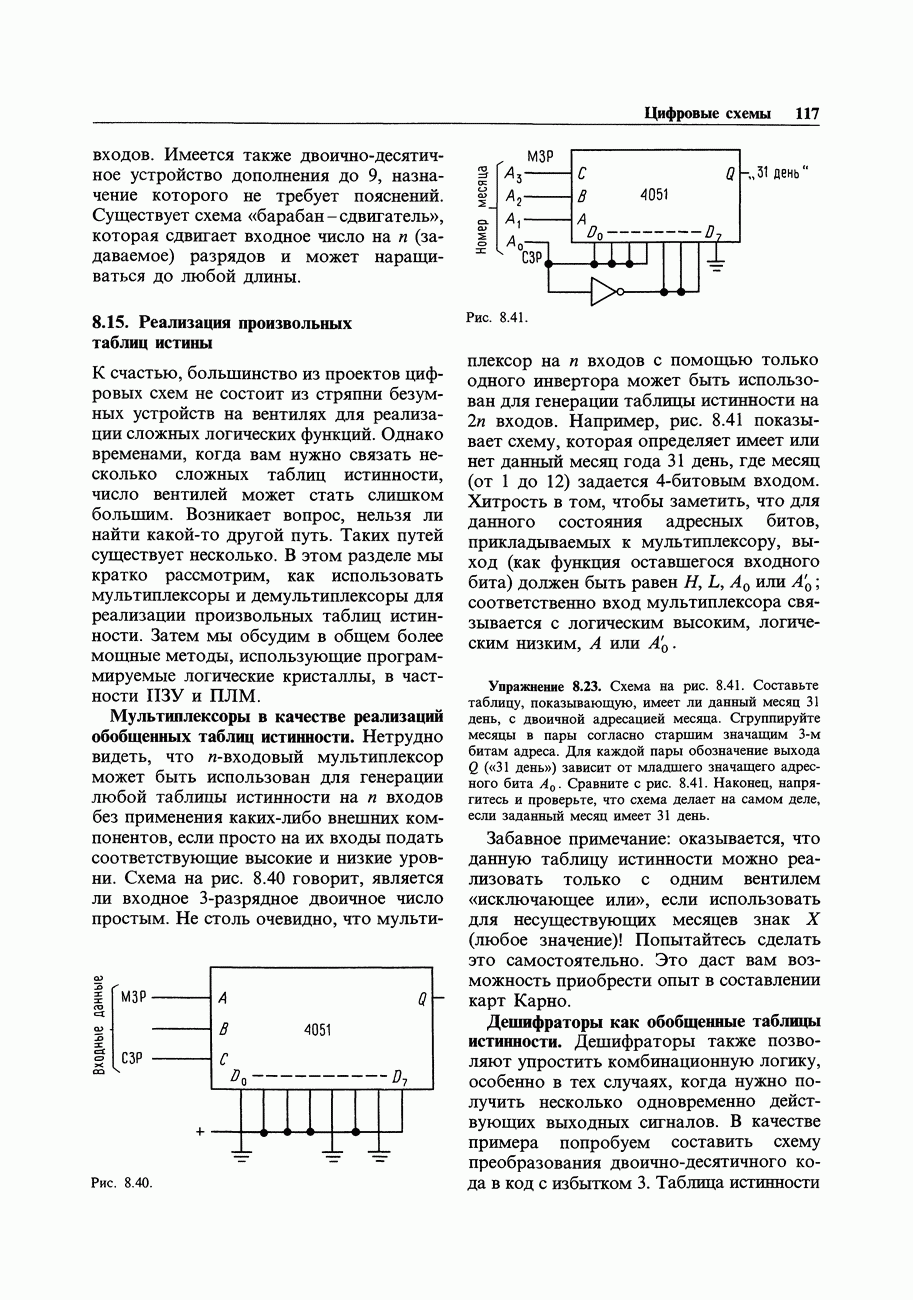
- 8.15. Реализация произвольных таблиц истины
- ПОСЛЕДОВАТЕЛЬНОСТНАЯ ЛОГИКА
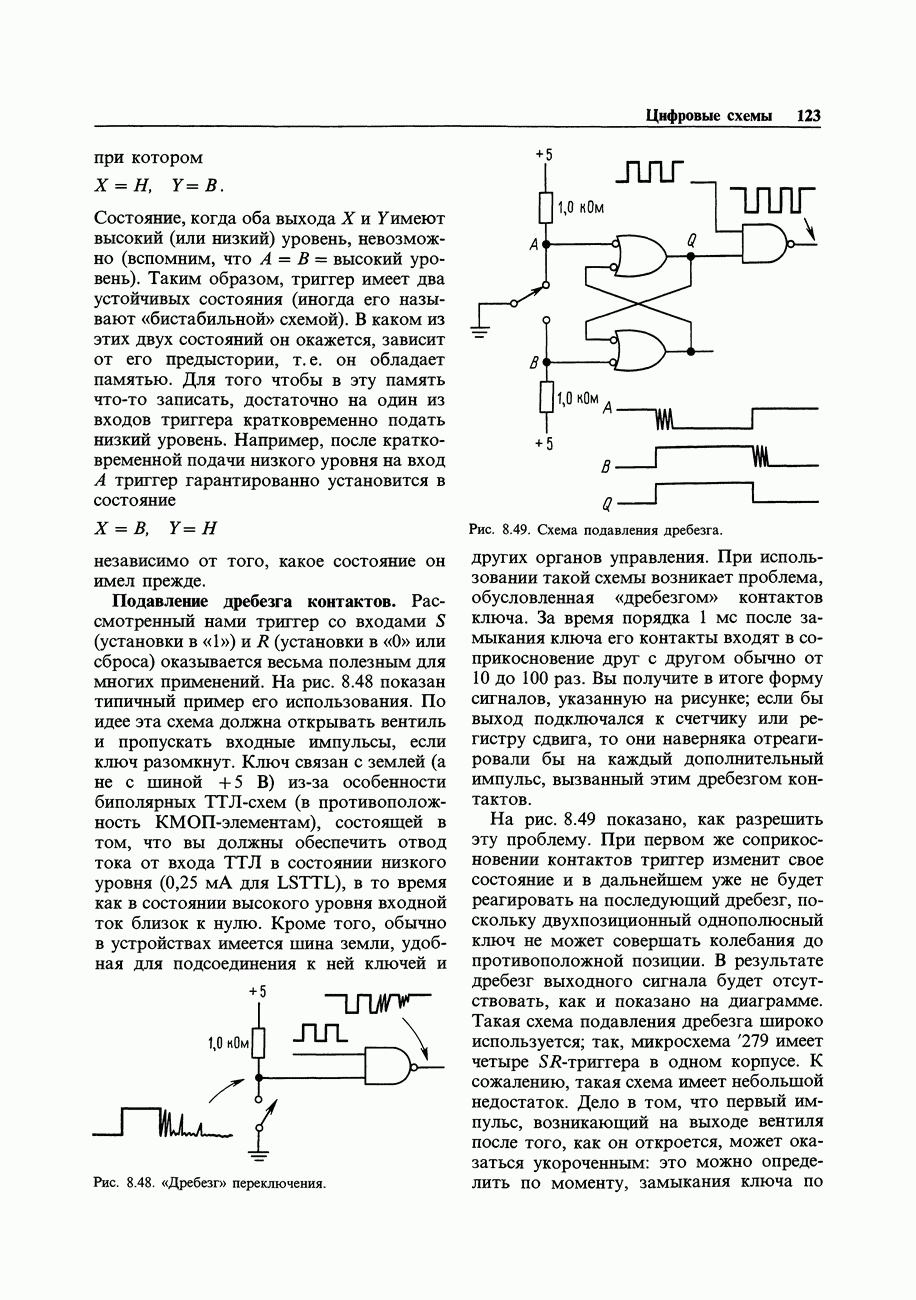
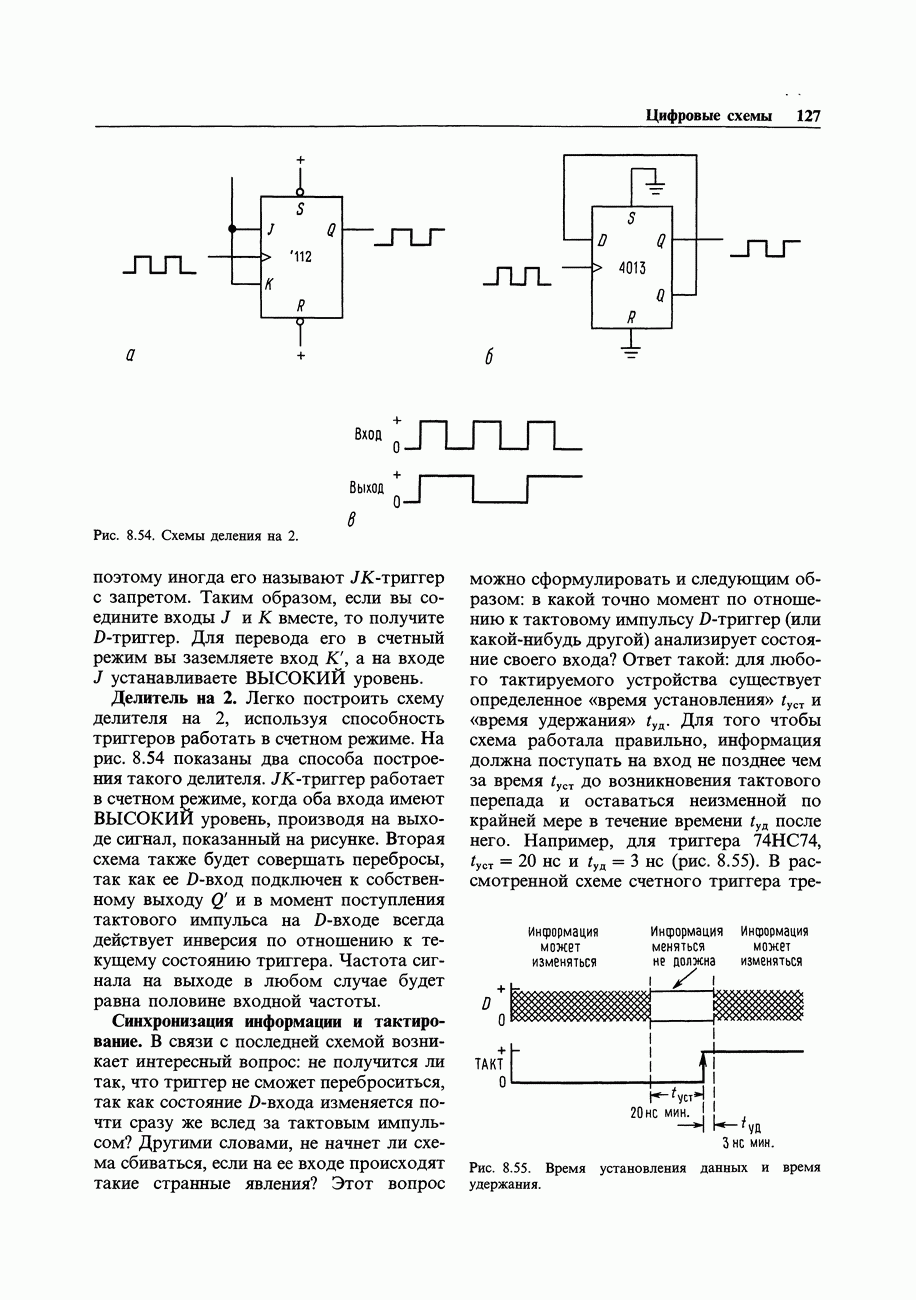
- 8.16. Устройства с памятью: триггеры
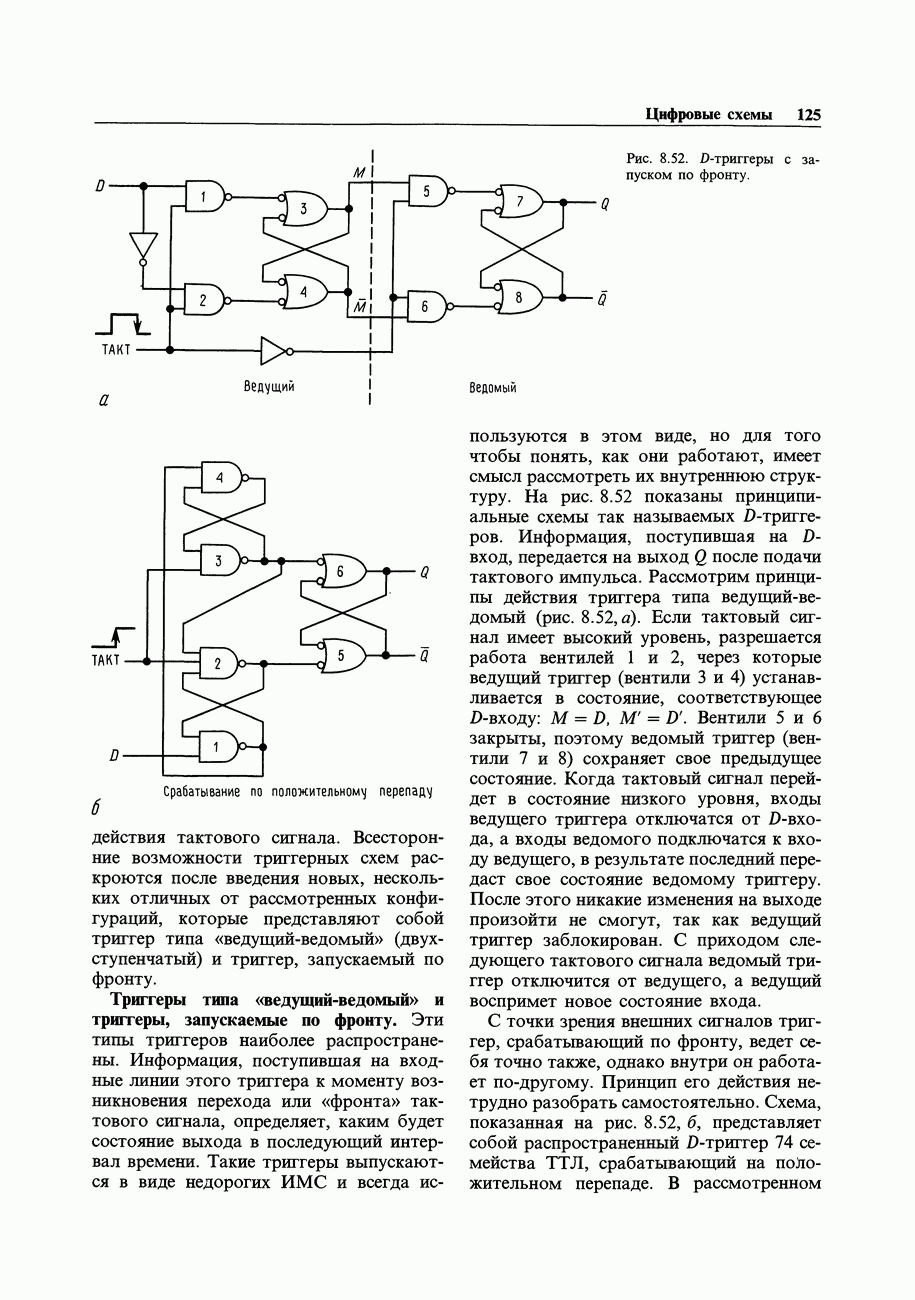
- 8.17. Тактируемые триггеры
- 8.18. Последовательностная логика-объединение памяти и вентилей
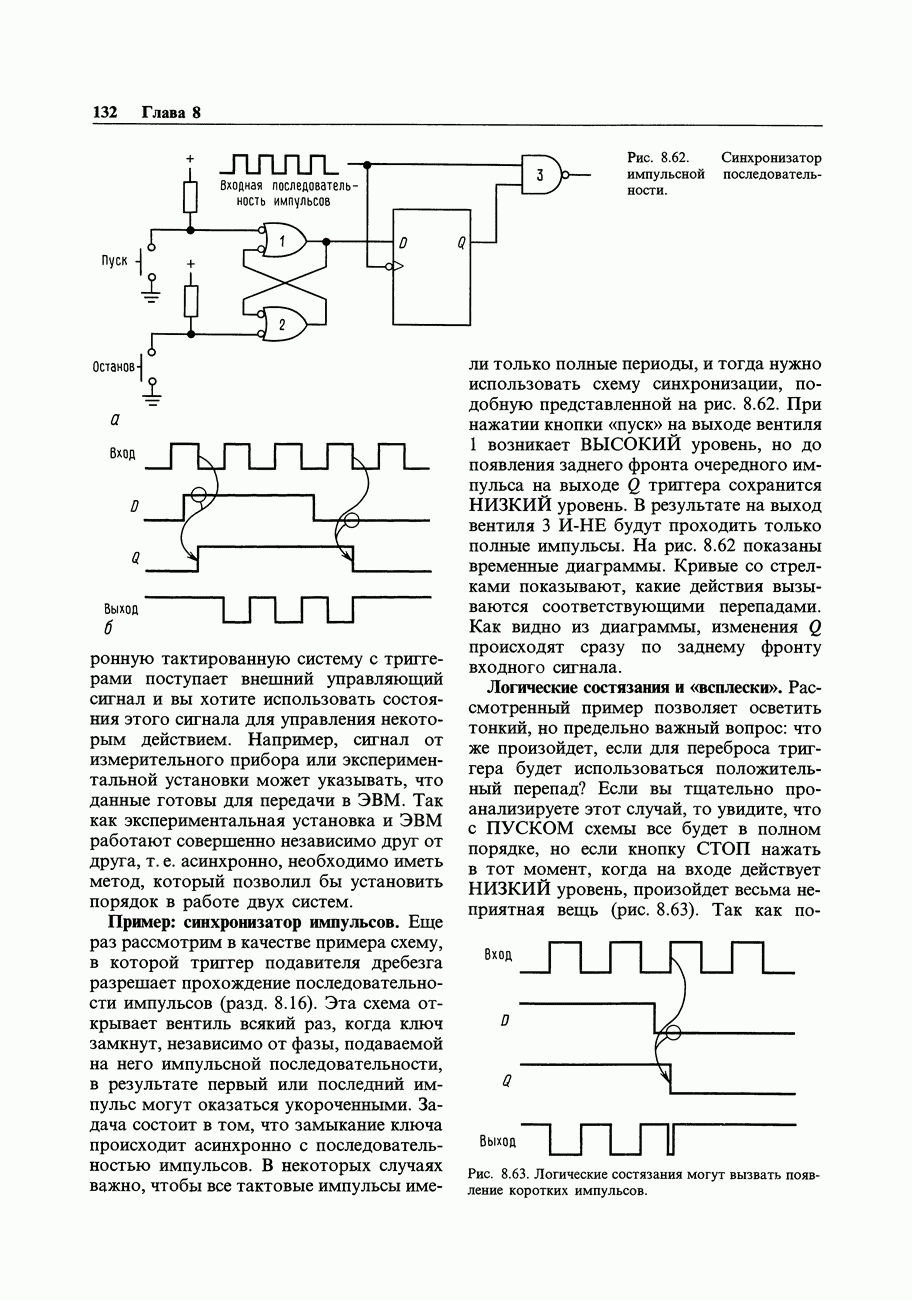
- 8.19. Синхронизатор
- МОНОСТАБИЛЬНЫЕ МУЛЬТИВИБРАТОРЫ
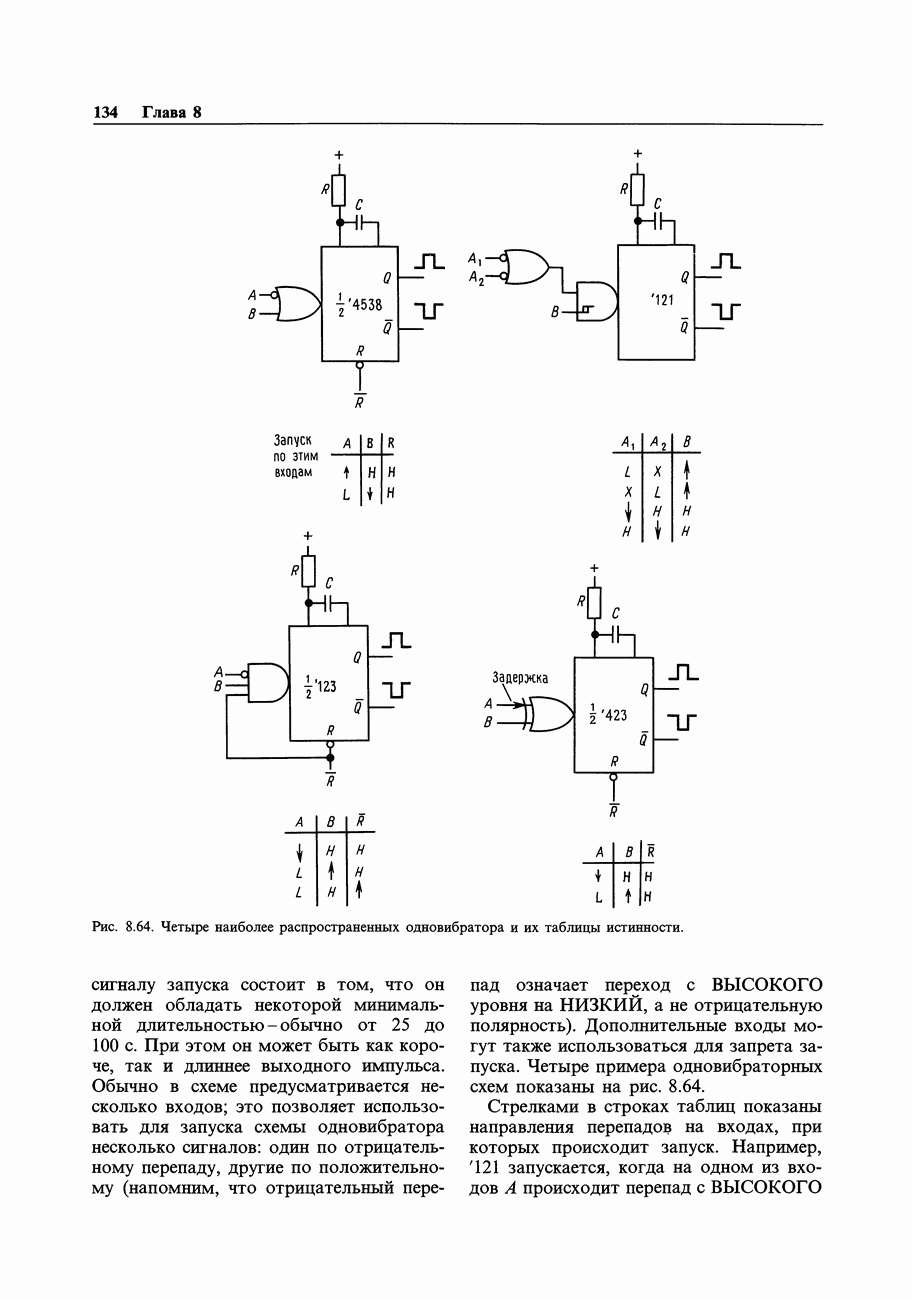
- 8.20. Характеристики одновибраторов
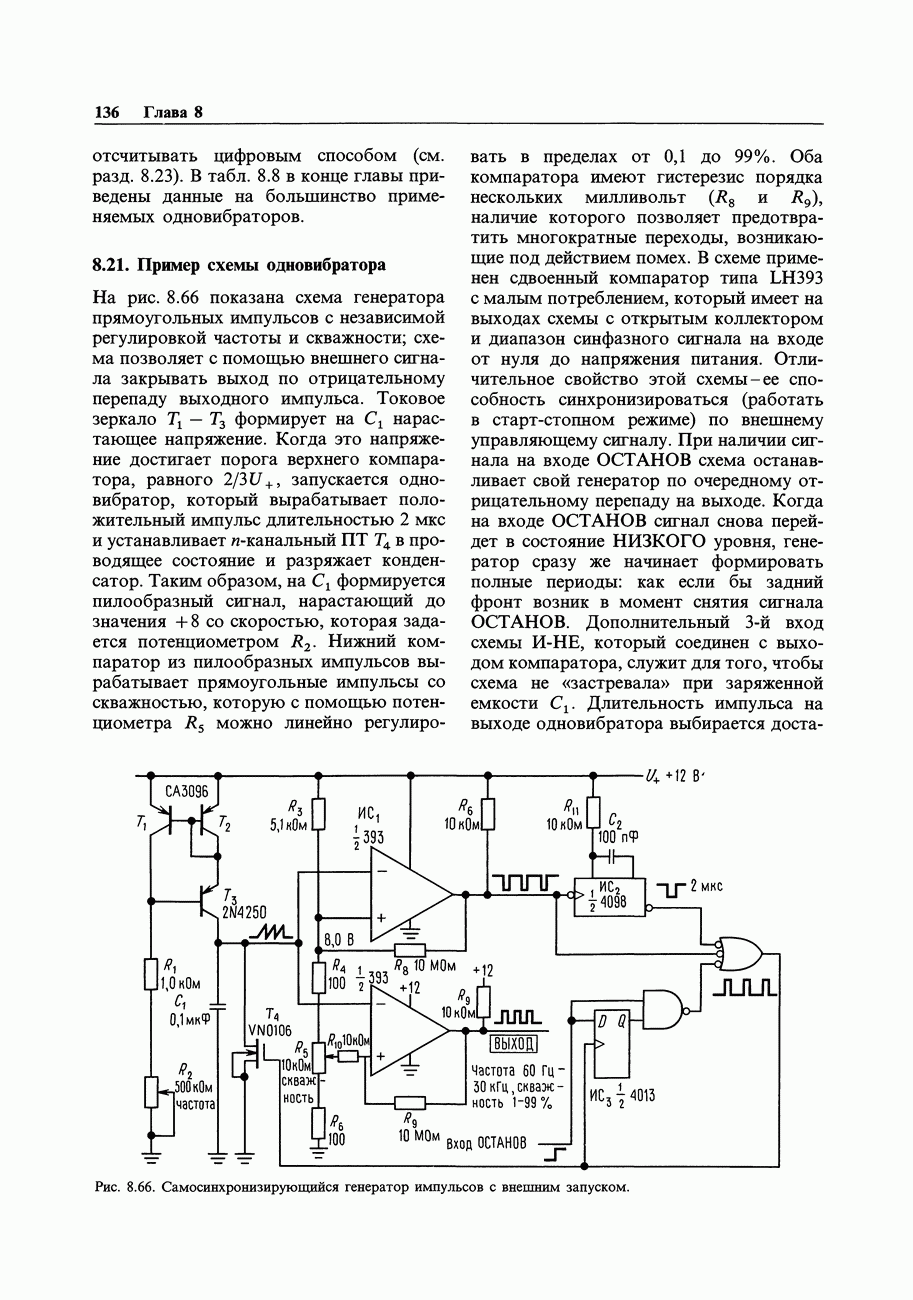
- 8.21. Пример схемы одновибратора
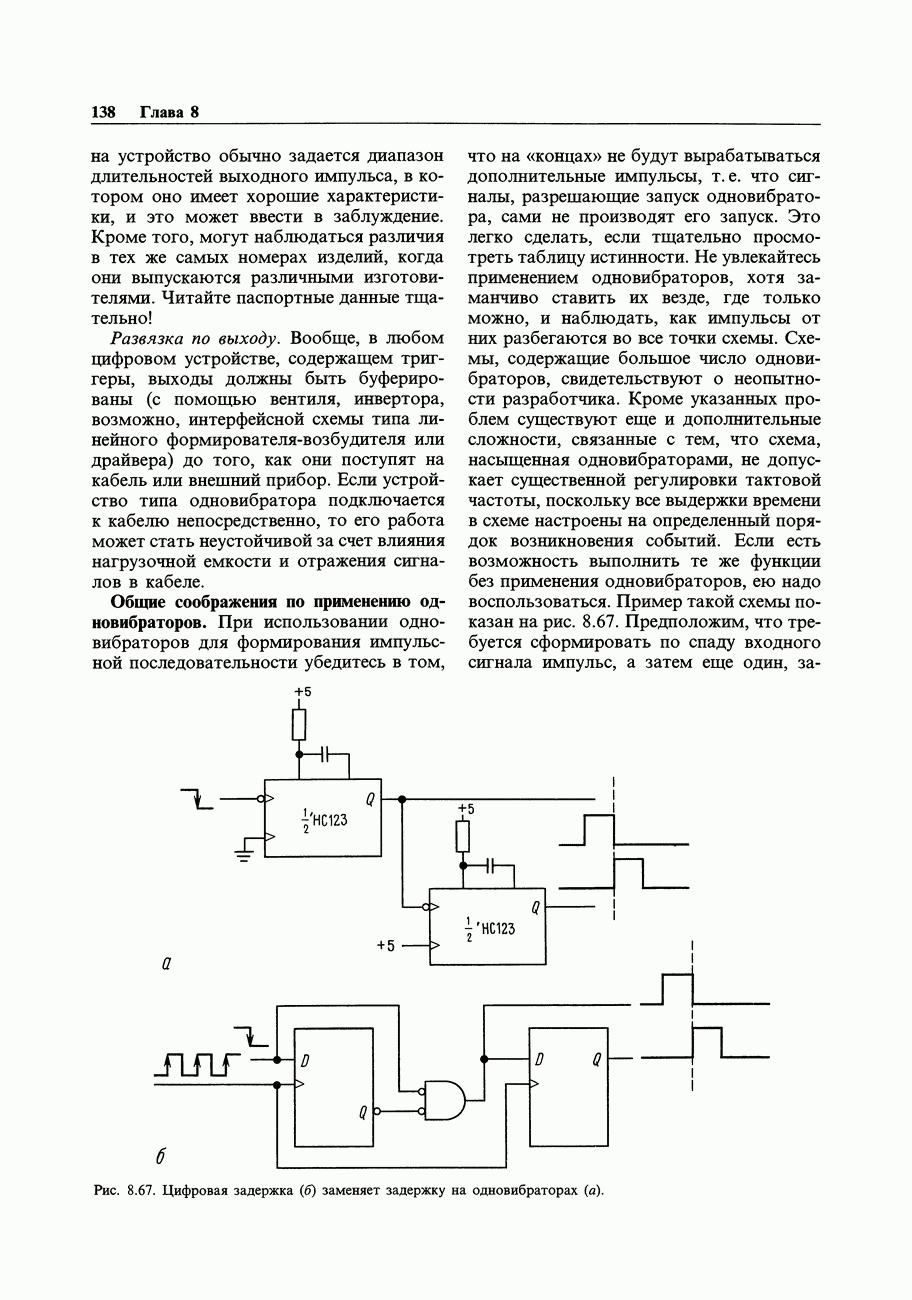
- 8.22. Предостережения относительно одновибраторов
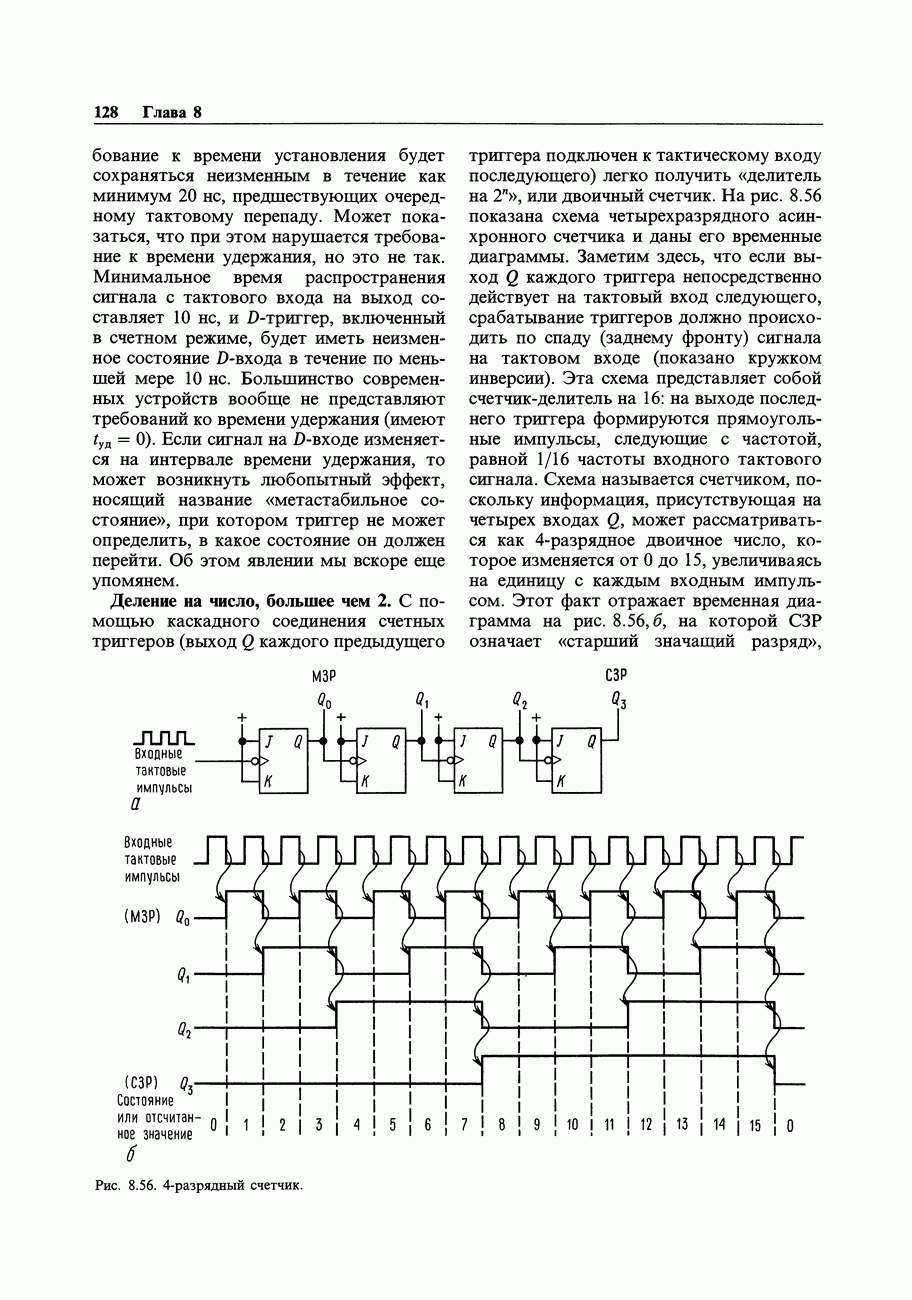
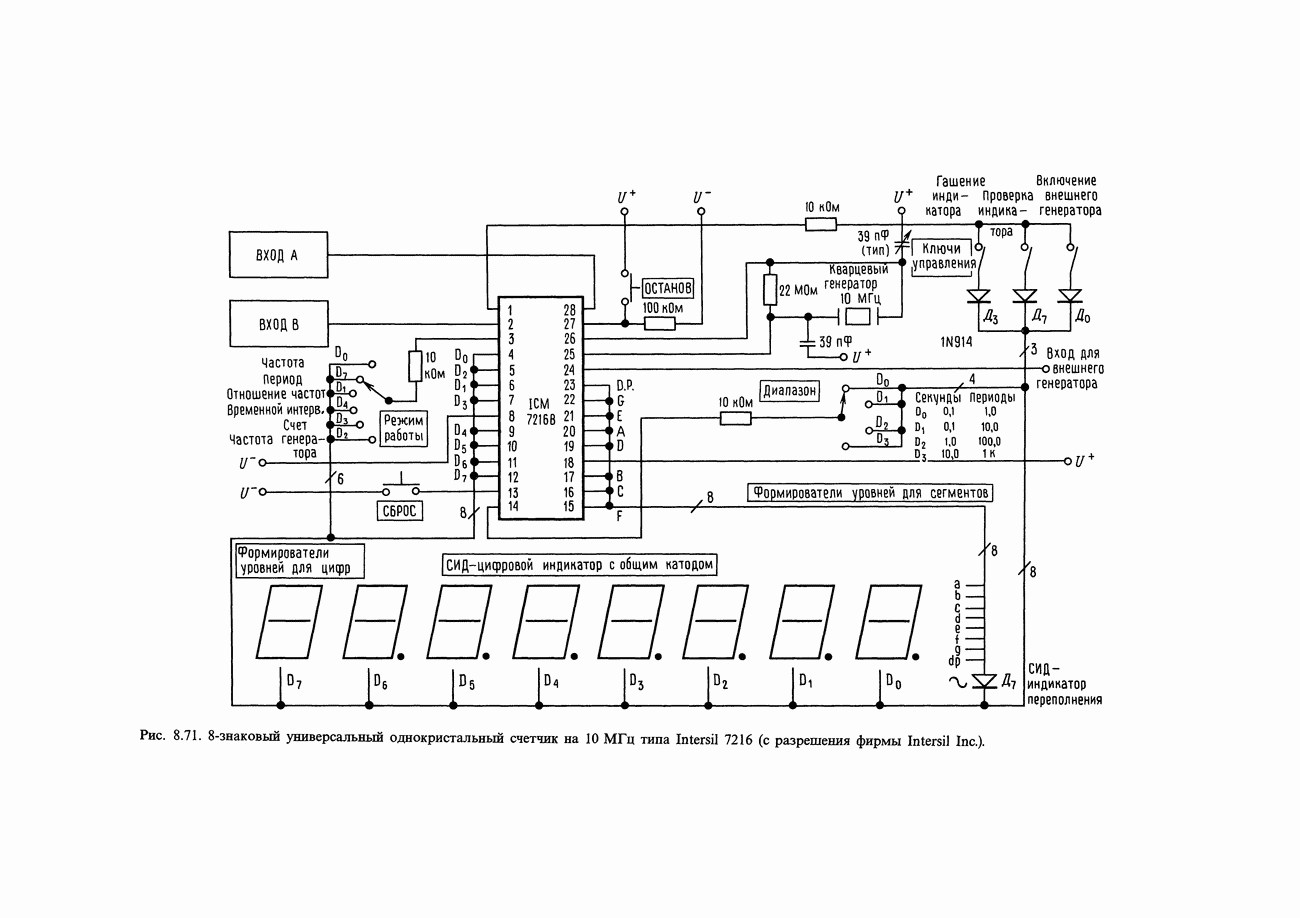
- 8.23. Получение выдержки времени с помощью счетчиков
- ПОСЛЕДОВАТЕЛЬНОСТНЫЕ ФУНКЦИИ, РЕАЛИЗУЕМЫЕ НА СТАНДАРТНЫХ ИМС
- 8.24. Фиксирующие схемы-защелки и регистры
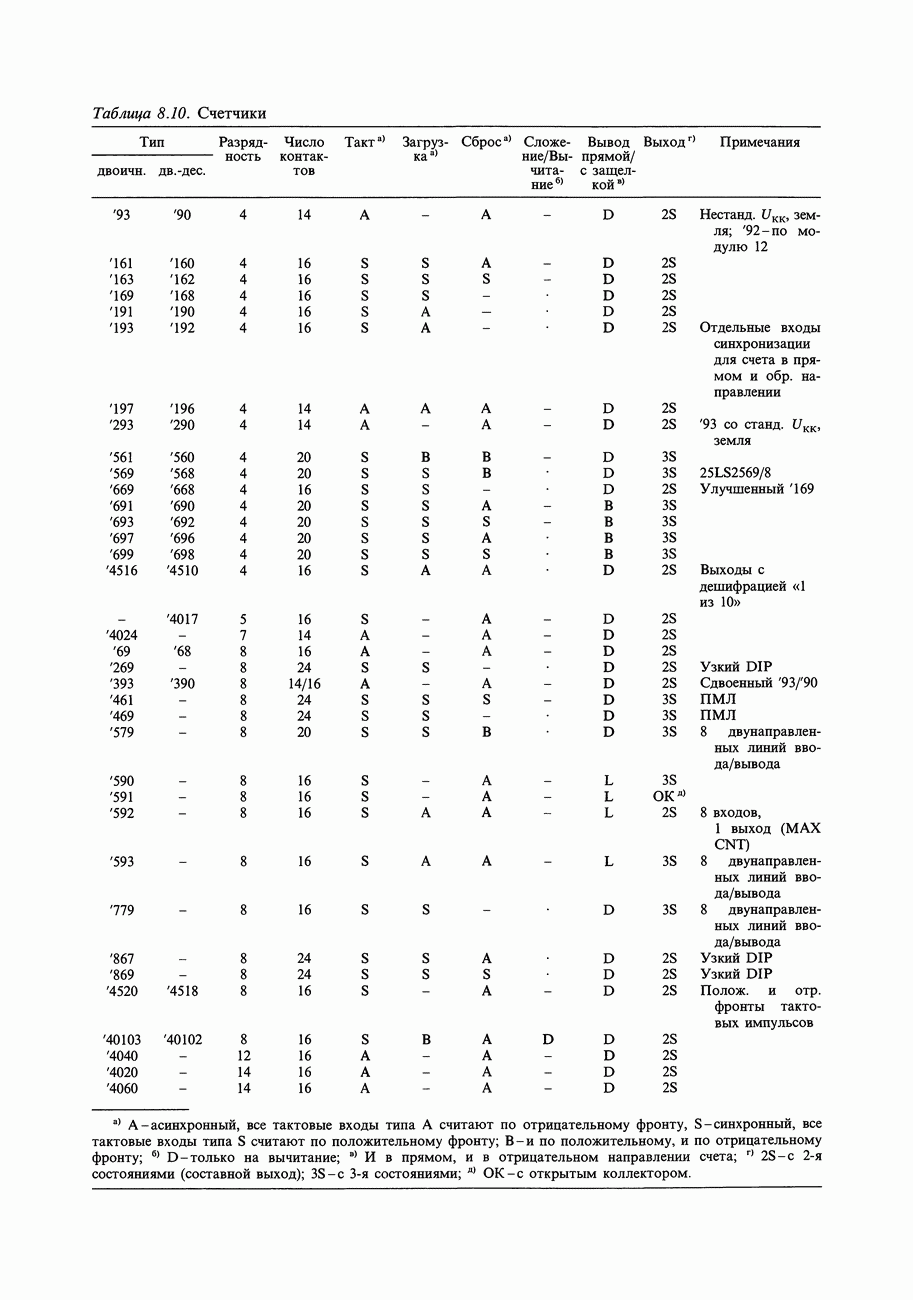
- 8.25. Счетчики
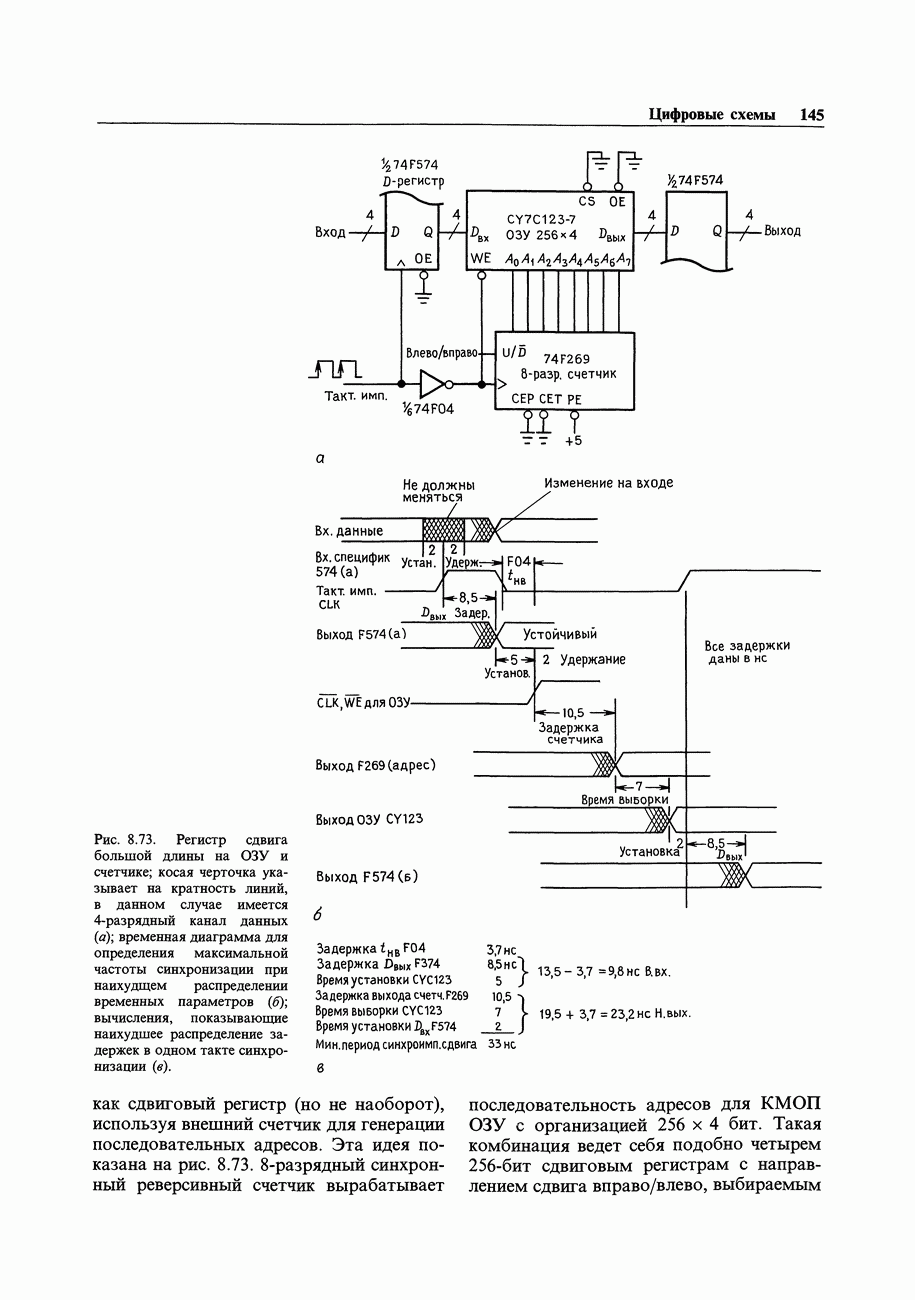
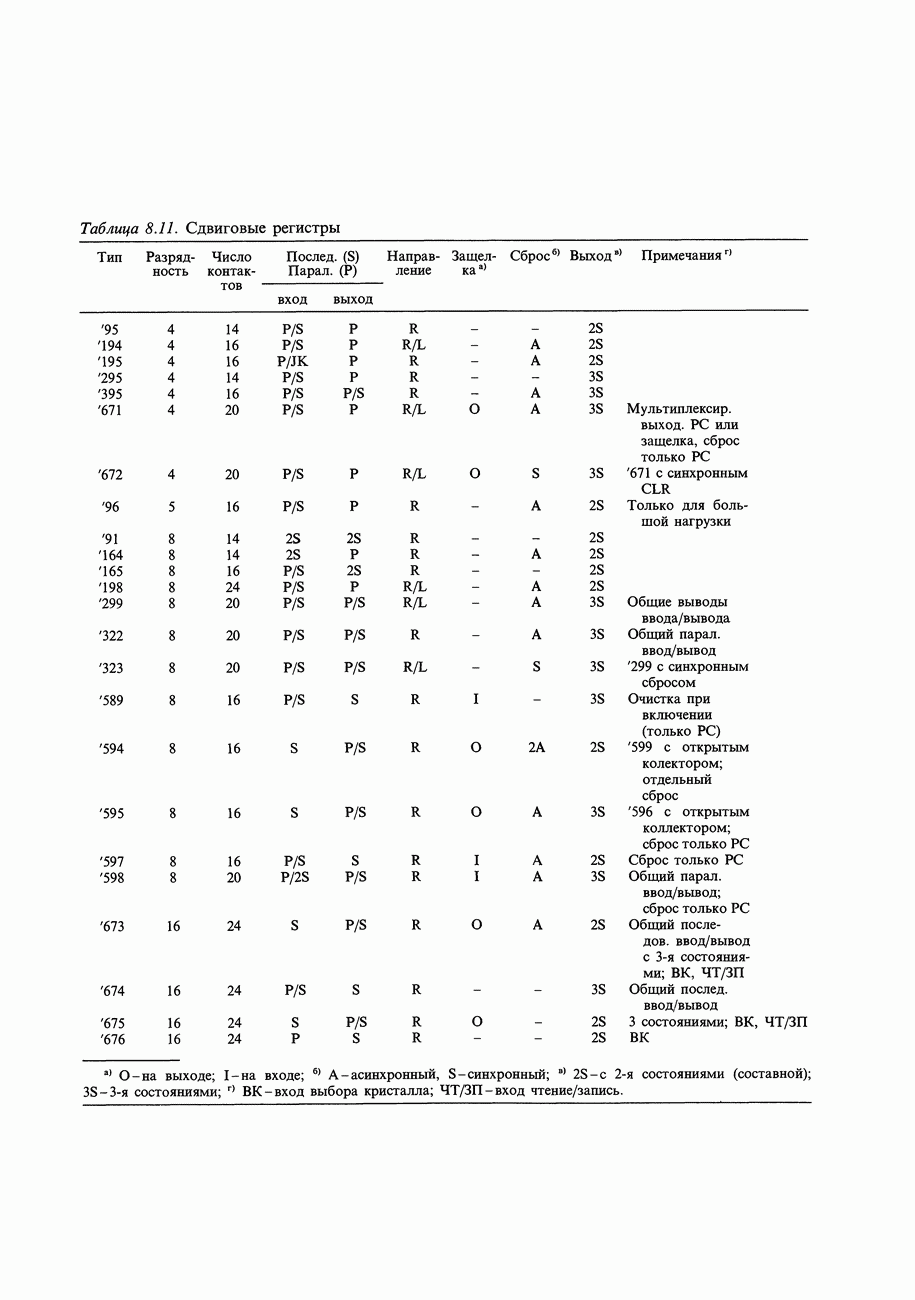
- 8.26. Регистры сдвига
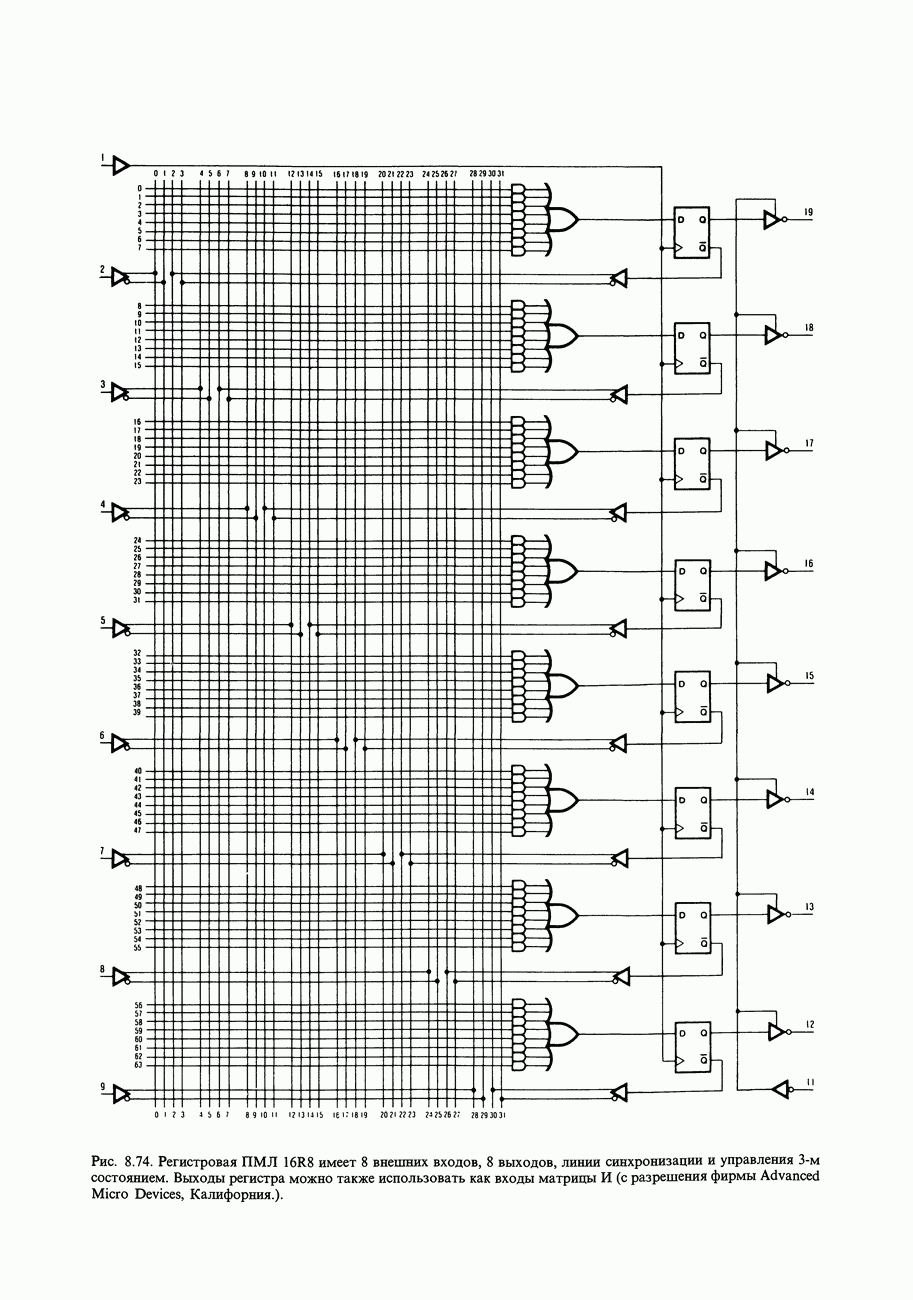
- 8.27. Последовательностные ПМЛ
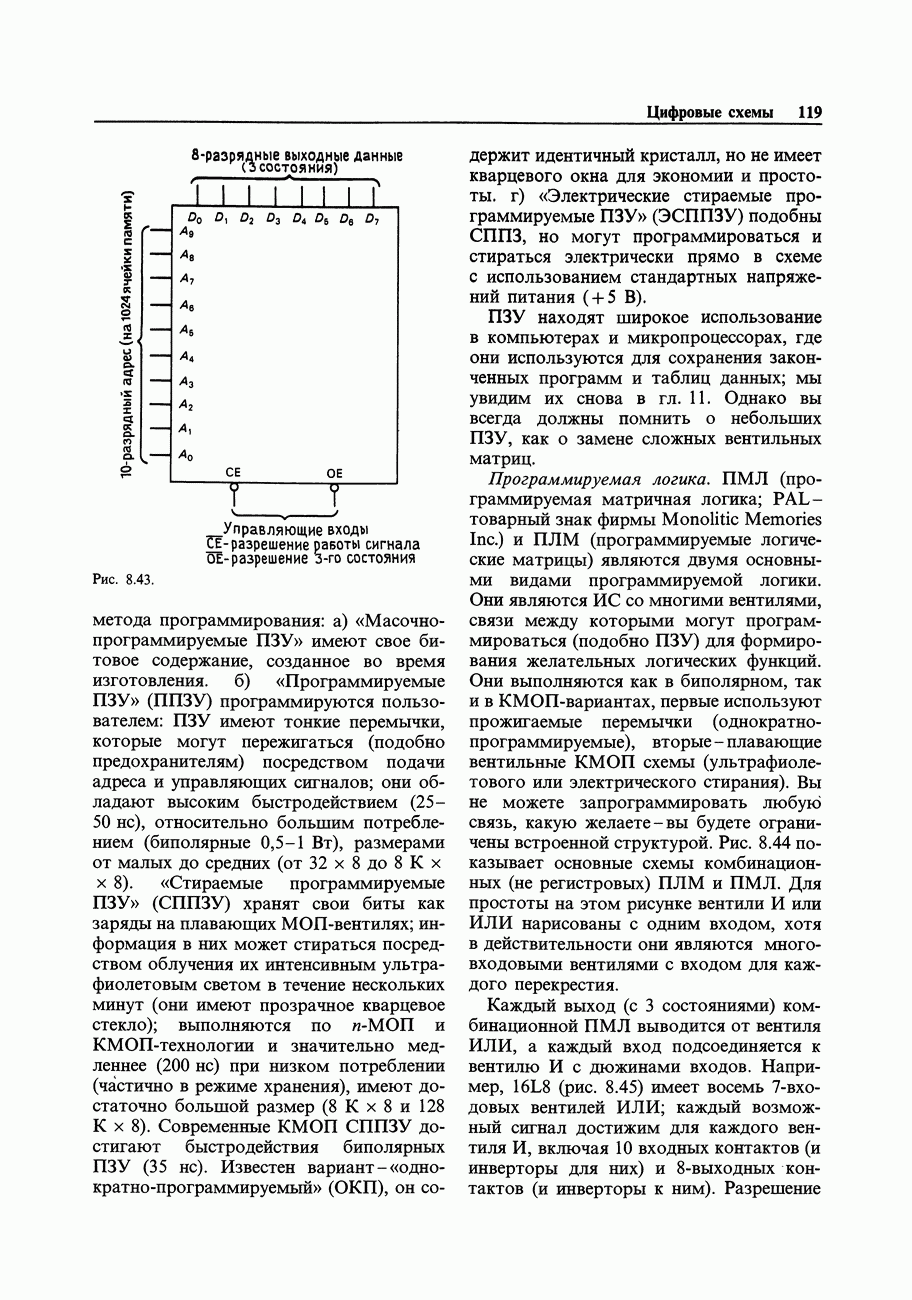
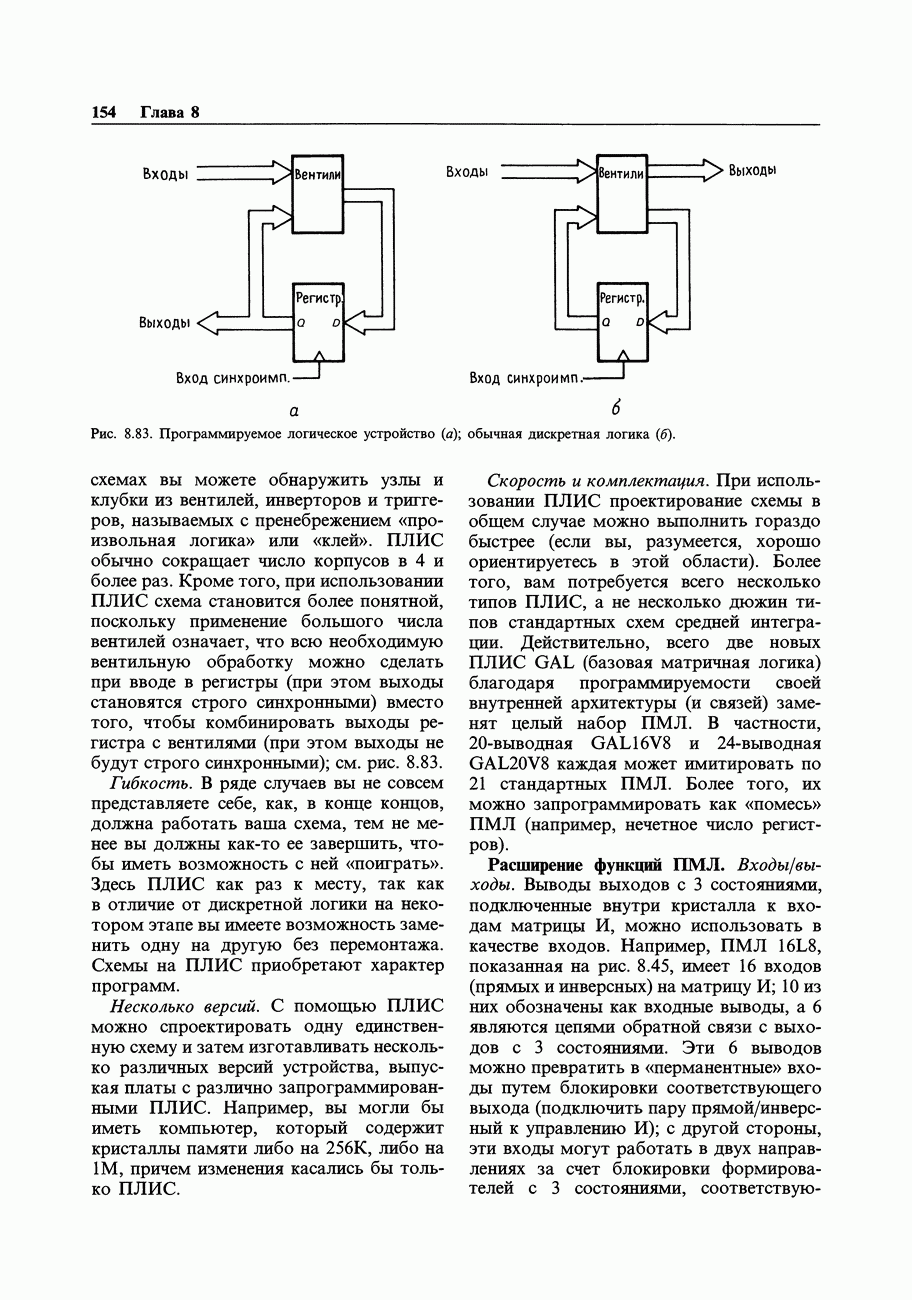
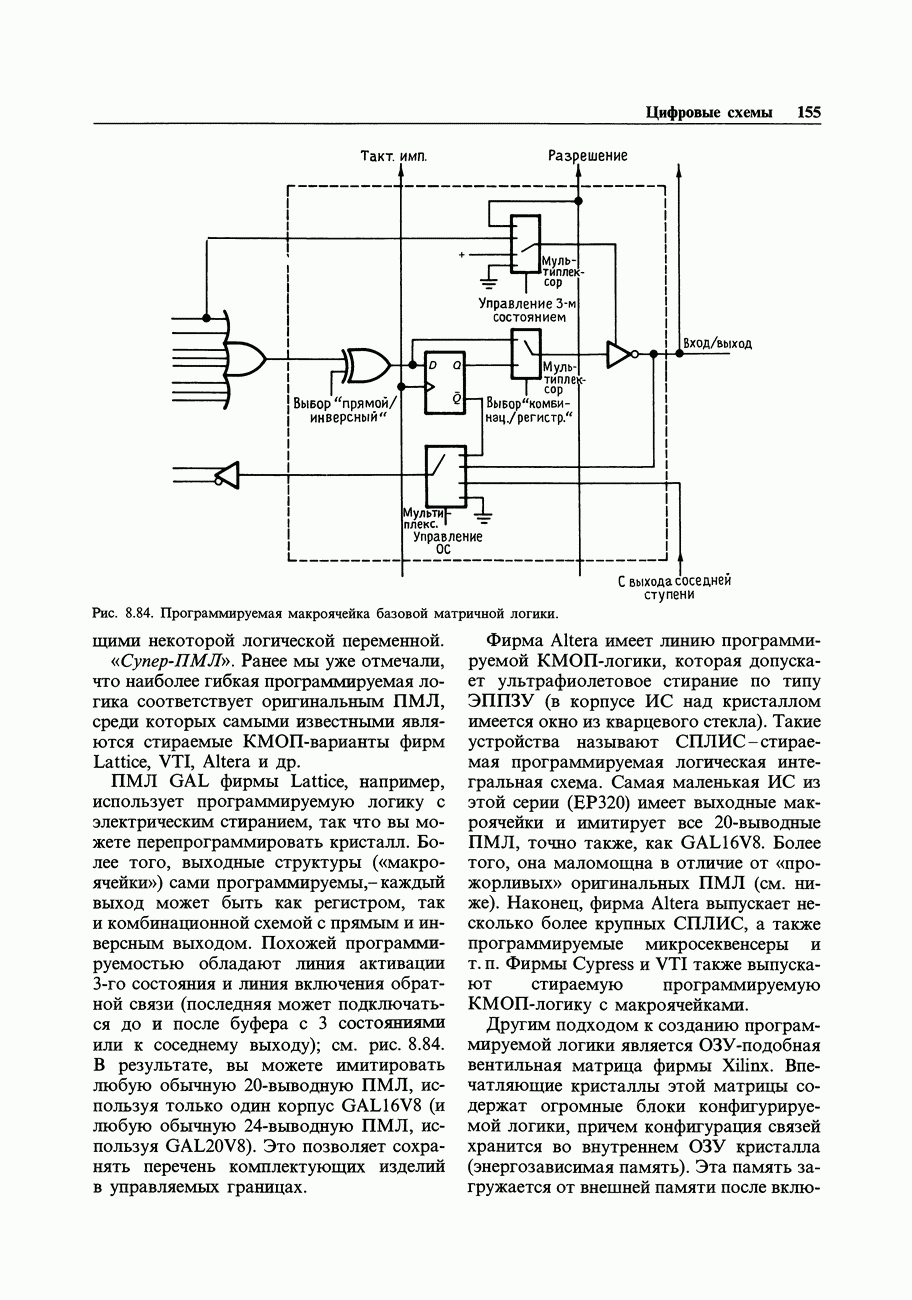
- Возможные применения программируемых логических интегральных схем (ПЛИС)
- 8.28. Разнообразные последовательностные схемы
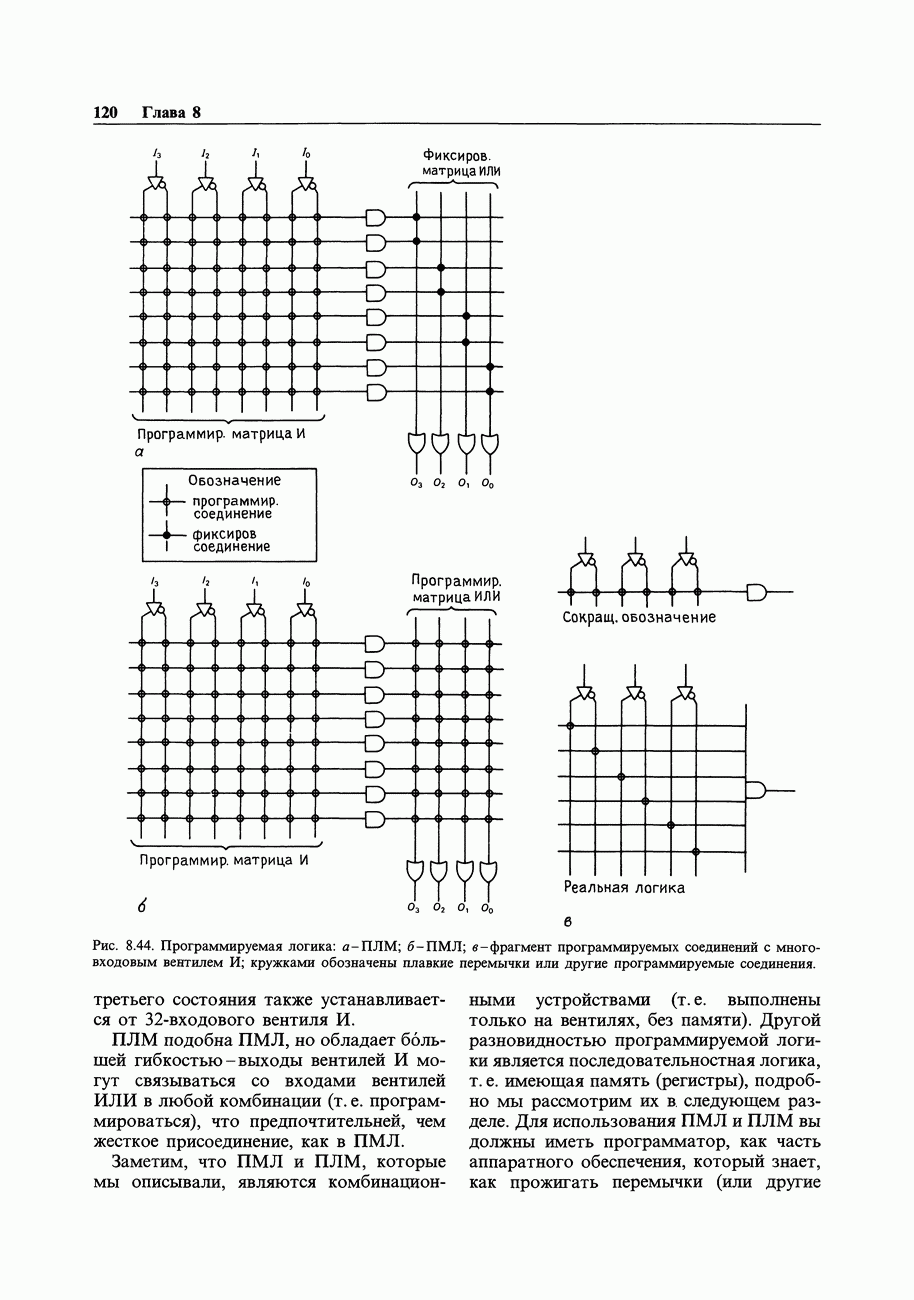
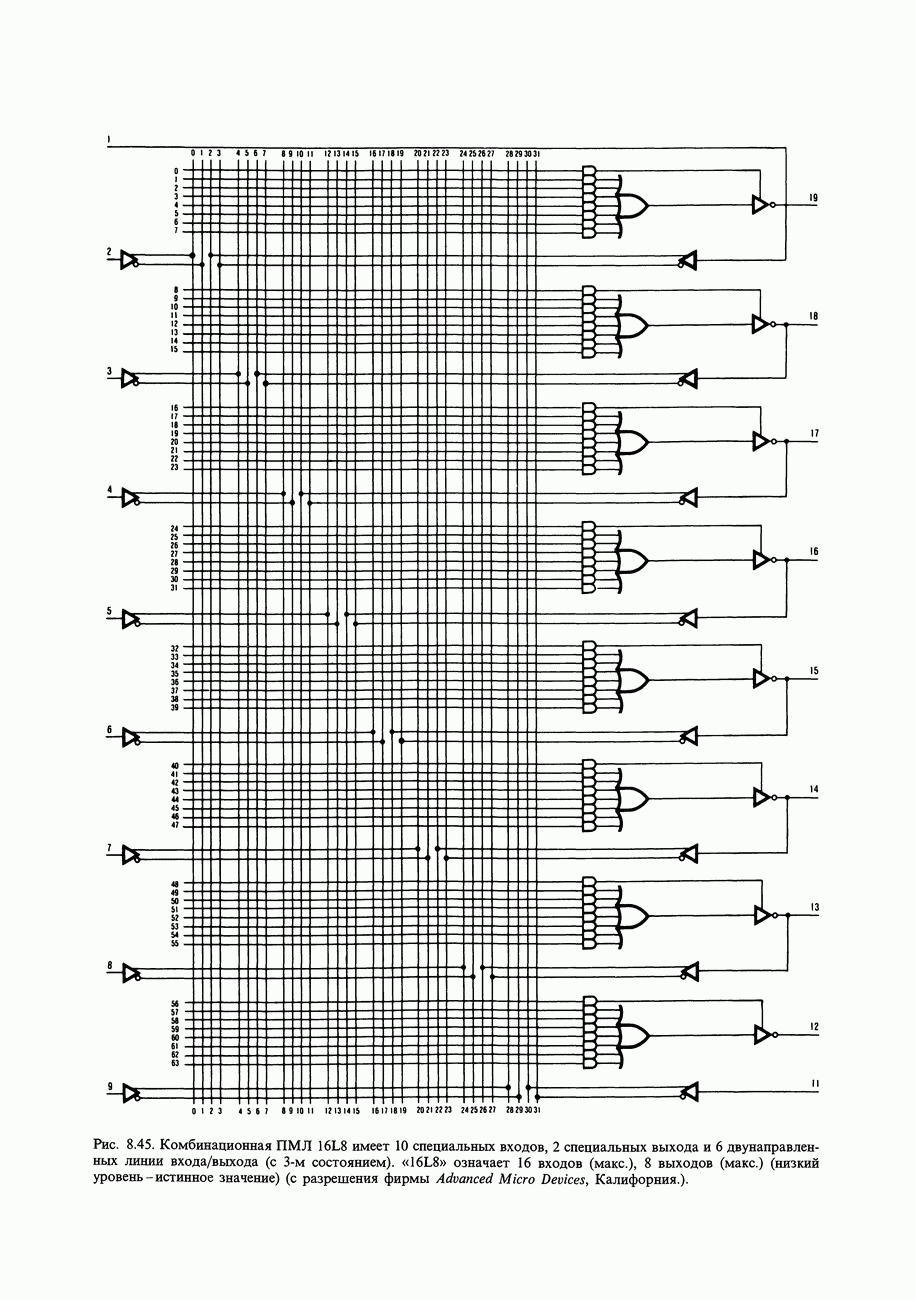
- НЕКОТОРЫЕ ТИПОВЫЕ ЦИФРОВЫЕ СХЕМЫ
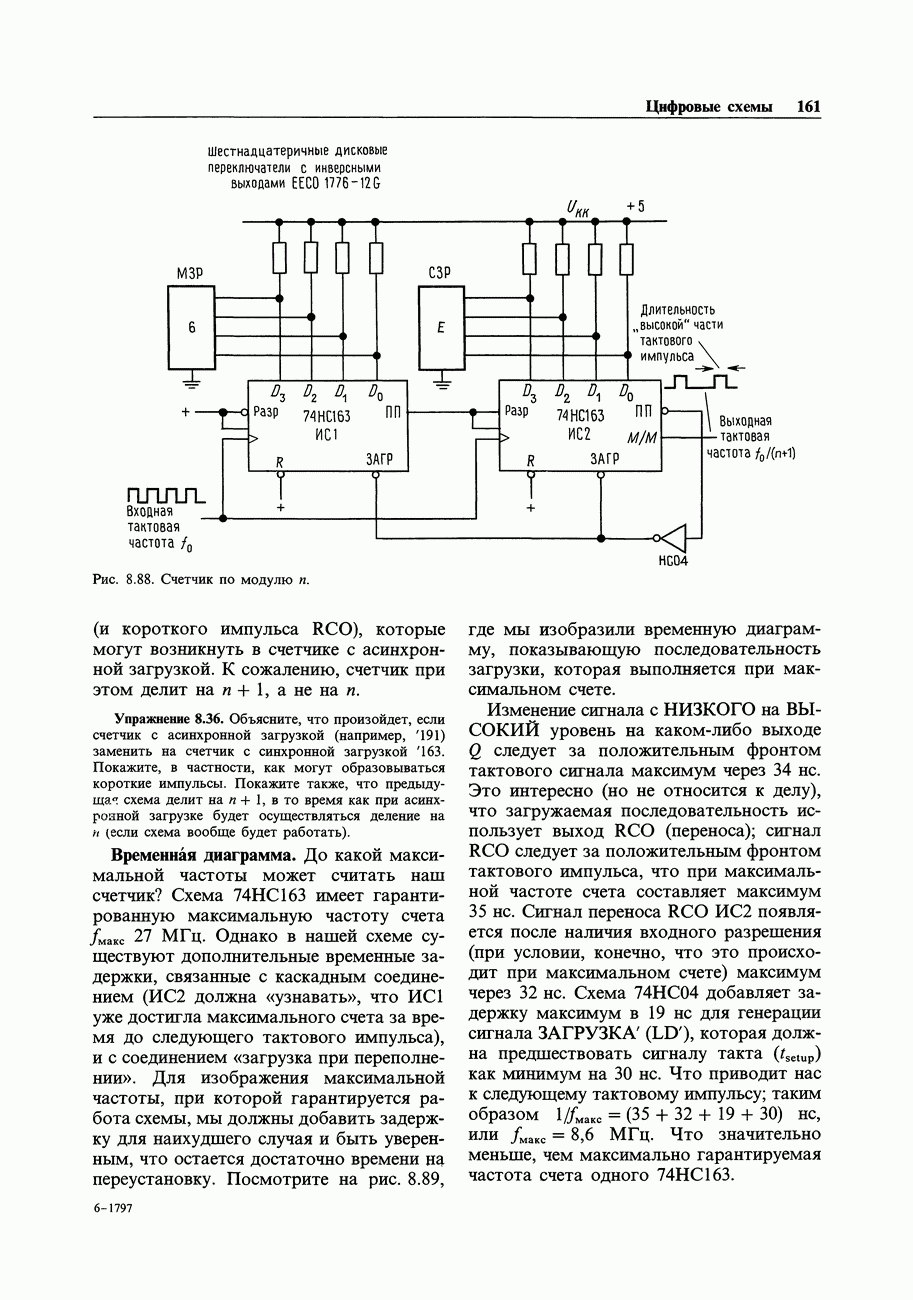
- 8.29. Счетчик по модулю n
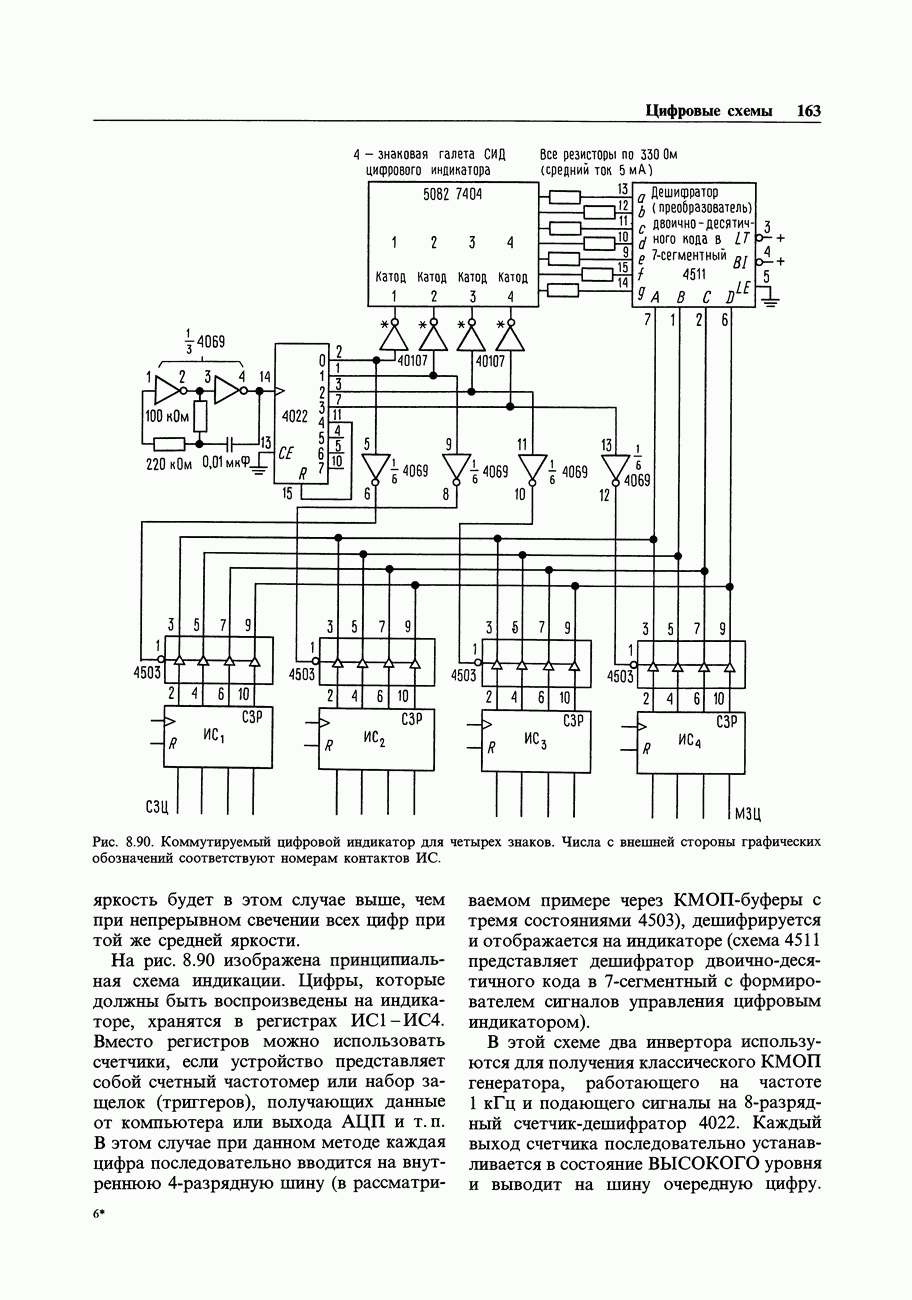
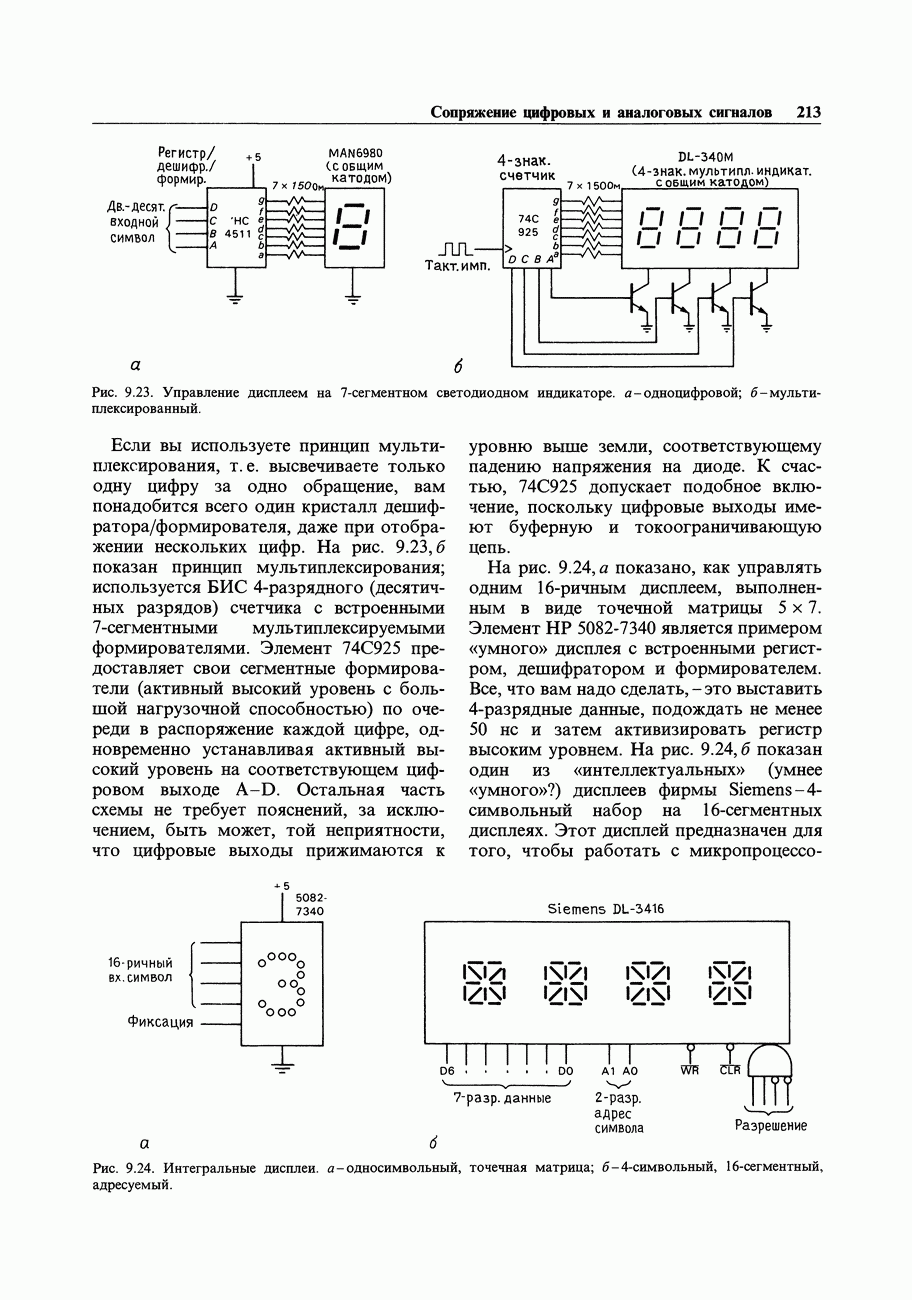
- 8.30. Мультиплексируемый цифровой индикатор на светодиодах
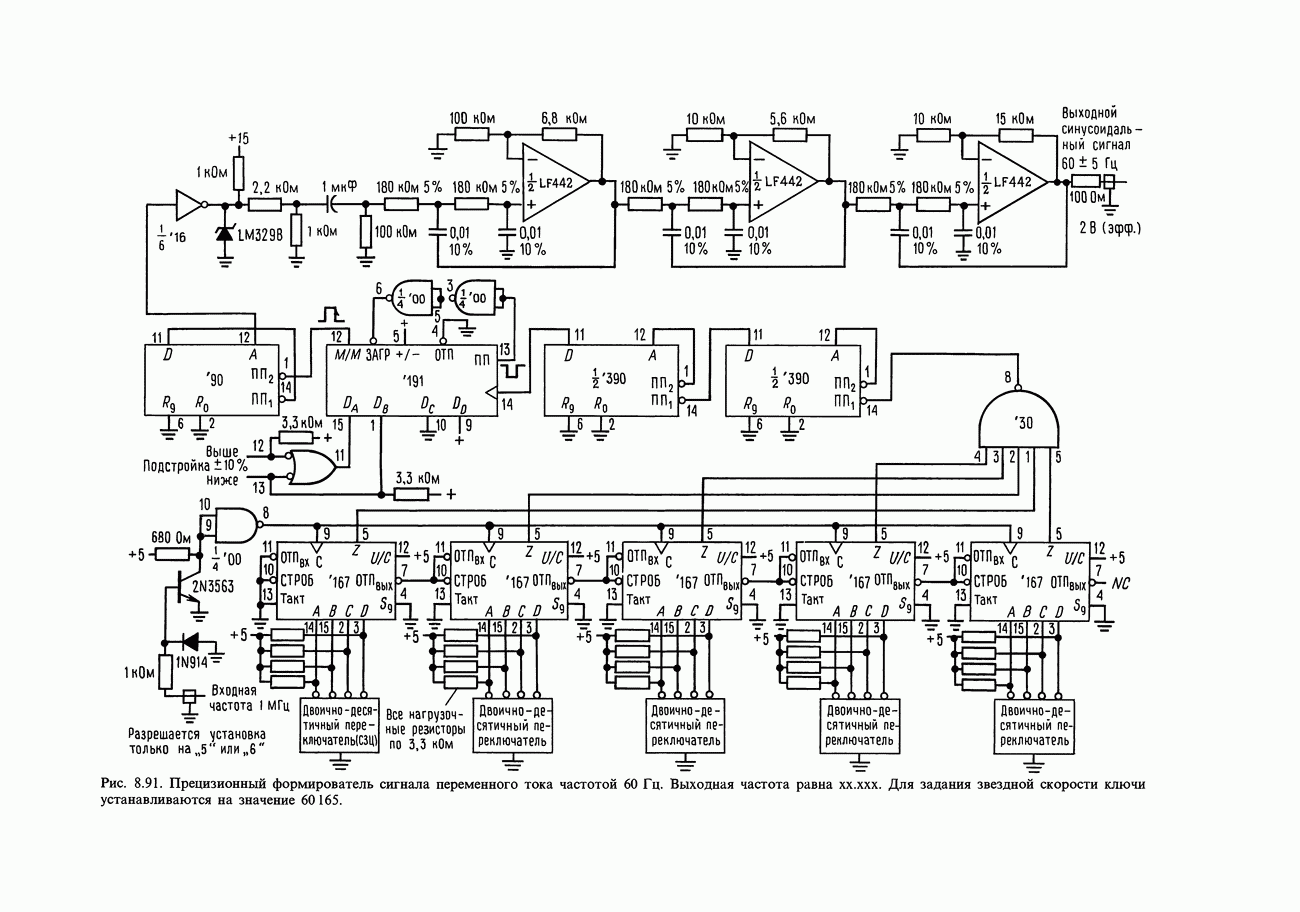
- 8.31. Привод звездного телескопа
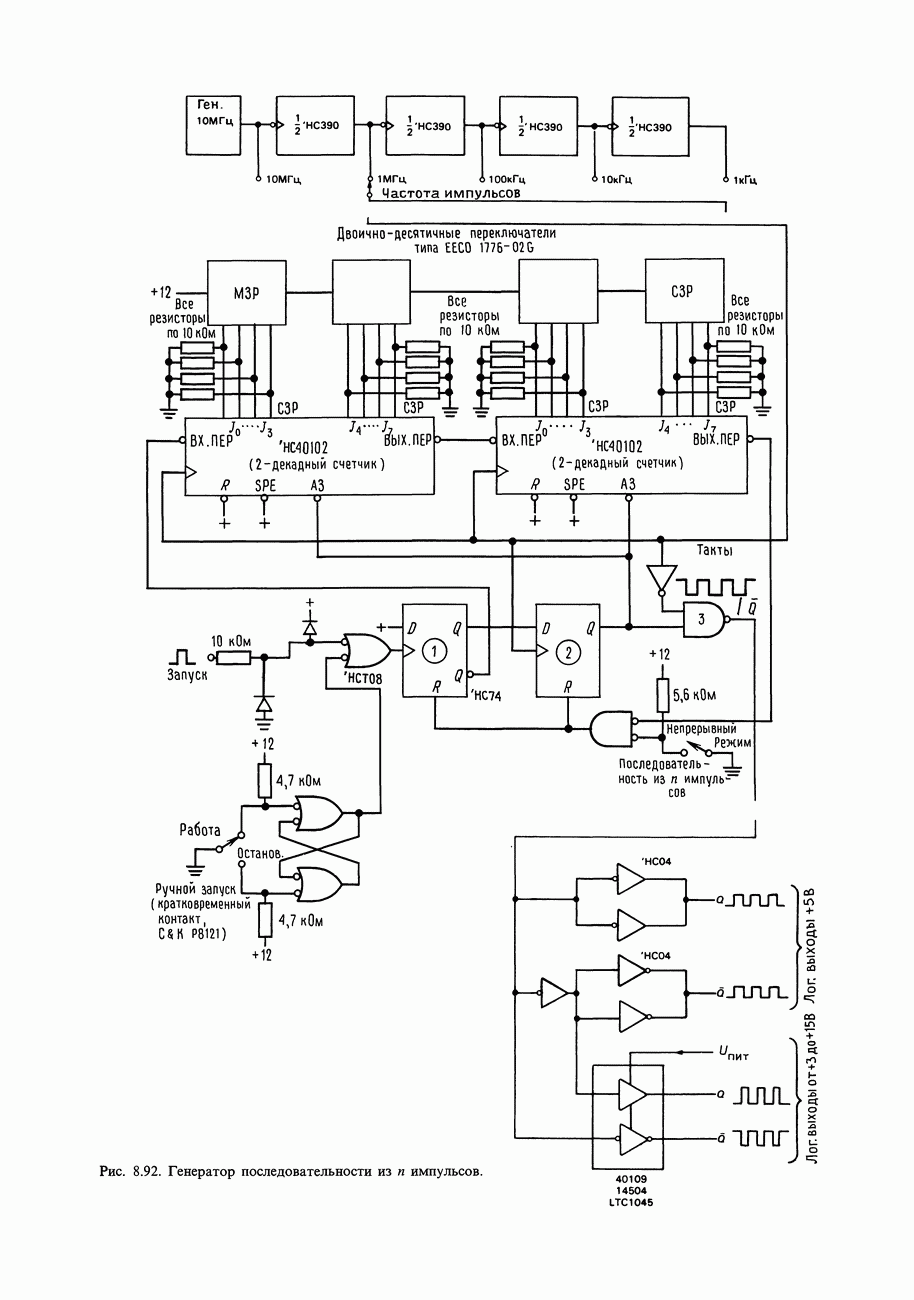
- 8.32. Генератор последовательности из n импульсов
- ПАТОЛОГИЯ В ЛОГИЧЕСКИХ СХЕМАХ
- 8.33. Проблемы статических режимов
- 8.34. Проблемы при переключениях
- 8.35. Прирожденные недостатки ТТЛ и КМОП
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
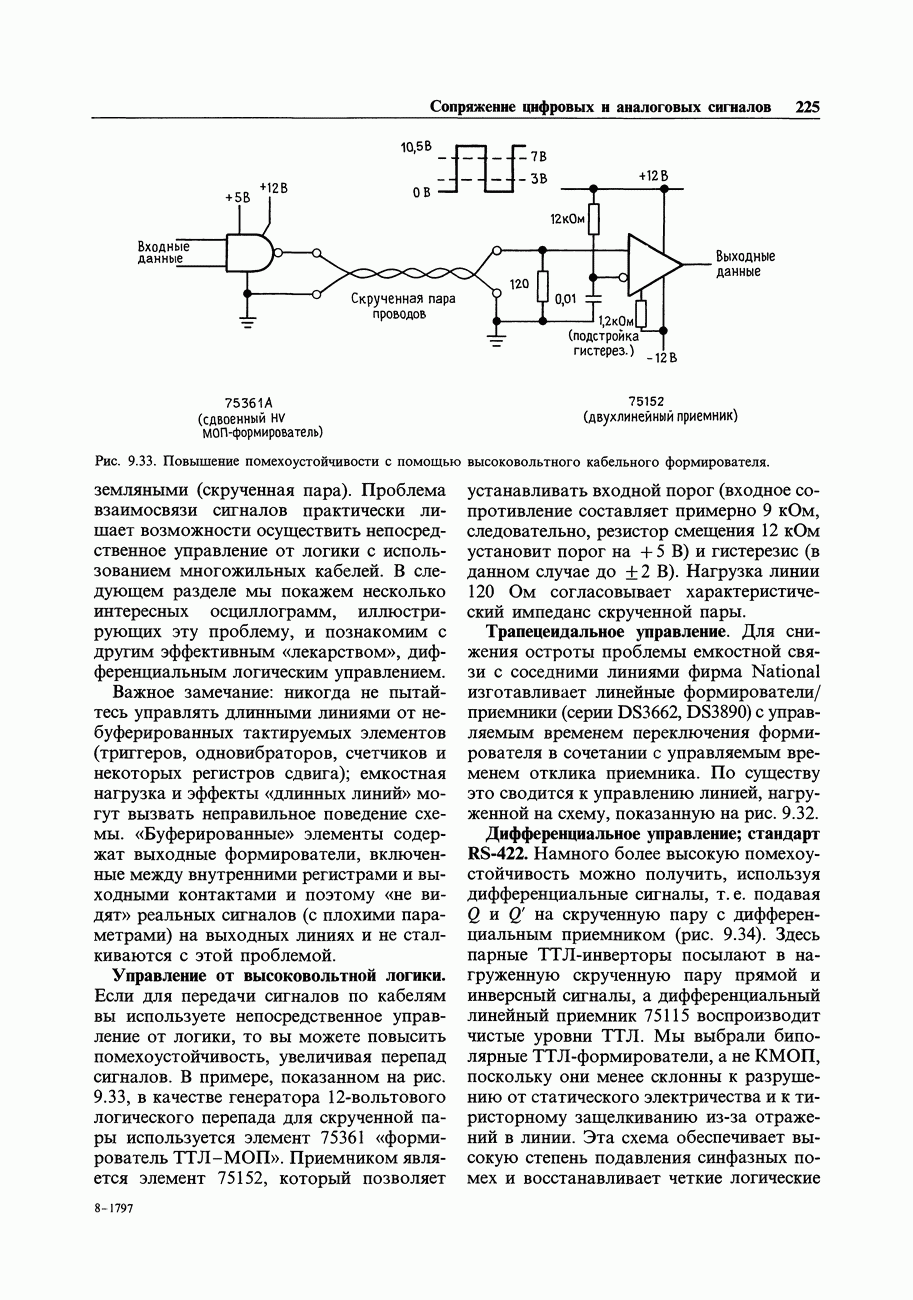
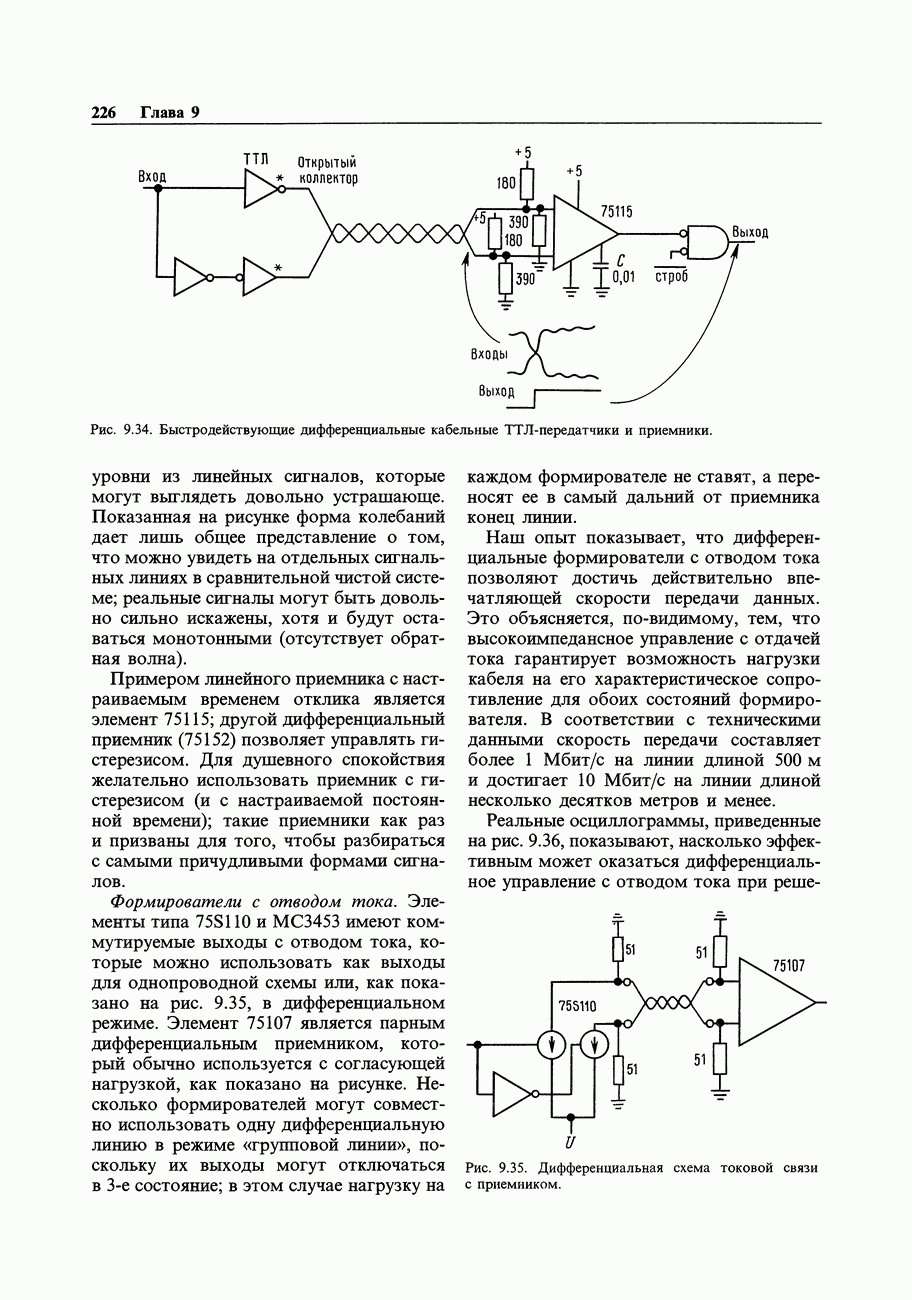
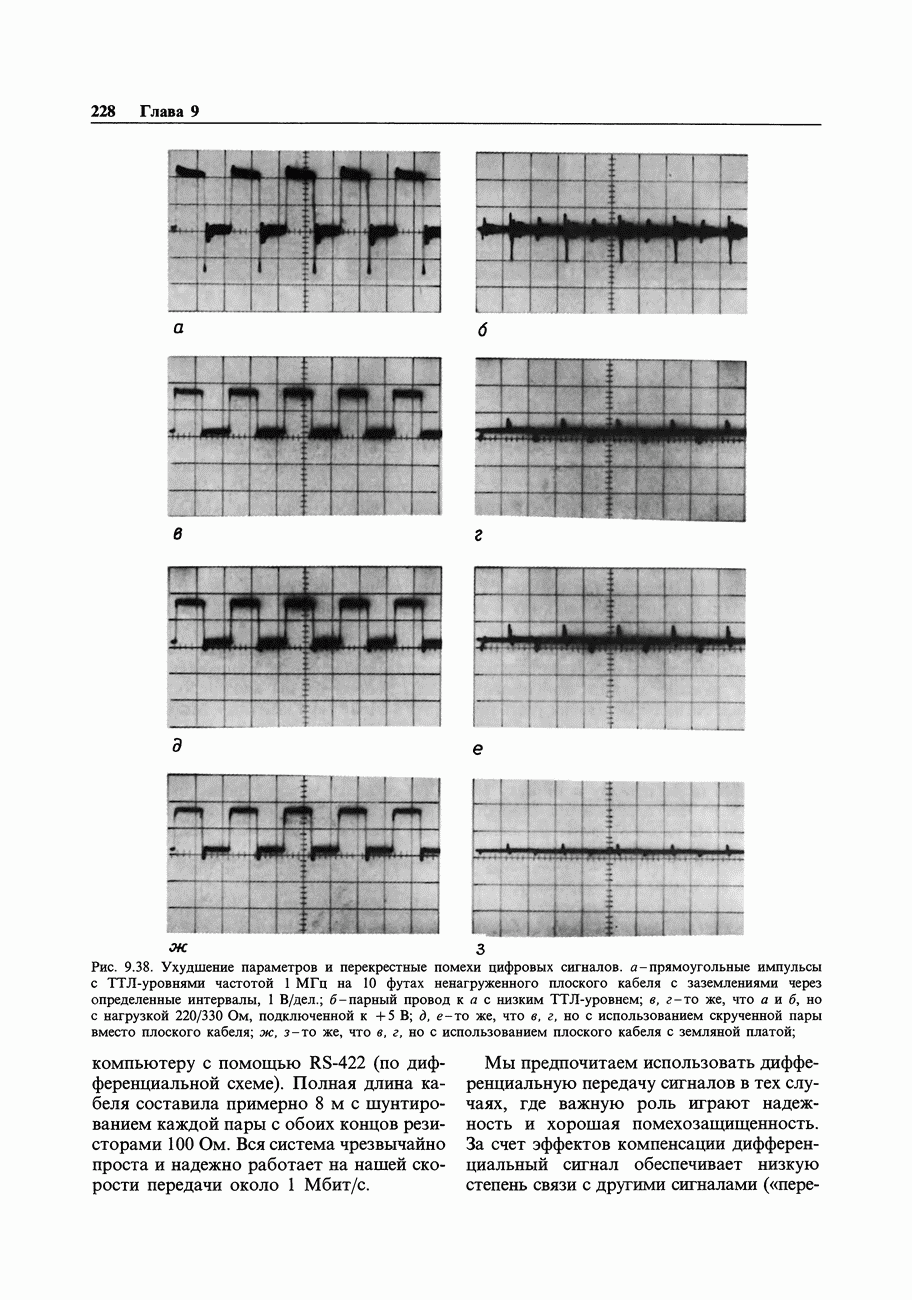
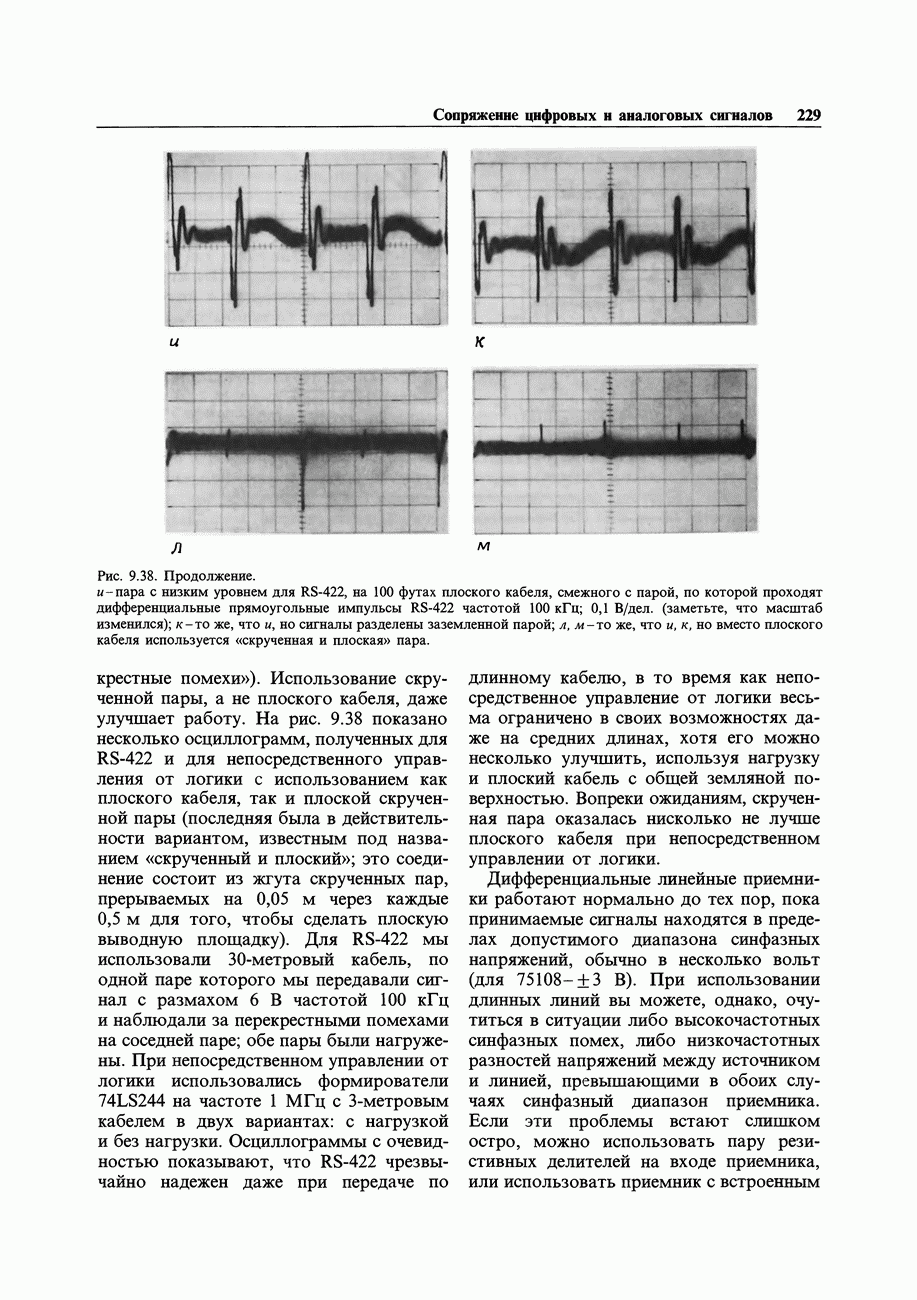
- ГЛАВА 9. СОПРЯЖЕНИЕ ЦИФРОВЫХ И АНАЛОГОВЫХ СИГНАЛОВ
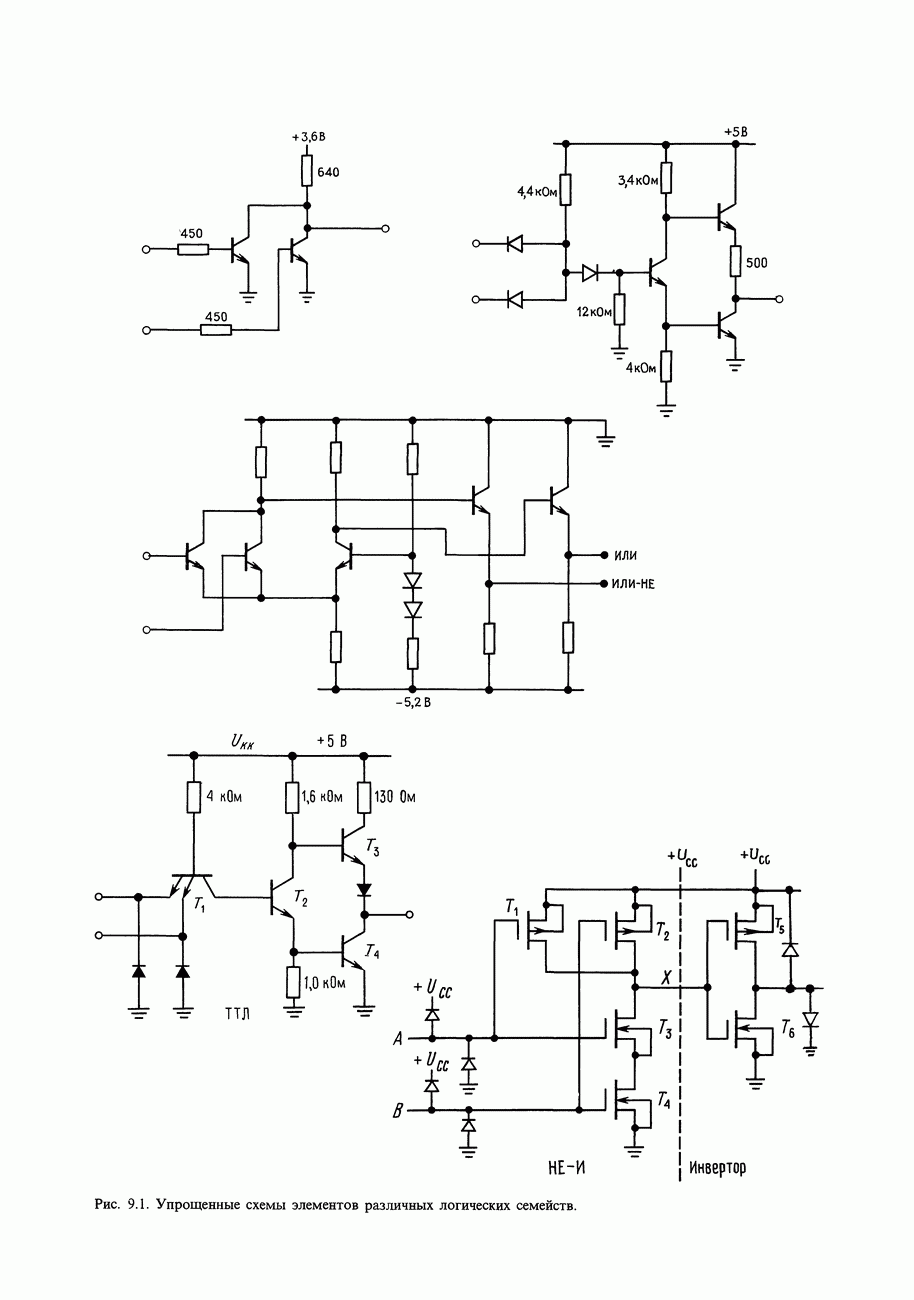
- 9.01. Хронология логических семейств
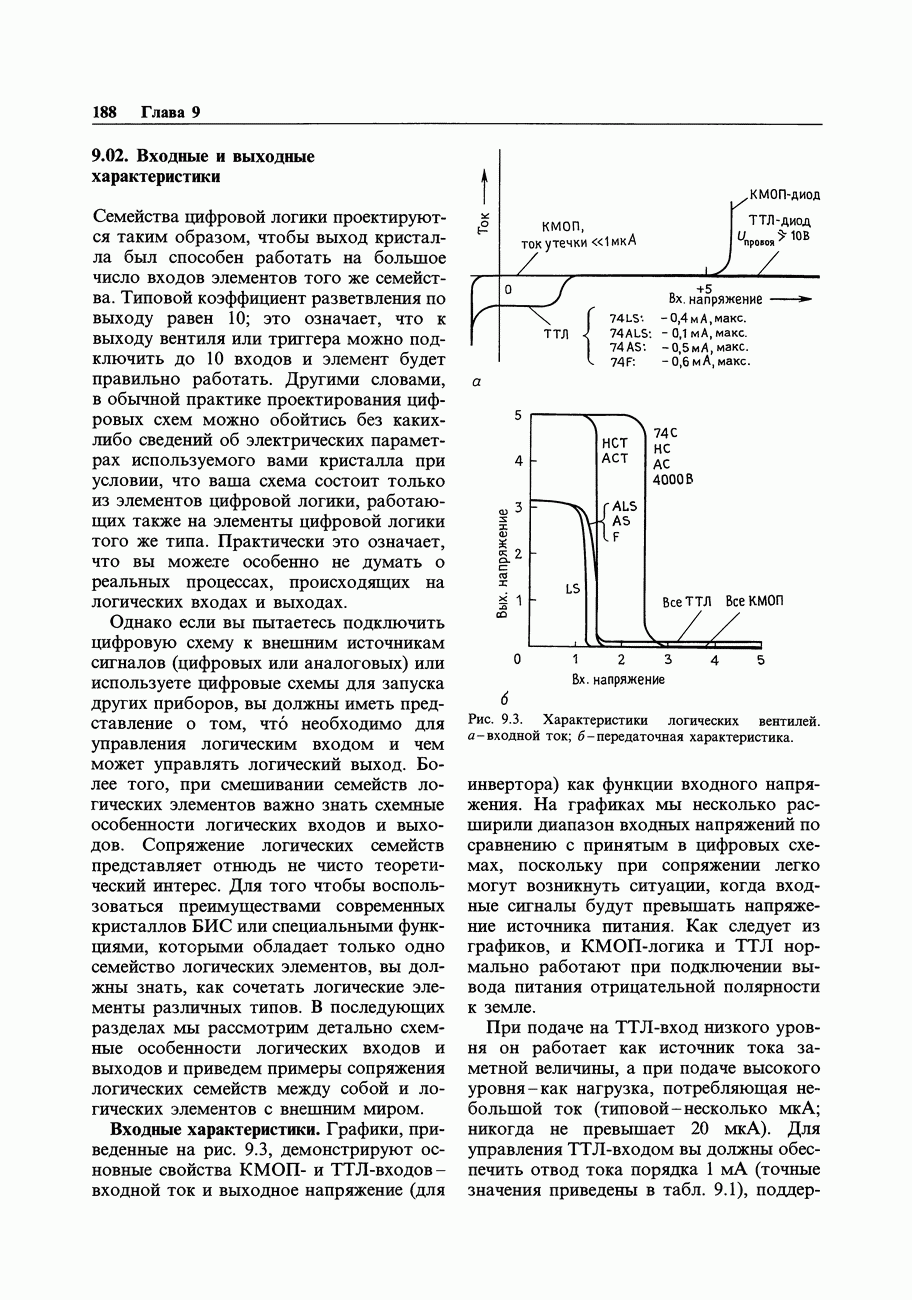
- 9.02. Входные и выходные характеристики
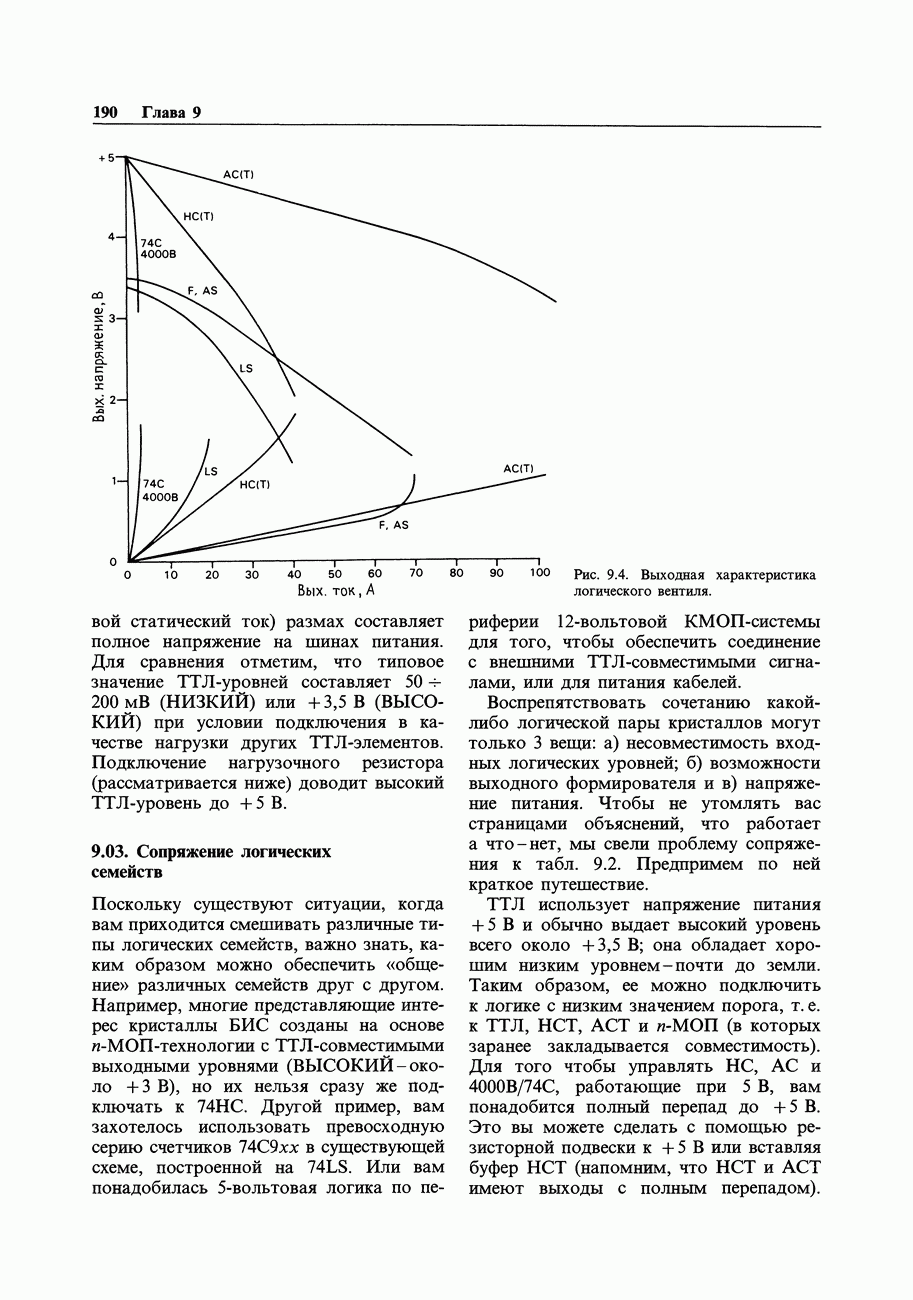
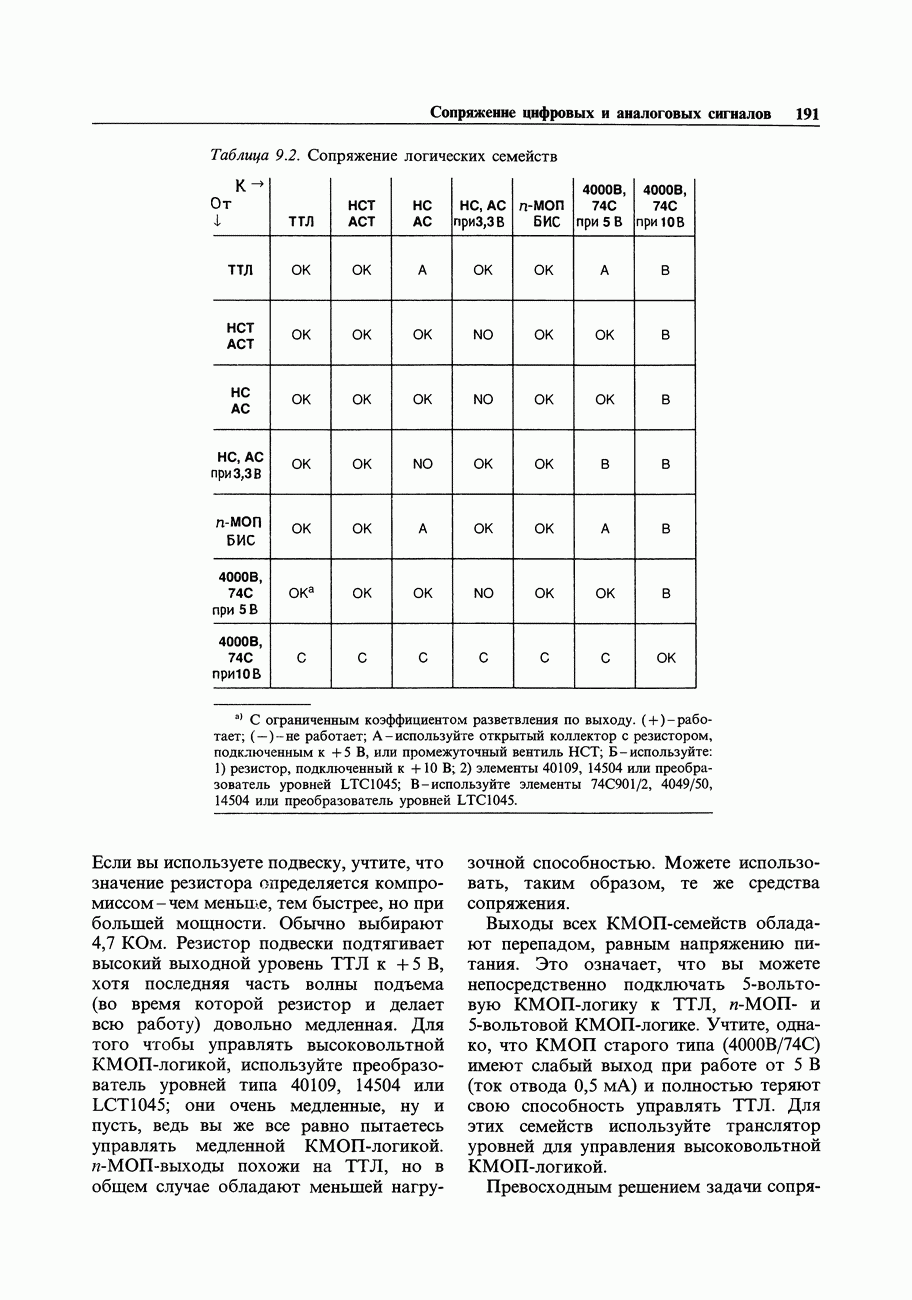
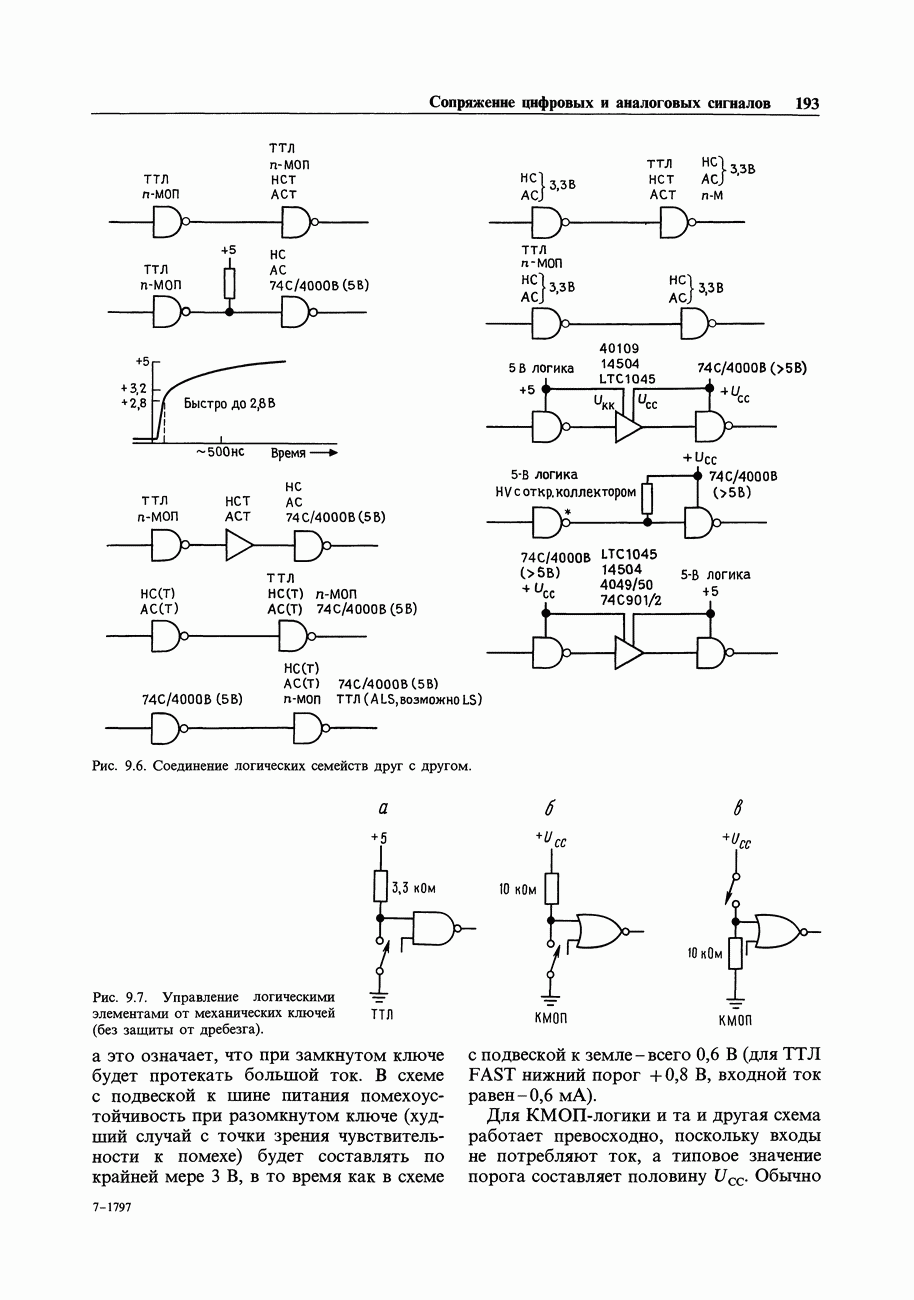
- 9.03. Сопряжение логических семейств
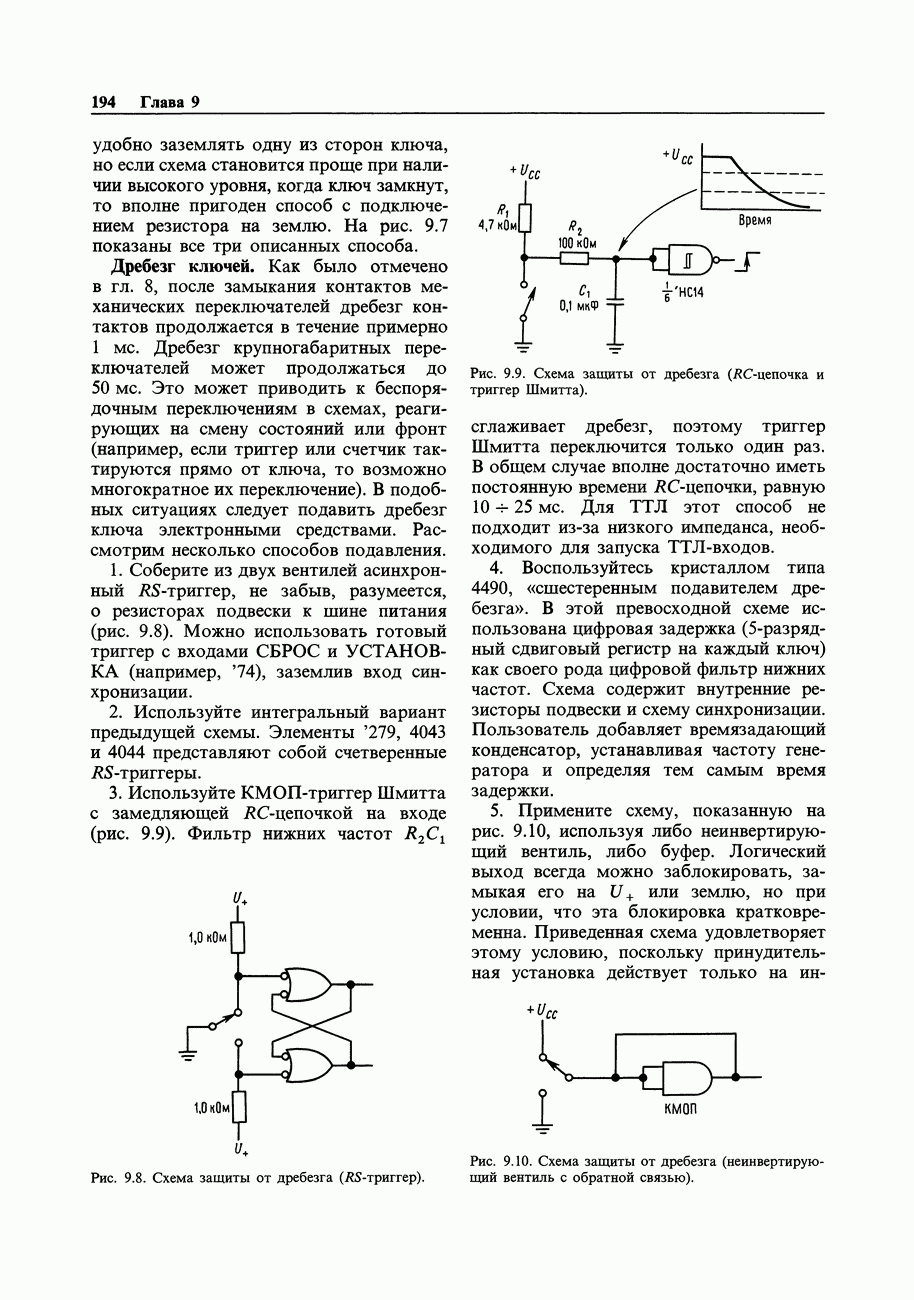
- 9.04. Управление КМОП-и ТТЛ-входами
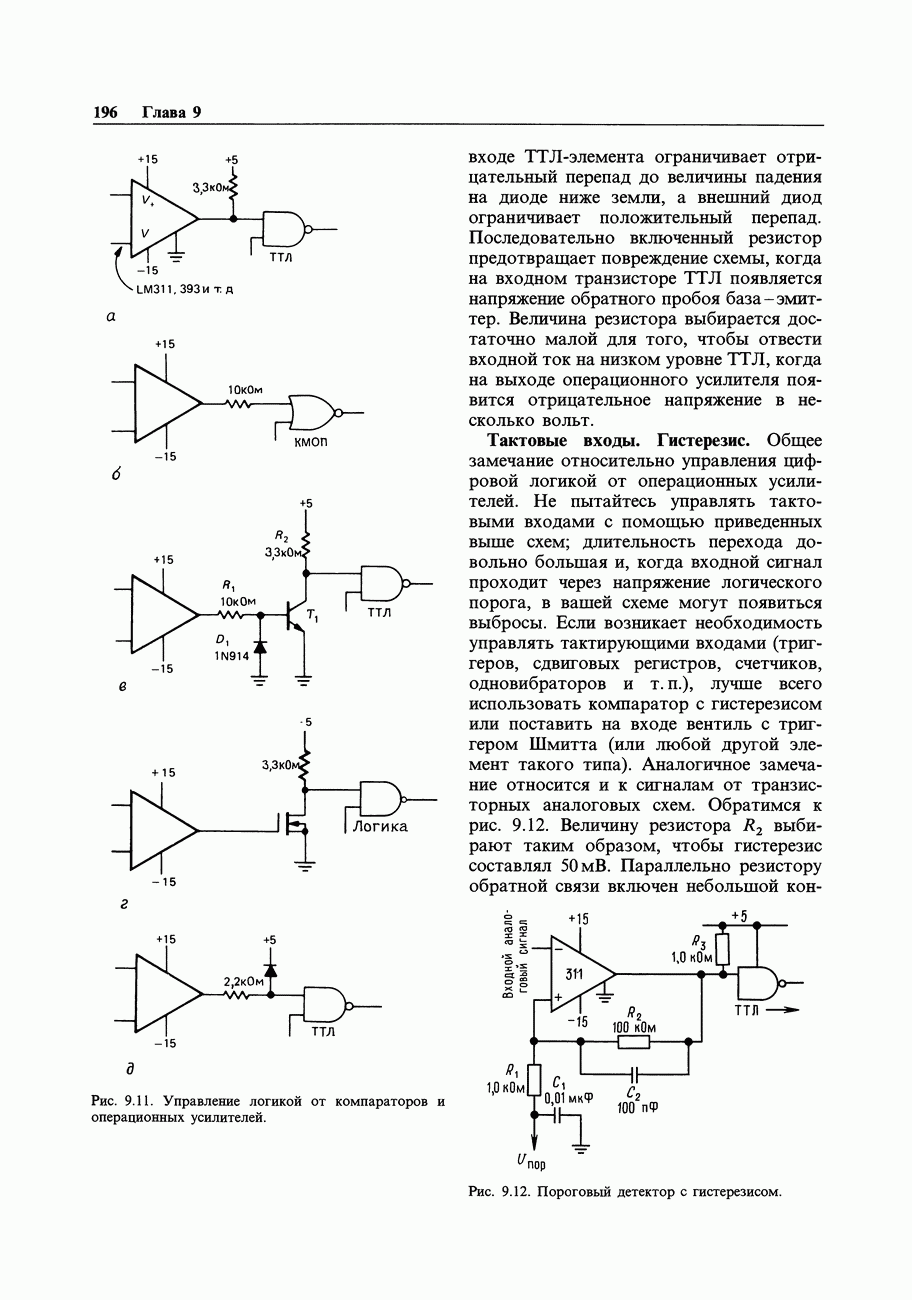
- 9.05. Управление цифровой логикой от компараторов и операционных усилителей
- 9.06. Некоторые замечания, касающиеся логических входов
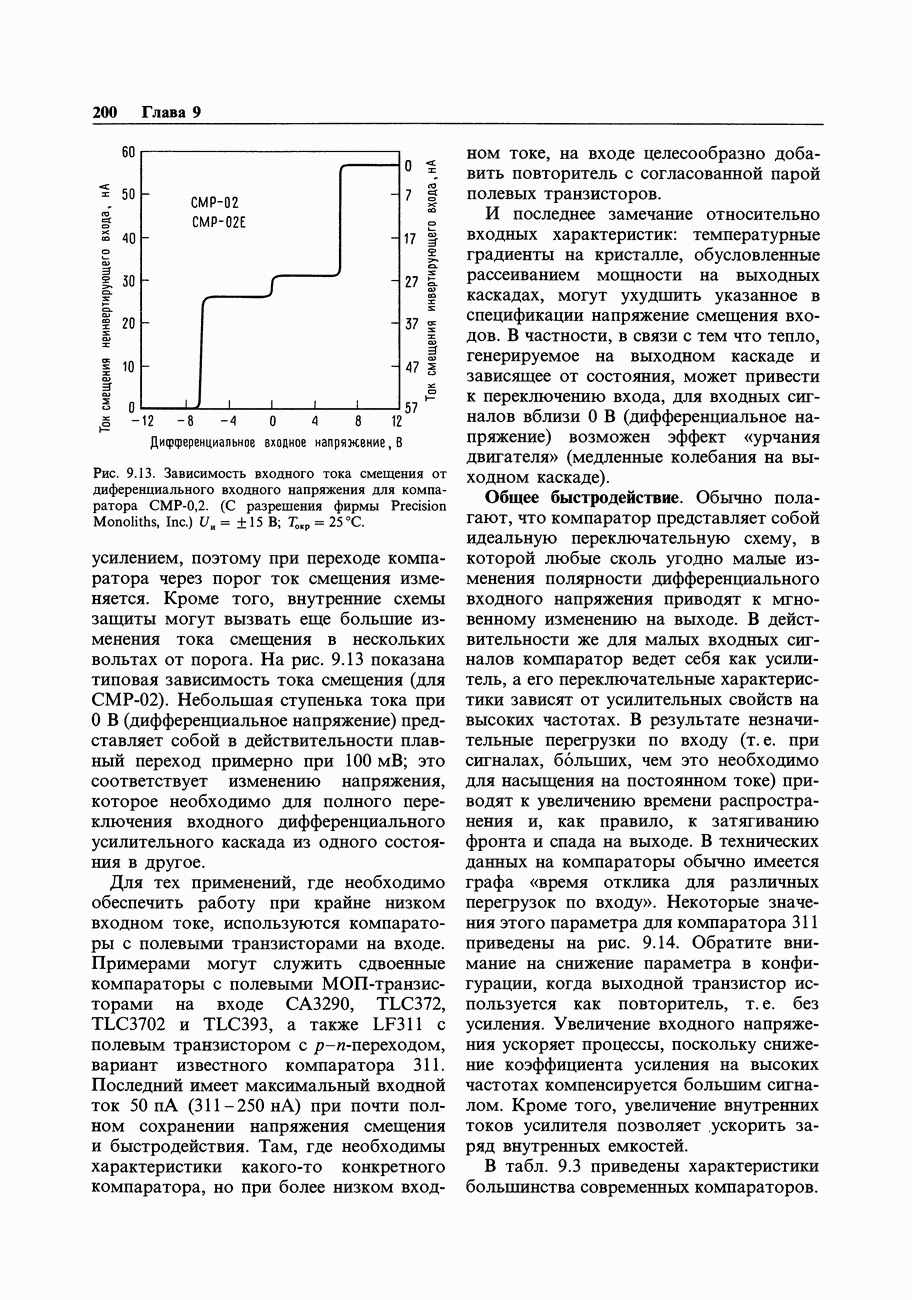
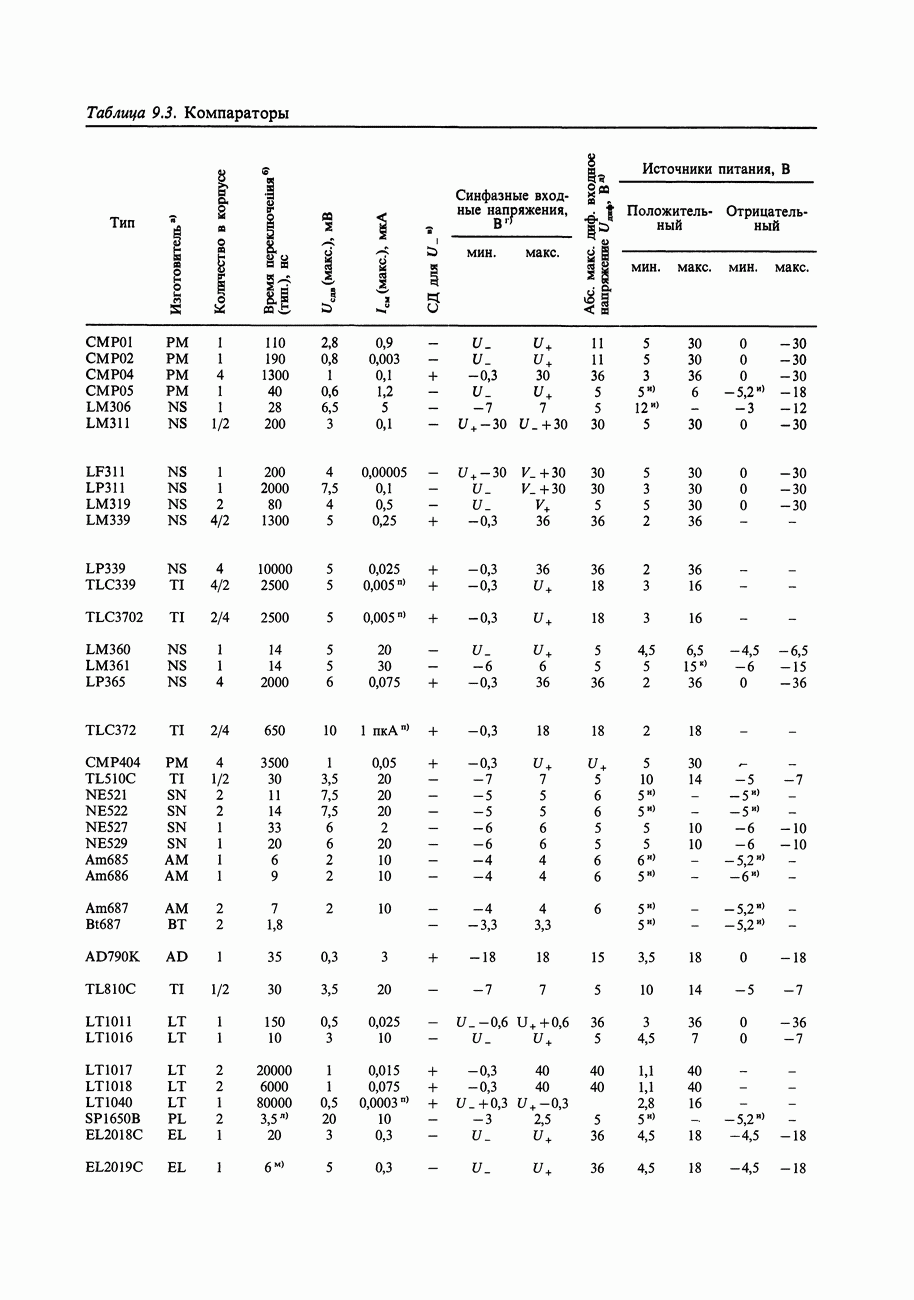
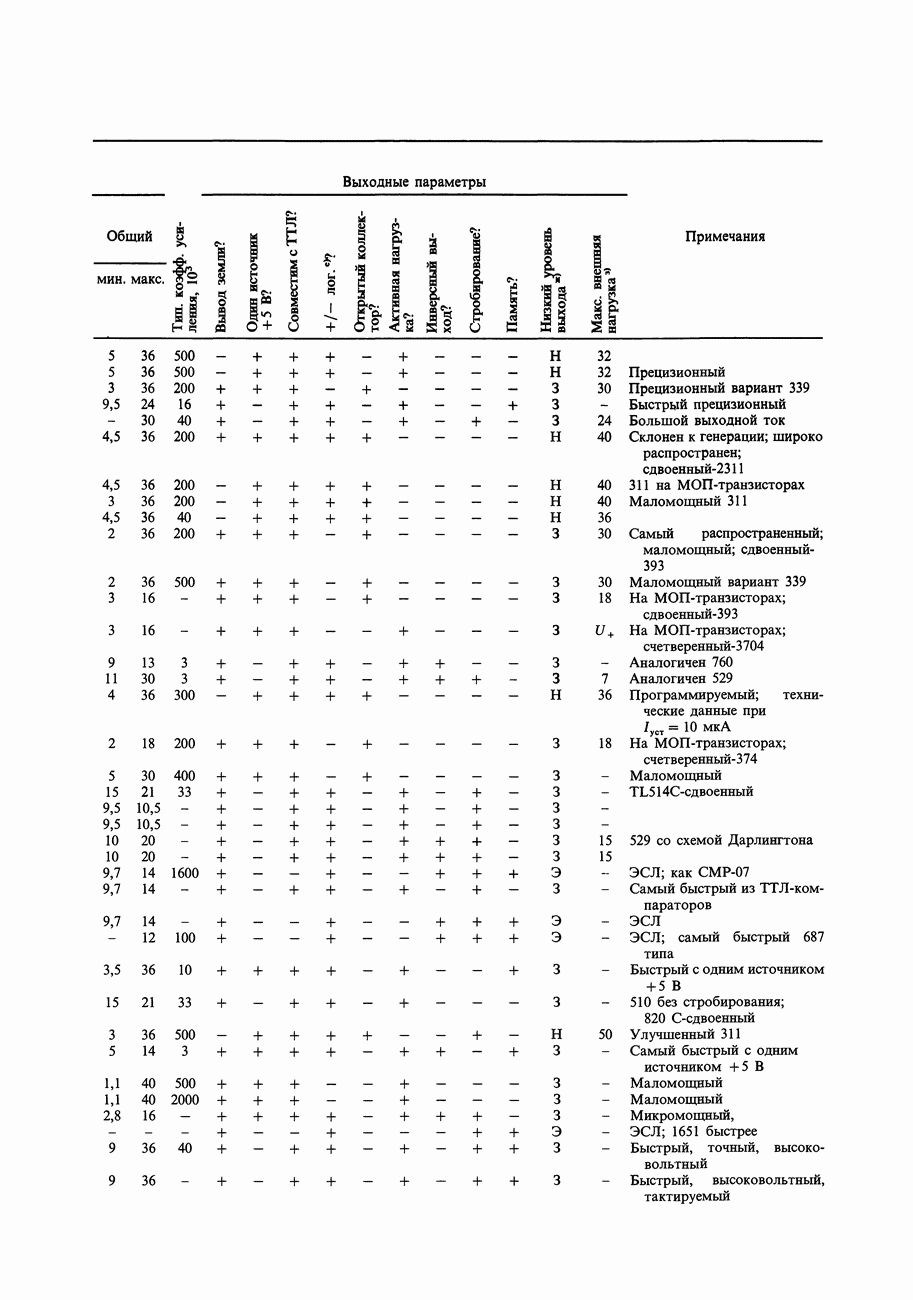
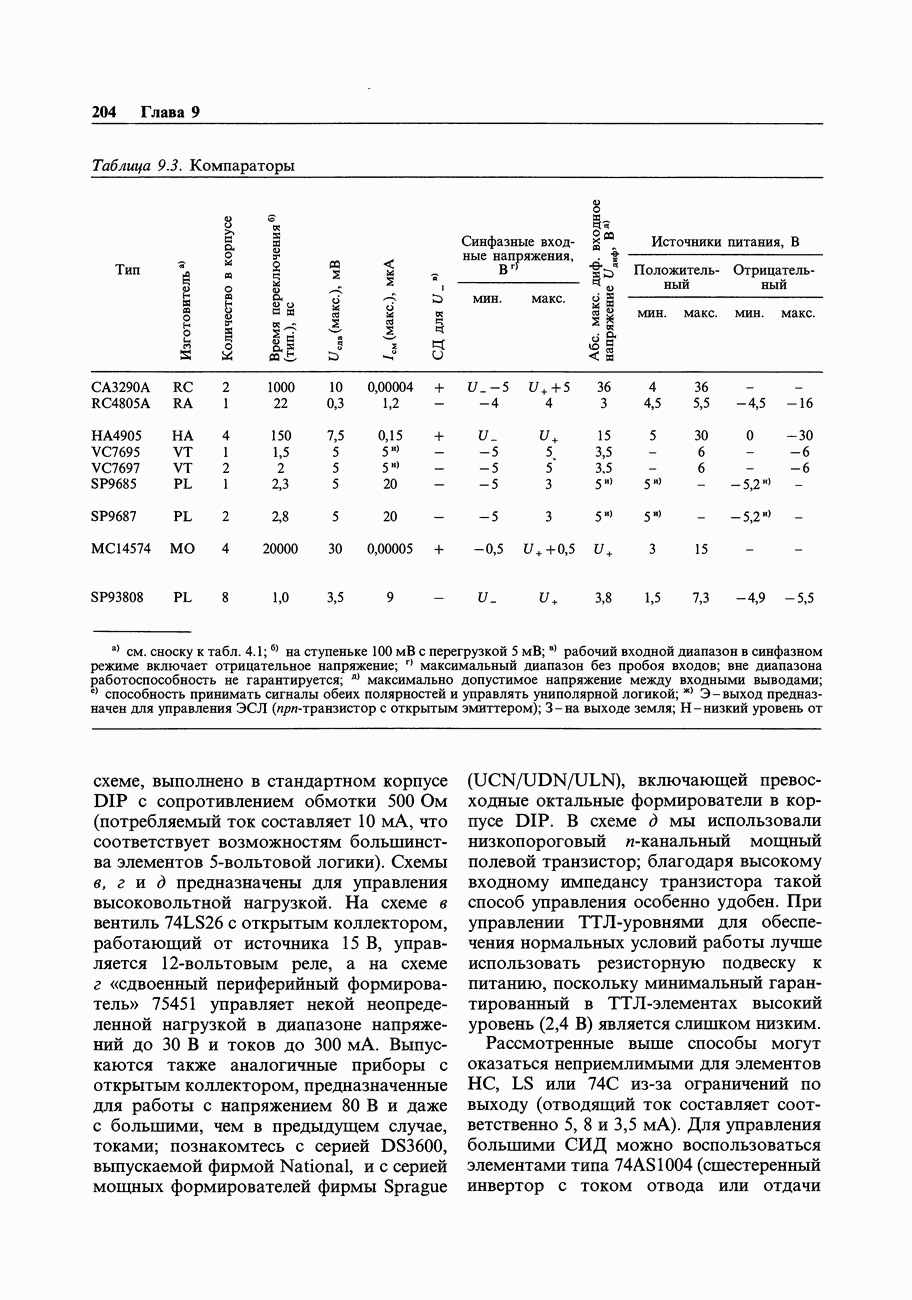
- 9.07. Компараторы
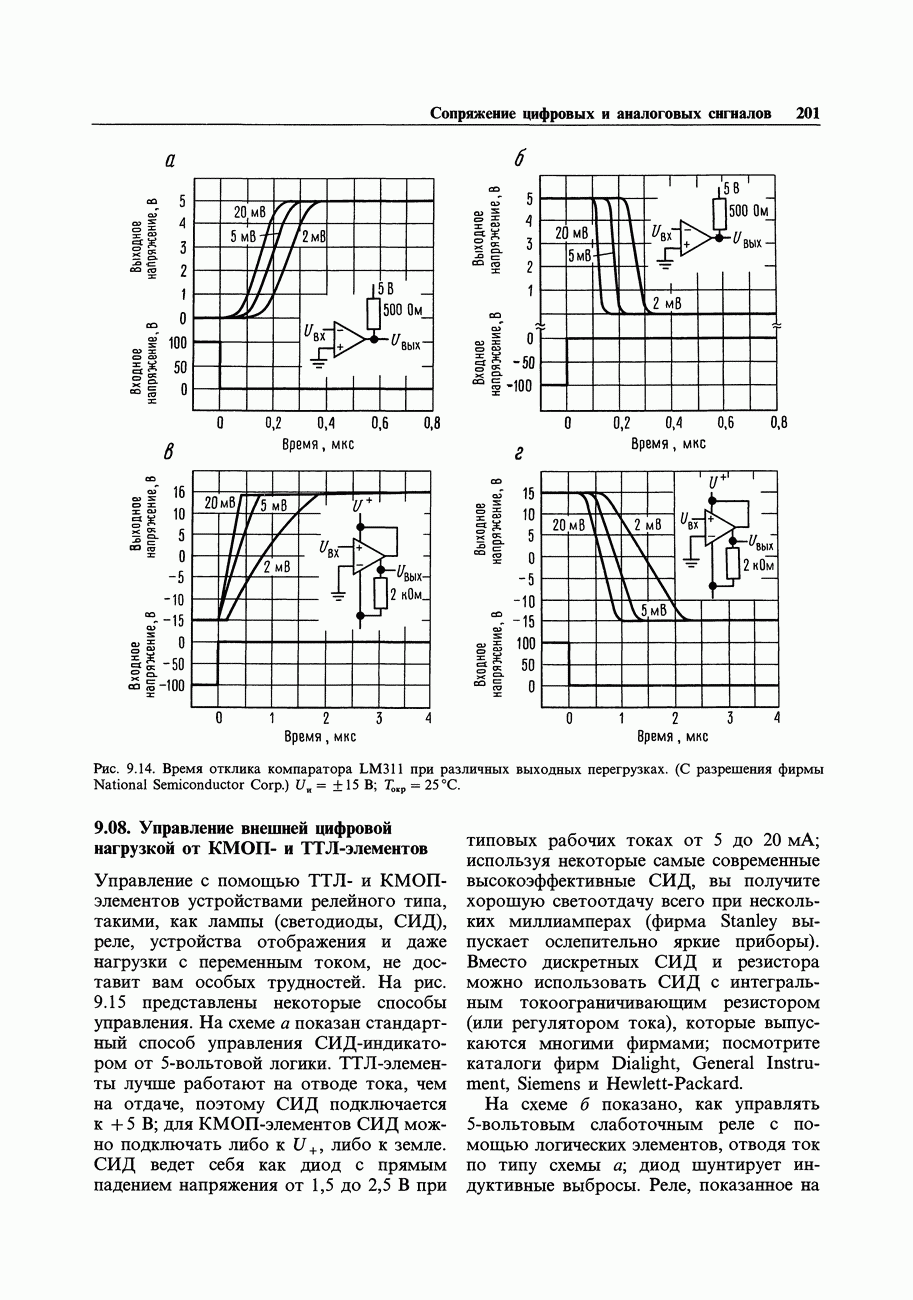
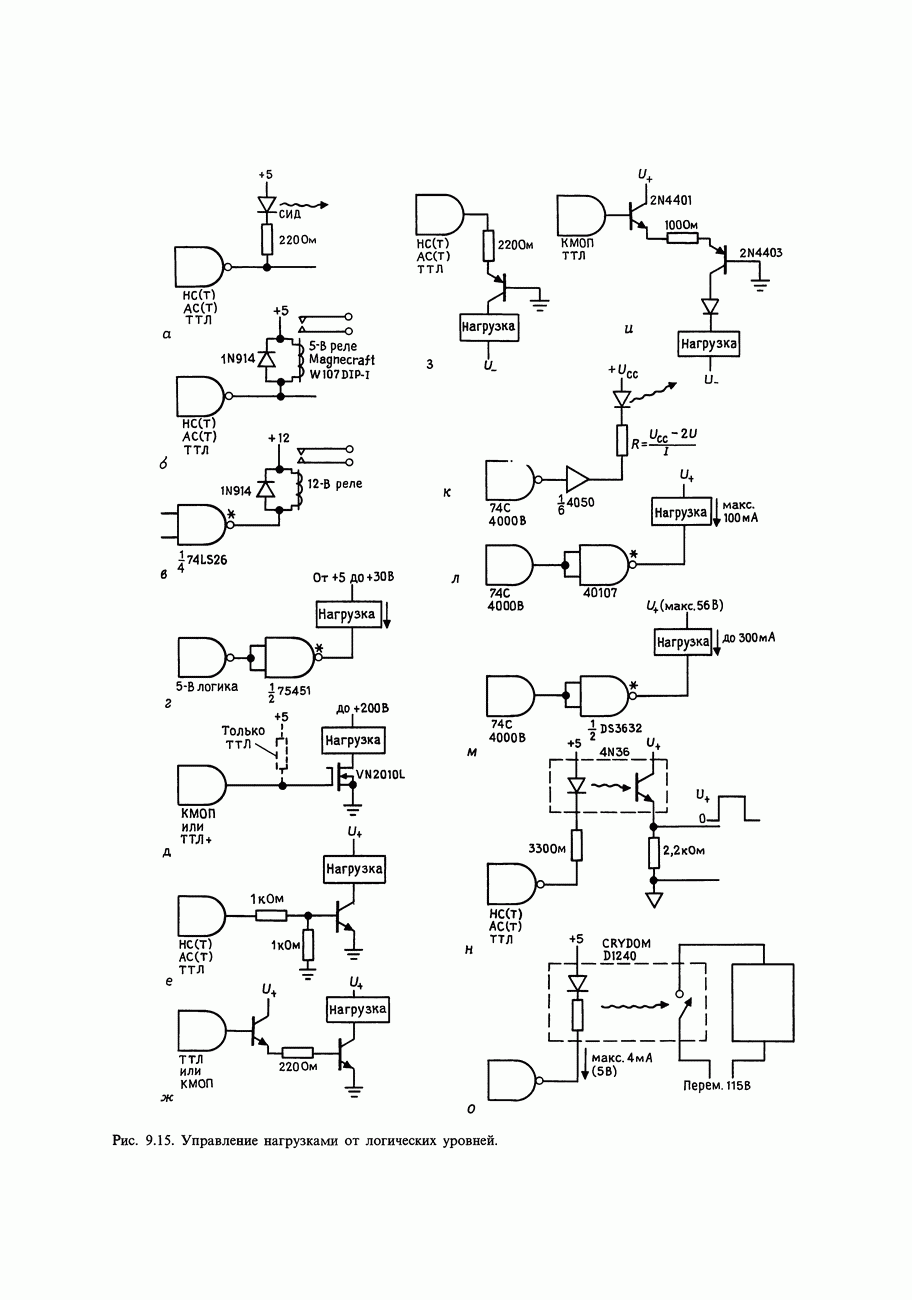
- 9.08. Управление внешней цифровой нагрузкой от КМОП- и ТТЛ-элементов
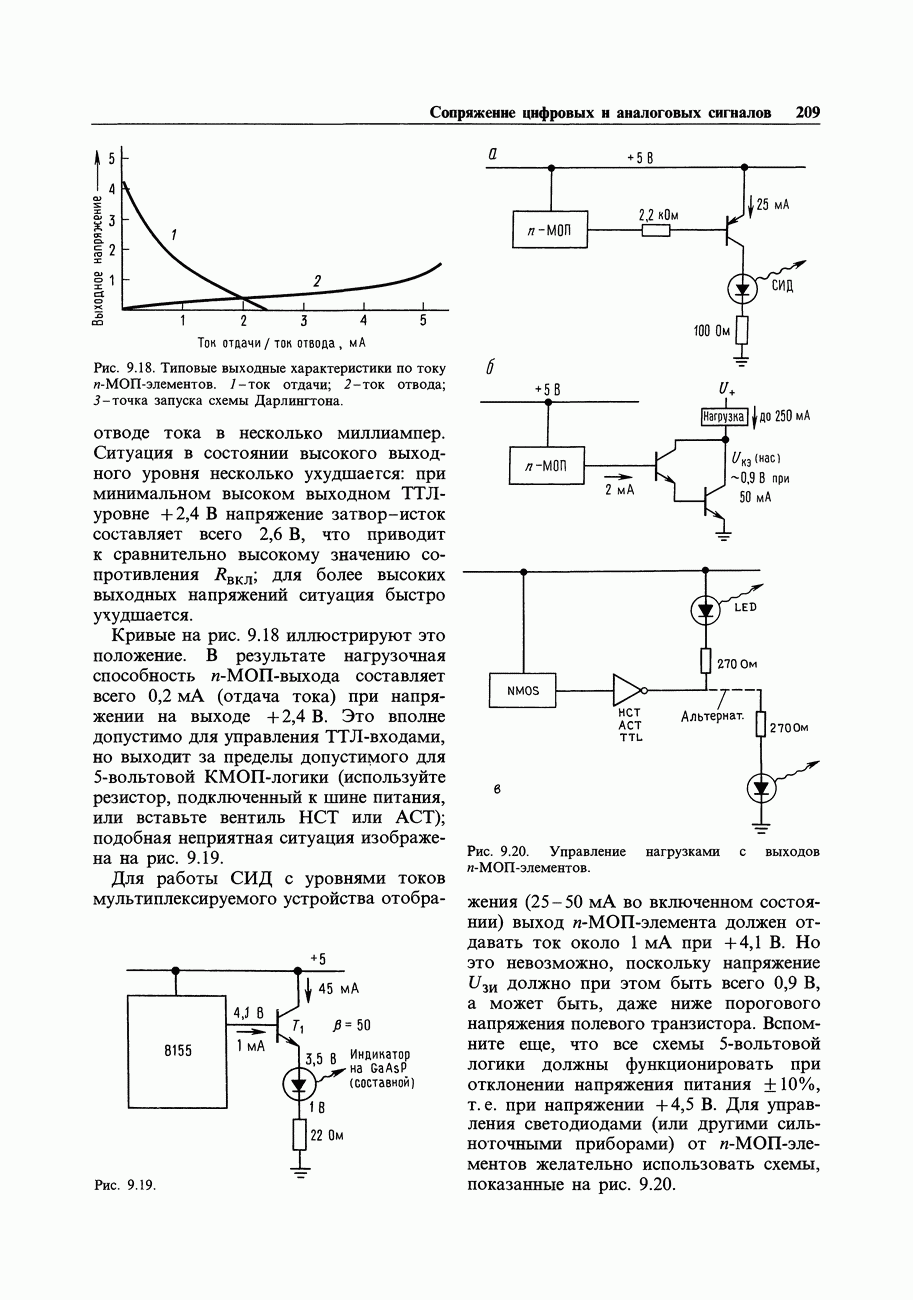
- 9.09. Сопряжение n-МОП БИС
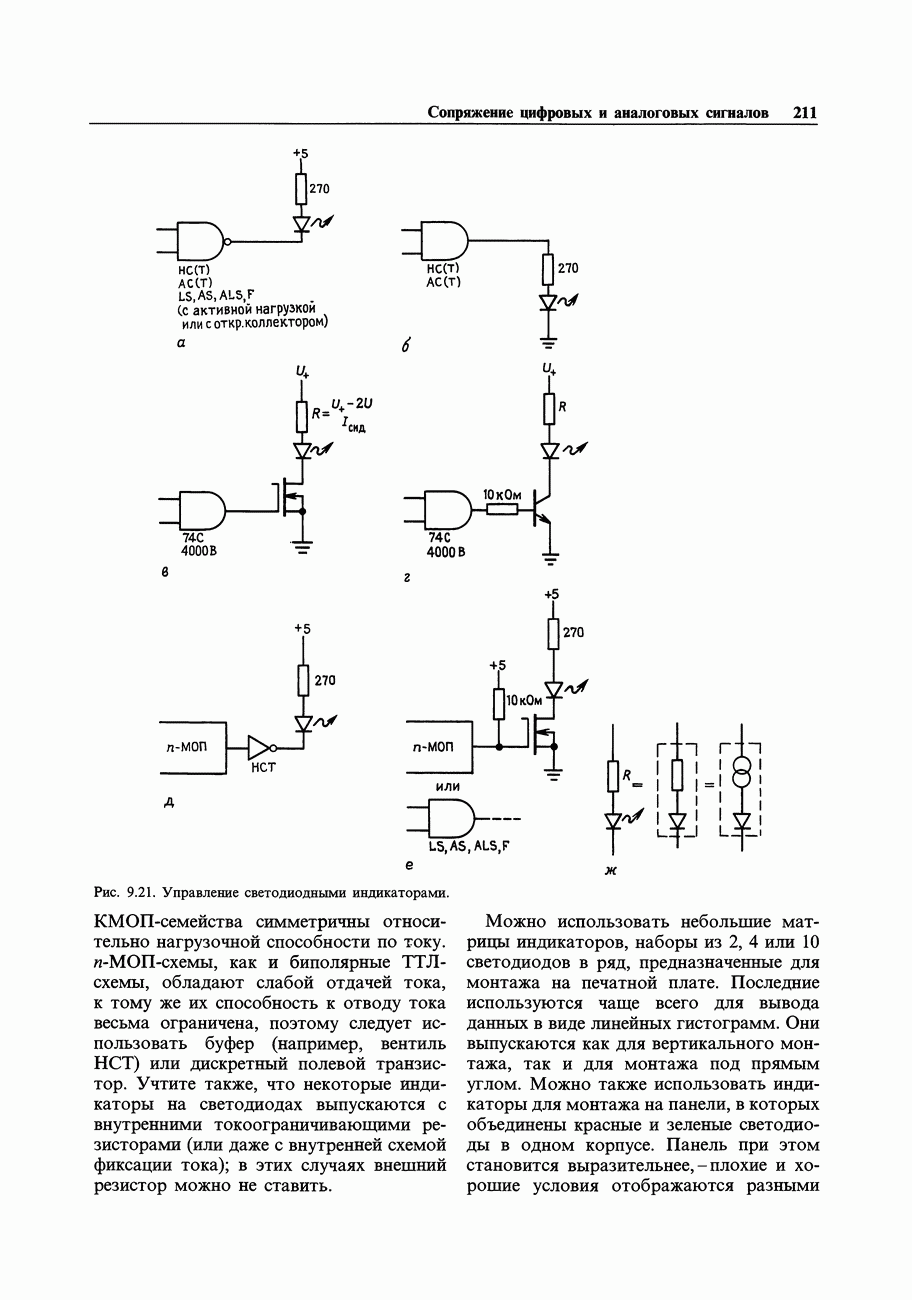
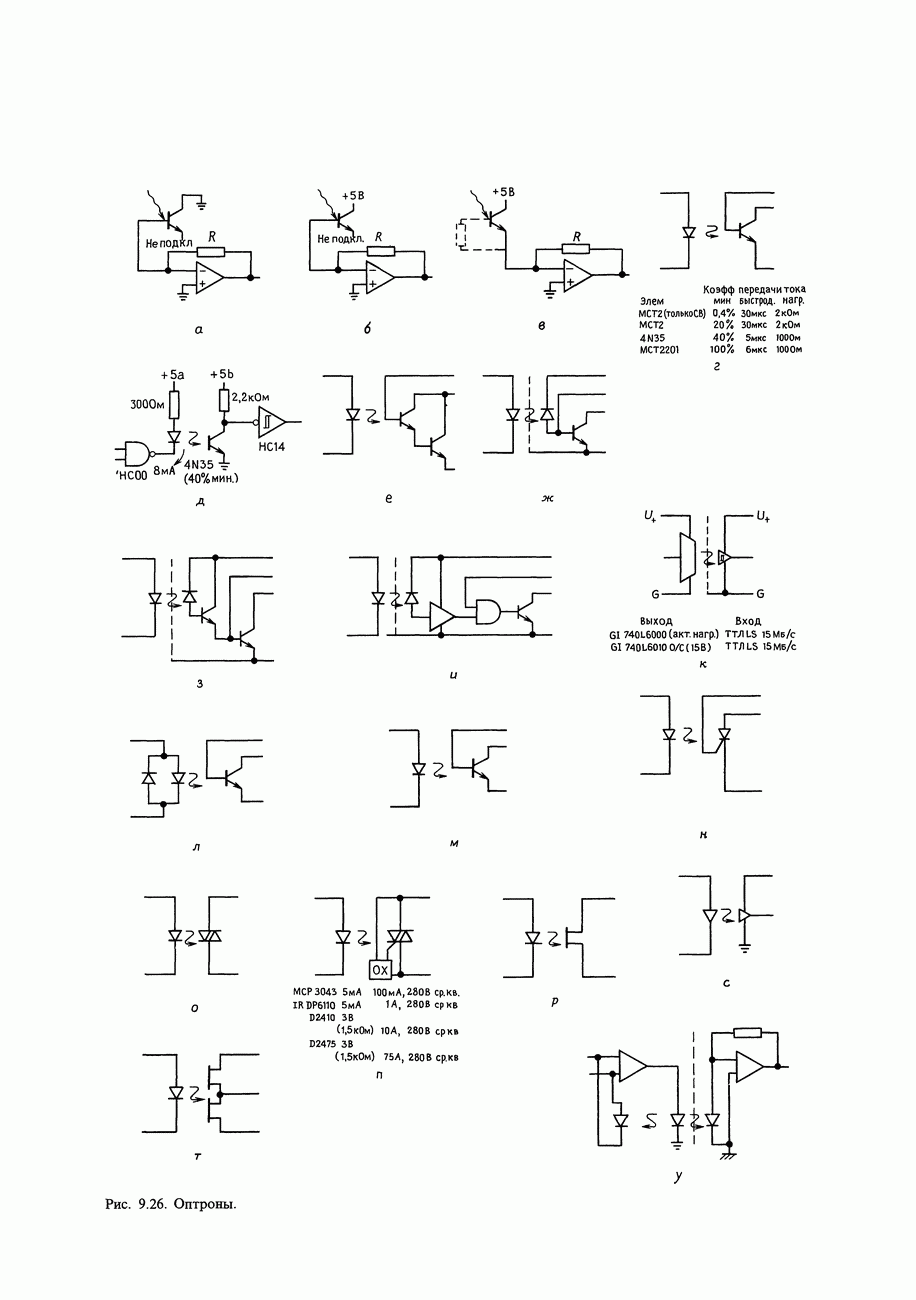
- 9.10. Оптоэлектроника
- ЦИФРОВЫЕ СИГНАЛЫ И ДЛИННЫЕ ЛИНИИ
- 9.11. Внутриплатные соединения
- 9.12. Межплатные соединения
- 9.13. Шины данных
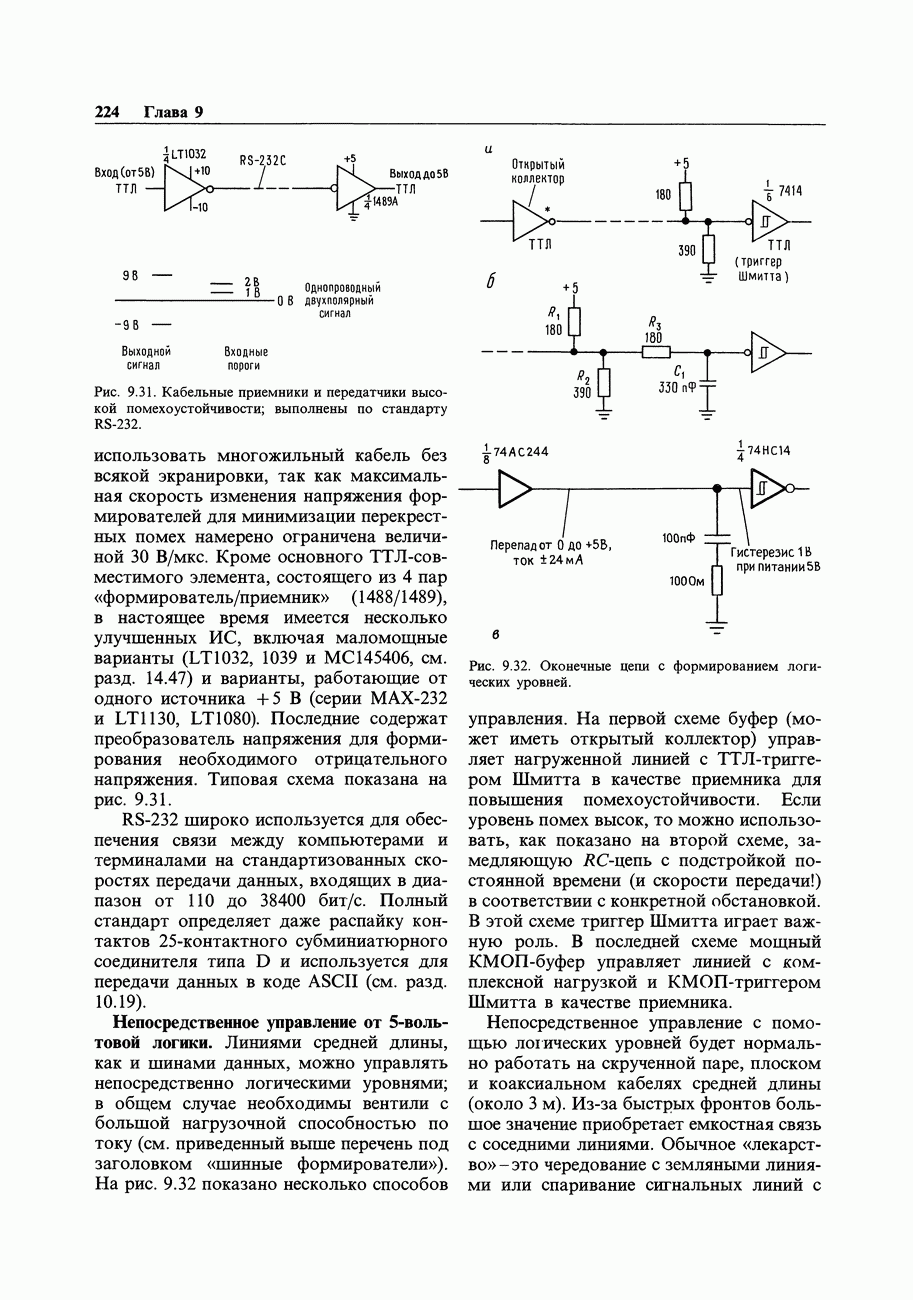
- 9.14. Кабельные связи
- АНАЛОГО-ЦИФРОВОЕ ПРЕОБРАЗОВАНИЕ
- 9.15. Введение в аналого-цифровое преобразование
- 9.16. Цифро-аналоговые преобразователи (ЦАП)
- 9.17. Интегрирующие ЦАП
- 9.18. ЦАП с умножением
- 9.19. Выбор ЦАП
- 9.20. Аналого-цифровые преобразователи
- 9.21. Методы уравновешивания заряда
- 9.22. Некоторые необычные АЦП и ЦАП
- 9.23. Выбор АЦП
- ПРИМЕРЫ А/Ц-ПРЕОБРАЗОВАНИЯ
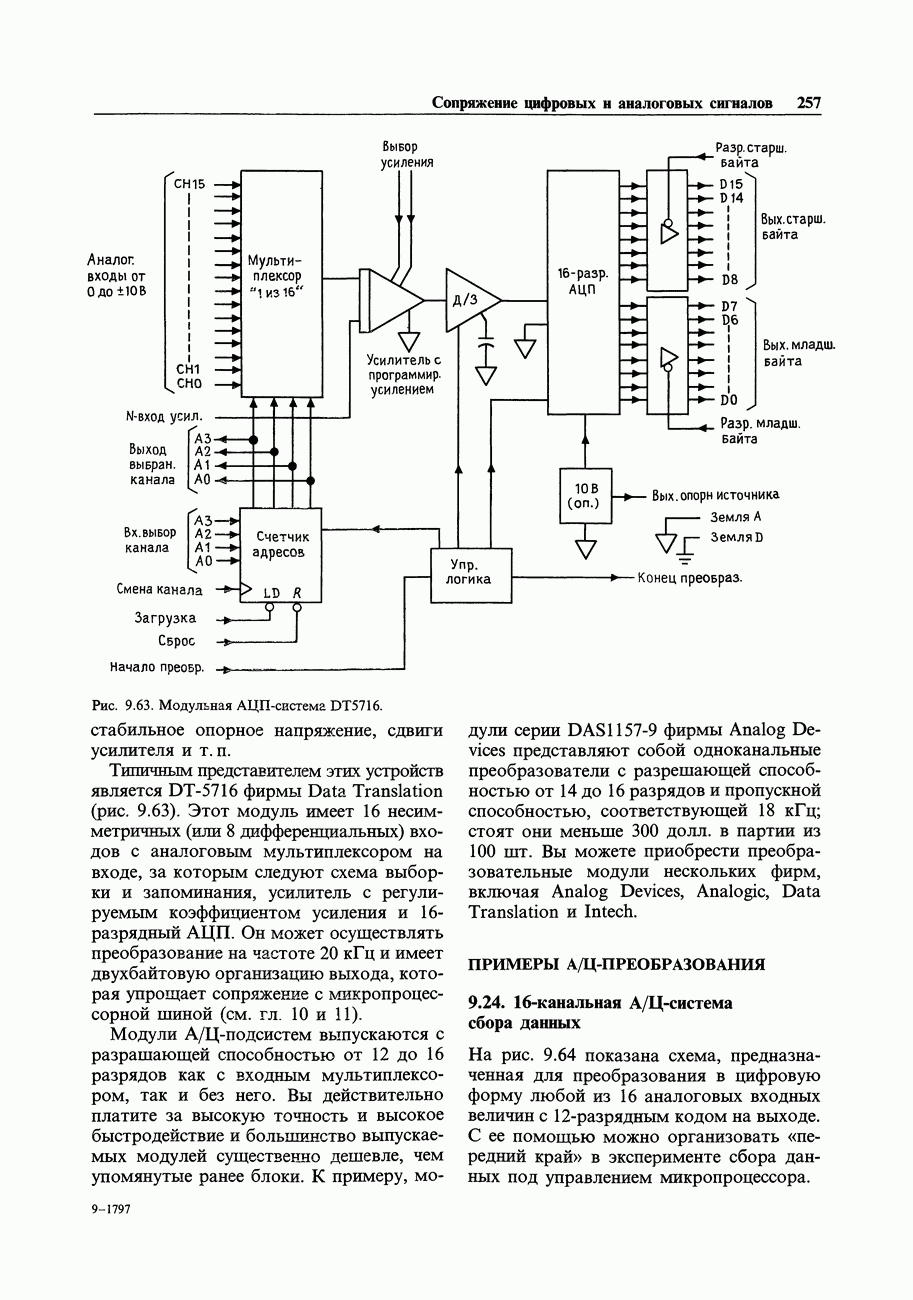
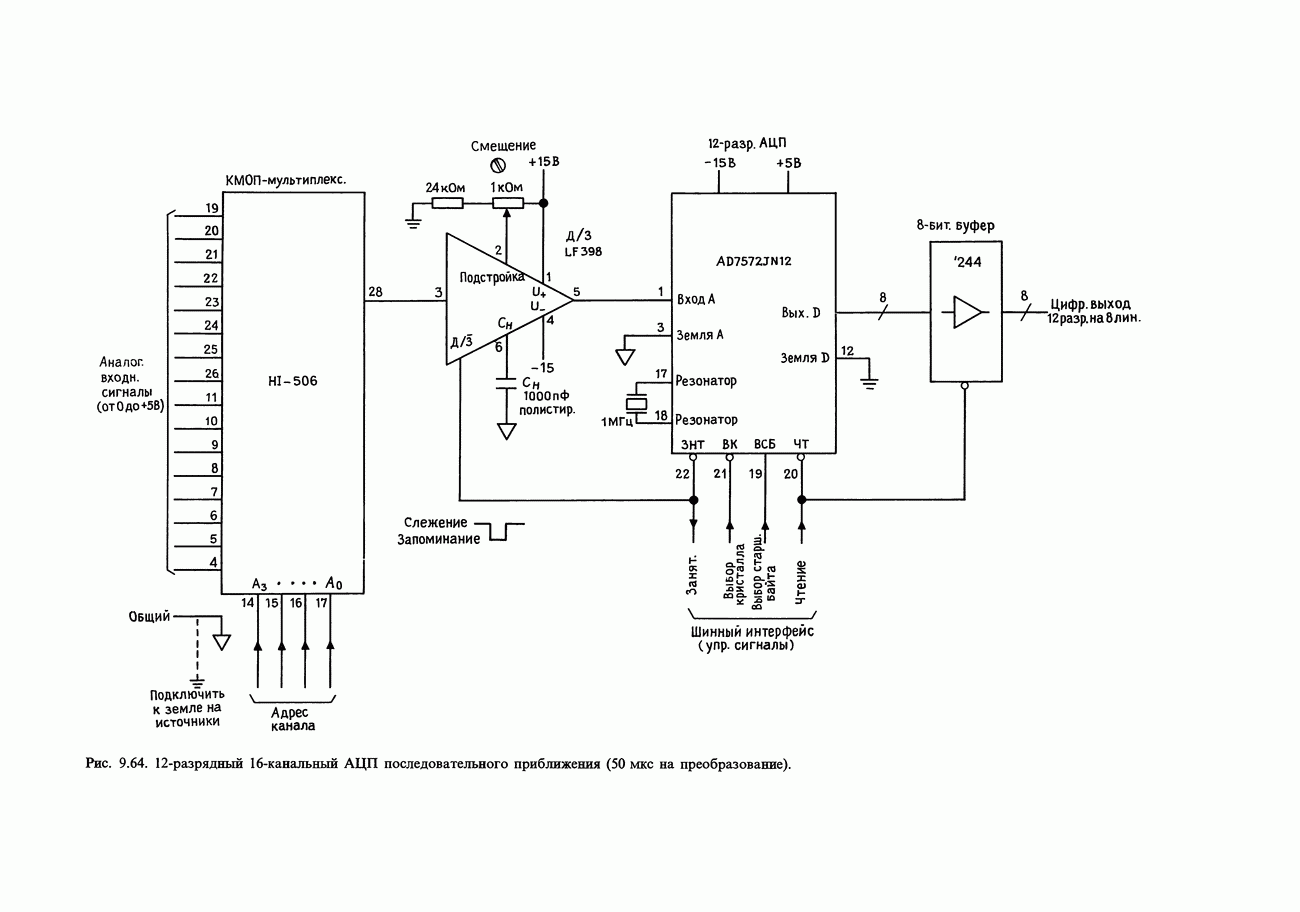
- 9.24. 16-канальная А/Ц-система сбора данных
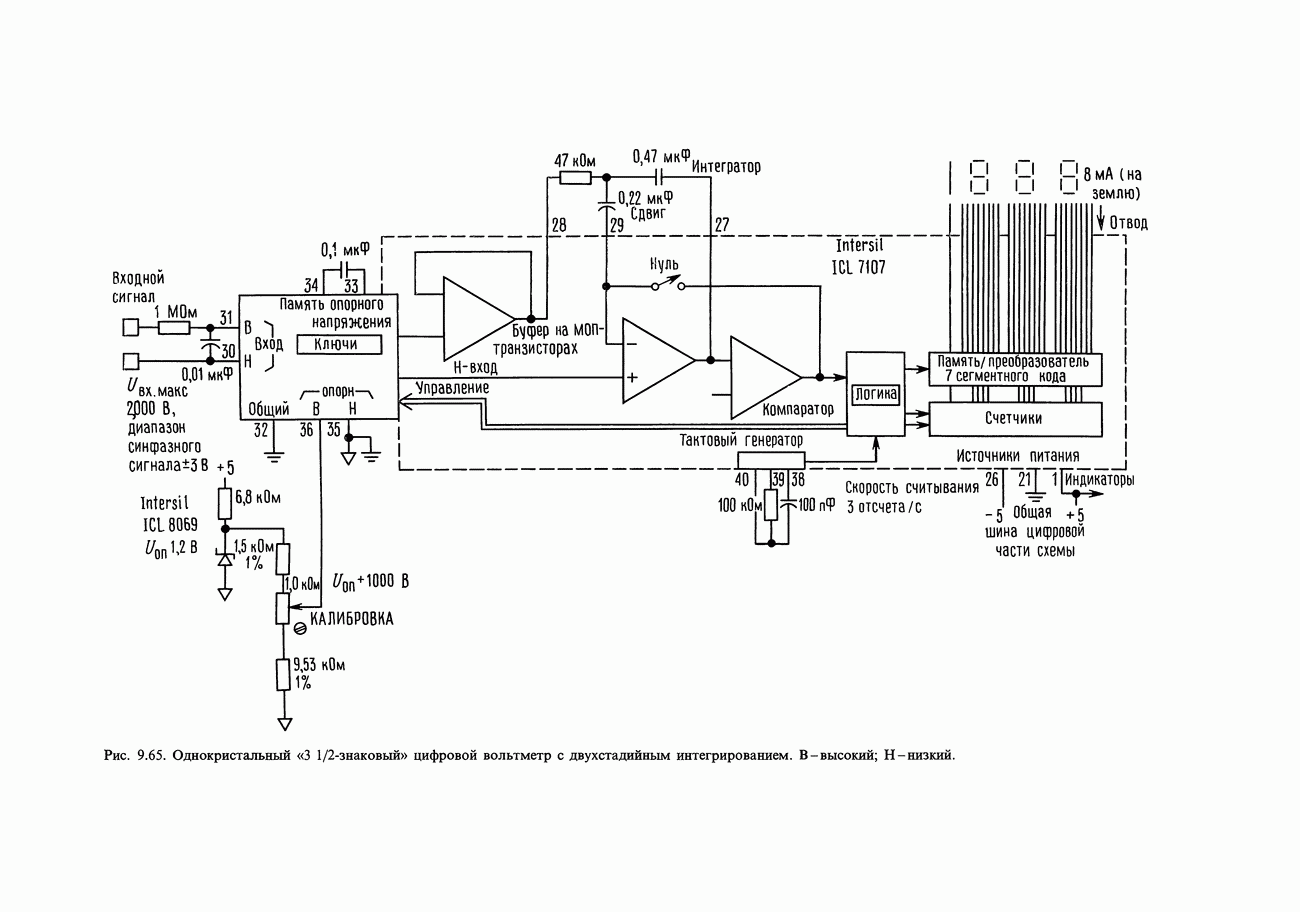
- 9.25. 3 1/2 — знаковый цифровой вольтметр
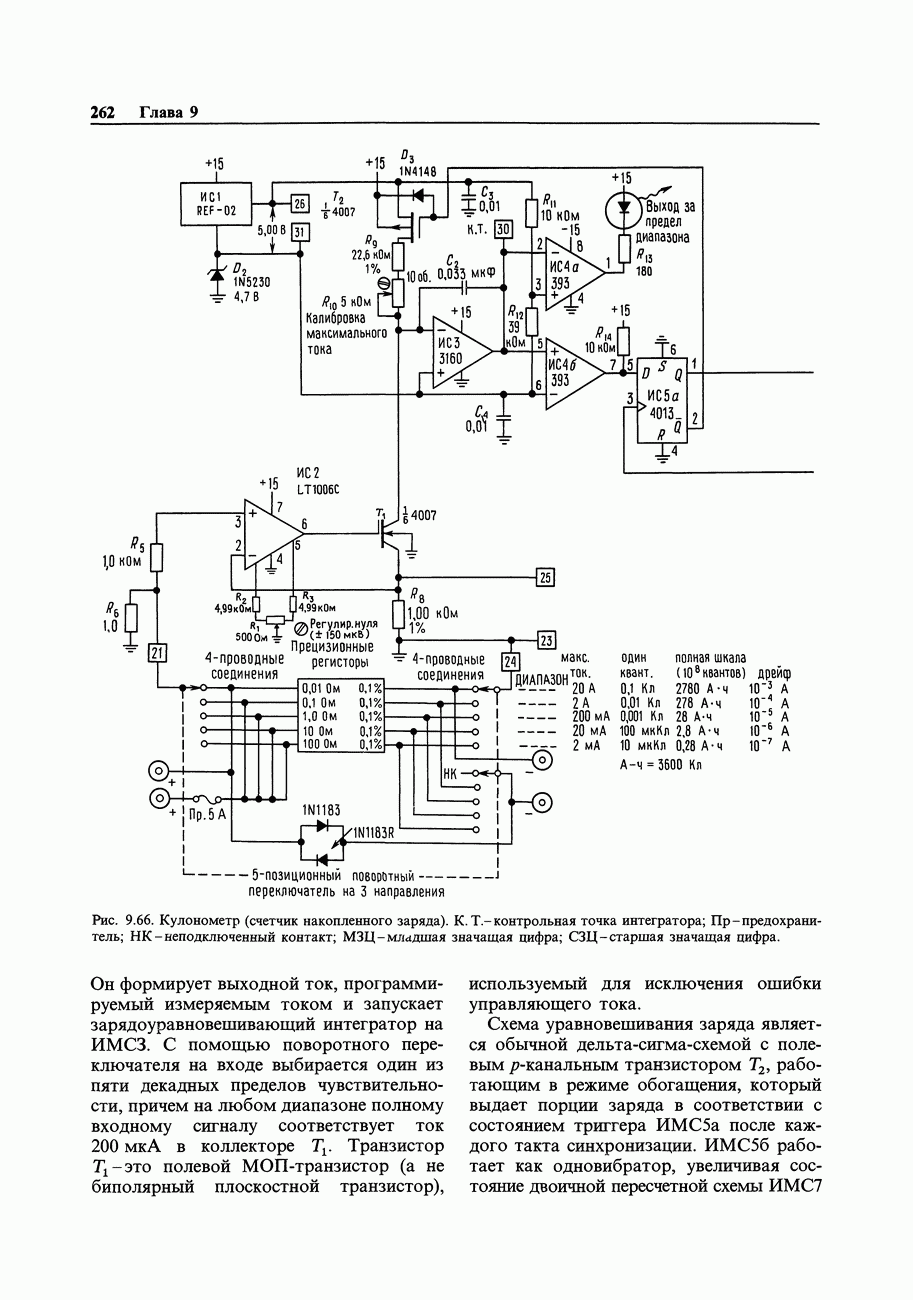
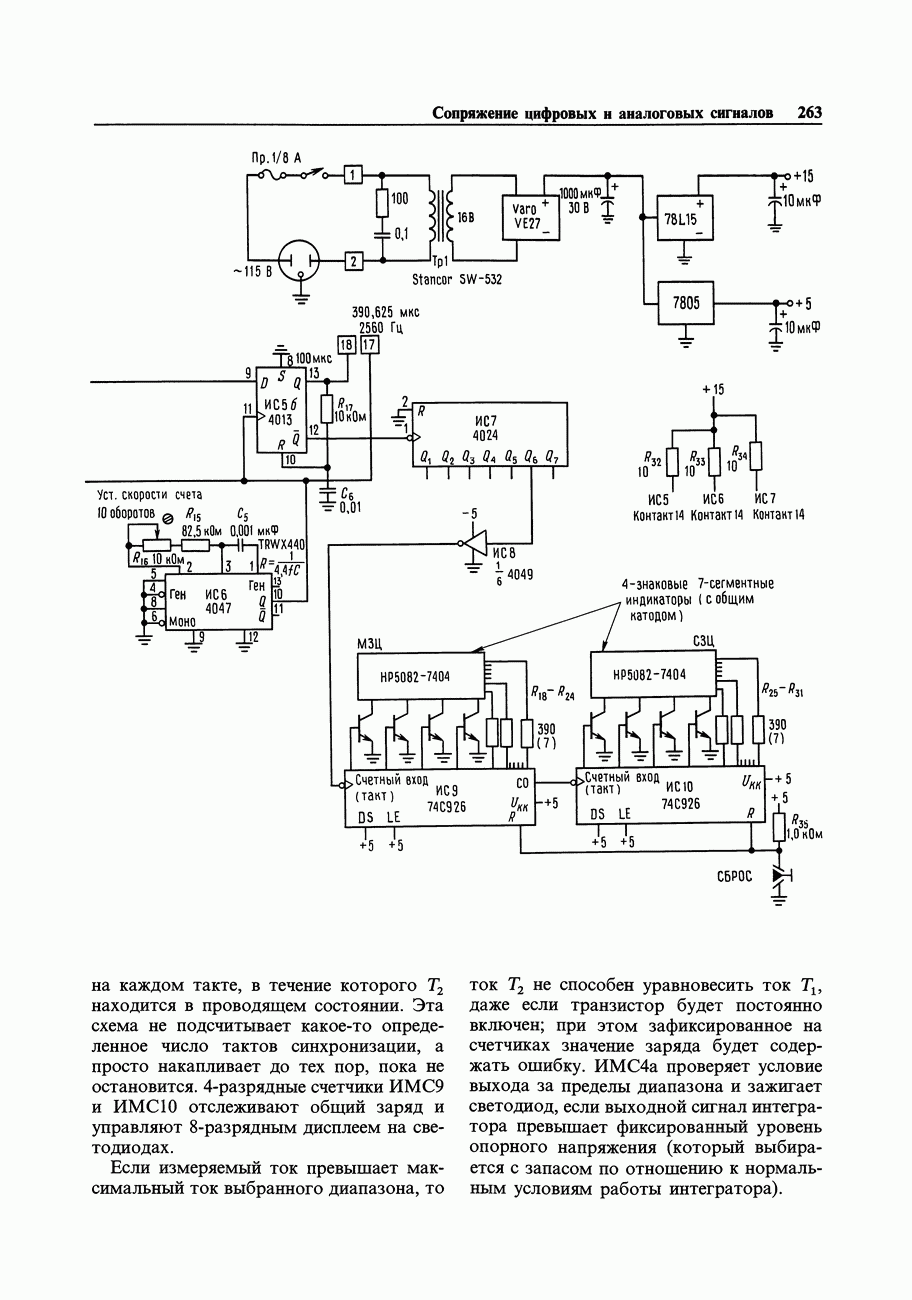
- 9.26. Кулонометр
- СХЕМЫ ФАЗОВОЙ АВТОПОДСТРОЙКИ ЧАСТОТЫ
- 9.28. Проектирование ФАПЧ
- 9.29. Пример разработки: умножитель частоты
- 9.30. Захват и слежение в системе ФАПЧ
- 9.31. Некоторые примеры применения систем ФАПЧ
- ПСЕВДОСЛУЧАЙНЫЕ ДВОИЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ГЕНЕРАТОРЫ ШУМА
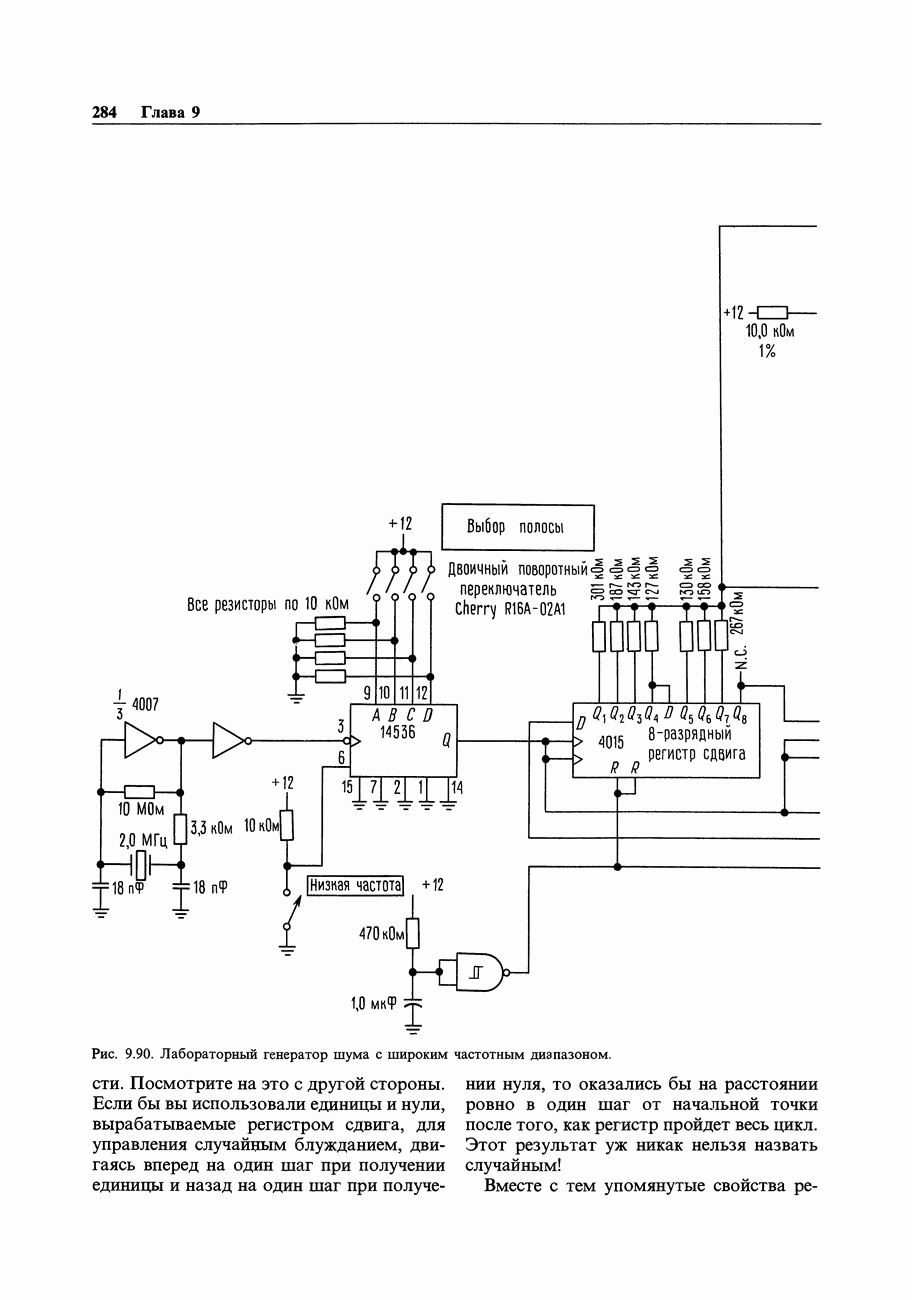
- 9.32. Цифровые методы генерации шума
- 9.33. Последовательности, генерируемые регистрами сдвига с обратными связями
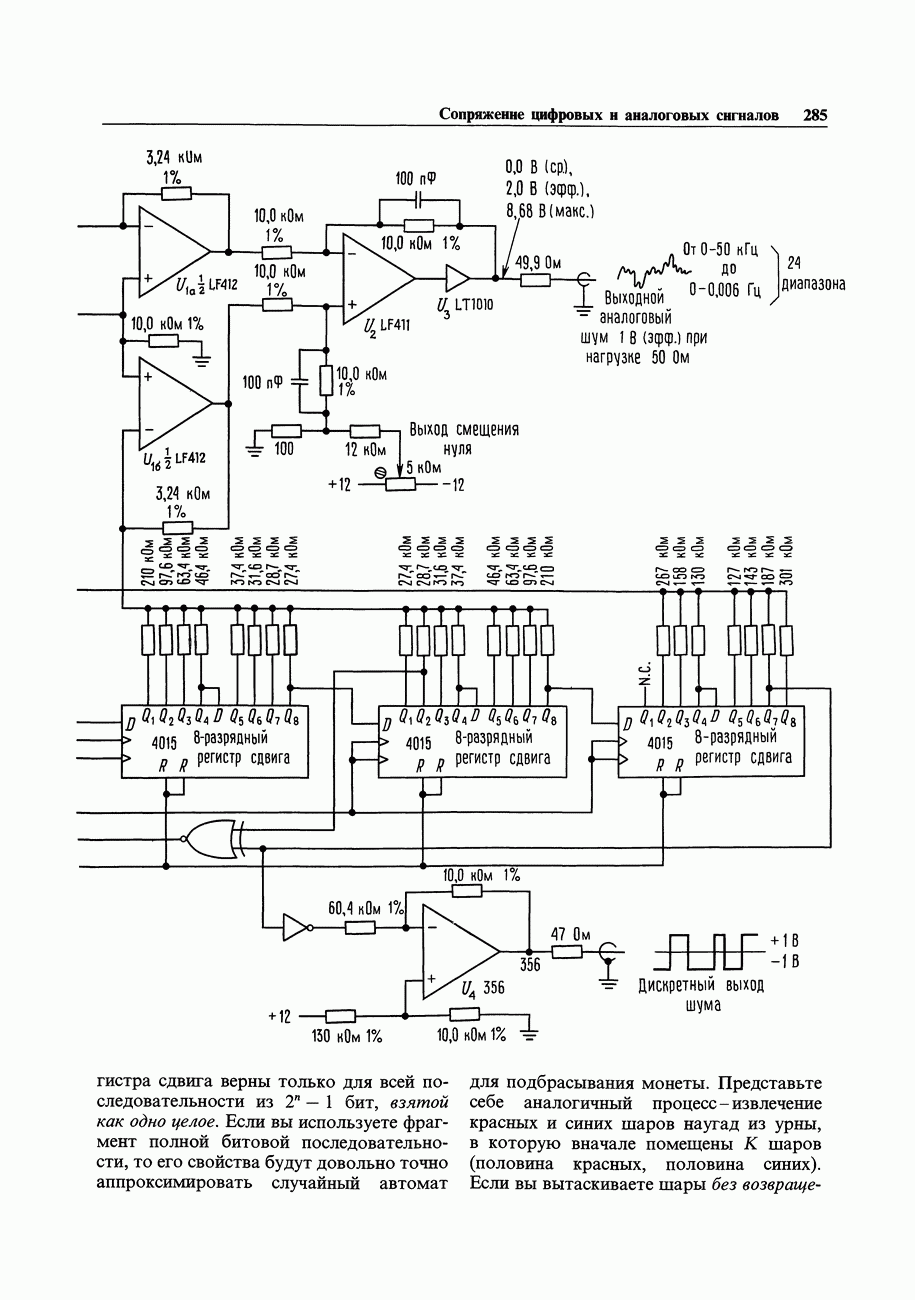
- 9.34. Формирование аналогового шума с использованием последовательностей максимальной длины
- 9.35. Энергетический спектр последовательности, сформированной при помощи регистра сдвига
- 9.36. Низкочастотная фильтрация
- 9.37. Краткое заключение
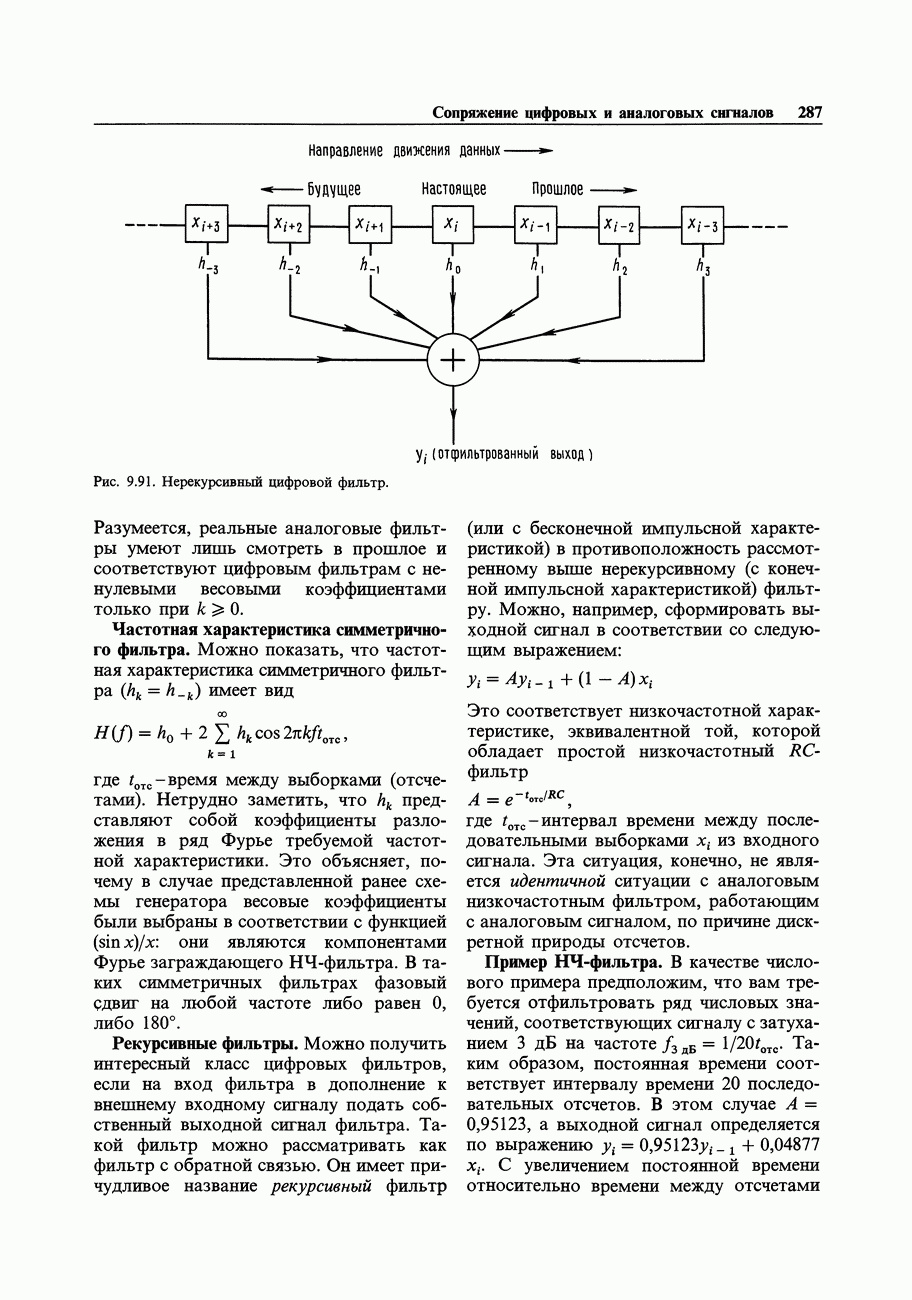
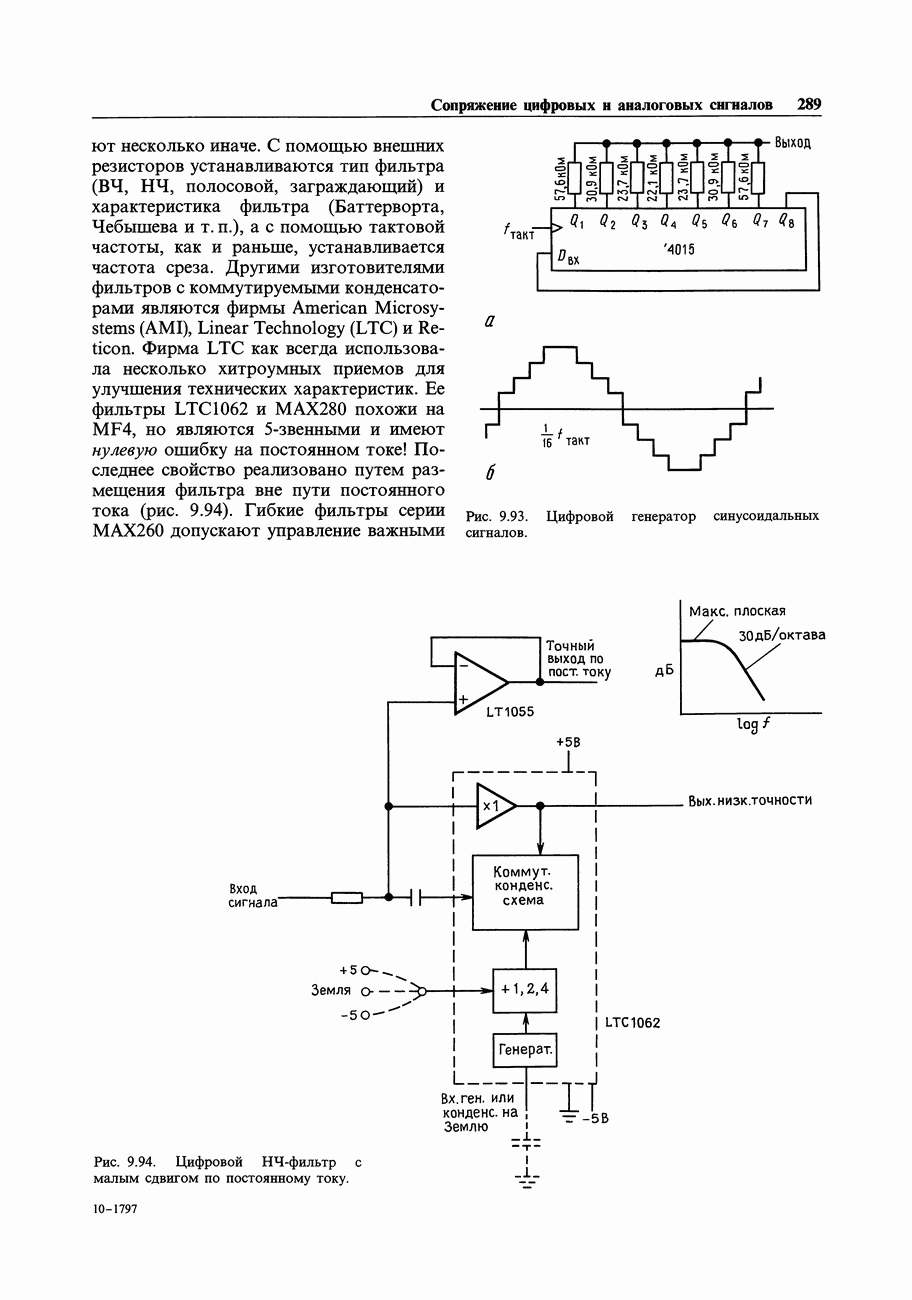
- 9.38. Цифровые фильтры
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 10. МИКРОЭВМ
- МИНИ-ЭВМ, МИКРОЭВМ И МИКРОПРОЦЕССОРЫ
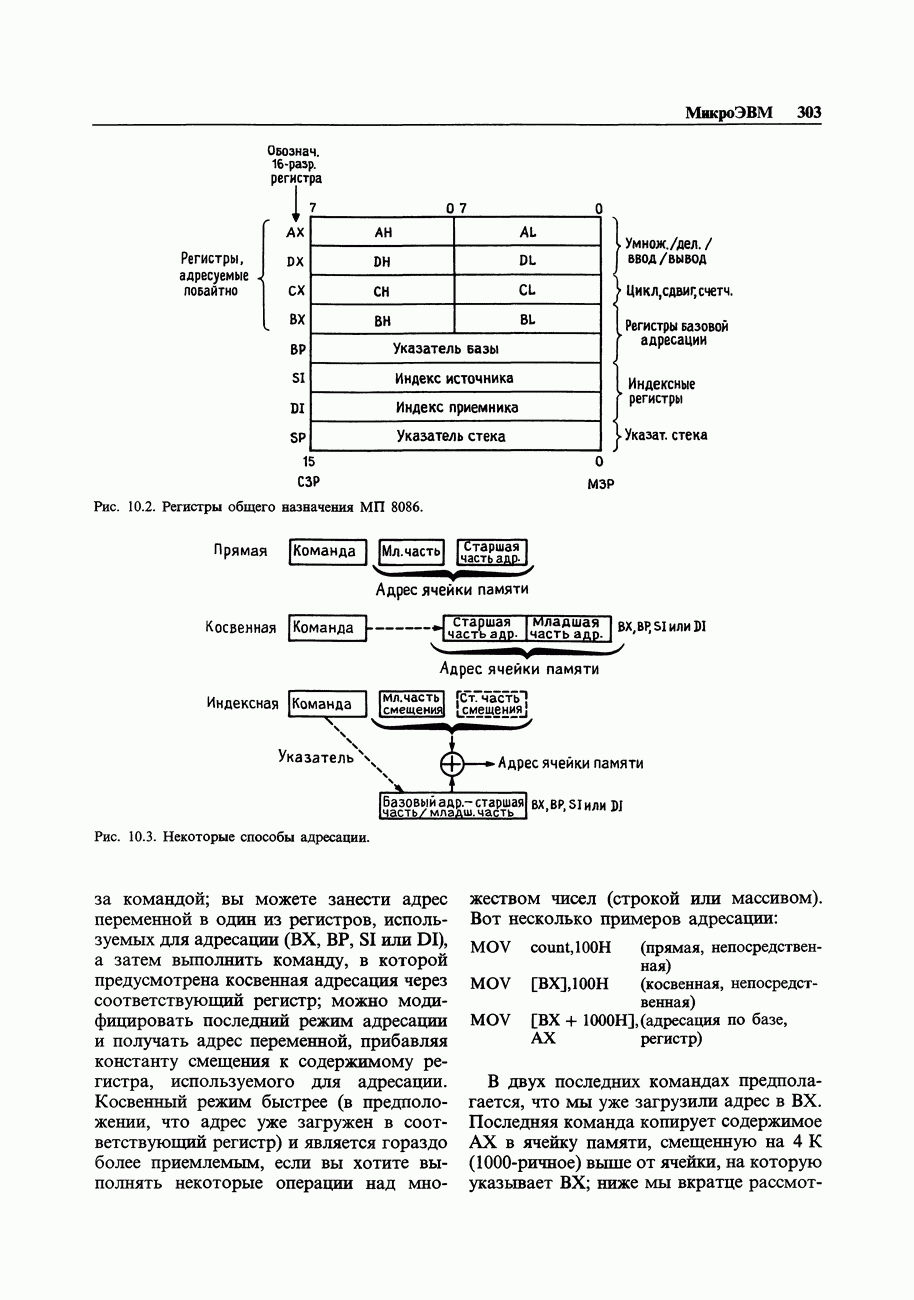
- 10.01. Архитектура микроЭВМ
- НАБОР КОМАНД КОМПЬЮТЕРА
- 10.02. Язык ассемблера и язык машинных кодов
- 10.03. Упрощенный набор команд процессора Intel 8086/8
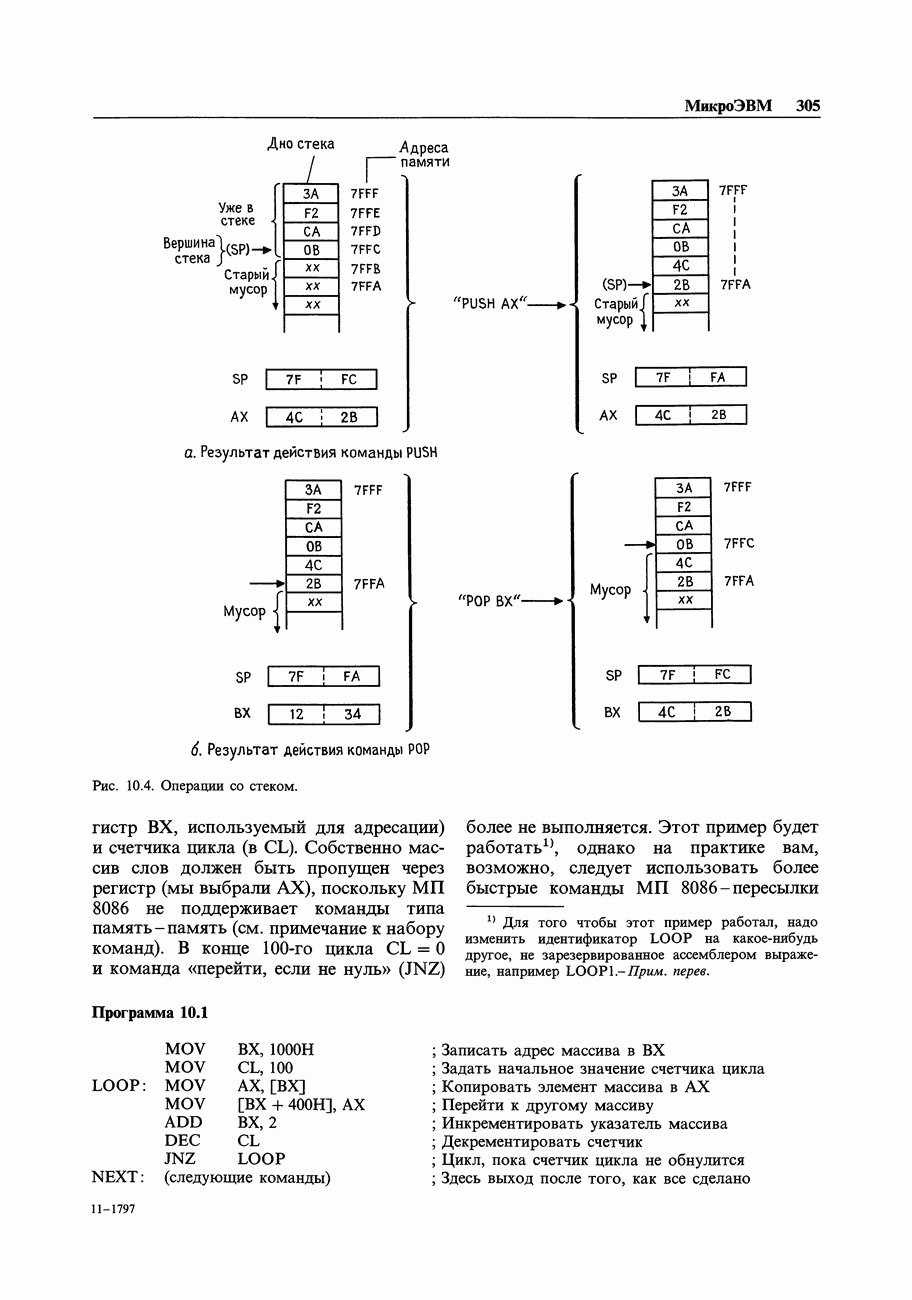
- 10.04. Программный пример
- СИГНАЛЫ МАГИСТРАЛИ И ЕЕ ФУНКЦИОНИРОВАНИЕ
- 10.05. Основные сигналы магистрали: данные, адрес, синхронизация
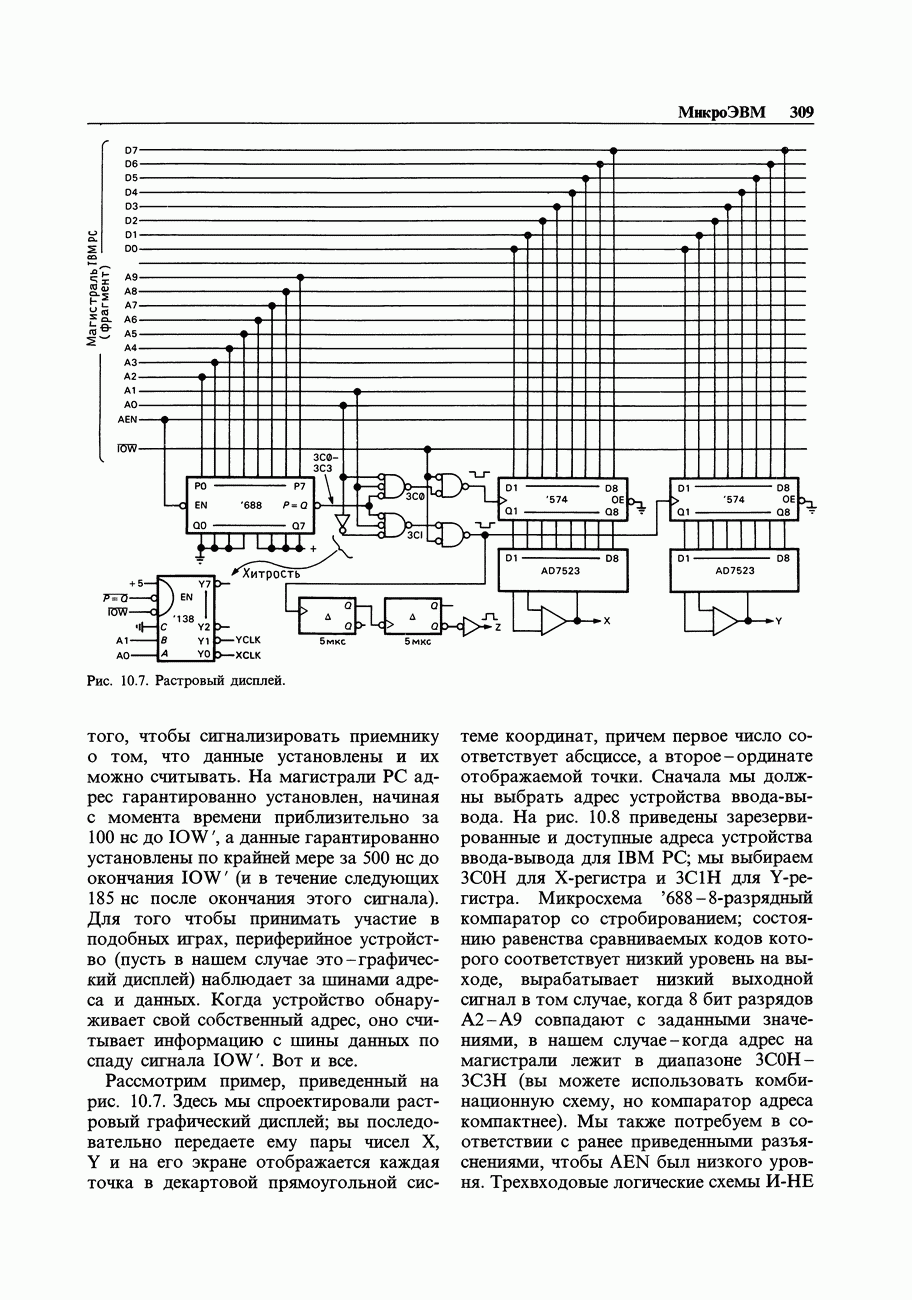
- 10.06. Программируемый ввод-вывод: вывод данных
- 10.07. Программируемый ввод-вывод: ввод данных
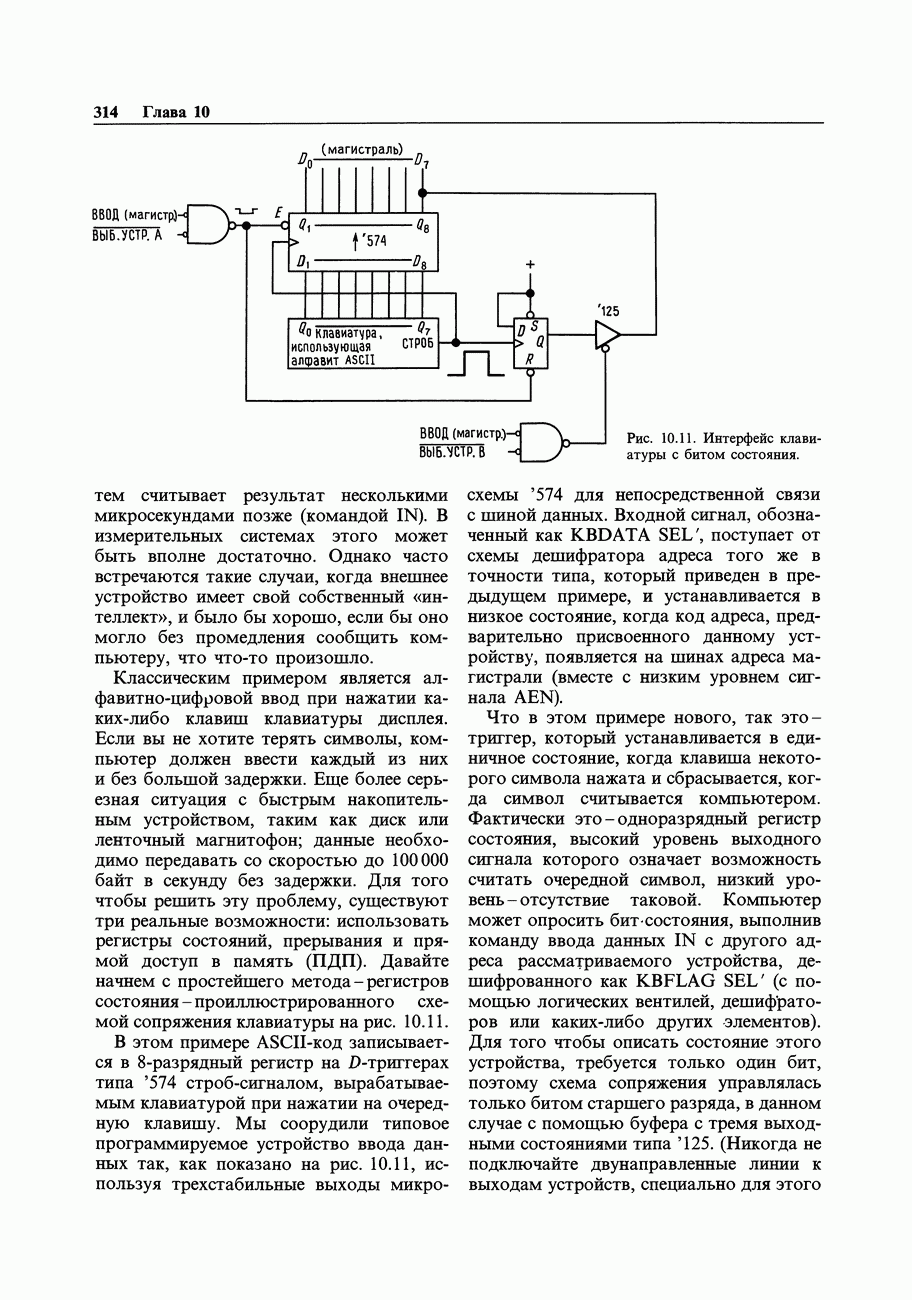
- 10.08. Программируемый ввод-вывод: регистры состояний
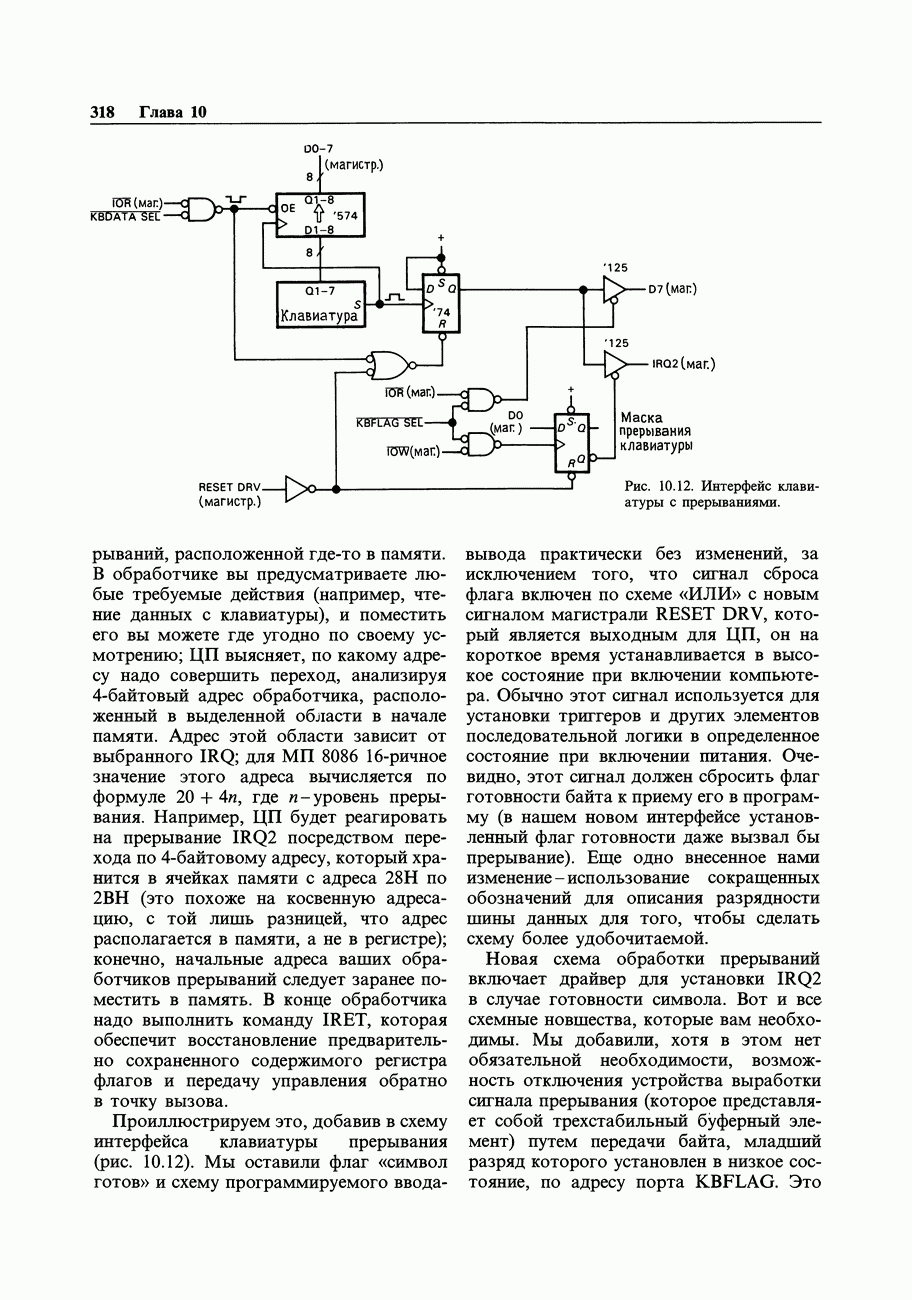
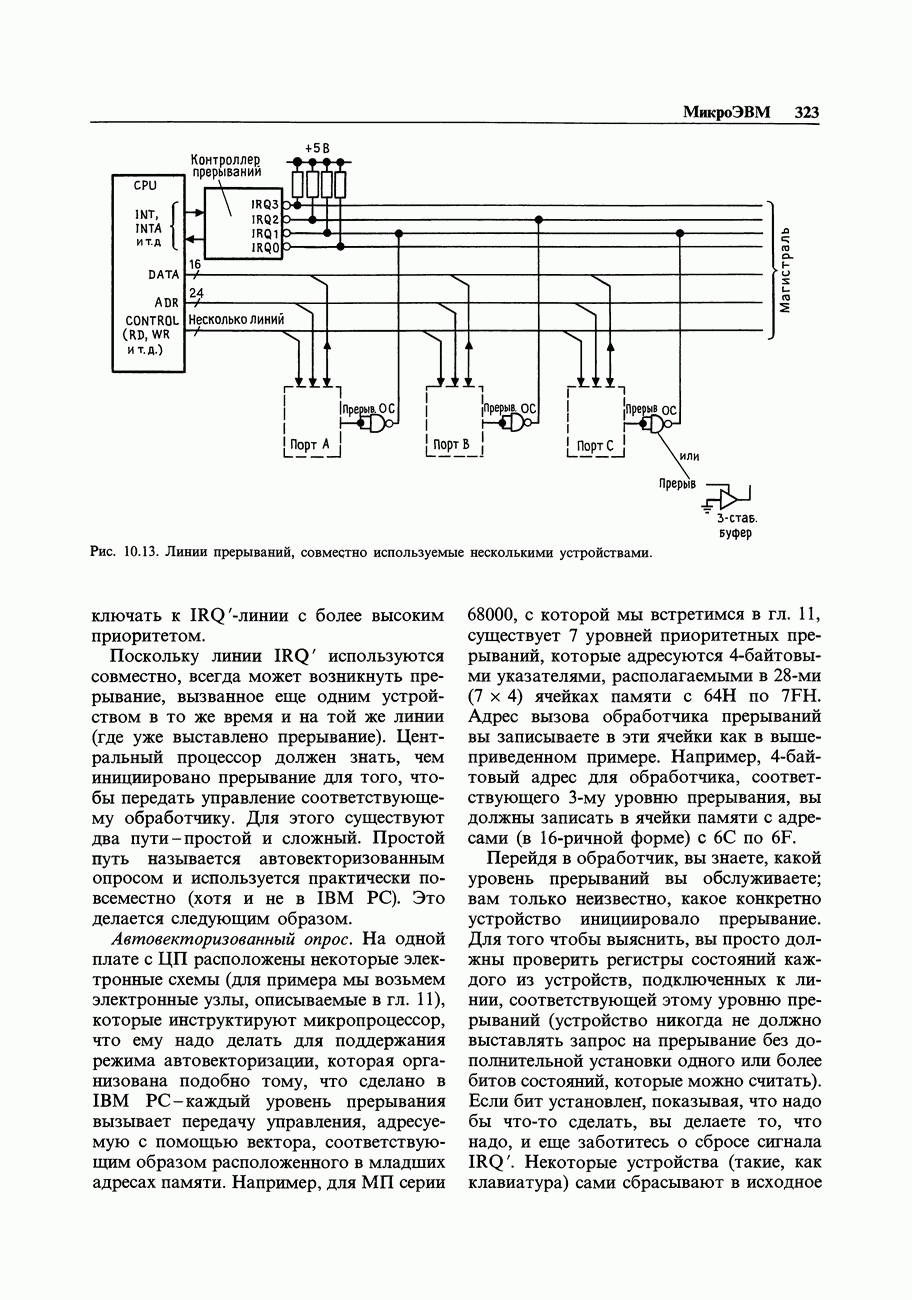
- 10.09. Прерывания
- 10.10. Обработка прерываний
- 10.11. Прерывания в целом
- 10.12. Прямой доступ в память
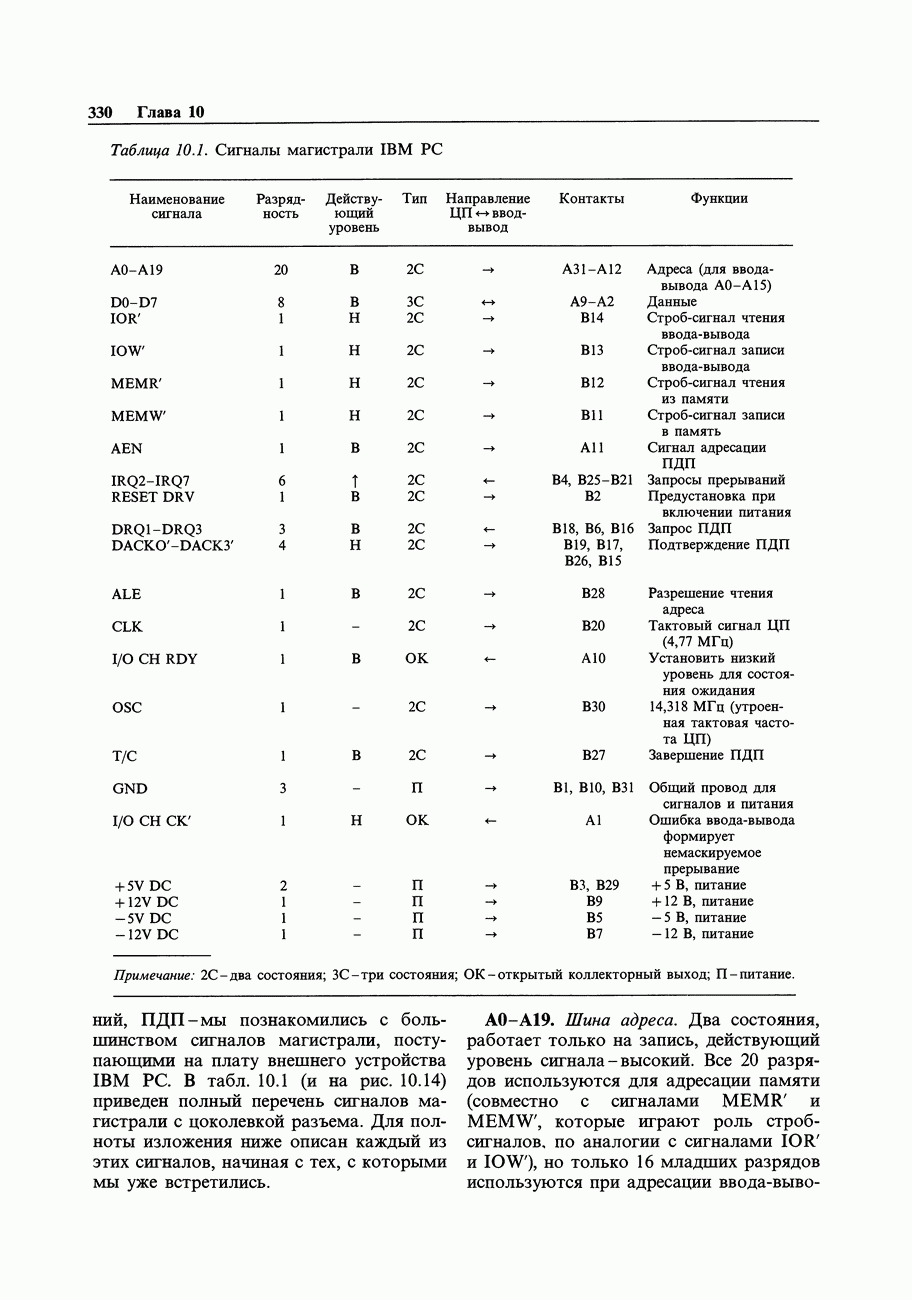
- 10.13. Сводный перечень сигналов магистрали IBM PC
- 10.14. Синхронный и асинхронный протоколы магистрали
- 10.15. Магистрали других микрокомпьютеров
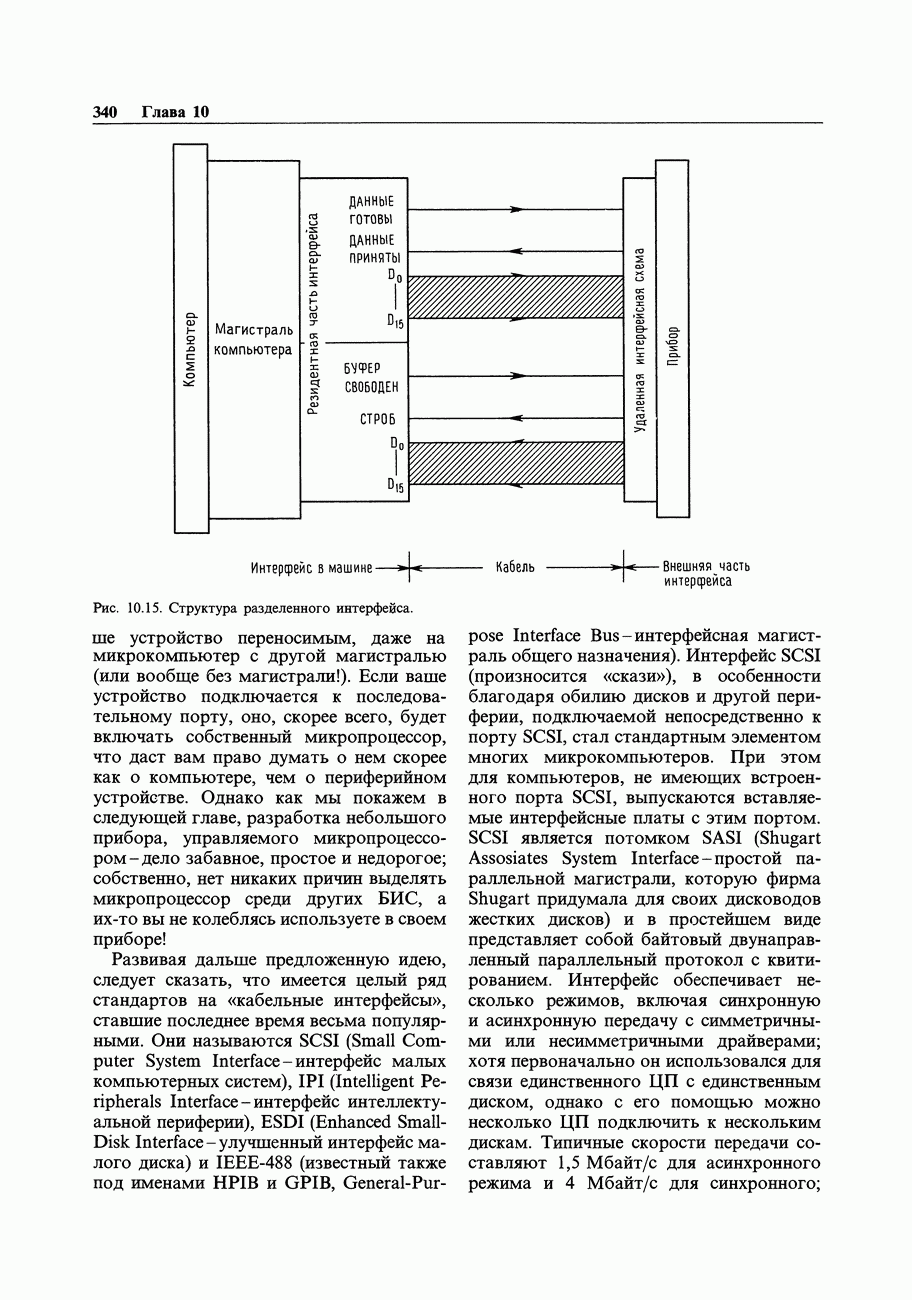
- 10.16. Подключение к компьютеру периферийных устройств
- СИСТЕМНЫЕ КОНЦЕПЦИИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- 10.17. Программирование
- 10.18. Операционные системы, файлы и использование памяти
- ПРИНЦИПЫ ПЕРЕДАЧИ ДАННЫХ
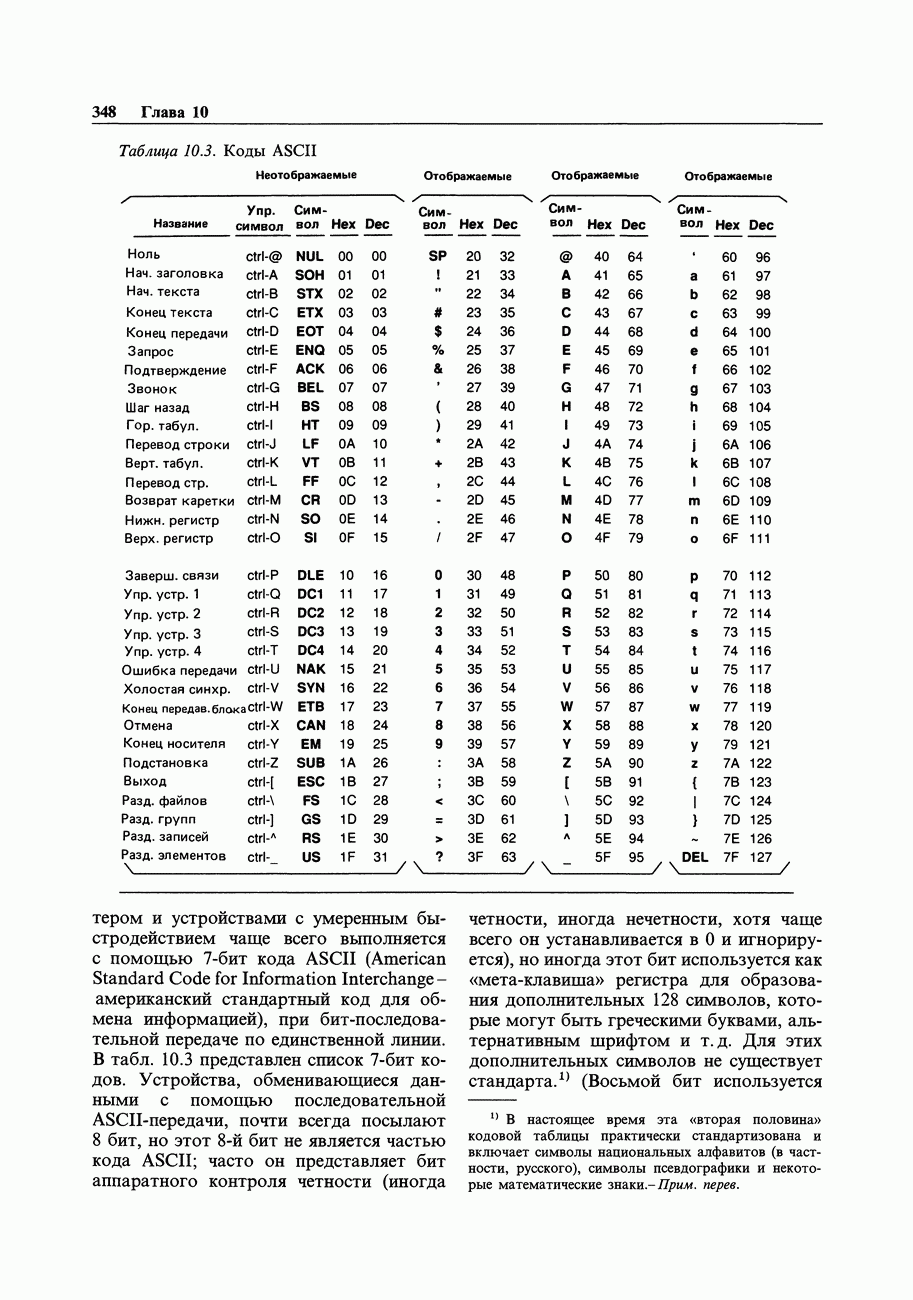
- 10.19. Последовательная связь и коды ASCII
- 10.20. Параллельная связь
- 10.21. Локальные вычислительные цепи
- 10.22. Пример интерфейса: аппаратная упаковка данных
- 10.23. Форматы чисел