| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.04. Вентили и таблицы истинности
Комбинационная и последовательная (последовательностная) логика.

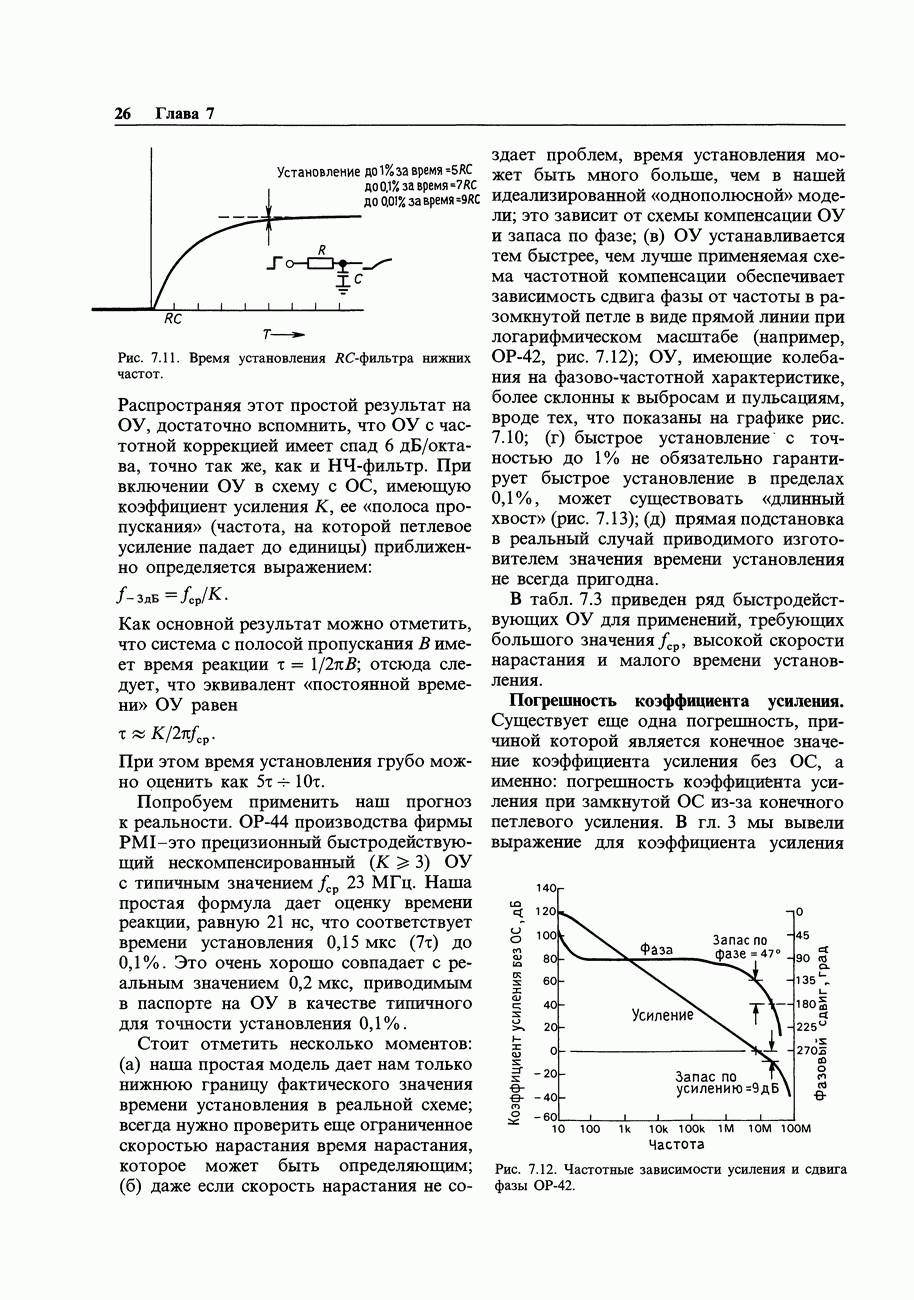
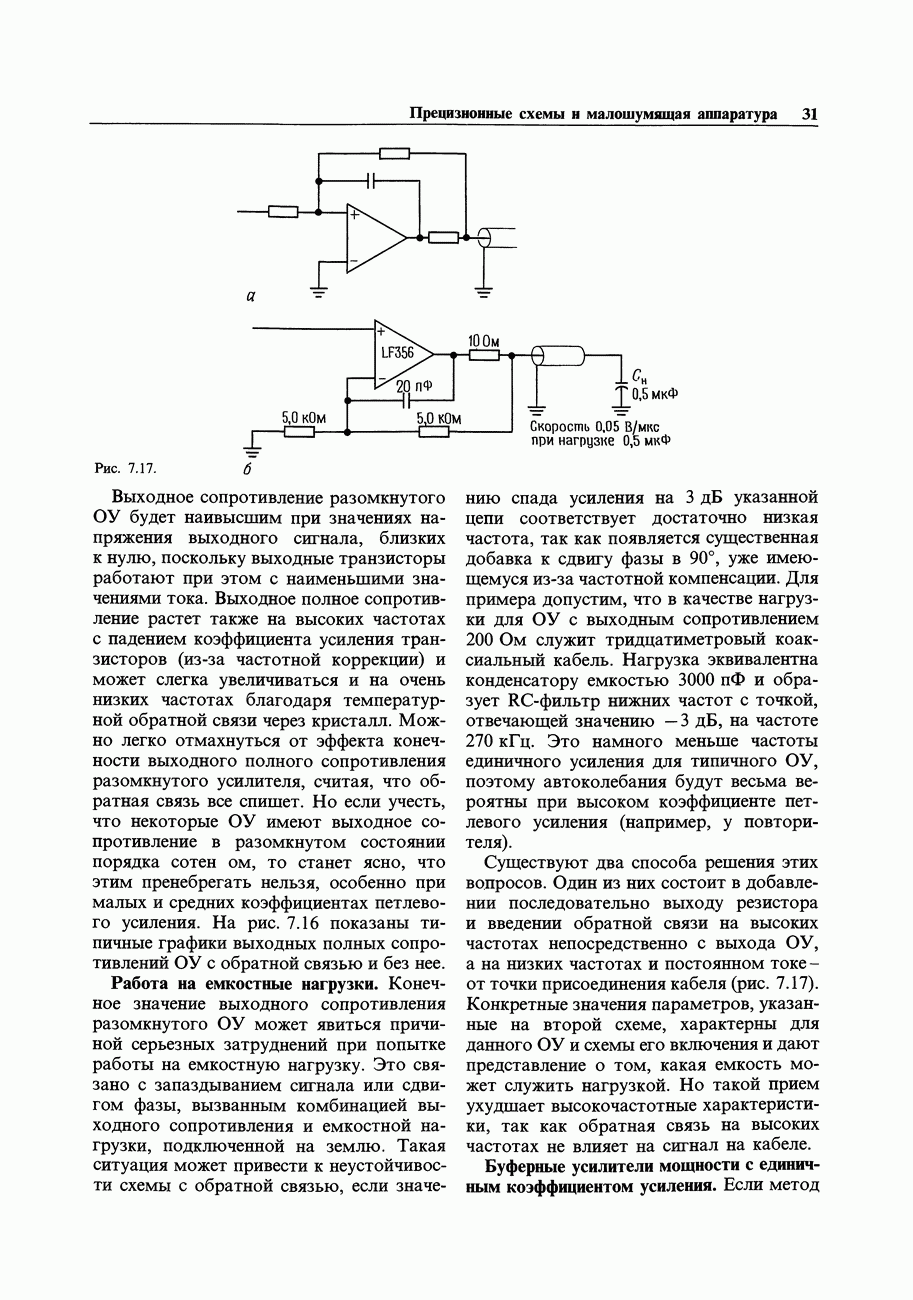
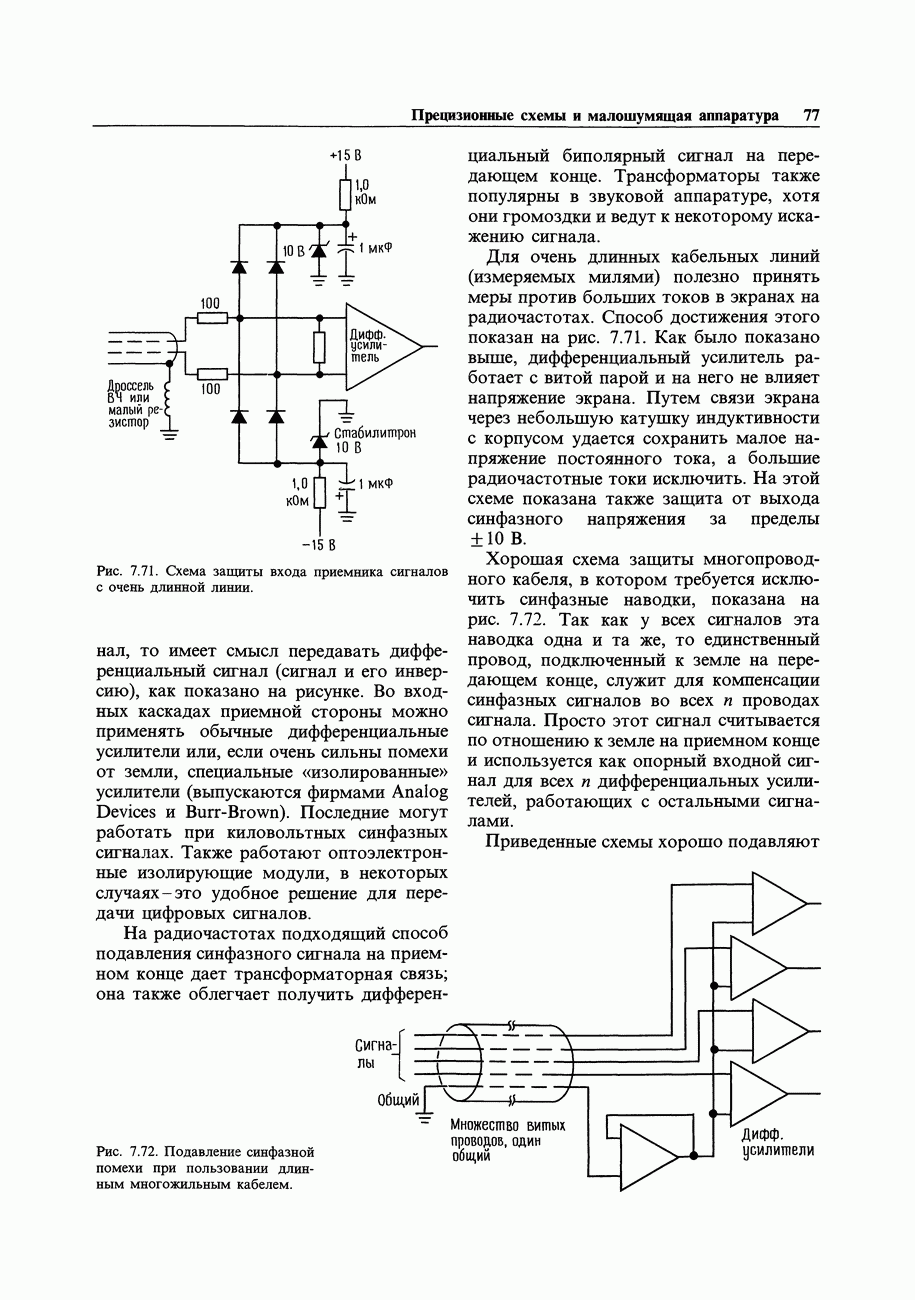
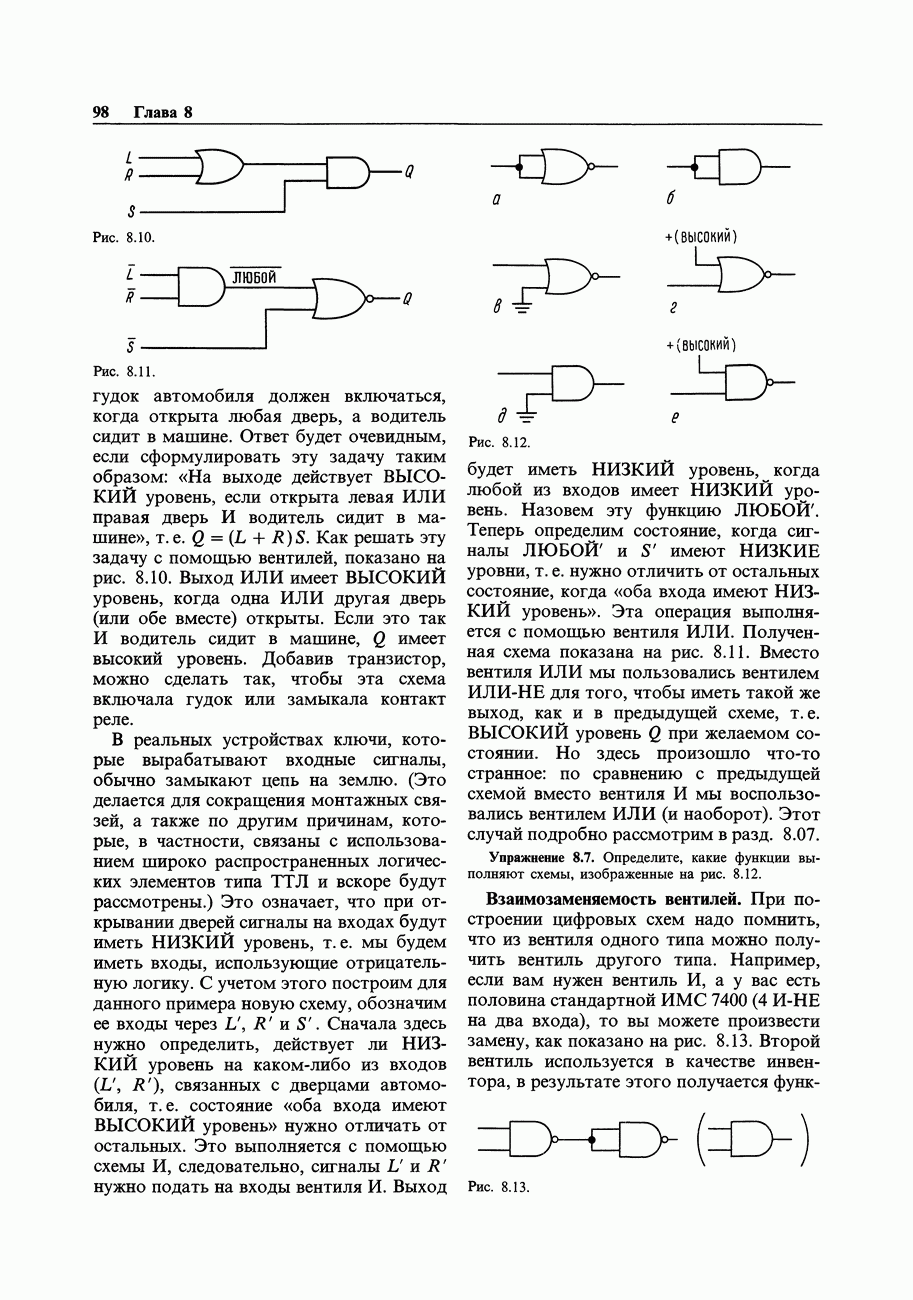
Рис. 8.2.

Рис. 8.3.
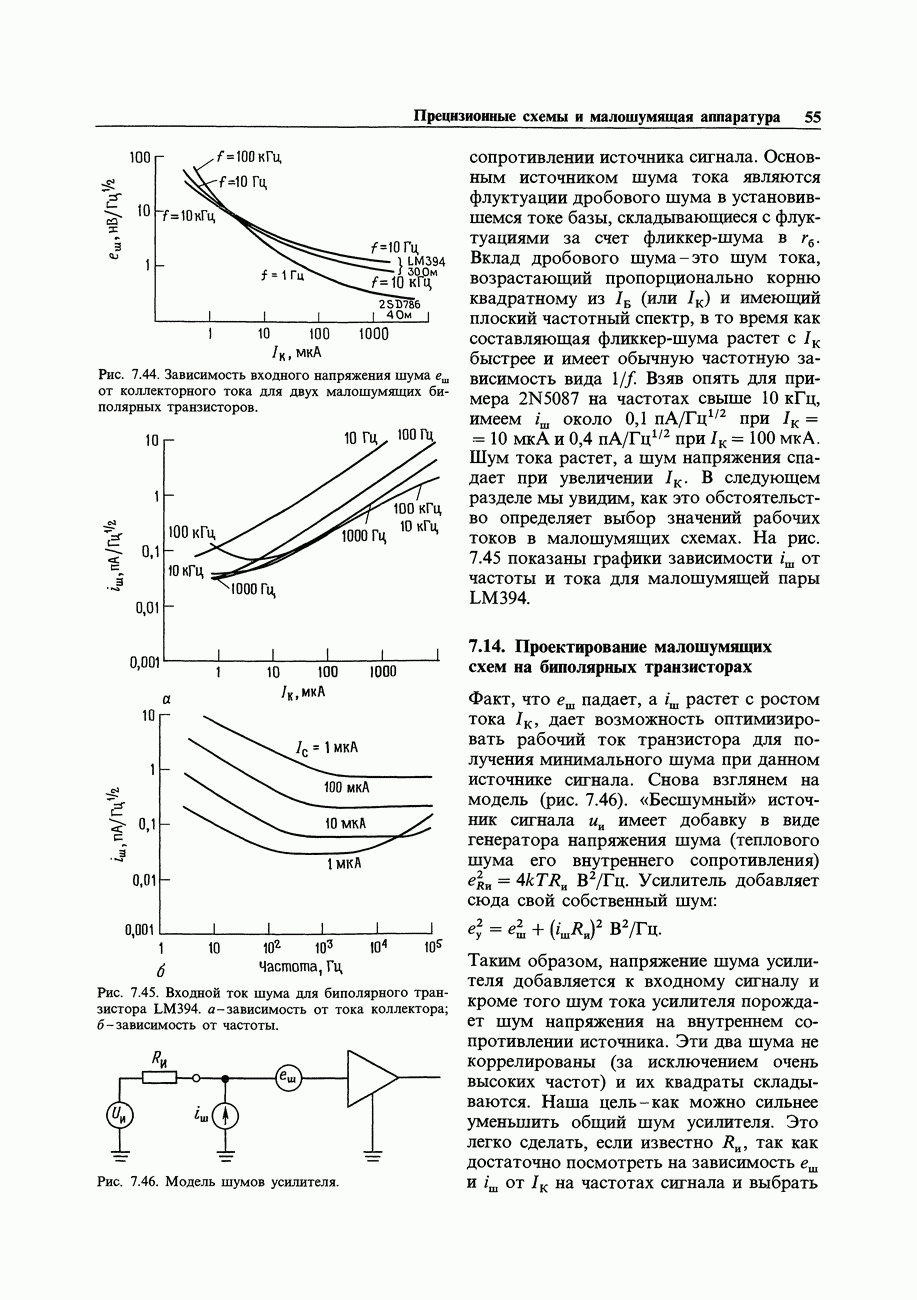
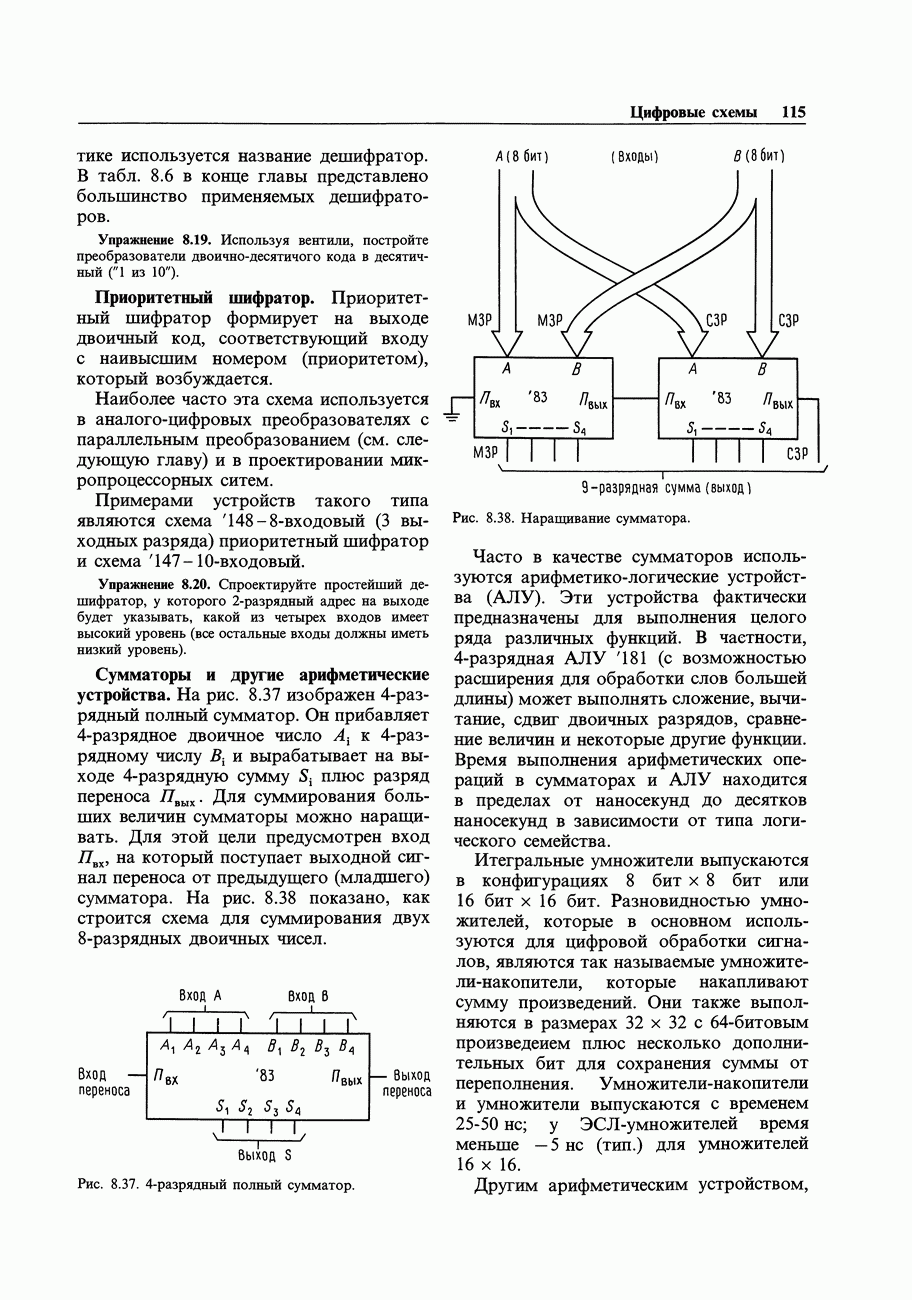
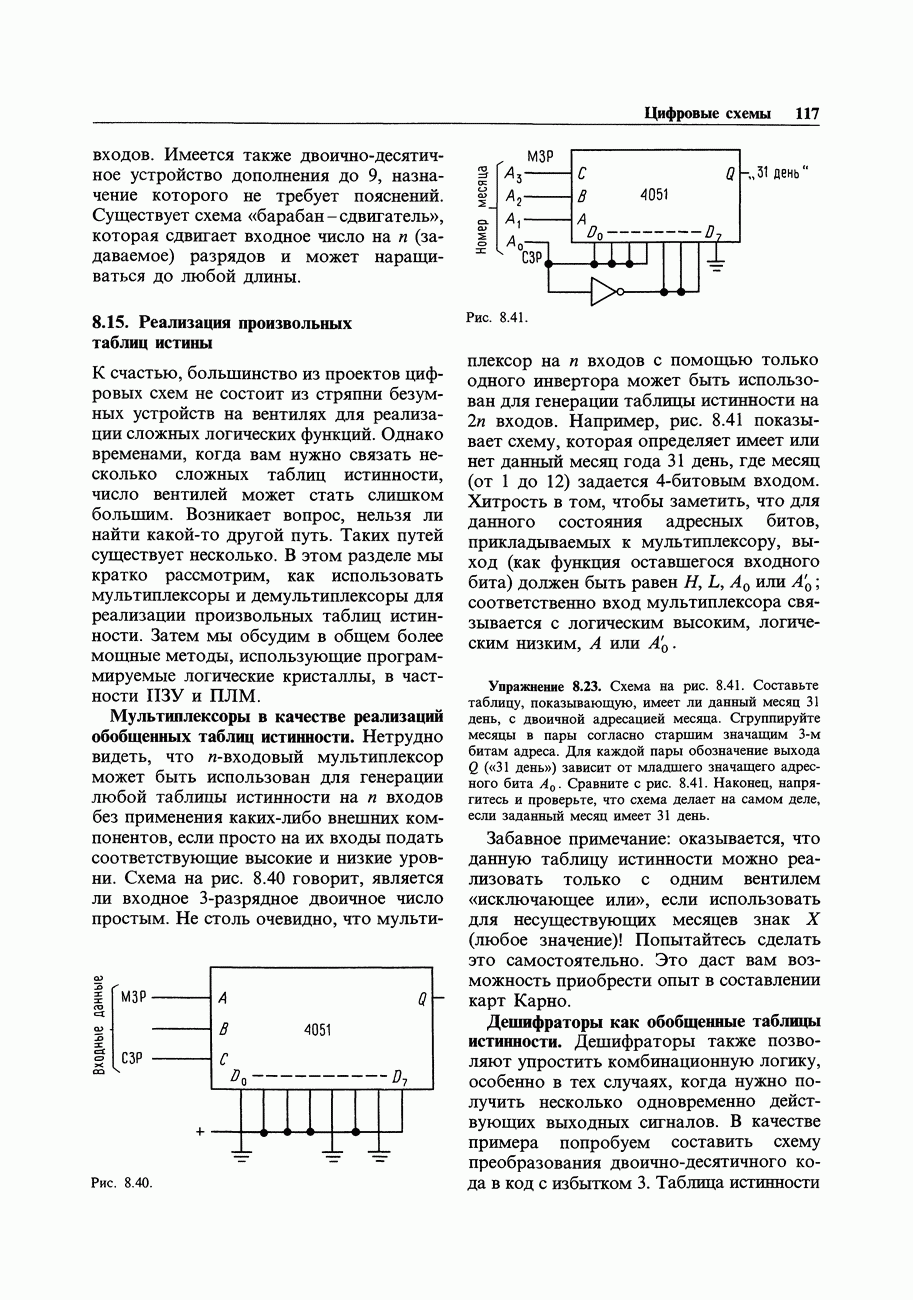
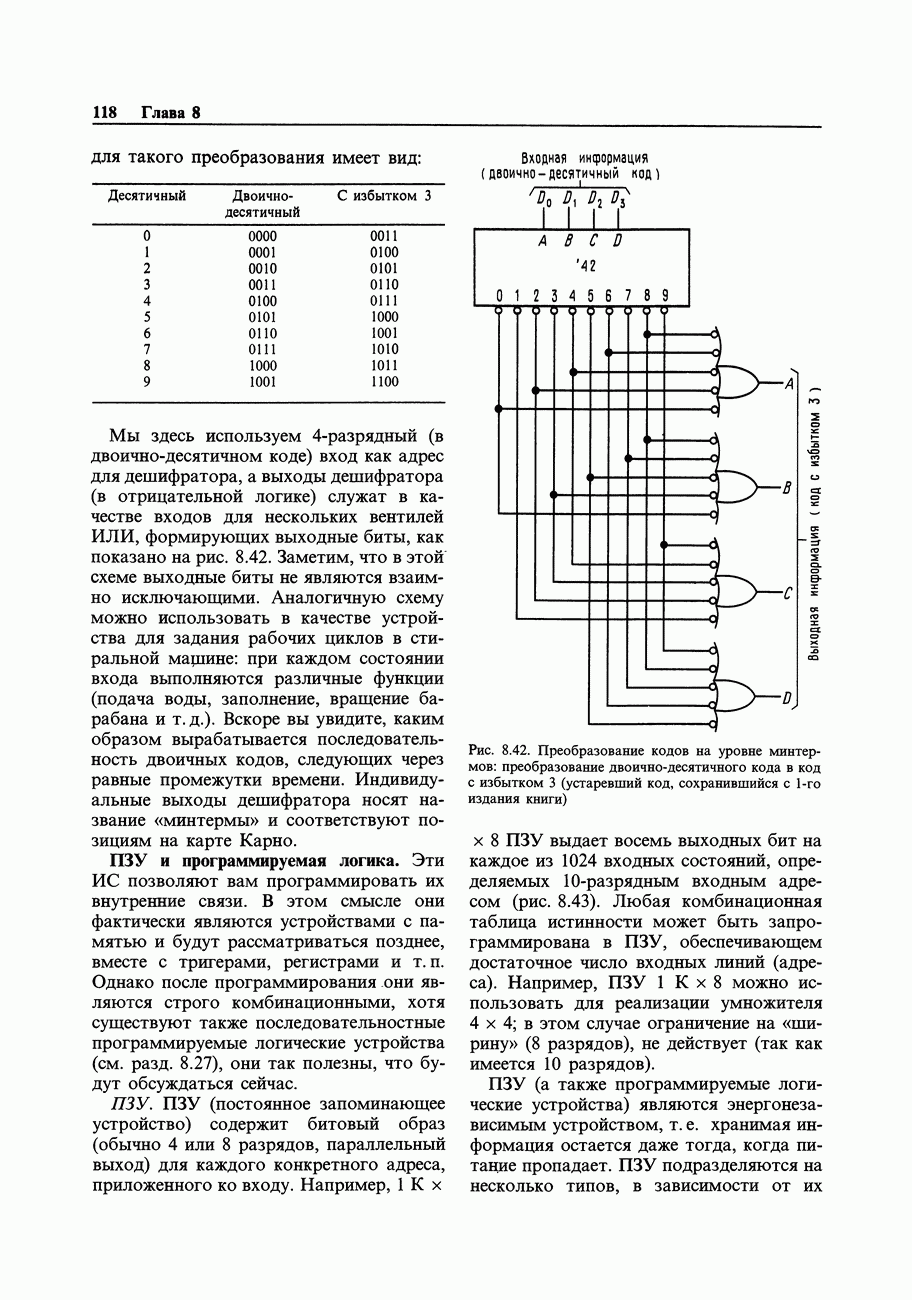
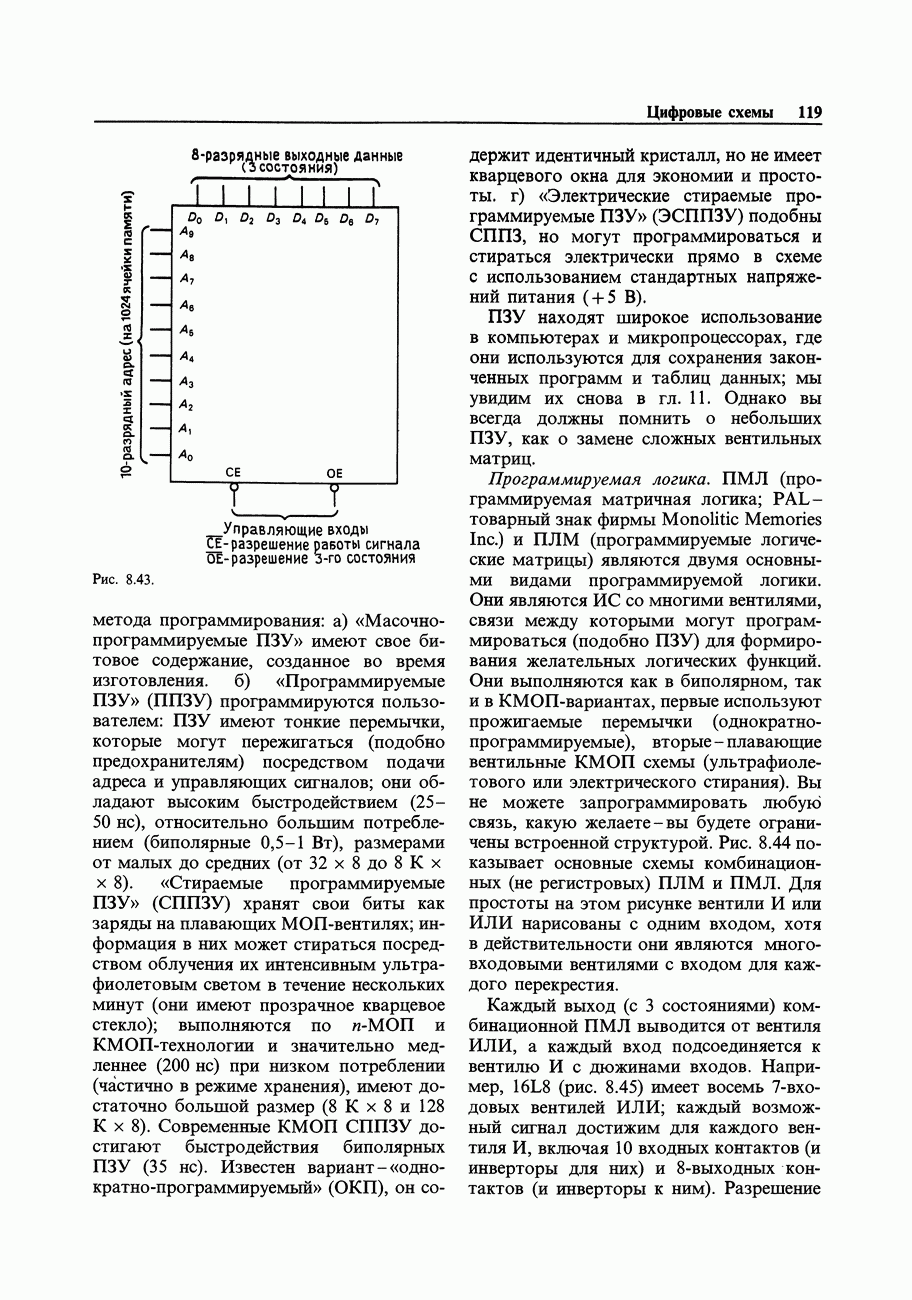
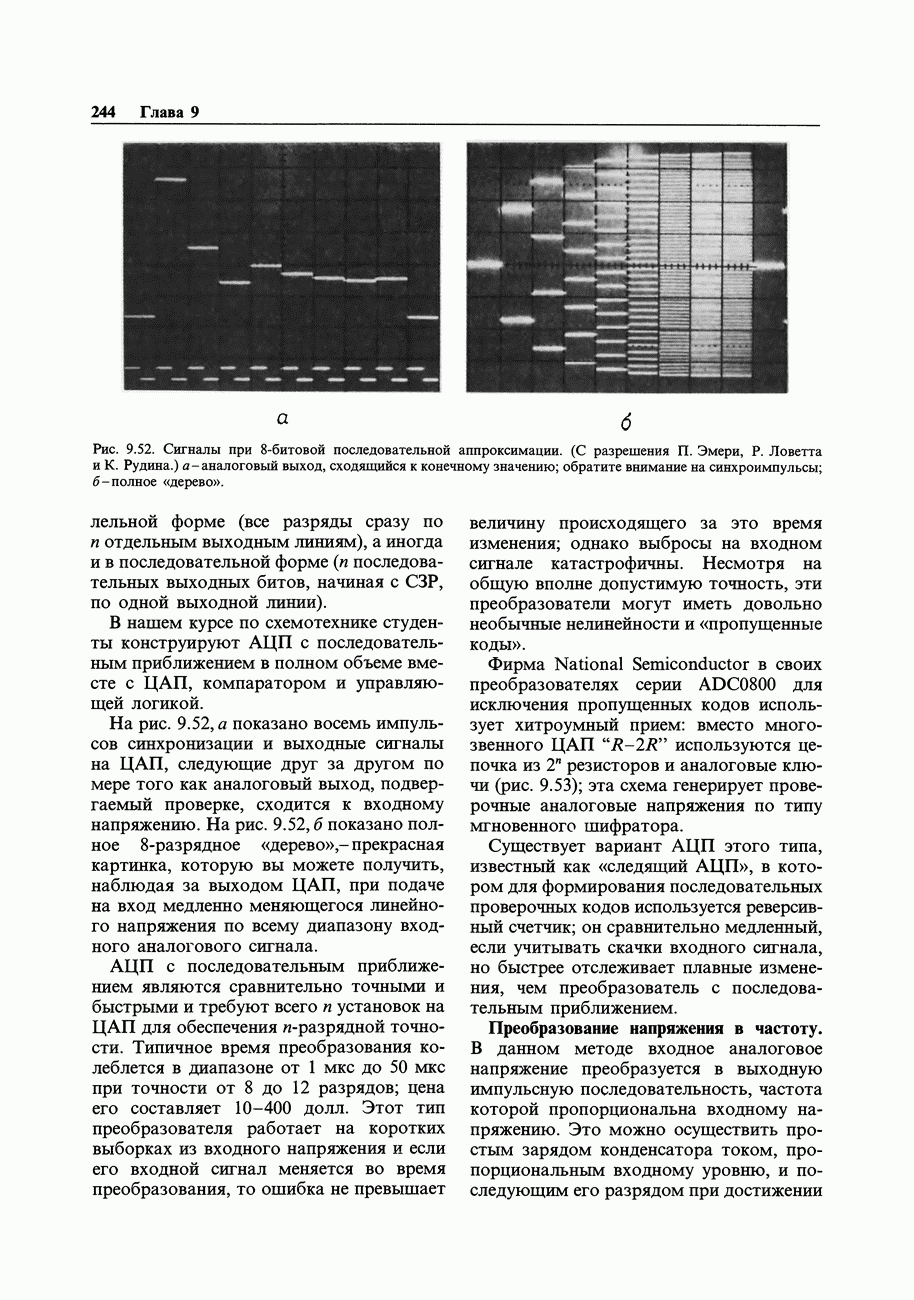
Сущность цифровой электроники - выработка выходных цифровых сигналов в соответствии с входными. Например, сумматор может принять на свои входы два 16-разрядных числа и сформировать на выходе 16-разрядную сумму (плюс перенос). Можно сделать также схему для умножения двух чисел. Такого типа операции должен уметь выполнять процессор ЭВМ. Другая задача - сравнение двух чисел с целью удостовериться в том, что «все системы действуют нормально». Возможно, вы захотите дополнить паритетным битом число, подлежащее передаче по каналу связи, так, чтобы общее количество «единиц» в нем стало четным: проверка паритета на приемной стороне обеспечивает простой контроль правильности передачи. Еще одна типичная задача заключается в том, чтобы взять какие-либо числа, выраженные в двоичном коде, а затем воспроизвести их на экране, отперфорировать или отпечатать в виде десятичных знаков. Состояние выхода (или выходов) во всех этих задачах является предопределенной функцией состояния входа или входов. Задачи, относящиеся к этому классу, называются «комбинационными» и могут быть решены с помощью вентилей - устройств, которые выполняют операции булевой алгебры в системах с двумя состояниями (двоичных).
Существует другой класс задач, которые нельзя решить лишь путем формирования комбинационных функций текущих значений входных сигналов и которые требуют знания их прежнего состояния. Для решения этих задач необходимо применять «последовательные» схемы. К задачам такого типа относится преобразование строки двоичных разрядов из последовательной формы (один разряд следует за другим во времени) в параллельную группу разрядов, подсчет числа единиц, распознавание заданной определенной кодовой комбинации и последовательности битов, или, например, формирование одного выходного импульса после поступления четырех входных. Для решения всех этих задач требуется в какой-либо форме цифровая память. Основным устройством для построения этой памяти служит триггер (или мультивибратор с двумя устойчивыми состояниями). Рассмотрим вначале вентили и комбинационную логику, так как они являются основой для построения любых цифровых схем. При переходе к последовательным логическим устройствам мир цифровой техники станет значительно более интересным, однако и вентили сами по себе также весьма любопытны.
Вентиль ИЛИ.
Выход вентиля ИЛИ имеет ВЫСОКИЙ уровень, если хотя бы на одном из его входов присутствует ВЫСОКИЙ уровень. Это можно выразить с помощью «таблицы истинности», представленной на рис. 8.2, где показан вентиль ИЛИ на 2 входа. В общем случае число входов не ограничено, однако в стандартном корпусе микросхемы обычно размещаются четыре -входовых вентиля, три
-входовых вентиля, три  -входовых или два
-входовых или два  -входовых. Например, на выходе
-входовых. Например, на выходе  -входового вентиля ИЛИ ВЫСОКИЙ уровень будет присутствовать в том случае, если он подан на любой из его входов. Для обозначения операции ИЛИ в булевой алгебре используется символ +. Функция «А ИЛИ В» записывается как А+В.
-входового вентиля ИЛИ ВЫСОКИЙ уровень будет присутствовать в том случае, если он подан на любой из его входов. Для обозначения операции ИЛИ в булевой алгебре используется символ +. Функция «А ИЛИ В» записывается как А+В.
Вентиль И.
Выход вентиля И имеет высокий уровень только в том случае, если ВЫСОКИЙ уровень присутствует на обоих его входах. Символическое изображение вентиля и его таблица истинности даны на рис. 8.3. Вентили И, выпускаемые промышленностью также как и вентили ИЛИ, могуть иметь 3, 4, а иногда и большее число входов.
Рис. 8.4.

Рис. 8.5.
Например,  -входовой вентиль И вырабатывает на выходе ВЫСОКИЙ уровень только в том случае, если на всех его входах действует ВЫСОКИЙ уровень.
-входовой вентиль И вырабатывает на выходе ВЫСОКИЙ уровень только в том случае, если на всех его входах действует ВЫСОКИЙ уровень.
Для обозначения операции И в булевой алгебре используется точка  , которая может быть опущена, функция «А и В» записывается как А В, или просто АВ.
, которая может быть опущена, функция «А и В» записывается как А В, или просто АВ.
Инвертор (функция НЕ).
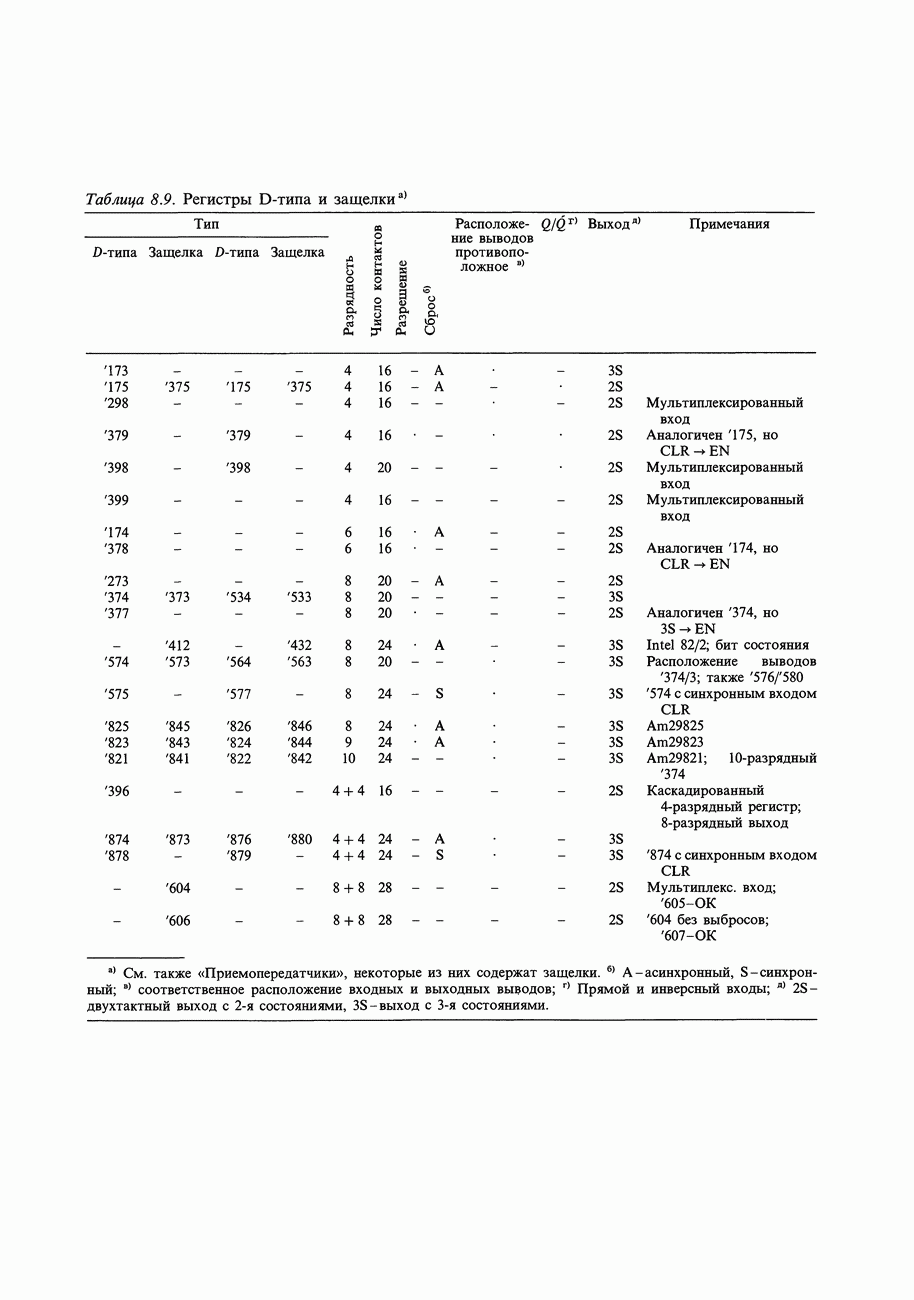
Иногда бывает нужно получить дополнение (инверсию) логического сигнала. Эту функцию выполняет инвертор - вентиль, который имеет только один вход (рис. 8.4). Для обозначения операции НЕ в булевой алгебре используется черта над символом или апостроф; «НЕ А» записывается как А или . Для удобства вместо
. Для удобства вместо  для указания отрицания часто используются символы
для указания отрицания часто используются символы  таким образом, НЕ А можно записать любым из следующих способов:
таким образом, НЕ А можно записать любым из следующих способов:  . Мы используем в этой книге запись А.
. Мы используем в этой книге запись А.
И-НЕ и ИЛИ-НЕ. Вентили могут совмещать инвертирование с выполнением функций И и ИЛИ.

Рис. 8.6.
Далее будет показано, что такие вентили имеют более широкое распространение, чем просто И и ИЛИ (рис. 8.5).

Рис. 8.7. Параллельные преобразователи двоичного, кода в код Грея  и кода Грея в двоичный (6).
и кода Грея в двоичный (6).
Исключающее ИЛИ.
Большой интерес представляет логическая функция «Исключающее ИЛИ», хотя она не относится к числу основных (рис. 8.6). На выходе вентиля «Исключающее ИЛИ» ВЫСОКИЙ уровень сформируется в том случае, если он будет подан на один из его входов (но не на оба одновременно).Другими словами, ВЫСОКИЙ уровень действует на выходе тогда, когда входы имеют различное состояние. Этот вентиль может иметь только два входа. Операция «Исключающее ИЛИ» подобна сложению двух бит по модулю 2.
Упражнение 8.5. Покажите, как вентиль «Исключающее ИЛИ» может быть использован в качестве «модифицируемого инвертора», который в зависимости от уровня на управляющем входе, может либо инвентировать входной сигнал, либо передавать его на выход без инверсии (буферировать).
Упражнение 8.6. Проверьте, действительно ли схемы, изображенные на рис. 8.7, преобразуют двоичный код в код Грея и наоборот.
| << Предыдущий параграф | Следующий параграф >> |
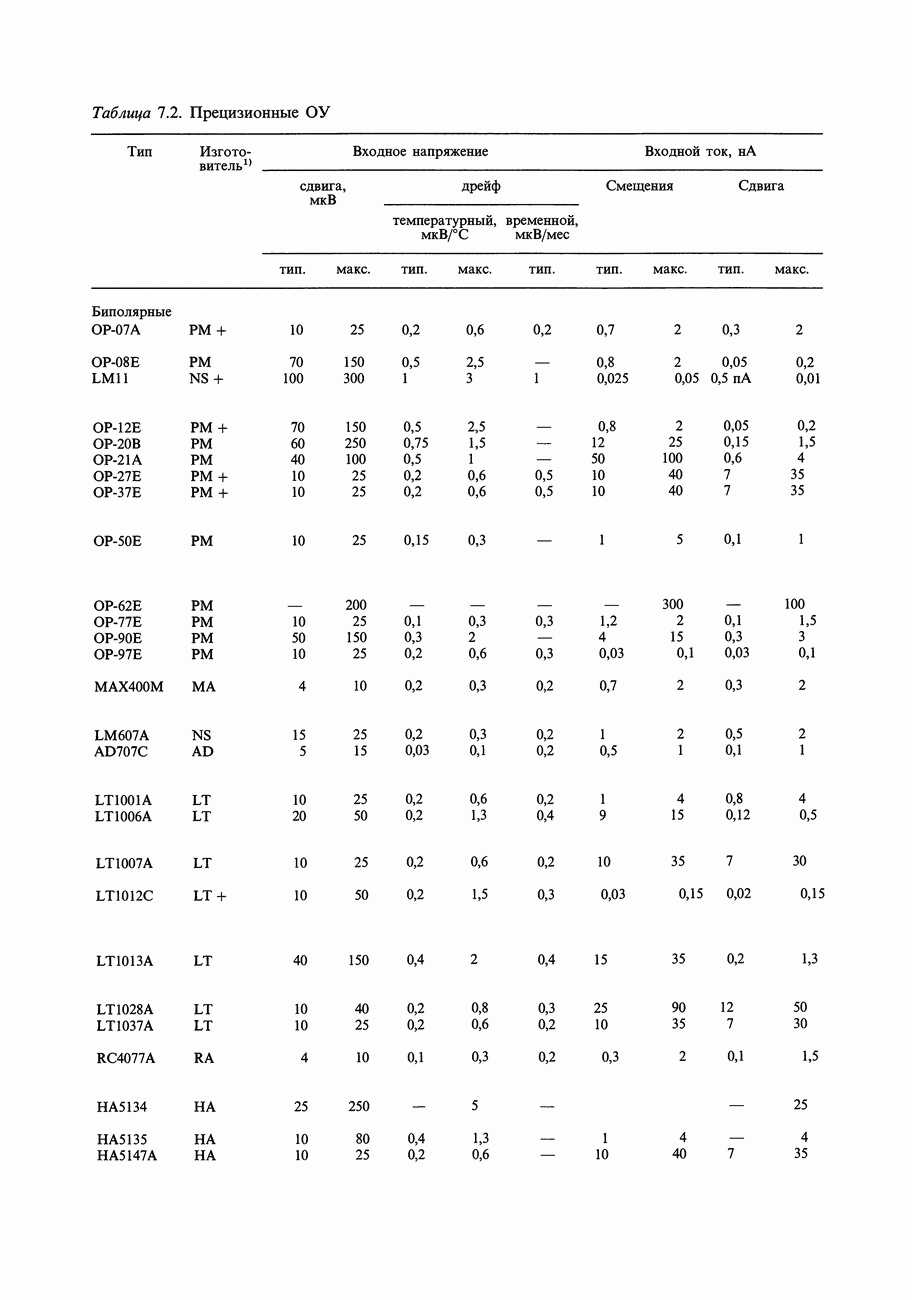
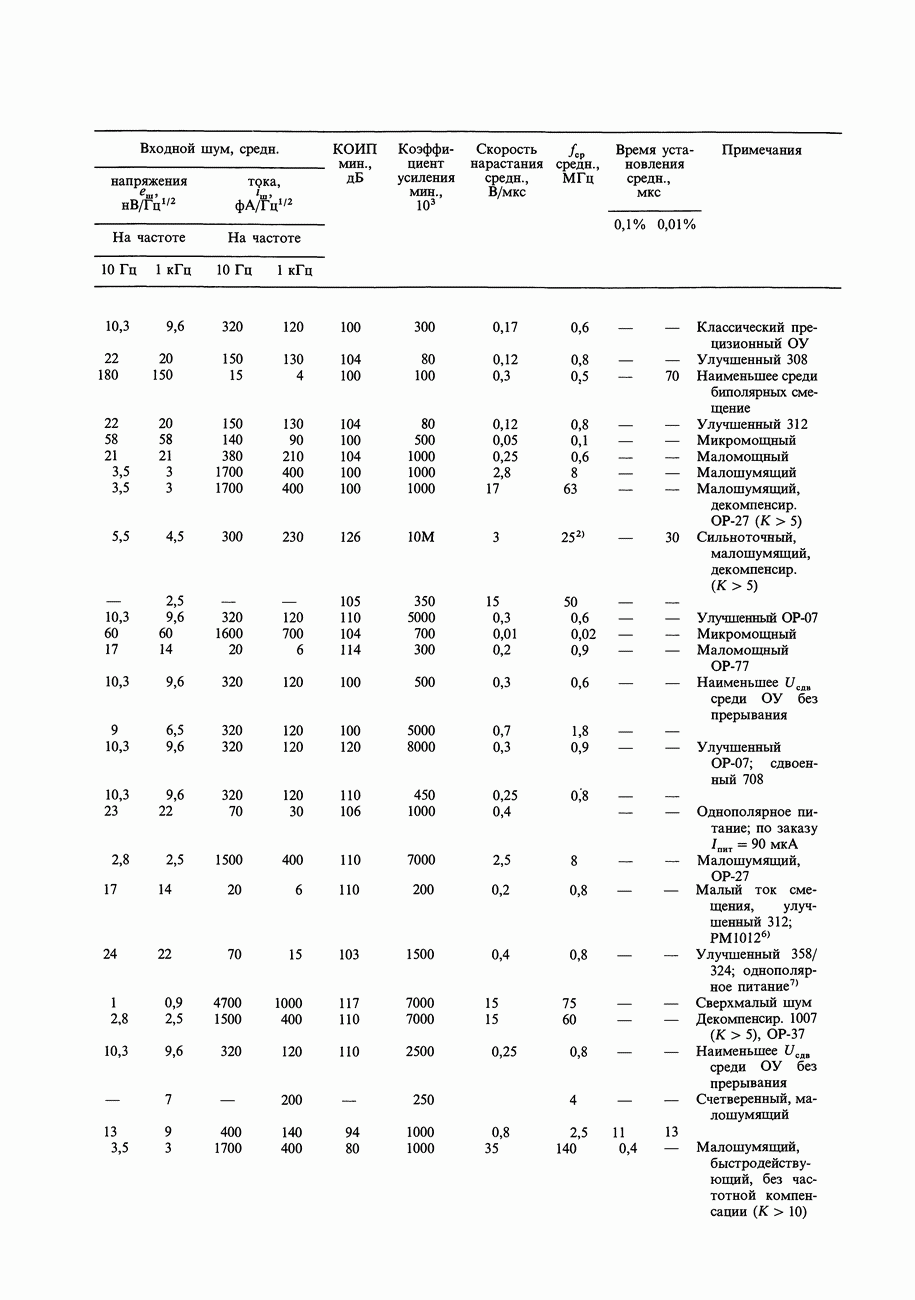
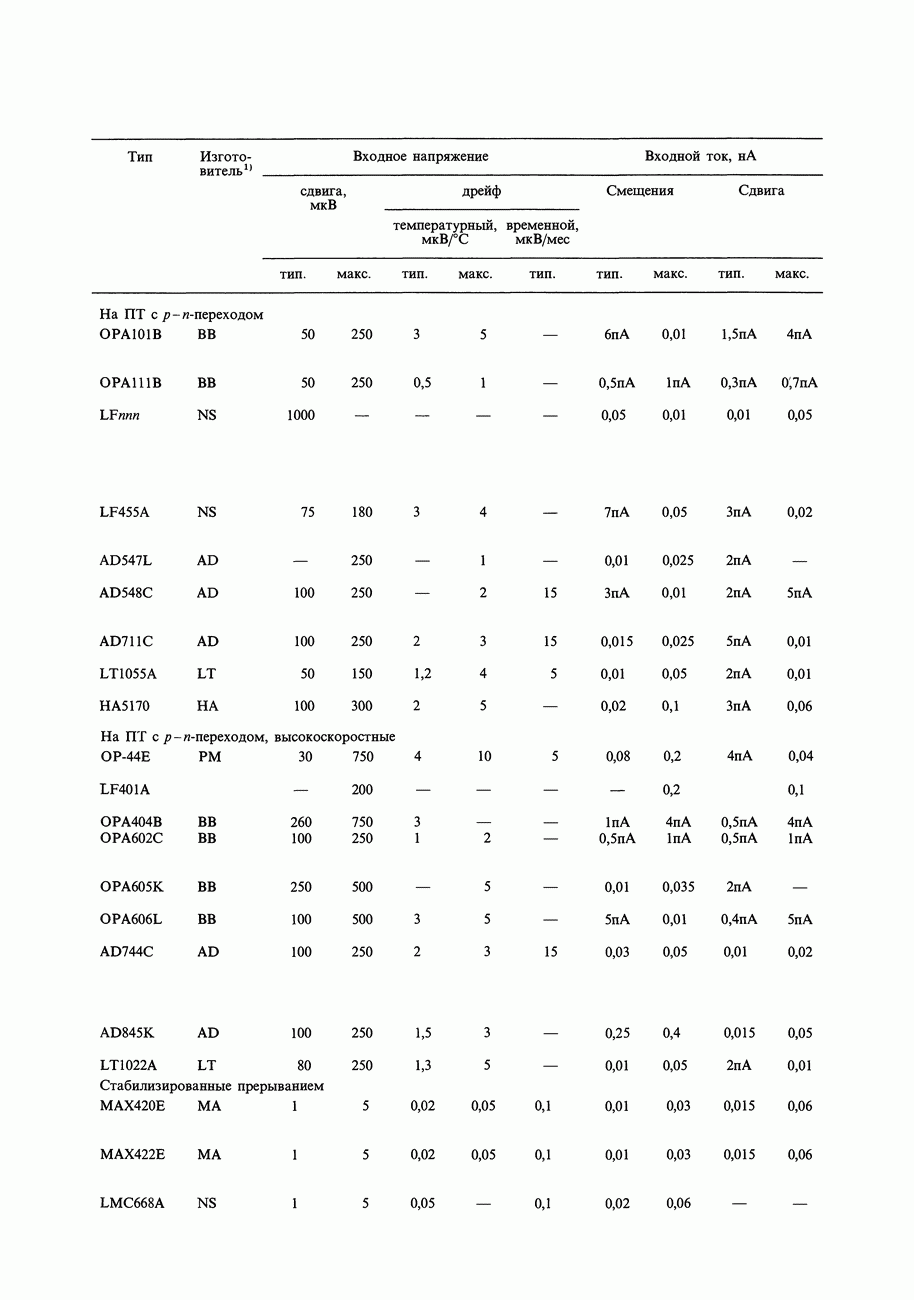
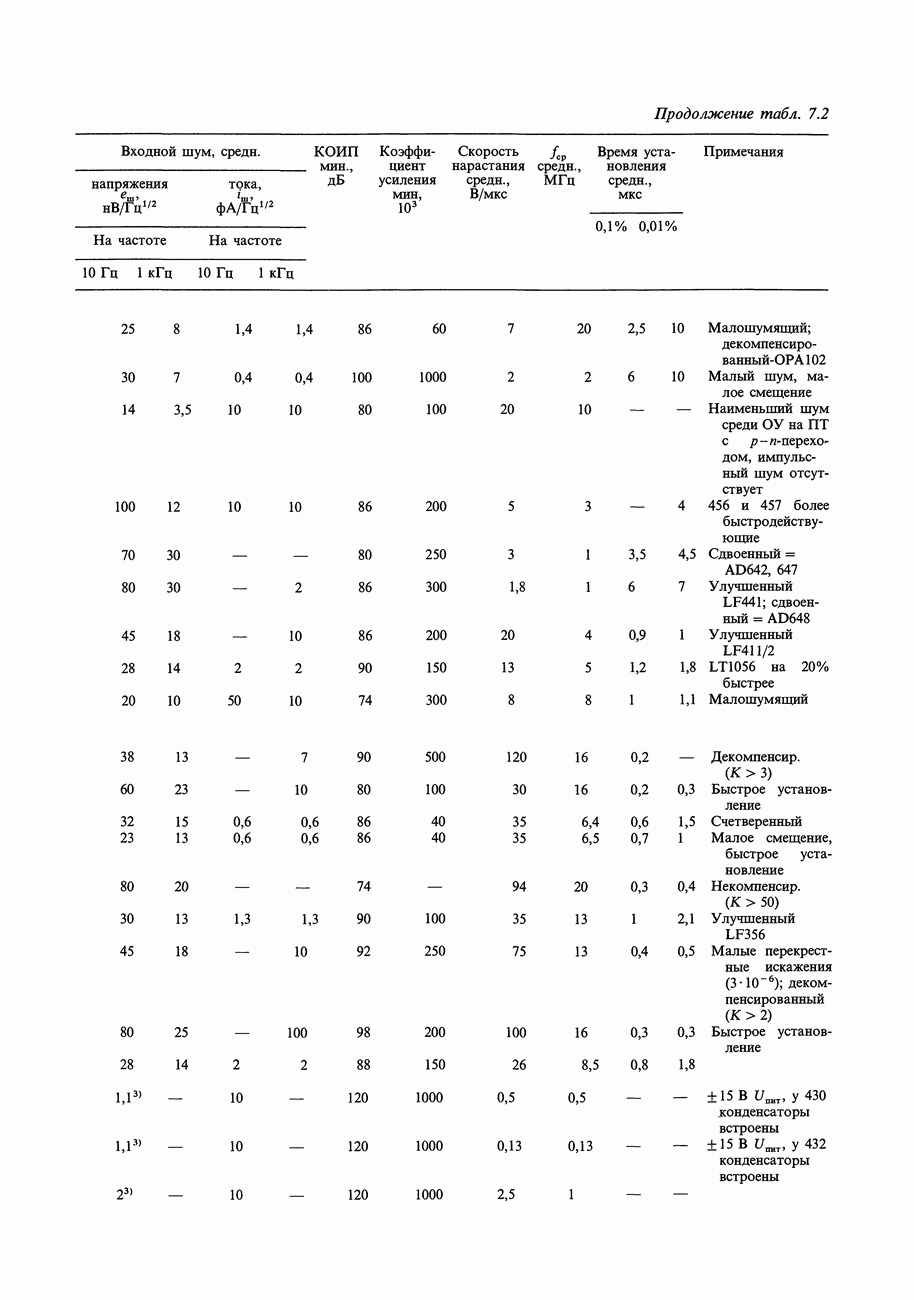
- ГЛАВА 7. ПРЕЦИЗИОННЫЕ СХЕМЫ И МАЛОШУМЯЩАЯ АППАРАТУРА
- 7.01. Соотношение точности и динамического диапазона
- 7.02. Бюджет погрешностей схемы
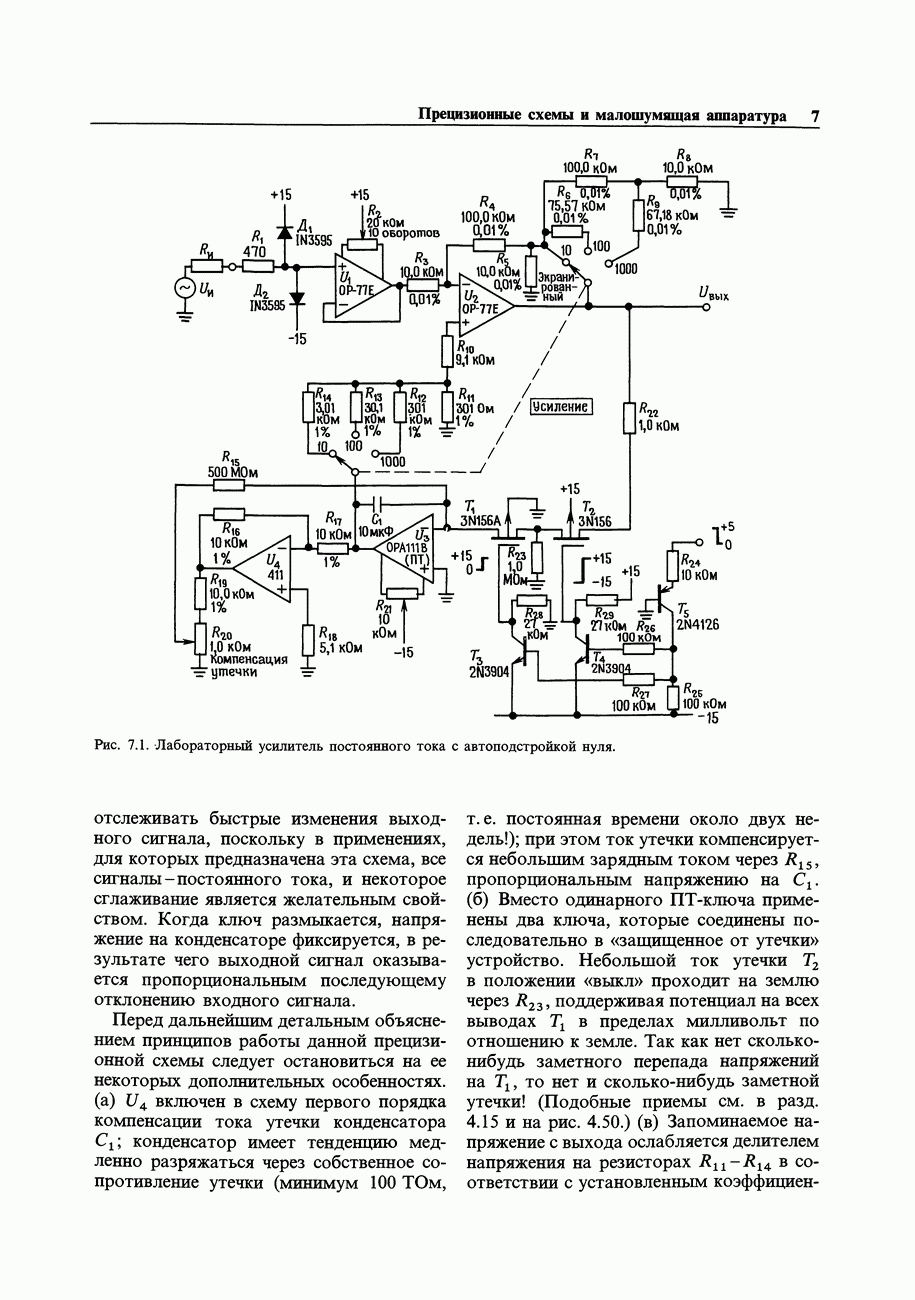
- 7.03. Пример схемы: прецизионный усилитель с автоматическим выбором нуля
- 7.04. «Бюджет погрешностей» при проектировании прецизионной схемы
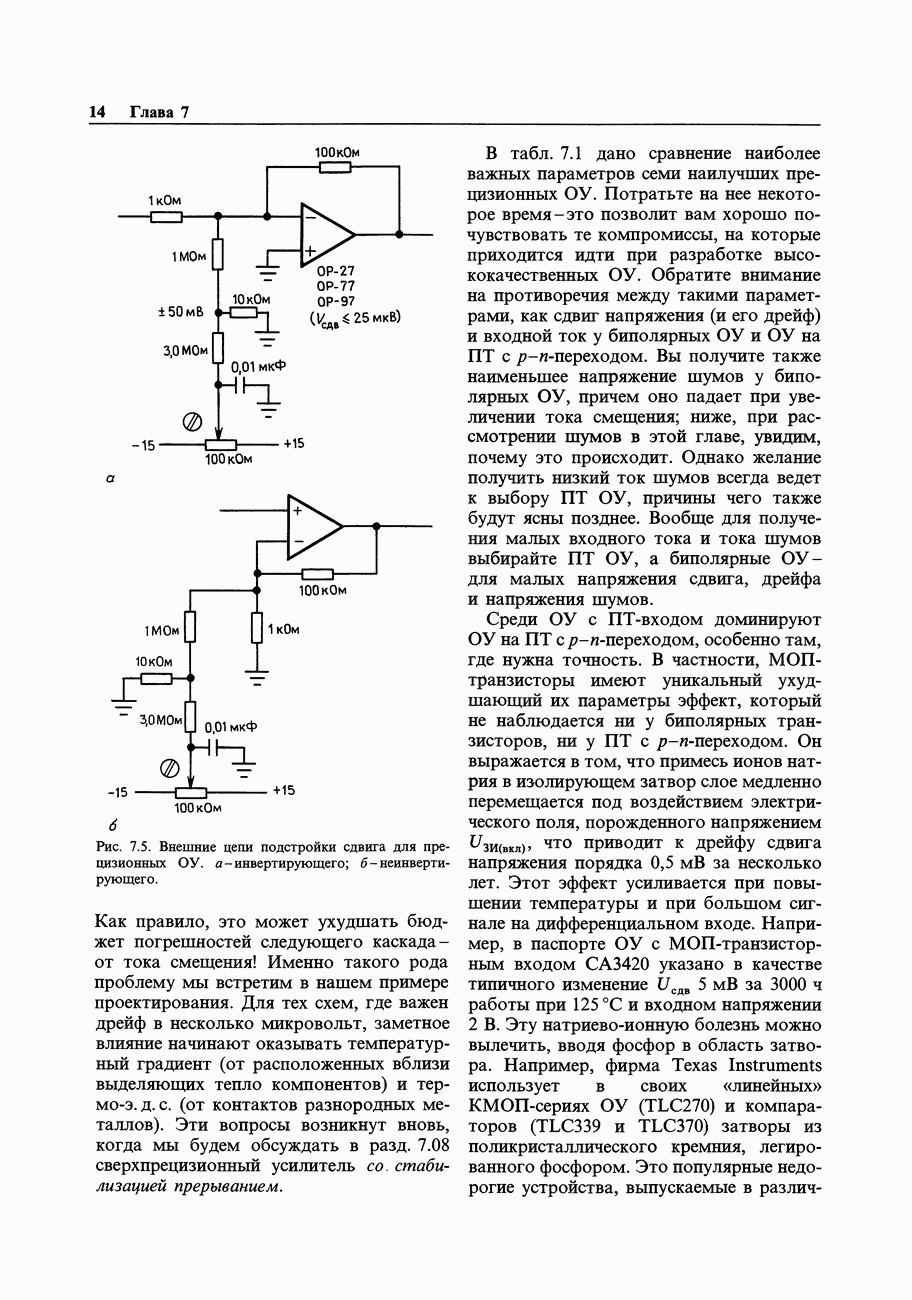
- 7.05. Погрешности внешних цепей
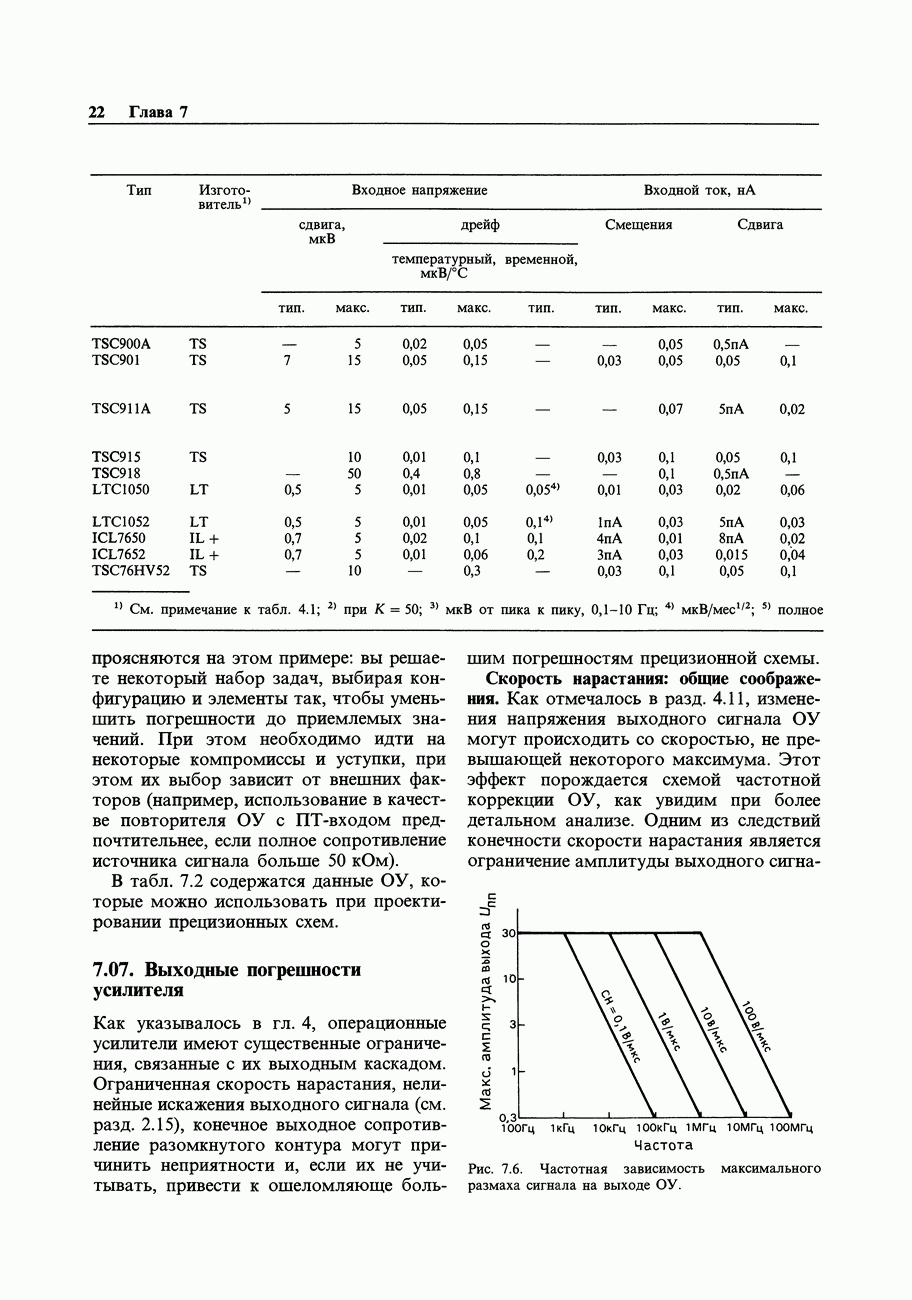
- 7.06. Входные погрешности усилителя
- 7.07. Выходные погрешности усилителя
- 7.08. Усилители с автоподстройкой нуля (стабилизированные прерыванием)
- Кое-что еще о схемах с прерыванием
- ДИФФЕРЕНЦИАЛЬНЫЕ И ИЗМЕРИТЕЛЬНЫЕ УСИЛИТЕЛИ
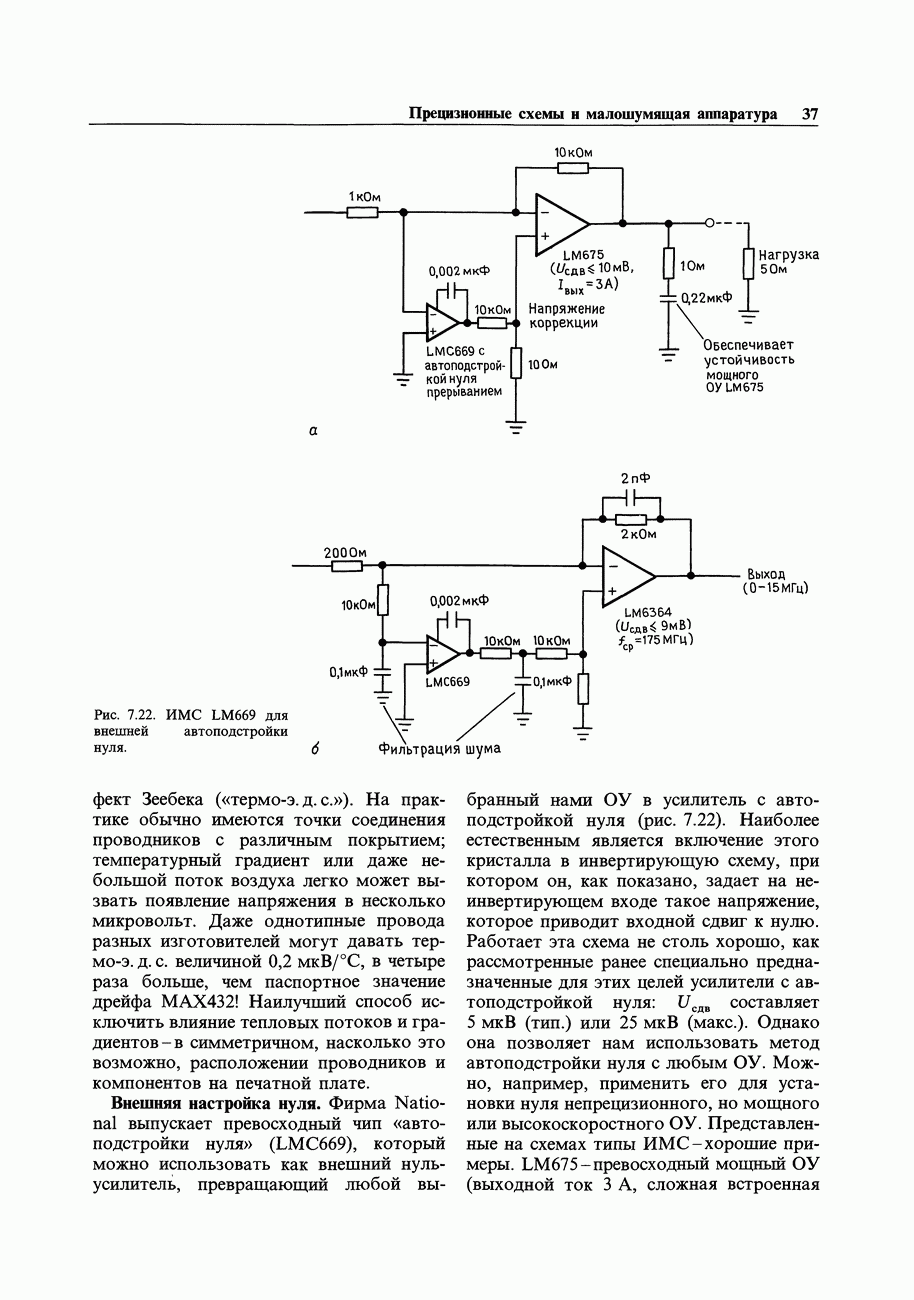
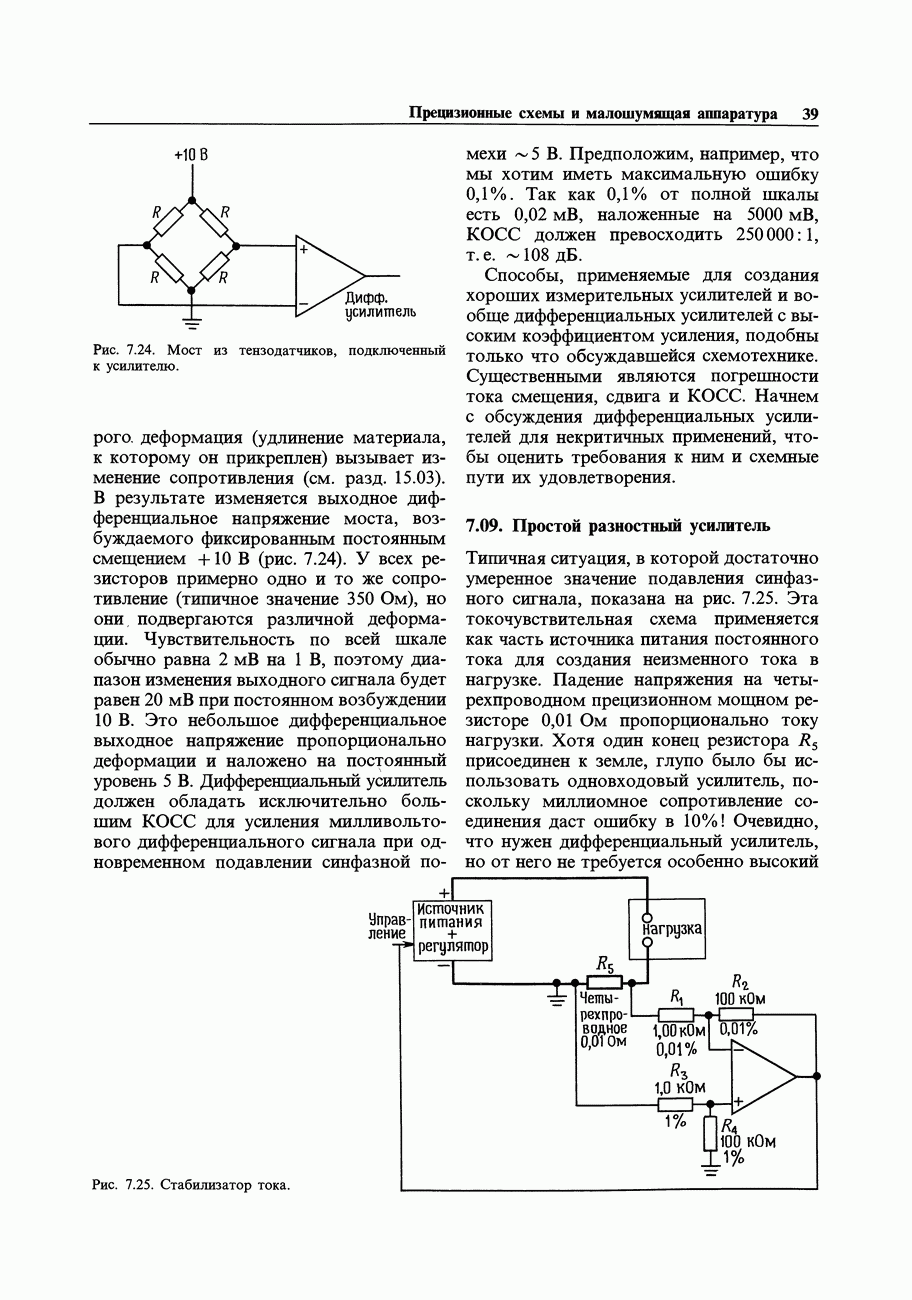
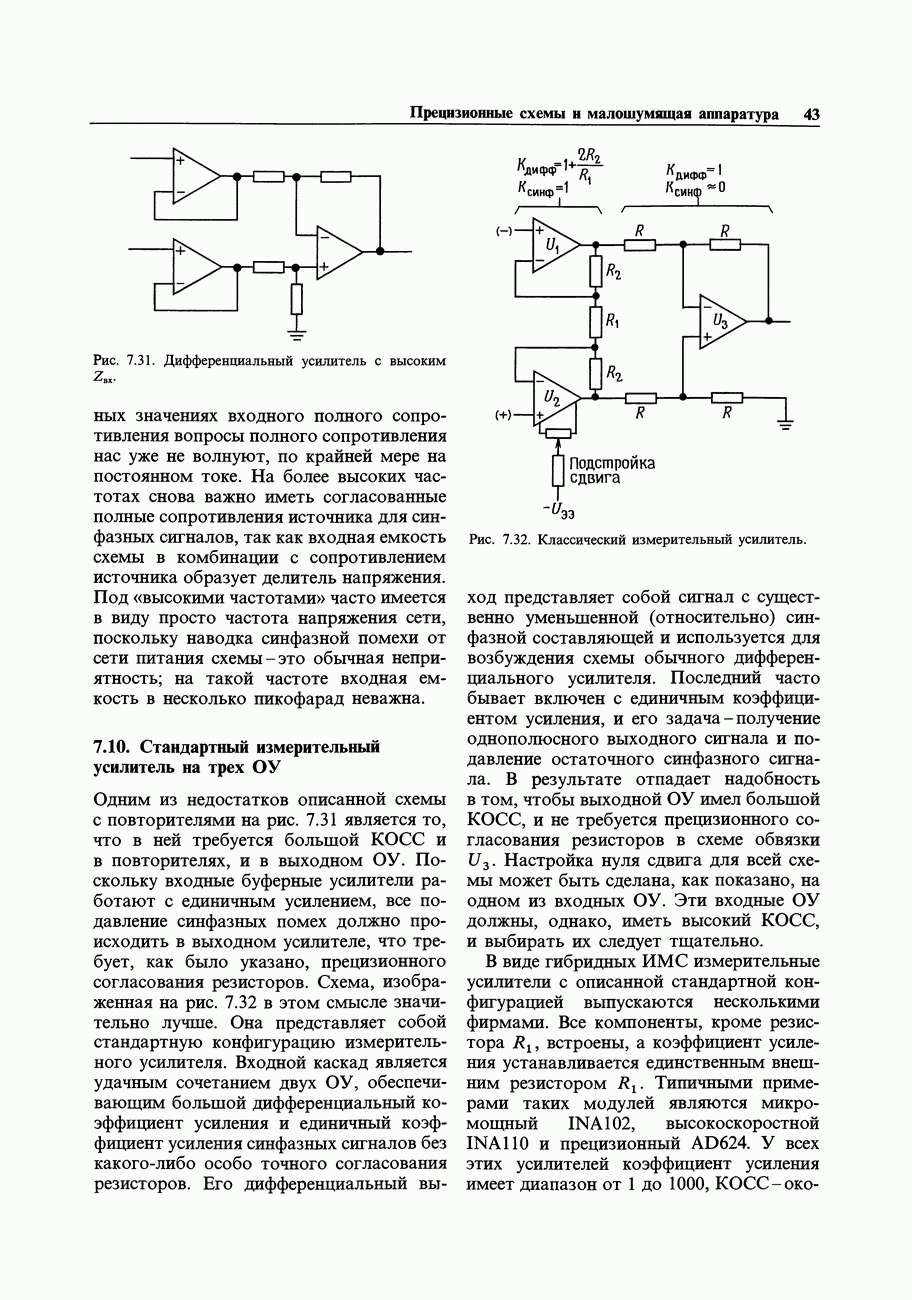
- 7.09. Простой разностный усилитель
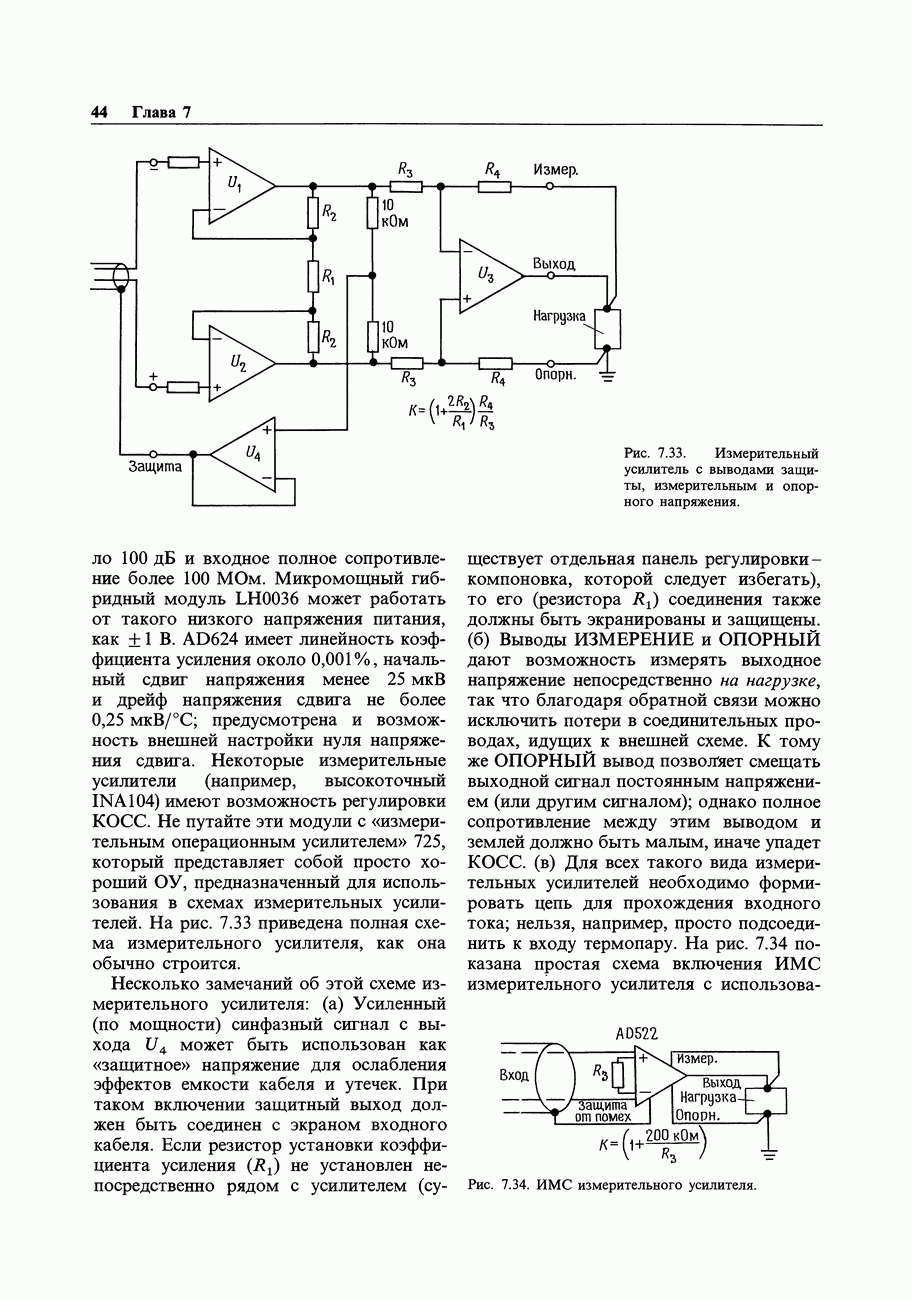
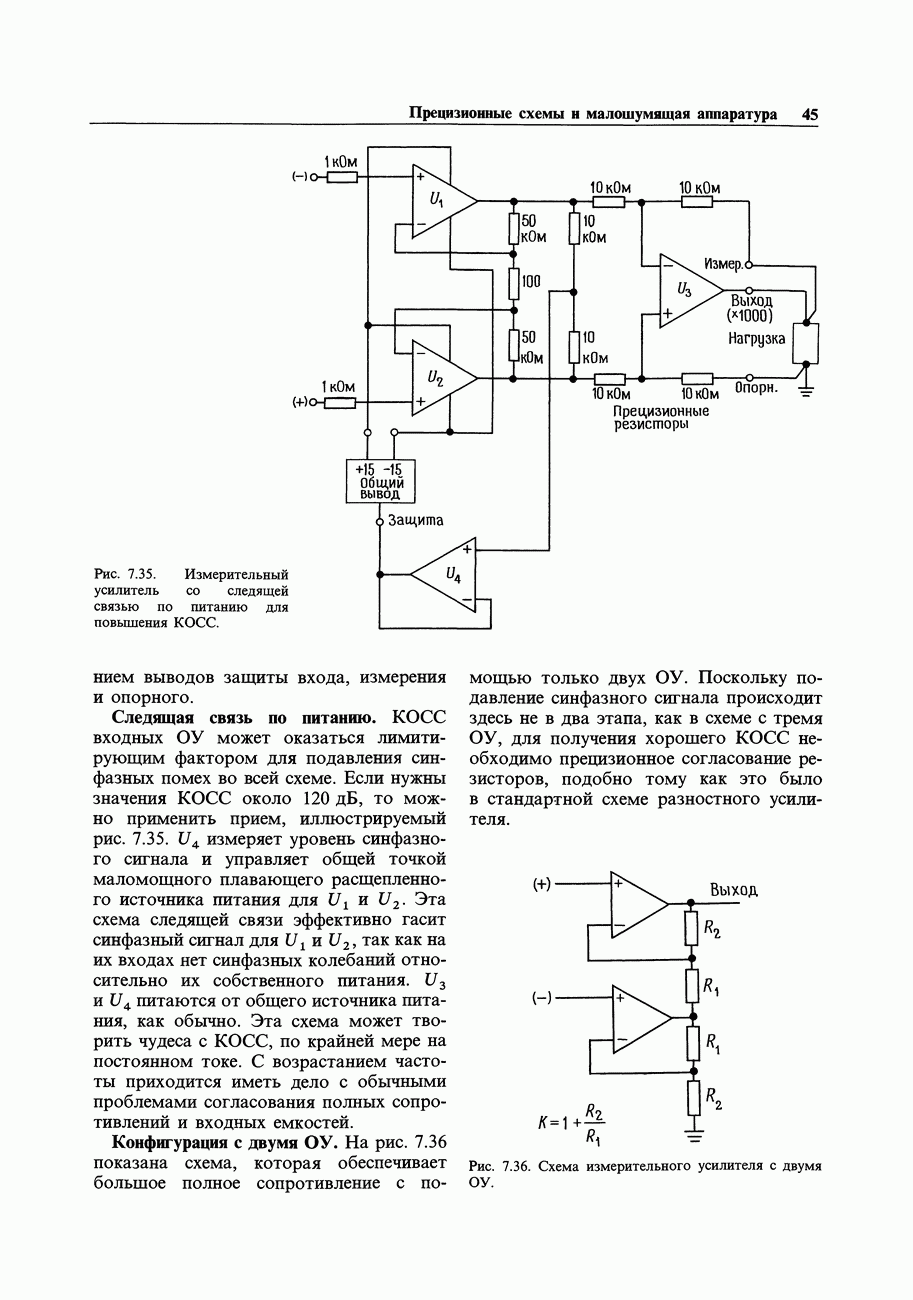
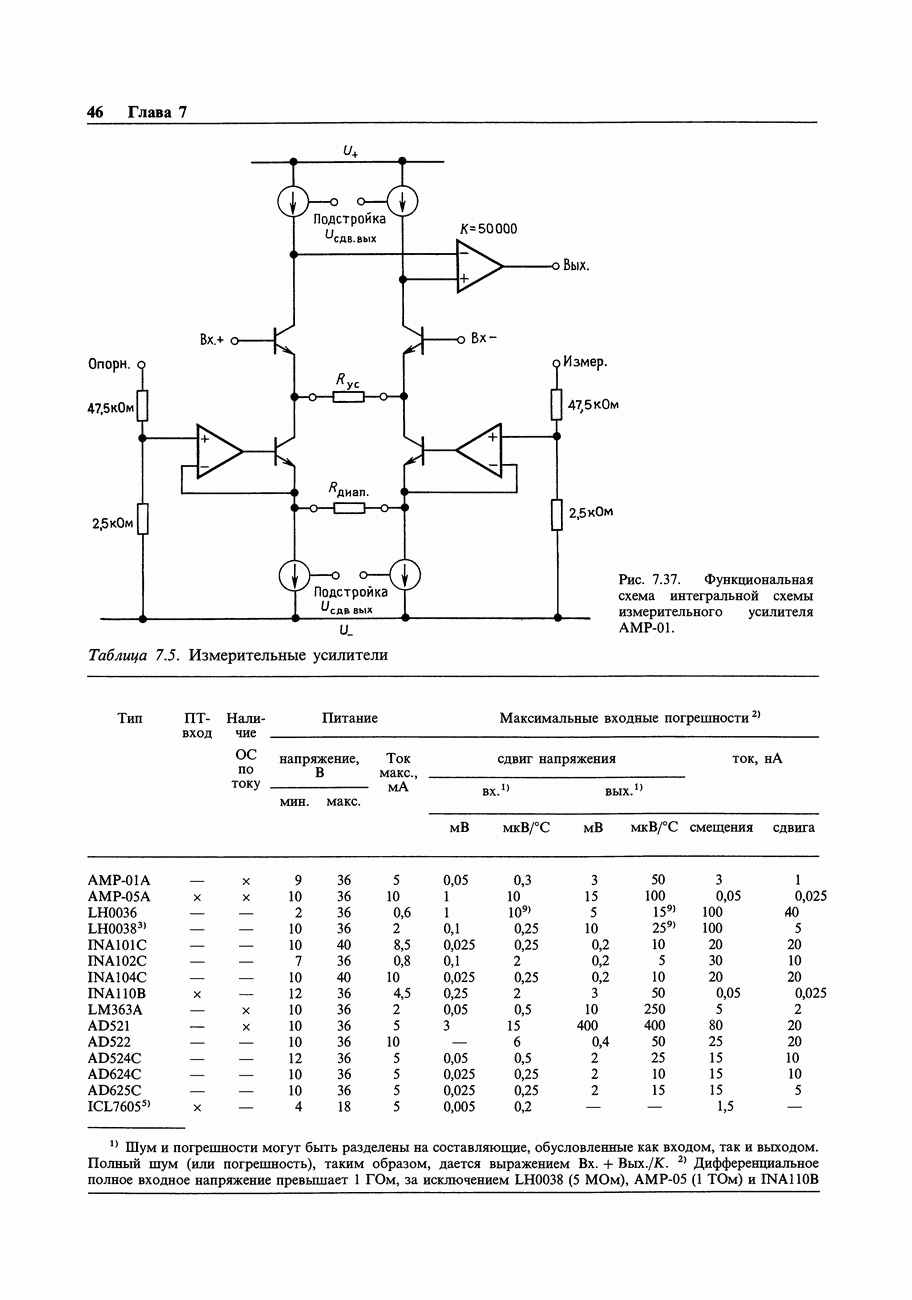
- 7.10. Стандартный измерительный усилитель на трех ОУ
- ШУМЫ УСИЛИТЕЛЕЙ
- 7.11. Происхождение и виды шумов
- 7.12. Отношение сигнал/шум и коэффициент шума
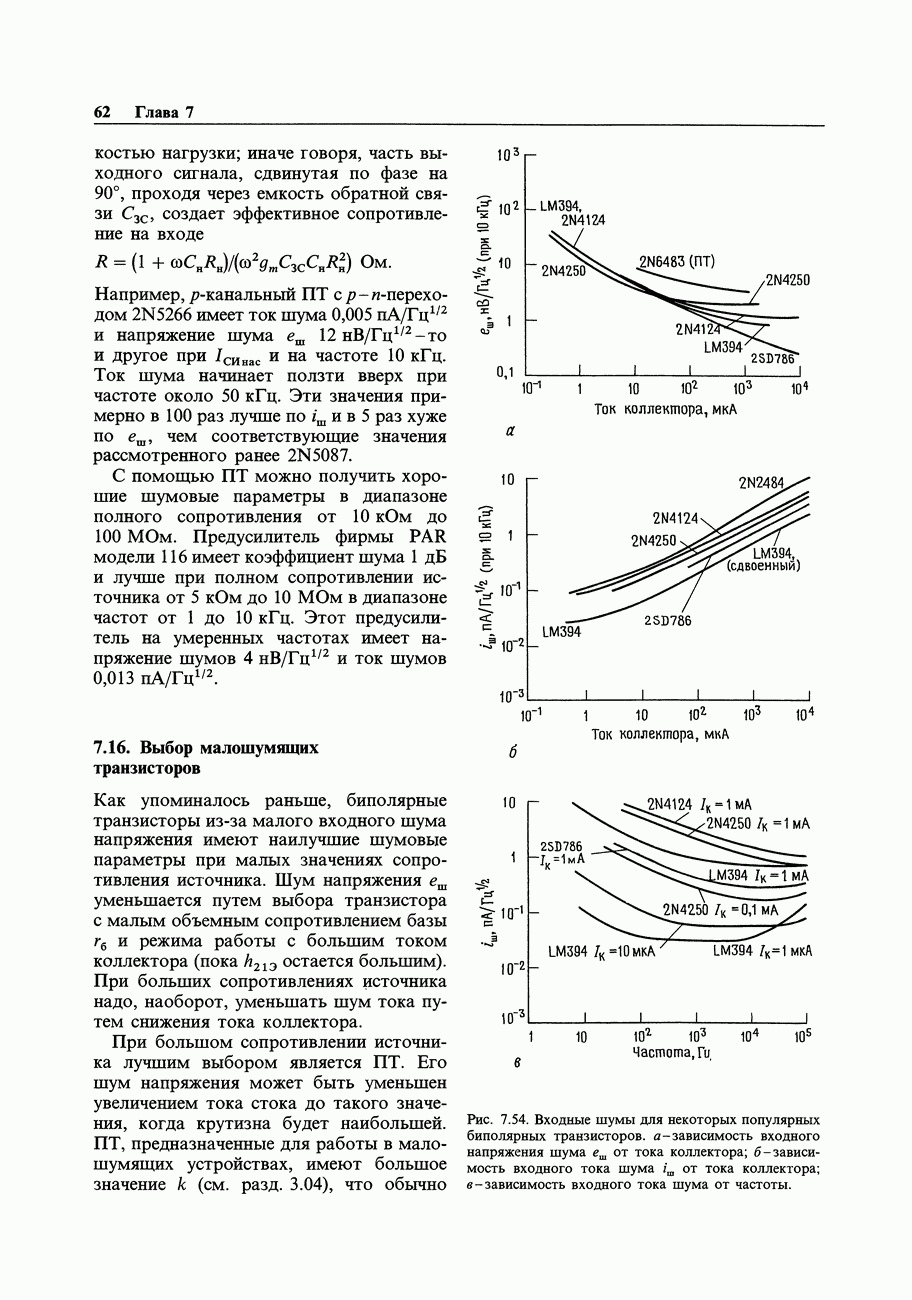
- 7.13. Шум тока и напряжения транзисторного усилителя
- 7.14. Проектирование малошумящих схем на биполярных транзисторах
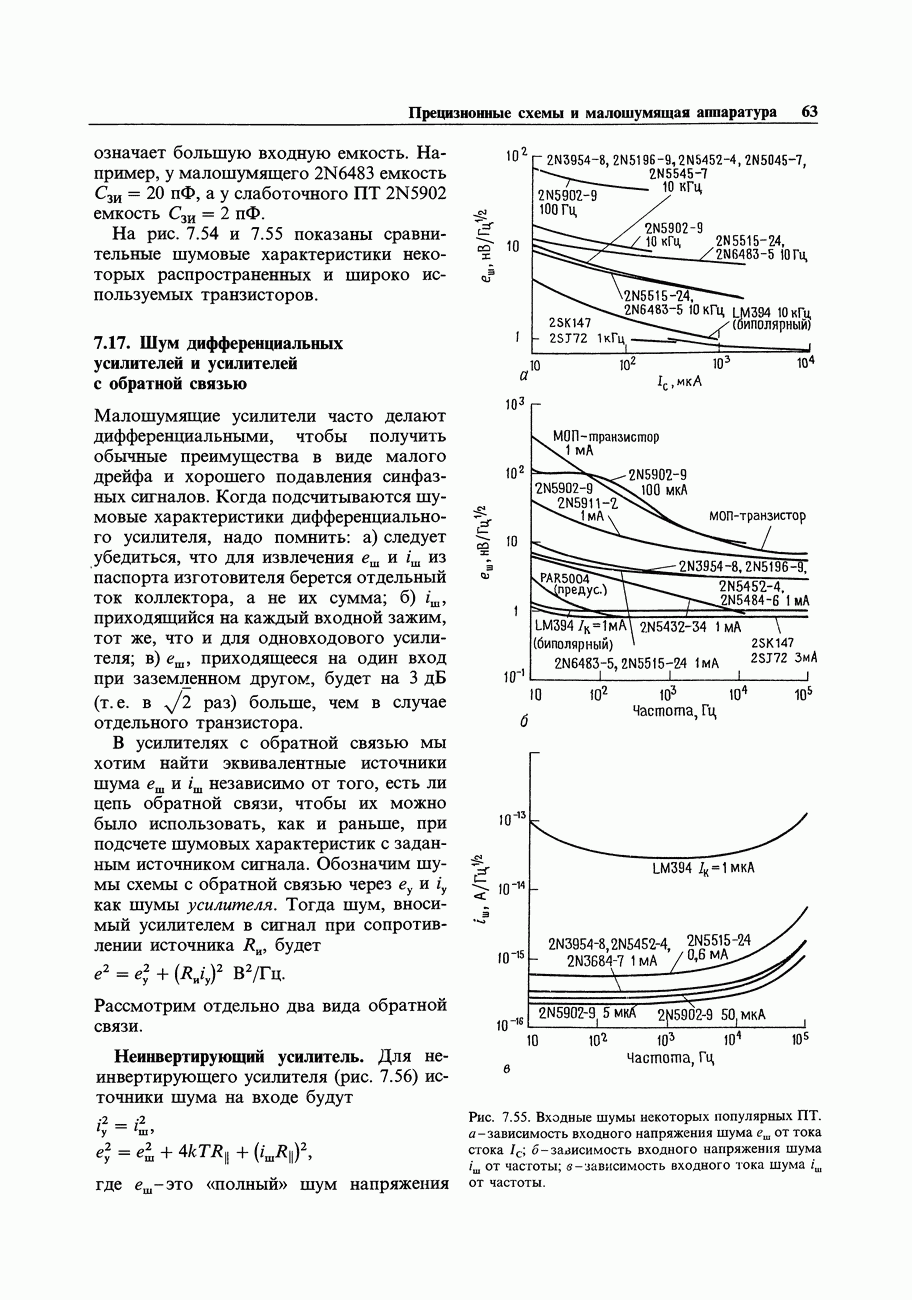
- 7.15. Шум ПТ
- 7.16. Выбор малошумящих транзисторов
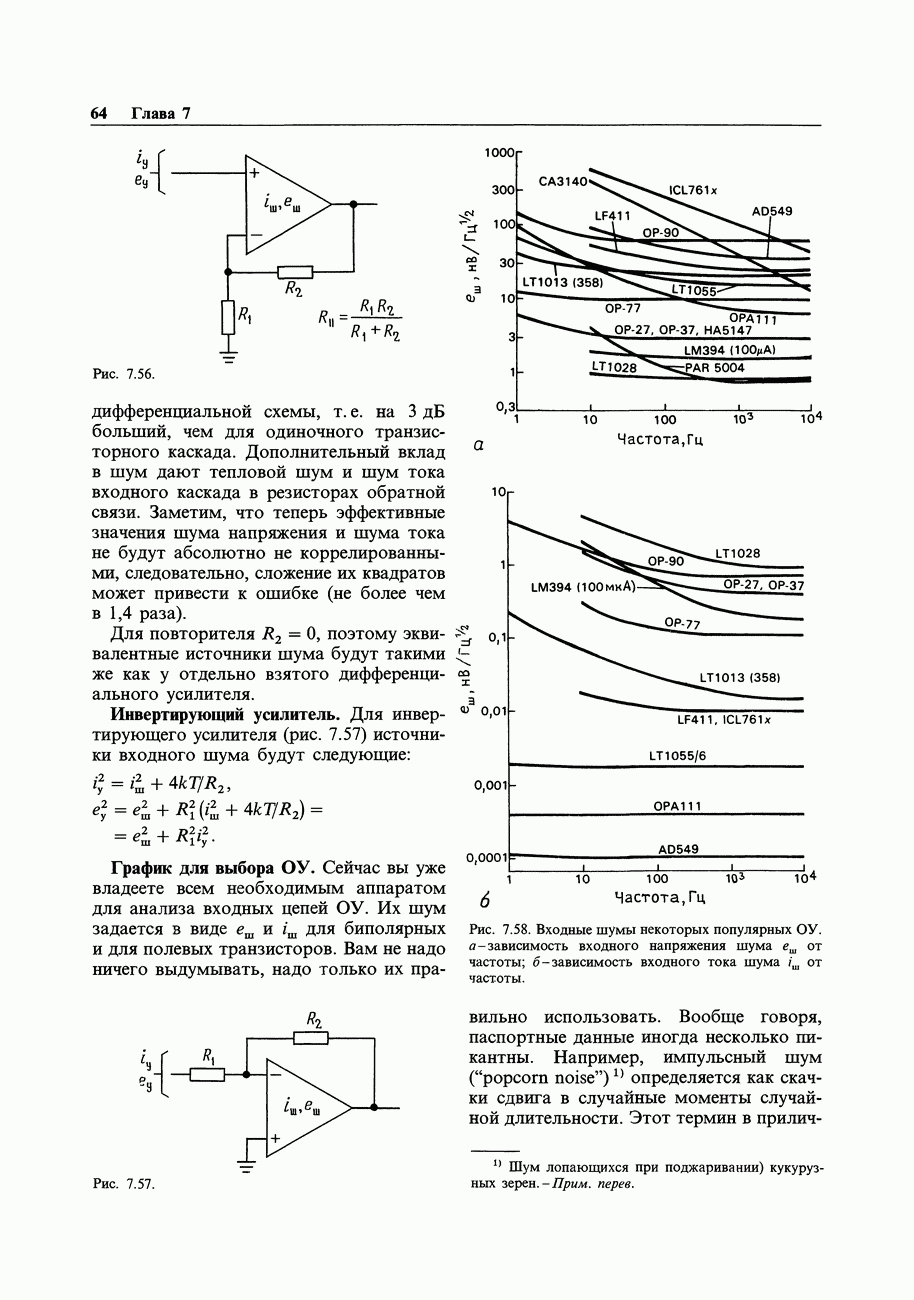
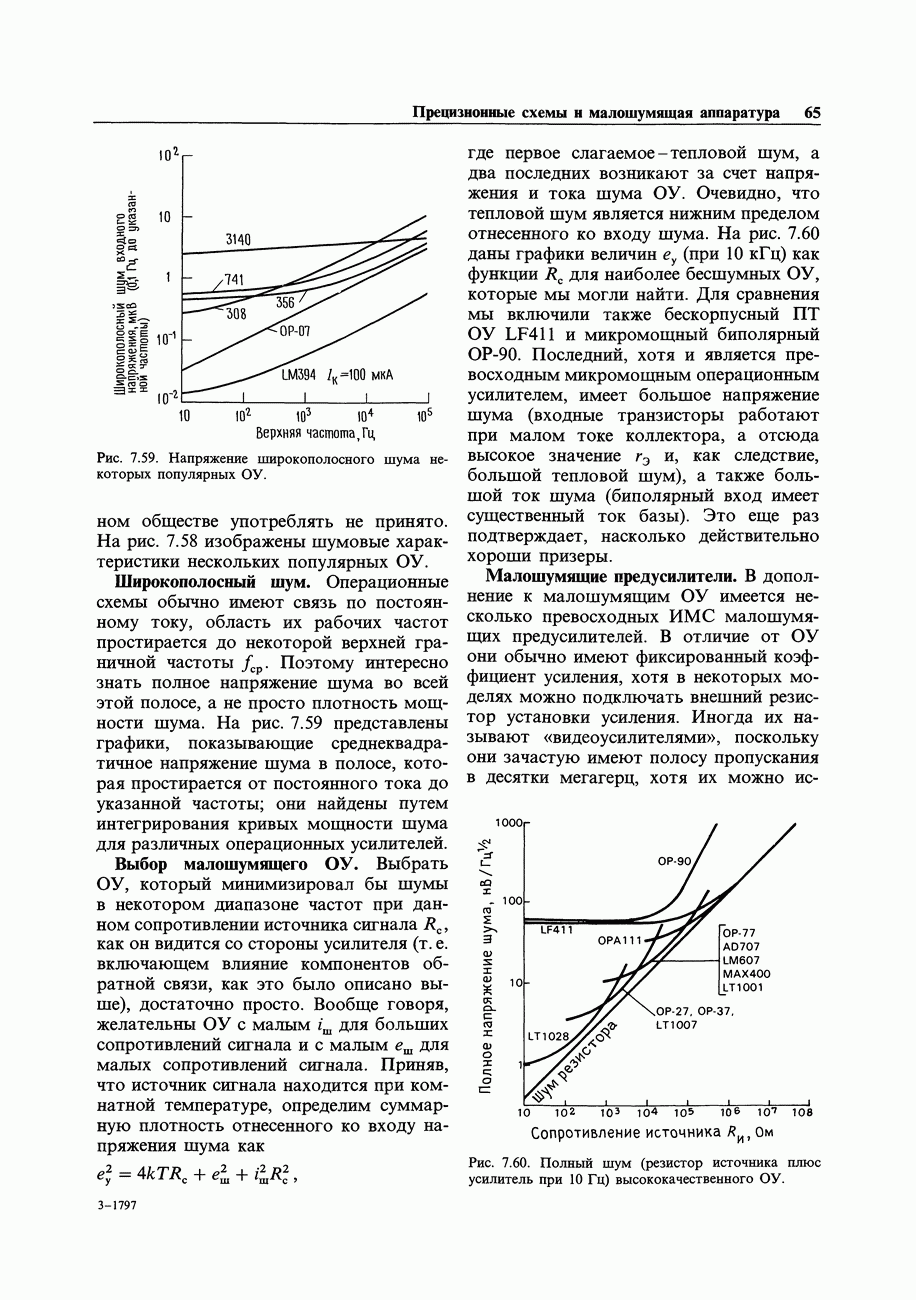
- 7.17. Шум дифференциальных усилителей и усилителей с обратной связью
- ИЗМЕРЕНИЕ ШУМА И ИСТОЧНИКИ ШУМА
- 7.18. Измерение без источника шума
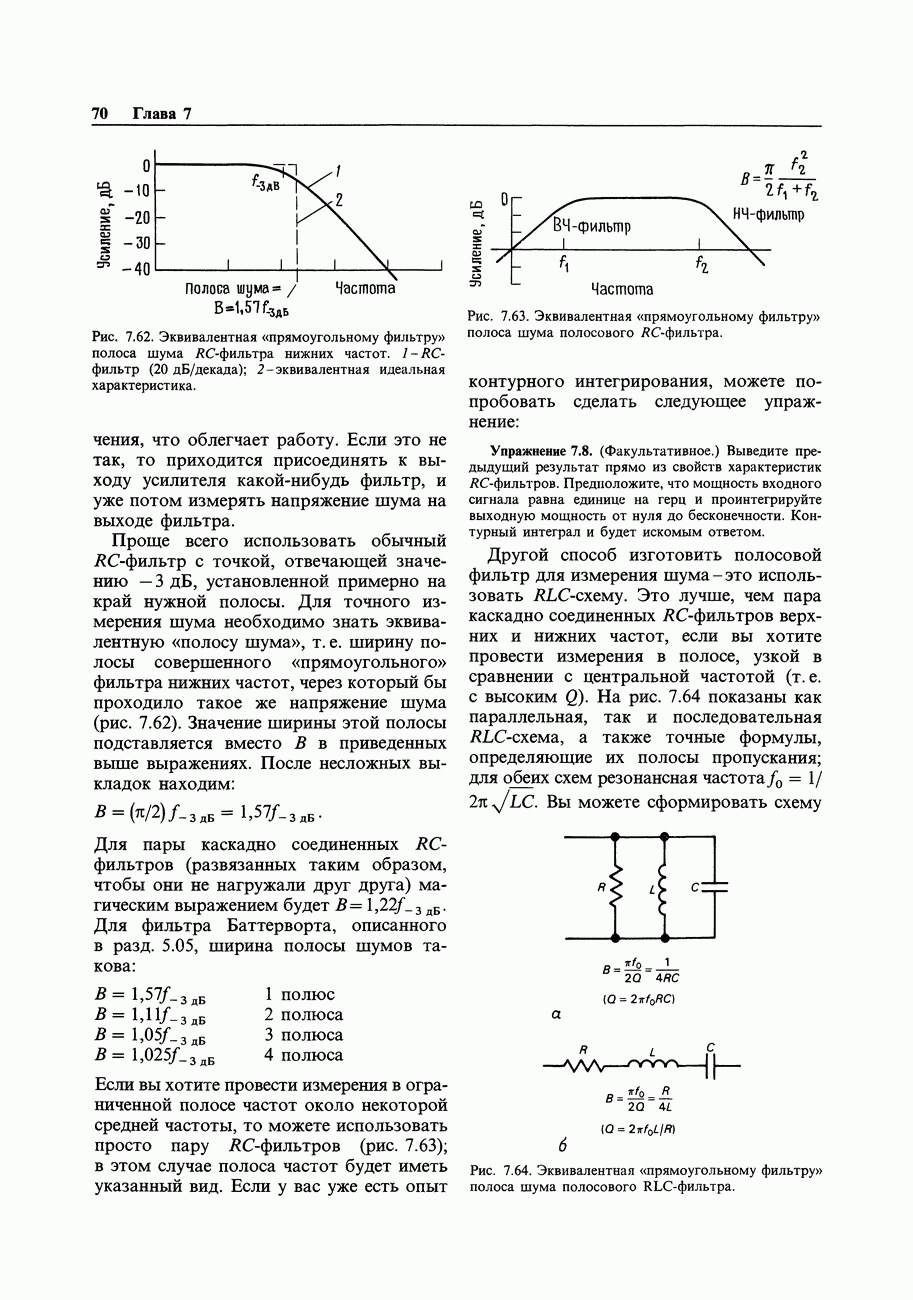
- 7.19. Измерение с источником шума
- 7.20. Генераторы шумов и сигналов
- 7.21. Ограничение полосы частот и измерение среднеквадратичного (эффективного) напряжения
- 7.22. Попурри на тему шумов
- ПОМЕХИ: ЭКРАНИРОВАНИЕ И ЗАЗЕМЛЕНИЕ
- 7.23. Помехи
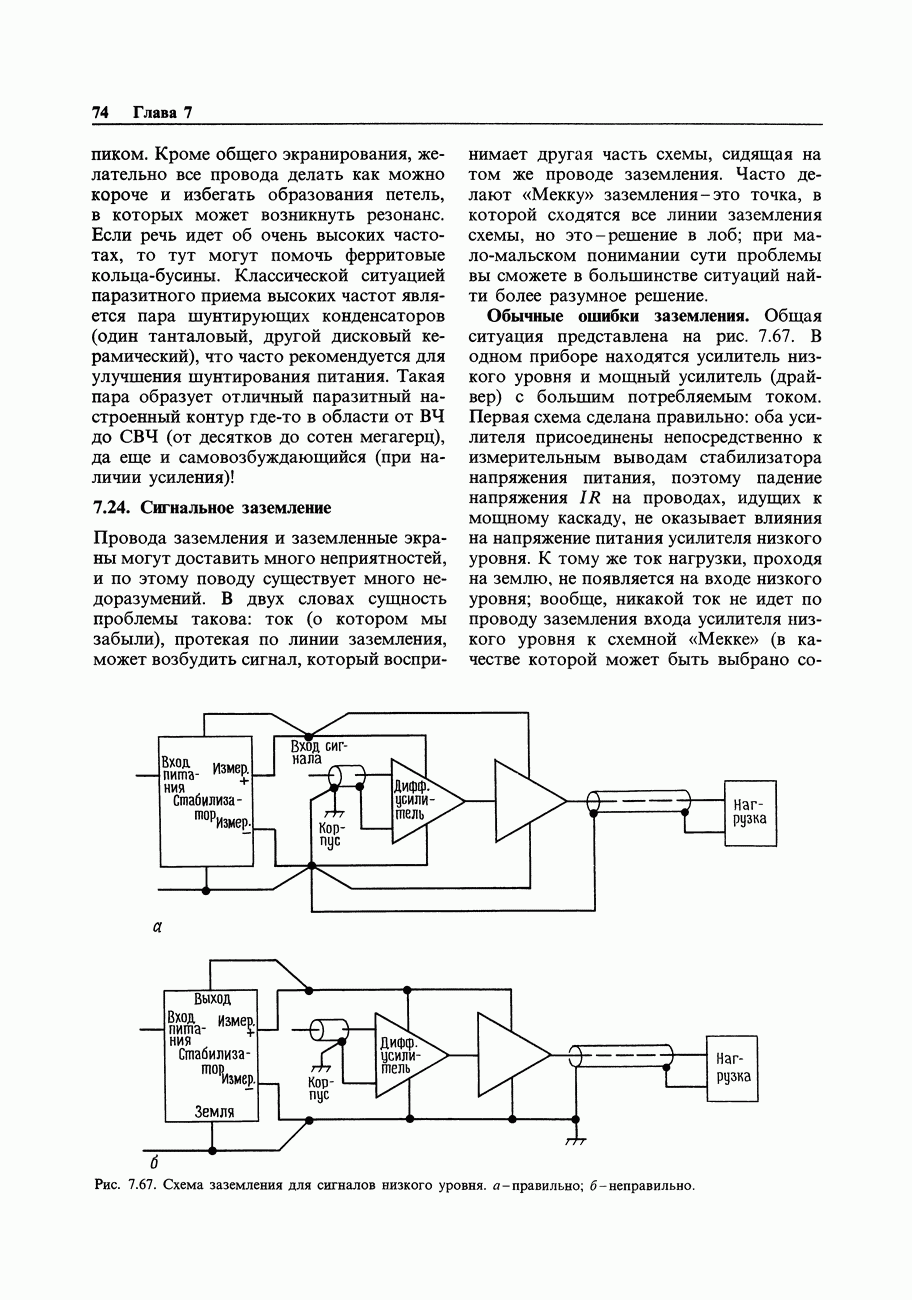
- 7.24. Сигнальное заземление
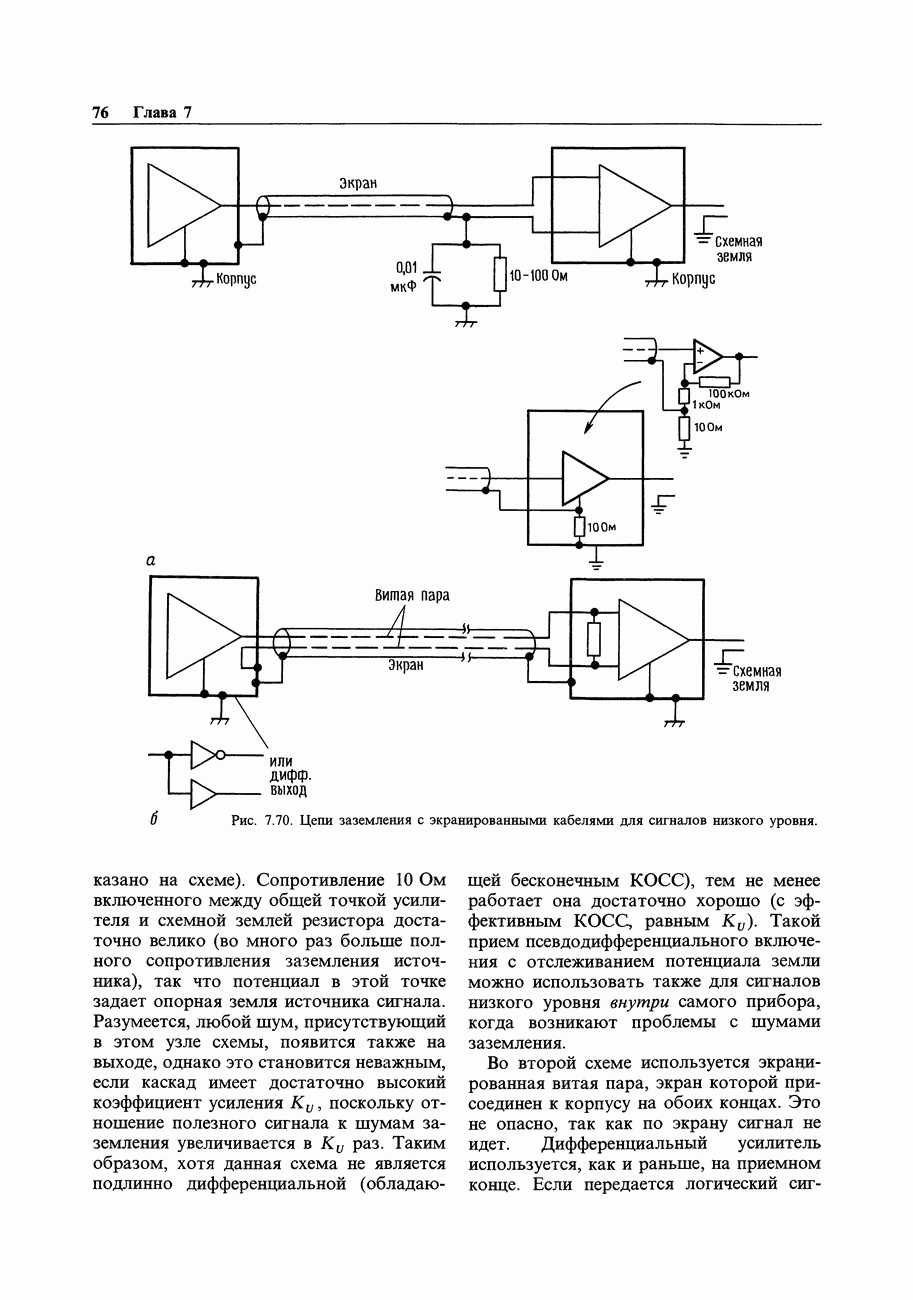
- 7.25. Межприборное заземление
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 8. ЦИФРОВЫЕ СХЕМЫ
- 8.01. Цифровые и аналоговые сигналы
- 8.02. Логические состояния
- ЛОГИЧЕСКИЕ УРОВНИ
- 8.03. Числовые коды
- 8.04. Вентили и таблицы истинности
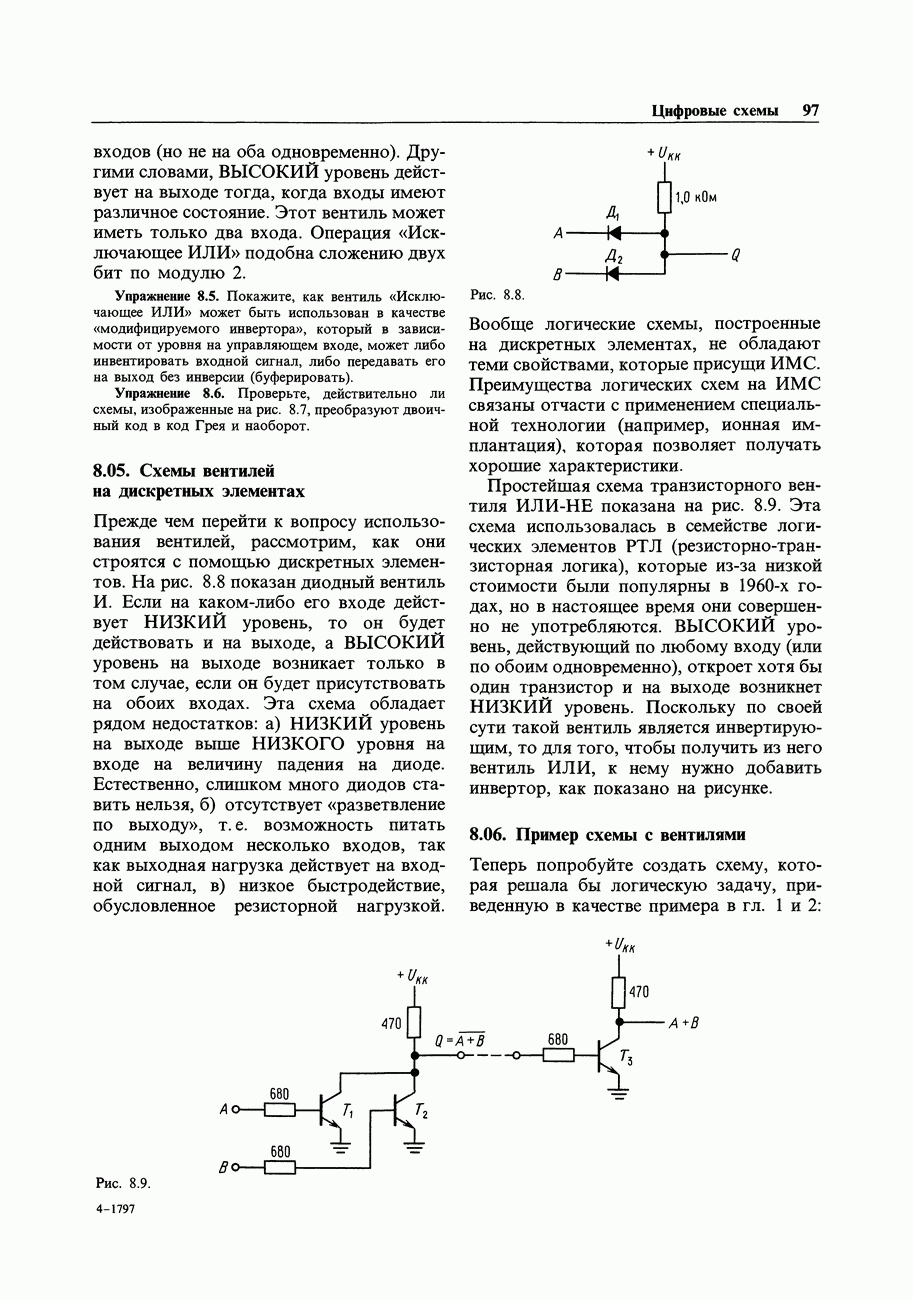
- 8.05. Схемы вентилей на дискретных элементах
- 8.06. Пример схемы с вентилями
- 8.07. Логические обозначения при заданных уровнях
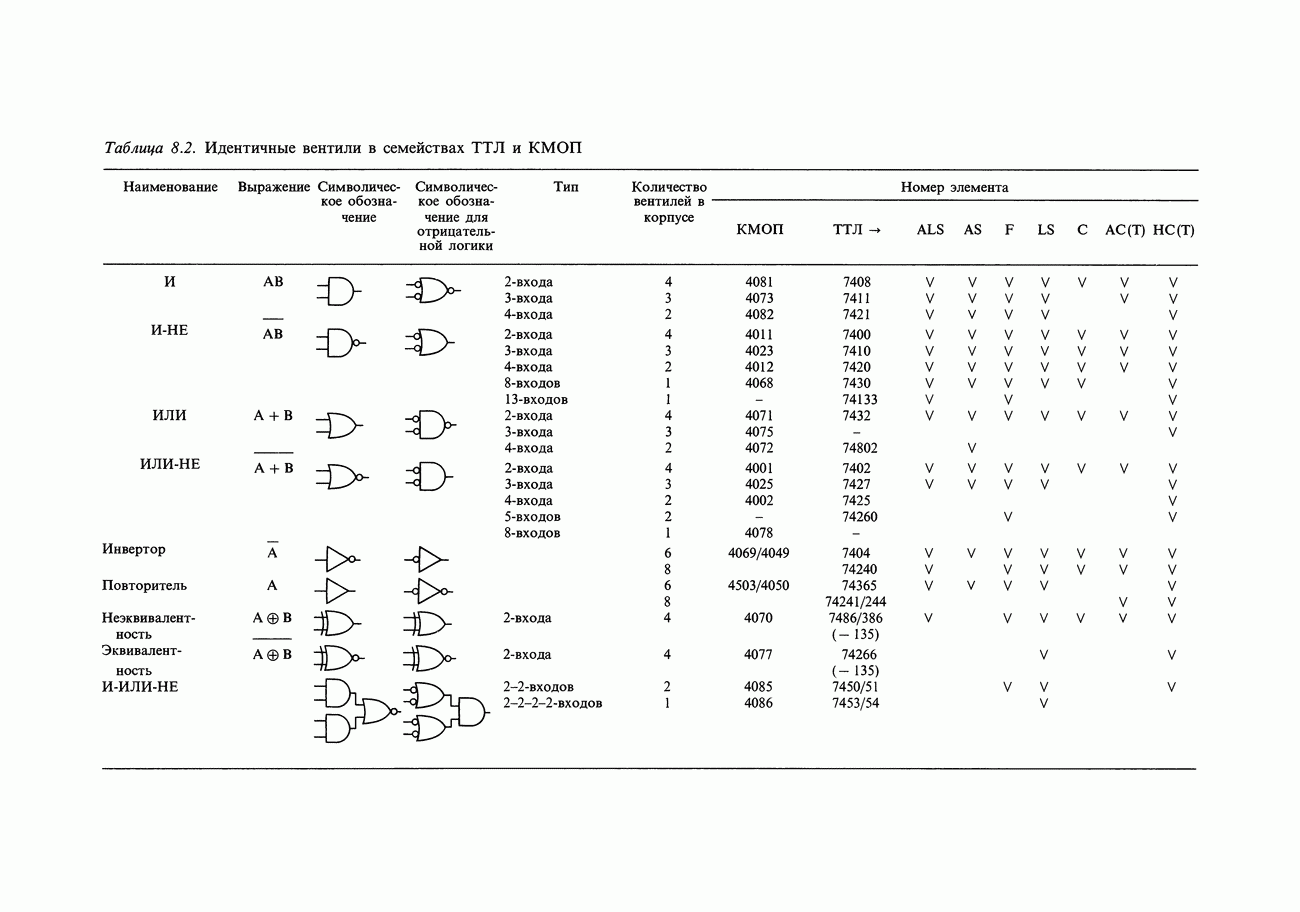
- 8.08. Каталог идентичных вентилей
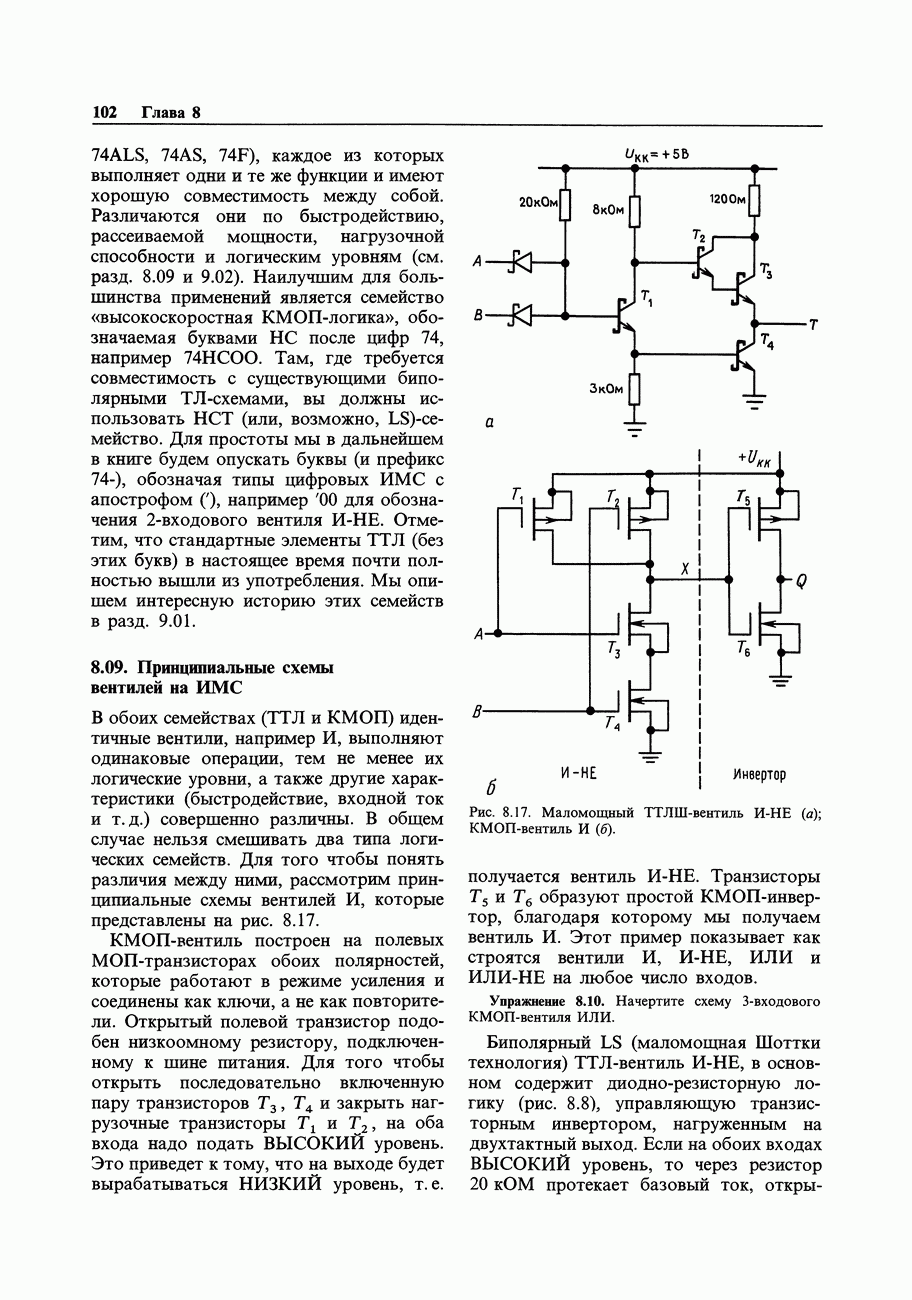
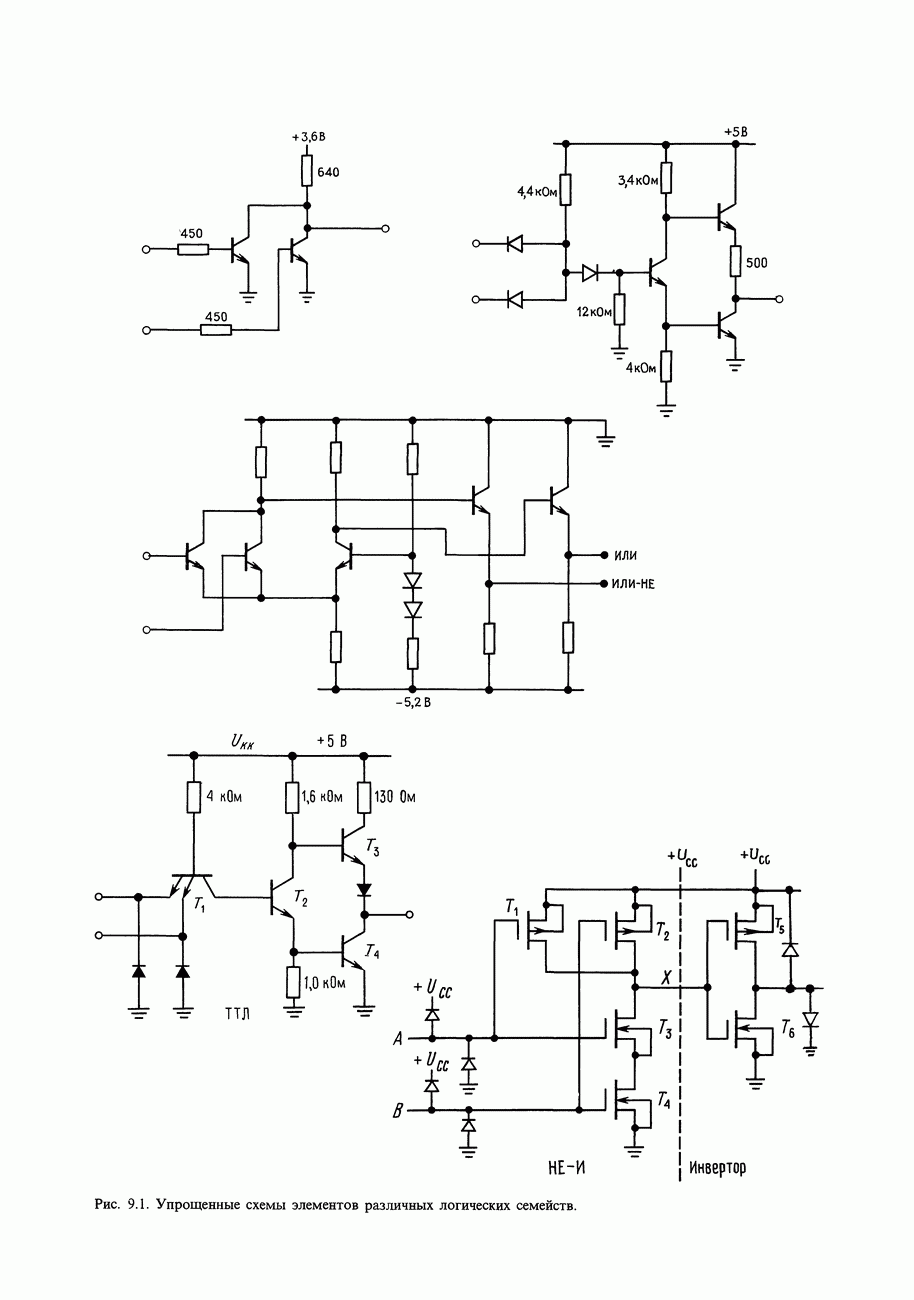
- 8.09. Принципиальные схемы вентилей на ИМС
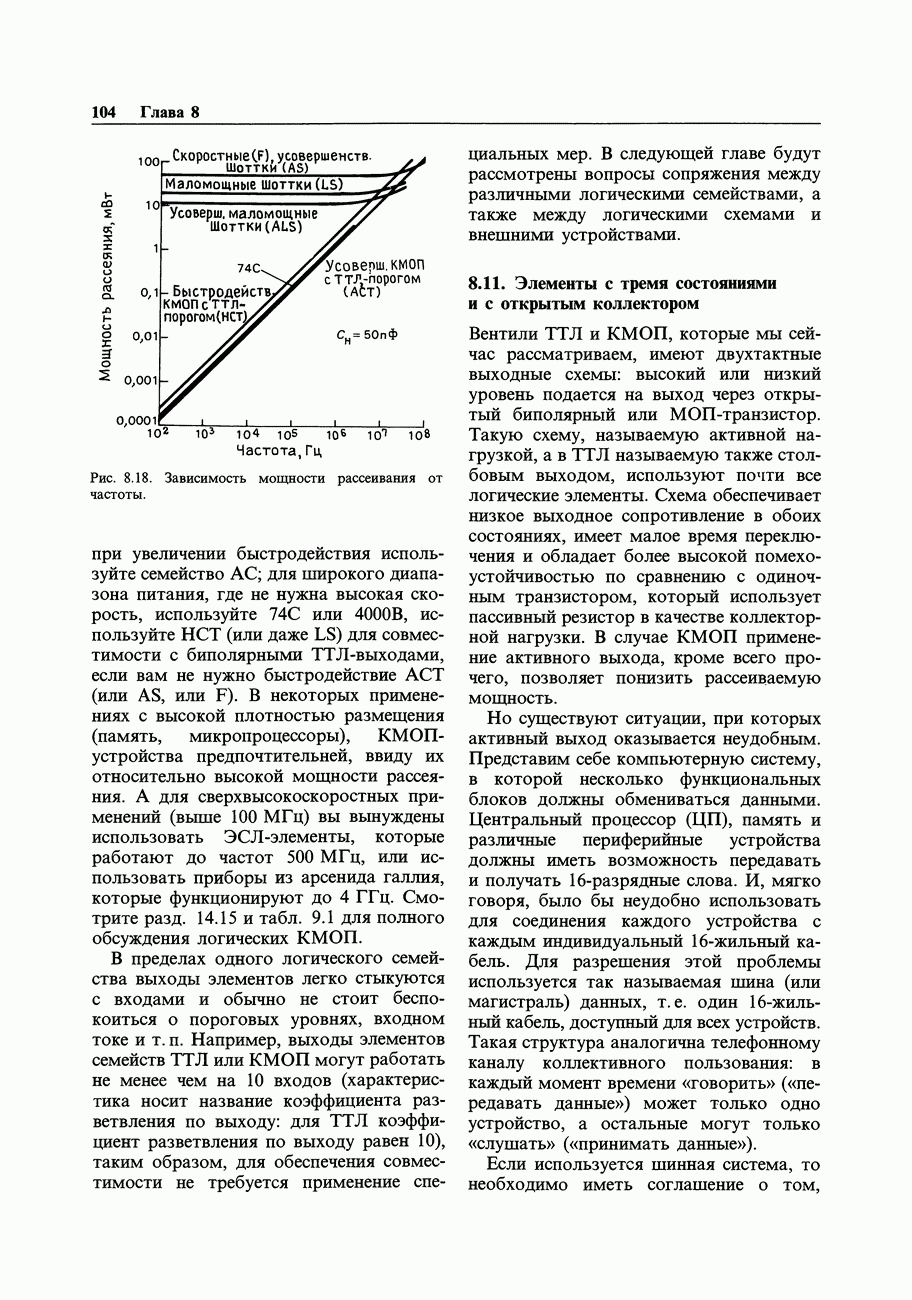
- 8.10. Характеристики ТТЛ и КМОП
- 8.11. Элементы с тремя состояниями и с открытым коллектором
- КОМБИНАЦИОННАЯ ЛОГИКА
- 8.12. Логические тождества
- 8.13. Минимизация и карты Карно
- 8.14. Комбинационные функциональные схемы, реализованные на стандартных ИМС
- 8.15. Реализация произвольных таблиц истины
- ПОСЛЕДОВАТЕЛЬНОСТНАЯ ЛОГИКА
- 8.16. Устройства с памятью: триггеры
- 8.17. Тактируемые триггеры
- 8.18. Последовательностная логика-объединение памяти и вентилей
- 8.19. Синхронизатор
- МОНОСТАБИЛЬНЫЕ МУЛЬТИВИБРАТОРЫ
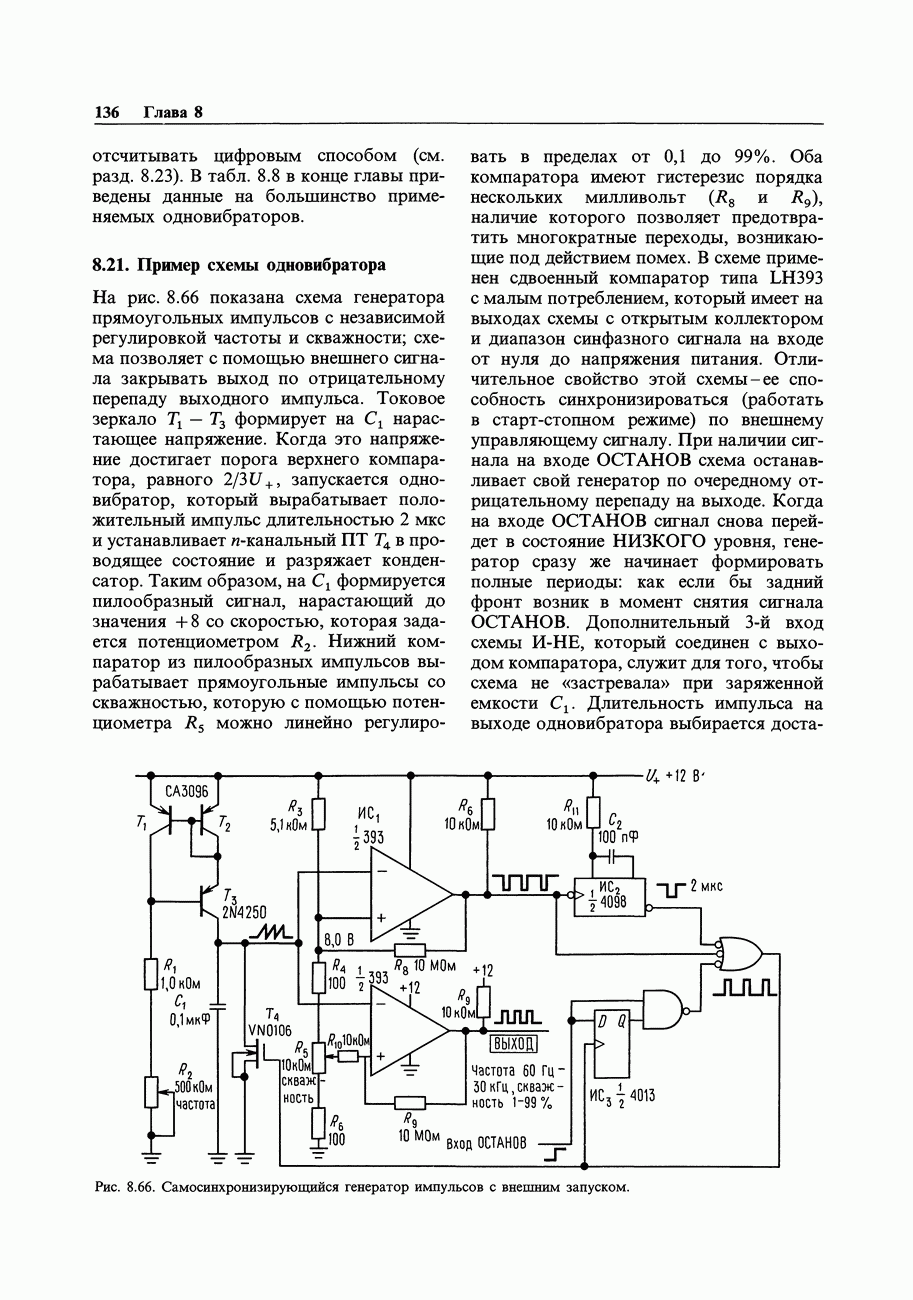
- 8.20. Характеристики одновибраторов
- 8.21. Пример схемы одновибратора
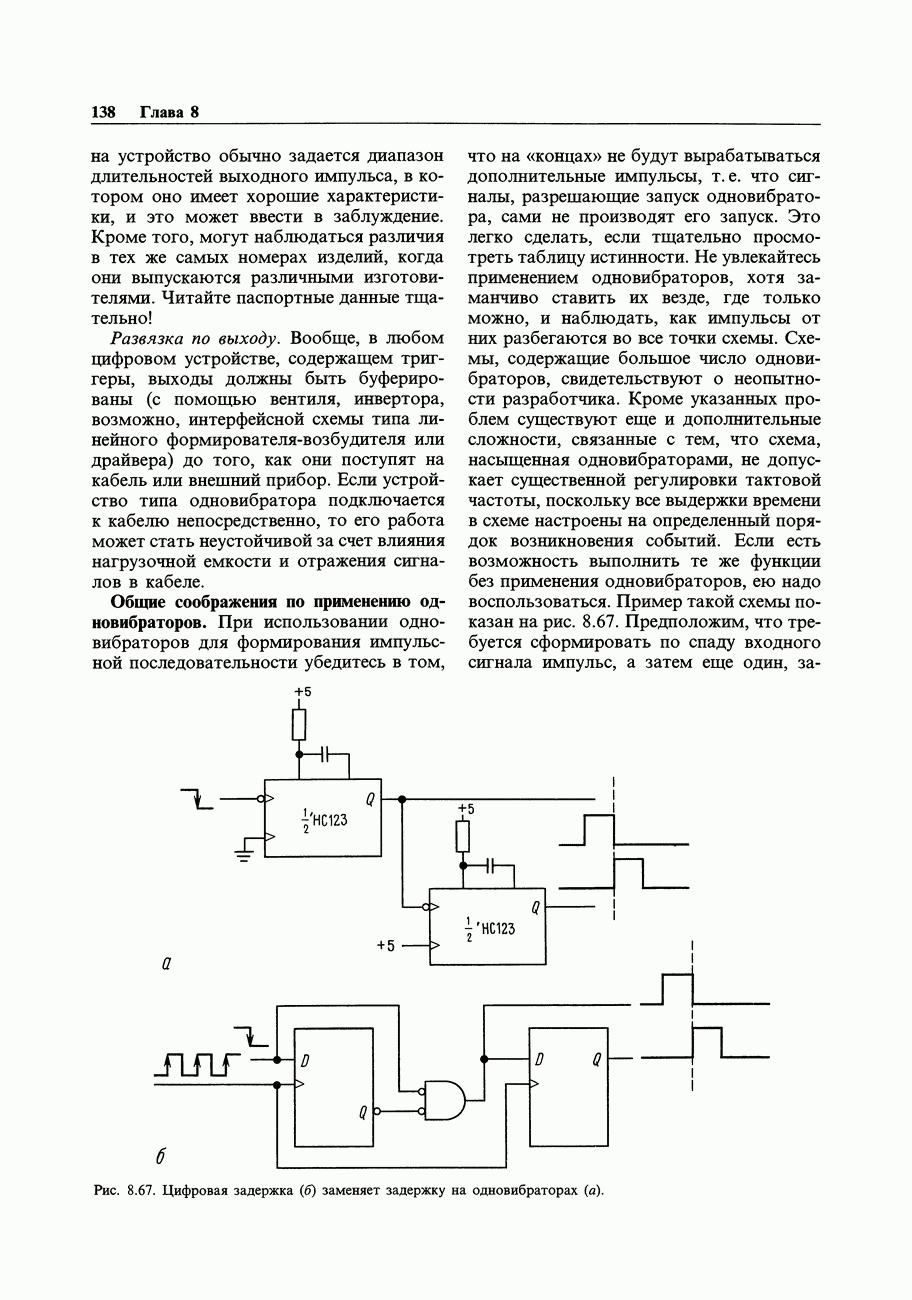
- 8.22. Предостережения относительно одновибраторов
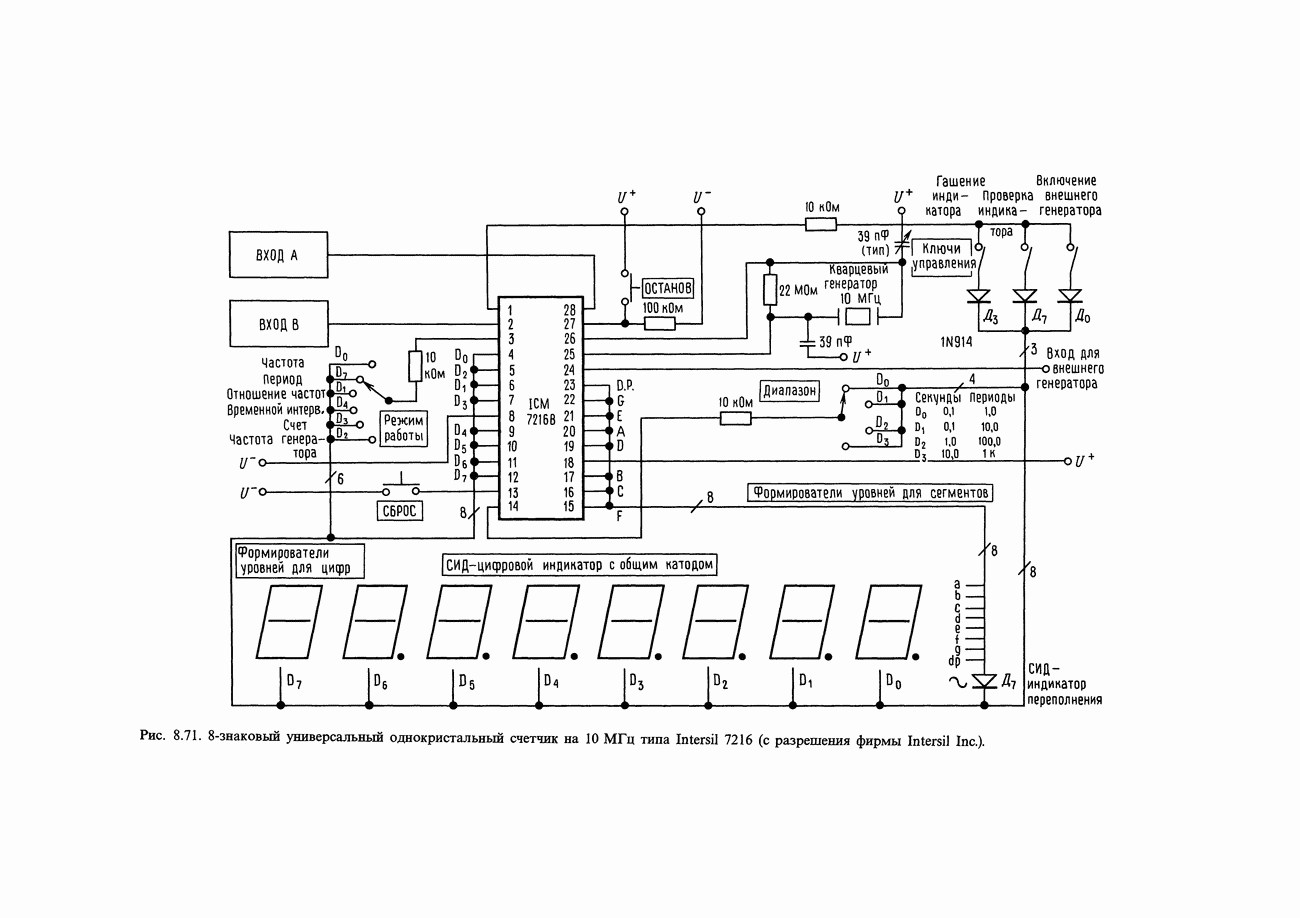
- 8.23. Получение выдержки времени с помощью счетчиков
- ПОСЛЕДОВАТЕЛЬНОСТНЫЕ ФУНКЦИИ, РЕАЛИЗУЕМЫЕ НА СТАНДАРТНЫХ ИМС
- 8.24. Фиксирующие схемы-защелки и регистры
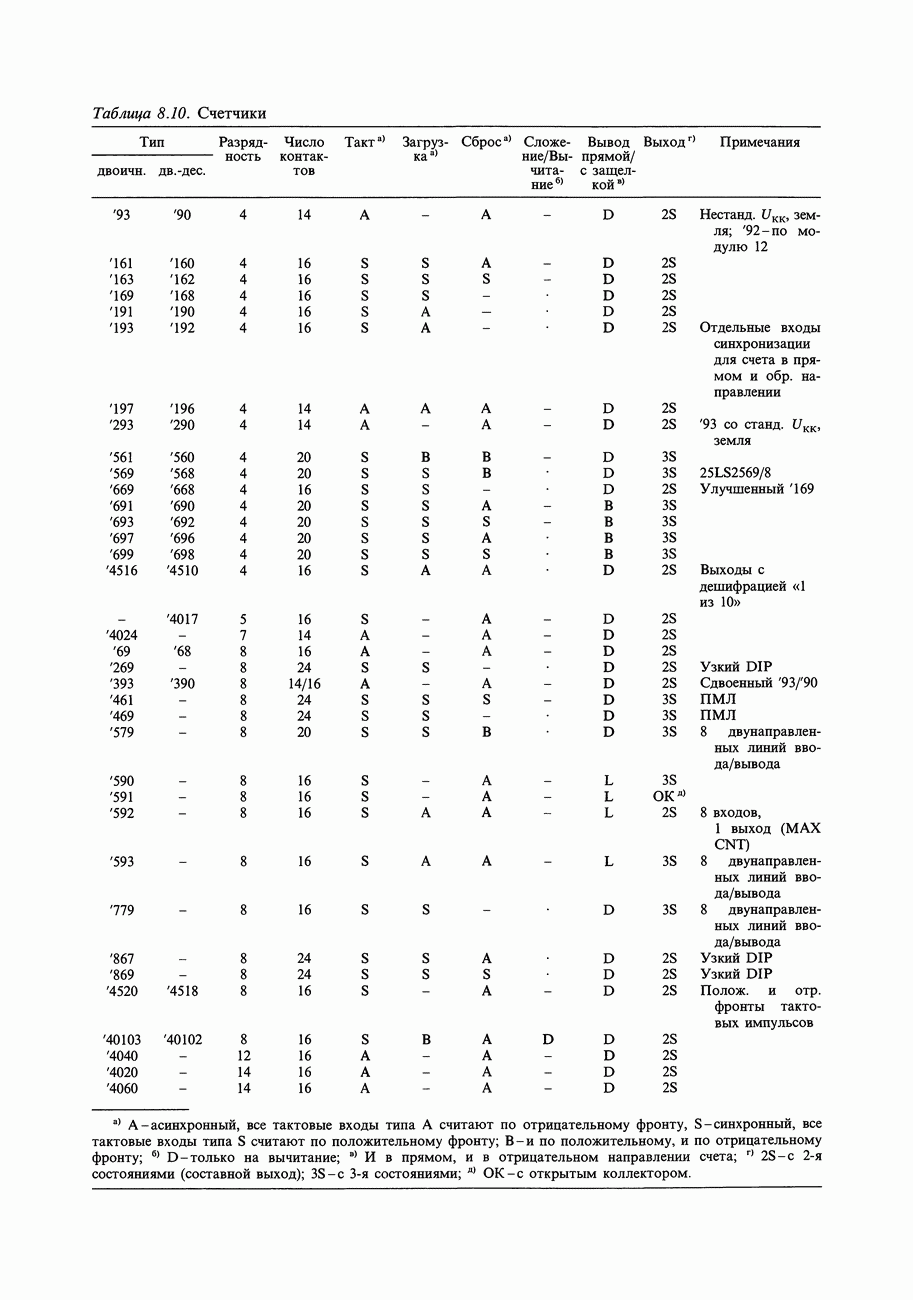
- 8.25. Счетчики
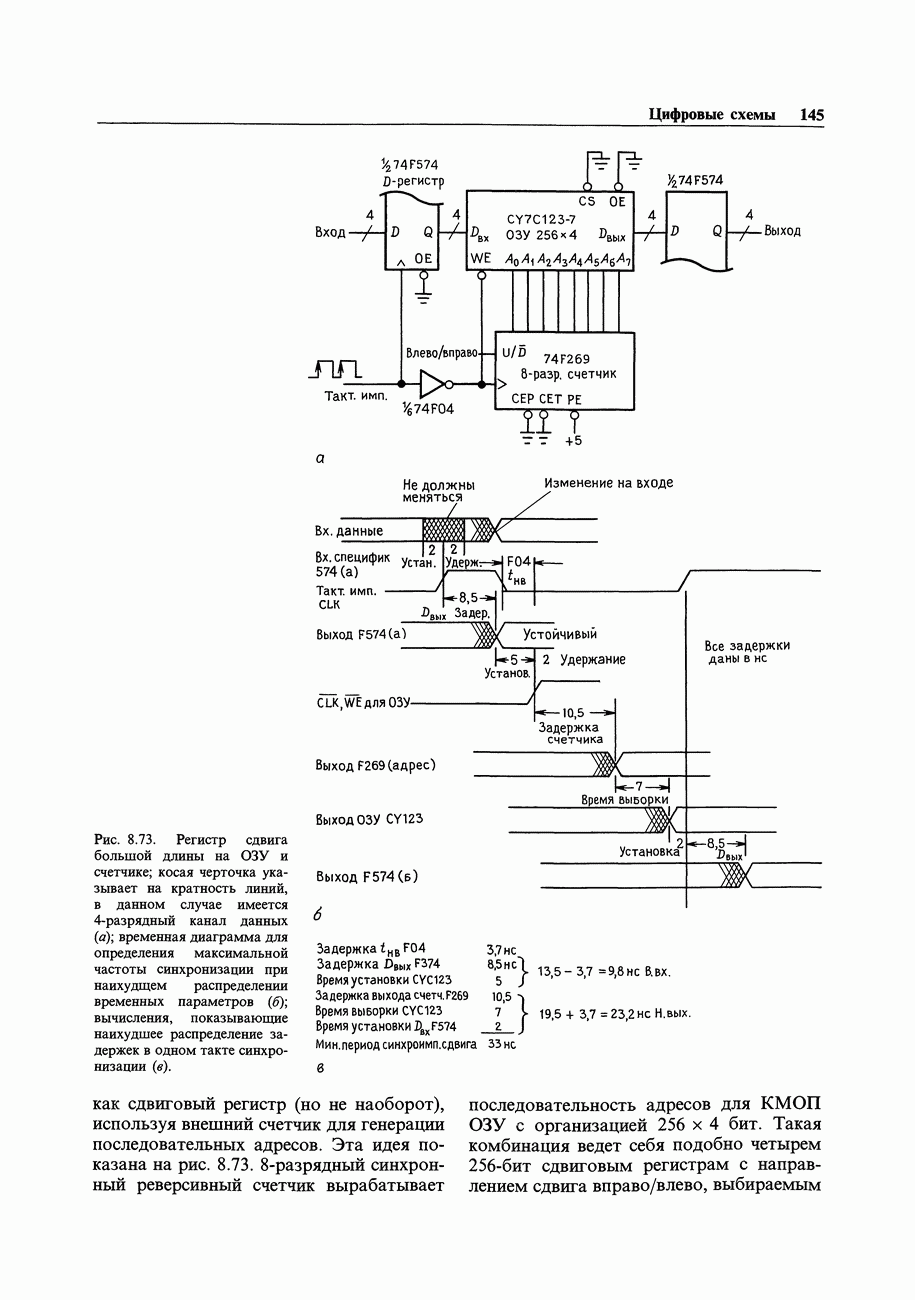
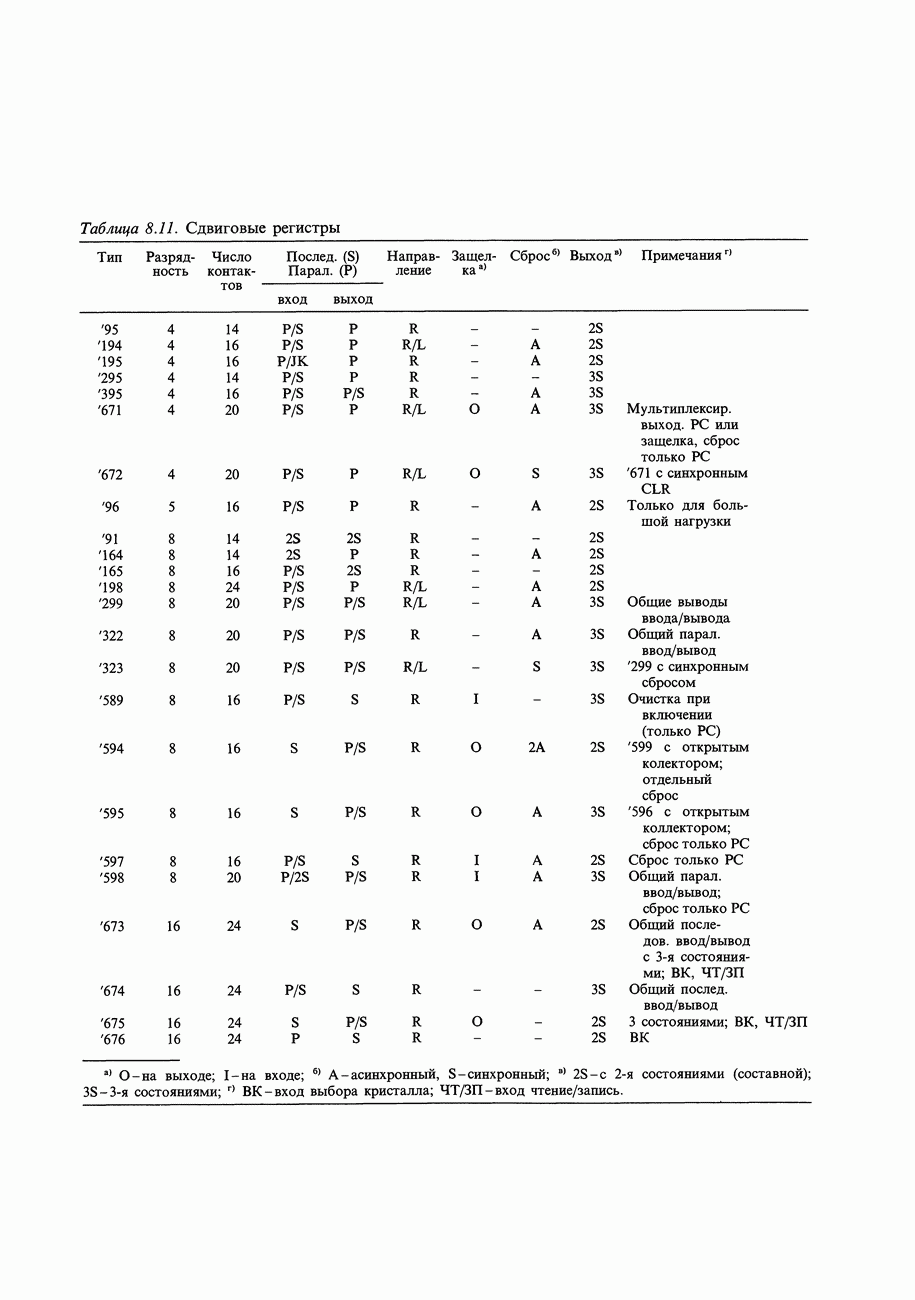
- 8.26. Регистры сдвига
- 8.27. Последовательностные ПМЛ
- Возможные применения программируемых логических интегральных схем (ПЛИС)
- 8.28. Разнообразные последовательностные схемы
- НЕКОТОРЫЕ ТИПОВЫЕ ЦИФРОВЫЕ СХЕМЫ
- 8.29. Счетчик по модулю n
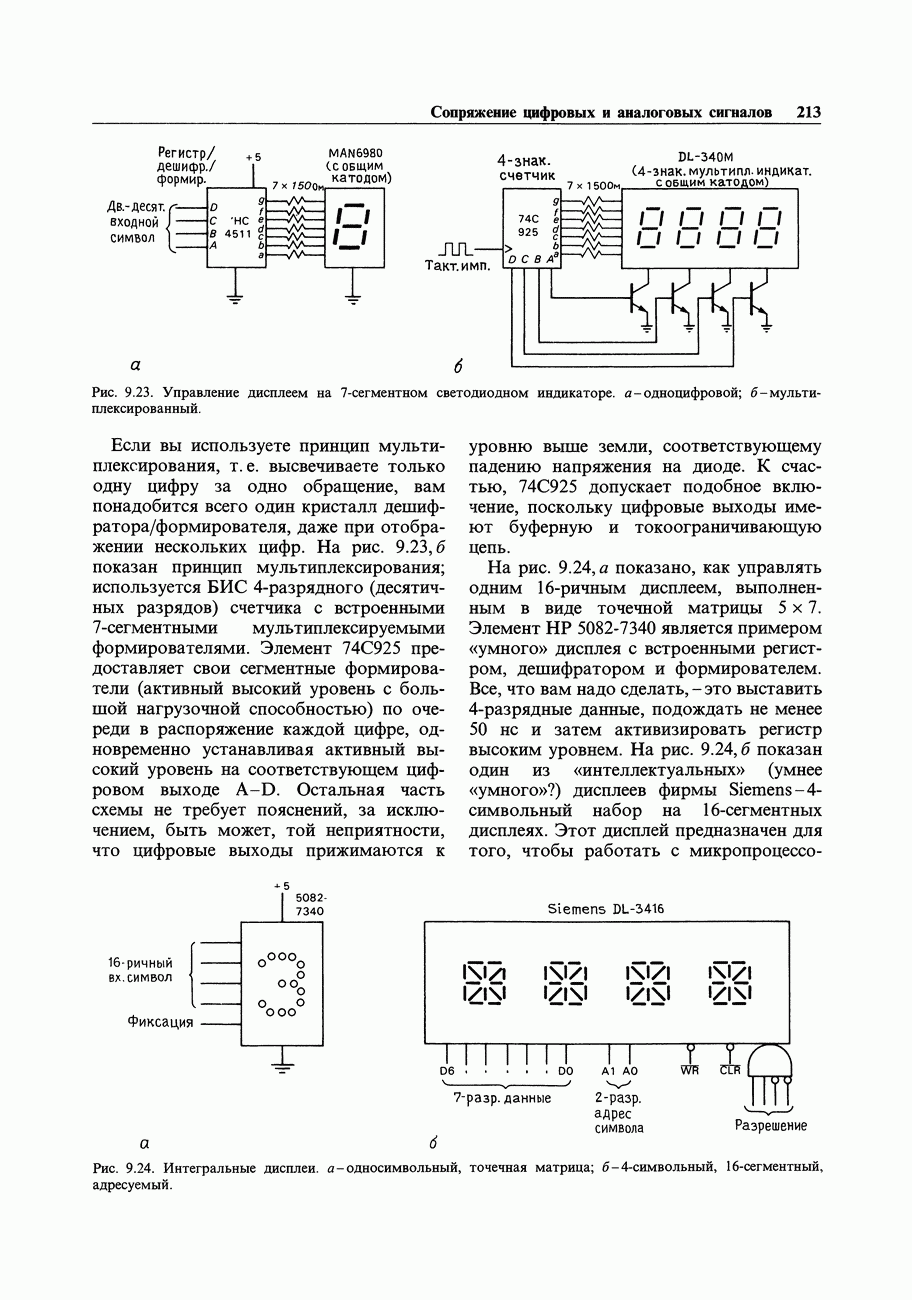
- 8.30. Мультиплексируемый цифровой индикатор на светодиодах
- 8.31. Привод звездного телескопа
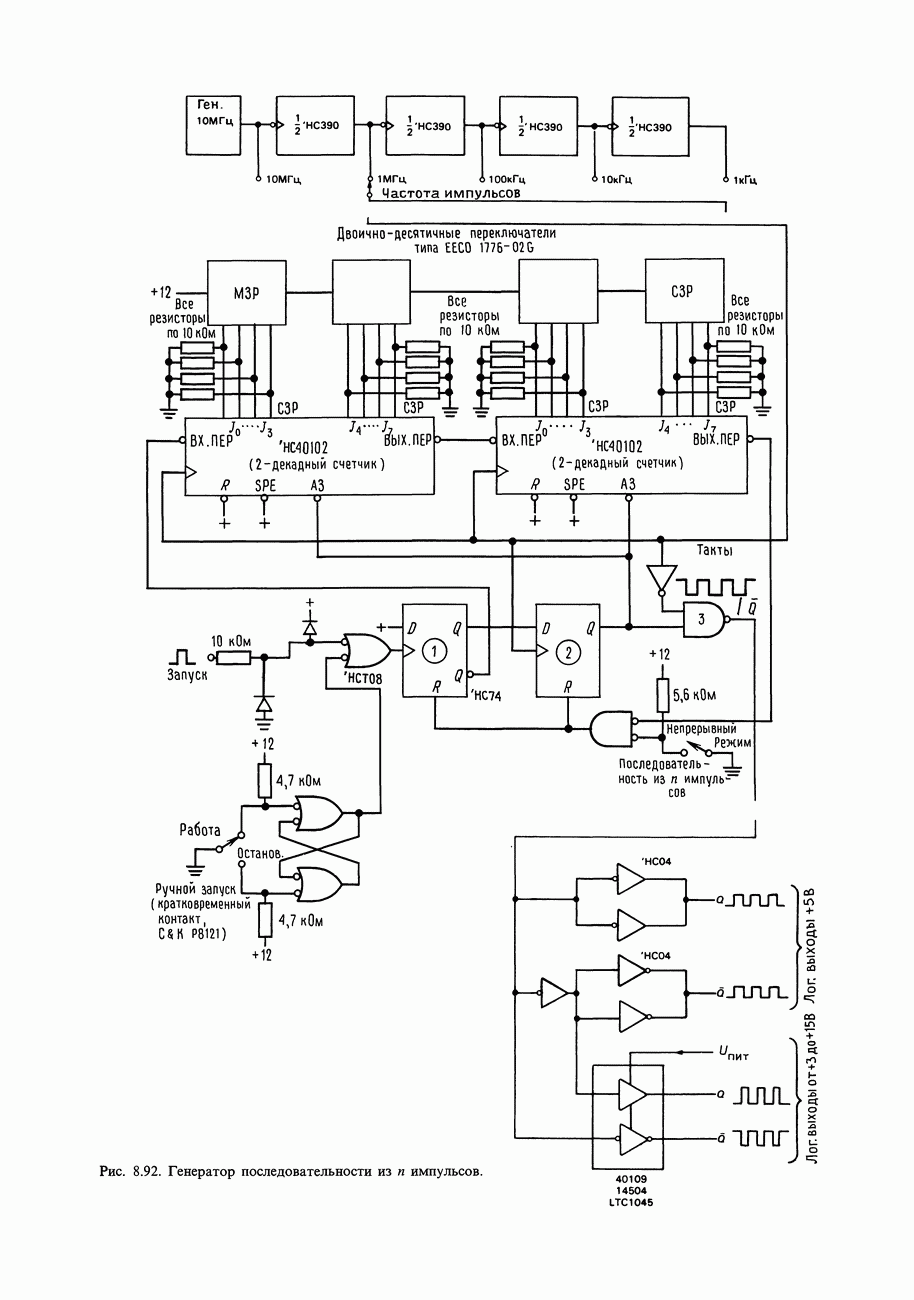
- 8.32. Генератор последовательности из n импульсов
- ПАТОЛОГИЯ В ЛОГИЧЕСКИХ СХЕМАХ
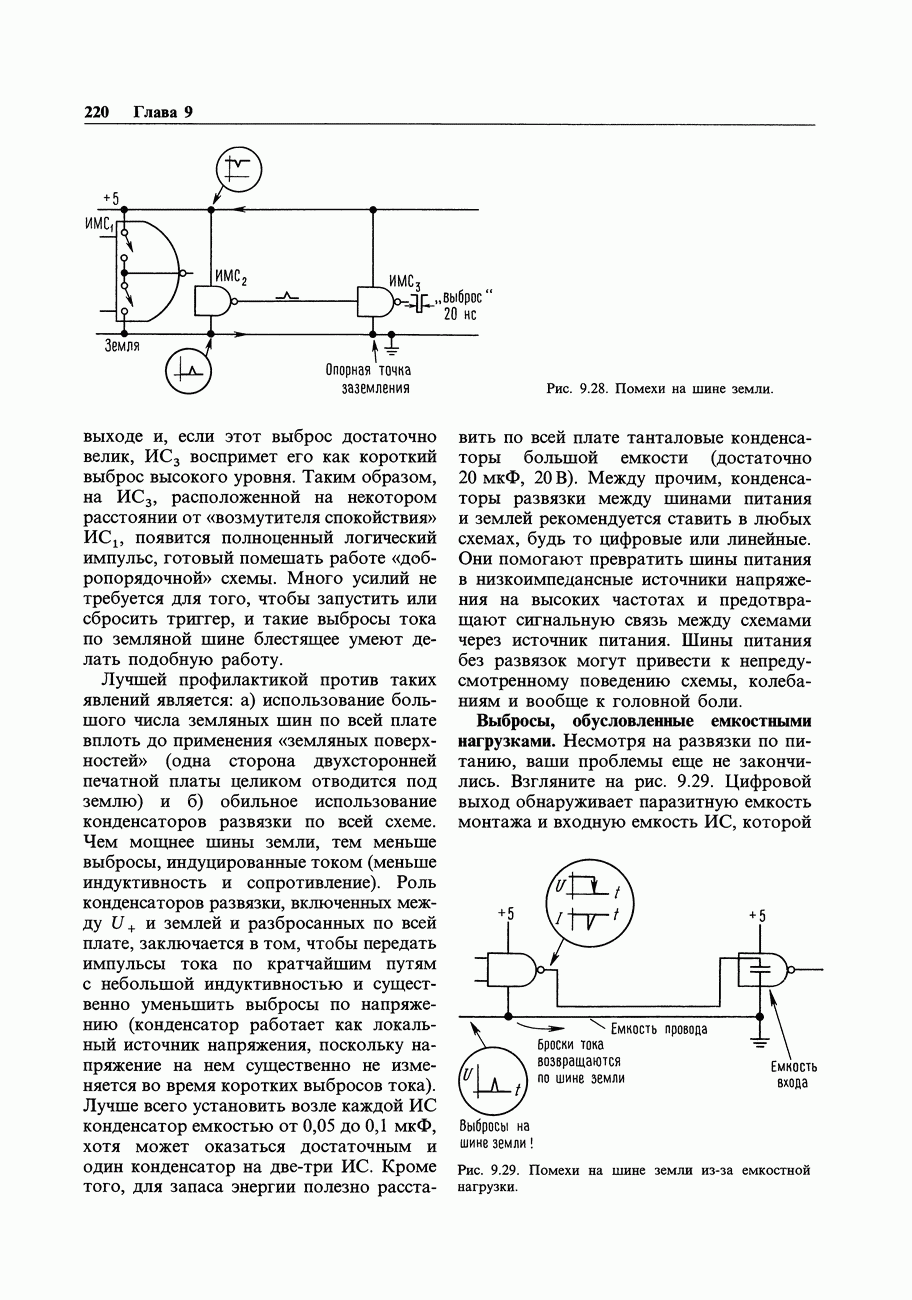
- 8.33. Проблемы статических режимов
- 8.34. Проблемы при переключениях
- 8.35. Прирожденные недостатки ТТЛ и КМОП
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 9. СОПРЯЖЕНИЕ ЦИФРОВЫХ И АНАЛОГОВЫХ СИГНАЛОВ
- 9.01. Хронология логических семейств
- 9.02. Входные и выходные характеристики
- 9.03. Сопряжение логических семейств
- 9.04. Управление КМОП-и ТТЛ-входами
- 9.05. Управление цифровой логикой от компараторов и операционных усилителей
- 9.06. Некоторые замечания, касающиеся логических входов
- 9.07. Компараторы
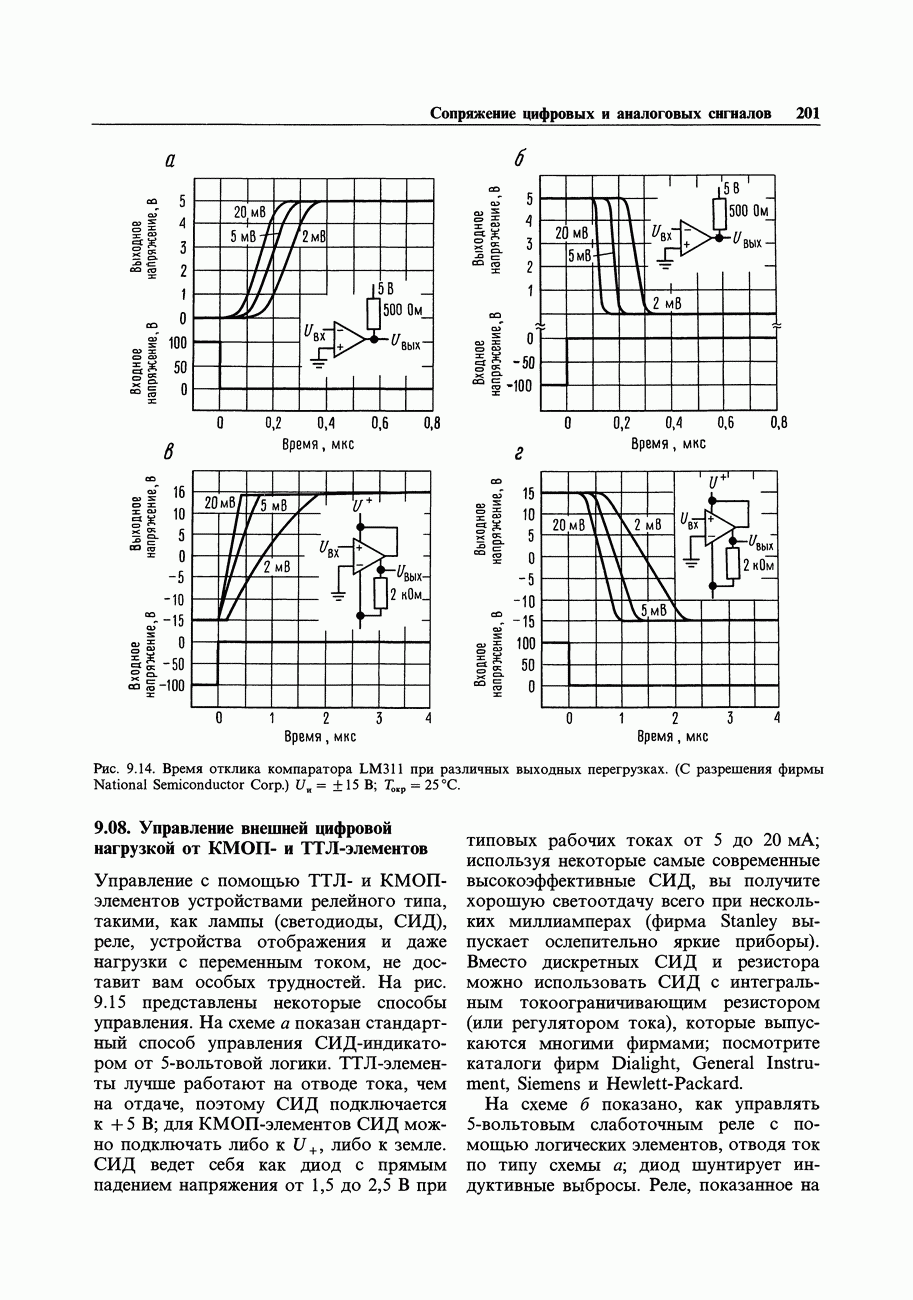
- 9.08. Управление внешней цифровой нагрузкой от КМОП- и ТТЛ-элементов
- 9.09. Сопряжение n-МОП БИС
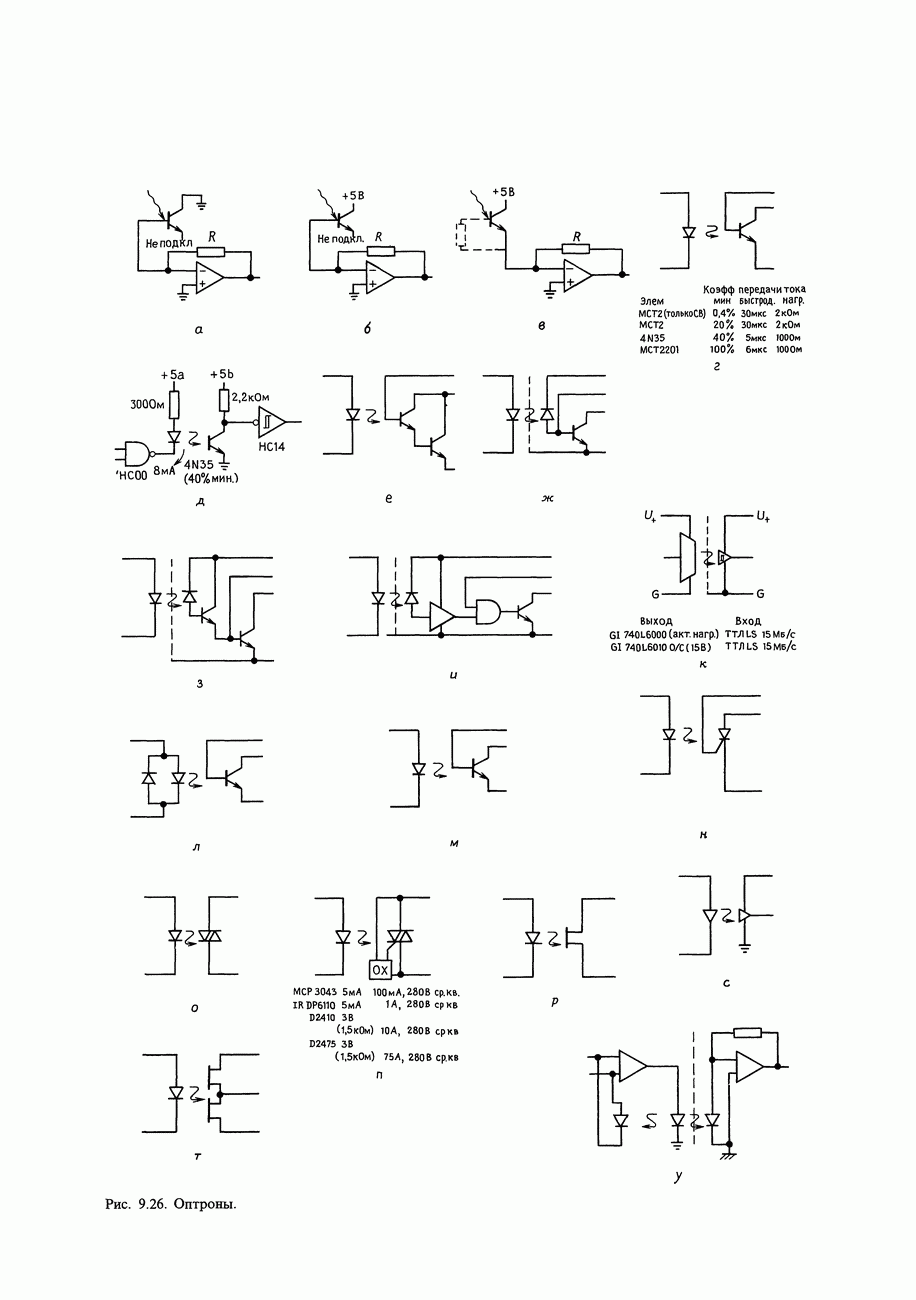
- 9.10. Оптоэлектроника
- ЦИФРОВЫЕ СИГНАЛЫ И ДЛИННЫЕ ЛИНИИ
- 9.11. Внутриплатные соединения
- 9.12. Межплатные соединения
- 9.13. Шины данных
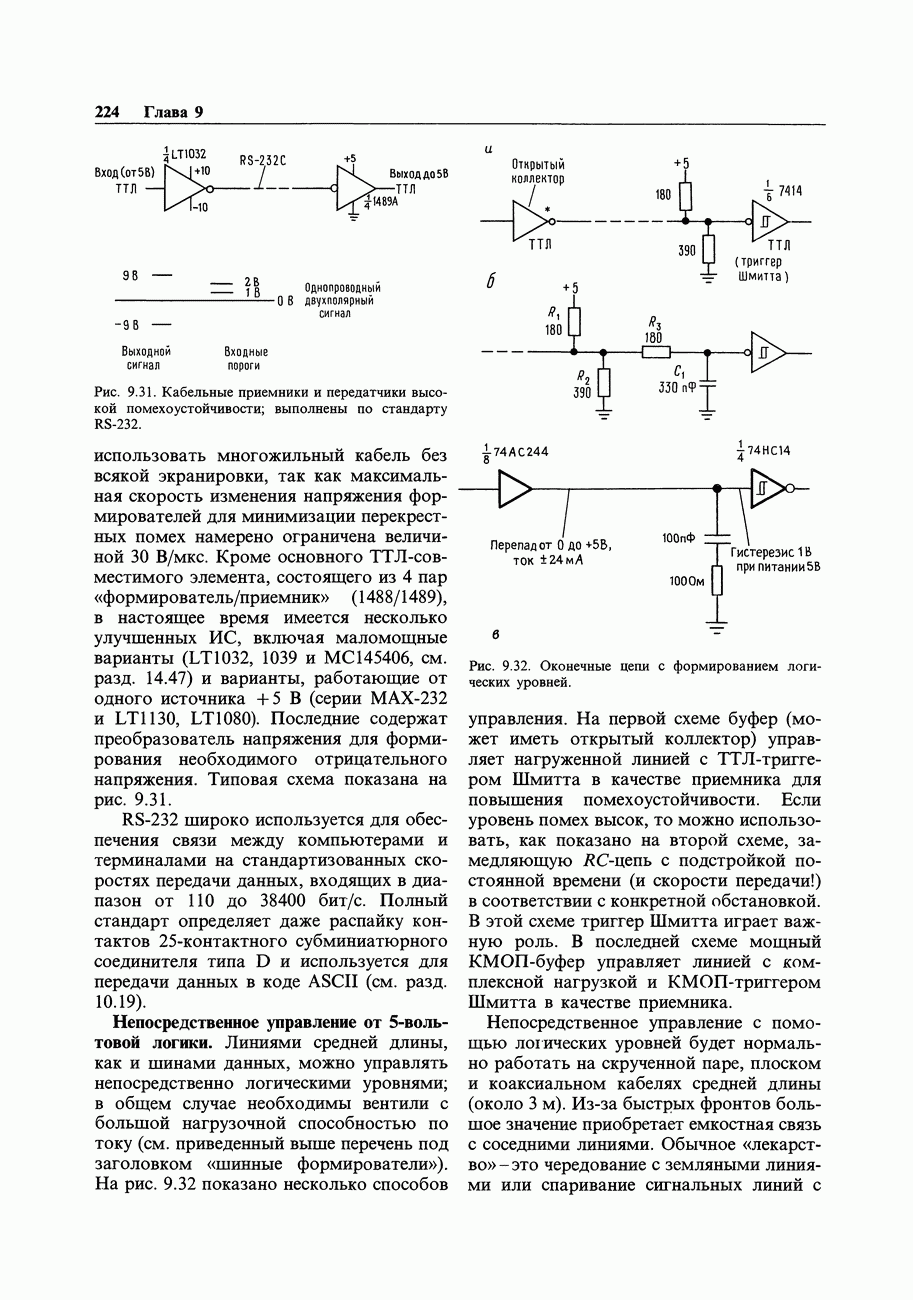
- 9.14. Кабельные связи
- АНАЛОГО-ЦИФРОВОЕ ПРЕОБРАЗОВАНИЕ
- 9.15. Введение в аналого-цифровое преобразование
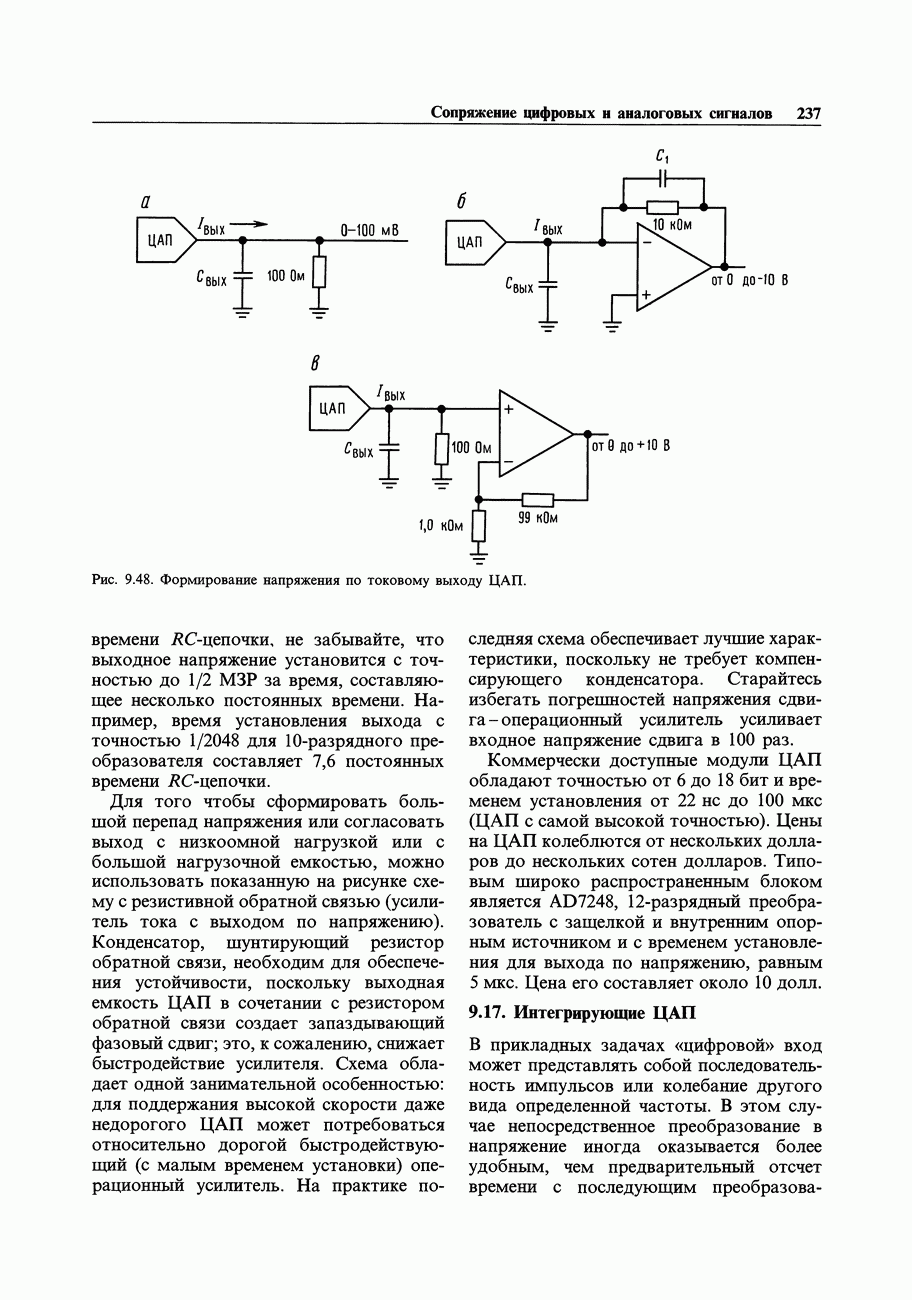
- 9.16. Цифро-аналоговые преобразователи (ЦАП)
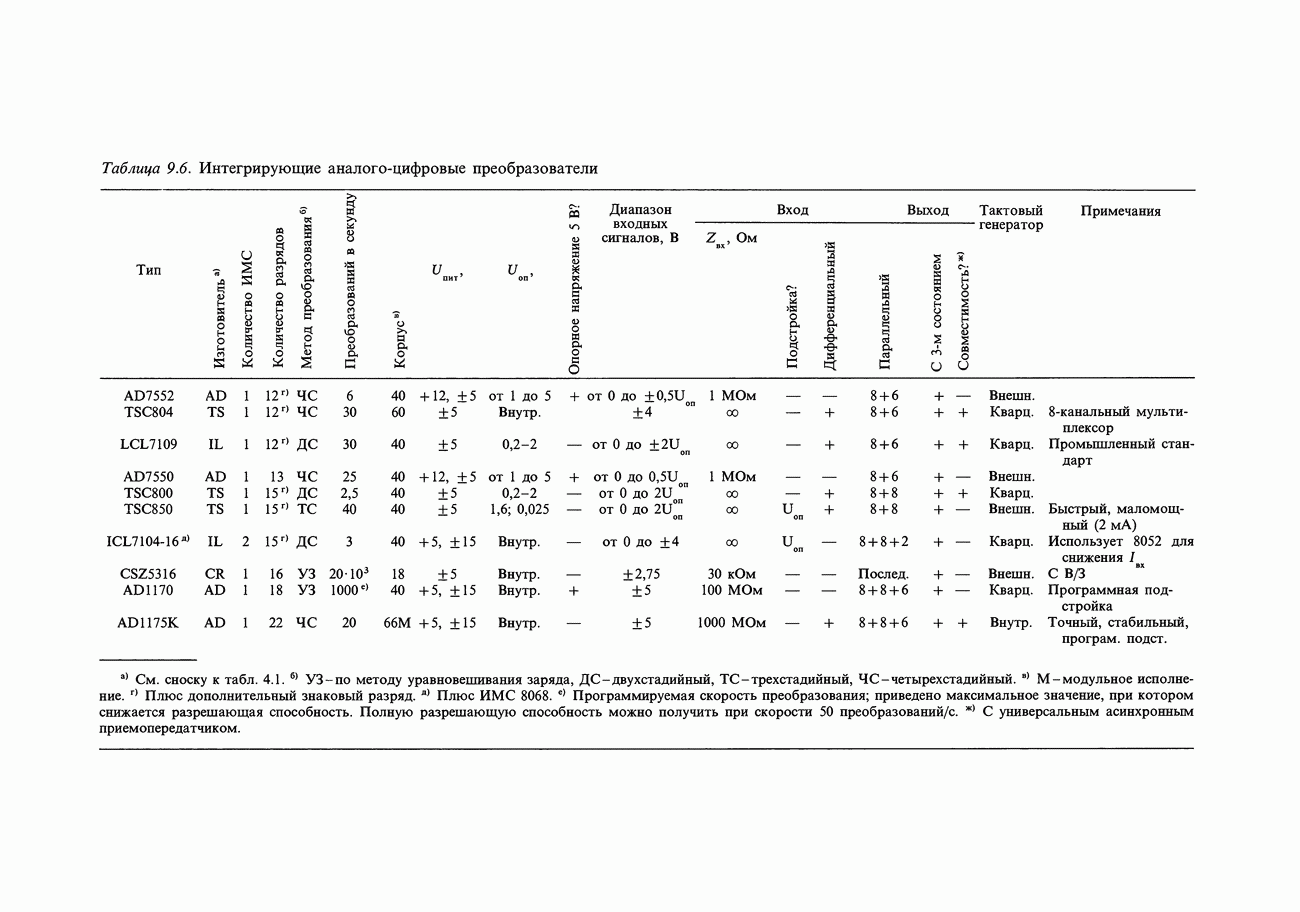
- 9.17. Интегрирующие ЦАП
- 9.18. ЦАП с умножением
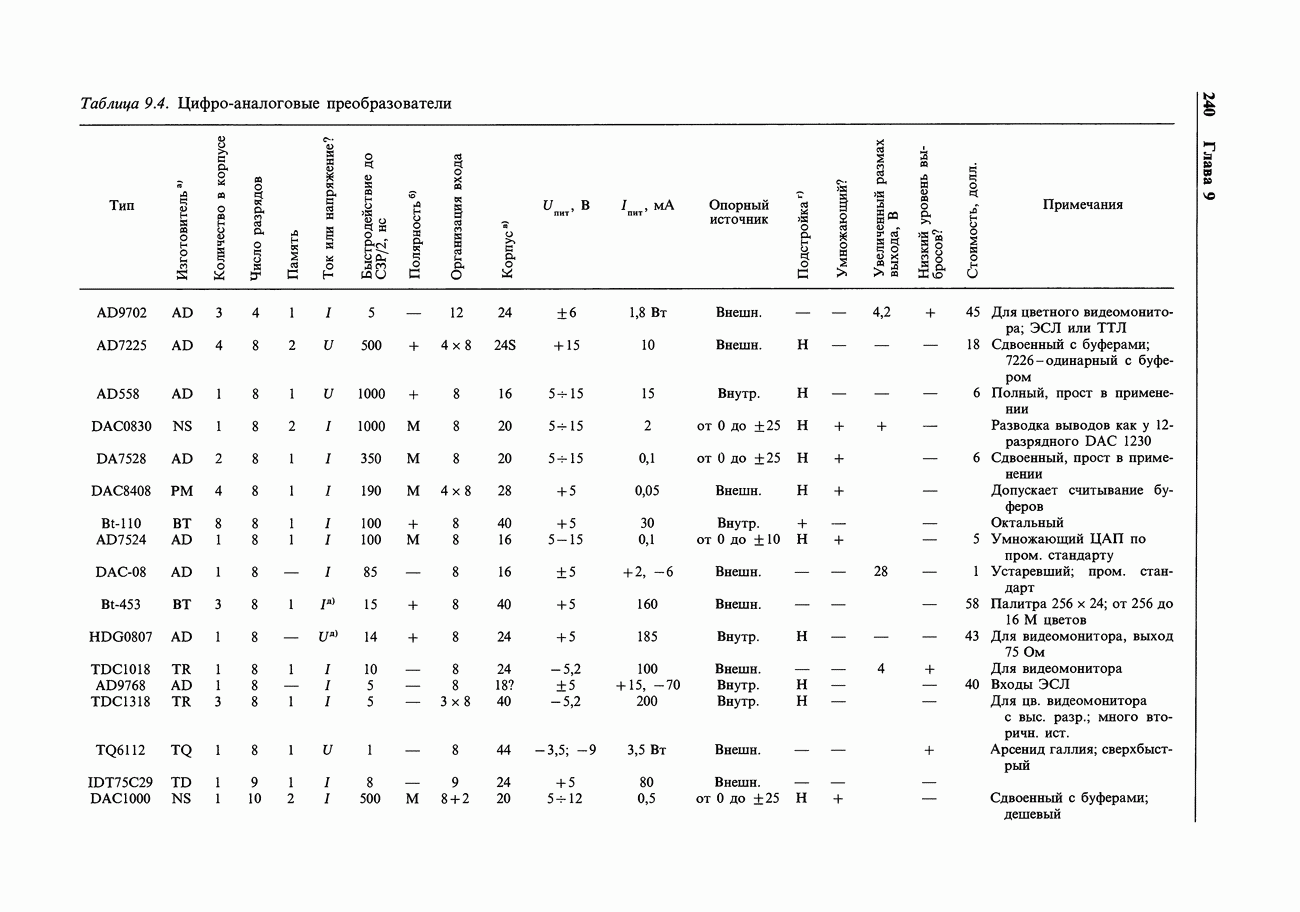
- 9.19. Выбор ЦАП
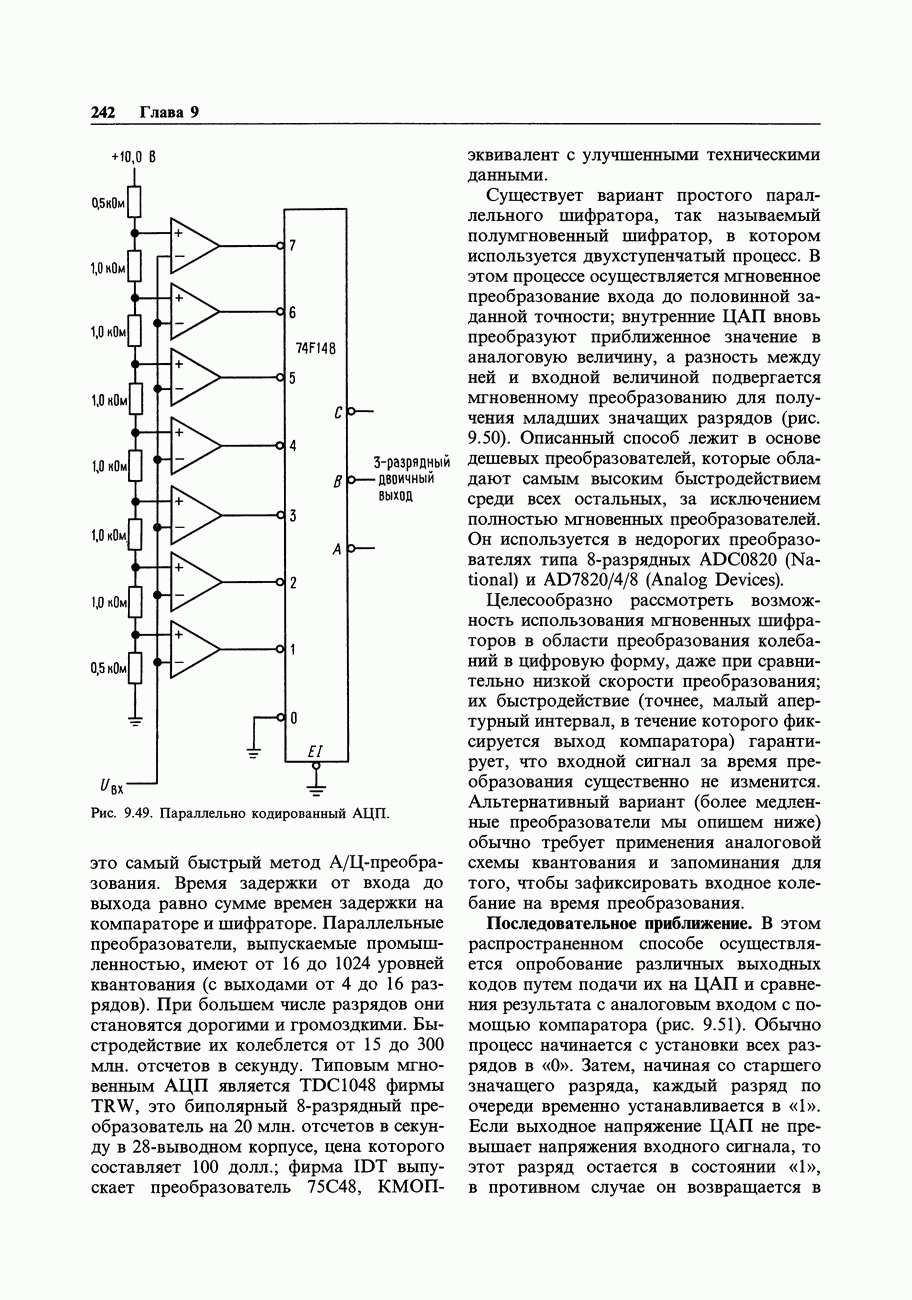
- 9.20. Аналого-цифровые преобразователи
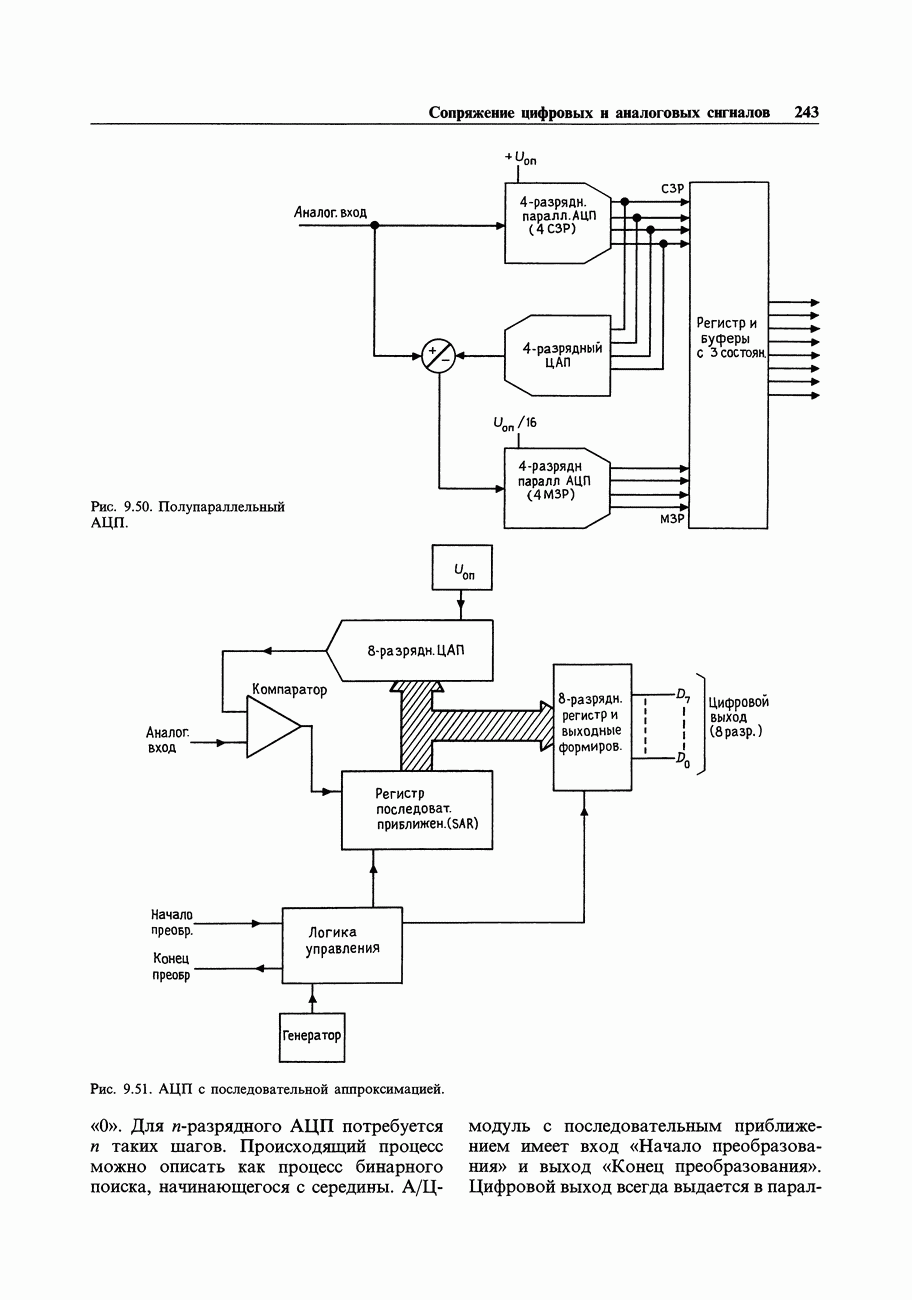
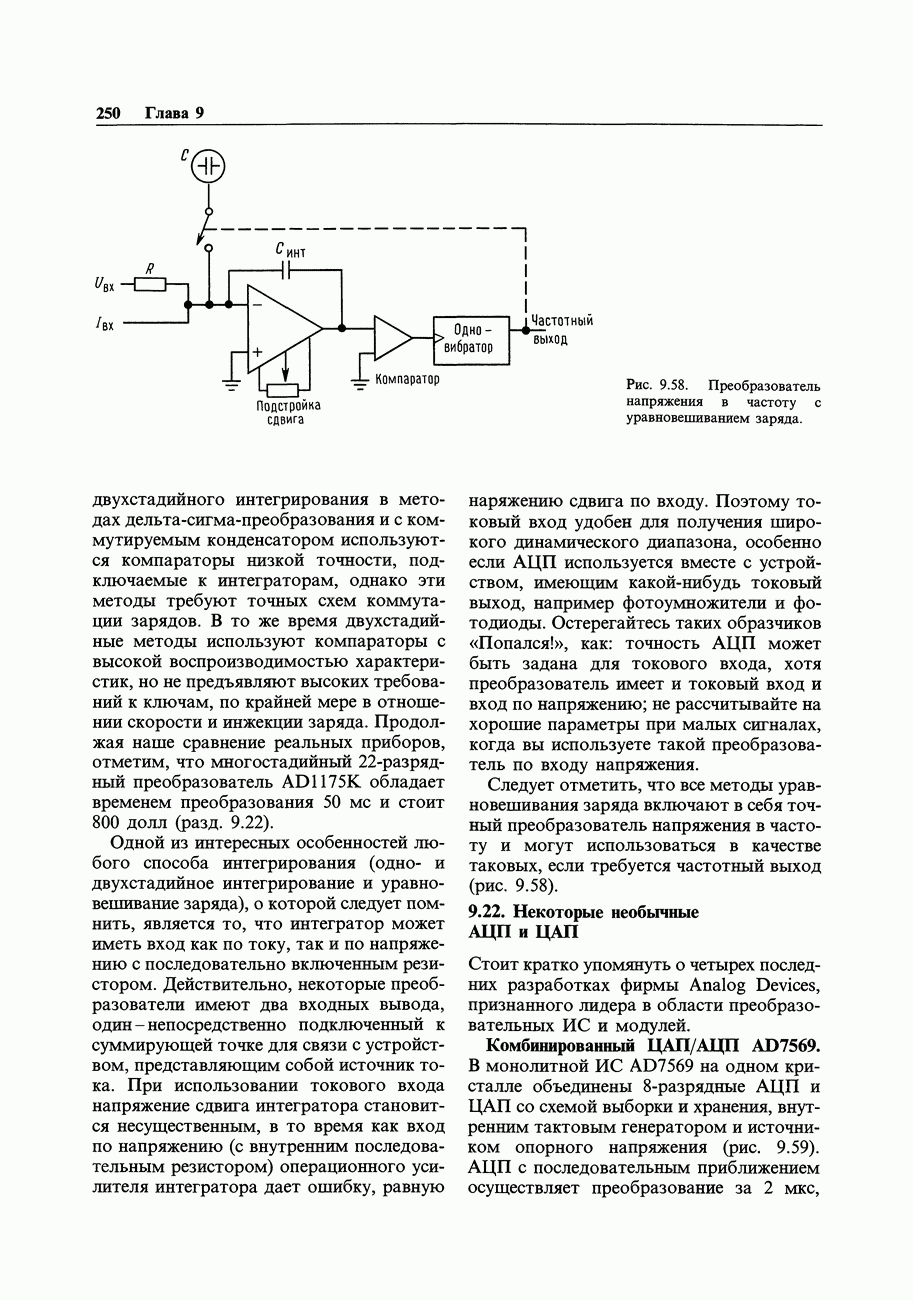
- 9.21. Методы уравновешивания заряда
- 9.22. Некоторые необычные АЦП и ЦАП
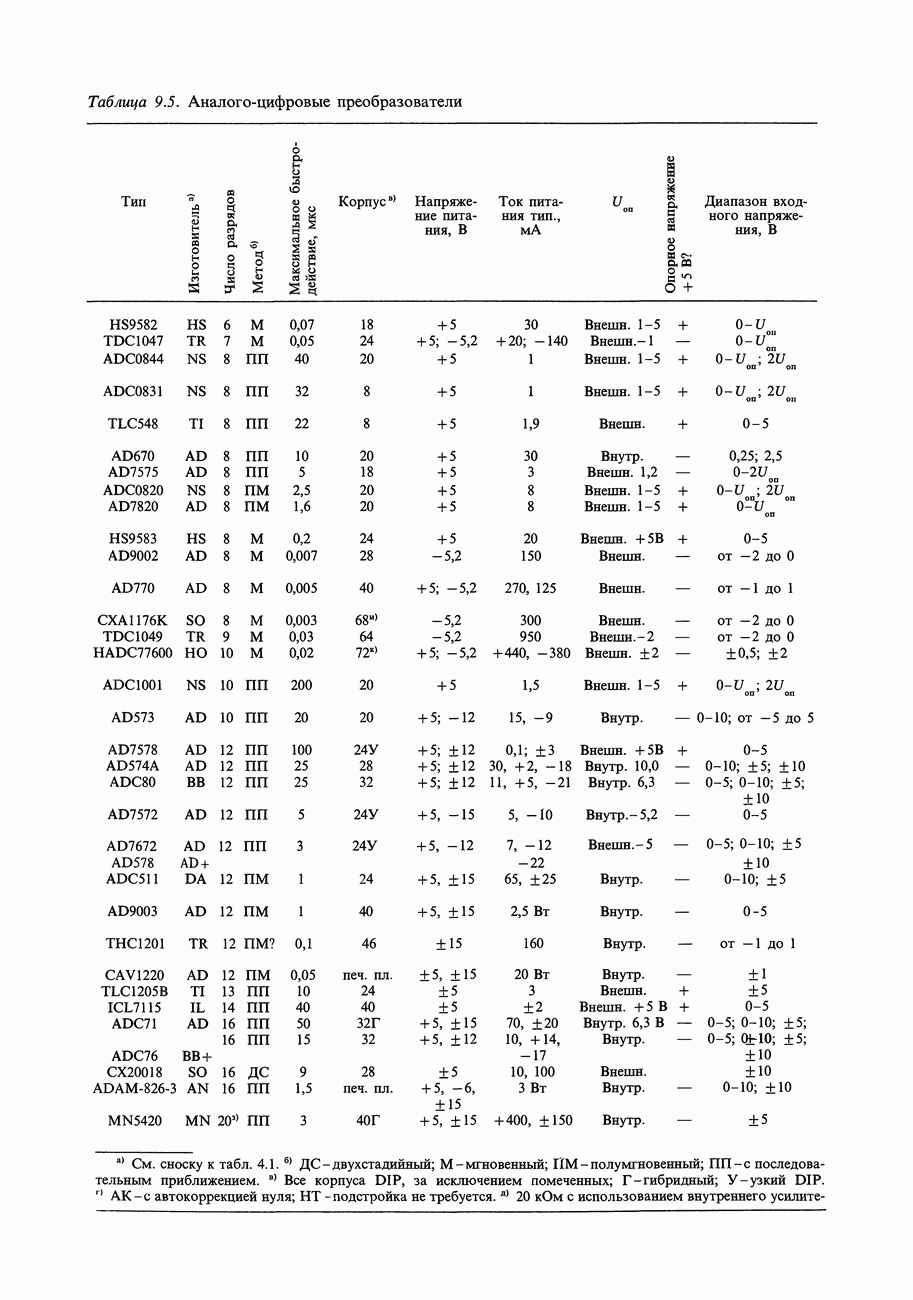
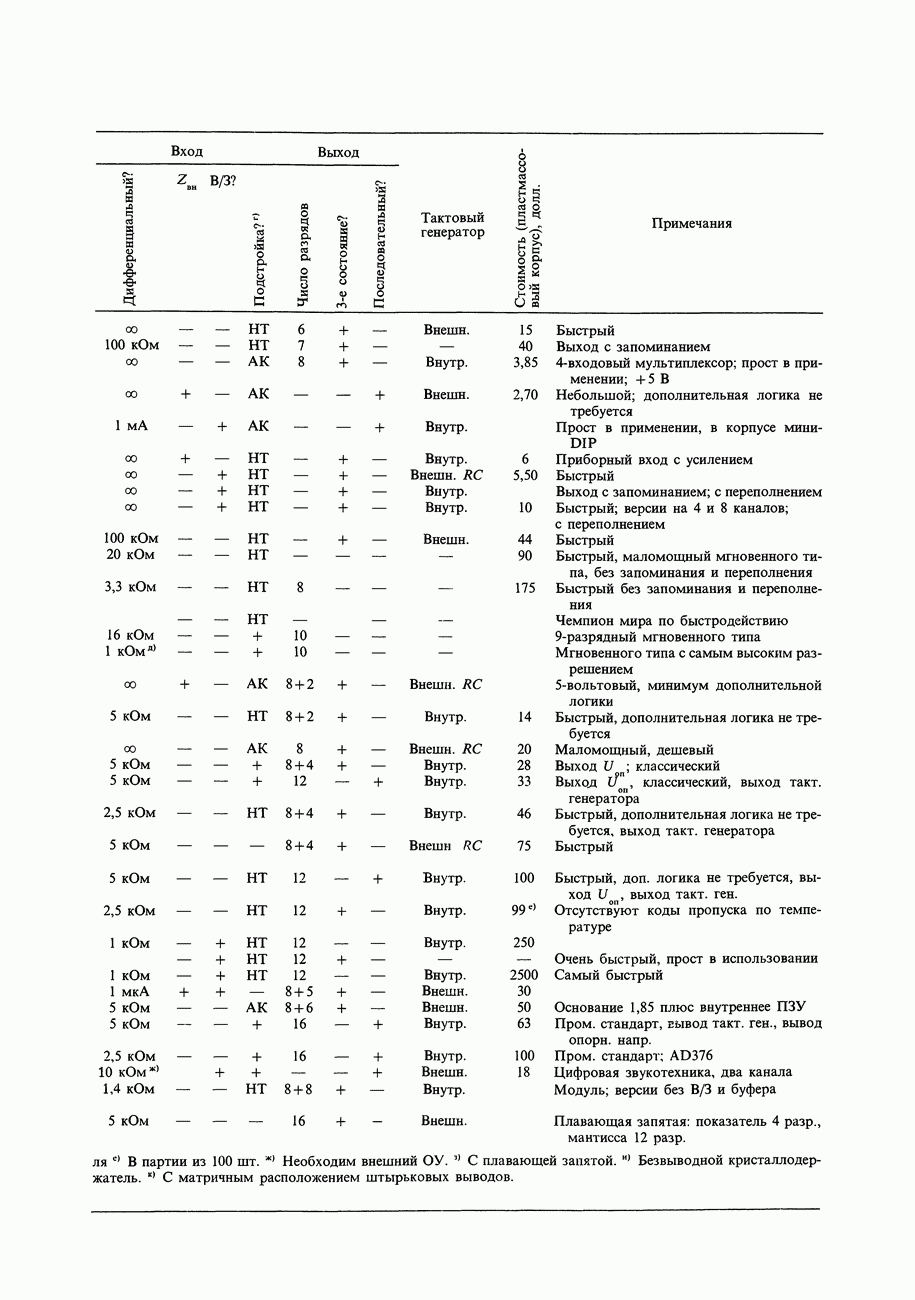
- 9.23. Выбор АЦП
- ПРИМЕРЫ А/Ц-ПРЕОБРАЗОВАНИЯ
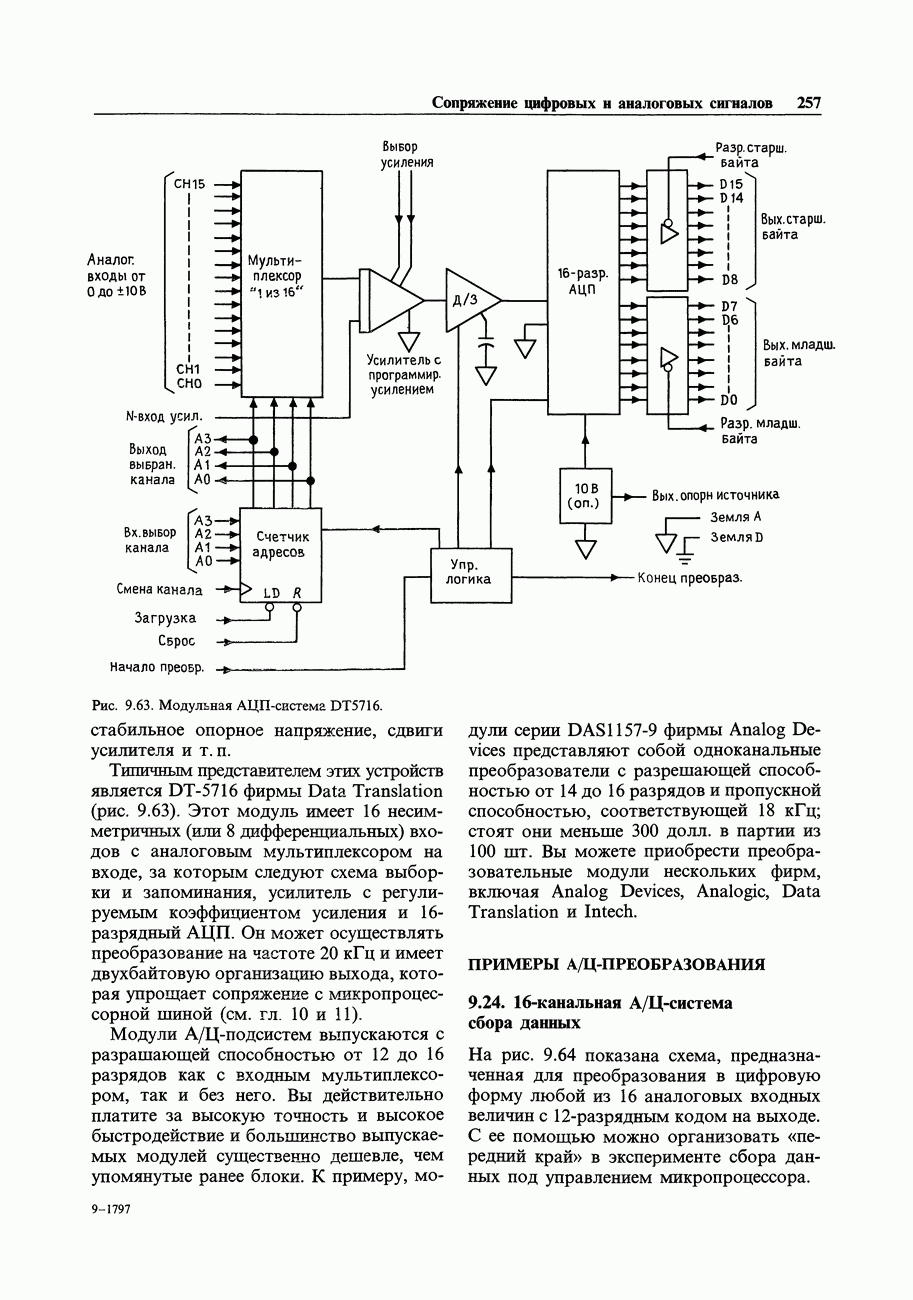
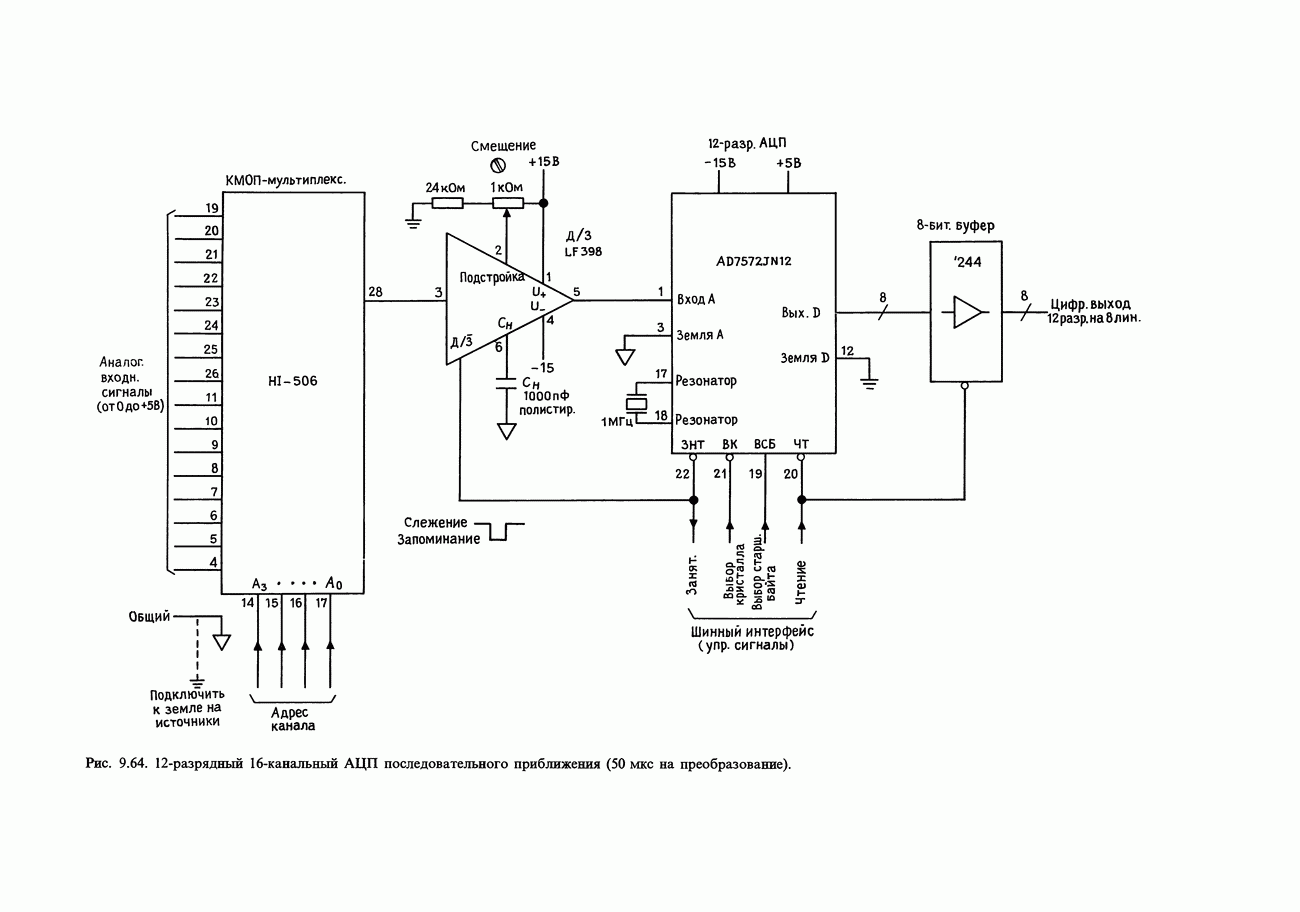
- 9.24. 16-канальная А/Ц-система сбора данных
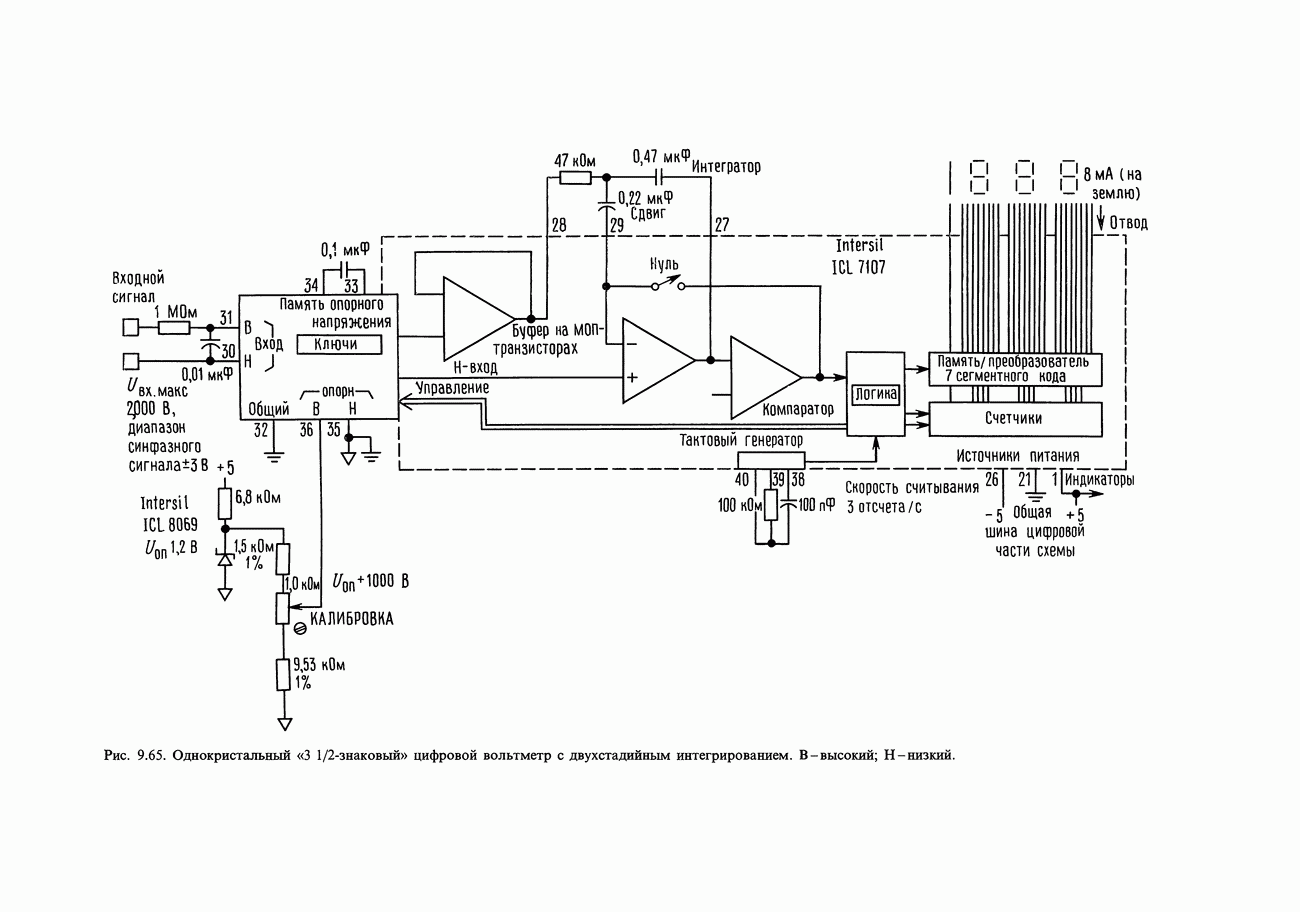
- 9.25. 3 1/2 — знаковый цифровой вольтметр
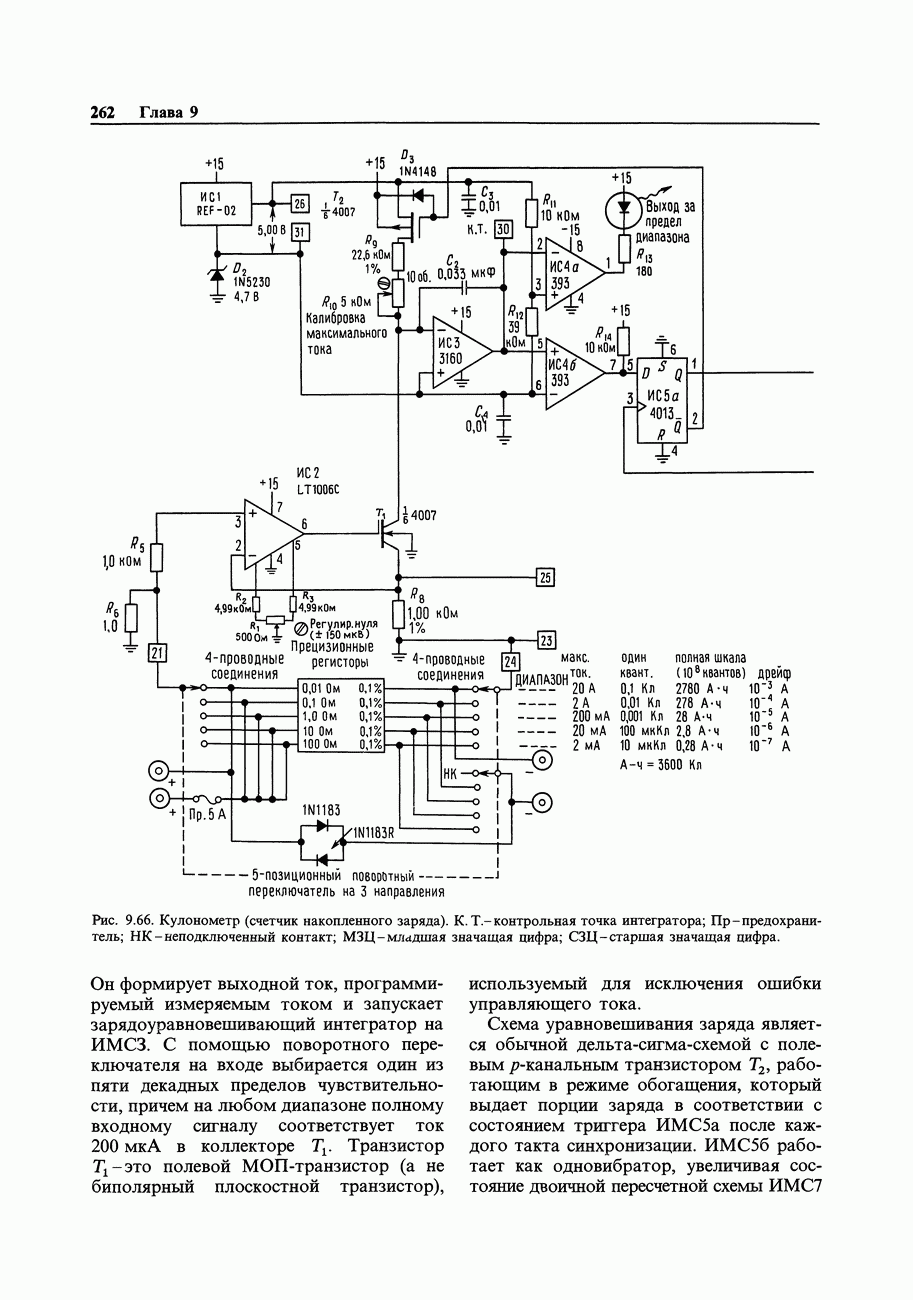
- 9.26. Кулонометр
- СХЕМЫ ФАЗОВОЙ АВТОПОДСТРОЙКИ ЧАСТОТЫ
- 9.28. Проектирование ФАПЧ
- 9.29. Пример разработки: умножитель частоты
- 9.30. Захват и слежение в системе ФАПЧ
- 9.31. Некоторые примеры применения систем ФАПЧ
- ПСЕВДОСЛУЧАЙНЫЕ ДВОИЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ГЕНЕРАТОРЫ ШУМА
- 9.32. Цифровые методы генерации шума
- 9.33. Последовательности, генерируемые регистрами сдвига с обратными связями
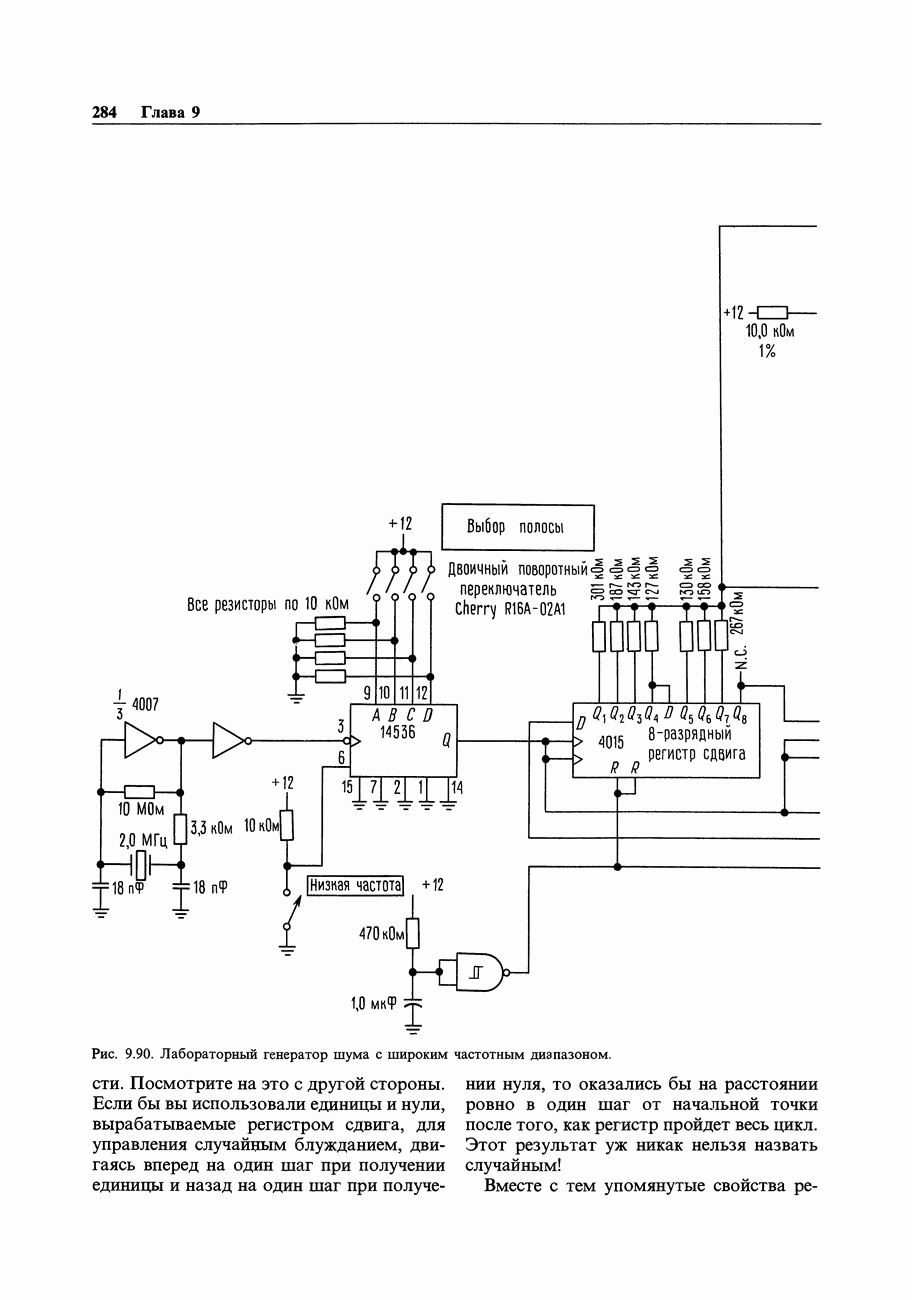
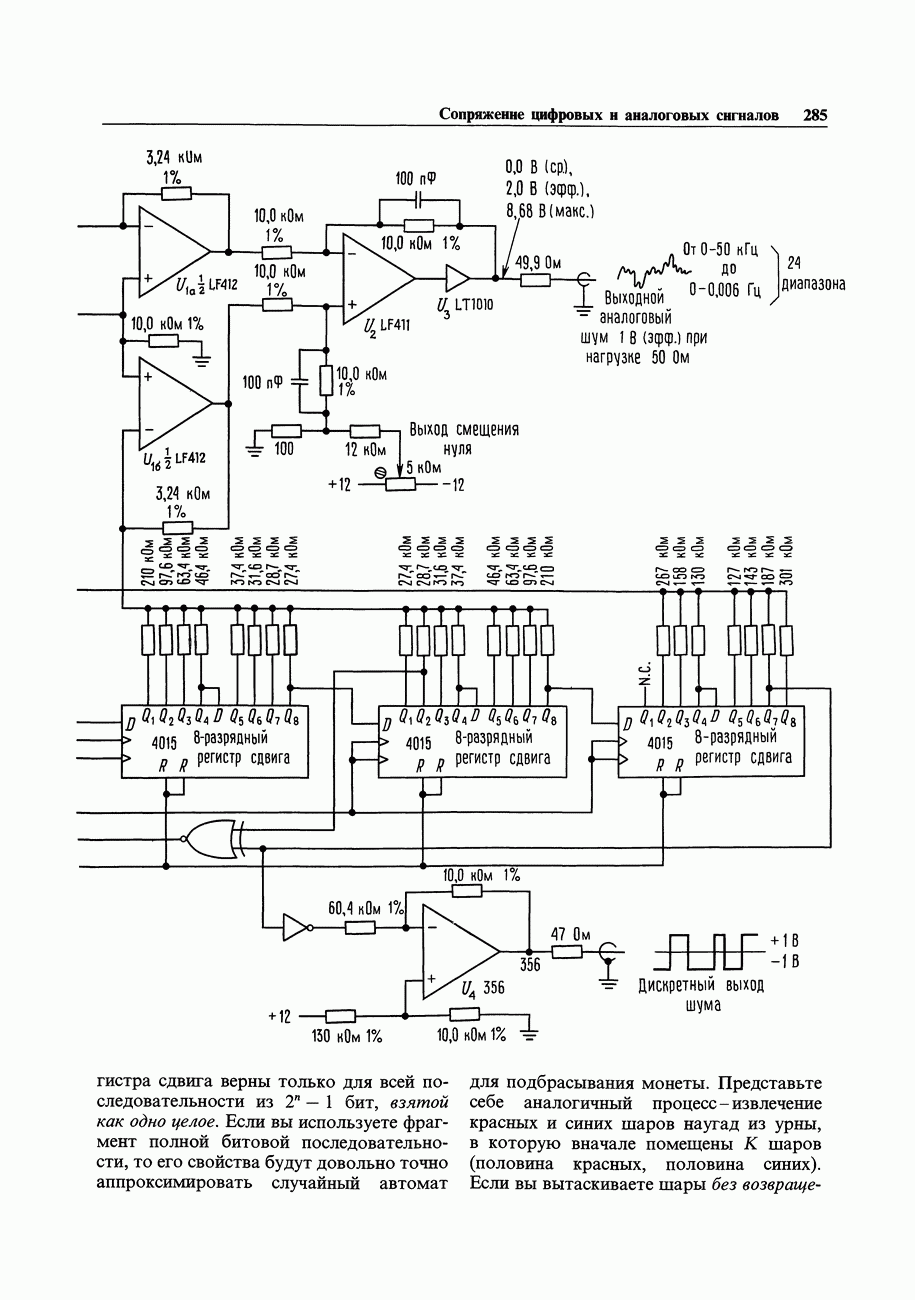
- 9.34. Формирование аналогового шума с использованием последовательностей максимальной длины
- 9.35. Энергетический спектр последовательности, сформированной при помощи регистра сдвига
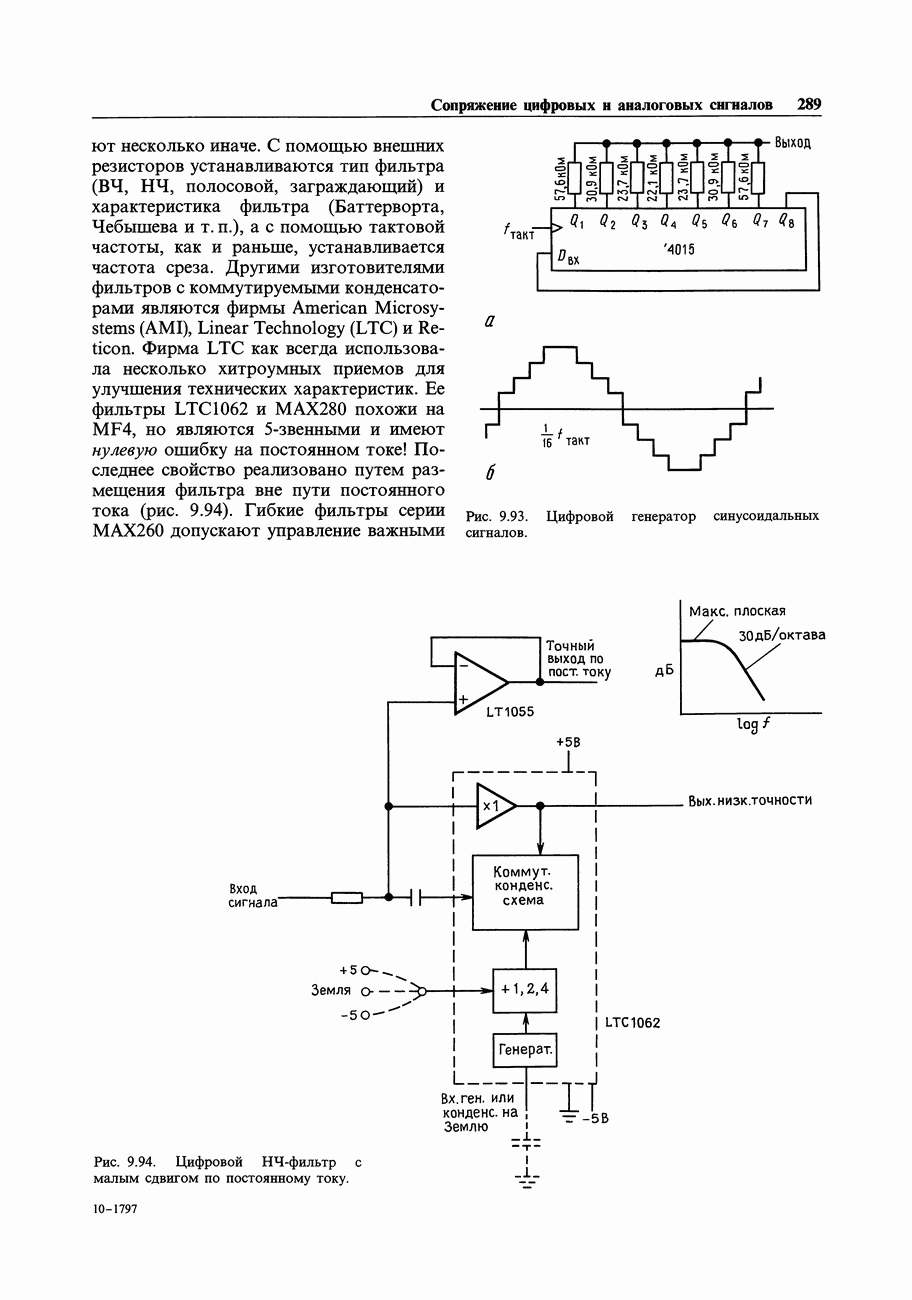
- 9.36. Низкочастотная фильтрация
- 9.37. Краткое заключение
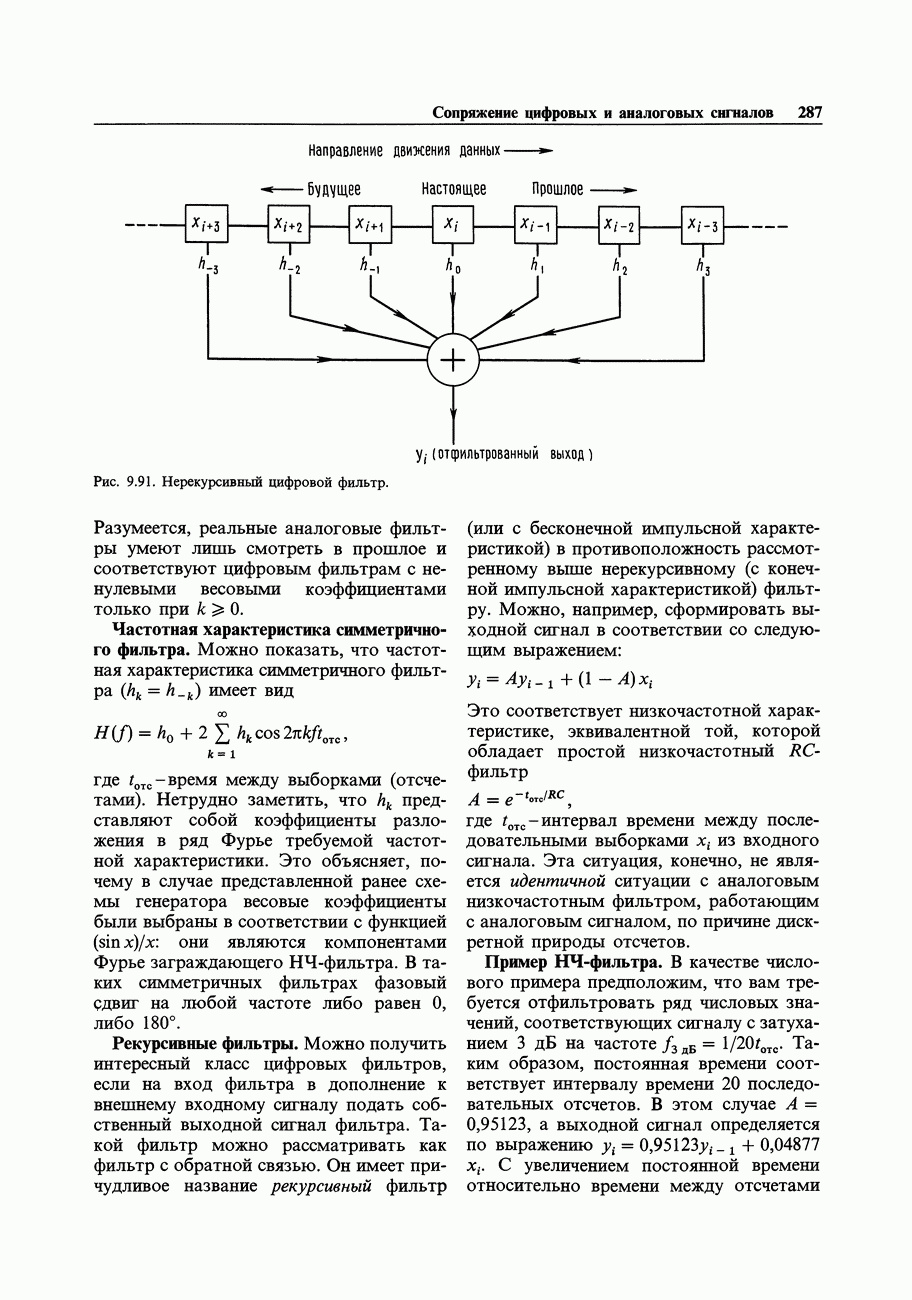
- 9.38. Цифровые фильтры
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 10. МИКРОЭВМ
- МИНИ-ЭВМ, МИКРОЭВМ И МИКРОПРОЦЕССОРЫ
- 10.01. Архитектура микроЭВМ
- НАБОР КОМАНД КОМПЬЮТЕРА
- 10.02. Язык ассемблера и язык машинных кодов
- 10.03. Упрощенный набор команд процессора Intel 8086/8
- 10.04. Программный пример
- СИГНАЛЫ МАГИСТРАЛИ И ЕЕ ФУНКЦИОНИРОВАНИЕ
- 10.05. Основные сигналы магистрали: данные, адрес, синхронизация
- 10.06. Программируемый ввод-вывод: вывод данных
- 10.07. Программируемый ввод-вывод: ввод данных
- 10.08. Программируемый ввод-вывод: регистры состояний
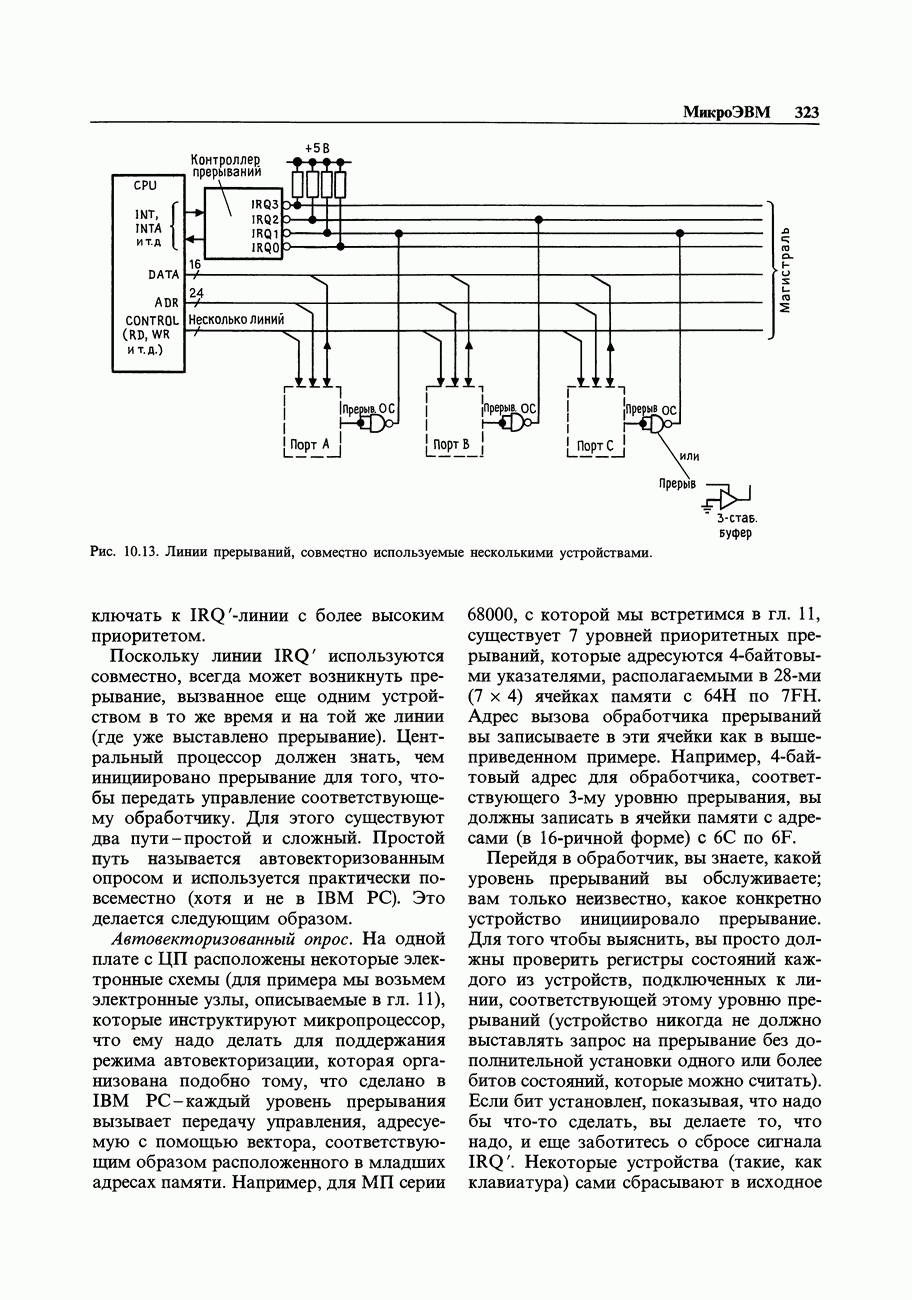
- 10.09. Прерывания
- 10.10. Обработка прерываний
- 10.11. Прерывания в целом
- 10.12. Прямой доступ в память
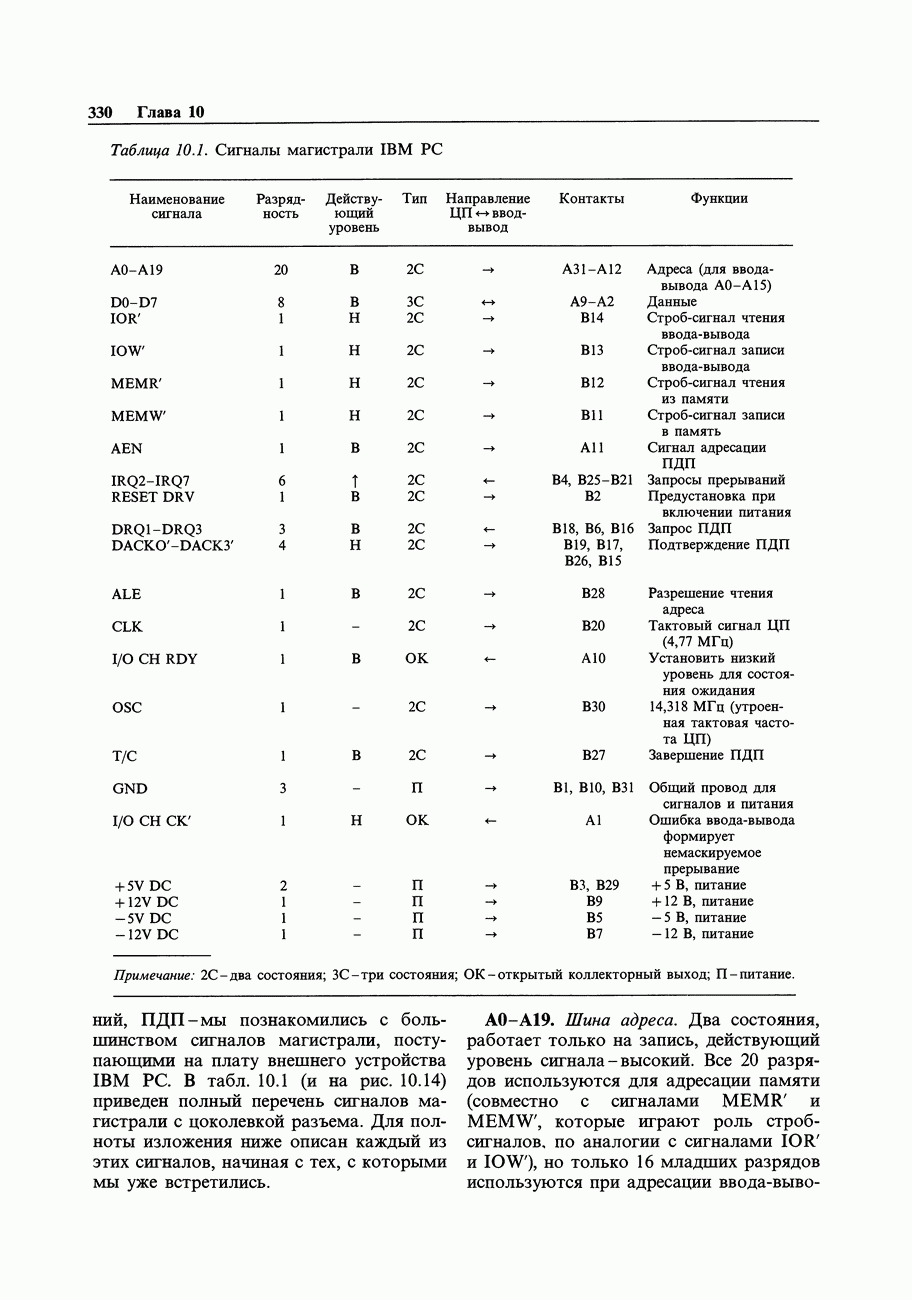
- 10.13. Сводный перечень сигналов магистрали IBM PC
- 10.14. Синхронный и асинхронный протоколы магистрали
- 10.15. Магистрали других микрокомпьютеров
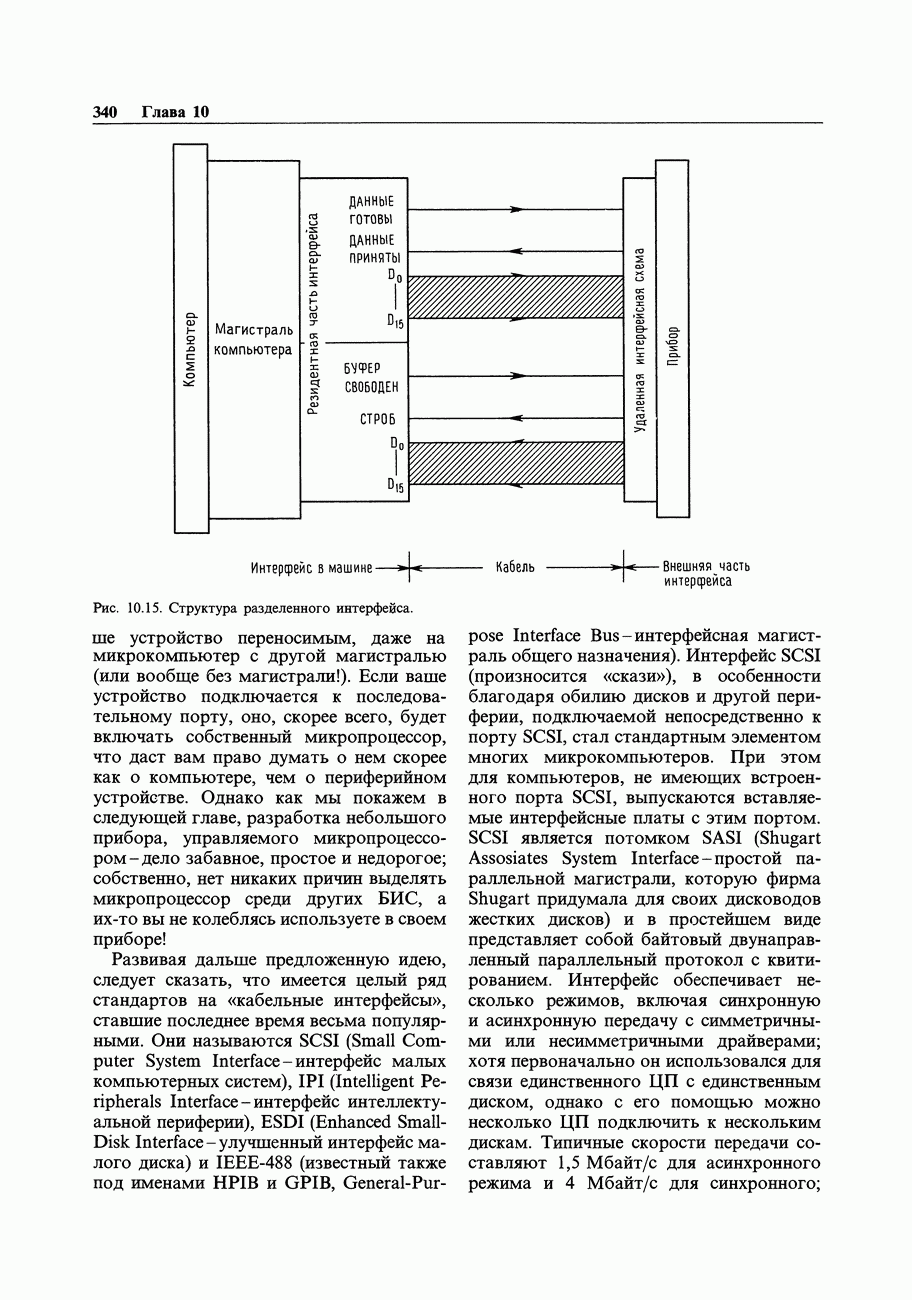
- 10.16. Подключение к компьютеру периферийных устройств
- СИСТЕМНЫЕ КОНЦЕПЦИИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- 10.17. Программирование
- 10.18. Операционные системы, файлы и использование памяти
- ПРИНЦИПЫ ПЕРЕДАЧИ ДАННЫХ
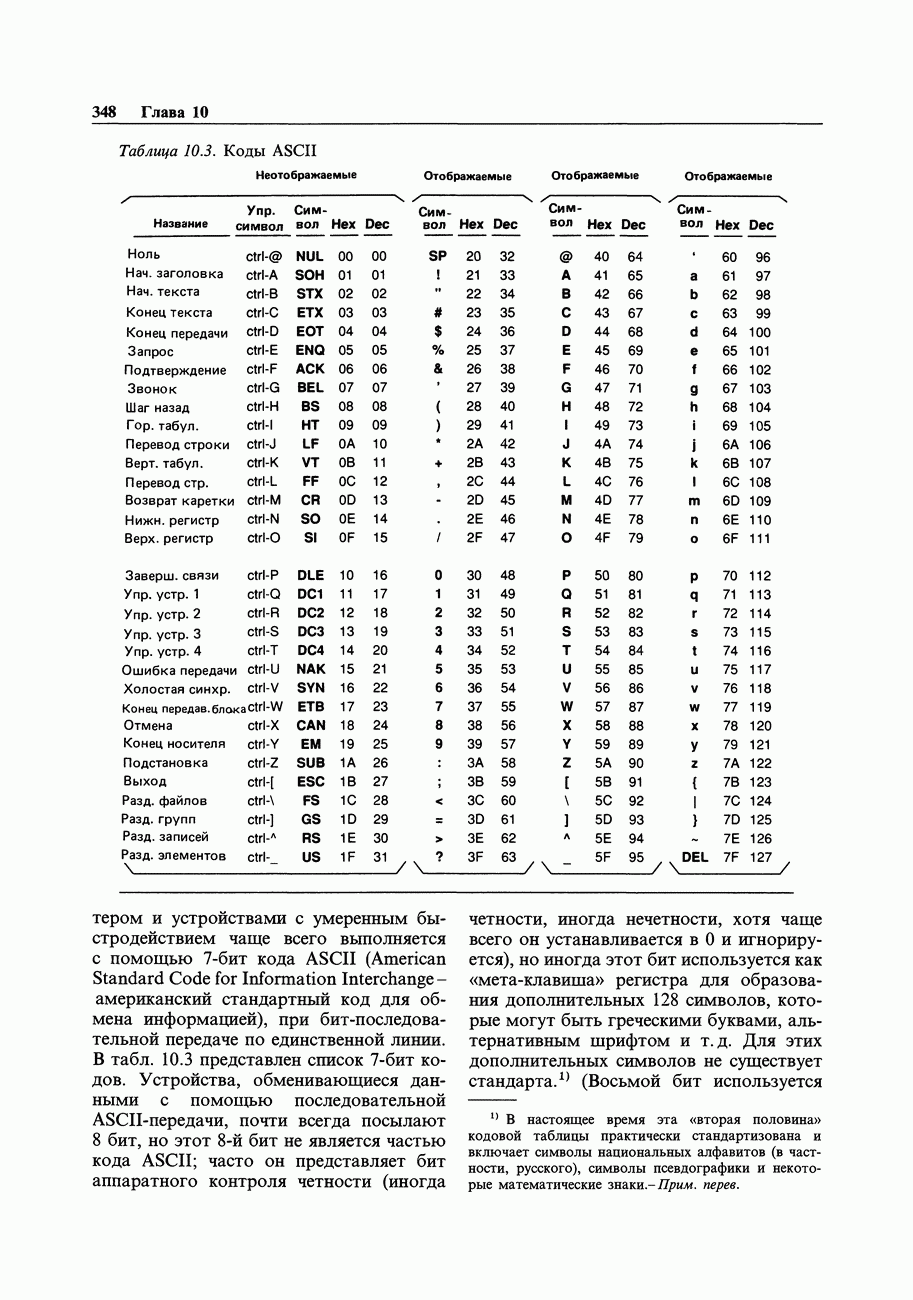
- 10.19. Последовательная связь и коды ASCII
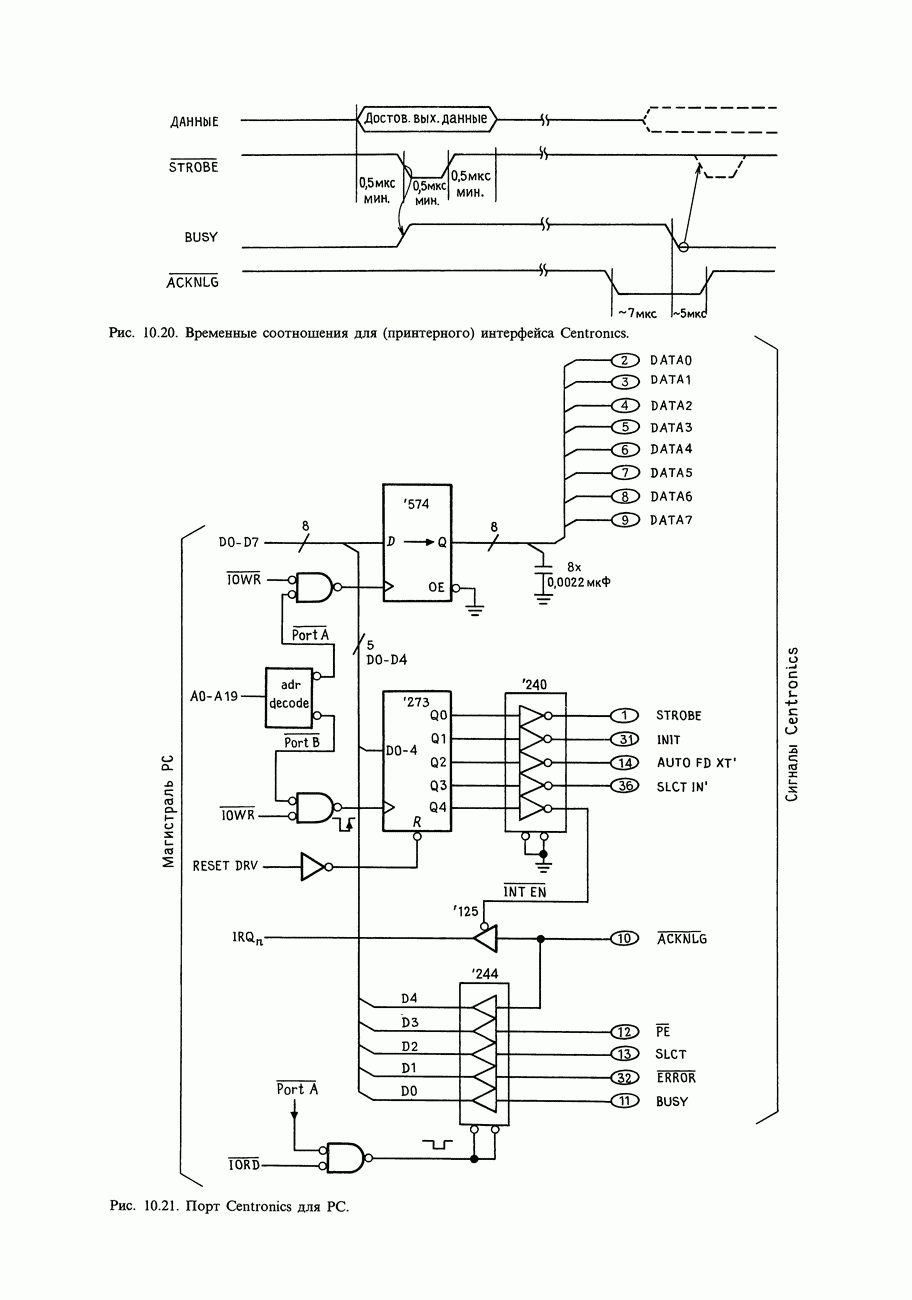
- 10.20. Параллельная связь
- 10.21. Локальные вычислительные цепи
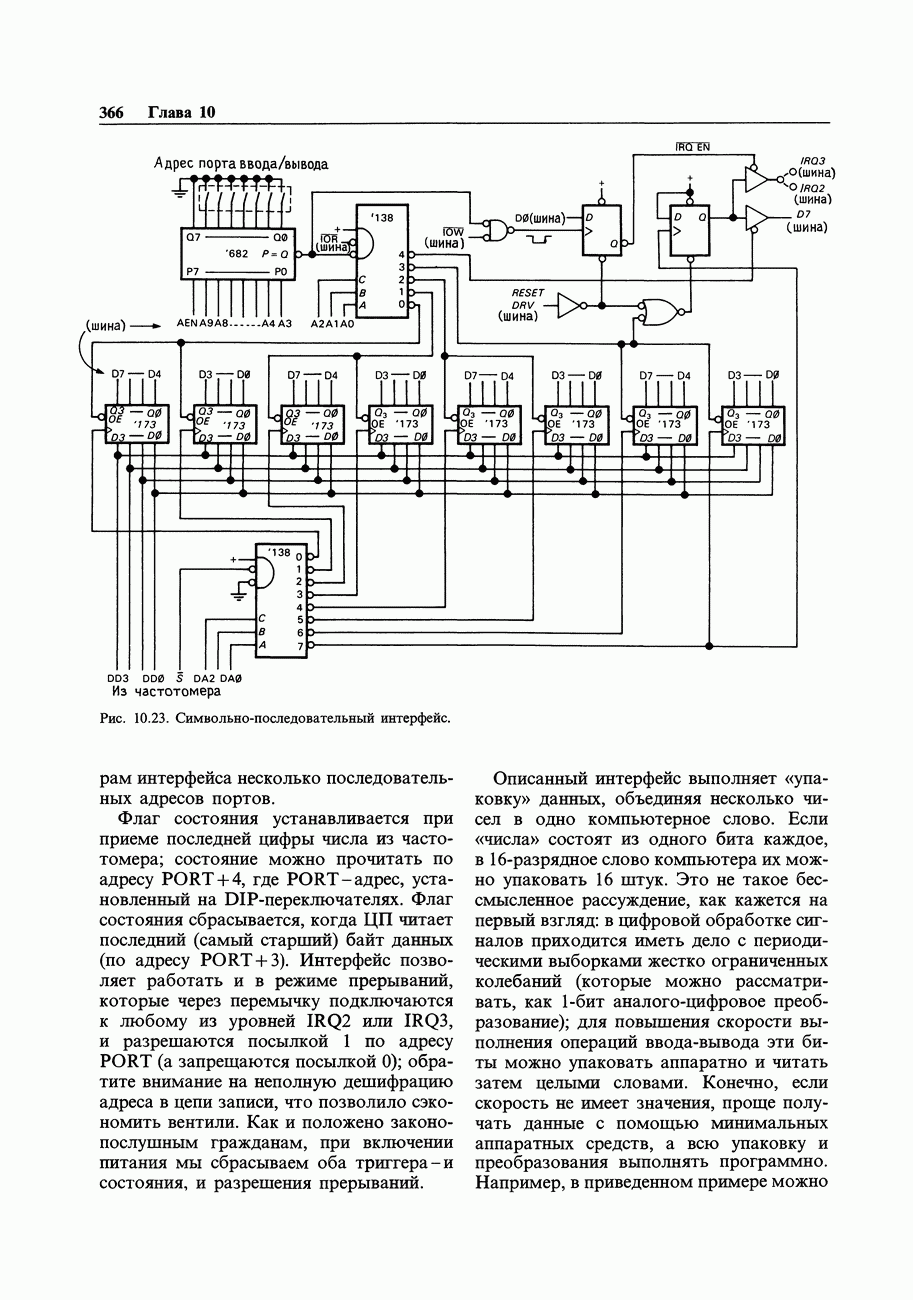
- 10.22. Пример интерфейса: аппаратная упаковка данных
- 10.23. Форматы чисел