| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
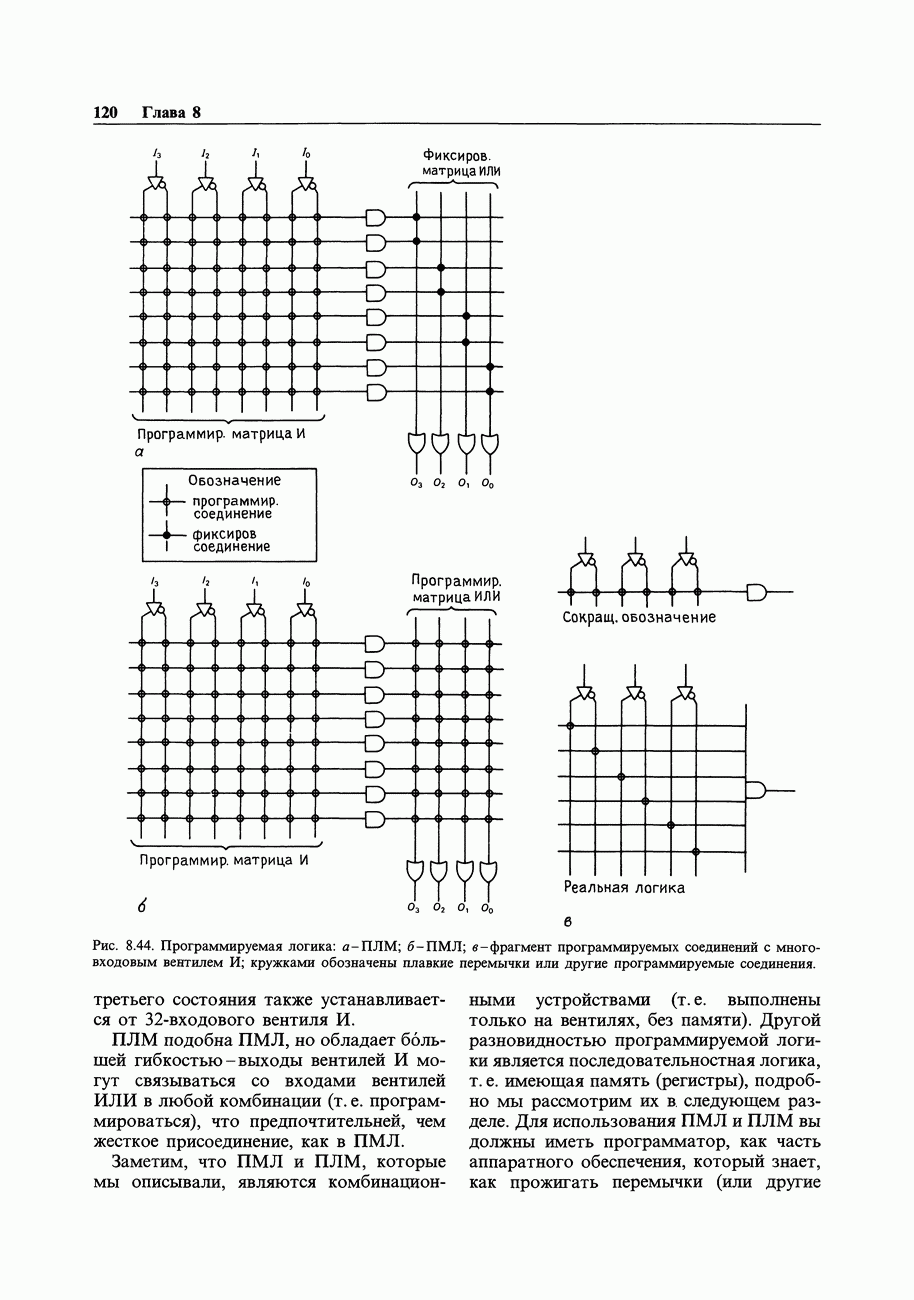
8.18. Последовательностная логика-объединение памяти и вентилей
После того как мы изучили свойства триггеров, посмотрим, что можно получить, если объединить их с рассмотренной ранее комбинационной (вентильной) логикой. Составленные из вентилей и триггеров схемы, представляют собой наиболее общую форму цифровой логики.

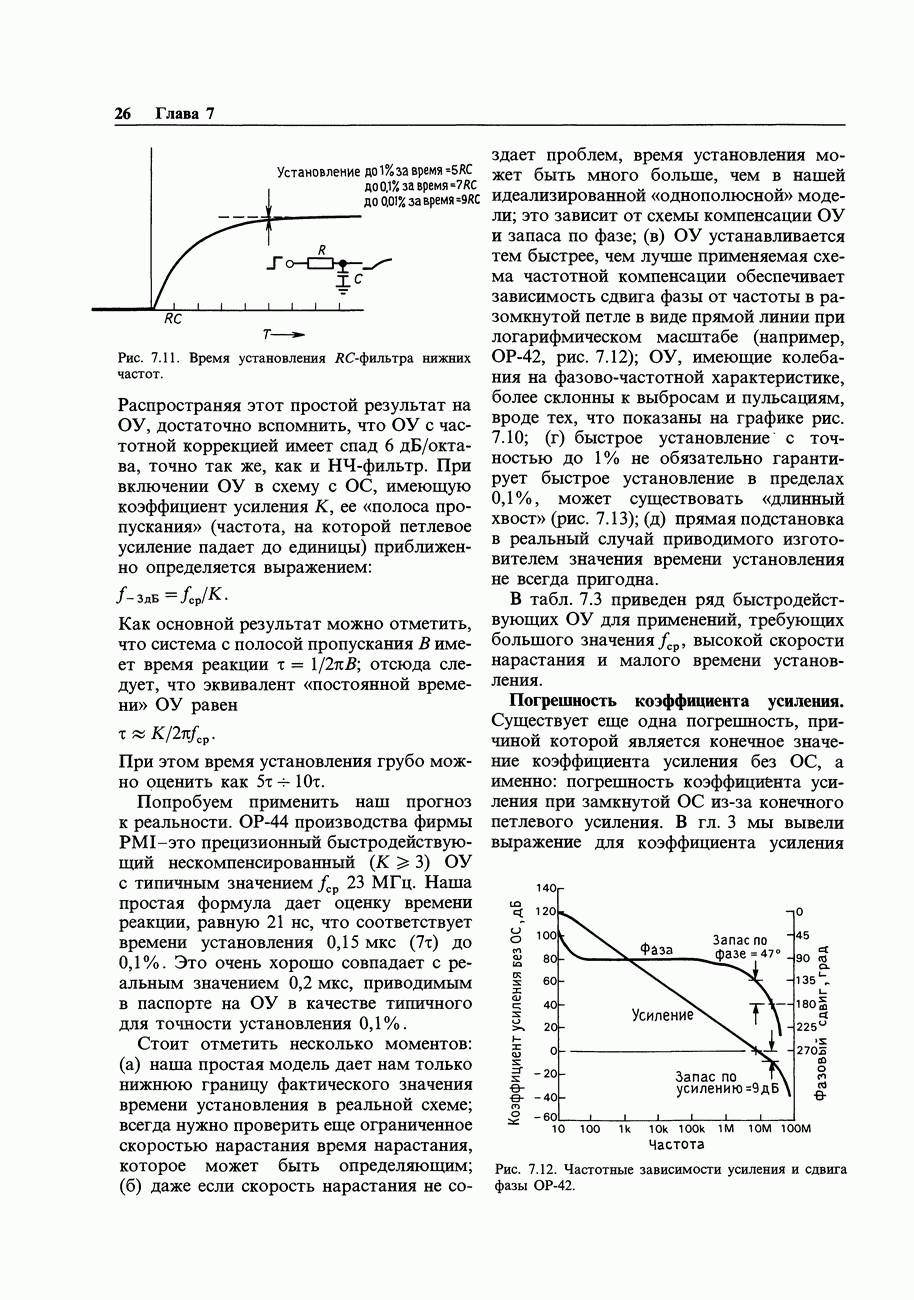
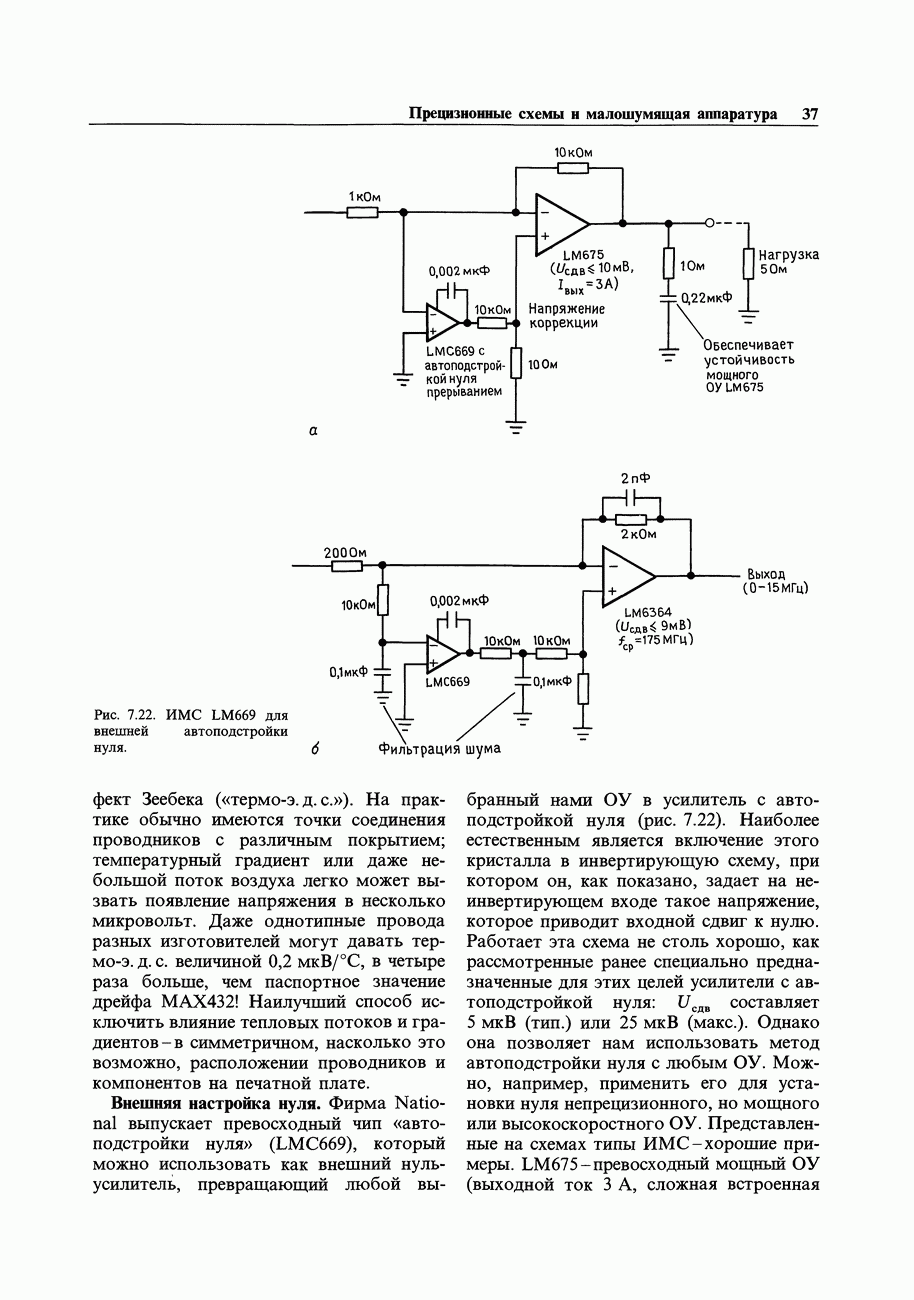
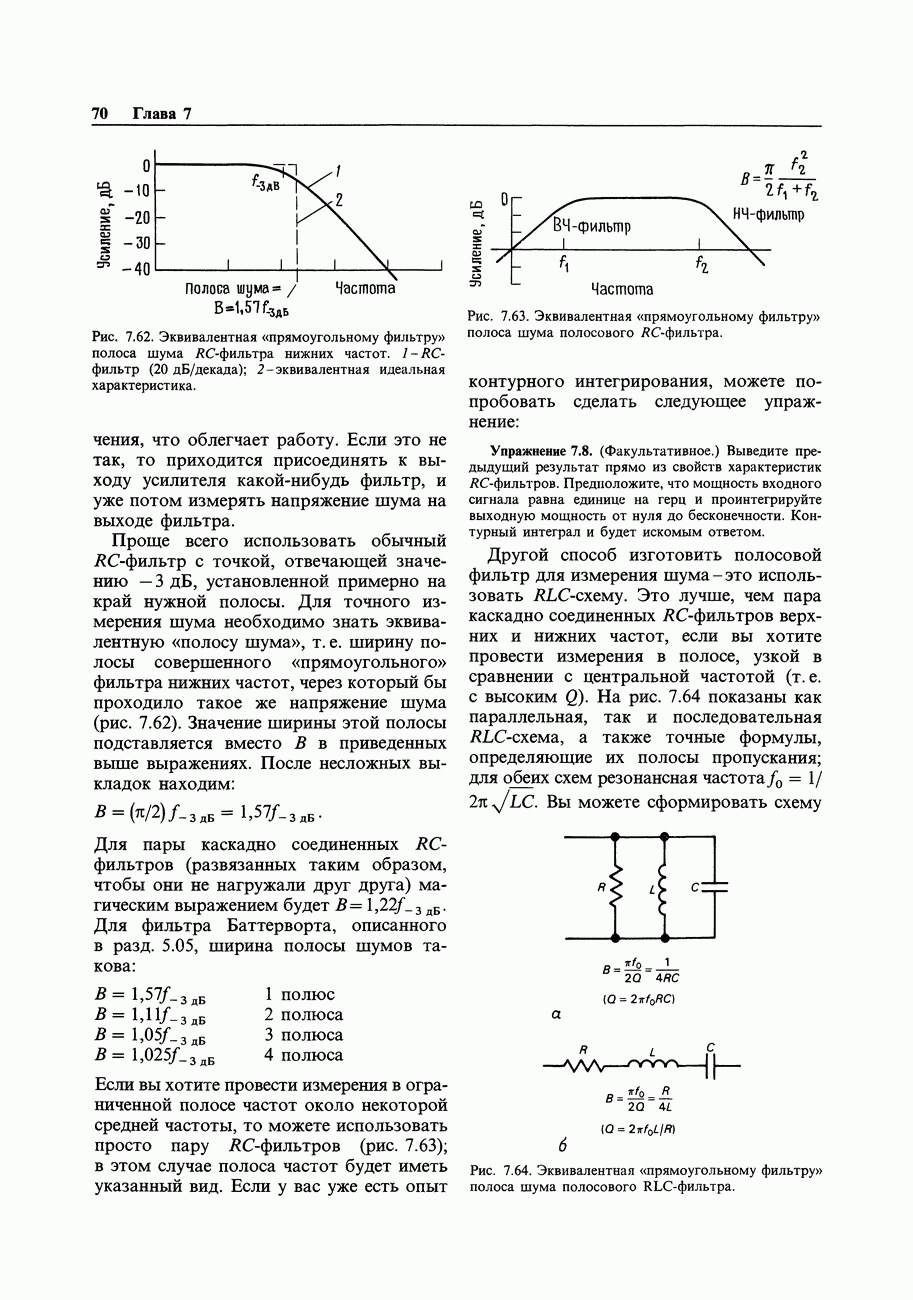
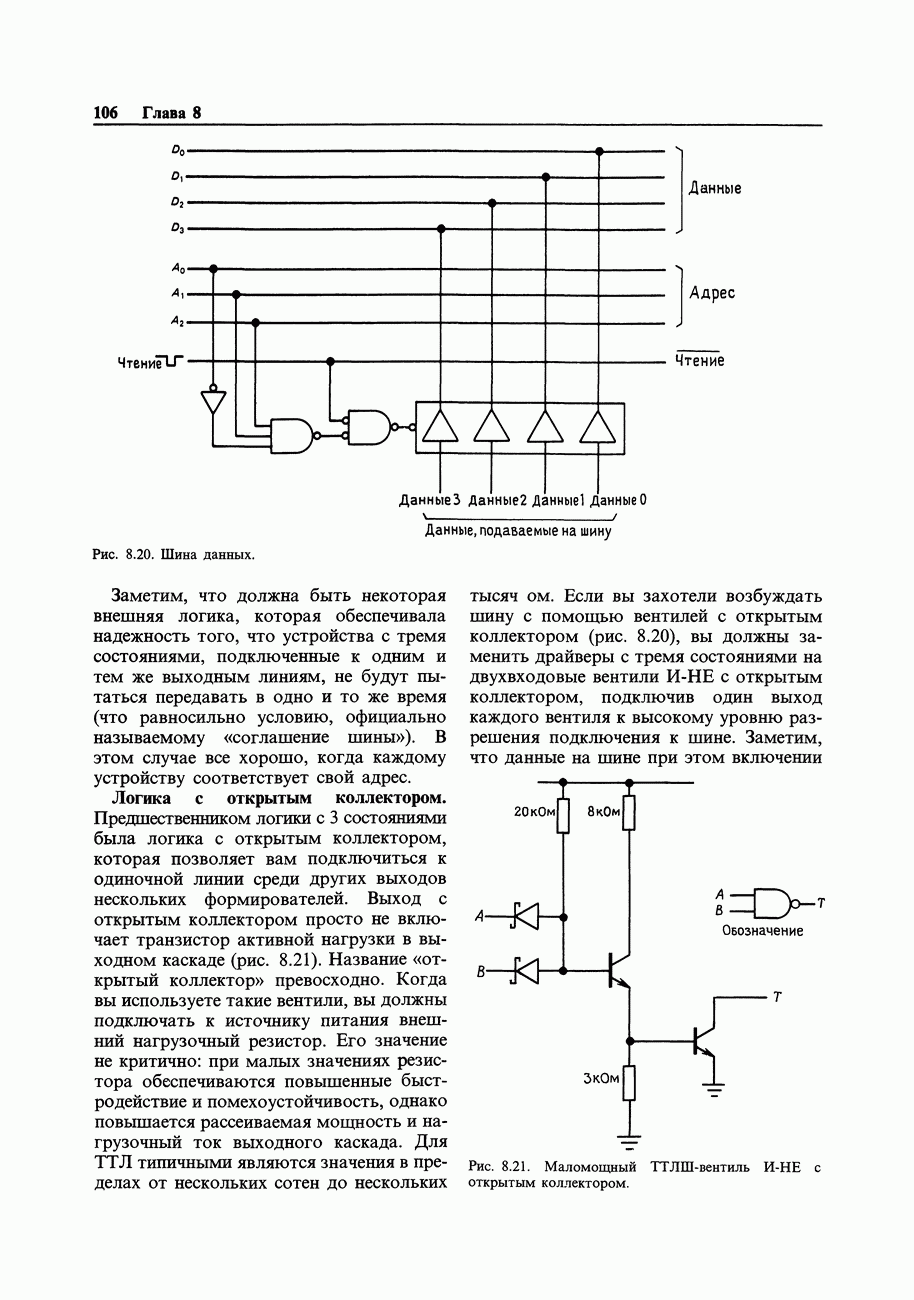
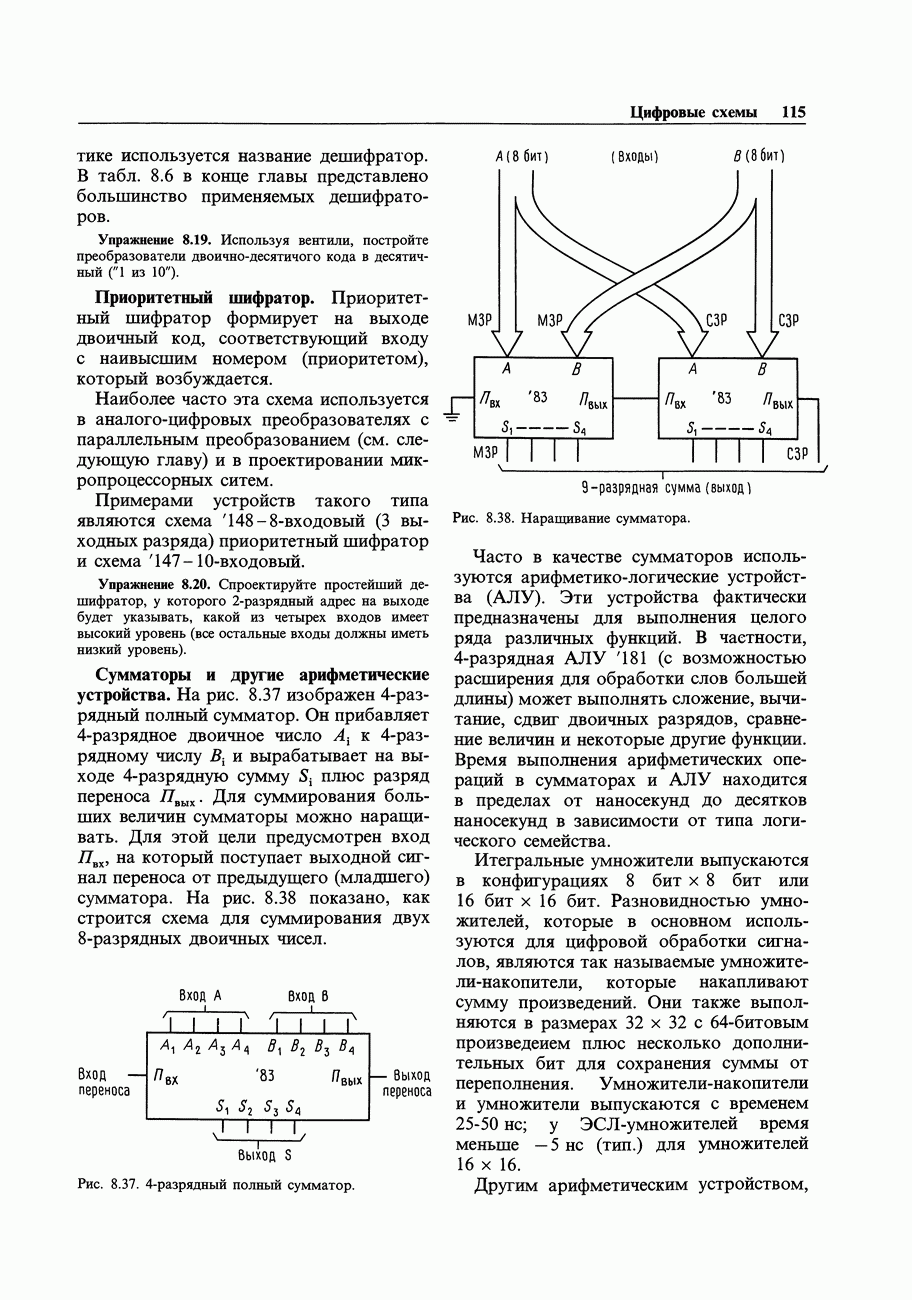
Рис. 8.57. Классическая последовательностная схема: регистры памяти и комбинационная логика. Эту схему можно легко реализовать с использованием однокристальных регистровых ПМЛ (см. разд. 8.27).
Синхронные тактируемые системы.
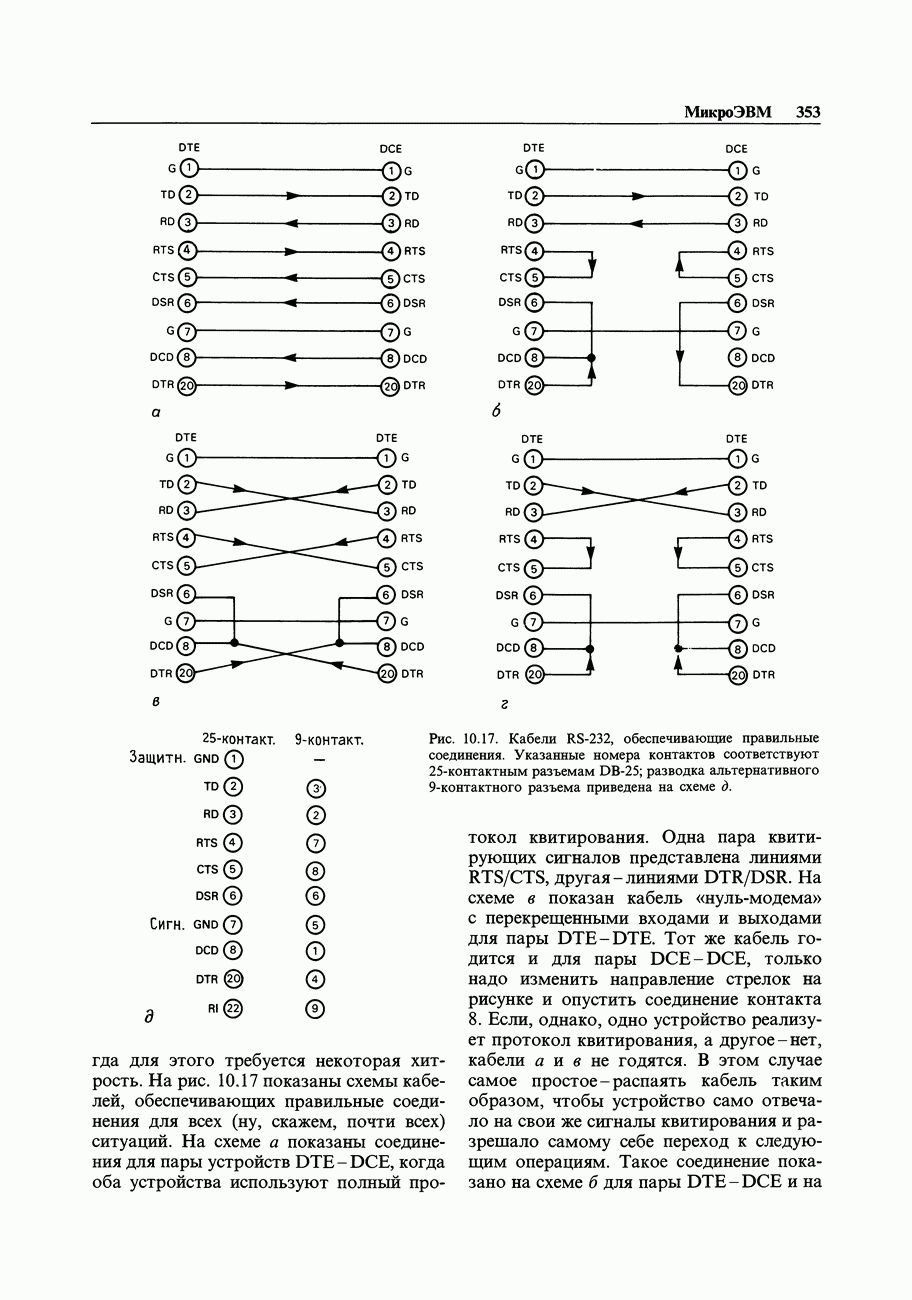
Мы уже упомянули в предыдущем разделе, что последовательностные логические схемы, в которых для управления всеми триггерами используется общий источник тактовых импульсов, имеют ряд преимуществ. В таких синхронных системах все действия происходят сразу же после возникновения тактового импульса и определяются тем состоянием, которое имеет место непосредственно перед его возникновением. Общая структура подобной системы показана на рис. 8.57.Все триггеры объединены в один общий регистр, представляющий собой не что иное, как набор  -триггеров, у которых тактовые входы соединены вместе, а индивидуальные
-триггеров, у которых тактовые входы соединены вместе, а индивидуальные  -входы и выходы Q выведены вовне. Каждый тактовый импульс вызывает передачу уровней, присутствующих на
-входы и выходы Q выведены вовне. Каждый тактовый импульс вызывает передачу уровней, присутствующих на  -входах, на соответствующие выходы Q. Блок, состоящий из вентилей, анализирует состояние выходов регистра и внешних входов, вырабатывает новую комбинацию сигнала для
-входах, на соответствующие выходы Q. Блок, состоящий из вентилей, анализирует состояние выходов регистра и внешних входов, вырабатывает новую комбинацию сигнала для  -входов регистра и выходные логические уровни.
-входов регистра и выходные логические уровни.

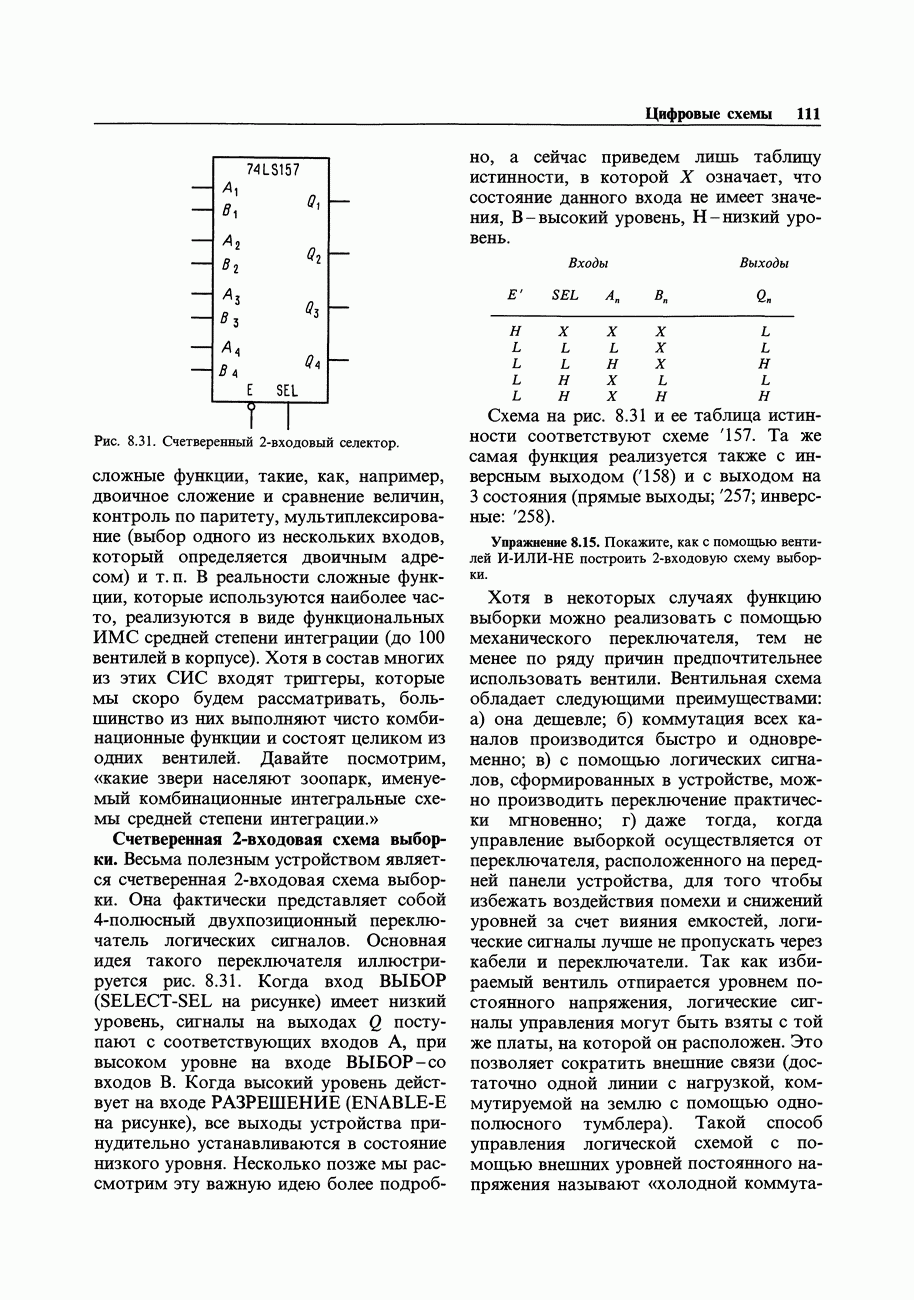
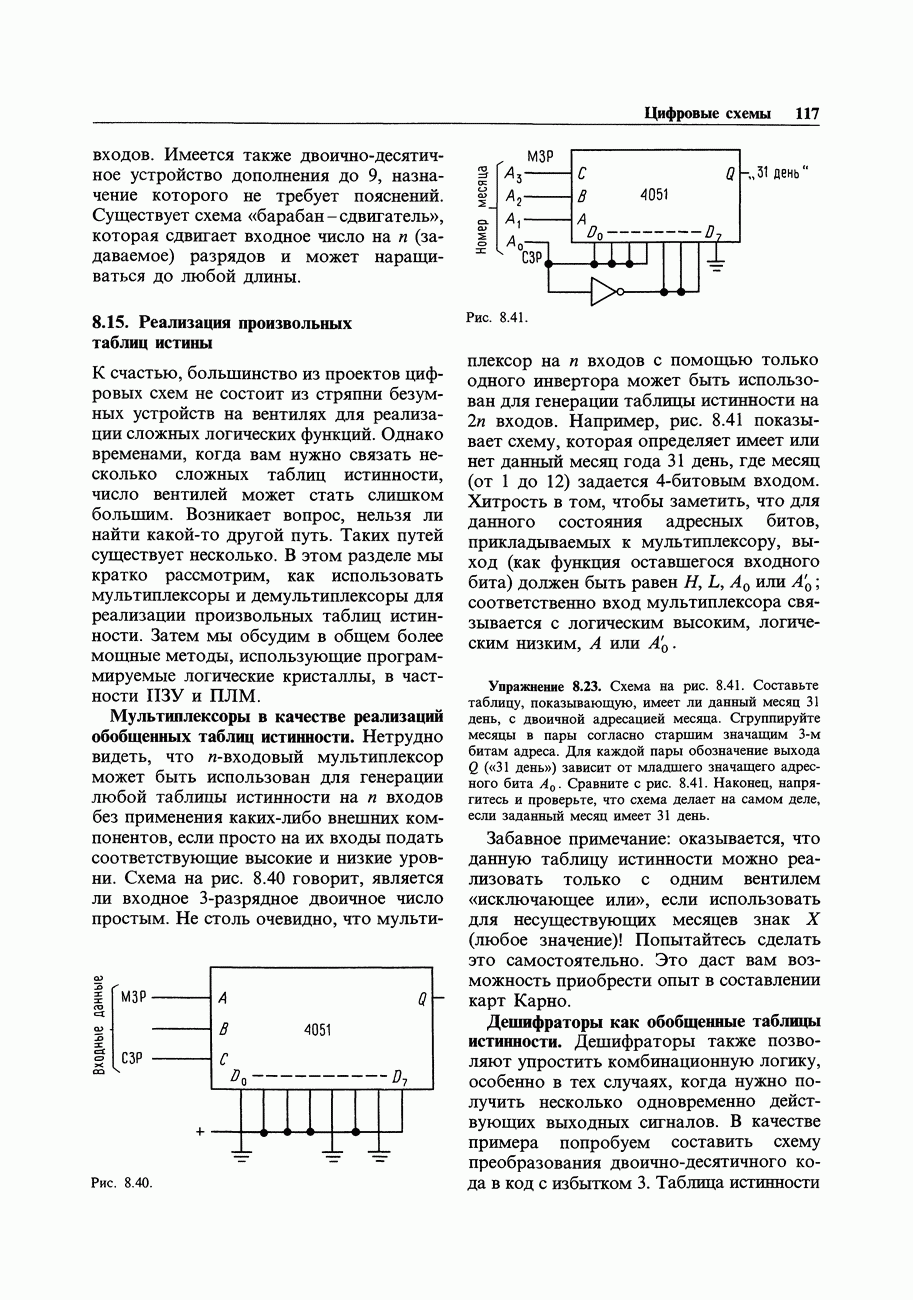
Рис. 8.58.
Эта с виду простая схема обладает очень большими возможностями. Рассмотрим пример.
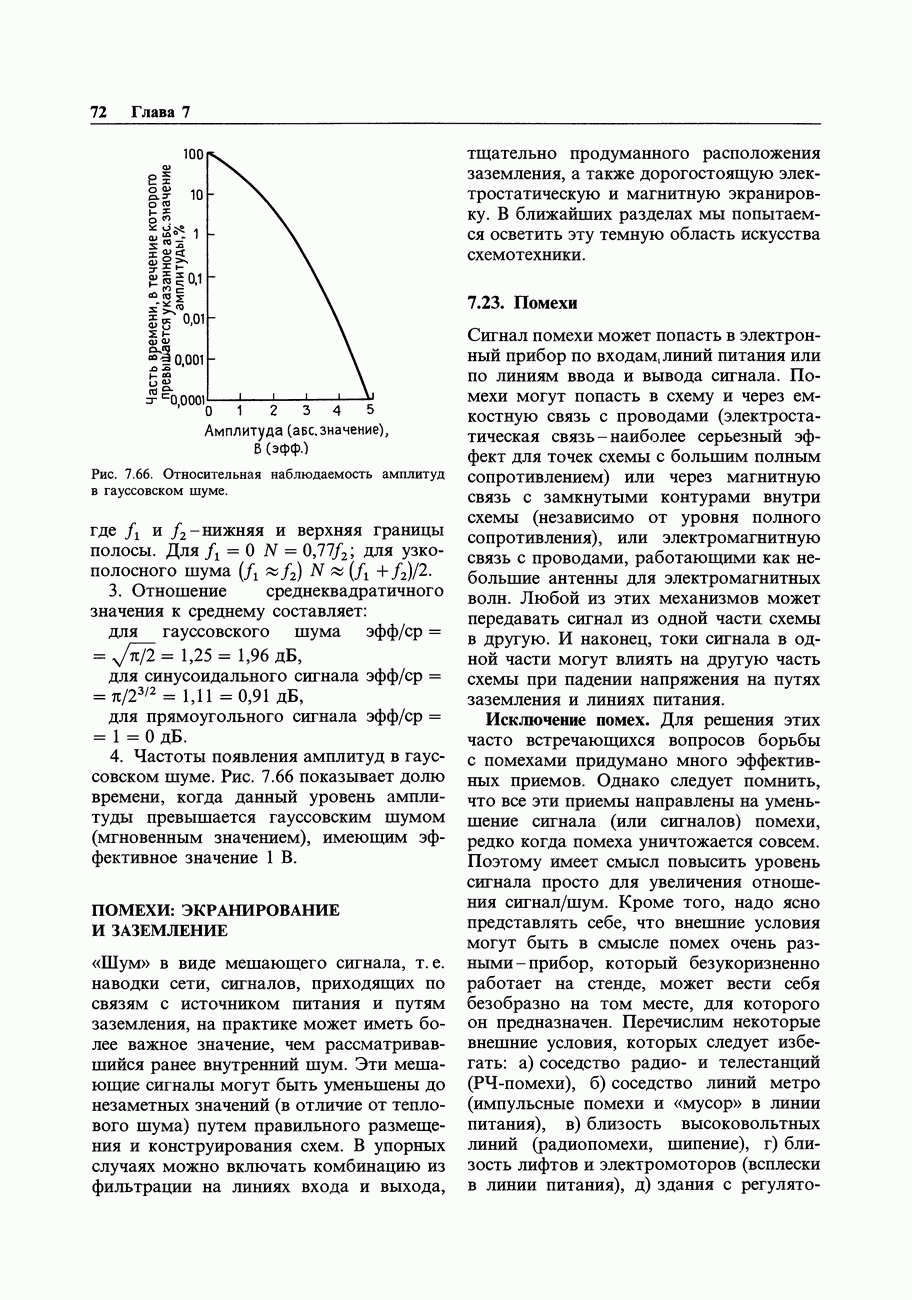
Пример: деление на 3. Попробуем построить схему синхронного делителя на 3 с помощью двух  -триггеров, тактируемых входным сигналом. В этом случае
-триггеров, тактируемых входным сигналом. В этом случае  будут входами регистра,
будут входами регистра,  - его выходами, общая тактовая линия будет представлять главный тактовый вход (рис. 8.58).
- его выходами, общая тактовая линия будет представлять главный тактовый вход (рис. 8.58).
1. Выберем три состояния:

2. Определим, что должно быть на выходах комбинационной схемы, для того чтобы получить последовательность этих состояний, т. е. что должно поступать на  -входы, для того чтобы получить требуемые состояния на выходах:
-входы, для того чтобы получить требуемые состояния на выходах:

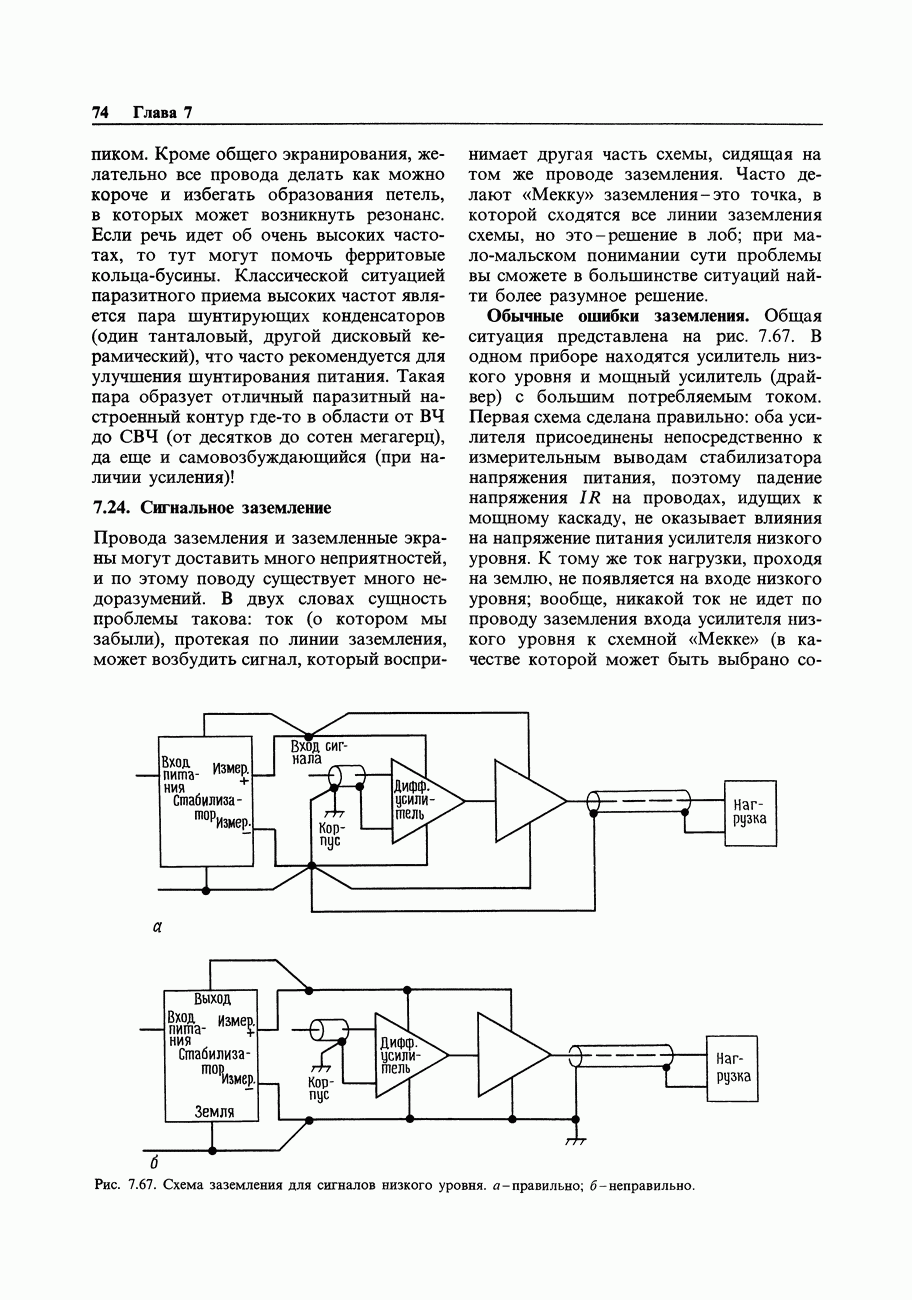
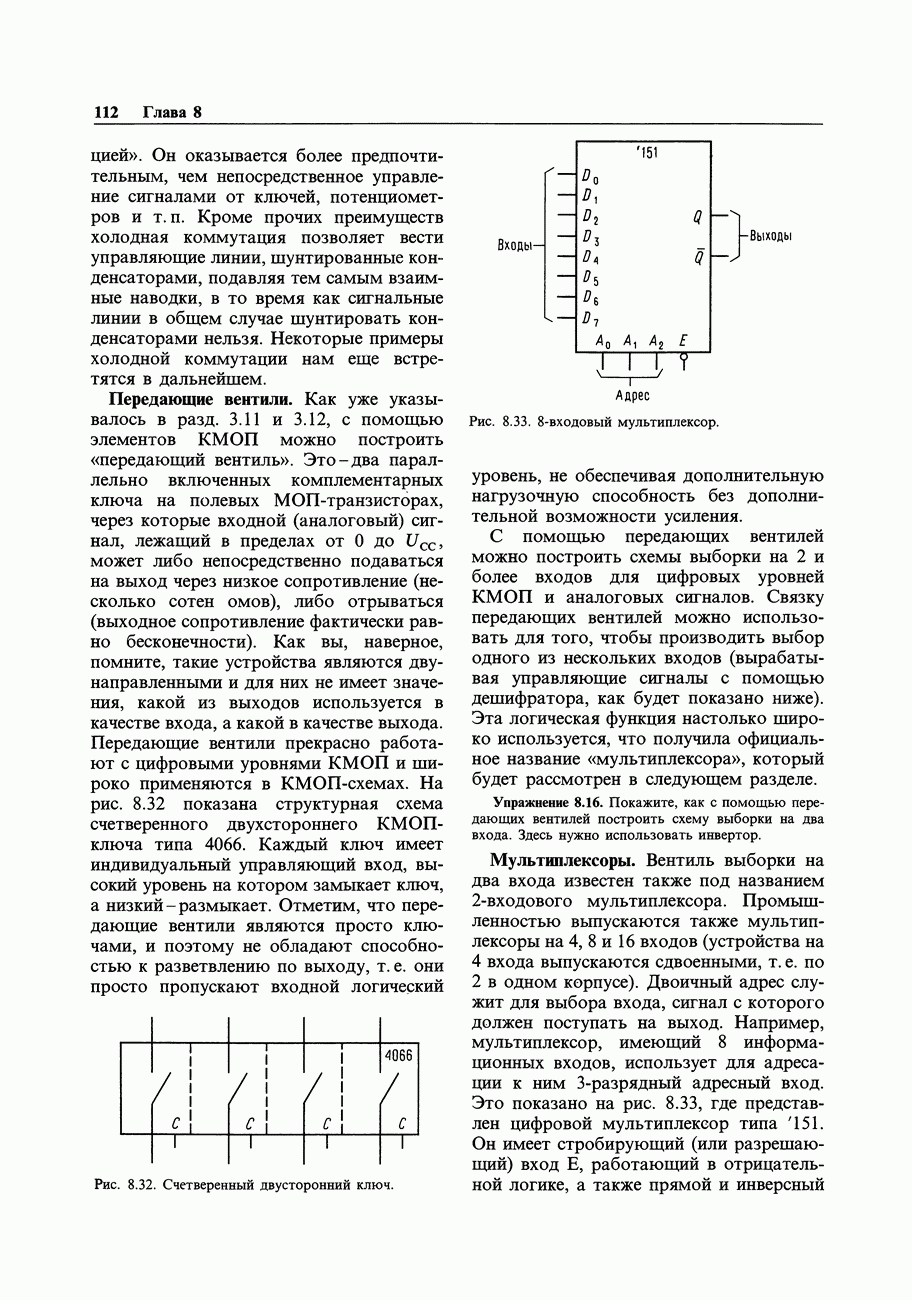
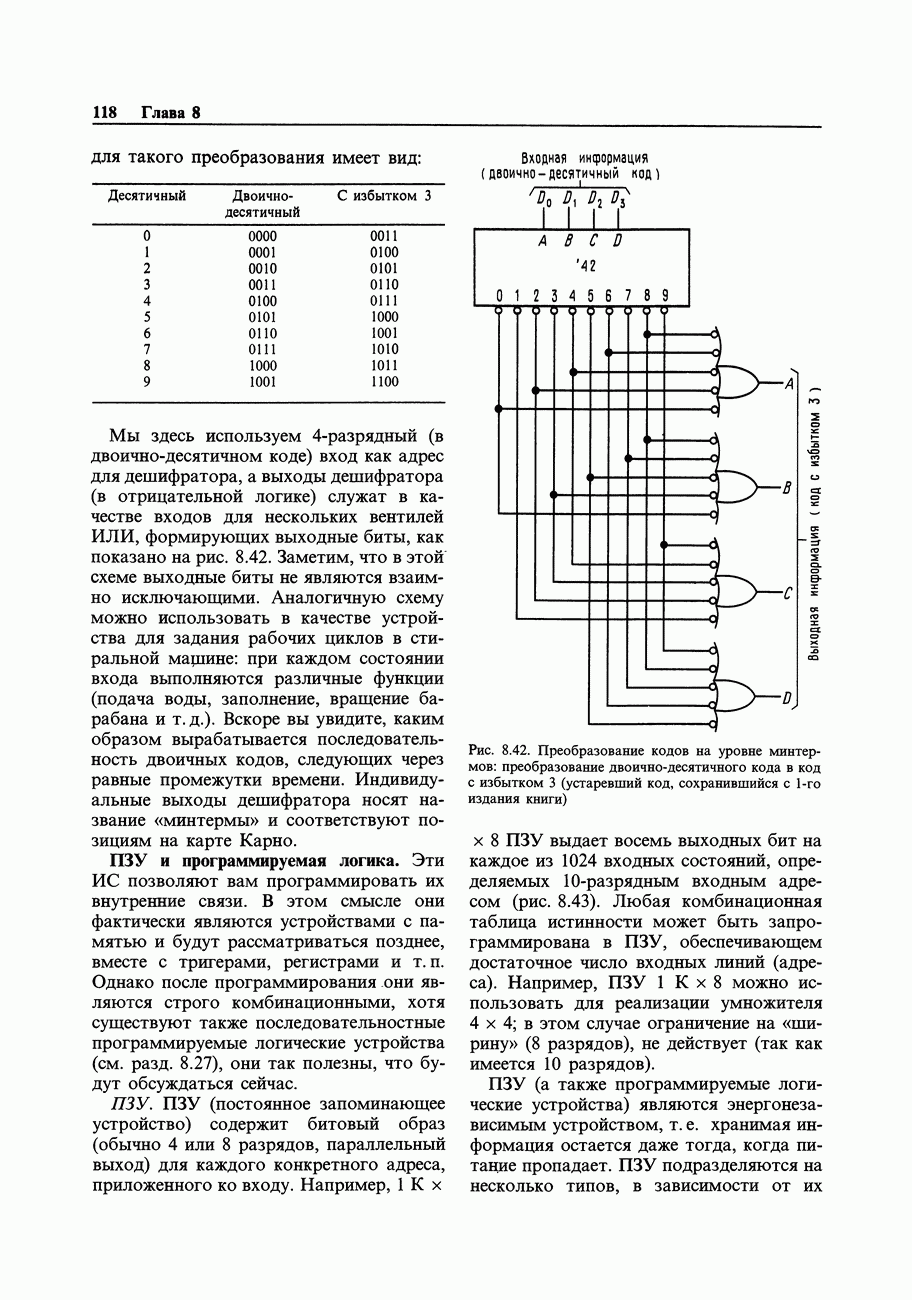
3. Построим вентильную схему, которая, с помощью имеющихся выходов, позволяла бы получить требуемые состояния на выходах. В общем случае можно использовать карту Карно, но для данного простого примера можно сразу увидеть, что  . Этому соответствует схема на рис. 8.59.
. Этому соответствует схема на рис. 8.59.

Рис. 8.59. Схема деления на 3.
Легко проверить, что эта схема работает так, как и было задумано. Так как она является синхронной, или тактируемой, сигналы на обоих выходах изменяются одновременно (если же выход первого триггера непосредственно подключить к тактовому входу второго, то получится асинхронный счетчик). В общем случае предпочитают использовать синхронные (или тактируемые) системы, так как они имеют более высокую помехоустойчивость. Это обусловлено тем, что к моменту возникновения тактового импульса триггеры находятся в установившемся состоянии, а на схемы, в которых входные сигналы анализируются только по фронтам тактовых импульсов, не действуют помехи, возникающие за счет емкостных связей от других триггеров или по каким-либо другим причинам. Еще одно преимущество состоит в том, что в тактируемых системах переходные состояния (вызванные задержками, в результате чего выходные сигналы изменяются не одновременно) не вызывают на выходах ложных сигналов, поскольку система не воспринимает никаких изменений, которые происходят после возникновения импульса. Далее мы проиллюстрируем это на ряде примеров.
Запрещенные состояния.
Что произойдет со схемой деления на 3, если ее триггеры каким-то образом окажутся в состоянии Это может произойти при включении питания, так как начальное состояние триггеров предсказать невозможно.
Это может произойти при включении питания, так как начальное состояние триггеров предсказать невозможно.

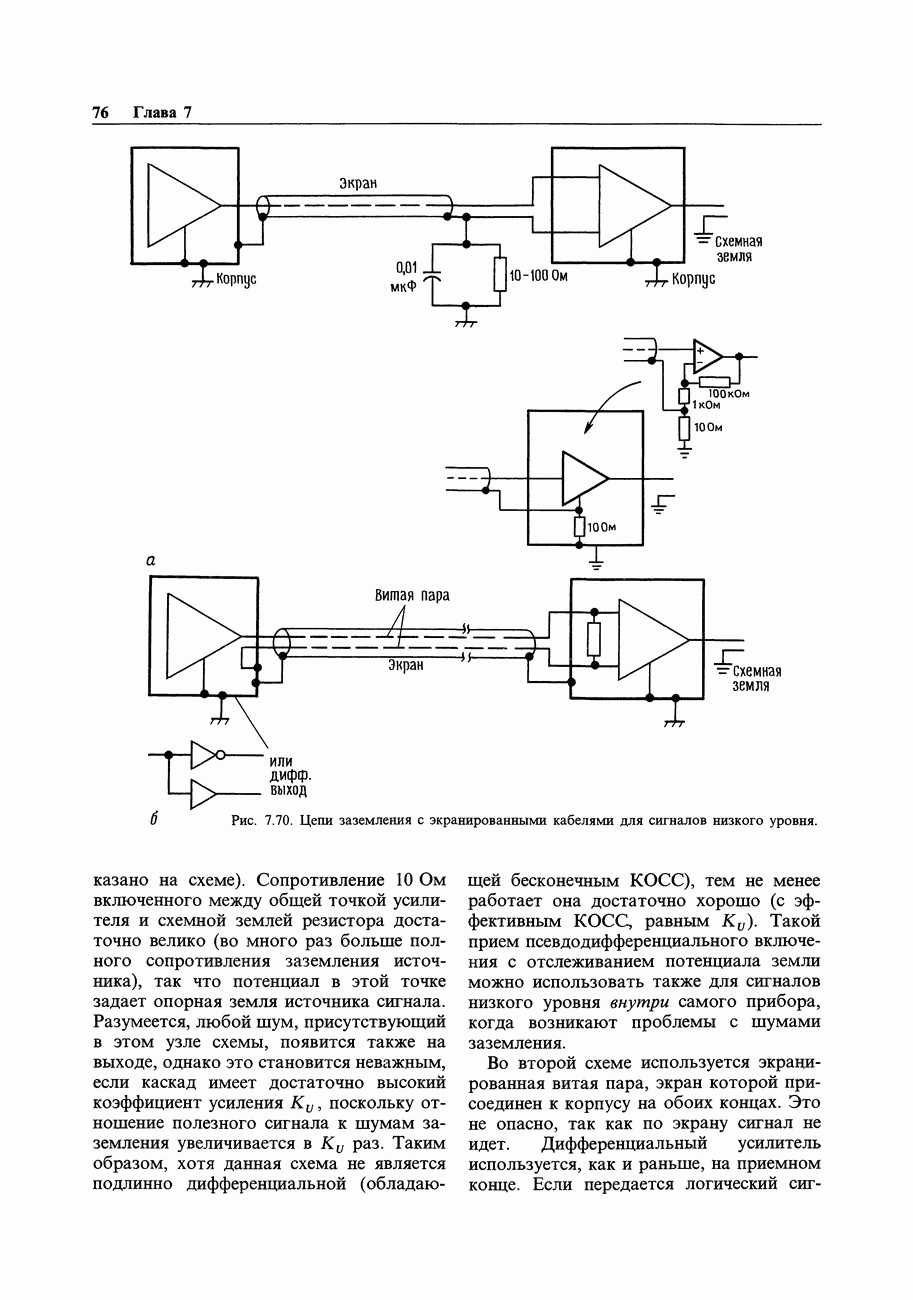
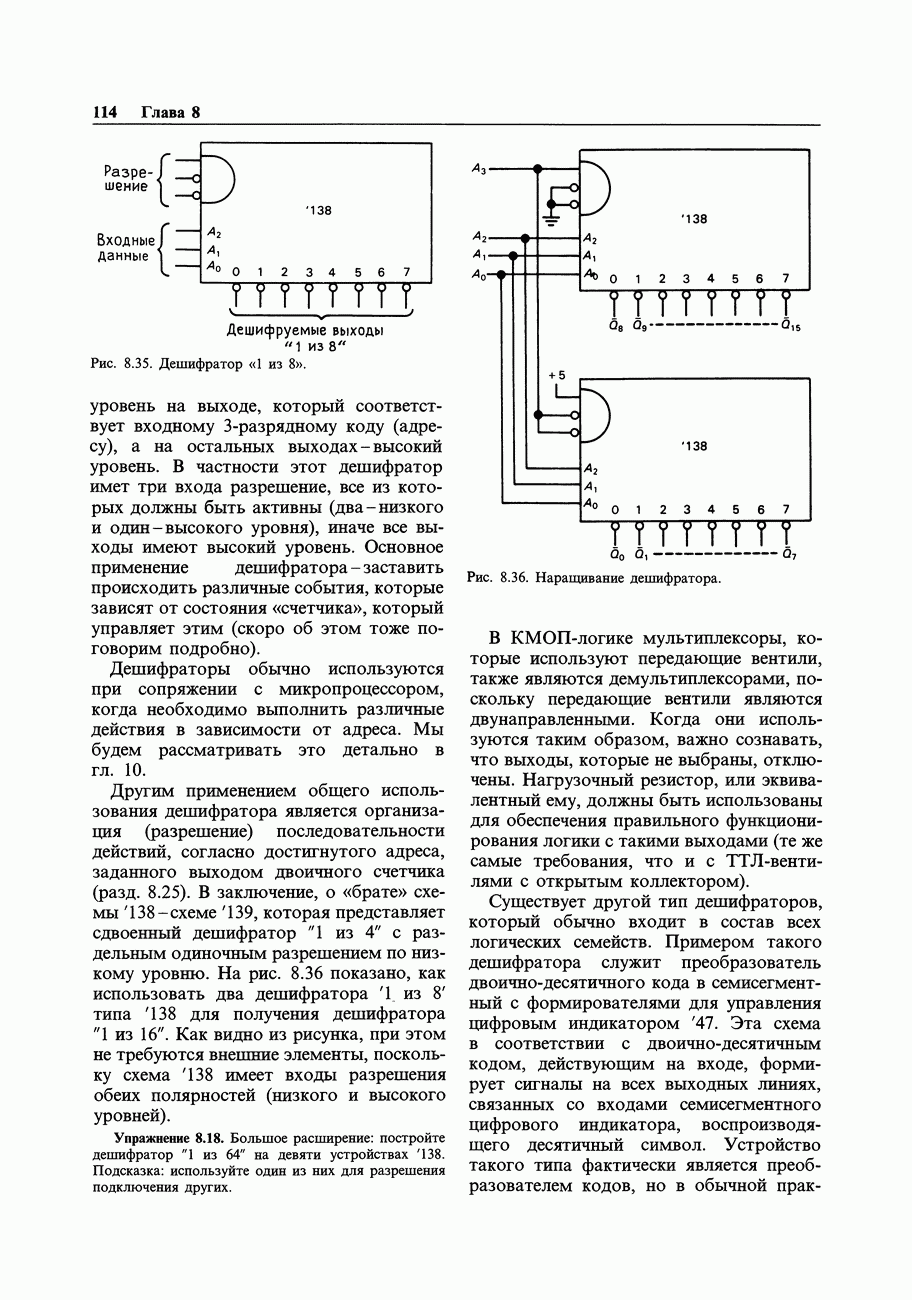
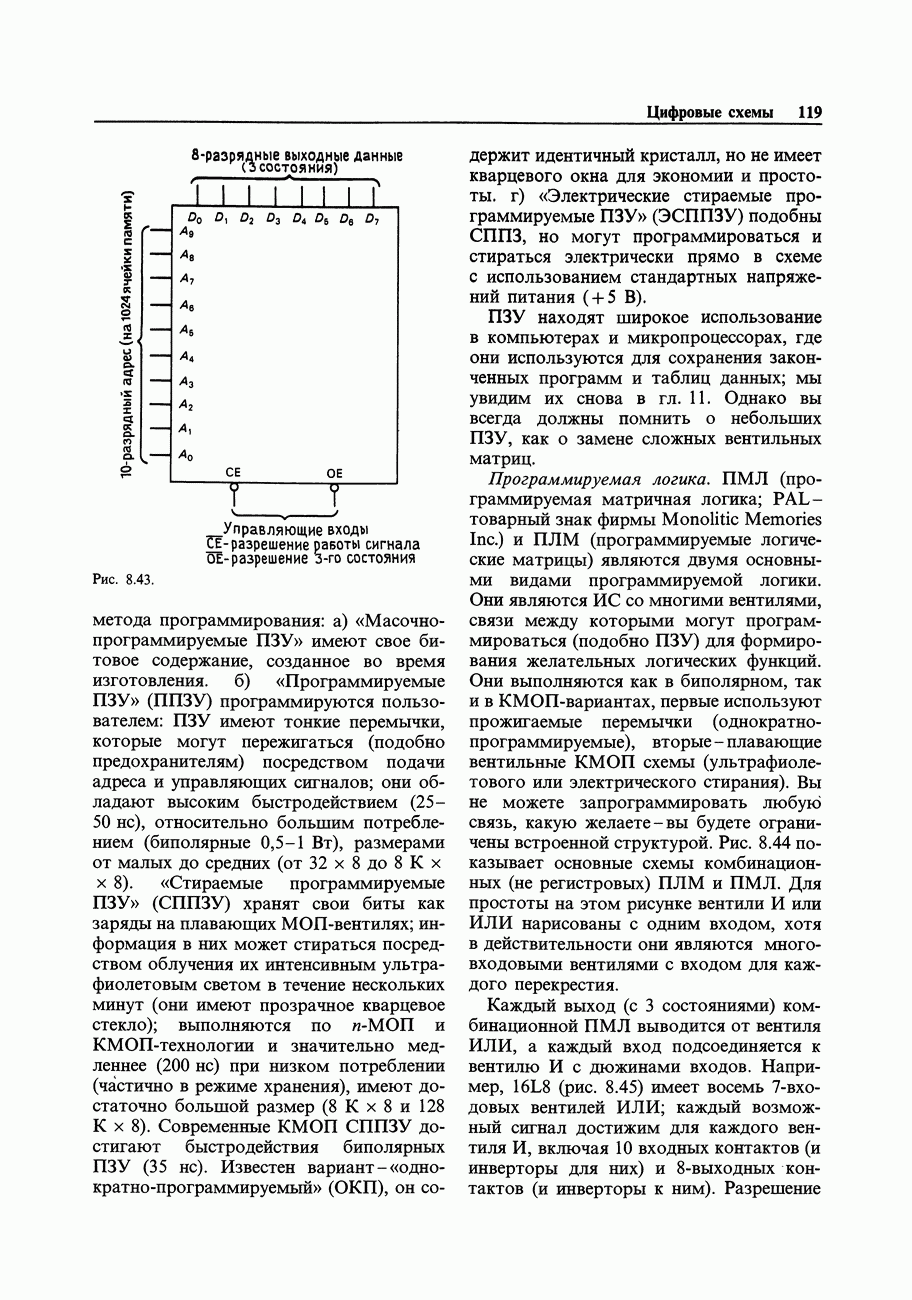
Рис. 8.60. Диаграмма состояний схемы деления на 3.
Из схемы видно, что первый тактовый импульс переведет ее в состояние (1, 0) и далее она будет функционировать как положено. В таких случаях важно производить проверку запрещенных состояний, поскольку схема может случайно оказаться в одном из них. (С другой стороны, все возможные состояния системы можно определить на начальном этапе разработки.) Диаграмма состояний, показанная для данного примера на рис. 8.60, может оказаться полезным диагностическим инструментом. Если в системе используются и другие переменные, то обычно для каждого перехода рядом со стрелкой записываются условия. Стрелки могут идти в обоих направлениях, а также из одного состояния к нескольким другим.
Упражнение 8.24. Постройте синхронную схему деления на 3 с помощью двух  -триггеров. Это можно выполнить (16 различными способами) без использования вентилей или инверторов. Когда вы будете составлять таблицу требуемых значений для входов
-триггеров. Это можно выполнить (16 различными способами) без использования вентилей или инверторов. Когда вы будете составлять таблицу требуемых значений для входов  , не забудьте, что для каждой точки J, К существуют две возможности. Например, если выход триггера переходит из 0 в 1, то
, не забудьте, что для каждой точки J, К существуют две возможности. Например, если выход триггера переходит из 0 в 1, то  (где
(где  -любое значение). Наконец, проверьте, не будет ли схема застревать в запрещенном состоянии (это наблюдается в четырех из 16 возможных решений этой задачи).
-любое значение). Наконец, проверьте, не будет ли схема застревать в запрещенном состоянии (это наблюдается в четырех из 16 возможных решений этой задачи).
Упражнение 8.25. Постройте синхронный  -разрядный реверсивный счетчик: он имеет тактовый вход и вход управления
-разрядный реверсивный счетчик: он имеет тактовый вход и вход управления  выходы являются выходами триггеров и
выходы являются выходами триггеров и  . Если вход
. Если вход  имеет ВЫСОКИЙ уровень, то он работает как обычный двоичный счетчик, а если НИЗКИЙ, то он считает в обратном
имеет ВЫСОКИЙ уровень, то он работает как обычный двоичный счетчик, а если НИЗКИЙ, то он считает в обратном  .
.
Диаграмма состоящий как инструмент проектирования.
Диаграмма состояний может оказаться полезной при разработке последовательной логики, особенно в тех случаях, когда переходы из одного состояния в другое могут происходить различным путем. Создавая такую схему, нужно сначала выбрать совокупность единственных состояний системы и каждому из них присвоить собственное имя (т. е. двоичный адрес). Здесь потребуется не менее триггеров, где
триггеров, где  - наименьшее целое, для которого
- наименьшее целое, для которого  больше или равно числу различных состояний системы. Далее устанавливают правила переходов из одного состояния в другое, т. е. все возможные условия для входа в каждое состояние и выхода из него. Таким образом, задача построения последовательной логики свелась к задаче построения комбинационной логики, которую всегда можно решить с помощью известных методов, например карты Карно. Реальный пример показан на рис. 8.61. Заметим, что здесь могут иметь место состояния, из которых нет перехода к другим состояниям (например, «получение диплома»).
больше или равно числу различных состояний системы. Далее устанавливают правила переходов из одного состояния в другое, т. е. все возможные условия для входа в каждое состояние и выхода из него. Таким образом, задача построения последовательной логики свелась к задаче построения комбинационной логики, которую всегда можно решить с помощью известных методов, например карты Карно. Реальный пример показан на рис. 8.61. Заметим, что здесь могут иметь место состояния, из которых нет перехода к другим состояниям (например, «получение диплома»).

Рис. 8.61. Диаграмма состояний.
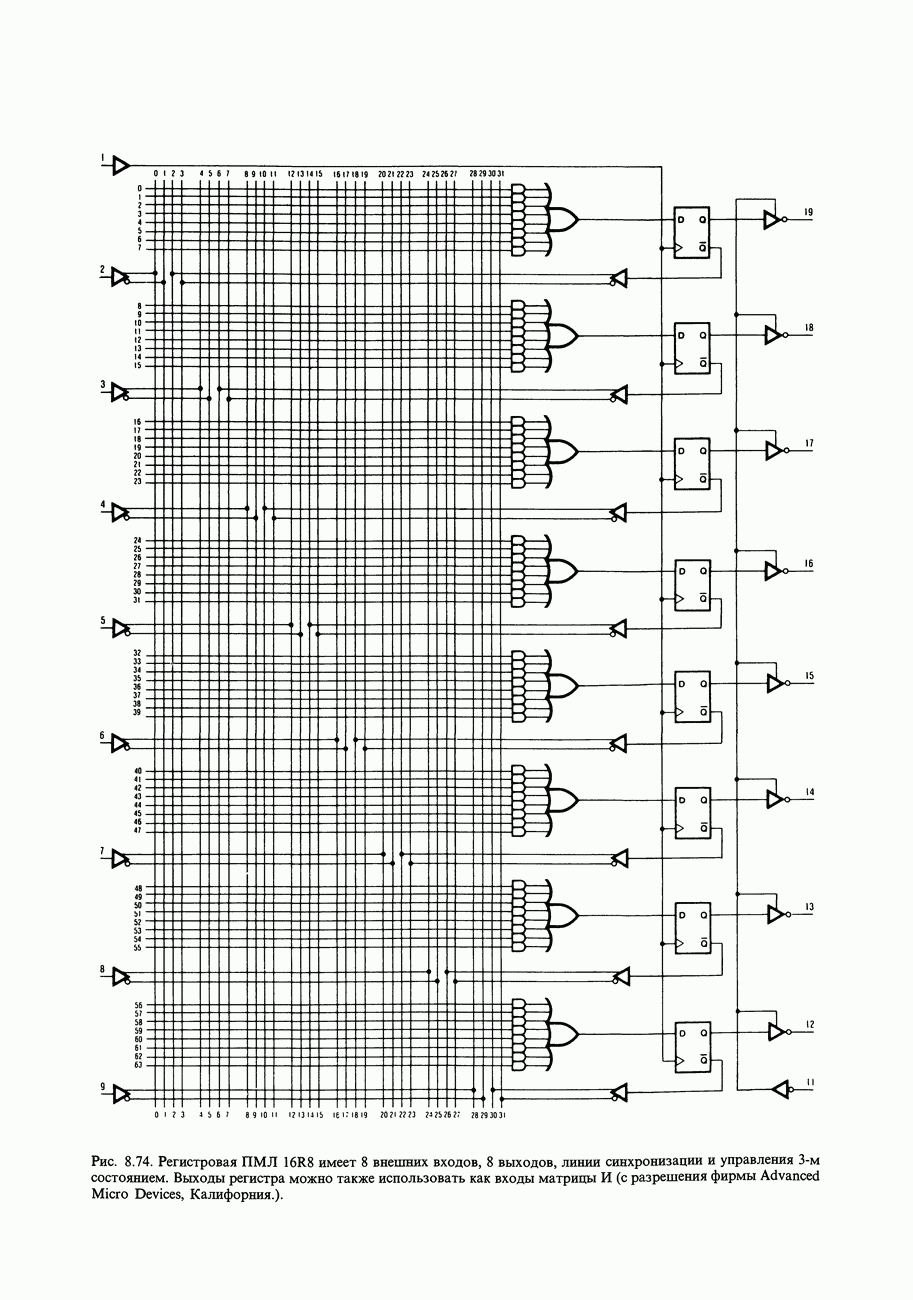
Регистровые ПЛМ. Программируемые логические ИС (ПМЛ и ПЛМ, смотрите разд. 8.15) выпускаются как с вентилями, так и с синхронно тактируемыми  -триггерами на одном кристалле. Они известны как регистровые ПМЛ и ПЛМ и являются идеальными для построения последовательностных схем. Вы узнаете, как это делать в разд. 8.27.
-триггерами на одном кристалле. Они известны как регистровые ПМЛ и ПЛМ и являются идеальными для построения последовательностных схем. Вы узнаете, как это делать в разд. 8.27.
| << Предыдущий параграф | Следующий параграф >> |
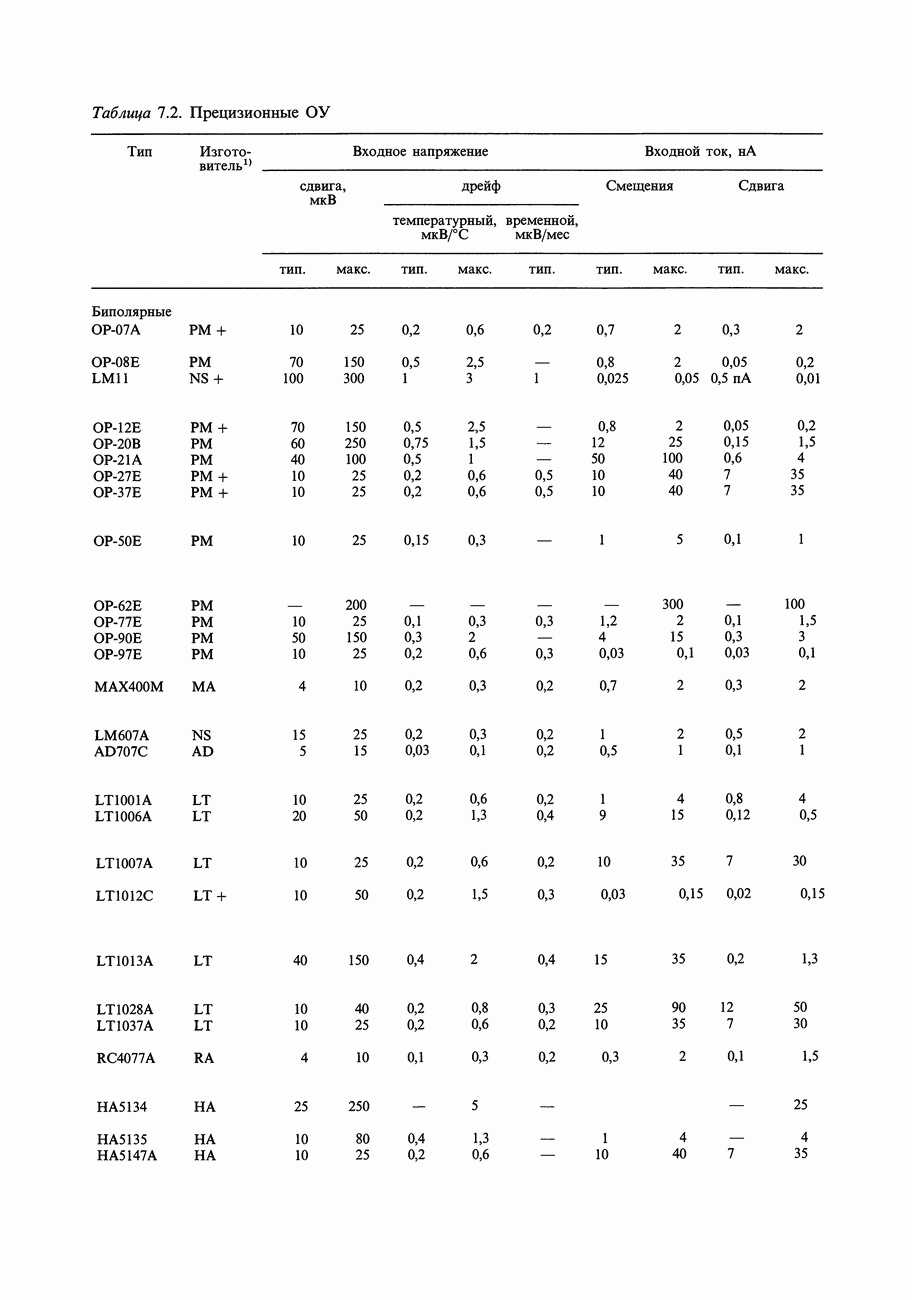
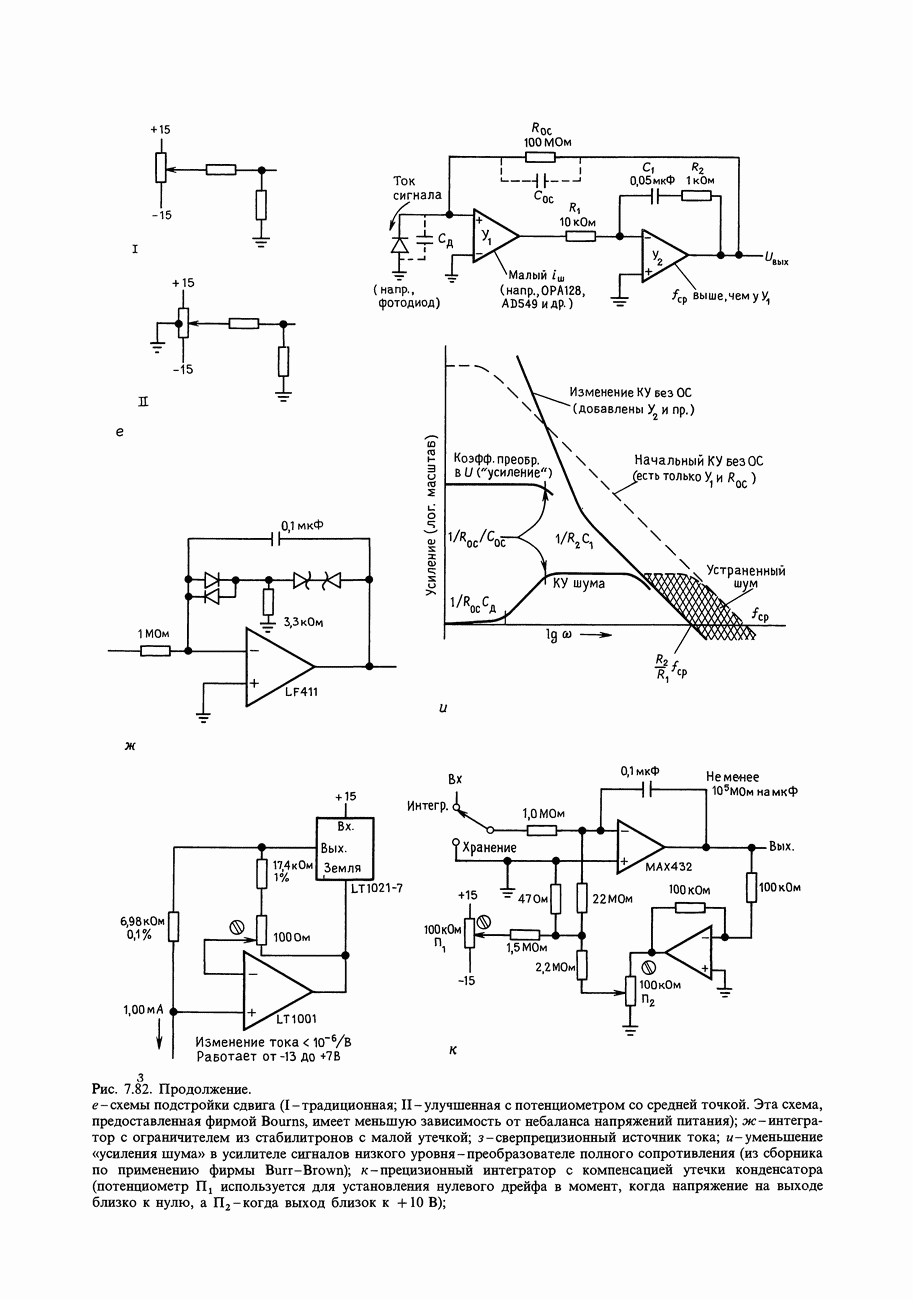
- ГЛАВА 7. ПРЕЦИЗИОННЫЕ СХЕМЫ И МАЛОШУМЯЩАЯ АППАРАТУРА
- 7.01. Соотношение точности и динамического диапазона
- 7.02. Бюджет погрешностей схемы
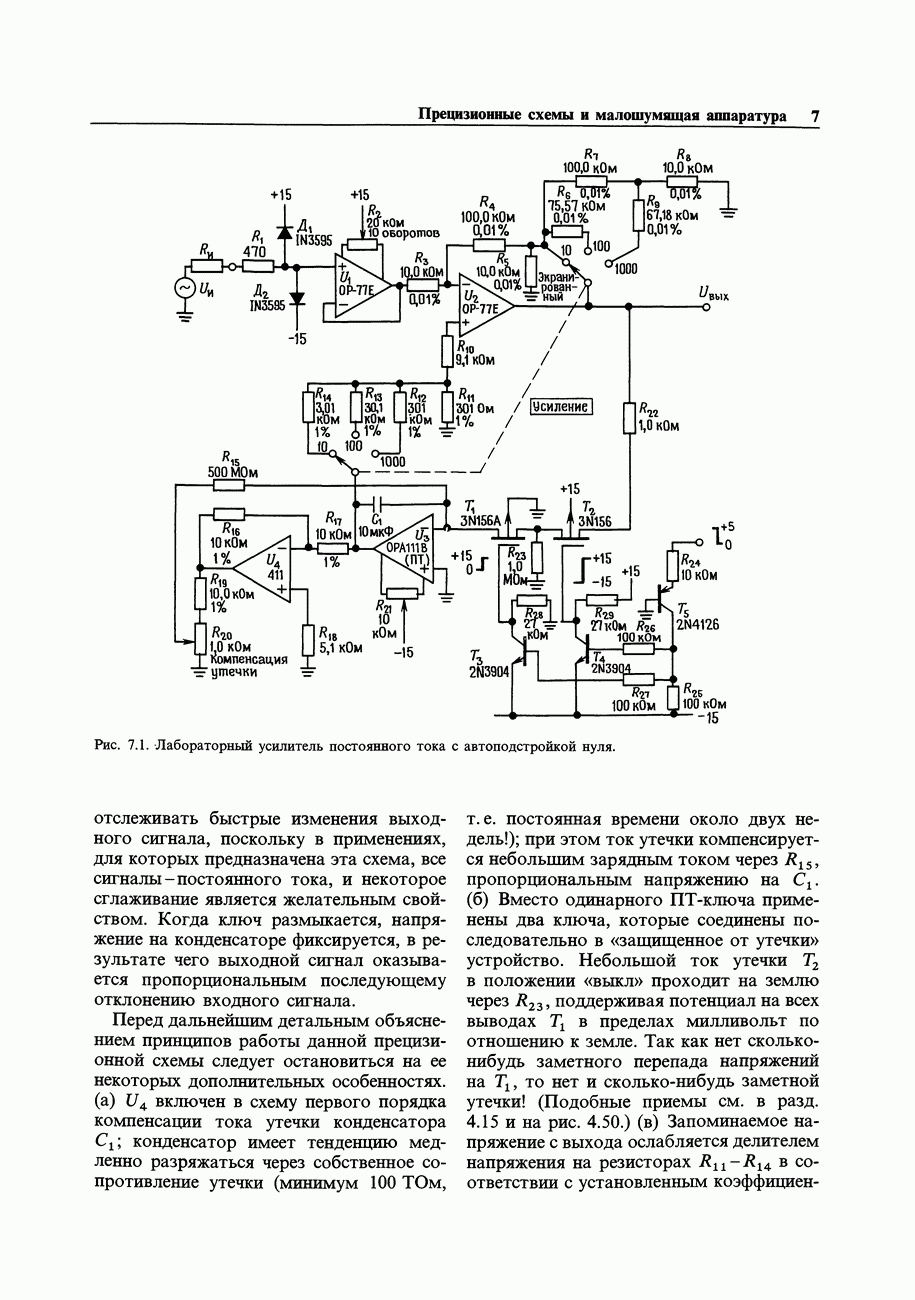
- 7.03. Пример схемы: прецизионный усилитель с автоматическим выбором нуля
- 7.04. «Бюджет погрешностей» при проектировании прецизионной схемы
- 7.05. Погрешности внешних цепей
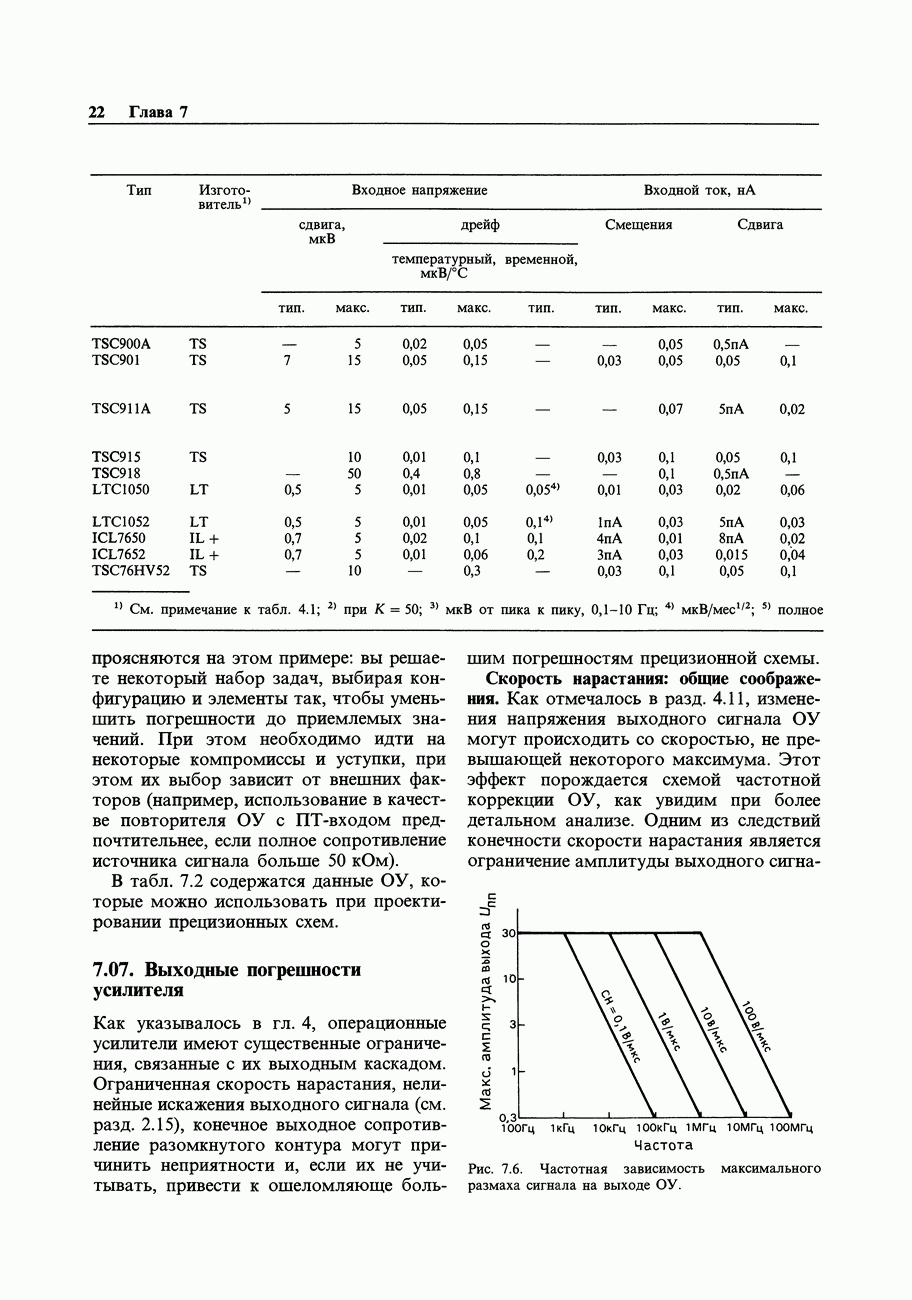
- 7.06. Входные погрешности усилителя
- 7.07. Выходные погрешности усилителя
- 7.08. Усилители с автоподстройкой нуля (стабилизированные прерыванием)
- Кое-что еще о схемах с прерыванием
- ДИФФЕРЕНЦИАЛЬНЫЕ И ИЗМЕРИТЕЛЬНЫЕ УСИЛИТЕЛИ
- 7.09. Простой разностный усилитель
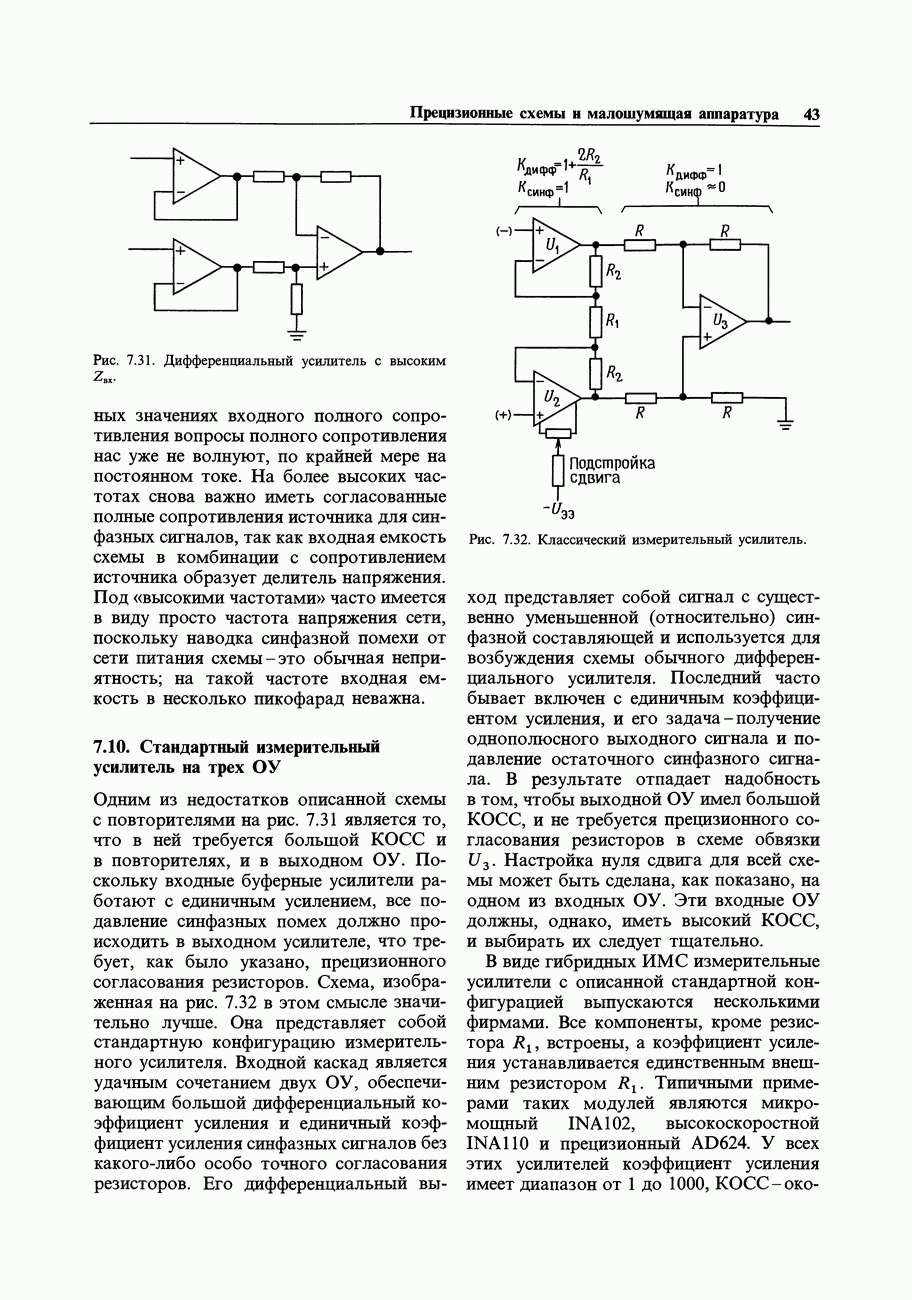
- 7.10. Стандартный измерительный усилитель на трех ОУ
- ШУМЫ УСИЛИТЕЛЕЙ
- 7.11. Происхождение и виды шумов
- 7.12. Отношение сигнал/шум и коэффициент шума
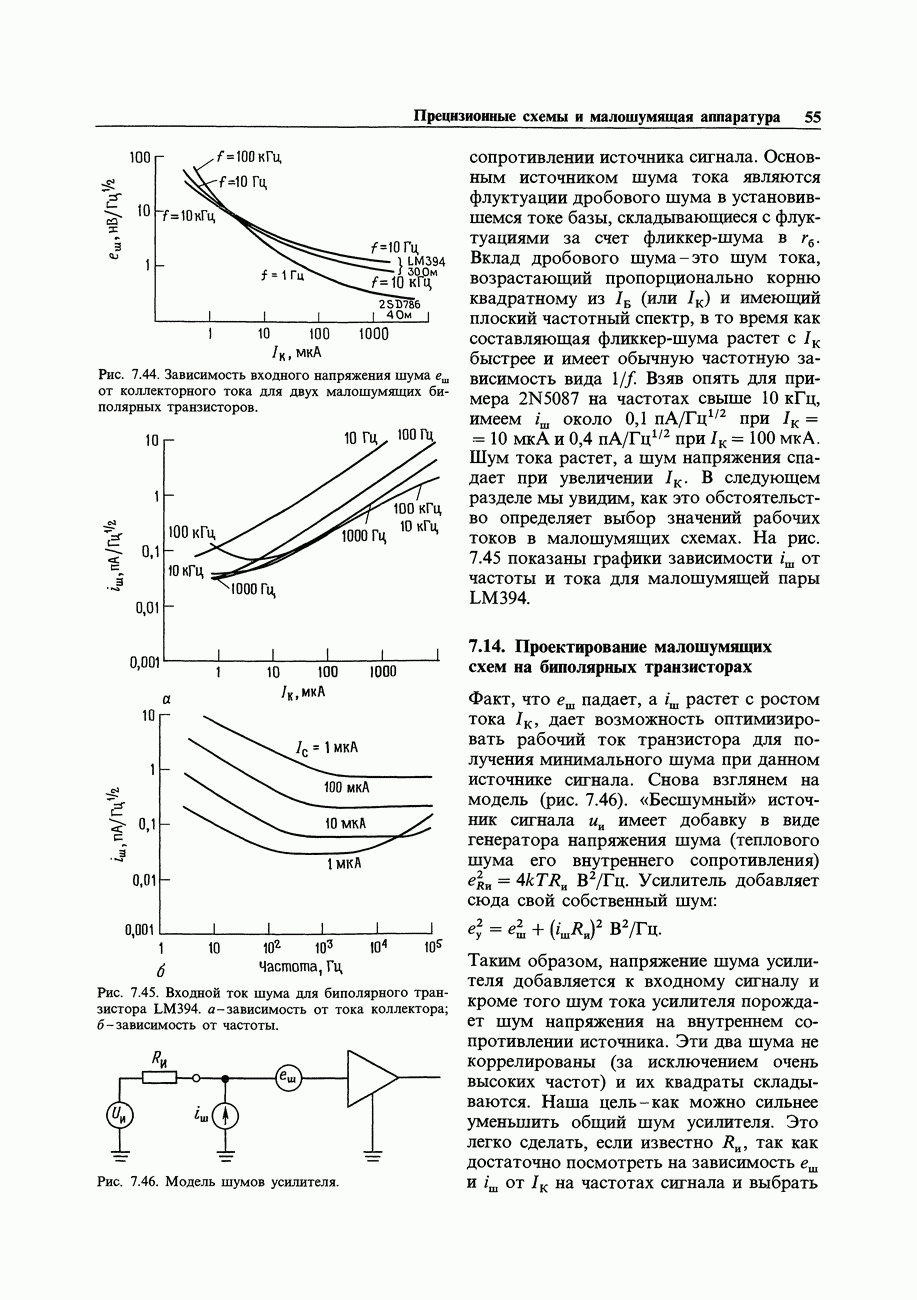
- 7.13. Шум тока и напряжения транзисторного усилителя
- 7.14. Проектирование малошумящих схем на биполярных транзисторах
- 7.15. Шум ПТ
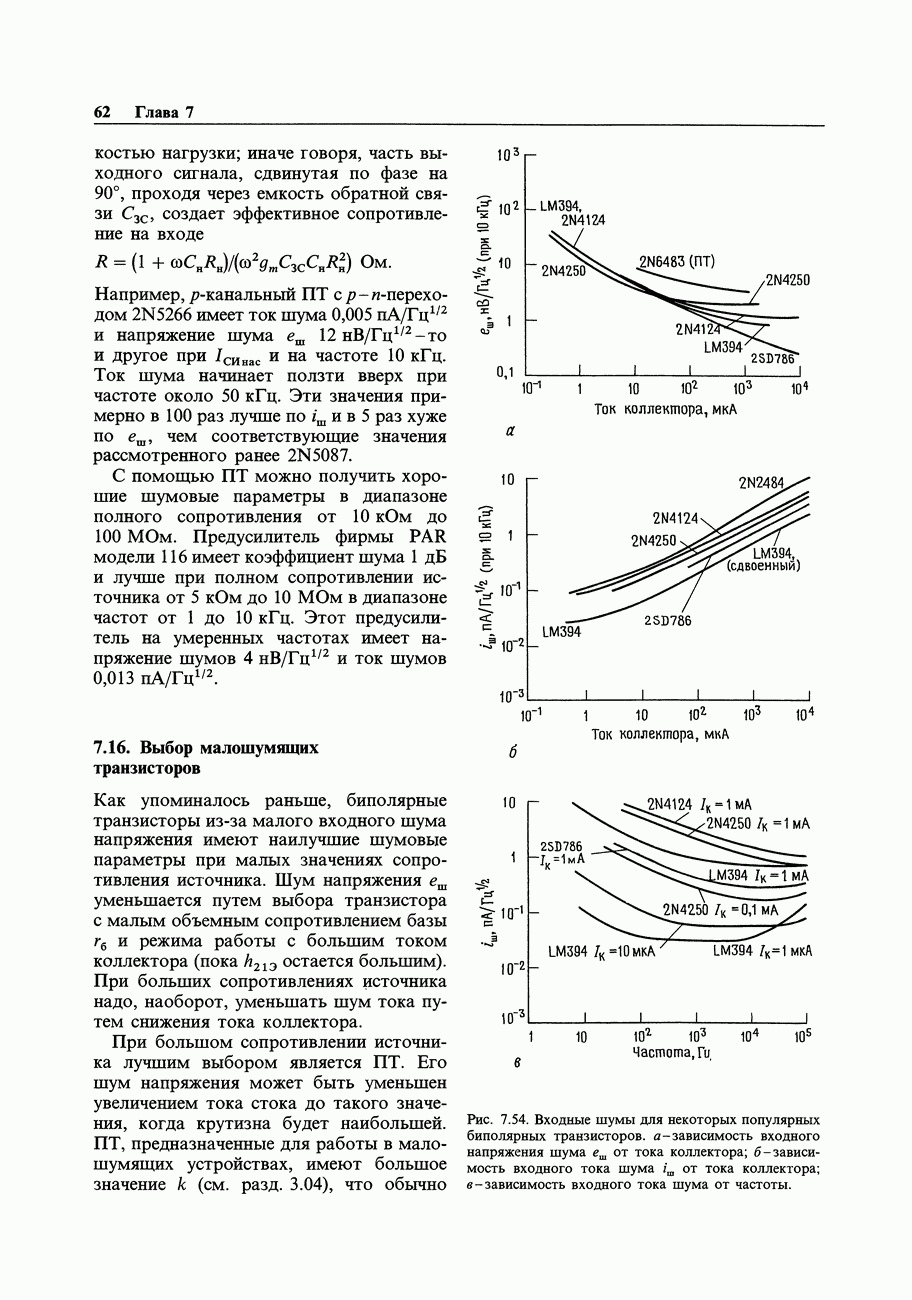
- 7.16. Выбор малошумящих транзисторов
- 7.17. Шум дифференциальных усилителей и усилителей с обратной связью
- ИЗМЕРЕНИЕ ШУМА И ИСТОЧНИКИ ШУМА
- 7.18. Измерение без источника шума
- 7.19. Измерение с источником шума
- 7.20. Генераторы шумов и сигналов
- 7.21. Ограничение полосы частот и измерение среднеквадратичного (эффективного) напряжения
- 7.22. Попурри на тему шумов
- ПОМЕХИ: ЭКРАНИРОВАНИЕ И ЗАЗЕМЛЕНИЕ
- 7.23. Помехи
- 7.24. Сигнальное заземление
- 7.25. Межприборное заземление
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 8. ЦИФРОВЫЕ СХЕМЫ
- 8.01. Цифровые и аналоговые сигналы
- 8.02. Логические состояния
- ЛОГИЧЕСКИЕ УРОВНИ
- 8.03. Числовые коды
- 8.04. Вентили и таблицы истинности
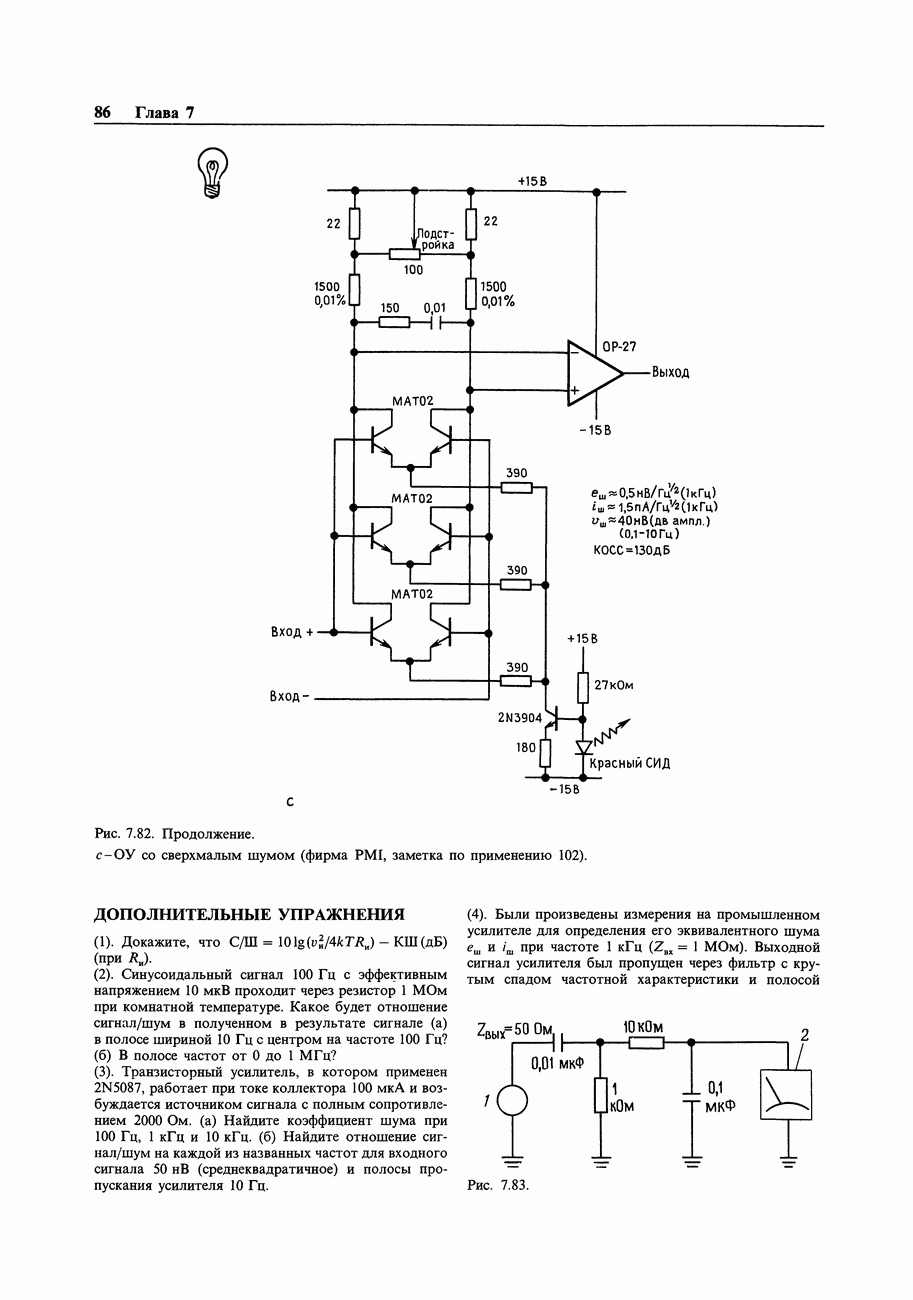
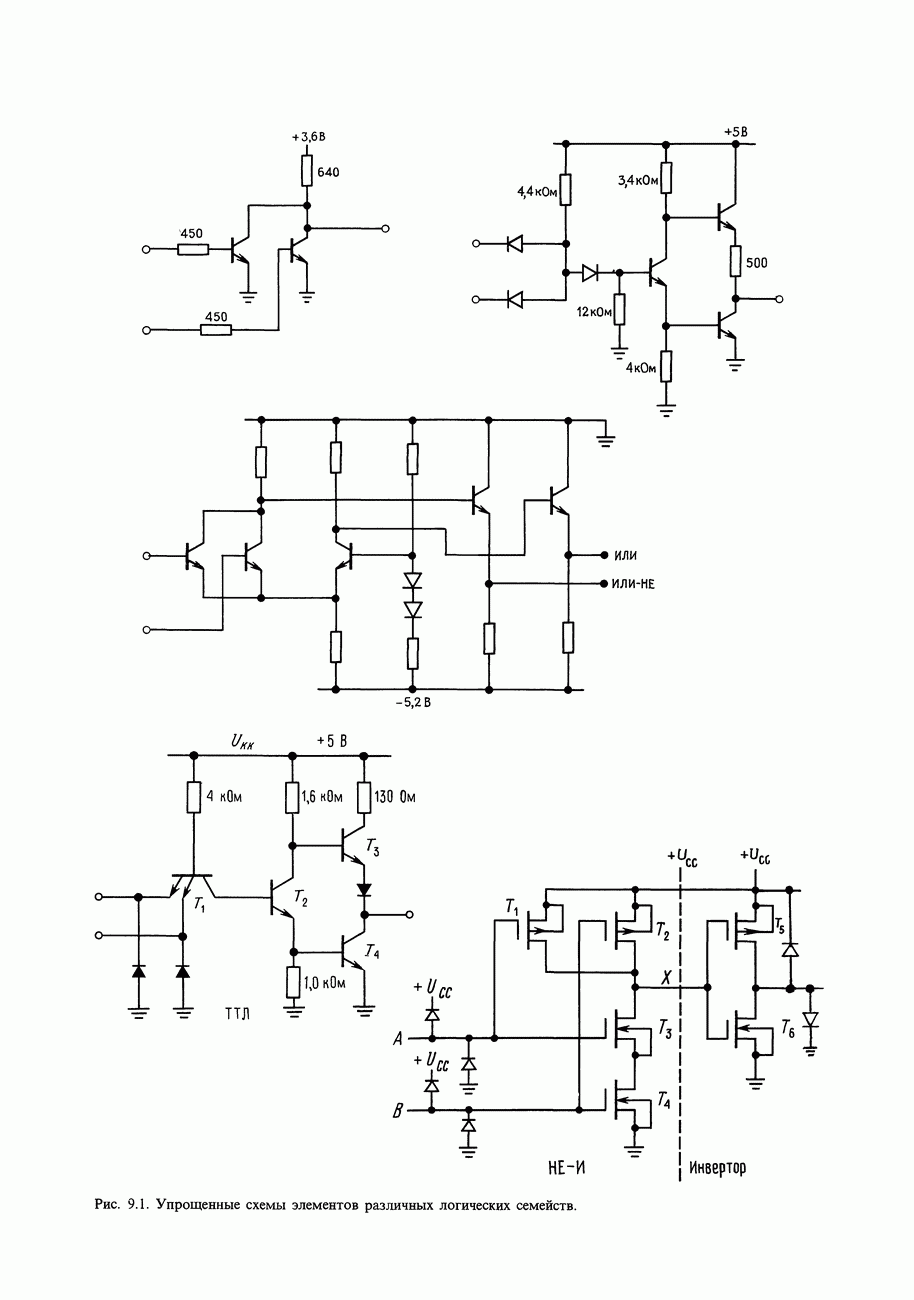
- 8.05. Схемы вентилей на дискретных элементах
- 8.06. Пример схемы с вентилями
- 8.07. Логические обозначения при заданных уровнях
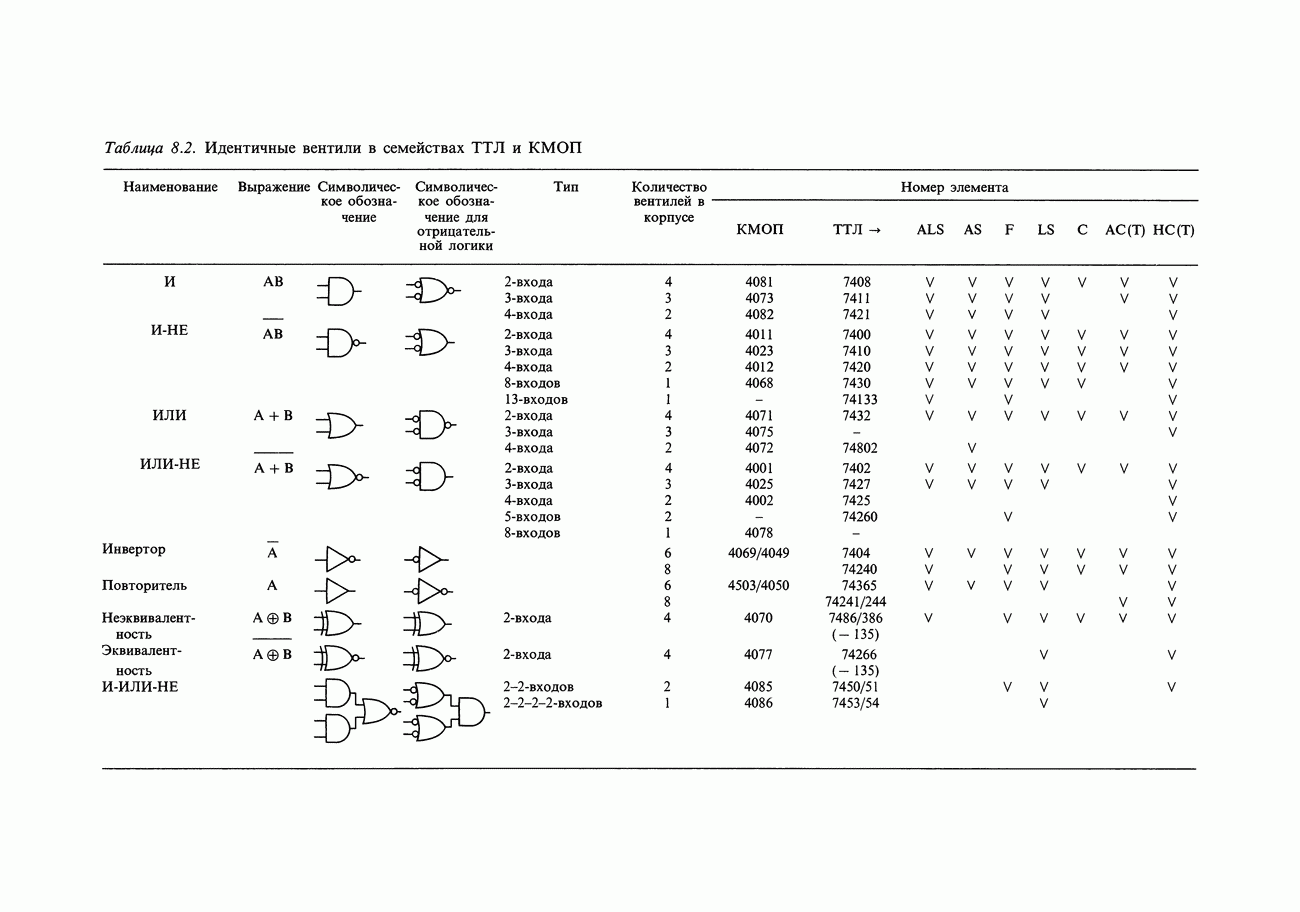
- 8.08. Каталог идентичных вентилей
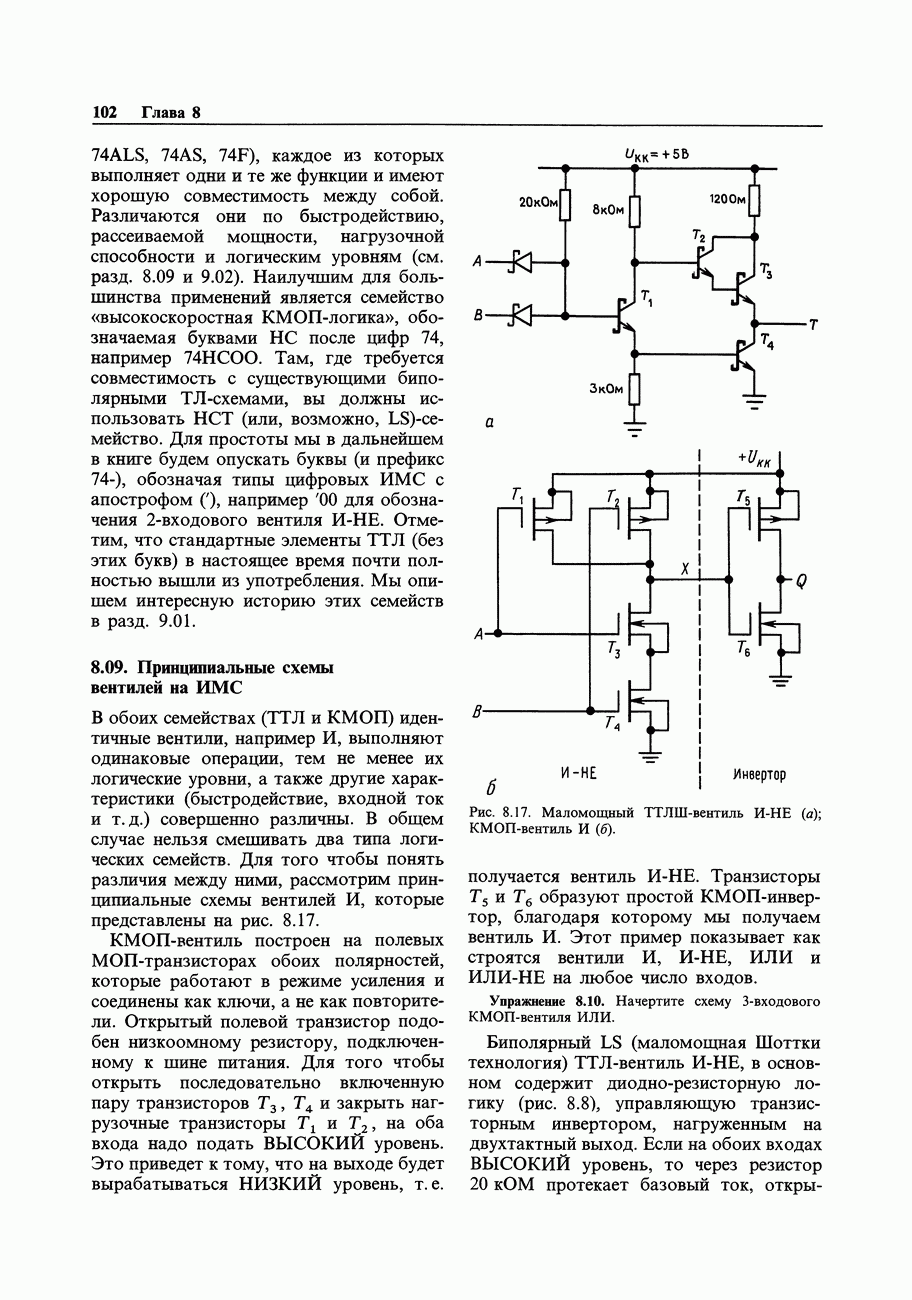
- 8.09. Принципиальные схемы вентилей на ИМС
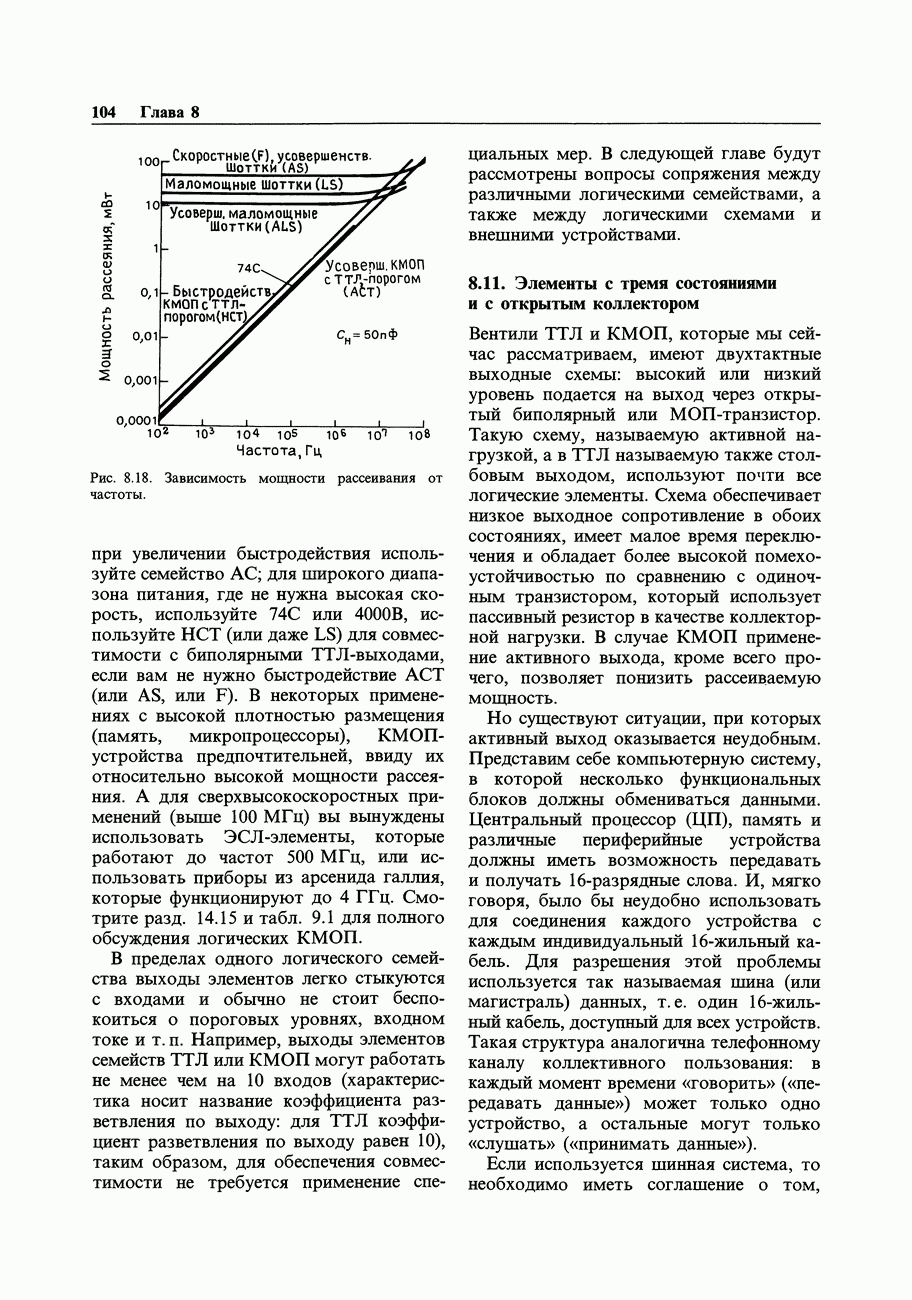
- 8.10. Характеристики ТТЛ и КМОП
- 8.11. Элементы с тремя состояниями и с открытым коллектором
- КОМБИНАЦИОННАЯ ЛОГИКА
- 8.12. Логические тождества
- 8.13. Минимизация и карты Карно
- 8.14. Комбинационные функциональные схемы, реализованные на стандартных ИМС
- 8.15. Реализация произвольных таблиц истины
- ПОСЛЕДОВАТЕЛЬНОСТНАЯ ЛОГИКА
- 8.16. Устройства с памятью: триггеры
- 8.17. Тактируемые триггеры
- 8.18. Последовательностная логика-объединение памяти и вентилей
- 8.19. Синхронизатор
- МОНОСТАБИЛЬНЫЕ МУЛЬТИВИБРАТОРЫ
- 8.20. Характеристики одновибраторов
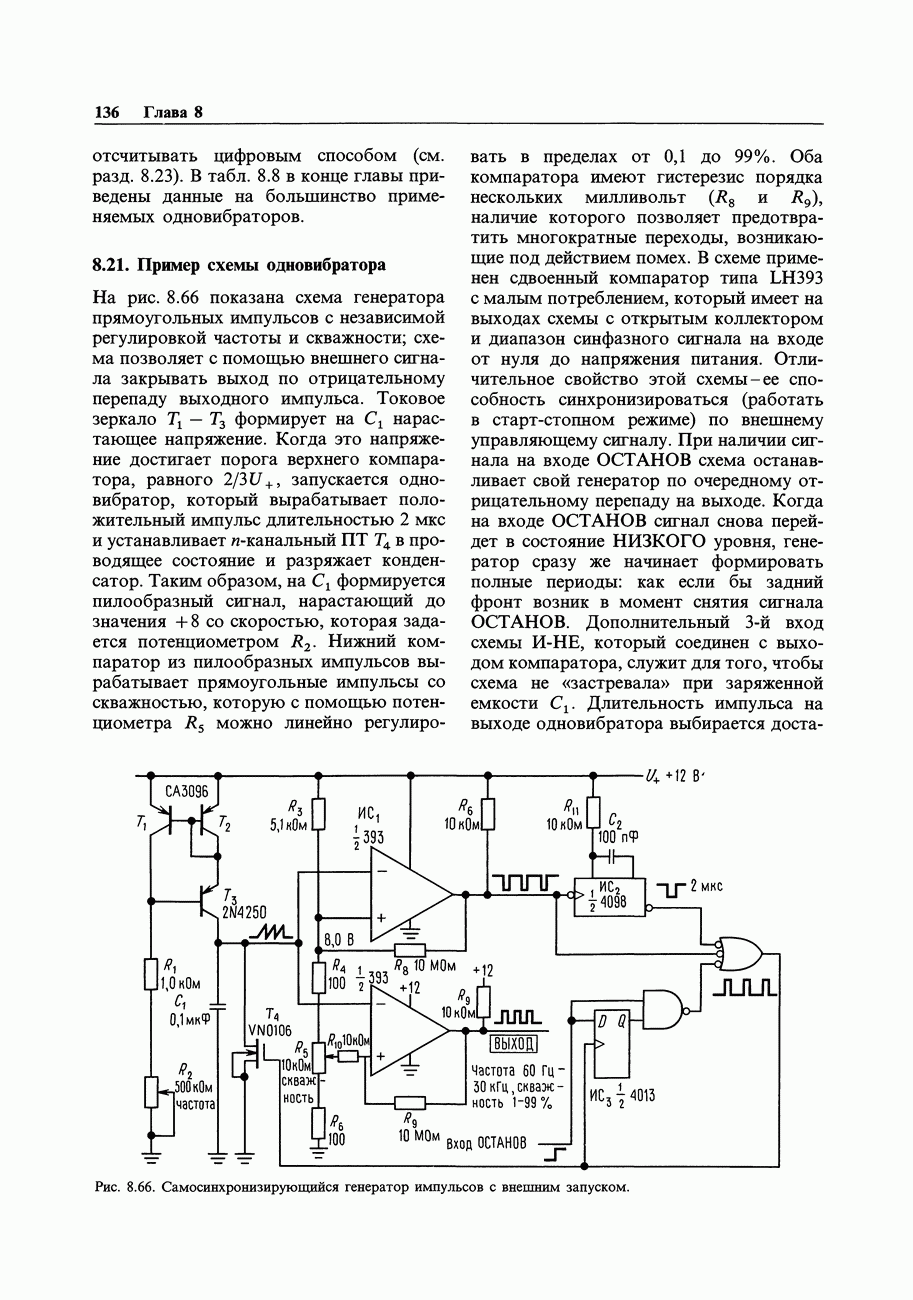
- 8.21. Пример схемы одновибратора
- 8.22. Предостережения относительно одновибраторов
- 8.23. Получение выдержки времени с помощью счетчиков
- ПОСЛЕДОВАТЕЛЬНОСТНЫЕ ФУНКЦИИ, РЕАЛИЗУЕМЫЕ НА СТАНДАРТНЫХ ИМС
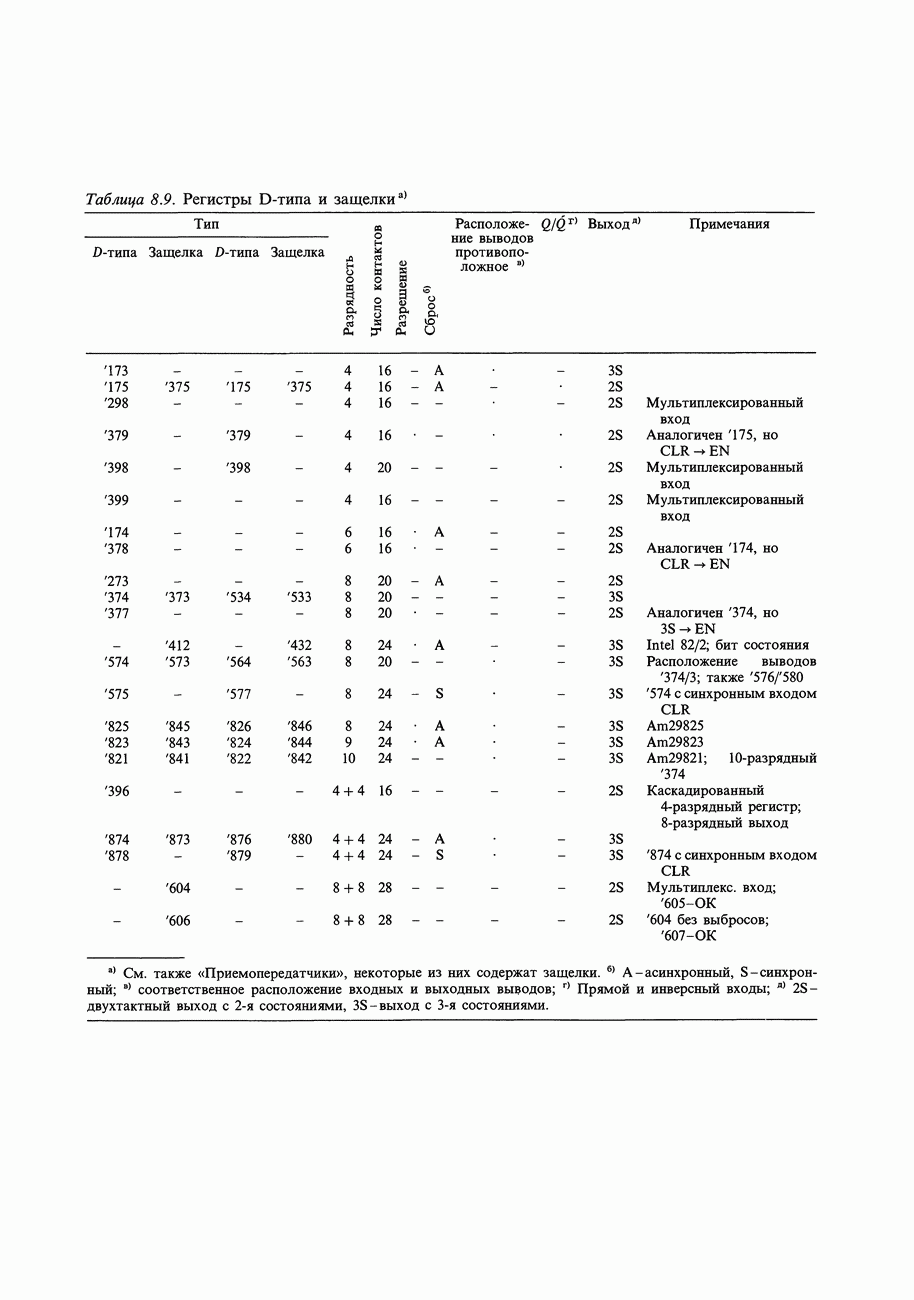
- 8.24. Фиксирующие схемы-защелки и регистры
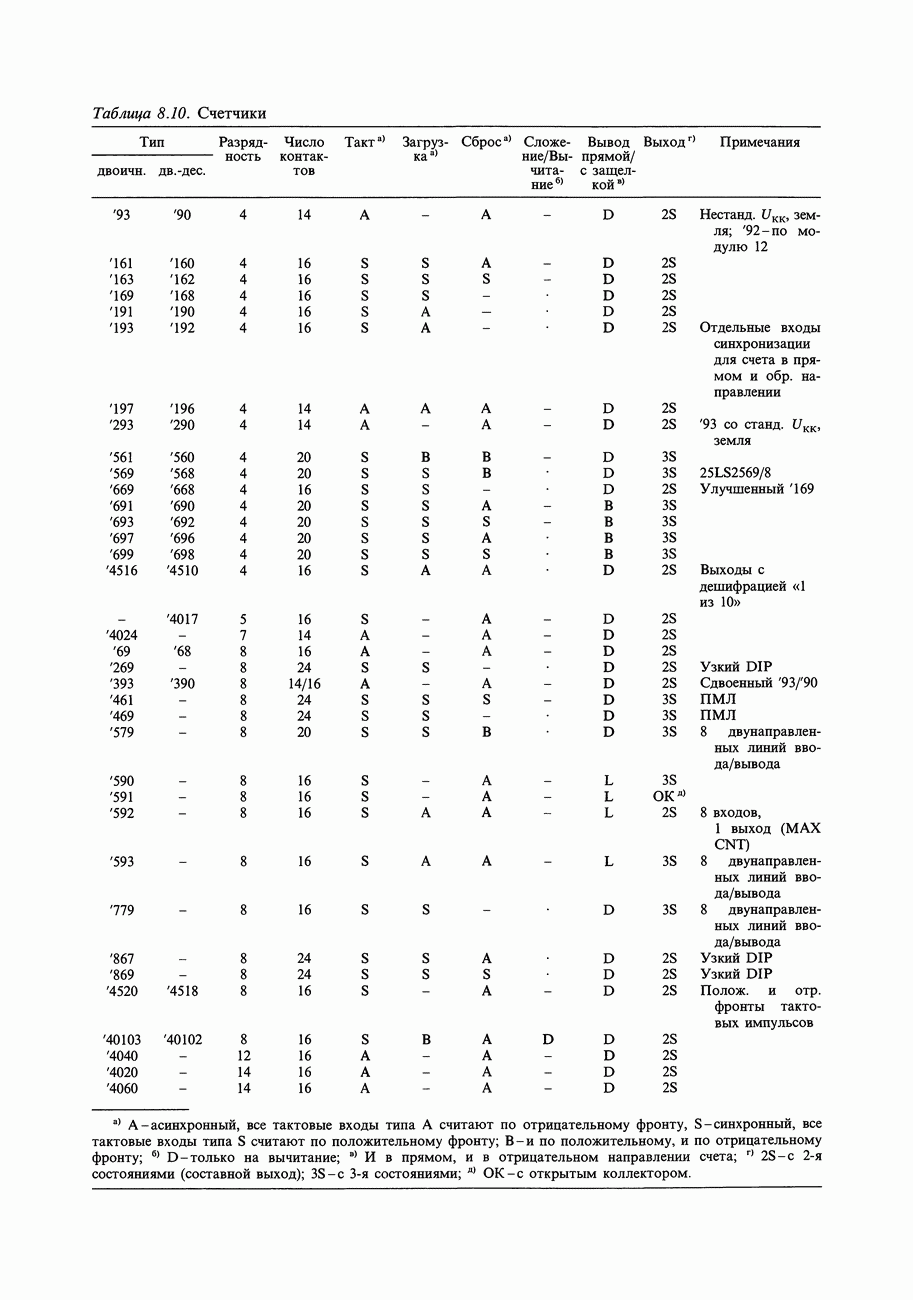
- 8.25. Счетчики
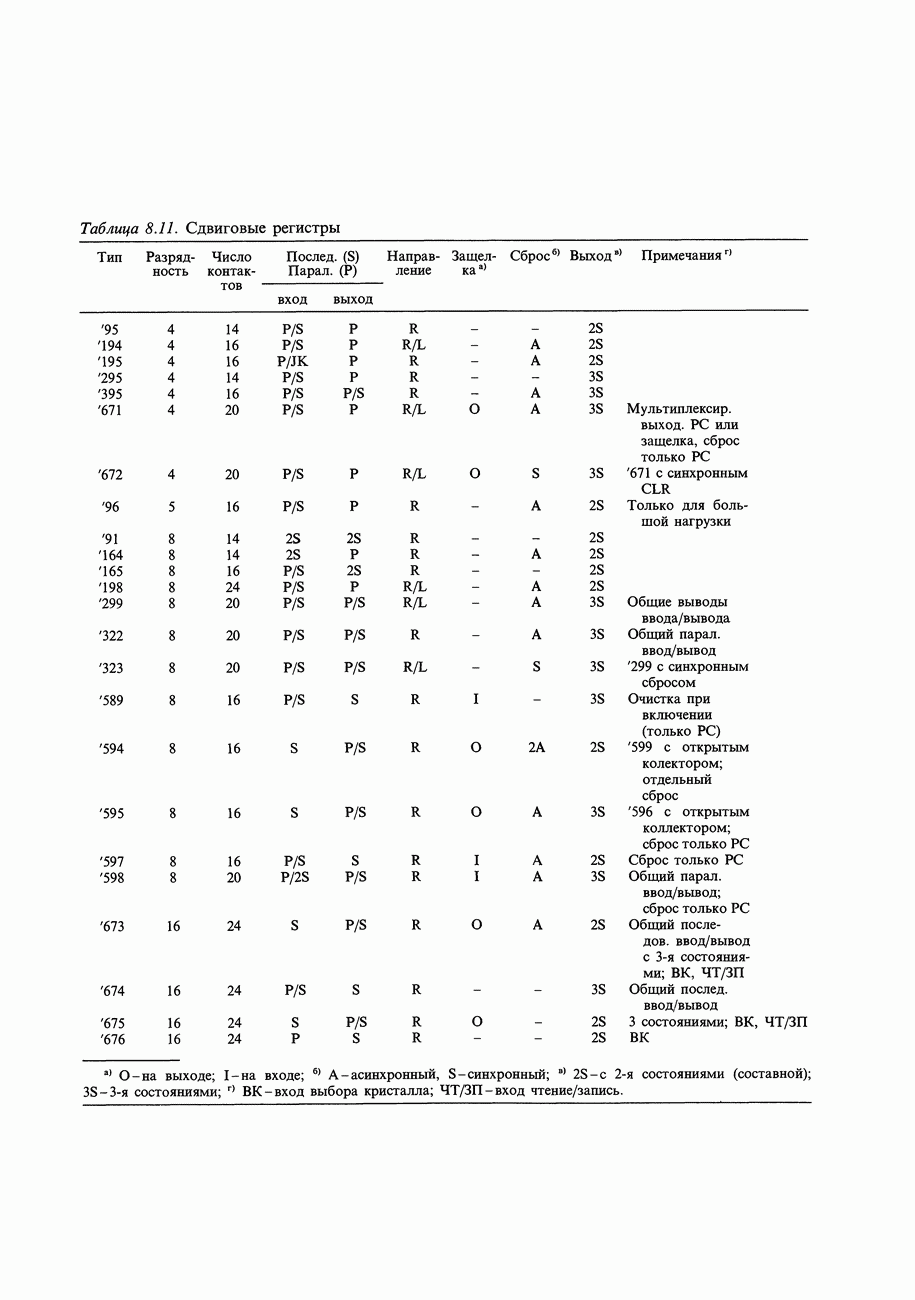
- 8.26. Регистры сдвига
- 8.27. Последовательностные ПМЛ
- Возможные применения программируемых логических интегральных схем (ПЛИС)
- 8.28. Разнообразные последовательностные схемы
- НЕКОТОРЫЕ ТИПОВЫЕ ЦИФРОВЫЕ СХЕМЫ
- 8.29. Счетчик по модулю n
- 8.30. Мультиплексируемый цифровой индикатор на светодиодах
- 8.31. Привод звездного телескопа
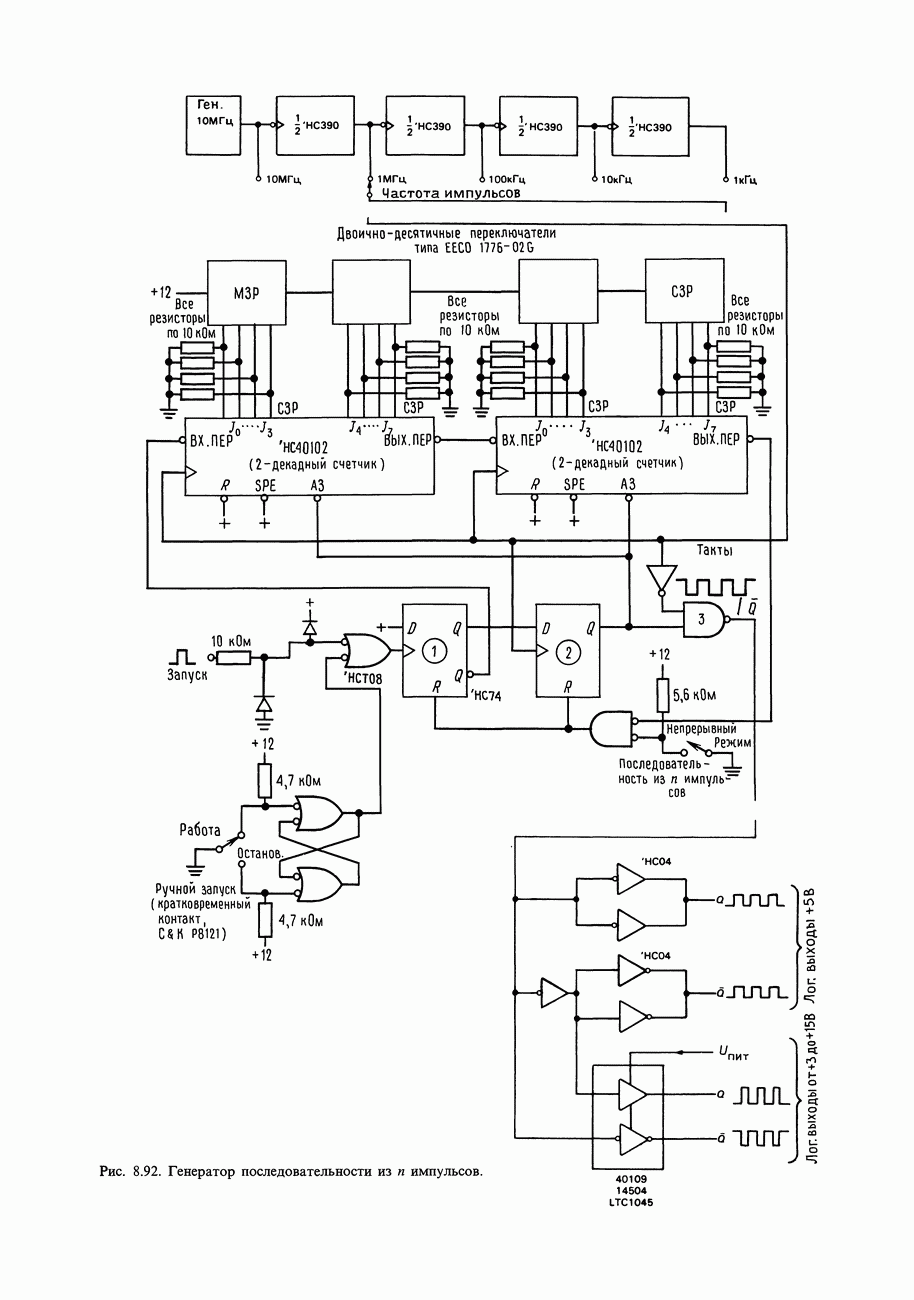
- 8.32. Генератор последовательности из n импульсов
- ПАТОЛОГИЯ В ЛОГИЧЕСКИХ СХЕМАХ
- 8.33. Проблемы статических режимов
- 8.34. Проблемы при переключениях
- 8.35. Прирожденные недостатки ТТЛ и КМОП
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 9. СОПРЯЖЕНИЕ ЦИФРОВЫХ И АНАЛОГОВЫХ СИГНАЛОВ
- 9.01. Хронология логических семейств
- 9.02. Входные и выходные характеристики
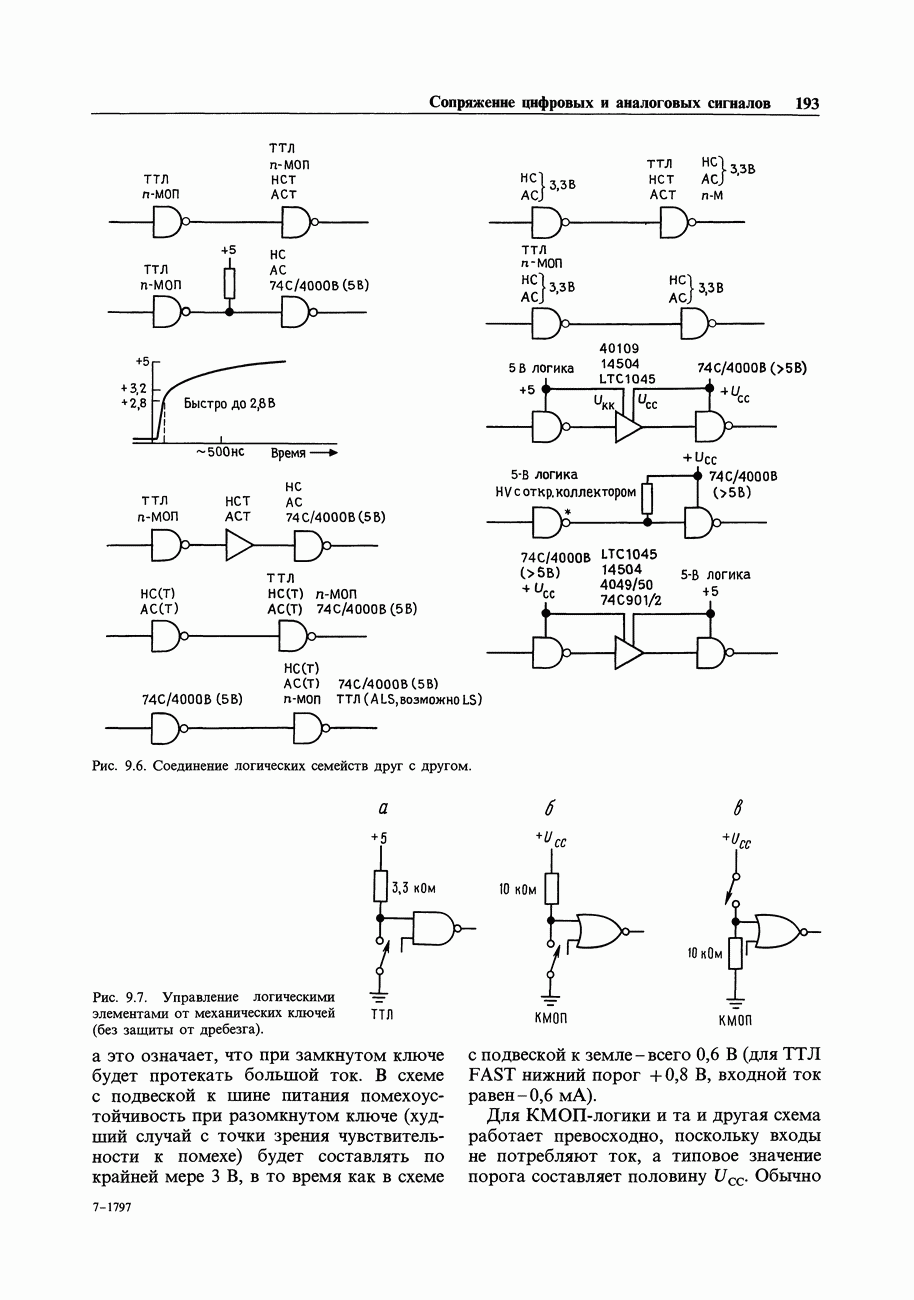
- 9.03. Сопряжение логических семейств
- 9.04. Управление КМОП-и ТТЛ-входами
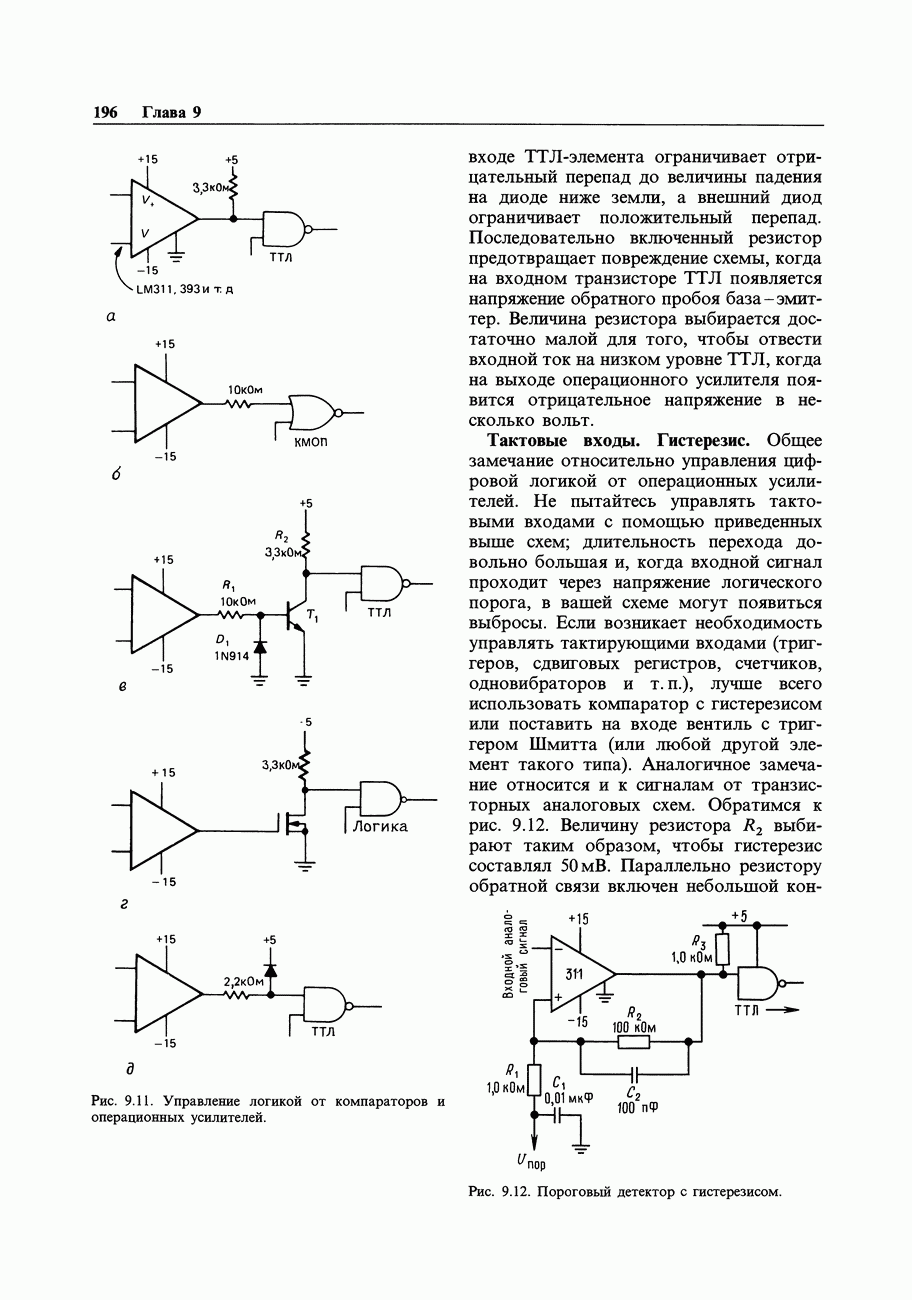
- 9.05. Управление цифровой логикой от компараторов и операционных усилителей
- 9.06. Некоторые замечания, касающиеся логических входов
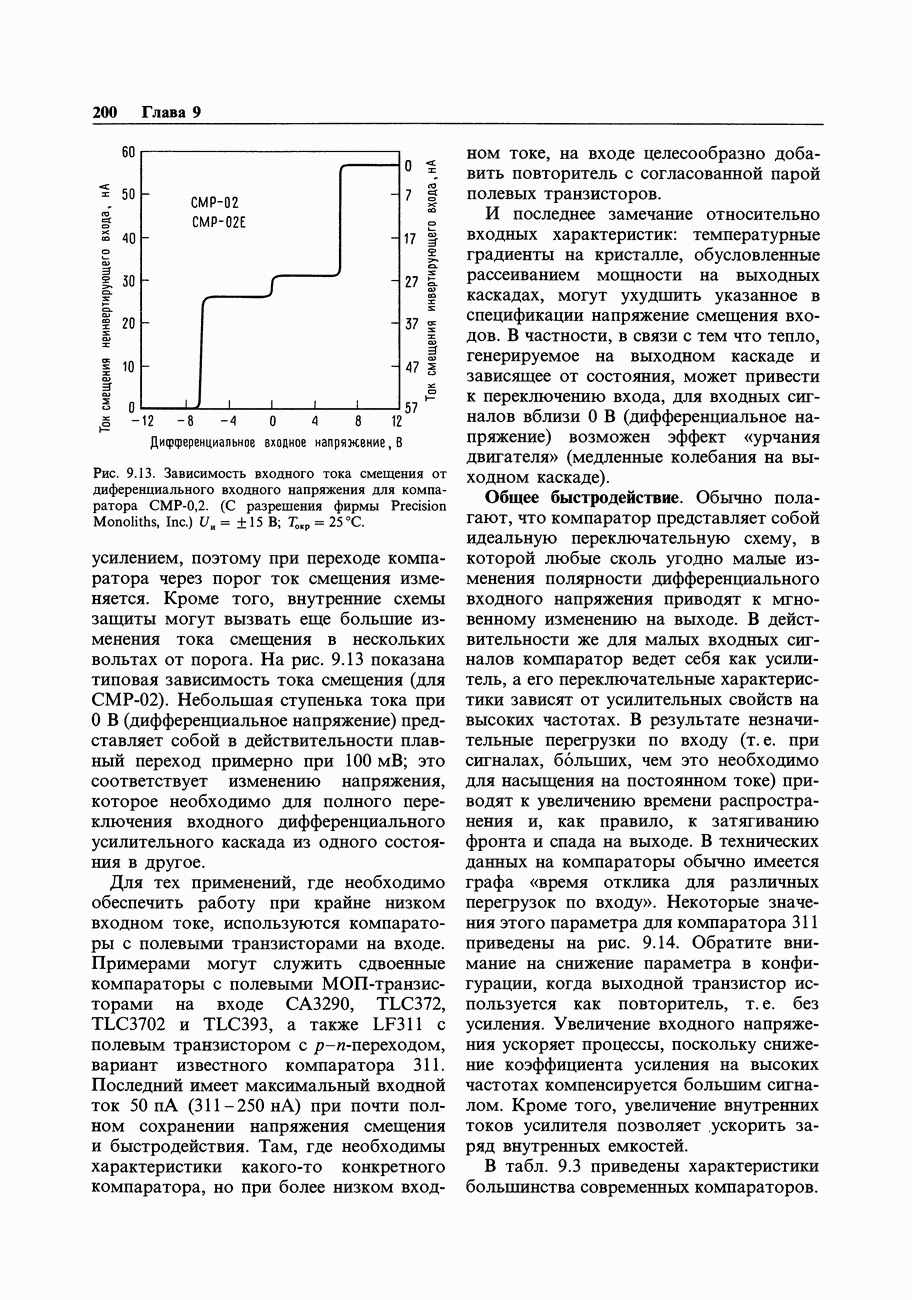
- 9.07. Компараторы
- 9.08. Управление внешней цифровой нагрузкой от КМОП- и ТТЛ-элементов
- 9.09. Сопряжение n-МОП БИС
- 9.10. Оптоэлектроника
- ЦИФРОВЫЕ СИГНАЛЫ И ДЛИННЫЕ ЛИНИИ
- 9.11. Внутриплатные соединения
- 9.12. Межплатные соединения
- 9.13. Шины данных
- 9.14. Кабельные связи
- АНАЛОГО-ЦИФРОВОЕ ПРЕОБРАЗОВАНИЕ
- 9.15. Введение в аналого-цифровое преобразование
- 9.16. Цифро-аналоговые преобразователи (ЦАП)
- 9.17. Интегрирующие ЦАП
- 9.18. ЦАП с умножением
- 9.19. Выбор ЦАП
- 9.20. Аналого-цифровые преобразователи
- 9.21. Методы уравновешивания заряда
- 9.22. Некоторые необычные АЦП и ЦАП
- 9.23. Выбор АЦП
- ПРИМЕРЫ А/Ц-ПРЕОБРАЗОВАНИЯ
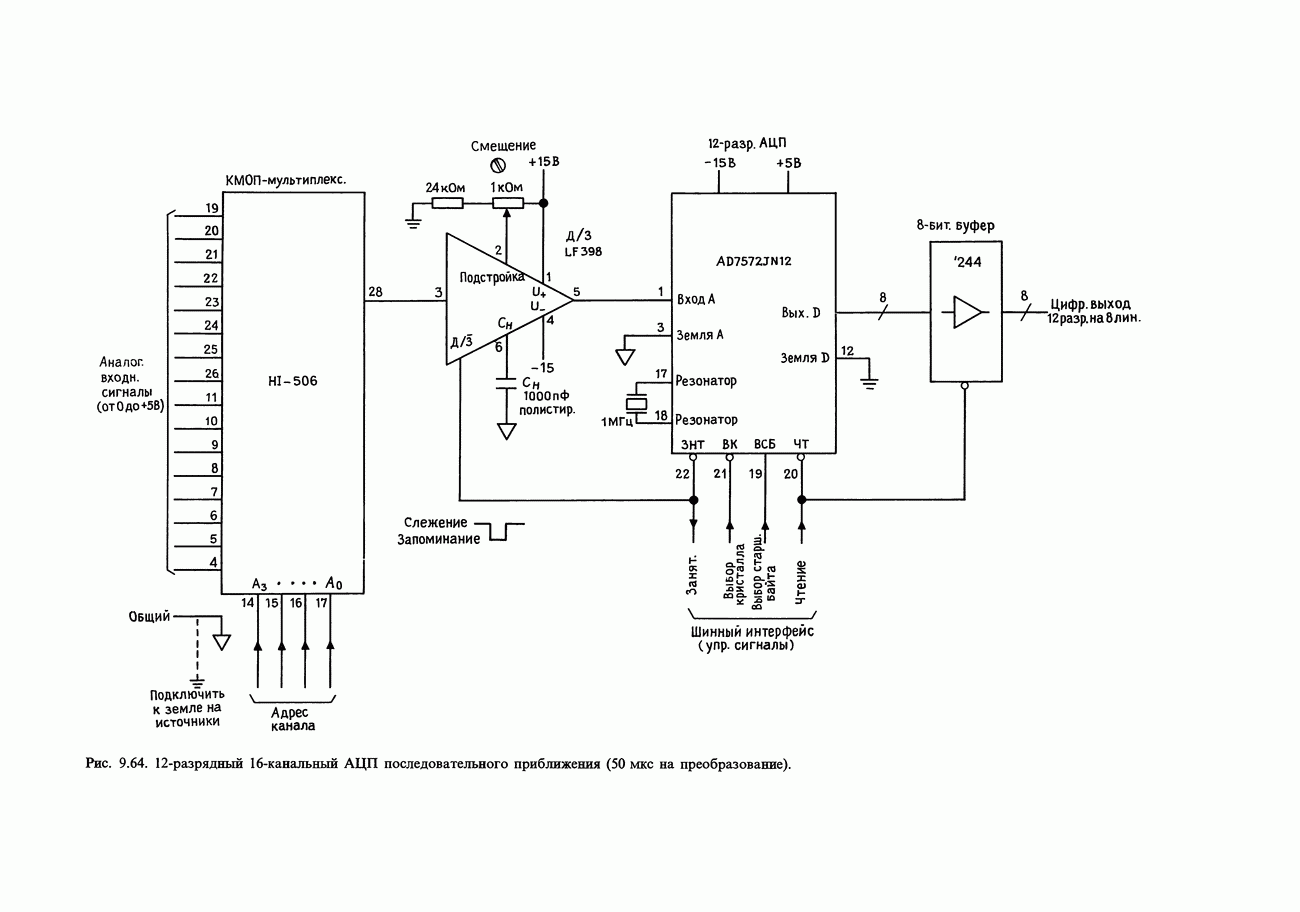
- 9.24. 16-канальная А/Ц-система сбора данных
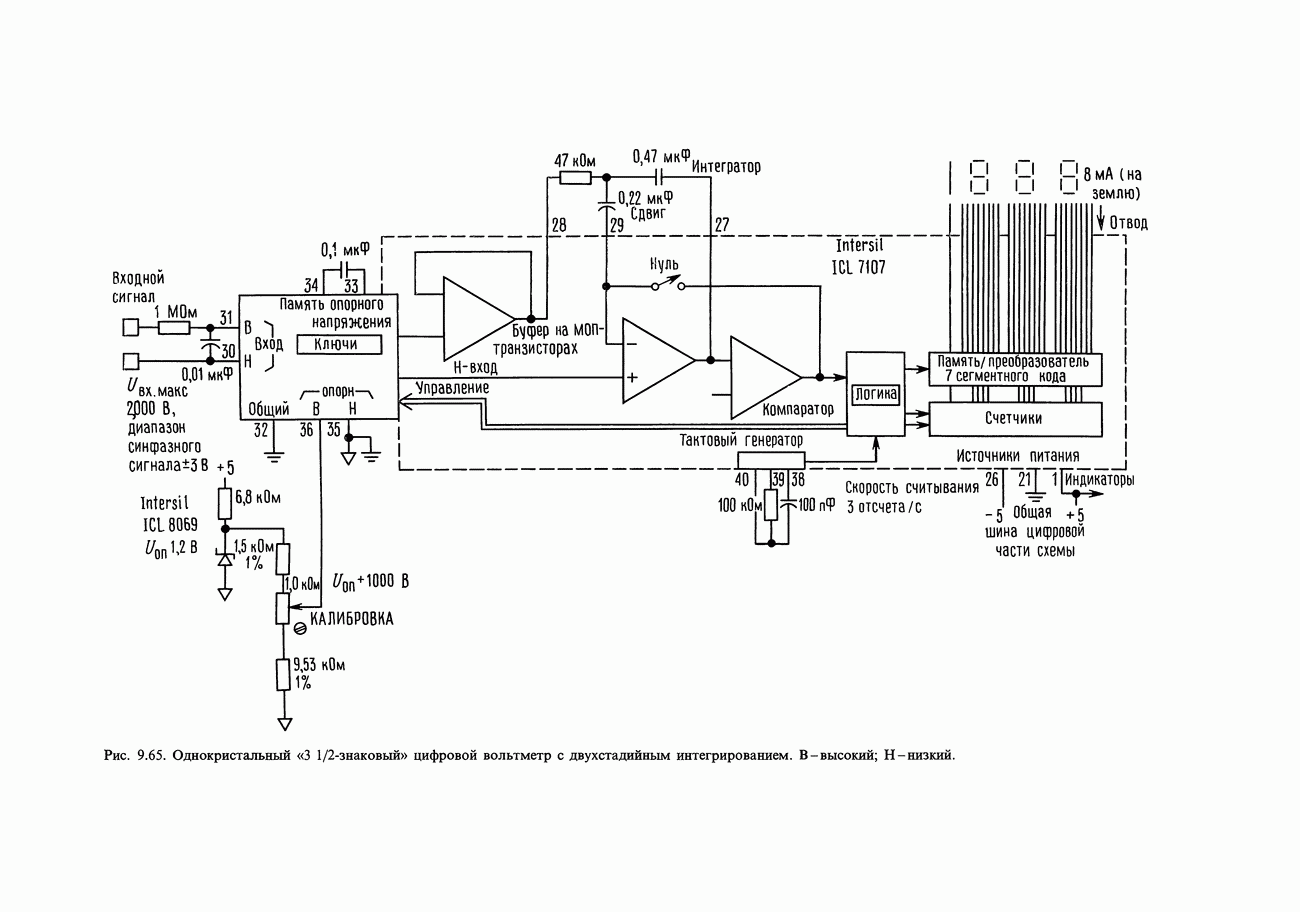
- 9.25. 3 1/2 — знаковый цифровой вольтметр
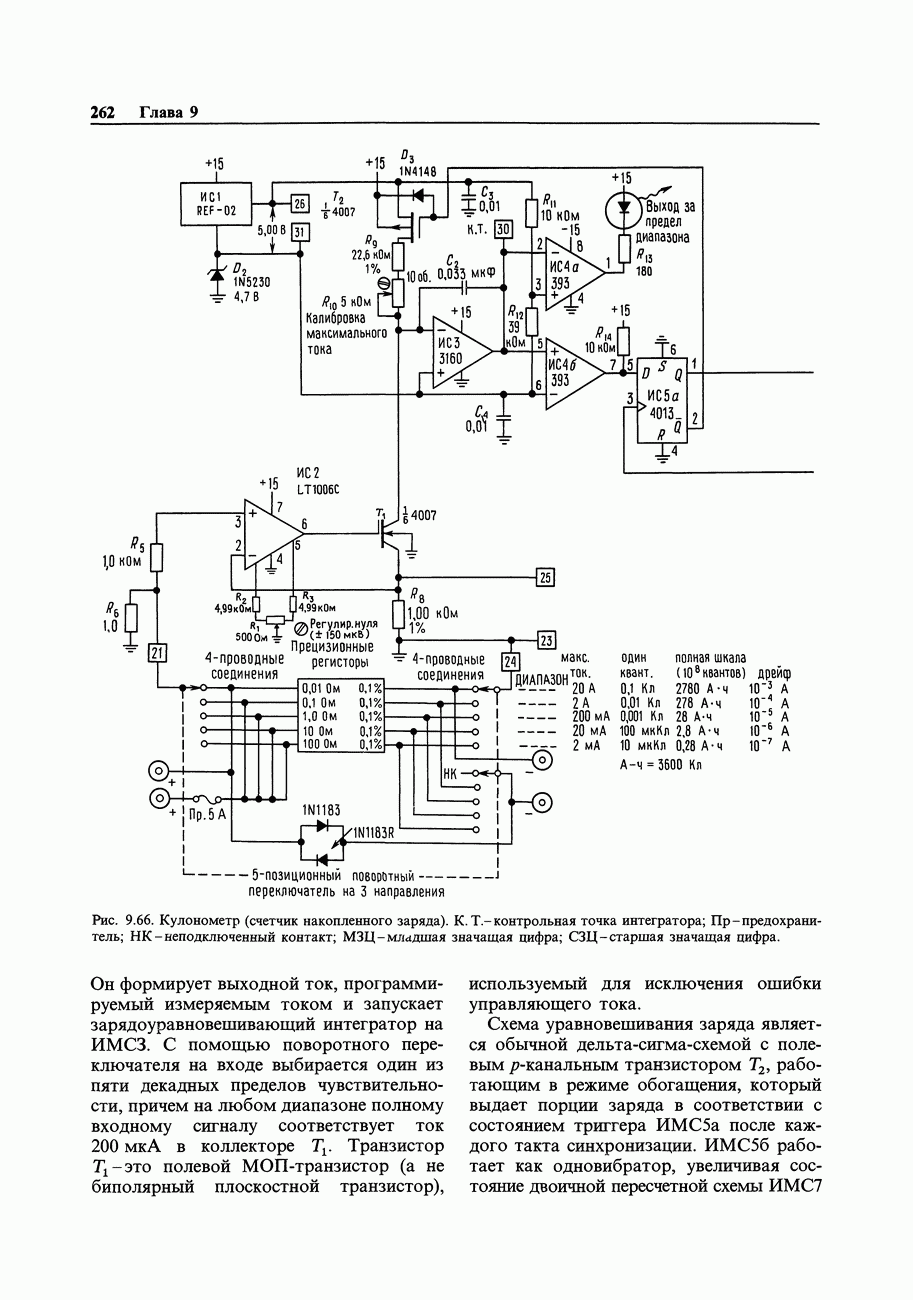
- 9.26. Кулонометр
- СХЕМЫ ФАЗОВОЙ АВТОПОДСТРОЙКИ ЧАСТОТЫ
- 9.28. Проектирование ФАПЧ
- 9.29. Пример разработки: умножитель частоты
- 9.30. Захват и слежение в системе ФАПЧ
- 9.31. Некоторые примеры применения систем ФАПЧ
- ПСЕВДОСЛУЧАЙНЫЕ ДВОИЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ГЕНЕРАТОРЫ ШУМА
- 9.32. Цифровые методы генерации шума
- 9.33. Последовательности, генерируемые регистрами сдвига с обратными связями
- 9.34. Формирование аналогового шума с использованием последовательностей максимальной длины
- 9.35. Энергетический спектр последовательности, сформированной при помощи регистра сдвига
- 9.36. Низкочастотная фильтрация
- 9.37. Краткое заключение
- 9.38. Цифровые фильтры
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 10. МИКРОЭВМ
- МИНИ-ЭВМ, МИКРОЭВМ И МИКРОПРОЦЕССОРЫ
- 10.01. Архитектура микроЭВМ
- НАБОР КОМАНД КОМПЬЮТЕРА
- 10.02. Язык ассемблера и язык машинных кодов
- 10.03. Упрощенный набор команд процессора Intel 8086/8
- 10.04. Программный пример
- СИГНАЛЫ МАГИСТРАЛИ И ЕЕ ФУНКЦИОНИРОВАНИЕ
- 10.05. Основные сигналы магистрали: данные, адрес, синхронизация
- 10.06. Программируемый ввод-вывод: вывод данных
- 10.07. Программируемый ввод-вывод: ввод данных
- 10.08. Программируемый ввод-вывод: регистры состояний
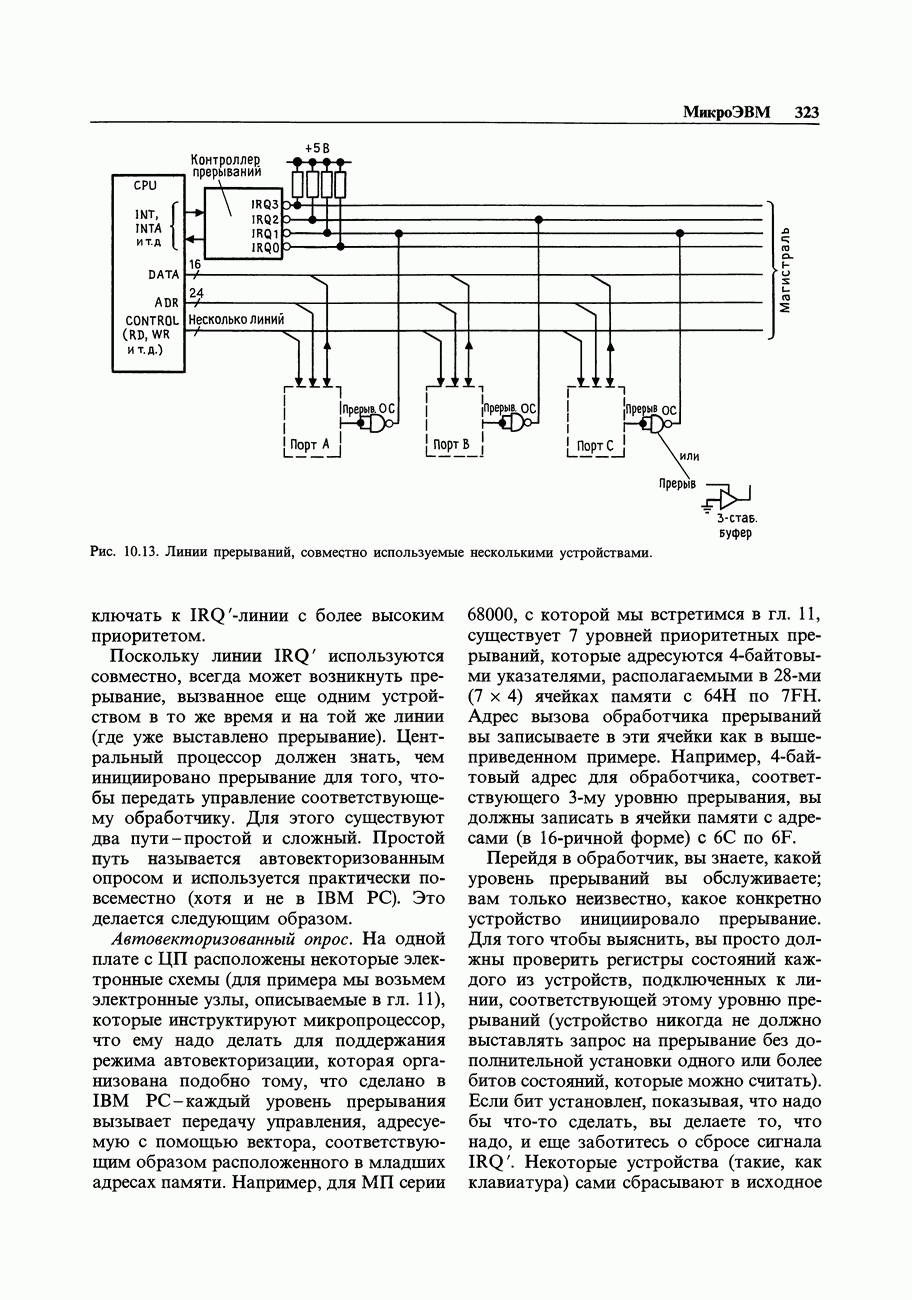
- 10.09. Прерывания
- 10.10. Обработка прерываний
- 10.11. Прерывания в целом
- 10.12. Прямой доступ в память
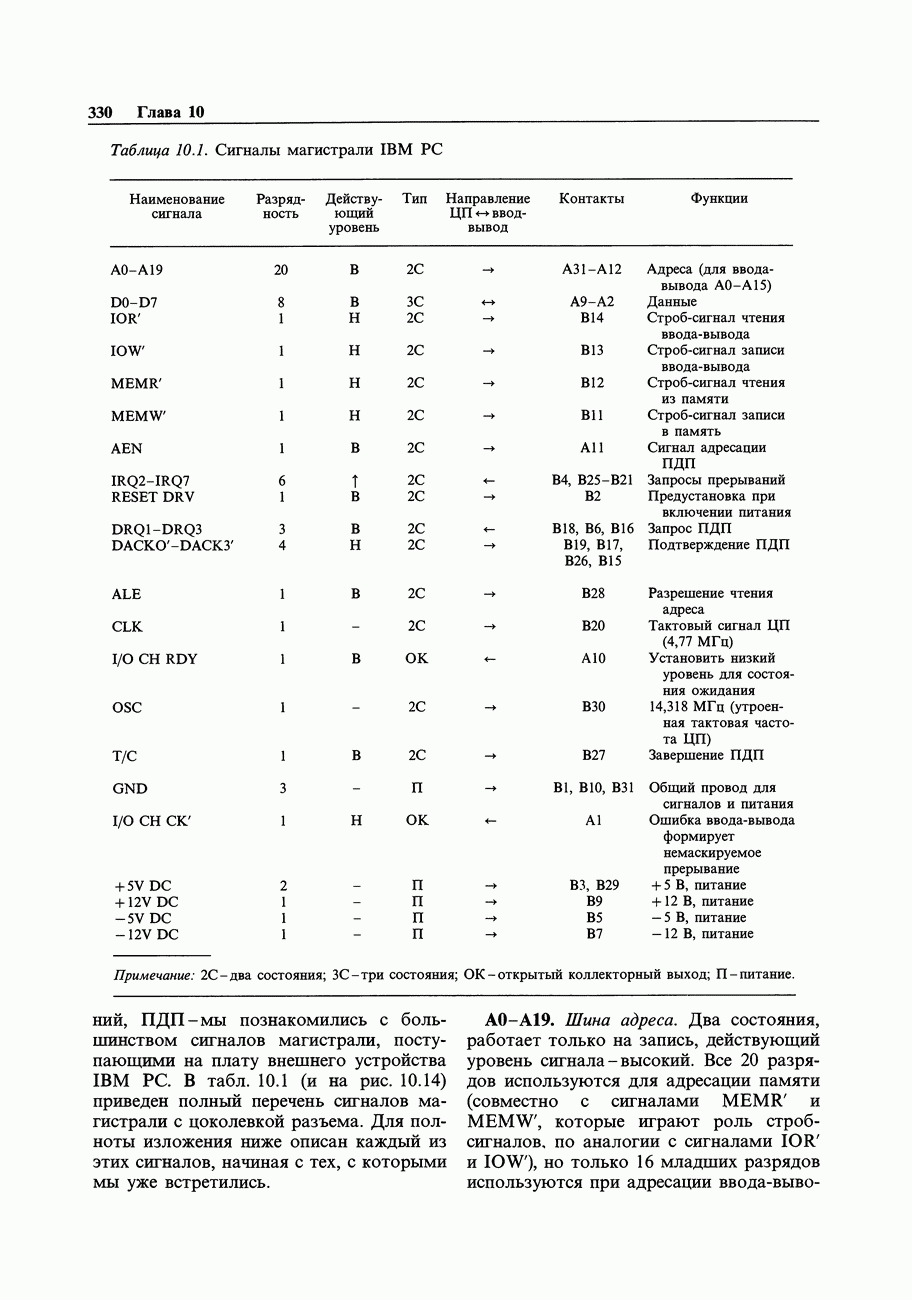
- 10.13. Сводный перечень сигналов магистрали IBM PC
- 10.14. Синхронный и асинхронный протоколы магистрали
- 10.15. Магистрали других микрокомпьютеров
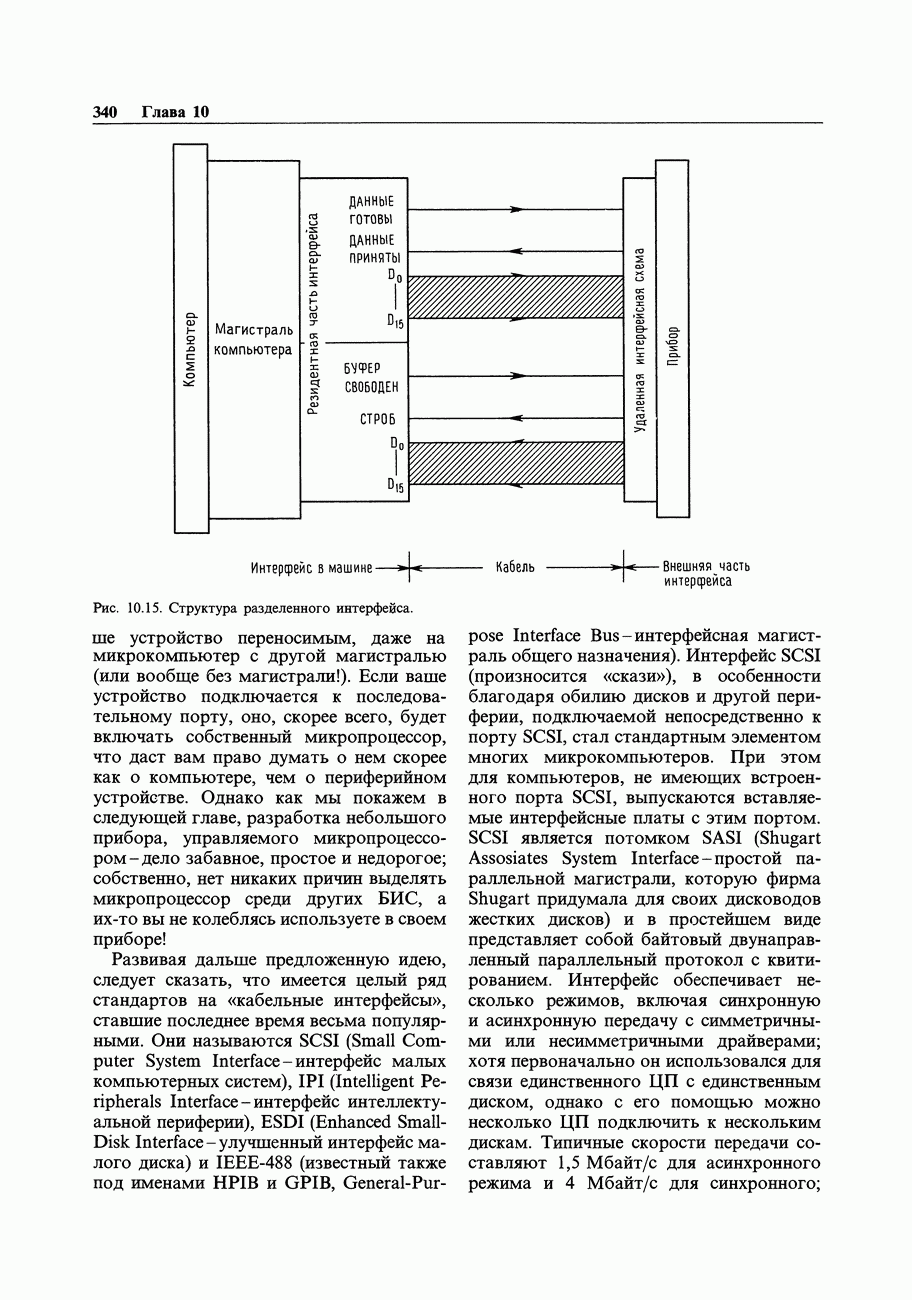
- 10.16. Подключение к компьютеру периферийных устройств
- СИСТЕМНЫЕ КОНЦЕПЦИИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- 10.17. Программирование
- 10.18. Операционные системы, файлы и использование памяти
- ПРИНЦИПЫ ПЕРЕДАЧИ ДАННЫХ
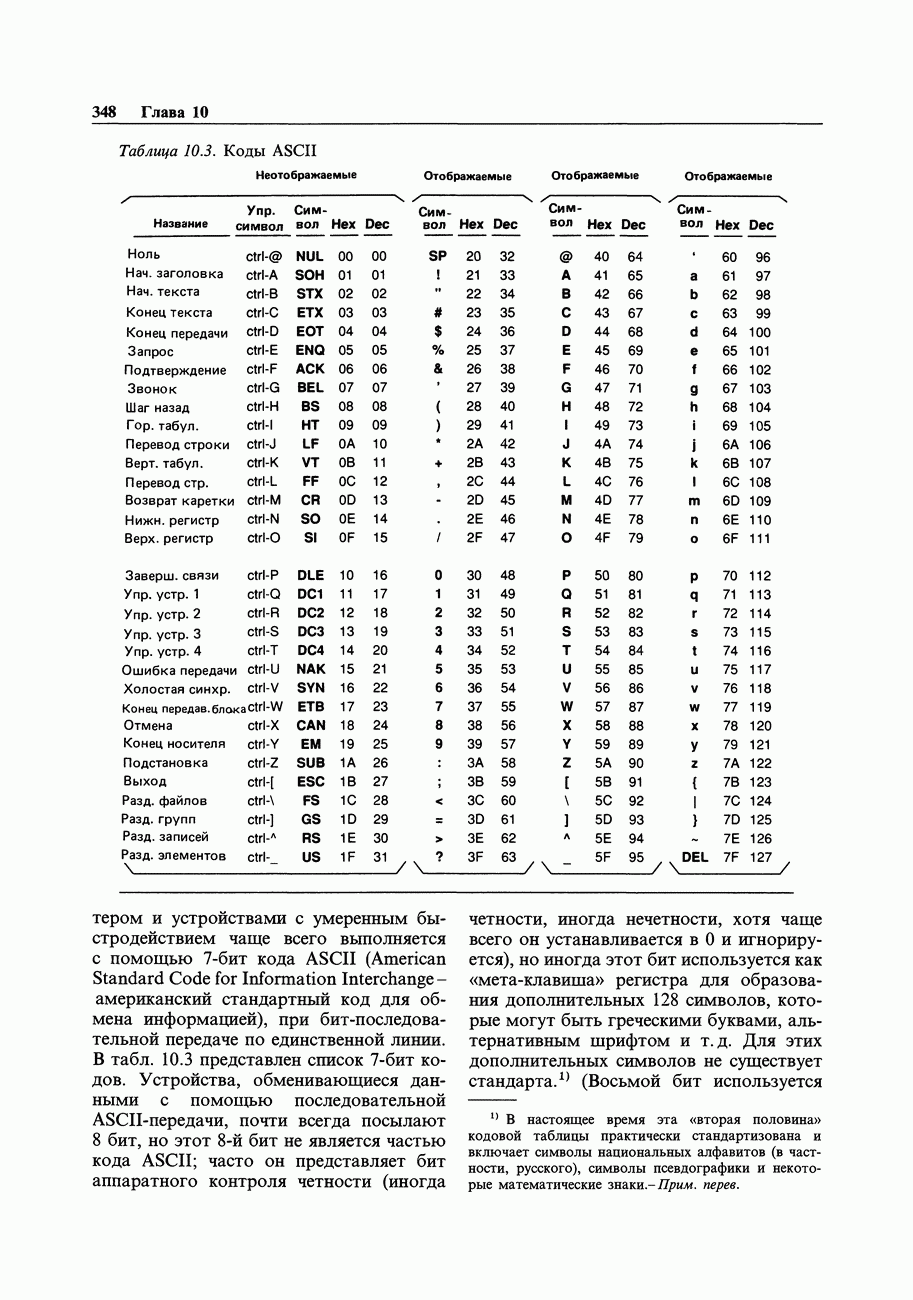
- 10.19. Последовательная связь и коды ASCII
- 10.20. Параллельная связь
- 10.21. Локальные вычислительные цепи
- 10.22. Пример интерфейса: аппаратная упаковка данных
- 10.23. Форматы чисел