Квазислучайные колебания и качественные вопросы небесной механики

Введение

Среди различных областей науки, где математика находит себе применение и является почетной гостьей, небесная механика занимает совершенно исключительное положение. С давних пор, уже почти 300 лет, ее задачи, и особенно «задача трех тел», служат полигоном, на котором поколение за поколением математиков испытывает мощь как старых, так и вновь изобретенных методов исследования. Естественность и простота постановок задач сочетаются с необычайным богатством и разнообразием их содержания. Попытки решить задачу трех тел или хотя бы получить какие-то частные результаты о свойствах ее решений явились отправной точкой для развития многих разделов науки. Многие результаты и поныне не утратили своего значения, другие представляют лишь исторический интерес; число опубликованных работ измеряется сотнями, если не тысячами.

На рубеже двух веков А. Пуанкаре подвел в своих «Новых методах небесной механики» итоги исследований XIX века и дал обильную пищу ученым XX века. Поражаешься богатству идей и понятий, содержащихся в этой книге: метод малого параметра, асимптотические ряды, исследование периодических решений, гомоклинические кривые, интегральные инварианты и т.д. Словом, значительная часть того, что теперь называется «качественной теорией дифференциальных уравнений», восходит к «Новым методам» Пуанкаре и, следовательно, к небесной механике.

Проникновение качественных методов в теорию нелинейных колебаний и в другие задачи нелинейной механики произошло позже, но так уж случилось, что именно с этими задачами стали преимущественно связывать качественную теорию дифференциальных уравнений.

Многие из этих задач приводят к исследованию потоков на двумерных многообразиях, где ситуация значительно проще (см., например, лекции А. Г. Кушиирепко), по зато и успехи существеннее, и методы плодотворнее.

Двумерная качественная теория дифференциальных уравнений получила значительное развитие, но сейчас она стала явно недостаточной, и современные конференции и симпозиумы это постоянно демонстрируют. Сейчас качественная теория развивается довольно бурно, и, по моему мнению, каждое ее возвращение к первоисточнику, а таковым я считаю небесную механику, придает ей новые силы и свежесть.

Одно такое возвращение состоялось, когда А.Н. Колмогоров, а затем В.И. Арнольд и Ю. Мозер получили свои замечательные результаты, касающиеся инвариантных торов и условно периодических движений в гамильтоновых системах. Вряд ли нужно напоминать, сколь значительным оказалось это продвижение в том, что Пуанкаре назвал «основной задачей динамики», и сколь стимулирующим было его воздействие на качественную теорию.

Сейчас, как мне кажется, назревает почва еще для одного возвращения, да и, пожалуй, оно уже началось. Будем надеяться, что и это возвращение окажется достаточно плодотворным.

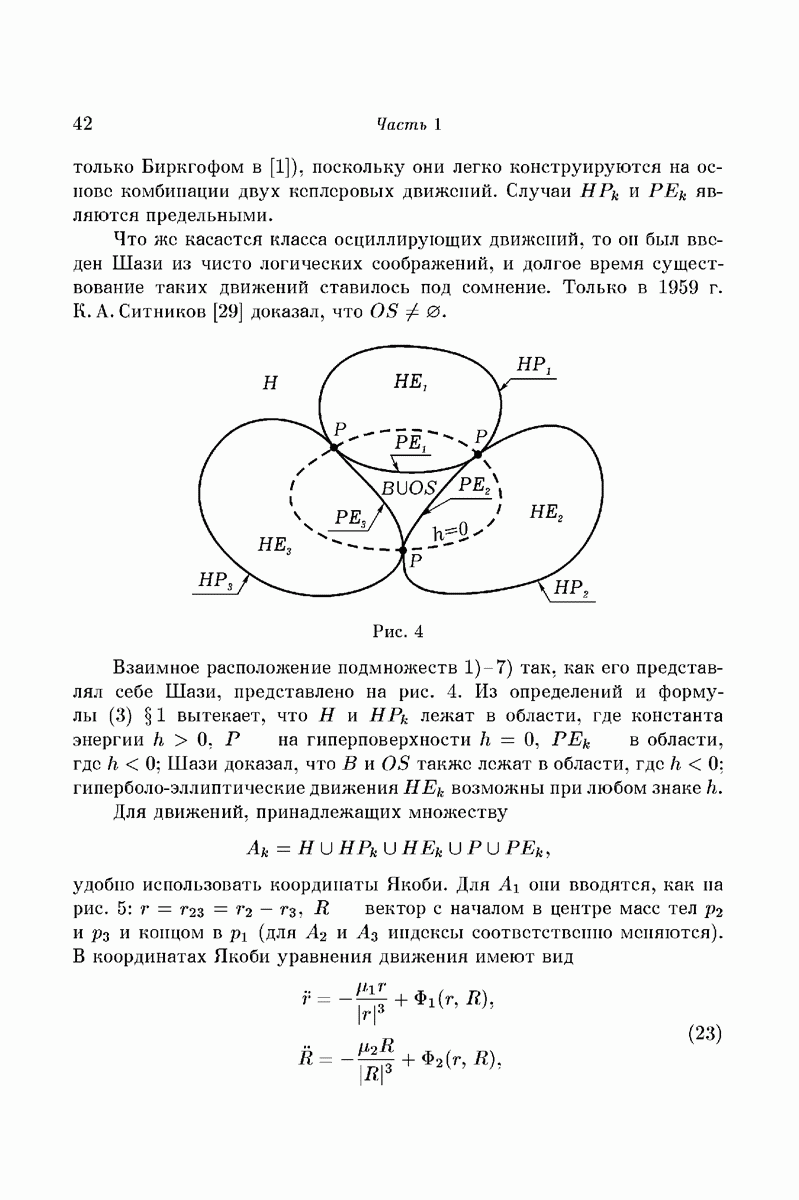
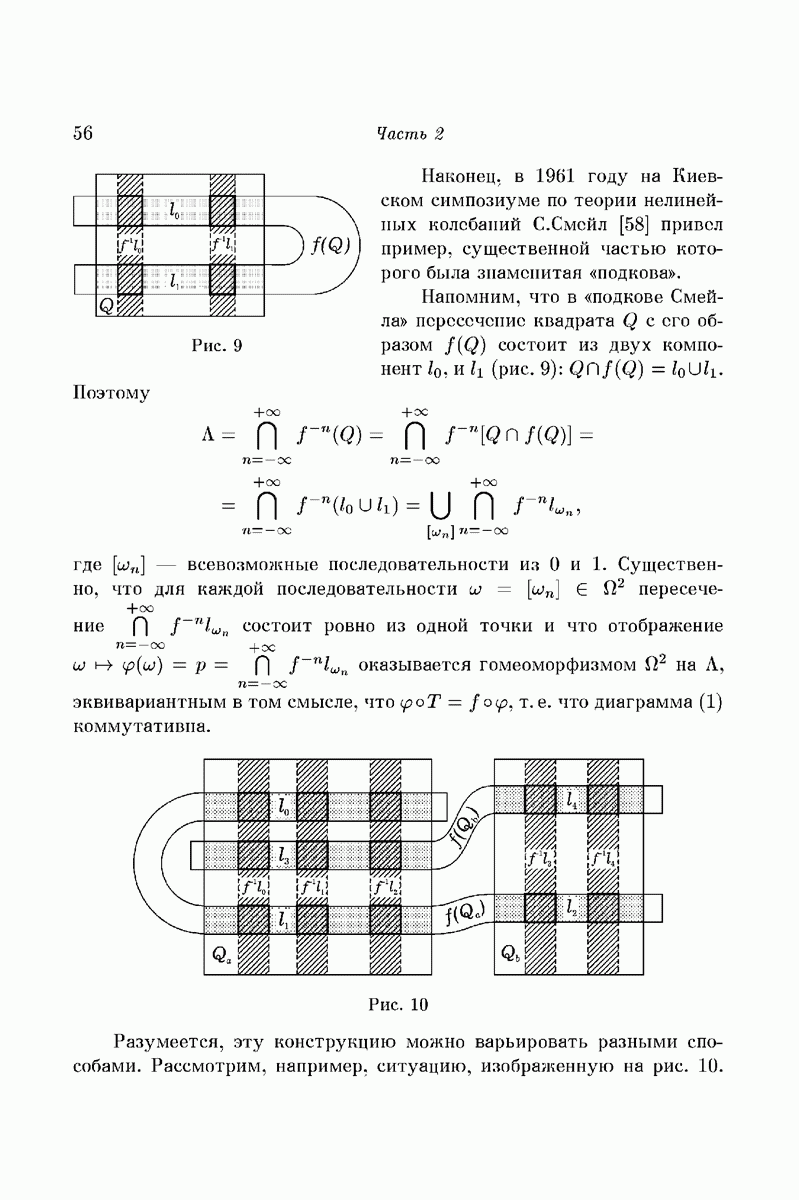
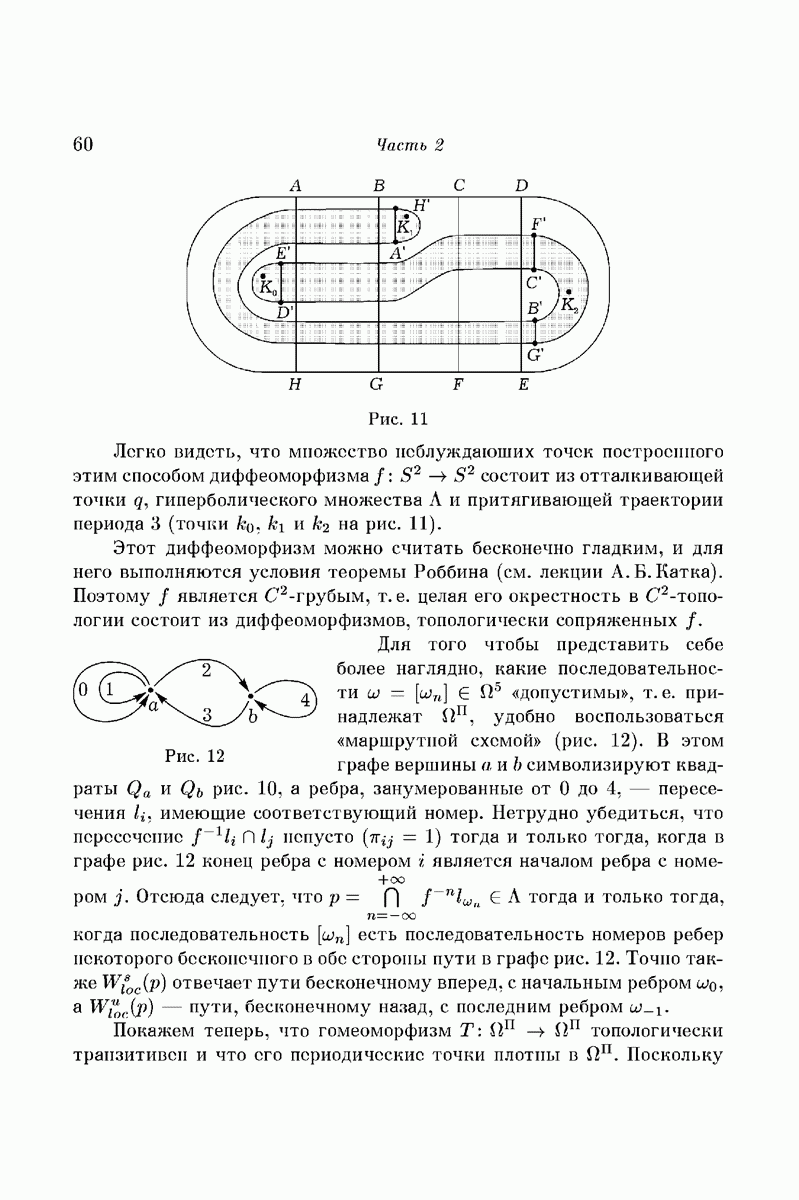
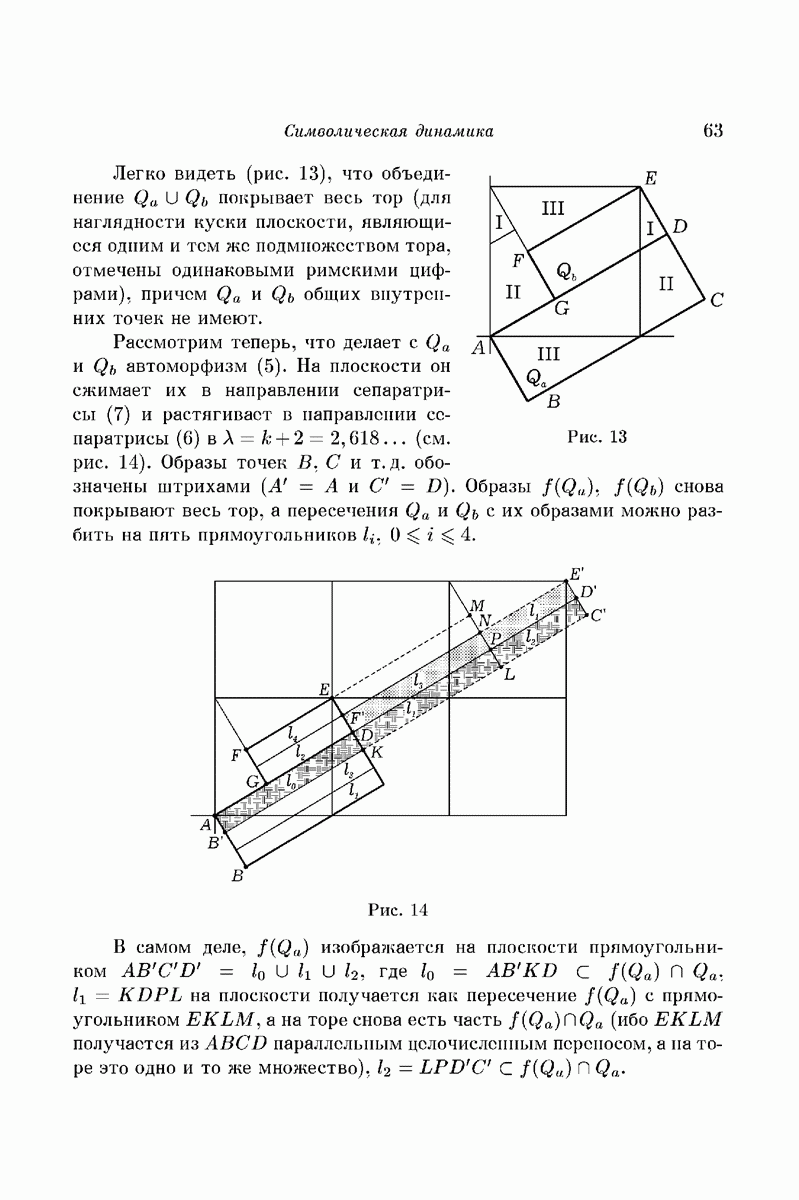
Кроме материалов летней украинской математической школы в Кацивели (июль 1971 года), далее широко использован русский вариант доклада [35], а также результаты, с которыми я ознакомился сравнительно недавно. Часть 1 содержит обзор некоторых направлений качественных исследований в задачах небесной механики. Часть 2 является наглядным введением в «символическую динамику»; я старался, чтобы технические детали возможно меньше заслоняли здесь существо дела. В части 3 я хотел показать, каким образом методы символической динамики могут оказаться полезными уже в простейших задачах теории нелинейных колебаний и что они позволяют сделать применительно к задачам, рассмотренных в части 1. Я приношу искреннюю благодарность организаторам школы, пригласившим меня прочитать эти лекции и проявившим незаурядное терпение, дожидаясь, пока они окажутся написанными.