| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Финальные движения в задаче трех тел и символическая динамика
В. М. Алексеев
1. Введение. «Задача трех тел» — одна из наиболее известных в математике, механике и астрономии. Годом ее рождения следует считать 1687 — дату выхода в свет ньютоновских «Philosophiac Naturalis Principia Mathematica». С тех пор уже почти 300 лет эта задача служит пробным камнем, на котором поколения математиков испытывают новые методы исследования. Оценивая роль, которую эта задача сыграла в истории математики, следует помнить, что именно она вместе с другими задачами небесной механики явилась отправной точкой в развитии многих идей как теории дифференциальных уравнений, так и смежных областей.
Среди работ, затерянных в безбрежном океане статей и монографий, посвященных задаче трех тел, многие результаты и поныне не утратили своего значения. XVIII в. оставил нам частные решения Л. Эйлера и Ж. Лагранжа, теорию возмущений и метод «вариации постоянных». XIX столетию принадлежит великое открытие «на копчике пера», сделанное У. Леверрье и Дж. Адамсом. Идея представления решений в виде степенных и тригонометрических рядов также в духе того столетия; для вычисления орбит небесных тел астрономы до сих пор нередко используют методы, восходящие к исследованиям того времени. Итог исследованиям XIX в. подвели «Новые методы небесной механики» Л. Пуанкаре и знаменитая теорема К. Зундмана об аналитической регуляризации любого решения задачи трех тел с ненулевым значением момента количества движения.
В XX в. характерен интерес к качественным проблемам. Постановки большинства тех из них, которые относятся к небесной механике и качественной теории дифференциальных уравнений, можно найти
уже у Пуанкаре [1]. Задачей трех тел стимулированы многие разделы знаменитой книги Дж. Биркгофа [3]; лекции K.Л. Зигеля [4], [5] почти целиком посвящены математическим проблемам, по преимуществу качественным, возникающим в небесной механике.
А. Уинтнер заметил однажды [6], что каждое поколение по-своему формулирует «основные проблемы в задаче трех тел» и по-своему их решает. Следуя Дж. Биркгофу [3], я считаю, что с чисто математической точки зрения сейчас такой основной проблемой является топологическое описание разбиения фазового пространства на траектории. Это описание должно включать классификацию различных типов движения, классификацию и изучение инвариантных интегральных многообразий, исследование эволюции системы и т. п.
Важные прикладные задачи, которые возникают в космической навигации, обычно не укладываются в рамки классической задачи трех тел и рассматриваться далее не будут.
Сформулированная выше проблема, по-видимому, еще далека от исчерпывающего разрешения, и потому мы ограничимся лишь ее более частным и грубым аспектом, а именно финальными движениями, т. е. поведением решений при 
Начало исследований в этом направлении было положено мемуарами Ж. Шази [7]-[9]. В [7] описаны все возможные односторонние (т.е. относящиеся только к  или только к
или только к  ) типы финальных движений. Как с математической, так и с космогонической точки зрения весьма интересно описать возможные типы эволюции системы, т. е. дать ответ на вопрос, в каких комбинациях могут сочетаться типы поведения при
) типы финальных движений. Как с математической, так и с космогонической точки зрения весьма интересно описать возможные типы эволюции системы, т. е. дать ответ на вопрос, в каких комбинациях могут сочетаться типы поведения при  Обзору достигнутых в этом направлении результатов посвящена первая половина этой статьи. Во второй половине я остановлюсь на методах, при помощи которых эти результаты были достигнуты.
Обзору достигнутых в этом направлении результатов посвящена первая половина этой статьи. Во второй половине я остановлюсь на методах, при помощи которых эти результаты были достигнуты.
Я хотел бы отметить, что А.Н. Колмогоров в 1954 г. привлек впервые мое внимание к обсуждаемым проблемам. С тех пор его дружеское внимание и ценные советы неоднократно помогали мне в моих исследованиях.
Результаты
2. Классификация финальных движении по Шази. Как хорошо известно, задача трех тел состоит в изучении движения тел (материальных точек  ) под действием ньютоновских сил взаимного притяжения. Через
) под действием ньютоновских сил взаимного притяжения. Через  обозначается далее масса тела
обозначается далее масса тела  обозначает расстояние между
обозначает расстояние между  определяются аналогично.
определяются аналогично.
В этой задаче  степеней свободы, и потому фазовое пространство 18-мерно. Выбором инерциальной системы можно добиться того, чтобы общий центр масс покоился в начале координат, что позволяет редуцировать задачу к 6 степеням свободы и 12-мерному фазовому пространству
степеней свободы, и потому фазовое пространство 18-мерно. Выбором инерциальной системы можно добиться того, чтобы общий центр масс покоился в начале координат, что позволяет редуцировать задачу к 6 степеням свободы и 12-мерному фазовому пространству  . После этого задача все еще имеет 4 алгебраических первых интеграла, что позволяет уменьшить размерность до 8 (см., например, [11]). Нам будет, однако, удобнее остановиться на рассмотрении
. После этого задача все еще имеет 4 алгебраических первых интеграла, что позволяет уменьшить размерность до 8 (см., например, [11]). Нам будет, однако, удобнее остановиться на рассмотрении  расслоенного на изоэнергетические гиперповерхности
расслоенного на изоэнергетические гиперповерхности  . Более мелкое расслоение, связанное с интегралами площадей, изучается в [12] и [13].
. Более мелкое расслоение, связанное с интегралами площадей, изучается в [12] и [13].
Согласно Шази [7],  разбивается на следующие подмножества:
разбивается на следующие подмножества:
1) Н. Гиперболические движения.
2)  . Гиперболо-параболические движения.
. Гиперболо-параболические движения.
3) Р. Параболические движения.
Здесь при  . Все
. Все  для Н и
для Н и  для Р.
для Р.
В случае  при
при  .
.
4)  . Гиперболо-эллиптические движения.
. Гиперболо-эллиптические движения.
5)  . Параболо-эллиптические движения.
. Параболо-эллиптические движения.
Здесь  для
для 
6) В. Ограниченные движения.

7) OS. Осциллирующие движения.


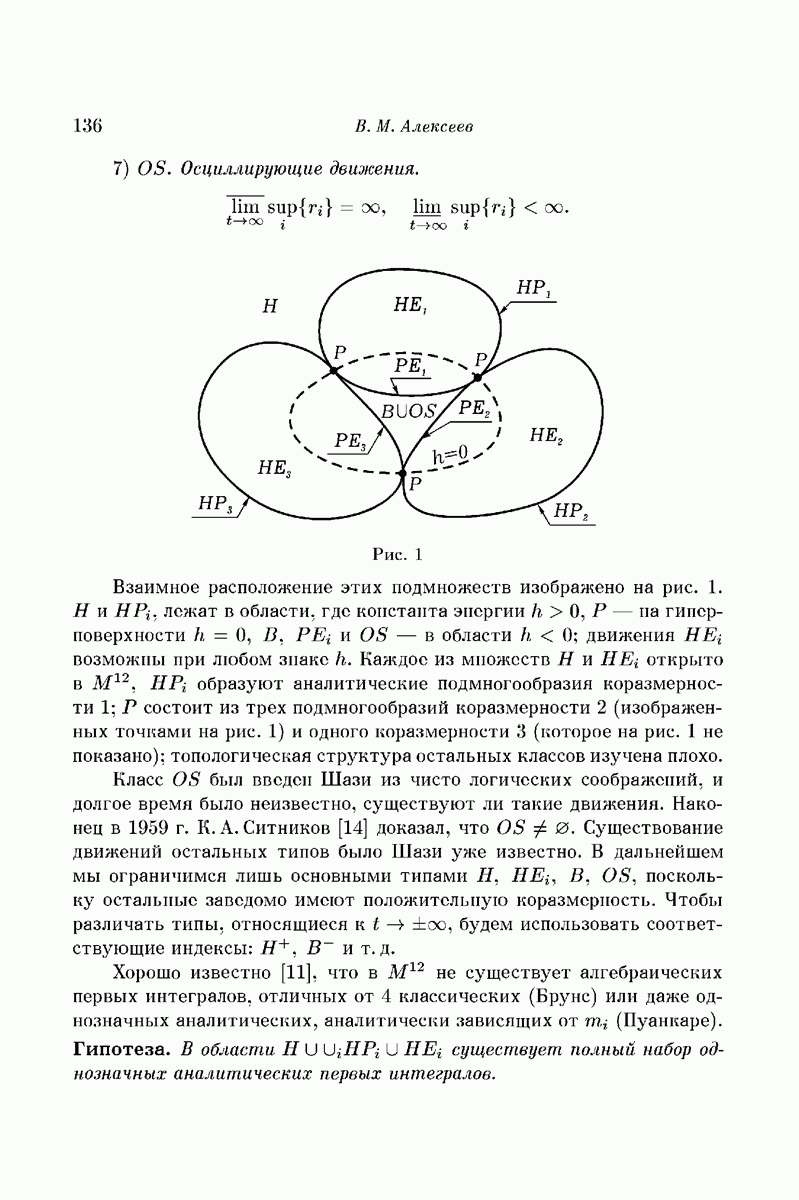
Рис. 1
Взаимное расположение этих подмножеств изображено на рис. 1. Н и  лежат в области, где константа энергии
лежат в области, где константа энергии  — на гиперповерхности
— на гиперповерхности  и OS — в области
и OS — в области  движения
движения  возможны при любом знаке h. Каждое из множеств Н и
возможны при любом знаке h. Каждое из множеств Н и  открыто в
открыто в  образуют аналитические подмногообразия коразмерности 1; Р состоит из трех подмногообразий коразмерности 2 (изображенных точками на рис. 1) и одного коразмерности 3 (которое на рис. 1 не показано); топологическая структура остальных классов изучена плохо.
образуют аналитические подмногообразия коразмерности 1; Р состоит из трех подмногообразий коразмерности 2 (изображенных точками на рис. 1) и одного коразмерности 3 (которое на рис. 1 не показано); топологическая структура остальных классов изучена плохо.
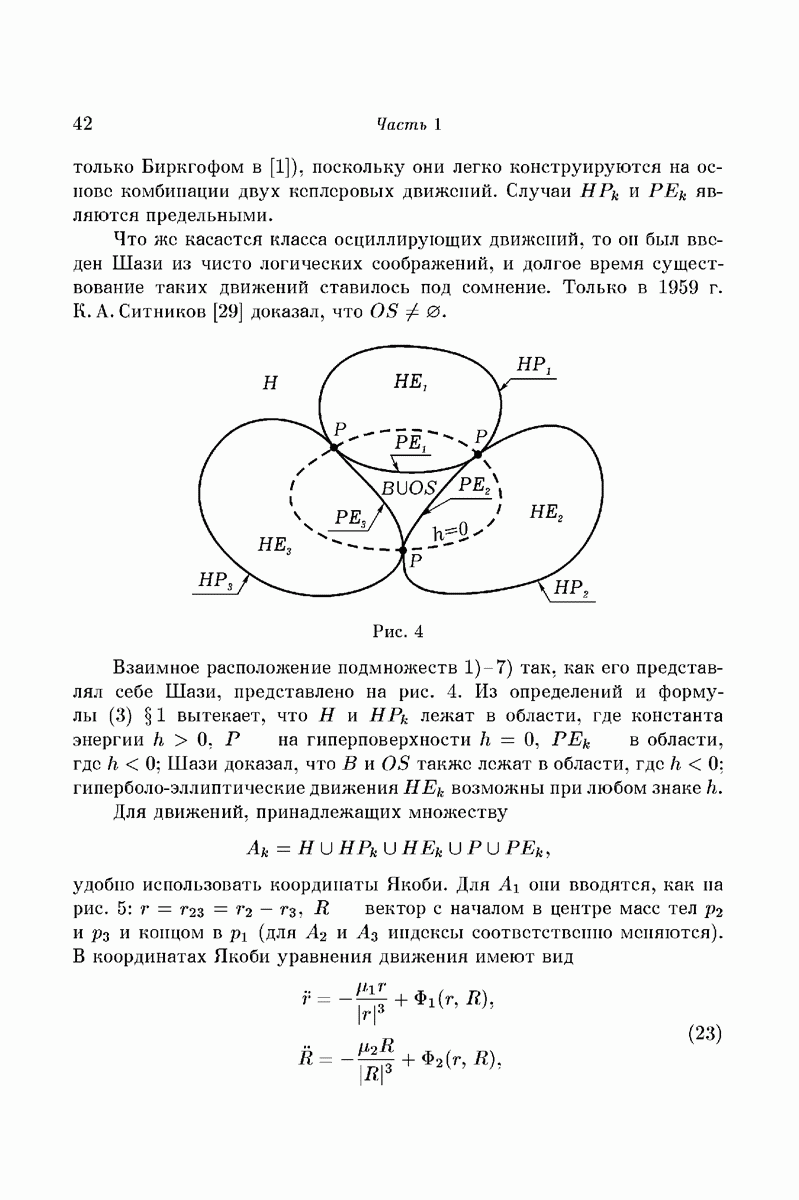
Класс OS был введен Шази из чисто логических соображений, и долгое время было неизвестно, существуют ли такие движения. Наконец в 1959 г. К. А. Ситников [14] доказал, что  . Существование движений остальных типов было Шази уже известно. В дальнейшем мы ограничимся лишь основными типами
. Существование движений остальных типов было Шази уже известно. В дальнейшем мы ограничимся лишь основными типами  , поскольку остальные заведомо имеют положительную коразмерность. Чтобы различать типы, относящиеся к
, поскольку остальные заведомо имеют положительную коразмерность. Чтобы различать типы, относящиеся к  будем использовать соответствующие индексы:
будем использовать соответствующие индексы:  и т.д.
и т.д.
Хорошо известно [11], что в  не существует алгебраических первых интегралов, отличных от 4 классических (Вруне) или даже однозначных аналитических, аналитически зависящих от
не существует алгебраических первых интегралов, отличных от 4 классических (Вруне) или даже однозначных аналитических, аналитически зависящих от  (Пуанкаре). Гипотеза. В области
(Пуанкаре). Гипотеза. В области  существует полный набор однозначных аналитических первых интегралов.
существует полный набор однозначных аналитических первых интегралов.
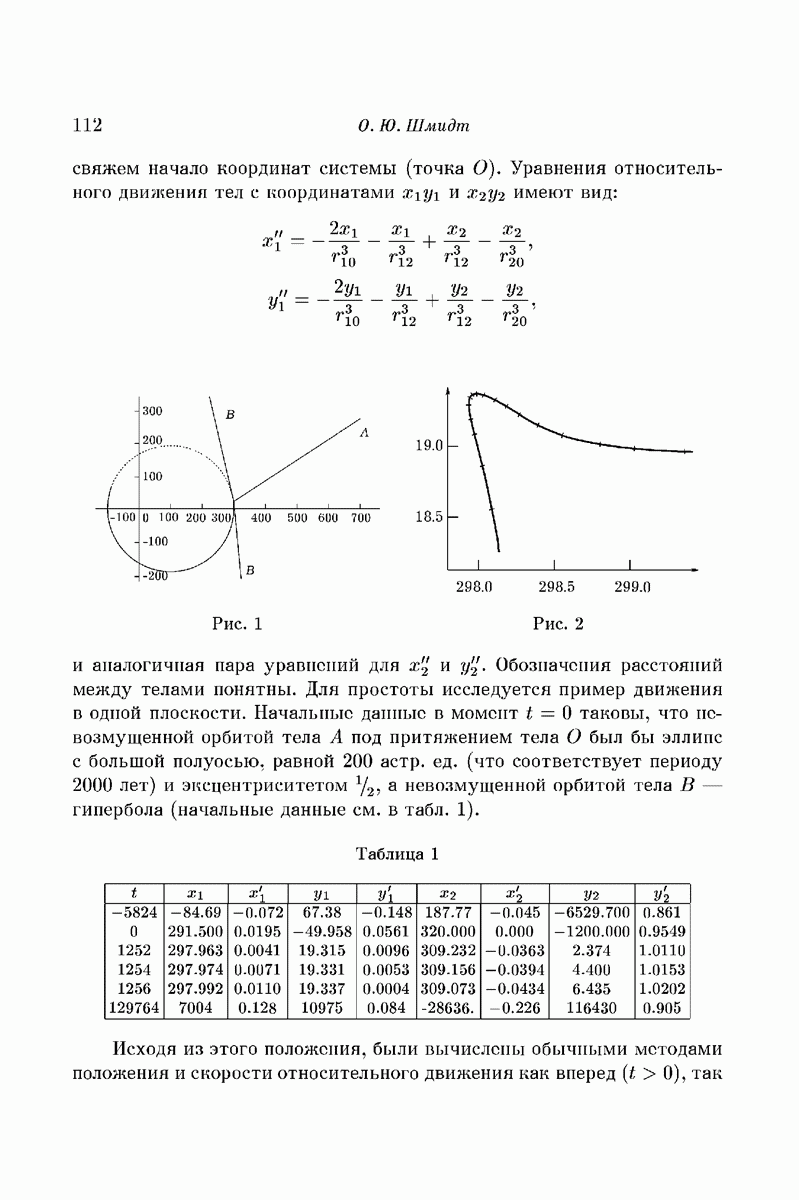
Таблица 1

Аргументы в пользу этой гипотезы содержатся в [7] и [9].
Область  оказывается весьма «разветвленной». Это связано с расположением в
оказывается весьма «разветвленной». Это связано с расположением в  множества S тех траекторий, на которых встречаются точки парных столкновений. Остается нерешенной Проблема ([4]). Не является ли S всюду плотным на некотором открытом в
множества S тех траекторий, на которых встречаются точки парных столкновений. Остается нерешенной Проблема ([4]). Не является ли S всюду плотным на некотором открытом в  подмножестве?
подмножестве?
Недавно Ю. Мозер предложил красивую интерпретацию зундмановской регуляризации парного столкновения в терминах геодезического потока на сфере 
3. Эволюция системы; область  (табл. 1). В мемуарах [8], [9] сформулировано утверждение о совпадении финальных типов одного и того же движения при
(табл. 1). В мемуарах [8], [9] сформулировано утверждение о совпадении финальных типов одного и того же движения при  и при
и при  и довольно долго математический и особенно астрономический мир был убежден, что такая замечательная симметрия действительно имеет место. Некоторый диссонанс вносили лишь примеры Беккера [17], которые явно принадлежали
и довольно долго математический и особенно астрономический мир был убежден, что такая замечательная симметрия действительно имеет место. Некоторый диссонанс вносили лишь примеры Беккера [17], которые явно принадлежали  . Однако Шази приписал это ошибкам численного интегрирования и невозможности проверить поведение решений на всей бесконечной оси времени.
. Однако Шази приписал это ошибкам численного интегрирования и невозможности проверить поведение решений на всей бесконечной оси времени.
В 1947 г. выводы Шази были поставлены под сомнение О. Ю. Шмидтом. Его космогоническая гипотеза, основанная на чисто гравитационном захвате, противоречила (по крайней мере, для задачи трех тел) симметричной картине Шази. Чтобы подкрепить свою гипотезу, Шмидт построил [18] численным интегрированием пример частичного
захвата  . В этом примере из трех независимых в прошлом звезд образуется устойчивая подсистема (двойная звезда), в то время как третья звезда снова уходит в бесконечность. Основанный на численном интегрировании пример Шмидта был уязвим для критики с тех же позиций, что и примеры [17]. Одно из выдвигавшихся возражений было преодолено Г. Ф. Хильми [19]. Ему удалось описать системами неравенств открытые подмножества в Н и
. В этом примере из трех независимых в прошлом звезд образуется устойчивая подсистема (двойная звезда), в то время как третья звезда снова уходит в бесконечность. Основанный на численном интегрировании пример Шмидта был уязвим для критики с тех же позиций, что и примеры [17]. Одно из выдвигавшихся возражений было преодолено Г. Ф. Хильми [19]. Ему удалось описать системами неравенств открытые подмножества в Н и  («критерии гиперболического и гиперболо-эллиптического движения»). Проверяя эти неравенства на концах промежутка интегрирования, можно сделать выводы о поведении решения на всей оси времени.
(«критерии гиперболического и гиперболо-эллиптического движения»). Проверяя эти неравенства на концах промежутка интегрирования, можно сделать выводы о поведении решения на всей оси времени.
Однако ошибки численного интегрирования оценить точно чрезвычайно трудно. Лишь построенный в 1953 г. К. А. Ситниковым [20] чисто качественными методами пример явился первым аккуратным доказательством возможности частичного захвата  а по симметрии и полного распада
а по симметрии и полного распада 
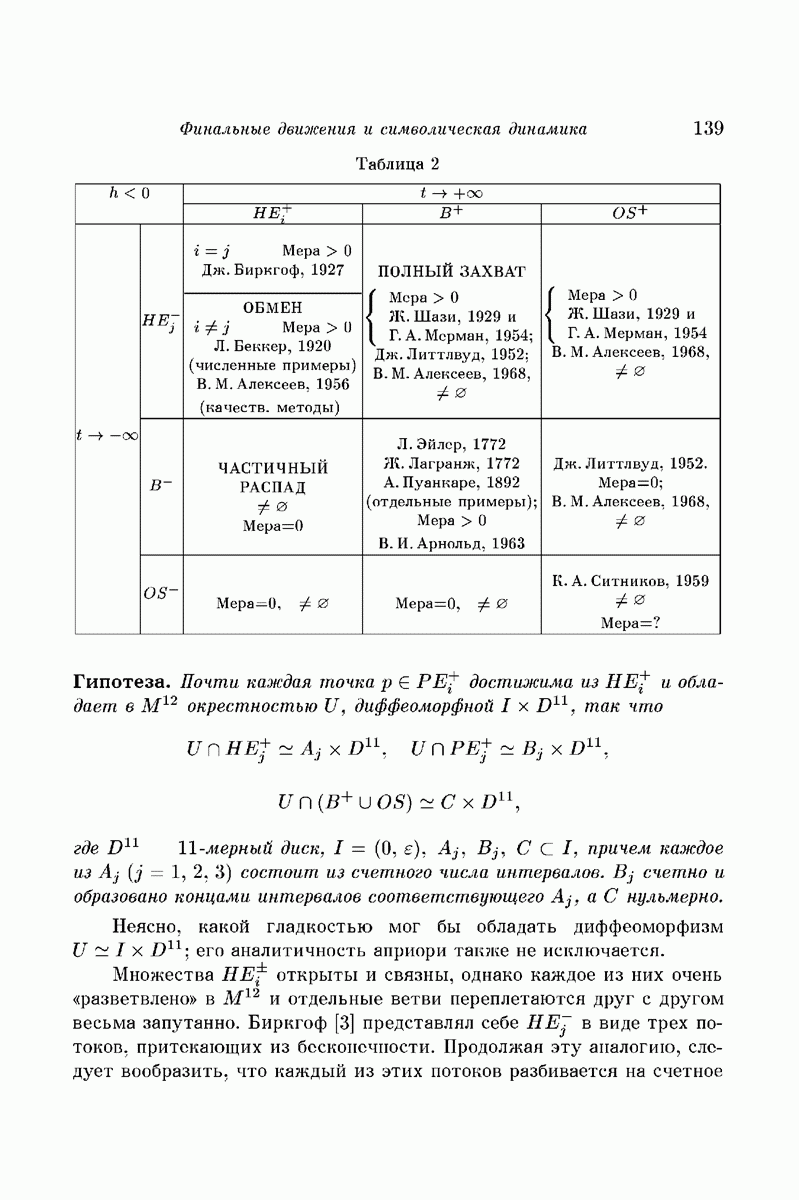
Пример Шмидта вызвал к жизни длинный ряд исследований, посвященных как критическому разбору работ Шази, так и всей проблеме финальных движений. Современное состояние этой проблемы вкратце отражено в таблицах 1 и 2. Каждая клетка отвечает одной из логически возможных комбинаций финальных движений в прошлом и будущем и описывает тем самым некоторый тип эволюции системы. Приведены авторы и даты работ, в которых были найдены соответствующие типы. Указана также и лебегова мера соответствующего множества в  . Следует иметь в виду, что из-за симметрии времени каждое исследование, относящееся к одной из клеток, в равной мере относится и к симметричной относительно главной диагонали клетке.
. Следует иметь в виду, что из-за симметрии времени каждое исследование, относящееся к одной из клеток, в равной мере относится и к симметричной относительно главной диагонали клетке.
В случае  (табл. 1) оказались осуществимыми все 5 логически возможных типов эволюции. Поскольку множества Н и
(табл. 1) оказались осуществимыми все 5 логически возможных типов эволюции. Поскольку множества Н и  открыты, это автоматически обеспечивает положительную вероятность
открыты, это автоматически обеспечивает положительную вероятность  каждого типа.
каждого типа.
4. Эволюция системы; случай  (табл. 2). В области
(табл. 2). В области  ситуация значительно сложнее, чем для
ситуация значительно сложнее, чем для  Прежде всего множества
Прежде всего множества  если и являются подмногообразиями коразмерности 1, то заведомо плохо вложенными в
если и являются подмногообразиями коразмерности 1, то заведомо плохо вложенными в  Неясно, являются ли они аналитическими. Автор придерживается следующей гипотезы, восходящей к А. Н. Колмогорову.
Неясно, являются ли они аналитическими. Автор придерживается следующей гипотезы, восходящей к А. Н. Колмогорову.
Таблица 2

Гипотеза. Почти каждая точка  достижима из
достижима из  и обладает в
и обладает в  окрестностью U, диффеоморфной
окрестностью U, диффеоморфной  так что
так что

где  диск,
диск,  , причем каждое из
, причем каждое из  состоит из счетного числа интервалов.
состоит из счетного числа интервалов.  счетно и образовано концами интервалов соответствующего
счетно и образовано концами интервалов соответствующего  а
а  нульмерно.
нульмерно.
Неясно, какой гладкостью мог бы обладать диффеоморфизм  его аналитичность априори также не исключается.
его аналитичность априори также не исключается.
Множества  открыты и связны, однако каждое из них очень «разветвлено» в
открыты и связны, однако каждое из них очень «разветвлено» в  и отдельные ветви переплетаются друг с другом весьма запутанно. Биркгоф [3] представлял себе
и отдельные ветви переплетаются друг с другом весьма запутанно. Биркгоф [3] представлял себе  в виде трех потоков, притекающих из бесконечности. Продолжая эту аналогию, следует вообразить, что каждый из этих потоков разбивается на счетное
в виде трех потоков, притекающих из бесконечности. Продолжая эту аналогию, следует вообразить, что каждый из этих потоков разбивается на счетное
число «ручейков», которые, подобно системе кровеносных капилляров, пронизывают фазовое пространство и собираются в три выходящих потока 
Анализ рассуждений Шази показал [21], что для доказательства равенства  они недостаточны, но все же можно утверждать, что
они недостаточны, но все же можно утверждать, что  совпадают в области
совпадают в области  точностью до множества нулевой лебеговой меры в
точностью до множества нулевой лебеговой меры в  («почти вся вода, приносимая потоками
(«почти вся вода, приносимая потоками  за исключением отдельных струек общей пулевой меры, уносится потоками
за исключением отдельных струек общей пулевой меры, уносится потоками  »).
»).
Тем самым возникли два вопроса: существуют ли в области  движения типа
движения типа  («полный захват») и
(«полный захват») и 
На оба эти вопроса автору удалось получить положительный ответ [22] [24]. Особенно интересно, что оказался возможным полный захват. В отличие от примеров Шмидта и Ситникова, при полном захвате образуется тройная звезда: к двойной звезде за счет чисто гравитационного взаимодействия присоединяется третье тело, прилетевшее из бесконечности. Ту же природу имеет захват кометы системой Солнце-Юпитер.
Строение множества  изучено плохо, хотя значительная доля публикаций по задаче трех тел относится именно к нему. Теория Колмогорова Арнольда Мозера позволила доказать существование условно-периодических движений во многих неинтегрируемых задачах механики. В частности, в 1963 г. В. И. Арнольд [25] показал, что
изучено плохо, хотя значительная доля публикаций по задаче трех тел относится именно к нему. Теория Колмогорова Арнольда Мозера позволила доказать существование условно-периодических движений во многих неинтегрируемых задачах механики. В частности, в 1963 г. В. И. Арнольд [25] показал, что  (при достаточно малой массе двух из трех тел) содержит подмножество положительной меры, состоящее из пятимерных торов, заполненных условно-периодическими движениями. См. также [5], [26], [27], [28].
(при достаточно малой массе двух из трех тел) содержит подмножество положительной меры, состоящее из пятимерных торов, заполненных условно-периодическими движениями. См. также [5], [26], [27], [28].
Условно-периодические движения образуют «регулярную» часть  но отнюдь его не исчерпывают. Во множестве
но отнюдь его не исчерпывают. Во множестве  существует также и «квазислучайпая» часть. Некоторое представление о ее строении можно получить, рассматривая один частный случай задачи трех тел (см. далее § 8).
существует также и «квазислучайпая» часть. Некоторое представление о ее строении можно получить, рассматривая один частный случай задачи трех тел (см. далее § 8).
Остается открытой
Проблема. Образует ли OS множество положительной или нулевой меры в  ?
?
Методы
5. «Эффект пограничного слоя» и разрывные решения идеальной кеплеровой задачи ([22], [23], [29]). Пусть М риманово многообразие,  — его замкнутое подмногообразие, W — нормальное расслоение над S, U — трубчатая окрестность S в М, диффеоморфная r-окрестности нулевого сечения W (так что
— его замкнутое подмногообразие, W — нормальное расслоение над S, U — трубчатая окрестность S в М, диффеоморфная r-окрестности нулевого сечения W (так что  можно считать координатами в U). Все векторные поля, о которых далее пойдет речь, принадлежат классу
можно считать координатами в U). Все векторные поля, о которых далее пойдет речь, принадлежат классу  на своей области определения и зависят от параметра
на своей области определения и зависят от параметра  непрерывно в точке
непрерывно в точке  относительно топологии равномерной сходимости на компактах.
относительно топологии равномерной сходимости на компактах.
Рассмотрим следующие системы дифференциальных уравнений: основную (определенную  )
)

которая в координатах  имеет вид
имеет вид

где 
вспомогательную (определенную в  )
)

предельные

и «систему пограничного слоя»

Здесь поля  и
и  удовлетворяют сформулированным выше условиям на всей U, их частные производные равномерно (по а) ограничены на
удовлетворяют сформулированным выше условиям на всей U, их частные производные равномерно (по а) ограничены на
каждом компакте в  определены на
определены на  (т. е. при
(т. е. при  ) и удовлетворяют дополнительно условию
) и удовлетворяют дополнительно условию

где 

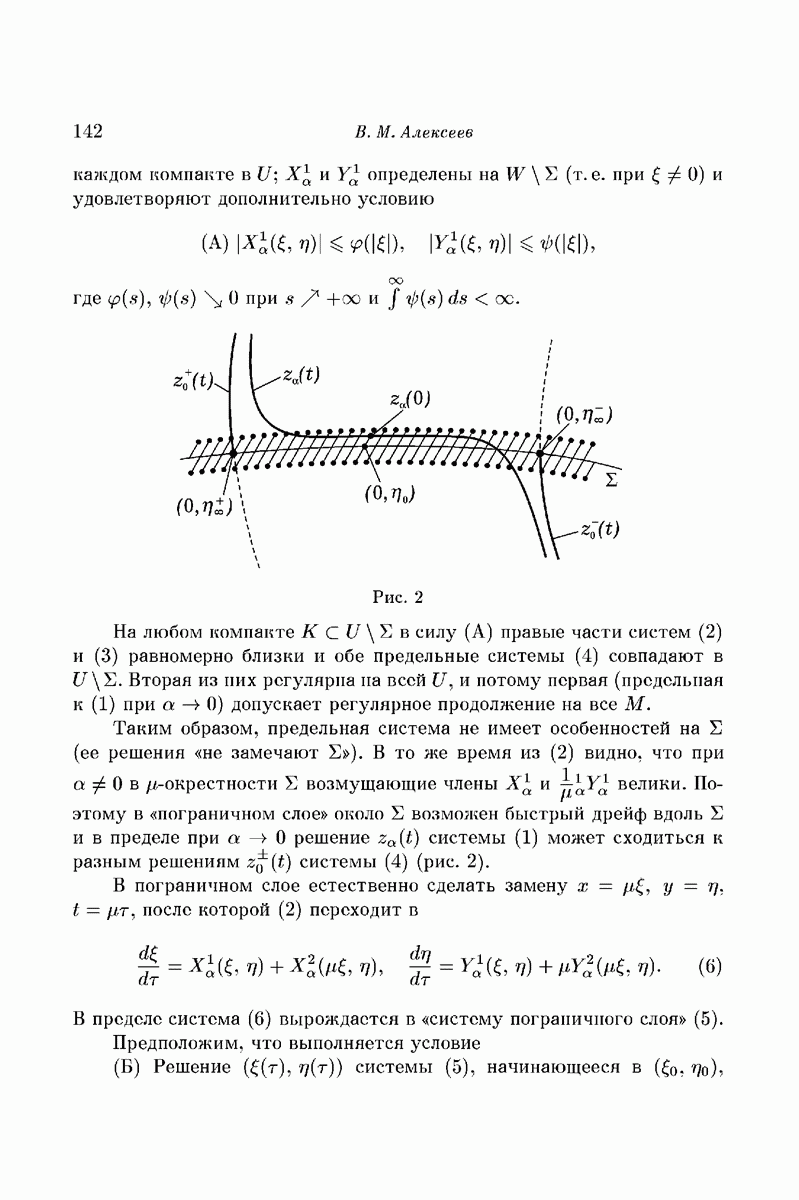
Рис. 2
На любом компакте  в силу (А) правые части систем (2) и (3) равномерно близки и обе предельные системы (4) совпадают в
в силу (А) правые части систем (2) и (3) равномерно близки и обе предельные системы (4) совпадают в  Вторая из них регулярна на всей U, и потому первая (предельная к (1) при
Вторая из них регулярна на всей U, и потому первая (предельная к (1) при  допускает регулярное продолжение на все М.
допускает регулярное продолжение на все М.
Таким образом, предельная система не имеет особенностей на  (ее решения «не замечают
(ее решения «не замечают  ). В то же время из (2) видно, что при
). В то же время из (2) видно, что при  в
в  -окрестности
-окрестности  возмущающие члены
возмущающие члены  и велики. Поэтому в «пограничном слое» около
и велики. Поэтому в «пограничном слое» около  возможен быстрый дрейф вдоль
возможен быстрый дрейф вдоль  и в пределе при
и в пределе при  решение
решение  системы (1) может сходиться к разным решениям
системы (1) может сходиться к разным решениям  системы (4) (рис. 2).
системы (4) (рис. 2).
В пограничном слое естественно сделать замену  , после которой (2) переходит в
, после которой (2) переходит в

В пределе система (6) вырождается в «систему пограничного слоя» (5). Предположим, что выполняется условие (Б) Решение  системы (5), начинающееся в
системы (5), начинающееся в  .
.
определено и лежит в  для
для  и, кроме того,
и, кроме того,

Теорема. Если  решение системы (1) такое, что
решение системы (1) такое, что
1) 
2) выполняются (А) и (Б);
3) 
4) решение системы (4) с начальными условиями  определено на
определено на  и лежит в
и лежит в  при
при  то для всех
то для всех 

Заметим, что  что, вообще говоря, не равно
что, вообще говоря, не равно  . Если же (Б) выполняется в усиленной форме, а именно:
. Если же (Б) выполняется в усиленной форме, а именно:  определено для всех
определено для всех  и
и

то (8) справедливо при  а при
а при 

где  — решение (4) с начальным условием
— решение (4) с начальным условием  определенное на
определенное на  и лежащее в
и лежащее в  на
на  .
.
При  налицо ситуация, изображенная на рис. 2. Рассмотрим теперь задачу трех тел типа «планетной системы»:
налицо ситуация, изображенная на рис. 2. Рассмотрим теперь задачу трех тел типа «планетной системы»:  Движением управляет в этом случае система вида (2), где
Движением управляет в этом случае система вида (2), где  а роль
а роль  играет «многообразие столкновений» тел
играет «многообразие столкновений» тел  описываемое уравнением
описываемое уравнением  Члены
Члены  в (2) относятся к взаимодействию тел
в (2) относятся к взаимодействию тел  в то время как во вспомогательной системе (3) мы этим взаимодействием пренебрегаем. Предельной системе (4) соответствует «идеальная кеплеровская задача», в которой
в то время как во вспомогательной системе (3) мы этим взаимодействием пренебрегаем. Предельной системе (4) соответствует «идеальная кеплеровская задача», в которой  покоится в начале координат,
покоится в начале координат,  описывают около
описывают около  кеплеровские орбиты. В зависимости от знака (приведенной к единице массы) энергии тела
кеплеровские орбиты. В зависимости от знака (приведенной к единице массы) энергии тела  в относительном движении около
в относительном движении около 
его орбита будет эллипсом  параболой
параболой  или гиперболой
или гиперболой  Таким образом, для предельной системы
Таким образом, для предельной системы  типы финальных движений одинаковы при
типы финальных движений одинаковы при  Именно это привело Шази
Именно это привело Шази  к ошибочному заключению о совпадении финальных движений при
к ошибочному заключению о совпадении финальных движений при  для любых масс. Его ошибка как раз связана с необходимостью учитывать при переходе от
для любых масс. Его ошибка как раз связана с необходимостью учитывать при переходе от  к
к  то,
то,  «эффект пограничного слоя». Этот эффект проявляется при близких прохождениях
«эффект пограничного слоя». Этот эффект проявляется при близких прохождениях  и система (5) описывает кеплеровское движение этих тел относительно равномерно движущегося общего центра тяжести; взаимодействием с
и система (5) описывает кеплеровское движение этих тел относительно равномерно движущегося общего центра тяжести; взаимодействием с  при этом пренебрегаем.
при этом пренебрегаем.
Теорема, сформулированная выше, дает возможность построить семейство решений реальной  задачи, сходящееся при то
задачи, сходящееся при то  к разным идеальным кеплеровским движениям для
к разным идеальным кеплеровским движениям для  . Тем самым для правильного описания предельного перехода следует учитывать и «разрывные» решения идеальной кеплеровской задачи, у которых скорости тел
. Тем самым для правильного описания предельного перехода следует учитывать и «разрывные» решения идеальной кеплеровской задачи, у которых скорости тел  меняются скачком в момент столкновения. На этой идее и основаны примеры обмена
меняются скачком в момент столкновения. На этой идее и основаны примеры обмена  в области
в области  указанные в табл. 2.
указанные в табл. 2.
Рассмотрим траекторию 70 в фазовом пространстве, отвечающую идеальному кеплеровскому движению, в котором  описывает гиперболу
описывает гиперболу  описывает эллипс
описывает эллипс  так что
так что  . Пусть
. Пусть  имеет единственную особую точку, а именно, в момент
имеет единственную особую точку, а именно, в момент  происходит столкновение тел
происходит столкновение тел  Вблизи отрицательной полутраектории
Вблизи отрицательной полутраектории  можно найти полутраекторию реальной (то,
можно найти полутраекторию реальной (то,  ) задачи, для которой также при
) задачи, для которой также при  тела
тела  сталкиваются. При зупдмаповской регуляризации решение продолжается таким образом, что тела
сталкиваются. При зупдмаповской регуляризации решение продолжается таким образом, что тела  (имеющие по предположению равные массы) обмениваются скоростями. Поэтому продолжение
(имеющие по предположению равные массы) обмениваются скоростями. Поэтому продолжение  полутрасктории
полутрасктории  оказывается не вблизи
оказывается не вблизи  , а вблизи идеальной траектории, на которой
, а вблизи идеальной траектории, на которой  поменялись ролями и которая содержится в
поменялись ролями и которая содержится в  Таким образом, траектория
Таким образом, траектория  . В движении, отвечающем траектории
. В движении, отвечающем траектории  , при
, при  движется вблизи гиперболы,
движется вблизи гиперболы,  вблизи эллипса, а при
вблизи эллипса, а при  — наоборот (рис. 3).
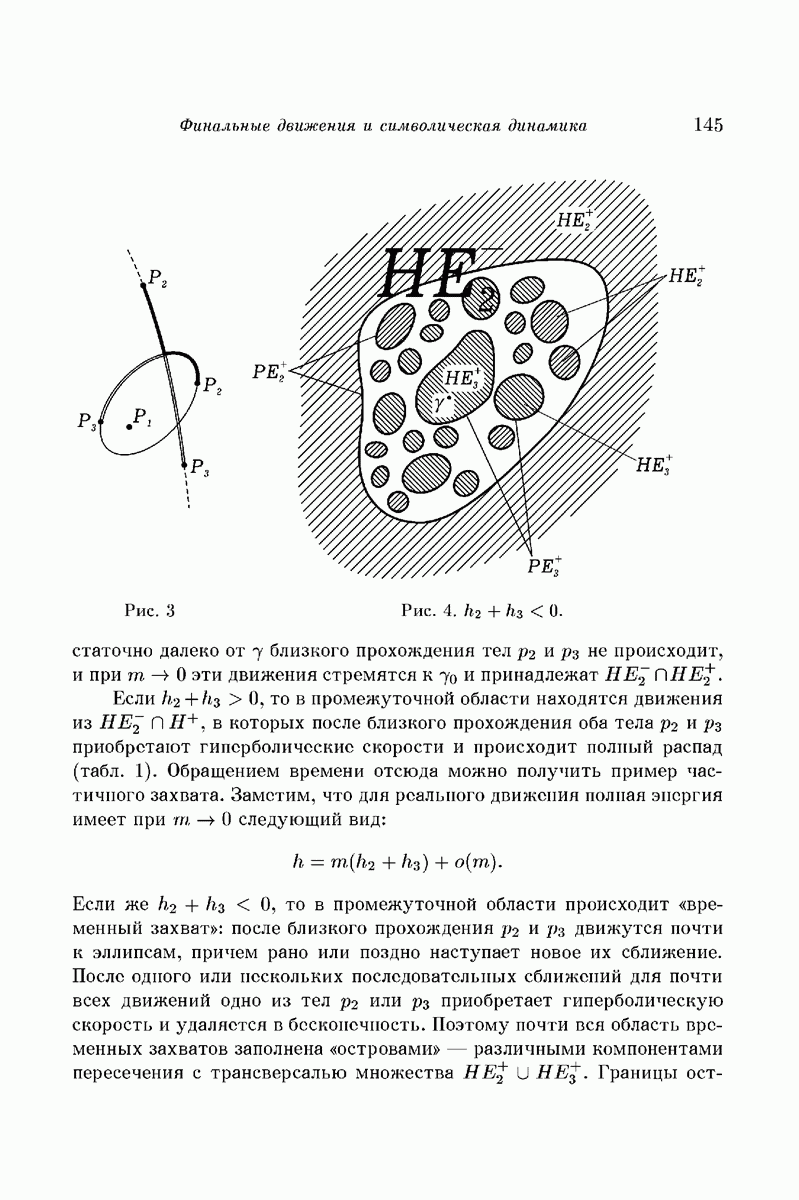
— наоборот (рис. 3).
В фазовом пространстве  траекторию
траекторию  можно включить в
можно включить в  -мерное многообразие «траекторий со столкновениями», т.е. достигающих Е. Приведя к нему двумерную трансверсаль, мы получим на этой трансверсали нечто вроде изображенного на рис. 4. Вблизи
-мерное многообразие «траекторий со столкновениями», т.е. достигающих Е. Приведя к нему двумерную трансверсаль, мы получим на этой трансверсали нечто вроде изображенного на рис. 4. Вблизи  лежат траектории с тем же финальным поведением, т.е. из
лежат траектории с тем же финальным поведением, т.е. из  . Достаточно
. Достаточно

Рис. 3

Рис. 4.  .
.
далеко от  близкого прохождения тел
близкого прохождения тел  не происходит, и при то
не происходит, и при то  эти движения стремятся к
эти движения стремятся к  и принадлежат
и принадлежат  .
.
Если  , то в промежуточной области находятся движения из
, то в промежуточной области находятся движения из  , в которых после близкого прохождения оба тела
, в которых после близкого прохождения оба тела  приобретают гиперболические скорости и происходит полный распад (табл. 1). Обращением времени отсюда можно получить пример частичного захвата. Заметим, что для реального движения полная энергия имеет при то,
приобретают гиперболические скорости и происходит полный распад (табл. 1). Обращением времени отсюда можно получить пример частичного захвата. Заметим, что для реального движения полная энергия имеет при то,  следующий вид:
следующий вид:

Если же  то в промежуточной области происходит «временный захват»: после близкого прохождения
то в промежуточной области происходит «временный захват»: после близкого прохождения  движутся почти к эллипсам, причем рано или поздно наступает новое их сближение. После одного или нескольких последовательных сближений для почти всех движений одно из тел
движутся почти к эллипсам, причем рано или поздно наступает новое их сближение. После одного или нескольких последовательных сближений для почти всех движений одно из тел  или
или  приобретает гиперболическую скорость и удаляется в бесконечность. Поэтому почти вся область временных захватов заполнена «островами» — различными компонентами пересечения с трансверсалью множества
приобретает гиперболическую скорость и удаляется в бесконечность. Поэтому почти вся область временных захватов заполнена «островами» — различными компонентами пересечения с трансверсалью множества  . Границы островов
. Границы островов
принадлежат  , а остальная часть области (лебеговой меры 0. но не пустая) заполнена ограниченными и осциллирующими движениями
, а остальная часть области (лебеговой меры 0. но не пустая) заполнена ограниченными и осциллирующими движениями 
Ввиду сложной топологической структуры аккуратное описание этой картины весьма затруднено. Можно надеяться, что недавняя работа Р. Истона [30] будет полезной в этом отношении.
6. Квазислучайные динамические системы. Теория классических динамических систем распадается на две большие ветви — топологическую «эргодическую теорию». Последняя имеет дело с отображениями, сохраняющими некоторую меру.
Ограничимся для простоты одним отображением  и нормированными мерами
и нормированными мерами  . Если S сохраняет меру
. Если S сохраняет меру  то определен инвариант — метрическая энтропия
то определен инвариант — метрическая энтропия  . Одно и то же S имеет, вообще говоря, много инвариантных мер (описываемых, например, теорией Крылова-Боголюбова).
. Одно и то же S имеет, вообще говоря, много инвариантных мер (описываемых, например, теорией Крылова-Боголюбова).
Предположим, что мы изучаем динамическую систему, регистрируя последовательные попадания траектории в множества  образующие разбиение пространства М, т. е. с помощью функции
образующие разбиение пространства М, т. е. с помощью функции  определяемой соотношениями
определяемой соотношениями  . Например, каждое
. Например, каждое  отвечает некоторому показанию прибора, и тогда
отвечает некоторому показанию прибора, и тогда  есть ряд последовательных показаний этого прибора, полученных при измерениях одного и того же движения с начальным состоянием
есть ряд последовательных показаний этого прибора, полученных при измерениях одного и того же движения с начальным состоянием  . Нормированная мера р. задает распределение вероятностей на М. Случайному выбору начальной точки отвечает случайная последовательность
. Нормированная мера р. задает распределение вероятностей на М. Случайному выбору начальной точки отвечает случайная последовательность  . Теорема Я. Г. Синап [31] утверждает, что при
. Теорема Я. Г. Синап [31] утверждает, что при  можно выбрать
можно выбрать  так, чтобы
так, чтобы  была «последовательностью Бернулли» в смысле теории вероятностей. Это делает естественным
была «последовательностью Бернулли» в смысле теории вероятностей. Это делает естественным
Определение  Динамическая система
Динамическая система  называется квазислучайной, если существует S-инвариантная борелевская мера
называется квазислучайной, если существует S-инвариантная борелевская мера  для которой
для которой  .
.
Аналогично метрической энтропии в [33] был определен топологический инвариант гомеоморфизма — топологическая энтропия  Теорема (Динабург [34] для
Теорема (Динабург [34] для  ; Гудмен [35]). Для гомеоморфизма S компакта
; Гудмен [35]). Для гомеоморфизма S компакта  , где
, где  берется по всем нормированным борелевским S-инвариантным мерам.Заметим, что существует [36] гомеоморфизм нульмерного компакта, для которого
берется по всем нормированным борелевским S-инвариантным мерам.Заметим, что существует [36] гомеоморфизм нульмерного компакта, для которого  не достигается, т.е. всегда
не достигается, т.е. всегда  .
.
Следствие. Динамическая система  квазислучайна тогда и только тогда, когда
квазислучайна тогда и только тогда, когда  .
.
7. Топологические марковские цепи («символическая динамика»). Почти во всех известных мне примерах квазислучайность динамической системы связана с существованием инвариантных марковских подмножеств.
Пусть  — тихоновское произведение счетного числа p-точий, т. е. пространство бесконечных последовательностей
— тихоновское произведение счетного числа p-точий, т. е. пространство бесконечных последовательностей  , где
, где  — гомеоморфизм сдвига на один символ влево.
— гомеоморфизм сдвига на один символ влево.
Каждая  -матрица
-матрица  из пулей и единиц определяет замкнутое инвариантное подмножество
из пулей и единиц определяет замкнутое инвариантное подмножество  условием
условием  . Для всех n. Ограничение
. Для всех n. Ограничение  называется топологической марковской цепью (т. м. ц.) с р состояниями и матрицей переходов
называется топологической марковской цепью (т. м. ц.) с р состояниями и матрицей переходов  .
.
Ориентированный граф Г с вершинами  и ребрами
и ребрами  для тех пар
для тех пар  для которых
для которых  однозначно определяет т.
однозначно определяет т.  . Совершенно аналогично, матрицей или графом определяются т. м. ц. со счетным и даже любым множеством состояний [32], [36], [37].
. Совершенно аналогично, матрицей или графом определяются т. м. ц. со счетным и даже любым множеством состояний [32], [36], [37].
Непрерывные отображения  называются топологически сопряженными, если существует гомеоморфизм
называются топологически сопряженными, если существует гомеоморфизм  такой, что коммутативна диаграмма
такой, что коммутативна диаграмма

Теорема (Вильяме [38]). Для того чтобы две т. м.ц.  с конечным числом состояний были топологически сопряженными, необходимо и достаточно, чтобы существовали такие лштрицы R и S с неотрицательными целыми элементами и такое целое
с конечным числом состояний были топологически сопряженными, необходимо и достаточно, чтобы существовали такие лштрицы R и S с неотрицательными целыми элементами и такое целое  , что
, что

(Здесь  — матрицы порядков
— матрицы порядков  соответственно.)
соответственно.)
Нетрудно убедиться в том, что число  периодических точек периода
периодических точек периода  в т. м. ц.
в т. м. ц.  равно
равно  где
где  — собственные числа матрицы
— собственные числа матрицы  . Так как у топологически сопряженных
. Так как у топологически сопряженных  числа
числа  должны совпадать, то при всех
должны совпадать, то при всех  откуда следует, что матрицы П и S имеют одинаковые отличные от 0 собственные числа (вместе с кратностью). Как показано в [38], это условие, однако, недостаточно. Спектральные свойства матрицы П определяют топологическую энтропию т. м. ц. А именно:
откуда следует, что матрицы П и S имеют одинаковые отличные от 0 собственные числа (вместе с кратностью). Как показано в [38], это условие, однако, недостаточно. Спектральные свойства матрицы П определяют топологическую энтропию т. м. ц. А именно:
Теорема (Перри [39]; [36]).  , где А — наибольшее положительное собственное значение матрицы
, где А — наибольшее положительное собственное значение матрицы  . Существует единственная борелевская Т-инвариантная мера р на
. Существует единственная борелевская Т-инвариантная мера р на  для которой
для которой  .
.
Топологическую энтропию т. м. ц. со счетным числом состояний и связь ее с метрическими энтропиями инвариантных мер исследовал Б. М. Гуревич [36], [37]. В частности, он доказал, что в этом случае топологическая энтропия всей цепи есть верхняя грань топологических подцепей с конечным числом состояний.
Динамические системы, связанные с гомеоморфизмом сдвига в пространстве последовательностей символов некоторого алфавита, впервые, по-видимому, рассматривались в связи с изучением геодезических на поверхностях отрицательной кривизны (см., например, [3], гл. VIII, § 11), а затем и сами по себе ([40]). За кругом вопросов, относящихся к таким системам, закрепилось название «символическая динамика». Возрождение интереса к идеям и методам символической динамики связано с работами С. Смейла [41], [42] и Я. Г. Синая [43], [44]. Последовательное употребление термина, «топологическая марковская цепь» начинается, по-видимому, с работ автора [32], хотя само понятие принадлежит математическому фольклору и по существу имеется, например, в [39]. Синай [43] использует это понятие, никак его не называя, а Смейл в [42] пользуется неудачным термином «subshift of finite type».
Пусть  — диффеоморфизм многообразия М. Назовем подмножество
— диффеоморфизм многообразия М. Назовем подмножество  инвариантным марковским подмножеством диффеоморфизма S, если существует т. м. ц.
инвариантным марковским подмножеством диффеоморфизма S, если существует т. м. ц.  и непрерывное отображение такие, что
и непрерывное отображение такие, что  , так что
, так что 
и диаграмма

коммутативна.
Тривиальные примеры инвариантных марковских подмножеств: неподвижная или периодическая точка, траектория  асимптотическая при
асимптотическая при  к периодическим или неподвижным точкам.
к периодическим или неподвижным точкам.
Если  — гомеоморфизм, то ограничение
— гомеоморфизм, то ограничение  топологически эквивалентно т. м. ц.
топологически эквивалентно т. м. ц.  и с помощью теорем Перри и Гуревича можно вычислить
и с помощью теорем Перри и Гуревича можно вычислить  . К сожалению,
. К сожалению,  может быть гомеоморфизмом лишь при
может быть гомеоморфизмом лишь при  Впрочем, в упоминаемых ниже важных примерах обратимость
Впрочем, в упоминаемых ниже важных примерах обратимость  нарушается, но лишь на множестве 1-й категории что дает возможность превратить
нарушается, но лишь на множестве 1-й категории что дает возможность превратить  в метрический изоморфизм и найти на А «меру максимальной энтропии».
в метрический изоморфизм и найти на А «меру максимальной энтропии».
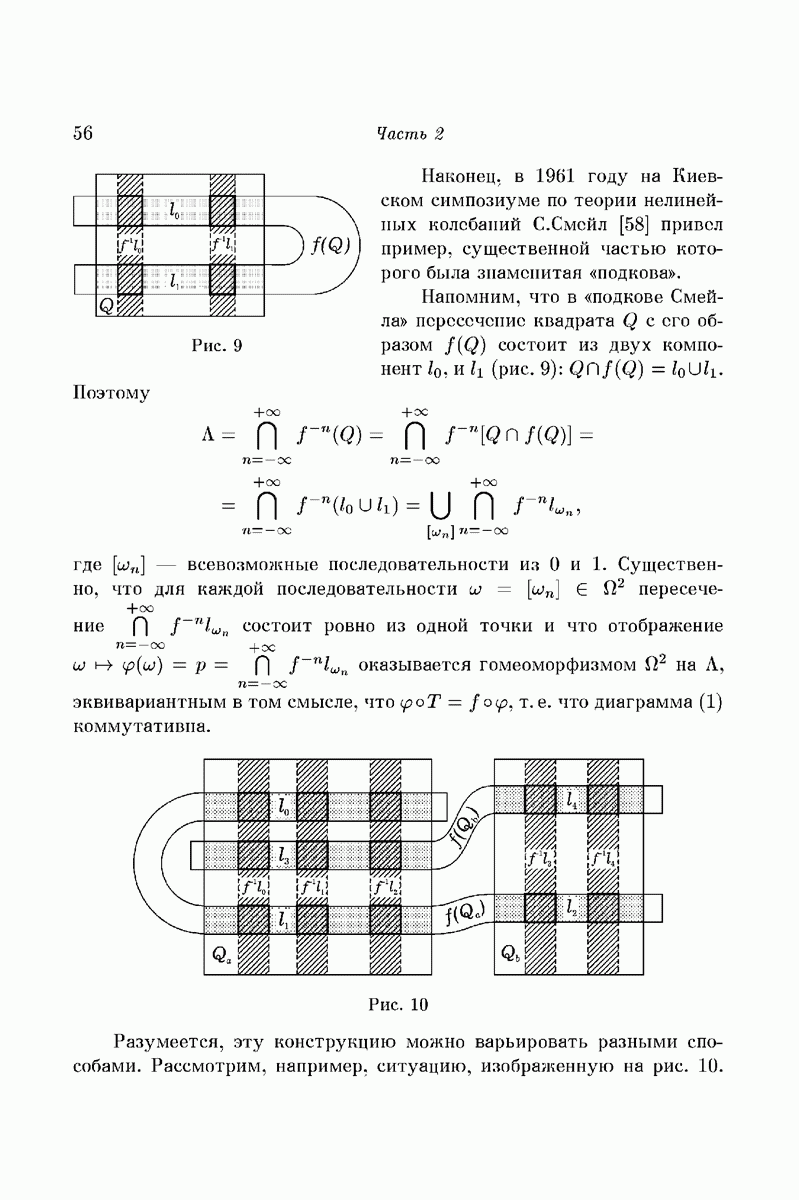
Пример 1. «Подкова Смейла» и ее модификации позволяют для любых  указать
указать  -открытое
-открытое  такое, что любой
такое, что любой  обладает инвариантным марковским подмножеством А, на котором
обладает инвариантным марковским подмножеством А, на котором  топологически эквивалентен
топологически эквивалентен  . Смейл [41] доказал это утверждение для матрицы П, состоящей из одних единиц («топологическая схема Бернулли»). В общем случае см. [32] и (45].
. Смейл [41] доказал это утверждение для матрицы П, состоящей из одних единиц («топологическая схема Бернулли»). В общем случае см. [32] и (45].
Пример 2. Пусть  — гиперболические периодические точки диффеоморфизма
— гиперболические периодические точки диффеоморфизма  — их устойчивые и неустойчивые инвариантные многообразия
— их устойчивые и неустойчивые инвариантные многообразия  причем предположим, что все W? имеют одинаковую размерность (все
причем предположим, что все W? имеют одинаковую размерность (все  имеют дополнительную размерность). Пусть далее
имеют дополнительную размерность). Пусть далее  ) — трансверсальные гомо- и гетероклинические точки, так что
) — трансверсальные гомо- и гетероклинические точки, так что  и в точке
и в точке  пересекаются трансверсально. Построим граф Г, структура которого до некоторой степени повторяет эту ситуацию. В него входят непересекающиеся циклы
пересекаются трансверсально. Построим граф Г, структура которого до некоторой степени повторяет эту ситуацию. В него входят непересекающиеся циклы  , причем число ребер в цикле
, причем число ребер в цикле  равно периоду
равно периоду  и пути
и пути  с числом ребер
с числом ребер  соединяющие вершины
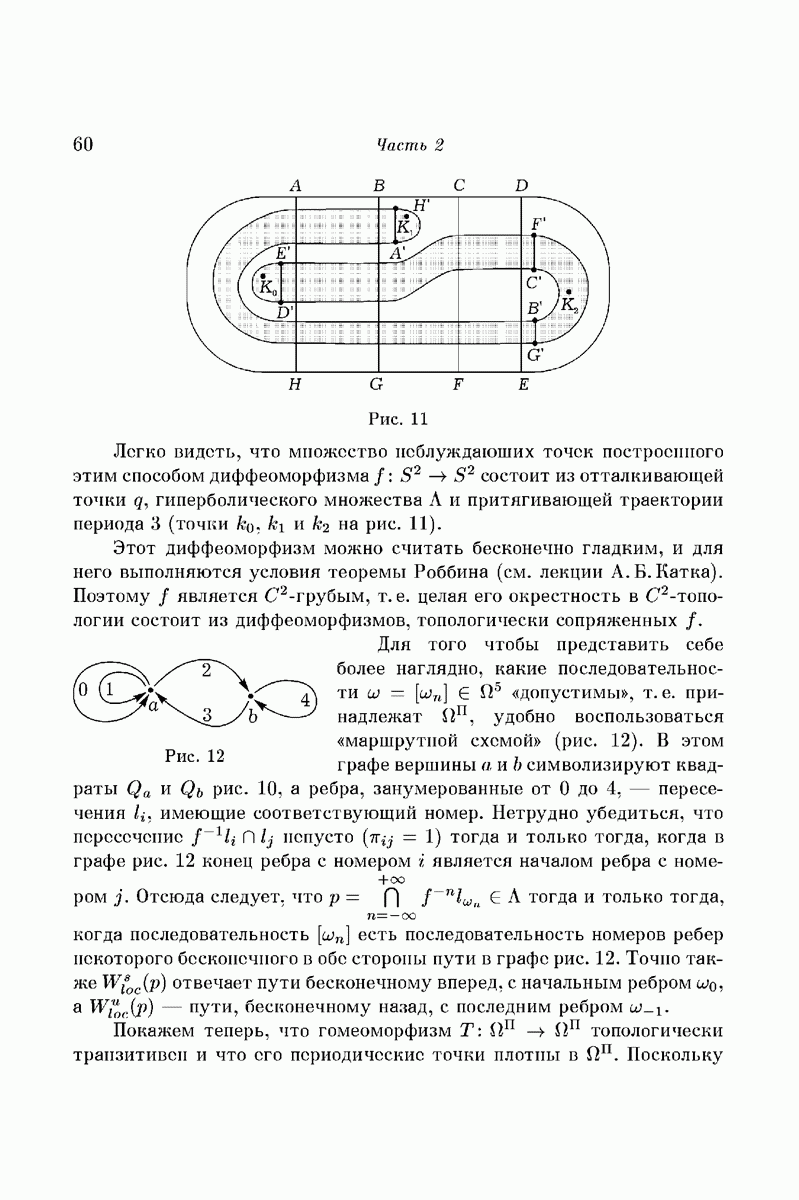
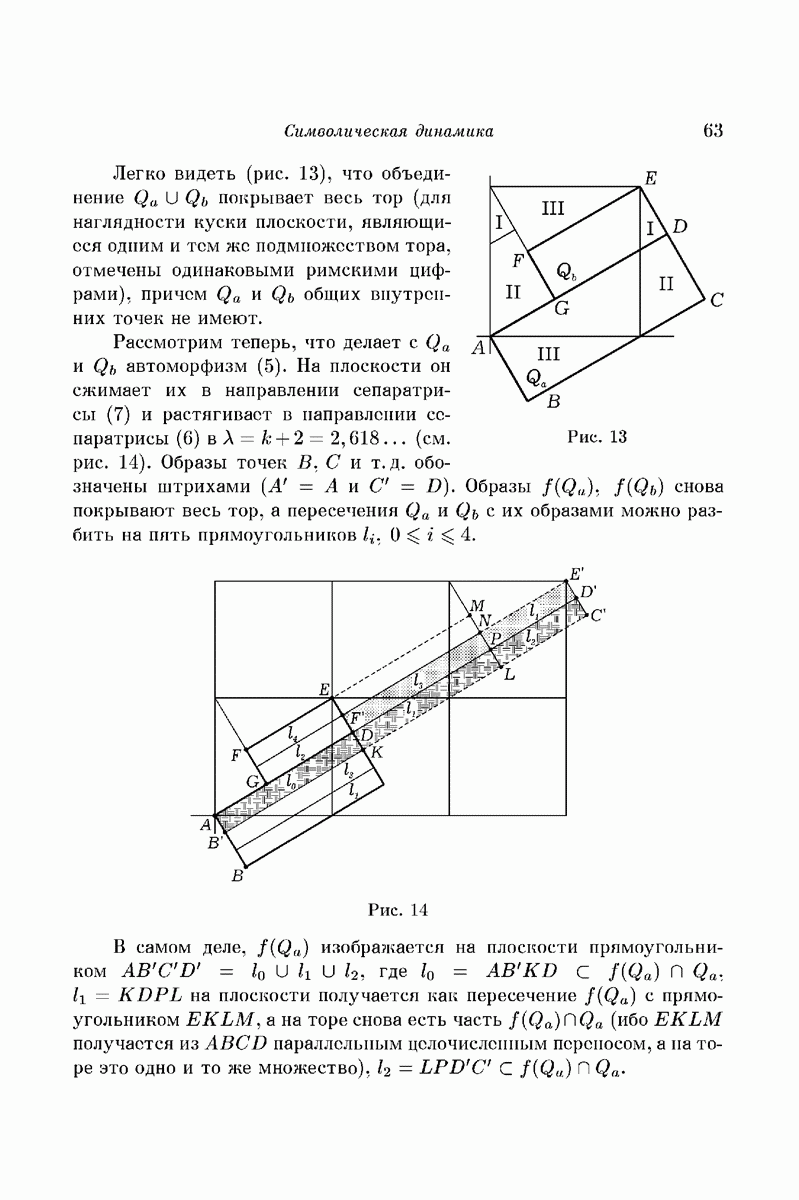
соединяющие вершины  (эти вершины можно брать на соответствующих циклах произвольно) (рис. 5).
(эти вершины можно брать на соответствующих циклах произвольно) (рис. 5).
Теорема  . Для любого открытого множества U, содержащего траектории точек
. Для любого открытого множества U, содержащего траектории точек  , существуют
, существуют

Рис. 5
 и открытое множество
и открытое множество  такие, что ограничение
такие, что ограничение  на максимальное
на максимальное  -инвариантное множество А, содержащееся в V, топологически эквивалентно т.м. ц., определяемой графом
-инвариантное множество А, содержащееся в V, топологически эквивалентно т.м. ц., определяемой графом  и
и  .
.
Заметим, что при различном выборе точек Q получаются различные графы Г. Соответственно меняются при этом V и А.
Пример 3. Пусть  — F-диффеоморфизм в смысле Д. В. Аносова. Я. Г. Синай [43], [44] доказал, что М является марковским множеством. Построение т. м. ц.
— F-диффеоморфизм в смысле Д. В. Аносова. Я. Г. Синай [43], [44] доказал, что М является марковским множеством. Построение т. м. ц.  и
и  -гомеоморфизма
-гомеоморфизма  было осуществлено им при помощи так называемого марковского разбиения многообразия М. Отображение
было осуществлено им при помощи так называемого марковского разбиения многообразия М. Отображение  склеивает лишь точки в
склеивает лишь точки в  образующие множество первой категории, и удается построить на М «меру максимальной энтропии» (подробнее см. [46], [47]).
образующие множество первой категории, и удается построить на М «меру максимальной энтропии» (подробнее см. [46], [47]).
Недавно Боуэн [48] распространил этот результат на произвольное базисное множество диффеоморфизма S, удовлетворяющего аксиоме А Смейла (см. [42]). Можно надеяться, что этот результат распространяется на произвольное инвариантное гиперболическое множество, обладающее дополнительным свойством «локальной максимальности» (важная роль этого свойства доказана Д. В. Аносовым [49]). Пока же автором получен более слабый результат [50] (отображение  существенно неоднозначно).
существенно неоднозначно).
Проблема. Пусть  . Существует ли у S марковское подмножество А, на котором
. Существует ли у S марковское подмножество А, на котором  ? А если
? А если  ?
?
Заметим, что теорема Перри накладывает ограничения на возможные
значения С, если желать, чтобы А было гомеоморфным образом т.м.ц. с конечным числом состояний: в этом случае С должно быть логарифмом алгебраического числа.
Если диффеоморфизм S обладает нетривиальным инвариантным марковским подмножеством, то это обычно позволяет построить траектории  с достаточно сложным поведением.
с достаточно сложным поведением.
Назовем т. м.ц.  транзитивной, если матрица П неприводима в смысле Перрона-Фробениуса ([51], гл. XIII). Методами символической динамики ([40]) легко доказывается
транзитивной, если матрица П неприводима в смысле Перрона-Фробениуса ([51], гл. XIII). Методами символической динамики ([40]) легко доказывается
Теорема. Транзитивная, т. м.ц.  топологически транзитивна (некоторые траектории и даже полутраектории плотны в
топологически транзитивна (некоторые траектории и даже полутраектории плотны в  ), периодические точки плотны в и для любых точек р и q существует точка
), периодические точки плотны в и для любых точек р и q существует точка  такая, что траектория
такая, что траектория  асимптотически сближается с траекторией
асимптотически сближается с траекторией  при
при  при
при  .
.
Если матрица П приводима, то воспользовавшись ее каноническим видом  можно выделить в
можно выделить в  «базисные» топологически транзитивные множества, аналогично «спектральному разложению» в [42] (см. также [50]).
«базисные» топологически транзитивные множества, аналогично «спектральному разложению» в [42] (см. также [50]).
С помощью отображения  эти свойства переносятся с т. м. ц. на марковское множество диффеоморфизма, что дает возможность исследовать последний. Предложенный автором метод «маршрутных схем» [32] оказался полезным при отыскании марковских подмножеств у динамических систем, отвечающих конкретным задачам. И в частности, именно это дало возможность заполнить «белые пятна» в табл. 2.
эти свойства переносятся с т. м. ц. на марковское множество диффеоморфизма, что дает возможность исследовать последний. Предложенный автором метод «маршрутных схем» [32] оказался полезным при отыскании марковских подмножеств у динамических систем, отвечающих конкретным задачам. И в частности, именно это дало возможность заполнить «белые пятна» в табл. 2.
8. Об одном частном случае задачи трех тел. Пусть  и в начальный момент
и в начальный момент  и их скорости симметричны относительно
и их скорости симметричны относительно  . Если выполнено обычное предположение о центре тяжести всей системы
. Если выполнено обычное предположение о центре тяжести всей системы  , то
, то  лежит на
лежит на  , и его скорость вертикальна (рис. 6). По соображениям симметрии подобное расположение тел
, и его скорость вертикальна (рис. 6). По соображениям симметрии подобное расположение тел  будет сохраняться для всех t, что позволяет свести исследование к системе с двумя степенями свободы.
будет сохраняться для всех t, что позволяет свести исследование к системе с двумя степенями свободы.
Этот частный случай задачи трех тел придуман давно (не позже 1895 г.), но счастливая идея исследовать на нем расположение в фазовом пространстве траекторий различных финальных типов принадлежит А.Н. Колмогорову. Именно для этого примера К. А. Ситникову [14] удалось доказать, что  (используя дополнительно симметрию
(используя дополнительно симметрию
времени, можно вывести из результата Ситникова неравенство  , что и отражено в табл. 2. В этом же примере автору удалось построить инвариантное марковское множество [24], [32].
, что и отражено в табл. 2. В этом же примере автору удалось построить инвариантное марковское множество [24], [32].

Рис. 6.
Пусть  (предположение
(предположение  вносит ничего принципиально нового). Тогда
вносит ничего принципиально нового). Тогда  описывают в XOY симметричные кеплеровские орбиты около О, которые в случае
описывают в XOY симметричные кеплеровские орбиты около О, которые в случае  будут эллипсами. В момент, когда
будут эллипсами. В момент, когда  проходит через О, состояние системы определяется скоростью этого тела и фазой
проходит через О, состояние системы определяется скоростью этого тела и фазой  (истинной или средней аномалией) эллиптического движения тел
(истинной или средней аномалией) эллиптического движения тел  Примем
Примем  за полярные координаты в некоторой плоскости Ф (ввиду симметрии относительно XOY знаком v можно пренебречь). Сдвиг вдоль траектории в фазовом пространстве от одного попадания
за полярные координаты в некоторой плоскости Ф (ввиду симметрии относительно XOY знаком v можно пренебречь). Сдвиг вдоль траектории в фазовом пространстве от одного попадания  в
в  к следующему определяет локальный диффеоморфизм
к следующему определяет локальный диффеоморфизм  . Оказывается, что можно указать такое открытое множество
. Оказывается, что можно указать такое открытое множество  , что максимальное инвариантное множество А, содержащееся в Г, является марковским и допускает описание в терминах символической динамики.
, что максимальное инвариантное множество А, содержащееся в Г, является марковским и допускает описание в терминах символической динамики.
Пусть  состоит из всевозможных последовательностей
состоит из всевозможных последовательностей  , где
, где  при
при  , где натуральное
, где натуральное  или 1; при
или 1; при  или 1; при
или 1; при  . И снабжается естественной топологией и на подмножестве
. И снабжается естественной топологией и на подмножестве  где
где  определен локальный гомеоморфизм Т сдвига на один символ влево:
определен локальный гомеоморфизм Т сдвига на один символ влево: 
Теорема ([32]). Существуют  , гомеоморфизм
, гомеоморфизм  и такое открытое множество
и такое открытое множество  , что
, что  является максимальным
является максимальным
инвариантным множеством в  и диаграмма
и диаграмма

коммутативна.
(Для случая  формулировка аналогичной теоремы приведена в [24]: в [52] приведены достаточные условия, при которых для отображения плоскости в плоскость можно доказать подобное же утверждение. Доказательства см. в [45].)
формулировка аналогичной теоремы приведена в [24]: в [52] приведены достаточные условия, при которых для отображения плоскости в плоскость можно доказать подобное же утверждение. Доказательства см. в [45].)
Выбор последовательности символов  следующим образом влияет на характер движения
следующим образом влияет на характер движения  . Взяв точку
. Взяв точку  в качестве начального условия, мы получим решение, для которого
в качестве начального условия, мы получим решение, для которого  возвращается в
возвращается в  раз при
раз при  раз при
раз при  . Между
. Между  возвращениями происходит
возвращениями происходит  целых оборотов тел
целых оборотов тел  около
около  символ
символ  указывает, что
указывает, что  возвращение происходит около момента максимального сближения (удаления) тел
возвращение происходит около момента максимального сближения (удаления) тел 
Если  , то после
, то после  возвращений
возвращений  уходит в бесконечность с предельной скоростью
уходит в бесконечность с предельной скоростью  . Аналогично, если
. Аналогично, если  , то
, то  определяет скорость ухода в бесконечность при
определяет скорость ухода в бесконечность при  .
.
Увеличение  влечет за собой также и увеличение размаха колебаний тела
влечет за собой также и увеличение размаха колебаний тела  .
.
Стандартными приемами «символической динамики» можно построить разнообразные примеры движения с предписанным заранее поведением. В частности, движение принадлежит  при
при  если
если  , если
, если  . Аналогично определяется и принадлежность к
. Аналогично определяется и принадлежность к  . Нетрудно убедиться, что при
. Нетрудно убедиться, что при  образуют полный набор финальных движений. Выбирая подходящим образом последовательности символов, убеждаемся, что верна
образуют полный набор финальных движений. Выбирая подходящим образом последовательности символов, убеждаемся, что верна
Теорема ([27], [45]). Существует такое  , что при
, что при  и при
и при  в рассматриваемом частном случае задачи трех тел реализуются все 16 логически возможных комбинаций финальных движений по Шази.
в рассматриваемом частном случае задачи трех тел реализуются все 16 логически возможных комбинаций финальных движений по Шази.
Например, последовательность  , в которой
, в которой  порождает решение, для которого происходит полный захват
порождает решение, для которого происходит полный захват  .
.
Кроме того, имеет место Следствие. При тех же условиях всякий однозначный аналитический первый интеграл есть функция интегралов энергии и момента.
Это следствие представляет некоторый интерес и не вытекает из упомянутой в § 2 теоремы Пуанкаре, поскольку речь идет о фиксированном значении масс.
Литература
[1] H. Poincare. Les methodes nouvelles de la mecanique celeste. Paris: Gauthier-Villars, 1892, t. 1, 1892, t. 2, 1899, t. 3.
[2] А.Пуанкаре. Избранные труды (серия «Классики науки»), М.: Наука, 1971, т. 1, 1972, т. 2.
[3] G. D. Birkhgoff. Dynamical systems. Amer. Math. Soc. Coll. Publ., 1927, 9 (Русский перевод: Дж. Биркгоф. Динамические системы. М.; Л.: Гостехиздат, 1940.)
[4] C.L. Siegel. Vorlesungen uber Himmelsmechanik. Berlin-Gottingen-Hridelberg: Springer-Verlag, 1956. (Русский перевод: К. JI. Зигель. Лекции по небесной механике. М.: ИЛ, 1959.)
[5] С. L. Siegel, J.K.Moser. Lectires on celestial mechanics. Berlin-Heidelberg-New York: Springer-Verlag, 1971. (Русский перевод отдельных глав имеется в книге: Ю. Мозер. Лекции о гамильтоновых системах. — М.: Мир 1973. С. 73-149.)
[6] A. Wintner. The analytical foundation of celestial mechanics. Princcton-Oxford, 1941. (Русский перевод: А.Уиптер. Аналитические основы небесной механики. М.: Наука, 1967.)
[7] J.Chazy. Sur Failure finale du m,ouvement, dans le probleme des trois corps quand le temps croit indefiniment. Ann. lEcole Norm. Sur. 3 ser., 1922. P. 29-130.
[8] J.Chazy. Sur Iallure finale du mouvement dans le probleme des trois corps. J. Math. Pures et Appl., 1929, 8. P. 353-380.
(см. скан)
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф |
- Квазислучайные колебания и качественные вопросы небесной механики
- Часть 1. О некоторых математических проблемах в небесной механике
- § 1. Основная задача небесной механики
- § 2. Геометрическая интерпретация задачи Кеплера
- § 3. Задача трех тел. Аналитические свойства решений
- § 4. Финальные движения в задаче трех тел
- § 5. Эволюция системы. Проблема захвата
- Часть 2. Символическая динамика
- Часть 3. Квазислучайные колебания некоторых нелинейных систем
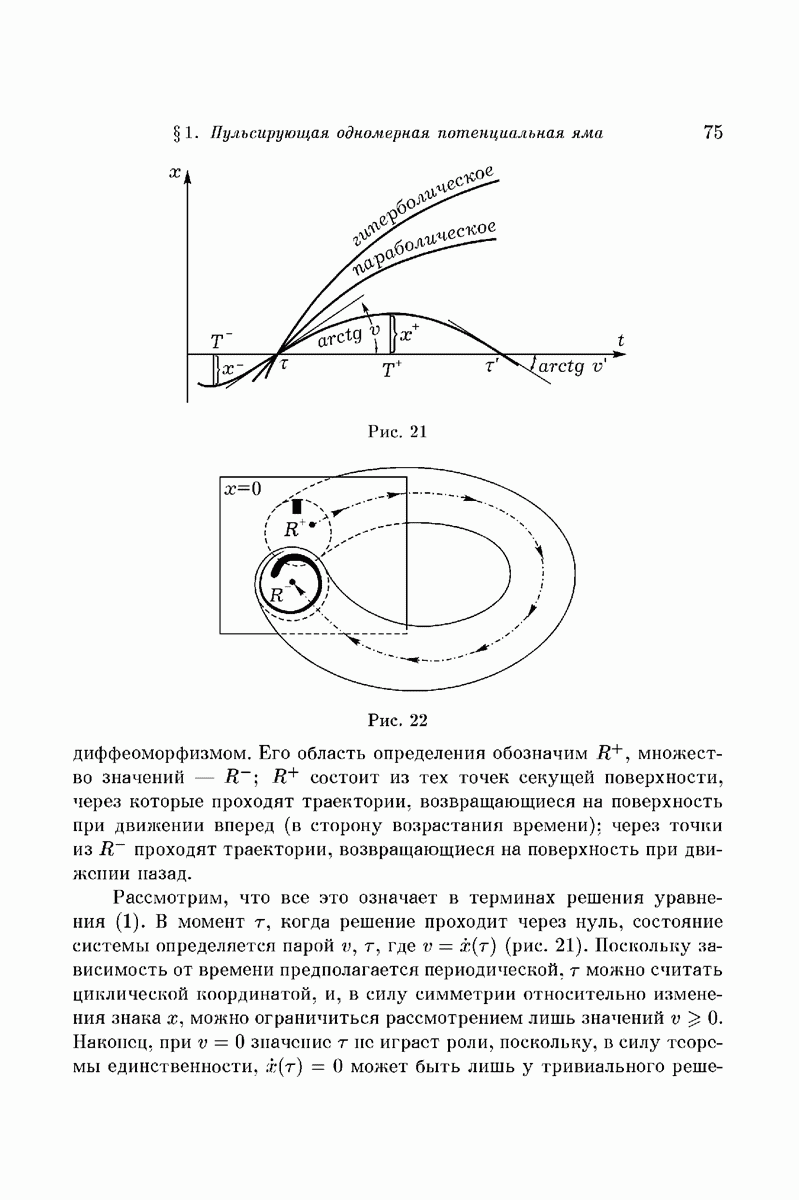
- § 1. Пульсирующая одномерная потенциальная яма
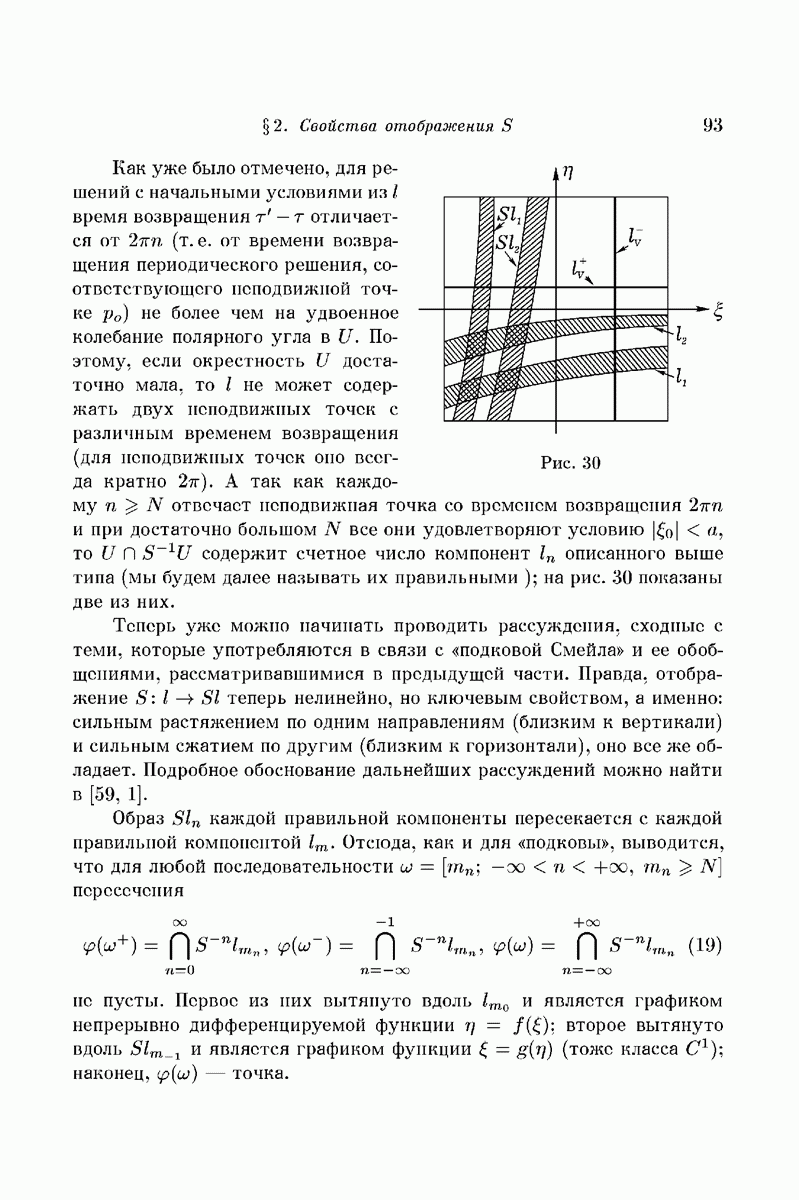
- § 2. Свойства отображения S
- § 3. Об одном частном случае задачи трех тел
- Литература
- О возможности захвата в небесной механике
- Литература
- О возможности захвата в задаче трех тел
- Обмен и захват в задаче трех тел
- Существование осциллирующих движений в задаче трех тел
- Финальные движения в задаче трех тел и символическая динамика