О возможности захвата в небесной механике

О. Ю. Шмидт

1. Возможность захвата одного псбсспого тела другим (или взаимного захвата двух тел) неоднократно выдвигалась как механизм для объяснения тех или других явлений космогонии, по встречала резкие возражения. Эти возражения указывали либо на невозможность захвата, либо на крайнюю его невероятность. Оставляя вопрос об оценке вероятности захвата до другой статьи, займемся сейчас выяснением самой возможности его.

2. Под «захватом» обычно понимается следующее явление: два небесных тела, первоначально двигавшиеся независимо друг от друга, под влиянием взаимного притяжения и тех или иных сопутствующих причин сходят со своих первоначальных орбит и в дальнейшем обращаются около общего центра тяжести по эллиптической (или возмущенной эллиптической) орбите. Возможно и такое определение: мы будем говорить, что произошел захват, если два тела до момента были всегда друг от друга на расстояниях, больших некоторой величины р, а после момента навсегда остаются на расстояниях меньших, чем р. Это — определение захвата, так сказать, навечно. Его можно было бы ослабить для «временного» захвата.

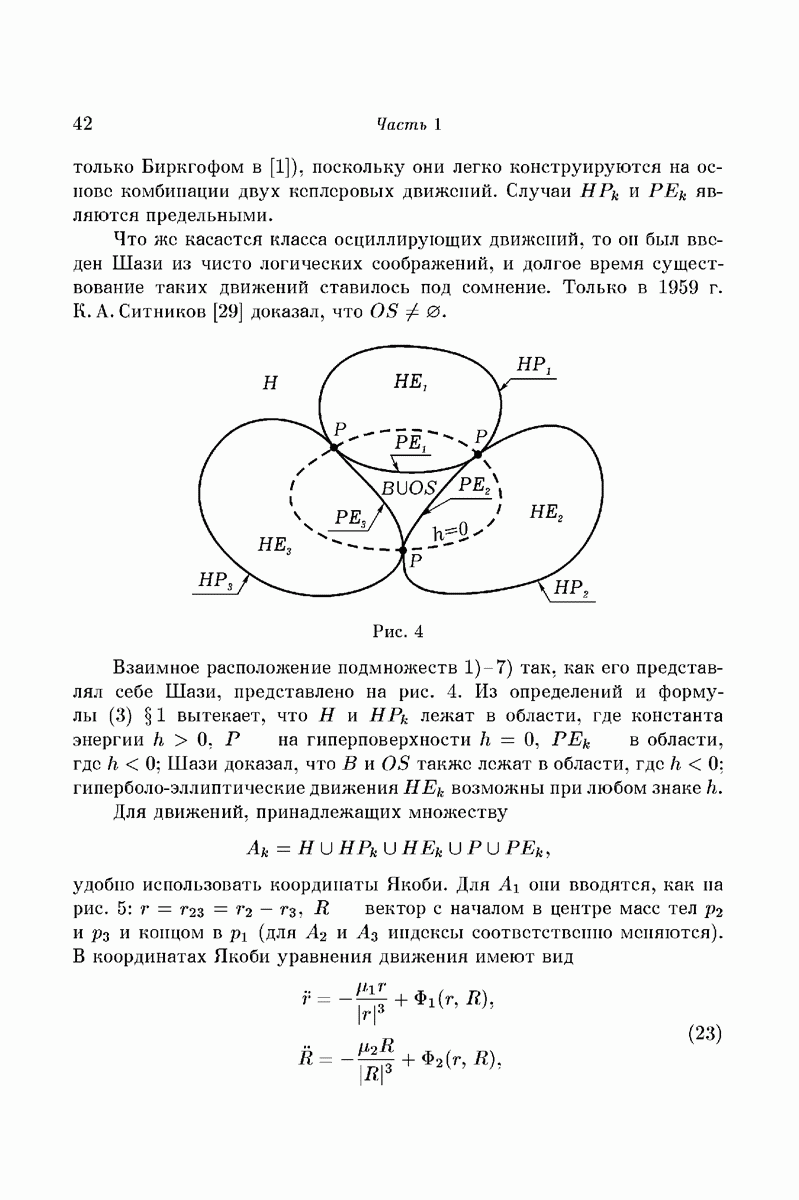
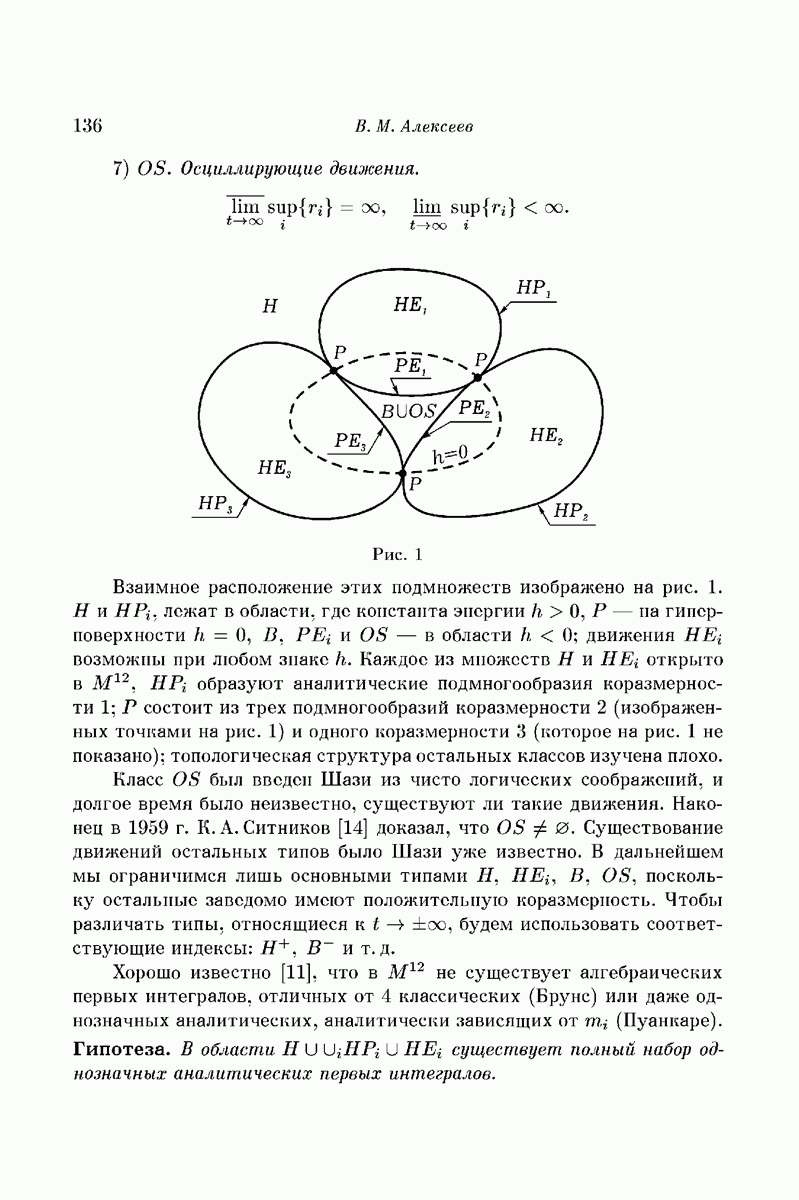
В случае ньютоновского притяжения захват невозможен при двух взаимно притягивающихся телах, необходимо по крайней мере три. Таким образом, вопрос о захвате упирается в знаменитую задачу трех тел. В этой связи наиболее детальное исследование принадлежит Chazy [1], который задался целью изучить движение в задаче трех тел, когда время возрастает бесконечно (allure finale). Chazy устанавливает следующие классы этих «финальных» состояний системы: 1) движения ограниченные, когда все три тела остаются в замкнутой области

около общего центра тяжести, и колебательные, когда тела попеременно то сближаются, то расходятся, не имея верхней границы расстояний, но и не уходят в бесконечность; 2) движения гиперболически-эллиптические, когда при бесконечном возрастании времени одно из тел уходит все дальше, а два других остаются на конечном расстоянии друг от друга, так что их относительное движение в пределе становится эллиптическим; 3) движения гиперболические, когда все три тела с течением времени безгранично расходятся.

В исследованиях Chazy существенную роль играет знак постоянной h в интеграле энергии, когда движение отнесено к центру тяжести системы. При возможны первые два класса упомянутых выше движений, при второй и третий. Для случая h < 0 Chazy в 1929 г. [1] доказал важную теорему: если в предельном прошлом (при ) движение принадлежало к одному из указанных классов, то и в предельном будущем (при ) оно будет принадлежать к тому же самому классу. Этот результат получил широкую известность. Его иногда считают доказательством невозможности захвата, забывая, что теорема Chazy 1929 г. относится только к случаю а сближение трех небесных тел, проходящих но независимым путям из бесконечности, предполагает как раз Правда, в 1932 г. Chazy [2] рассмотрел и этот последний случай и пришел к тому же выводу, но в отличие от первого мемуара дал строгого доказательства, ограничиваясь суждениями по аналогии. Ниже будет приведен пример, опровергающий утверждение Chazy для , а именно пример, когда движение было «гиперболическим» в прошлом и становится «гиперболически-эллиптическим» в будущем.

3. Явление захвата лежит в основе предложенной мною теории происхождения планетных систем и двойных звезд [7, 8]. Поэтому передо мной стояла настоятельная задача: доказать прежде всего принципиальную возможность захвата. Для этого достаточно найти хотя бы один пример в задаче трех тел, приводящий к захвату. В литературе таких примеров нет. Только Becker [3] вычислил несколько орбит своеобразного «обмена», когда проходящая мимо двойной звезды третья звезда вырывает одну из звезд парной системы и сама становится на ее место. Этот случай не решает нашего вопроса.

По скоростям и положениям (в некоторый момент) трех пришедших из бесконечности тел очень трудно догадаться, как будет протекать их встреча и не произойдет ли захвата. Подобрать такие условия

практически невозможно. Но задача сильно упрощается, если одновременно с захватом рассматривать параллельно разрывы пары тел под воздействием третьего тела. Разрывом двойной звезды занимались неоднократно: Opik [4], Lyttlcton [5], Chandrasckhar [6], по эти авторы прошли мимо того важного обстоятельства, что каждому случаю разрыва взаимно-однозначно соответствует случай захвата. В самом деле, как известно, уравнения небесной механики допускают изменение знака времени. Если в начальном положении система имеет координаты и скорости а через время пришла в положение с координатами и скоростями то другая система, начав движение с тех же координат но с противоположными скоростями — придет через время в то же положение в котором вначале была первая система, и со скоростями, равными точно Например, если первоначально две звезды обращались по эллипсам друг около друга, а затем проходящая третья звезда разорвала связь, так что через некоторое время все три звезды уже расходились в разные стороны с гиперболическими относительными скоростями, то фиксировав положение звезд в один из таких последующих моментов и придав им обратно направленные скорости (той же величины, как в первом случае), мы получим ту же картину движения в обратном порядке (как в пущенной наоборот кинопленке) и, начав с взаимно-гиперболических движений трех звезд, кончим эллиптическим движением двух из них, т. е. образованием двойной звезды путем захвата.

Подобрать условия для разрыва пары уже гораздо легче. И действительно, первый же предложенный мной численный пример дал отчетливую картину разрыва двойной звезды, а рассматриваемый в обратном направлении дал, следовательно, пример образования двойной звезды путем захвата. Вычисления были проведены О. П. Крамер и В.И. Ковригиной, под общим руководством Н. Н. Парийского. Начато вычисление ряда дальнейших примеров.

4. Рассматривается движение трех тел с одинаковыми массами, равными массе Солнца, которая берется за единицу. Единицей расстояния служит астрономическая единица, а единицей времени год, деленный на 277. При этих условиях постоянная тяготения равна 1, что упрощает вычисление. Мы будем иметь дело с относительным движением по отношению к одному из трех тел, с которым мы неизменно

свяжем начало координат системы (точка О). Уравнения относительного движения тел с координатами имеют вид:

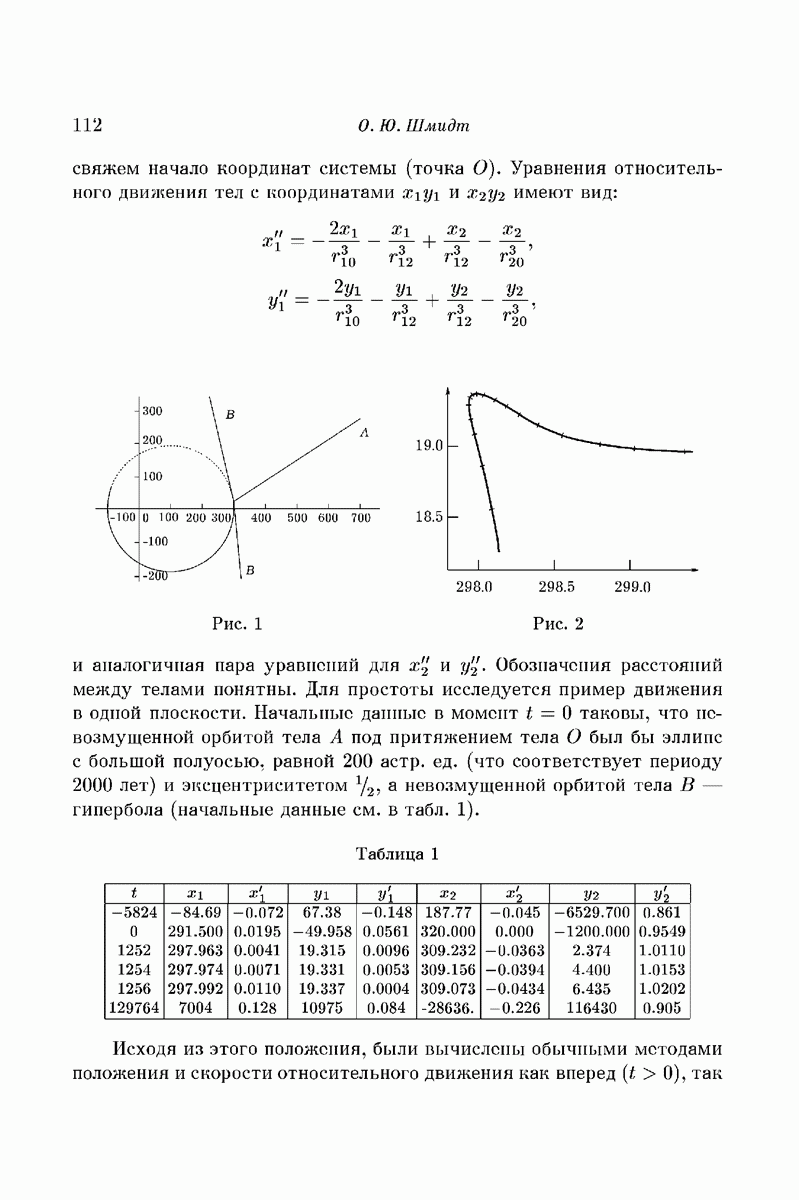
Рис. 1

Рис. 2

и аналогичная пара уравнений для . Обозначения расстояний между телами понятны. Для простоты исследуется пример движения в одной плоскости. Начальные данные в момент t = 0 таковы, что невозмущенной орбитой тела А под притяжением тела О был бы эллипс с большой полуосью, равной 200 астр. ед. (что соответствует периоду 2000 лет) и эксцентриситетом , а невозмущенной орбитой тела В — гипербола (начальные данные см. в табл. 1).

Таблица 1

Исходя из этого положения, были вычислены обычными методами положения и скорости относительного движения как вперед , так

и назад На рис. 1 воспроизведены траектории движения, а на рис. 2 — в большем масштабе тот участок траектории тела А, на котором произошел разрыв пары. При этом отмечены точки, соответствующие тем моментам времени, для которых вычислялись положения и скорости. В табл. 1 даны начальные данные и для иллюстрации приведены некоторые строчки из результатов вычисления.

Мы видим, что с возрастанием t действительно произошел разрыв пары. В том, что движение в дальнейшем останется гиперболическим по отношению к телу О, убеждает не только рисунок, но и следующее простое рассуждение. Из наших уравнений видно, что как только и станут больше в дальнейшем ускорение тела А будет всегда меньше, чем т.е. меньше того ускорения, которое соответствует притяжению одним телом, помещенным в точке О, с четверной массой. Из табл. 1 видно, что скорость тела А в последних строках значительно больше, чем была бы параболическая скорость в указанном для сравнения случае. Таким образом, и в дальнейшем А останется на гиперболе. Движение, обратно направленное, дает захват с образованием двойной звезды и эллиптической орбитой.

Рассмотренный пример не является исключительным. Ясно, что небольшие изменения в начальных данных, в том числе и в третьем измерении, дадут небольшие изменения и в области разрыва (захвата). Множество начальных данных, приводящих к захвату, имеет положительную меру, а не меру нуль.

5. Итак, захват в задаче трех тел возможен, как и разрыв двойной звезды, притом этот захват (разрыв) будет не временным, а постоянным. Движение системы трех тел, гиперболически-эллиптическое в прошлом, может стать гиперболическим в будущем, и наоборот.

Вероятность захвата хотя и мала, но положительна (не нуль). Поэтому при наличии в Галактике около 1011 звезд и времени никак не меньше миллиардов лет, можно быть уверенным, что в Галактике есть случаи, когда эта возможность была реализована, т. е. хотя бы некоторая часть визуально-двойных звезд образовалась путем захвата. Это теперь уже не гипотеза, а факт. Отсюда еще нельзя непосредственно сделать вывод, что все визуально-двойные звезды образовались таким путем. Но можно построить теорию для тех двойных звезд, которые произошли путем захвата, т. е. вывести закономерности и формулы, которым должны подчиняться эксцентриситеты, длины осей и наклоны орбит, и затем сравнить эти формулы с данными наблюдений. Это

сделано в моих работах [7], причем совпадение теоретических и эмпирических закономерностей оказалось очень хорошим.

Таким образом, не малая часть, а все или, по крайней мере, подавляющая часть визуально-двойных звезд произошла путем захвата.