§ 3. Об одном частном случае задачи трех тел

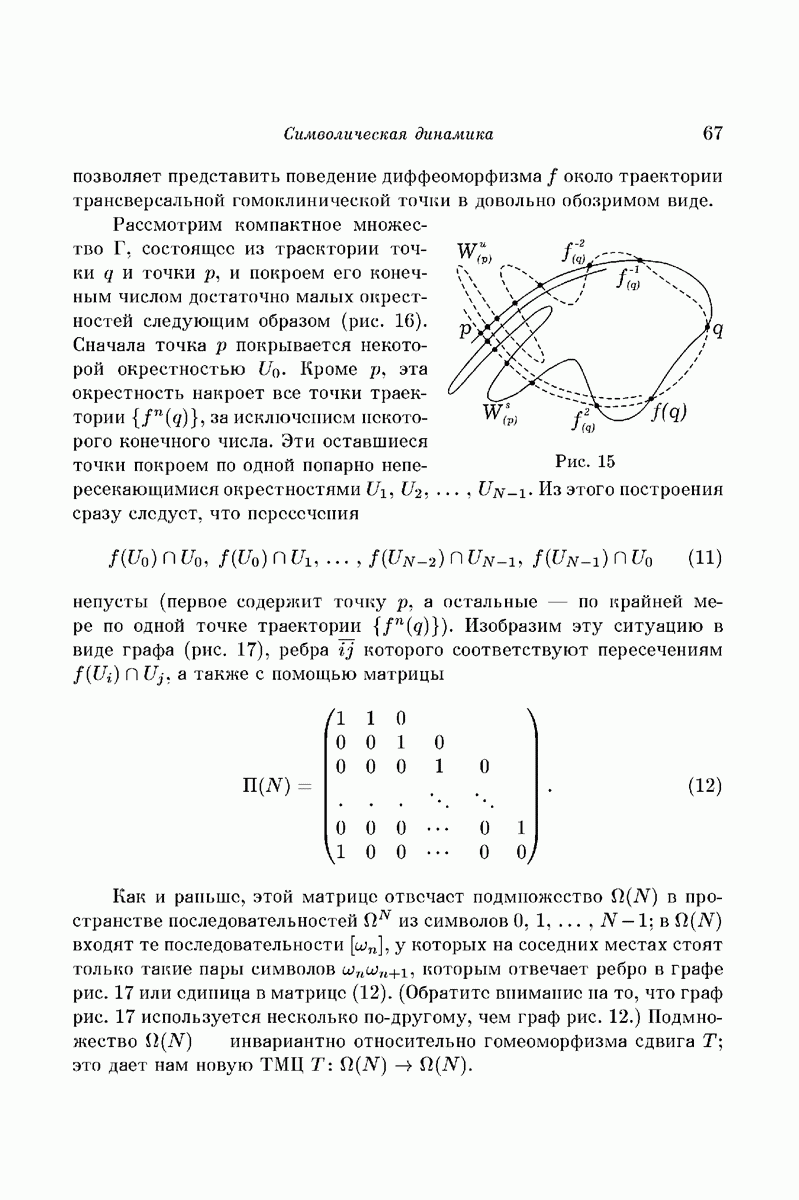
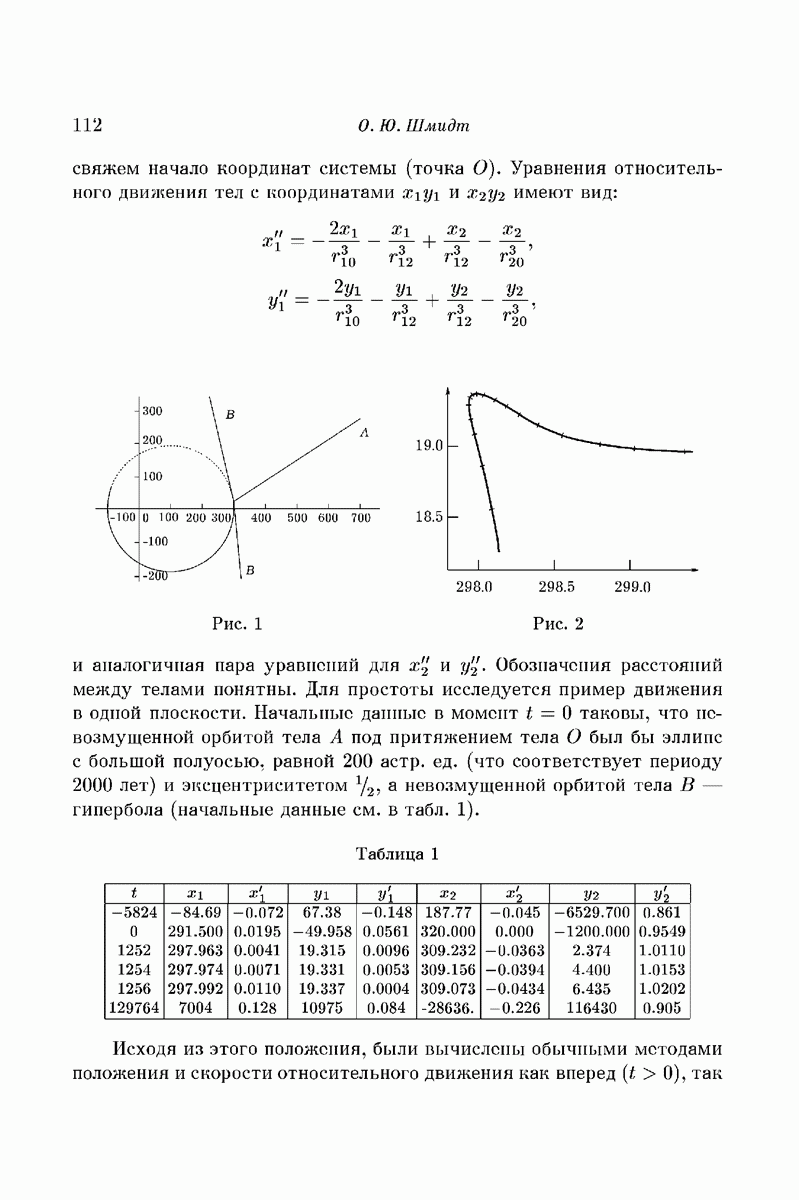
Рассмотрим снова, как и в лекции 1, движение трех тел (материальных точек) взаимодействующих друг с другом по закону Ньютона; — масса тела .

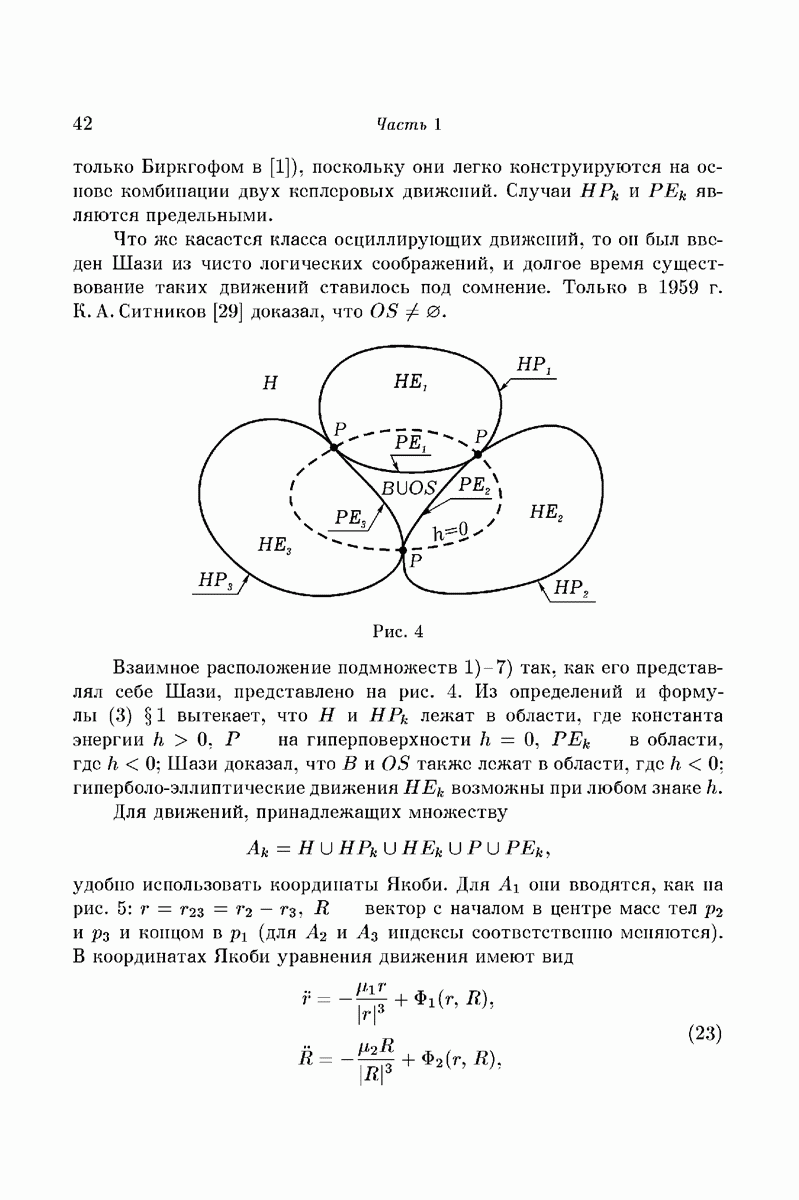
Предположим, что и что в начальный момент тела и их скорости симметричны относительно QZ, а тело лежит на этой оси и его скорость направлена вдоль нее (рис. 32). По соображениям симметрии подобное расположение тел будет сохраняться для всех t, что позволяет свести исследование к системе с двумя степенями свободы.

Этот частный случай задачи трех тел придумай давно (я знаю ссылку на работу 1895 года), но счастливая идея: исследовать на нем

Рис. 32

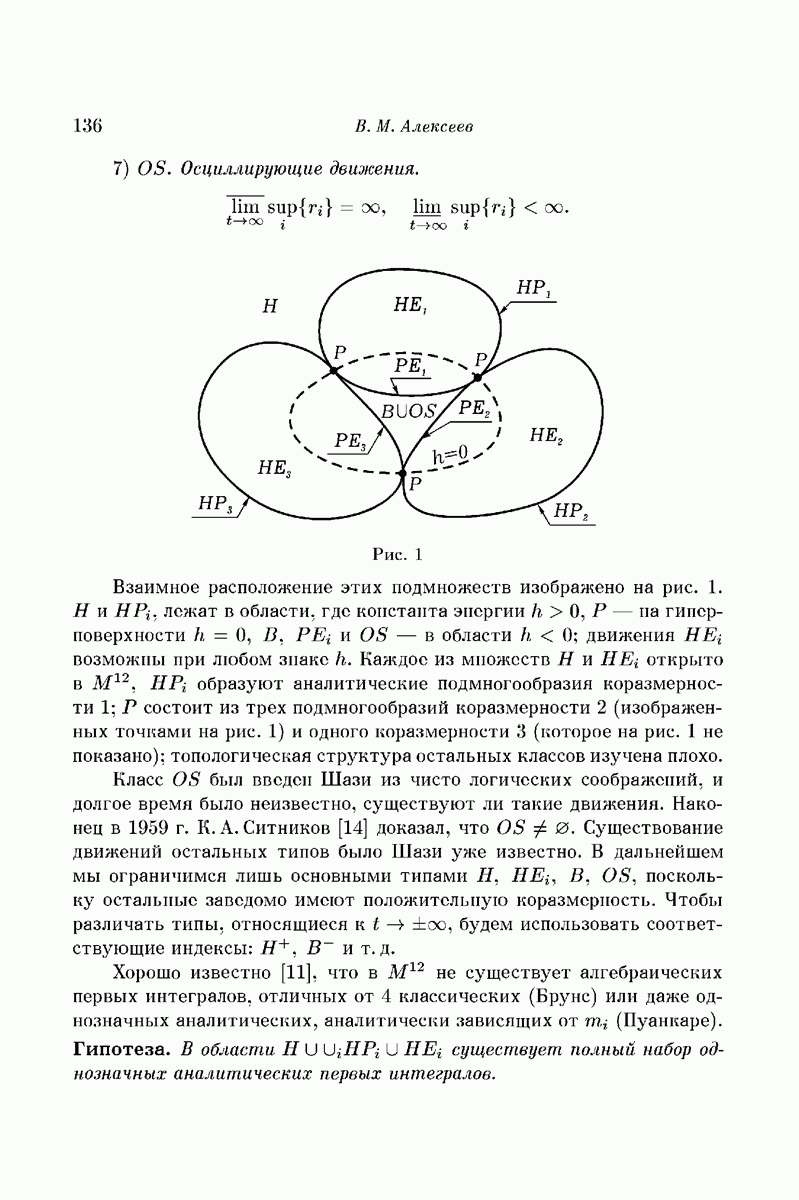
расположение в фазовом пространстве траекторий различных финальных типов, принадлежит А. Н. Колмогорову. Именно для этого примера К. А. Ситникову удалось доказать [29] существование осциллирующих движений (см. часть 1), а автору — возможность применения методов «символической динамики».

Пусть (предположение не вносит ничего принципиально нового). Если выполнено обычное соглашение о центре тяжести системы (формула (2) в части 1), то описывают в плоскости XOY кеплеровы орбиты, симметричные относительно 0; в случае они будут эллипсами, что мы и предположим далее. При подходящем выборе единиц можно считать, что период обращения тел по этим эллипсам равен а гравитационная постоянная и суммарная масса тел — единице. Обозначим через половину расстояния (т.е. расстояние от каждого из тел до точки 0). Тогда уравнение движения тела положение которого определяется лишь одной координатой z, имеет вид

Это уравнение принадлежит классу, рассмотренному в § 1; легко проверяется, что его правая часть удовлетворяет предположениям А Е, причем

Полярные координаты , игравшие столь важную роль в §§ 1-2, интерпретируются теперь так. В момент, когда проходит через 0 и все три тела располагаются на одной прямой («прямолинейная конфигурация»), состояние системы определяется двумя величинами: скоростью

тела и фазой эллиптического движения тел (в качестве можно взять среднюю или истинную аномалию По соображениям симметрии можно ограничиться лишь модулем v скорости Тогда заданием полярных координат точки на плоскости Ф движение полностью определяется с точностью до направления скорости.

Если орбиты тел круговые, то (в силу соглашения о выборе единиц) и уравнение (28) интегрируется. Начальные условия , принадлежащие окружности порождают параболические движения, при — гиперболические, при — ограниченные (движение тела при этом будет периодическим так же, как и движение пары но периоды этих двух движений на множестве полной меры несоизмеримы).

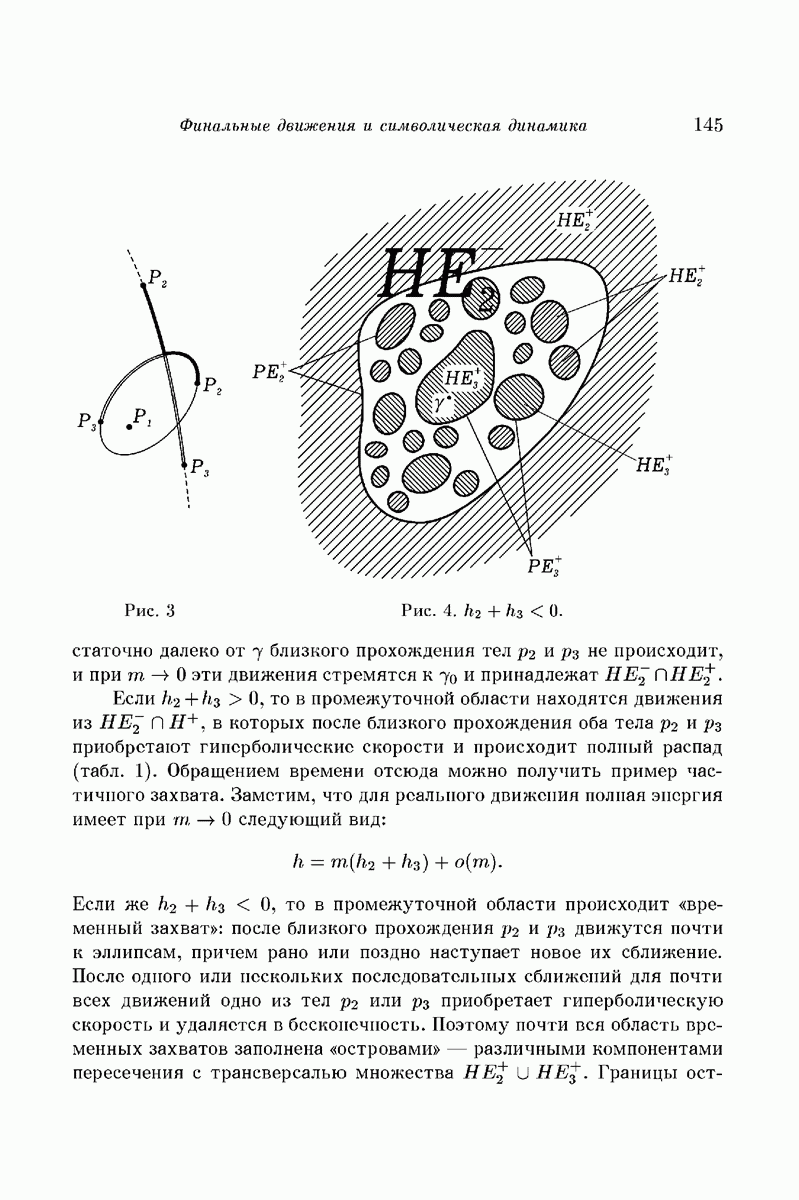
В том же случае, когда тела обращаются около 0 по эллипсам, кривые параболических начальных данных и друг с другом не совпадают. Если эллипсы мало отличаются от окружностей, то удастся доказать «типичность» уравнения. Используя разложения по эксцентриситету эллипсов как по малому параметру, можно убедиться в том, что кривые и асимптотические близкие к окружности имеют ровно две трансверсальные точки пересечения (как на рис. 3). 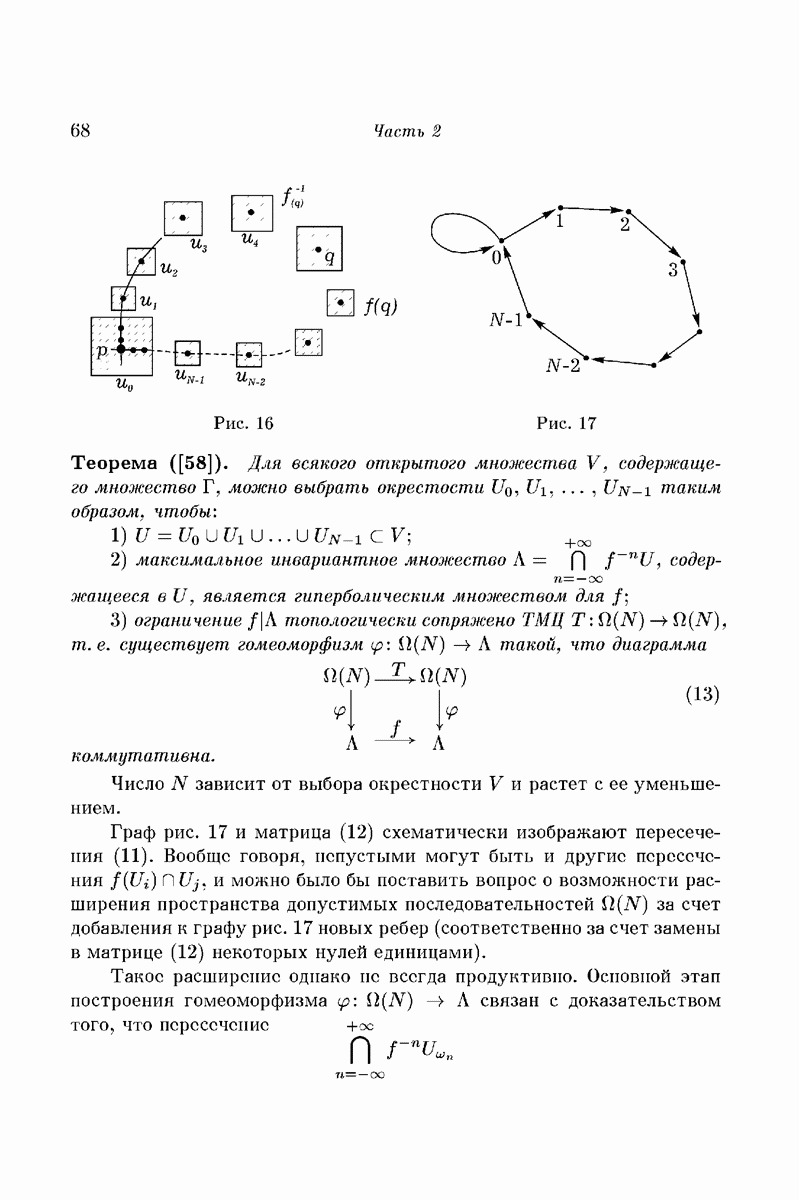Одной точке пересечения, близкой к (0,2), соответствуют моменты наибольшего сближения тел Другой, близкой к — моменты наибольшего удаления. Следуя рассуждениям предыдущего параграфа, можно определить окрестности точек пересечения, «хорошие» с точки зрения возможности использования символической динамики. В фазовом пространстве этим окрестностям отвечает некоторое открытое подмножество V многообразия прямолинейных конфигурации. Оно зависит от двух параметров N и ; формулируемая ниже теорема справедлива, если достаточно мало, а N достаточно велико. Теорема 3. Множество решений рассматриваемого частного случая задачи трех тел, когда моменты прямолинейных конфигураций их состояния принадлежат V, находится во взаимно однозначном соответствии со множеством всех символических последовательностей вида

где — натуральные числа или части, отделенные в (29) пунктиром, могут и отсутствовать или , и тогда последовательность в соответствующую сторону бесконечна.

Число прямолинейных конфигураций на решении определяется символами в (29): если , то прохождение через О происходит вблизи момента наибольшего сближения тел если — вблизи момента наибольшего удаления. Символ стоящий между показывает число полных оборотов тел вокруг 0, протекающих между возвращением к 0. Символы или если они присутствуют, показывают, что тело уходит в бесконечность при или при соответственно со скоростью или .

Термин «решение» в этой теореме означает траекторию в фазовом пространстве, на которой в качестве нулевой точки выделено одно из состояний с прямолинейной конфигурацией (из § 1 следует, что на каждой траектории такие состояния найдутся). Этому состоянию присвоен номер 0, и ему отвечает в последовательности (29) символ ; остальные состояния с прямолинейной конфигурацией нумеруются от нулевого в обе стороны. Выбор другой прямолинейной конфигурации в качестве пулевой приводит к изменению нумерации символов в последовательности (29), но сама последовательность остается той же самой. Принадлежность движения к тому или иному (финальному типу по Шази определяется последовательностью (29) так же, как и в § 2, только классы в смысле § 1 превращаются здесь в и .

Если масса тела отлична от нуля, то задача становится более сложной, и результаты, основанные на изучении уравнения (1), к ней непосредственно не применимы. Все же и в этом случае удается, по крайней мере при (см. [63]), построить отображение S с теми же свойствами, что и в § 2. Это делает справедливым

Следствие. Существует такое , что при и при h < 0 в рассматриваемом частном случае задачи трех тел реализуются все 16 логически возможных комбинаций финальных типов движения по Шази.

Например, любая последовательность

в которой порождает решение, для которого происходит полный захват (часть 1, § 5). Стандартными приемами символической динамики можно построить и другие примеры движения

с предписанным заранее разнообразным поведением. Так, последовательности

отвечает движение тела, которое можно интерпретировать следующим образом. Космический корабль, прилетевший в систему двойной звезды из бесконечности со скоростью вышел сначала на орбиту, близкую к периодической (маятниковой) с периодом . На этой орбите он проделал полных колебаний, причем в течение каждого дважды возвращался в точку относительно равновесия (в центр масс двойной звезды поочередно в моменты наибольшего сближения и наибольшего удаления компонент двойной звезды. Затем корабль перешел на орбиту, близкую к периодической с периодом проделал на ней полных колебаний, причем каждое из его возвращений к точке равновесия происходило около моментов сближения компонент двойной звезды. Наконец, вернувшись на первоначальную орбиту, корабль проделал около нее полтора колебания и ушел в бесконечность со скоростью в ту же сторону, откуда пришел. Замечательно, что все эти эволюции оказываются возможными только за счет сил гравитации и не требуют расхода топлива. Правда, точность задания начальных условий должна быть необычайно высока.

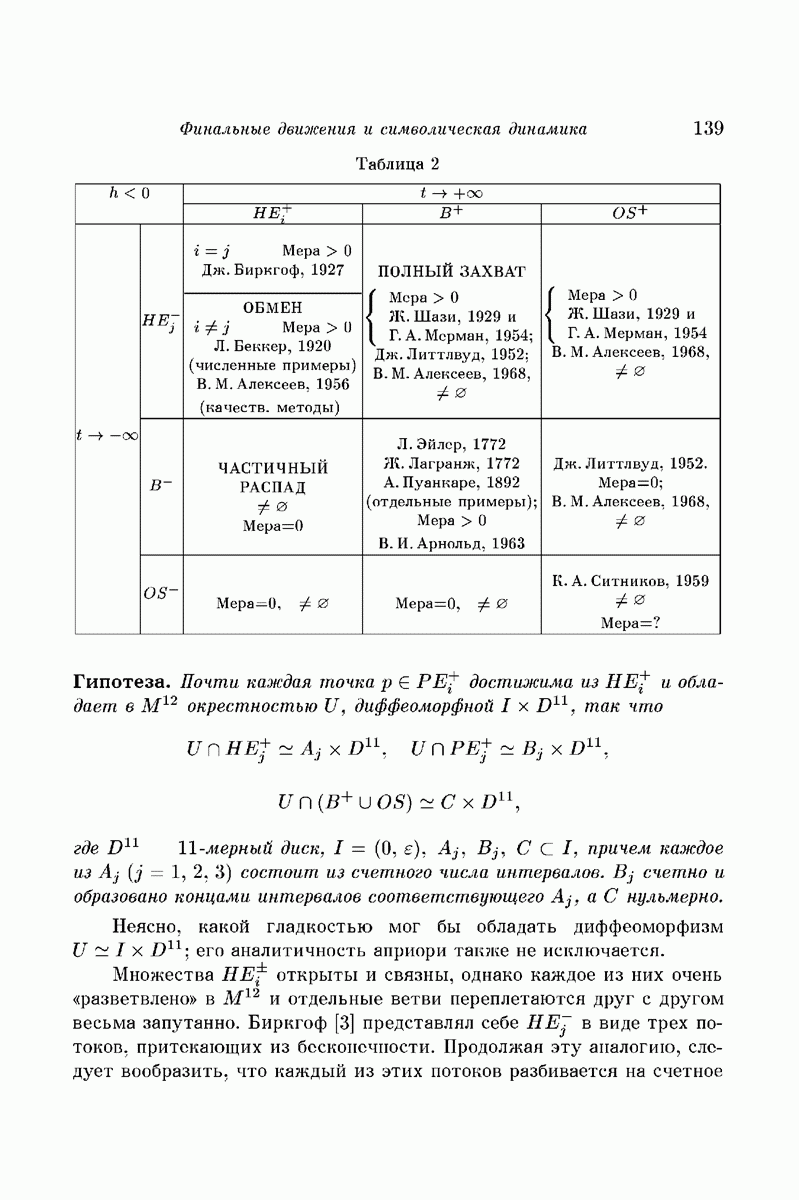
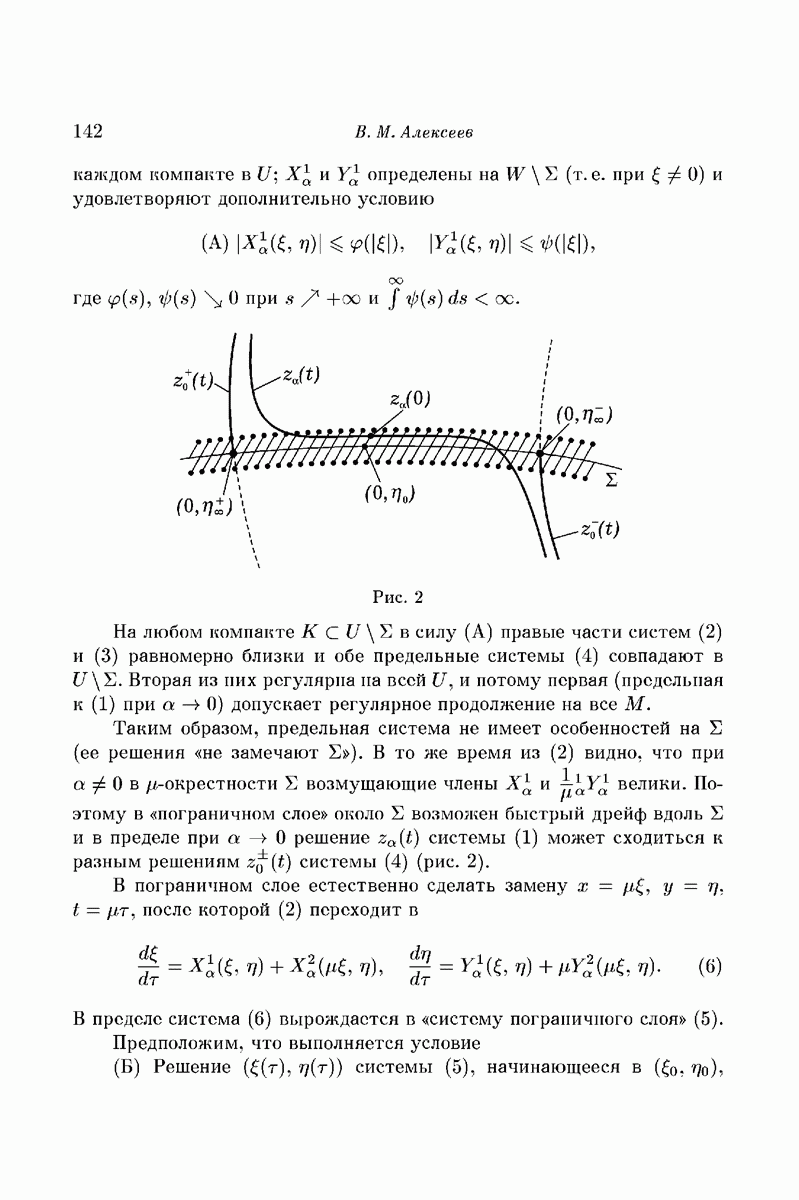
Теорема 3 и ее следствие позволили получить ответ на ряд теоретических вопросов небесной механики, из которых вопрос о полном захвате, вероятно, наиболее интересен. Тем не менее, целый ряд проблем, как уже было отмечено в части 1, остается не решенным. Применительно к рассматриваемому здесь примеру это, в первую очередь, вопрос о мерс множеств осциллирующих движений Кроме того, было бы чрезвычайно интересно распространить эти результаты на случай «полномерного» фазового пространства задачи трех тел, не говоря уж об общей задаче n тел.