| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Финальные движения в задаче трех тел
Исследование качественных свойств решений задачи трех тел продвинулись сравнительно далеко в направлении изучения финальных движений, т. е. поведения решений при  . Давний и стойкий интерес, который проявляют к этим вопросам как специалисты, так и не специалисты, вполне объясним. Здесь затрагиваются проблемы, возникающие в области, где математика и механика граничат с философией: происхождение и судьба Солнечной системы, эволюция звездных скоплений и т. д.
. Давний и стойкий интерес, который проявляют к этим вопросам как специалисты, так и не специалисты, вполне объясним. Здесь затрагиваются проблемы, возникающие в области, где математика и механика граничат с философией: происхождение и судьба Солнечной системы, эволюция звездных скоплений и т. д.
Один из первых результатов в этой области был получен Лапласом и Лагранжем, которые доказали, что в первом приближении (т.е. если пренебречь членами, содержащими квадраты отношений масс планет к массе Солнца) движение планет может быть описано чисто тригонометрическими рядами [9]. Этот результат был истолкован как доказательство устойчивости Солнечной системы; с ним же связано происхождение понятия «устойчивости в смысле Лаграпжа» в общей теории динамических систем. К сожалению, надежды на справедливость аналогичного утверждения в следующих приближениях теории возмущений не оправдались, и в настоящее время вопрос об устойчивости как реальной Солнечной системы, так и вообще планетарных систем гравитирующих точек остается открытым; мы еще вернемся к этому вопросу далее.
Простейшей и в то же время наиболее наглядной характеристикой движения является асимптотика попарных расстояний между телами при  .
.
Ньютоновский характер сил взаимодействия порождает две типичные асимптотики для ухода в бесконечность: гиперболическую  и параболическую
и параболическую  . В одномерной кеплеровой задаче это очевидно: из интеграла энергии
. В одномерной кеплеровой задаче это очевидно: из интеграла энергии

находим, что

Те же три случая мы имеем и в задаче двух тел. В зависимости от знака константы полной энергия h (энергии относительного движения этих двух тел, если центр масс не предполагается покоящимся) движения разделяются на
Н. гиперболические:  ;
;
Р. параболические:  ;
;
В. ограниченные (или эллиптические):  .
.
(Здесь и далее  расстояние между телами
расстояние между телами  ; С — некоторая постоянная, не обязанная быть одной и той же во всех формулах.)
; С — некоторая постоянная, не обязанная быть одной и той же во всех формулах.)
В случае произвольного числа тел положение оказывается гораздо более сложным. Все же Саари удалось доказать [48] некоторое условное утверждение, согласно которому три упомянутых выше типа поведения попарных расстояний при  являются основными. Согласно Саари, все n тел разбиваются на скопления, внутри которых попарные расстояния ограничены; скопления группируются в подсистемы так, что внутри одной подсистемы расстояния между скоплениями имеют порядок наконец, расстояния центров масс подсистем от общего центра масс всей системы имеют порядок
являются основными. Согласно Саари, все n тел разбиваются на скопления, внутри которых попарные расстояния ограничены; скопления группируются в подсистемы так, что внутри одной подсистемы расстояния между скоплениями имеют порядок наконец, расстояния центров масс подсистем от общего центра масс всей системы имеют порядок  . Этот красивый результат получен, однако, в предположении, что выполняется ряд не проверяемых эффективно условий, важнейшим из которых является отсутствие осциллирующих троек
. Этот красивый результат получен, однако, в предположении, что выполняется ряд не проверяемых эффективно условий, важнейшим из которых является отсутствие осциллирующих троек  , где
, где  , а отношение хотя и не ограничено, не стремится к бесконечности.
, а отношение хотя и не ограничено, не стремится к бесконечности.
Вернемся к задаче трех тел. Здесь мы имеем всего три попарных расстояния, которые мы для краткости обозначим

Величины р связаны между собой неравенствами треугольника, что уменьшает число логически возможных комбинаций их асимптотик. Еще в 1922 г. французский астроном и математик Ж. Шази описал все возможные в задаче трех тел типы финальных движений [38]. Согласно Шази, все фазовое пространство разбивается на следующие подмножества:
1) Н. Гиперболические движения:  .
.
2)  . Гиперболо-параболические движения:
. Гиперболо-параболические движения:

3) Р. Параболические движения:

Во всех трех случаях происходит распад системы трех тел (тройной звезды) на отдельные составляющие компоненты; различие лишь в скорости удаления компонент друг от друга. Например, для движений из  система распадается на две подсистемы: одна состоит из одного тела
система распадается на две подсистемы: одна состоит из одного тела  , другая — из тел
, другая — из тел  , которые удаляются друг от друга параболически
, которые удаляются друг от друга параболически  , в то время как подсистемы расходятся гиперболически
, в то время как подсистемы расходятся гиперболически  .
.
4)  . Гиперболо-эллиптические движения:
. Гиперболо-эллиптические движения:

5)  . Параболо-эллиптические движения:
. Параболо-эллиптические движения:

В этих двух случаях система распадается на двойную звезду и одно тело, расстояние между которыми стремится к бесконечности гиперболически или параболически; каждый случай разбивается на три подслучая в соответствии с тем, какое из трех тел удаляется от пары остальных; например, для движений  расстояние между телами
расстояние между телами  ограничено, в то время как
ограничено, в то время как  неограниченно от них удаляется параболически.
неограниченно от них удаляется параболически.
6)  . Ограниченные движения: все
. Ограниченные движения: все  .
.
7)  . Осциллирующие движения: по крайней мере одно из
. Осциллирующие движения: по крайней мере одно из  не ограничено, но не стремится к бесконечности.
не ограничено, но не стремится к бесконечности.
Существование движений типов Н, Р и В было Шази уже известно; примеры доставляют, скажем, лагранжевы решения, в которых треугольник  — равносторонний (меняющихся размеров). В существовании движений гиперболо-эллиптического типа он не сомневался (хотя более или менее строгое доказательство было дано, по-видимому,
— равносторонний (меняющихся размеров). В существовании движений гиперболо-эллиптического типа он не сомневался (хотя более или менее строгое доказательство было дано, по-видимому,
только Биркгофом в [1]), поскольку они легко конструируются на основе комбинации двух кеплеровых движений. Случаи  и
и  являются предельными.
являются предельными.
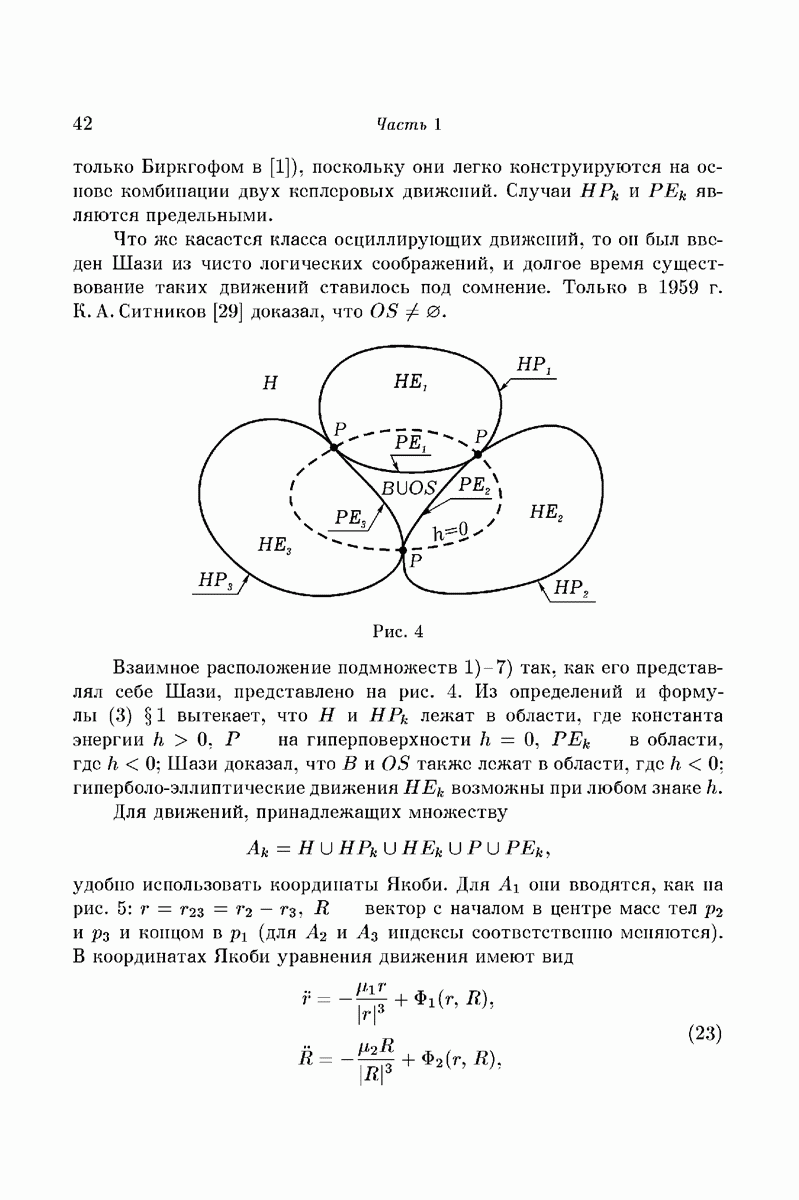
Что же касается класса осциллирующих движений, то он был введен Шази из чисто логических соображений, и долгое время существование таких движений ставилось под сомнение. Только в 1959 г. К. А. Ситников [29] доказал, что  .
.

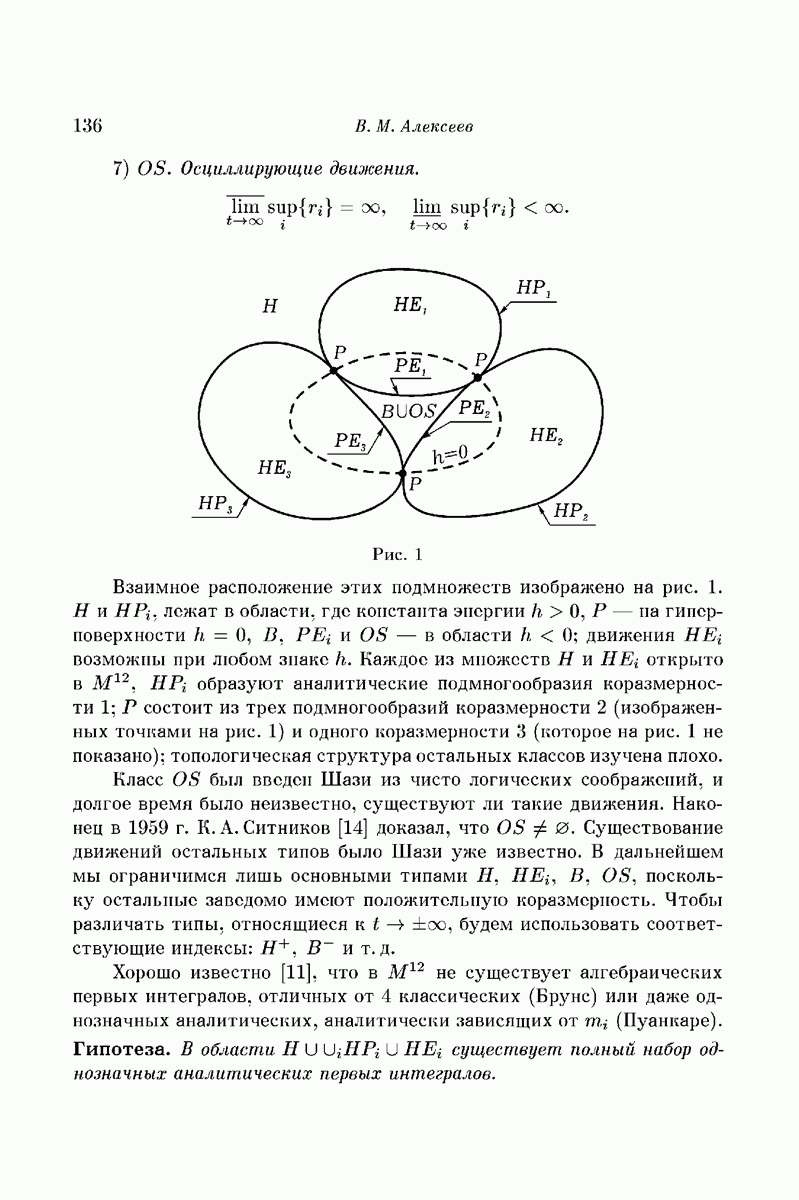
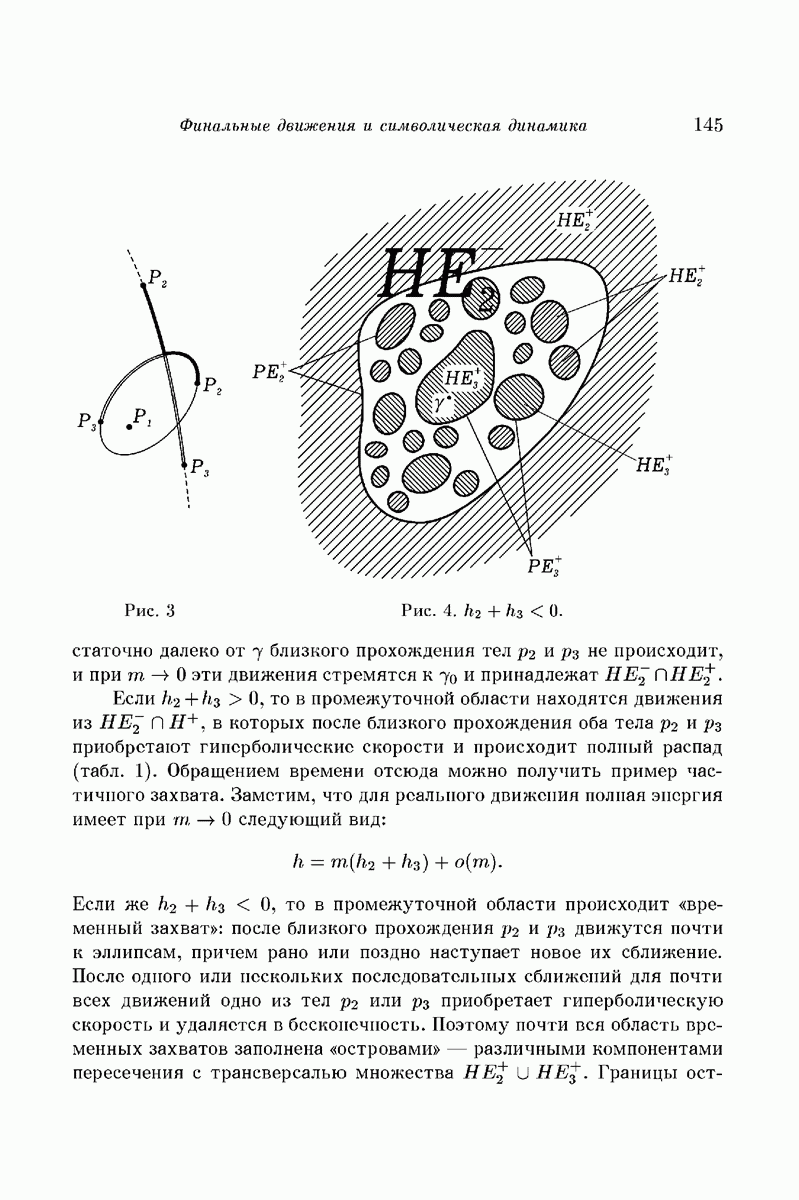
Рис. 4
Взаимное расположение подмножеств  так, как его представлял себе Шази, представлено на рис. 4. Из определений и формулы (3) § 1 вытекает, что Н и
так, как его представлял себе Шази, представлено на рис. 4. Из определений и формулы (3) § 1 вытекает, что Н и  лежат в области, где константа энергии
лежат в области, где константа энергии  на гиперповерхности
на гиперповерхности  в области, где
в области, где  ; Шази доказал, что В и OS также лежат в области, где h < 0; гиперболо-эллиптические движения
; Шази доказал, что В и OS также лежат в области, где h < 0; гиперболо-эллиптические движения  возможны при любом знаке h. Для движений, принадлежащих множеству
возможны при любом знаке h. Для движений, принадлежащих множеству

удобно использовать координаты Якоби. Для  они вводятся, как на рис. 5:
они вводятся, как на рис. 5:  вектор с началом в центре масс тел
вектор с началом в центре масс тел  и концом в
и концом в  (для
(для  и
и  индексы соответственно меняются). В координатах Якоби уравнения движения имеют вид
индексы соответственно меняются). В координатах Якоби уравнения движения имеют вид

где  — некоторые константы, зависящие только от масс
— некоторые константы, зависящие только от масс  а функции
а функции  . Для движений из множества
. Для движений из множества  при
при  отношение
отношение  достаточно быстро, так что система (23) асимптотически распадается на две кеплеровы подсистемы. Шази доказал, что элементы, определяющие мгновенные кеплеровы орбиты в этих двух подсистемах, стремятся при
достаточно быстро, так что система (23) асимптотически распадается на две кеплеровы подсистемы. Шази доказал, что элементы, определяющие мгновенные кеплеровы орбиты в этих двух подсистемах, стремятся при  к определенным пределам. В частности, существуют предельные относительные энергии
к определенным пределам. В частности, существуют предельные относительные энергии

и принадлежность движений к различным финальным типам можно описать в терминах этих величин так:


Рис. 5
Обе кеплеровы подсистемы, на которые распадается асимптотически система (23), могут быть проинтегрированы до конца, поэтому представляется весьма правдоподобной Гипотеза. В области

задача трех тел имеет полный набор однозначных аналитических первых интегралов.
Шази считал это утверждение верным, нужные интегралы он предлагал строить из предельных значений элементов мгновенных кеплеровых орбит в подсистемах, однако его аргументы, приведенные в [38] и [40], не кажутся мне исчерпывающими. Если, тем не менее, оно верно, то было бы интересно изучить поведение интегралов около границы (25), которая весьма сложна.
| << Предыдущий параграф | Следующий параграф >> |
- Квазислучайные колебания и качественные вопросы небесной механики
- Часть 1. О некоторых математических проблемах в небесной механике
- § 1. Основная задача небесной механики
- § 2. Геометрическая интерпретация задачи Кеплера
- § 3. Задача трех тел. Аналитические свойства решений
- § 4. Финальные движения в задаче трех тел
- § 5. Эволюция системы. Проблема захвата
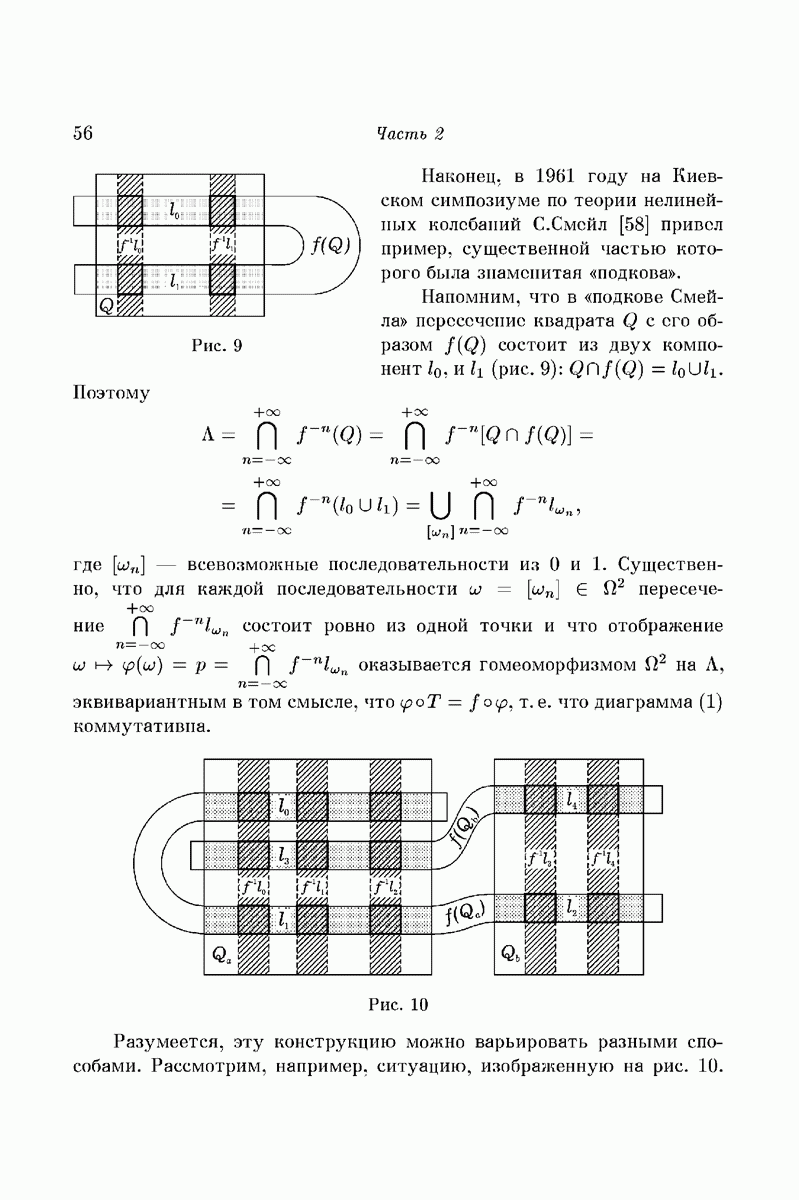
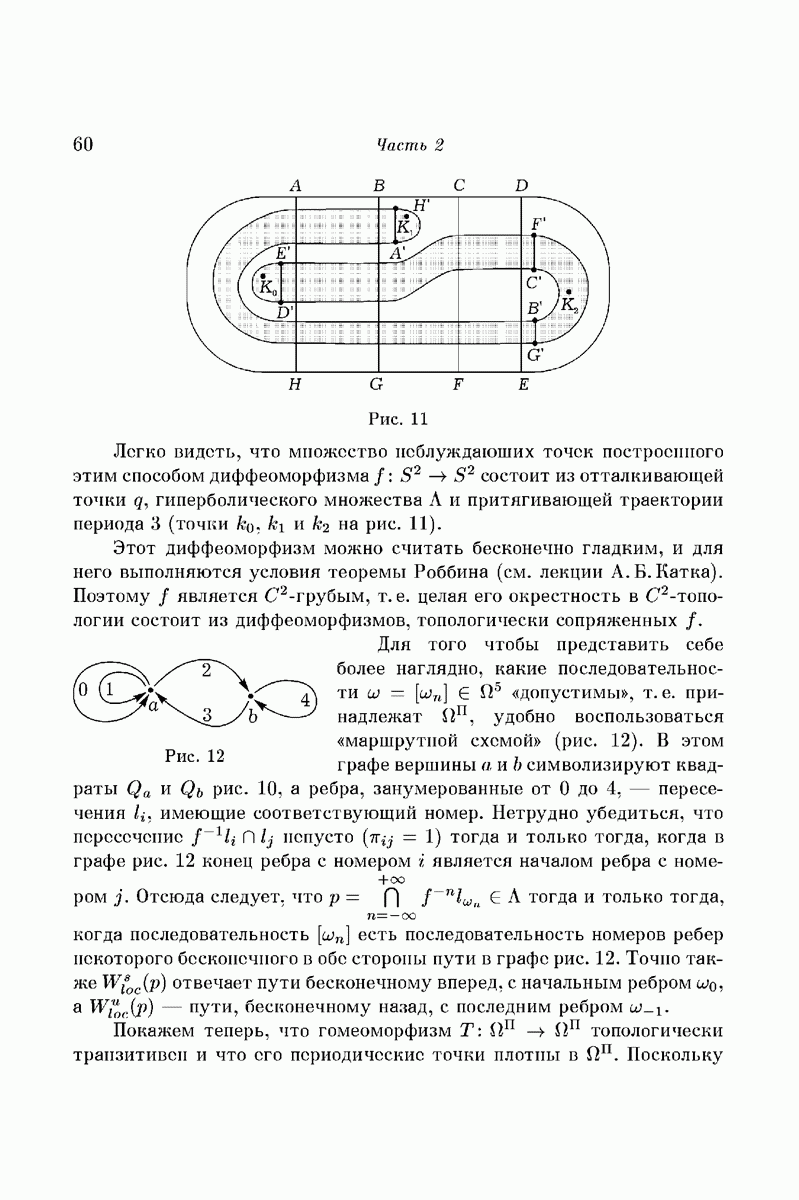
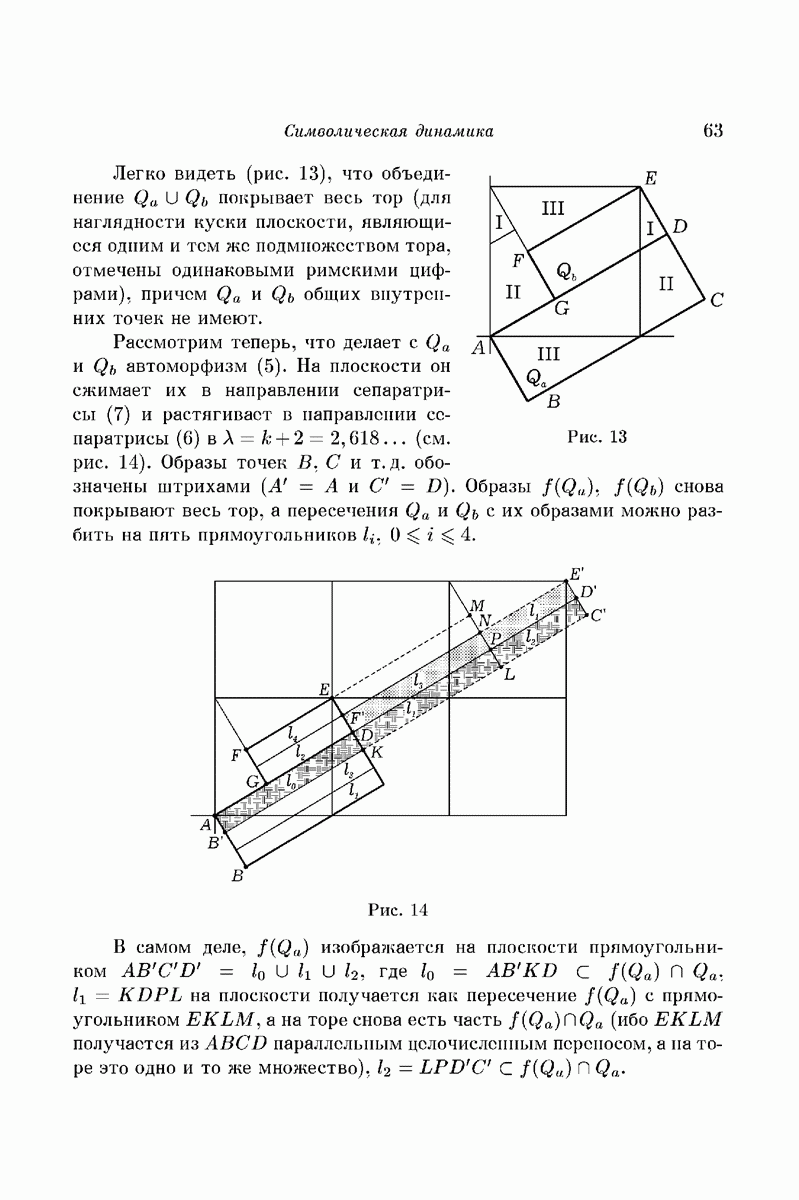
- Часть 2. Символическая динамика
- Часть 3. Квазислучайные колебания некоторых нелинейных систем
- § 1. Пульсирующая одномерная потенциальная яма
- § 2. Свойства отображения S
- § 3. Об одном частном случае задачи трех тел
- Литература
- О возможности захвата в небесной механике
- Литература
- О возможности захвата в задаче трех тел
- Обмен и захват в задаче трех тел
- Существование осциллирующих движений в задаче трех тел
- Финальные движения в задаче трех тел и символическая динамика