Часть 3. Квазислучайные колебания некоторых нелинейных систем

§ 1. Пульсирующая одномерная потенциальная яма

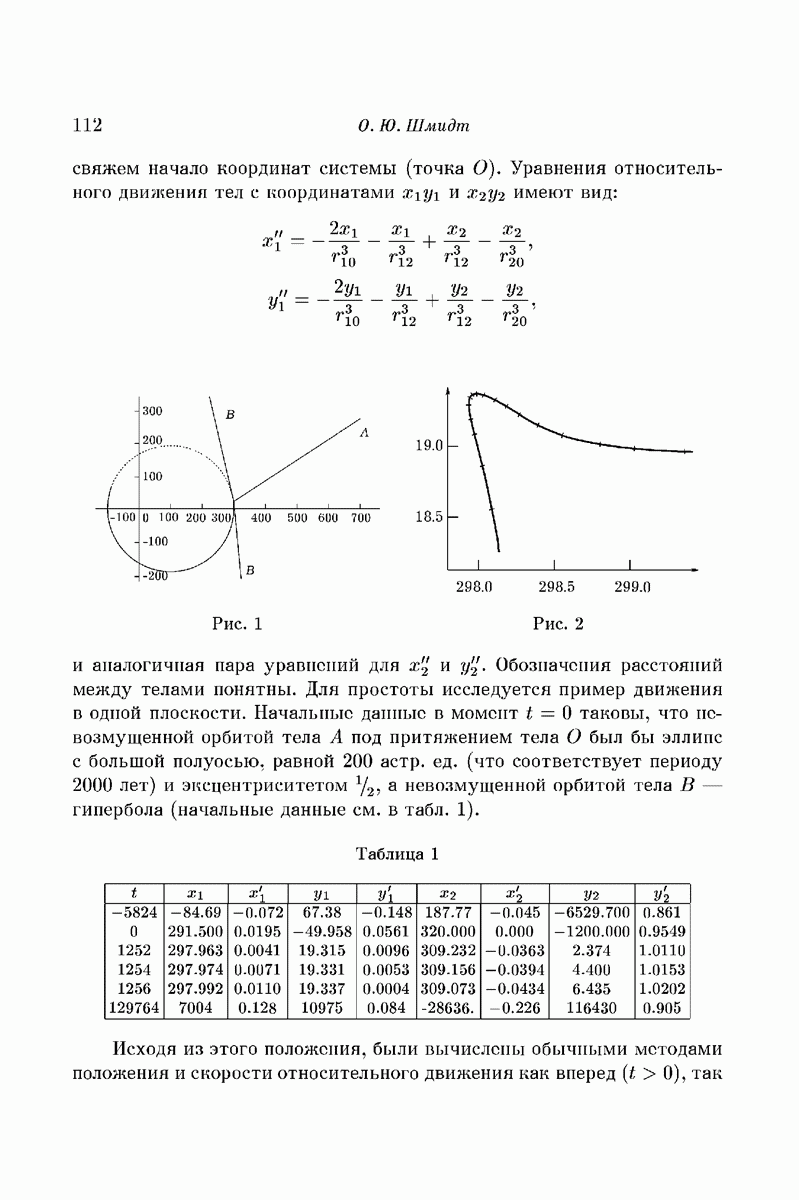
Рассмотрим простейшую псиптегрируемую динамическую систему, а именно: одномерный осциллятор в периодически меняющемся потенциальном поле. Эта система описывается дифференциальным уравнением

где периодически зависит от t. Выбор предположений, касающихся зависимости Q от определился несколькими соображениями. С одной стороны, эти предположения должны быть настолько общими, чтобы отчетливо проявилась суть изучаемого явления. С другой стороны, хотелось, чтобы рассматриваемый класс включал уравнение, описывающее движение в одном частном случае задачи трех тел. Наконец, в-третьих, некоторые предположения, в частности выбор профиля потенциала в виде симметричной «ямы», просто облегчают вычисления, которые, впрочем, остаются достаточно громоздкими. Подробно эти вычисления проведены в [59] и [63] (см. также [62]).

Нашей конечной целью является построение семейства решений уравнения (1), исследование которого можно проводить методами символической динамики. Поскольку, однако, в предыдущей части речь шла лишь об отображениях, первым нашим шагом должно быть построение секущей поверхности в смысле Пуанкаре и соответствующего отображения (функции последования) S. При этом используются лишь самые общие свойства функции Q, сформулированные ниже как «основные предположения». При выполнении еще и дополнительных предположений для отображения S удается построить инвариантное множество достаточно сложной структуры, на котором действие S изоморфно «топологической марковской цепи». Переходя обратно от отображения S

к фазовому потоку, мы получаем искомое «квазислучайное» семейство траекторий. Стандартные приемы символической динамики позволяют теперь построить решения уравнения (1) с весьма разнообразным поведением.

Итак, рассмотрим движение материальной точки (частицы) в поле с периодически меняющимся потенциалом U(х, t), график которого имеет вид симметричной потенциальной ямы (рис. 20). Предположим, что сила, действующая на частицу, всегда направлена к точке и вдали от этой точки убывает с расстоянием.

Рис. 20

Последнее означает, что при больших график U как функции от вогнут вниз. Профиль потенциальной ямы, как уже было сказано, периодически пульсирует, но качественный его характер остается одним и тем же. Предполагается также, что пульсации затухают при , причем значительно быстрее, чем убывает величина силы. Точные формулировки соответствующих предположений будут выражены для удобства в терминах функции (силы), а не (потенциала).

Основные предположения

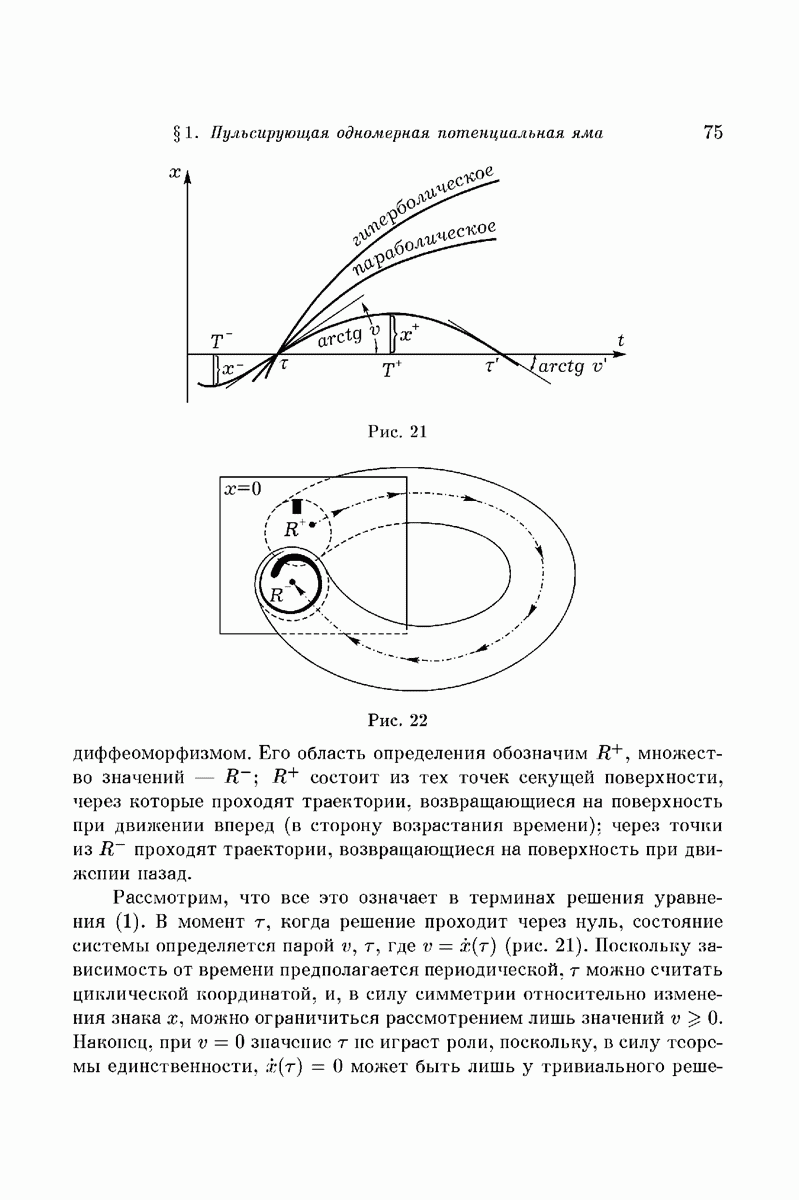
В силу А и Б график решения x(t) уравнения (1) как функции от t вогнут вниз при и вверх при (рис. 21). Поэтому каждое решение уравнения (1) имеет хотя бы один нуль, а следовательно, каждая траектория фазового потока рассматриваемой задачи пересекает хотя бы один раз поверхность . Ее мы и возьмем в качестве секущей.

Для построения функций последования нужно, чтобы траектории пересекали секущую поверхность не менее двух раз (рис. 22). Без дополнительных предположений относительно Q этим свойством обладают, вообще говоря, не все траектории, а потому функция последования определена не на всей секущей поверхности и является лишь локальным

Рис. 21

Рис. 22

диффеоморфизмом. Его область определения обозначим множество значений — состоит из тех точек секущей поверхности, через которые проходят траектории, возвращающиеся на поверхность при движении вперед (в сторону возрастания времени); через точки из проходят траектории, возвращающиеся на поверхность при движении назад.

Рассмотрим, что все это означает в терминах решения уравнения (1). В момент , когда решение проходит через нуль, состояние системы определяется парой , где (рис. 21). Поскольку зависимость от времени предполагается периодической, можно считать циклической координатой, и, в силу симметрии относительно изменения знака можно ограничиться рассмотрением лишь значений . Наконец, при значение играет роли, поскольку, в силу теоремы единственности, может быть лишь у тривиального решения

(напомним, что в силу нечетности ) Это позволяет считать полярными координатами на некоторой плоскости Ф. (Более аккуратно следовало бы описать Ф как фактор-пространство, получаемое из секущей поверхности при помощи некоторых отождествлений, учитывающих указанные симметрии уравнения; подробнее мы на этом не останавливаемся.)

Заданием u, t решение определяется однозначно (рис. 21). Посмотрим, что может произойти с нетривиальным решением при . В силу вогнутости в области скорость монотонно убывает. Поэтому возможны два случая. Если при всех , то существует предел

Можно доказать (используя только А и Б), что в этом случае при даже если . Если , то решение называется гиперболическим, если — параболическим. Аналогия с небесной механикой (см. часть 1) очевидна.

Если же наступит момент, когда обратится в нуль (ближайший к такой момент на ) мы обозначим далее символом то возрастание решения сменяется убыванием и оно возвращается к значению в некоторый момент (снова так мы обозначаем ближайший к момент на ), когда (рис. 21). В фазовом пространстве соответствующая траектория возвращается на секущую поверхность (рис. 22), и, следовательно, можно определить функцию последования S равенством , где (знак минус появился в силу соглашения: рассматривать лишь значения ).

При все рассуждения повторяются: решение может опять оказаться гиперболическим или параболическим или же вернется к пулю в некоторый момент . В последнем случае на паре определено отображение где и т.д. При подходящих начальных условиях решение может иметь бесконечное число нулей, и стало быть, определены все степени отображения S. Стандартным в теории дифференциальных уравнений рассуждением, основанным на теореме единственности, можно убедиться в том, что пули решения не могут иметь точки накопления.

Таким образом, при выполнении условий А и Б решения уравнения (1) следующим образом классифицируются по их поведению при .

1) 0. Тривиальное решение .

2) Колеблющиеся решения, имеющие при бесконечно много нулей. В свою очередь они подразделяются на:

3) П. Параболические решения.

4) Н. Гиперболические решения. Если фиксирован момент обращения решения в пуль, то гиперболические и параболические решения можно еще подразделить по числу их нулей при Соответствующие классы обозначаются далее ( число нулей).

Аналогичную классификацию можно провести и при . Соответствующие классы обозначаются теми же буквами, только с добавлением индекса минус: и т.п.

В стационарном случае, когда сила Q и потенциал не зависят от времени, уравнение (1) интегрируется в квадратурах. При этом имеет место закон сохранения энергии

(3)

и поведение решений определяется величиной константы h. Если , то решение будет периодическим и, следовательно, принадлежит классам . Если же , то решение монотонно, имеет ровно один нуль и стремится к бесконечности при . При решение гиперболично и принадлежит при — параболично и принадлежит Поэтому приходится рассматривать отдельно два существенно различных случая в соответствии с тем, конечна или бесконечна величина . Обратим особое внимание на то, что поведение решений при одно и то же.

Естественно предположить, что свойства решений нестационарного уравнения (1) будут в какой-то степени аналогичны свойствам решений усредненного уравнения

В соответствии со сказанным выше мы будем различать два случая.

а) Потенциальная яма бесконечной глубины

В этом случае все нетривиальные решения усредненного уравнения (4) периодичны.

б) Потенциальная яма конечной глубины. В этом случае уравнение (4) имеет также гиперболические и параболические решения.

Если отвлечься от идей символической динамики, то наши результаты, касающиеся уравнения (1), относятся, с одной стороны, к поведению его решений при , а с другой — к тому, в каких комбинациях могут сочетаться типы поведения при , т.е. к аналогу проблем эволюции в небесной механике. Эти результаты получены при условии, что функция Q, кроме основных предположений АВ, удовлетворяет еще ряду дополнительных предположений. Говоря коротко, одностороннее поведение решений уравнения (1) оказывается аналогичным поведению решений усредненного уравнения (4), а двустороннее — нет; в то время как у уравнения (4) тип решения при и при один и тот же, у уравнения (1) эти типы могут сочетаться произвольно.

Технические предположения (последняя только в случае ) непрерывны для всех х и t.

Д. Существует интегрируемая функция , такая, что для всех и всех ,

Е. Отношение

Для стационарного уравнения, а следовательно, и для усредненного уравнения (4) справедлив закон сохранения энергии (3). В нестационарном случае энергия не сохраняется, но все же удается сконструировать «эпергоподобпую» величину , которая позволяет классифицировать решения так же, как это делается с помощью константы энергии в стационарном случае. Энергия частицы складывается из кинетической и потенциальной; это обстоятельство послужит нам наводящим соображением. А именно: у решения, возвращающегося к нулю (т.е. такого, что ) , скорость обращается в нуль в момент (рис. 21) и энергия в этот момент сводится лишь к потенциальному члену , где — максимальное значение, достигнутое решением в точке поворота. Если же решение гиперболично или параболично (т. е. ), то потенциальный член стремится к константе и энергия равна . Основываясь на этом, определим функцию

Лемма. Функция конечна и непрерывна во всей плоскости Ф, непрерывно дифференцируема в имеет единственный минимум в точке 0, а ее линии уровня диффеоморфны окружностям.

Аналогично определяется функция , связанная с поведением решения при . В стационарном случае, очевидно, имеет место равенство , но для произвольного

уравнения (1) функции и h не обязаны совпадать, что является чрезвычайно важным обстоятельством.

Следствие. Если , то все нетривиальные решения уравнения (1) колеблющиеся. Если , то множества Н и открыты и являются соответственно внешней и внутренней областями, ограниченными гладкими жордановыми кривыми .

Рис. 23

Все это сразу следует из леммы и определения функций h. В частности, . В следующем параграфе будет доказано, что области имеют одинаковую площадь. А так как обе они содержат точку 0, то ограничивающие их кривые не могут лежать одна в другой и, значит, пересекаются (рис. 23). Определение. При выполнении предположений АЕ уравнение (1) называется типичным:

в случае когда хотя бы в одной своей общей точке кривые имеют различные касательные;

в случае когда уравнение имеет хотя бы один простой корень.

(Существование корней у этого уравнения очевидно, ибо функция — периодическая с нулевым средним.)

Теорема 1. Если выполняются предположения и уравнение (1) типично, то:

1) Существует такое N, что для каждого уравнение (1) имеет решение периода (антипериода ).

2) Если при (в частности, всегда при ), то реализуются все логически возможные комбинации типов поведения нетривиальных решений при причем для каждой комбинации, кроме для соответствующее множество начальных условий имеет мощность континуума (в частности, существуют колеблющиеся решения, не ограниченные при или при или в обоих случаях). Все множества , так что по крайней мере счетно (это относится к ).

3) В случае решения, стремящиеся в обе стороны к бесконечности, могут иметь любое количество нулей. Множество начальных условий, отвечающих гиперболическим в обе стороны решениям, открыто. Множество начальных условий, отвечающих решениям, колеблющимся в одну сторону и стремящимся к бесконечности в другую, хотя и не пусто, но имеет лебегову меру нуль.

Заметим, что если Q достаточно гладко, мало, то, согласно теории Колмогорова-Арнольда-Мозера, множество ограниченных колеблющихся решений будет не только не пусто, но и содержит внутренние точки.

Как уже отмечалось, предположения АЕ выбирались так, чтобы развиваемая теория была применима к одному частному случаю задачи трех тел, который будет рассмотрен в § 3. Однако можно поставить целый ряд вопросов, остающихся пока открытыми, но несомненно представляющих интерес и с точки зрения общей теории нелинейных колебаний.

1) Можно ли ослабить предположения так, чтобы утверждение приведенного выше следствия все еще было справедливым? Тот же вопрос можно сформулировать раздельно для случаев . Какую роль во всем этом играет предположение В?

2) При каком минимальном условии на Q уравнение (1) все еще имеет счетное число субгармоник? Можно ли при этом отбросить или ослабить предположение В? То же относительно предположений ?

3) Можно ли в формулировке теоремы ослабить или отбросить условие

4) Являются ли области В звездными относительно точки при ? Ясно, что из положительного ответа на второй вопрос следует и положительный ответ на первый. Отрицательный ответ на первый вопрос был бы физически парадоксален, т. к. при этом с увеличением начальной скорости гиперболическое движение сменялось бы возвращающимся к нулю.

5) Если Q имеет большую гладкость, чем это предусмотрено в D, то будут ли более гладкими кривые ? То же в случае аналитичности ?

6) Образуют ли типичные уравнения открытое всюду плотное (в подходящей топологии) множество среди всех уравнений (1)?

7) Что можно сказать о мере множества неограниченных колеблющихся решений? То же о мере множества колеблющихся ограниченных решений для произвольного Q (а не только близкого к стационарному)?