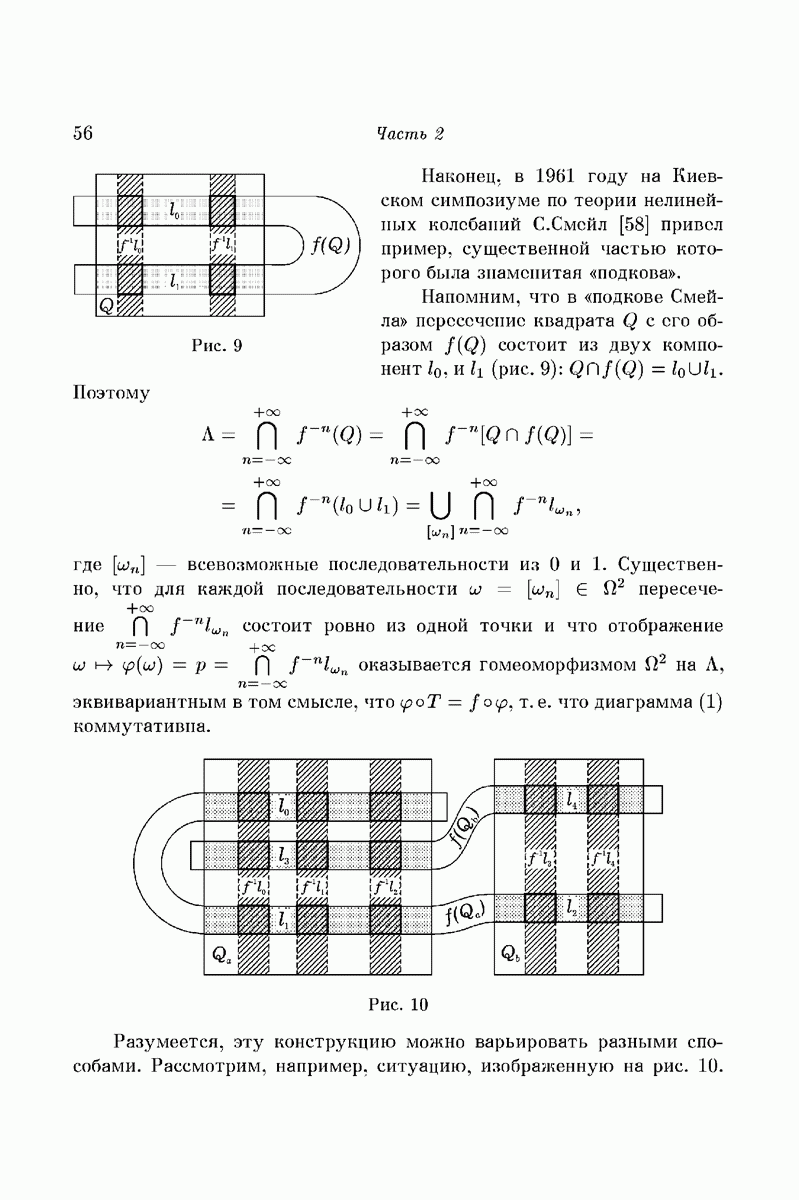
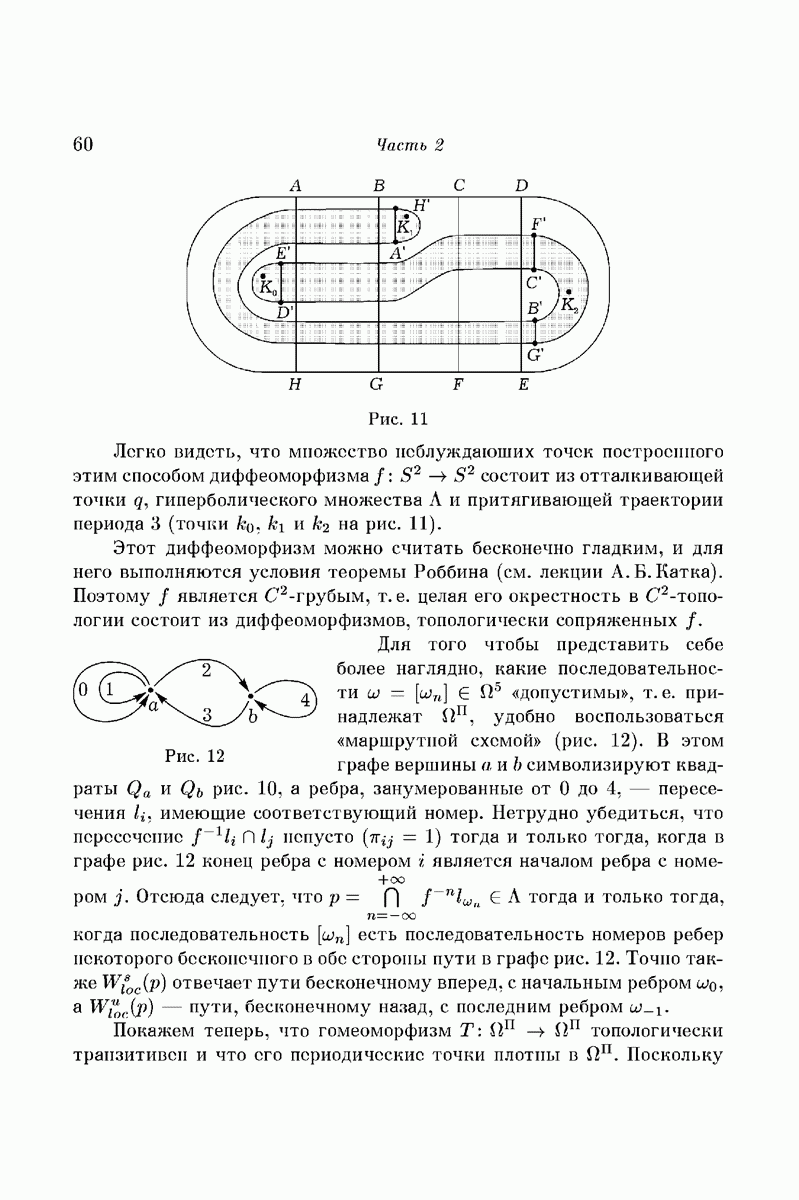
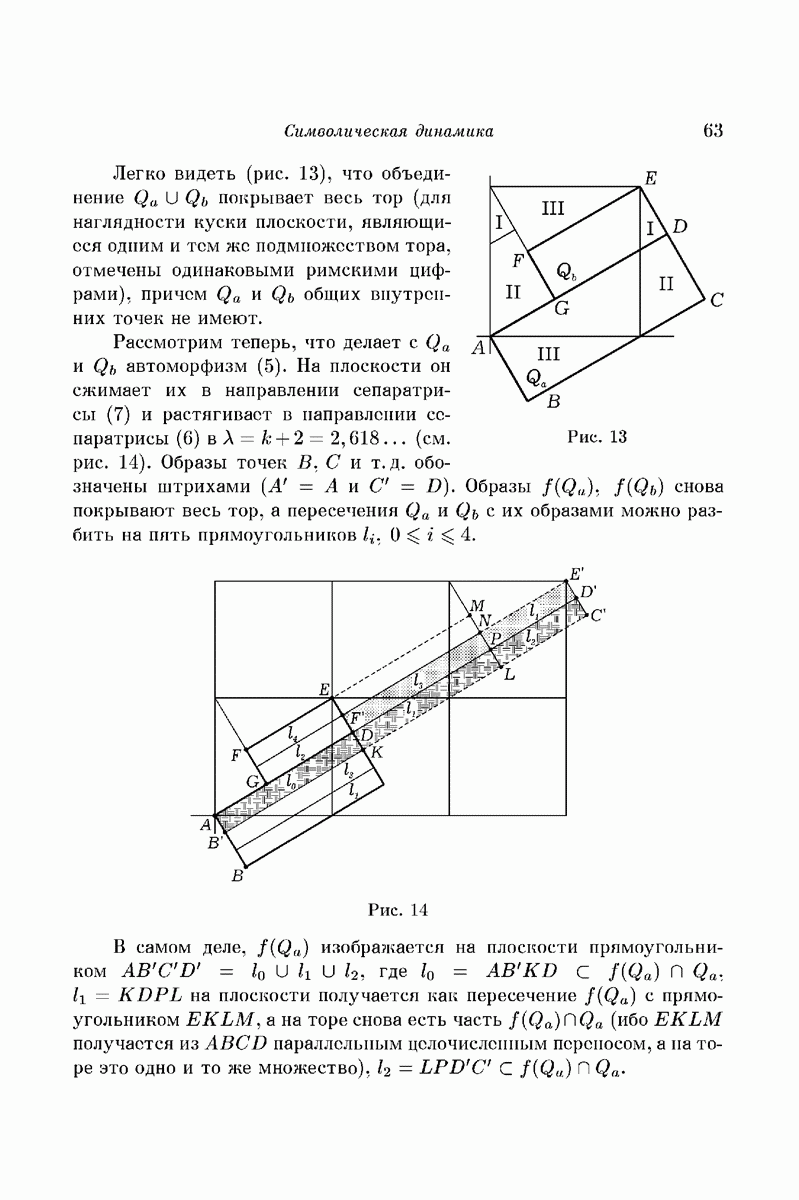
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Существование осциллирующих движений в задаче трех тел
К. Ситников
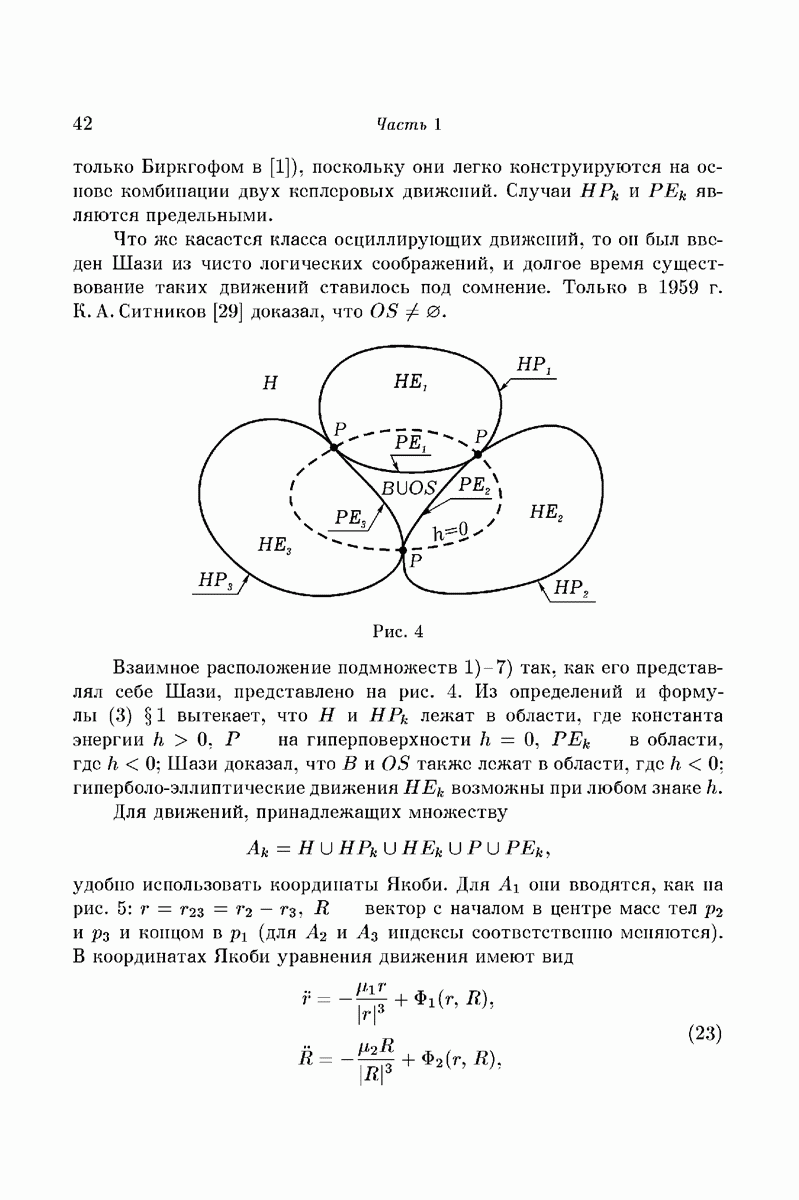
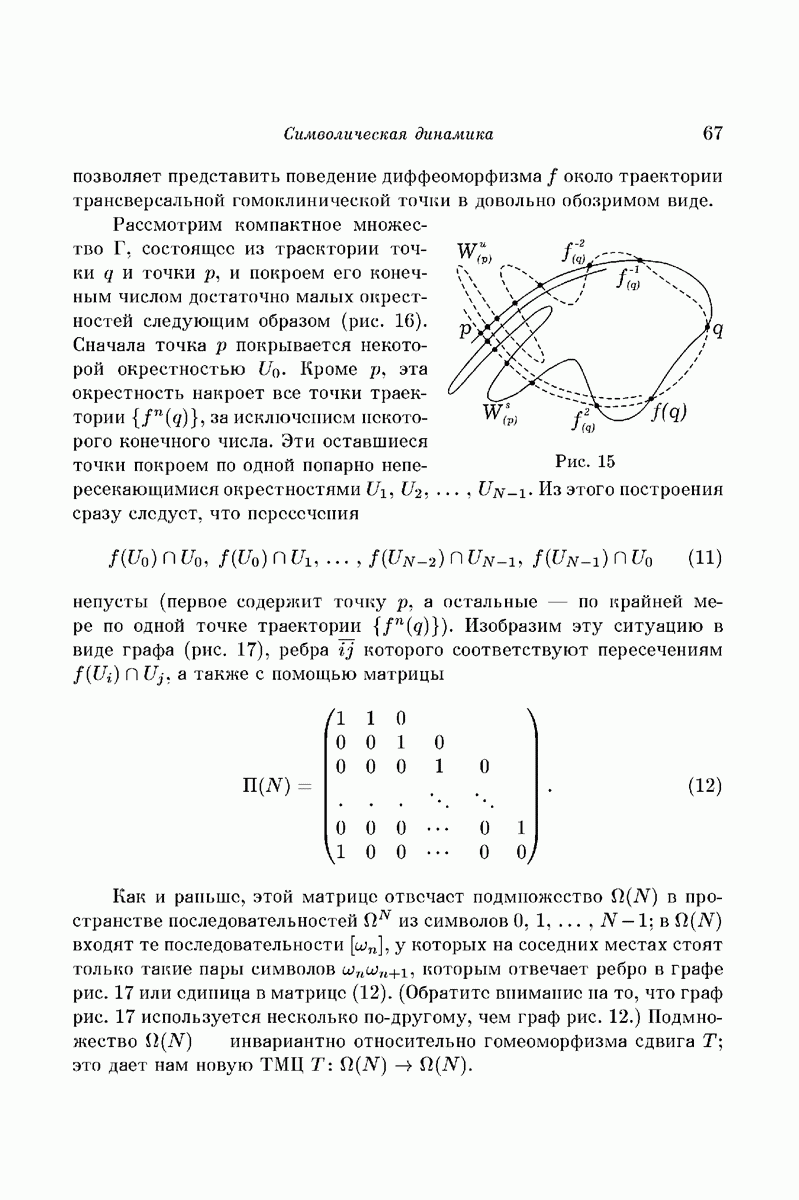
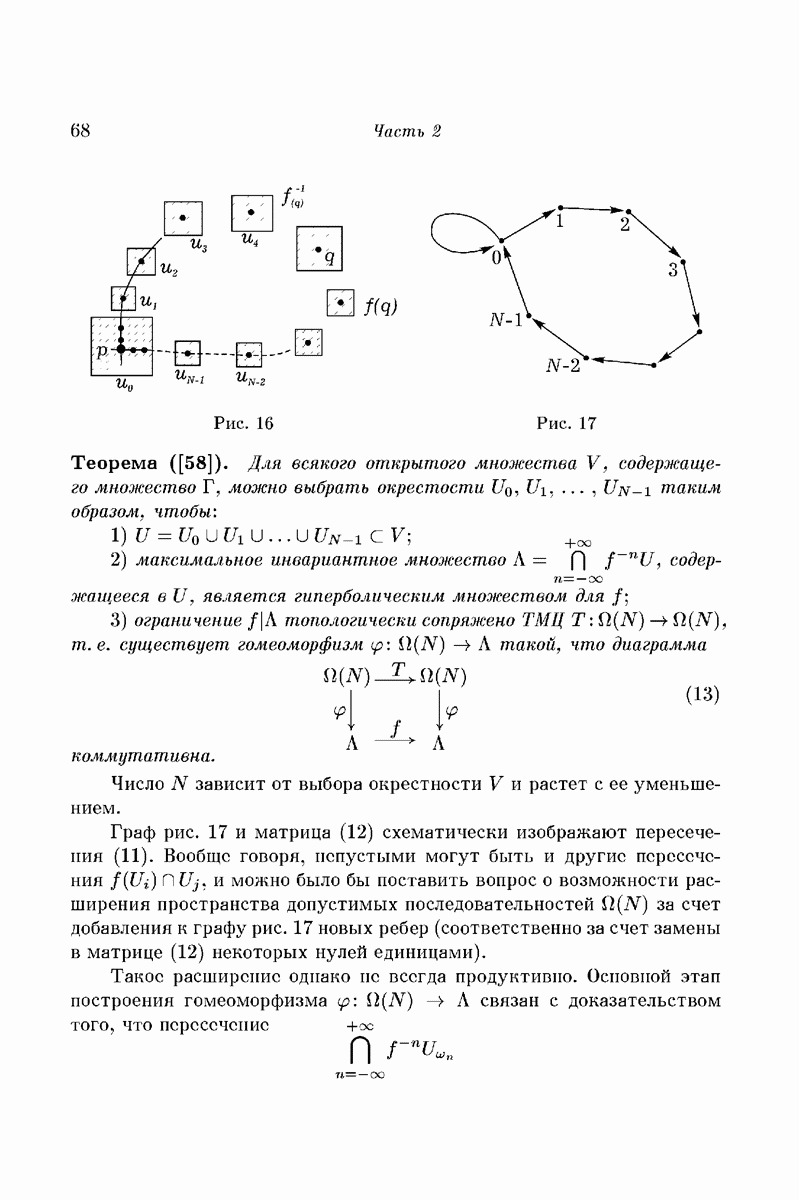
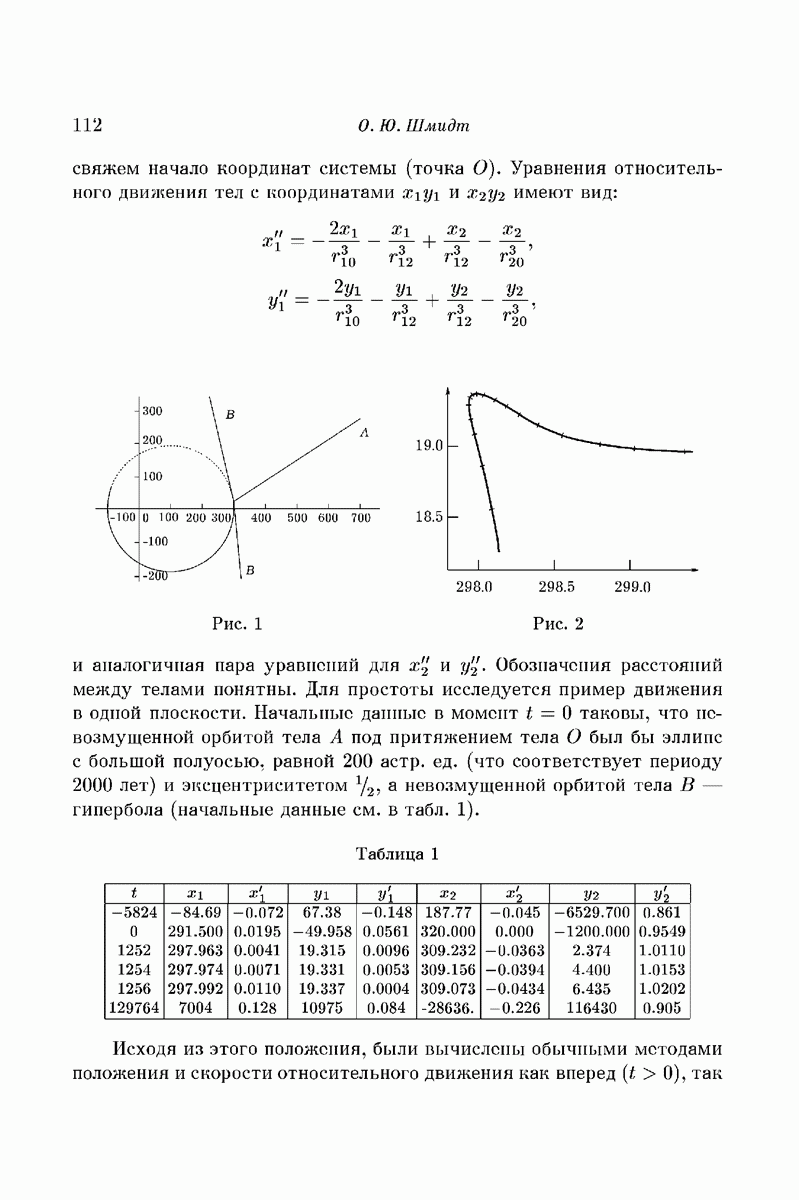
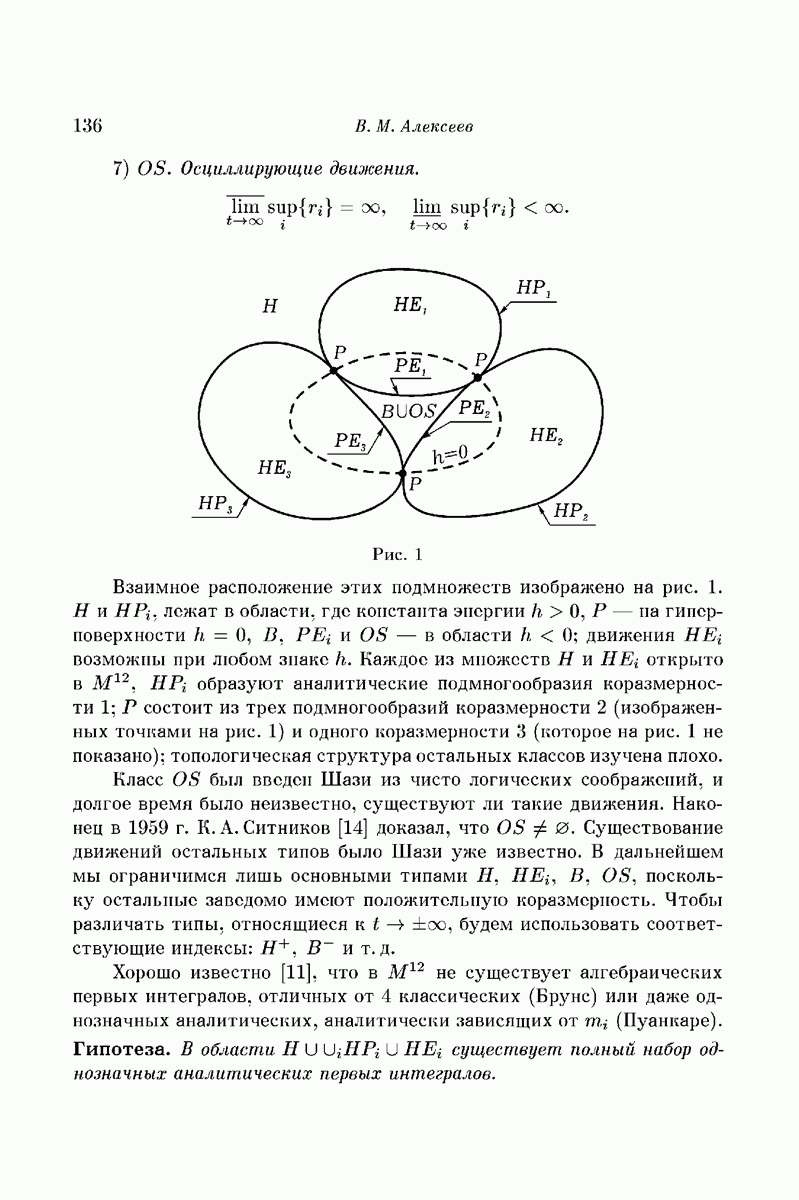
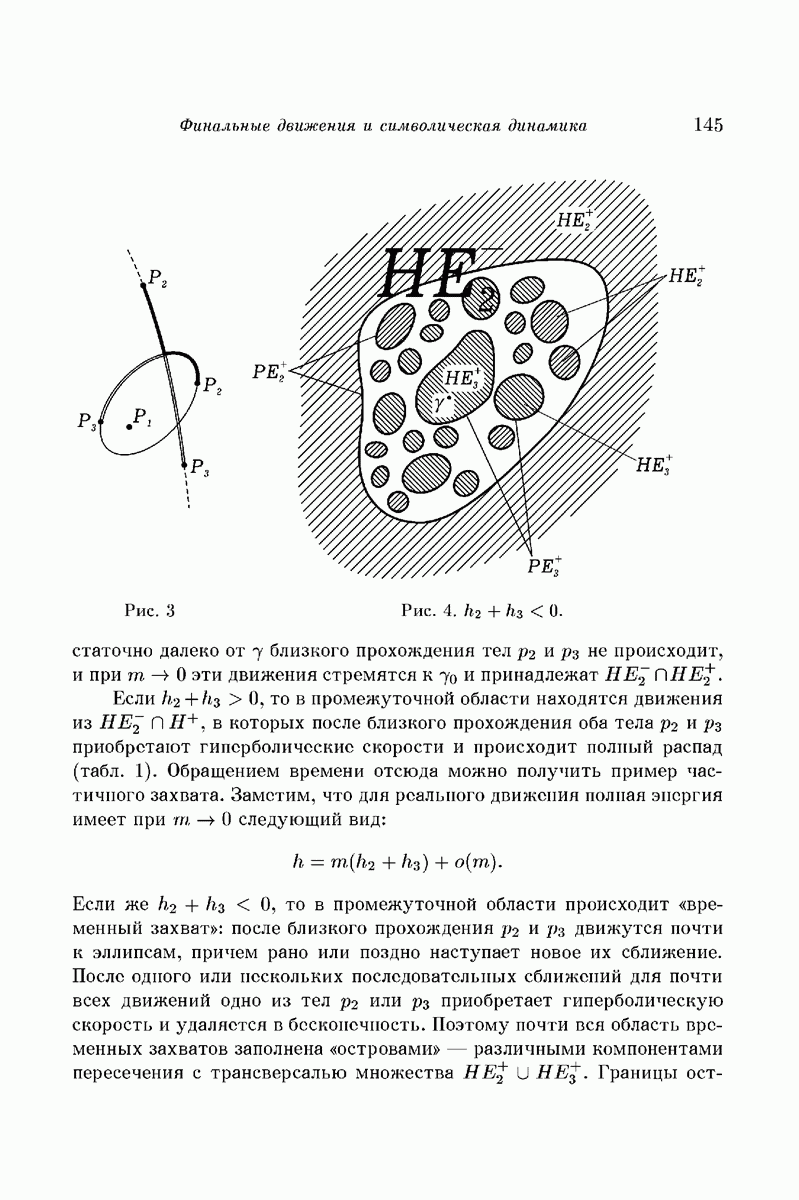
В этой работе строится система трех тел, движущихся под действием сил взаимного ньютоновского тяготения, в которой имеет место явление осцилляции, т.е. при  расстояние между телами (1) и (2) ограничено, а расстояния между каждым из них и телом (3) не ограничено и не стремится к бесконечности. Этот вопрос был поставлен теоремами Лагранжа и Пуассона об инвариантности больших осей в надлежащих приближениях [1, 2]. Вначале мы построим такую систему в ограниченной задаче трех тел, когда тело (3) имеет бесконечно малую массу, а затем перейдем к конечной произвольно малой массе тела (3).
расстояние между телами (1) и (2) ограничено, а расстояния между каждым из них и телом (3) не ограничено и не стремится к бесконечности. Этот вопрос был поставлен теоремами Лагранжа и Пуассона об инвариантности больших осей в надлежащих приближениях [1, 2]. Вначале мы построим такую систему в ограниченной задаче трех тел, когда тело (3) имеет бесконечно малую массу, а затем перейдем к конечной произвольно малой массе тела (3).
Пусть имеется в пространстве инерциальная прямоугольная система координат OXYZ. Возьмем систему двух тел (1) и (2) одинаковой произвольной массы М, центр тяжести которых все время находится в начале координат О и которые движутся под действием сил взаимного тяготения по эллипсам, лежащим в плоскости OXY, большие оси и эксцентриситеты которых равны произвольным R и  Состояние этой системы определяется углом
Состояние этой системы определяется углом  образуемым радиусом-вектором
образуемым радиусом-вектором  тела (1) с осью X. Определим теперь систему трех тел (1), (2) и (3), зависящую от двух параметров
тела (1) с осью X. Определим теперь систему трех тел (1), (2) и (3), зависящую от двух параметров  следующим образом: зададим при
следующим образом: зададим при  угол
угол  и координаты тела (3) бесконечно малой массы равными
и координаты тела (3) бесконечно малой массы равными  , а компоненты его скорости равными
, а компоненты его скорости равными  . Мы докажем, что для каждого значения
. Мы докажем, что для каждого значения  и любой последовательности чисел
и любой последовательности чисел  (в частности, для любой последовательности, стремящейся к бесконечности) существует такое значение
(в частности, для любой последовательности, стремящейся к бесконечности) существует такое значение  что в системе
что в системе  при t > 0 тело (3) бесконечное число раз проходит через
при t > 0 тело (3) бесконечное число раз проходит через
точку О, удаляясь от нее после к-го прохождения на расстояние, большее  .
.
Легко видеть, что тело (3) при всех t находится на оси Z. Далее, для любого  существует минимальное
существует минимальное  при котором координата
при котором координата  тела (3) при t > 0 монотонно возрастает до плюс бесконечности. Лемма 1. Для любых
тела (3) при t > 0 монотонно возрастает до плюс бесконечности. Лемма 1. Для любых  существует такое положительное
существует такое положительное  при котором тело (3) первый раз возвратится в точку О в момент времени t.
при котором тело (3) первый раз возвратится в точку О в момент времени t.
Вначале мы докажем, что если  достаточно близко к
достаточно близко к  то время первого возвращения будет сколь угодно большим. Действительно, если
то время первого возвращения будет сколь угодно большим. Действительно, если  достаточно близко к то, на основании непрерывной зависимости решения уравнения движения тела (3) от начальных условий, максимальное удаление а тела (3) от точки О будет сколь угодно большим. При движении «вверх» во всех точках отрезка [0, а], величина скорости тела (3) меньше
достаточно близко к то, на основании непрерывной зависимости решения уравнения движения тела (3) от начальных условий, максимальное удаление а тела (3) от точки О будет сколь угодно большим. При движении «вверх» во всех точках отрезка [0, а], величина скорости тела (3) меньше  и поэтому время первого возвращения стремится к бесконечности вместе с
и поэтому время первого возвращения стремится к бесконечности вместе с  .
.
Возьмем теперь такое  при котором время первого возвращения
при котором время первого возвращения  . При изменении начальной скорости тела (3) от 0 до
. При изменении начальной скорости тела (3) от 0 до  время его первого возвращения в точку О будет непрерывно изменяться от 0 до t, и утверждение леммы следует из того, что непрерывная функция принимает все свои промежуточные значения.
время его первого возвращения в точку О будет непрерывно изменяться от 0 до t, и утверждение леммы следует из того, что непрерывная функция принимает все свои промежуточные значения.
Лемма 2. Существует такое число S (зависящее от R и  что: если в системе
что: если в системе  в момент времени
в момент времени  тела (1) и (2) находятся на минимальном расстоянии, а в момент
тела (1) и (2) находятся на минимальном расстоянии, а в момент  на максимальном; если
на максимальном; если  — ближайший к
— ближайший к  из больших моментов, обладающих этим свойством; если отрезок
из больших моментов, обладающих этим свойством; если отрезок  делится точкой О пополам и если при убывании времени от 0 координата
делится точкой О пополам и если при убывании времени от 0 координата  монотонно возрастает больше, чем до S, то при возрастании времени от 0 координата
монотонно возрастает больше, чем до S, то при возрастании времени от 0 координата  монотонно убывает до минус бесконечности.
монотонно убывает до минус бесконечности.
Вначале мы докажем, что если условия леммы выполнены с достаточно большим S, то  . Действительно, ускорение, испытываемое телом (3) в точке z в момент времени
. Действительно, ускорение, испытываемое телом (3) в точке z в момент времени  равное
равное  больше по абсолютной величине, чем при
больше по абсолютной величине, чем при  . Поэтому величина скорости тела (3) в
. Поэтому величина скорости тела (3) в  при достаточно большом S больше
при достаточно большом S больше  . Так как во всех точках отрезка —
. Так как во всех точках отрезка —  скорость тела (3) больше, чем в его
скорость тела (3) больше, чем в его
конце  то время его прохождения меньше
то время его прохождения меньше  . Это время меньше полупериода
. Это время меньше полупериода  обращения тел (1) и (2) по эллипсам, равного, как известно,
обращения тел (1) и (2) по эллипсам, равного, как известно,  и поэтому
и поэтому  .
.
В каждой точке z отрезка  ускорение тела (3) будет по абсолютной величине больше его ускорения в точке —z, так как в первом случае тела (1) и (2) находятся на меньшем расстоянии, чем во втором. Отсюда следует, что
ускорение тела (3) будет по абсолютной величине больше его ускорения в точке —z, так как в первом случае тела (1) и (2) находятся на меньшем расстоянии, чем во втором. Отсюда следует, что  . Будем сравнивать при каждом
. Будем сравнивать при каждом  ускорение
ускорение  тела (3), находящегося в точке
тела (3), находящегося в точке  с ускорением
с ускорением  создаваемым телами (1) и (2) в момент времени
создаваемым телами (1) и (2) в момент времени  в симметричной относительно плоскости OXY точке
в симметричной относительно плоскости OXY точке  Докажем, что
Докажем, что

при t, до которого  монотонно возрастает, а первое неравенство, кроме того, при
монотонно возрастает, а первое неравенство, кроме того, при  где n — целое число. Разность
где n — целое число. Разность  равная
равная

будет при  положительна, так как при этих
положительна, так как при этих  при
при  отрицательна, при
отрицательна, при  отрицательна и при
отрицательна и при  положительна. Для каждого
положительна. Для каждого  соответствующая ему пара радиусов-векторов
соответствующая ему пара радиусов-векторов  встречается по одному разу в каждой из других частей в моменты времени
встречается по одному разу в каждой из других частей в моменты времени  при этом
при этом  Координаты тела (3) в эти моменты равны
Координаты тела (3) в эти моменты равны 
Рассмотрим значения  , где
, где 
Из этих свойств  имеющих место и для следующих периодов, вытекают неравенства (1). Из этих неравенств следует, что
имеющих место и для следующих периодов, вытекают неравенства (1). Из этих неравенств следует, что  при t, до которых
при t, до которых  монотонно возрастает. Допустим противное, и пусть
монотонно возрастает. Допустим противное, и пусть  — первое значение
— первое значение  для которого
для которого  Для каждого
Для каждого  ускорение тела (3) при
ускорение тела (3) при  меньше
меньше  , так как
, так как  и функция
и функция  убывает при
убывает при  даже если бы тело (3) имело большее ускорение, равное
даже если бы тело (3) имело большее ускорение, равное  то, в силу неравенств (1) и в силу того, что
то, в силу неравенств (1) и в силу того, что  равенство
равенство  не могло бы иметь места.
не могло бы иметь места.
Из неравенств (1) следует, что при возрастании времени тело (3) во всех достаточно далеких точках будет иметь скорость, меньшую —а, а потому, если S больше также  то
то  монотонно убывает до минус бесконечности. Лемма 2 доказана.
монотонно убывает до минус бесконечности. Лемма 2 доказана.
Существование осцилляции. Итак, для заданных  требуется найти
требуется найти  Возьмем
Возьмем  и интервал
и интервал  имеющий своим правым концом значение настолько малый, чтобы при каждом
имеющий своим правым концом значение настолько малый, чтобы при каждом  принадлежащем
принадлежащем  тело (3) монотонно удалялось от точки О на расстояние, большее S (см. лемму 2).
тело (3) монотонно удалялось от точки О на расстояние, большее S (см. лемму 2).
Возьмем моменты времени  при которых тела (1) и (2) находятся на минимальном и максимальном расстояниях, настолько большими, чтобы найденные для них по лемме 1 значения
при которых тела (1) и (2) находятся на минимальном и максимальном расстояниях, настолько большими, чтобы найденные для них по лемме 1 значения  принадлежали
принадлежали  . В системе
. В системе  отрезок, пройденный телом (3) за время от
отрезок, пройденный телом (3) за время от  до
до  лежит ниже точки О, а в системе
лежит ниже точки О, а в системе  выше, а так как его положение и длина изменяются непрерывно при изменении
выше, а так как его положение и длина изменяются непрерывно при изменении  то найдется такое
то найдется такое  лежащее между
лежащее между  и что в системе
и что в системе  этот отрезок будет делиться точкой О пополам. Следовательно, по лемме 2, в системе
этот отрезок будет делиться точкой О пополам. Следовательно, по лемме 2, в системе  тело (3) после первого возвращения в точку О монотонно уходит в минус бесконечность. В системе
тело (3) после первого возвращения в точку О монотонно уходит в минус бесконечность. В системе  положения тела (3) в моменты времени
положения тела (3) в моменты времени  будут симметричны относительно плоскости OXY, и поэтому после первого возвращения в точку О тело (3) будет «опускаться» лишь до конечной высоты, равной высоте первого «подъема».
будут симметричны относительно плоскости OXY, и поэтому после первого возвращения в точку О тело (3) будет «опускаться» лишь до конечной высоты, равной высоте первого «подъема».
Изменяя  от
от  до
до  возьмем первое ее значение (О), при котором тело (3) после первого возвращения в точку О монотонно уходит в минус бесконечность, и возьмем настолько малый интервал
возьмем первое ее значение (О), при котором тело (3) после первого возвращения в точку О монотонно уходит в минус бесконечность, и возьмем настолько малый интервал  , имеющий своим концом
, имеющий своим концом  , чтобы при каждом
, чтобы при каждом  принадлежащем
принадлежащем
 , тело (3) после первого возвращения в точку О удалялось от нее лишь на конечное расстояние, но большее S и
, тело (3) после первого возвращения в точку О удалялось от нее лишь на конечное расстояние, но большее S и  из
из  .
.
Аналогичным образом в  находим такое
находим такое  что при значении
что при значении  равном
равном  тело (3) после второго возвращения в точку О монотонно уходит в плюс бесконечность, и такой интервал
тело (3) после второго возвращения в точку О монотонно уходит в плюс бесконечность, и такой интервал  , имеющий своим концом
, имеющий своим концом  что при значениях
что при значениях  принадлежащих
принадлежащих  тело (3) после второго возвращения в точку О удаляется от нее на конечное расстояние, большее
тело (3) после второго возвращения в точку О удаляется от нее на конечное расстояние, большее  и S. При этом
и S. При этом  , т.е.
, т.е.  вместе со своими концами содержится в
вместе со своими концами содержится в  .
.
Продолжая этот процесс дальше, мы получим убывающую последовательность интервалов  причем
причем  обладает тем свойством, что при значениях
обладает тем свойством, что при значениях  принадлежащих
принадлежащих  тело (3) к раз возвращается в точку О, после чего удаляется от нее лишь на конечное расстояние, но большее
тело (3) к раз возвращается в точку О, после чего удаляется от нее лишь на конечное расстояние, но большее  а при значении
а при значении  равном одному из концов
равном одному из концов  тело (3) после
тело (3) после  возвращения уходит в бесконечность. Отсюда следует, что существует
возвращения уходит в бесконечность. Отсюда следует, что существует  принадлежащее всем
принадлежащее всем  которое и будет искомым, т.е. в системе
которое и будет искомым, т.е. в системе  тело (3) будет совершать осцилляции, если
тело (3) будет совершать осцилляции, если 
Случай конечной массы тела (3). Зададим при  положения и скорости тел (1), (2), (3) в иперциальпой системе координат OXYZ такими же, как и в системе
положения и скорости тел (1), (2), (3) в иперциальпой системе координат OXYZ такими же, как и в системе  массы тел (1) и (2) по-прежнему равны М, а масса тела (3) равна то. Получаем систему, зависящую от трех параметров
массы тел (1) и (2) по-прежнему равны М, а масса тела (3) равна то. Получаем систему, зависящую от трех параметров  и то. Мы докажем, что существует такое а, что для любых
и то. Мы докажем, что существует такое а, что для любых  существует такое
существует такое  что в системе
что в системе  то при
то при  тело (3) бесконечное число раз проходит через центр тяжести О тел (1) и (2), удаляясь от него после
тело (3) бесконечное число раз проходит через центр тяжести О тел (1) и (2), удаляясь от него после  прохождения на расстояние, большее
прохождения на расстояние, большее  а расстояние тел (1) и (2) всегда меньше
а расстояние тел (1) и (2) всегда меньше 
Лемма 3. Для любых  существует такое
существует такое  что в любой системе
что в любой системе  то при
то при  для любого значения времени
для любого значения времени  движение тел (1) и (2) при
движение тел (1) и (2) при  отличается меньше чем на
отличается меньше чем на  от движения тел (1) и (2) по некоторым эллипсам с параметрами R и е (равными параметрам «основных» эллипсов) только под действием сил взаимного тяготения (без влияния тела
от движения тел (1) и (2) по некоторым эллипсам с параметрами R и е (равными параметрам «основных» эллипсов) только под действием сил взаимного тяготения (без влияния тела  ).
).
Все время  разбиваем на интервалы произвольной длины Т и на каждом из них аппроксимируем движения тел (1) и (2) в системе
разбиваем на интервалы произвольной длины Т и на каждом из них аппроксимируем движения тел (1) и (2) в системе  то эллиптическими движениями. Выбираем моменты времени
то эллиптическими движениями. Выбираем моменты времени  при которых расстояния тел (1) и (2) минимальны и максимальны
при которых расстояния тел (1) и (2) минимальны и максимальны
в этих аппроксимациях. При этом если  достаточно мало, то при любых
достаточно мало, то при любых  имеем в силу леммы
имеем в силу леммы  где n пробегает все целые числа,
где n пробегает все целые числа,  и е сколь угодно мало.
и е сколь угодно мало.
Схема построения примера осцилляции остается такой же, как в ограниченной задаче. В системе  выбираем достаточно большие
выбираем достаточно большие  . При возрастании
. При возрастании  от 0 время возвращения тела (3) в точку О будет расти до бесконечности, а времена
от 0 время возвращения тела (3) в точку О будет расти до бесконечности, а времена  этих выбранных минимума и максимума изменяются в ограниченных пределах разрывным образом, но величины их скачков сколь угодно малы, если то достаточно мало. Поэтому существуют такие
этих выбранных минимума и максимума изменяются в ограниченных пределах разрывным образом, но величины их скачков сколь угодно малы, если то достаточно мало. Поэтому существуют такие  и при которых времена возвращений будут сколь угодно мало отличаться от соответствующих
и при которых времена возвращений будут сколь угодно мало отличаться от соответствующих  . Построение продолжается дальше, причем лемма 2 для системы
. Построение продолжается дальше, причем лемма 2 для системы  , то, от в предположении, что те достаточно мало, сохраняет свою силу.
, то, от в предположении, что те достаточно мало, сохраняет свою силу.
Литература
[1] J. Chazy. Math, pure et appl, 8, 354 (1929).
[2] H. Poincare. Methodes nouvelles de la mecanique celeste. 3, Paris, 1899. P. 141.
| << Предыдущий параграф | Следующий параграф >> |
- Квазислучайные колебания и качественные вопросы небесной механики
- Часть 1. О некоторых математических проблемах в небесной механике
- § 1. Основная задача небесной механики
- § 2. Геометрическая интерпретация задачи Кеплера
- § 3. Задача трех тел. Аналитические свойства решений
- § 4. Финальные движения в задаче трех тел
- § 5. Эволюция системы. Проблема захвата
- Часть 2. Символическая динамика
- Часть 3. Квазислучайные колебания некоторых нелинейных систем
- § 1. Пульсирующая одномерная потенциальная яма
- § 2. Свойства отображения S
- § 3. Об одном частном случае задачи трех тел
- Литература
- О возможности захвата в небесной механике
- Литература
- О возможности захвата в задаче трех тел
- Обмен и захват в задаче трех тел
- Существование осциллирующих движений в задаче трех тел
- Финальные движения в задаче трех тел и символическая динамика