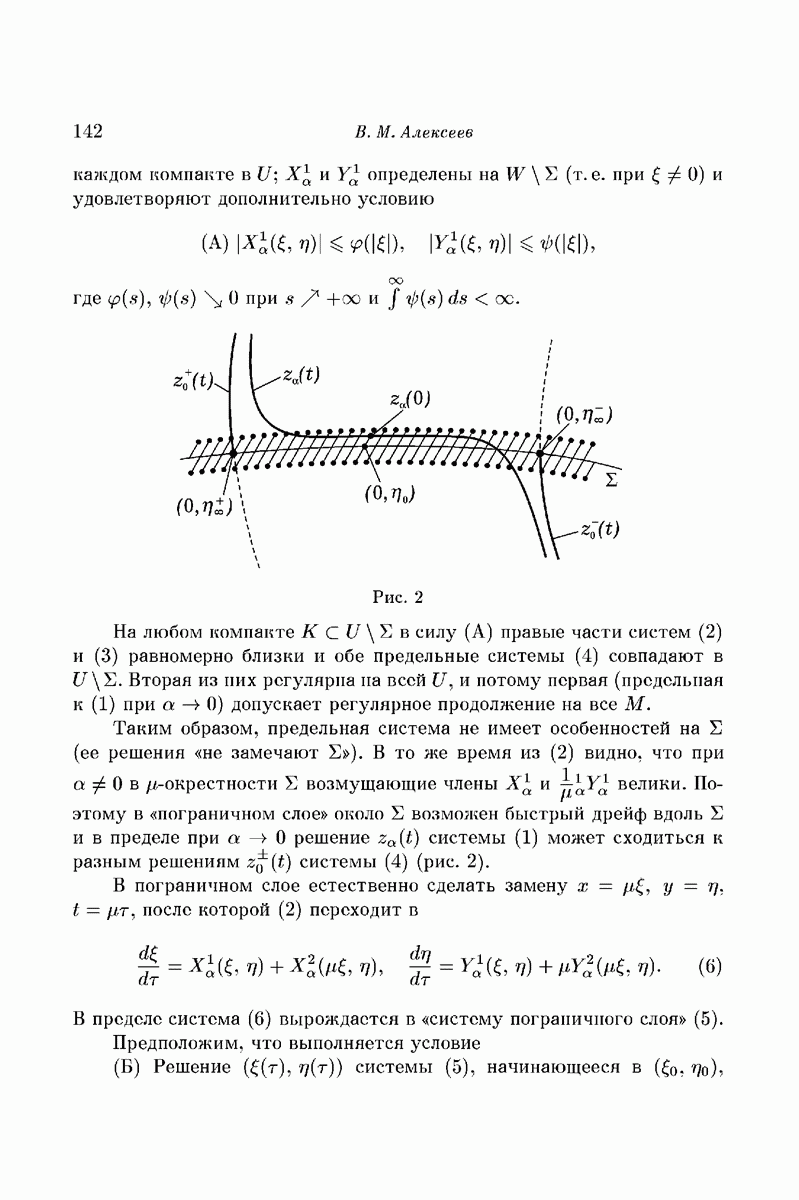
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Часть 2. Символическая динамика
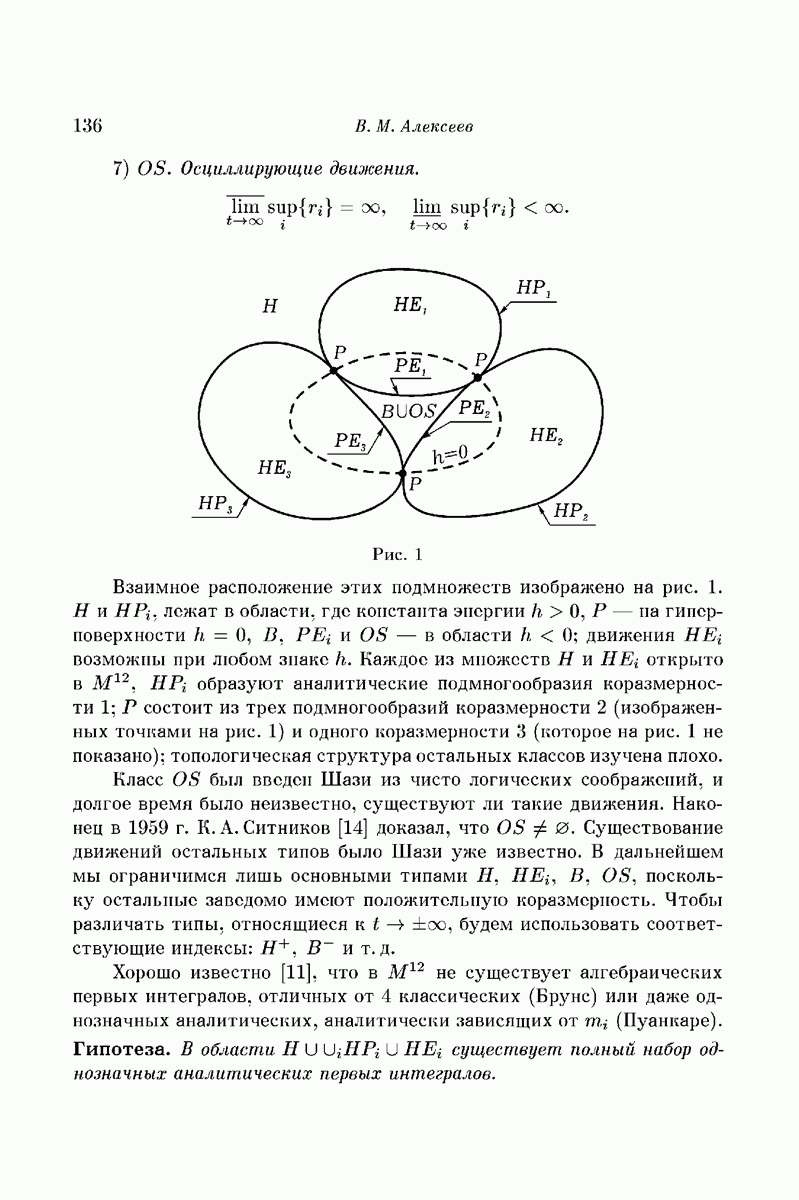
В последние годы в качественной теории дифференциальных уравнений значительное внимание уделяется «неправильно устроенным» объектам, для описания которых классические аналитические средства: асимптотические формулы, ряды теории возмущений и т. п., оказались непригодными. Примером может служить инвариантное множество, связанное с «подковой Смейла», которое было рассмотрено в лекциях А. В. Катка.
Здесь мы имели дело с диффеоморфизмом двумерной сферы  , который, при желании, мог бы быть задан явными формулами и мог бы быть класса
, который, при желании, мог бы быть задан явными формулами и мог бы быть класса  . Максимальное множество А, инвариантное относительно этого диффеоморфизма и содержащееся в квадрате Q, — объект вполне естественно определенный — является произведением двух канторовых множеств (и, стало быть, само гомеоморфно канторову множеству), а действие f на
. Максимальное множество А, инвариантное относительно этого диффеоморфизма и содержащееся в квадрате Q, — объект вполне естественно определенный — является произведением двух канторовых множеств (и, стало быть, само гомеоморфно канторову множеству), а действие f на  топологически сопряжено «преобразованию пекаря». Как мы видели, это действие довольно сложно: в А содержится всюду плотное подмножество Р, состоящее из периодических точек диффеоморфизма
топологически сопряжено «преобразованию пекаря». Как мы видели, это действие довольно сложно: в А содержится всюду плотное подмножество Р, состоящее из периодических точек диффеоморфизма  для любых
для любых  из А найдется счетное подмножество таких точек
из А найдется счетное подмножество таких точек  , что траектория
, что траектория  асимптотичпа при
асимптотичпа при  к траектории
к траектории  , а при
, а при  — к траектории
— к траектории  и т.д. Кроме того, множество А не разложимо, поскольку существуют точки
и т.д. Кроме того, множество А не разложимо, поскольку существуют точки  , траектории которых всюду плотны в
, траектории которых всюду плотны в  .
.
Трудно представить себе, каким образом эту сложную ситуацию можно было бы адекватно описать аналитическими формулами в классическом духе. В то же время действие ограничения  на множестве А полностью определяется тем, что
на множестве А полностью определяется тем, что  топологически сопряжено гомеоморфизму сдвига
топологически сопряжено гомеоморфизму сдвига  в пространстве
в пространстве  бесконечных в обе стороны двоичных последовательностей. Существование гомеоморфизма
бесконечных в обе стороны двоичных последовательностей. Существование гомеоморфизма
 с коммутативной диаграммой
с коммутативной диаграммой

позволяет установить как уже упомянутые свойства диффеоморфизма  так и некоторые другие. Таким образом, последовательность двоичных символов является как бы кодом траектории
так и некоторые другие. Таким образом, последовательность двоичных символов является как бы кодом траектории  точки
точки  изучал коды и сдвиг, мы изучаем с топологической точки зрения действие f на
изучал коды и сдвиг, мы изучаем с топологической точки зрения действие f на  .
.
Кодировка траекторий гладких динамических систем последовательностями натуральных чисел или последовательностями символов некоторого конечного алфавита впервые, по-видимому, была применена для описания глобального поведения геодезических на поверхностях отрицательной кривизны (Ж. Адамар, М. Морс и другие; см., например, [1] гл. 8, § 11). Это послужило толчком для изучения различных свойств гомеоморфизма сдвига в различных подпространствах пространства  р-ичных последовательностей. Весь круг связанных с этим идей и понятий получил название «символической динамики» ([52]). Однако некоторое время после этого отображение
р-ичных последовательностей. Весь круг связанных с этим идей и понятий получил название «символической динамики» ([52]). Однако некоторое время после этого отображение  изучалось главным образом с точки зрения эргодической теории, тем более что оно тесно связано с эргодическими динамическими системами вероятностного происхождения — марковскими цепями и, в частности, со схемой Бернулли. Мы еще вернемся далее к этой связи.
изучалось главным образом с точки зрения эргодической теории, тем более что оно тесно связано с эргодическими динамическими системами вероятностного происхождения — марковскими цепями и, в частности, со схемой Бернулли. Мы еще вернемся далее к этой связи.
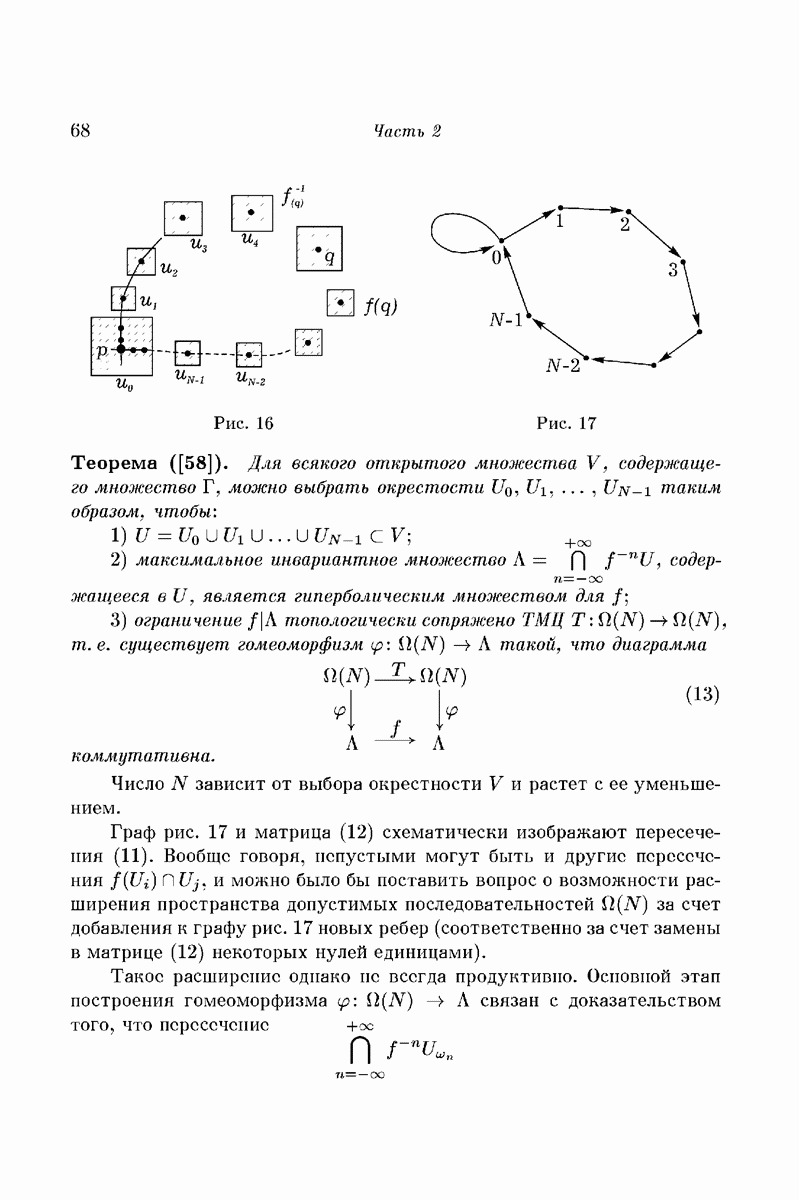
С другой стороны, при изучении колебаний, описываемых уравнением второго порядка

где  — подходящие нелинейности, а возмущающая сила р периодична, Н. Левинсон [53], М. Картрайт и Дж. Литлвуд [54] обнаружили ситуацию, в которой также появлялось естественным образом пространство
— подходящие нелинейности, а возмущающая сила р периодична, Н. Левинсон [53], М. Картрайт и Дж. Литлвуд [54] обнаружили ситуацию, в которой также появлялось естественным образом пространство  . А именно: в рассматривавшихся ими примерах диссипативных систем, описываемых уравнением (2), множество «предельных режимов» содержит подмножество, находящееся во взаимно однозначном соответствии с точками из
. А именно: в рассматривавшихся ими примерах диссипативных систем, описываемых уравнением (2), множество «предельных режимов» содержит подмножество, находящееся во взаимно однозначном соответствии с точками из  (изложение работы Лсвинсопа можно найти также в [55], § 15).
(изложение работы Лсвинсопа можно найти также в [55], § 15).
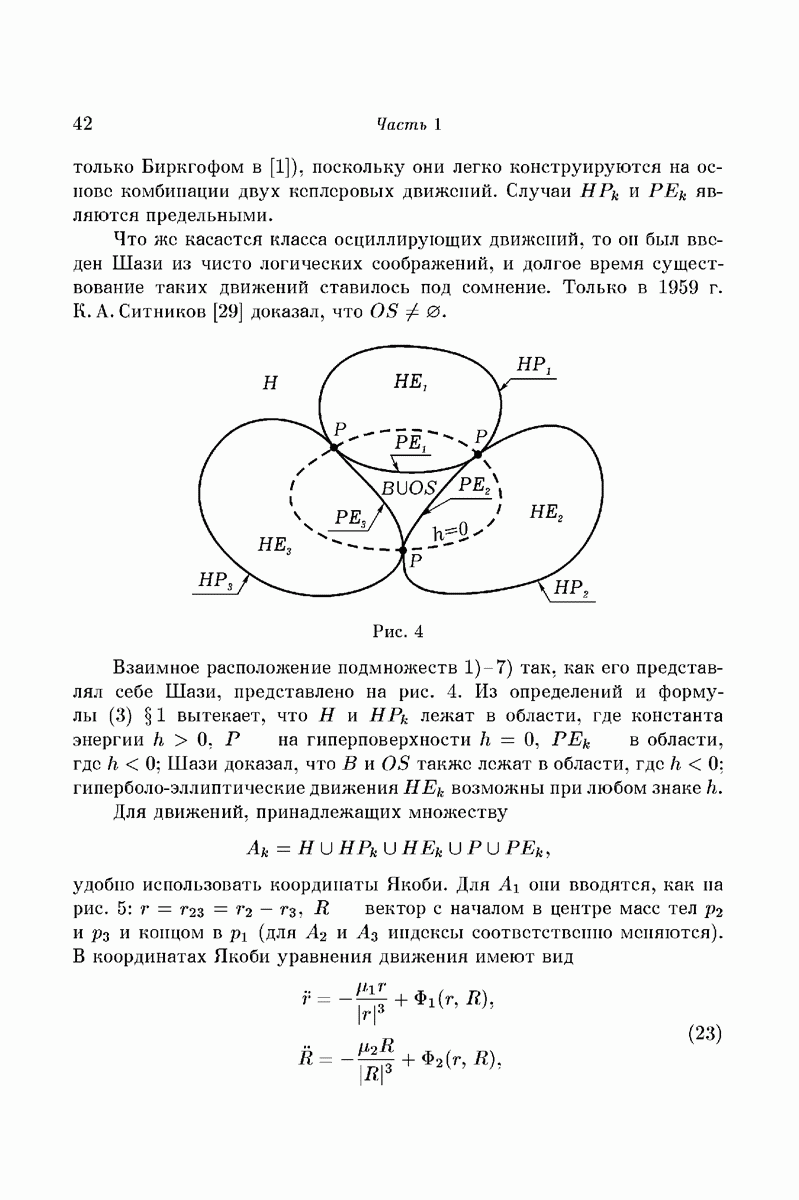
Наконец, в 1961 году на Киевском симпозиуме по теории нелинейных колебаний С. Смейл [58] привел пример, существенной частью которого была знаменитая «подкова».

Рис. 9
Напомним, что в «подкове Смейла» псрсссчспис квадрата Q с его образом  состоит из двух компонент
состоит из двух компонент  . Поэтому
. Поэтому

где  — всевозможные последовательности из 0 и 1. Существенно, что для каждой последовательности
— всевозможные последовательности из 0 и 1. Существенно, что для каждой последовательности  пересечение
пересечение  состоит ровно из одной точки и что отображение
состоит ровно из одной точки и что отображение  оказывается гомеоморфизмом
оказывается гомеоморфизмом  на
на  , эквивариантным в том смысле, что
, эквивариантным в том смысле, что  , т. е. что диаграмма (1) коммутативна.
, т. е. что диаграмма (1) коммутативна.

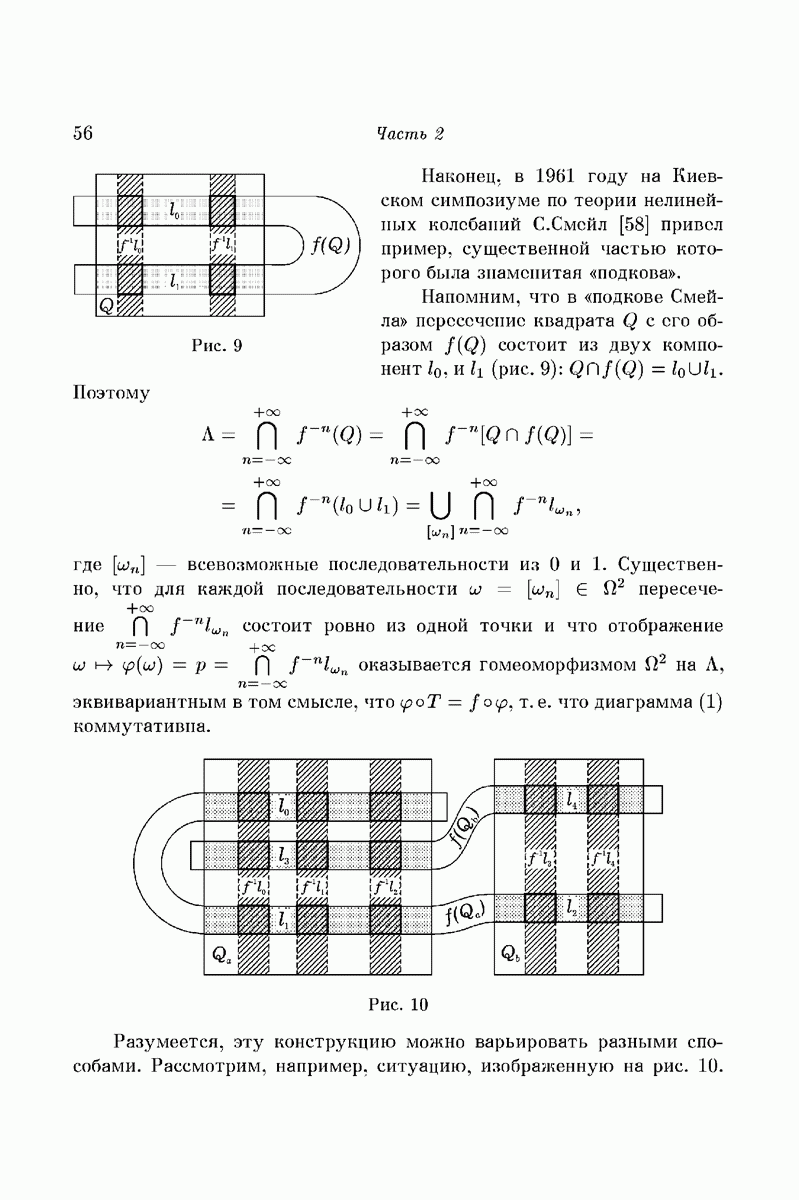
Рис. 10
Разумеется, эту конструкцию можно варьировать разными способами. Рассмотрим, например, ситуацию, изображенную на рис. 10.
Множество Q состоит теперь из двух прямоугольников  , а пересечение
, а пересечение  — из пяти компонент
— из пяти компонент

Как и в случае «подковы», предполагается, что  — прямоугольники, которые надо в дальнейшем представлять себе лежащими в плоскости и со сторонами параллельными оси координат. Прилагательные «горизонтальный» и «вертикальный» относятся именно к такому представлению. Отображения
— прямоугольники, которые надо в дальнейшем представлять себе лежащими в плоскости и со сторонами параллельными оси координат. Прилагательные «горизонтальный» и «вертикальный» относятся именно к такому представлению. Отображения  предполагаются линейными (гиперболическими поворотами), сжимающими в вертикальном и растягивающими в горизонтальном направлениях. Пусть снова
предполагаются линейными (гиперболическими поворотами), сжимающими в вертикальном и растягивающими в горизонтальном направлениях. Пусть снова  — максимальное инвариантное множество, содержащееся в Q. Тогда, как и выше,
— максимальное инвариантное множество, содержащееся в Q. Тогда, как и выше,

но теперь символы  принадлежат алфавиту из пяти букв 0,1,2,3,4. Каждой точке
принадлежат алфавиту из пяти букв 0,1,2,3,4. Каждой точке  можно поставить в соответствие ровно одну последовательность
можно поставить в соответствие ровно одну последовательность  так, что
так, что  . Однако теперь уже не для всякой последовательности
. Однако теперь уже не для всякой последовательности  пересечение
пересечение  . Чтобы убедиться в этом, рассмотрим пересечение
. Чтобы убедиться в этом, рассмотрим пересечение

Множества  содержатся в
содержатся в  и поэтому не пересекаются с
и поэтому не пересекаются с  , которые лежат в
, которые лежат в  . Напротив,
. Напротив,  лежат в
лежат в  и пересекаются с
и пересекаются с  но не с
но не с  .
.
Поэтому в выражении  пересечения
пересечения  будут
будут
непусты не для всех пар  , а лишь для тех, для которых в матрице
, а лишь для тех, для которых в матрице

соответствующие элементы  равны 1. Точно так же доказывается, что если
равны 1. Точно так же доказывается, что если  .
.
Обозначим через  подмножество в пространстве
подмножество в пространстве  состоящее из тех последовательностей
состоящее из тех последовательностей  для которых
для которых  при всех n. Пространство
при всех n. Пространство  может быть наделено тихоновской топологией; в этой топологии окрестность последовательности состоит из всех последовательностей
может быть наделено тихоновской топологией; в этой топологии окрестность последовательности состоит из всех последовательностей  совпадающих с на некотором (фиксированном для данной окрестности) отрезке номеров
совпадающих с на некотором (фиксированном для данной окрестности) отрезке номеров  . Легко видеть, что
. Легко видеть, что

где  только тогда, когда для каждого n начиная с некоторого места (своего для разных
только тогда, когда для каждого n начиная с некоторого места (своего для разных  этой топологии пространство
этой топологии пространство  компактно, а подмножество замкнуто, а потому также компактно;
компактно, а подмножество замкнуто, а потому также компактно;  гомеоморфизм, относительно которого подмножество
гомеоморфизм, относительно которого подмножество  инвариантно.
инвариантно.
По аналогии с теорией вероятностей гомеоморфизм  называется топологической марковской цепыо (ТМЦ), а матрица
называется топологической марковской цепыо (ТМЦ), а матрица  — матрицей допустимых переходов этой цепи.
— матрицей допустимых переходов этой цепи.
Рассуждая так же, как и в случае «подковы», мы установим, что отображение  является гомеоморфизмом между
является гомеоморфизмом между  и
и  . При этом
. При этом

так что гомеоморфизм  эквивариантен и диаграмма
эквивариантен и диаграмма

коммутативна.
Односторонним последовательностям

можно сопоставить пересечения

Первое из них является вертикальным, второе — горизонтальным отрезками, проходящими в Q через точку

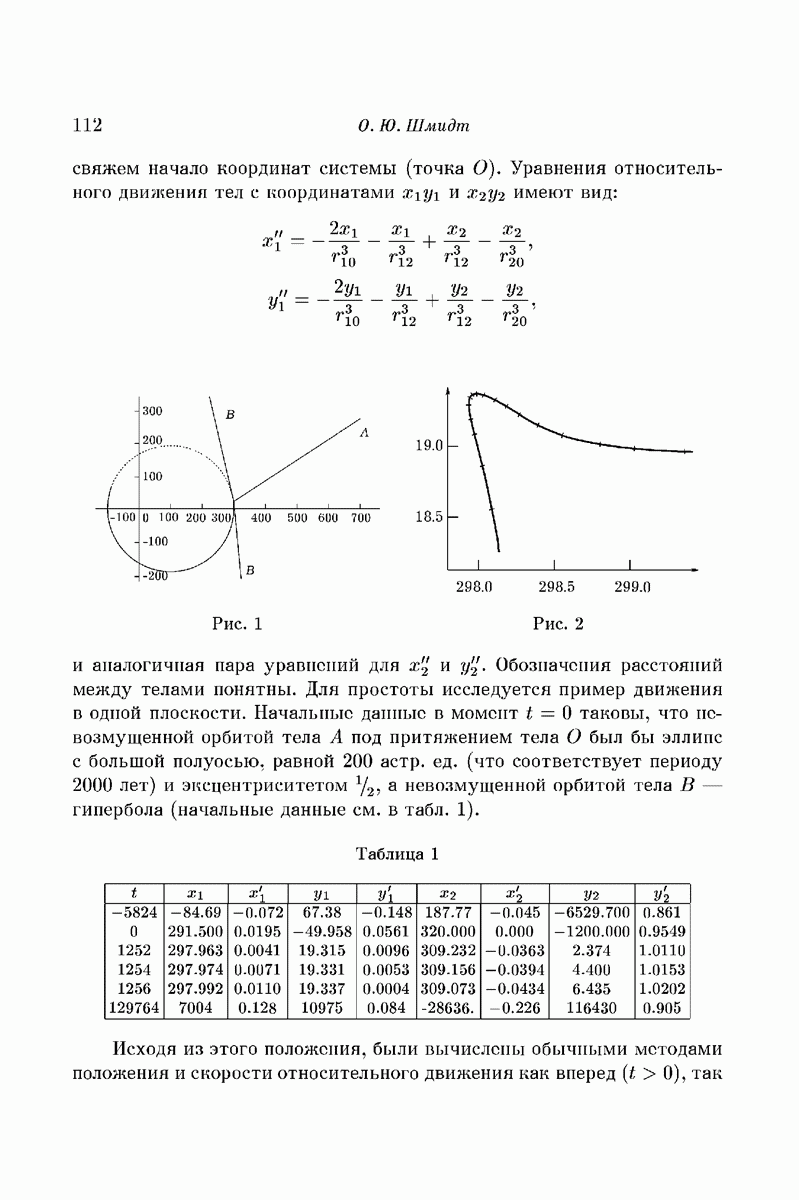
отвечающую полной последовательности  составленной из
составленной из  и
и  . Из определения видно, что и
. Из определения видно, что и  удовлетворяют соотношениям
удовлетворяют соотношениям

Касательные  проведенные в каждой точке
проведенные в каждой точке  , определяют на
, определяют на  (так же, как и в случае «подковы») структуру гиперболического множества (см. лекции А. В. Катка). Сами
(так же, как и в случае «подковы») структуру гиперболического множества (см. лекции А. В. Катка). Сами  и являются локальными кусками листов инвариантных слоений, связанных с гиперболическим множеством
и являются локальными кусками листов инвариантных слоений, связанных с гиперболическим множеством  .
.
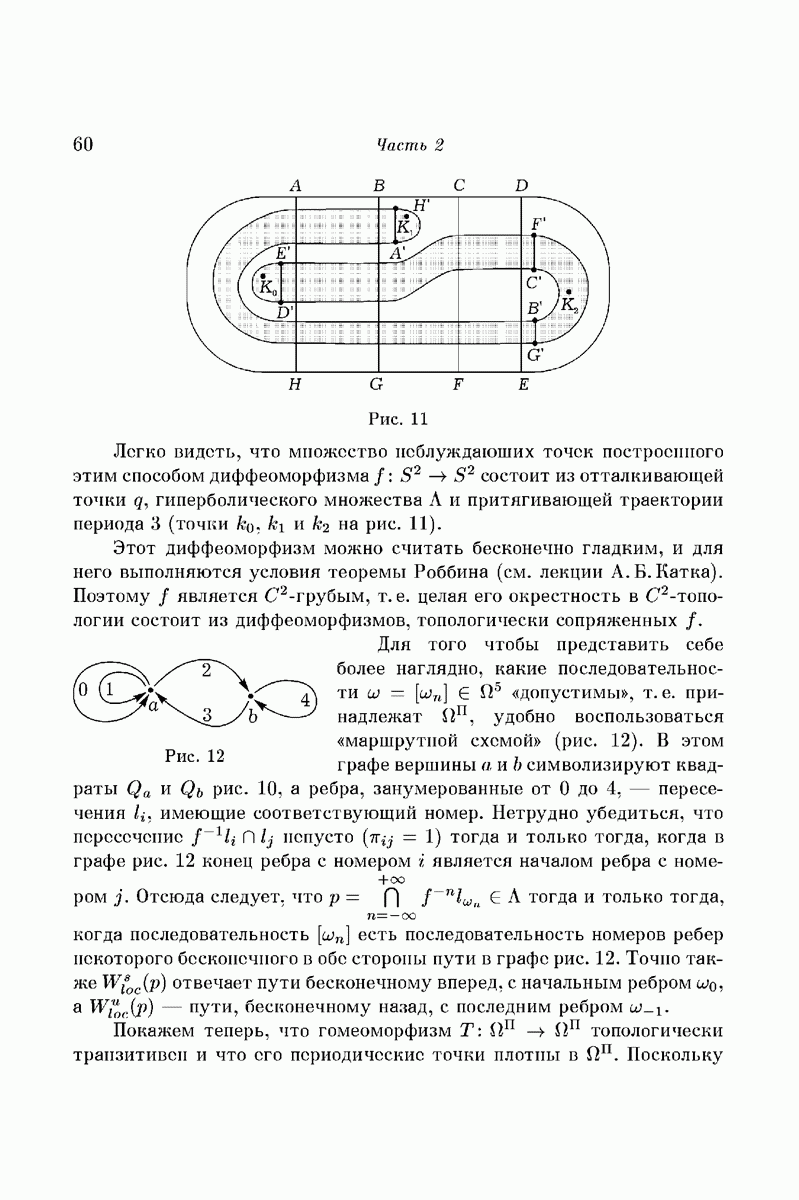
Локальный диффеоморфизм  легко продолжить до глобального диффеоморфизма двумерной сферы. Первый этап соответствующего построения — отображение диска в себя — представлен на рис. 11. Далее можно действовать, как в случае «подковы», и продолжить
легко продолжить до глобального диффеоморфизма двумерной сферы. Первый этап соответствующего построения — отображение диска в себя — представлен на рис. 11. Далее можно действовать, как в случае «подковы», и продолжить  так, чтобы вне диска он имел единственную отталкивающую точку
так, чтобы вне диска он имел единственную отталкивающую точку 

Рис. 11
Легко видеть, что множество нсблуждаюших точек построенного этим способом диффеоморфизма  состоит из отталкивающей точки
состоит из отталкивающей точки  , гиперболического множества
, гиперболического множества  и притягивающей траектории периода
и притягивающей траектории периода  (точки
(точки  на рис. 11).
на рис. 11).
Этот диффеоморфизм можно считать бесконечно гладким, и для него выполняются условия теоремы Роббина (см. лекции А.В. Катка). Поэтому f является  -грубым, т.е. целая его окрестность в
-грубым, т.е. целая его окрестность в  -топологии состоит из диффеоморфизмов, топологически сопряженных
-топологии состоит из диффеоморфизмов, топологически сопряженных  .
.

Рис. 12
Для того чтобы представить себе более наглядно, какие последовательности  «допустимы», т. е. принадлежат удобно воспользоваться «маршрутной схемой» (рис. 12). В этом графе вершины а и b символизируют квадраты
«допустимы», т. е. принадлежат удобно воспользоваться «маршрутной схемой» (рис. 12). В этом графе вершины а и b символизируют квадраты  рис. 10, а ребра, занумерованные от 0 до 4, — пересечения
рис. 10, а ребра, занумерованные от 0 до 4, — пересечения  имеющие соответствующий номер. Нетрудно убедиться, что пересечение
имеющие соответствующий номер. Нетрудно убедиться, что пересечение  непусто
непусто  тогда и только тогда, когда в графе рис. 12 конец ребра с номером
тогда и только тогда, когда в графе рис. 12 конец ребра с номером  является началом ребра с номером j. Отсюда следует, что
является началом ребра с номером j. Отсюда следует, что  тогда и только тогда, когда последовательность
тогда и только тогда, когда последовательность  есть последовательность номеров ребер некоторого бесконечного в обе стороны пути в графе рис. 12. Точно также
есть последовательность номеров ребер некоторого бесконечного в обе стороны пути в графе рис. 12. Точно также  отвечает пути бесконечному вперед, с начальным ребром
отвечает пути бесконечному вперед, с начальным ребром  — пути, бесконечному назад, с последним ребром
— пути, бесконечному назад, с последним ребром  .
.
Покажем теперь, что гомеоморфизм  топологически транзитивен и что его периодические точки плотны в
топологически транзитивен и что его периодические точки плотны в  . Поскольку
. Поскольку
ограничение  на
на  топологически сопряжено
топологически сопряжено  обладает на
обладает на  теми же свойствами.
теми же свойствами.
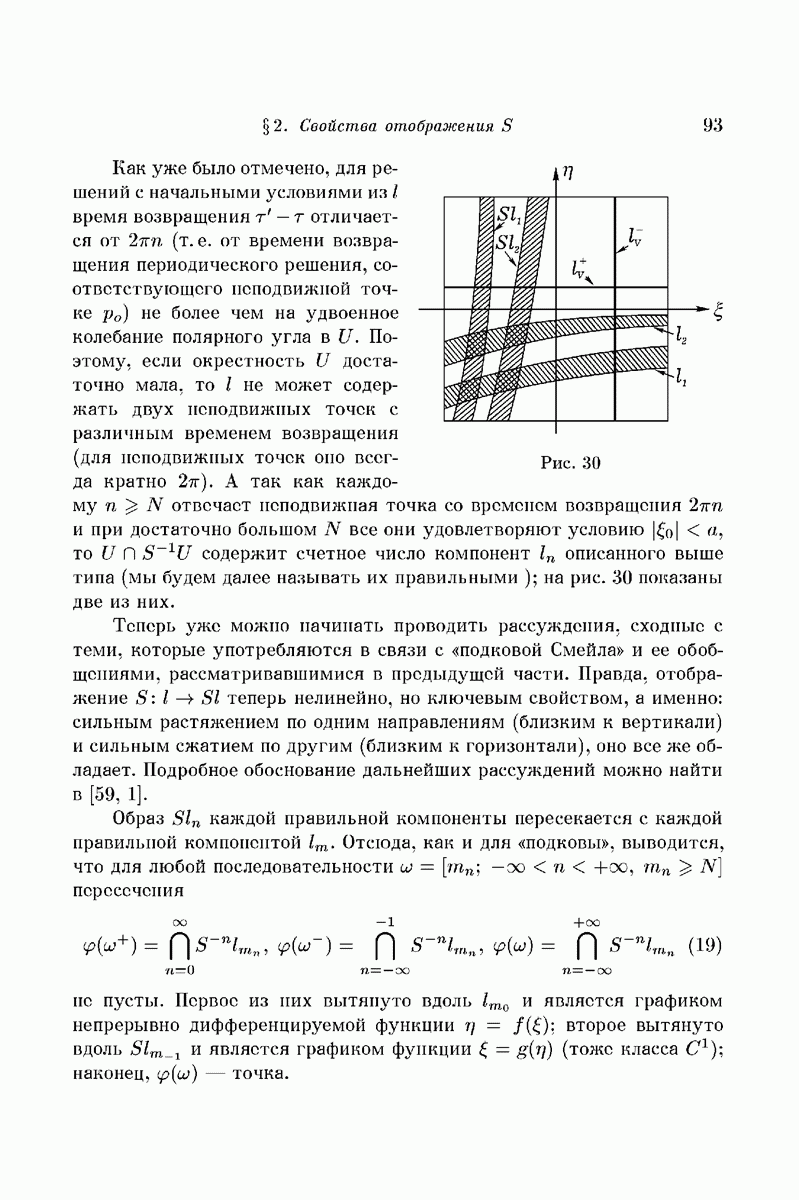
Пусть  произвольная последовательность в
произвольная последовательность в  и U — некоторая ее окрестность, состоящая из всевозможных последовательностей
и U — некоторая ее окрестность, состоящая из всевозможных последовательностей  совпадающих с
совпадающих с  на отрезке номеров
на отрезке номеров  . Пусть этот отрезок в начинается символом
. Пусть этот отрезок в начинается символом  и оканчивается символом
и оканчивается символом  .
.
Рассмотрим граф рис. 12. Очевидно, что для любой пары  и
и  его ребер в этом графе существует путь, в котором V — начальное ребро, а
его ребер в этом графе существует путь, в котором V — начальное ребро, а  — конечное. В частности, существует путь
— конечное. В частности, существует путь  , скажем, состоящий из к ребер, начальное ребро которого имеет номер
, скажем, состоящий из к ребер, начальное ребро которого имеет номер  , а конечное номер
, а конечное номер  . Построим теперь периодическую последовательность
. Построим теперь периодическую последовательность  следующим образом. На отрезке
следующим образом. На отрезке  (иначе
(иначе  не попадет в U). Символы же
не попадет в U). Символы же  возьмем равными номерам ребер, входящих в путь 7. Построенному блоку из —
возьмем равными номерам ребер, входящих в путь 7. Построенному блоку из —  к символов отвечает замкнутый путь в графе. Вся последовательность
к символов отвечает замкнутый путь в графе. Вся последовательность  получается теперь периодическим повторением этого блока.
получается теперь периодическим повторением этого блока.
Таким образом, любая окрестность любой точки  содержит периодическую последовательность из
содержит периодическую последовательность из  и этим доказано, что периодические точки гомеоморфизма Т плотны в
и этим доказано, что периодические точки гомеоморфизма Т плотны в  . Применяя близкие рассуждения, можно построить последовательность
. Применяя близкие рассуждения, можно построить последовательность  , траектория которой и даже только полутраектория
, траектория которой и даже только полутраектория  всюду плотна в
всюду плотна в  .
.
Занумеруем в произвольном порядке всевозможные конечные блоки  , в которых символы от 0 до 4 встречаются в допустимом порядке (т.е. для соседних символов
, в которых символы от 0 до 4 встречаются в допустимом порядке (т.е. для соседних символов  и
и  или соответствующая блоку последовательность ребер в графе рис. 12 образует путь). Пусть блок
или соответствующая блоку последовательность ребер в графе рис. 12 образует путь). Пусть блок  начинается символом и оканчивается символом
начинается символом и оканчивается символом  . Как уже отмечалось, существует допустимый блок символов
. Как уже отмечалось, существует допустимый блок символов  с началом и концом
с началом и концом  . Возьмем теперь последовательность
. Возьмем теперь последовательность

в которой элементы  произвольны,
произвольны,  , а далее стоят
, а далее стоят
поочередно блоки  так, что конец одного блока является началом следующего.
так, что конец одного блока является началом следующего.
Пусть теперь U окрестность произвольной точки  состоящая из последовательностей, совпадающих с на отрезке номеров
состоящая из последовательностей, совпадающих с на отрезке номеров  . Пусть блок
. Пусть блок  занумерован нами как
занумерован нами как  и его начало стоит в
и его начало стоит в  на месте с номером N. Тогда
на месте с номером N. Тогда  . Поэтому положительная полутраектория
. Поэтому положительная полутраектория  точки
точки  рано или поздно попадает в любую окрестность любой точки
рано или поздно попадает в любую окрестность любой точки  т.е. всюду плотна. Следовательно,
т.е. всюду плотна. Следовательно,  топологически транзитивно, что и утверждалось.
топологически транзитивно, что и утверждалось.
Рассмотренный только что диффеоморфизм  может показаться слишком искусственным. Однако символическая динамика появляется и в более естественных примерах.
может показаться слишком искусственным. Однако символическая динамика появляется и в более естественных примерах.
Возьмем уже встречавшийся в лекциях А. Г. Кушнирспко и А. Б. Катка автоморфизм тора  задаваемый формулами
задаваемый формулами

Как линейное отображение плоскости (5) является гиперболическим поворотом с неподвижной точкой  и инвариантными прямыми:
и инвариантными прямыми:
растягивающаяся сепаратриса 
сжимающаяся сепаратриса 
(здесь  — золотое сечение).
— золотое сечение).
Рассмотрим на плоскости XOY прямоугольники:  , стороны которого АВ и AD — отрезки сепаратрис (6) и (7), ВС и CD — отрезки прямых, параллельных тем же сепаратрисам, но проходящих через точки (1,0) и (1,1) (заметим, что
, стороны которого АВ и AD — отрезки сепаратрис (6) и (7), ВС и CD — отрезки прямых, параллельных тем же сепаратрисам, но проходящих через точки (1,0) и (1,1) (заметим, что  вершины единичного квадрата изображают одну и ту же точку на торе, а поэтому AD и ВС — отрезки одной и той же сепаратрисы; то же относится и к АВ и CD), и
вершины единичного квадрата изображают одну и ту же точку на торе, а поэтому AD и ВС — отрезки одной и той же сепаратрисы; то же относится и к АВ и CD), и  , сторона DG которого лежит на AD, EF и ED — отрезки прямых, параллельных сепаратрисам (6) и (7) и проходящих через (1,1), a FG лежит на прямой, параллельной сепаратрисе (7) и проходящей через (0,1) (снова все это разные отрезки одной и той же пары сепаратрис на торе).
, сторона DG которого лежит на AD, EF и ED — отрезки прямых, параллельных сепаратрисам (6) и (7) и проходящих через (1,1), a FG лежит на прямой, параллельной сепаратрисе (7) и проходящей через (0,1) (снова все это разные отрезки одной и той же пары сепаратрис на торе).
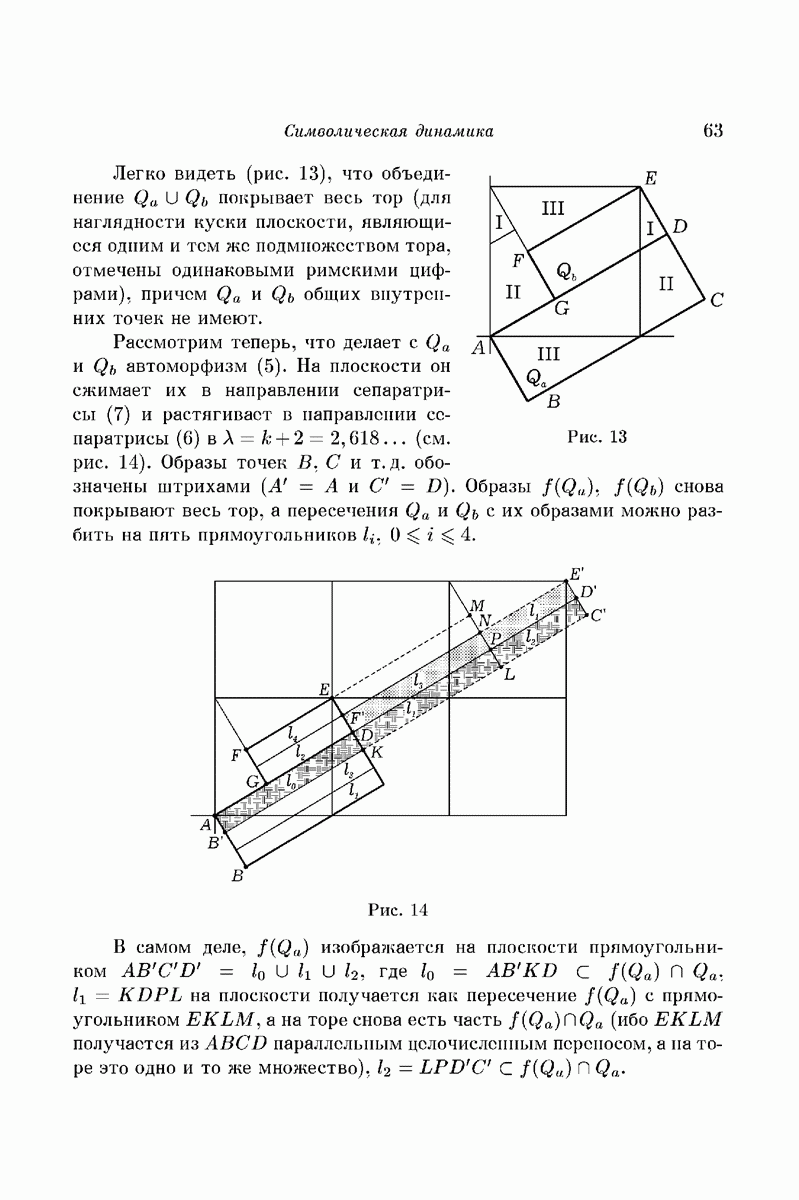
Легко видеть (рис. 13), что объединение  покрывает весь тор (для наглядности куски плоскости, являющиеся одним и тем же подмножеством тора, отмечены одинаковыми римскими цифрами), причем
покрывает весь тор (для наглядности куски плоскости, являющиеся одним и тем же подмножеством тора, отмечены одинаковыми римскими цифрами), причем  общих внутренних точек не имеют.
общих внутренних точек не имеют.

Рис. 13
Рассмотрим теперь, что делает с  автоморфизм (5). На плоскости он сжимает их в направлении сепаратрисы (7) и растягивает в направлении сепаратрисы (6) в
автоморфизм (5). На плоскости он сжимает их в направлении сепаратрисы (7) и растягивает в направлении сепаратрисы (6) в  (см. рис. 14). Образы точек В, С и т.д. обозначены штрихами
(см. рис. 14). Образы точек В, С и т.д. обозначены штрихами  . Образы
. Образы  снова покрывают весь тор, а пересечения
снова покрывают весь тор, а пересечения  с их образами можно разбить на пять прямоугольников
с их образами можно разбить на пять прямоугольников  .
.

Рис. 14
В самом деле,  изображается на плоскости прямоугольником
изображается на плоскости прямоугольником  где
где  на плоскости получается как пересечение
на плоскости получается как пересечение  с прямоугольником EKLM, а на торе снова есть часть
с прямоугольником EKLM, а на торе снова есть часть  (ибо EKLM получается из ABCD параллельным целочисленным переносом, а на торе это одно и то же множество),
(ибо EKLM получается из ABCD параллельным целочисленным переносом, а на торе это одно и то же множество),  .
.
Точно так же  , где
, где  . Мы видим теперь, что пересечения
. Мы видим теперь, что пересечения  устроены точно так же, как на рис. 10, однако теперь
устроены точно так же, как на рис. 10, однако теперь  , так что не остается «лишних» точек, но зато некоторые точки тора покрыты дважды (на рис. 10 различные
, так что не остается «лишних» точек, но зато некоторые точки тора покрыты дважды (на рис. 10 различные  ; попарно не пересекаются, а теперь они могут пересекаться, хотя только по границе). Отображения
; попарно не пересекаются, а теперь они могут пересекаться, хотя только по границе). Отображения  являются гиперболическими поворотами, и мы можем провести те же построения, которые были применены для исследования «подковы Смейла» и диффеоморфизма рис. 10 и 11. Снова появляются пространство
являются гиперболическими поворотами, и мы можем провести те же построения, которые были применены для исследования «подковы Смейла» и диффеоморфизма рис. 10 и 11. Снова появляются пространство  , где
, где  — матрица (3), и
— матрица (3), и  .
.
Теорема ([57]). Существует отображение  непрерывное и гомеоморфное на дополнении множества первой категории в смысле Бэра в такое, что
непрерывное и гомеоморфное на дополнении множества первой категории в смысле Бэра в такое, что  и диаграмма
и диаграмма

коммутативна.
Упоминаемое здесь множество первой категории получается как прообраз сторон прямоугольников  и всех их сдвигов под действием автоморфизма f. Прообраз каждой стороны оказывается в нигде не плотным, поэтому множество, где
и всех их сдвигов под действием автоморфизма f. Прообраз каждой стороны оказывается в нигде не плотным, поэтому множество, где  не является гомеоморфизмом, представляет собой счетное объединение нигде
не является гомеоморфизмом, представляет собой счетное объединение нигде  плотных множеств, что, собственно говоря, и является определением «множества первой категории».
плотных множеств, что, собственно говоря, и является определением «множества первой категории».
Какие следствия мы можем извлечь из этой теоремы? Прежде всего мы уже видели, что периодические точки сдвига Т плотны в  . Если
. Если  , то из диаграммы (8) видно, что
, то из диаграммы (8) видно, что  , а потому
, а потому  периодическая точка автоморфизма
периодическая точка автоморфизма  . Пусть q произвольная точка тора и
. Пусть q произвольная точка тора и  . По доказанному выше, существует последовательность периодических точек
. По доказанному выше, существует последовательность периодических точек  но тогда
но тогда  — последовательность периодических точек автоморфизма
— последовательность периодических точек автоморфизма  сходящаяся
сходящаяся  . Следовательно, периодические точки автоморфизма
. Следовательно, периодические точки автоморфизма  плотны в
плотны в  .
.
Точно так же доказывается, что в  существует всюду плотная (полу)траектория, в силу чего
существует всюду плотная (полу)траектория, в силу чего  оказывается топологически транзитивным.
оказывается топологически транзитивным.
Проанализировав, какие точки в  отождествляются при отображении
отождествляются при отображении  , мы можем любой топологический вопрос, относящийся к свойствам автоморфизма
, мы можем любой топологический вопрос, относящийся к свойствам автоморфизма  , выразить в терминах «топологической динамики». Во многих случаях этот подход оказывается весьма удобным.
, выразить в терминах «топологической динамики». Во многих случаях этот подход оказывается весьма удобным.
Далее, рассмотрим в пространстве всевозможные «цилиндры»

При отображении  такой цилиндр переходит в пересечение
такой цилиндр переходит в пересечение

Пусть р обозначает обычную лебегову меру (площадь), перенесенную на тор с плоскости. Припишем каждому цилиндру (9) меру, которую обозначим 

Нетрудно проверить, что так определенная на всех цилиндрах мера удовлетворяет условиям известной теоремы А. Н. Колмогорова, и тем самым и может быть продолжена на все борелевские множества в  . Автоморфизм (5) сохраняет площадь:
. Автоморфизм (5) сохраняет площадь:  , так как определитель его матрицы
, так как определитель его матрицы  ; тем же свойством обладает и отображение Т. Чтобы доказать это, возьмем сначала произвольный цилиндр
; тем же свойством обладает и отображение Т. Чтобы доказать это, возьмем сначала произвольный цилиндр  образом которого будет цилиндр
образом которого будет цилиндр  , где
, где  . Из формулы (10) следует, что
. Из формулы (10) следует, что

Определим в  новую меру v равенством
новую меру v равенством  . Тогда на всех цилиндрах выполняется равенство
. Тогда на всех цилиндрах выполняется равенство

Из теоремы А.Н. Колмогорова следует, что в этом случае  , т.е.
, т.е.  , что и означает инвариантность меры
, что и означает инвариантность меры  .
.
Из равенства (10) можно вывести, что для любого борелевского подмножества тора выполняется равенство  . Множества в
. Множества в  , на которых
, на которых  не взаимно однозначно, имеют меры 0. Поскольку в метрической теории динамических систем («Эргодической теории») принято пренебрегать множествами меры 0, с этой точки зрения
не взаимно однозначно, имеют меры 0. Поскольку в метрической теории динамических систем («Эргодической теории») принято пренебрегать множествами меры 0, с этой точки зрения  оказывается изоморфизмом отображений пространств с мерой
оказывается изоморфизмом отображений пространств с мерой  . При этом мера v в пространстве
. При этом мера v в пространстве  есть не что иное, как распределение вероятностей некоторой марковской цепи. Это означает, что найдутся такие
есть не что иное, как распределение вероятностей некоторой марковской цепи. Это означает, что найдутся такие  что для любого цилиндра
что для любого цилиндра

Матрица  называется в теории вероятностей матрицей вероятностей перехода,
называется в теории вероятностей матрицей вероятностей перехода,  — стационарными вероятностями состояний данной цепи.
— стационарными вероятностями состояний данной цепи.
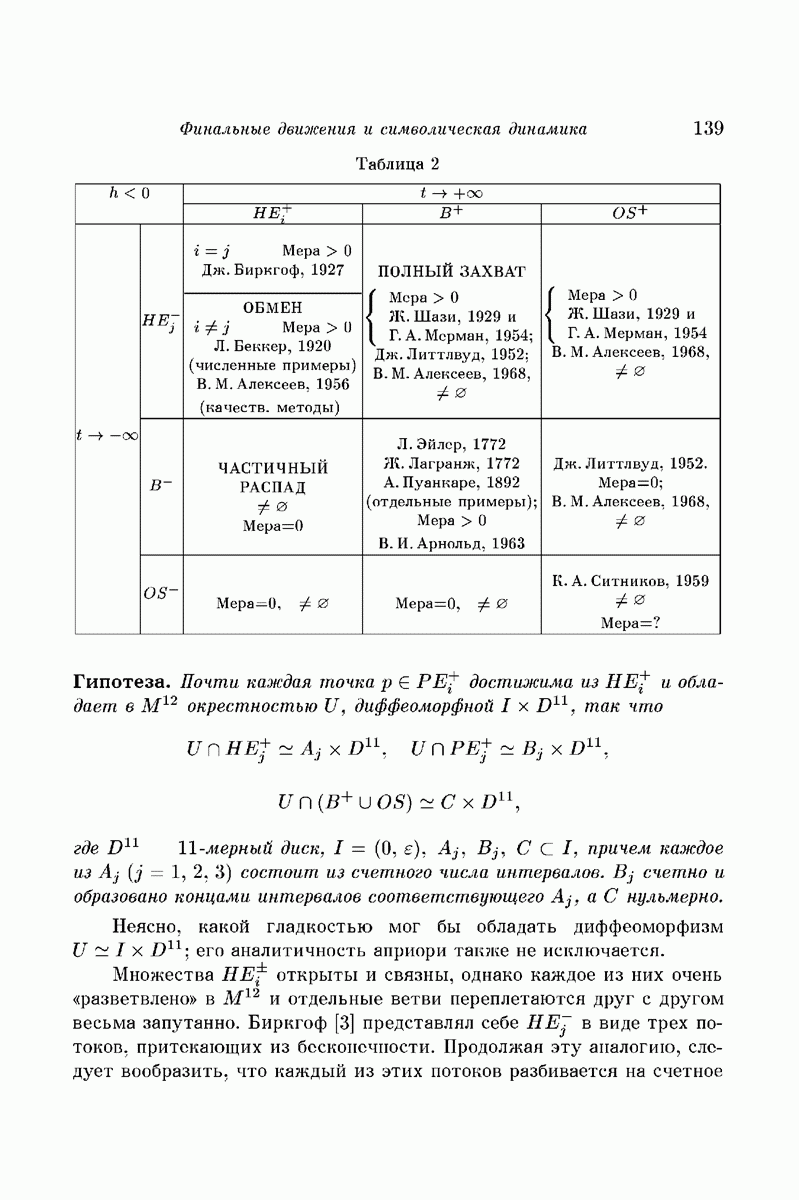
Аналогичными рассуждениями Р. Адлер и Б. Вейс установили ([57]), что любой эргодический автоморфизм двумерного тора, задаваемый целочисленной унимодулярной матрицей, изоморфен, с точки зрения эргодической теории, некоторой стационарной марковской цепи. Этот изоморфизм позволил им провести классификацию всех таких автоморфизмов. Единственным инвариантом при этом оказалась энтропия автоморфизма в смысле А.Н. Колмогорова, равная логарифму модуля того из собственных чисел матрицы автоморфизма, у которого этот модуль больше  эргодического автоморфизма тора одно из собственных чисел обязательно таково).
эргодического автоморфизма тора одно из собственных чисел обязательно таково).
Еще одна ситуация, в которой применимы методы символической динамики, связана с так называемыми гомоклиническими точками. Пусть р — гиперболическая неподвижная точка диффеоморфизма  произвольного многообразия, и пусть
произвольного многообразия, и пусть  — ее инвариантные устойчивое и неустойчивое многообразия (см. лекции А. Г. Кушниренко). Точка
— ее инвариантные устойчивое и неустойчивое многообразия (см. лекции А. Г. Кушниренко). Точка  называется гомоклинической точкой точки р. Ее траектория
называется гомоклинической точкой точки р. Ее траектория  двояко-асимптотична в том смысле, что
двояко-асимптотична в том смысле, что  как при
как при  так и при
так и при  Если в точке q многообразия
Если в точке q многообразия  пересекаются трансверсально (т.е. касательные плоскости
пересекаются трансверсально (т.е. касательные плоскости  порождают все касательное пространство
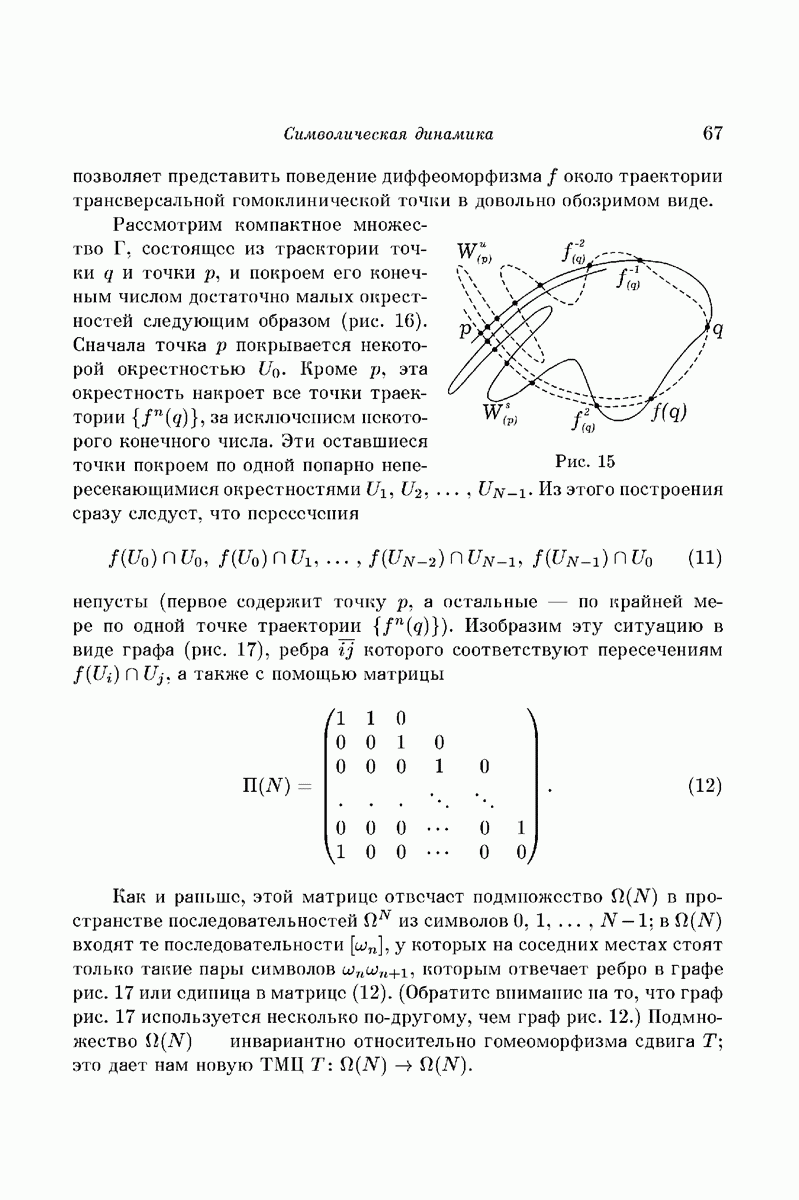
порождают все касательное пространство  точки q), то точка q называется трансверсальной гомоклинической точкой. В лекциях А. Г. Кушниренко уже отмечалось, что гомоклинические точки связаны с чрезвычайно запутанной картиной типа, изображенной на рис. 15. Символическая динамика
точки q), то точка q называется трансверсальной гомоклинической точкой. В лекциях А. Г. Кушниренко уже отмечалось, что гомоклинические точки связаны с чрезвычайно запутанной картиной типа, изображенной на рис. 15. Символическая динамика
позволяет представить поведение диффеоморфизма  около траектории трансверсальной гомоклинической точки в довольно обозримом виде.
около траектории трансверсальной гомоклинической точки в довольно обозримом виде.
Рассмотрим компактное множество Г, состоящее из траектории точки q и точки р, и покроем его конечным числом достаточно малых окрестностей следующим образом (рис. 16). Сначала точка р покрывается некоторой окрестностью 

Рис. 15
Кроме р, эта окрестность накроет все точки траектории  за исключением некоторого конечного числа. Эти оставшиеся точки покроем по одной попарно непересекающимися окрестностями
за исключением некоторого конечного числа. Эти оставшиеся точки покроем по одной попарно непересекающимися окрестностями  . Из этого построения сразу следует, что пересечения
. Из этого построения сразу следует, что пересечения

непусты (первое содержит точку р, а остальные — по крайней мере по одной точке траектории  . Изобразим эту ситуацию в виде графа (рис. 17), ребра
. Изобразим эту ситуацию в виде графа (рис. 17), ребра  , которого соответствуют пересечениям
, которого соответствуют пересечениям  , а также с помощью матрицы
, а также с помощью матрицы

Как и раньше, этой матрице отвечает подмножество  в пространстве последовательностей
в пространстве последовательностей  из символов
из символов  входят те последовательности у которых на соседних местах стоят только такие пары символов
входят те последовательности у которых на соседних местах стоят только такие пары символов  , которым отвечает ребро в графе рис. 17 или единица в матрице (12). (Обратите внимание на то, что граф рис. 17 используется несколько по-другому, чем граф рис. 12.) Подмножество
, которым отвечает ребро в графе рис. 17 или единица в матрице (12). (Обратите внимание на то, что граф рис. 17 используется несколько по-другому, чем граф рис. 12.) Подмножество  инвариантно относительно гомеоморфизма сдвига Т; это дает нам новую
инвариантно относительно гомеоморфизма сдвига Т; это дает нам новую  .
.

Рис. 16

Рис. 17
Теорема ([58]). Для всякого открытого множества V, содержащего множество Г, можно выбрать окрестости  таким образом, чтобы:
таким образом, чтобы:
1) 
2) максимальное инвариантное множество  содержащееся в U, является гиперболическим множеством, для
содержащееся в U, является гиперболическим множеством, для  ;
;
3) ограничение  топологически сопряжено
топологически сопряжено  существует гомеоморфизм
существует гомеоморфизм  такой, что диаграмма
такой, что диаграмма

коммутативна.
Число N зависит от выбора окрестности V и растет с ее уменьшением.
Граф рис. 17 и матрица (12) схематически изображают пересечения (11). Вообще говоря, непустыми могут быть и другие пересечения  и можно было бы поставить вопрос о возможности расширения пространства допустимых последовательностей
и можно было бы поставить вопрос о возможности расширения пространства допустимых последовательностей  за счет добавления к графу рис. 17 новых ребер (соответственно за счет замены в матрице (12) некоторых нулей единицами).
за счет добавления к графу рис. 17 новых ребер (соответственно за счет замены в матрице (12) некоторых нулей единицами).
Такое расширение однако  всегда продуктивно. Основной этап построения гомеоморфизма
всегда продуктивно. Основной этап построения гомеоморфизма  связан с доказательством того, что пересечение
связан с доказательством того, что пересечение


Рис. 18. «Хорошее» пересечение

Рис. 19. «Плохие» пересечения
непусто, когда допустимы все попарные пересечения  («марковское свойство»). Для «подковы Смейла» и диффеоморфизма рис. 10 это утверждение легко следовало из линейности отображений
(«марковское свойство»). Для «подковы Смейла» и диффеоморфизма рис. 10 это утверждение легко следовало из линейности отображений  и простых геометрических соображений. В общей ситуации, с которой мы сталкиваемся в окрестности траектории гомоклинической точки, доказательство подобного «марковского свойства» становится нетривиальным. Для его справедливости нужно, чтобы пересечения
и простых геометрических соображений. В общей ситуации, с которой мы сталкиваемся в окрестности траектории гомоклинической точки, доказательство подобного «марковского свойства» становится нетривиальным. Для его справедливости нужно, чтобы пересечения  были не только непусты, но еще и достаточно «хороши». Не вдаваясь в подробности, поясню сказанное рисунками 18 и 19; более подробно о том, что значит «хорошее» пересечение, см. в [59].
были не только непусты, но еще и достаточно «хороши». Не вдаваясь в подробности, поясню сказанное рисунками 18 и 19; более подробно о том, что значит «хорошее» пересечение, см. в [59].
С другой стороны, сформулированная выше теорема утверждает, что множество  является максимальным инвариантным множеством в некоторой своей окрестности, поэтому его расширение возможно лишь за счет добавления траекторий, достаточно далеко уходящих от
является максимальным инвариантным множеством в некоторой своей окрестности, поэтому его расширение возможно лишь за счет добавления траекторий, достаточно далеко уходящих от  . Дело обстояло совсем не так в случае исходного множества Г. Оно так же инвариантно, и из условия трансверсальности пересечения
. Дело обстояло совсем не так в случае исходного множества Г. Оно так же инвариантно, и из условия трансверсальности пересечения  в гомоклинической точке можно вывести, что Г — гиперболическое множество. Однако оно не является «локально максимальным», поскольку теорема как раз и утверждает, что любая окрестность V, содержащая Г, содержит большее инвариантное множество
в гомоклинической точке можно вывести, что Г — гиперболическое множество. Однако оно не является «локально максимальным», поскольку теорема как раз и утверждает, что любая окрестность V, содержащая Г, содержит большее инвариантное множество  .
.
Перейдем к обсуждению следствий, которые можно извлечь из
сформулированной выше теоремы. Как и в предыдущих случаях и теми же самыми рассуждениями, доказывается, что  действует на
действует на  топологически транзитивно и что периодические точки плотны в
топологически транзитивно и что периодические точки плотны в  . Каждая траектория
. Каждая траектория  взаимно однозначно кодируется последовательностью
взаимно однозначно кодируется последовательностью  . С помощью рис. 17 легко сообразить, что эта последовательность устроена следующим образом. В ней всегда есть пули; после каждого пуля может стоять либо пуль, либо единица, причем последняя всегда является началом блока
. С помощью рис. 17 легко сообразить, что эта последовательность устроена следующим образом. В ней всегда есть пули; после каждого пуля может стоять либо пуль, либо единица, причем последняя всегда является началом блока  . Таким образом,
. Таким образом,  состоит из пулей, в которые вкраплены блоки а (не исключено, что несколько или даже бесконечно много блоков а могут при этом идти подряд):
состоит из пулей, в которые вкраплены блоки а (не исключено, что несколько или даже бесконечно много блоков а могут при этом идти подряд):

Число блоков (т может быть конечным или бесконечным: они могут встречаться в последовательности  неограниченно далеко вправо или влево, или в обе стороны.
неограниченно далеко вправо или влево, или в обе стороны.
При отображении  последовательность
последовательность  перейдет в точку
перейдет в точку  . Для примера рассмотрим
. Для примера рассмотрим  как в (14). Ей отвечает точка
как в (14). Ей отвечает точка  . В силу (13)
. В силу (13)

Аналогично,  и дальнейшие итерации
и дальнейшие итерации  дважды пройдут последовательно все окрестности
дважды пройдут последовательно все окрестности  затем
затем  три раза попадет в
три раза попадет в  и т.д.
и т.д.
Пусть  и
и  Рассмотрим подмножество
Рассмотрим подмножество  инвариантное относительно
инвариантное относительно  и состоящее из последовательностей, у которых
и состоящее из последовательностей, у которых  . В силу инвариантности тогда и на всех местах, помер которых делится
. В силу инвариантности тогда и на всех местах, помер которых делится  должны стоять пули:
должны стоять пули:  и, чтобы описать
и, чтобы описать  достаточно выяснить, какие блоки из
достаточно выяснить, какие блоки из  символа могут встретиться между двумя нулями. Снова обратившись к рис. 17, мы найдем, что таковыми могут быть только следующие s блоков:
символа могут встретиться между двумя нулями. Снова обратившись к рис. 17, мы найдем, что таковыми могут быть только следующие s блоков:

Таким образом, каждая последовательность  имеет вид
имеет вид

где индексы  могут принимать независимо любое значение
могут принимать независимо любое значение  . Ясно, что
. Ясно, что  находится во взаимно-однозначном соответствии с множеством всех последовательностей из s символов. Преобразование Тк сдвигает (15) на s символов влево, что приводит к появлению на месте блока
находится во взаимно-однозначном соответствии с множеством всех последовательностей из s символов. Преобразование Тк сдвигает (15) на s символов влево, что приводит к появлению на месте блока  блока
блока  . Это в точности то же самое, что делает сдвиг Т на
. Это в точности то же самое, что делает сдвиг Т на  . Это доказывает, что гомеоморфизм сопряжен с гомеоморфизмом
. Это доказывает, что гомеоморфизм сопряжен с гомеоморфизмом  .
.
Отображение переносит эту сопряженность на многообразие. Так как у всех последовательностей из  то
то  .
.
И мы получаем
Следствие. Если р — гиперболическая неподвижная точка диффеоморфизма  , обладающая трансверсальной гомоклинической точкой, то для любой окрестности
, обладающая трансверсальной гомоклинической точкой, то для любой окрестности  и любого натурального s найдутся такие к и подмножество
и любого натурального s найдутся такие к и подмножество  инвариантное относительно
инвариантное относительно  что ограничение
что ограничение  топологически сопряжено гомеоморфизму сдвига в пространстве s-ичных последовательностей. (Для s = 1 это утверждение тривиально).
топологически сопряжено гомеоморфизму сдвига в пространстве s-ичных последовательностей. (Для s = 1 это утверждение тривиально).
Именно так был сформулирован первоначальный результат С. Смейла [60], показавший возможность использования методов «символической динамики» в общей гомоклинической ситуации. При этом Смейл предполагал еще, что диффеоморфизм f приводим к линейному в некоторой окрестности точки р за счет подходящего выбора системы локальных координат — предположение, хотя и несущественное с точки зрения «общего положения» (ибо сколь угодно малым изменением  можно добиться его выполнения), но все же излишнее.
можно добиться его выполнения), но все же излишнее.
Вернемся к пространству  . Каждая последовательность, ему принадлежащая, однозначно с точностью до сдвига восстанавливается, если будут указаны длины серий из пулей, разделяемых блоками
. Каждая последовательность, ему принадлежащая, однозначно с точностью до сдвига восстанавливается, если будут указаны длины серий из пулей, разделяемых блоками  Таким образом, элементы из
Таким образом, элементы из  могут быть закодированы последовательностями натуральных чисел, а именно
могут быть закодированы последовательностями натуральных чисел, а именно

соответствует элементу

Если в  все символы
все символы  при
при  , то последовательность (16) будет ограничена справа (можно завершить ее символом
, то последовательность (16) будет ограничена справа (можно завершить ее символом  ), точно так же она может быть ограничена слева или даже состоять из конечного числа символов (если w содержит лишь конечное число блоков а). Заметим, что если
), точно так же она может быть ограничена слева или даже состоять из конечного числа символов (если w содержит лишь конечное число блоков а). Заметим, что если  при
при  , то
, то  стремится при
стремится при  к последовательности, состоящей из одних нулей. Последовательность из одних нулей неподвижная точка отображения сдвига и переходит при отображении
к последовательности, состоящей из одних нулей. Последовательность из одних нулей неподвижная точка отображения сдвига и переходит при отображении  в неподвижную точку р диффеоморфизма
в неподвижную точку р диффеоморфизма  . Отсюда следует, что последовательностям (16), ограниченным справа, отвечают точки, траектории которых
. Отсюда следует, что последовательностям (16), ограниченным справа, отвечают точки, траектории которых  — асимптотичпы к р. Аналогично, последовательностям (16), ограниченным слева (с двух сторон), отвечают точки, траектории которых
— асимптотичпы к р. Аналогично, последовательностям (16), ограниченным слева (с двух сторон), отвечают точки, траектории которых  -асимптотичны (двоякоасимптотичны) к р. Подобное описание (в терминах последовательностей (16)) траекторий, остающихся в окрестности замыкания траектории гомоклинической точки, предложено Л. П. Шильниковым [61] (правда не для диффеоморфизма, а для потока, но это не очень существенно. Приведенное выше описание в терминах ТМЦ представляется мне более отвечающим сути явления, тем более что оно без труда переносится на более сложные ситуации.
-асимптотичны (двоякоасимптотичны) к р. Подобное описание (в терминах последовательностей (16)) траекторий, остающихся в окрестности замыкания траектории гомоклинической точки, предложено Л. П. Шильниковым [61] (правда не для диффеоморфизма, а для потока, но это не очень существенно. Приведенное выше описание в терминах ТМЦ представляется мне более отвечающим сути явления, тем более что оно без труда переносится на более сложные ситуации.
| << Предыдущий параграф | Следующий параграф >> |
- Квазислучайные колебания и качественные вопросы небесной механики
- Часть 1. О некоторых математических проблемах в небесной механике
- § 1. Основная задача небесной механики
- § 2. Геометрическая интерпретация задачи Кеплера
- § 3. Задача трех тел. Аналитические свойства решений
- § 4. Финальные движения в задаче трех тел
- § 5. Эволюция системы. Проблема захвата
- Часть 2. Символическая динамика
- Часть 3. Квазислучайные колебания некоторых нелинейных систем
- § 1. Пульсирующая одномерная потенциальная яма
- § 2. Свойства отображения S
- § 3. Об одном частном случае задачи трех тел
- Литература
- О возможности захвата в небесной механике
- Литература
- О возможности захвата в задаче трех тел
- Обмен и захват в задаче трех тел
- Существование осциллирующих движений в задаче трех тел
- Финальные движения в задаче трех тел и символическая динамика