О возможности захвата в задаче трех тел

Г. Ф. Хильми

1. Мы будем рассматривать задачу, известную в науке под именем проблемы трех тел, т.е. задачу о движении трех тел, которые мы будем считать материальными точками, притягивающимися по закону Ньютона. Эти точки мы обозначим через их массы соответственно через а через обозначим расстояния между точками . Кроме того, через р мы обозначим расстояние точки от центра тяжести точек . Движения точек мы будем описывать в координатах Якоби; пусть х, у, z — координаты точки относительно осей с началом в точке и — координаты точки относительно осей с началом в центре тяжести точек Координатные оси обеих систем предполагаются параллельными. Интеграл энергии в координатах Якоби имеет вид:

где

и Н — постоянная интеграция.

2. К числу фундаментальных задач, возникающих в проблеме трех тел, принадлежит задача о возможности и мере (вероятности) захвата. Обычное в астрономии представление о явлении захвата может быть точно выражено следующим определением.

Определение 1. Мы будем говорить, что имеет место явление захвата между телами , если

и если можно указать такой момент времени Т и такое положительное число Р, что

В результате недостаточно строгих исследований Ж. Шази в науке широко распространилось убеждение, что захват практически невозможен. Это означает следующее: если захват и возможен, то мера того множества точек, которое в фазовом пространстве системы трех тел изображает начальные состояния, приводящие к захвату, равна пулю. Несмотря на такое состояние вопроса, акад. О.Ю. Шмидт, на основании индуктивных небесно-механических и космогонических соображений, пришел к выводу, что в случаях, когда , захват возможен и имеет положительную вероятность. Не имея в своем распоряжении математического доказательства этого факта, О.Ю. Шмидт в основу своих разнообразных космогонических исследований положил смелую «рабочую гипотезу» о возможности захвата, осуществляющегося с положительной вероятностью. В 1947 г. появилась работа О.Ю. Шмидта, специально посвященная вопросу о возможности захвата, в которой пересматривается и существенно продвигается эта проблема. В этой работе доказано существование и положительная вероятность ослабленной формы захвата, однако именно той, которая имеет значение в космогонии и в статистической небесной механике. Определение захвата, рассмотренного О.Ю. Шмидтом, может быть сформулировано следующим образом.

Определение 2. Пусть два положительных числа, которые мы назовем параметрами захвата. Мы будем говорить, что на временном отрезке осуществилось явление ослабленного захвата между телами , если в момент времени

и все три относительные скорости гиперболические, а в момент

скорость относительно эллиптическая, скорость относительно точки с массой, равной помещенной в центре тяжести , будет гиперболической.

Параметры захвата имеют определенный астрономический смысл: это среднее расстояние между звездами в данной достаточно

большой (в статистическом смысле) части Галактики, а — это то расстояние между звездами, при котором при данном значении их надлежит рассматривать как двойную систему, если их относительная скорость эллиптическая.

Возможность ослабленного захвата О.Ю. Шмидт доказал, непосредственно подобрав начальные условия, при которых он осуществляется.

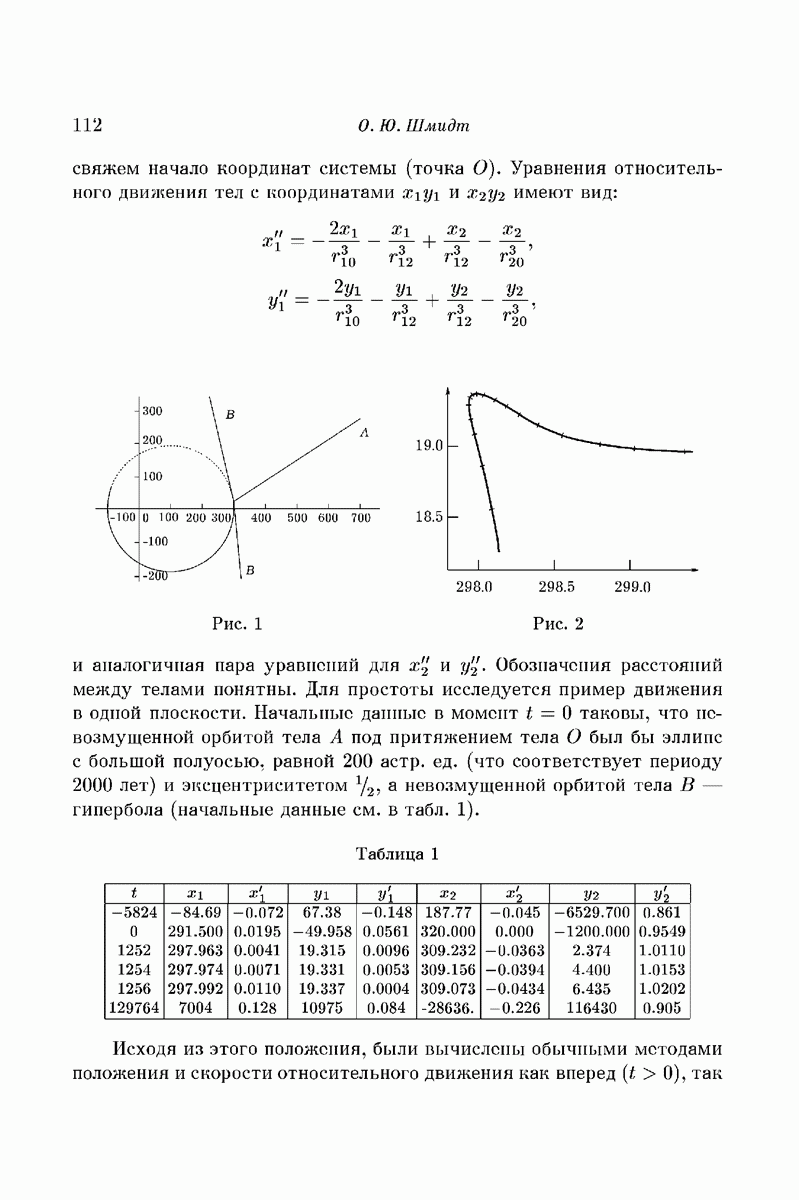
О.Ю. Шмидт рассматривал движение трех тел в одной плоскости, с одинаковыми массами, равными массе Солнца, принятой за единицу. Единицей расстояния служила астрономическая единица длины, а единицей времени год, деленный на . Точка бралась неподвижной, координаты точки точки задавались относительно осей с центром в Начальные данные в момент таковы, что невозмущенной орбитой точки под притяжением был бы эллипс с большой полуосью, равной 200 астр. ед. и эксцентриситетом а невозмущенной орбитой точки гипербола. В этом случае движение трех тел было изучено от момента времени до численным интегрированием проблемы трех тел. Предварительные вычисления были сделаны лично О.Ю. Шмидтом, а затем точные и подробные вычисления были выполнены в Геофизическом институте Академии наук СССР под руководством Н. Н. Парийского. Начальные положения и скорости тел , а также их положения и скорости для крайних моментов времени свсдспы в табл. 1.

Таблица 1

Пользуясь данными табл. 1, легко установить, что в рассматриваемом случае осуществляется ослабленный захват. Из существования хотя бы одного примера осуществления ослабленного захвата и из общих свойств решений дифференциальных уравнений следует, как это было указано в работе О.Ю. Шмидта, что множество начальных данных, приводящих к подобному захвату, имеет положительную меру, а не меру нуль.

3. Решение проблемы захвата в постановке, рассмотренной О. Ю. Шмидтом, совершенно достаточно для астрономических приложений.

Однако, опираясь на указанный О.Ю. Шмидтом пример движения трех тел, проблему захвата можно решить и как проблему математической небесной механики, понимая захват в обычном, более общем смысле, и таким образом построить математическую теорию захвата.

Мы будем исходить из следующих, принадлежащих автору, теорем, громоздкие и длинные доказательства которых отложим до полной публикации.

Теорема 1. Пусть

Если в некоторый момент времени

то все три расстояния, Гц, , неограниченно возрастают при

Теорема 2. постоянная, энергия можно указать два положительных числа R и и такой момент времени , что

где , то при всех точка монотонно удаляется в бесконечность от центра тяжести точек , а взаимное расстояние точек остается не превышающим R.

Определение 3. Мы будем говорить, что на временном отрезке между телами осуществился захват специального типа, если в момент выполняются условия теоремы 1, а в момент — условия теоремы 2.

Легко убедиться, что захват специального типа есть частный случай захвата в обычном смысле, т. е. в смысле определения 2.

Теорема 3. При движении трех тел под влиянием взаимных притяжений захват возможен.

Справедливость теоремы непосредственно следует из теорем 1 и 2 и примера, указанного О.Ю. Шмидтом. Пользуясь приведенными выше результатами вычислений, легко убедиться, что при выполняются условия теоремы 1, а при — условия теоремы 2. Таким образом, при начальных условиях, предложенных О.Ю. Шмидтом, осуществляется не только ослабленный захват, по и захват специального типа, а следовательно, и обычный захват в смысле определения 2. Теорема доказана.

Теорема 4. Мера множества тех точек в фазовом пространстве системы трех тел, которые изображают начальные состояния системы, приводящие к захвату, не может быть равной нулю.

Мы не будем здесь излагать подробного доказательства. Основные же черты этого доказательства следующие. Рассмотрим 12-мерное евклидово пространство с координатами и будем величины рассматривать как функции этих координат. Пусть Е множество всех точек фазового пространства в которых и — множество всех точек, в которых

Так как непрерывные функции от координат фазового пространства, то множества Е и суть множества открытые.

Обозначим через G множество тех точек из Е, которые, описывая свои фазовые орбиты, через некоторый промежуток времени переходят в множество 8. Очевидно, что каждая точка множества и соответствует начальным условиям, приводящим к захвату специального типа. В силу теоремы 3 множество пустое множество. Из того, что множества Е и открытые, и из общих теорем о непрерывной зависимости решений дифференциальных уравнений от начальных параметров следует, что и множество G есть множество открытое. Но тогда

а так как , то множество не может быть множеством меры нуль.

Я пользуюсь случаем, чтобы выразить глубокую признательность московским ученым и моим учителям акад. О.Ю. Шмидту, чл.-корр. АН СССР В.В. Степанову, чл.-корр. АН СССР П.С. Александрову, чл.-корр. АН СССР М.Ф. Субботину и проф. А.А. Маркову. Своим интересом к работе и ценными советами они мне оказали неоценимую услугу.

Литература

[1] J. Chazy. de Math., 8 (1929).

[2] J. Chazy. Bull. Astr., 8 (1932).

[3] О.Ю. Шмидт. ДАН, 58, № 2 (1947).