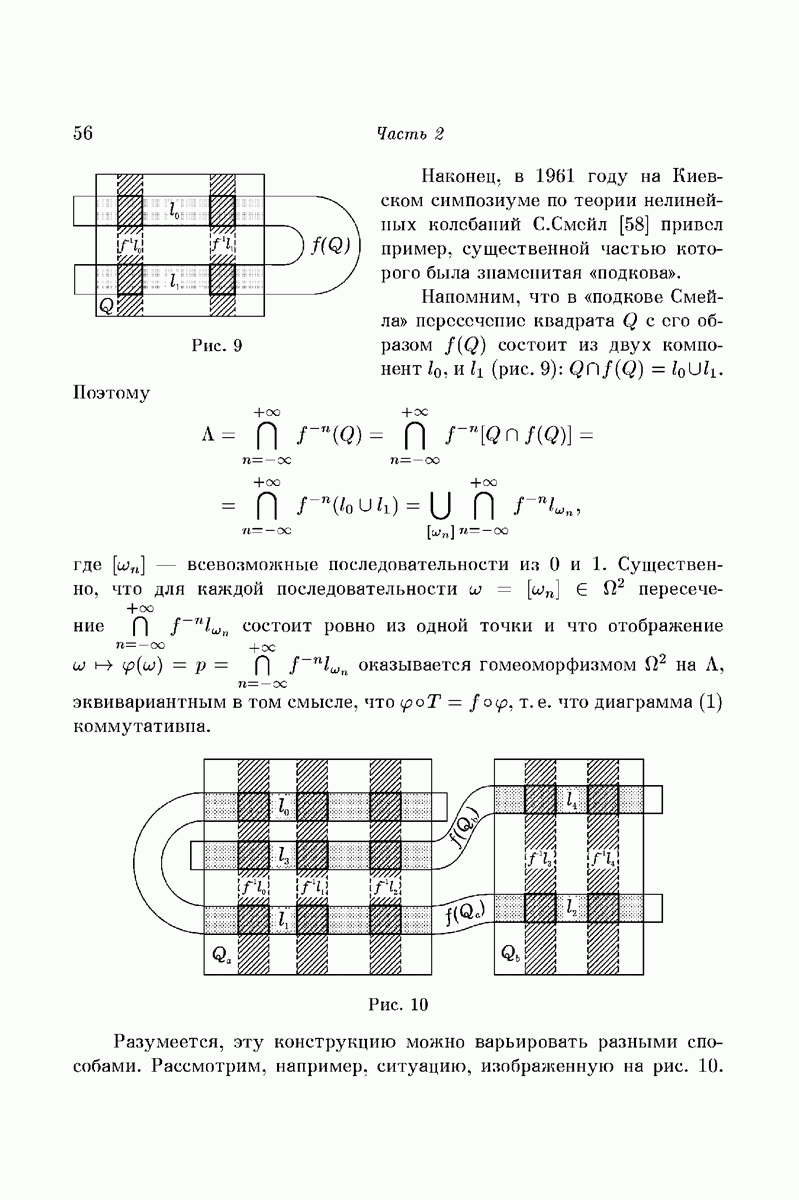
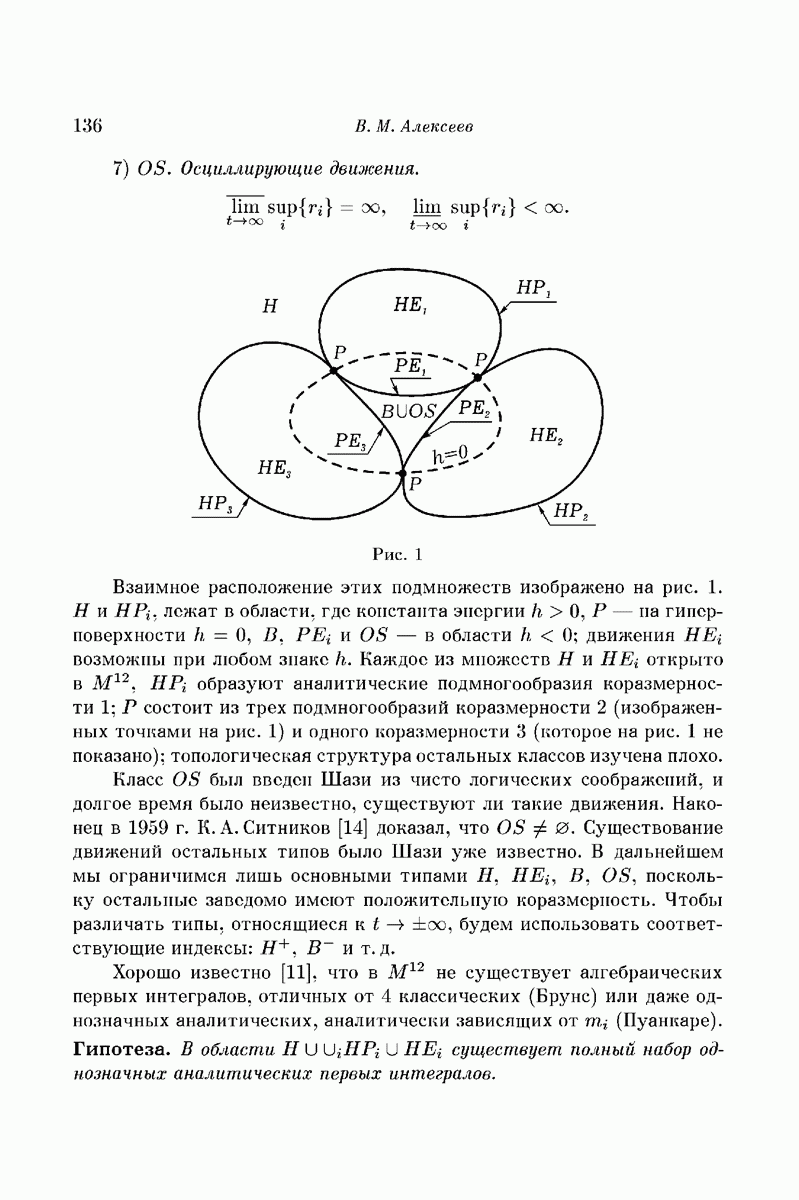
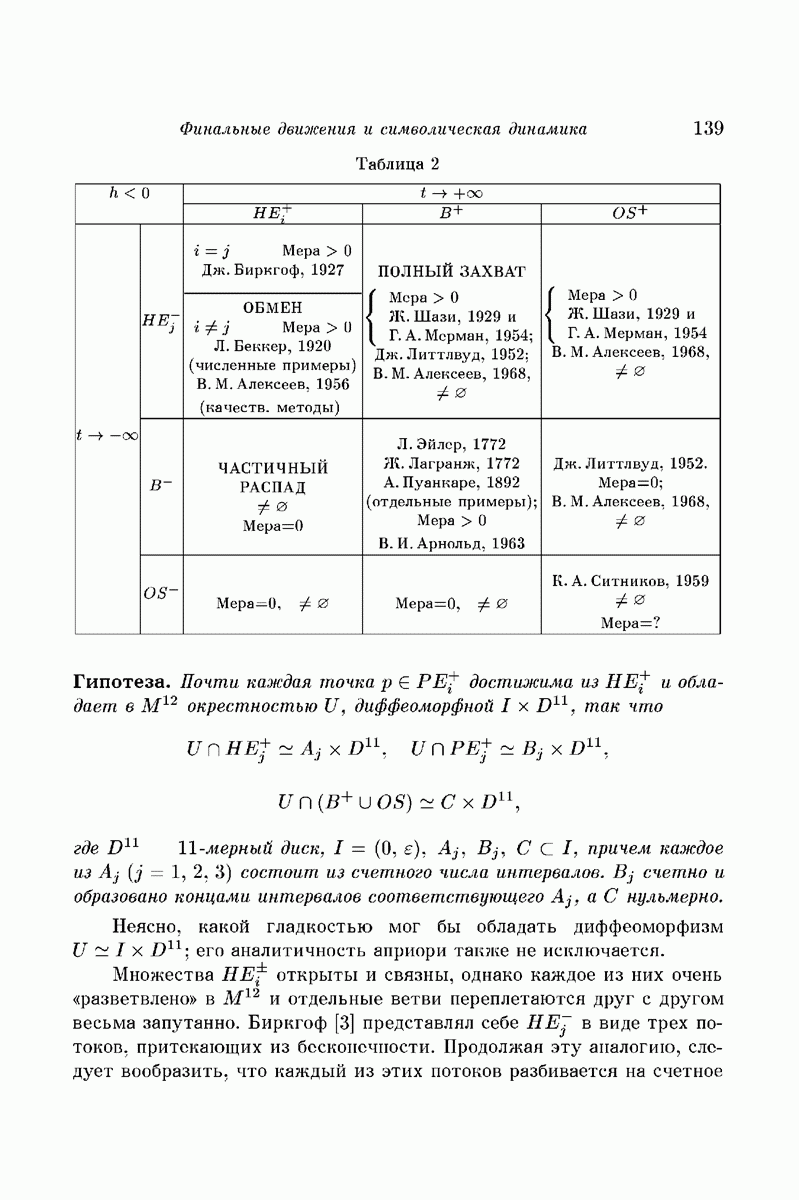
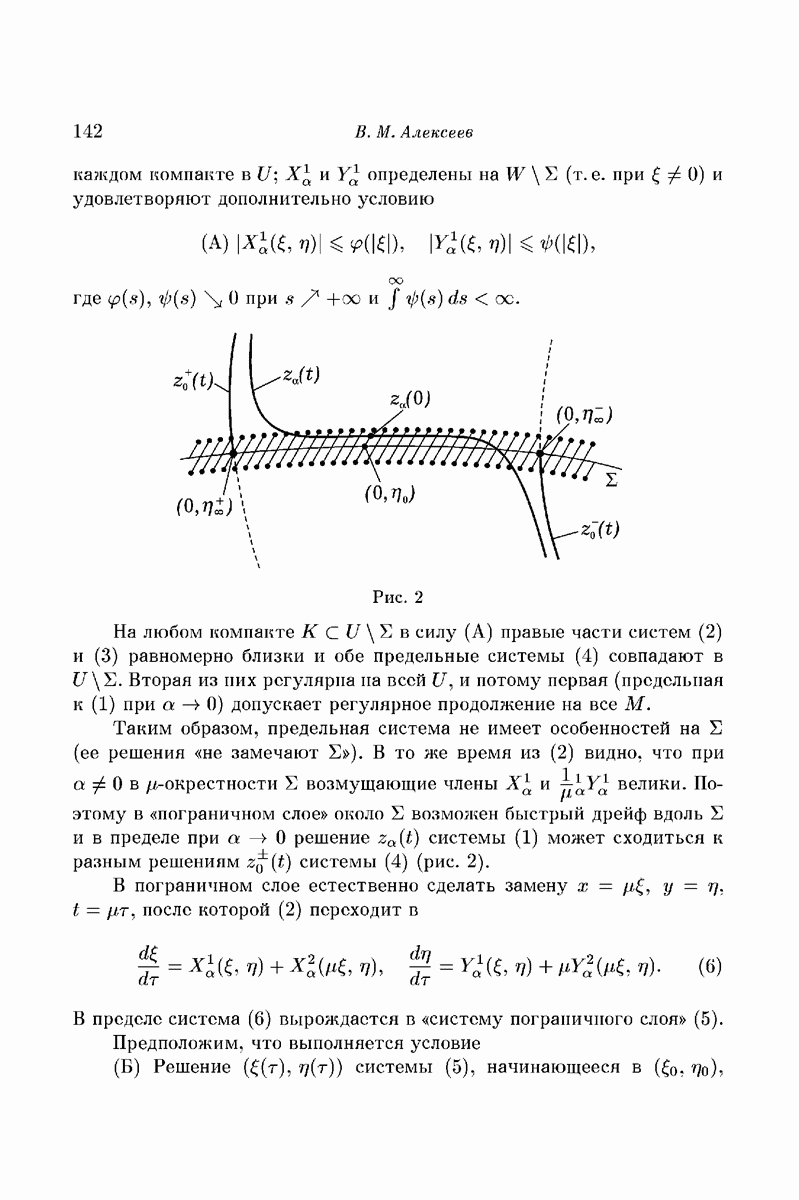
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Геометрическая интерпретация задачи Кеплера
Если  и центр масс тел
и центр масс тел  и покоится в соответствии с (2) в начале координат, то систему (1) можно упростить. А именно, исключив
и покоится в соответствии с (2) в начале координат, то систему (1) можно упростить. А именно, исключив  с помощью (2), мы получим для
с помощью (2), мы получим для  такое же уравнение, как если бы тело
такое же уравнение, как если бы тело  двигалось в ньютоновском поле тяготения, создаваемом неподвижной массой
двигалось в ньютоновском поле тяготения, создаваемом неподвижной массой  расположенной в начале («задача Кеплера»), При надлежащем выборе системы единиц
расположенной в начале («задача Кеплера»), При надлежащем выборе системы единиц  , а тогда для
, а тогда для  имеем уравнение
имеем уравнение

Дальнейшие рассуждения практически не зависят от числа координат, так что в  можно было бы считать вектором из
можно было бы считать вектором из  . Для простоты мы ограничимся, однако, случаем
. Для простоты мы ограничимся, однако, случаем 
Фазовое пространство задачи Кеплера имеет (при  ) размерность 4. Фиксируя значения интегралов энергии h и момента С, мы получаем двумерное интегральное многообразие. При
) размерность 4. Фиксируя значения интегралов энергии h и момента С, мы получаем двумерное интегральное многообразие. При  оно будет компактным. Если заменить (6) уравнением движения в поле произвольной центральной силы
оно будет компактным. Если заменить (6) уравнением движения в поле произвольной центральной силы

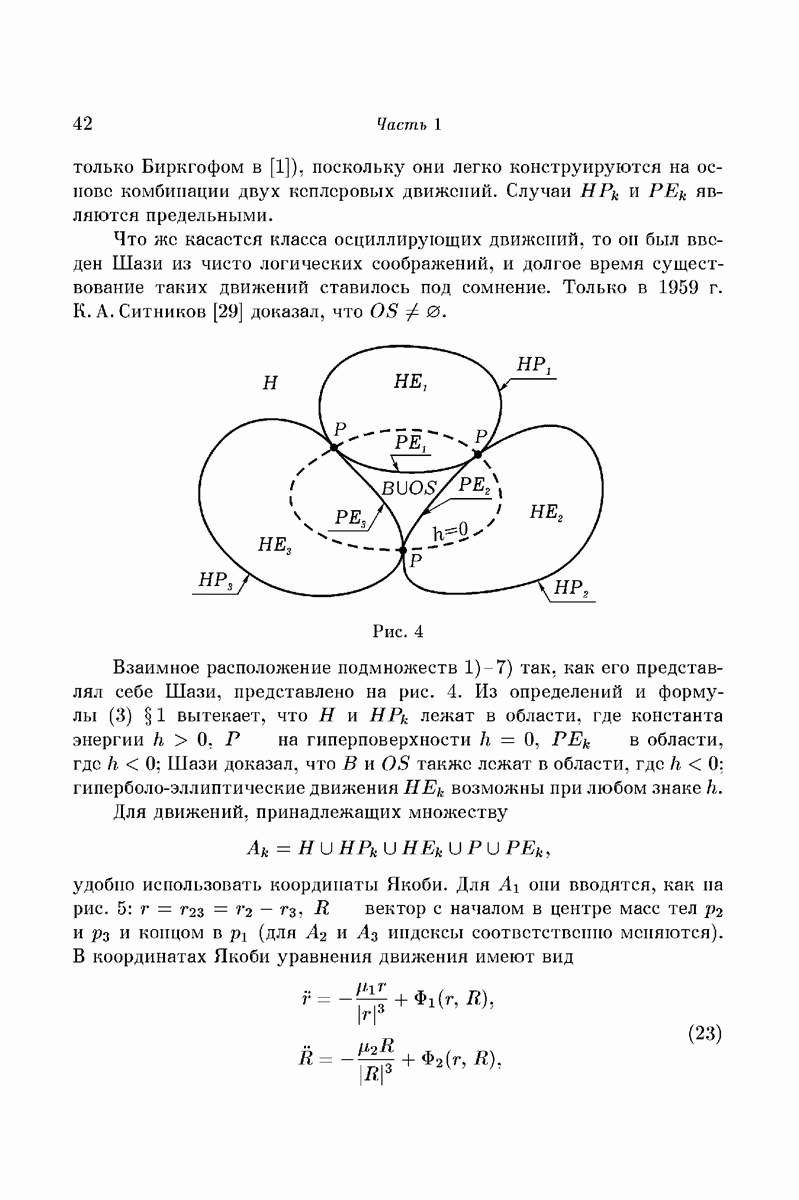
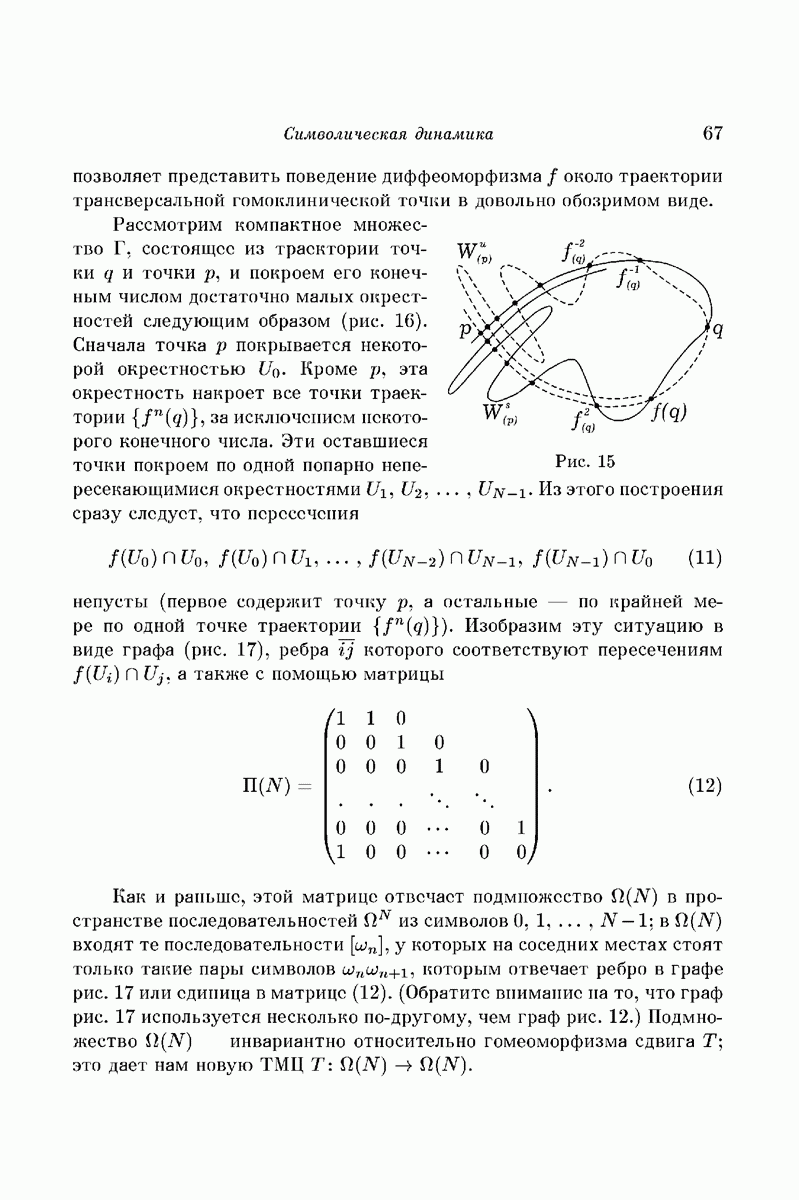
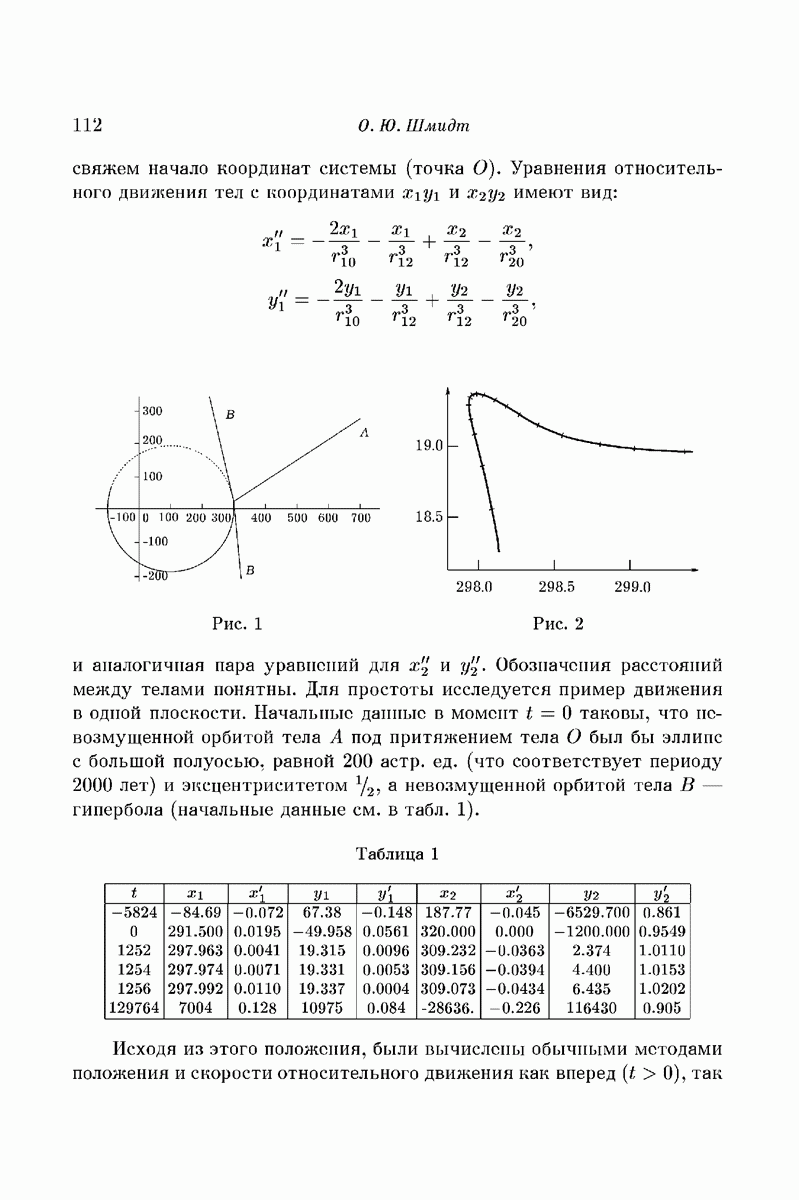
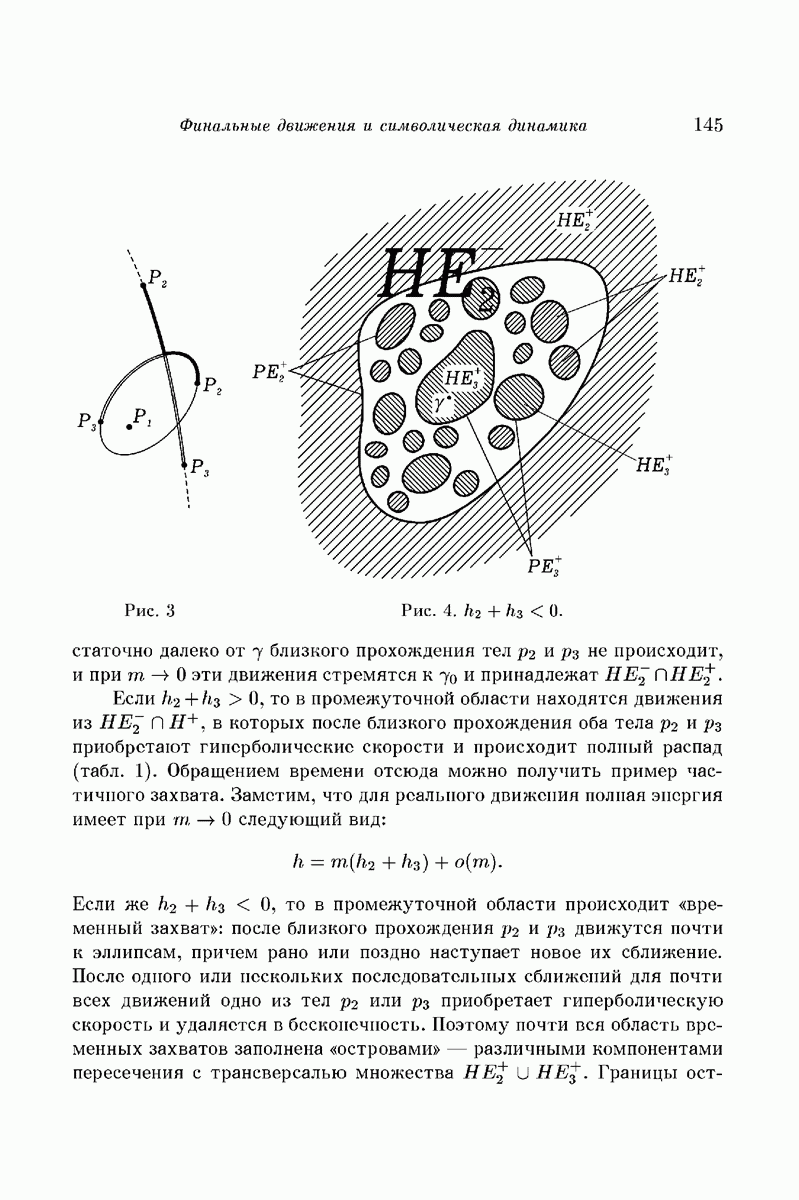
то в типичном случае такое многообразие оказывается двумерным тором, а каждая из лежащих на нем траекторий образует всюду плотную обмотку. Проектируя траекторию из фазового пространства в координатное, мы находим, что не уходящая в бесконечность типичная орбита материальной точки, управляемой уравнением (7), заполняет всюду плотно некоторое кольцо (рис. 1). В исключительных резонансных случаях инвариантные торы распадаются в семейства периодических траекторий.
Если же сила притяжения к неподвижному центру убывает как то исключительный случай становится правилом, происходит вырождение. Не уходящая в бесконечность орбита всегда является эллипсом (рис. 2), а в фазовом пространстве все двумерные торы распадаются в семейства периодических траекторий.
Естественно ожидать, что такое вырождение обязано своим происхождением наличию еще одного первого интеграла [4, § 50]. Известно,

Рис. 1

Рис. 2
что классические интегралы (3) и (4) связаны (по теореме Э. Нетер) с инвариантностью уравнений (1) относительно сдвигов по времени (интеграл энергии) и относительно вращений (интеграл момента). Это заставляет думать, что и новый интеграл должен быть следствием некоторой «скрытой симметрии» кеплеровой задачи.
Геометрическая интерпретация случая  , данная Ю. Мозером в [44], позволяет указать явно эту симметрию; впрочем, Мозер отмечает, что еще в 1935 году
, данная Ю. Мозером в [44], позволяет указать явно эту симметрию; впрочем, Мозер отмечает, что еще в 1935 году  использовал ключевое для этих рассуждений преобразование с целью объяснить вырождение уровней энергии в квантовой модели атома водорода (подобный эффект физики обычно также связывают со «скрытой симметрией»).
использовал ключевое для этих рассуждений преобразование с целью объяснить вырождение уровней энергии в квантовой модели атома водорода (подобный эффект физики обычно также связывают со «скрытой симметрией»).
Ю.С. Осипов [25] распространил рассуждения Мозера на случай произвольного h, дав несколько иное доказательство, которое с незначительными изменениями будет воспроизведено, далее.
Напомним сначала определение геодезического потока на римановом многообразии  (см., например, [17]). Этим термином обозначается динамическая система
(см., например, [17]). Этим термином обозначается динамическая система  действующая в многообразии
действующая в многообразии  единичных касательных векторов многообразия
единичных касательных векторов многообразия 
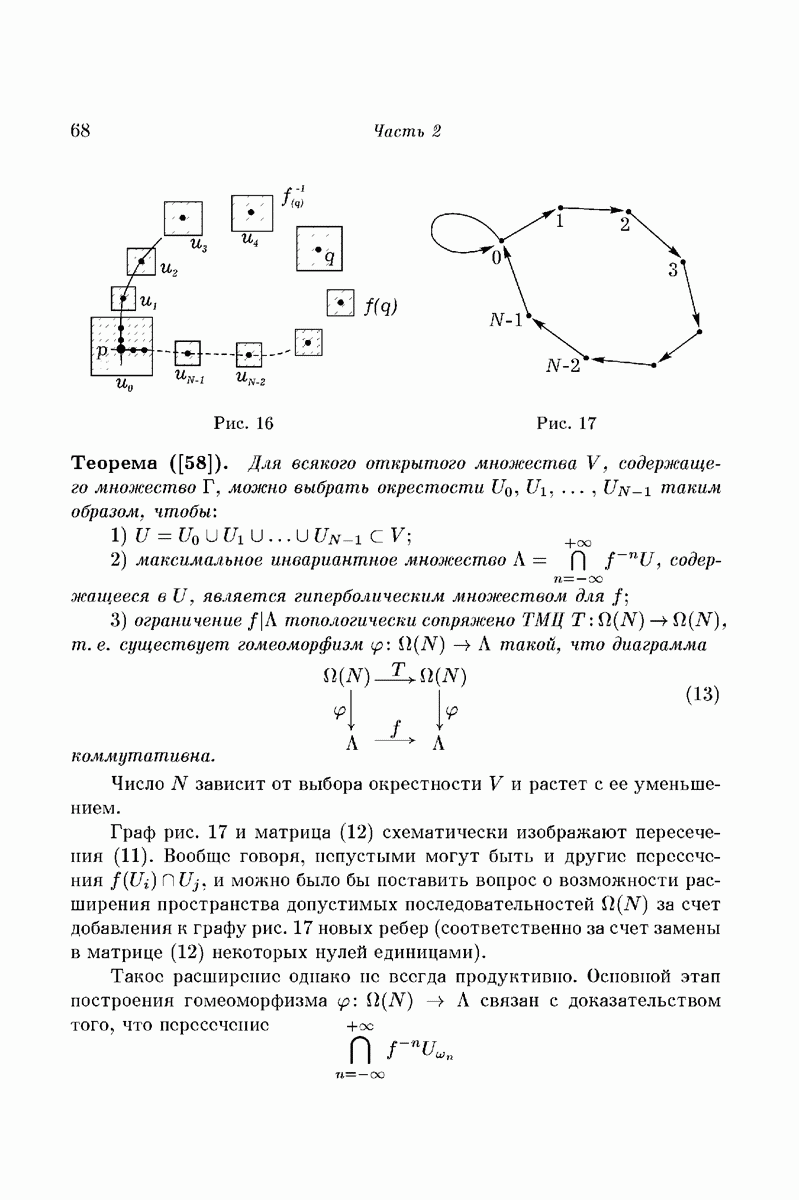
Пусть  — единичный касательный вектор в точке р
— единичный касательный вектор в точке р  Проведем через р (ориентированную) геодезическую в направлении вектора
Проведем через р (ориентированную) геодезическую в направлении вектора  и, отложив на ней дугу длины S. получим точку р и единичный вектор
и, отложив на ней дугу длины S. получим точку р и единичный вектор  , касающийся в ней той же (ориентированной) геодезической. По определению, преобразование
, касающийся в ней той же (ориентированной) геодезической. По определению, преобразование  переводит
переводит  (рис. 3).
(рис. 3).
Теорема. Фазовый поток плоской кеплеровой задачи (6) на многообразии
постоянной энергии h с точностью до замены времени эквивалентен геодезическому потоку на поверхности постоянной гауссовой кривизны  . После пополнения одной точкой эта поверхность изометрична сфере при
. После пополнения одной точкой эта поверхность изометрична сфере при  эвклидовой плоскости при
эвклидовой плоскости при  и плоскости Лобачевского при
и плоскости Лобачевского при  .
.
Как уже было сказано, аналогичное утверждение имеет место при любой размерности  . Читателям предоставляется произвести соответствующие изменения в формулировке. Доказательство.
. Читателям предоставляется произвести соответствующие изменения в формулировке. Доказательство.

Рис. 3
Произведем замену времени, введя новое независимое переменное а, соотношением

В канонических переменных  уравнения кеплеровой задачи имеют гамильтопов вид
уравнения кеплеровой задачи имеют гамильтопов вид

где

На эквиэнергетическом интегральном многообразии  можно преобразовать уравнения (9) следующим образом:
можно преобразовать уравнения (9) следующим образом:

так как Н — h на этом многообразии тождественно равно 0. На том же многообразии

что дает возможность преобразовать уравнения далее:

и аналогично

Таким образом, замена времени (8) превращает гамильтоновы уравнения (9) на эквиэнергетической поверхности Н = h в гамильтоновы уравнения

на поверхности  Заметим, что при
Заметим, что при  поверхность
поверхность  состоит из двух «пол»; по смыслу проделанных преобразований надо взять из них ту, на которой
состоит из двух «пол»; по смыслу проделанных преобразований надо взять из них ту, на которой  .
.
Исключим теперь  из уравнений (10):
из уравнений (10):

Отсюда

причем

Многообразие  проектируется на все пространство
проектируется на все пространство  в случае
в случае  на область
на область  в случае
в случае  и (с учетом выбора полы) на область
и (с учетом выбора полы) на область  в случае
в случае  Эти открытые подмножества в
Эти открытые подмножества в  будем для краткости обозначать М. Введем в
будем для краткости обозначать М. Введем в  новую риманову метрику так. чтобы в ней вектор скорости — стал единичным:
новую риманову метрику так. чтобы в ней вектор скорости — стал единичным:

Нетрудно усмотреть, что (12) являются уравнениями геодезических линий новой метрики, причем, по самому ее построению, параметр s имеет смысл длины дуги.
Согласно (13), компоненты ко- и контравариантных метрических тензоров [10] равны соответственно

откуда находим символы Кристоффеля:

Следовательно, уравнения геодезических имеют вид

что совпадает с (12).
Рассмотрим отображение  многообразия
многообразия  в касательное расслоение
в касательное расслоение  определяемое равенством
определяемое равенством  , где
, где

Легко видеть, что это отображение устанавливает взаимно однозначное соответствие между многообразием  (или его полой, если
(или его полой, если  и многообразием W единичных касательных векторов. Остается проверить, что фазовый поток, определяемый системой (10), переходит при отображении
и многообразием W единичных касательных векторов. Остается проверить, что фазовый поток, определяемый системой (10), переходит при отображении  в геодезический поток
в геодезический поток  .
.
В самом деле, траектория  потока (10) переходит в
потока (10) переходит в  где, по доказанному,
где, по доказанному,  — геодезическая,
— геодезическая,  — единичный (в метрике
— единичный (в метрике  ) касательный к ней вектор. Геодезическая, проходящая через точку
) касательный к ней вектор. Геодезическая, проходящая через точку  в направлении вектора
в направлении вектора  совпадает с
совпадает с  , а так как вектор — единичный, то s — длина дуги на этой геодезической. Поэтому отображение
, а так как вектор — единичный, то s — длина дуги на этой геодезической. Поэтому отображение  геодезического потока переводит
геодезического потока переводит  что и утверждалось.
что и утверждалось.
Метрика (13) хорошо известна.
При  стереографическая проекция
стереографическая проекция

переводит М в проколотую сферу  радиуса
радиуса  , причем метрика (13) переходит в обычную евклидову. Таким образом, риманово многообразие Моказывается поверхностью положительной постоянной (гауссовой) кривизны
, причем метрика (13) переходит в обычную евклидову. Таким образом, риманово многообразие Моказывается поверхностью положительной постоянной (гауссовой) кривизны  . При
. При  инверсия
инверсия

переводит  снова в себя, а метрика (13) становится евклидовой
снова в себя, а метрика (13) становится евклидовой

При h > 0 инверсия

отображает  на внутренность единичного круга с выколотым центром, а метрика (13) переходит (с точностью до постоянного множителя) в обычную метрику модели Пуанкаре плоскости Лобачевского
на внутренность единичного круга с выколотым центром, а метрика (13) переходит (с точностью до постоянного множителя) в обычную метрику модели Пуанкаре плоскости Лобачевского

Этим доказательство теоремы завершается.
Доказанная эквивалентность (с точностью до замены времени (8)) между фазовым потоком задачи (6) на эквиэнергетическом многообразии Н = h и геодезическим потоком на многообразии М с метрикой (13) позволяет, прежде всего, произвести «регуляризацию» задачи Кеплера.
Уравнение (6) имеет особенность при  Если постоянная площадей (интеграл момента) с
Если постоянная площадей (интеграл момента) с  то, как нетрудно проверить,
то, как нетрудно проверить,  отделен от 0 положительной константой, так что решение не имеет особенностей и является аналитической функцией t на всей оси
отделен от 0 положительной константой, так что решение не имеет особенностей и является аналитической функцией t на всей оси  Напротив, если
Напротив, если  то движение происходит по прямой, проходящей через начало, и обязательно
то движение происходит по прямой, проходящей через начало, и обязательно  при некотором
при некотором  Не ограничивая общности, можно считать, что
Не ограничивая общности, можно считать, что  . В случае реальной механической задачи в момент
. В случае реальной механической задачи в момент  происходит столкновение движущейся точки с неподвижным центром притяжения (в задаче двух тел это означает столкновение движущихся точек в их центре масс), и бессмысленно говорить о том, что будет при
происходит столкновение движущейся точки с неподвижным центром притяжения (в задаче двух тел это означает столкновение движущихся точек в их центре масс), и бессмысленно говорить о том, что будет при  так как при тесном сближении, и подавно при столкновении, становится непригодным идеализированное представление физического объекта в виде материальной точки. Однако, с математической точки зрения, естественно попытаться продолжить
так как при тесном сближении, и подавно при столкновении, становится непригодным идеализированное представление физического объекта в виде материальной точки. Однако, с математической точки зрения, естественно попытаться продолжить  на
на  так, чтобы полученная вектор-функция была бы в некотором смысле «регулярной». Говоря здесь и в следующем параграфе о «продолжении решения за момент столкновения», мы будем всегда иметь в виду лишь эту, чисто математическую, постановку вопроса.
так, чтобы полученная вектор-функция была бы в некотором смысле «регулярной». Говоря здесь и в следующем параграфе о «продолжении решения за момент столкновения», мы будем всегда иметь в виду лишь эту, чисто математическую, постановку вопроса.
Регуляризацию решения  можно попытаться произвести при помощи предельного перехода, подобрав семейство решений
можно попытаться произвести при помощи предельного перехода, подобрав семейство решений  задачи (6) так, чтобы при а
задачи (6) так, чтобы при а  они не содержали особенностей (т. е. находились бы в области с
они не содержали особенностей (т. е. находились бы в области с  ) и чтобы
) и чтобы

при  . Если при этом правая часть (17) существует и при
. Если при этом правая часть (17) существует и при 
то этот предел можно считать продолжением  за момент столкновения. Другую возможность подсказывает аналитический характер задачи. В самом деле, в комплексной области можно обойти особую точку
за момент столкновения. Другую возможность подсказывает аналитический характер задачи. В самом деле, в комплексной области можно обойти особую точку  и получить значения
и получить значения  при помощи аналитического продолжения. Разумеется, вопрос о физическом смысле «комплексного времени» будет бессодержательным: это такая же математическая абстракция, как и сама идея продолжения движения за момент столкновения.
при помощи аналитического продолжения. Разумеется, вопрос о физическом смысле «комплексного времени» будет бессодержательным: это такая же математическая абстракция, как и сама идея продолжения движения за момент столкновения.
Поскольку в особой точке  , из интеграла энергии находим, что
, из интеграла энергии находим, что

Поэтому решению с особенностью отвечает геодезическая метрики (13), уходящая в бесконечно удаленную (в смысле координат  ), но не в смысле длины дуги) точку
), но не в смысле длины дуги) точку  .
.
Многообразие М с метрикой (13) не является полным метрическим пространством, но становится таковым после пополнения точкой  . Согласно (14) (16), пополненное пространство
. Согласно (14) (16), пополненное пространство  изометричпо сфере при
изометричпо сфере при  эвклидовой плоскости при
эвклидовой плоскости при  и плоскости Лобачевского при
и плоскости Лобачевского при  Точке
Точке  при этом соответствует «Северный полюс»
при этом соответствует «Северный полюс»  сферы при
сферы при  и точка
и точка  в остальных случаях. На всех трех поверхностях дуга геодезической, оканчивающаяся в некоторой точке q, однозначно продолжается до полной геодезической, проходящей через q (рис. 3). Поэтому и геодезическая метрики (13), отвечающая решению кеплеровой задачи с особенностью, имеет однозначное продолжение за точку р. Легко видеть, что это продолжение является регуляризацией в смысле (17).
в остальных случаях. На всех трех поверхностях дуга геодезической, оканчивающаяся в некоторой точке q, однозначно продолжается до полной геодезической, проходящей через q (рис. 3). Поэтому и геодезическая метрики (13), отвечающая решению кеплеровой задачи с особенностью, имеет однозначное продолжение за точку р. Легко видеть, что это продолжение является регуляризацией в смысле (17).
Рассмотрим теперь ситуацию с точки зрения теории аналитических функций. Уравнения геодезических на сфере, евклидовой плоскости и плоскости Лобачевского не имеют вещественных особенностей. Поэтому вдоль геодезической координаты  связанные с
связанные с  формулами (14) (16), являются аналитическими (и даже элементарными) функциями длины дуги s, не имеющими на вещественной оси
формулами (14) (16), являются аналитическими (и даже элементарными) функциями длины дуги s, не имеющими на вещественной оси  особых точек. «Прокол» поверхности в точке-образе
особых точек. «Прокол» поверхности в точке-образе  порождает у функций
порождает у функций  «устранимую особую точку» (по стандартной терминологии курсов ТФКП). Ясно, что ее обход по пути, близкому к вещественной оси, приводит к тому же результату, что и продолжение
«устранимую особую точку» (по стандартной терминологии курсов ТФКП). Ясно, что ее обход по пути, близкому к вещественной оси, приводит к тому же результату, что и продолжение
геодезической в полном многообразии М. Что же касается переменных  в их зависимости от «физического времени» t, связанного с s соотношением (8), аналитичность нарушается.
в их зависимости от «физического времени» t, связанного с s соотношением (8), аналитичность нарушается.
В самом деле, пусть при  геодезическая проходит на
геодезическая проходит на  через «прокол». Учитывая, что
через «прокол». Учитывая, что  — длина дуги и обозначая через
— длина дуги и обозначая через  единичный вектор, касающийся геодезической в точке прокола, имеем
единичный вектор, касающийся геодезической в точке прокола, имеем

и (только для h < 0) из уравнения сферы

Отсюда в силу (14) (16) и (11) получаем

Далее, согласно (8),

и потому

Таким образом,  являются аналитическими функциями «униформизирующей переменной» s, причем скорость
являются аналитическими функциями «униформизирующей переменной» s, причем скорость  имеет относительно этой переменной простой полюс в точке столкновения,
имеет относительно этой переменной простой полюс в точке столкновения,  остаются голоморфными. Как функции t координаты и скорости имеют алгебраическую особенность (точку ветвления):
остаются голоморфными. Как функции t координаты и скорости имеют алгебраическую особенность (точку ветвления):

За момент столкновения эти функции могут быть продолжены (с сохранением вещественности) единственным образом.
Теперь рассмотрим, каким образом соответствие между фазовым потоком задачи Кеплера и геодезическим потоком на М связано с наличием дополнительных первых интегралов, отсутствующих в случае произвольной центральной силы (7). Поверхности  в высшей степени однородны: на каждой из них действует трехпараметрическая группа движений, т. е. преобразований,
в высшей степени однородны: на каждой из них действует трехпараметрическая группа движений, т. е. преобразований,  меняющих метрику, а, следовательно, и сохраняющих геодезический поток. Согласно теореме Нетер, каждой однопараметрической подгруппе из этой группы, а точнее говоря, ее инфинитезимальной образующей, т. е. элементу алгебры Ли, отвечает первый интеграл. Известно, что геодезические, параметризованные длиной дуги, являются экстремалями интеграла действия ([7], § 12)
меняющих метрику, а, следовательно, и сохраняющих геодезический поток. Согласно теореме Нетер, каждой однопараметрической подгруппе из этой группы, а точнее говоря, ее инфинитезимальной образующей, т. е. элементу алгебры Ли, отвечает первый интеграл. Известно, что геодезические, параметризованные длиной дуги, являются экстремалями интеграла действия ([7], § 12)

(точкой обозначено дифференцирование по  ).
).
Преобразования, не меняющие метрику, оставляют инвариантным и этот интеграл. Если  — векторное поле, порождающее однопараметрическую группу движений (т. е. являющееся ее инфинитезимальной образующей), то соответствующий первый интеграл выглядит так ([2], § 16):
— векторное поле, порождающее однопараметрическую группу движений (т. е. являющееся ее инфинитезимальной образующей), то соответствующий первый интеграл выглядит так ([2], § 16):

Подставляя сюда значения коэффициентов метрики (13) и используя (11), преобразуем это выражение к виду
 (20)
(20)
(разумеется, минусы можно было бы опустить без всякого ущерба, они оставлены лишь для согласования с классическими формулами).
Алгебра Ли группы движений поверхности  трехмерна. Векторные поля, отвечающие трем одпопараметрическим подгруппам, легко вычислить. Это будут:
трехмерна. Векторные поля, отвечающие трем одпопараметрическим подгруппам, легко вычислить. Это будут:

(вращение плоскости  около начала);
около начала);

(движения, оставляющие на месте геодезическую 

(движения, оставляющие на месте геодезическую 
В координатах  также соответствует вращению плоскости около начала (около оси Ох о для
также соответствует вращению плоскости около начала (около оси Ох о для  . Что же касается б) и в), то они отвечают при
. Что же касается б) и в), то они отвечают при  вращению сферы около двух взаимно перпендикулярных горизонтальных осей, проходящих через ее центр, с угловой скоростью
вращению сферы около двух взаимно перпендикулярных горизонтальных осей, проходящих через ее центр, с угловой скоростью  При
При  поля б) и в) порождают параллельные переносы плоскости
поля б) и в) порождают параллельные переносы плоскости  (это согласуется и с предельным переходом
(это согласуется и с предельным переходом  при котором радиус сферы
при котором радиус сферы  но линейная скорость ее «южного полюса», где
но линейная скорость ее «южного полюса», где  остается постоянной). При
остается постоянной). При  поля б) и в) порождают подгруппы неевклидовых параллельных переносов вдоль координатных осей
поля б) и в) порождают подгруппы неевклидовых параллельных переносов вдоль координатных осей  .
.
Подставляя выражения для  в (20), находим следующие первые интегралы:
в (20), находим следующие первые интегралы:

(это классический интеграл момента, см. (4)),

Последние два выражения можно преобразовать, используя уже найденный интеграл момента и интеграл энергии

откуда видно, что  суть не что иное, как компоненты так называемого «инвариантного вектора Лапласа». В
суть не что иное, как компоненты так называемого «инвариантного вектора Лапласа». В  этот вектор записывается так:
этот вектор записывается так:

а применительно к плоскому случаю, где

мы получаем для компонент вектора  найденные выше выражения.
найденные выше выражения.
Инвариантный вектор I и является тем дополнительным первым интегралом, который является специфическим для ньютоновского закона взаимодействия ([4], §15).
Найденные интегралы связаны соотношением

что и естественно, поскольку фазовое пространство плоской кеплеровой задачи четырехмерно. И потому не более трех первых интегралов могут быть независимыми.
Геометрическая интерпретация задачи Кеплера позволяет дать прозрачное истолкование употребляемых в небесной механике элементов: средней, истинной и эксцентрической аномалиям и т.п. ([44]). Заметим еще, что  равно эксцентриситету орбиты.
равно эксцентриситету орбиты.
| << Предыдущий параграф | Следующий параграф >> |
- Квазислучайные колебания и качественные вопросы небесной механики
- Часть 1. О некоторых математических проблемах в небесной механике
- § 1. Основная задача небесной механики
- § 2. Геометрическая интерпретация задачи Кеплера
- § 3. Задача трех тел. Аналитические свойства решений
- § 4. Финальные движения в задаче трех тел
- § 5. Эволюция системы. Проблема захвата
- Часть 2. Символическая динамика
- Часть 3. Квазислучайные колебания некоторых нелинейных систем
- § 1. Пульсирующая одномерная потенциальная яма
- § 2. Свойства отображения S
- § 3. Об одном частном случае задачи трех тел
- Литература
- О возможности захвата в небесной механике
- Литература
- О возможности захвата в задаче трех тел
- Обмен и захват в задаче трех тел
- Существование осциллирующих движений в задаче трех тел
- Финальные движения в задаче трех тел и символическая динамика