| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Протокол подбрасывания монеты
1. Алиса выбирает случайное число х из  вычисляет
вычисляет  и посылает у Бобу.
и посылает у Бобу.
2. Боб выбирает случайный бит  случайное число к из
случайное число к из  вычисляет
вычисляет  и посылает
и посылает  Алисе.
Алисе.
3. Алиса выбирает случайный бит с и посылает его Бобу.
4. Боб посылает Алисе 
5. Алиса проверяет, выполняется ли сравнение  уьдк
уьдк  Если да, то результатом выполнения протокола будет бит
Если да, то результатом выполнения протокола будет бит 
Значение  это криптографический аналог того ящика, о котором шла речь в описании физической реализации. В самом деле, из значения
это криптографический аналог того ящика, о котором шла речь в описании физической реализации. В самом деле, из значения  Алиса не может извлечь никакой информации о бите
Алиса не может извлечь никакой информации о бите  Поскольку к выбирается случайным образом из
Поскольку к выбирается случайным образом из  значение
значение  в обоих случаях, при
в обоих случаях, при  является случайным элементом группы, порожденной
является случайным элементом группы, порожденной  и поэтому не несет никакой информации о значении бита
и поэтому не несет никакой информации о значении бита  (разумеется, Алиса может попытаться обманывать, выбирая значение у, не принадлежащее группе, порожденной
(разумеется, Алиса может попытаться обманывать, выбирая значение у, не принадлежащее группе, порожденной  однако Боб легко обнаружит такой обман, проверяя сравнение
однако Боб легко обнаружит такой обман, проверяя сравнение 
С другой стороны, Боб может обманывать, т. е. открывать значение бита  по своему желанию и как 0, и как 1, но только в том случае, если он умеет вычислять дискретные логарифмы. Это вытекает из следующих соображений. Поскольку, как уже отмечалось выше, можно считать, что значение
по своему желанию и как 0, и как 1, но только в том случае, если он умеет вычислять дискретные логарифмы. Это вытекает из следующих соображений. Поскольку, как уже отмечалось выше, можно считать, что значение  заведомо принадлежит группе, порожденной
заведомо принадлежит группе, порожденной  существует единственное число а
существует единственное число а  такое, что
такое, что  Для того, чтобы открыть значение
Для того, чтобы открыть значение  Боб должен послать Алисе на шаге 4 число
Боб должен послать Алисе на шаге 4 число  а для того, чтобы открыть значение
а для того, чтобы открыть значение  число
число  Отсюда
Отсюда  Пусть
Пусть  полиномиальная вероятностная машина Тьюринга, которую Боб использует для осуществления такого обмана. Тогда следующий алгоритм будет вычислять дискретные логарифмы.
полиномиальная вероятностная машина Тьюринга, которую Боб использует для осуществления такого обмана. Тогда следующий алгоритм будет вычислять дискретные логарифмы.
1. Передаем входное значение у машине 
2. Получив в ответ значение  запоминаем состояние машины
запоминаем состояние машины 
3. Выбираем случайный бит с и передаем его 
4. Получив от  значения
значения  запоминаем эти величины, восстанавливаем ранее запомненное состояние машины
запоминаем эти величины, восстанавливаем ранее запомненное состояние машины  и переходим на шаг 3.
и переходим на шаг 3.
5. Как только среди пар  найдутся
найдутся  вычисляем
вычисляем  дискретный логарифм величины у.
дискретный логарифм величины у.
На основе этих соображений можно построить доказательство следующего утверждения: в предположении трудности задачи дискретного логарифмирования приведенный выше протокол подбрасывания монеты является стойким. Заметим, что для данного протокола достаточно весьма слабой формы этого предположения. Поскольку Алиса может прекратить выполнение протокола, если с момента передачи значения у Бобу до момента получения от него значений  и к проходит более, скажем, 30 секунд, достаточно предположить, что задача дискретного логарифмирования не может быть решена за такое время.
и к проходит более, скажем, 30 секунд, достаточно предположить, что задача дискретного логарифмирования не может быть решена за такое время.
Если из приведенного выше протокола подбрасывания монеты вычленить шаги 1, 2 и 4, то получим так называемый протокол привязки к биту (bit commitment). Шаги 1 и 2 в таком протоколе называются этапом привязки, а шаг 4 — этапом открытия бита. В этом протоколе для значения  в которое упаковывается бит
в которое упаковывается бит  (аналог ящика в физической реализации) обычно используется термин блоб (blob), для Алисы — получатель, а для Боба — отправитель. Говоря неформально, от протокола привязки к биту требуется такая конструкция блоба, которая обеспечивает одновременное выполнение следующих двух требований:
(аналог ящика в физической реализации) обычно используется термин блоб (blob), для Алисы — получатель, а для Боба — отправитель. Говоря неформально, от протокола привязки к биту требуется такая конструкция блоба, которая обеспечивает одновременное выполнение следующих двух требований:
1) после выполнения этапа привязки получатель не может самостоятельно определить, какой бит упакован в блоб;
2) на этапе открытия бита отправитель может открыть любой блоб либо только как 0, либо только как 1.
В нашем случае требование 1) выполняется безусловно, т. е. вне зависимости от того, какими вычислительными ресурсами обладает получатель, он не может самостоятельно узнать, какой бит находится в блобе. В таких случаях говорят, что протокол гарантирует безусловную безопасность отправителя. В то же время безопасность получателя основывается на недоказанном предположении о вычислительной трудности задачи дискретного логарифмирования. Такая асимметрия типична для многих типов криптографических протоколов. Она имеется, например, в доказательствах с вычислительно нулевым разглашением. Но существует и другой тип протоколов привязки к биту, в которых уже безопасность получателя безусловна, а безопасность отправителя основывается на недоказанных предположениях. Для многих типов криптографических протоколов с указанной выше асимметрией построены такого рода двойственные протоколы.
Протокол привязки к биту — один из основных типов примитивных криптографических протоколов. Он находит многочисленные
применения в криптографии. В качестве иллюстрации рассмотрим способ повышения эффективности доказательств с нулевым разглашением на примере рассмотренного в главе 2 протокола для задачи ИЗОМОРФИЗМ ГРАФОВ. В этом протоколе главная проблема — большое количество раундов, растущее пропорционально размеру графа. Достаточно естественная идея — выполнить все эти последовательные раунды параллельно. На первом шаге  выбирает
выбирает  случайных перестановок
случайных перестановок  вычисляет
вычисляет  и посылает все эти
и посылает все эти  графов
графов  На втором шаге V выбирает
На втором шаге V выбирает  случайных битов
случайных битов  и посылает их
и посылает их  а на третьем
а на третьем  формирует все
формирует все  требуемых перестановок и посылает их
требуемых перестановок и посылает их 
Но будет ли такой протокол доказательством с нулевым разглашением? Прежде всего заметим, что этот протокол трехраундовый, а как показывает уже упоминавшийся в разделе 2 результат Гольдрайха и Кравчика, трехраундовых доказательств с нулевым разглашением скорее всего не существует. Тот метод, который использовался в главе 2 для построения моделирующей машины, срабатывал, поскольку при последовательном выполнении протокола моделирующая машина могла угадать на каждом раунде запрос  проверяющего с вероятностью 1/2. В параллельном же варианте вероятность угадывания равна
проверяющего с вероятностью 1/2. В параллельном же варианте вероятность угадывания равна  т. е. пренебрежимо мала. Кроме того, проверяющий формирует свои запросы
т. е. пренебрежимо мала. Кроме того, проверяющий формирует свои запросы  уже получив от
уже получив от  все графы
все графы  и может выбирать их (запросы) зависящими достаточно сложным образом от всех этих графов. Это также представляется непреодолимым препятствием при попытке построения моделирующей машины.
и может выбирать их (запросы) зависящими достаточно сложным образом от всех этих графов. Это также представляется непреодолимым препятствием при попытке построения моделирующей машины.
Зависимость  от
от  можно предотвратить следующим образом. Проверяющий V выбирает свои запросы в самом начале выполнения протокола, еще до того, как увидит
можно предотвратить следующим образом. Проверяющий V выбирает свои запросы в самом начале выполнения протокола, еще до того, как увидит  Каждый бит
Каждый бит  упаковывается в блоб
упаковывается в блоб  и V посылает все блобы
и V посылает все блобы  доказывающему. Только после этого
доказывающему. Только после этого  посылает V все графы
посылает V все графы  В ответ V открывает блобы, а
В ответ V открывает блобы, а  получив
получив  формирует требуемые перестановки и посылает их
формирует требуемые перестановки и посылает их 
В результате количество раундов в протоколе возросло, но осталось константой (достаточно 5 раундов). При использовании протокола привязки к биту, обеспечивающего безусловную безопасность отправителя, даже обладающий неограниченными вычислительными возможностями доказывающий не может извлечь из блобов  никакой информации о запросах
никакой информации о запросах  Поэтому корректность протокола сохраняется.
Поэтому корректность протокола сохраняется.
Итак, второе из указанных выше препятствий устранено. А как быть с первым? Оказывается, моделирующей машине совсем необязательно угадывать запросы  Следующая замечательная идея
Следующая замечательная идея
многократно использовалась в работах, посвященных криптографическим протоколам (см. [15]). Моделирующая машина  получив от V блобы, запоминает состояние машины V, выбирает графы
получив от V блобы, запоминает состояние машины V, выбирает графы  как случайные перестановки графа
как случайные перестановки графа  и передает их
и передает их  В ответ V открывает блобы, и
В ответ V открывает блобы, и  получает запросы
получает запросы  После этого моделирующая машина формирует графы
После этого моделирующая машина формирует графы  как ответы на запросы
как ответы на запросы  восстанавливает запомненное состояние машины V и передает ей
восстанавливает запомненное состояние машины V и передает ей  Поскольку протокол привязки к биту предполагается стойким, машина
Поскольку протокол привязки к биту предполагается стойким, машина  вновь получит те же самые биты
вновь получит те же самые биты  и успешно завершит моделирование, выдавая
и успешно завершит моделирование, выдавая  требуемые перестановки, а также блобы
требуемые перестановки, а также блобы  и те сообщения, которые были выданы машиной V для их открытия.
и те сообщения, которые были выданы машиной V для их открытия.
Предположим, что то предположение, на котором основывается стойкость протокола привязки к биту, стало доказанным фактом. Например, удалось доказать, что не существует полиномиальных алгоритмов для задачи дискретного логарифмирования. Даже в этом случае полиномиально ограниченный отправитель в приведенном выше протоколе привязки к биту может угадать х хоть и с малой, но ненулевой вероятностью, и обмануть получателя. Из-за этого рассмотренный нами параллельный вариант протокола будет доказательством лишь со статистически нулевым разглашением. А исходный последовательный вариант (см. главу 2) обладал свойством абсолютно нулевого разглашения. В работе Беллара, Микали и Островски [15], где был предложен описанный выше способ преобразования последовательных протоколов в параллельные, используется специальная конструкция блобов для задачи ИЗОМОРФИЗМ ГРАФОВ, сохраняющая свойство абсолютно нулевого разглашения.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму изданию
- Глава 1. Основные понятия криптографии
- 2. Предмет криптографии
- 3. Математические основы
- 4. Новые направления
- 5. Заключение
- Глава 2. Криптография и теория сложности
- 2. Криптография и гипотеза P != NP
- 3. Односторонние функции
- 4. Псевдослучайные генераторы
- 5. Доказательства с нулевым разглашением
- Глава 3. Криптографические протоколы
- 2. Целостность. Протоколы аутентификации и электронной подписи
- Схема аутентификации Шнорра
- Схема электронной подписи Шнорра
- 3. Неотслеживаемость. Электронные деньги
- 4. Протоколы типа «подбрасывание монеты по телефону»
- Протокол подбрасывания монеты
- 5. Еще раз о разделении секрета
- 6. Поиграем в «кубики». Протоколы голосования
- Протокол Шаума и Педерсена
- 7. За пределами стандартных предположений. Конфиденциальная передача сообщений
- 8. Вместо заключения
- Глава 4. Алгоритмические проблемы теории чисел
- 2. Система шифрования RSA
- 3. Сложность теоретико-числовых алгоритмов
- 4. Как отличить составное число от простого
- 5. Алгоритм, доказывающий непростоту числа
- 5. Как строить большие простые числа
- 6. Как проверить большое число на простоту
- 7. Как раскладывают составные числа на множители
- 8. Дискретное логарифмирование
- 9. Заключение
- Глава 5. Математика разделения секрета
- 2. Разделение секрета для произвольных структур доступа
- 3. Линейное разделение секрета.
- 4. Идеальное разделение секрета и матроиды
- Глава 6. Компьютер и криптография
- 2. Немного теории
- Что надо знать перед написанием программы шифрования
- 3. Как зашифровать файл?
- 4. Поучимся на чужих ошибках
- 5. Вместо заключения
- Глава 7. Олимпиады по криптографии для школьников
- 2. Шифры замены
- А. Конан Дойл, «Пляшущие человечки»
- Ж. Верн, «Путешествие к центру Земли»
- 3. Шифры перестановки
- 4. Многоалфавитные шифры замены с периодическим ключом
- 5. Условия задач олимпиад по математике и криптографии
- 6. Указания и решения
- Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
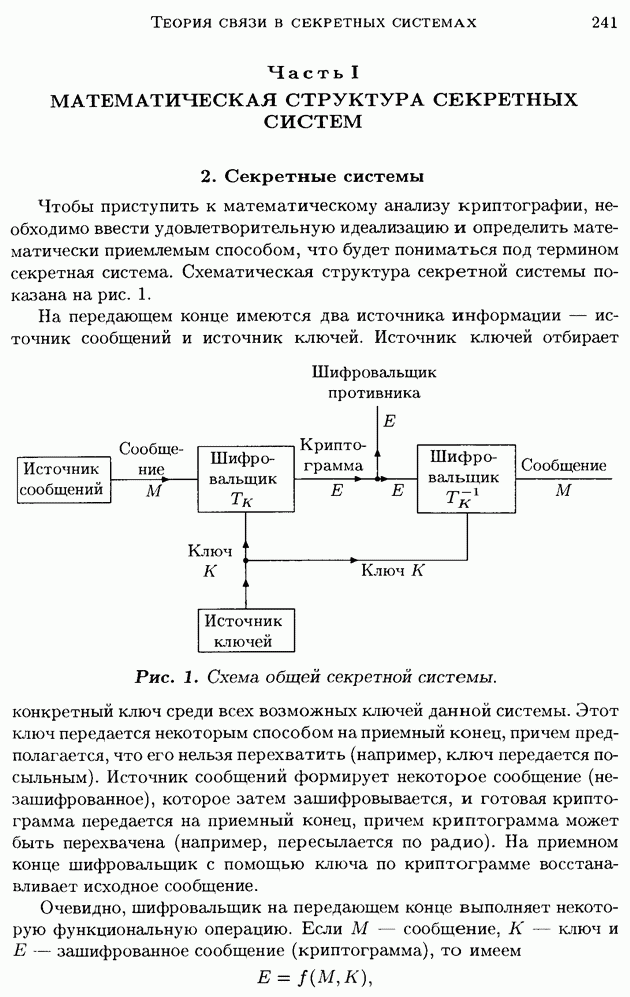
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность