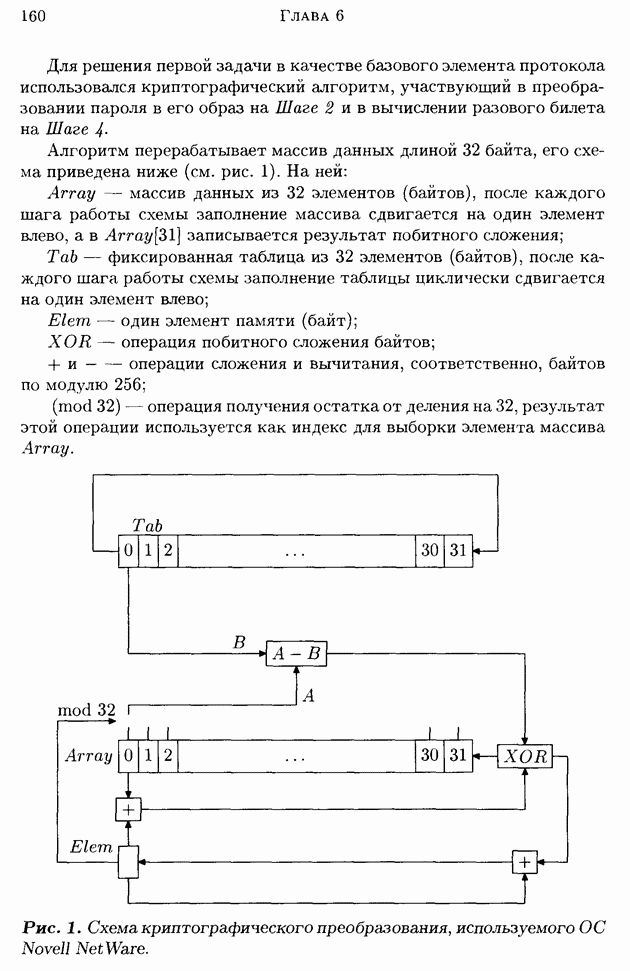
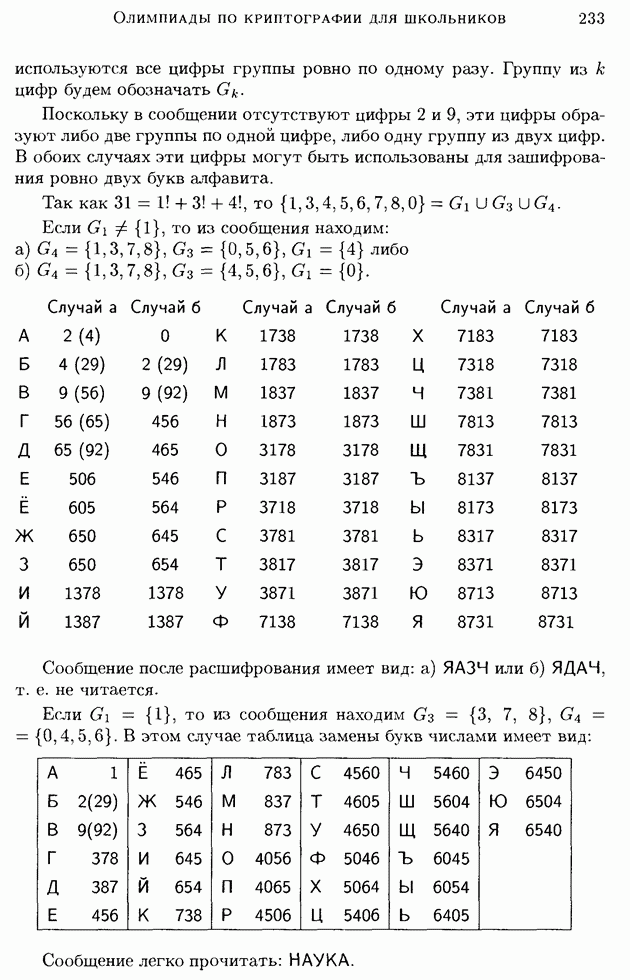
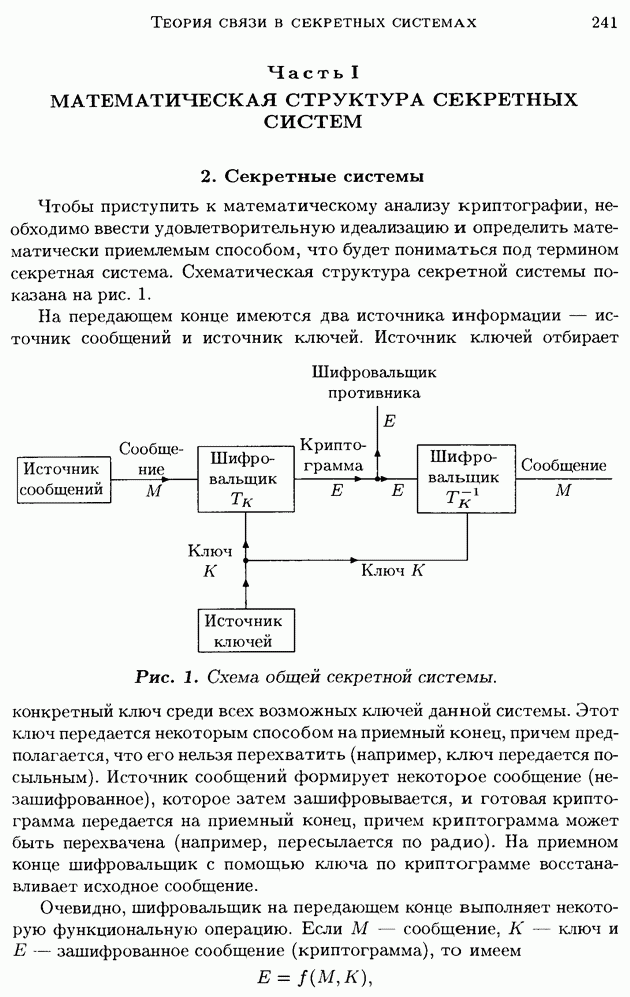
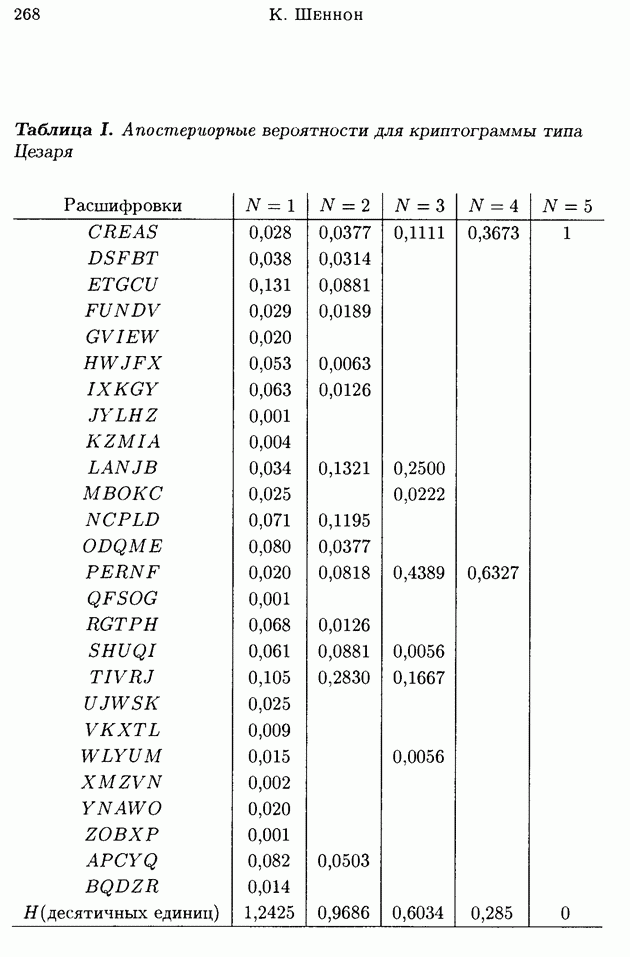
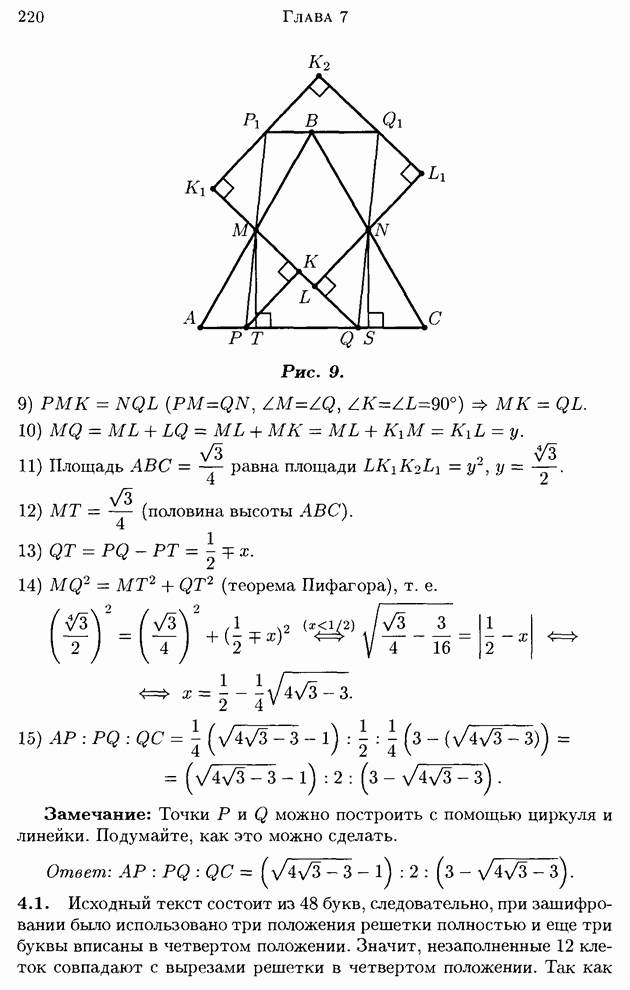| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Односторонние функции
Говоря неформально, односторонняя функция — это эффективно вычислимая функция, для задачи инвертирования которой не существует эффективных алгоритмов. Под инвертированием понимается массовая задача нахождения по заданному значению функции одного (любого) значения из прообраза (заметим, что обратная функция, вообще говоря, может не существовать).
Поскольку понятие односторонней функции — центральное в математической криптографии, ниже мы даем его формальное определение.
Пусть  множество всех двоичных строк длины
множество всех двоичных строк длины  Под функцией
Под функцией  мы понимаем семейство
мы понимаем семейство  где
где  Для простоты изложения мы предполагаем, что
Для простоты изложения мы предполагаем, что  пробегает весь натуральный ряд и что каждая из функций
пробегает весь натуральный ряд и что каждая из функций  всюду определена.
всюду определена.
Функция  называется честной, если существует полином
называется честной, если существует полином  такой, что
такой, что  для всех
для всех 
Определение 1. Честная функция  называется односторонней, если
называется односторонней, если
1. Существует полиномиальный алгоритм, который для всякого х вычисляет 
2. Для любой полиномиальной вероятностной машины Тьюринга А выполнено следующее. Пусть строка х выбрана наудачу из множества  (обозначается
(обозначается  Тогда для любого полинома
Тогда для любого полинома  и всех достаточно больших
и всех достаточно больших 

Вероятность здесь определяется случайным выбором строки х и случайными величинами, которые А использует в своей работе.
Условие 2 качественно означает следующее. Любая полиномиальная вероятностная машина Тьюринга А может по данному у найти х из уравнения  лишь с пренебрежимо малой вероятностью.
лишь с пренебрежимо малой вероятностью.
Заметим, что требование честности нельзя опустить. Поскольку длина входного слова  машины А равна
машины А равна  ей может не хватить полиномиального (от
ей может не хватить полиномиального (от  ) времени просто на выписывание строки х, если
) времени просто на выписывание строки х, если  слишком сильно «сжимает» входные значения.
слишком сильно «сжимает» входные значения.
Ясно, что из предположения о существовании односторонних функций следует, что  Однако, не исключена следующая ситуация:
Однако, не исключена следующая ситуация:  но односторонних функций нет.
но односторонних функций нет.
Существование односторонних функций является необходимым условием для стойкости многих типов криптографических схем. В некоторых случаях этот факт устанавливается достаточно просто. Обратимся опять к примеру 1. Рассмотрим функцию  такую, что
такую, что  Она вычислима с помощью алгоритма
Она вычислима с помощью алгоритма  за полиномиальное время. Покажем, что если
за полиномиальное время. Покажем, что если  не односторонняя функция, то криптосистема
не односторонняя функция, то криптосистема
нестойкая. Предположим, что существует полиномиальный вероятностный алгоритм А, который инвертирует  с вероятностью по крайней мере
с вероятностью по крайней мере  для некоторого полинома
для некоторого полинома  Здесь
Здесь  длина ключа
длина ключа  Противник может подать на вход алгоритму А ключ
Противник может подать на вход алгоритму А ключ  и получить с указанной вероятностью некоторое значение
и получить с указанной вероятностью некоторое значение  из прообраза. Далее противник подает
из прообраза. Далее противник подает  на вход алгоритма
на вход алгоритма  и получает пару ключей
и получает пару ключей  Хотя
Хотя  не обязательно совпадает с
не обязательно совпадает с  тем не менее, по определению криптосистемы
тем не менее, по определению криптосистемы  для любого открытого текста
для любого открытого текста  Поскольку
Поскольку  найден с вероятностью по крайней мере
найден с вероятностью по крайней мере  которая в криптографии не считается пренебрежимо малой, криптосистема нестойкая.
которая в криптографии не считается пренебрежимо малой, криптосистема нестойкая.
Для других криптографических схем подобный результат доказывается не столь просто. В работе Импальяццо и Луби [7] доказана необходимость односторонних функций для существования целого ряда стойких криптографических схем.
Из всего сказанного следует, что предположение о существовании односторонних функций является самым слабым криптографическим предположением, которое может оказаться достаточным для доказательства существования стойких криптографических схем различных типов. На выяснение того, является ли это условие и в самом деле достаточным, направлены значительные усилия специалистов. Трудность задачи построения криптографических схем из односторонних функций можно пояснить на следующем примере. Пусть  односторонняя функция и нам требуется построить криптосистему с секретным ключом. В такой криптосистеме имеется только один ключ — секретный, который известен и отправителю, и получателю шифрованного сообщения. Алгоритмы шифрования
односторонняя функция и нам требуется построить криптосистему с секретным ключом. В такой криптосистеме имеется только один ключ — секретный, который известен и отправителю, и получателю шифрованного сообщения. Алгоритмы шифрования  и дешифрования
и дешифрования  оба зависят от этого секретного ключа К и таковы, что
оба зависят от этого секретного ключа К и таковы, что  для любого открытого текста
для любого открытого текста  Ясно, что если криптограмму
Ясно, что если криптограмму  сообщения
сообщения  вычислять как
вычислять как  то противник, перехвативший
то противник, перехвативший  может вычислить
может вычислить  лишь с пренебрежимо малой вероятностью. Но во-первых, непонятно, каким образом сможет восстановить сообщение
лишь с пренебрежимо малой вероятностью. Но во-первых, непонятно, каким образом сможет восстановить сообщение  из криптограммы законный получатель? Во-вторых, из того, что функция
из криптограммы законный получатель? Во-вторых, из того, что функция  односторонняя следует лишь, что противник не может вычислить все сообщение целиком. А это — весьма низкий уровень стойкости. Желательно, чтобы противник, знающий криптограмму
односторонняя следует лишь, что противник не может вычислить все сообщение целиком. А это — весьма низкий уровень стойкости. Желательно, чтобы противник, знающий криптограмму  не мог вычислить ни одного бита открытого текста.
не мог вычислить ни одного бита открытого текста.
На настоящий момент доказано, что существование односторонних функций является необходимым и достаточным условием для существования стойких криптосистем с секретным ключом, а также стойких криптографических протоколов нескольких типов, включая протоколы электронной подписи. С другой стороны, имеется результат
Импальяццо и Рудиха [9], который является достаточно сильным аргументом в пользу того, что для некоторых типов криптографических схем (включая протоколы распределения ключей типа Диффи-Хеллмана) требуются более сильные предположения, чем предположение о существовании односторонних функций. К сожалению, этот результат слишком сложный, чтобы его можно было разъяснить в настоящей главе.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму изданию
- Глава 1. Основные понятия криптографии
- 2. Предмет криптографии
- 3. Математические основы
- 4. Новые направления
- 5. Заключение
- Глава 2. Криптография и теория сложности
- 2. Криптография и гипотеза P != NP
- 3. Односторонние функции
- 4. Псевдослучайные генераторы
- 5. Доказательства с нулевым разглашением
- Глава 3. Криптографические протоколы
- 2. Целостность. Протоколы аутентификации и электронной подписи
- Схема аутентификации Шнорра
- Схема электронной подписи Шнорра
- 3. Неотслеживаемость. Электронные деньги
- 4. Протоколы типа «подбрасывание монеты по телефону»
- Протокол подбрасывания монеты
- 5. Еще раз о разделении секрета
- 6. Поиграем в «кубики». Протоколы голосования
- Протокол Шаума и Педерсена
- 7. За пределами стандартных предположений. Конфиденциальная передача сообщений
- 8. Вместо заключения
- Глава 4. Алгоритмические проблемы теории чисел
- 2. Система шифрования RSA
- 3. Сложность теоретико-числовых алгоритмов
- 4. Как отличить составное число от простого
- 5. Алгоритм, доказывающий непростоту числа
- 5. Как строить большие простые числа
- 6. Как проверить большое число на простоту
- 7. Как раскладывают составные числа на множители
- 8. Дискретное логарифмирование
- 9. Заключение
- Глава 5. Математика разделения секрета
- 2. Разделение секрета для произвольных структур доступа
- 3. Линейное разделение секрета.
- 4. Идеальное разделение секрета и матроиды
- Глава 6. Компьютер и криптография
- 2. Немного теории
- Что надо знать перед написанием программы шифрования
- 3. Как зашифровать файл?
- 4. Поучимся на чужих ошибках
- 5. Вместо заключения
- Глава 7. Олимпиады по криптографии для школьников
- 2. Шифры замены
- А. Конан Дойл, «Пляшущие человечки»
- Ж. Верн, «Путешествие к центру Земли»
- 3. Шифры перестановки
- 4. Многоалфавитные шифры замены с периодическим ключом
- 5. Условия задач олимпиад по математике и криптографии
- 6. Указания и решения
- Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность