| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Сложность теоретико-числовых алгоритмов
Сложность алгоритмов теории чисел обычно принято измерять количеством арифметических операций (сложений, вычитаний, умножений и делений с остатком), необходимых для выполнения всех действий, предписанных алгоритмом. Впрочем, это определение не учитывает величины чисел, участвующих в вычислениях. Ясно, что перемножить два стозначных числа значительно сложнее, чем два однозначных, хотя при этом и в том, и в другом случае выполняется лишь одна арифметическая операция. Поэтому иногда учитывают еще и величину чисел, сводя дело к так называемым битовым операциям, т. е. оценивая количество необходимых операций с цифрами 0 и 1, в двоичной записи чисел. Это зависит от рассматриваемой задачи, от целей автора и т. д.
На первый взгляд странным также кажется, что операции умножения и деления приравниваются по сложности к операциям сложения и вычитания. Житейский опыт подсказывает, что умножать числа значительно сложнее, чем складывать их. В действительности же, вычисления можно организовать так, что на умножение или деление больших чисел понадобится не намного больше битовых операций, чем на сложение. В книге [7] описывается алгоритм Шёнхаге - Штрассена, основанный на так называемом быстром преобразовании Фурье, и требующий  битовых операций для умножения двух
битовых операций для умножения двух  -разрядных двоичных чисел. Таким же количеством битовых операций можно обойтись при выполнении деления с остатком двух двоичных чисел, записываемых не более, чем
-разрядных двоичных чисел. Таким же количеством битовых операций можно обойтись при выполнении деления с остатком двух двоичных чисел, записываемых не более, чем  цифрами. Для сравнения отметим, что сложение
цифрами. Для сравнения отметим, что сложение  -разрядных двоичных чисел требует
-разрядных двоичных чисел требует  битовых операций.
битовых операций.
Говоря в этой статье о сложности алгоритмов, мы будем иметь в виду количество арифметических операций. При построении эффективных алгоритмов и обсуждении верхних оценок сложности обычно хватает интуитивных понятий той области математики, которой принадлежит алгоритм. Формализация же этих понятий требуется лишь тогда, когда речь идет об отсутствии алгоритма или доказательстве нижних оценок сложности. Более детальное и формальное обсуждение этих вопросов см. в главе 2.
Приведем теперь примеры достаточно быстрых алгоритмов с оценками их сложности. Здесь и в дальнейшем мы не будем придерживаться формального описания алгоритмов, стараясь в первую очередь объяснить смысл выполняемых действий.
Следующий алгоритм вычисляет  за
за  арифметических операций. При этом, конечно, предполагается, что натуральные числа
арифметических операций. При этом, конечно, предполагается, что натуральные числа  не превосходят по величине
не превосходят по величине 
1. Алгоритм вычисления a^d (mod m)
1. Представим  в двоичной системе счисления
в двоичной системе счисления  где
где  цифры в двоичном представлении, равны 0 или
цифры в двоичном представлении, равны 0 или 
2. Положим  и затем для
и затем для  вычислим
вычислим

 есть искомый вычет
есть искомый вычет 
Справедливость этого алгоритма вытекает из сравнения

легко доказываемого индукцией по 
Так как каждое вычисление на шаге 2 требует не более трех умножений по модулю  и этот шаг выполняется
и этот шаг выполняется  раз, то сложность алгоритма может быть оценена величиной
раз, то сложность алгоритма может быть оценена величиной 
Второй алгоритм — это классический алгоритм Евклида вычисления наибольшего общего делителя целых чисел. Мы предполагаем заданными два натуральных числа  и вычисляем их наибольший общий делитель
и вычисляем их наибольший общий делитель 
2. Алгоритм Евклида
1. Вычислим  остаток от деления числа а на
остаток от деления числа а на 
2. Если  то
то  есть искомое число.
есть искомое число.
3. Если  то заменим пару чисел
то заменим пару чисел  парой
парой  и перейдем к шагу 1.
и перейдем к шагу 1.
Не останавливаясь на объяснении, почему алгоритм действительно находит  докажем некоторую оценку его сложности. Теорема 3. При вычислении наибольшего общего делителя
докажем некоторую оценку его сложности. Теорема 3. При вычислении наибольшего общего делителя  с помощью алгоритма Евклида будет выполнено не более
с помощью алгоритма Евклида будет выполнено не более  операций деления с остатком, где
операций деления с остатком, где  есть количество цифр в десятичной записи меньшего из чисел
есть количество цифр в десятичной записи меньшего из чисел 
Доказательство. Положим  и определим
и определим  последовательность делителей, появляющихся в процессе выполнения шага 1 алгоритма Евклида. Тогда
последовательность делителей, появляющихся в процессе выполнения шага 1 алгоритма Евклида. Тогда

Пусть также  — последовательность Фибоначчи. Индукцией по
— последовательность Фибоначчи. Индукцией по  от
от  до
до  легко доказывается неравенство
легко доказывается неравенство  . А так как
. А так как  то имеем неравенства
то имеем неравенства 
Немного подправив алгоритм Евклида, можно достаточно быстро решать сравнения  при условии, что
при условии, что  Эта задача равносильна поиску целых решений уравнения
Эта задача равносильна поиску целых решений уравнения 
3. Алгоритм решения уравнения ах + by = 1
0. Определим матрицу 
1. Вычислим  остаток от деления числа а на
остаток от деления числа а на 
2. Если  то второй столбец матрицы
то второй столбец матрицы  дает вектор
дает вектор  решений уравнения.
решений уравнения.
3. Если  то заменим матрицу
то заменим матрицу  матрицей
матрицей  Заменим пару чисел
Заменим пару чисел  парой
парой  и перейдем к шагу 1.
и перейдем к шагу 1.
Если обозначить через  матрицу
матрицу  возникающую в процессе работы алгоритма перед шагом 2 после к делений с остатком (шаг 1),
возникающую в процессе работы алгоритма перед шагом 2 после к делений с остатком (шаг 1),
то в обозначениях из доказательства теоремы 1 в этот момент выполняется векторное равенство  Его легко доказать индукцией по k. Поскольку числа
Его легко доказать индукцией по k. Поскольку числа  взаимно просты, имеем
взаимно просты, имеем  и это доказывает, что алгоритм действительно дает решение уравнения
и это доказывает, что алгоритм действительно дает решение уравнения  Буквой
Буквой  мы обозначили количество делений с остатком, которое в точности такое же, как и в алгоритме Евклида.
мы обозначили количество делений с остатком, которое в точности такое же, как и в алгоритме Евклида.
Три приведенных выше алгоритма относятся к разряду так называемых полиномиальных алгоритмов. Это название носят алгоритмы, сложность которых оценивается сверху степенным образом в зависимости от длины записи входящих чисел (см. подробности в главе 2). Если наибольшее из чисел, подаваемых на вход алгоритма, не превосходит  то сложность алгоритмов этого типа оценивается величиной
то сложность алгоритмов этого типа оценивается величиной  где с — некоторая абсолютная постоянная. Во всех приведенных выше примерах
где с — некоторая абсолютная постоянная. Во всех приведенных выше примерах 
Полиномиальные алгоритмы в теории чисел — большая редкость. Да и оценки сложности алгоритмов чаще всего опираются на какие-либо не доказанные, но правдоподобные гипотезы, обычно относящиеся к аналитической теории чисел.
Для некоторых задач эффективные алгоритмы вообще не известны. Иногда в таких случаях все же можно предложить последовательность действий, которая, «если повезет», быстро приводит к требуемому результату. Существует класс так называемых вероятностных алгоритмов, которые дают правильный результат, но имеют вероятностную оценку времени работы. Обычно работа этих алгоритмов зависит от одного или нескольких параметров. В худшем случае они работают достаточно долго. Но удачный выбор параметра определяет быстрое завершение работы. Такие алгоритмы, если множество «хороших» значений параметров велико, на практике работают достаточно эффективно, хотя и не имеют хороших оценок сложности.
Мы будем иногда использовать слова детерминированный алгоритм, чтобы отличать алгоритмы в обычном смысле от вероятностных алгоритмов.
Как пример, рассмотрим вероятностный алгоритм, позволяющий эффективно находить решения полиномиальных сравнений по простому модулю. Пусть  простое число, которое предполагается большим, и
простое число, которое предполагается большим, и  многочлен, степень которого предполагается ограниченной. Задача состоит в отыскании решений сравнения
многочлен, степень которого предполагается ограниченной. Задача состоит в отыскании решений сравнения

Например, речь может идти о решении квадратичных сравнений, если степень многочлена  равна 2. Другими словами, мы должны отыскать в поле
равна 2. Другими словами, мы должны отыскать в поле  все элементы, удовлетворяющие уравнению
все элементы, удовлетворяющие уравнению 
Согласно малой теореме Ферма, все элементы поля  являются однократными корнями многочлена
являются однократными корнями многочлена  Поэтому, вычислив наибольший общий делитель
Поэтому, вычислив наибольший общий делитель  мы найдем многочлен
мы найдем многочлен  множество корней которого в поле
множество корней которого в поле  совпадает с множеством корней многочлена
совпадает с множеством корней многочлена  причем все эти корни однократны. Если окажется, что многочлен
причем все эти корни однократны. Если окажется, что многочлен  имеет нулевую степень, т. е. лежит в поле
имеет нулевую степень, т. е. лежит в поле  это будет означать, что сравнение (8) не имеет решений.
это будет означать, что сравнение (8) не имеет решений.
Для вычисления многочлена  удобно сначала вычислить многочлен
удобно сначала вычислить многочлен  пользуясь алгоритмом, подобным описанному выше алгоритму возведения в степень (напомним, что число
пользуясь алгоритмом, подобным описанному выше алгоритму возведения в степень (напомним, что число  предполагается большим). А затем с помощью аналога алгоритма Евклида вычислить
предполагается большим). А затем с помощью аналога алгоритма Евклида вычислить  Все это выполняется за полиномиальное количество арифметических операций.
Все это выполняется за полиномиальное количество арифметических операций.
Таким образом, обсуждая далее задачу нахождения решений сравнения (8), мы можем предполагать, что в кольце многочленов  справедливо равенство
справедливо равенство

4. Алгоритм нахождения делителей многочлена f(x) в кольце Fp[x]
1. Выберем каким-либо способом элемент 
2. Вычислим наибольший общий делитель

3. Если многочлен  окажется собственным делителем
окажется собственным делителем  то многочлен
то многочлен  распадется на два множителя и с каждым из них независимо нужно будет проделать все операции, предписываемые настоящим алгоритмом для многочлена
распадется на два множителя и с каждым из них независимо нужно будет проделать все операции, предписываемые настоящим алгоритмом для многочлена 
4. Если окажется, что  или
или  следует перейти к шагу 1 и, выбрав новое значение 6, продолжить выполнение алгоритма.
следует перейти к шагу 1 и, выбрав новое значение 6, продолжить выполнение алгоритма.
Количество операций на шаге 2 оценивается величиной  если вычисления проводить так, как это указывалось выше при нахождении
если вычисления проводить так, как это указывалось выше при нахождении  Выясним теперь, сколь долго придется выбирать числа 6, пока на шаге 2 не будет найден собственный делитель
Выясним теперь, сколь долго придется выбирать числа 6, пока на шаге 2 не будет найден собственный делитель 
Количество решений уравнения  в поле
в поле  не превосходит
не превосходит  Это означает, что подмножество
Это означает, что подмножество  состоящее из элементов 6, удовлетворяющих условиям
состоящее из элементов 6, удовлетворяющих условиям

состоит не менее, чем из  элементов. Учитывая теперь, что каждый ненулевой элемент
элементов. Учитывая теперь, что каждый ненулевой элемент  удовлетворяет одному из равенств
удовлетворяет одному из равенств 
либо  заключаем, что для
заключаем, что для  одно из чисел
одно из чисел  а 2 будет корнем многочлена
а 2 будет корнем многочлена  другое — нет. Для таких элементов 5 многочлен
другое — нет. Для таких элементов 5 многочлен  определенный на шаге 2 алгоритма, будет собственным делителем многочлена
определенный на шаге 2 алгоритма, будет собственным делителем многочлена 
Итак, существует не менее «удачных» выборов элемента 6, при которых на шаге 2 алгоритма многочлен  распадется на два собственных множителя. Следовательно, при «случайном» выборе элемента
распадется на два собственных множителя. Следовательно, при «случайном» выборе элемента  вероятность того, что многочлен не разложится на множители после к повторений шагов алгоритма 1-4, не превосходит
вероятность того, что многочлен не разложится на множители после к повторений шагов алгоритма 1-4, не превосходит  Вероятность с ростом к убывает очень быстро. И действительно, на практике этот алгоритм работает достаточно эффективно.
Вероятность с ростом к убывает очень быстро. И действительно, на практике этот алгоритм работает достаточно эффективно.
Заметим, что при оценке вероятности мы использовали только два корня многочлена  При
При  эта вероятность, конечно, еще меньше. Более тонкий анализ с использованием оценок А. Вейля для сумм характеров показывает, что вероятность для многочлена
эта вероятность, конечно, еще меньше. Более тонкий анализ с использованием оценок А. Вейля для сумм характеров показывает, что вероятность для многочлена  не распасться на множители при однократном проходе шагов алгоритма 1-4, не превосходит
не распасться на множители при однократном проходе шагов алгоритма 1-4, не превосходит  Здесь постоянная в
Здесь постоянная в  зависит от
зависит от  Детали доказательства см. в [24]. В настоящее время известно элементарное доказательство оценки А. Вейля (см. [9]).
Детали доказательства см. в [24]. В настоящее время известно элементарное доказательство оценки А. Вейля (см. [9]).
В книге [6] описывается принадлежащий Берлекэмпу детерминированный алгоритм решения сравнения (8), требующий  арифметических операций. Он практически бесполезен при больших
арифметических операций. Он практически бесполезен при больших  а вот при маленьких
а вот при маленьких  и не очень больших
и не очень больших  он работает не очень долго.
он работает не очень долго.
Если в сравнении (8) заменить простой модуль  составным модулем
составным модулем  то задача нахождения решений соответствующего сравнения становится намного более сложной. Известные алгоритмы ее решения основаны на сведении сравнения к совокупности сравнений (8) по простым модулям — делителям
то задача нахождения решений соответствующего сравнения становится намного более сложной. Известные алгоритмы ее решения основаны на сведении сравнения к совокупности сравнений (8) по простым модулям — делителям  следовательно, они требуют разложения числа
следовательно, они требуют разложения числа  на простые сомножители, что, как уже указывалось, является достаточно трудоемкой задачей.
на простые сомножители, что, как уже указывалось, является достаточно трудоемкой задачей.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму изданию
- Глава 1. Основные понятия криптографии
- 2. Предмет криптографии
- 3. Математические основы
- 4. Новые направления
- 5. Заключение
- Глава 2. Криптография и теория сложности
- 2. Криптография и гипотеза P != NP
- 3. Односторонние функции
- 4. Псевдослучайные генераторы
- 5. Доказательства с нулевым разглашением
- Глава 3. Криптографические протоколы
- 2. Целостность. Протоколы аутентификации и электронной подписи
- Схема аутентификации Шнорра
- Схема электронной подписи Шнорра
- 3. Неотслеживаемость. Электронные деньги
- 4. Протоколы типа «подбрасывание монеты по телефону»
- Протокол подбрасывания монеты
- 5. Еще раз о разделении секрета
- 6. Поиграем в «кубики». Протоколы голосования
- Протокол Шаума и Педерсена
- 7. За пределами стандартных предположений. Конфиденциальная передача сообщений
- 8. Вместо заключения
- Глава 4. Алгоритмические проблемы теории чисел
- 2. Система шифрования RSA
- 3. Сложность теоретико-числовых алгоритмов
- 4. Как отличить составное число от простого
- 5. Алгоритм, доказывающий непростоту числа
- 5. Как строить большие простые числа
- 6. Как проверить большое число на простоту
- 7. Как раскладывают составные числа на множители
- 8. Дискретное логарифмирование
- 9. Заключение
- Глава 5. Математика разделения секрета
- 2. Разделение секрета для произвольных структур доступа
- 3. Линейное разделение секрета.
- 4. Идеальное разделение секрета и матроиды
- Глава 6. Компьютер и криптография
- 2. Немного теории
- Что надо знать перед написанием программы шифрования
- 3. Как зашифровать файл?
- 4. Поучимся на чужих ошибках
- 5. Вместо заключения
- Глава 7. Олимпиады по криптографии для школьников
- 2. Шифры замены
- А. Конан Дойл, «Пляшущие человечки»
- Ж. Верн, «Путешествие к центру Земли»
- 3. Шифры перестановки
- 4. Многоалфавитные шифры замены с периодическим ключом
- 5. Условия задач олимпиад по математике и криптографии
- 6. Указания и решения
- Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
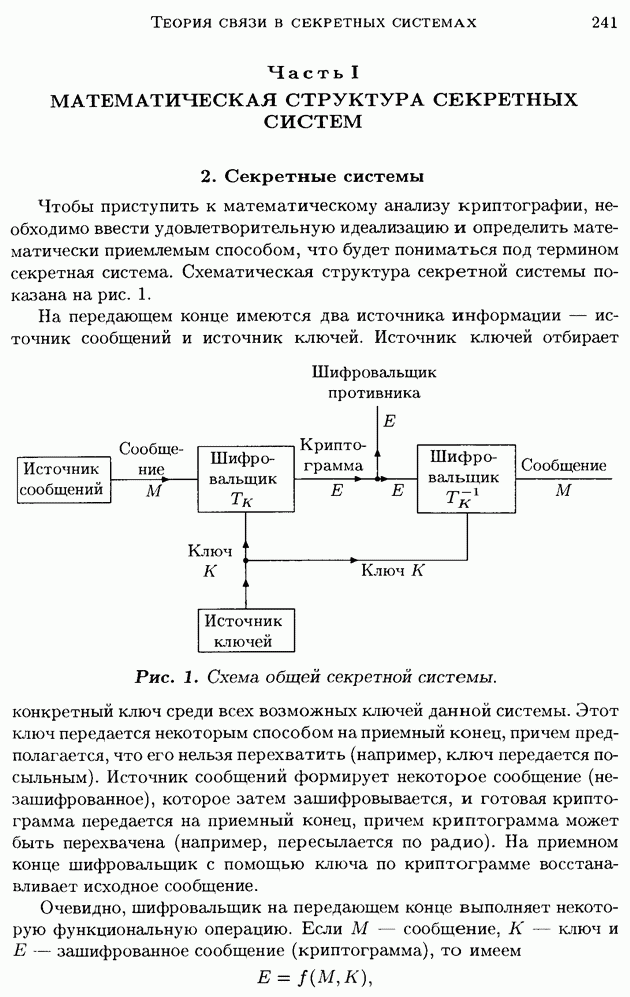
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность