| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Как отличить составное число от простого
Существует довольно эффективный способ убедиться, что заданное число является составным, не разлагая это число на множители. Согласно малой теореме Ферма, если число N простое, то для любого целого а, не делящегося на  выполняется сравнение
выполняется сравнение

Если же при каком-то а это сравнение нарушается, можно утверждать, что  составное. Проверка (9) не требует больших вычислений, это следует из алгоритма 1. Вопрос только в том, как найти для составного N целое число а, не удовлетворяющее (9). Можно, например,
составное. Проверка (9) не требует больших вычислений, это следует из алгоритма 1. Вопрос только в том, как найти для составного N целое число а, не удовлетворяющее (9). Можно, например,
пытаться найти необходимое число а, испытывая все целые числа подряд, начиная с 2. Или попробовать выбирать эти числа случайным образом на отрезке 
К сожалению, такой подход не всегда дает то, что хотелось бы. Имеются составные числа  обладающие свойством (9) для любого целого а с условием
обладающие свойством (9) для любого целого а с условием  Такие числа называются числами Кар-майкла. Рассмотрим, например, число
Такие числа называются числами Кар-майкла. Рассмотрим, например, число  Так как 560 делится на каждое из чисел 2, 10, 16, то с помощью малой теоремы Ферма легко проверить, что 561 есть число Кармайкла. Можно доказать
Так как 560 делится на каждое из чисел 2, 10, 16, то с помощью малой теоремы Ферма легко проверить, что 561 есть число Кармайкла. Можно доказать  что любое из чисел Кармайкла имеет вид
что любое из чисел Кармайкла имеет вид  где все простые
где все простые  различны, причем
различны, причем  делится на каждую разность
делится на каждую разность  Лишь недавно, см. [10], была решена проблема о бесконечности множества таких чисел.
Лишь недавно, см. [10], была решена проблема о бесконечности множества таких чисел.
В 1976 г. Миллер предложил заменить проверку (9) проверкой несколько иного условия. Детали последующего изложения можно найти в [8]. Если  простое число,
простое число,  где
где  нечетно, то согласно малой теореме Ферма для каждого а с условием
нечетно, то согласно малой теореме Ферма для каждого а с условием  хотя бы одна из скобок в произведении
хотя бы одна из скобок в произведении

делится на  Обращение этого свойства можно использовать, чтобы отличать составные числа от простых.
Обращение этого свойства можно использовать, чтобы отличать составные числа от простых.
Пусть  нечетное составное число,
нечетное составное число,  где
где  нечетно. Назовем целое число
нечетно. Назовем целое число  «хорошим» для
«хорошим» для  если нарушается одно из двух условий:
если нарушается одно из двух условий:
а) N не делится на а;
Р)  или существует целое к,
или существует целое к,  такое, что
такое, что

Из сказанного ранее следует, что для простого числа N не существует хороших чисел а. Если же N составное число, то, как доказал Рабин, их существует не менее 
Теперь можно построить вероятностный алгоритм, отличающий составные числа от простых.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму изданию
- Глава 1. Основные понятия криптографии
- 2. Предмет криптографии
- 3. Математические основы
- 4. Новые направления
- 5. Заключение
- Глава 2. Криптография и теория сложности
- 2. Криптография и гипотеза P != NP
- 3. Односторонние функции
- 4. Псевдослучайные генераторы
- 5. Доказательства с нулевым разглашением
- Глава 3. Криптографические протоколы
- 2. Целостность. Протоколы аутентификации и электронной подписи
- Схема аутентификации Шнорра
- Схема электронной подписи Шнорра
- 3. Неотслеживаемость. Электронные деньги
- 4. Протоколы типа «подбрасывание монеты по телефону»
- Протокол подбрасывания монеты
- 5. Еще раз о разделении секрета
- 6. Поиграем в «кубики». Протоколы голосования
- Протокол Шаума и Педерсена
- 7. За пределами стандартных предположений. Конфиденциальная передача сообщений
- 8. Вместо заключения
- Глава 4. Алгоритмические проблемы теории чисел
- 2. Система шифрования RSA
- 3. Сложность теоретико-числовых алгоритмов
- 4. Как отличить составное число от простого
- 5. Алгоритм, доказывающий непростоту числа
- 5. Как строить большие простые числа
- 6. Как проверить большое число на простоту
- 7. Как раскладывают составные числа на множители
- 8. Дискретное логарифмирование
- 9. Заключение
- Глава 5. Математика разделения секрета
- 2. Разделение секрета для произвольных структур доступа
- 3. Линейное разделение секрета.
- 4. Идеальное разделение секрета и матроиды
- Глава 6. Компьютер и криптография
- 2. Немного теории
- Что надо знать перед написанием программы шифрования
- 3. Как зашифровать файл?
- 4. Поучимся на чужих ошибках
- 5. Вместо заключения
- Глава 7. Олимпиады по криптографии для школьников
- 2. Шифры замены
- А. Конан Дойл, «Пляшущие человечки»
- Ж. Верн, «Путешествие к центру Земли»
- 3. Шифры перестановки
- 4. Многоалфавитные шифры замены с периодическим ключом
- 5. Условия задач олимпиад по математике и криптографии
- 6. Указания и решения
- Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
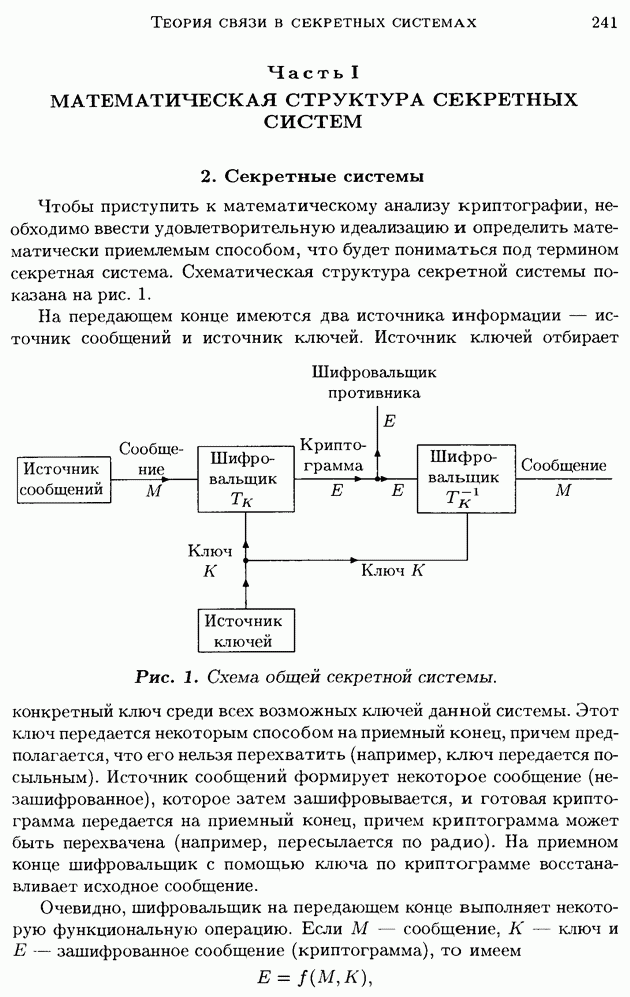
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность