| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Протокол Шаума и Педерсена
1. Доказывающий выбирает к  вычисляет
вычисляет  и посылает
и посылает  проверяющему.
проверяющему.
2. Проверяющий выбирает запрос  и посылает
и посылает  доказывающему.
доказывающему.
3. Доказывающий вычисляет  и посылает s проверяющему.
и посылает s проверяющему.
4. Проверяющий убеждается, что  и принимает доказательство. В противном случае, если хотя бы одно из этих сравнений не выполняется, — отвергает.
и принимает доказательство. В противном случае, если хотя бы одно из этих сравнений не выполняется, — отвергает.
Читатель, который ознакомился со вторым разделом данной главы, без труда обнаружит сходство этого протокола со схемой аутентификации Шнорра. Такому читателю будет полезно попытаться самостоятельно провести анализ стойкости данного протокола.
В принципе центр может доказать утверждение  каждому желающему. Неудобство в том, что протокол интерактивный. Но используя тот же прием, которым схема аутентификации Шнорра преобразуется в схему электронной подписи (см. раздел 2), можно и этот протокол сделать неинтерактивным. В таком случае центр может просто опубликовать неинтерактивное доказательство вместе с итогом
каждому желающему. Неудобство в том, что протокол интерактивный. Но используя тот же прием, которым схема аутентификации Шнорра преобразуется в схему электронной подписи (см. раздел 2), можно и этот протокол сделать неинтерактивным. В таком случае центр может просто опубликовать неинтерактивное доказательство вместе с итогом 
Конечно, предположение о том, что все избиратели доверяют одному центру подсчета голосов, весьма далеко от реальности. Можно создать  центров
центров  Тогда предположение о том, что по крайней мере
Тогда предположение о том, что по крайней мере  центров из
центров из  честные, где, например,
честные, где, например,  выглядит более реалистичным.
выглядит более реалистичным.
В этом случае центры совместно выбирают и публикуют три случайных порождающих  группы
группы  Бюллетень избирателя У, формируется так же, как и в предыдущем варианте:
Бюллетень избирателя У, формируется так же, как и в предыдущем варианте:  Но теперь центры не в состоянии сами дешифровать эту криптограмму. Вместо этого каждый из них вычисляет
Но теперь центры не в состоянии сами дешифровать эту криптограмму. Вместо этого каждый из них вычисляет  Избиратель V, с помощью описанной в предыдущем разделе схемы проверяемого разделения секрета создает доли
Избиратель V, с помощью описанной в предыдущем разделе схемы проверяемого разделения секрета создает доли  секретного значения
секретного значения
 и передает долю
и передает долю  центру
центру  Далее, выполняя вычисления над долями (см. раздел 5), центры вычисляют
Далее, выполняя вычисления над долями (см. раздел 5), центры вычисляют  Если при этом хотя бы
Если при этом хотя бы  центров честные, то остальные не смогут восстановить ни одно из значений Полученный результат S проверяется: должно выполняться сравнение
центров честные, то остальные не смогут восстановить ни одно из значений Полученный результат S проверяется: должно выполняться сравнение  Если оно выполнено, то значение S публикуется, и этого значения достаточно для вычисления итога голосования. В самом деле,
Если оно выполнено, то значение S публикуется, и этого значения достаточно для вычисления итога голосования. В самом деле,  Правда, для того чтобы получить итог
Правда, для того чтобы получить итог  необходимо вычислить дискретный логарифм полученной величины. Но поскольку абсолютное значение
необходимо вычислить дискретный логарифм полученной величины. Но поскольку абсолютное значение  невелико (заведомо не превосходит количества избирателей I) это можно сделать простым перебором.
невелико (заведомо не превосходит количества избирателей I) это можно сделать простым перебором.
В этой схеме возникает новая проблема — необходимо обеспечить протокол, с помощью которого центры совместно выбирают порождающие  причем так, что ни один из них не является известной степенью другого. Эту проблему можно решить следующим способом. Пусть
причем так, что ни один из них не является известной степенью другого. Эту проблему можно решить следующим способом. Пусть  вероятностный алгоритм, который генерирует три случайных порождающих. Его можно рассматривать как детерминированный алгоритм, который получает на входе помимо чисел
вероятностный алгоритм, который генерирует три случайных порождающих. Его можно рассматривать как детерминированный алгоритм, который получает на входе помимо чисел  еще и случайную строку
еще и случайную строку  требуемой длины. В разделе 4 был описан протокол подбрасывания монеты, который очевидным образом обобщается на случай
требуемой длины. В разделе 4 был описан протокол подбрасывания монеты, который очевидным образом обобщается на случай  участников. С помощью такого обобщенного протокола центры могут по биту сгенерировать строку
участников. С помощью такого обобщенного протокола центры могут по биту сгенерировать строку  (существуют и более эффективные схемы). Если хотя бы один из центров честный, то
(существуют и более эффективные схемы). Если хотя бы один из центров честный, то  случайная строка. По окончании выполнения протокола центры публикуют
случайная строка. По окончании выполнения протокола центры публикуют  Поскольку алгоритм
Поскольку алгоритм  предполагается общеизвестным, всякий желающий может проверить, что
предполагается общеизвестным, всякий желающий может проверить, что  получены с помощью строки
получены с помощью строки 
Все проблемы решены? Отнюдь! Если в случае одного центра последний расшифровывал все бюллетени и проверял их правильность, отбрасывая недействительные, то в случае  центров нечестный избиратель может попытаться с помощью недействительного бюллетеня сорвать выборы или исказить их итог. Эту проблему можно решить, если потребовать, чтобы вместе с бюллетенем каждый избиратель публиковал доказательство, что бюллетень построен правильно. Другими словами, требуется протокол, с помощью которого для данного бюллетеня
центров нечестный избиратель может попытаться с помощью недействительного бюллетеня сорвать выборы или исказить их итог. Эту проблему можно решить, если потребовать, чтобы вместе с бюллетенем каждый избиратель публиковал доказательство, что бюллетень построен правильно. Другими словами, требуется протокол, с помощью которого для данного бюллетеня  избиратель
избиратель  доказывал, что он знает
доказывал, что он знает  такие, что
такие, что  При этом протокол не должен давать проверяющему никакой полезной для него информации о значениях
При этом протокол не должен давать проверяющему никакой полезной для него информации о значениях  Пример такого протокола дан в работе [22]; мы его не воспроизводим здесь ввиду громоздкости.
Пример такого протокола дан в работе [22]; мы его не воспроизводим здесь ввиду громоздкости.
Теперь, наконец, все? Опять нет! ... Впрочем, поставим на этом точку. Надеемся, что читатель уже убедился в том, что протоколы голосования — нетривиальный объект и всевозможные его технические
аспекты можно обсуждать еще очень долго. К тому же мы рассматривали только два основных требования к протоколам голосования — анонимность и правильность подсчета голосов. А ведь существуют и другие. Причем новые требования могут возникать уже в процессе анализа протоколов голосования, когда обнаруживается, что последние обладают некоторыми неожиданными свойствами, которых нет в ныне общепринятых неэлектронных системах выборов. Например, при использовании описанной выше конструкции бюллетеня избиратель  знает значения
знает значения  которые он впоследствии может использовать для доказательства, что голосовал данным определенным образом (например, «за», а не «против»). Это создает возможности покупки голосов и требует разработки соответствующей криптографической защиты.
которые он впоследствии может использовать для доказательства, что голосовал данным определенным образом (например, «за», а не «против»). Это создает возможности покупки голосов и требует разработки соответствующей криптографической защиты.
Дальнейшие подробности протоколов голосования см. в работах [22], [23], из которых заимствованы изложенные выше идеи построения таких протоколов.
И последнее, о чем хотелось бы сказать в этом разделе. Всюду выше мы обсуждали (неформально) лишь стойкость различных криптографических примитивов, используемых в протоколе голосования, по отдельности. Но при композиции стойких криптографических протоколов может получиться нестойкий. Исследование стойкости композиций протоколов — еще одна, и зачастую весьма непростая, задача теоретической криптографии.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму изданию
- Глава 1. Основные понятия криптографии
- 2. Предмет криптографии
- 3. Математические основы
- 4. Новые направления
- 5. Заключение
- Глава 2. Криптография и теория сложности
- 2. Криптография и гипотеза P != NP
- 3. Односторонние функции
- 4. Псевдослучайные генераторы
- 5. Доказательства с нулевым разглашением
- Глава 3. Криптографические протоколы
- 2. Целостность. Протоколы аутентификации и электронной подписи
- Схема аутентификации Шнорра
- Схема электронной подписи Шнорра
- 3. Неотслеживаемость. Электронные деньги
- 4. Протоколы типа «подбрасывание монеты по телефону»
- Протокол подбрасывания монеты
- 5. Еще раз о разделении секрета
- 6. Поиграем в «кубики». Протоколы голосования
- Протокол Шаума и Педерсена
- 7. За пределами стандартных предположений. Конфиденциальная передача сообщений
- 8. Вместо заключения
- Глава 4. Алгоритмические проблемы теории чисел
- 2. Система шифрования RSA
- 3. Сложность теоретико-числовых алгоритмов
- 4. Как отличить составное число от простого
- 5. Алгоритм, доказывающий непростоту числа
- 5. Как строить большие простые числа
- 6. Как проверить большое число на простоту
- 7. Как раскладывают составные числа на множители
- 8. Дискретное логарифмирование
- 9. Заключение
- Глава 5. Математика разделения секрета
- 2. Разделение секрета для произвольных структур доступа
- 3. Линейное разделение секрета.
- 4. Идеальное разделение секрета и матроиды
- Глава 6. Компьютер и криптография
- 2. Немного теории
- Что надо знать перед написанием программы шифрования
- 3. Как зашифровать файл?
- 4. Поучимся на чужих ошибках
- 5. Вместо заключения
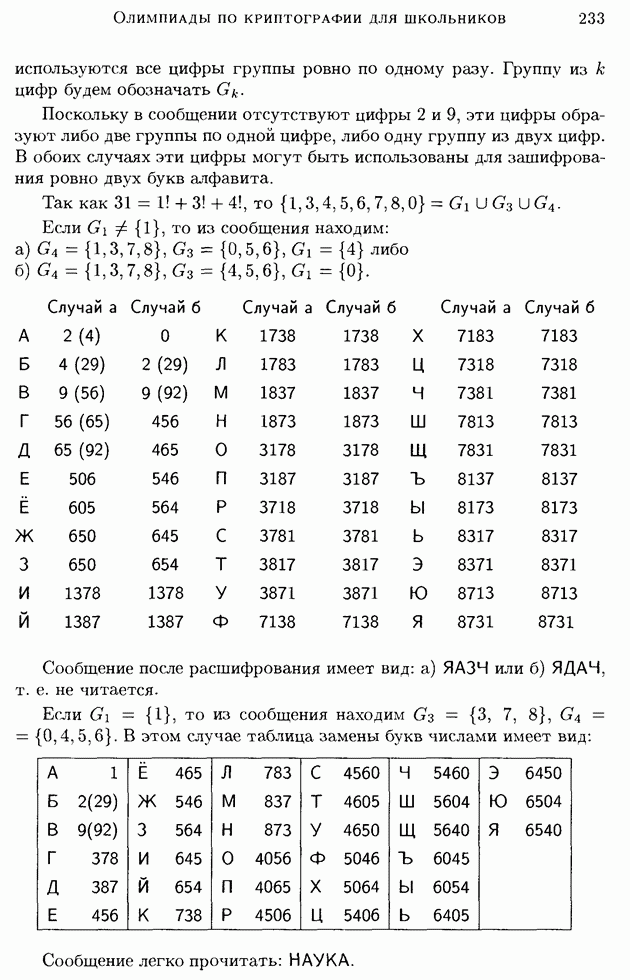
- Глава 7. Олимпиады по криптографии для школьников
- 2. Шифры замены
- А. Конан Дойл, «Пляшущие человечки»
- Ж. Верн, «Путешествие к центру Земли»
- 3. Шифры перестановки
- 4. Многоалфавитные шифры замены с периодическим ключом
- 5. Условия задач олимпиад по математике и криптографии
- 6. Указания и решения
- Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
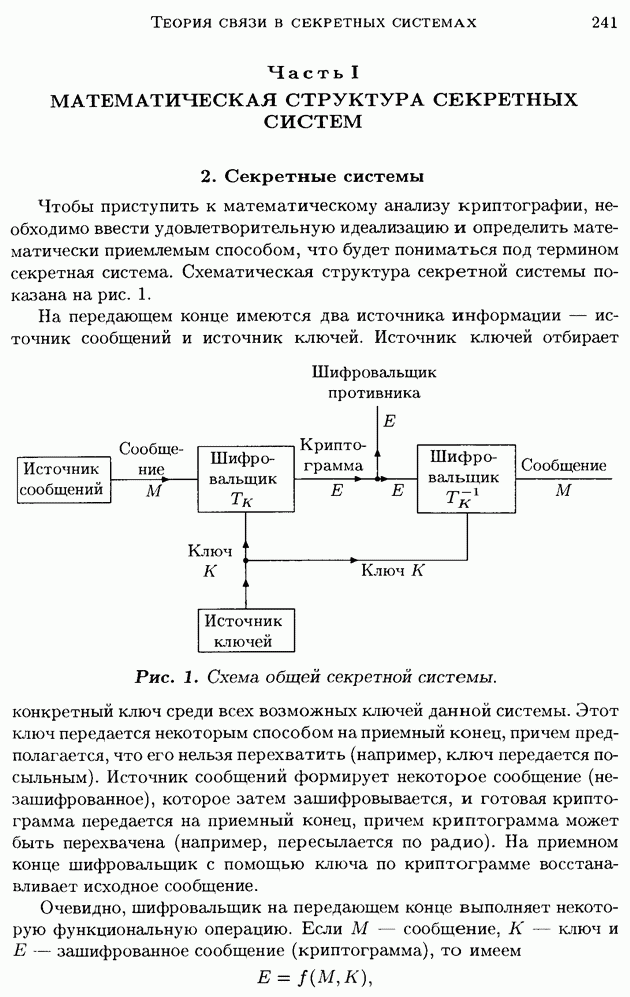
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
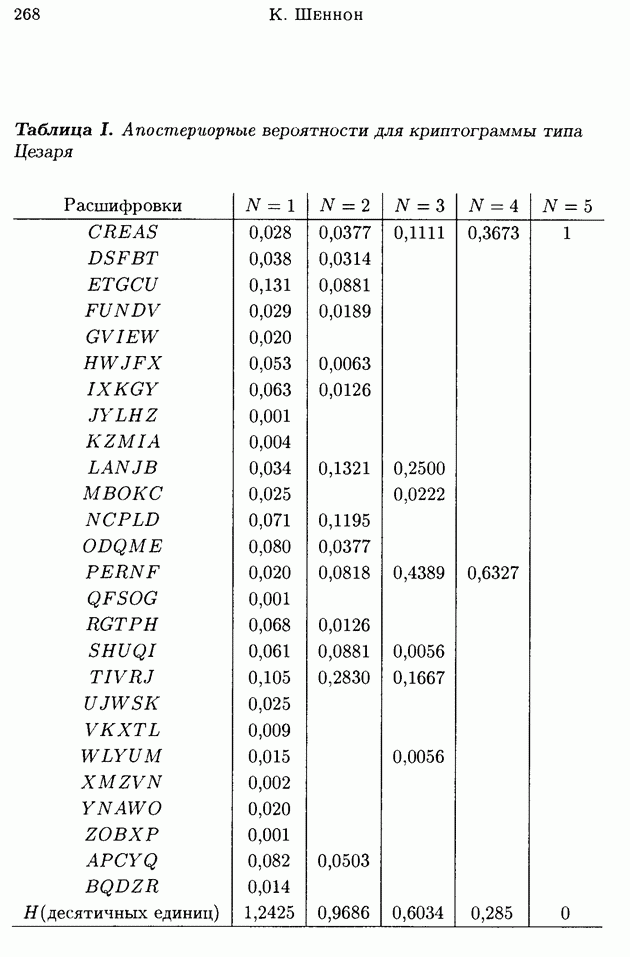
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность