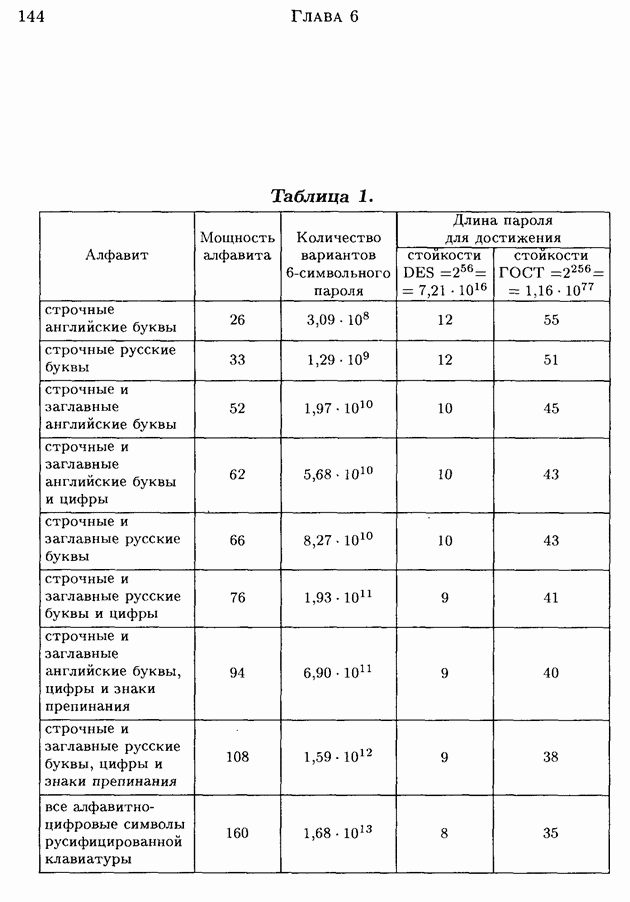
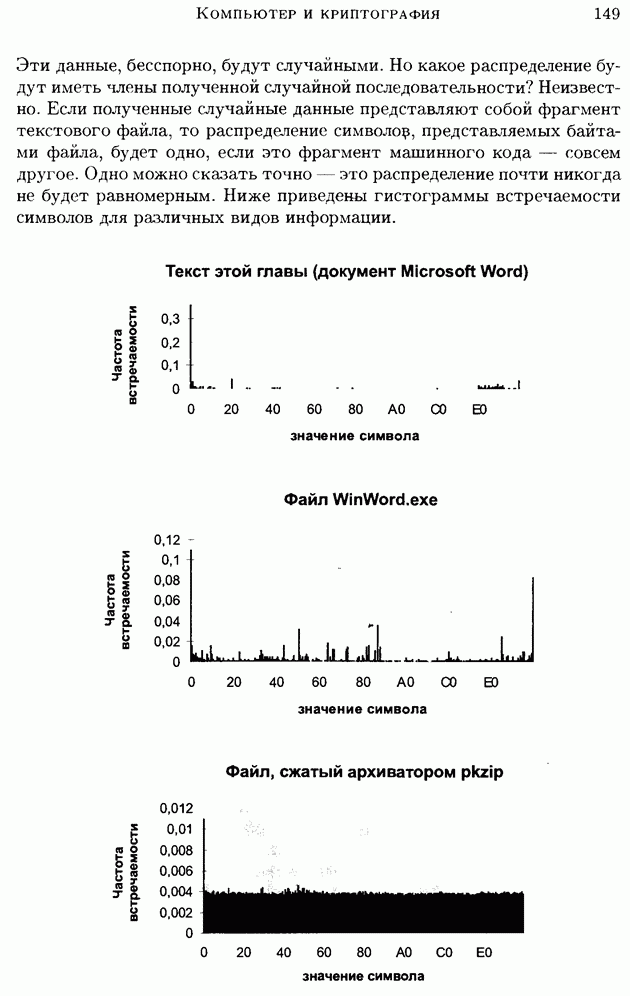
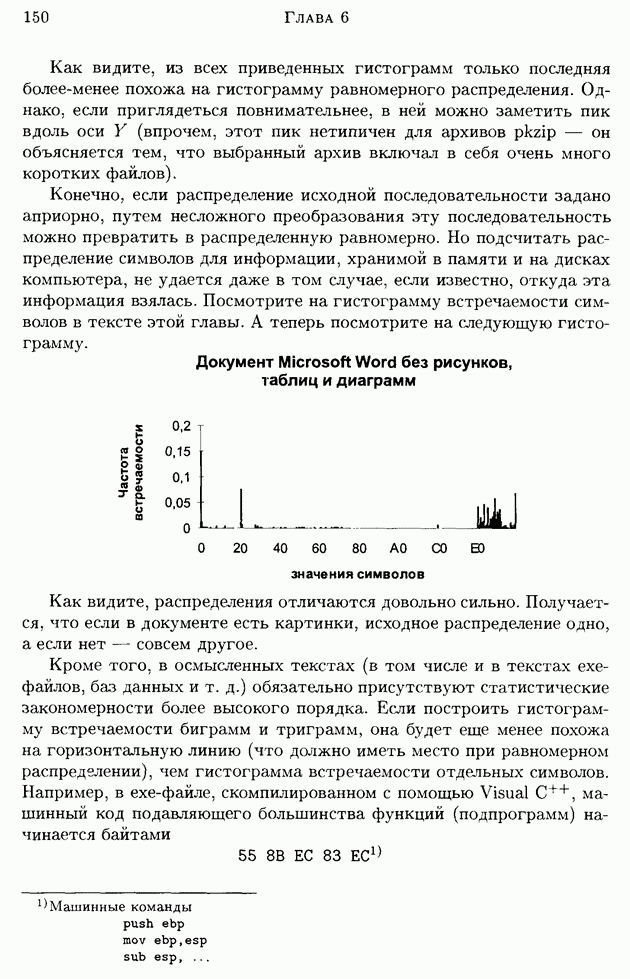
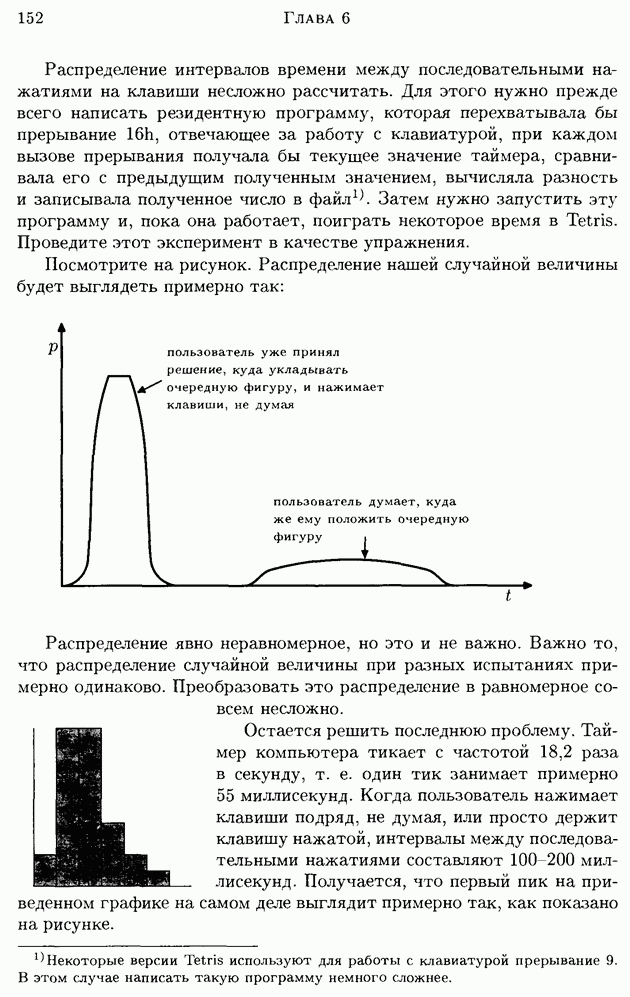
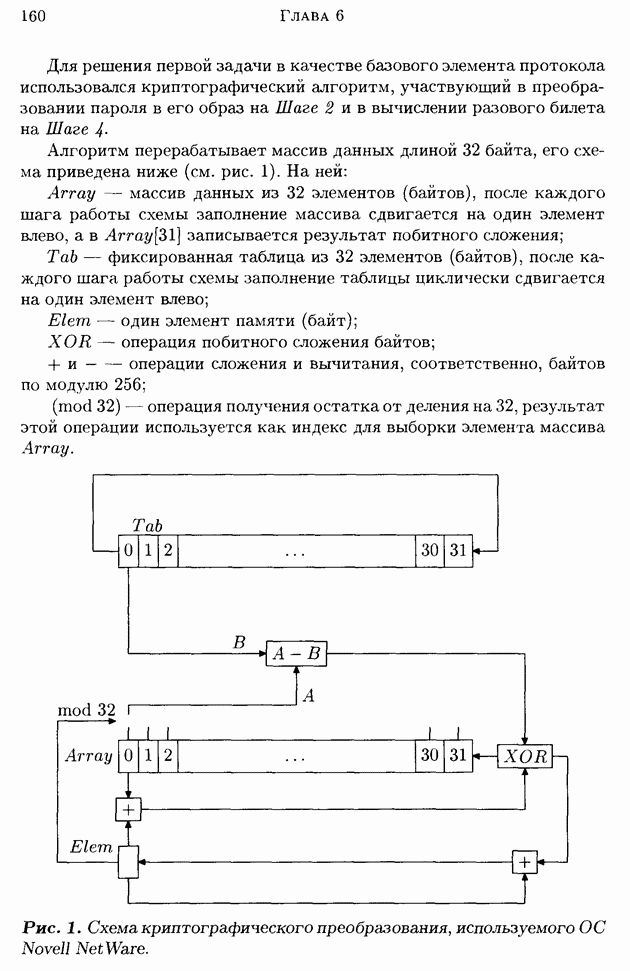
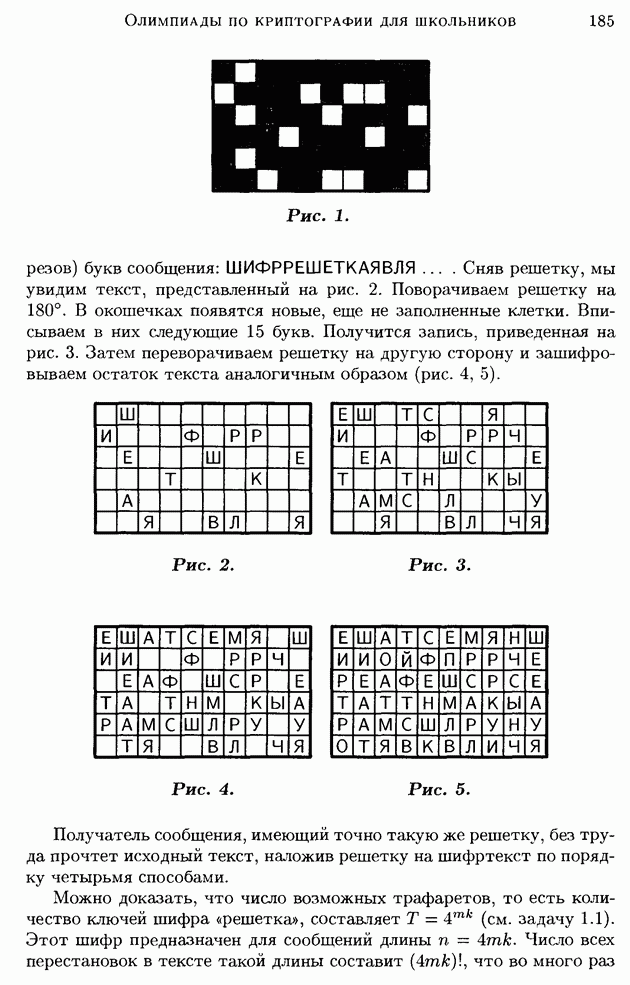
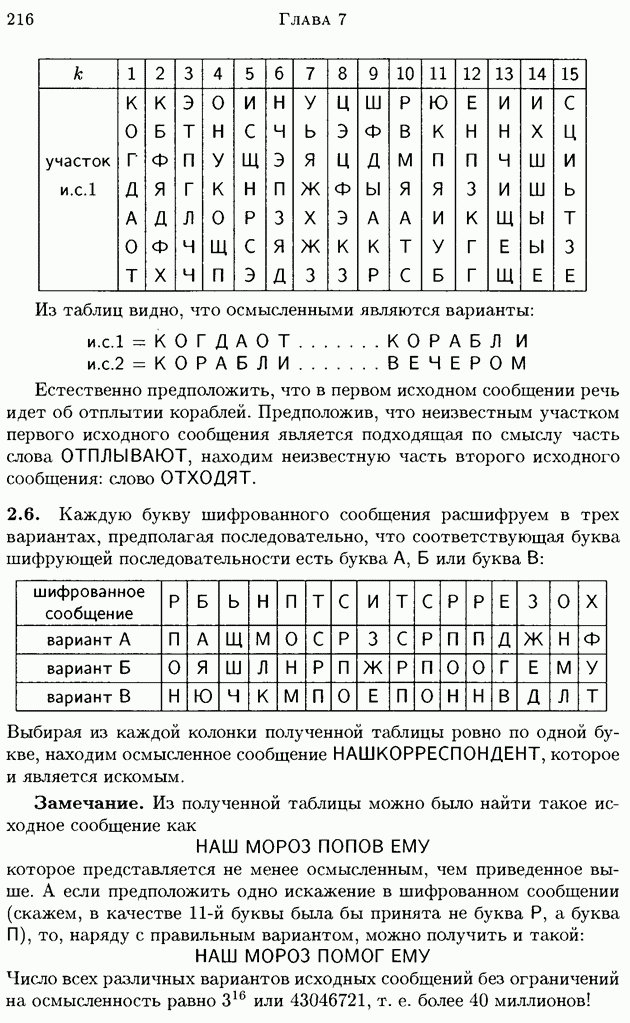
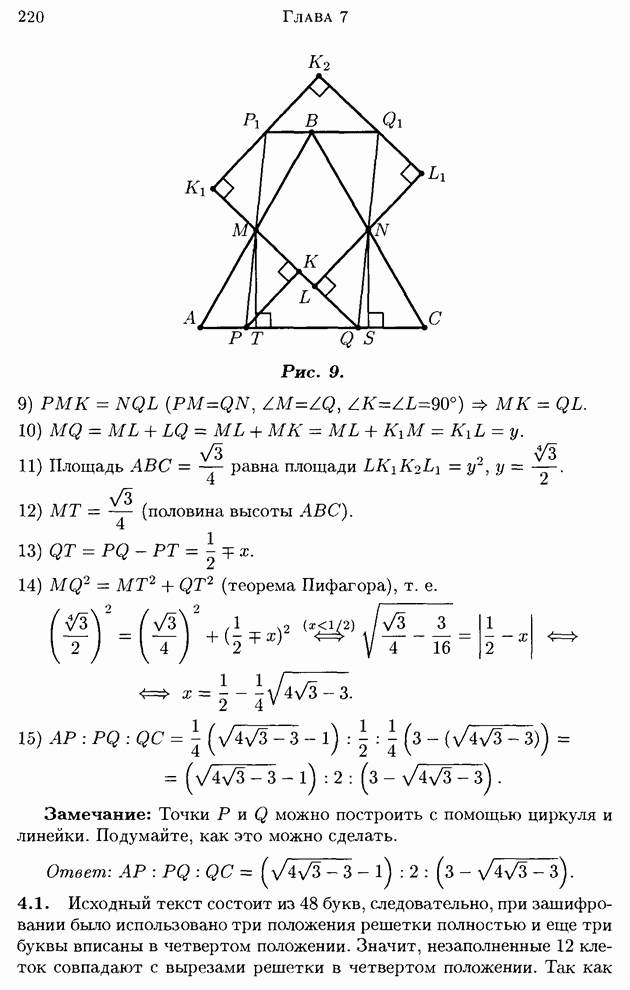| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
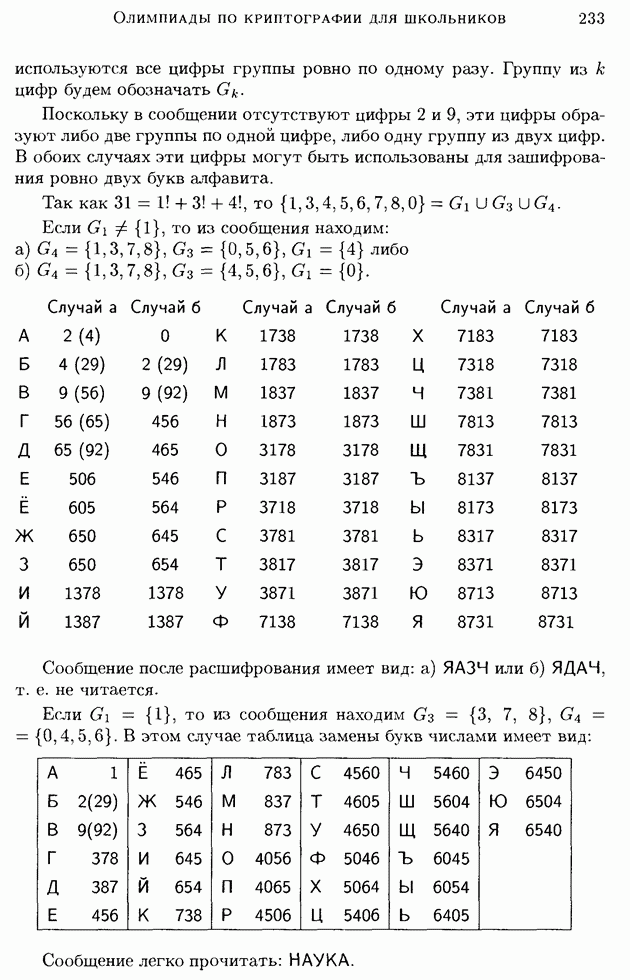
11. Ненадежность
Предположим теперь, что для английского текста используется шифр простой подстановки и что перехвачено определенное число, скажем  букв зашифрованного текста. Если N достаточно велико, скажем более 50, то почти всегда существует единственное решение шифра, т. е. единственная последовательность, имеющая смысл на английском языке, в которую переводится перехваченный материал с помощью простой подстановки. Для меньших N шансы на неединственность решения увеличиваются; для
букв зашифрованного текста. Если N достаточно велико, скажем более 50, то почти всегда существует единственное решение шифра, т. е. единственная последовательность, имеющая смысл на английском языке, в которую переводится перехваченный материал с помощью простой подстановки. Для меньших N шансы на неединственность решения увеличиваются; для  вообще говоря, будет существовать некоторое число подходящих отрывков осмысленного английского текста, в то время как для
вообще говоря, будет существовать некоторое число подходящих отрывков осмысленного английского текста, в то время как для  окажется подходящей значительная часть (порядка 1/8) всех возможных значащих английских последовательностей такой длины, так как из восьми букв редко повторится больше чем одна. При
окажется подходящей значительная часть (порядка 1/8) всех возможных значащих английских последовательностей такой длины, так как из восьми букв редко повторится больше чем одна. При  очевидно, возможна любая буква и апостериорная вероятность любой буквы будет равна ее априорной вероятности. Для одной буквы система является совершенно секретной.
очевидно, возможна любая буква и апостериорная вероятность любой буквы будет равна ее априорной вероятности. Для одной буквы система является совершенно секретной.
Это происходит, вообще говоря, со всеми разрешимыми шифрами. Прежде чем перехвачена криптограмма, можно представить себе априорные вероятности, связанные с различными возможными сообщениями, а также с различными ключами. После того как материал перехвачен, шифровальщик противника вычисляет их апостериорные вероятности. При увеличении числа N вероятности некоторых сообщений возрастают, но для большинства сообщений они убывают до тех пор, пока не останется только одно сообщение, имеющее вероятность, близкую к единице, в то время как полная вероятность всех других близка к нулю.
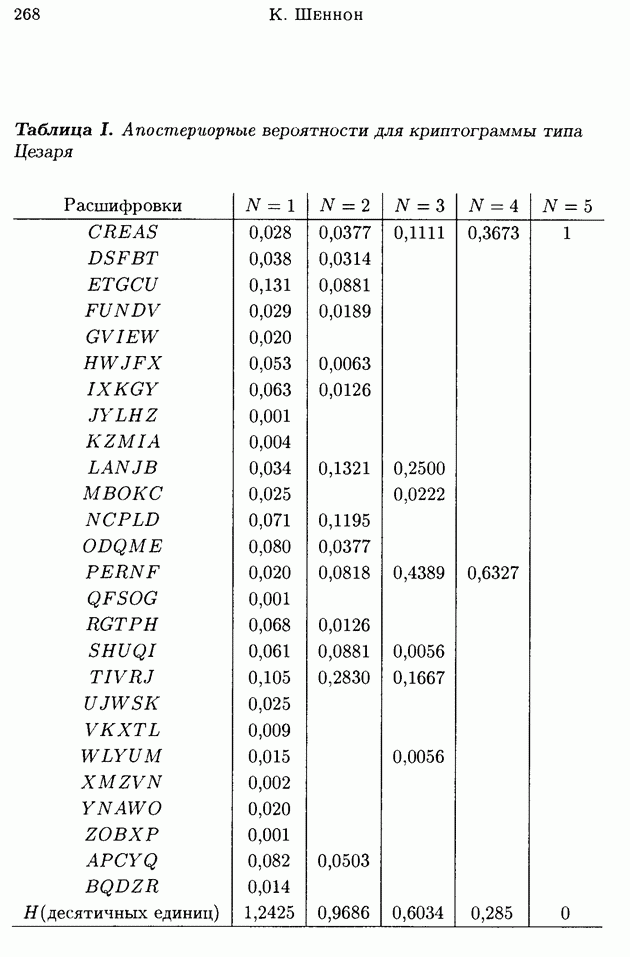
Для самых простых систем эти вычисления можно эффективно выполнить. Таблица I дает апостериорные вероятности для шифра Цезаря, примененного к английскому тексту, причем ключ выбирался случайно из 26 возможных ключей. Для того чтобы можно было использовать обычные таблицы частот букв, диграмм и триграмм, текст был начат в случайном месте (на страницу открытой наугад книги был случайно опущен карандаш). Сообщение, выбранное таким способом, начинается с «creases to» (карандаш опущен на третью букву слова increases). Если известно, что сообщение начинается не с середины, а с начала некоторого предложения, то нужно пользоваться иной таблицей, соответствующей частотам букв, диграмм и триграмм, стоящих в начале предложения.
(см. скан)
Шифр Цезаря со случайным ключом является чистым, и выбор частного ключа не влияет на апостериорные вероятности. Чтобы определить эти вероятности, надо просто выписать возможные расшифровки с помощью всех ключей и вычислить их априорные вероятности. Апостериорные вероятности получатся из этих последних в результате деления их на их сумму. Эти возможные расшифровки, образующие остаточный класс этого сообщения, найдены с помощью стандартного процесса последовательного «пробегания алфавита», в таблице I они даны слева. Для одной перехваченной буквы апостериорные вероятности равны априорным вероятностям для всех букв (они приведены в таблице под рубрикой 
Для двух перехваченных букв эти вероятности равны априорным вероятностям диграмм, пронормированным на их сумму (они приведены в столбце  Триграммные частоты получены аналогично и приведены в столбце
Триграммные частоты получены аналогично и приведены в столбце  Для четырех- и пятибуквенных последовательностей вероятности находились из триграммных частот с помощью умножения, так как с некоторым приближением
Для четырех- и пятибуквенных последовательностей вероятности находились из триграммных частот с помощью умножения, так как с некоторым приближением

Заметим, что для трех букв число возможных сообщений снижается до четырех сообщений достаточно высокой вероятности, причем вероятности всех других сообщений малы по сравнению с вероятностями этих четырех сообщений. Для четырех букв имеются два возможных сообщения и для пяти — только одно, а именно правильная дешифровка.
В принципе это может быть проведено для любой системы, однако в том случае, когда объем ключа не очень мал, число возможных сообщений настолько велико, что вычисления становятся практически невыполнимыми.
Получаемое таким образом множество апостериорных вероятностей описывает, как постепенно, по мере получения зашифрованного материала, становятся более точными сведения шифровальщика противника относительно сообщения и ключа.
Это описание, однако, является слишком исчерпывающим и слишком сложным для наших целей. Хотелось бы иметь упрощенное описание такого приближения к единственности возможного решения.
Аналогичная ситуация возникает в теории связи, когда передаваемый сигнал искажается шумом. Здесь необходимо ввести подходящую меру неопределенности того, что действительно было передано, при
условии, что известен только искаженный шумом вариант — принятый сигнал.
В «Математической теории связи» показано, что естественной математической мерой этой неопределенности является условная энтропия передаваемого сигнала при условии, что принятый сигнал известен. Эта условная энтропия для удобства будет называться ненадежностью.
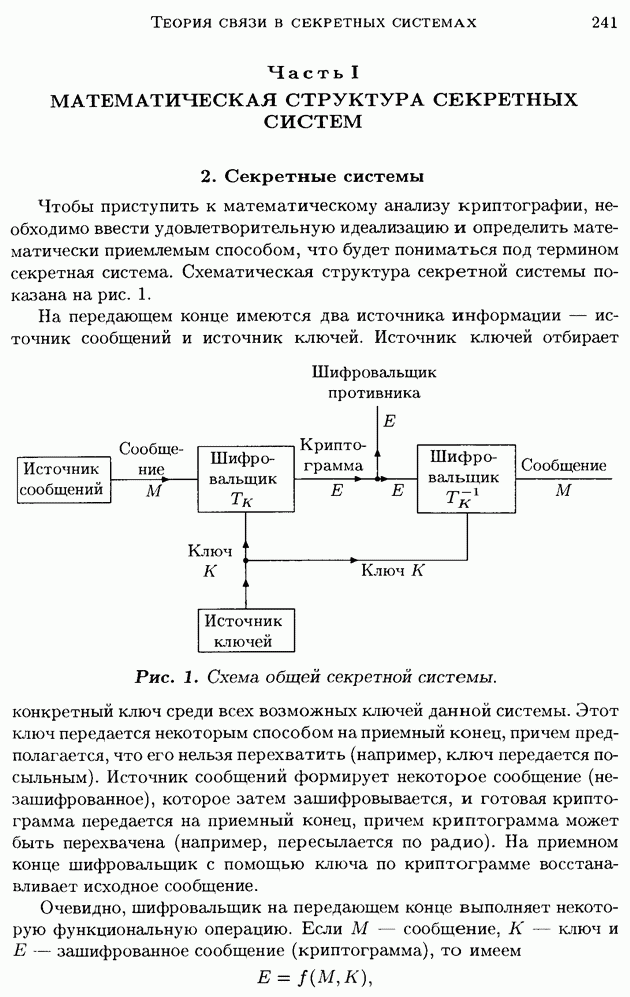
С криптографической точки зрения секретная система почти тождественна системе связи при наличии шума. На сообщение (передаваемый сигнал) действует некоторый статистический элемент (секретная система с ее статистически выбранным ключом). В результате получается криптограмма (аналог искаженного сигнала), подлежащая дешифрированию. Основное различие заключается в следующем: во-первых, в том, что преобразование при помощи шифра имеет обычно более сложную природу, чем возникающее за счет шума в канале; и, во-вторых, ключ в секретной системе обычно выбирается из конечного множества, в то время как шум в канале чаще является непрерывным, выбранным по существу из бесконечного множества.
Учитывая эти соображения, естественно использовать ненадежность в качестве теоретической меры секретности. Следует отметить, что имеются две основные ненадежности: ненадежность ключа и ненадежность сообщения. Они будут обозначаться через  соответственно. Их величины определяются соотношениями
соответственно. Их величины определяются соотношениями

где  криптограмма, сообщение и ключ;
криптограмма, сообщение и ключ;
 вероятность ключа К и криптограммы
вероятность ключа К и криптограммы 
 апостериорная вероятность ключа К, если перехвачена криптограмма
апостериорная вероятность ключа К, если перехвачена криптограмма 
 аналогичные вероятности, но не для ключа, а для сообщения.
аналогичные вероятности, но не для ключа, а для сообщения.
Суммирование в  проводится по всем возможным криптограммам определенной длины (скажем, N) и по всем возможным ключам. Для
проводится по всем возможным криптограммам определенной длины (скажем, N) и по всем возможным ключам. Для  суммирование проводится по всем сообщениям и криптограммам длины
суммирование проводится по всем сообщениям и криптограммам длины  Таким образом,
Таким образом,  являются функциями от
являются функциями от  числа перехваченных букв. Это будет иногда указываться в обозначении так:
числа перехваченных букв. Это будет иногда указываться в обозначении так:  Заметим, что эти ненадежности являются «полными», т. е. не делятся на N с тем,
Заметим, что эти ненадежности являются «полными», т. е. не делятся на N с тем,
чтобы получить скорость ненадежности, которая рассматривалась в работе «Математическая теория связи».
Те же самые рассуждения, которые были использованы в «Математической теории связи» для обоснования введения ненадежности в качестве меры неопределенности в теории связи, применимы и здесь. Так, из того, что ненадежность равна нулю, следует, что одно сообщение (или ключ) имеет единичную вероятность, а все другие — нулевую. Этот случай соответствует полной осведомленности шифровальщика. Постепенное убывание ненадежности с ростом N соответствует увеличению сведений об исходном ключе или сообщении. Кривые ненадежности сообщения и ключа, нанесенные на график как функции от  мы будем называть характеристиками ненадежности рассматриваемой секретной системы.
мы будем называть характеристиками ненадежности рассматриваемой секретной системы.
Величины  для криптограммы шифра Цезаря, рассмотренной выше, сосчитаны и приведены в нижней строке табл.
для криптограммы шифра Цезаря, рассмотренной выше, сосчитаны и приведены в нижней строке табл.  Числа
Числа  в этом случае равны и даны в десятичных единицах (т. е. при вычислениях в качестве основания логарифма бралось 10). Следует отметить, что ненадежность здесь сосчитана для частной криптограммы, так как суммирование ведется только по
в этом случае равны и даны в десятичных единицах (т. е. при вычислениях в качестве основания логарифма бралось 10). Следует отметить, что ненадежность здесь сосчитана для частной криптограммы, так как суммирование ведется только по  (или К), но не по
(или К), но не по  В общем случае суммирование должно было бы проводиться по всем перехваченным криптограммам длины
В общем случае суммирование должно было бы проводиться по всем перехваченным криптограммам длины  в результате чего получилась бы средняя неопределенность. Вычислительные трудности не позволяют сделать это практически.
в результате чего получилась бы средняя неопределенность. Вычислительные трудности не позволяют сделать это практически.
| << Предыдущий параграф |
- Предисловие ко второму изданию
- Глава 1. Основные понятия криптографии
- 2. Предмет криптографии
- 3. Математические основы
- 4. Новые направления
- 5. Заключение
- Глава 2. Криптография и теория сложности
- 2. Криптография и гипотеза P != NP
- 3. Односторонние функции
- 4. Псевдослучайные генераторы
- 5. Доказательства с нулевым разглашением
- Глава 3. Криптографические протоколы
- 2. Целостность. Протоколы аутентификации и электронной подписи
- Схема аутентификации Шнорра
- Схема электронной подписи Шнорра
- 3. Неотслеживаемость. Электронные деньги
- 4. Протоколы типа «подбрасывание монеты по телефону»
- Протокол подбрасывания монеты
- 5. Еще раз о разделении секрета
- 6. Поиграем в «кубики». Протоколы голосования
- Протокол Шаума и Педерсена
- 7. За пределами стандартных предположений. Конфиденциальная передача сообщений
- 8. Вместо заключения
- Глава 4. Алгоритмические проблемы теории чисел
- 2. Система шифрования RSA
- 3. Сложность теоретико-числовых алгоритмов
- 4. Как отличить составное число от простого
- 5. Алгоритм, доказывающий непростоту числа
- 5. Как строить большие простые числа
- 6. Как проверить большое число на простоту
- 7. Как раскладывают составные числа на множители
- 8. Дискретное логарифмирование
- 9. Заключение
- Глава 5. Математика разделения секрета
- 2. Разделение секрета для произвольных структур доступа
- 3. Линейное разделение секрета.
- 4. Идеальное разделение секрета и матроиды
- Глава 6. Компьютер и криптография
- 2. Немного теории
- Что надо знать перед написанием программы шифрования
- 3. Как зашифровать файл?
- 4. Поучимся на чужих ошибках
- 5. Вместо заключения
- Глава 7. Олимпиады по криптографии для школьников
- 2. Шифры замены
- А. Конан Дойл, «Пляшущие человечки»
- Ж. Верн, «Путешествие к центру Земли»
- 3. Шифры перестановки
- 4. Многоалфавитные шифры замены с периодическим ключом
- 5. Условия задач олимпиад по математике и криптографии
- 6. Указания и решения
- Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность