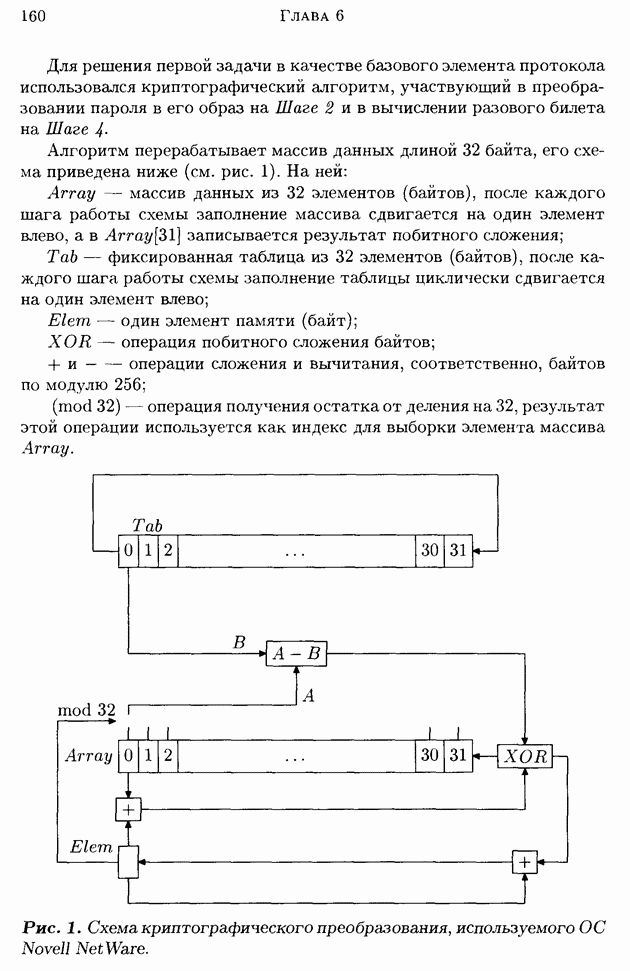
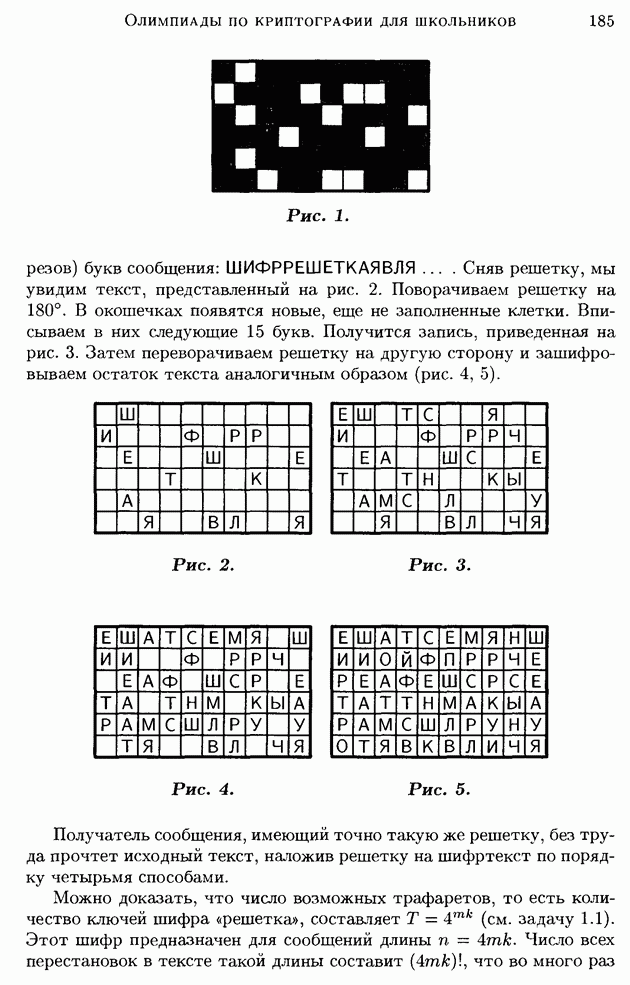
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Еще раз о разделении секрета
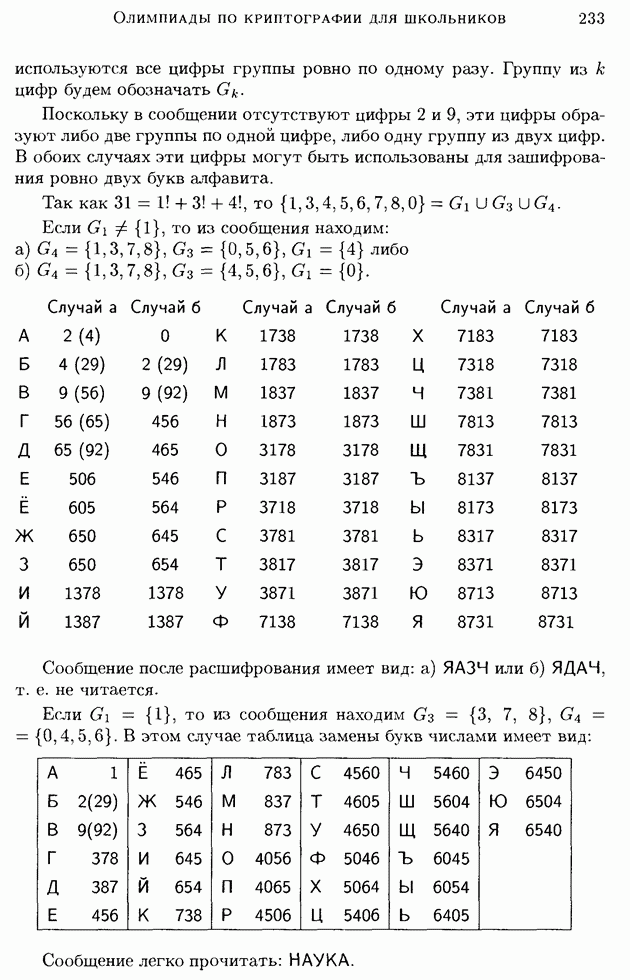
В работе [16] со ссылкой на книгу «Gent und seine schonheiten» (Thill-Verlag, Briissel, 1990) описывается следующий исторический пример. В XIII-XIV веках в  Генте была построена ратушная башня. В «секрете» (secreet), самом надежном помещении башни, хранились уставы и привилегии, имевшие важное значение. Помещение имело две двери, каждая с тремя замками, ключи от которых находились во владении различных цехов. Документы хранились в шкафу, который, в свою очередь, также запирался на три ключа. Один из этих ключей хранился у фогта, а два других — у главного шеффена.
Генте была построена ратушная башня. В «секрете» (secreet), самом надежном помещении башни, хранились уставы и привилегии, имевшие важное значение. Помещение имело две двери, каждая с тремя замками, ключи от которых находились во владении различных цехов. Документы хранились в шкафу, который, в свою очередь, также запирался на три ключа. Один из этих ключей хранился у фогта, а два других — у главного шеффена.
Мы привели этот пример в разделе, посвященном протоколам разделения секрета, главным образом для того, чтобы показать, что хотя криптографические протоколы — сравнительно молодая отрасль криптографии, задачи, которые решаются с помощью протоколов, возникли очень давно и имеют свою историю.
Почему «еще раз о разделении секрета»? В главе 5 разделение секрета рассматривается в основном как математическая, прежде всего комбинаторная, задача. Здесь же мы его обсуждаем как криптографический протокол. При этом предполагается, что читатель знаком с главой 5.
В протоколе разделения секрета имеются  участников
участников  которых мы будем называть процессорами, и один выделенный участник
которых мы будем называть процессорами, и один выделенный участник  называемый дилером (или, иногда, лидером). Протокол состоит из двух фаз.
называемый дилером (или, иногда, лидером). Протокол состоит из двух фаз.
На фазе разделения секрета дилер, знающий некоторый секрет  генерирует
генерирует  долей секрета
долей секрета  и посылает
и посылает  процессору
процессору  по защищенному каналу связи. На фазе восстановления секрета любое подмножество из не менее чем
по защищенному каналу связи. На фазе восстановления секрета любое подмножество из не менее чем  процессоров, где
процессоров, где  параметр протокола, однозначно восстанавливает секрет, обмениваясь сообщениями по защищенным каналам связи. А любое подмножество из не более чем
параметр протокола, однозначно восстанавливает секрет, обмениваясь сообщениями по защищенным каналам связи. А любое подмножество из не более чем  процессоров не может восстановить секрет (что означают слова «не может восстановить» будет пояснено ниже).
процессоров не может восстановить секрет (что означают слова «не может восстановить» будет пояснено ниже).
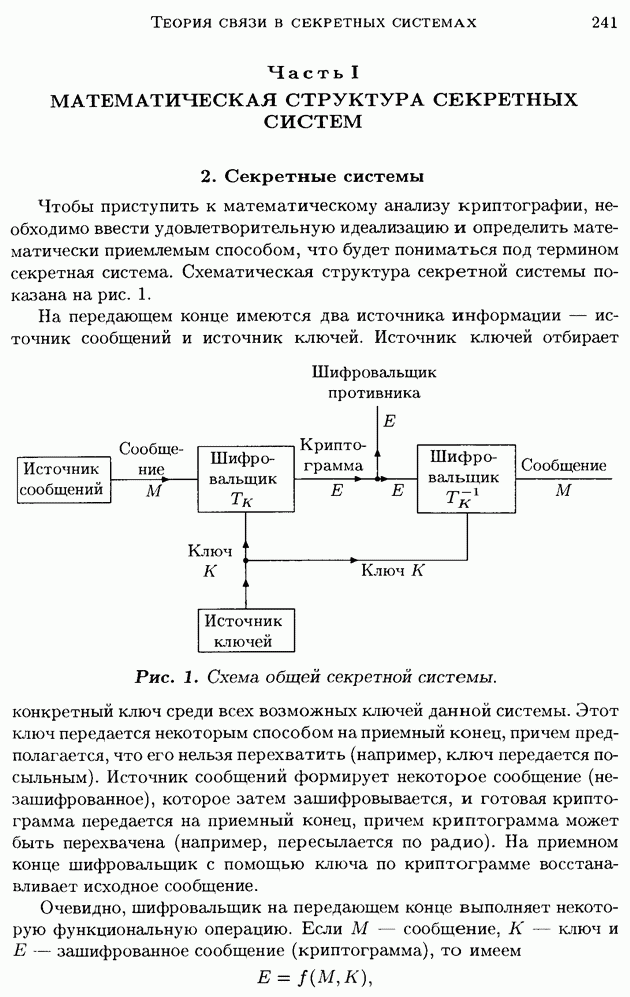
Как и в других типах криптографических протоколов, в протоколе разделения секрета участники, вообще говоря, не доверяют друг другу и каждый из них может оказаться противником. В том числе и дилер. Можно ли обеспечить какую-либо защиту честных участников даже и в этом случае? Безусловно, нечестный дилер может просто саботировать выполнение протокола. Но если дилер пытается обмануть более хитрым способом, то от этого, оказывается, можно защититься следующим образом. Фаза разделения секрета начинается с того, что дилер публикует секрет s в «зашифрованном» виде (точнее было бы сказать — выполняет привязку к строке  по аналогии с привязкой к биту). С помощью этой информации каждый процессор
по аналогии с привязкой к биту). С помощью этой информации каждый процессор  может проверить, что значение
может проверить, что значение  полученное им от дилера, действительно является долей секрета
полученное им от дилера, действительно является долей секрета  Такой протокол называется протоколом проверяемого разделения секрета. В обычных схемах разделения секрета рассматривается пассивный противник, а именно, противником являются не более чем
Такой протокол называется протоколом проверяемого разделения секрета. В обычных схемах разделения секрета рассматривается пассивный противник, а именно, противником являются не более чем  участников, которые, объединив свои доли, пытаются получить какую-либо информацию о значении секрета. На фазе восстановления секрета в протоколе проверяемого разделения секрета действует активный противник: нечестные участники могут преследовать цель сорвать восстановление значения s честными участниками, посылая им вместо своих долей секрета любую другую
участников, которые, объединив свои доли, пытаются получить какую-либо информацию о значении секрета. На фазе восстановления секрета в протоколе проверяемого разделения секрета действует активный противник: нечестные участники могут преследовать цель сорвать восстановление значения s честными участниками, посылая им вместо своих долей секрета любую другую
информацию. От протокола требуется, чтобы честные участники, если их по крайней мере  всегда правильно восстанавливали значение
всегда правильно восстанавливали значение 
Рассмотрим конструкцию протокола проверяемого разделения секрета из работы [17]. Конструкция основана на задаче дискретного логарифмирования.
В соответствии со схемой Шамира дилер выбирает случайный полином  степени
степени  где
где  вычисляет
вычисляет  и публикует
и публикует  После этого для всякого
После этого для всякого  дилер вычисляет
дилер вычисляет  и посылает это значение процессору
и посылает это значение процессору  по защищенному каналу. Процессор
по защищенному каналу. Процессор  проверяя равенство
проверяя равенство

убеждается, что  доля секрета
доля секрета  В самом деле,
В самом деле,

Конструкцию протокола для фазы восстановления секрета рассмотрим в наиболее простом случае, когда дилер честный. На этой фазе каждый процессор  посылает каждому другому процессору
посылает каждому другому процессору  свою долю
свою долю  Всякий честный участник
Всякий честный участник  получив некоторое значение
получив некоторое значение  от
от  проверяет это значение, как описано выше, и отбрасывает все доли
проверяет это значение, как описано выше, и отбрасывает все доли  не прошедшие проверку. Поскольку честных участников не менее
не прошедшие проверку. Поскольку честных участников не менее  получит по крайней мере
получит по крайней мере  правильных долей секрета. Используя алгоритм восстановления секрета из схемы Шамира,
правильных долей секрета. Используя алгоритм восстановления секрета из схемы Шамира,  восстановит значение
восстановит значение 
В отличие от схем разделения секрета, рассматриваемых в главе 5, стойкость данного протокола основывается на предположении о вычислительной трудности задачи дискретного логарифмирования. Поэтому, если в обычных схемах разделения секрета требуется, чтобы любое подмножество участников, не составляющее кворума, не получало никакой информации о секрете, то во многих схемах проверяемого разделения секрета такое подмножество лишь «не может восстановить» секрет. В том смысле, что для его восстановления требуется решить некоторую гипотетически трудную вычислительную задачу. В рассмотренном выше примере всякий участник мог бы узнать секрет  если бы он умел вычислять дискретные логарифмы.
если бы он умел вычислять дискретные логарифмы.
Одно из возможных приложений схем разделения секрета — организация хранения криптографических ключей. Свойство проверяемости представляется далеко не лишним для таких приложений. Но круг приложений схем проверяемого разделения секрета существенно шире.
Предположим, что с помощью описанной выше схемы разделены два секрета  и что оба эти секреты являются числами. Теперь представим себе ситуацию, что после этого потребовалась разделить секрет
и что оба эти секреты являются числами. Теперь представим себе ситуацию, что после этого потребовалась разделить секрет  Конечно, это может сделать дилер с помощью того же протокола. А могут ли процессоры выполнить то же самое без участия дилера?
Конечно, это может сделать дилер с помощью того же протокола. А могут ли процессоры выполнить то же самое без участия дилера?
Пусть  полиномы, которые использовались для разделения секретов
полиномы, которые использовались для разделения секретов  соответственно. Пусть
соответственно. Пусть  для
для  Для любого
Для любого  пусть
пусть  доли секретов
доли секретов  полученные процессором
полученные процессором  Ясно, что
Ясно, что  также полином степени
также полином степени 
Поэтому каждый процессор  может вычислить долю
может вычислить долю  секрета s просто по формуле
секрета s просто по формуле  Эти доли проверяемы с помощью значений
Эти доли проверяемы с помощью значений 
Рабин и Бен-Op показали [18], что выполняя такого рода вычисления над долями секретов, процессоры могут вычислить любую функцию над конечным полем «проверяемым образом». Этот результат относится к области протоколов конфиденциального вычисления (secure multi party computation). Типичная задача здесь такая. Требуется вычислить значение функции  на некотором наборе значений аргументов
на некотором наборе значений аргументов  С помощью схемы проверяемого разделения секрета вычисляются доли
С помощью схемы проверяемого разделения секрета вычисляются доли  этих значений. В начале выполнения протокола доля
этих значений. В начале выполнения протокола доля  известна процессору
известна процессору  и только ему. Протокол должен обеспечивать вычисление значения
и только ему. Протокол должен обеспечивать вычисление значения  таким образом, чтобы для некоторого параметра
таким образом, чтобы для некоторого параметра 
1) в результате выполнения протокола любое подмножество из не более чем  процессоров не получало никакой информации о значениях
процессоров не получало никакой информации о значениях  других процессоров (кроме той, которая следует из известных им долей и значения функции
других процессоров (кроме той, которая следует из известных им долей и значения функции 
2) при любых действиях нечестных участников остальные участники вычисляют правильное значение  если только количество нечестных участников не превосходит
если только количество нечестных участников не превосходит 
Протоколы конфиденциального вычисления, ввиду своей общности, представляют несомненный теоретический интерес. Кроме того, многие типы прикладных криптографических протоколов (например, протоколы голосования) по существу являются частными случаями протоколов конфиденциального вычисления.
При различных предположениях о процессорах и о сети связи доказан ряд теорем следующего типа: если  не превосходит некоторого порогового значения (зависящего от
не превосходит некоторого порогового значения (зависящего от  и от предположений), то всякая вычислимая функция имеет протокол конфиденциального вычисления.
и от предположений), то всякая вычислимая функция имеет протокол конфиденциального вычисления.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму изданию
- Глава 1. Основные понятия криптографии
- 2. Предмет криптографии
- 3. Математические основы
- 4. Новые направления
- 5. Заключение
- Глава 2. Криптография и теория сложности
- 2. Криптография и гипотеза P != NP
- 3. Односторонние функции
- 4. Псевдослучайные генераторы
- 5. Доказательства с нулевым разглашением
- Глава 3. Криптографические протоколы
- 2. Целостность. Протоколы аутентификации и электронной подписи
- Схема аутентификации Шнорра
- Схема электронной подписи Шнорра
- 3. Неотслеживаемость. Электронные деньги
- 4. Протоколы типа «подбрасывание монеты по телефону»
- Протокол подбрасывания монеты
- 5. Еще раз о разделении секрета
- 6. Поиграем в «кубики». Протоколы голосования
- Протокол Шаума и Педерсена
- 7. За пределами стандартных предположений. Конфиденциальная передача сообщений
- 8. Вместо заключения
- Глава 4. Алгоритмические проблемы теории чисел
- 2. Система шифрования RSA
- 3. Сложность теоретико-числовых алгоритмов
- 4. Как отличить составное число от простого
- 5. Алгоритм, доказывающий непростоту числа
- 5. Как строить большие простые числа
- 6. Как проверить большое число на простоту
- 7. Как раскладывают составные числа на множители
- 8. Дискретное логарифмирование
- 9. Заключение
- Глава 5. Математика разделения секрета
- 2. Разделение секрета для произвольных структур доступа
- 3. Линейное разделение секрета.
- 4. Идеальное разделение секрета и матроиды
- Глава 6. Компьютер и криптография
- 2. Немного теории
- Что надо знать перед написанием программы шифрования
- 3. Как зашифровать файл?
- 4. Поучимся на чужих ошибках
- 5. Вместо заключения
- Глава 7. Олимпиады по криптографии для школьников
- 2. Шифры замены
- А. Конан Дойл, «Пляшущие человечки»
- Ж. Верн, «Путешествие к центру Земли»
- 3. Шифры перестановки
- 4. Многоалфавитные шифры замены с периодическим ключом
- 5. Условия задач олимпиад по математике и криптографии
- 6. Указания и решения
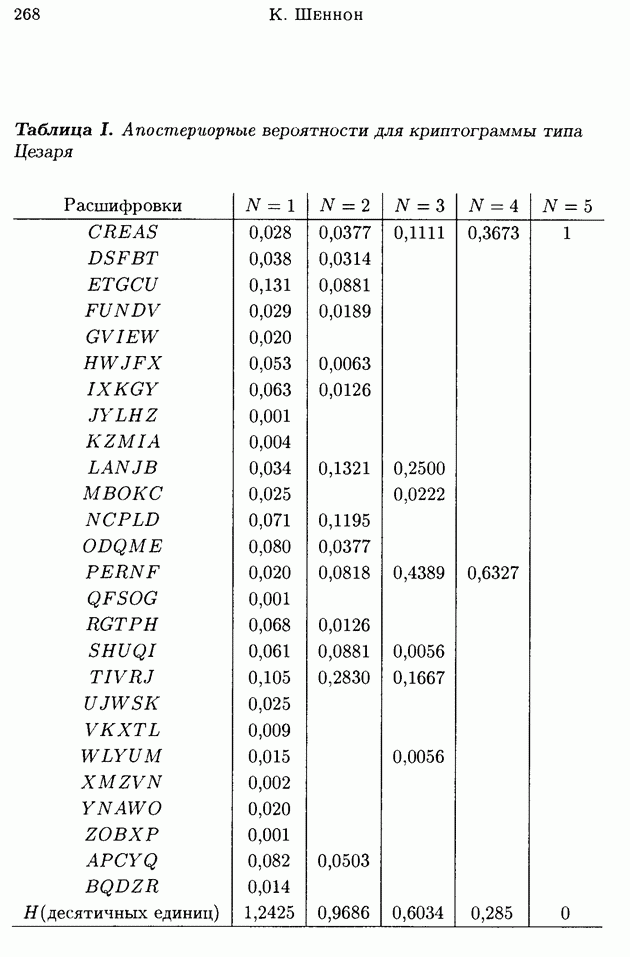
- Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность