| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Идеальное разделение секрета и матроиды
Начнем с определения идеальных СРС. Для этого вернемся к комбинаторному определению совершенной СРС. Следующее определение совершенной СРС [3] является даже более общим, чем вероятностное определение 1, поскольку условие (2) заменено в нем на более слабое.
Для произвольного множества  обозначим через
обозначим через  -матрицу, полученную из матрицы V удалением столбцов,
-матрицу, полученную из матрицы V удалением столбцов,
номера которых не принадлежат множеству В. Пусть  обозначает число различных строк в матрице
обозначает число различных строк в матрице 
Определение 3. Матрица V задает БД-совершенную СРС, реализующую структуру доступа  если
если

где  если
если  в противном случае.
в противном случае.
Это определение отличается от определений 1 и 2 тем, что на неразрешенные множества А накладывается довольно слабое условие, а именно, если множество строк V с данными значениями координат из множества А непусто, то все возможные значения секрета встречаются в нулевой координате этих строк (без требований «одинаково часто» как в комбинаторном определении 2 или же «с априорной вероятностью» как в вероятностном определении 1). Легко видеть, что матрица любой совершенной вероятностной СРС задает БД-совершенную СРС, но обратное неверно.
Для произвольной комбинаторной СРС, задаваемой матрицей V, определим на множествах  функцию
функцию  где
где  Легко проверить, что
Легко проверить, что  для любых множеств
для любых множеств  а условие (4) может быть переписано в виде
а условие (4) может быть переписано в виде

Лемма. Для любой БД-совершенной СРС если  то
то 
Доказательство. По условиям леммы  Следовательно,
Следовательно,

Так как мы предполагаем, что все точки  существенные, т. е. для любого
существенные, т. е. для любого  найдется подмножество А такое, что
найдется подмножество А такое, что  то из леммы вытекает
то из леммы вытекает
Следствие. Для любой БД-совершенной  для всех
для всех 
Следствие означает, как мы и предупреждали в начале статьи, что для совершенных СРС «размер» проекции не может быть меньше «размера» секрета. Поэтому БД-совершенная СРС называется идеальной, если  для всех
для всех 
Замечание. Неравенство  справедливо и для совершенных вероятностных СРС, поскольку их матрицы задают БД-совершенные СРС.
справедливо и для совершенных вероятностных СРС, поскольку их матрицы задают БД-совершенные СРС.
Естественный вопрос состоит в том, для каких структур доступа  существуют реализующие их идеальные (вероятностные или
существуют реализующие их идеальные (вероятностные или
комбинаторные) СРС. Как уже отмечалось во введении, наилучший на сегодняшний день ответ использует слово «матроид». Напомним определение матроидов и некоторые их основные свойства (см. [6]).
Матроидом называется конечное множество X и семейство I его подмножеств, называемых независимыми (остальные множества называются зависимыми), если выполнены следующие свойства:

Пример 4. Множество X — это множество векторов в некотором линейном векторном пространстве, а независимые подмножества — это линейно независимые подмножества векторов.
Собственно с этого примера и началась теория матроидов, вначале как попытка дать аксиоматическое определение линейной независимости векторов через «внутренние свойства», т. е. не апеллируя к понятию вектора. К счастью, попытка не удалась, так как нашлись матроиды, не представимые как линейные (т. е. как системы векторов), а сама теория матроидов разрослась далеко за пределы «линейной алгебры» (см. [6]).
Пример 5 (матроид Вамоса). Рассмотрим следующее множество:  и положим
и положим  Матроид Вамоса определяется как матроид, в котором множества
Матроид Вамоса определяется как матроид, в котором множества  а также все подмножества из пяти или более элементов являются зависимыми. Известно, что этот матроид не является линейным.
а также все подмножества из пяти или более элементов являются зависимыми. Известно, что этот матроид не является линейным.
Матроид также можно определить через так называемую ранговую функцию  матроида, определяемую как максимальная мощность независимого подмножества
матроида, определяемую как максимальная мощность независимого подмножества  Очевидно, что независимые множества (и только они) задаются условием
Очевидно, что независимые множества (и только они) задаются условием  Ранговая функция матроида обладает свойствами
Ранговая функция матроида обладает свойствами

Обратно, пусть некоторая функция  обладает свойствами (6). Назовем независимыми те множества А, для которых
обладает свойствами (6). Назовем независимыми те множества А, для которых  Тогда эти множества задают матроид, а функция
Тогда эти множества задают матроид, а функция  является его ранговой функцией. Возможно также определить матроид через минимальные зависимые множества, называемые циклами. Матроид называется связным, если для любых двух его точек существует содержащий их цикл.
является его ранговой функцией. Возможно также определить матроид через минимальные зависимые множества, называемые циклами. Матроид называется связным, если для любых двух его точек существует содержащий их цикл.
Теперь мы можем сформулировать основной результат. Теорема ([3]). Для любой БД-совершенной идеальной СРС, реализующей структуру доступа  независимые множества, определяемые условием
независимые множества, определяемые условием  задают связный матроид на множестве
задают связный матроид на множестве  Все циклы этого матроида, содержащие точку 0, имеют вид
Все циклы этого матроида, содержащие точку 0, имеют вид  где
где 
Главным в доказательстве теоремы является «проверка» целочисленности функции  . В самом деле,
. В самом деле,  очевидно обладает остальными свойствами (6) и, следовательно, при условии целочисленности является ранговой функцией и задает матроид. Доказательство этой теоремы и несколько более общих утверждений можно найти в [7].
очевидно обладает остальными свойствами (6) и, следовательно, при условии целочисленности является ранговой функцией и задает матроид. Доказательство этой теоремы и несколько более общих утверждений можно найти в [7].
Отметим, что из второй части утверждения теоремы следует, что разным идеальным СРС, реализующим данную структуру доступа  всегда соответствует один и тот же матроид, поскольку матроид однозначно определяется всеми циклами, проходящими через фиксированную точку (см. [6]). Тем самым, каждой идеально реализуемой структуре доступа соответствует однозначно определенный матроид.
всегда соответствует один и тот же матроид, поскольку матроид однозначно определяется всеми циклами, проходящими через фиксированную точку (см. [6]). Тем самым, каждой идеально реализуемой структуре доступа соответствует однозначно определенный матроид.
В связи с теоремой возникает несколько естественных вопросов. Прежде всего, не порождают ли идеальные СРС все матроиды? Нет, например, матроид Вамоса не может быть получен как матроид идеальной СРС [8]. С другой стороны, линейные матроиды есть ни что иное как рассмотренные в п. 3 идеальные одномерные линейные СРС. В связи с этим возникает вопрос о существовании структуры доступа  которую невозможно реализовать в виде идеальной одномерной линейной СРС, но можно в виде идеальной многомерной линейной СРС. Недавно такой пример был построен [9], и, значит, мы можем говорить о многомерных линейных матроидах как классе матроидов более общем, чем линейные.
которую невозможно реализовать в виде идеальной одномерной линейной СРС, но можно в виде идеальной многомерной линейной СРС. Недавно такой пример был построен [9], и, значит, мы можем говорить о многомерных линейных матроидах как классе матроидов более общем, чем линейные.
Итак, идеальных СРС больше, чем линейных матроидов, но меньше, чем всех матроидов. Уточнить, «насколько больше», представляется довольно сложной задачей. В частности, существует ли идеально реализуемая структура доступа  которую невозможно реализовать как идеальную линейную многомерную
которую невозможно реализовать как идеальную линейную многомерную 
Литература к главе 5
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму изданию
- Глава 1. Основные понятия криптографии
- 2. Предмет криптографии
- 3. Математические основы
- 4. Новые направления
- 5. Заключение
- Глава 2. Криптография и теория сложности
- 2. Криптография и гипотеза P != NP
- 3. Односторонние функции
- 4. Псевдослучайные генераторы
- 5. Доказательства с нулевым разглашением
- Глава 3. Криптографические протоколы
- 2. Целостность. Протоколы аутентификации и электронной подписи
- Схема аутентификации Шнорра
- Схема электронной подписи Шнорра
- 3. Неотслеживаемость. Электронные деньги
- 4. Протоколы типа «подбрасывание монеты по телефону»
- Протокол подбрасывания монеты
- 5. Еще раз о разделении секрета
- 6. Поиграем в «кубики». Протоколы голосования
- Протокол Шаума и Педерсена
- 7. За пределами стандартных предположений. Конфиденциальная передача сообщений
- 8. Вместо заключения
- Глава 4. Алгоритмические проблемы теории чисел
- 2. Система шифрования RSA
- 3. Сложность теоретико-числовых алгоритмов
- 4. Как отличить составное число от простого
- 5. Алгоритм, доказывающий непростоту числа
- 5. Как строить большие простые числа
- 6. Как проверить большое число на простоту
- 7. Как раскладывают составные числа на множители
- 8. Дискретное логарифмирование
- 9. Заключение
- Глава 5. Математика разделения секрета
- 2. Разделение секрета для произвольных структур доступа
- 3. Линейное разделение секрета.
- 4. Идеальное разделение секрета и матроиды
- Глава 6. Компьютер и криптография
- 2. Немного теории
- Что надо знать перед написанием программы шифрования
- 3. Как зашифровать файл?
- 4. Поучимся на чужих ошибках
- 5. Вместо заключения
- Глава 7. Олимпиады по криптографии для школьников
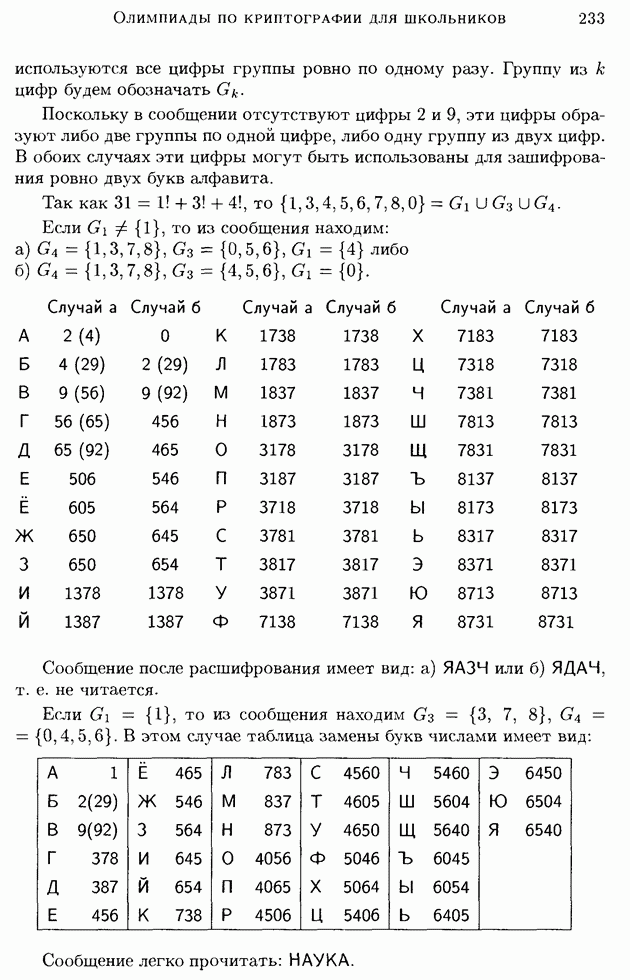
- 2. Шифры замены
- А. Конан Дойл, «Пляшущие человечки»
- Ж. Верн, «Путешествие к центру Земли»
- 3. Шифры перестановки
- 4. Многоалфавитные шифры замены с периодическим ключом
- 5. Условия задач олимпиад по математике и криптографии
- 6. Указания и решения
- Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
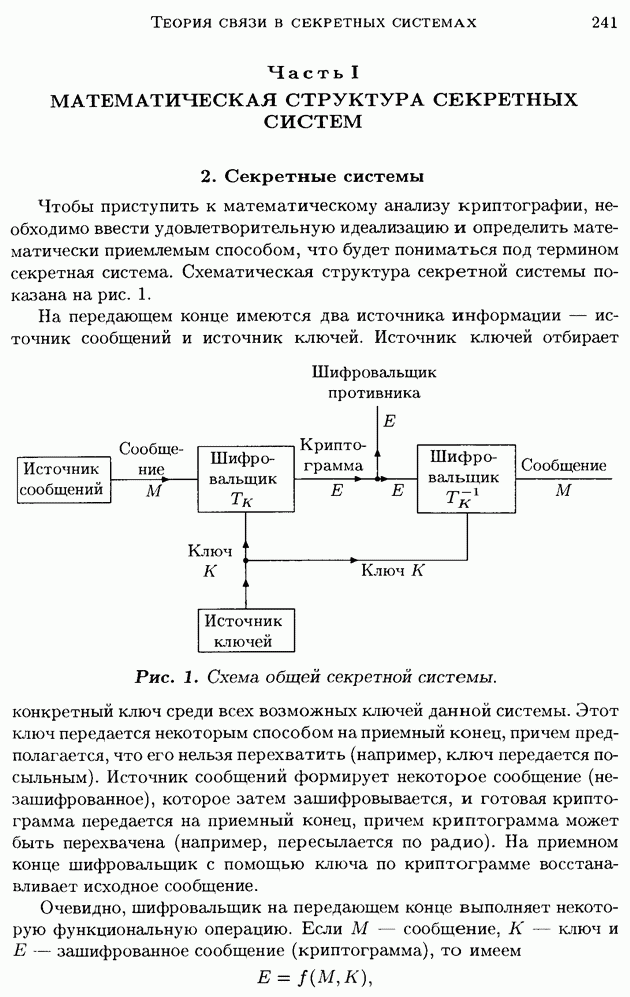
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
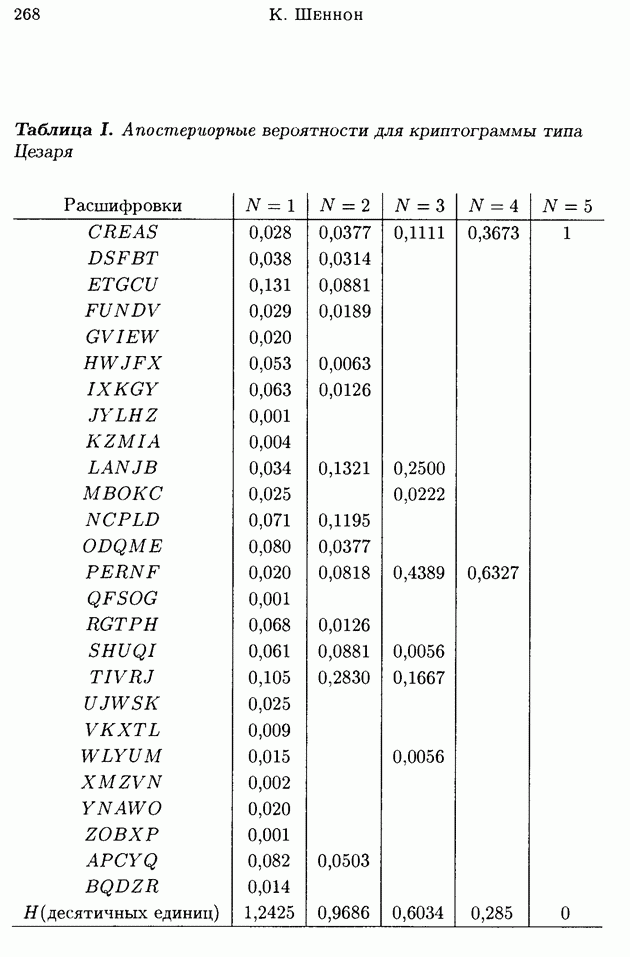
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность