| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Шифры перестановки
Шифр, преобразования из которого изменяют только порядок следования символов исходного текста, но не изменяют их самих, называется шифром перестановки 
Рассмотрим преобразование из ШП, предназначенное для зашифрования сообщения длиной  символов. Его можно представить с помощью таблицы
символов. Его можно представить с помощью таблицы

где  номер места шифртекста, на которое попадает первая буква исходного сообщения при выбранном преобразовании,
номер места шифртекста, на которое попадает первая буква исходного сообщения при выбранном преобразовании,  номер места для второй буквы и т. д. В верхней строке таблицы выписаны по порядку числа от 1 до
номер места для второй буквы и т. д. В верхней строке таблицы выписаны по порядку числа от 1 до  а в нижней — те же числа, но в произвольном порядке. Такая таблица называется подстановкой степени
а в нижней — те же числа, но в произвольном порядке. Такая таблица называется подстановкой степени 
Зная подстановку, задающую преобразование, можно осуществить как зашифрование, так и расшифрование текста. Например, если для преобразования используется подстановка

и в соответствии с ней зашифровывается слово  то получится
то получится  Попробуйте расшифровать сообщение
Попробуйте расшифровать сообщение  полученное в результате преобразования с помощью указанной выше подстановки.
полученное в результате преобразования с помощью указанной выше подстановки.
В качестве упражнения читателю предлагается самостоятельно выписать подстановки, задающие преобразования в описанных ниже трех
примерах шифров перестановки. Ответы помещены в конце раздела.
Читатель, знакомый с методом математической индукции, может легко убедиться в том, что существует  (обозначается
(обозначается  читается
читается  факториал») вариантов заполнения нижней строки таблицы (6). Таким образом, число различных преобразований шифра перестановки, предназначенного для зашифрования сообщений длины
факториал») вариантов заполнения нижней строки таблицы (6). Таким образом, число различных преобразований шифра перестановки, предназначенного для зашифрования сообщений длины  меньше либо равно
меньше либо равно  (заметим, что в это число входит и вариант преобразования, оставляющий все символы на своих местах!).
(заметим, что в это число входит и вариант преобразования, оставляющий все символы на своих местах!).
С увеличением числа  значение
значение  растет очень быстро. Приведем таблицу значений
растет очень быстро. Приведем таблицу значений  для первых 10 натуральных чисел:
для первых 10 натуральных чисел:
(см. скан)
При больших  для приближенного вычисления
для приближенного вычисления  можно пользоваться известной формулой Стирлинга
можно пользоваться известной формулой Стирлинга

где 
Примером ШП, предназначенного для зашифрования сообщений длины  является шифр, в котором в качестве множества ключей взято множество всех подстановок степени
является шифр, в котором в качестве множества ключей взято множество всех подстановок степени  а соответствующие им преобразования шифра задаются, как было описано выше. Число ключей такого шифра равно
а соответствующие им преобразования шифра задаются, как было описано выше. Число ключей такого шифра равно 
Для использования на практике такой шифр не удобен, так как при больших значениях  приходится работать с длинными таблицами.
приходится работать с длинными таблицами.
Широкое распространение получили шифры перестановки, использующие некоторую геометрическую фигуру. Преобразования из этого шифра состоят в том, что в фигуру исходный текст вписывается по ходу одного «маршрута», а затем по ходу другого выписывается с нее. Такой шифр называют маршрутной перестановкой. Например, можно вписывать исходное сообщение в прямоугольную таблицу, выбрав такой маршрут: по горизонтали, начиная с левого верхнего угла поочередно слева направо и справа налево. Выписывать же сообщение будем по другому маршруту: по вертикали, начиная с верхнего правого угла и двигаясь поочередно сверху вниз и снизу вверх.
Зашифруем, например, указанным способом фразу:

используя прямоугольник размера 
(см. скан)
Зашифрованная фраза выглядит так:

Теоретически маршруты могут быть значительно более изощренными, однако запутанность маршрутов усложняет использование таких шифров.
Ниже приводятся описания трех разновидностей шифров перестановки, встречавшихся в задачах олимпиад.
Шифр «Сцитала». Одним из самых первых шифровальных приспособлений был жезл («Сцитала»), применявшийся еще во времена войны Спарты против Афин в V веке до н. э. Это был цилиндр, на который виток к витку наматывалась узкая папирусная лента (без просветов и нахлестов), а затем на этой ленте вдоль его оси записывался необходимый для передачи текст. Лента сматывалась с цилиндра и отправлялась адресату, который, имея цилиндр точно такого же диаметра, наматывал ленту на него и прочитывал сообщение. Ясно, что такой способ шифрования осуществляет перестановку местами букв сообщения.
Шифр «Сцитала», как видно из решения задачи 2.1, реализует не более  перестановок
перестановок  по прежнему, — длина сообщения). Действительно, этот шифр, как нетрудно видеть, эквивалентен следующему шифру маршрутной перестановки: в таблицу, состоящую из
по прежнему, — длина сообщения). Действительно, этот шифр, как нетрудно видеть, эквивалентен следующему шифру маршрутной перестановки: в таблицу, состоящую из  столбцов, построчно записывают сообщение, после чего выписывают буквы по столбцам. Число задействованных столбцов таблицы не может превосходить длины сообщения.
столбцов, построчно записывают сообщение, после чего выписывают буквы по столбцам. Число задействованных столбцов таблицы не может превосходить длины сообщения.
Имеются еще и чисто физические ограничения, накладываемые реализацией шифра «Сцитала». Естественно предположить, что диаметр жезла не должен превосходить 10 сантиметров. При высоте строки в 1 сантиметр на одном витке такого жезла уместится не более 32 букв  Таким образом, число перестановок, реализуемых «Сцита-лой», вряд ли превосходит 32.
Таким образом, число перестановок, реализуемых «Сцита-лой», вряд ли превосходит 32.
Шифр «Поворотная решетка». Для использования шифра, называемого поворотной решеткой, изготавливается трафарет из прямоугольного листа клетчатой бумаги размера  клеток. В трафарете вырезано тк клеток так, что при наложении его на чистый лист бумаги того же размера четырьмя возможными способами его вырезы полностью покрывают всю площадь листа.
клеток. В трафарете вырезано тк клеток так, что при наложении его на чистый лист бумаги того же размера четырьмя возможными способами его вырезы полностью покрывают всю площадь листа.
Буквы сообщения последовательно вписываются в вырезы трафарета (по строкам, в каждой строке слева направо) при каждом из четырех его возможных положений в заранее установленном порядке.
Поясним процесс шифрования на примере. Пусть в качестве ключа используется решетка  приведенная на рис. 1.
приведенная на рис. 1.
Зашифруем с ее помощью текст

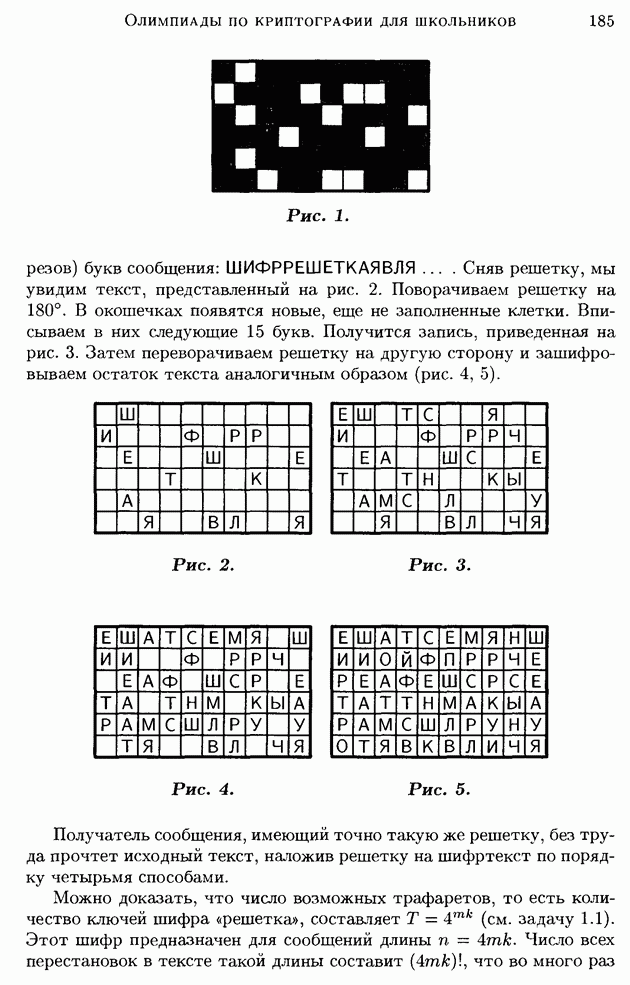
Наложив решетку на лист бумаги, вписываем первые 15 (по числу

Рис. 1.
вырезов) букв сообщения:  Сняв решетку, мы увидим текст, представленный на рис. 2. Поворачиваем решетку на 180°. В окошечках появятся новые, еще не заполненные клетки. Вписываем в них следующие 15 букв. Получится запись, приведенная на рис. 3. Затем переворачиваем решетку на другую сторону и зашифровываем остаток текста аналогичным образом (рис. 4, 5).
Сняв решетку, мы увидим текст, представленный на рис. 2. Поворачиваем решетку на 180°. В окошечках появятся новые, еще не заполненные клетки. Вписываем в них следующие 15 букв. Получится запись, приведенная на рис. 3. Затем переворачиваем решетку на другую сторону и зашифровываем остаток текста аналогичным образом (рис. 4, 5).

Рис. 2.

Рис. 3.

Рис. 4.

Рис. 5.
Получатель сообщения, имеющий точно такую же решетку, без труда прочтет исходный текст, наложив решетку на шифртекст по порядку четырьмя способами.
Можно доказать, что число возможных трафаретов, то есть количество ключей шифра «решетка», составляет  (см. задачу 1.1). Этот шифр предназначен для сообщений длины
(см. задачу 1.1). Этот шифр предназначен для сообщений длины  Число всех перестановок в тексте такой длины составит
Число всех перестановок в тексте такой длины составит  что во много раз
что во много раз
больше числа  Однако, уже при размере трафарета
Однако, уже при размере трафарета  число возможных решеток превосходит 4 миллиарда.
число возможных решеток превосходит 4 миллиарда.
Широко распространена разновидность шифра маршрутной перестановки, называемая «шифром вертикальной перестановки» (ШВП). В нем снова используется прямоугольник, в который сообщение вписывается обычным способом (по строкам слева направо). Выписываются буквы по вертикали, а столбцы при этом берутся в порядке, определяемом ключом. Пусть, например, этот ключ таков: (5,4,1,7,2,6,3), и с его помощью надо зашифровать сообщение:

Впишем сообщение в прямоугольник, столбцы которого пронумерованы в соответствии с ключом:
(см. скан)
Теперь, выбирая столбцы в порядке, заданном ключом, и выписывая последовательно буквы каждого из них сверху вниз, получаем такую криптограмму:

Число ключей ШВП не более  где
где  число столбцов таблицы. Как правило,
число столбцов таблицы. Как правило,  гораздо меньше, чем длина текста
гораздо меньше, чем длина текста  (сообщение укладывается в несколько строк по
(сообщение укладывается в несколько строк по  букв), а, значит, и
букв), а, значит, и  много меньше
много меньше 
Пользуясь приведенной выше формулой Стирлинга при больших  попытайтесь оценить, во сколько раз число возможных перестановок
попытайтесь оценить, во сколько раз число возможных перестановок  столбцами меньше числа всех перестановок на тексте длины
столбцами меньше числа всех перестановок на тексте длины  кратном
кратном 
В случае, когда ключ ШВП не рекомендуется записывать, его можно извлекать из какого-то легко запоминающегося слова или предложения. Для этого существует много способов. Наиболее распространенный состоит в том, чтобы приписывать буквам числа в соответствии с обычным алфавитным порядком букв. Например, пусть ключевым словом будет  Присутствующая в нем буква А получает номер 1. Если какая-то буква входит несколько раз, то ее появления нумеруются последовательно слева направо. Поэтому второе вхождение буквы А получает номер 2. Поскольку буквы
Присутствующая в нем буква А получает номер 1. Если какая-то буква входит несколько раз, то ее появления нумеруются последовательно слева направо. Поэтому второе вхождение буквы А получает номер 2. Поскольку буквы  в этом слове нет, то буква В получает номер 3 и так далее. Процесс продолжается до тех
в этом слове нет, то буква В получает номер 3 и так далее. Процесс продолжается до тех
пор, пока все буквы не получат номера. Таким образом, мы получаем следующий ключ:

Перейдем к вопросу о методах вскрытия шифров перестановки. Проблема, возникающая при восстановлении сообщения, зашифрованного ШП, состоит не только в том, что число возможных ключей велико даже при небольших длинах текста. Если и удастся перебрать все допустимые варианты перестановок, не всегда ясно, какой из этих вариантов истинный. Например, пусть требуется восстановить исходный текст по криптограмме  и нам ничего не известно, кроме того, что применялся шифр перестановки. Какой вариант «осмысленного» исходного текста признать истинным:
и нам ничего не известно, кроме того, что применялся шифр перестановки. Какой вариант «осмысленного» исходного текста признать истинным:  или
или  А может быть
А может быть  Приведем пример еще более запутанной ситуации. Пусть требуется восстановить сообщение по криптограмме
Приведем пример еще более запутанной ситуации. Пусть требуется восстановить сообщение по криптограмме

полученной шифром перестановки. Возможны, как минимум, два варианта исходного сообщения:

Эти варианты имеют прямо противоположный смысл и в имеющихся условиях у нас нет возможности определить, какой из вариантов истинный.
Иногда, за счет особенностей реализации шифра, удается получить информацию об использованном преобразовании (перестановке). Рассмотрим шифр «Сцитала» из задачи 2.1. Выше уже рассматривался вопрос о количестве перестановок, реализуемых «Сциталой». Их оказалось не более 32. Это число невелико, поэтому можно осуществить перебор всех вариантов. При достаточной длине сообщения, мы, скорее всего, получим единственный читаемый вариант текста. Однако, используя информацию о расположении линий, оставленных шифровальщиком, удается определить диаметр стержня, а значит, и возникающую перестановку букв (см. задачу 2.1).
В рассмотренном примере шифровальщик по неосторожности оставил на папирусе следы, позволяющие нам легко прочитать сообщение. Возможны и другие ситуации, когда не очень «грамотное» использование шифра облегчает вскрытие переписки.
В задаче 5.2 содержится пример текста, зашифрованного ШВП. По условию пробелы между словами при записи текста в таблицу опускались. Поэтому заключаем, что все столбцы, содержащие пробел в последней строке, должны стоять в конце текста. Таким образом, возникает разбиение столбцов на две группы (содержащие 6 букв, и
содержащие 5 букв). Для завершения восстановления исходного текста достаточно найти порядок следования столбцов в каждой из групп в отдельности, что гораздо проще.
Аналогичная ситуация возникает и при «неполном» использовании шифра «решетка» (см. задачу 4.1). Пусть имеется решетка размера  и зашифрованное с ее помощью сообщение длины
и зашифрованное с ее помощью сообщение длины  к, не содержащее пробелов. Незаполненные к мест в решетке при условии, что к
к, не содержащее пробелов. Незаполненные к мест в решетке при условии, что к  соответствуют вырезам в четвертом положении решетки. На основе такой информации, происходит резкое уменьшение числа допустимых решеток (их будет
соответствуют вырезам в четвертом положении решетки. На основе такой информации, происходит резкое уменьшение числа допустимых решеток (их будет  Читателю предлагается самостоятельно подсчитать число допустимых решеток при
Читателю предлагается самостоятельно подсчитать число допустимых решеток при 
На примере решения задачи 5.2 продемонстрируем еще один подход к вскрытию шифров вертикальной перестановки — лингвистический. Он основан на том, что в естественных языках некоторые комбинации букв встречаются очень часто, другие — гораздо реже, а многие вообще не встречаются (например — 
Будем подбирать порядок следования столбцов друг за другом так, чтобы во всех строках этих столбцов получались «читаемые» отрезки текста. В приведенном решении задачи восстановление текста начинается с подбора цепочки из трех столбцов первой группы, содержащей в последней строке сочетание  так как естественно предположить, что сообщение заканчивается точкой. Далее подбираются столбцы, продолжающие участки текста в других строках, и т. д.
так как естественно предположить, что сообщение заканчивается точкой. Далее подбираются столбцы, продолжающие участки текста в других строках, и т. д.
Сочетание лингвистического метода с учетом дополнительной информации довольно быстро может привести к вскрытию сообщения.
В заключение рассказа о шифрах перестановки приведем историю с зашифрованным автографом А. С. Пушкина, описанную в романе В. Каверина «Исполнение желаний».
Главный герой романа — студент-историк  Трубачевский, — занимавшийся работой в архиве своего учителя — академика Бауэра С. И., — нашел в одном из секретных ящиков пушкинского бюро фрагмент недописанной X главы «Евгения Онегина». Это был перегнутый вдвое полулист плотной голубоватой бумаги с водяным знаком 1829 года. На листе было написано следующее.
Трубачевский, — занимавшийся работой в архиве своего учителя — академика Бауэра С. И., — нашел в одном из секретных ящиков пушкинского бюро фрагмент недописанной X главы «Евгения Онегина». Это был перегнутый вдвое полулист плотной голубоватой бумаги с водяным знаком 1829 года. На листе было написано следующее.
(см. скан)
(см. скан)
Без особых усилий Трубачевский прочитал рукопись, и ничего не понял. Он переписал ее, получилась бессвязная чепуха, в которой одна строка, едва начавшая мысль, перебивается другой, а та — третьей, еще более бессмысленной и бессвязной. Он попробовал разбить рукопись на строфы, — опять не получилось. Стал искать рифмы, — как будто и рифм не было, хотя на белый стих все это мало похоже. Просчитал строку — четырехстопный ямб, размер, которым написан «Евгений Онегин».
Трубачевский с азартом взялся за рукопись, пытался читать ее, пропуская по одной строке, потом по две, по три, надеясь случайно угадать тайную последовательность, в которой были записаны строки. У него ничего не получалось. Тогда он стал читать третью строку вслед за первой, пятую за третьей, восьмую за пятой, предположив, что пропуски должны увеличиваться в арифметической прогрессии. Все то же! Отчаявшись, он бросил эту затею. Однако, она не давала ему покоя ни на лекции, ни в трамвае ... Как шахматист, играющий в уме, он не только знал наизусть каждую строчку, он видел ее в десяти комбинациях сразу.
Прошло время. Однажды, когда он смотрел на светлые пятна окон подходящего к перрону поезда, каким-то внутренним зрением он
увидел перед собой всю рукопись — и с такой необыкновенной отчетливостью, как это бывает только во сне.
Сможете ли вы прочитать эти стихи? Ответ вы найдете в романе В. Каверина.
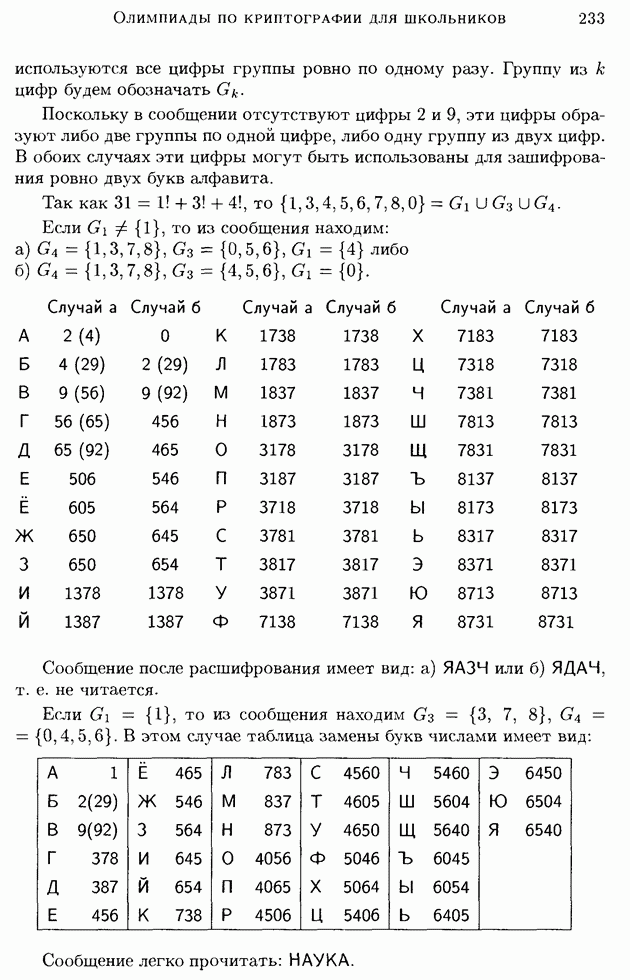
Ответы к упражнению.
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму изданию
- Глава 1. Основные понятия криптографии
- 2. Предмет криптографии
- 3. Математические основы
- 4. Новые направления
- 5. Заключение
- Глава 2. Криптография и теория сложности
- 2. Криптография и гипотеза P != NP
- 3. Односторонние функции
- 4. Псевдослучайные генераторы
- 5. Доказательства с нулевым разглашением
- Глава 3. Криптографические протоколы
- 2. Целостность. Протоколы аутентификации и электронной подписи
- Схема аутентификации Шнорра
- Схема электронной подписи Шнорра
- 3. Неотслеживаемость. Электронные деньги
- 4. Протоколы типа «подбрасывание монеты по телефону»
- Протокол подбрасывания монеты
- 5. Еще раз о разделении секрета
- 6. Поиграем в «кубики». Протоколы голосования
- Протокол Шаума и Педерсена
- 7. За пределами стандартных предположений. Конфиденциальная передача сообщений
- 8. Вместо заключения
- Глава 4. Алгоритмические проблемы теории чисел
- 2. Система шифрования RSA
- 3. Сложность теоретико-числовых алгоритмов
- 4. Как отличить составное число от простого
- 5. Алгоритм, доказывающий непростоту числа
- 5. Как строить большие простые числа
- 6. Как проверить большое число на простоту
- 7. Как раскладывают составные числа на множители
- 8. Дискретное логарифмирование
- 9. Заключение
- Глава 5. Математика разделения секрета
- 2. Разделение секрета для произвольных структур доступа
- 3. Линейное разделение секрета.
- 4. Идеальное разделение секрета и матроиды
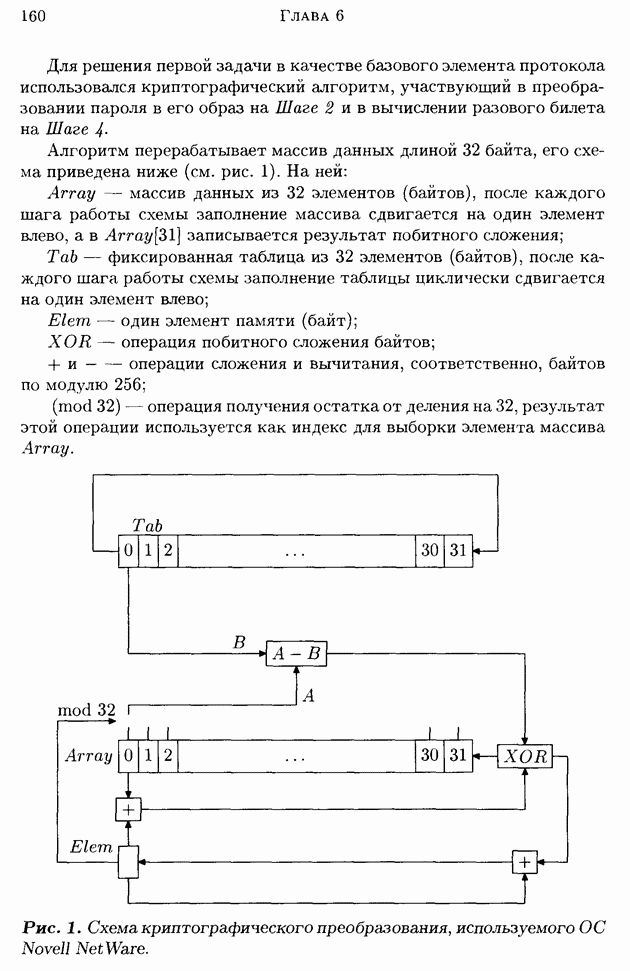
- Глава 6. Компьютер и криптография
- 2. Немного теории
- Что надо знать перед написанием программы шифрования
- 3. Как зашифровать файл?
- 4. Поучимся на чужих ошибках
- 5. Вместо заключения
- Глава 7. Олимпиады по криптографии для школьников
- 2. Шифры замены
- А. Конан Дойл, «Пляшущие человечки»
- Ж. Верн, «Путешествие к центру Земли»
- 3. Шифры перестановки
- 4. Многоалфавитные шифры замены с периодическим ключом
- 5. Условия задач олимпиад по математике и криптографии
- 6. Указания и решения
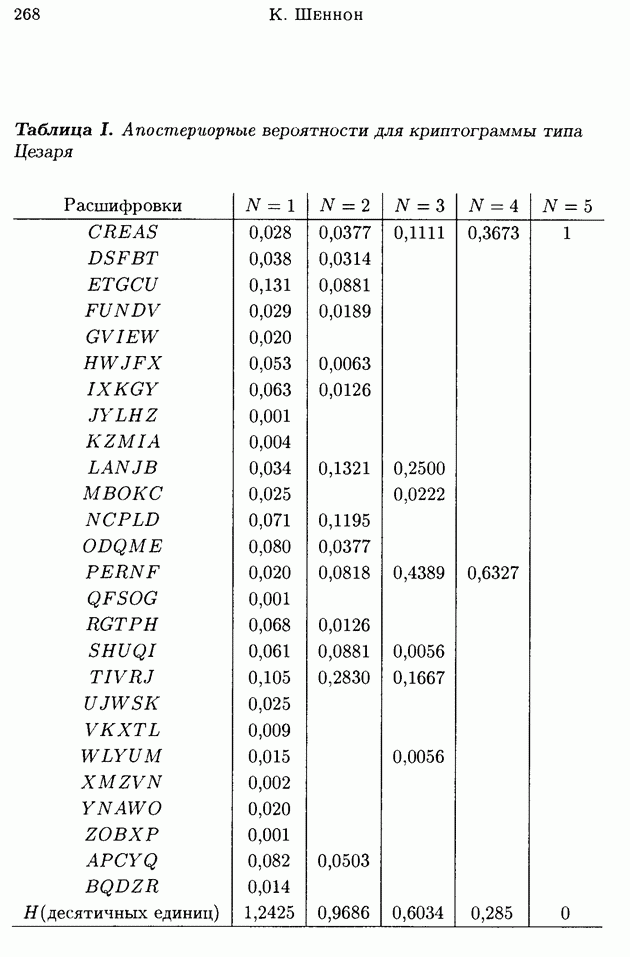
- Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
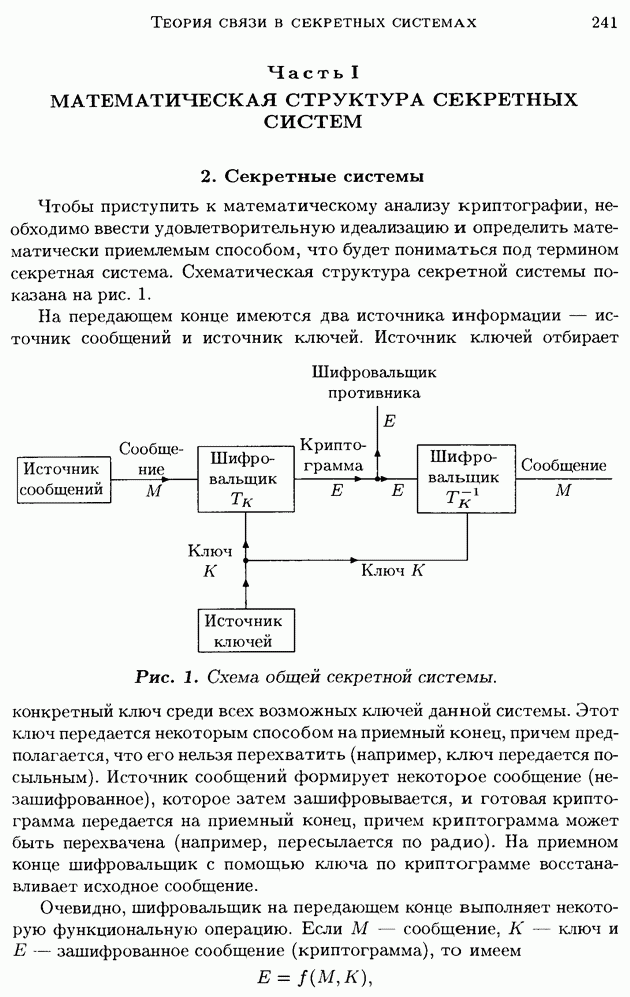
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность