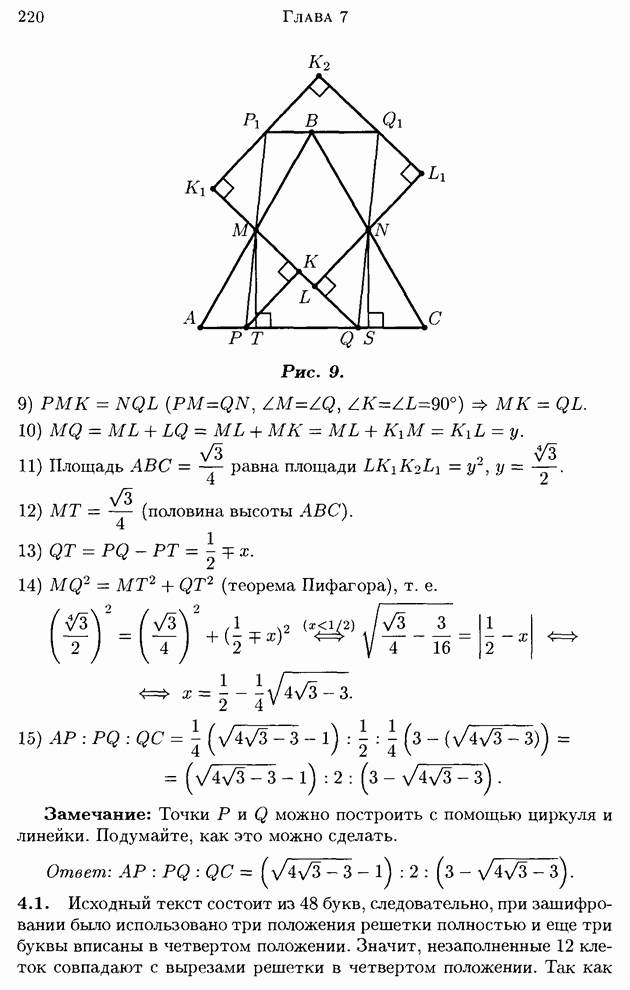| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
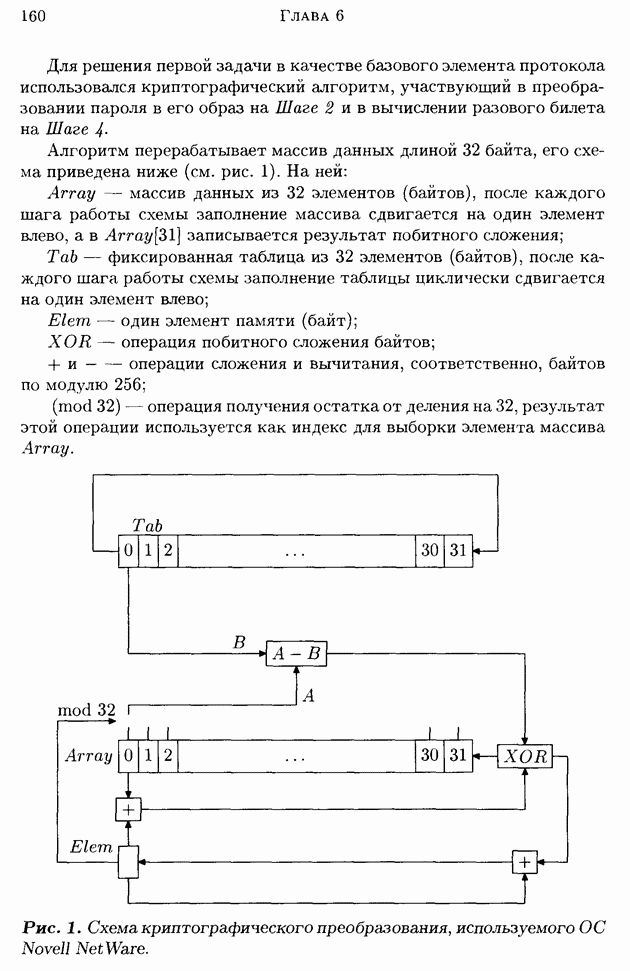
6. Указания и решения
1.1. Все клетки квадрата размера  разобьем на непересекающиеся группы по четыре клетки в каждой. Отнесем клетки к одной и той же группе, если при каждом повороте квадрата до его самосовмещения они перемещаются на места клеток этой же группы. На рисунке показано такое разбиение на группы всех клеток квадрата
разобьем на непересекающиеся группы по четыре клетки в каждой. Отнесем клетки к одной и той же группе, если при каждом повороте квадрата до его самосовмещения они перемещаются на места клеток этой же группы. На рисунке показано такое разбиение на группы всех клеток квадрата  причем клетки одной группы помечены одной и той же цифрой. Всего таких групп будет
причем клетки одной группы помечены одной и той же цифрой. Всего таких групп будет  (целое, так как
(целое, так как  четное число). При наложении трафарета на квадрат ровно одна клетка из каждой группы окажется под его вырезами. Каждому трафарету поставим в соответствие упорядоченный набор всех клеток из таких групп, оказавшихся под вырезами трафарета при наложении его на квадрат помеченной стороной вверх. Такое соответствие является взаимнооднозначным, поскольку каждому ключу будет однозначно соответствовать упорядоченный набор из
четное число). При наложении трафарета на квадрат ровно одна клетка из каждой группы окажется под его вырезами. Каждому трафарету поставим в соответствие упорядоченный набор всех клеток из таких групп, оказавшихся под вырезами трафарета при наложении его на квадрат помеченной стороной вверх. Такое соответствие является взаимнооднозначным, поскольку каждому ключу будет однозначно соответствовать упорядоченный набор из  клеток (по одной из каждой группы), вырезанных в трафарете, и наоборот. Всего таких наборов
клеток (по одной из каждой группы), вырезанных в трафарете, и наоборот. Всего таких наборов  В самом деле, существует ровно четыре различных варианта выбора клетки из каждой группы независимо от выбранных клеток из других таких групп. Таким образом, число различных ключей шифра «поворотная решетка» при четных значениях
В самом деле, существует ровно четыре различных варианта выбора клетки из каждой группы независимо от выбранных клеток из других таких групп. Таким образом, число различных ключей шифра «поворотная решетка» при четных значениях  равно
равно 
1.2. Легко видеть, что  Отсюда
Отсюда  где
где  корни многочлена
корни многочлена  Получаем
Получаем
(см. скан)
Ответ: ТАКДЕРЖАТЬ
1.3. Ответ: начиная с 54.
1.4. Разложим числа то и  на простые множители:
на простые множители:  . Обозначим буквой
. Обозначим буквой  число
число  равное произведению
равное произведению  Найдем все его делители
Найдем все его делители  вида:
вида:  где числа х, у, z и u принимают только значения 0 и 1. Тогда, как нетрудно видеть, числа
где числа х, у, z и u принимают только значения 0 и 1. Тогда, как нетрудно видеть, числа  окажутся взаимно простыми. Полагая
окажутся взаимно простыми. Полагая  получим все искомые пары
получим все искомые пары  В самом деле, в указанных выше условиях наибольший общий делитель такой пары равен
В самом деле, в указанных выше условиях наибольший общий делитель такой пары равен  а ее наименьшее общее кратное равно
а ее наименьшее общее кратное равно  Таким
Таким
образом, искомое число упорядоченных пар совпадает с числом всех делителей  вида:
вида:  которое равно числу всех упорядоченных наборов длины 4 и состоящих только из 0 и 1. Число всех таких наборов равно
которое равно числу всех упорядоченных наборов длины 4 и состоящих только из 0 и 1. Число всех таких наборов равно  так как для каждого места в наборах существует ровно 2 варианта его значений независимо от значений на других местах. В общем случае число
так как для каждого места в наборах существует ровно 2 варианта его значений независимо от значений на других местах. В общем случае число  представляется в виде
представляется в виде  где
где  различные простые числа,
различные простые числа,  натуральные числа. Число всех делителей вида:
натуральные числа. Число всех делителей вида:  где числа х,
где числа х,  принимают только по два значения (0 и соответствующий натуральный показатель степени в представлении числа
принимают только по два значения (0 и соответствующий натуральный показатель степени в представлении числа  равно
равно  где k — число всех простых делителей числа
где k — число всех простых делителей числа  Если число различных простых множителей в каноническом разложении числа
Если число различных простых множителей в каноническом разложении числа  равно к, то число различных упорядоченных пар
равно к, то число различных упорядоченных пар  равно
равно 
Ответ: 16 пар (пары  и
и  разные). В общем случае число упорядоченных пар равно
разные). В общем случае число упорядоченных пар равно  где k — число всех простых делителей
где k — число всех простых делителей 
1.5. Из последней строчки легко заметить, что  Тогда из первого столбца находим, что
Тогда из первого столбца находим, что  Затем из последнего столбца находим
Затем из последнего столбца находим  Итак,
Итак,

Из средней строки ясно, что  Из первого столбца находим
Из первого столбца находим  Из средней строки можно вычислить значения Н и 3:
Из средней строки можно вычислить значения Н и 3:  Получим
Получим

Далее, последовательно вычисляем значения:  Расставим буквы в порядке возрастания их цифровых значений и получим текст ШИФРЗАМЕНЫ
Расставим буквы в порядке возрастания их цифровых значений и получим текст ШИФРЗАМЕНЫ
Ответ: ШИФРЗАМЕНЫ
1.6. Ответ: например, 
Обозначим  набор
набор  выписанный в обратном порядке.
выписанный в обратном порядке.

В общем случае можно показать, что множество искомых наборов состоит из слов вида:

2.1. Рассмотрим один виток ленты на развертке цилиндра (разрез по горизонтальной линии). По условию высота  опущенная на сторону
опущенная на сторону  равна
равна  Угол
Угол  равен (
равен ( Отсюда
Отсюда  равно
равно  Так как высота строки равна
Так как высота строки равна  то всего на одном витке
то всего на одном витке  букв.
букв.
Ответ: чтобы прочитать текст, надо разрезать ленту на участки по  букв и сложить их рядом.
букв и сложить их рядом.

Рис. 8.
2.2. Согласно условию, исходное сообщение состоит из двух пятерок цифр:  Пусть
Пусть  последние две цифры суммы чисел, изображенных этими пятерками. Через
последние две цифры суммы чисел, изображенных этими пятерками. Через  обозначим последнюю цифру суммы чисел
обозначим последнюю цифру суммы чисел  Пусть
Пусть  обозначает цифру переноса (цифру десятков) суммы
обозначает цифру переноса (цифру десятков) суммы  По условию имеем, что
По условию имеем, что 
Пусть  первый член,
первый член,  разность арифметической прогрессии, которую коммерсант использовал при шифровании. Тогда из условия получаем:
разность арифметической прогрессии, которую коммерсант использовал при шифровании. Тогда из условия получаем:

Обозначим символом  равенство остатков от деления на 10 чисел
равенство остатков от деления на 10 чисел  Тогда записи
Тогда записи  имеют одинаковый
имеют одинаковый
смысл. Если  то
то  Всегда
Всегда  так как остаток от деления единствен.
так как остаток от деления единствен.
Из соотношений (4), (5), (9) и (10) находим соответственно:

Подставляя эти значения в равенства (11) и (12), получим следующие равенства:  Отсюда следует, что
Отсюда следует, что

Подставив X из (17) и из (18) в (1), (2),(3), (13), (14), (6), (7), (8), (15), (16), найдем выражения для цифр исходного сообщения:

Найденные выражения дают два варианта исходных сообщений:

2.3. Ответ: а — любое, b - не должно делиться на 2 и на 5.
Указание. Обозначим через  остаток от деления значения многочлена
остаток от деления значения многочлена  на 10. Для однозначного расшифрования необходимо и достаточно, чтобы разным значениям х соответствовали разные значения
на 10. Для однозначного расшифрования необходимо и достаточно, чтобы разным значениям х соответствовали разные значения  Поэтому
Поэтому  принимают все значения от 0 до 9. Найдем эти значения:
принимают все значения от 0 до 9. Найдем эти значения:

где  остаток от деления числа у на 10.
остаток от деления числа у на 10.
Отсюда, пользуясь свойствами остатков, замечаем, что  должно быть нечетным (иначе
должно быть нечетным (иначе  будут только четные числа) и
будут только четные числа) и  не должно делиться на 5 (иначе
не должно делиться на 5 (иначе  будут только 0 и 5). Непосредственной проверкой можно убедиться, что при любом а и при всех
будут только 0 и 5). Непосредственной проверкой можно убедиться, что при любом а и при всех  удовлетворяющим приведенным условиям, гарантируется однозначность расшифрования.
удовлетворяющим приведенным условиям, гарантируется однозначность расшифрования.
2.4. Обозначим через  остаток от деления на 26 суммы чисел, которые соответствуют первым
остаток от деления на 26 суммы чисел, которые соответствуют первым  буквам алфавита
буквам алфавита 
Если среди чисел  есть нуль:
есть нуль:  то искомой ключевой комбинацией является цепочка первых
то искомой ключевой комбинацией является цепочка первых  букв алфавита.
букв алфавита.
Если среди чисел  нет нуля, то обязательно найдутся два одинаковых числа:
нет нуля, то обязательно найдутся два одинаковых числа:  (считаем, что
(считаем, что  Тогда искомой ключевой комбинацией является участок алфавита, начинающийся с
Тогда искомой ключевой комбинацией является участок алфавита, начинающийся с  и заканчивающийся
и заканчивающийся  буквой.
буквой.
2.5. Если две буквы с порядковыми номерами  и То зашифрованы в буквы с порядковыми номерами
и То зашифрованы в буквы с порядковыми номерами  с помощью одной и той же буквы, то остатки от деления чисел
с помощью одной и той же буквы, то остатки от деления чисел  на 30 равны между собой и совпадают с порядковым номером шифрующей буквы (порядковым номером буквы Я удобно считать число 0). Тогда, с учетом соглашения о порядковом номере буквы Я, справедливо, что
на 30 равны между собой и совпадают с порядковым номером шифрующей буквы (порядковым номером буквы Я удобно считать число 0). Тогда, с учетом соглашения о порядковом номере буквы Я, справедливо, что  равен остатку от деления числа
равен остатку от деления числа  на 30, а, вместе с тем,
на 30, а, вместе с тем,  равен остатку от деления числа
равен остатку от деления числа  на 30. Если каждое из выражений в скобках заменить соответствующим остатком от деления на 30, то упомянутая связь не нарушится.
на 30. Если каждое из выражений в скобках заменить соответствующим остатком от деления на 30, то упомянутая связь не нарушится.
Представим в виде набора порядковых номеров известные шифрованные сообщения (обозначим их соответственно  и слово КОРАБЛИ:
и слово КОРАБЛИ:
(см. скан)
Возможны 15 вариантов (номер варианта обозначим буквой к) расположения слова КОРАБЛИ в каждом из двух исходных сообщений  и. с. 2).
и. с. 2).
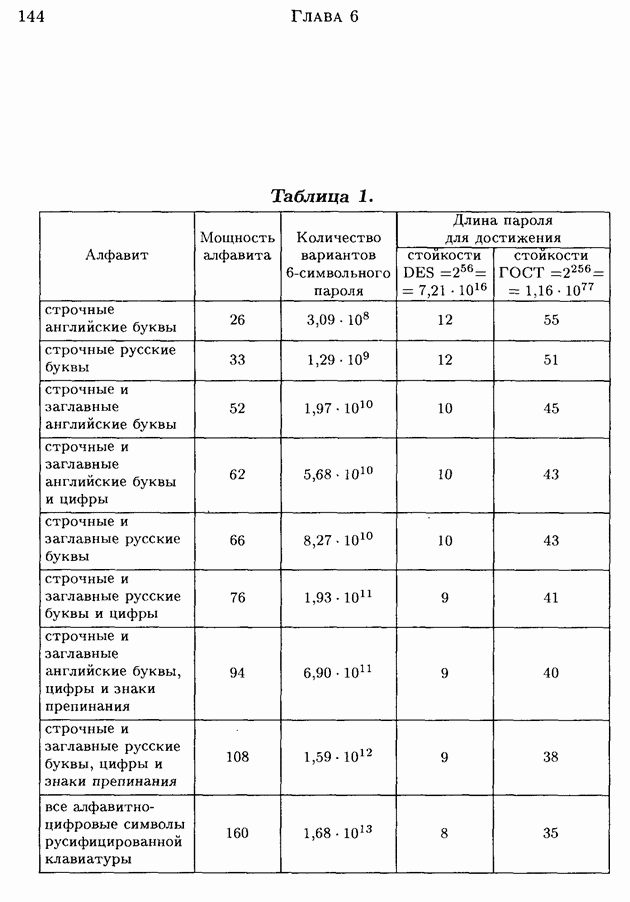
Вначале для каждого из 15 вариантов расположения слова КОРАБЛИ в и. с. 1 найдем соответствующий участок и. с. 2. Имеем:
(см. скан)
Поэтому для участка и. с. 2 получаем следующие 15 вариантов:
(см. скан)
Теперь для каждого из 15 вариантов расположения слова КОРАБЛИ в и. с. 2 найдем соответствующий участок и. с. 1. Имеем:
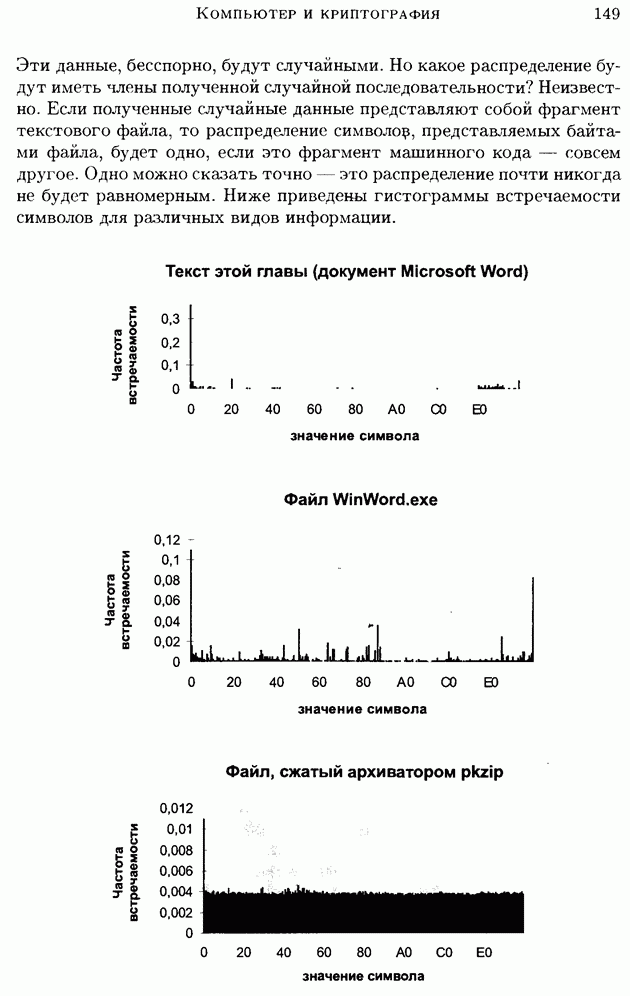
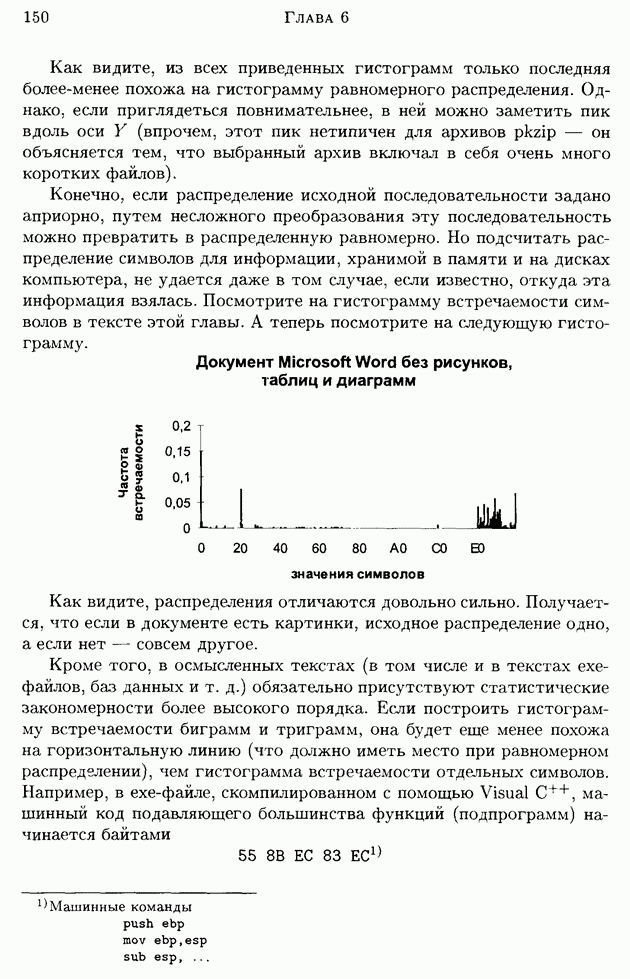
(см. скан)
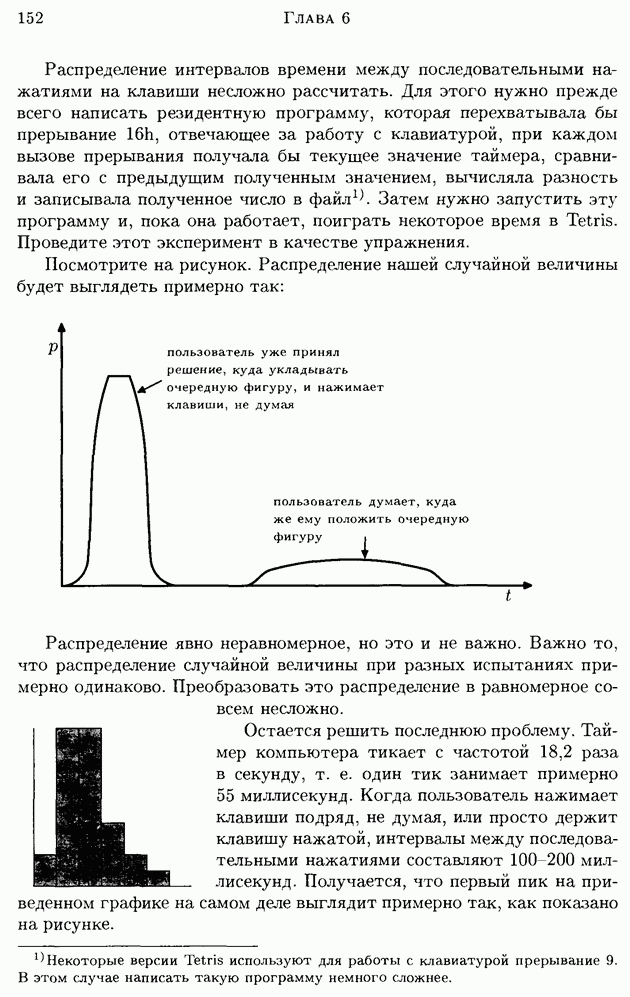
Поэтому для участка и. с. 1 получаем следующие 15 вариантов:
(см. скан)
Заменим порядковые номера в найденных вариантах участков и. с. 1 и и. с. 2 на буквы русского алфавита. Получаем следующие таблицы:
(см. скан)
(см. скан)
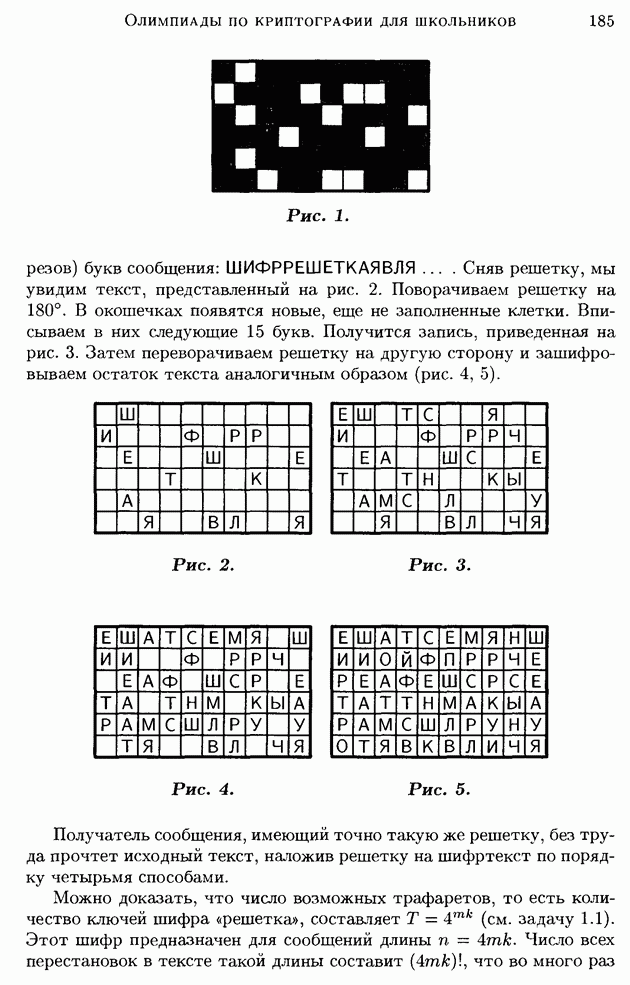
Из таблиц видно, что осмысленными являются варианты:

Естественно предположить, что в первом исходном сообщении речь идет об отплытии кораблей. Предположив, что неизвестным участком первого исходного сообщения является подходящая по смыслу часть слова ОТПЛЫВАЮТ, находим неизвестную часть второго исходного сообщения: слово ОТХОДЯТ.
2.6. Каждую букву шифрованного сообщения расшифруем в трех вариантах, предполагая последовательно, что соответствующая буква шифрующей последовательности есть буква  или буква В:
или буква В:
(см. скан)
Выбирая из каждой колонки полученной таблицы ровно по одной букве, находим осмысленное сообщение НАШКОРРЕСПОНДЕНТ, которое и является искомым.
Замечание. Из полученной таблицы можно было найти такое исходное сообщение как

которое представляется не менее осмысленным, чем приведенное выше. А если предположить одно искажение в шифрованном сообщении (скажем, в качестве 11-й буквы была бы принята не буква  а буква
а буква  то, наряду с правильным вариантом, можно получить и такой:
то, наряду с правильным вариантом, можно получить и такой:

Число всех различных вариантов исходных сообщений без ограничений на осмысленность равно  или 43046721, т. е. более 40 миллионов!
или 43046721, т. е. более 40 миллионов!
3.1. Если каждый из 993 абонентов связан с 99 абонентами, то для этого потребуется  линий связи, которое не может быть целым числом.
линий связи, которое не может быть целым числом.
Ответ: нельзя.
3.2. Несложно заметить, что рассматриваемый шифр обладает тем свойством, что при зашифровании разные буквы заменяются разными. Следовательно, при зашифровании разных слов получаются разные слова. С другой стороны, одинаковые буквы заменяются на одинаковые независимо от цикла шифрования, так как используется один и тот же ключ. Следовательно, при зашифровании одинаковых слов получаются одинаковые слова. Таким образом, число различных слов, которые можно получить в указанном процессе шифрования с начальным словом СРОЧНО, совпадает с наименьшим номером цикла шифрования, дающем это начальное слово.
Так как буква С повторяется в каждом цикле шифрования, номер которого кратен 5, а буквы  в каждом цикле, номера которых кратны 13, 7, 2 и 3 соответственно, то слово
в каждом цикле, номера которых кратны 13, 7, 2 и 3 соответственно, то слово  появится впервые в цикле с номером, равным
появится впервые в цикле с номером, равным 
Ответ: 2730.
3.3. Если символы одного отрезка занумеровать последовательно числами от 1 до 12, то после передачи его из  символы расположатся в порядке (2,4,6,8,10,12,1,3,5,7,9,11), а после передачи этого отрезка (замена символов не меняет порядка) из
символы расположатся в порядке (2,4,6,8,10,12,1,3,5,7,9,11), а после передачи этого отрезка (замена символов не меняет порядка) из  в порядке (4,8,12,3,7,11,2,6,10,1,5,9). Переставим символы перехваченных отрезков в соответствии с их номерами до передачи из пункта А. Получим отрезки вида:
в порядке (4,8,12,3,7,11,2,6,10,1,5,9). Переставим символы перехваченных отрезков в соответствии с их номерами до передачи из пункта А. Получим отрезки вида:
(см. скан)
Поскольку в пунктах  одинаковые буквы заменялись одинаковыми, а разные — разными, то найденные отрезки можно рассматривать как замену одинаковых символов исходного текста одинаковыми, а разных — разными. Сравнивая места одинаковых букв слова
одинаковые буквы заменялись одинаковыми, а разные — разными, то найденные отрезки можно рассматривать как замену одинаковых символов исходного текста одинаковыми, а разных — разными. Сравнивая места одинаковых букв слова
КРИПТОГРАФИЯ и места одинаковых символов в отрезках, находим, что слово КРИПТОГРАФИЯ зашифровано во втором отрезке. Это дает возможность найти исходное сообщение, используя гипотезы о частых буквах русского языка и смысле исходного сообщения.
Ответ:
(см. скан)
3.4. Докажем, что 20 является периодом рассматриваемой последовательности. Заметим, что у двух натуральных чисел  совпадают цифры единиц тогда и только тогда, когда их разность делится на 10. Таким образом, мы достигнем цели, если докажем, что разность
совпадают цифры единиц тогда и только тогда, когда их разность делится на 10. Таким образом, мы достигнем цели, если докажем, что разность  пп делится на 10 для всех натуральных значений
пп делится на 10 для всех натуральных значений  Исходя из того, что
Исходя из того, что  делится на
делится на  получаем, что
получаем, что  делится на
делится на  Кроме того,
Кроме того,  Пп
Пп  делится на
делится на  для всех
для всех  Вместе с тем,
Вместе с тем,

где каждое из слагаемых делится на 2 (так как содержит произведение  и делится на 5 (поскольку первое слагаемое есть произведение пяти последовательных чисел, а второе содержит множитель 5). Следовательно,
и делится на 5 (поскольку первое слагаемое есть произведение пяти последовательных чисел, а второе содержит множитель 5). Следовательно,  пп делится на 10. Число
пп делится на 10. Число

делится на 10, так как каждое из слагаемых делится на 10.
Проверим, что 20 является наименьшим периодом. Выписывая первые 20 значений последовательности 

легко убедиться, что она не имеет периода меньшей длины.
3.5. Для того, чтобы найти исходное сообщение, найдем сначала цифровое сообщение, полученное из него с помощью таблицы замены. Согласно этой таблице на нечетных местах цифрового образа исходного сообщения могут быть только цифры 0, 1, 2 и 3. Последовательно рассматривая эти значения для каждого нечетного места цифрового сообщения с использованием соответствующей цифры шифрованного сообщения, найдем соответствующие варианты значений цифр шифрующего отрезка. Для этого вычислим остатки от деления разностей цифр шифрованного и варианта цифрового сообщений:
(см. скан)
По задаче 3.4 последовательность, из которой выбран шифрующий отрезок, является периодической с периодом 20. Из таблицы вариантов значений цифр шифрующего отрезка видим, что 5-я его цифра может быть равна  или 8, а его 25-я цифра
или 8, а его 25-я цифра  или 5. Отсюда получаем, что
или 5. Отсюда получаем, что  На периоде последовательности, из которой выбран шифрующий отрезок, есть две цифры
На периоде последовательности, из которой выбран шифрующий отрезок, есть две цифры  Поэтому рассмотрим два случая. Если
Поэтому рассмотрим два случая. Если  то
то  Это противоречит таблице вариантов значений цифр шифрующего отрезка, в которой
Это противоречит таблице вариантов значений цифр шифрующего отрезка, в которой  может быть равна 4, 5, 6 или 7. Если же
может быть равна 4, 5, 6 или 7. Если же  то соответствующий шифрующий отрезок: 1636567490147656369016365674 хорошо согласуется с таблицей вариантов значений его цифр. Вычитая цифры найденного отрезка из соответствующих цифр шифрованного сообщения и заменяя разности их остатками от деления на 10, получим по таблице замены пар цифр на буквы исходное сообщение:
то соответствующий шифрующий отрезок: 1636567490147656369016365674 хорошо согласуется с таблицей вариантов значений его цифр. Вычитая цифры найденного отрезка из соответствующих цифр шифрованного сообщения и заменяя разности их остатками от деления на 10, получим по таблице замены пар цифр на буквы исходное сообщение:
(см. скан)
3.6. Обозначения понятны из рис. 9.
(см. скан)

Рис. 9.
(см. скан)
Замечание: Точки  можно построить с помощью циркуля и линейки. Подумайте, как это можно сделать.
можно построить с помощью циркуля и линейки. Подумайте, как это можно сделать.
Ответ:  .
.
4.1. Исходный текст состоит из 48 букв, следовательно, при зашифровании было использовано три положения решетки полностью и еще три буквы вписаны в четвертом положении. Значит, незаполненные 12 клеток совпадают с вырезами решетки в четвертом положении. Так как
(см. скан)
текст вписывается последовательно, то неизвестные нам три выреза могут располагаться только в первой строке таблицы и первых пяти клетках второй строки (до первого известного выреза). Считаем, что трафарет лежит в четвертом положении. Учитывая, что в одну клетку листа нельзя вписать две буквы, получаем, что вырезы могут быть только в отмеченных знаком  местах трафарета
местах трафарета  места известных вырезов):
места известных вырезов):
Очевидно, что из отмеченных в первой строке двух клеток вырезается только одна (так как они совмещаются поворотом). Получаем два возможных варианта решетки (либо первый  либо второй
либо второй  в первой строке). Читаемый текст получается при втором варианте.
в первой строке). Читаемый текст получается при втором варианте.
Ответ:
ПОЛЬЗУЯСЬШИФРОМРЕШЕТКАНЕЛЬЗЯОСТАВЛЯТЬПУСТЫЕМЕСТА
4.2. Один из вариантов решения состоит из следующих этапов.
(см. скан)
Получили текст:
(см. скан)
Получили текст:
(см. скан)
(см. скан)
Итак,
(см. скан)
Ответ: Бегают по лесу стаи зверей — Не за добычей, не на водопой: Денно и нощно они егерей Ищут веселой толпой.
4.3. Ответ: 
4.4. Занумеруем буквы латинского алфавита последовательно числами от 1 до 24. Пусть  некоторое число от 1 до
некоторое число от 1 до  число, в которое переходит х на втором этапе. Тогда перестановочность этапов можно записать в следующем виде:
число, в которое переходит х на втором этапе. Тогда перестановочность этапов можно записать в следующем виде:

Это означает, что соседние числа  на втором этапе переходят в соседние же числа
на втором этапе переходят в соседние же числа  т. е. второй этап — тоже сдвиг. Последовательное применение двух сдвигов — очевидно тоже сдвиг и остается рассмотреть 24 варианта различных сдвигов. Читаемый текст определяется однозначно. Осложнения, связанные с переходом
т. е. второй этап — тоже сдвиг. Последовательное применение двух сдвигов — очевидно тоже сдвиг и остается рассмотреть 24 варианта различных сдвигов. Читаемый текст определяется однозначно. Осложнения, связанные с переходом  устраняются либо переходом к остаткам при делении на 24, либо выписыванием после буквы
устраняются либо переходом к остаткам при делении на 24, либо выписыванием после буквы  второй раз алфавита
второй раз алфавита 
Ответ: INTER ARMA SILENT MUSAE (интер арма сйлент музэ — когда гремит оружие, музы молчат).
4.5. Составим возможные варианты переданных букв:
(см. скан)
Выбирая вторую и последнюю группу букв (где есть короткие колонки букв), определяем слова, им соответствующие:  В исходных словах 33 буквы, поэтому буквы
В исходных словах 33 буквы, поэтому буквы  уже использованы и их можно вычеркнуть из всех колонок:
уже использованы и их можно вычеркнуть из всех колонок:
Из нескольких вариантов, например, в третьей группе:
ГНОЙ ГНОМ ГРОМ
выбираем варианты так, чтобы каждая буква использовалась один раз. Продолжая таким образом, получим ответ. Ответ:
БЫК ВЯЗ ГНОЙ ДИЧЬ ПЛЮЩ СЪЁМ ЦЕХ ШУРФ ЭТАЖ
4.6. Заметим, что  для всех натуральных k. Складывая почленно эти равенства при
для всех натуральных k. Складывая почленно эти равенства при  получим
получим  По условию
По условию  Следовательно, справедливо соотношение
Следовательно, справедливо соотношение 
Ясно, что при расшифровании так же, как и при зашифровании, вместо чисел  можно воспользоваться их остатками от деления на 30. Так как для каждого целого неотрицательного
можно воспользоваться их остатками от деления на 30. Так как для каждого целого неотрицательного 

где  некоторое целое число, то получаем следующие остатки при делении чисел
некоторое целое число, то получаем следующие остатки при делении чисел  на 30:
на 30:
(см. скан)
Заключительный этап представлен в таблице:
(см. скан)
4.7. Ответ:

5.1. Указание. Найдите допустимые варианты для остатков от деления неизвестных х и у на 7. Таких вариантов будет восемь. Учитывая принадлежность неизвестных к заданному диапазону, найдите допустимые варианты для (х,у) (19 вариантов). Для каждой пары  найдите
найдите  В диапазон 10.. 20 попадают только три решения: (12,16,11), (13,17,17), (13,18,12).
В диапазон 10.. 20 попадают только три решения: (12,16,11), (13,17,17), (13,18,12).
5.2. Так как при записывании сообщения в таблицу пробелы опускались, можно сделать вывод, что столбцы, содержащие пробел в последней клетке, до перестановки стояли в конце таблицы. Таким образом, столбцы можно разбить на две группы, как показано на рис. 10. При этом для получения исходного текста потребуется переставлять столбцы только внутри групп.

Рис. 10.
Естественно предположить, что сообщение оканчивалось точкой. Поэтому на третьем с конца месте в первой группе должен быть столбец, оканчивающийся на  на втором — на
на втором — на  на последнем — на К. Получаем два варинта (рис. 10), из которых первый является явно «нечитаемым».
на последнем — на К. Получаем два варинта (рис. 10), из которых первый является явно «нечитаемым».

Рис. 11.

Рис. 12.
Таким образом, удалось зафиксировать последние три столбца первой
группы. Переставляя столбцы второй группы, ищем «читаемые» продолжения зафиксированных столбцов (рис. 11). Действуя далее аналогичным образом с оставшимися столбцами первой группы, достаточно легко получаем исходное сообщение.
Ответ:
(см. скан)
5.4. Во втором случае известны пары цифр, которыми шифруются буквы  а в первом — пары цифр для тех же букв, за исключением буквы «н».
а в первом — пары цифр для тех же букв, за исключением буквы «н».
Ответ: во втором случае легче.
5.5. Ответ: 481.
5.6. Можно заметить, что последовательность букв  входит как подпоследовательность в каждый из шифртекстов первой тройки:
входит как подпоследовательность в каждый из шифртекстов первой тройки:

На основе этого наблюдения можно предположить, что шифрование заключается в следующем. В каждый промежуток между буквами исходного сообщения (начало и конец также считаются промежутками) вставляются одна либо две буквы в соответствии с известным только отправителю и получателю ключом.
Очевидно, что первая буква сообщения должна попасть на 2-е или 3-е место шифрованного текста. Сравнивая буквы, стоящие на указанных местах в подлежащих расшифрованию криптограммах, делаем вывод, что одно и то же исходное сообщение соответствует первому и третьему шифртексту и что первая буква этого сообщения — 
Рассуждая далее аналогичным образом, заключаем, что второй буквой повторяющегося сообщения является О (сопоставили  из 1-й криптограммы и
из 1-й криптограммы и  из 3-й) и так далее. В итоге получим, что первой и третьей криптограмме соответствует исходное сообщение
из 3-й) и так далее. В итоге получим, что первой и третьей криптограмме соответствует исходное сообщение
ПОВТОРЕНИЕМАТЬУЧЕНИЯ
Теперь расшифруем вторую криптограмму. Первой буквой сообщения могут быть только С или И. Далее, подбирая к каждой из них возможные варианты последующих букв и вычеркивая заведомо «нечитаемые» цепочки букв, получим:

(см. скан)
В итоге получим исходное сообщение СМОТРИВКОРЕНЬ.
Ответ: 1,3 — ПОВТОРЕНИЕМАТЬУЧЕНИЯ 2 — СМОТРИВКОРЕНЬ
5.7. Обратив внимание на то, что некоторые символы в тексте условий задач пятой олимпиады набраны выделенным шрифтом, и выписав эти символы в порядке их следования, получаем текст:

6.1. Так как каждый из 1997 абонентов связан ровно с N другими, то общее число направлений связи равно  Отсюда общее число связанных пар абонентов равно
Отсюда общее число связанных пар абонентов равно  так как каждая связанная пара имеет ровно 2 направления связи. Поскольку число 1997/2 должно быть целым, а число 1997 — нечетное, то число N должно быть четным.
так как каждая связанная пара имеет ровно 2 направления связи. Поскольку число 1997/2 должно быть целым, а число 1997 — нечетное, то число N должно быть четным.
Докажем, что для каждого  существует система связи из 1997 абонентов, в которой каждый связан ровно с N другими. В самом деле, расположив всех абонентов на окружности и связав каждого из них с
существует система связи из 1997 абонентов, в которой каждый связан ровно с N другими. В самом деле, расположив всех абонентов на окружности и связав каждого из них с  ближайшими к нему по часовой стрелке и с ближайшими к нему против часовой стрелки, получим пример такой сети связи.
ближайшими к нему по часовой стрелке и с ближайшими к нему против часовой стрелки, получим пример такой сети связи.
6.2. Покажем, что на диагонали присутствуют все числа от 1 до 1997. Пусть число а  не стоит на диагонали. Тогда, в силу симметрии таблицы, число а встречается четное количество раз. С другой стороны, так как число а по одному разу встречается в каждой строке, всего в таблице чисел а нечетное количество (1997). Получили противоречие.
не стоит на диагонали. Тогда, в силу симметрии таблицы, число а встречается четное количество раз. С другой стороны, так как число а по одному разу встречается в каждой строке, всего в таблице чисел а нечетное количество (1997). Получили противоречие.
Всего на диагонали 1997 клеток, поэтому каждое число из множества  встретится на диагонали ровно по одному разу. Вычисляя сумму арифметической прогрессии, находим ответ. Ответ: 1995003.
встретится на диагонали ровно по одному разу. Вычисляя сумму арифметической прогрессии, находим ответ. Ответ: 1995003.
6.3. Ответ: ШЕСТАЯОЛИМПИАДАПОКРИПТОГРАФИИПОСВЯЩЕ  АСЕМ И ДЕСЯТИ ПЯТИЛ ЕТИЮСПЕЦИАЛЬНОЙСЛУЖБЫ РОССИИ
АСЕМ И ДЕСЯТИ ПЯТИЛ ЕТИЮСПЕЦИАЛЬНОЙСЛУЖБЫ РОССИИ
Указание. Пусть некоторая буква а при зашифровании первым способом заменялась на букву (3. Тогда количество повторов буквы (3 в первой криптограмме будет равно числу повторов буквы а во второй криптограмме.
6.4. а) Определим моменты остановок после начала шифрования. Для этого каждой букве русского алфавита припишем ее порядковый номер:  Тогда буквам из шифруемого слова будут соответствовать номера:
Тогда буквам из шифруемого слова будут соответствовать номера:  Моменты остановок будем указывать числом одношаговых (на один зубец) поворотов I колеса до соответствующей остановки.
Моменты остановок будем указывать числом одношаговых (на один зубец) поворотов I колеса до соответствующей остановки.
(см. скан)
Искомый шифртекст: 515355128523864354
б) Пусть  количество одношаговых поворотов
количество одношаговых поворотов  колеса от начала до остановки с номером
колеса от начала до остановки с номером 
 — цифра, на которую указывает стрелка II колеса в момент остановки с номером
— цифра, на которую указывает стрелка II колеса в момент остановки с номером 
 цифра III колеса, на которую указывает стрелка III колеса в момент остановки с номером k.
цифра III колеса, на которую указывает стрелка III колеса в момент остановки с номером k.
Тогда, учитывая, что начальное положение стрелок соответствует букве А на первом колесе и 0 на II и III колесах, справедливы равенства

для подходящих неотрицательных целых чисел 
Заметим, что  Отсюда справедливы равенства
Отсюда справедливы равенства

Подставляя эти значения в равенства (1) и (2), получим

Следовательно,

Правая и левая части делятся на 70, то есть имеют вид  для подходящего неотрицательного целого
для подходящего неотрицательного целого  Поэтому
Поэтому

Подставляя  в (1), получим
в (1), получим

Учитывая условие  и то, что остановка колес происходит в момент первого появления шифруемой буквы под стрелкой I колеса, имеем
и то, что остановка колес происходит в момент первого появления шифруемой буквы под стрелкой I колеса, имеем
(см. скан)
6.5. Указание. Рассмотрим некоторую расстановку ненулевых цифр на окружности. Упорядоченную пару  соседних цифр на этой окружности назовем
соседних цифр на этой окружности назовем  -соседней, если
-соседней, если  является соседней с а по часовой стрелке. Пару
является соседней с а по часовой стрелке. Пару  назовем
назовем  -соседней, если существует цифра
-соседней, если существует цифра  для которой пары
для которой пары  и
и  являются
являются  -соседними.
-соседними.
Каждой расстановке ненулевых цифр на окружности однозначно соответствует цепочка  -соседних пар вида:
-соседних пар вида:  которой, в свою очередь, однозначно соответствует цепочка
которой, в свою очередь, однозначно соответствует цепочка  -соседних пар вида:
-соседних пар вида:

Если из цепочки  удалить любую пару, то по оставшимся парам она восстанавливается однозначно.
удалить любую пару, то по оставшимся парам она восстанавливается однозначно.
Если из цепочки  удалить две соседние пары, то она также восстанавливается однозначно.
удалить две соседние пары, то она также восстанавливается однозначно.
Удаление из  любых трех пар приводит к неоднозначности восстановления цепочки
любых трех пар приводит к неоднозначности восстановления цепочки  В этом можно убедиться, рассмотрев следующие фрагменты цепочки вида
В этом можно убедиться, рассмотрев следующие фрагменты цепочки вида 

Таким образом, при наличии двух указанных в условии задачи цифровых текстов нам будут известны некоторые  -соседние пары, в которых первая цифра берется из первой криптограммы, а вторая — из второй. Поэтому с учетом вышесказанного получаем условие однозначного восстановления порядка расстановки цифр на данной окружности.
-соседние пары, в которых первая цифра берется из первой криптограммы, а вторая — из второй. Поэтому с учетом вышесказанного получаем условие однозначного восстановления порядка расстановки цифр на данной окружности.
Ответ: для однозначного восстановления расстановки цифр на окружности необходимо и достаточно, чтобы в одном из цифровых текстов было не менее 7 ненулевых цифр (это соответствует удалению из цепочки  -соседних пар вида
-соседних пар вида  не более двух из них).
не более двух из них).
6.6. Последовательность остатков от деления чисел  на 24 — периодическая с периодом 2, так как для любого натурального
на 24 — периодическая с периодом 2, так как для любого натурального  справедливо:
справедливо:

Кроме того,  кратно 24, то есть остатки
кратно 24, то есть остатки  равны.
равны.
6.7. Ответ:  все решения имеют вид
все решения имеют вид 
Указание. При а 0 рассматриваемое уравнение равносильно  которое имеет не более двух решений.
которое имеет не более двух решений.
При  из графика функции в левой части уравнения видно, что если
из графика функции в левой части уравнения видно, что если  число решений будет четным, поэтому не может быть равно 1997. Если
число решений будет четным, поэтому не может быть равно 1997. Если  то уравнение имеет ровно 2 решения. Если же
то уравнение имеет ровно 2 решения. Если же  то уравнение имеет ровно 1997 решений. 7.1. Для того, чтобы сохранилась связь при выходе из строя любых двух узлов, необходимо, чтобы в каждый узел входило не менее трех линий связи.
то уравнение имеет ровно 1997 решений. 7.1. Для того, чтобы сохранилась связь при выходе из строя любых двух узлов, необходимо, чтобы в каждый узел входило не менее трех линий связи.

Ситуация недопустима, ибо при выходе из строя узлов  узел А становится недоступным. Значит, всего линий должно быть не менее
узел А становится недоступным. Значит, всего линий должно быть не менее 
Вот два примера, удовлетворяющие условиям задачи с 15-ю линиями связи:

Приведем доказательство для первого примера. Если вышли из строя два узла на одном пятиугольнике, то связь сохранится через другие пятиугольники. Если вышли из строя по одному узлу на разных пятиугольниках, то связь сохранится по линиям, соединяющим эти пятиугольники.
Ответ: 15.
7.2. Процедура зашифрования может быть полностью описана квадратной таблицей  На пересечении строки с номером
На пересечении строки с номером  и столбца с номером
и столбца с номером  записываем цифру, в которую при зашифровании переходит цифра
записываем цифру, в которую при зашифровании переходит цифра  если она стоит в пароле после цифры
если она стоит в пароле после цифры  Из однозначности расшифрования следует, что в каждой строке каждая цифра встречается ровно один раз.
Из однозначности расшифрования следует, что в каждой строке каждая цифра встречается ровно один раз.
Обозначим через  зашифрованные пароли и два известных пароля в порядке, определяемом условием задачи. Процедура зашифрования сохраняет длину, поэтому
зашифрованные пароли и два известных пароля в порядке, определяемом условием задачи. Процедура зашифрования сохраняет длину, поэтому  не могут соответствовать ни
не могут соответствовать ни  ни
ни  Предположив, что соотвествует
Предположив, что соотвествует  получим часть таблицы, в которой в одной строке две одинаковые цифры. Это означает, что предположение неверно. Составляя таблицы, убеждаемся, что
получим часть таблицы, в которой в одной строке две одинаковые цифры. Это означает, что предположение неверно. Составляя таблицы, убеждаемся, что  не шифруется ни в ни в
не шифруется ни в ни в  ни в
ни в  В результате таких рассуждений остается только один вариант перехода
В результате таких рассуждений остается только один вариант перехода  Заполнение таблицы будет следующим:
Заполнение таблицы будет следующим:
(см. скан)
Очевидно, что в строке с номером 2 в последней клетке стоит 1. Знание этой таблицы позволяет однозначно расшифровать  получится 5830829. Пароли, соответствующие
получится 5830829. Пароли, соответствующие  восстанавливаются не полностью.
восстанавливаются не полностью.
Ответ: полностью можно расшифровать только 5393511, получится 5830829.
7.3. Сообщение состоит из  буквы. Поэтому
буквы. Поэтому  или
или  (при
(при  получается нечитаемый текст). При
получается нечитаемый текст). При  не получается осмысленного текста при всех шести возможных вариантах перестановки букв
не получается осмысленного текста при всех шести возможных вариантах перестановки букв  Рассмотрим случай
Рассмотрим случай 
(см. скан)
Соседние буквы при перестановке переходят в буквы, отстоящие друг от друга на одинаковое расстояние: буква на  месте переходит на место, определяемое остатком от деления
месте переходит на место, определяемое остатком от деления  на 17, а буква на
на 17, а буква на  месте — на место, определяемое остатком от деления
месте — на место, определяемое остатком от деления  на 17. Это верно для любого х. Поэтому есть всего 16 вариантов переходов соседних букв (исходный текст нечитаем), которые определяют однозначно переходы всех остальных букв. Перебирая их, получаем нечитаемые тексты во всех случаях, кроме одного, который дает текст:
на 17. Это верно для любого х. Поэтому есть всего 16 вариантов переходов соседних букв (исходный текст нечитаем), которые определяют однозначно переходы всех остальных букв. Перебирая их, получаем нечитаемые тексты во всех случаях, кроме одного, который дает текст:
(см. скан)
Из трех вариантов начала текста легко определяется истинный вариант.
Ответ:
ЧТОБЫПОЛУЧИТЬПЯТЬНУЖНООТЛИЧНОЗНАТЬПОЛУЧИЛОСЬНЕПЛОХО
7.4. Последовательность обхода доски показана на рисунке:
(см. скан)
Ответ: Кавалергардов век недолог И потому так сладок он. Труба трубит, откинут полог 
7.5. Из однородности всех членов следует, что неравенство эквивалентно неравенству  при условии
при условии 
Пусть с — минимальное из чисел  Тогда
Тогда


Находим минимум квадратного трехчлена с параметром с и положительным коэффициентом при  Минимум достигается в точке
Минимум достигается в точке  при этом значение А будет положительным.
при этом значение А будет положительным.
7.6. Если мелом с квадратным сечением нарисовать на доске отрезок прямой так, чтобы стороны сечения были параллельны краям доски, то площадь полученной линии будет равна площади ступенчатой линии с такими же концами (см. рис. 13).
Если на доске нарисовать некоторый (выпуклый) многоугольник, то найдутся такие граничные «точки» этого многоугольника, которые являются ближайшими к одному из краев доски. Площадь границы прямоугольника, содержащей все такие «точки», равна площади границы нарисованного выпуклого многоугольника (см. рис. 14).

Рис. 13.

Рис. 14.
Такой прямоугольник назовем окаймляющим. Ясно, что площадь окаймляющего прямоугольника не меньше площади соответствующего многоугольника. Значит, для любого многоугольника данной площади найдется прямоугольник такой же площади, но с площадью границы не большей, чем площадь границы исходного многоугольника.
Если многоугольник со сторонами  имеет площадь
имеет площадь  то плошадь его границы равна
то плошадь его границы равна

Минимум достигается в случае, когда возводимое в квадрат выражение равно 0. В этом случае  что влечет
что влечет  Таким образом, наименьшую площадь границы, равную
Таким образом, наименьшую площадь границы, равную  имеет квадрат со стороной
имеет квадрат со стороной 
Ответ: квадрат со стороной  площадь его границы —
площадь его границы — 
7.7. Если группа цифр, из которой образуются числа, состоит из к цифр, то существует ровно  различных чисел, для записи которых
различных чисел, для записи которых
используются все цифры группы ровно по одному разу. Группу из к цифр будем обозначать 
Поскольку в сообщении отсутствуют цифры 2 и 9, эти цифры образуют либо две группы по одной цифре, либо одну группу из двух цифр. В обоих случаях эти цифры могут быть использованы для зашифрования ровно двух букв алфавита.
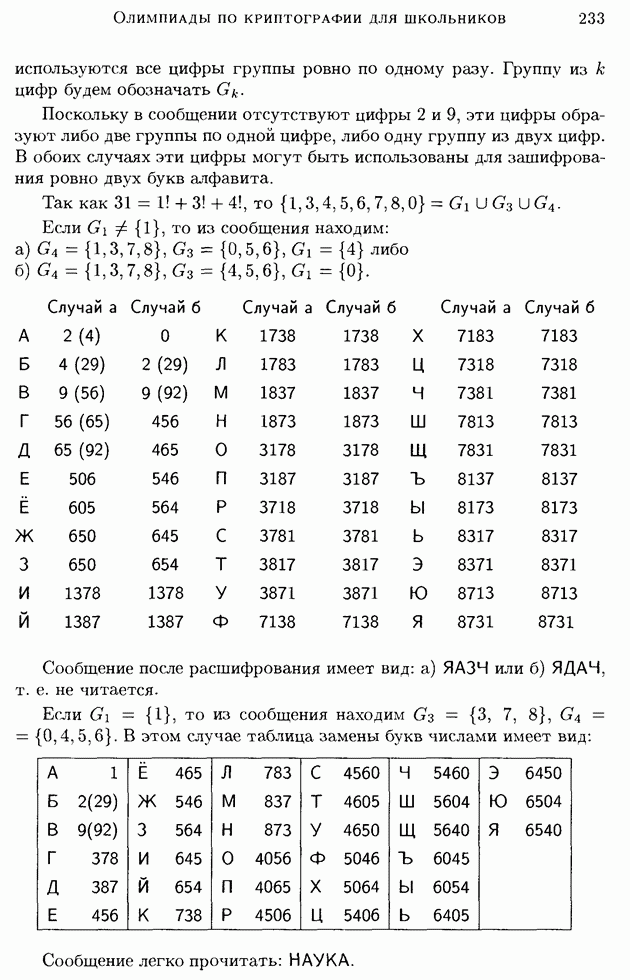
Так как  то
то  Если
Если  то из сообщения находим:
то из сообщения находим:

(см. скан)
Сообщение после расшифрования имеет вид: а)  или б)
или б)  т. е. не читается.
т. е. не читается.
Если  то из сообщения находим
то из сообщения находим  В этом случае таблица замены букв числами имеет вид:
В этом случае таблица замены букв числами имеет вид:
(см. скан)
Сообщение легко прочитать: НАУКА.
Литература к главе 7
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму изданию
- Глава 1. Основные понятия криптографии
- 2. Предмет криптографии
- 3. Математические основы
- 4. Новые направления
- 5. Заключение
- Глава 2. Криптография и теория сложности
- 2. Криптография и гипотеза P != NP
- 3. Односторонние функции
- 4. Псевдослучайные генераторы
- 5. Доказательства с нулевым разглашением
- Глава 3. Криптографические протоколы
- 2. Целостность. Протоколы аутентификации и электронной подписи
- Схема аутентификации Шнорра
- Схема электронной подписи Шнорра
- 3. Неотслеживаемость. Электронные деньги
- 4. Протоколы типа «подбрасывание монеты по телефону»
- Протокол подбрасывания монеты
- 5. Еще раз о разделении секрета
- 6. Поиграем в «кубики». Протоколы голосования
- Протокол Шаума и Педерсена
- 7. За пределами стандартных предположений. Конфиденциальная передача сообщений
- 8. Вместо заключения
- Глава 4. Алгоритмические проблемы теории чисел
- 2. Система шифрования RSA
- 3. Сложность теоретико-числовых алгоритмов
- 4. Как отличить составное число от простого
- 5. Алгоритм, доказывающий непростоту числа
- 5. Как строить большие простые числа
- 6. Как проверить большое число на простоту
- 7. Как раскладывают составные числа на множители
- 8. Дискретное логарифмирование
- 9. Заключение
- Глава 5. Математика разделения секрета
- 2. Разделение секрета для произвольных структур доступа
- 3. Линейное разделение секрета.
- 4. Идеальное разделение секрета и матроиды
- Глава 6. Компьютер и криптография
- 2. Немного теории
- Что надо знать перед написанием программы шифрования
- 3. Как зашифровать файл?
- 4. Поучимся на чужих ошибках
- 5. Вместо заключения
- Глава 7. Олимпиады по криптографии для школьников
- 2. Шифры замены
- А. Конан Дойл, «Пляшущие человечки»
- Ж. Верн, «Путешествие к центру Земли»
- 3. Шифры перестановки
- 4. Многоалфавитные шифры замены с периодическим ключом
- 5. Условия задач олимпиад по математике и криптографии
- 6. Указания и решения
- Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
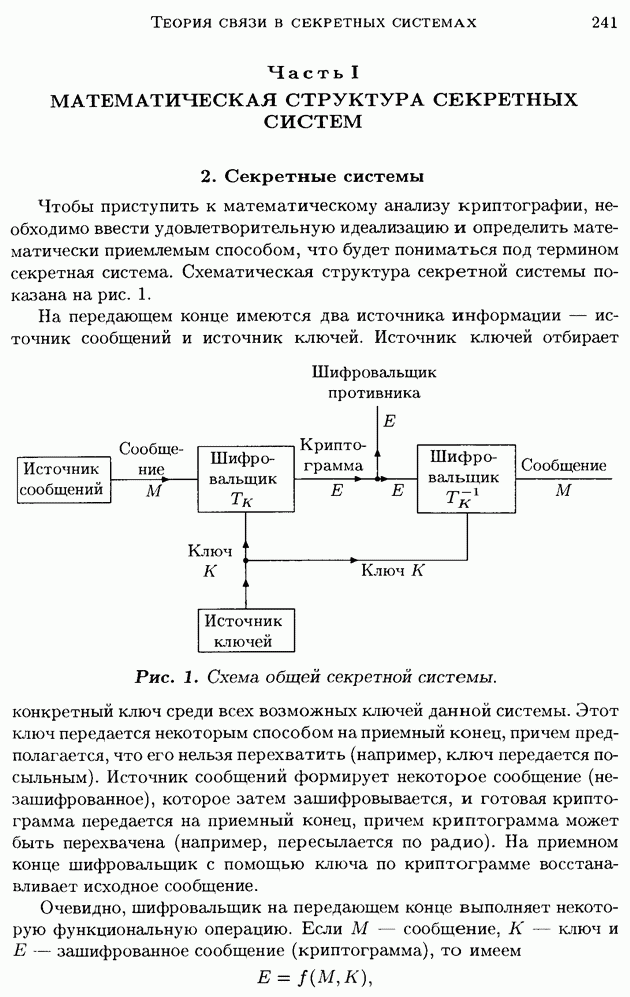
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность