| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
9. Заключение
Мы затронули в этой главе лишь небольшую часть вопросов, связанных с теоретико-числовыми алгоритмами и оценками их сложности. Мы не описывали перспективные исследования, связанные с распространением алгоритмов решета на поля алгебраических чисел (решето числового поля), и использование их для разложения целых чисел на множители или решения задачи дискретного логарифмирования, см. [20]. Именно с помощью этих алгоритмов достигнуты теоретические оценки сложности разложения на множители

Не были затронуты эллиптические кривые, т. е. определенные с точностью до обратимого множителя пропорциональности множества точек

обладающие групповой структурой. С их помощью удалось построить весьма эффективные алгоритмы разложения чисел на множители и проверки целых чисел на простоту. В отличие от мультипликативной группы  порядок группы
порядок группы  при одном и том же
при одном и том же  меняется в зависимости от целых параметров
меняется в зависимости от целых параметров  Это оказывается весьма существенным, например, при разложении чисел
Это оказывается весьма существенным, например, при разложении чисел  на множители. Мы
на множители. Мы
отсылаем читателей за подробностями использования эллиптических кривых к статье [21].
Литература к главе 4
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие ко второму изданию
- Глава 1. Основные понятия криптографии
- 2. Предмет криптографии
- 3. Математические основы
- 4. Новые направления
- 5. Заключение
- Глава 2. Криптография и теория сложности
- 2. Криптография и гипотеза P != NP
- 3. Односторонние функции
- 4. Псевдослучайные генераторы
- 5. Доказательства с нулевым разглашением
- Глава 3. Криптографические протоколы
- 2. Целостность. Протоколы аутентификации и электронной подписи
- Схема аутентификации Шнорра
- Схема электронной подписи Шнорра
- 3. Неотслеживаемость. Электронные деньги
- 4. Протоколы типа «подбрасывание монеты по телефону»
- Протокол подбрасывания монеты
- 5. Еще раз о разделении секрета
- 6. Поиграем в «кубики». Протоколы голосования
- Протокол Шаума и Педерсена
- 7. За пределами стандартных предположений. Конфиденциальная передача сообщений
- 8. Вместо заключения
- Глава 4. Алгоритмические проблемы теории чисел
- 2. Система шифрования RSA
- 3. Сложность теоретико-числовых алгоритмов
- 4. Как отличить составное число от простого
- 5. Алгоритм, доказывающий непростоту числа
- 5. Как строить большие простые числа
- 6. Как проверить большое число на простоту
- 7. Как раскладывают составные числа на множители
- 8. Дискретное логарифмирование
- 9. Заключение
- Глава 5. Математика разделения секрета
- 2. Разделение секрета для произвольных структур доступа
- 3. Линейное разделение секрета.
- 4. Идеальное разделение секрета и матроиды
- Глава 6. Компьютер и криптография
- 2. Немного теории
- Что надо знать перед написанием программы шифрования
- 3. Как зашифровать файл?
- 4. Поучимся на чужих ошибках
- 5. Вместо заключения
- Глава 7. Олимпиады по криптографии для школьников
- 2. Шифры замены
- А. Конан Дойл, «Пляшущие человечки»
- Ж. Верн, «Путешествие к центру Земли»
- 3. Шифры перестановки
- 4. Многоалфавитные шифры замены с периодическим ключом
- 5. Условия задач олимпиад по математике и криптографии
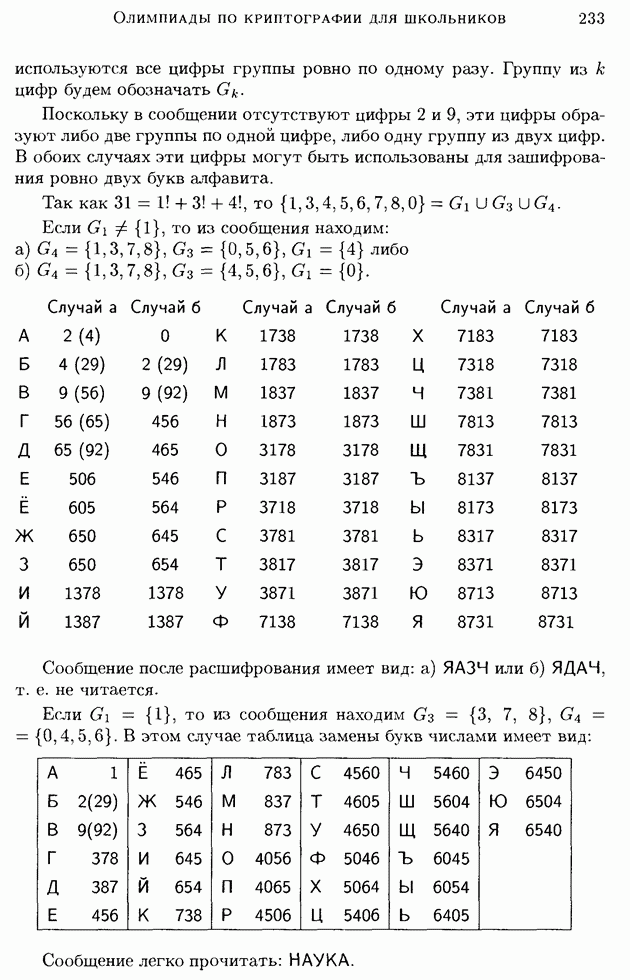
- 6. Указания и решения
- Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
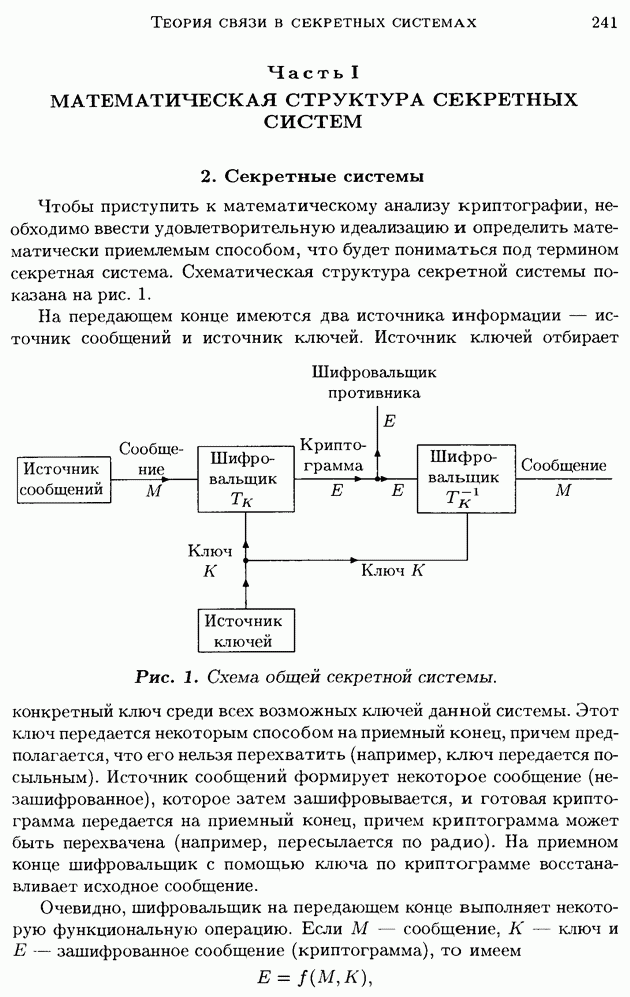
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
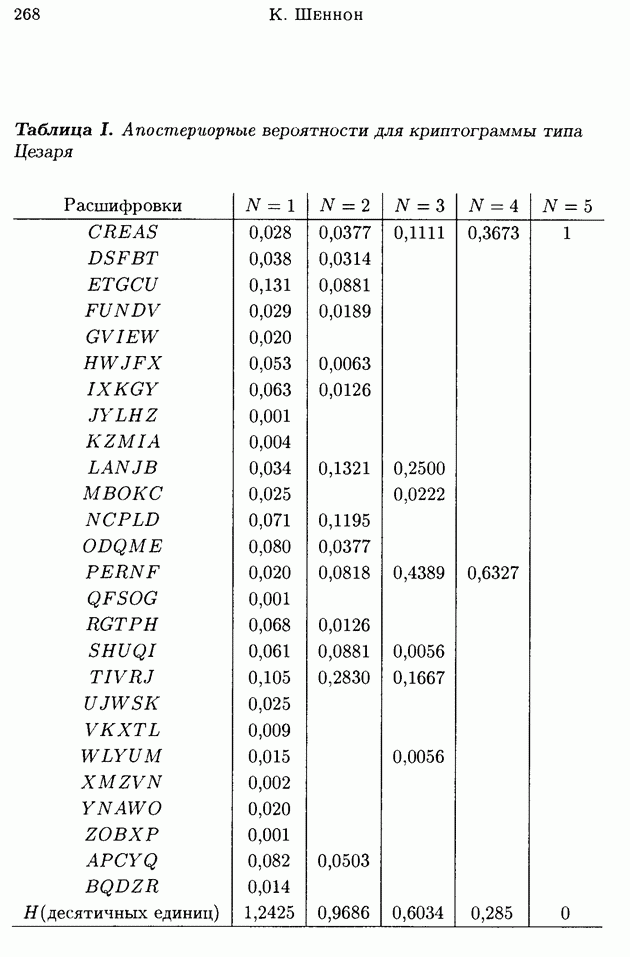
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность