| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6. Как проверить большое число на простоту
Есть некоторое отличие в постановках задач предыдущего и настоящего разделов. Когда мы строим простое число  мы обладаем некоторой дополнительной информацией о нем, возникающей в процессе построения. Например, такой информацией является знание простых делителей числа
мы обладаем некоторой дополнительной информацией о нем, возникающей в процессе построения. Например, такой информацией является знание простых делителей числа  Эта информация иногда облегчает доказательство простоты
Эта информация иногда облегчает доказательство простоты 
В этом разделе мы предполагаем лишь, что нам задано некоторое число  например, выбранное случайным образом на каком-то промежутке, и требуется установить его простоту, или доказать, что оно является составным. Эту задачу за полиномиальное количество операций решает указанный в п. 4 алгоритм Миллера. Однако, справедливость полученного с его помощью утверждения зависит от недоказанной расширенной гипотезы Римана. Если число N выдержало
например, выбранное случайным образом на каком-то промежутке, и требуется установить его простоту, или доказать, что оно является составным. Эту задачу за полиномиальное количество операций решает указанный в п. 4 алгоритм Миллера. Однако, справедливость полученного с его помощью утверждения зависит от недоказанной расширенной гипотезы Римана. Если число N выдержало
испытания алгоритмом 5 для 100 различных значений параметра а, то, по-видимому, можно утверждать, что оно является простым с вероятностью большей, чем  Эта вероятность очень близка к единице, однако все же оставляет некоторую тень сомнения на простоте числа
Эта вероятность очень близка к единице, однако все же оставляет некоторую тень сомнения на простоте числа  В дальнейшем в этом разделе мы будем считать, что заданное число N является простым, а нам требуется лишь доказать это.
В дальнейшем в этом разделе мы будем считать, что заданное число N является простым, а нам требуется лишь доказать это.
В настоящее время известны детерминированные алгоритмы различной сложности для доказательства простоты чисел. Мы остановимся подробнее на одном из них, предложенном в 1983 г. в совместной работе Адлемана, Померанца и Рамели [13]. Для доказательства простоты или непростоты числа N этот алгоритм требует  арифметических операций. Здесь с — некоторая положительная абсолютная постоянная. Функция
арифметических операций. Здесь с — некоторая положительная абсолютная постоянная. Функция  хоть и медленно, но все же возрастает с ростом
хоть и медленно, но все же возрастает с ростом  поэтому алгоритм не является полиномиальным. Но все же его практические реализации позволяют достаточно быстро тестировать числа на простоту. Существенные усовершенствования и упрощения в первоначальный вариант алгоритма были внесены в работах
поэтому алгоритм не является полиномиальным. Но все же его практические реализации позволяют достаточно быстро тестировать числа на простоту. Существенные усовершенствования и упрощения в первоначальный вариант алгоритма были внесены в работах  Ленстры и А. Коена [14, 15]. Мы будем называть описываемый ниже алгоритм алгоритмом Адлемана-Ленстры.
Ленстры и А. Коена [14, 15]. Мы будем называть описываемый ниже алгоритм алгоритмом Адлемана-Ленстры.
В основе алгоритма лежит использование сравнений типа малой теоремы Ферма, но в кольцах целых чисел круговых полей, т. е. полей, порожденных над полем  числами
числами  корнями из 1. Пусть
корнями из 1. Пусть  простое нечетное число и с — первообразный корень по модулю
простое нечетное число и с — первообразный корень по модулю  т. е. образующий элемент мультипликативной группы поля
т. е. образующий элемент мультипликативной группы поля  которая циклична. Для каждого целого числа х, не делящегося на
которая циклична. Для каждого целого числа х, не делящегося на  можно определить его индекс,
можно определить его индекс,  называемый также дискретным логарифмом, с помощью сравнения
называемый также дискретным логарифмом, с помощью сравнения  Рассмотрим далее два простых числа
Рассмотрим далее два простых числа  с условием, что
с условием, что  делится на
делится на  но не делится на
но не делится на 
Следующая функция, определенная на множестве целых чисел,

является характером по модулю  и порядок этого характера равен
и порядок этого характера равен  Сумма
Сумма

называется суммой Гаусса. Формулируемая ниже теорема 3 представляет собой аналог малой теоремы Ферма, используемый в алгоритме Адлемана - Ленстры.
Теорема 5. Пусть  нечетное простое число,
нечетное простое число,  Тогда в кольце
Тогда в кольце  выполняется сравнение
выполняется сравнение

Если при каких-либо числах  сравнение из теоремы 3 нарушается, можно утверждать, что N составное число. В противном случае, если сравнение выполняется, оно дает некоторую информацию о возможных простых делителях числа
сравнение из теоремы 3 нарушается, можно утверждать, что N составное число. В противном случае, если сравнение выполняется, оно дает некоторую информацию о возможных простых делителях числа  Собрав такую информацию для различных
Собрав такую информацию для различных  в конце концов удается установить, что N имеет лишь один простой делитель и является простым.
в конце концов удается установить, что N имеет лишь один простой делитель и является простым.
В случае  легко проверить, что сравнение из теоремы 3 равносильно хорошо известному в элементарной теории чисел сравнению
легко проверить, что сравнение из теоремы 3 равносильно хорошо известному в элементарной теории чисел сравнению

где — так называемый символ Якоби. Хорошо известно также, что последнее сравнение выполняется не только для простых  но и для любых целых
но и для любых целых  взаимно простых с
взаимно простых с  Заметим также, что для вычисления символа Якоби существует быстрый алгоритм, основанный на законе взаимности Гаусса и, в некотором смысле, подобный алгоритму Евклида вычисления наибольшего общего делителя. Следующий пример показывает, каким образом выполнимость нескольких сравнений типа (13) дает некоторую информацию о возможных простых делителях числа
Заметим также, что для вычисления символа Якоби существует быстрый алгоритм, основанный на законе взаимности Гаусса и, в некотором смысле, подобный алгоритму Евклида вычисления наибольшего общего делителя. Следующий пример показывает, каким образом выполнимость нескольких сравнений типа (13) дает некоторую информацию о возможных простых делителях числа 
Пример 1 (X. Ленстра). Пусть  натуральное число,
натуральное число,  для которого выполнены сравнения
для которого выполнены сравнения

а кроме того с некоторым целым числом  имеем
имеем

Как уже указывалось, при простом N сравнения (14) выполняются для любого а, взаимно простого с  а сравнение (15) означает, что
а сравнение (15) означает, что  есть первообразный корень по модулю
есть первообразный корень по модулю  Количество первообразных корней равно
Количество первообразных корней равно  т. е. достаточно велико. Таким образом, число
т. е. достаточно велико. Таким образом, число  с условием (15) при простом N может быть найдено достаточно быстро с помощью случайного выбора и последующей проверки (15).
с условием (15) при простом N может быть найдено достаточно быстро с помощью случайного выбора и последующей проверки (15).
Докажем, что из выполнимости (14-15) следует, что каждый делитель  числа N удовлетворяет одному из сравнений
числа N удовлетворяет одному из сравнений

Не уменьшая общности, можно считать, что  простое число. Введем теперь обозначения
простое число. Введем теперь обозначения  где
где  нечетные
нечетные
числа. Из (15) и сравнения  следует, что
следует, что  Далее, согласно (14), выполняются следующие сравнения
Далее, согласно (14), выполняются следующие сравнения

означающие (в силу того, что символ Якоби может равняться лишь — 1 или  что
что

При  это равенство означает, что
это равенство означает, что  при
при  , и, следовательно,
, и, следовательно,  Если же
Если же  , то имеем
, то имеем  Этим (16) доказано.
Этим (16) доказано.
Информация такого рода получается и в случае произвольных простых чисел  с указанными выше свойствами.
с указанными выше свойствами.
Опишем (очень грубо) схему алгоритма Адлемана - Ленстры для проверки простоты 
1) выбираются различные простые числа  и различные простые нечетные
и различные простые нечетные  такие, что
такие, что
а) для каждого  все простые делители числа
все простые делители числа  содержатся среди
содержатся среди  не делятся на квадрат простого числа,
не делятся на квадрат простого числа,

2) для каждой пары выбранных чисел  проводятся тесты, подобные сравнению из теоремы 3. Если N не удовлетворяет какому-либо из этих тестов — оно составное. В противном случае
проводятся тесты, подобные сравнению из теоремы 3. Если N не удовлетворяет какому-либо из этих тестов — оно составное. В противном случае
3) определяется не очень большое множество чисел, с которыми только и могут быть сравнимы простые делители  А именно, каждый простой делитель
А именно, каждый простой делитель  числа N должен удовлетворять сравнению вида
числа N должен удовлетворять сравнению вида

4) проверяется, содержит ли найденное множество делители  Если при этом делители не обнаружены, утверждается, что
Если при этом делители не обнаружены, утверждается, что  простое число.
простое число.
Если число N составное, оно обязательно имеет простой делитель  меньший
меньший  который сам содержится среди возможных остатков. Именно на этом свойстве основано применение пункта 4) алгоритма. Пример 2. Если выбрать следующие множества простых чисел
который сам содержится среди возможных остатков. Именно на этом свойстве основано применение пункта 4) алгоритма. Пример 2. Если выбрать следующие множества простых чисел

то таким способом удается проверять простоту чисел 
Отметим, что в работе [13] для тестирования использовались не сравнения теоремы 3, а закон взаимности для степенных вычетов и так называемые суммы Якоби. Сумма Якоби

определяется для двух характеров  по модулю
по модулю  Если характеры имеют порядок
Если характеры имеют порядок  то соответствующая сумма Якоби принадлежит кольцу
то соответствующая сумма Якоби принадлежит кольцу  Поскольку числа
Поскольку числа  участвующие в алгоритме, сравнительно невелики, то вычисления с суммами Якоби производятся в полях существенно меньшей степени, чем вычисления с суммами Гаусса. Это главная причина, по которой суммы Якоби предпочтительнее для вычислений. При
участвующие в алгоритме, сравнительно невелики, то вычисления с суммами Якоби производятся в полях существенно меньшей степени, чем вычисления с суммами Гаусса. Это главная причина, по которой суммы Якоби предпочтительнее для вычислений. При  выполняется классическое соотношение
выполняется классическое соотношение

связывающее суммы Гаусса с суммами Якоби и позволяющее переписать сравнение теоремы 3 в терминах сумм Якоби (см. [16]). Так, при  соответствующее сравнение, справедливое для простых
соответствующее сравнение, справедливое для простых  отличных от 2, 3, 7, принимает вид
отличных от 2, 3, 7, принимает вид

где  некоторый корень кубический из 1.
некоторый корень кубический из 1.
В 1984 г. в работе [15] было внесено существенное усовершенствование в алгоритм, позволившее освободиться от требования неделимости чисел  на квадраты простых чисел. В результате, например, выбрав число
на квадраты простых чисел. В результате, например, выбрав число  и взяв S равным произведению простых чисел
и взяв S равным произведению простых чисел  с условием, что
с условием, что  делится на
делится на  получим
получим  что позволяет доказывать простоту чисел
что позволяет доказывать простоту чисел  записываемых сотней десятичных знаков. При этом вычисления будут проводиться в полях, порожденных корнями из 1 степеней 16, 9, 5 и 7.
записываемых сотней десятичных знаков. При этом вычисления будут проводиться в полях, порожденных корнями из 1 степеней 16, 9, 5 и 7.
Мой персональный компьютер с процессором Pentium-150, пользуясь реализацией этого алгоритма на языке UBASIC, доказал простоту записываемого 65 десятичными знаками, большего из простых чисел в примере Ривеста, Шамира и Адлемана (см. раздел 1) за 8 секунд. Сравнение этих 8 секунд и 17 лет, потребовавшихся для разложения на множители предложенного в примере числа, конечно, впечатляет.
Отметим, что оценка сложности этого алгоритма представляет собой трудную задачу аналитической теории чисел. Как уже указывалось, количество операций оценивается величиной  Однако соответствующие числа
Однако соответствующие числа  возникающие в процессе доказательства, не могут быть явно указаны в зависимости от
возникающие в процессе доказательства, не могут быть явно указаны в зависимости от  Доказано лишь
Доказано лишь
существование чисел  для которых достигается оценка. Впрочем, есть вероятностный вариант алгоритма, доказывающий простоту простого числа N с вероятностью большей
для которых достигается оценка. Впрочем, есть вероятностный вариант алгоритма, доказывающий простоту простого числа N с вероятностью большей  за
за  арифметических операций. А в предположении расширенной гипотезы Римана эта оценка сложности может быть получена при эффективно указанных
арифметических операций. А в предположении расширенной гипотезы Римана эта оценка сложности может быть получена при эффективно указанных 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму изданию
- Глава 1. Основные понятия криптографии
- 2. Предмет криптографии
- 3. Математические основы
- 4. Новые направления
- 5. Заключение
- Глава 2. Криптография и теория сложности
- 2. Криптография и гипотеза P != NP
- 3. Односторонние функции
- 4. Псевдослучайные генераторы
- 5. Доказательства с нулевым разглашением
- Глава 3. Криптографические протоколы
- 2. Целостность. Протоколы аутентификации и электронной подписи
- Схема аутентификации Шнорра
- Схема электронной подписи Шнорра
- 3. Неотслеживаемость. Электронные деньги
- 4. Протоколы типа «подбрасывание монеты по телефону»
- Протокол подбрасывания монеты
- 5. Еще раз о разделении секрета
- 6. Поиграем в «кубики». Протоколы голосования
- Протокол Шаума и Педерсена
- 7. За пределами стандартных предположений. Конфиденциальная передача сообщений
- 8. Вместо заключения
- Глава 4. Алгоритмические проблемы теории чисел
- 2. Система шифрования RSA
- 3. Сложность теоретико-числовых алгоритмов
- 4. Как отличить составное число от простого
- 5. Алгоритм, доказывающий непростоту числа
- 5. Как строить большие простые числа
- 6. Как проверить большое число на простоту
- 7. Как раскладывают составные числа на множители
- 8. Дискретное логарифмирование
- 9. Заключение
- Глава 5. Математика разделения секрета
- 2. Разделение секрета для произвольных структур доступа
- 3. Линейное разделение секрета.
- 4. Идеальное разделение секрета и матроиды
- Глава 6. Компьютер и криптография
- 2. Немного теории
- Что надо знать перед написанием программы шифрования
- 3. Как зашифровать файл?
- 4. Поучимся на чужих ошибках
- 5. Вместо заключения
- Глава 7. Олимпиады по криптографии для школьников
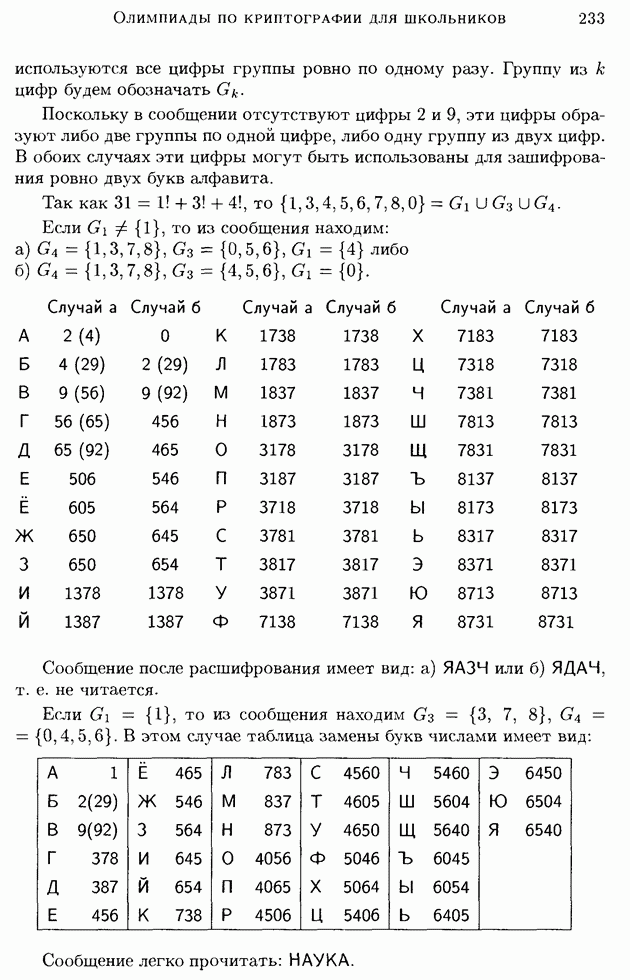
- 2. Шифры замены
- А. Конан Дойл, «Пляшущие человечки»
- Ж. Верн, «Путешествие к центру Земли»
- 3. Шифры перестановки
- 4. Многоалфавитные шифры замены с периодическим ключом
- 5. Условия задач олимпиад по математике и криптографии
- 6. Указания и решения
- Приложение. Отрывок из статьи К. Шеннона «Теория связи в секретных системах»
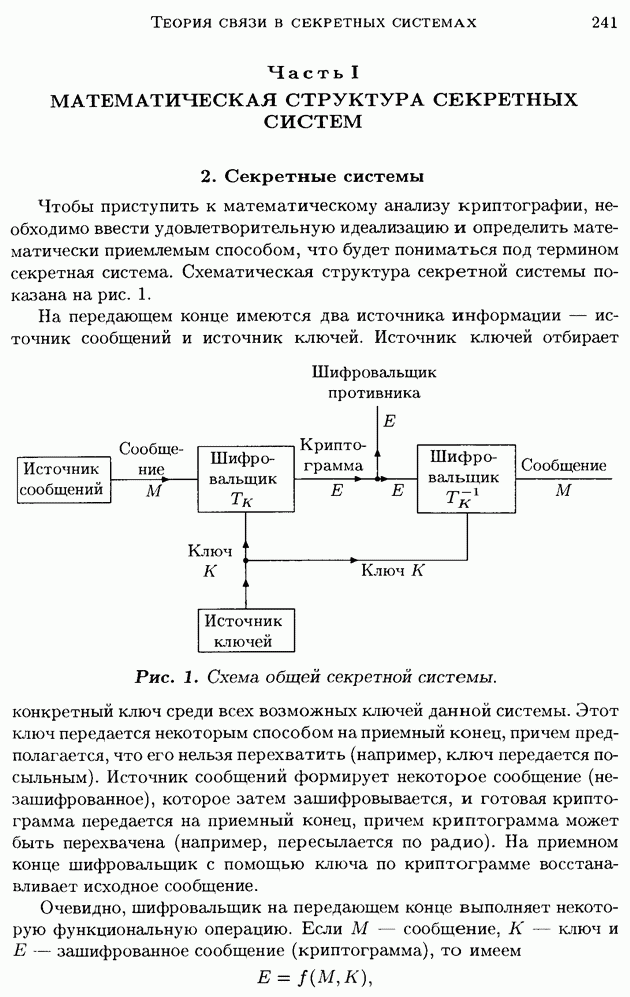
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
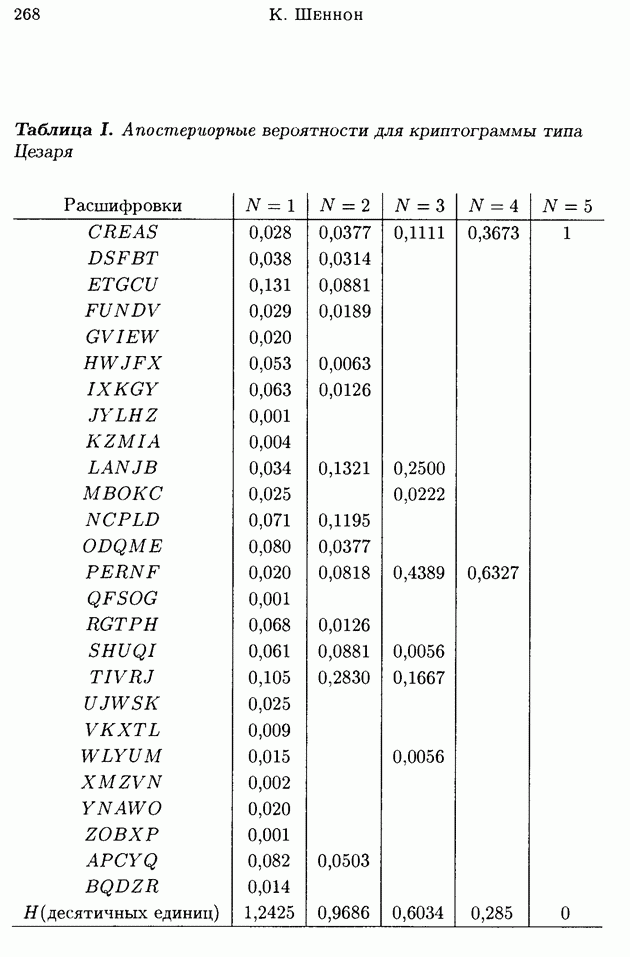
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность