| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.1.2. Методы многомерного шкалирования
В дальнейшем развитие методов психосемантики шло по линии разработки удобных пакетов прикладных программ, основанных на методах многомерного шкалирования (МШ), факторного анализа, а также специализированных методов (статистической) обработки репертуарных решеток [Франселла, Баннистер,
1987]. Примерами пакетов такого типа являются системы KELLY [Похилько, Страхов, 1990], MADONNA [Терехина, 1988], MEDIS [Алексеева, Воинов и др., 1989]. С другой стороны, специфика ряда конкретных приложений, прежде всего — в инженерии знаний, требовала также развития иных (не численных) методов обработки психосемантических данных, использующих — в той или иной форме — парадигму логического вывода на знаниях. Ярким примером этого направления служит система AQUINAS [Boose et al., 1989; Boose, 1990]. Однако анализ практического применения систем обоих типов к задачам инженерии знаний приводит к выводу о несовершенстве имеющихся методик и необходимости их развития в соответствии с современными требованиями инженерии знаний. Наибольшие перспективы в этой области, по-видимому, у методов многомерного шкалирования).
Многомерное шкалирование (МШ) сегодня — это математический инструментарий, предназначенный для обработки данных о попарных сходствах, связях или отношениях между анализируемыми объектами с целью представления этих объектов в виде точек некоторого координатного пространства. МШ представляет собой один из разделов прикладной статистики, научной дисциплины,
разрабатывающей и систематизирующей понятия, приемы, математические методы и модели, предназначенные для сбора, стандартной записи, систематизации и обработки статистических данных с целью их лаконичного представления, интерпретации и получения научных и практических выводов.
Традиционно МШ используется для решения трех типов задач:
1. Поиск и интерпретация латентных (то есть скрытых, непосредственно не наблюдаемых) переменных, объясняющих заданную структуру попарных расстояний (связей, близостей).
2. Верификация геометрической конфигурации системы анализируемых объектов в координатном пространстве латентных переменных.
3. Сжатие исходного массива данных с минимальными потерями в их информативности.
Независимо от задачи МШ всегда используется как инструмент наглядного представления (визуализации) исходных данных. МШ широко применяется в исследованиях по антропологии, педагогике, психологии, экономике, социологии [Дэйвисон, 1988].
В основе данного подхода лежит интерактивная процедура субъективного шкалирования, когда испытуемому (то есть эксперту) предлагается оценить сходство между различными элементами П с помощью некоторой градуированной шкалы (например, от 0 до 9, или от -2 до +2). После такой процедуры аналитик располагает численно представленными стандартизованными данными, поддающимися обработке существующими пакетами прикладных программ, реализующими различные алгоритмы формирования концептов более высокого уровня абстракции и строящими геометрическую интерпретацию семантического пространства в евклидовой системе координат.
Основной тип данных в МШ — меры близости между двумя объектами  Если мера близости такова, что самые большие значения
Если мера близости такова, что самые большие значения  соответствуют парам наиболее похожих объектов, то
соответствуют парам наиболее похожих объектов, то  — мера сходства, если, наоборот, наименее похожим, то
— мера сходства, если, наоборот, наименее похожим, то  — мера различия.
— мера различия.
МШ использует дистанционную модель различия, используя понятие расстояния в геометрии как аналогию сходства и различия понятий (рис. 5.3).
Для того чтобы функция  определенная на парах объектов
определенная на парах объектов  была евклидовым расстоянием, она должна удовлетворять следующим Четырем аксиомам:
была евклидовым расстоянием, она должна удовлетворять следующим Четырем аксиомам:

Тогда, согласно обычной формуле евклидова расстояния, мера различия двух объектов  и
и  со значениями признака к у объектов
со значениями признака к у объектов  и
и  соответственно y и х :
соответственно y и х :


Рис. 5.3. Расстояние в евклидовой метрике
Дистанционная модель была многократно проверена в социологии и психологии [Monahan, Lockhead, 1977; Петренко, 1988; Шмелев, 1983], что дает возможность оценить ее пригодность для использования.
В большинстве работ по МШ используется матричная алгебра. Геометрическая интерпретация позволяет представить абстрактные понятия матричной алгебры в конкретной графической форме. Для облегчения интерпретации решения задачи МШ к первоначально оцененной матрице координат стимулов X применяется вращение.
Среди множества алгоритмов МШ широко используются различные модификации метрических методов Торгерсона [Torgerson, 1958], а также неметрические модели, например Крускала [Kruskal, 1964].
При сравнении методов МШ с другими методами анализа, теоретически применимыми в инженерии знаний (иерархический кластерный анализ [Дюран, Оделл, 1977] или факторный анализ [Иберла, 1980]), МШ выигрывает за счет возможности дать наглядное количественное координатное представление, зачастую более простое и поэтому легче интерпретируемое экспертами.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- 1. Введение в интеллектуальные системы
- 1.1. Краткая история искусственного интеллекта
- 1.1.2. Зарождение нейрокибернетики
- 1.1.3. От кибернетики «черного ящика» к ИИ
- 1.1.4. История искусственного интеллекта в России
- 1.2. Основные направления исследований в области искусственного интеллекта
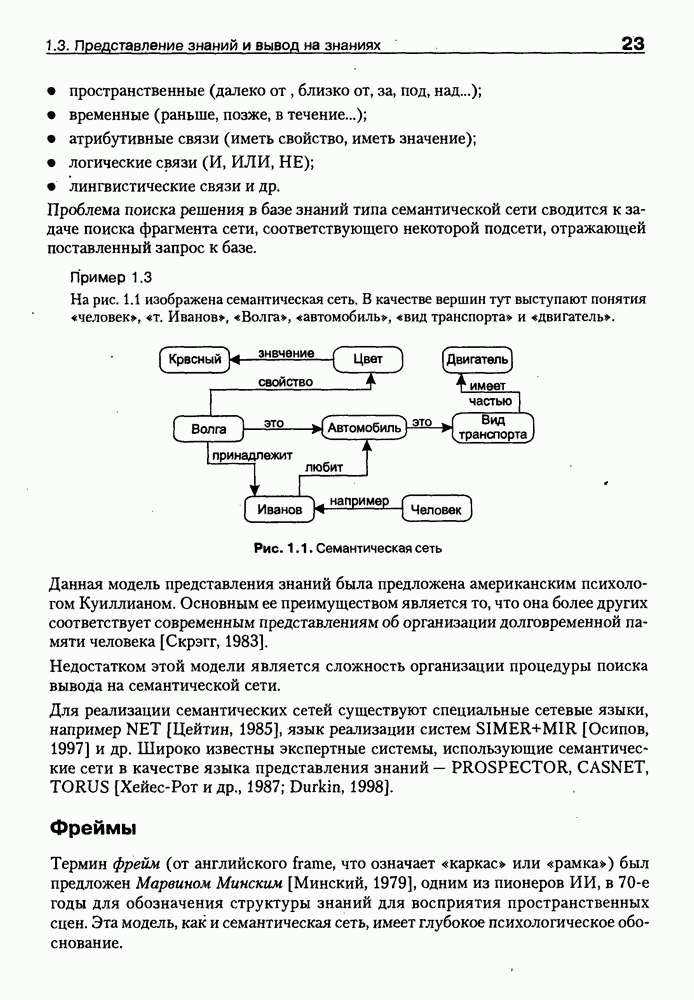
- 1.3. Представление знаний и вывод на знаниях
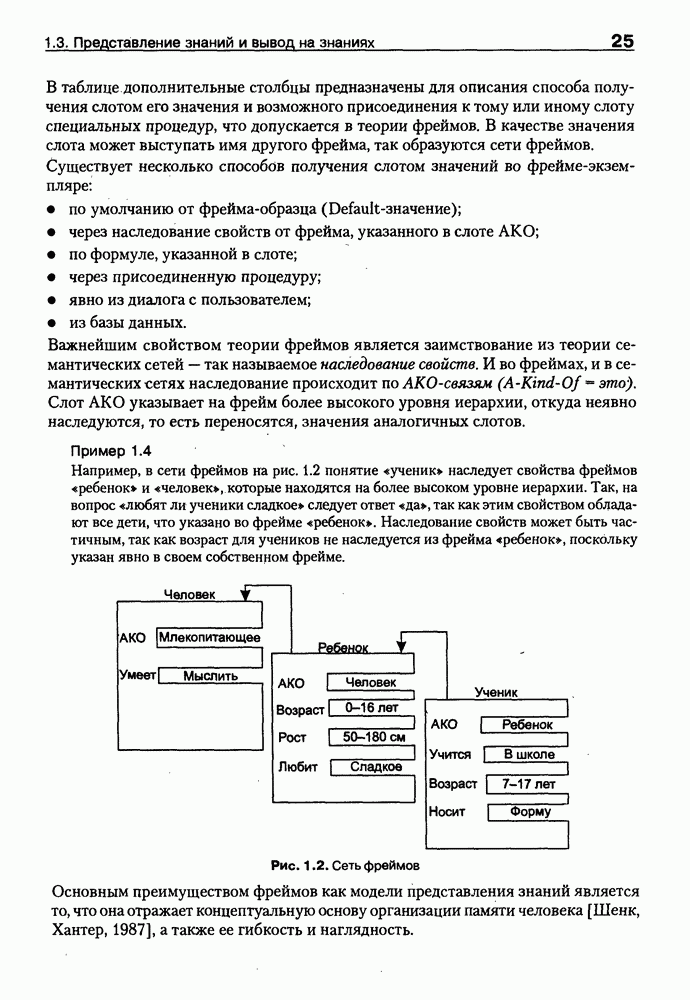
- 1.3.2. Модели представления знаний
- 1.3.3. Вывод на знаниях
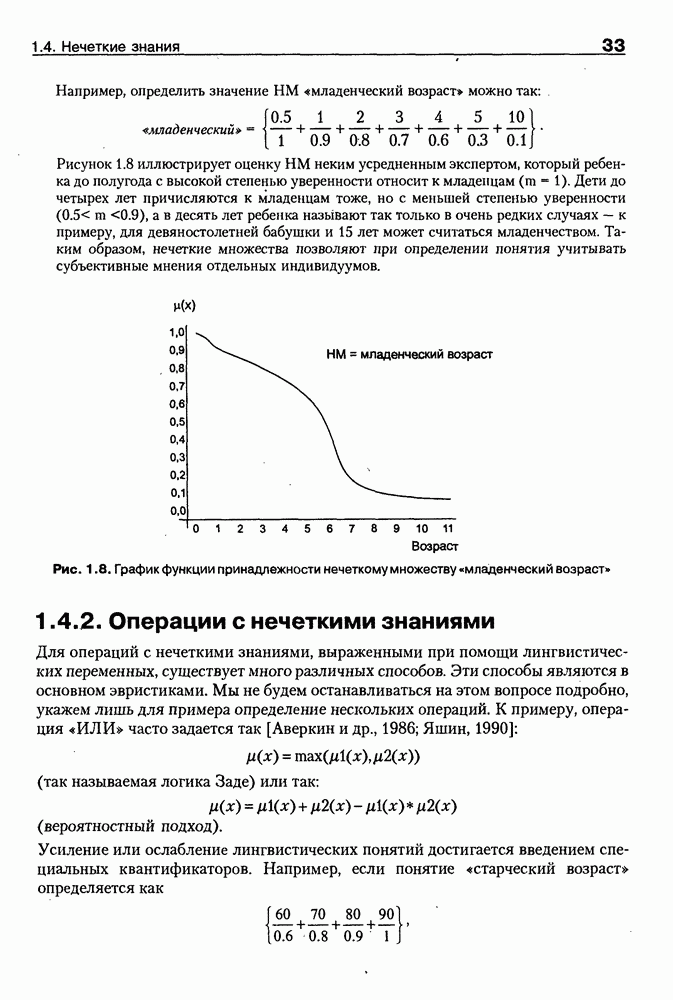
- 1.4. Нечеткие знания
- 1.4.2. Операции с нечеткими знаниями
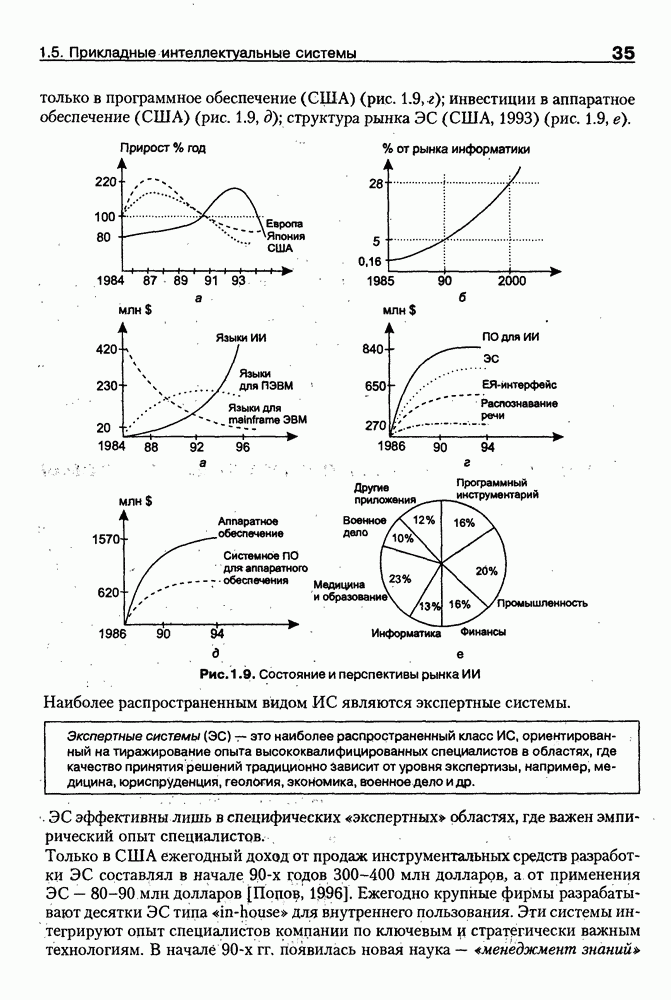
- 1.5. Прикладные интеллектуальные системы
- 2. Разработка систем, основанных на знаниях
- 2.1. Введение в экспертные системы. Определение и структура
- 2.2. Классификация систем, основанных на знаниях
- 2.2.2. Классификация по связи с реальным временем
- 2.2.3. Классификация по типу ЭВМ
- 2.2.4. Классификация по степени интеграции с другими программами
- 2.3. Коллектив разработчиков
- 2.4. Технология проектирования и разработки
- 3. Теоретические аспекты инженерии знаний
- 3.1. Поле знаний
- 3.1.2. Семиотическая модель поля знаний
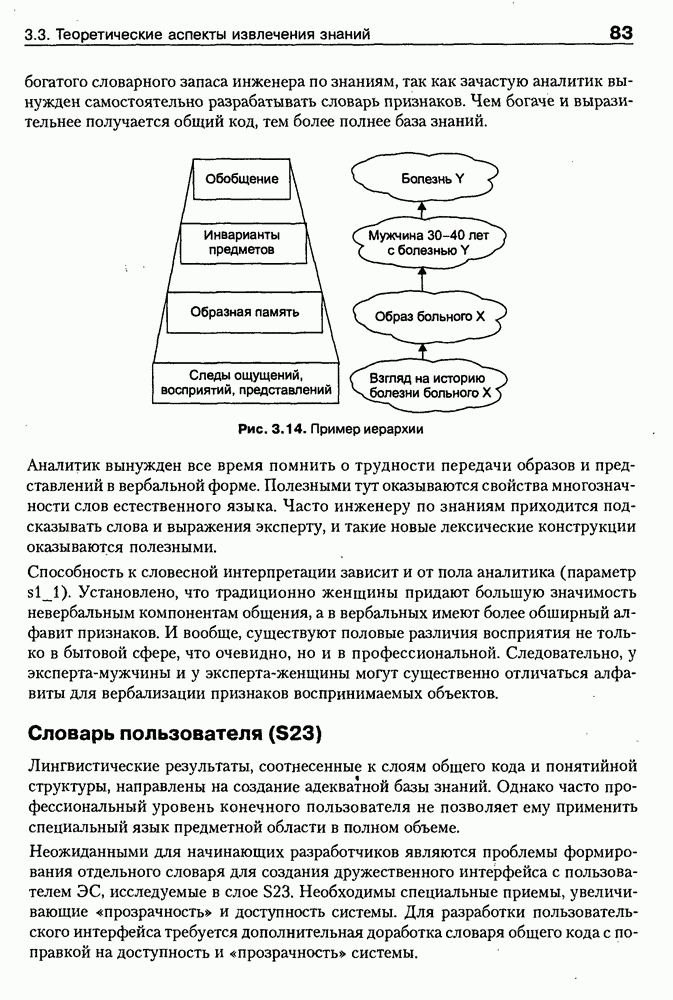
- 3.1.3. «Пирамида» знаний
- 3.2. Стратегии получения знаний
- 3.3. Теоретические аспекты извлечения знаний
- 3.3.2. Лингвистический аспект
- 3.3.3. Гносеологический аспект извлечения знаний
- 3.4. Теоретические аспекты структурирования знаний
- 3.4.2. Иерархический подход
- 3.4.3. Традиционные методологии структурирования
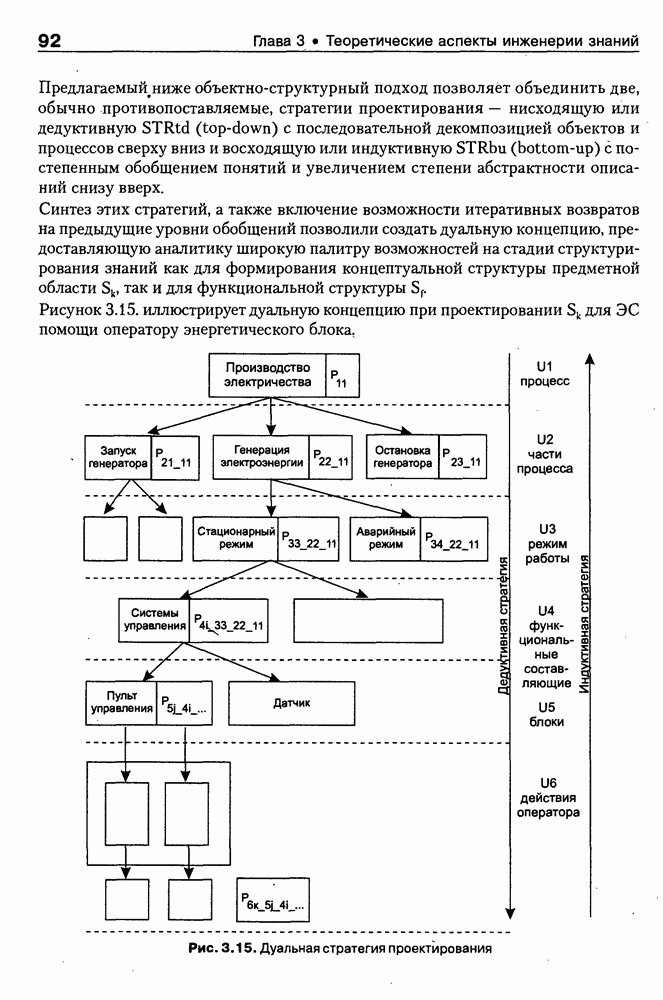
- 3.4.4. Объектно-структурный подход (ОСП)
- 4. Технологии инженерии знаний
- 4.1. Классификация методов практического извлечения знаний
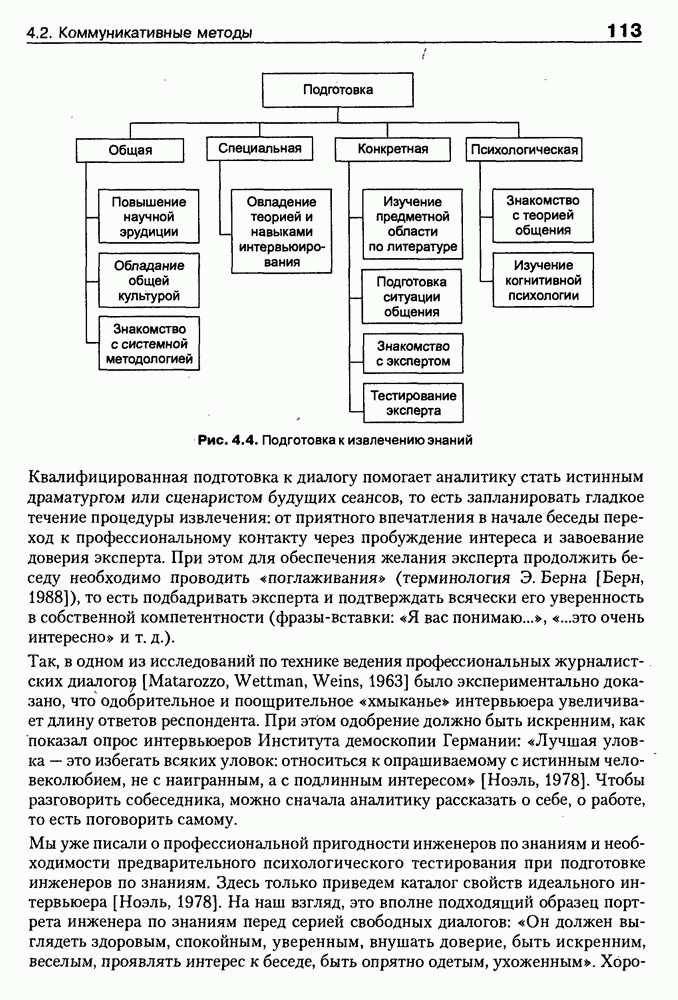
- 4.2. Коммуникативные методы
- 4.2.2. Активные индивидуальные методы
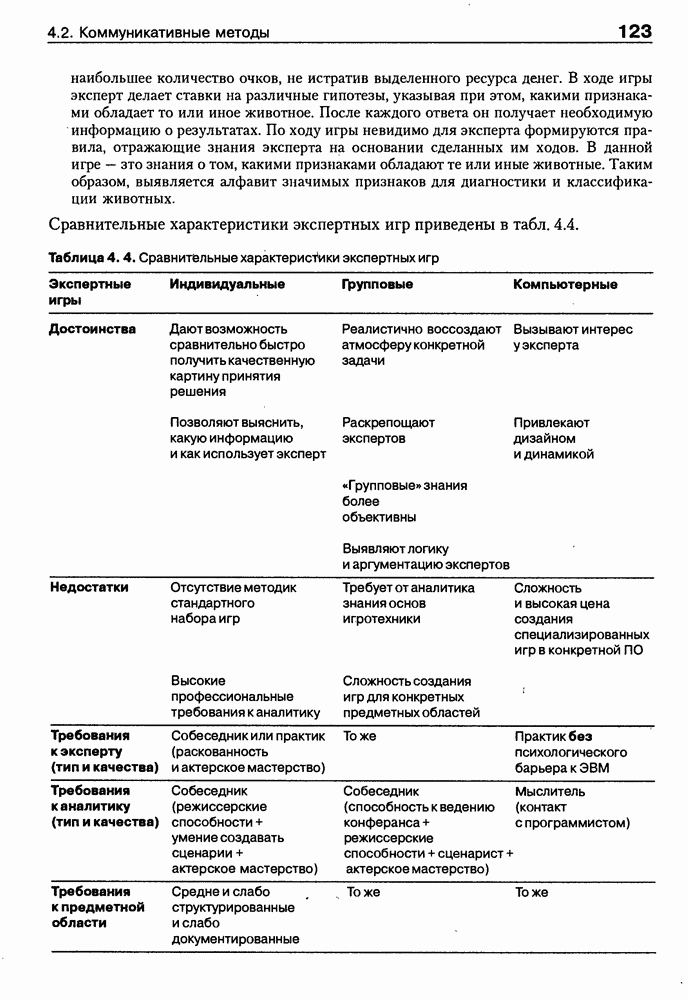
- 4.2.3. Активные групповые методы
- 4.3. Текстологические методы
- 4.4. Простейшие методы структурирования
- 4.4.2. Специальные методы структурирования
- 4.5. Состояние и перспективы автоматизированного приобретения знаний
- 4.5.2. Современное состояние автоматизированных систем приобретения знаний
- 4.6. Примеры методов и систем приобретения знаний
- 4.6.2. Имитация консультаций
- 4.6.3. Интегрированные среды приобретения знаний
- 4.6.4. Приобретение знаний из текстов
- 4.6.5. Инструментарий прямого приобретения знаний SIMER + MIR
- 5. Новые тенденции и прикладные аспекты инженерии знаний
- 5.1. Латентные структуры знаний и психосемантика
- 5.1.2. Методы многомерного шкалирования
- 5.1.3. Использование метафор для выявления «скрытых» структур знаний
- 5.2. Метод репертуарных решеток
- 5.2.2. Методы выявления конструктов
- 5.2.3. Анализ репертуарных решеток
- 5.2.4. Автоматизированные методы
- 5.3. Управление знаниями
- 5.3.2. Управление знаниям и корпоративная память
- 5.3.3. Системы OMIS
- 5.3.4. Особенности разработки OMIS
- 5.4. Визуальное проектирование баз знаний как инструмент познания
- 5.4.2. База знаний как познавательный инструмент
- 5.5. Проектирование гипермедиа БД и адаптивных обучающих систем
- 5.5.2. От мультимедиа к гипермедиа
- 5.5.3. На пути к адаптивным обучающим системам
- 6. Программный инструментарий разработки систем, основанных на знаниях
- 6.1. Технологии разработки программного обеспечения — цели, принципы, парадигмы
- 6.1.2. Модели процесса разработки ПО
- 6.1.3. Инструментальные средства поддержки разработки систем ПО
- 6.2. Методологии создания и модели жизненного цикла интеллектуальных систем
- 6.3. Языки программирования для ИИ и языки представления знаний
- 6.4. Инструментальные пакеты для ИИ
- 6.5. WorkBench-системы
- 7. Пример разработки системы, основанной на знаниях
- 7.1.2. Декларативное представление данных и знаний
- 7.1.3. Процедурные средства языка
- 7.2. Психодиагностика — пример предметной области для построения экспертных систем
- 7.2.2. Батарея психодиагностических ЭС «Ориентир»
- 7.3. Разработка и реализация психодиагностической ЭС «Cattell»
- 7.3.2. Общение с пользователем и опрос испытуемых
- 7.3.3. Вывод портретов и генерация их текстовых представлений
- 7.3.4. Помощь и объяснения в ЭС «Cattell»
- 8. Представление данных и знаний в Интернете
- 8.1.2. HTML — язык гипертекстовой разметки Интернет-документов
- 8.1.3. Возможности представления знаний на базе языка HTML
- 8.2. Онтологии и онтологические системы
- 8.2.2. Модели онтологии и онтологической системы
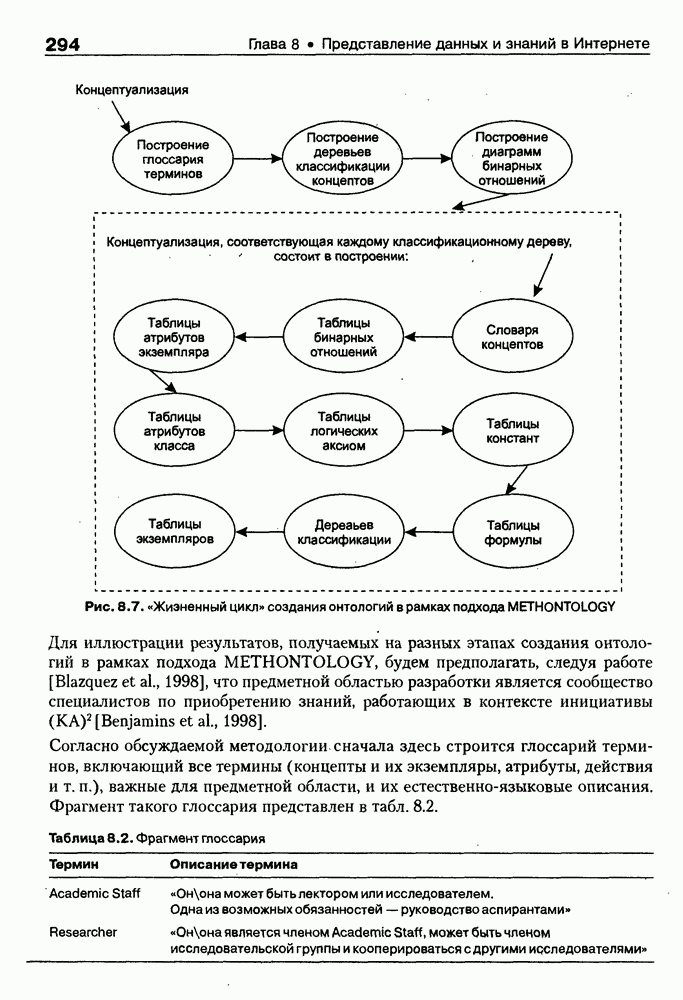
- 8.2.3. Методологии создания и «жизненный цикл» онтологий
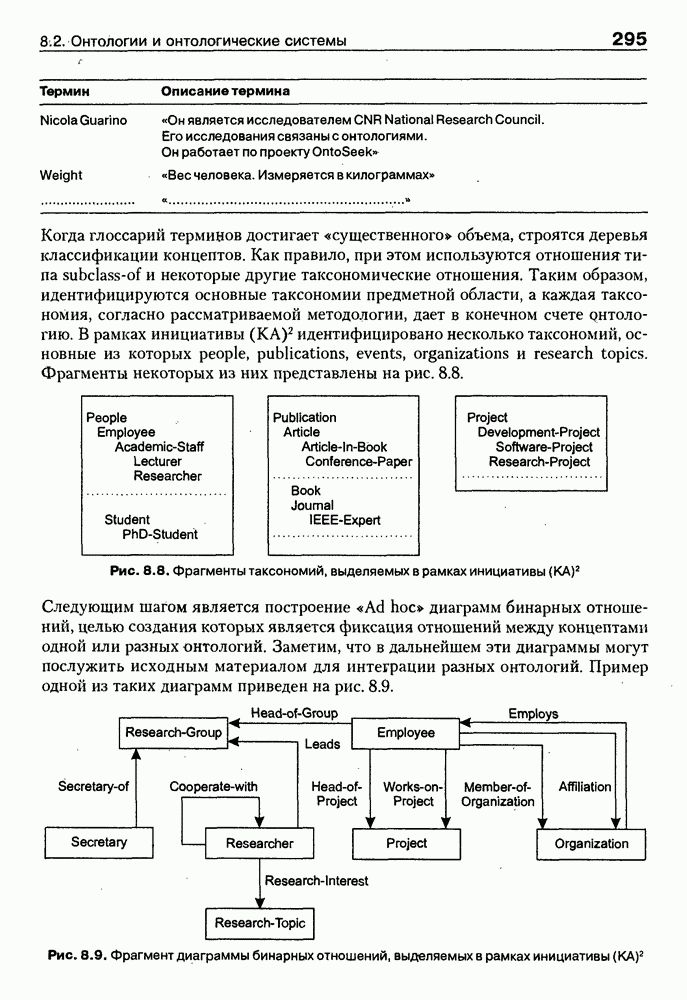
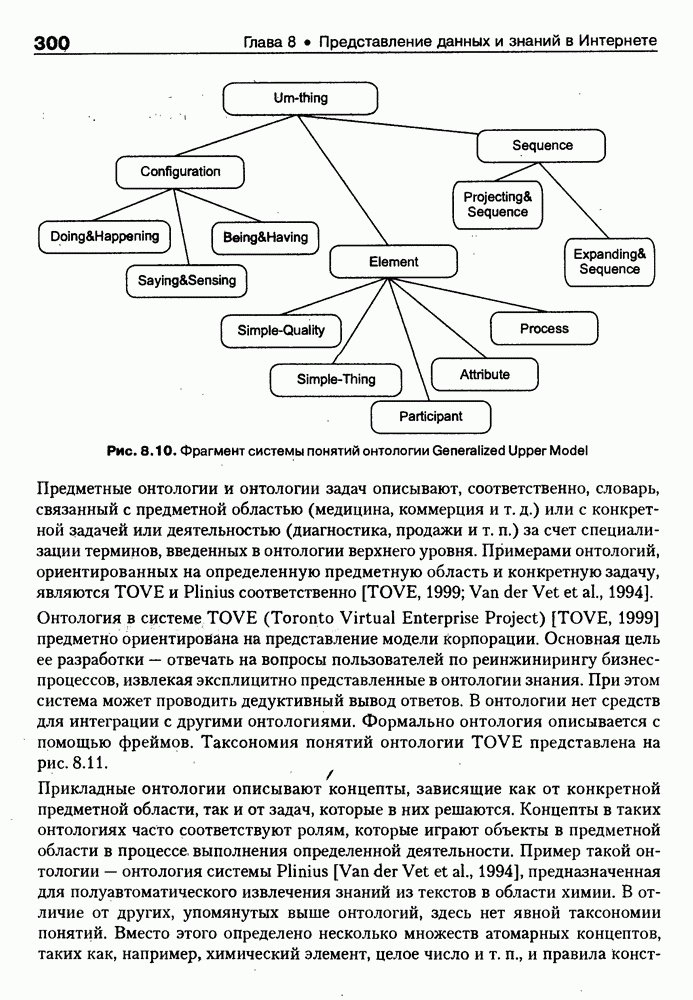
- 8.2.4. Примеры онтологий
- 8.3. Системы и средства представления онтологических знаний
- 8.3.2. Инициатива и инструментарий Ontobroker
- 8.3.3. Проект SHOE — спецификация онтологий и инструментарий
- 8.3.4. Другие подходы и тенденции
- 9. Интеллектуальные Интернет-технологии
- 9.1. Программные агенты и мультиагентные системы
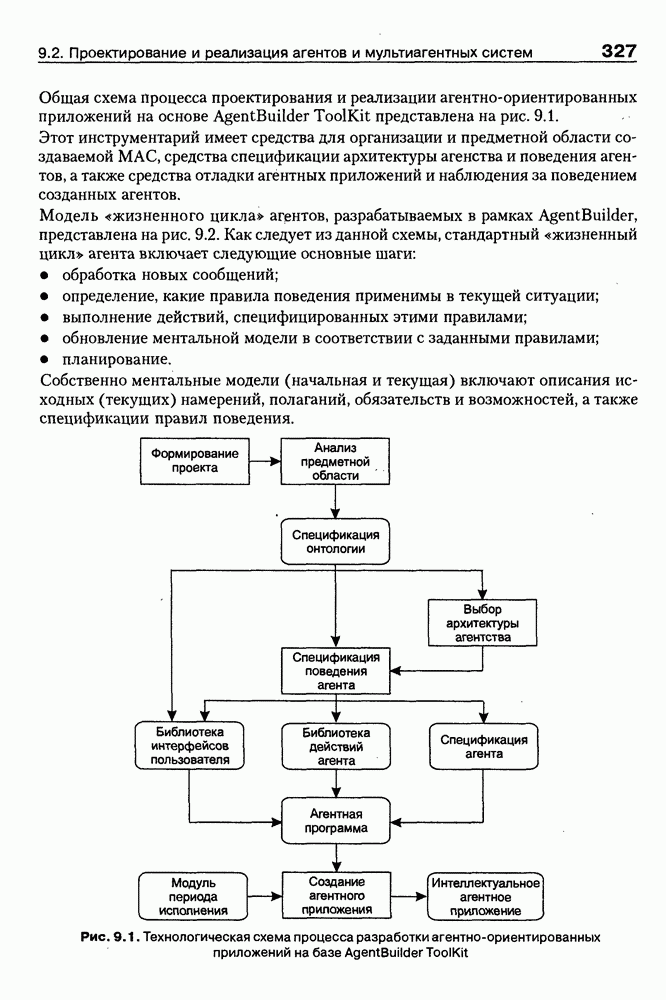
- 9.2. Проектирование и реализация агентов и мультиагентных систем
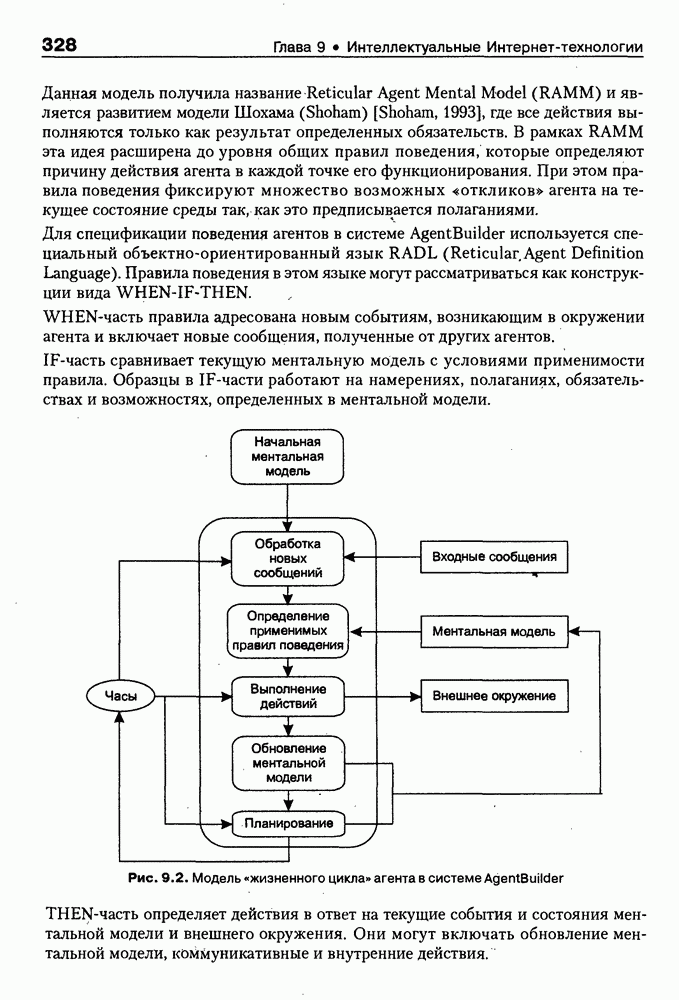
- 9.2.2. Инструментарий AgentBuilder
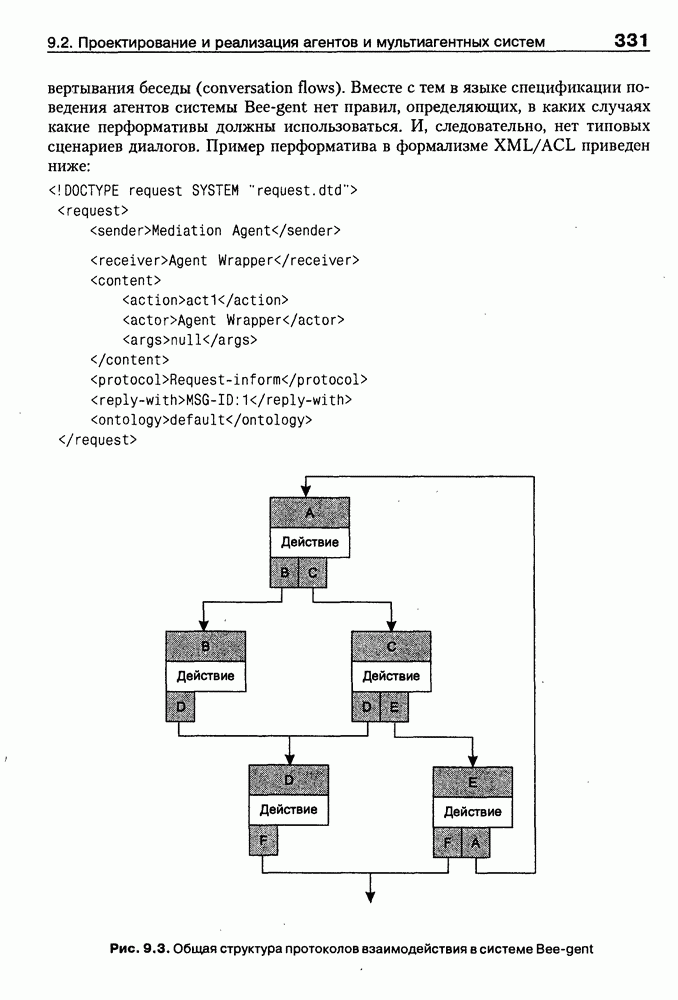
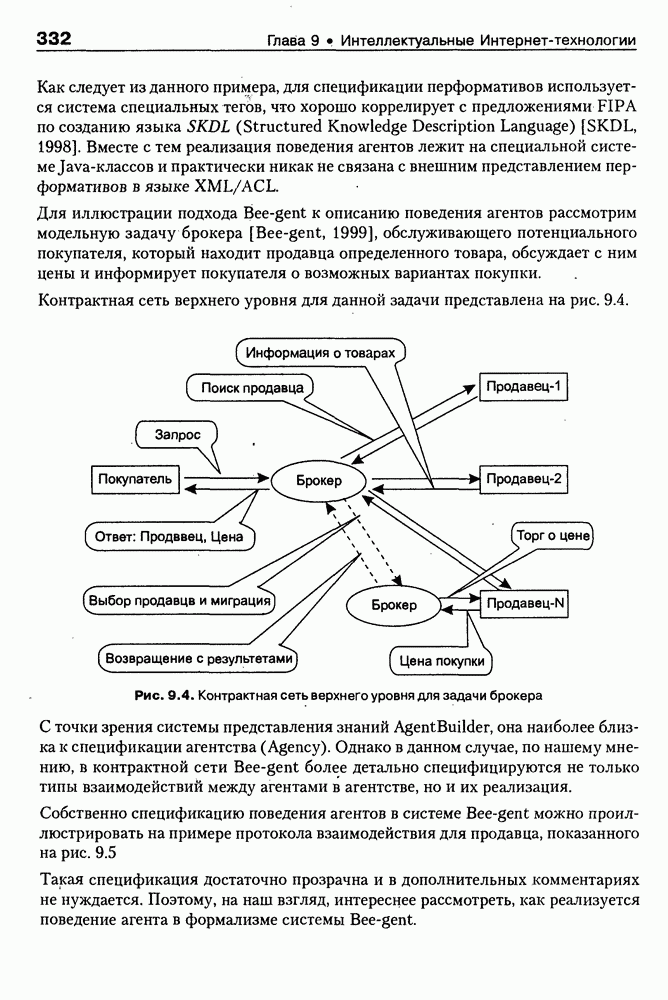
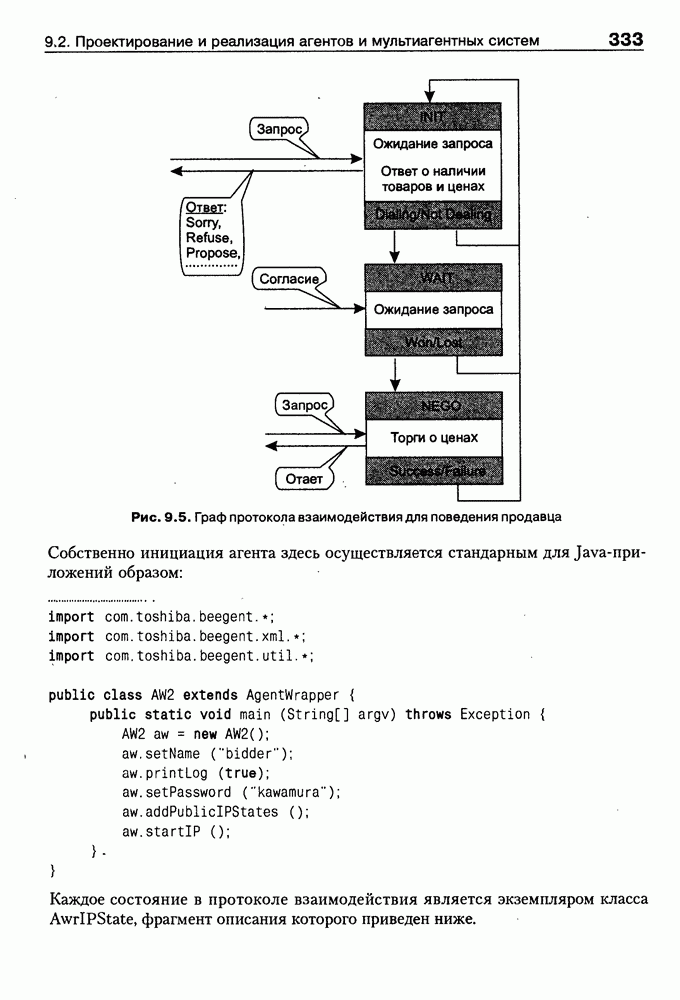
- 9.2.3. Система Bee-gent
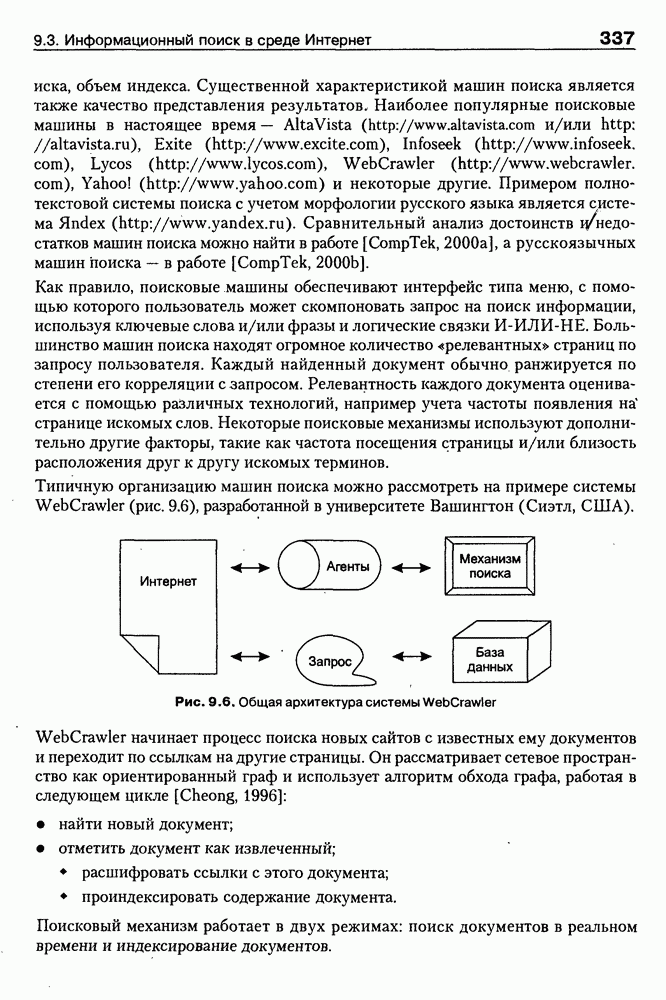
- 9.3. Информационный поиск в среде Интернет
- 9.3.2. Неспециализированные и специализированные поисковые агенты
- 9.3.3. Системы интеллектуальных поисковых агентов
- Заключение
- Литература