| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
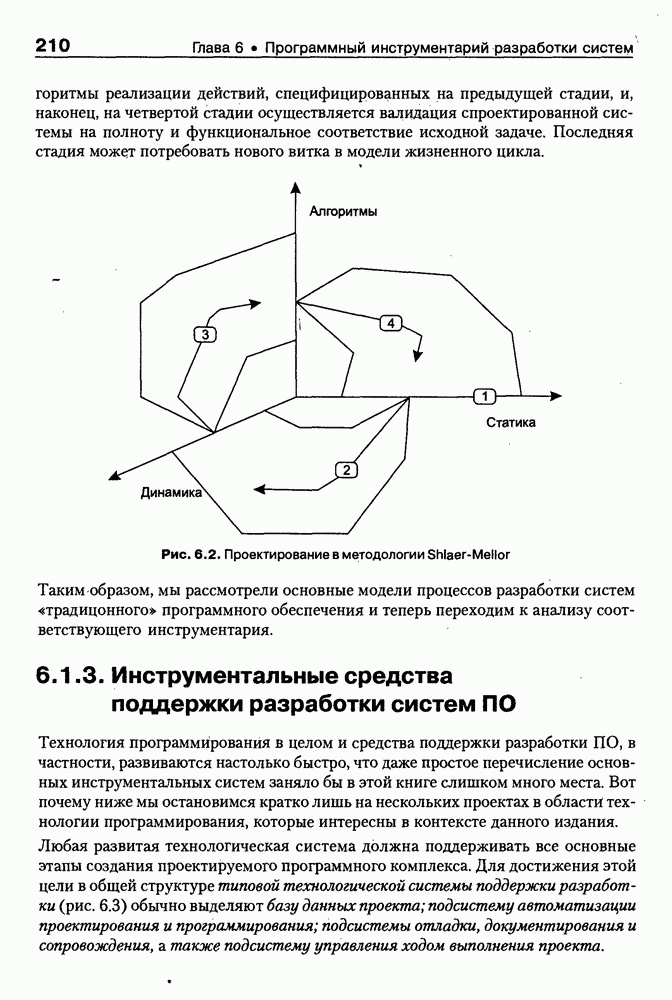
8.2.2. Модели онтологии и онтологической системы
Выше уже отмечалось, что понятие онтологии предполагает определение и использование взаимосвязанной и взаимосогласованной совокупности трех
компонент: таксономии терминов, определений терминов и правил их обработки. Учитывая это, введем следующее определение понятия модели онтологии:
Под формальной моделью онтологии О будем понимать упорядоченную тройку вида:

где
X — конечное множество концептов (понятий, терминов) предметной области, которую представляет онтология О;
 — конечное множество отношений между концептами (понятиями, терминами) заданной предметной области;
— конечное множество отношений между концептами (понятиями, терминами) заданной предметной области;
Ф — конечное множество функций интерпретации (аксиоматизация), заданных на концептах и/или отношениях онтологии О.
Заметим, что естественным ограничением, накладываемым на множество X, является его конечность и непустота. Иначе обстоит дело с компонентами Ф и 91 в определении онтологии О. Понятно, что и в этом случае Ф и 91 должны быть конечными множествами. Рассмотрим, однако, граничные случаи, связанные с их пустотой.
Пусть  Тогда онтология О трансформируется в простой словарь:
Тогда онтология О трансформируется в простой словарь:

Такая вырожденная онтология может быть полезна для спецификации, пополнения и поддержки словарей ПО, но онтологии-словари имеют ограниченное использование, поскольку не вводят эксплицитно смысла терминов. Хотя в некоторых случаях, когда используемые термины принадлежат очень узкому (например, техническому) словарю и их смыслы уже заранее хорошо согласованы в пределах определенного (например, научного) сообщества, такие онтологии применяются на практике. Известными примерами онтологий этого типа являются индексы машин поиска информации в сети Интернет.
Иная ситуация в случае использования терминов обычного естественного языка или в тех случаях, когда общаются программные агенты. В этом случае необходимо характеризовать предполагаемый смысл элементов словаря с помощью подходящей аксиоматизации, цель использования которой — в исключении нежелательных моделей и в том, чтобы интерпретация была единой для всех участников общения.
Другой вариант соответствует случаю  но Ф 0. Тогда каждому элементу множества терминов из X может быть поставлена в соответствие функция интерпретации
но Ф 0. Тогда каждому элементу множества терминов из X может быть поставлена в соответствие функция интерпретации  из Ф. Формально это утверждение может быть записано следующим образом.
из Ф. Формально это утверждение может быть записано следующим образом.
Пусть

причем

где  — множество интерпретируемых терминов;
— множество интерпретируемых терминов;
 — множество интерпретирующих терминов.
— множество интерпретирующих терминов.
Тогда

такие что

где
Пустота пересечения множеств  исключает циклические интерпретации, а введение в рассмотрение функции к аргументов призвано обеспечить более полную интерпретацию. Вид отображения
исключает циклические интерпретации, а введение в рассмотрение функции к аргументов призвано обеспечить более полную интерпретацию. Вид отображения  из Ф определяет выразительную мощность и практическую полезность этого вида онтологии. Так, если предположить, что функция интерпретации задается оператором присваивания значений
из Ф определяет выразительную мощность и практическую полезность этого вида онтологии. Так, если предположить, что функция интерпретации задается оператором присваивания значений  где
где  — имя интерпретации
— имя интерпретации  то онтология трансформируется в пассивный словарь
то онтология трансформируется в пассивный словарь 

Такой словарь пассивен, так как все определения терминов из  берутся из уже существующего и фиксированного множества
берутся из уже существующего и фиксированного множества  Практическая ценность его выше, чем простого словаря! но явно недостаточна, например, для представления знаний в задачах обработки информации в Интернете в силу динамического характера этой среды.
Практическая ценность его выше, чем простого словаря! но явно недостаточна, например, для представления знаний в задачах обработки информации в Интернете в силу динамического характера этой среды.
Для того чтобы учесть последнее обстоятельство, предположим, что часть интерпретирующих терминов из множества  задается процедурно, а не декларативно. Смысл таких терминов «вычисляется» каждый раз при их интерпретации. Ценность такого словаря для задач обработки информации в среде Интернет выше, чем у предыдущей модели, но все еще недостаточна, так как интерпретируемые элементы из
задается процедурно, а не декларативно. Смысл таких терминов «вычисляется» каждый раз при их интерпретации. Ценность такого словаря для задач обработки информации в среде Интернет выше, чем у предыдущей модели, но все еще недостаточна, так как интерпретируемые элементы из  никак не связаны между собой и, следовательно, играют лишь роль ключей входа в онтологию.
никак не связаны между собой и, следовательно, играют лишь роль ключей входа в онтологию.
Для представления модели онтологии, которая нужна для решения задач обработки информации в Интернете, очевидно, требуется отказаться от предположения 
Итак, предположим, что множество отношений на концептах онтологии не пусто, и рассмотрим возможные варианты его формирования.
Для этого введем в рассмотрение специальный подкласс онтологий — простую таксономию следующим образом:

Под таксономической структурой будем понимать иерархическую систему понятий, связанных между собой отношением  («бытьэлементом класса»).
(«бытьэлементом класса»).
Отношение  имеет фиксированную заранее семантику и позволяет организовывать структуру понятий онтологии в виде дерева. Такой подход имеет свои преимущества и недостатки, но в общем случае является адекватным и удобным для представления иерархии понятий.
имеет фиксированную заранее семантику и позволяет организовывать структуру понятий онтологии в виде дерева. Такой подход имеет свои преимущества и недостатки, но в общем случае является адекватным и удобным для представления иерархии понятий.
Результаты анализа частных случаев модели онтологии приведены в таблице 8.1.
Таблица 8.1. Классификация моделей онтологии

Далее можно обобщить частные случаи модели онтологии таким образом, чтобы обеспечить возможность:
• представления множества концептов X в виде сетевой структуры;
• использования достаточно богатого множества отношений  , включающего не только таксономические отношения, но и отношения, отражающие специфику конкретной предметной области, а также средства расширения множества
, включающего не только таксономические отношения, но и отношения, отражающие специфику конкретной предметной области, а также средства расширения множества  ;
;
• использования декларативных и процедурных интерпретаций и отношений, включая возможность определения новых интерпретаций.
Тогда можно ввести в рассмотрение модель расширяемой онтологии и исследовать ее свойства. Однако, учитывая техническую направленность данной книги, мы не будем делать этого здесь, а желающих познакомиться с такой моделью отсылаем к работе [Maikevich et al., 1999]. Как показано в этой работе, модель расширяемой онтологии является достаточно мощной для спецификации процессов формирования пространств знаний в среде Интернет. Вместе с тем и эта модель является неполной в силу своей пассивности даже там, где определены соответствующие процедурные интерпретации и введены специальные функции пополнения онтологии. Ведь единственной точкой управления активностью в такой модели является запрос на интерпретацию определенного концепта. Этот запрос выполняется всегда одинаково и инициирует запуск соответствующей процедуры. А собственно вывод ответа на запрос и/или поиск необходимой для этого информации остается вне модели и должен реализовываться другими средствами.
Учитывая вышесказанное, а также необходимость эксплицитной спецификации процессов функционирования онтологии, введем в рассмотрение понятие онтологической системы
Под формальной моделью онтологической системы  будем понимать триплет вида:
будем понимать триплет вида:

где
 онтология верхнего уровня (метаонтология);
онтология верхнего уровня (метаонтология);
 — множество предметных онтологий и онтологий задач предметной области;
— множество предметных онтологий и онтологий задач предметной области;
Е — модель машины вывода, ассоциированной с онтологической системой 
Использование системы онтологий и специальной машины вывода позволяет решать в такой модели различные задачи. Расширяя систему моделей  можно учитывать предпочтения пользователя, а изменяя модель машины вывода, вводить специализированные критерии релевантности получаемой в процессе поиска информации и формировать специальные репозитории накопленных данных, а также пополнять при необходимости используемые онтологии, о
можно учитывать предпочтения пользователя, а изменяя модель машины вывода, вводить специализированные критерии релевантности получаемой в процессе поиска информации и формировать специальные репозитории накопленных данных, а также пополнять при необходимости используемые онтологии, о
В модели  имеются три онтологические компоненты:
имеются три онтологические компоненты:
• метаонтология;
• предметная онтология;
• онтология задач.
Как указывалось выше, метаонтология оперирует общими концептами и отношениями, которые не зависят от конкретной предметной области. Концептами метауровня являются общие понятия, такие как «объект», «свойство», «значение» и т. д. Тогда на уровне метаонтологии мы получаем интенсиональное описание свойств предметной онтологии и онтологии задач. Онтология метауровня является статической, что дает возможность обеспечить здесь эффективный вывод.
Предметная онтология  содержит понятия, описывающие конкретную предметную область, отношения, семантически значимые для данной предметной области, и множество интерпретаций этих понятий и отношений (декларативных и процедурных). Понятия предметной области специфичны в каждой прикладной онтологии, но отношения — более универсальны. Поэтому в качестве базиса обычно выделяют такие отношения модели предметной онтологии, как partjof, kindjof, contained_in, member_of, seealso и некоторые другие.
содержит понятия, описывающие конкретную предметную область, отношения, семантически значимые для данной предметной области, и множество интерпретаций этих понятий и отношений (декларативных и процедурных). Понятия предметной области специфичны в каждой прикладной онтологии, но отношения — более универсальны. Поэтому в качестве базиса обычно выделяют такие отношения модели предметной онтологии, как partjof, kindjof, contained_in, member_of, seealso и некоторые другие.
Отношение  определено на множестве концептов, является отношением принадлежности и показывает, что концепт может быть частью других концептов. Оно является отношением типа «часть-целое» и по свойствам близко к отношению
определено на множестве концептов, является отношением принадлежности и показывает, что концепт может быть частью других концептов. Оно является отношением типа «часть-целое» и по свойствам близко к отношению  и может быть задано соответствующими аксиомами. Аналогичным образом можно ввести и другие отношения типа «часть-целое».
и может быть задано соответствующими аксиомами. Аналогичным образом можно ввести и другие отношения типа «часть-целое».
Иначе обстоит дело с отношением see also. Оно обладает другой семантикой и другими свойствами. Поэтому целесообразно вводить его не декларативно, а процедурно, подобно тому, как это делается при определении новых типов в языках программирования, где поддерживаются абстрактные типы данных;

Заметим, что и отношение see_also «не вполне» транзитивно. Действительно, если предположить, что (XI  то можно считать, что (XI
то можно считать, что (XI  Однако по мере увеличения длины цепочки объектов,
Однако по мере увеличения длины цепочки объектов,
связанных данным отношением, справедливость транзитивного переноса свойства connected_with падает. Поэтому в случае отношения see also мы имеем дело не с отношением частичного порядка (как, например, в случае отношения is_a), а с отношением толерантности. Однако для простоты это ограничение может быть перенесено из определения отношения в функцию его интерпретации.
Анализ различных предметных областей показывает, что введенный выше набор отношений является достаточным для начального описания соответствующих онтологий. Понятно, что этот базис является открытым и может пополняться в зависимости от предметной области и целей, стоящих перед прикладной системой, в которой такая онтология используется.
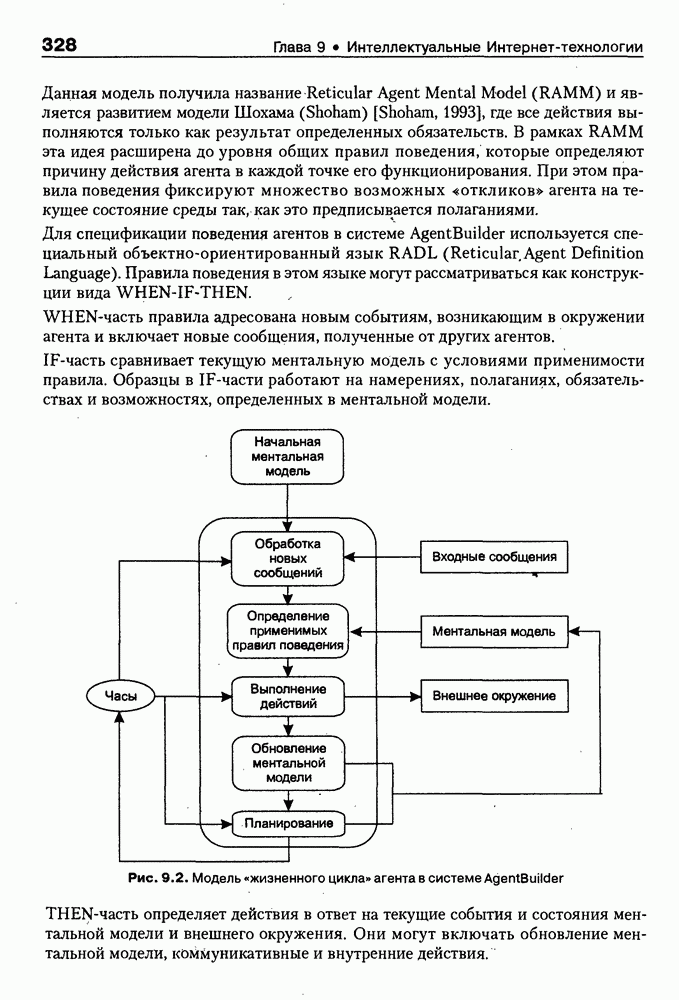
Онтология задач в качестве понятий содержит типы решаемых задач, а отношения этой онтологии, как правило, специфицируют декомпозицию задач на подзадачи. Вместе с тем, если прикладной системой решается единственный тип задач (например, задачи поиска релевантной запросу информации), то онтология задач может в данном случае описываться словарной моделью, рассмотренной выше. Таким образом, модель онтологической системы позволяет описывать необходимые для ее функционирования онтологии разных уровней. Взаимосвязь между онтологиями показана на рис. 8.6.

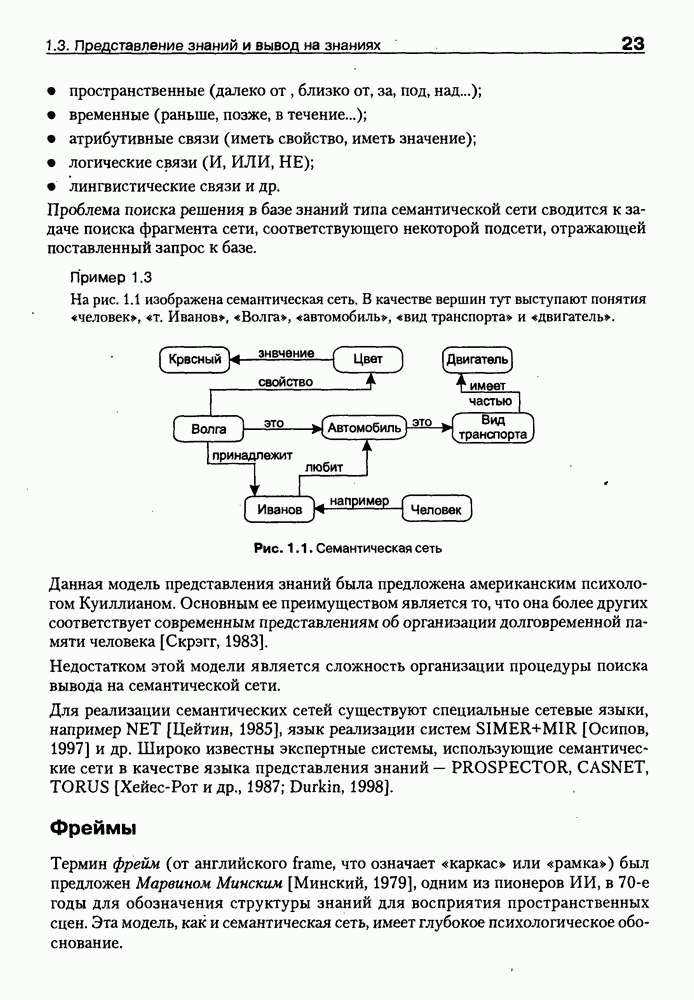
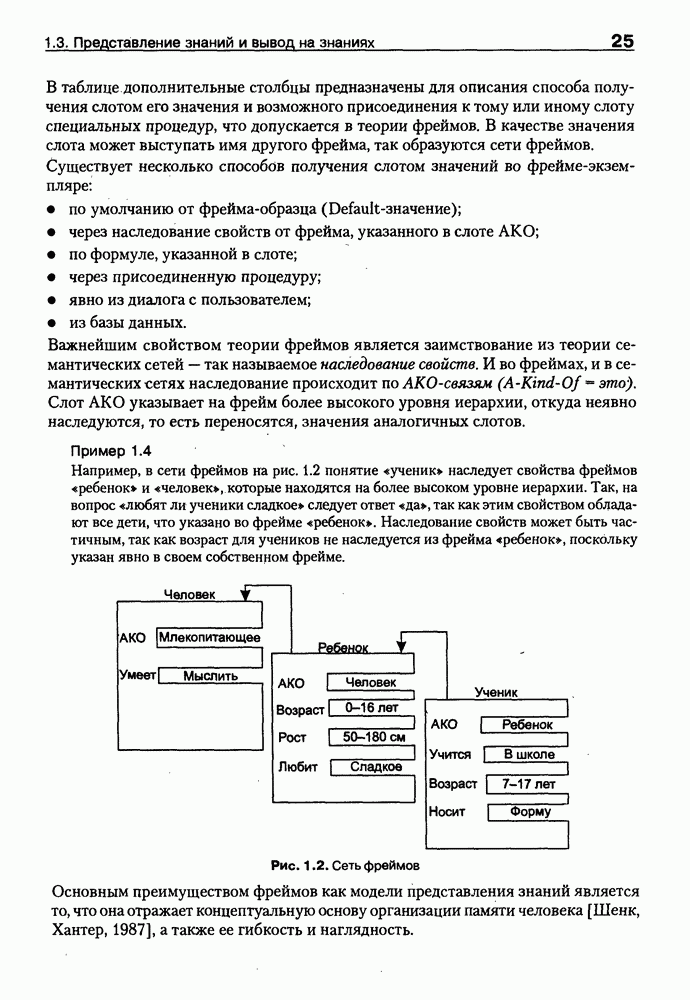
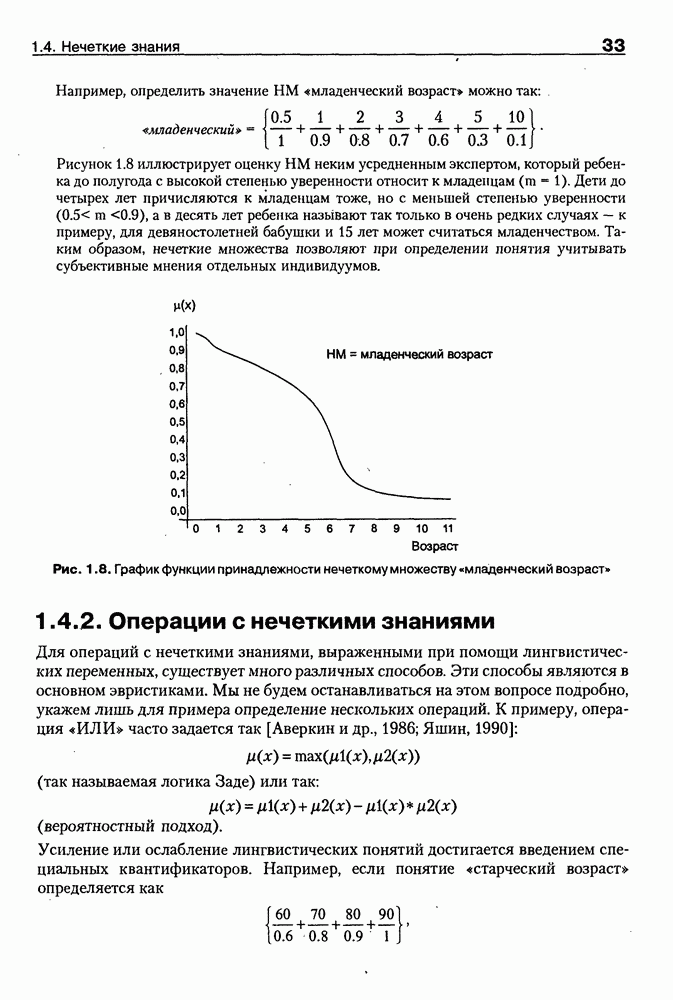
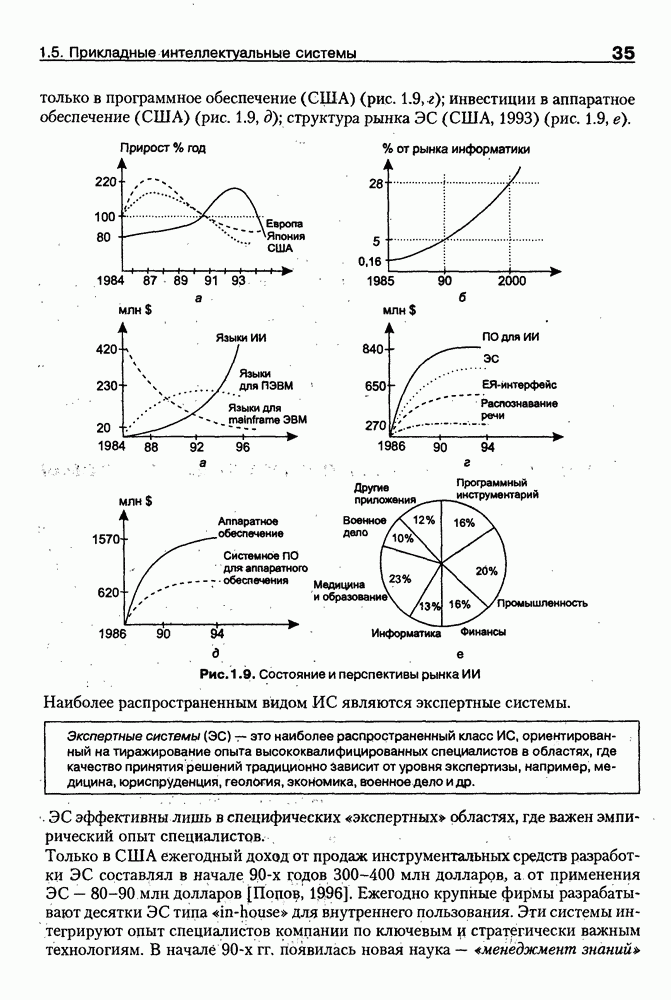
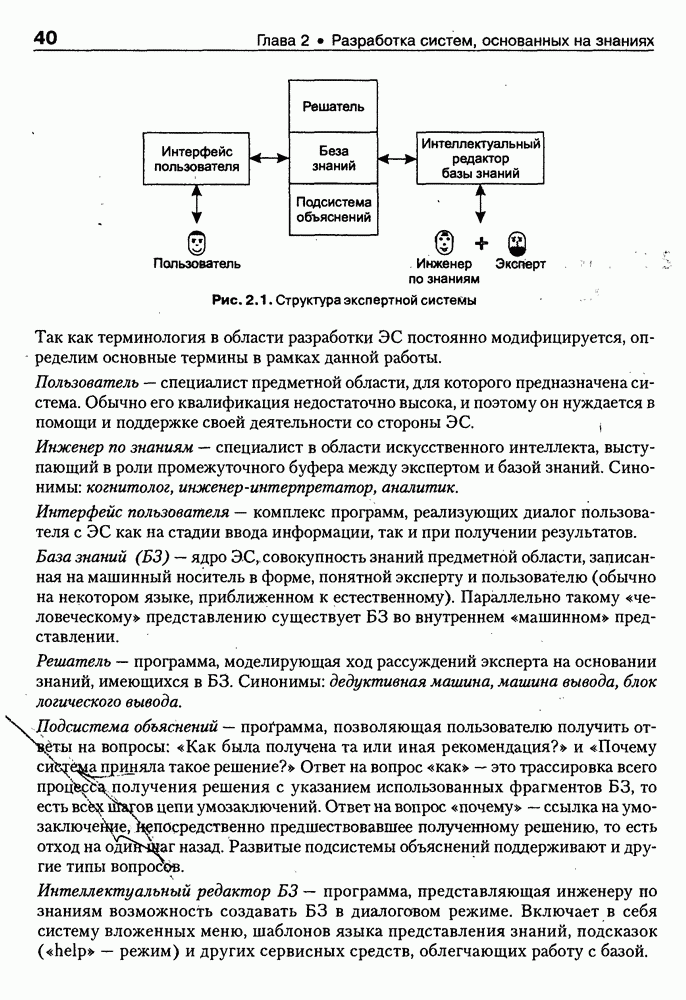
Рис. 8.6. Взаимосвязь между онтологиями онтологической системы
Машина вывода онтологической системы в общем случае может опираться на сетевое представление онтологий всех уровней. При этом ее функционирование будет связано:
• с активацией понятий и/или отношений, фиксирующих решаемую задачу (описание исходной ситуации);
• определением целевого состояния (ситуации);
• выводом на сети, заключающемся в том, что от узлов исходной ситуации распространяются волны активации, использующие свойства отношений, с ними связанных. Критерием остановки процесса является достижение целевой ситуации или превышение длительности исполнения (time-out).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- 1. Введение в интеллектуальные системы
- 1.1. Краткая история искусственного интеллекта
- 1.1.2. Зарождение нейрокибернетики
- 1.1.3. От кибернетики «черного ящика» к ИИ
- 1.1.4. История искусственного интеллекта в России
- 1.2. Основные направления исследований в области искусственного интеллекта
- 1.3. Представление знаний и вывод на знаниях
- 1.3.2. Модели представления знаний
- 1.3.3. Вывод на знаниях
- 1.4. Нечеткие знания
- 1.4.2. Операции с нечеткими знаниями
- 1.5. Прикладные интеллектуальные системы
- 2. Разработка систем, основанных на знаниях
- 2.1. Введение в экспертные системы. Определение и структура
- 2.2. Классификация систем, основанных на знаниях
- 2.2.2. Классификация по связи с реальным временем
- 2.2.3. Классификация по типу ЭВМ
- 2.2.4. Классификация по степени интеграции с другими программами
- 2.3. Коллектив разработчиков
- 2.4. Технология проектирования и разработки
- 3. Теоретические аспекты инженерии знаний
- 3.1. Поле знаний
- 3.1.2. Семиотическая модель поля знаний
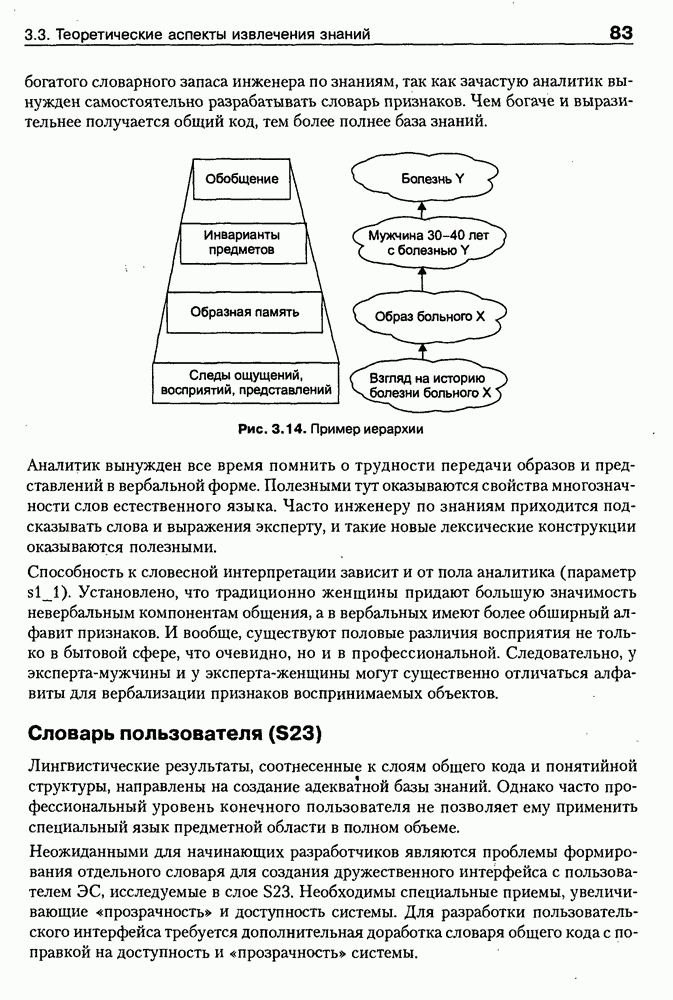
- 3.1.3. «Пирамида» знаний
- 3.2. Стратегии получения знаний
- 3.3. Теоретические аспекты извлечения знаний
- 3.3.2. Лингвистический аспект
- 3.3.3. Гносеологический аспект извлечения знаний
- 3.4. Теоретические аспекты структурирования знаний
- 3.4.2. Иерархический подход
- 3.4.3. Традиционные методологии структурирования
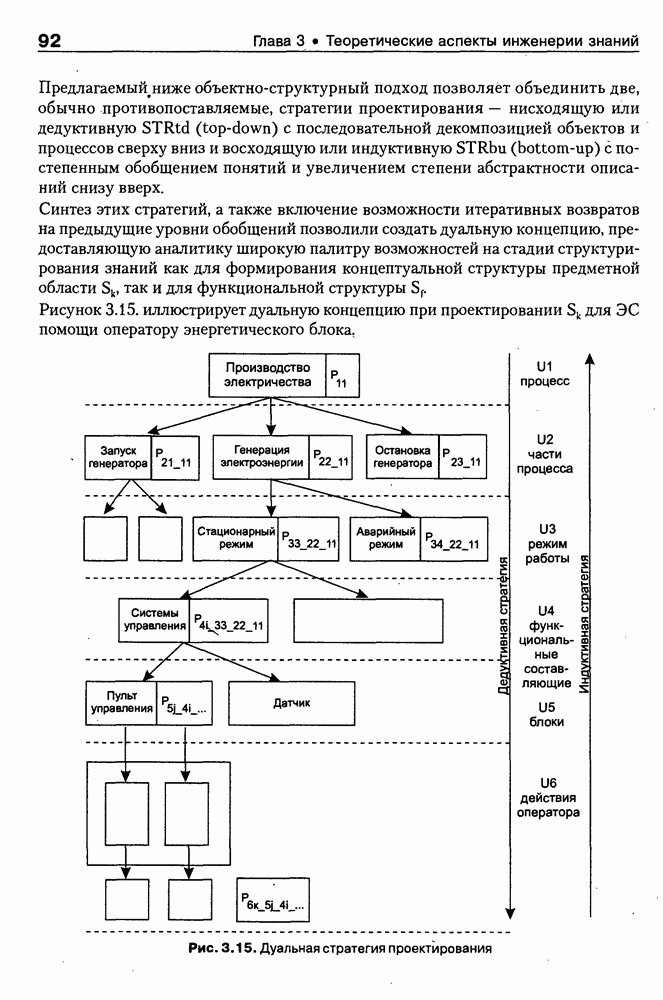
- 3.4.4. Объектно-структурный подход (ОСП)
- 4. Технологии инженерии знаний
- 4.1. Классификация методов практического извлечения знаний
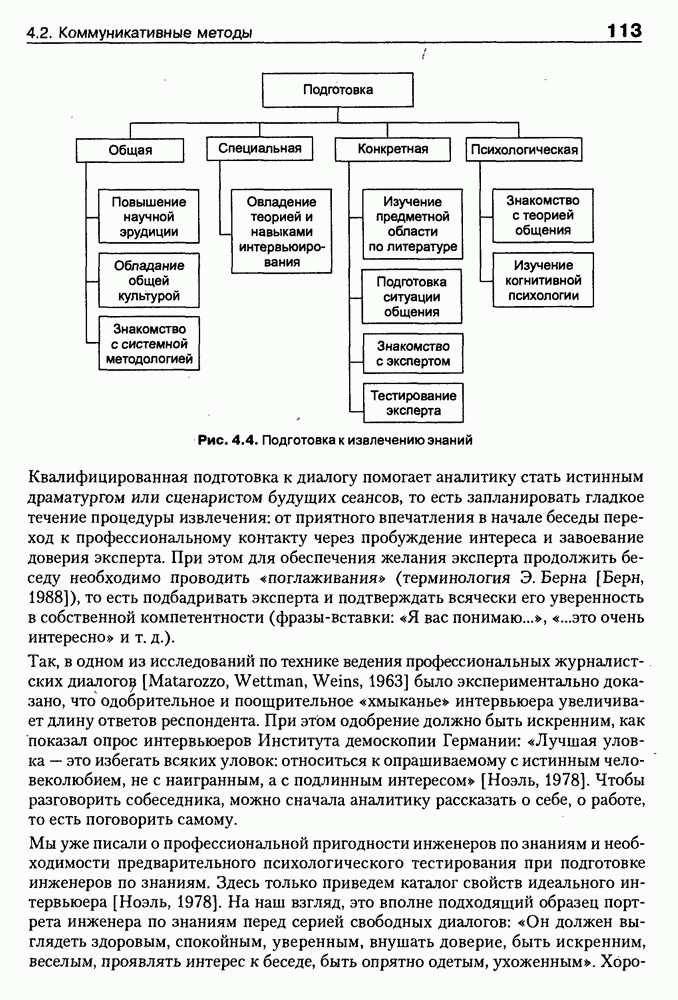
- 4.2. Коммуникативные методы
- 4.2.2. Активные индивидуальные методы
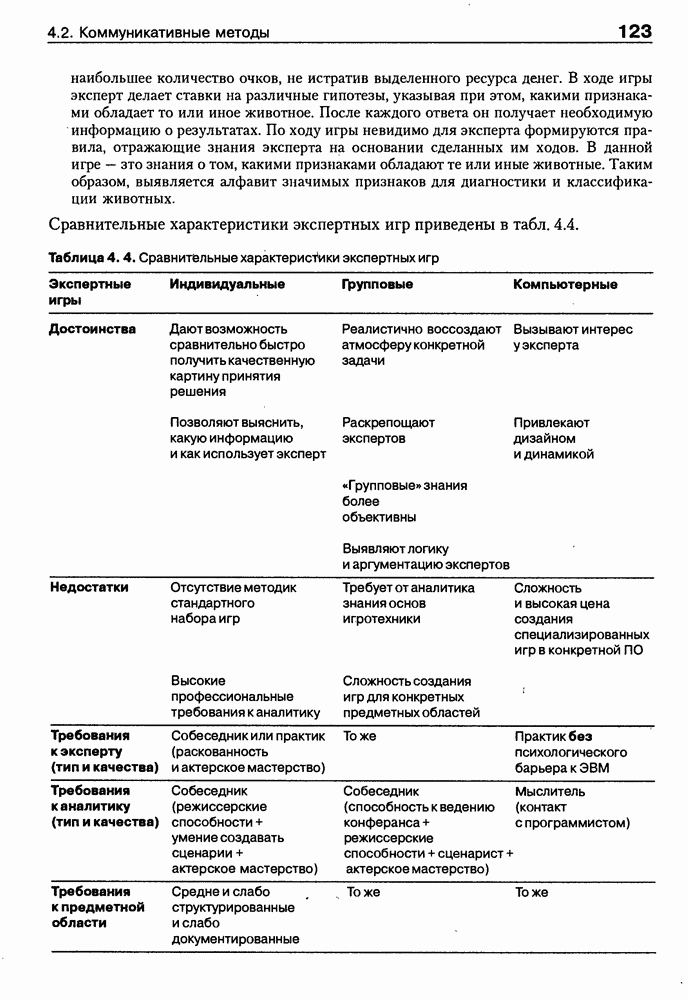
- 4.2.3. Активные групповые методы
- 4.3. Текстологические методы
- 4.4. Простейшие методы структурирования
- 4.4.2. Специальные методы структурирования
- 4.5. Состояние и перспективы автоматизированного приобретения знаний
- 4.5.2. Современное состояние автоматизированных систем приобретения знаний
- 4.6. Примеры методов и систем приобретения знаний
- 4.6.2. Имитация консультаций
- 4.6.3. Интегрированные среды приобретения знаний
- 4.6.4. Приобретение знаний из текстов
- 4.6.5. Инструментарий прямого приобретения знаний SIMER + MIR
- 5. Новые тенденции и прикладные аспекты инженерии знаний
- 5.1. Латентные структуры знаний и психосемантика
- 5.1.2. Методы многомерного шкалирования
- 5.1.3. Использование метафор для выявления «скрытых» структур знаний
- 5.2. Метод репертуарных решеток
- 5.2.2. Методы выявления конструктов
- 5.2.3. Анализ репертуарных решеток
- 5.2.4. Автоматизированные методы
- 5.3. Управление знаниями
- 5.3.2. Управление знаниям и корпоративная память
- 5.3.3. Системы OMIS
- 5.3.4. Особенности разработки OMIS
- 5.4. Визуальное проектирование баз знаний как инструмент познания
- 5.4.2. База знаний как познавательный инструмент
- 5.5. Проектирование гипермедиа БД и адаптивных обучающих систем
- 5.5.2. От мультимедиа к гипермедиа
- 5.5.3. На пути к адаптивным обучающим системам
- 6. Программный инструментарий разработки систем, основанных на знаниях
- 6.1. Технологии разработки программного обеспечения — цели, принципы, парадигмы
- 6.1.2. Модели процесса разработки ПО
- 6.1.3. Инструментальные средства поддержки разработки систем ПО
- 6.2. Методологии создания и модели жизненного цикла интеллектуальных систем
- 6.3. Языки программирования для ИИ и языки представления знаний
- 6.4. Инструментальные пакеты для ИИ
- 6.5. WorkBench-системы
- 7. Пример разработки системы, основанной на знаниях
- 7.1.2. Декларативное представление данных и знаний
- 7.1.3. Процедурные средства языка
- 7.2. Психодиагностика — пример предметной области для построения экспертных систем
- 7.2.2. Батарея психодиагностических ЭС «Ориентир»
- 7.3. Разработка и реализация психодиагностической ЭС «Cattell»
- 7.3.2. Общение с пользователем и опрос испытуемых
- 7.3.3. Вывод портретов и генерация их текстовых представлений
- 7.3.4. Помощь и объяснения в ЭС «Cattell»
- 8. Представление данных и знаний в Интернете
- 8.1.2. HTML — язык гипертекстовой разметки Интернет-документов
- 8.1.3. Возможности представления знаний на базе языка HTML
- 8.2. Онтологии и онтологические системы
- 8.2.2. Модели онтологии и онтологической системы
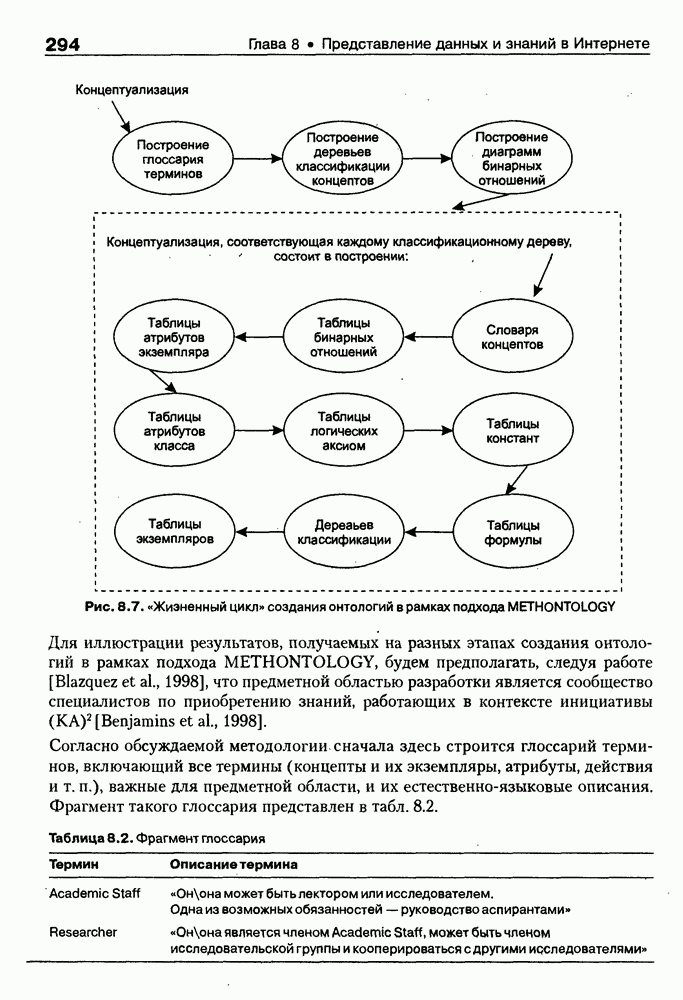
- 8.2.3. Методологии создания и «жизненный цикл» онтологий
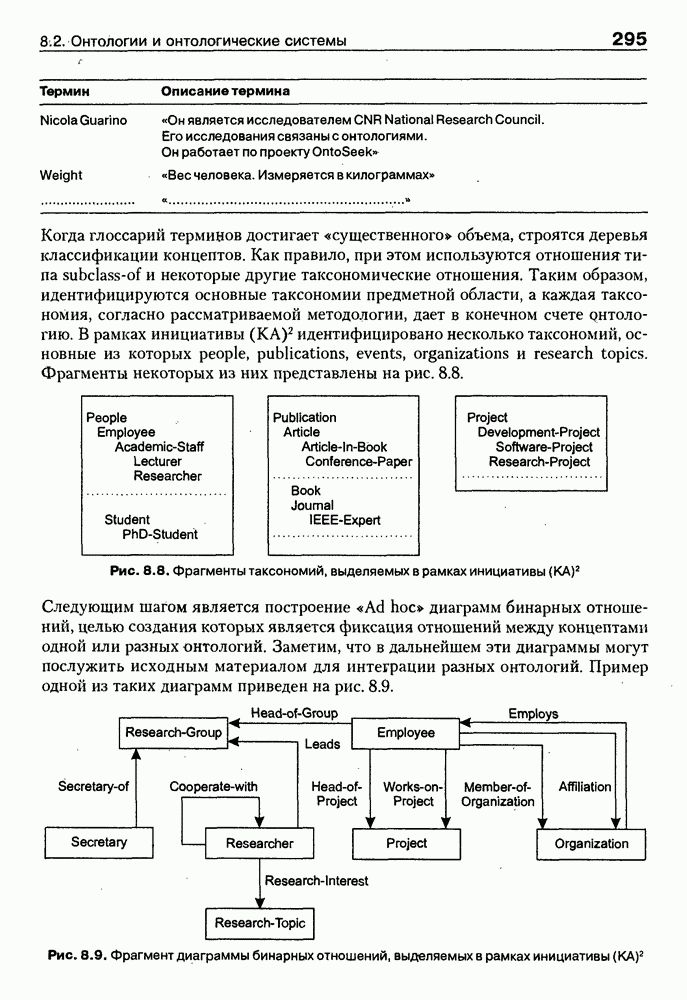
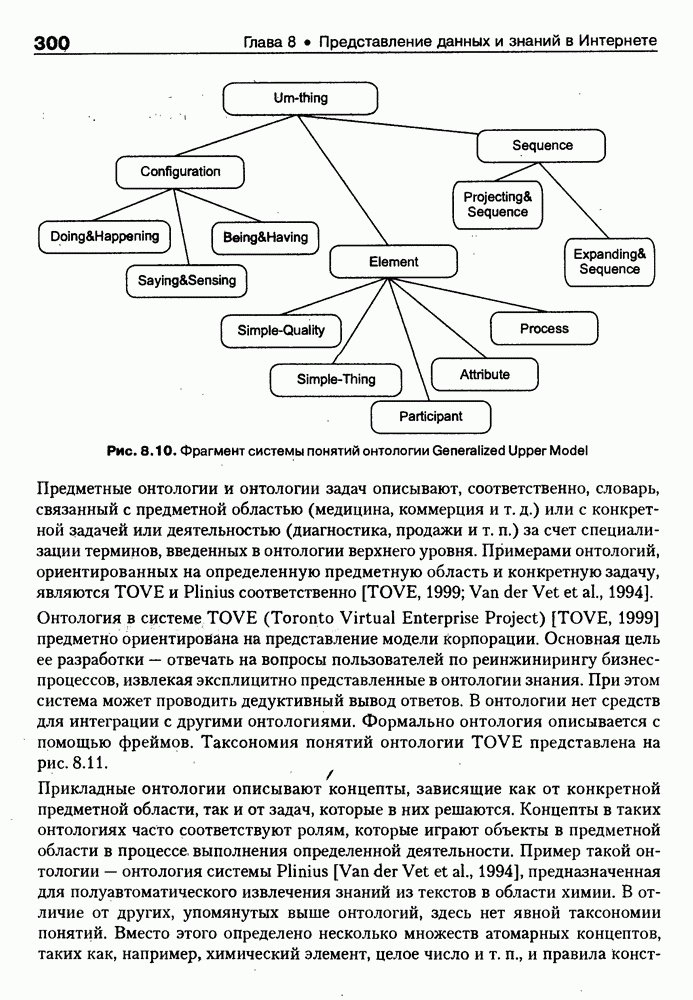
- 8.2.4. Примеры онтологий
- 8.3. Системы и средства представления онтологических знаний
- 8.3.2. Инициатива и инструментарий Ontobroker
- 8.3.3. Проект SHOE — спецификация онтологий и инструментарий
- 8.3.4. Другие подходы и тенденции
- 9. Интеллектуальные Интернет-технологии
- 9.1. Программные агенты и мультиагентные системы
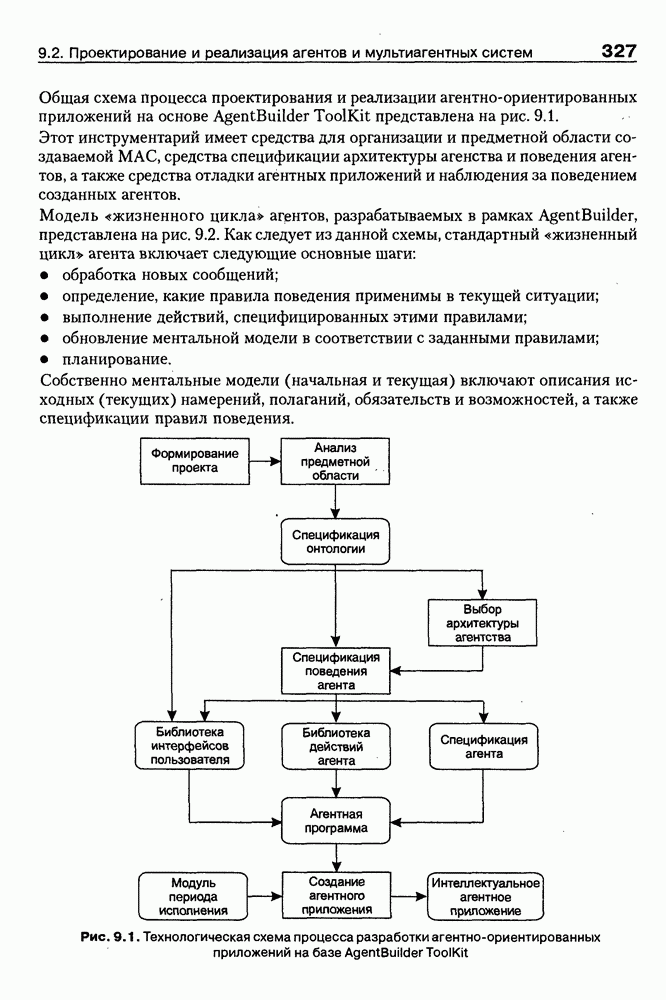
- 9.2. Проектирование и реализация агентов и мультиагентных систем
- 9.2.2. Инструментарий AgentBuilder
- 9.2.3. Система Bee-gent
- 9.3. Информационный поиск в среде Интернет
- 9.3.2. Неспециализированные и специализированные поисковые агенты
- 9.3.3. Системы интеллектуальных поисковых агентов
- Заключение
- Литература