| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
Ряд задач может быть решен с применением рекурсии. Вот один из примеров:
Для заданных трех чисел  соединить точки с координатами
соединить точки с координатами

 что в результате дает звезду. Последовательно (как часть задачи!) выполнить подобную работу еще пять раз, но теперь с другими тремя числами:
что в результате дает звезду. Последовательно (как часть задачи!) выполнить подобную работу еще пять раз, но теперь с другими тремя числами:

Выполнение задачи продолжается до тех пор, пока задаваемая величина  будет не меньше 0.1. Для начальной (или главной) задачи задаваемые числа будут равня
будет не меньше 0.1. Для начальной (или главной) задачи задаваемые числа будут равня  Как и ранее, будем использовать автоматическое масштабирование и размещение. Ниже приводится программа, решающая поставленную задачу.
Как и ранее, будем использовать автоматическое масштабирование и размещение. Ниже приводится программа, решающая поставленную задачу.
(см. скан)

Рис. 2.14. Результат работы программы STARS
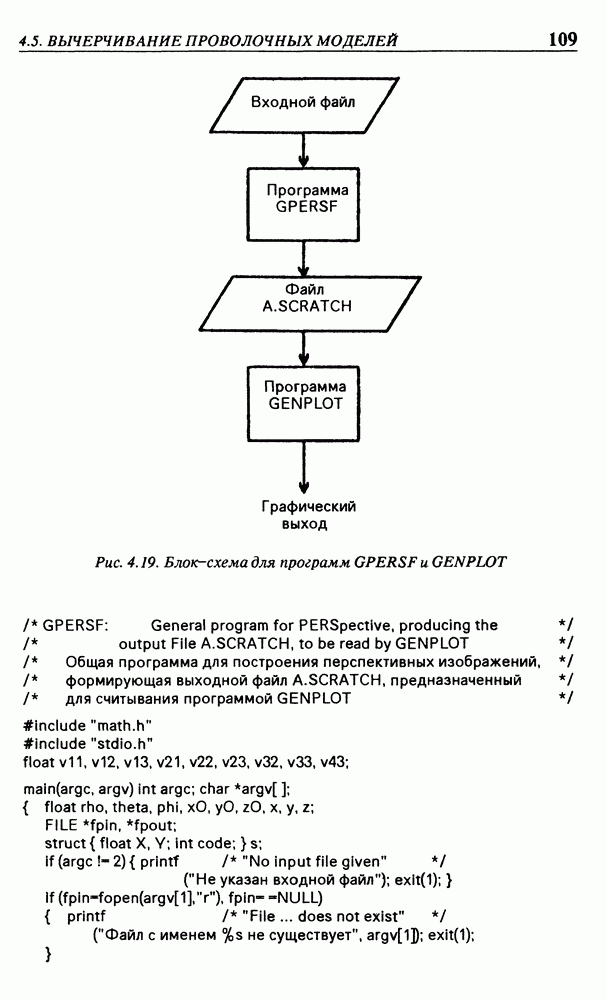
После этой программы должна быть вызвана программа GENPLOT, описанная в предыдущем параграфе, результат их совместной работы показан на рис. 2.14.
Следующим примером может быть известное “Пифагорово дерево”. Оно часто изображается так, как показано на рис. 2.15. Каждый из прямоугольных треугольников в этом дереве имеет внутренний угол, равный 45°. Опять воспользуемся генератором случайных чисел для создания более общей программы, которая может сформировать не только рис. 2.15, но также генерировать и менее регулярные деревья. Углы, задаваемые равными 45° для рис. 2.15, в общем случае будут задаваться случайным образом в пределах между  где значение
где значение  задается в качестве входного параметра вместе с параметром
задается в качестве входного параметра вместе с параметром  определяющим глубину рекурсии. Регулярная версия, изображенная на рис. 2.15, получается при задании
определяющим глубину рекурсии. Регулярная версия, изображенная на рис. 2.15, получается при задании  в 7. На рисунке параметр
в 7. На рисунке параметр  определяет количество треугольников на
определяет количество треугольников на
пути от корня до листьев дерева. Сердцевиной программы будет рекурсивная функция square jmdjriangle (“квадрат и треугольник”) с параметром  определяющим глубину рекурсии, в качестве первого аргумента. Если значение параметра
определяющим глубину рекурсии, в качестве первого аргумента. Если значение параметра  больше нуля, то задачей функции square jmdjriangle, как это определяется названием, будет вычертить квадрат и над ним треугольник, а затем еще дважды обратиться к самой себе с соответствующими новыми аргументами, первый из которых задается равным
больше нуля, то задачей функции square jmdjriangle, как это определяется названием, будет вычертить квадрат и над ним треугольник, а затем еще дважды обратиться к самой себе с соответствующими новыми аргументами, первый из которых задается равным  Размер и положение квадрата полностью определяются четырьмя параметрами:
Размер и положение квадрата полностью определяются четырьмя параметрами:  рис. 2.16). Для вычерчивания треугольника необходимо знать угол а. Этот угол, выраженный в градусах, равен
рис. 2.16). Для вычерчивания треугольника необходимо знать угол а. Этот угол, выраженный в градусах, равен  где deviation равно одному из целых чисел ряда
где deviation равно одному из целых чисел ряда  выбираемому случайным образом, как это делалось в параграфе 2.6.
выбираемому случайным образом, как это делалось в параграфе 2.6.
На рис. 2.16 необходимые точки пронумерованы последовательными числами 0, 1,2, 3, 4. Координаты  точки О задаются в обращении к функции. Для вычисления остальных точек вначале рассмотрим более простую ситуацию при
точки О задаются в обращении к функции. Для вычисления остальных точек вначале рассмотрим более простую ситуацию при  то есть когда сторона 0 1 квадрата занимает горизонтальное положение.
то есть когда сторона 0 1 квадрата занимает горизонтальное положение.

Рис. 2.15. “Пифагорово дерево”, регулярная версия

Рис. 2.16. Нумерация точек
В этом положении координаты точек определить очень просто. Они записываются в массивах х и у. Затем вся конструкция поворачивается вокруг точки О на угол  таким же образом, как это выполнялось в параграфе 2.3. Результат поворота записывается в массивах
таким же образом, как это выполнялось в параграфе 2.3. Результат поворота записывается в массивах 
(см. скан)
(см. скан)
Эта программа формирует файл  который должен быть обработан программой GENPLOT из параграфа 2.5. Графический результат работы программы для
который должен быть обработан программой GENPLOT из параграфа 2.5. Графический результат работы программы для  показан на рис. 2.17.
показан на рис. 2.17.

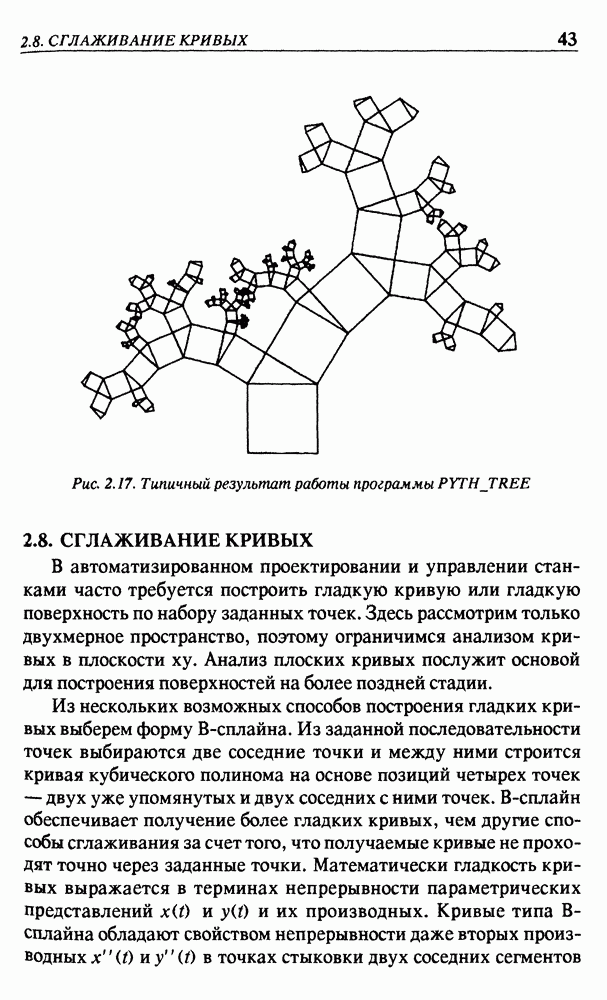
Рис. 2.17. Типичный результат работы программы PYTHTREE
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
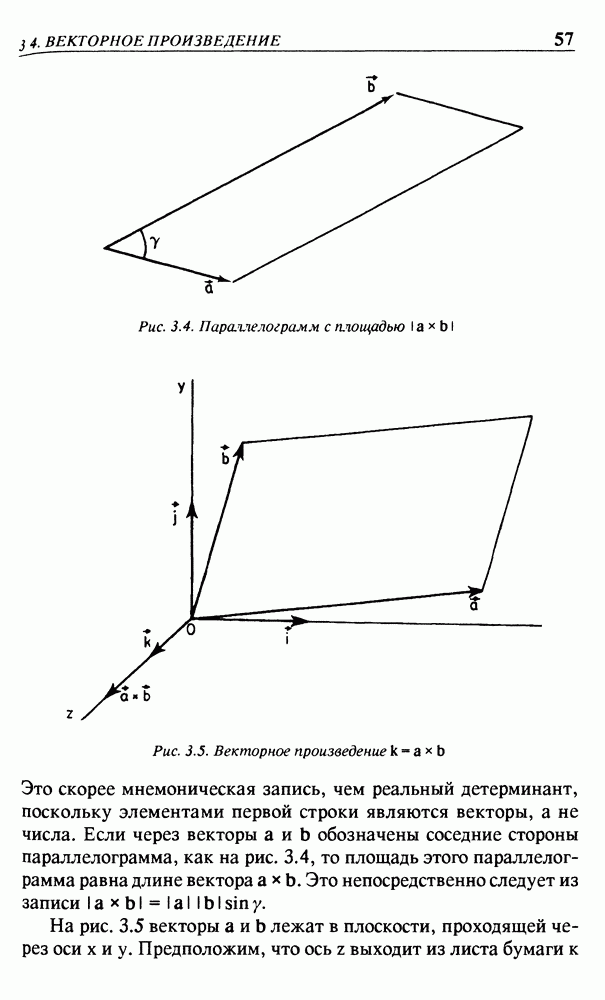
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
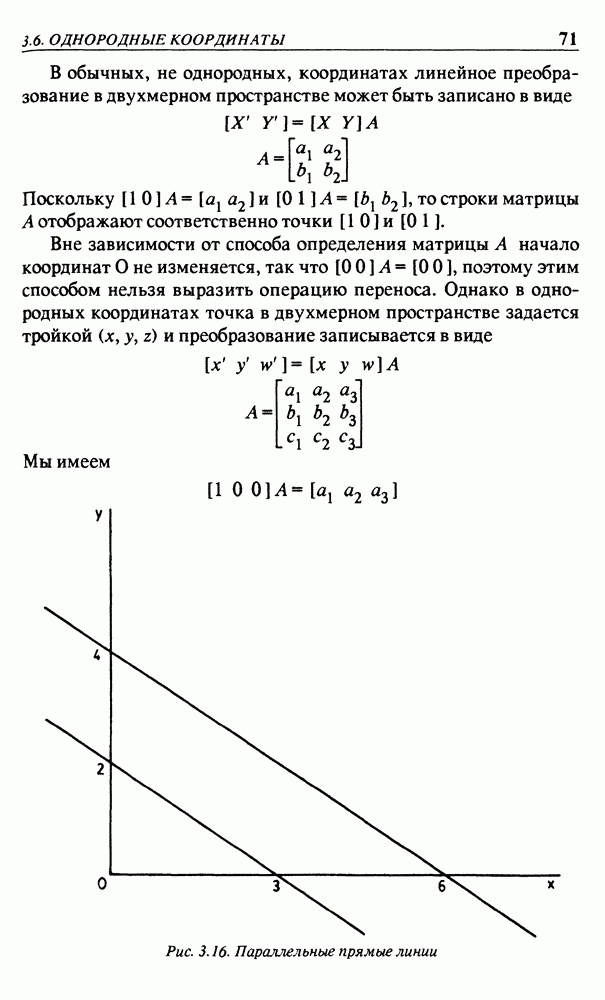
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
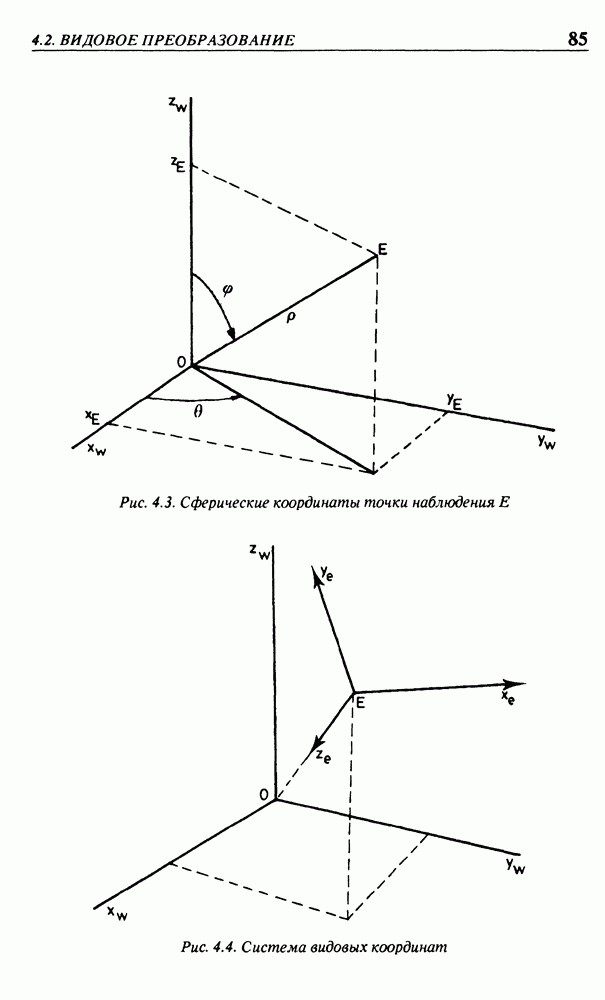
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
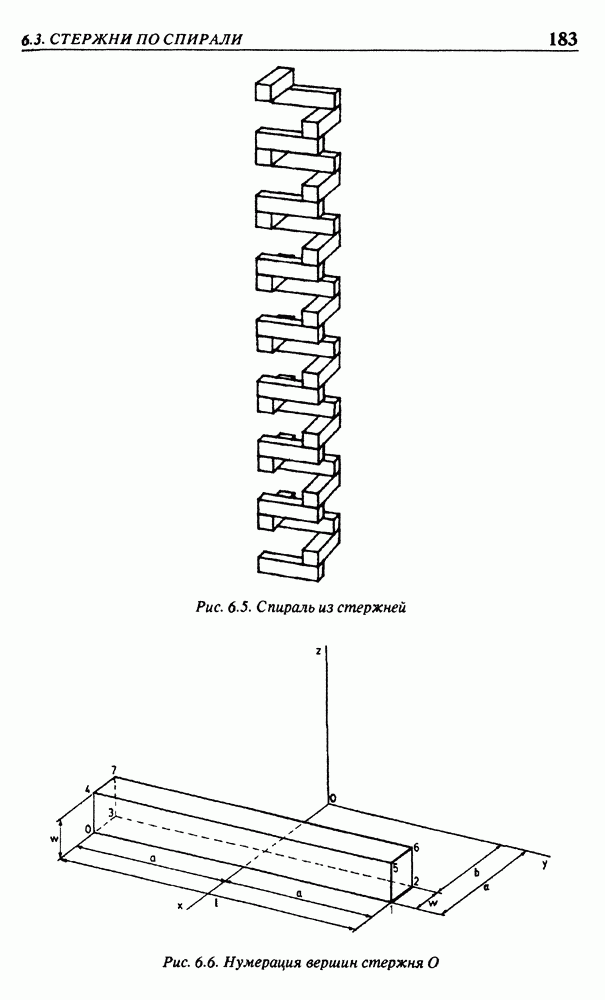
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
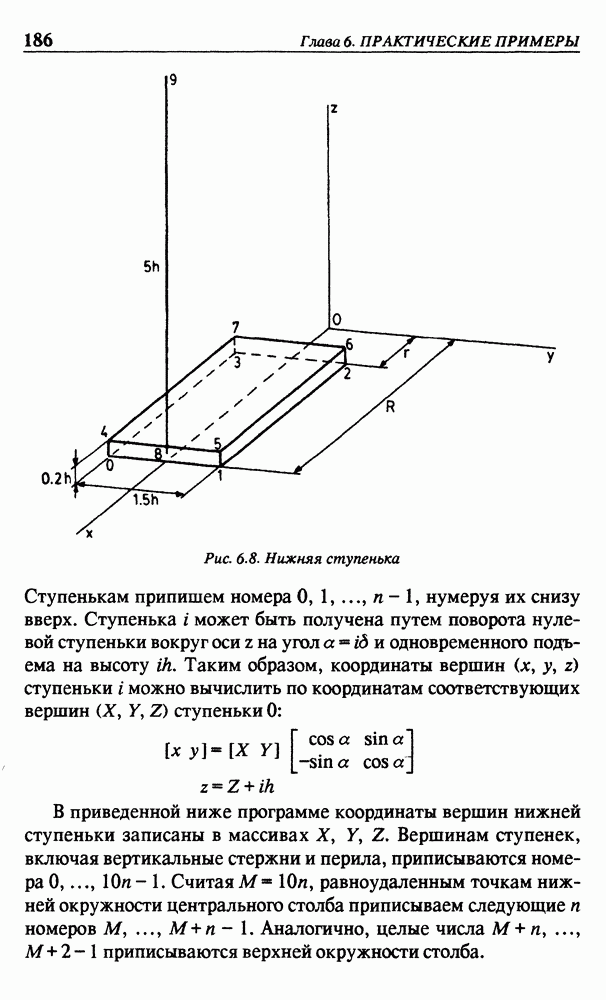
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
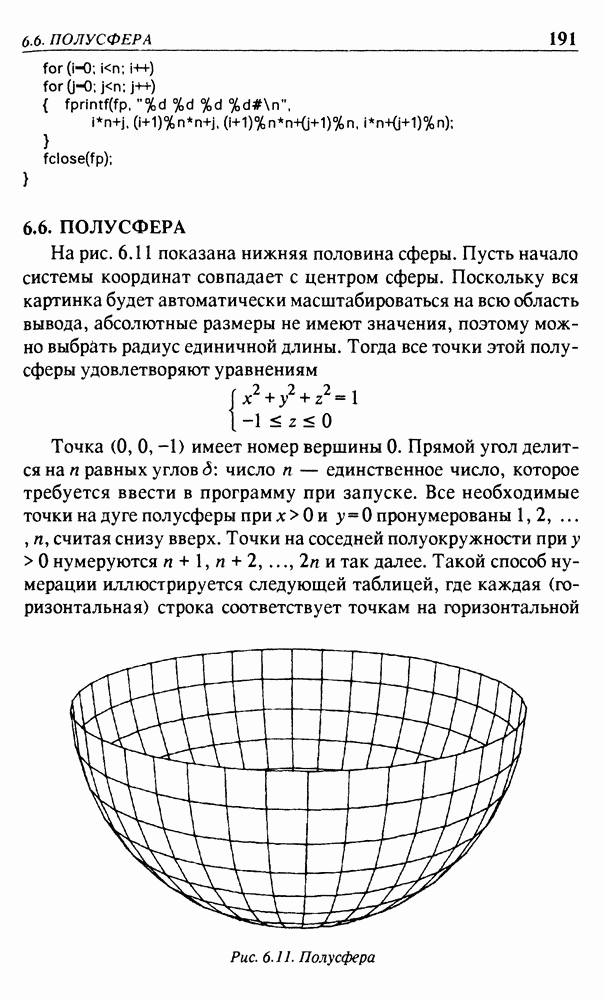
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА