| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
Улучшим теперь программу HIDLIN из параграфа 5.3 с целью повышения удобства для пользователя и увеличения эффективности. Дадим возможность пользователю определить грани объекта в виде полигонов, а программа сама будет

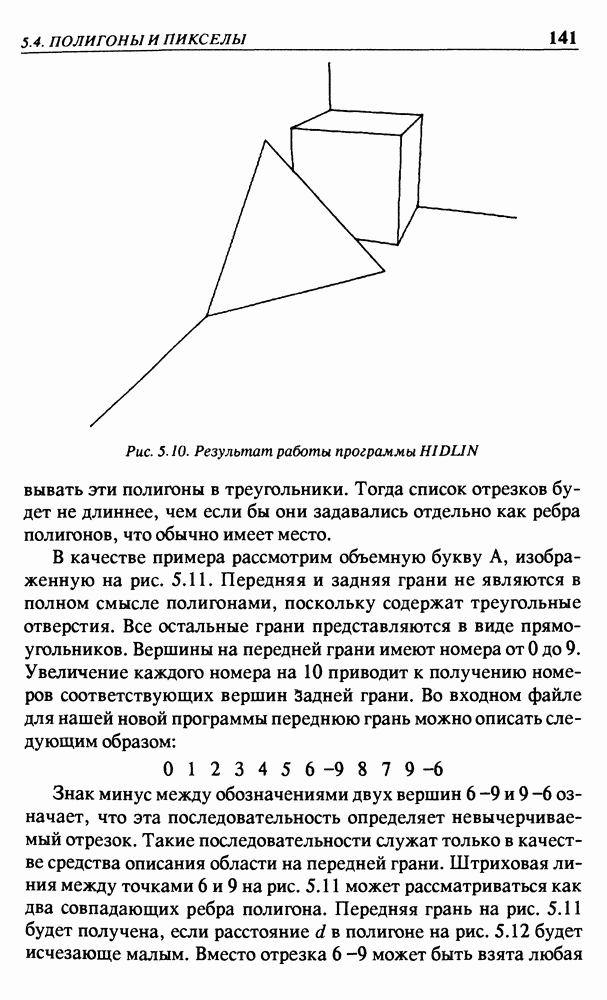
Рис. 5.10. Результат работы программы HIDUN
преобразовывать эти полигоны в треугольники. Тогда список отрезков будет не длиннее, чем если бы они задавались отдельно как ребра полигонов, что обычно имеет место.
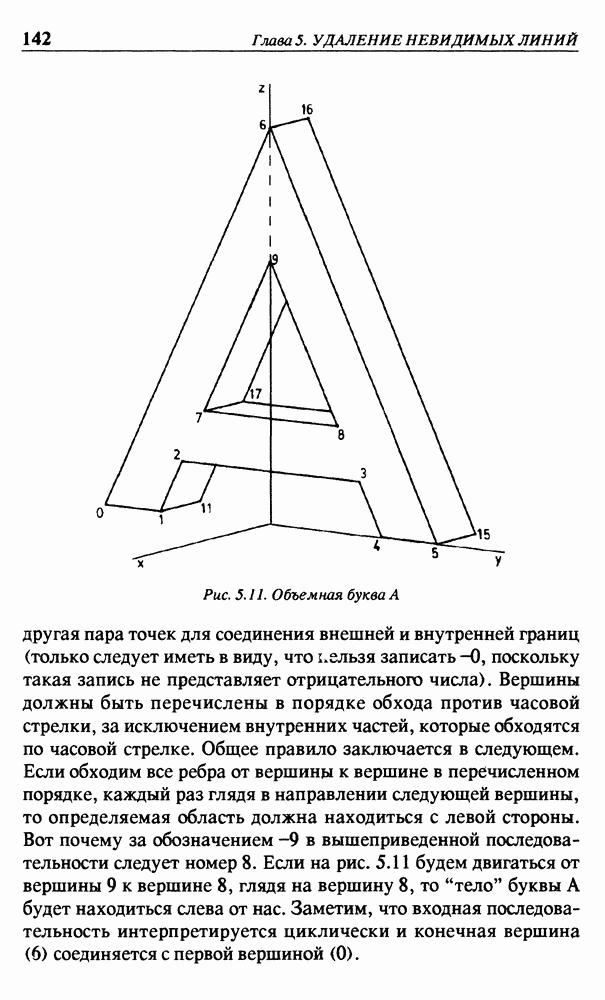
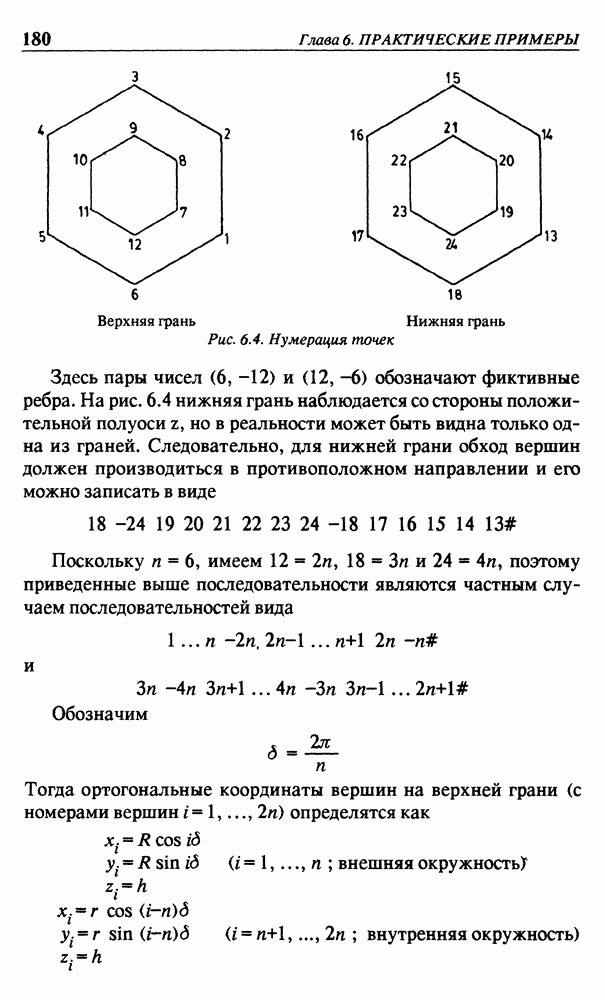
В качестве примера рассмотрим объемную букву А, изображенную на рис. 5.11. Передняя и задняя грани не являются в полном смысле полигонами, поскольку содержат треугольные отверстия. Все остальные грани представляются в виде прямоугольников. Вершины на передней грани имеют номера от 0 до 9. Увеличение каждого номера на 10 приводит к получению номеров соответствующих вершин Задней грани. Во входном файле для нашей новой программы переднюю грань можно описать следующим образом:

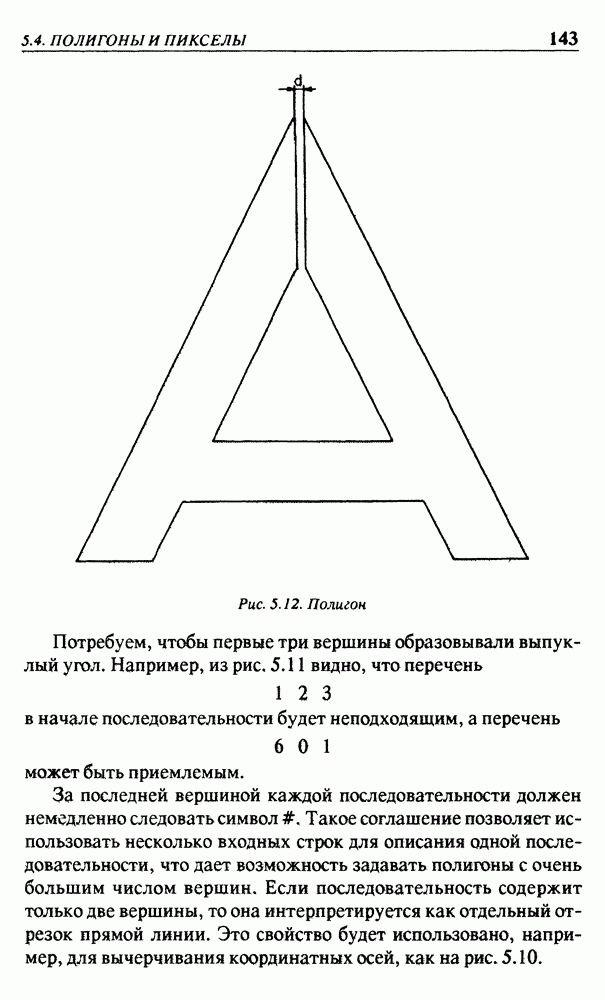
Знак минус между обозначениями двух вершин 6 -9 и 9 -6 означает, что эта последовательность определяет невычерчиваемый отрезок. Такие последовательности служат только в качестве средства описания области на передней грани. Штриховая линия между точками 6 и 9 на рис. 5.11 может рассматриваться как два совпадающих ребра полигона. Передняя грань на рис. 5.11 будет получена, если расстояние  в полигоне на рис. 5.12 будет исчезающе малым. Вместо отрезка 6 -9 может быть взята любая
в полигоне на рис. 5.12 будет исчезающе малым. Вместо отрезка 6 -9 может быть взята любая

Рис. 5.11. Объемная буква А
другая пара точек для соединения внешней и внутренней границ (только следует иметь в виду, что нельзя записать -0, поскольку такая запись не представляет отрицательного числа). Вершины должны быть перечислены в порядке обхода против часовой стрелки, за исключением внутренних частей, которые обходятся по часовой стрелке. Общее правило заключается в следующем. Если обходим все ребра от вершины к вершине в перечисленном порядке, каждый раз глядя в направлении следующей вершины, то определяемая область должна находиться с левой стороны. Вот почему за обозначением -9 в вышеприведенной последовательности следует номер 8. Если на рис. 5.11 будем двигаться от вершины 9 к вершине 8, глядя на вершину 8, то “тело” буквы А будет находиться слева от нас. Заметим, что входная последовательность интерпретируется циклически и конечная вершина (6) соединяется с первой вершиной (0).

Рис. 5.12. Полигон
Потребуем, чтобы первые три вершины образовывали выпуклый угол. Например, из рис, 5.11 видно, что перечень

в начале последовательности будет неподходящим, а перечень

может быть приемлемым.
За последней вершиной каждой последовательности должен немедленно следовать символ Такое соглашение позволяет использовать несколько входных строк для описания одной последовательности, что дает возможность задавать полигоны с очень большим числом вершин. Если последовательность содержит только две вершины, то она интерпретируется как отдельный отрезок прямой линии. Это свойство будет использовано, например, для вычерчивания координатных осей, как на рис. 5.10.
Как и ранее, файл начинается с координат

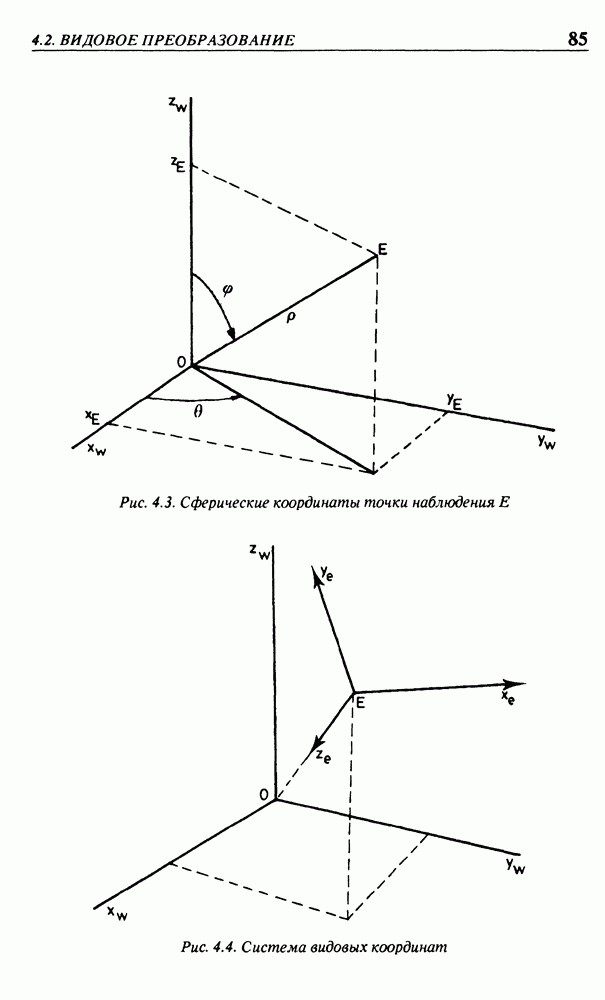
центральной точки О, которая будет использована в качестве нового начала системы координат. Также потребуются сферические  точки наблюдения Е относительно точки О (рис. 4.3), но вместо считывания их из файла программа запросит пользователя ввести эти три числа. Таким образом, программу можно будет запускать на выполнение несколько раз с различными точками наблюдения без изменения файла. Прямая линия
точки наблюдения Е относительно точки О (рис. 4.3), но вместо считывания их из файла программа запросит пользователя ввести эти три числа. Таким образом, программу можно будет запускать на выполнение несколько раз с различными точками наблюдения без изменения файла. Прямая линия  определяет направление наблюдения. Номер каждой вершины и ее координаты х, у, z опять считываются из файла. Затем перечисляются номера вершин, определяющих грани, как было описано ранее. Помните, что для определения направления обхода по часовой стрелке на грань следует смотреть снаружи объекта. Примем соглашение, что комментарии могут появляться в любом месте вне перечня чисел и все комментарии заключаются в скобки, они не должны быть вложенными. Для определения начала последней части входных данных указывается слово Faces (“грани”). Фактически проверяется только первая буква (прописная
определяет направление наблюдения. Номер каждой вершины и ее координаты х, у, z опять считываются из файла. Затем перечисляются номера вершин, определяющих грани, как было описано ранее. Помните, что для определения направления обхода по часовой стрелке на грань следует смотреть снаружи объекта. Примем соглашение, что комментарии могут появляться в любом месте вне перечня чисел и все комментарии заключаются в скобки, они не должны быть вложенными. Для определения начала последней части входных данных указывается слово Faces (“грани”). Фактически проверяется только первая буква (прописная  а остальные пропускаются, поэтому подойдет и слово
а остальные пропускаются, поэтому подойдет и слово  Полный список входных данных для вычерчивания буквы А (рис. 5.11) приведен ниже:
Полный список входных данных для вычерчивания буквы А (рис. 5.11) приведен ниже:

(см. скан)
Программа, которую предстоит разработать, будет гораздо удобнее программы HIDLIN из параграфа 5.3, поскольку вместо треугольника и отрезков прямых теперь можно будет задавать грани объекта со сложной формой. Однако это не единственное усовершенствование. В программе HIDLIN мы имели набор треугольников. Видимость каждого отрезка проверялась относительно каждого треугольника. Поэтому при повышении сложности объекта, например, оба списка удлиняются в два раза, затраты вычислительного времени возрастают в четыре раза. Будем говорить, что программа HIDLIN имеет квадратичную сложно  по затратам времени.
по затратам времени.
Для сложных объектов наша новая программа будет работать значительно быстрее программы HIDLIN. Как и ранее, будем иметь набор отрезков и набор треугольников, но видимость каждого данного отрезка теперь будет проверяться только относительно части набора треугольников. Например, отрезок  лежащий в левой верхней части экрана, не будет проверяться относительно треугольника ABC в правой нижней части экрана. Для реализации этого алгоритма разделим экран на Nscreen х Nscreen равных прямоугольников, где
лежащий в левой верхней части экрана, не будет проверяться относительно треугольника ABC в правой нижней части экрана. Для реализации этого алгоритма разделим экран на Nscreen х Nscreen равных прямоугольников, где  некоторое положительное целое число. Для рис. 5.13 выбрано
некоторое положительное целое число. Для рис. 5.13 выбрано 

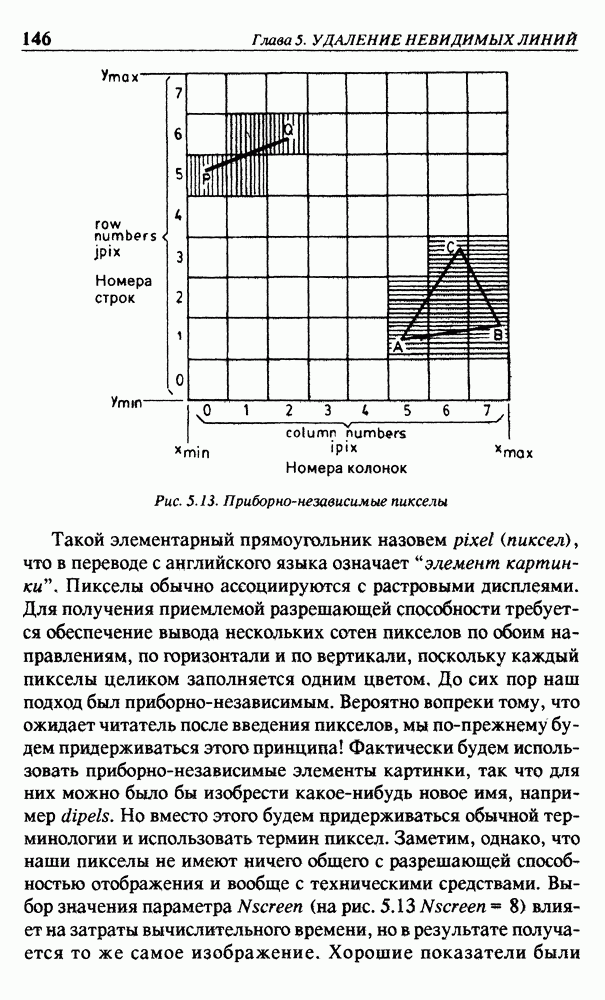
Рис. 5.13. Приборно-независимые пикселы
Такой элементарный прямоугольник назовем  (пиксел), что в переводе с английского языка означает “элемент картинки. Пикселы обычно ассоциируются с растровыми дисплеями. Для получения приемлемой разрешающей способности требуется обеспечение вывода нескольких сотен пикселов по обоим направлениям, по горизонтали и по вертикали, поскольку каждый пикселы целиком заполняется одним цветом. До сих пор наш подход был приборно-независимым. Вероятно вопреки тому, что ожидает читатель после введения пикселов, мы по-прежнему будем придерживаться этого принципа! Фактически будем использовать приборно-независимые элементы картинки, так что для них можно было бы изобрести какое-нибудь новое имя, например
(пиксел), что в переводе с английского языка означает “элемент картинки. Пикселы обычно ассоциируются с растровыми дисплеями. Для получения приемлемой разрешающей способности требуется обеспечение вывода нескольких сотен пикселов по обоим направлениям, по горизонтали и по вертикали, поскольку каждый пикселы целиком заполняется одним цветом. До сих пор наш подход был приборно-независимым. Вероятно вопреки тому, что ожидает читатель после введения пикселов, мы по-прежнему будем придерживаться этого принципа! Фактически будем использовать приборно-независимые элементы картинки, так что для них можно было бы изобрести какое-нибудь новое имя, например  Но вместо этого будем придерживаться обычной терминологии и использовать термин пиксел. Заметим, однако, что наши пикселы не имеют ничего общего с разрешающей способностью отображения и вообще с техническими средствами. Выбор значения параметра
Но вместо этого будем придерживаться обычной терминологии и использовать термин пиксел. Заметим, однако, что наши пикселы не имеют ничего общего с разрешающей способностью отображения и вообще с техническими средствами. Выбор значения параметра  (на рис. 5.13 Nscreen
(на рис. 5.13 Nscreen  ) влияет на затраты вычислительного времени, но в результате получается то же самое изображение. Хорошие показатели были
) влияет на затраты вычислительного времени, но в результате получается то же самое изображение. Хорошие показатели были
получены при  то есть при использовании 30 30 -900 пикселов.
то есть при использовании 30 30 -900 пикселов.
Повышение эффективности основано на идее формирования списков треугольников для каждого пиксела. Такой список пикселов содержит только те треугольники, которые частично или полностью покрывают пиксел. Треугольник ABC на рис. 5.13 будет занесен в списки только для заштрихованных пикселов из колонок 5, 6, 7. Как и в программе  будет существовать один общий массив
будет существовать один общий массив  элементами которого являются структуры, содержащие номера вершин А, В, С и коэффициенты
элементами которого являются структуры, содержащие номера вершин А, В, С и коэффициенты  из уравнения плоскости
из уравнения плоскости  Напомним, что видовые координаты вершины А записаны в элемент массива
Напомним, что видовые координаты вершины А записаны в элемент массива  и так далее. В зависимости от контекста термин “треугольник ABC” означает либо исходный треугольник в трехмерном пространстве, либо его проекцию на экран. Будем, например, говорить, что сторона треугольника
и так далее. В зависимости от контекста термин “треугольник ABC” означает либо исходный треугольник в трехмерном пространстве, либо его проекцию на экран. Будем, например, говорить, что сторона треугольника  на рис. 5.13 лежит в пикселных колонках 5, 6, 7. Это несколько упростит изложение, поскольку в противном случае пришлось бы говорить о центральной проекции
на рис. 5.13 лежит в пикселных колонках 5, 6, 7. Это несколько упростит изложение, поскольку в противном случае пришлось бы говорить о центральной проекции  исходной стороны треугольника
исходной стороны треугольника  В списках пикселов будут указываться только значения индексов
В списках пикселов будут указываться только значения индексов  обозначающих треугольники, необходимые параметры которых могут быть вызваны из
обозначающих треугольники, необходимые параметры которых могут быть вызваны из  Будем говорить, что треугольник, частично или полностью покрывающий пиксел, ассоциирован с этим пикселом.
Будем говорить, что треугольник, частично или полностью покрывающий пиксел, ассоциирован с этим пикселом.
После того, как будут сформированы все пикселные списки, можно начать вычерчивание отрезков прямых линий. Для каждого отрезка PQ начнем с построения наборов всех треугольников, ассоциированных с пикселами, содержащими точки отрезка  На рис. 5.13 такие пикселы заштрихованы в колонках 0, 1, 2. Затем отрезок PQ проверяется на видимость только относительно треугольников из этого набора. На первый взгляд кажется, что реализация такой простой идеи потребует очень большой дополнительной работы, так как, во-первых, все треугольники должны быть записаны в пикселных списках и, во-вторых, проверке на видимость каждого отрезка прямой линии должно предшествовать формирование набора треугольников, которые могут его закрыть. Но дополнительная работа для этих действий зависит только линейно от числа треугольников и отрезков. Поэтому для этого способа ожидается линейная зависимость сложности.
На рис. 5.13 такие пикселы заштрихованы в колонках 0, 1, 2. Затем отрезок PQ проверяется на видимость только относительно треугольников из этого набора. На первый взгляд кажется, что реализация такой простой идеи потребует очень большой дополнительной работы, так как, во-первых, все треугольники должны быть записаны в пикселных списках и, во-вторых, проверке на видимость каждого отрезка прямой линии должно предшествовать формирование набора треугольников, которые могут его закрыть. Но дополнительная работа для этих действий зависит только линейно от числа треугольников и отрезков. Поэтому для этого способа ожидается линейная зависимость сложности.
В параграфе 5.3 координаты области вывода вычислялись не программой  а постпроцессором
а постпроцессором  Последняя программа сначала определяет минимальные и максимальные значения координат (считываемых из файла
Последняя программа сначала определяет минимальные и максимальные значения координат (считываемых из файла  и затем использует их для вычисления коэффициента масштабирования
и затем использует их для вычисления коэффициента масштабирования  и параметров переноса
и параметров переноса  как было описано в параграфе 2.6. Сейчас предпочтительнее перенести эти действия в нашу новую программу HIDLINPX. В любом случае нам потребуются максимальные и минимальные значения координат, поскольку иначе нельзя будет ассоциировать точки на экране с пикселами. И будет напрасная трата времени, если эту работу выполнять дважды. Внутри программы будут использованы экранные координаты
как было описано в параграфе 2.6. Сейчас предпочтительнее перенести эти действия в нашу новую программу HIDLINPX. В любом случае нам потребуются максимальные и минимальные значения координат, поскольку иначе нельзя будет ассоциировать точки на экране с пикселами. И будет напрасная трата времени, если эту работу выполнять дважды. Внутри программы будут использованы экранные координаты  вычисленные путем “чистых” перспективных преобразований в соответствии с уравнениями (4.10) и (4.11), что означает размещение плоскости экрана на расстоянии 1 от точки наблюдения Е.
вычисленные путем “чистых” перспективных преобразований в соответствии с уравнениями (4.10) и (4.11), что означает размещение плоскости экрана на расстоянии 1 от точки наблюдения Е.
Экранные координаты всех точек объектов должны быть вычислены как можно раньше, чтобы обеспечить возможность вычисления их минимальных и максимальных значений  Полученные таким образом размеры проекции на экран не следует путать с областью вывода, в которую впоследствии будет отображаться картинка. Соответствие между размером проекции и областью вывода устанавливается по координатам границ области вывода
Полученные таким образом размеры проекции на экран не следует путать с областью вывода, в которую впоследствии будет отображаться картинка. Соответствие между размером проекции и областью вывода устанавливается по координатам границ области вывода  которые запрашиваются у пользователя во время выполнения программы. Приводимый ниже фрагмент программы тесно связан с материалом, изложенным в параграфе 2.6, и показывает, что фактически вычисляется:
которые запрашиваются у пользователя во время выполнения программы. Приводимый ниже фрагмент программы тесно связан с материалом, изложенным в параграфе 2.6, и показывает, что фактически вычисляется:
(см. скан)

Затем можно вычислить видовые координаты  на основании значений экранных координат
на основании значений экранных координат  следующим образом:
следующим образом:

Интересно сравнить эти две формулы с параграфом 4.3, где утверждалось, что коэффициент масштабирования есть просто расстояние  между точкой наблюдения Е и плоскостью, в которой можем представить область вывода. Экран и область вывода располагаются в двух параллельных плоскостях (обе перпендикулярны к направлению линии наблюдения
между точкой наблюдения Е и плоскостью, в которой можем представить область вывода. Экран и область вывода располагаются в двух параллельных плоскостях (обе перпендикулярны к направлению линии наблюдения  причем первая плоскость находится на расстоянии 1, а вторая — на расстоянии
причем первая плоскость находится на расстоянии 1, а вторая — на расстоянии  точки наблюдения Е.
точки наблюдения Е.
Координаты точек в области вывода будут использоваться только при вызовах действительных “команд черчения”, то есть в обращениях к функциям move и  Внутри программы будут применяться только экранные координаты, которые лежат в пределах вычисленных границ
Внутри программы будут применяться только экранные координаты, которые лежат в пределах вычисленных границ  И именно эта область будет разделена на
И именно эта область будет разделена на  пикселов. Обсудим теперь взаимосвязь между
пикселов. Обсудим теперь взаимосвязь между  номером столбца пикселов. Взаимосвязь между
номером столбца пикселов. Взаимосвязь между  и номером строки
и номером строки  будет аналогичной. Как видно из рис. 5.13, мы имеем
будет аналогичной. Как видно из рис. 5.13, мы имеем

Теоретически горизонтальный размер пиксела равен

(Скоро мы увидим, что практически полезно несколько скорректировать это уравнение.) Тогда число  получается путем усечения значения частного
получается путем усечения значения частного

до целого числа. Результат вычисления по этой формуле имеет неприятное следствие, которое заключается в том, что значение  соответствует
соответствует  а это превышает максимально допустимое значение
а это превышает максимально допустимое значение  Одним из решений мог
Одним из решений мог  бы быть расширение экрана на один столбец (и на одну строку), который использовался бы для точек столбца
бы быть расширение экрана на один столбец (и на одну строку), который использовался бы для точек столбца  (и строки
(и строки  По причине экономии такое решение не
По причине экономии такое решение не
рационально, и поэтому будем настаивать на применении только  столбцов пикселов с номерами от 0 до
столбцов пикселов с номерами от 0 до  Это легко получить путем небольшого увеличения значения параметра
Это легко получить путем небольшого увеличения значения параметра  Умножим его на величину
Умножим его на величину  где константе epsilon приписано небольшое положительное значение, скажем
где константе epsilon приписано небольшое положительное значение, скажем  Теперь, поскольку значения
Теперь, поскольку значения  уже определены, вычислим
уже определены, вычислим

Каждый раз при необходимости определить пиксел, ассоциированный с точкой ( , его позиция вычисляется операторами
, его позиция вычисляется операторами

Заметим, что отсечение дробной части в языке Си выполняется неявно при любом присвоении значения с плавающей точкой целочисленной переменной. Поэтому вполне достаточно объявить тип  для переменных
для переменных  и
и 
Может также потребоваться и обратная операция

Так будет найдено значение X, соответствующее левой границе колонки пикселов с номером  Экранные координаты
Экранные координаты  точки в центре пиксела
точки в центре пиксела  вычисляются операторами
вычисляются операторами

Посмотрим теперь, как можно использовать пикселы для хранения информации о треугольниках, с которыми они ассоциированы. Будем использовать линейный список узлов, а каждый узел содержит номер треугольника  и указатель на следующей узел, если он существует. Если нет, то поле указателя будет иметь значение
и указатель на следующей узел, если он существует. Если нет, то поле указателя будет иметь значение  Начальный указатель каждого списка помещен в двухмерный массив
Начальный указатель каждого списка помещен в двухмерный массив  Пиксел
Пиксел  соответствует элементу
соответствует элементу 
Ради эффективности некоторым из треугольников, ассоциированных с пикселом, будет дана специальная трактовка. К этим специальным треугольникам отнесем те, которые полностью покрывают пиксел. (Треугольник полностью покрывает пиксел, если он весь лежит внутри треугольника.) Для данного пиксела  все эти специальные треугольники могут быть
все эти специальные треугольники могут быть
проигнорированы, за исключением только одного, который расположен ближе всех к точке наблюдения! Здесь термины “близкий” и расстояние до треугольника” относятся к точке в трехмерном пространстве, в которой прямая линия, проходящая через точку Е и центр пиксела, пересекает плоскость треугольника. Если есть треугольники, полностью покрывающие пиксел, то номер, идентифицирующий ближний из них, также будет сохранен в массиве  вместе с расстоянием до этого треугольника. Поля для этих двух новых элементов называются
вместе с расстоянием до этого треугольника. Поля для этих двух новых элементов называются  и
и  На рис. 5.14 показан типичный набор треугольников, ассоциированных с пикселом. В процессе запоминания треугольников пиксел может иметь структуру данных, показанную на рис. 5.15. Только треугольники 18 и 23 покрывают пиксел полностью. Поскольку треугольник 18 является ближайшим к глазу, то его номер и расстояние до него записываются в элементы массива
На рис. 5.14 показан типичный набор треугольников, ассоциированных с пикселом. В процессе запоминания треугольников пиксел может иметь структуру данных, показанную на рис. 5.15. Только треугольники 18 и 23 покрывают пиксел полностью. Поскольку треугольник 18 является ближайшим к глазу, то его номер и расстояние до него записываются в элементы массива  Треугольники 3 и 5 не полностью закрывают пиксел, следовательно, расстояние до них не существенно на данном этапе. В процессе запоминания треугольников ближайший треугольник, с номером 18 в данном примере, записывается в линейный список не сразу, поскольку впоследствии может обнаружиться другой закрывающий треугольник, более близкий. Ближайший закрывающий треугольник добавляется в список в
Треугольники 3 и 5 не полностью закрывают пиксел, следовательно, расстояние до них не существенно на данном этапе. В процессе запоминания треугольников ближайший треугольник, с номером 18 в данном примере, записывается в линейный список не сразу, поскольку впоследствии может обнаружиться другой закрывающий треугольник, более близкий. Ближайший закрывающий треугольник добавляется в список в

Рис. 5-14. Пиксел и ассоциированные треугольники

Рис. 5.15. Структура данных для пиксела
самом конце процесса. После окончания этого процесса список для каждого пиксела будет содержать все треугольники, ассоциированные с пикселом.
Теперь нужно разобраться с другой интересной проблемой программирования. Для данного треугольника ABC с экранными координатами вершин  и
и  необходимо найти, какой пиксел с ним ассоциирован и какие из них, если есть таковые, полностью покрываются этим треугольником. Эта проблема совсем не тривиальная, поскольку необходимо рассмотреть очень много ситуаций. Первая из подзадач заключается в поиске одной стороны треугольника, являющейся его границей сверху или снизу. Припишем номера 0,1,2 сторонам треугольника
необходимо найти, какой пиксел с ним ассоциирован и какие из них, если есть таковые, полностью покрываются этим треугольником. Эта проблема совсем не тривиальная, поскольку необходимо рассмотреть очень много ситуаций. Первая из подзадач заключается в поиске одной стороны треугольника, являющейся его границей сверху или снизу. Припишем номера 0,1,2 сторонам треугольника  соответственно, как показано на рис. 5.16. Здесь получилось так, что сторона 0 расположена сверху, а стороны 1 и 2 — снизу. Нам нужно закодировать эту ситуацию и занести соответствующие коды в массив
соответственно, как показано на рис. 5.16. Здесь получилось так, что сторона 0 расположена сверху, а стороны 1 и 2 — снизу. Нам нужно закодировать эту ситуацию и занести соответствующие коды в массив  содержащий три элемента
содержащий три элемента

то есть 1 и 0 являются кодами для положения сверху и снизу, соответственно. Для аналитического определения этих значений используем точку, лежащую далеко внизу. Обозначим экранные координаты точки V как  где, например,
где, например,  Тогда
Тогда  если, и только если, обе точки
если, и только если, обе точки  лежат по одну сторону от прямой линии А. Последнее утверждение легко проверить путем подстановки координат точек
лежат по одну сторону от прямой линии А. Последнее утверждение легко проверить путем подстановки координат точек  в левую часть уравнения, описывающего прямую
в левую часть уравнения, описывающего прямую 


Рис. 5.16. Нумерация сторон
Если точки  дают одинаковые знаки при такой подстановке, то они находятся по одну и ту же сторону от прямой А, а это означает, что данная сторона находится сверху. Запись на языке Си получается очень краткая:
дают одинаковые знаки при такой подстановке, то они находятся по одну и ту же сторону от прямой А, а это означает, что данная сторона находится сверху. Запись на языке Си получается очень краткая:

где через  и
и  обозначены детерминанты
обозначены детерминанты

Аналогично вычисляются детерминанты

после чего получаем остальные элементы массива

Следующим шагом будет определение координат концевых точек слева  и справа
и справа  для каждой из сторон
для каждой из сторон  Так, для рис. 5.16 будем иметь
Так, для рис. 5.16 будем иметь  и так далее.
и так далее.
Найдем номера  и
и  колонок пикселов, в которых расположены самые крайние левая и правая вершины треугольника
колонок пикселов, в которых расположены самые крайние левая и правая вершины треугольника  После этого для треугольника ABC можно скорректировать список пикселов, ограничив
После этого для треугольника ABC можно скорректировать список пикселов, ограничив  только пикселами в диапазоне номеров столбцов от
только пикселами в диапазоне номеров столбцов от  до
до  Для каждого столбца
Для каждого столбца  в этом диапазоне введем границы по строкам
в этом диапазоне введем границы по строкам  Все пикселы в диапазоне
Все пикселы в диапазоне  ассоциируются с треугольником. Этот диапазон включает (возможно пустой) поддиапазон
ассоциируются с треугольником. Этот диапазон включает (возможно пустой) поддиапазон  Все пикселы в этом поддиапазоне полностью покрываются треугольником. На рис. 5.17 показана сторона с номером 1 треугольника
Все пикселы в этом поддиапазоне полностью покрываются треугольником. На рис. 5.17 показана сторона с номером 1 треугольника  Предположим, что эта сторона — нижняя граница, то есть для нее
Предположим, что эта сторона — нижняя граница, то есть для нее  тогда эта сторона треугольника позволит определить значения
тогда эта сторона треугольника позволит определить значения  для значений
для значений  в диапазоне
в диапазоне  где целые числа
где целые числа  и
и  получаются в результате усечения частного при вычислении
получаются в результате усечения частного при вычислении

Вычислим наклон сторон треугольника

(В отличие от двух предыдущих вычислений здесь отсечения не будет, поскольку переменная slope имеет тип переменной с плавающей точкой.) Предположим, что при последовательных вычислениях от столбца  до столбца
до столбца  рассматривается столбец
рассматривается столбец  Определим номер строки
Определим номер строки  для точки I на рис.
для точки I на рис.

Рис. 5.17. Сторона треугольника и столбцы пикселов
5.17, в которой сторона треугольника пересекает границу между столбцами пикселов  и
и  Этот номер строки можно найти по значениям экранных координат
Этот номер строки можно найти по значениям экранных координат  точки пересечения I:
точки пересечения I:

Пусть  будет старое значение
будет старое значение  вычисленное для столбца с номером
вычисленное для столбца с номером  Тоща имеем
Тоща имеем

где функция  определяет минимальное значение одного из двух аргументов, а функция
определяет минимальное значение одного из двух аргументов, а функция  максимальное значение. На рис. 5.17 имеем
максимальное значение. На рис. 5.17 имеем  Для столбца пикселов
Для столбца пикселов  припишем усеченное частное от деления
припишем усеченное частное от деления  а если это номер строки для крайней левой конечной точки, то
а если это номер строки для крайней левой конечной точки, то  Аналогично усеченный номер строки
Аналогично усеченный номер строки  самой правой конечной точки берется в столбце на самом краю справа,
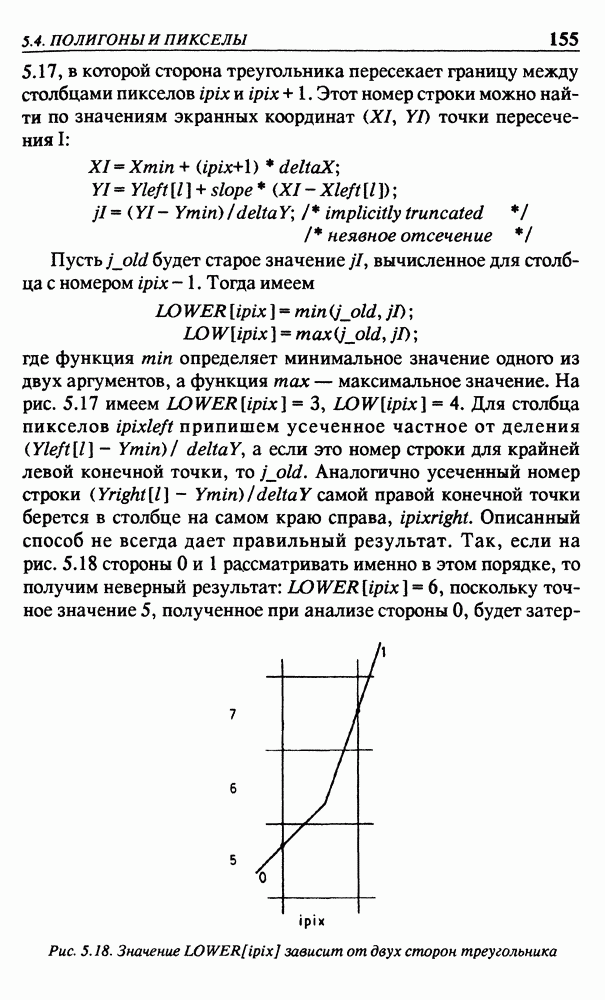
самой правой конечной точки берется в столбце на самом краю справа,  Описанный способ не всегда дает правильный результат. Так, если на рис. 5.18 стороны 0 и 1 рассматривать именно в этом порядке, то получим неверный результат:
Описанный способ не всегда дает правильный результат. Так, если на рис. 5.18 стороны 0 и 1 рассматривать именно в этом порядке, то получим неверный результат:  поскольку точное значение 5, полученное при анализе стороны 0, будет
поскольку точное значение 5, полученное при анализе стороны 0, будет

Рис. 5.18. Значение  зависит от двух сторон треугольника
зависит от двух сторон треугольника
затерто результатом анализа стороны 1. Поэтому вначале присвоим всем элементам массива  очень большие значения и разрешим только уменьшать их. Также всем элементам массива
очень большие значения и разрешим только уменьшать их. Также всем элементам массива  должны быть присвоены очень маленькие значения, которые затем можно только увеличивать. Значения массивов
должны быть присвоены очень маленькие значения, которые затем можно только увеличивать. Значения массивов  и
и  определяются аналогично.
определяются аналогично.
Теперь для треугольника ABC (данные для которого зафиксированы в массиве  определены диапазоны столбцов
определены диапазоны столбцов  и элементы массивов
и элементы массивов  поэтому можно скорректировать матрицу
поэтому можно скорректировать матрицу  и линейный список. Если диапазон номеров пикселов в столбце
и линейный список. Если диапазон номеров пикселов в столбце 

не пуст и  определяет номер строки в этом диапазоне, то пиксел
определяет номер строки в этом диапазоне, то пиксел  полностью закрывается треугольником
полностью закрывается треугольником  Затем исследуем точку
Затем исследуем точку  в которой прямая линия, проходящая через точку наблюдения Е и центр
в которой прямая линия, проходящая через точку наблюдения Е и центр  пиксела, пересекает треугольник ABC (см. рис. 5.19). Напомним, что плоскость ABC расположена на расстоянии
пиксела, пересекает треугольник ABC (см. рис. 5.19). Напомним, что плоскость ABC расположена на расстоянии  от точки Е и имеет вектор нормали
от точки Е и имеет вектор нормали  . Числа
. Числа  хранятся в массиве
хранятся в массиве  Компонента вектора
Компонента вектора  в направлении вектора нормали
в направлении вектора нормали  равна
равна  Следовательно, длина вектора
Следовательно, длина вектора  может быть вычислена из скалярного произведения
может быть вычислена из скалярного произведения


Рис. 5.19. Расстояния в треугольнике
Поскольку треугольники  и
и  подобны, то имеем
подобны, то имеем

Следовательно,

В поля  всех элементов матрицы
всех элементов матрицы  первоначально записаны значения -1, а всем полям
первоначально записаны значения -1, а всем полям  присвоены начальные значения
присвоены начальные значения  Для каждого пиксела
Для каждого пиксела  который полностью покрывается треугольником у, эти два поля изменяются, если значение
который полностью покрывается треугольником у, эти два поля изменяются, если значение  будет меньше записанного в
будет меньше записанного в  . В этом случае новое расстояние до треугольника
. В этом случае новое расстояние до треугольника  записывается в поле
записывается в поле  а значение у — в поле
а значение у — в поле 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
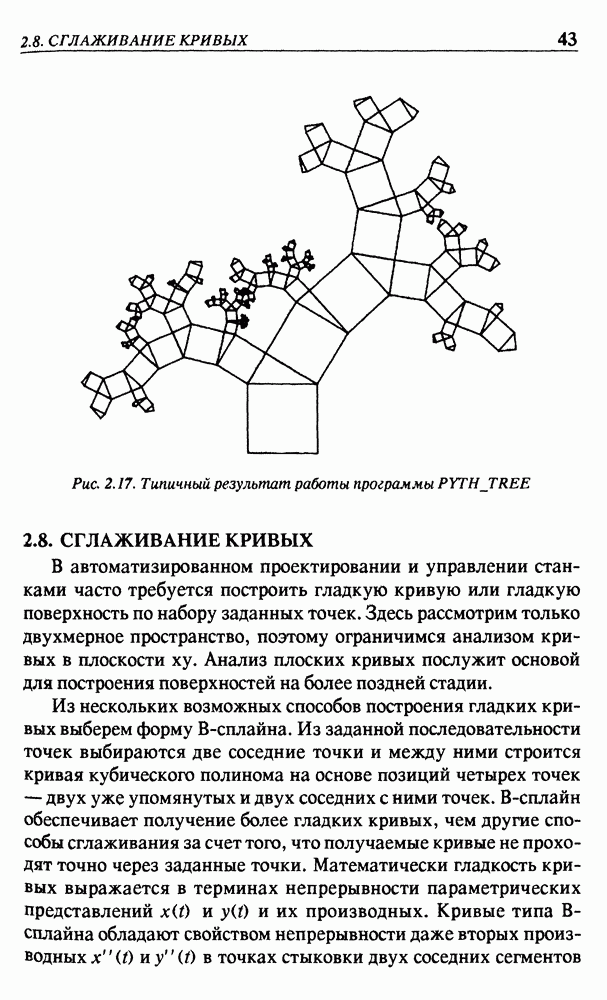
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
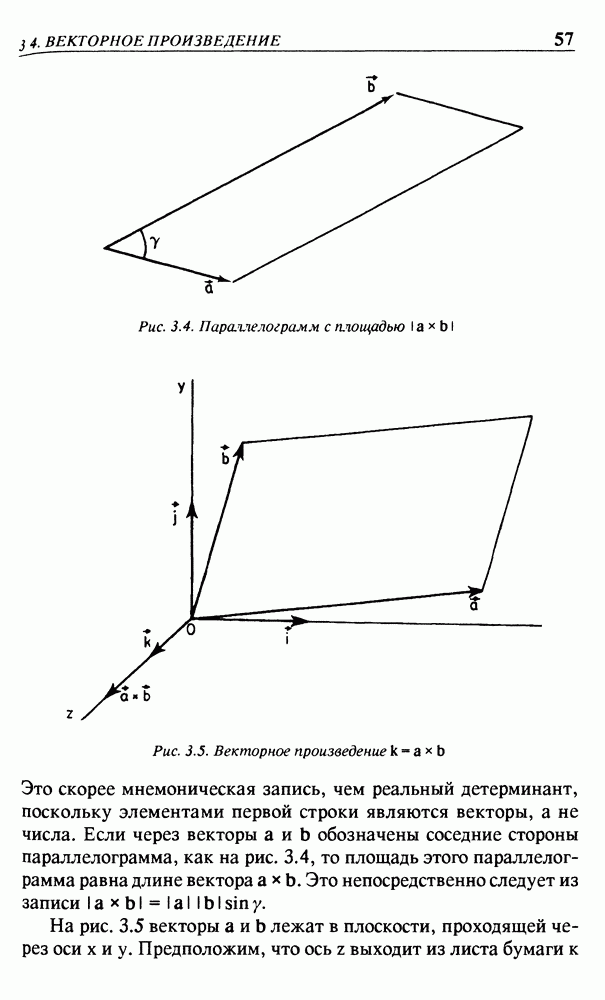
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
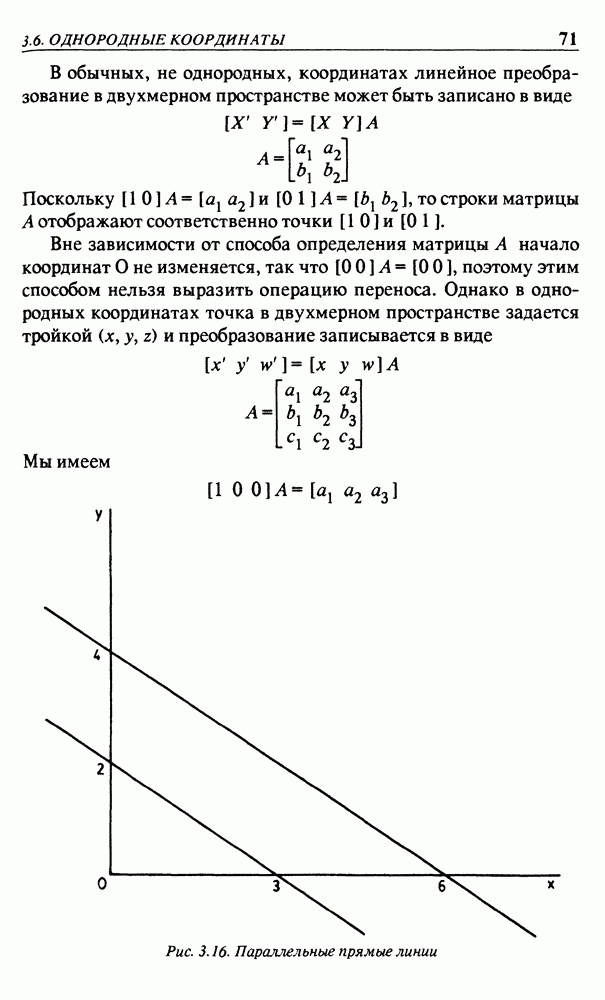
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
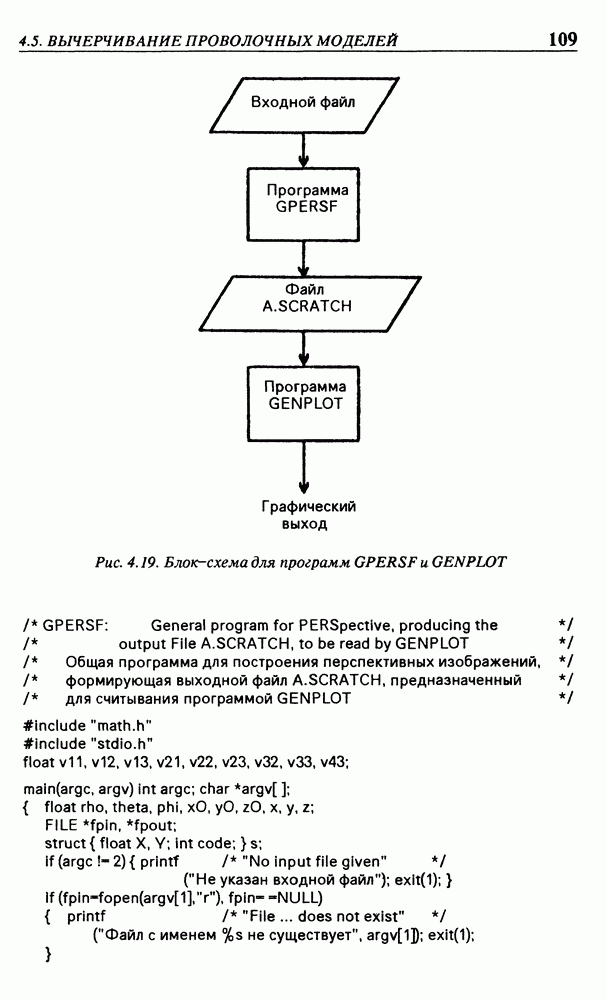
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
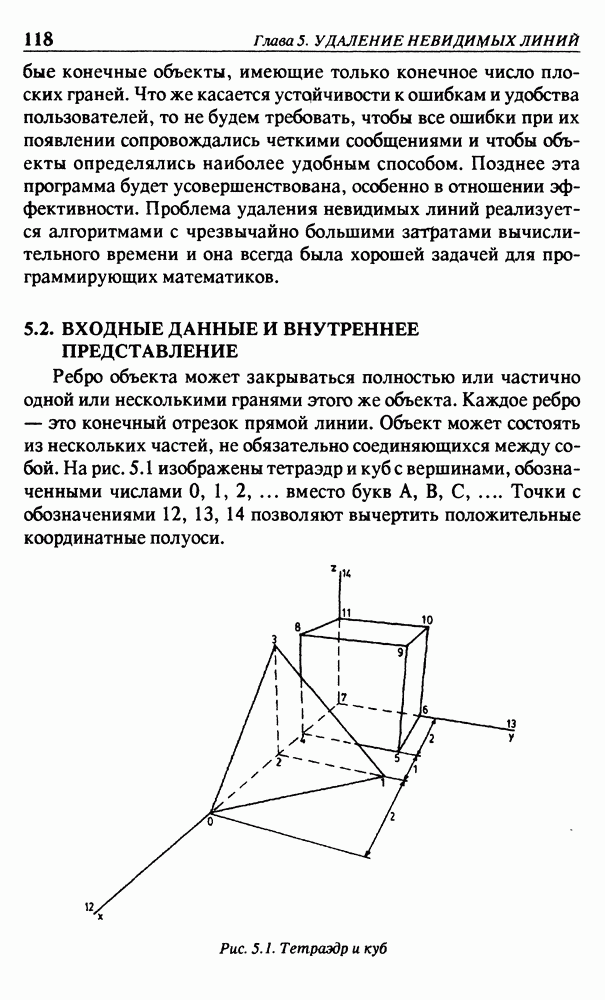
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
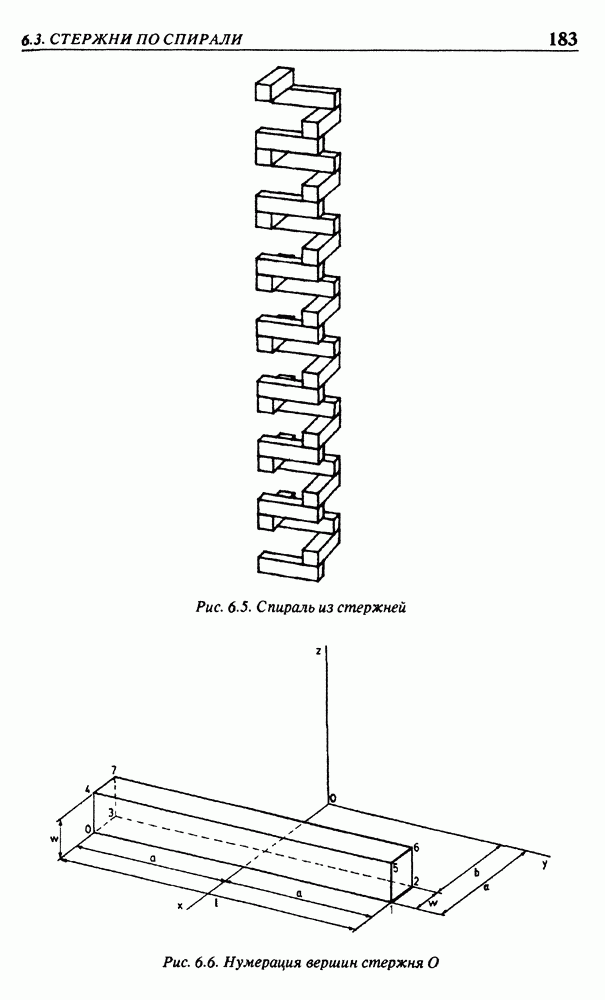
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
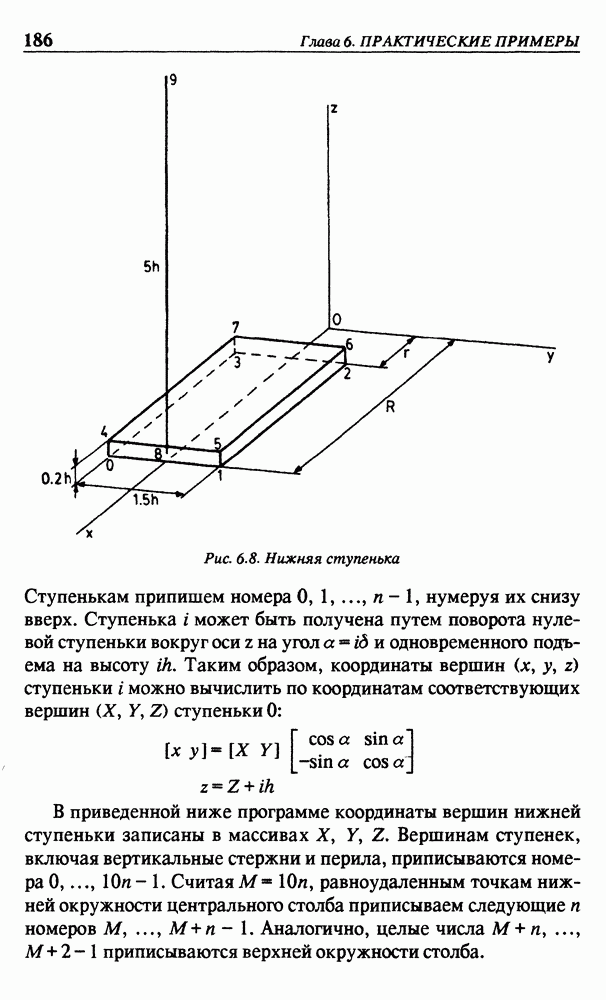
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
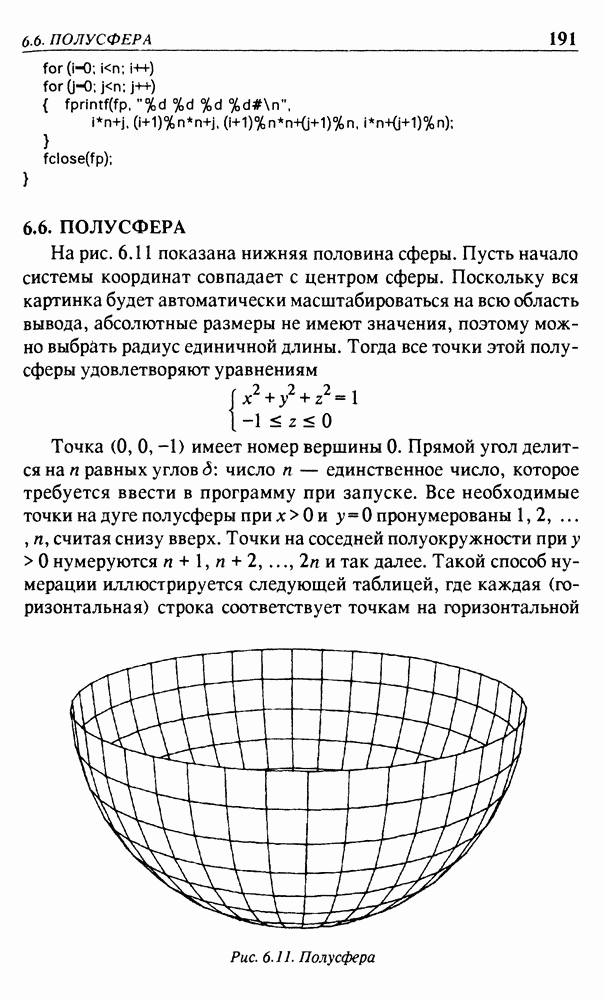
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА