| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3. ДЕТЕРМИНАНТЫ
Перед описанием векторного произведения обратим внимание на детерминанты. Чтобы решить следующую систему двух линейных уравнений:

необходимо умножить первое уравнение на коэффициент  а второе — на коэффициент
а второе — на коэффициент  и сложить, тогда нолучим
и сложить, тогда нолучим

После этого можно первое уравнение умножить на  а второе
а второе
— на  и также сложить. В результате получим
и также сложить. В результате получим

Если  не равно нулю, то можно выполнить деление и найти
не равно нулю, то можно выполнить деление и найти

Выражение в делителе можно записать в форме

В этом случае оно называется детерминантом второго порядка. Следовательно,

С помощью детерминантов уравнение (3.3) может быть записано в виде

где

Заметим, что  получается путем замены
получается путем замены  столбца в
столбца в  на правую часть системы уравнений
на правую часть системы уравнений  или 2). Такой способ решения системы линейных уравнений называется “правилом Крамера”. Этот способ пригоден не только для системы двух уравнений (хотя с точки зрения затрат машинного времени он оказывается очень дорогим для больших систем). Определим детерминант третьего порядка в виде уравнения
или 2). Такой способ решения системы линейных уравнений называется “правилом Крамера”. Этот способ пригоден не только для системы двух уравнений (хотя с точки зрения затрат машинного времени он оказывается очень дорогим для больших систем). Определим детерминант третьего порядка в виде уравнения

и детерминант четвертого порядка

и так далее.
Детерминанты имеют много интересных свойств, некоторые из них перечислены ниже.
1. Значение детерминанта не изменится, если строки записать в виде столбцов в том же порядке, например:

2. Если произвести взаимную замену двух строк (или двух столбцов), то значение детерминанта будет умножено на -1:

3. Если любую строку (или столбец) умножить на коэффициент, то значение детерминанта также будет умножено на этот коэффициент. Например:

4. Если строка (или столбец) изменяется путем добавления соответствующих элементов другой строки (или столбца), умноженных на константу, то значение детерминанта не изменится. Например:

5. Если строка (или столбец) является линейной комбинацией некоторых других строк (или столбцов), то значение детерминанта равно нулю. Например:

Существует много полезных применений детерминантов. Детерминантные уравнения, выражающие геометрические свойства, элегантны и легки для запоминания. Например, уравнение для прямой линии в двухмерном пространстве,  проходящей через две точки
проходящей через две точки  может быть записано в виде
может быть записано в виде

Такая запись становится очевидной, если, во-первых, рассматривать уравнение (3.5) как специальное обозначение линейных уравнений по х и у и, следовательно, представляющих прямую линию в пространстве  и, во-вторых, можно убедиться, что координаты обеих точек
и, во-вторых, можно убедиться, что координаты обеих точек  удовлетворяют этому уравнению, поскольку при их подстановке в первую строку получим две одинаковые строки. Аналогично, плоскость в трехмерном пространстве,
удовлетворяют этому уравнению, поскольку при их подстановке в первую строку получим две одинаковые строки. Аналогично, плоскость в трехмерном пространстве,  проходящая через три точки
проходящая через три точки  будет описываться уравнением
будет описываться уравнением 

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
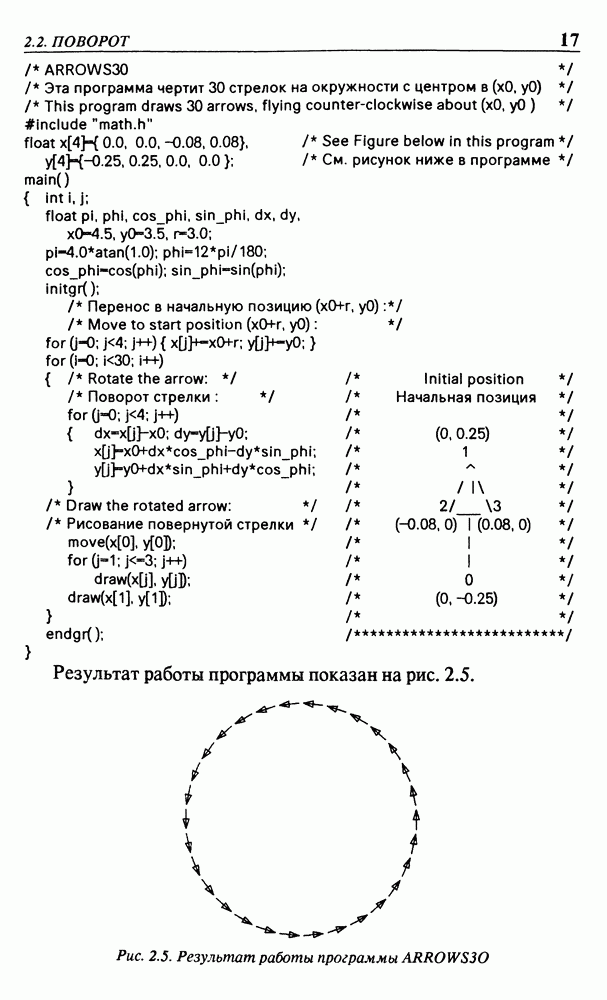
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
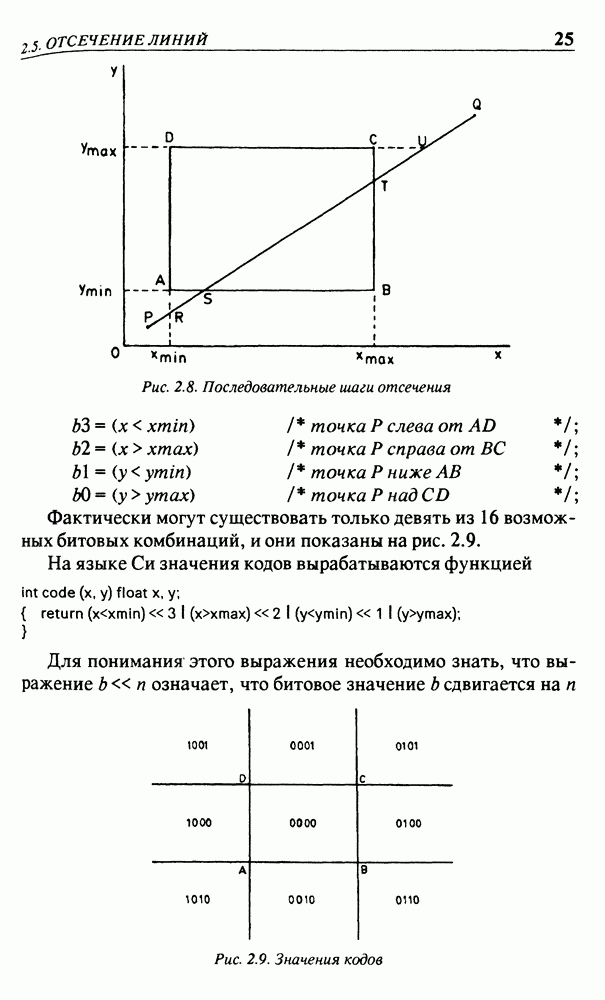
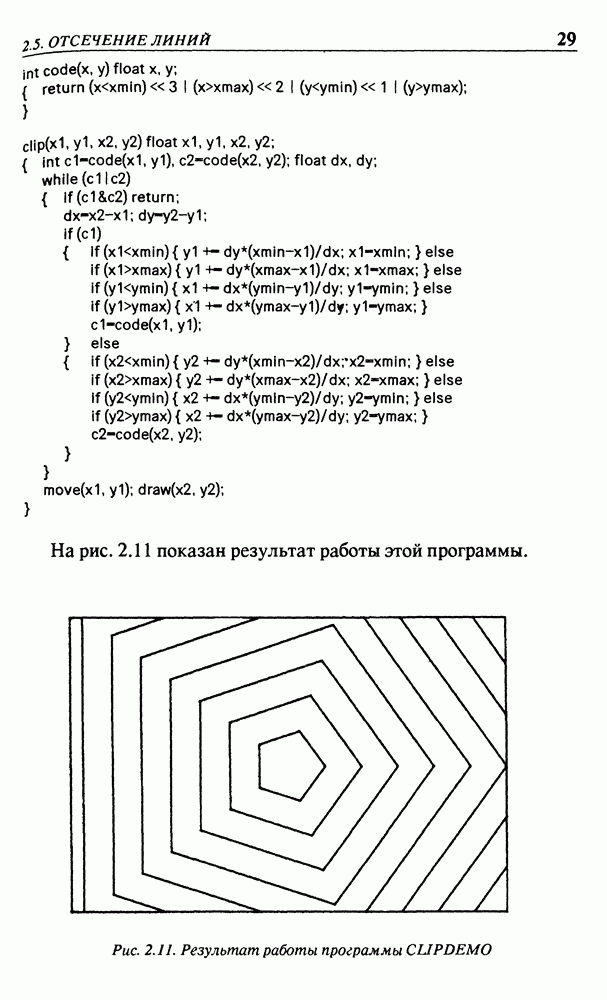
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
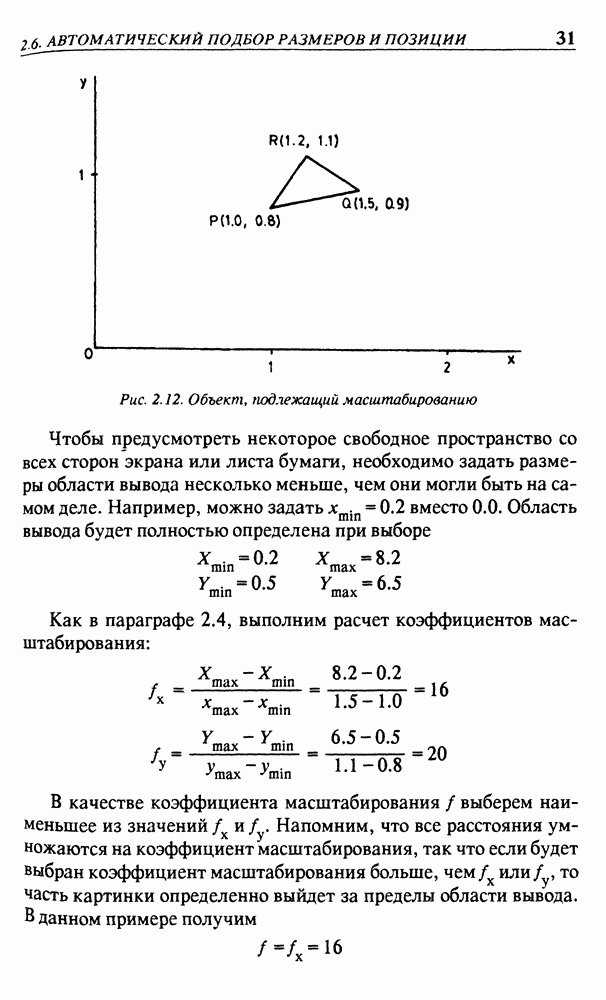
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
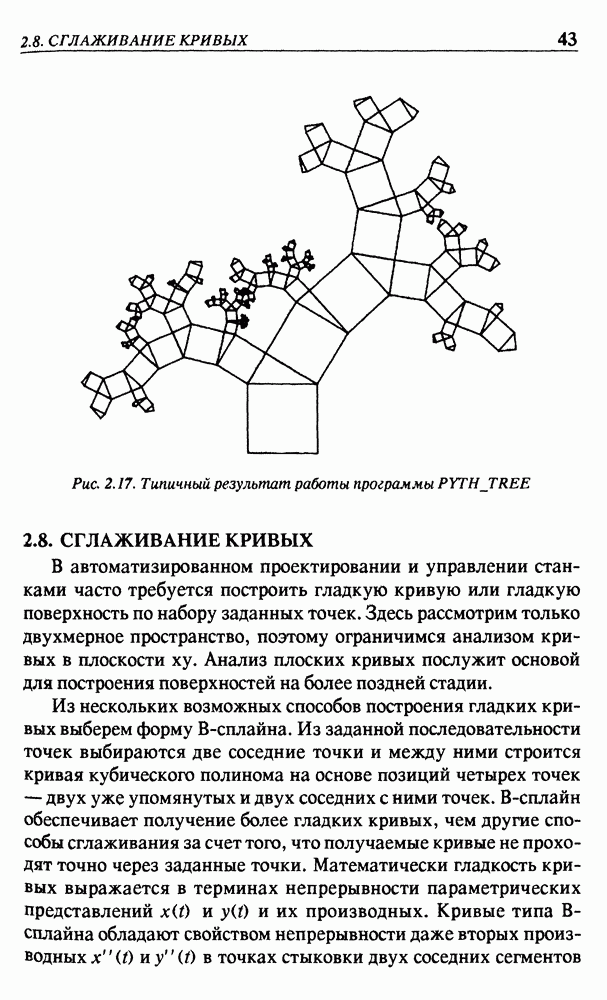
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
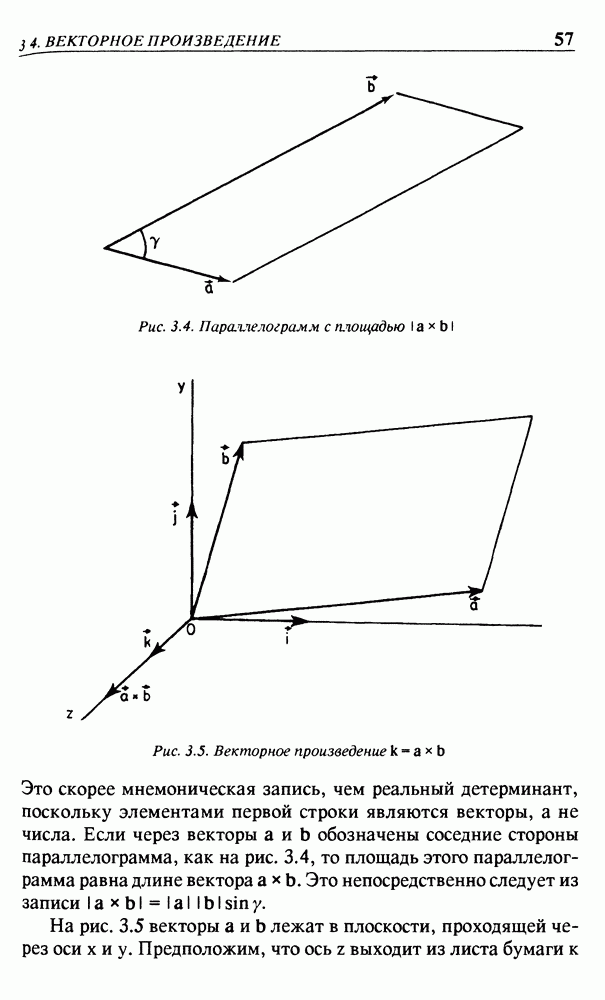
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
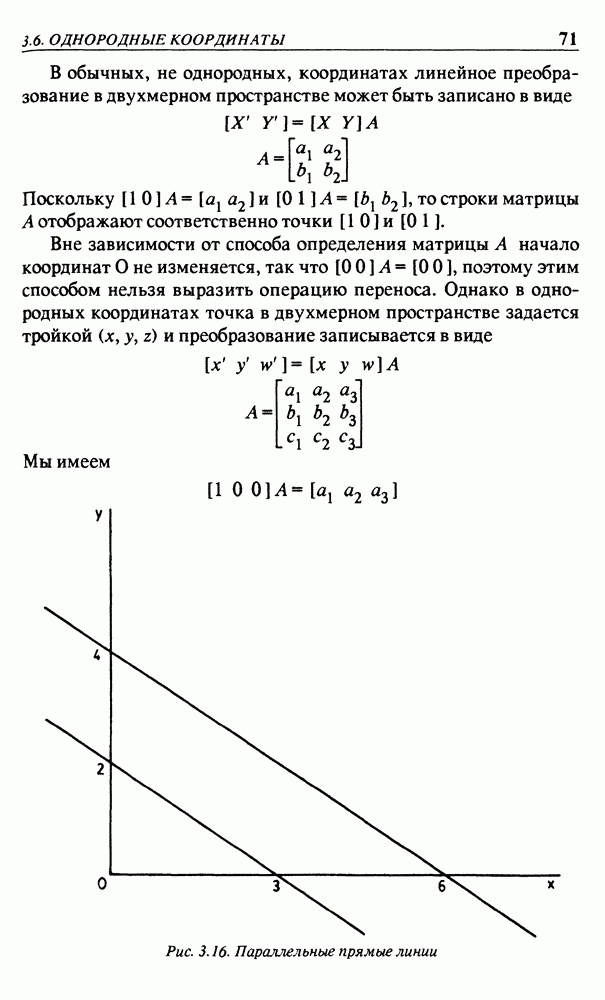
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
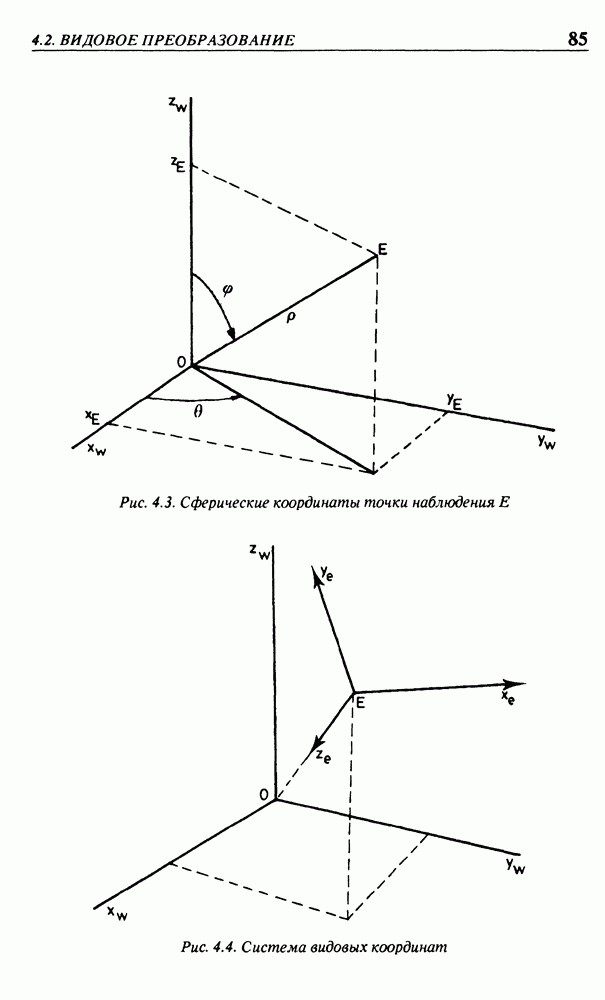
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
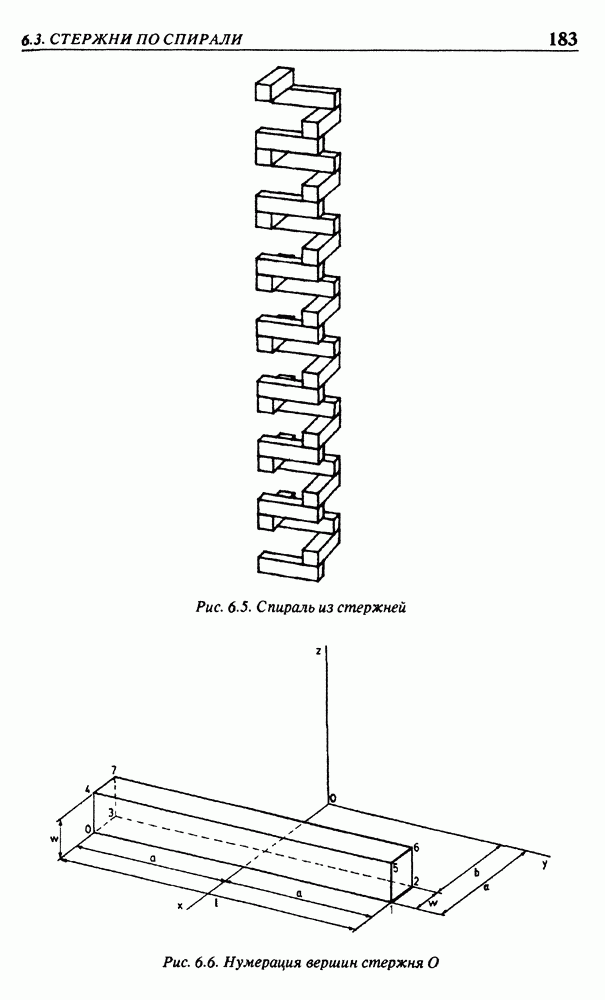
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
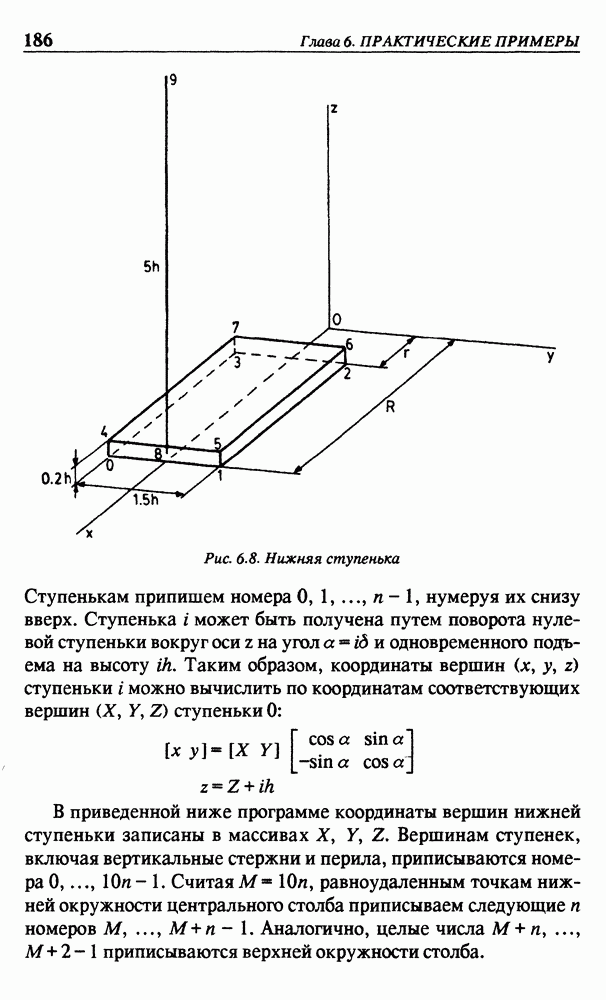
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
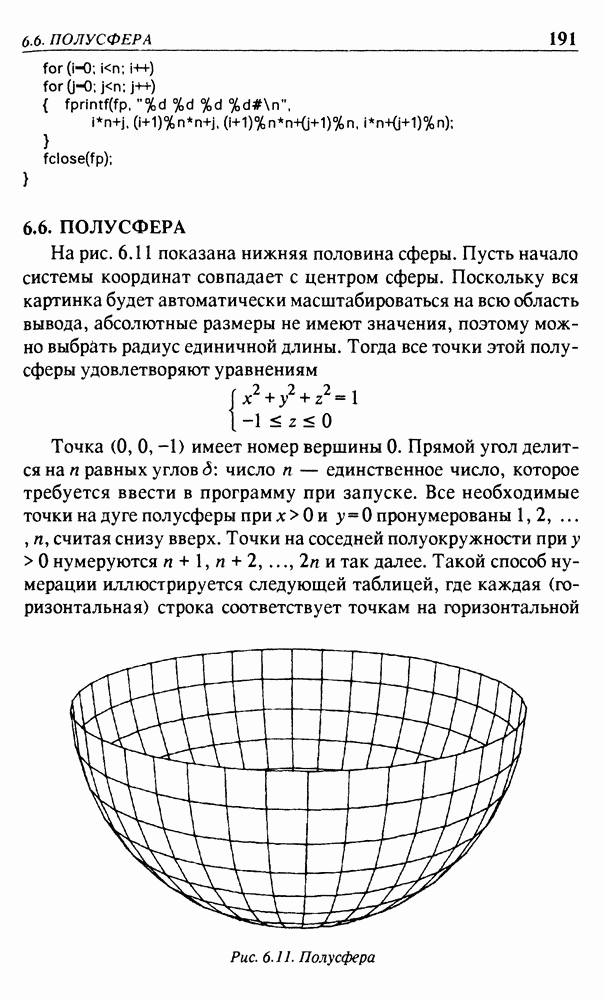
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА