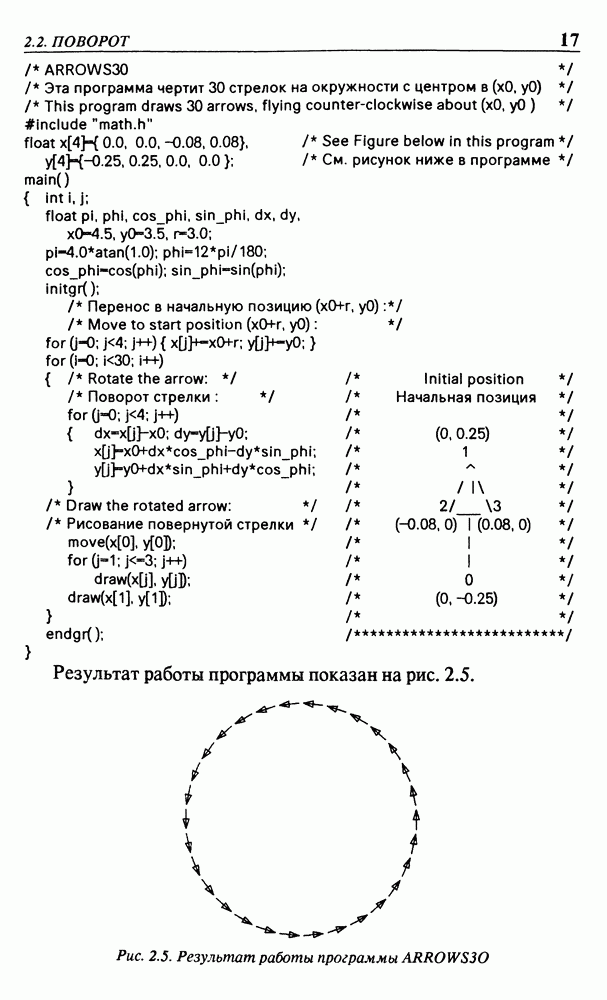
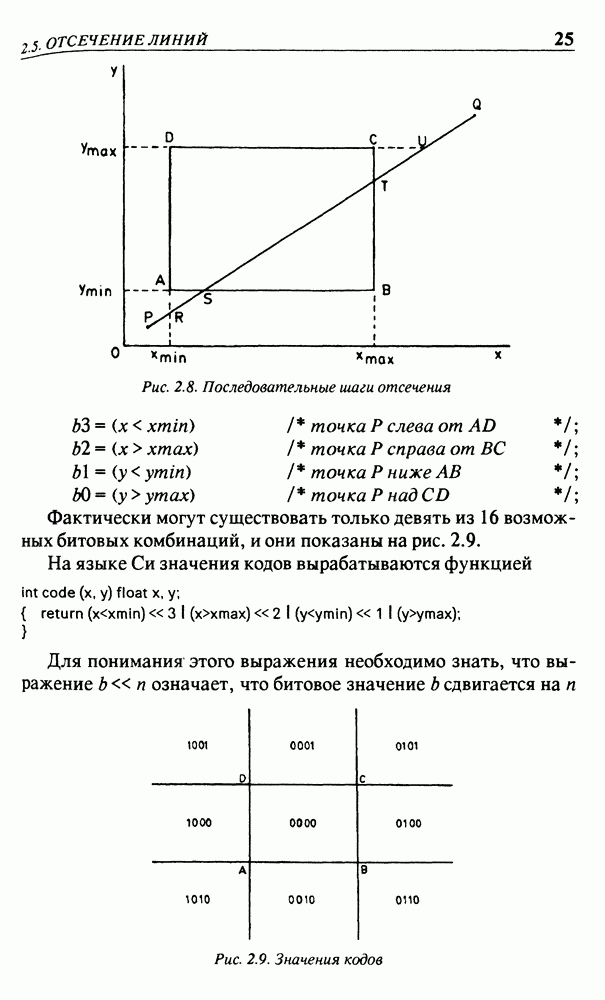
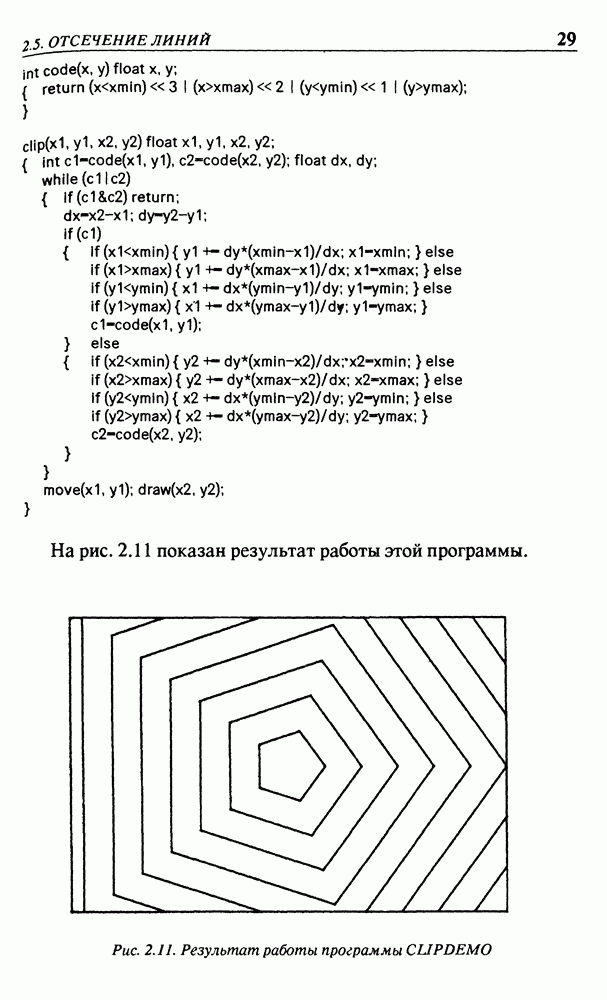
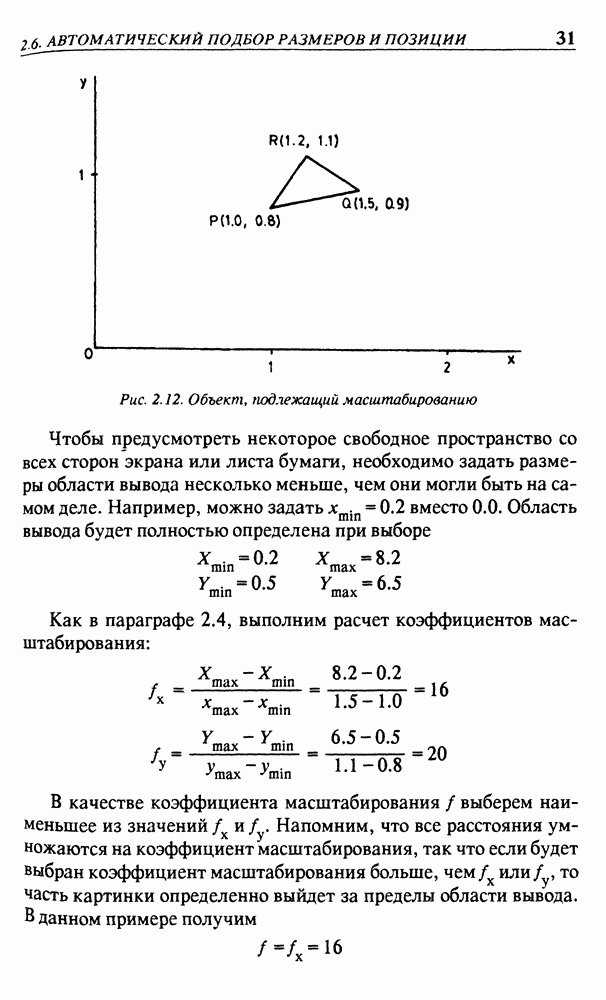
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
В этом параграфе рассматривается математически интересная задача, связанная с построением перспективной проекции, и поэтому ее часто включают в книги по трехмерной машинной графике. Здесь будут обсуждаться только геометрические свойства. Хот» рассуждения сравнительно просты, но они довольны длинные и носят теоретический характер. Цель заключается в более четком понимании обозначений типа  Читатели, интересующиеся практическими аспектами графического программирования, могут вполне пропустить этот параграф без серьезных последствий для понимания остальных частей книги. К изучению этого параграфа можно вернуться на более поздней стадии.
Читатели, интересующиеся практическими аспектами графического программирования, могут вполне пропустить этот параграф без серьезных последствий для понимания остальных частей книги. К изучению этого параграфа можно вернуться на более поздней стадии.
В параграфе 2.3 уже использовалась запись  для обозначения матрицы, состоящей только из одной строки, иногда называемой вектором-строкой. Такая запись может также рассматриваться как частный случай записи
для обозначения матрицы, состоящей только из одной строки, иногда называемой вектором-строкой. Такая запись может также рассматриваться как частный случай записи  где числа
где числа  называются однородными координатами. Эти три числа однородных координат применяются для обозначения точки в двухмерном пространстве. В проективной геометрии однородные координаты применялись задолго до возникновения и распространения машинной графики. В главе 4 будем рассматривать перспективные преобразования. Фактически они являются центральным проецированием, исследуемым в различных книгах по проективной геометрии. Здесь обсудим лишь вкратце несколько задач из этой увлекательной, но достаточно трудной для
называются однородными координатами. Эти три числа однородных координат применяются для обозначения точки в двухмерном пространстве. В проективной геометрии однородные координаты применялись задолго до возникновения и распространения машинной графики. В главе 4 будем рассматривать перспективные преобразования. Фактически они являются центральным проецированием, исследуемым в различных книгах по проективной геометрии. Здесь обсудим лишь вкратце несколько задач из этой увлекательной, но достаточно трудной для
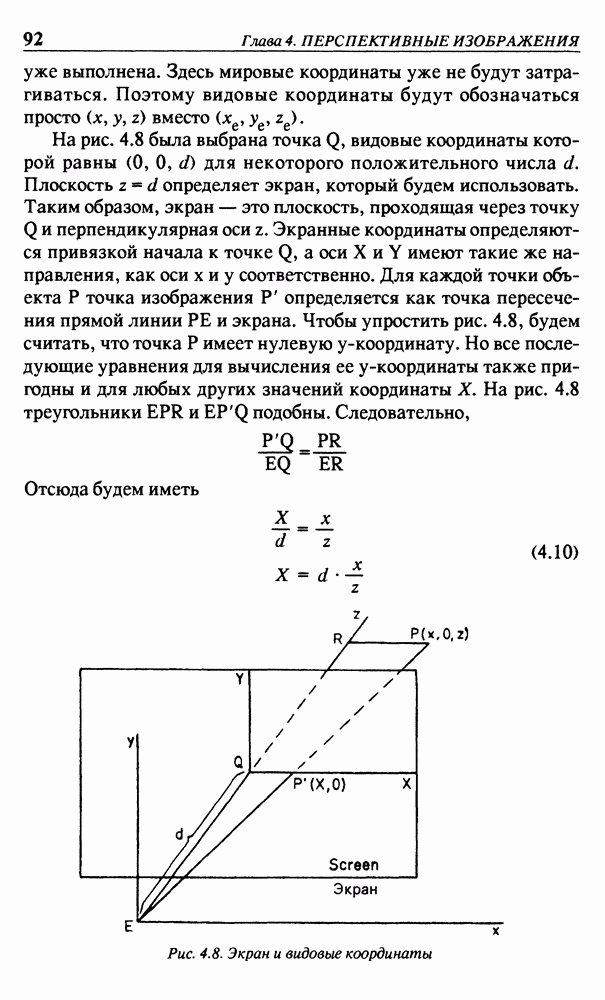
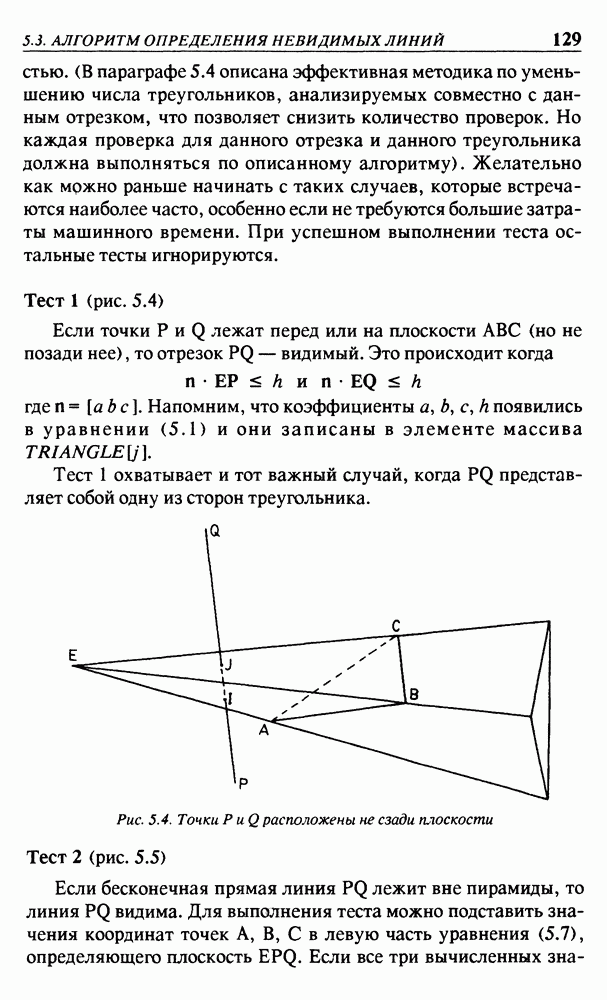
понимания ветви математики, избегая формальных определений и строгих доказательств теории. На рис. 3.15 имеем ось х и ось  так что точка задается парой координат
так что точка задается парой координат  Любая точка
Любая точка  не лежащая на оси х, имеет свою центральную проекцию
не лежащая на оси х, имеет свою центральную проекцию  определяемую как точка пересечения прямой линии
определяемую как точка пересечения прямой линии  с прямой линией
с прямой линией  описываемой уравнением
описываемой уравнением  Точка начала координат является центром проекции. Отрезок прямой линии
Точка начала координат является центром проекции. Отрезок прямой линии  может рассматриваться как луч света из объекта Р в глаз, расположенный в точке О. Для точек
может рассматриваться как луч света из объекта Р в глаз, расположенный в точке О. Для точек  и
и  получим два подобных треугольника
получим два подобных треугольника  и
и  так что
так что

Все точки  со свойством
со свойством  лежат на линии
лежат на линии  и имеют одну и ту же проекцию
и имеют одну и ту же проекцию  Если будем интересоваться только проекциями на прямую линию
Если будем интересоваться только проекциями на прямую линию  а не фактическими значениями
а не фактическими значениями  то имеет значение только их отношение. Вполне естественно использовать только одну координату X вместо пары (X, 1), если учитывать только точки на прямой линии
то имеет значение только их отношение. Вполне естественно использовать только одну координату X вместо пары (X, 1), если учитывать только точки на прямой линии  Если же все-таки требуется использовать координатную пару, то подойдет любая пара чисел
Если же все-таки требуется использовать координатную пару, то подойдет любая пара чисел  удовлетворяющая условию
удовлетворяющая условию  если принять такое соглашение. В геометрическом смысле координатная пара
если принять такое соглашение. В геометрическом смысле координатная пара  любой точки Р, отличной от О, на прямой
любой точки Р, отличной от О, на прямой

Рис. 3.15. Двухмерная центральная проекция
линии  может служить обозначением точки
может служить обозначением точки  Это и реализуется в случае применения однородных координат.
Это и реализуется в случае применения однородных координат.
В общем случае любая точка  в
в  -мерном пространстве записывается как точка
-мерном пространстве записывается как точка  в
в  -мерном пространстве, где
-мерном пространстве, где  любое ненулевое вещественное число. Эта группа из
любое ненулевое вещественное число. Эта группа из  чисел определяет однородные координаты исходной точки в
чисел определяет однородные координаты исходной точки в  -мерном пространстве. Читатель, возможно, знаком с определением проекции, которая является отображением множества точек в
-мерном пространстве. Читатель, возможно, знаком с определением проекции, которая является отображением множества точек в  -мерном пространстве в одну в
-мерном пространстве в одну в  -мерном пространстве. Однородные координаты возникли из-за необходимости обратного преобразования из
-мерном пространстве. Однородные координаты возникли из-за необходимости обратного преобразования из  -мерного пространства в
-мерного пространства в  -мерное пространство. Точка (5,7) в двухмерном пространстве, например, может быть записана в однородных координатах как (15, 21, 3) или как (500, 700, 100) и так далее. Хотя все операции относятся к двухмерному пространству, эти тройки можно принимать за точки в трехмерном пространстве. Очевидно, что обозначение
-мерное пространство. Точка (5,7) в двухмерном пространстве, например, может быть записана в однородных координатах как (15, 21, 3) или как (500, 700, 100) и так далее. Хотя все операции относятся к двухмерному пространству, эти тройки можно принимать за точки в трехмерном пространстве. Очевидно, что обозначение  представляет собой обычную запись точки в двухмерном пространстве для точки
представляет собой обычную запись точки в двухмерном пространстве для точки  в трехмерном пространстве. Точка Р является центральной проекцией для любой точки
в трехмерном пространстве. Точка Р является центральной проекцией для любой точки  если
если  Как и ранее, точка начала координат О будет центром проекций, а все точки проецируются на плоскость
Как и ранее, точка начала координат О будет центром проекций, а все точки проецируются на плоскость 
Для определения термина однородные (координаты) воспользуемся уравнением

описывающим прямую линию в двухмерном пространстве. Заменяя  на
на  получаем
получаем

или

Уравнение (3.7) обычно принято называть однородным, поскольку оно имеет одинаковую структуру в терминах  Отсюда числа
Отсюда числа  закономерно называть однородными координатами точки (
закономерно называть однородными координатами точки ( . Если опять
. Если опять  что двухмерное пространство располагается в плоскости
что двухмерное пространство располагается в плоскости  в координатной системе
в координатной системе  то уравнение (3.7) описывает плоскость, проходящую через начало координат и заданную прямую линию.
то уравнение (3.7) описывает плоскость, проходящую через начало координат и заданную прямую линию.
Если считать, что запись  используется как иная форма записи для
используется как иная форма записи для  то необходимо будет потребовать, чтобы значение
то необходимо будет потребовать, чтобы значение  не было равно нулю. Однако при этом однородные координаты едва ли имели какие-либо преимущества перед обычными координатами и читатель мог бы вообще выразить сомнение относительно наличия каких-то преимуществ. Например, рассмотрим систему из двух линейных уравнений, каждое из которых описывает прямую линию в двухмерном пространстве:
не было равно нулю. Однако при этом однородные координаты едва ли имели какие-либо преимущества перед обычными координатами и читатель мог бы вообще выразить сомнение относительно наличия каких-то преимуществ. Например, рассмотрим систему из двух линейных уравнений, каждое из которых описывает прямую линию в двухмерном пространстве:

Если две прямые линии параллельны, то они не пересекаются и не существует пары чисел  , удовлетворяющей системе (3.8). Таким образом, для нахождения общей точки для прямых линий необходимо применять правило с некоторым исключением, которое не совсем элегантно. При замене координат
, удовлетворяющей системе (3.8). Таким образом, для нахождения общей точки для прямых линий необходимо применять правило с некоторым исключением, которое не совсем элегантно. При замене координат  на однородные координаты
на однородные координаты  ситуация несколько улучшится
ситуация несколько улучшится

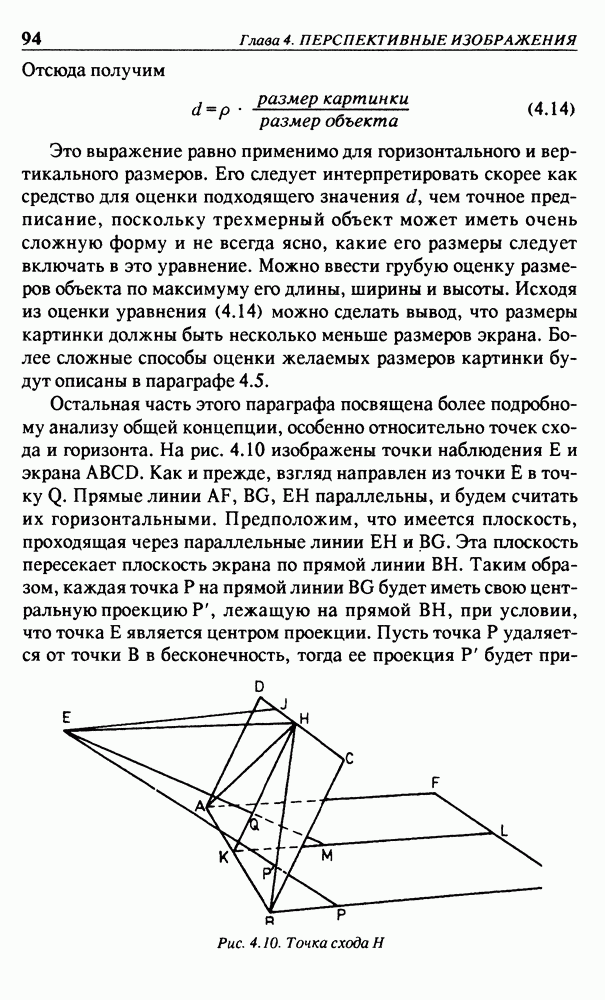
Уравнения из системы (3.9) можно интерпретировать как плоскости, проходящие через точку начала координат О. Эта система имеет, по крайней мере, одно тривиальное решение  Для геометрической интерпретации зададим для коэффициентов конкретные значения. Пусть, например, заменим систему (3.8) на систему
Для геометрической интерпретации зададим для коэффициентов конкретные значения. Пусть, например, заменим систему (3.8) на систему

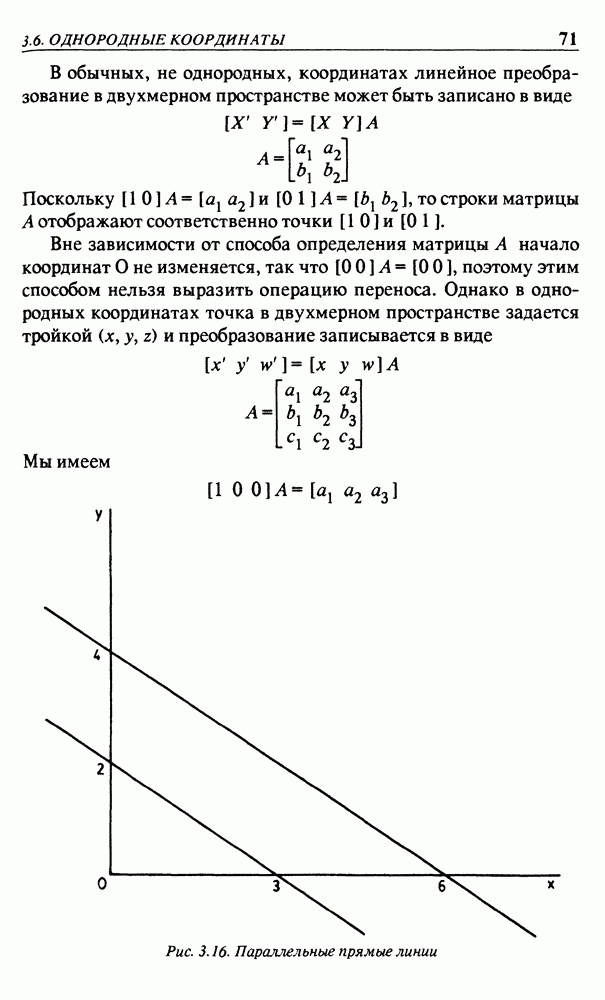
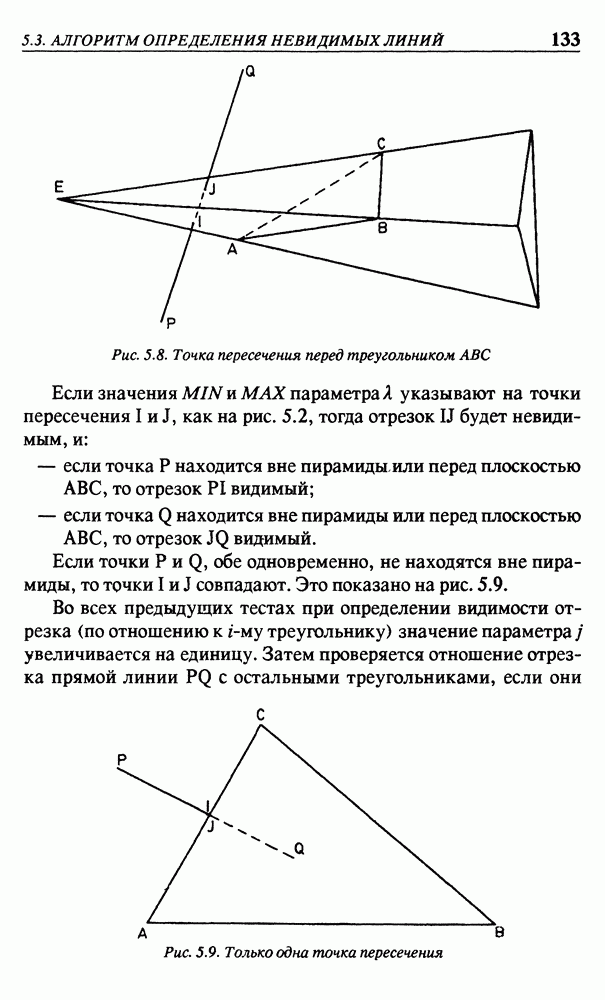
описывающую две параллельные прямые линии, изображенные на рис. 3.16. Тогда систему уравнений (3.9) можно заменить на

Эта система эквивалентна системе

так что решение состоит из всех троек  , где k — любое вещественное число. В трехмерном пространстве эти точки образуют прямую линию, проходящую через точки О и (3, -2, 0),
, где k — любое вещественное число. В трехмерном пространстве эти точки образуют прямую линию, проходящую через точки О и (3, -2, 0),
причем эта прямая линия представляет собой линию пересечения двух плоскостей, заданных уравнениями  Возвращаясь к двухмерному пространству плоскости
Возвращаясь к двухмерному пространству плоскости  напомним, что каждая точка
напомним, что каждая точка  ассоциируется с прямой линией
ассоциируется с прямой линией  в трехмерном пространстве. Для ненулевых значений
в трехмерном пространстве. Для ненулевых значений  эта ассоциация почти тривиальна. Теперь станет понятной очень важная причина применения однородных координат. Для каждой прямой линии в двухмерном пространстве добавим один объект, называемый бесконечно удаленной точкой. Эта бесконечно удаленная точка не может быть обозначена в обычной системе коор динат, а в системе однородных координат — может. Например, бесконечно удаленная точка на прямой линии, описываемой уравнением
эта ассоциация почти тривиальна. Теперь станет понятной очень важная причина применения однородных координат. Для каждой прямой линии в двухмерном пространстве добавим один объект, называемый бесконечно удаленной точкой. Эта бесконечно удаленная точка не может быть обозначена в обычной системе коор динат, а в системе однородных координат — может. Например, бесконечно удаленная точка на прямой линии, описываемой уравнением  записывается как (3, -2, 0) или в виде любой тройки
записывается как (3, -2, 0) или в виде любой тройки  для ненулевого
для ненулевого  Поскольку эти тройки являются решением системы уравнений (3.10), то бесконечно удаленную точку можно считать точкой пересечения двух параллельных линий, изображенных на рис. 3.16. Считается, что бесконечно удаленная точка находится в двухмерном пространстве. Как мы видели, каждая точка в двухмерном пространстве ассоциируется с прямой линией в трехмерном пространстве, поэтому желательно выяснить, с какой прямой линией ассоциируется бесконечно удаленная точка
Поскольку эти тройки являются решением системы уравнений (3.10), то бесконечно удаленную точку можно считать точкой пересечения двух параллельных линий, изображенных на рис. 3.16. Считается, что бесконечно удаленная точка находится в двухмерном пространстве. Как мы видели, каждая точка в двухмерном пространстве ассоциируется с прямой линией в трехмерном пространстве, поэтому желательно выяснить, с какой прямой линией ассоциируется бесконечно удаленная точка  Поскольку эта линия должна проходить через точку начала координат
Поскольку эта линия должна проходить через точку начала координат  то искомая линия должна быть линией, проходящей через точку О и точку (3, -2,0), то есть лежащей в плоскости
то искомая линия должна быть линией, проходящей через точку О и точку (3, -2,0), то есть лежащей в плоскости 
Вполне резонно назвать точку (3, -2, 0) бесконечно удаленной точкой, поскольку ее можно рассматривать как предельную точку (3, -2, w) при  стремящемся к нулю, а эта тройка в однородных координатах эквивалентна точке
стремящемся к нулю, а эта тройка в однородных координатах эквивалентна точке  , которая при малых значениях
, которая при малых значениях  удалена очень далеко. Введение бесконечно удаленной точки позволяет утверждать, что любые две различные прямые пересекаются в одной точке. Аналогично в проективной геометрии можно утверждать, что две любые различные плоскости имеют линию пересечения. Если плоскости параллельны, то все точки этой линии пересечения в однородных координатах записываются в виде
удалена очень далеко. Введение бесконечно удаленной точки позволяет утверждать, что любые две различные прямые пересекаются в одной точке. Аналогично в проективной геометрии можно утверждать, что две любые различные плоскости имеют линию пересечения. Если плоскости параллельны, то все точки этой линии пересечения в однородных координатах записываются в виде  . Этот вопрос не будем рассматривать детально, а лучше вернемся к двухмерному пространству и покажем другие новые проявления возможностей, предоставляемых однородными координатами.
. Этот вопрос не будем рассматривать детально, а лучше вернемся к двухмерному пространству и покажем другие новые проявления возможностей, предоставляемых однородными координатами.
В обычных, не однородных, координатах линейное преобразование в двухмерном пространстве может быть записано в виде 

Поскольку  то строки матрицы А отображают соответственно точки
то строки матрицы А отображают соответственно точки 
Вне зависимости от способа определения матрицы А начало координат О не изменяется, так что  поэтому этим способом нельзя выразить операцию переноса. Однако в однородных координатах точка в двухмерном пространстве задается тройкой
поэтому этим способом нельзя выразить операцию переноса. Однако в однородных координатах точка в двухмерном пространстве задается тройкой  и преобразование записывается в виде
и преобразование записывается в виде

Мы имеем


Рис. 3.16. Параллельные прямые линии
Так как точка [100] — бесконечно удаленная точка на оси х, то первая строка  матрицы А представляет собой отображение этой бесконечно удаленной точки на оси х. Аналогично вторая строка матрицы
матрицы А представляет собой отображение этой бесконечно удаленной точки на оси х. Аналогично вторая строка матрицы  будет отображением бесконечно удаленной точки на оси у. Поскольку
будет отображением бесконечно удаленной точки на оси у. Поскольку

то можно считать, что третья строка матрицы  является отображением точки начала координат [001]. Это означает, что однородные координаты позволяют выразить любые преобразования путем матричного умножения. Фактически в этом нет ничего нового и это свойство уже использовалось в параграфе 2.3. Однако операция переноса — не единственное новое свойство, предоставляемое таким матричным умножением. С его помощью можно преобразовать параллельные прямые линии в пересекающиеся. Покажем это на примере преобразования полного прямоугольного квадранта в треугольник.
является отображением точки начала координат [001]. Это означает, что однородные координаты позволяют выразить любые преобразования путем матричного умножения. Фактически в этом нет ничего нового и это свойство уже использовалось в параграфе 2.3. Однако операция переноса — не единственное новое свойство, предоставляемое таким матричным умножением. С его помощью можно преобразовать параллельные прямые линии в пересекающиеся. Покажем это на примере преобразования полного прямоугольного квадранта в треугольник.
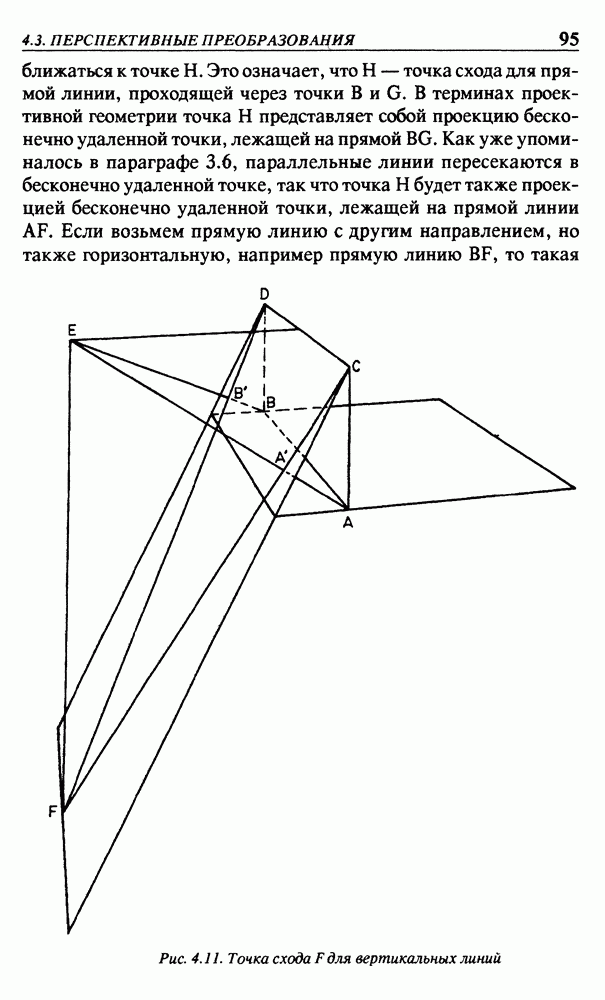
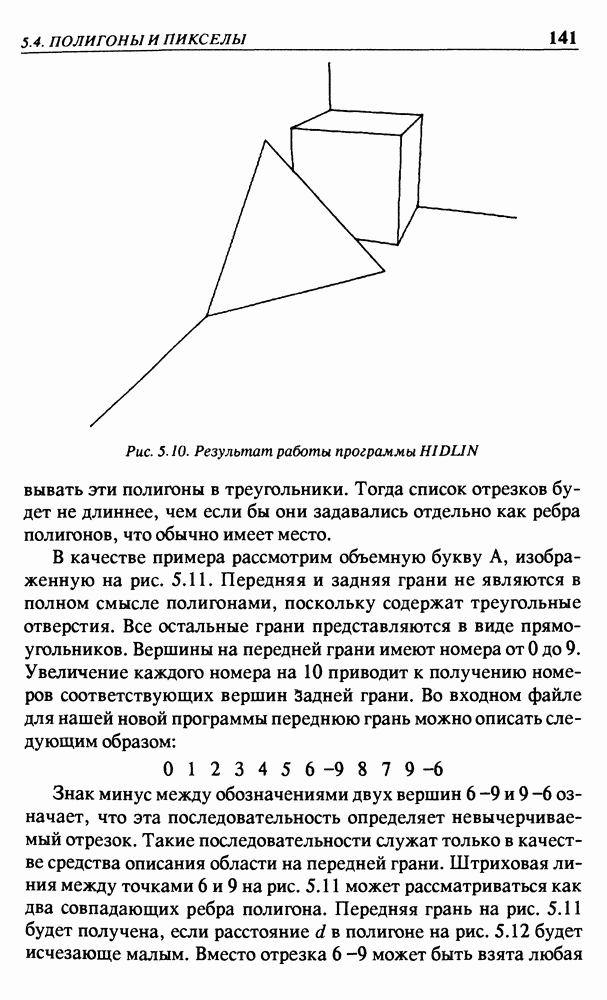
На рис. 3.17 изображен произвольный треугольник, вершины которого заданы в прямоугольной системе координат точками  Добавим третью координату, равную 1, как формальное средство образования однородных координат. Исключением являются бесконечно удаленные точки (1, 0, 0) и (0, 1, 0) на координатных осях, у которых третья однородная координата равна нулю. Образуем матрицу М, такую, что матричное умножение
Добавим третью координату, равную 1, как формальное средство образования однородных координат. Исключением являются бесконечно удаленные точки (1, 0, 0) и (0, 1, 0) на координатных осях, у которых третья однородная координата равна нулю. Образуем матрицу М, такую, что матричное умножение

отобразит точку О на точку С, точку (1, 0, 0) — на точку А и точку (0, 1, 0) — на точку В. Для любых ненулевых значений  точки
точки  будут точками требуемого изображения треугольника, если
будут точками требуемого изображения треугольника, если

Это легко проверить, поскольку имеем очевидное соотношение

правая часть которого является просто другим обозначением точки А на рис. 3.17. На первый взгляд кажется, что константы  в уравнении (3.11) не нужны и могут быть установлены
в уравнении (3.11) не нужны и могут быть установлены

Рис. 3.17. Квадрант, преобразованный в треугольник
равными 1. Однако они нужны для того, чтобы можно было задать заранее установленное отображение  для так называемой единичной точки
для так называемой единичной точки  Точка
Точка  может быть выбрана в любом месте внутри треугольника. Поскольку точка
может быть выбрана в любом месте внутри треугольника. Поскольку точка  отображается на точку
отображается на точку  то имеем
то имеем

— сокращенное обозначение следующей системы трех линейных уравнений относительно переменных 

Система имеет единственное решение, которое следует из того факта, что тройки  обозначают вершины треугольника. Решение этой системы для
обозначают вершины треугольника. Решение этой системы для  у и подстановка результата в уравнение (3.11) дает искомое значение матрицы М.
у и подстановка результата в уравнение (3.11) дает искомое значение матрицы М.
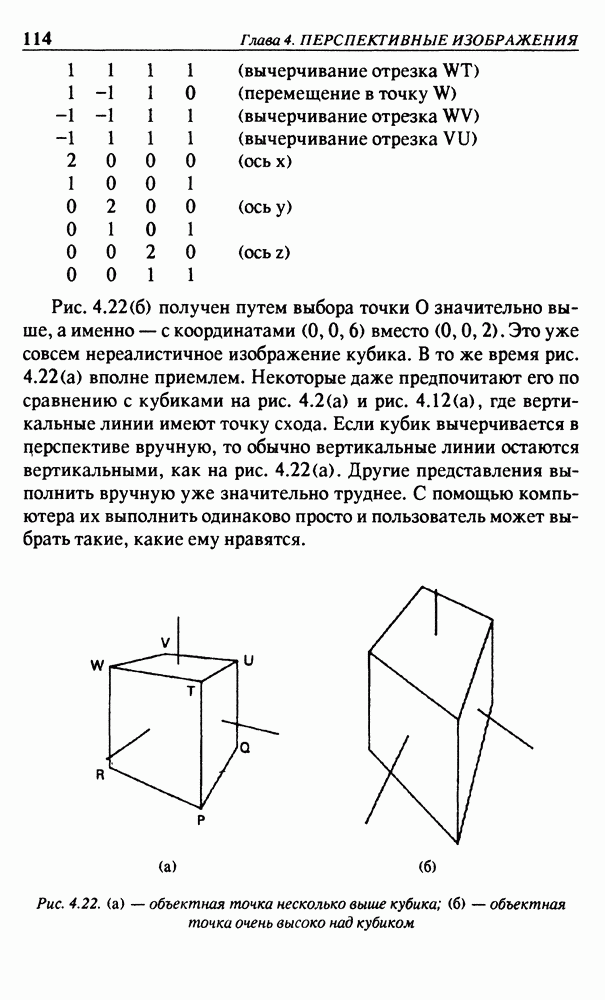
Прямые линии преобразуются в прямые линии, но их параллелизм не сохраняется. Например, вертикальная линия, проходящая через точку  на рис. 3.17, превращается в прямую линию, проходящую через точки
на рис. 3.17, превращается в прямую линию, проходящую через точки  Это дает геометрическое средство для нахождения проекции Р для точки Р. Имея вычисленное значение матрицы М, точку проекции Р можно найти аналитически как произведение
Это дает геометрическое средство для нахождения проекции Р для точки Р. Имея вычисленное значение матрицы М, точку проекции Р можно найти аналитически как произведение

Заметим, что все бесконечно удаленные точки отображаются на отрезок  а все бесконечно удаленные точки параллельных линий — на единственную точку на отрезке
а все бесконечно удаленные точки параллельных линий — на единственную точку на отрезке  Это дает основание рассматривать весь квадрант как плоскую перспективу, в которой треугольник ABC является картиной, а отрезок
Это дает основание рассматривать весь квадрант как плоскую перспективу, в которой треугольник ABC является картиной, а отрезок  представляет собой линию горизонта.
представляет собой линию горизонта.
На этом закончим анализ однородных координат. Другие интересные свойства однородных координат читатель может найти в учебниках по проективной геометрии, например в книге Hopkins and Hails (1953).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
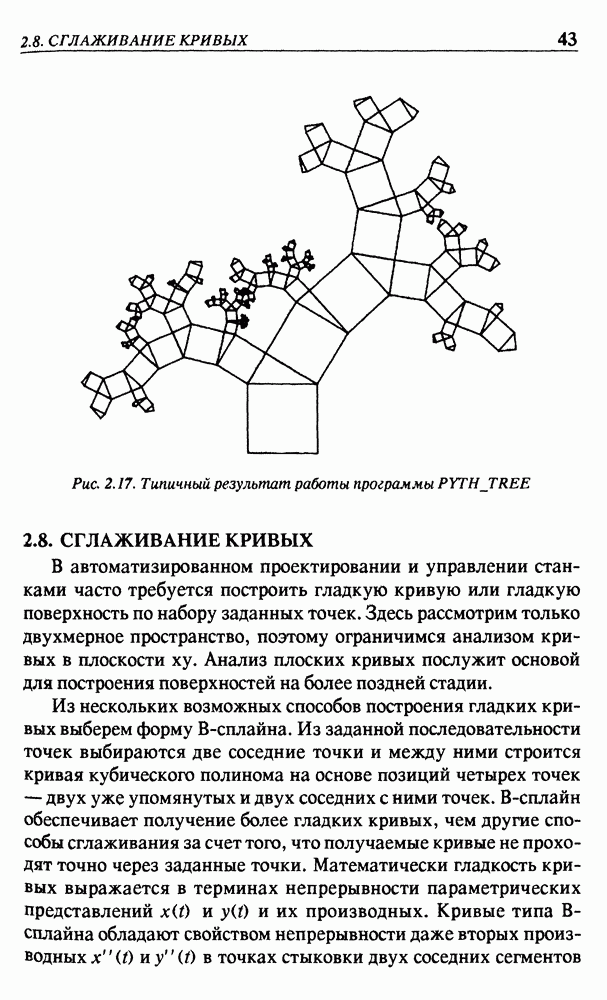
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
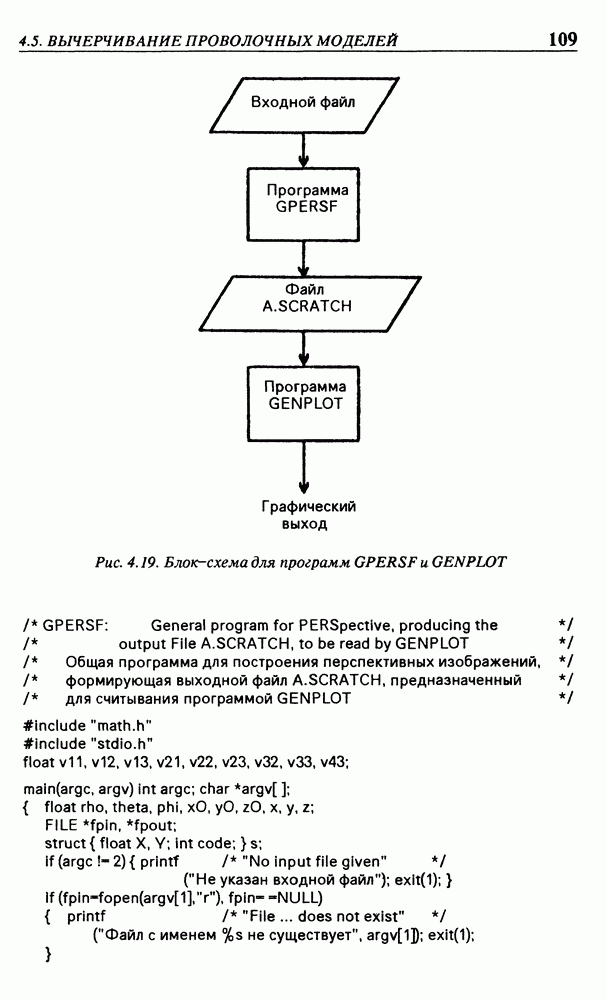
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
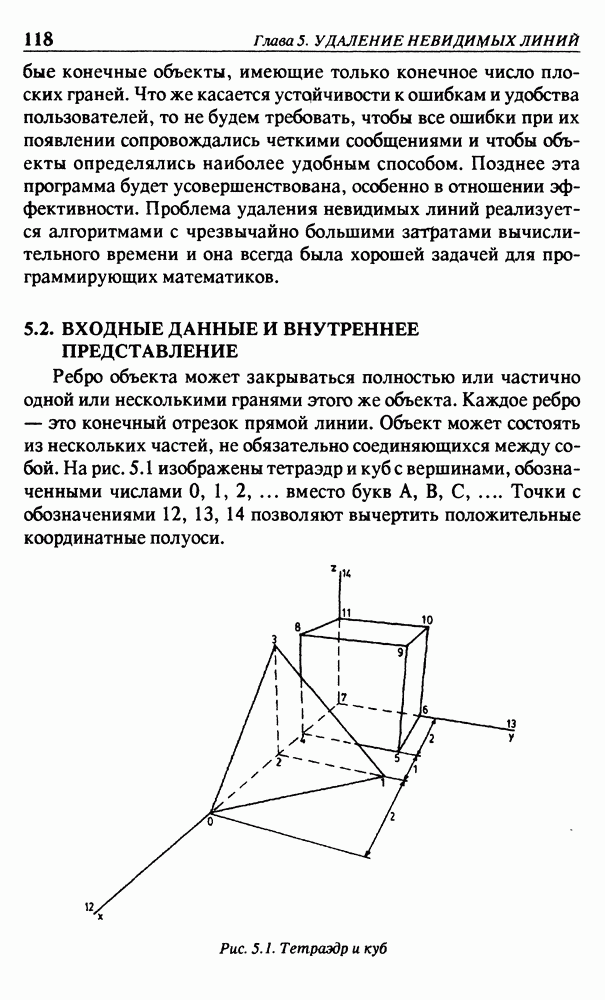
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
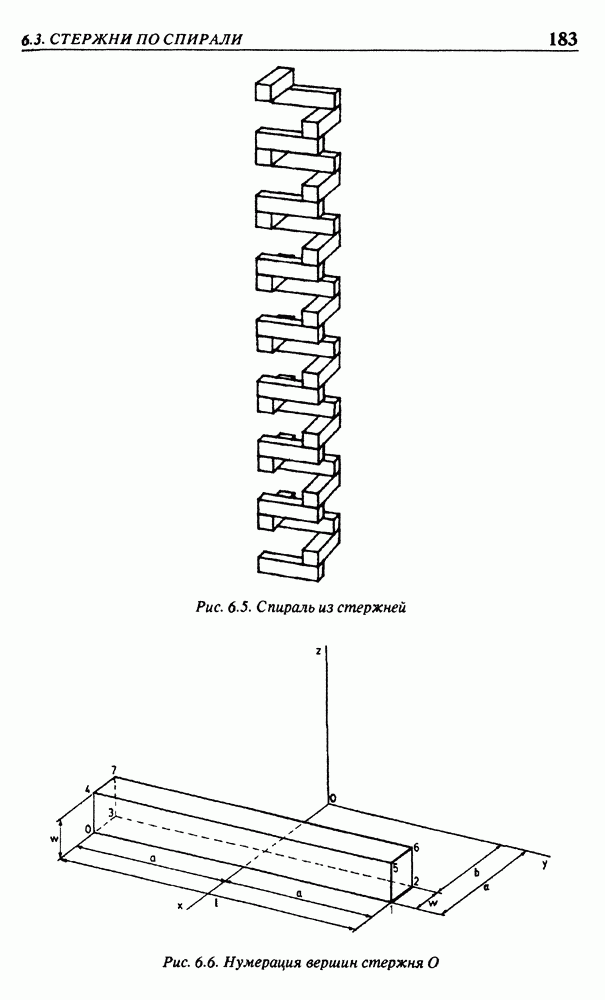
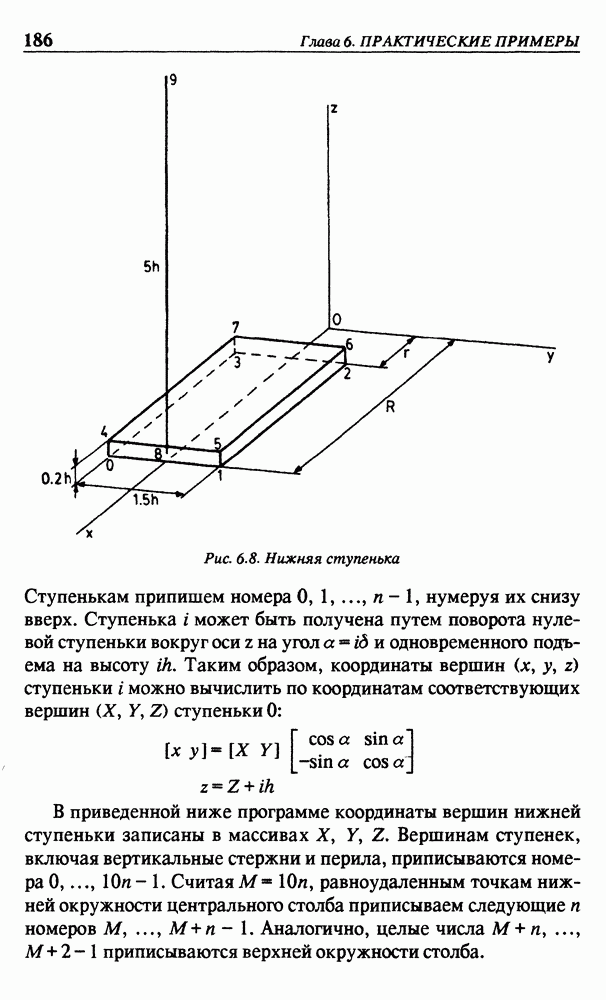
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
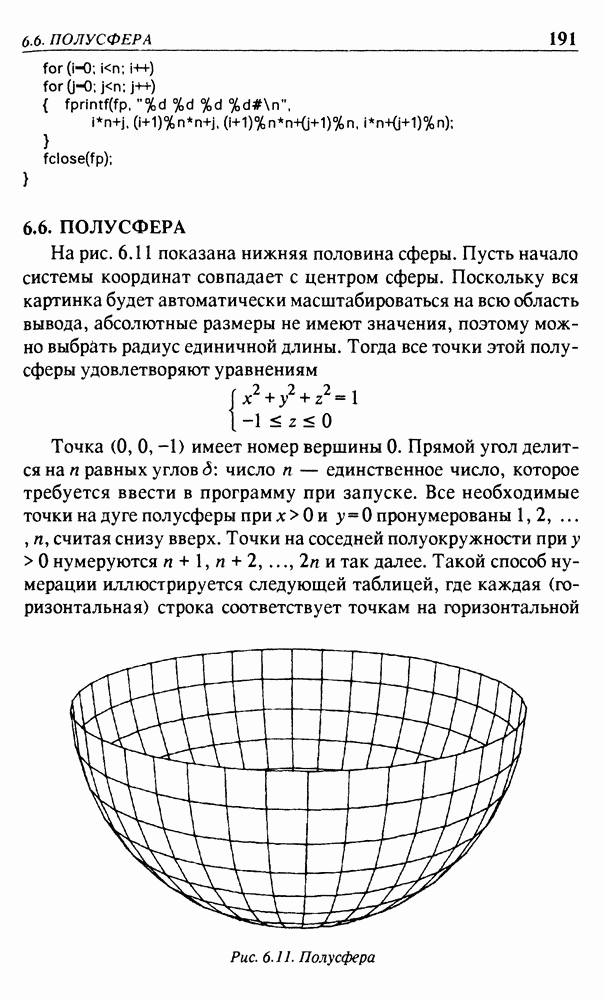
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА