| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
Программа HIDLINPX составлялась с целью получения чертежей сплошных объектов. Но мы уже видели на двух примерах, что она также применима и для других целей. Во-первых, она может вычерчивать “свободные” отрезки прямых линий, например координатные оси, если номера их конечных точек имеются во входном файле после ключевого слова “Faces”. Во-вторых, в параграфе 6.6 мы рассматривали поверхность полусферы как некоторую математическую абстракцию. Теперь продвинемся еще на шаг дальше в применении программы HIDLINPX для целей, далеких от первоначально поставленных.
Иногда требуется графически представить функцию от двух переменных

Для этого необходимо определить прямоугольный домен

В принципе функция  может быть любой функцией двух переменных. В качестве примера воспользуемся квадратичной функцией
может быть любой функцией двух переменных. В качестве примера воспользуемся квадратичной функцией

(В качестве коэффициента мы не применяем букву  потому, что этой буквой обозначено имя функции.) Программа будет запрашивать значения коэффициентов
потому, что этой буквой обозначено имя функции.) Программа будет запрашивать значения коэффициентов  а также целые числа
а также целые числа  и Эти два целых числа используются для вычисления длины и ширины элементарных прямоугольников:
и Эти два целых числа используются для вычисления длины и ширины элементарных прямоугольников:

Углы этих прямоугольников образуют сетку точек  для которых будут вычисляться значения
для которых будут вычисляться значения  Полученные таким образом точки в трехмерном пространстве соединяются отрезками прямых линий, параллельными плоскостям либо
Полученные таким образом точки в трехмерном пространстве соединяются отрезками прямых линий, параллельными плоскостям либо  либо
либо  Именно эти отрезки и будут вычерчиваться. На рис. 6.12 показана функция
Именно эти отрезки и будут вычерчиваться. На рис. 6.12 показана функция

для которой было задано

С каждой точкой сетки  ассоциируется пара чисел
ассоциируется пара чисел  Для точки (х, у, z) на поверхности, соответствующей точке сетки
Для точки (х, у, z) на поверхности, соответствующей точке сетки  приписывается номер вершины
приписывается номер вершины 

Рис. 6.12. Квадратичная функция двух переменных

Рис. 6.13. (а) - точки на поверхности; (б) - два треугольника
Тогда имеем

Нумерация вершин показана на рис.  где
где 
На рис. 6.13(a) мы видим поверхность из конца положительной полуоси  Например, точки 1, 2, 5, 6 — точки поверхности. К сожалению, в общем случае эти точки не лежат в одной плоскости, поэтому их нельзя использовать в качестве вершин полигона. Если точку 1 соединить с точкой 6, то получатся два треугольника, которые решат эту проблему. Общий случай показан на рис.
Например, точки 1, 2, 5, 6 — точки поверхности. К сожалению, в общем случае эти точки не лежат в одной плоскости, поэтому их нельзя использовать в качестве вершин полигона. Если точку 1 соединить с точкой 6, то получатся два треугольника, которые решат эту проблему. Общий случай показан на рис.  где
где  Хотя эти два треугольника и не лежат в одной плоскости, они могут быть использованы в качестве требуемого полигона при условии, что ребро
Хотя эти два треугольника и не лежат в одной плоскости, они могут быть использованы в качестве требуемого полигона при условии, что ребро  вычерчиваться не будет. В зависимости от положения точки наблюдения любая из сторон треугольников может быть видимой, поэтому после слова Faces в файле данных каждый треугольник необходимо определить дважды:
вычерчиваться не будет. В зависимости от положения точки наблюдения любая из сторон треугольников может быть видимой, поэтому после слова Faces в файле данных каждый треугольник необходимо определить дважды:

Знак минус предотвратит вычерчивание отрезка  .
.
Кроме поверхностей функциональных зависимостей можно также вычертить части положительных координатных полуосей там, где они видны. Их длину должен указать пользователь. Наконец, программа запрашивает некоторое значение координаты  чтобы можно было вычислить положение “центральной точки объекта”, необходимой для программы HIDLINPX. Эта величина не особенно критична, поэтому для нее годится грубая оценка.
чтобы можно было вычислить положение “центральной точки объекта”, необходимой для программы HIDLINPX. Эта величина не особенно критична, поэтому для нее годится грубая оценка.
Для квадратичных функций двух переменных следующая программа носит довольно общий характер. Для других функций  необходимо заменить функцию
необходимо заменить функцию  конце программы и исключить элементы программы, относящиеся к определению коэффициентов
конце программы и исключить элементы программы, относящиеся к определению коэффициентов 
(см. скан)
(см. скан)
УПРАЖНЕНИЯ
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
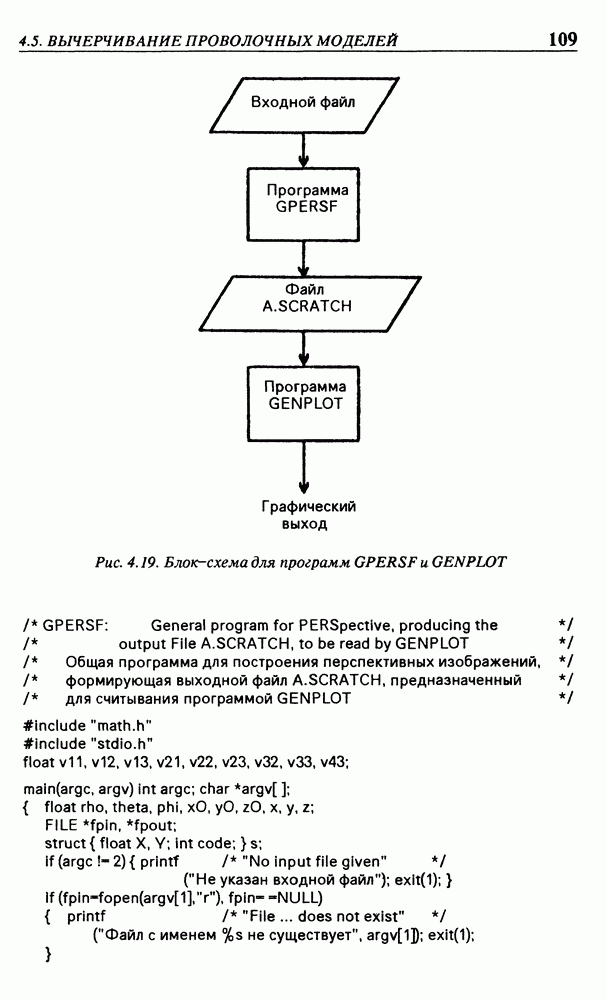
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
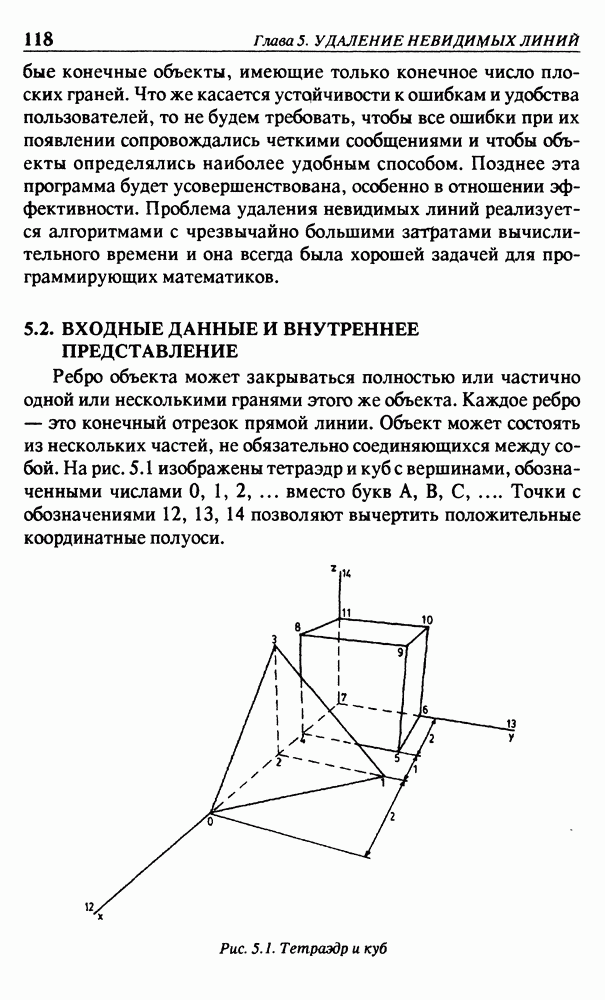
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
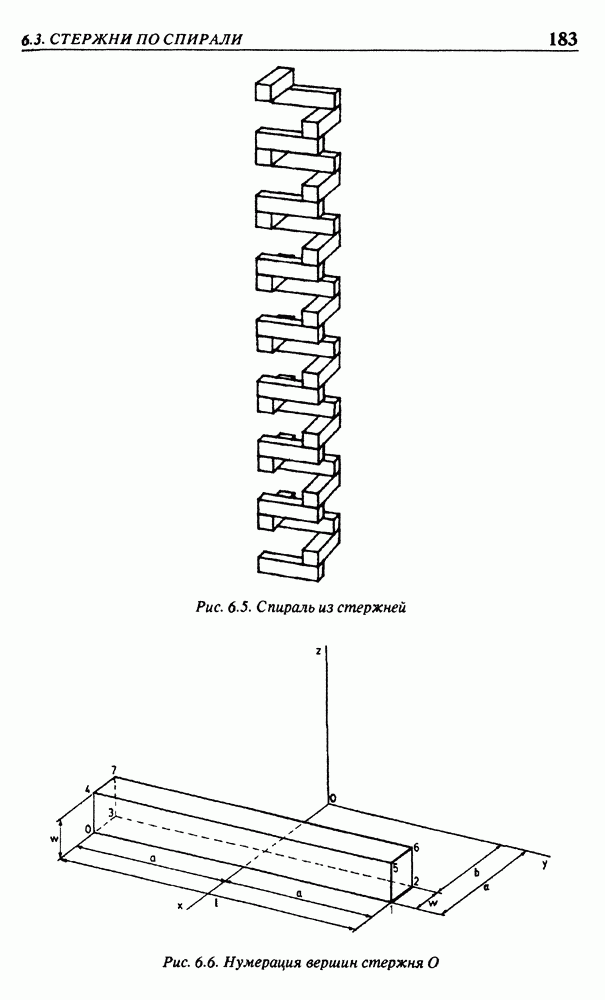
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
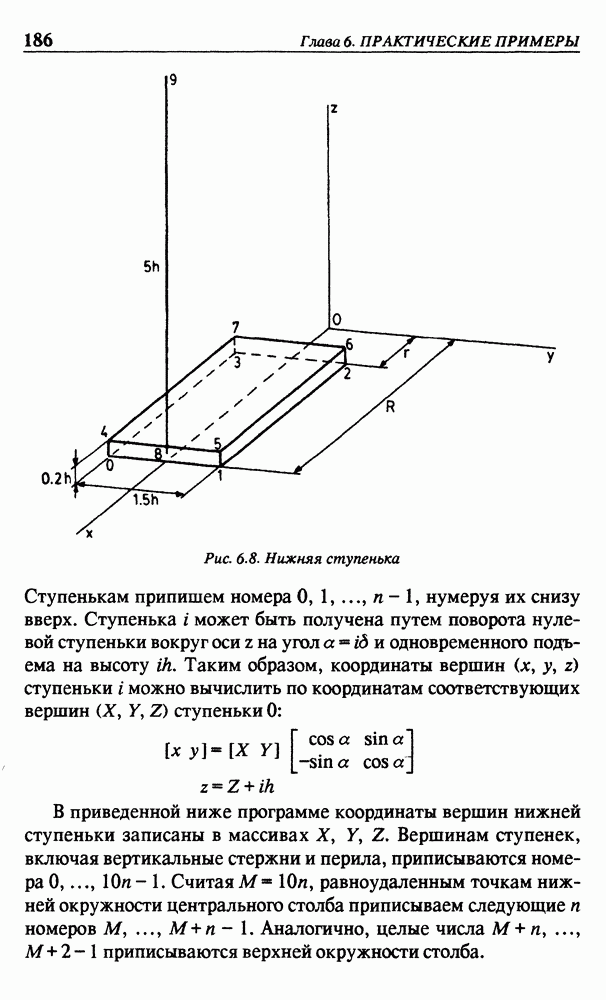
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
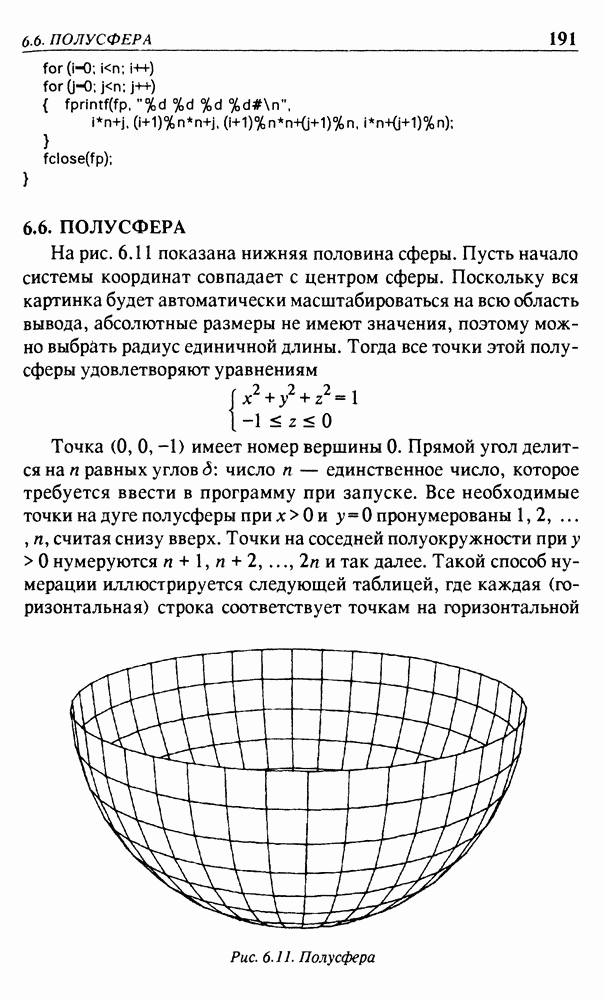
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА