| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.4. ОКНА И ОБЛАСТИ ВЫВОДА
Часто встречаются ситуации, когда требуется вычертить объекты, размеры которых заданы в единицах совершенно несовместимых с экранной системой координат. Например, размеры здания могут быть в сотни раз больше размеров желаемого изображения. С другой стороны, молекула в реальности значительно меньше ее изображения на картинке. Наконец, имеются такие приложения, в которых объект является не какой-либо физической реальностью, а лишь графическим представлением соотношений между некоторыми значениями, например, на рис. 2.6 показана динамика доходов некоей фирмы в начале двадцатого века.
Проблемно-ориентированные размеры выражаются в так называемых мировых координатах. На рис. 2.6 числа 1901, 1902,

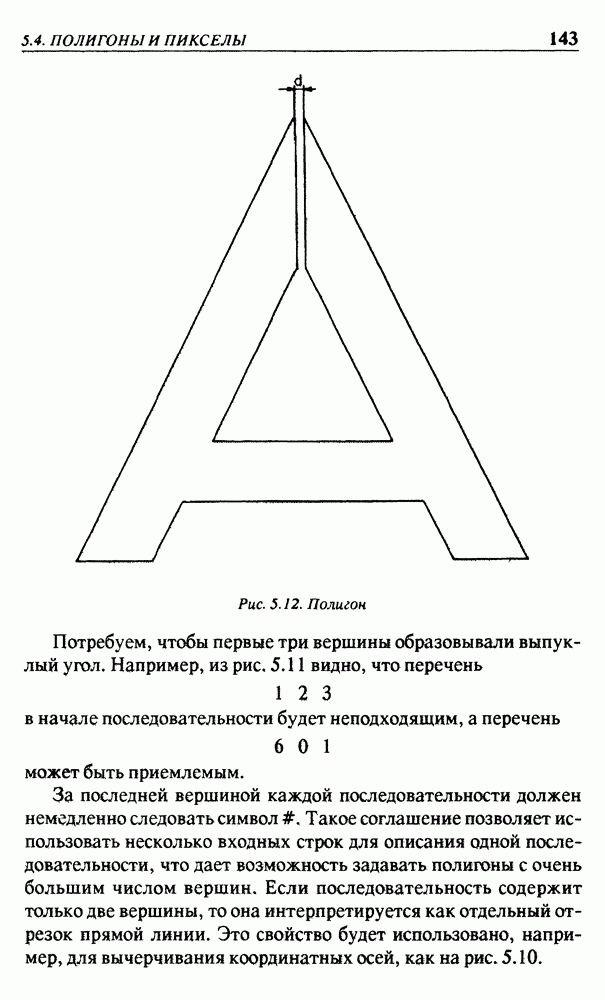
Рис. 2.6. Столбчатая диаграмма в окне
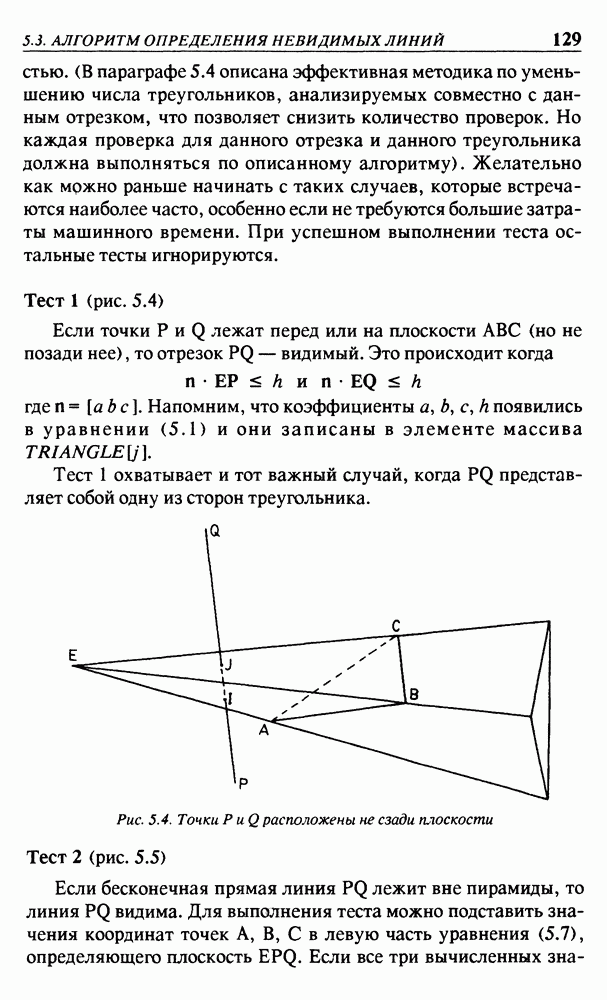
 выражают значения в мировых координатах. Введем теперь концепцию окна. Окно — это прямоугольник, в пределах которого вычерчивается объект (или его часть), как показано на рис. 2.6. Стороны прямоугольника параллельны координатным осям. Во избежание затруднений в понимании происходящего очень важно отметить, что окно относится к объекту, но не к изображению, которое будет сформировано. Если, как обычно, введем горизонтальную ось х и вертикальную ось у, то окно на рис. 2.6 полностью определится значениями:
выражают значения в мировых координатах. Введем теперь концепцию окна. Окно — это прямоугольник, в пределах которого вычерчивается объект (или его часть), как показано на рис. 2.6. Стороны прямоугольника параллельны координатным осям. Во избежание затруднений в понимании происходящего очень важно отметить, что окно относится к объекту, но не к изображению, которое будет сформировано. Если, как обычно, введем горизонтальную ось х и вертикальную ось у, то окно на рис. 2.6 полностью определится значениями:

Очевидно, что размеры и положение окна определяются в системе мировых координат. Эти значения могут показаться неожиданными для читателя, поскольку окно вводится для определения желаемого изображения на картинке и, на первый взгляд, более приемлемым было бы задать эти значения в дюймах, чем указать какое-то фиктивное значение дохода, равное  в качестве минимального значения
в качестве минимального значения  по оси у. Однако задание окна в системе мировых координат является обычным и очень Удобным на практике.
по оси у. Однако задание окна в системе мировых координат является обычным и очень Удобным на практике.
Необходимо также задать прямоугольную область на экране, которая определит размеры желаемой картинки. Эта область называется областью вывода. Она задается аналогично окну, то есть указываются минимальные и максимальные значения по
координатным осям  в единицах измерения на экране.
в единицах измерения на экране.  значения будут обозначаться прописными буквами
значения будут обозначаться прописными буквами  пичным примером задания области вывода могут быть значения
пичным примером задания области вывода могут быть значения
Хтгйп 

Теперь окно нужно отобразить на область вывода. Например заданное значение в мировых координатах  должно бьпп преобразовано в экранную координату
должно бьпп преобразовано в экранную координату  Вначале вычисля ются коэффициенты масштабирования по осям:
Вначале вычисля ются коэффициенты масштабирования по осям:

В нашем случае найдем, что  расстояние
расстояние  точки изображения от левого края области вывода вычисляется умножением коэффициента
точки изображения от левого края области вывода вычисляется умножением коэффициента  на соответ ствующее расстояние
на соответ ствующее расстояние  от исходной точки до левого
от исходной точки до левого  окна. Расстояние
окна. Расстояние  находится аналогично. Следовательно координаты точки изображения будут определены из соотношений
находится аналогично. Следовательно координаты точки изображения будут определены из соотношений

Закончим этот параграф тремя замечаниями:
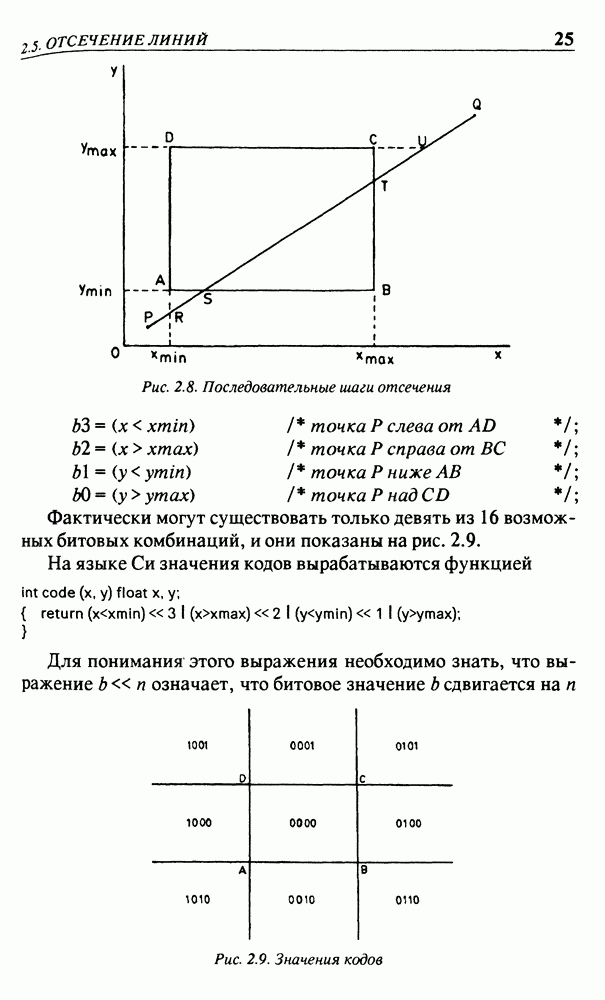
1. Окно совсем не обязательно должно охватывать весь объект целиком. Если оно не охватывает весь объект, то части  екта, находящиеся вне окна, не вычерчиваются — они дол
екта, находящиеся вне окна, не вычерчиваются — они дол  быть отсечены. Эта операция носит название отсече ние, более подробно она обсуждается в параграфе 2.5.
быть отсечены. Эта операция носит название отсече ние, более подробно она обсуждается в параграфе 2.5.
2. В общем случае коэффициенты  различны. Для столб чатой диаграммы это как раз то, что надо. Но совсем не
различны. Для столб чатой диаграммы это как раз то, что надо. Но совсем не  дится, когда угловые соотношения на изображении должнь быть точно такими же, как на объекте. В этом случае в
дится, когда угловые соотношения на изображении должнь быть точно такими же, как на объекте. В этом случае в  честве коэффициента масштабирования следует выбрать наименьшее из значений
честве коэффициента масштабирования следует выбрать наименьшее из значений  Поэтому рекомендуется
Поэтому рекомендуется
заменить выражение (2.12) на формулы, основанные на пересчете координат относительно центров окна и области вывода. Это будет описано в параграфе 2.6.
3. Размеры и положение окна не всегда известны заранее. В параграфе 2.6 будет показан способ их вычисления вместо задания пользователем.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
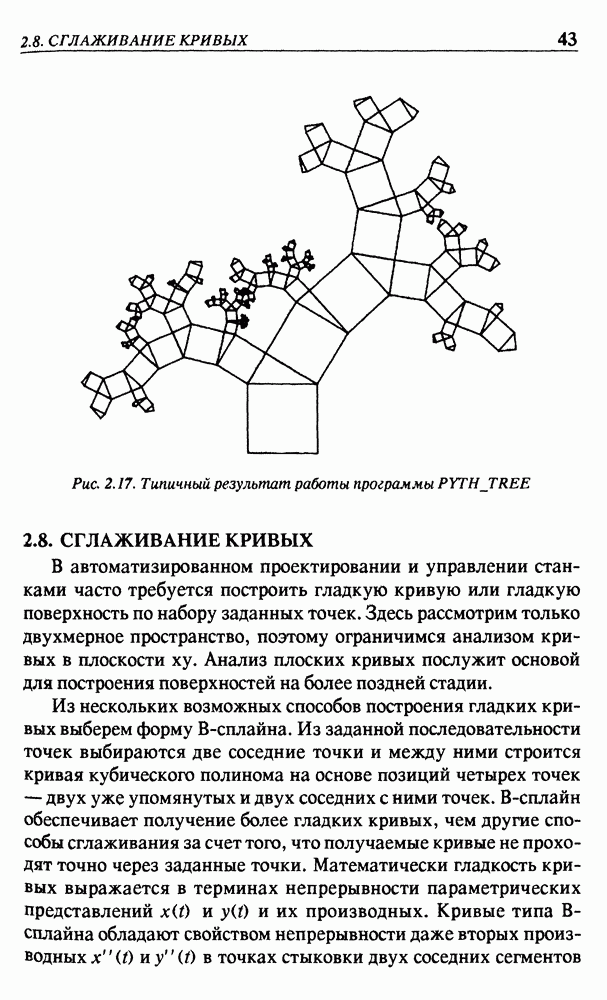
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
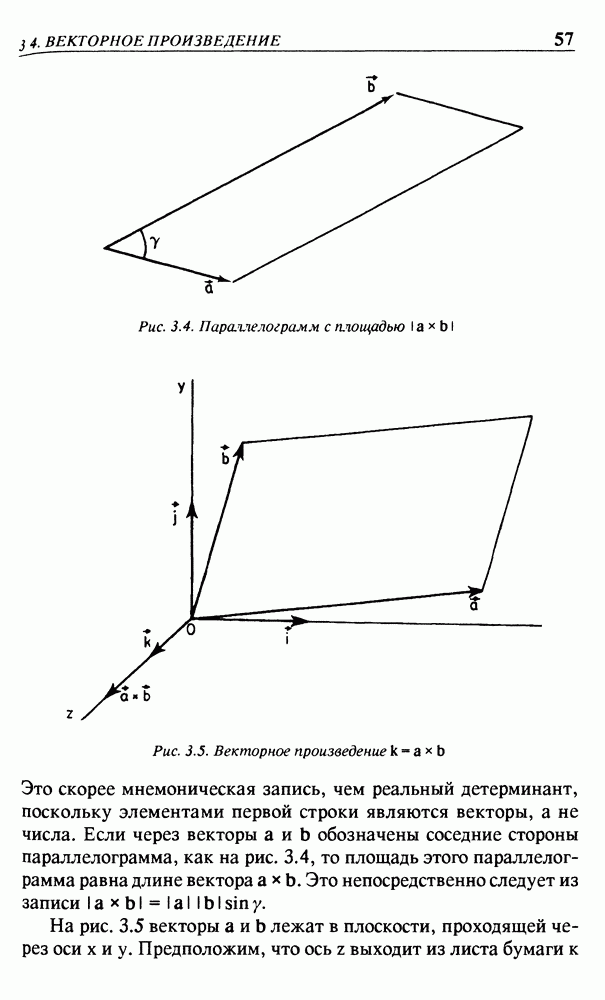
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
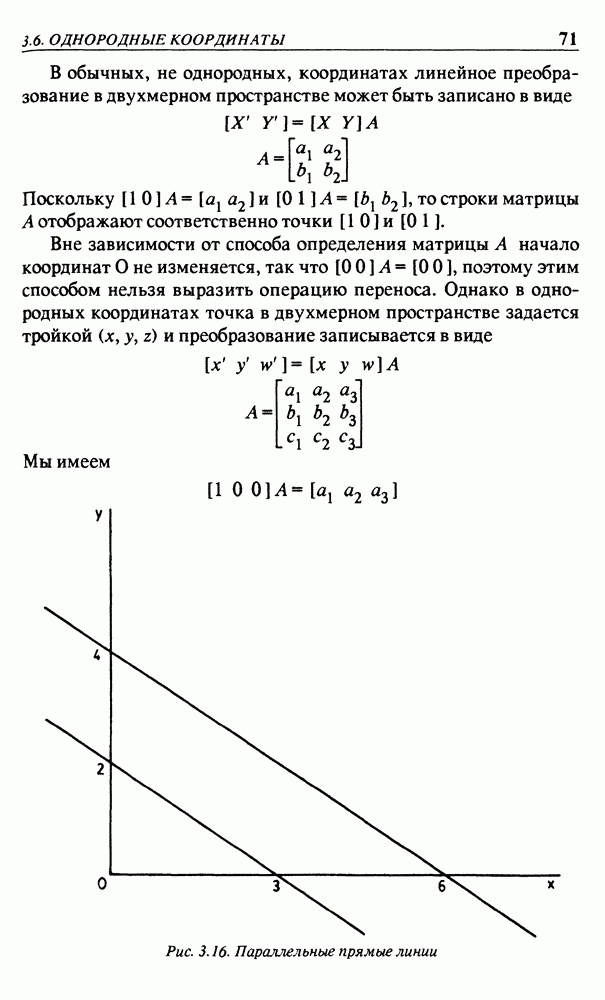
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
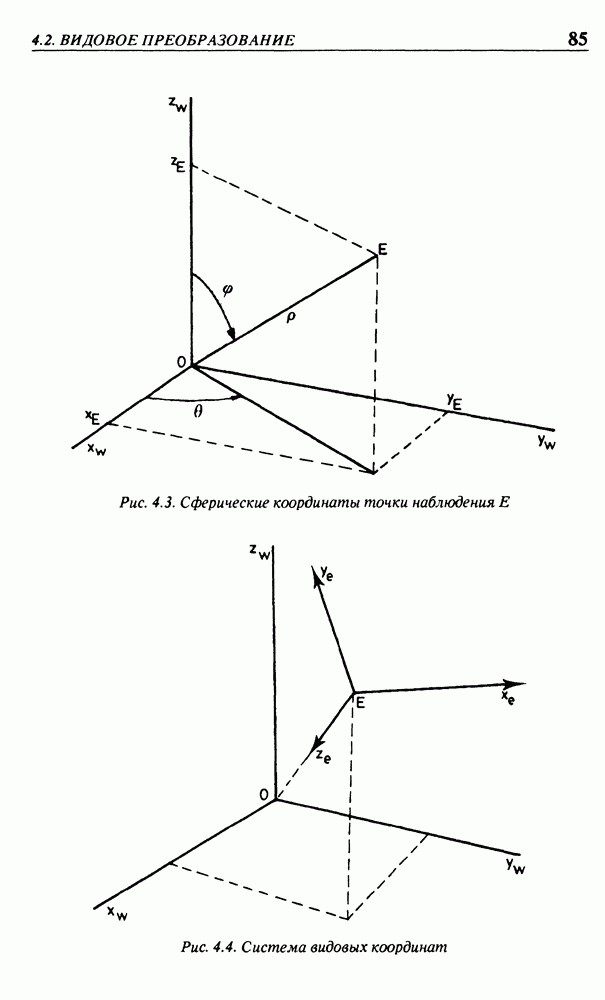
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
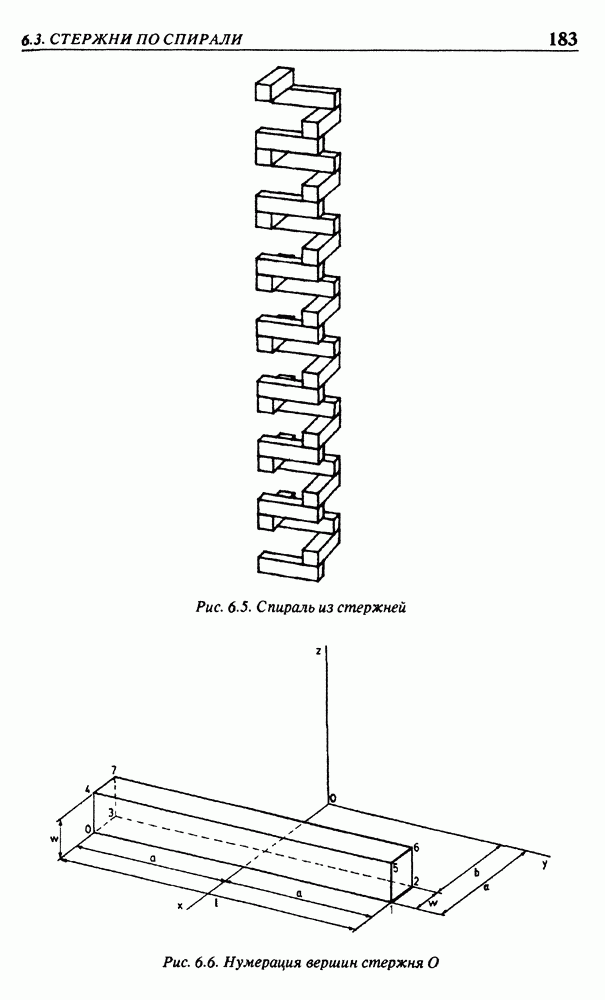
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
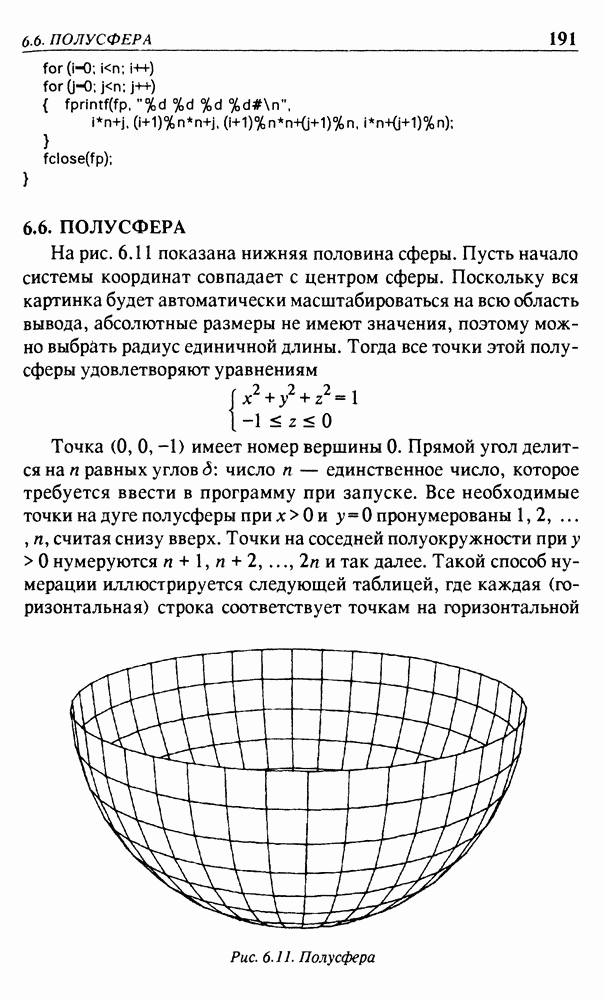
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА