| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.2. ПОЛЫЙ ЦИЛИНДР
Большое число объектов имеет кривые поверхности. Такие поверхности можно аппроксимировать полигонами. Для примера рассмотрим полый цилиндр, показанный на рис. 6.3(б). Для некоторого достаточно большого целого числа  выберем
выберем  равноудаленных точек на внешней окружности (с радиусом
равноудаленных точек на внешней окружности (с радиусом  на верхней грани и столько же аналогичных точек на нижней грани. Затем аппроксимируем внешний цилиндр с помощью призмы, вершинами которой являются эти
на верхней грани и столько же аналогичных точек на нижней грани. Затем аппроксимируем внешний цилиндр с помощью призмы, вершинами которой являются эти  точек. Есть также и внутренний цилиндр с радиусом
точек. Есть также и внутренний цилиндр с радиусом  Оба цилиндра имеют высоту А и ось, совпадающую с осью z нашей системы координат. Внутренний цилиндр также аппроксимируется призмой аналогично внешнему цилиндру. Нижняя грань лежит в плоскости
Оба цилиндра имеют высоту А и ось, совпадающую с осью z нашей системы координат. Внутренний цилиндр также аппроксимируется призмой аналогично внешнему цилиндру. Нижняя грань лежит в плоскости  а верхняя грань — в плоскости
а верхняя грань — в плоскости  Подлежащий вычерчиванию объект и его положение полностью определяются значениями
Подлежащий вычерчиванию объект и его положение полностью определяются значениями  и А. Сначала рассмотрим случай
и А. Сначала рассмотрим случай  а затем позднее обобщим его для произвольного
а затем позднее обобщим его для произвольного 
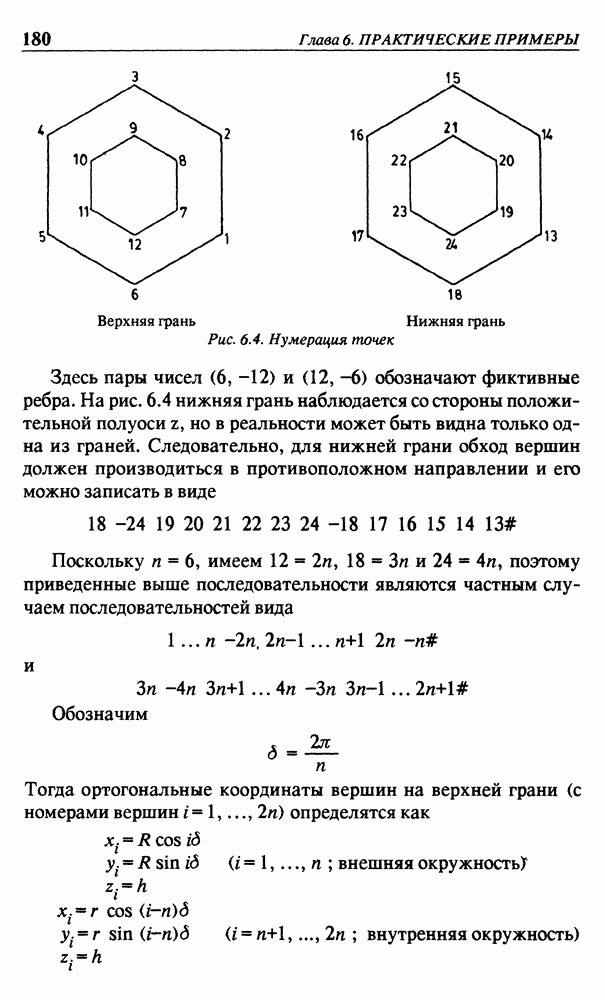
Пронумеруем вершины, как показано на рис. 6.4. Для каждой вершины  на верхней грани
на верхней грани  существует вертикальное ребро, соединяющее ее с вершиной
существует вертикальное ребро, соединяющее ее с вершиной  Верхняя грань может быть описана последовательностью
Верхняя грань может быть описана последовательностью


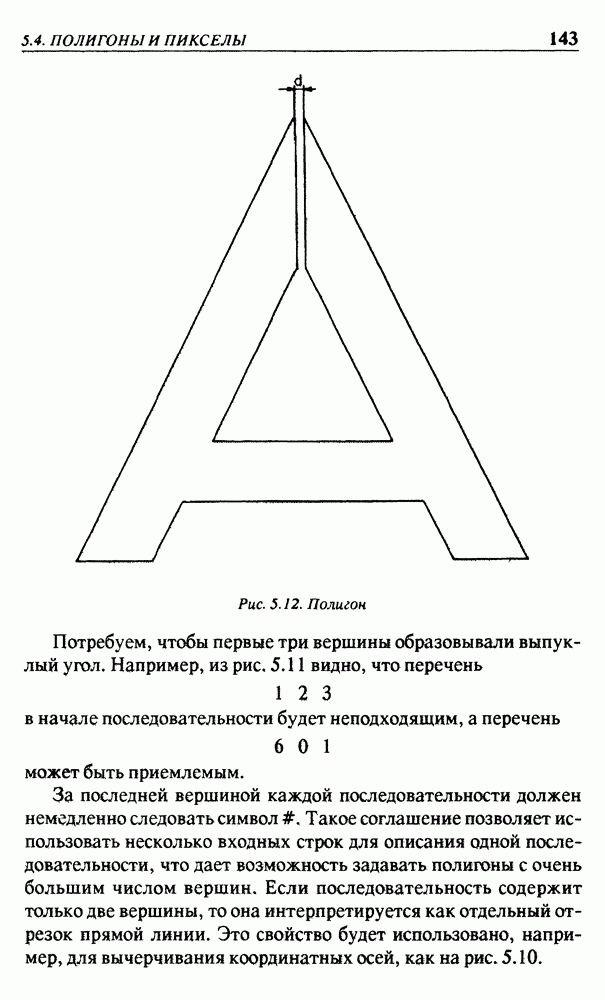
Рис. 6.3. 

Рис. 6.4. Нумерация точек
Здесь пары чисел (6, -12) и (12, -6) обозначают фиктивные ребра. На рис. 6.4 нижняя грань наблюдается со стороны положительной полуоси  но в реальности может быть видна только одна из граней. Следовательно, для нижней грани обход вершин должен производиться в противоположном направлении и его можно записать в виде
но в реальности может быть видна только одна из граней. Следовательно, для нижней грани обход вершин должен производиться в противоположном направлении и его можно записать в виде

Поскольку  имеем
имеем  поэтому приведенные выше последовательности являются частным случаем последовательностей вида
поэтому приведенные выше последовательности являются частным случаем последовательностей вида

и

Обозначим

Тогда ортогональные координаты вершин на верхней грани (с номерами вершин  определятся как
определятся как

Для нижней грани будем иметь

Ниже приведена программа для вычерчивания полой призмы. Выбрав достаточно большое целое число  получим хорошую аппроксимацию цилиндра, что демонстрирует рис. 6.3(б).
получим хорошую аппроксимацию цилиндра, что демонстрирует рис. 6.3(б).
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
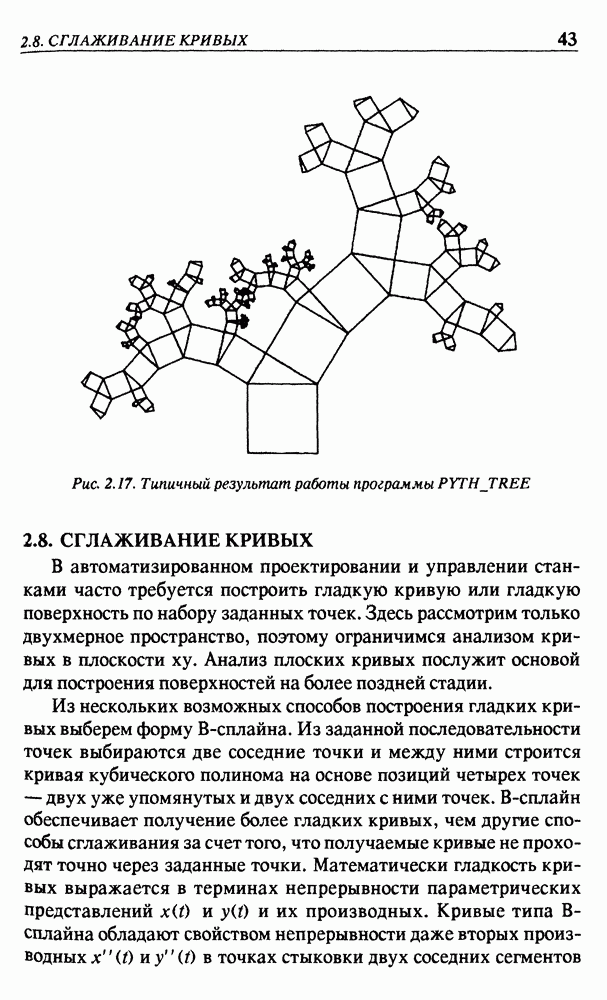
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
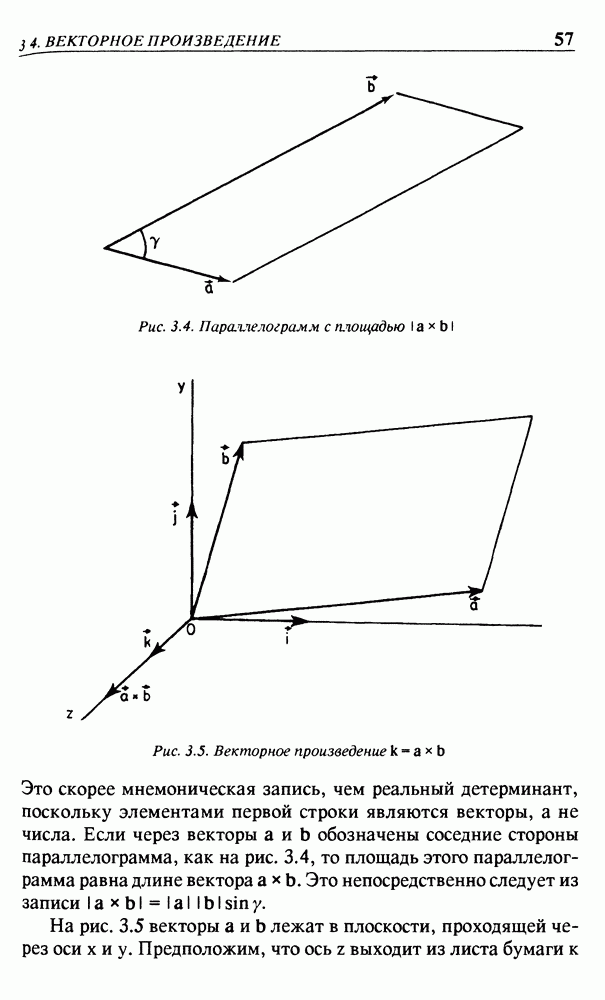
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
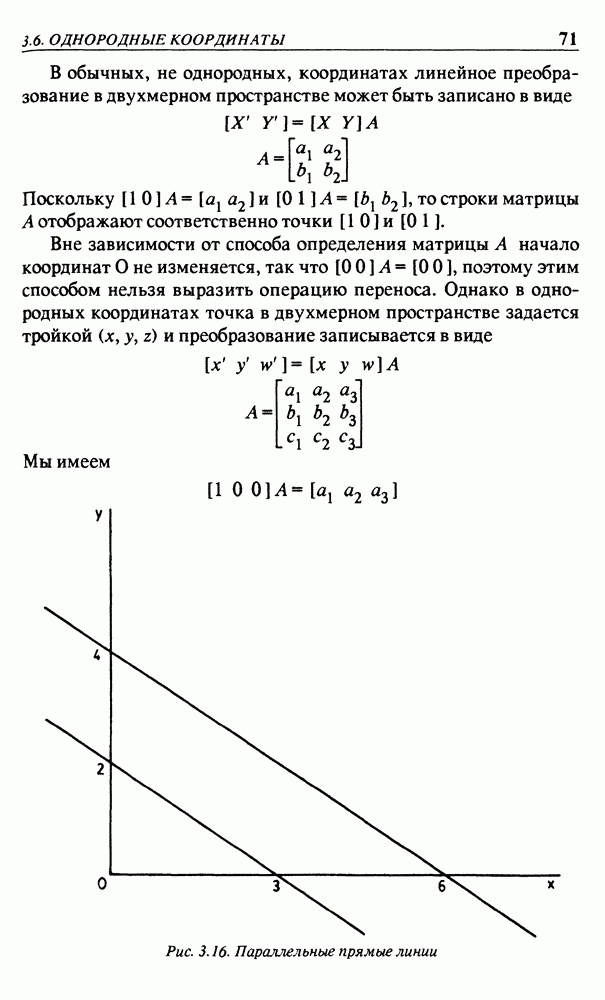
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
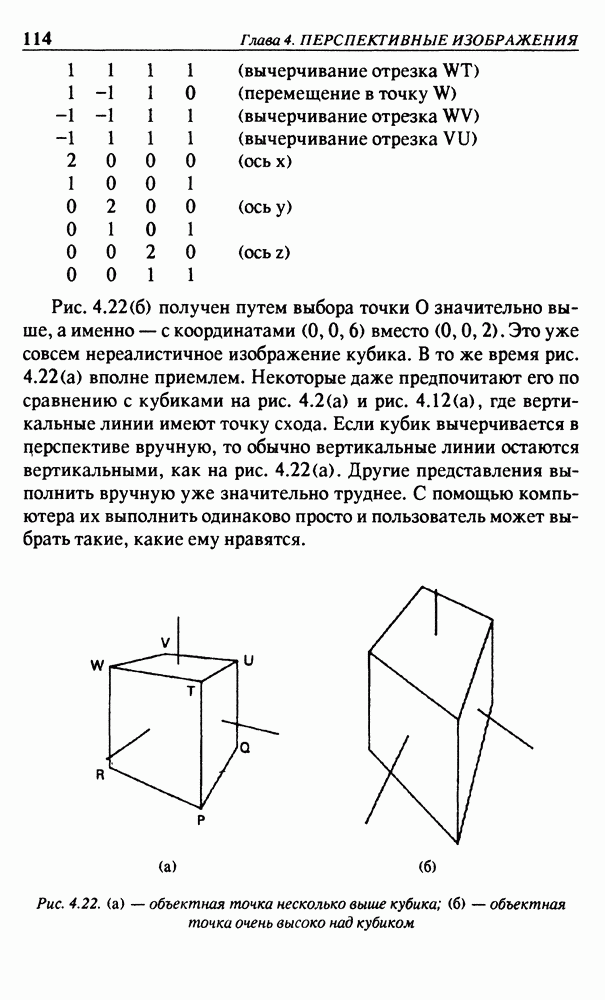
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
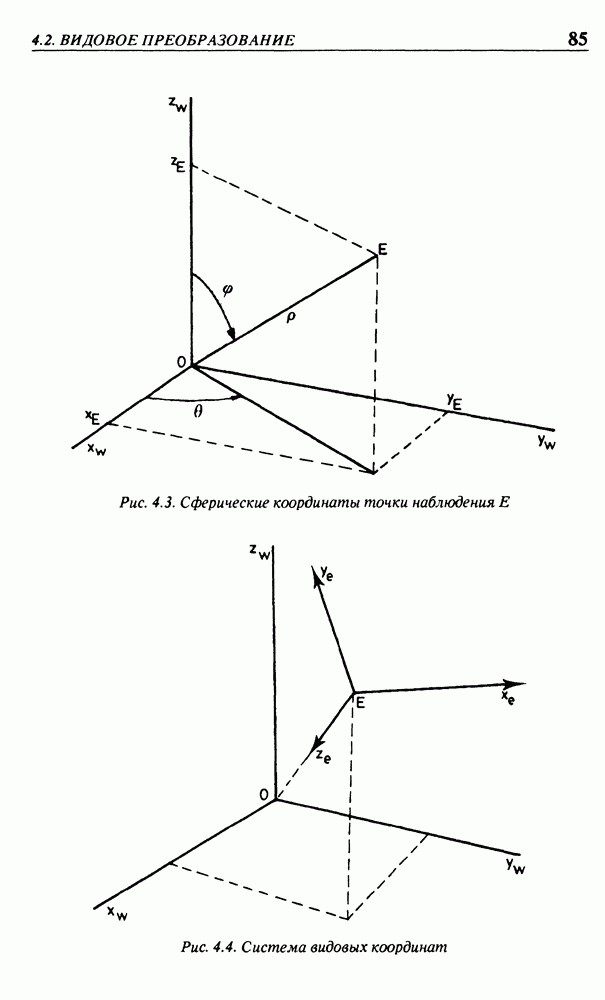
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
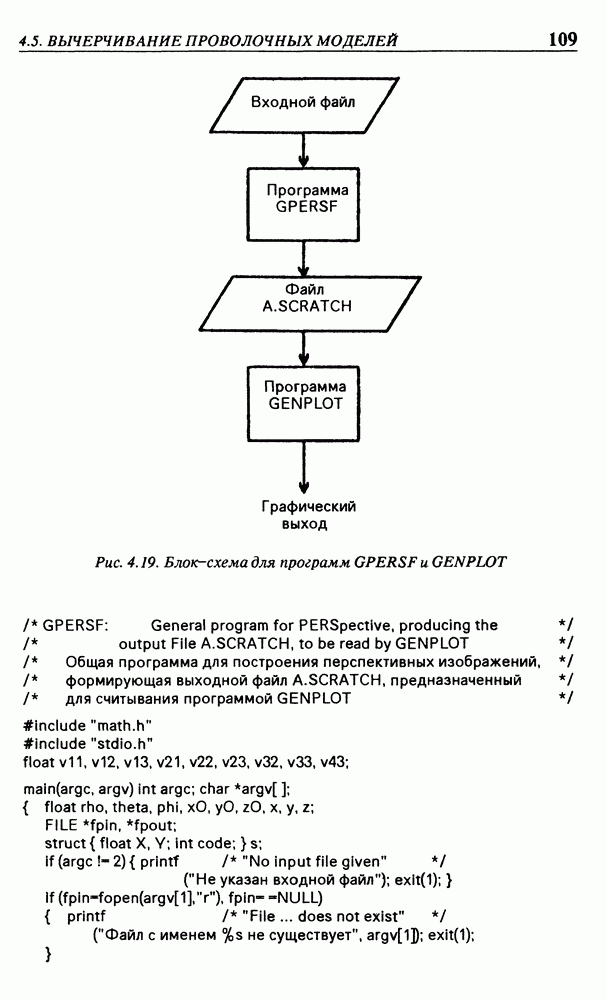
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
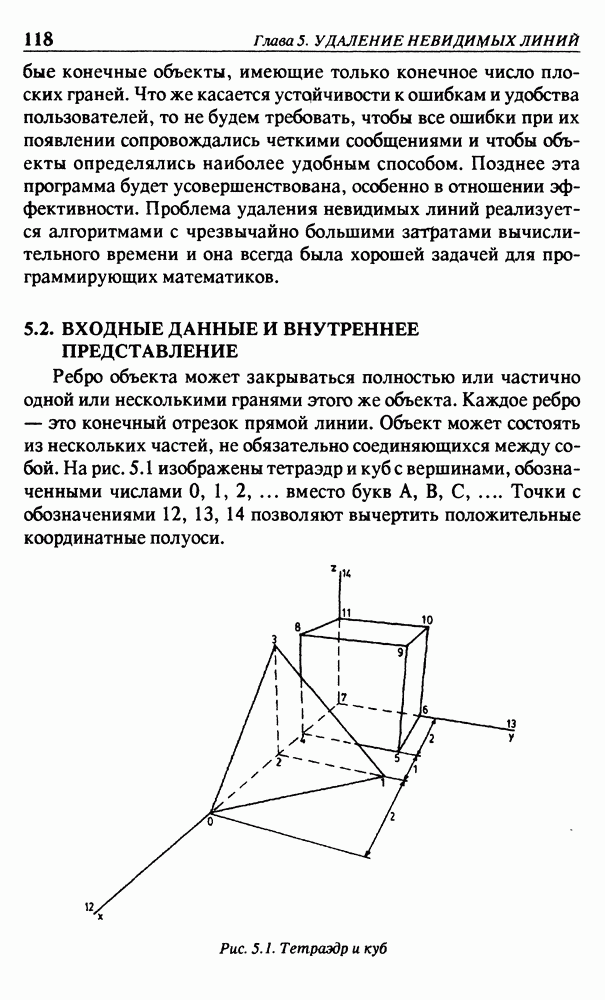
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
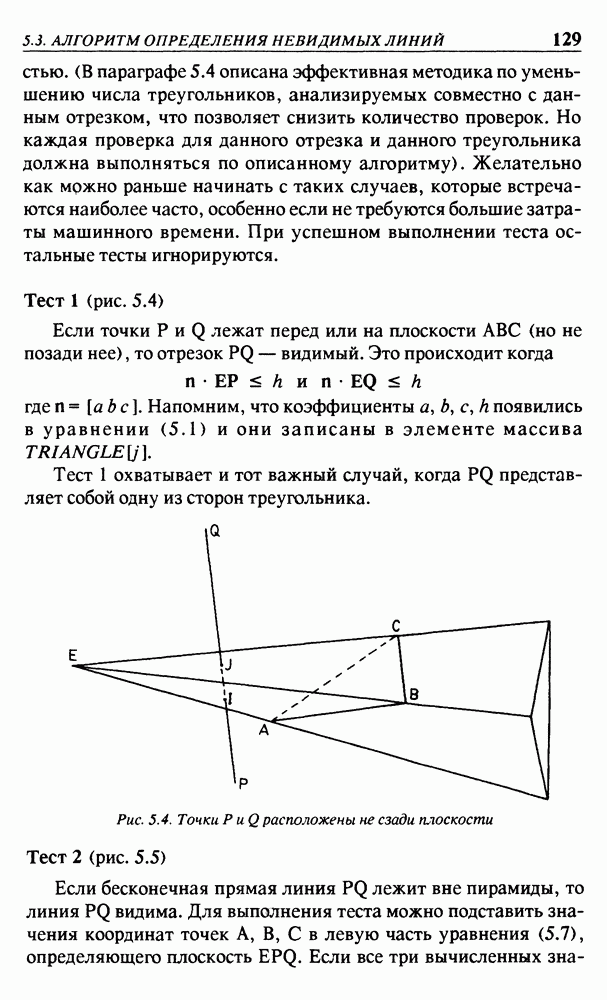
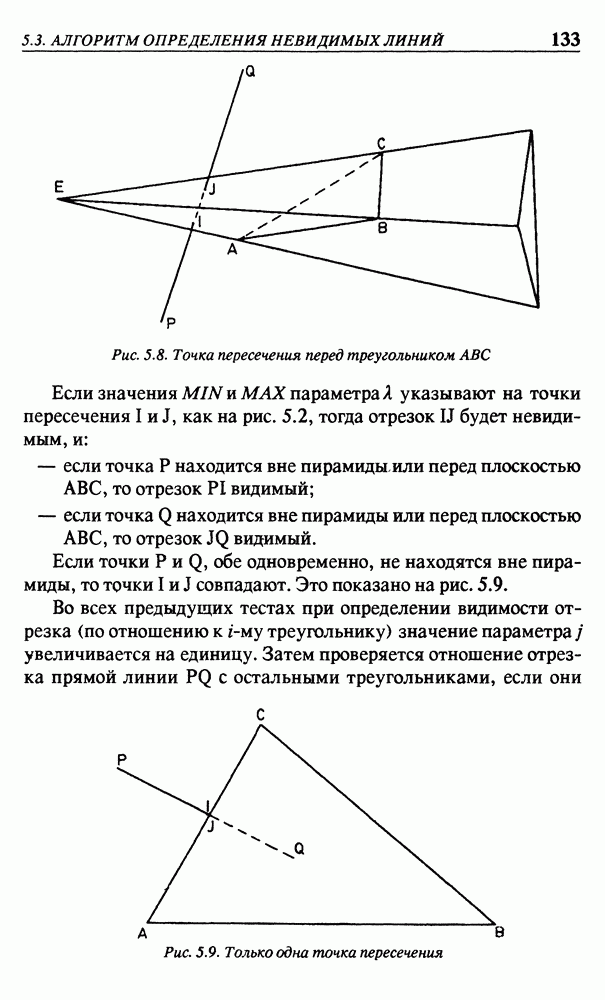
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
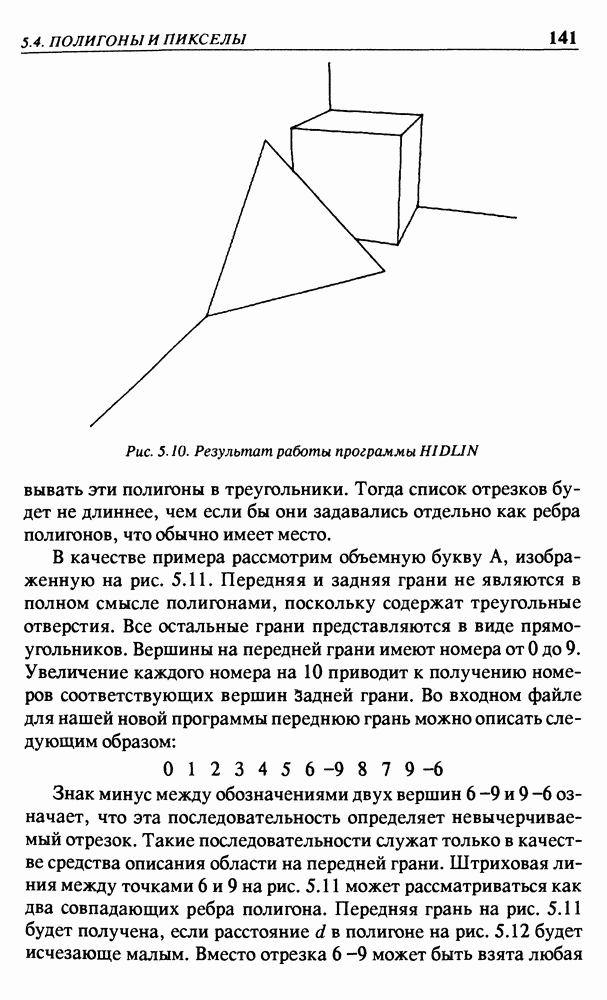
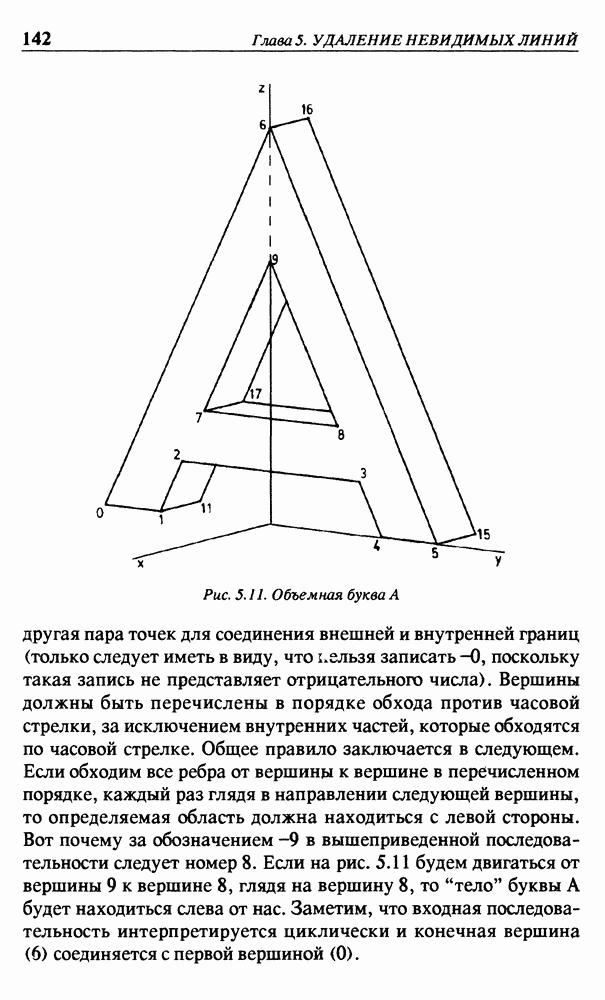
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
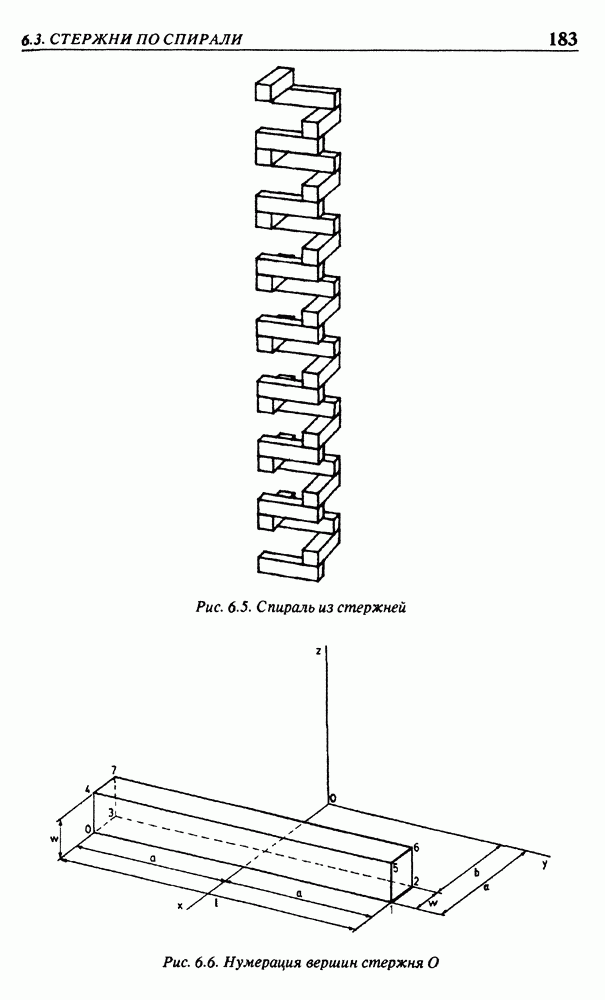
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
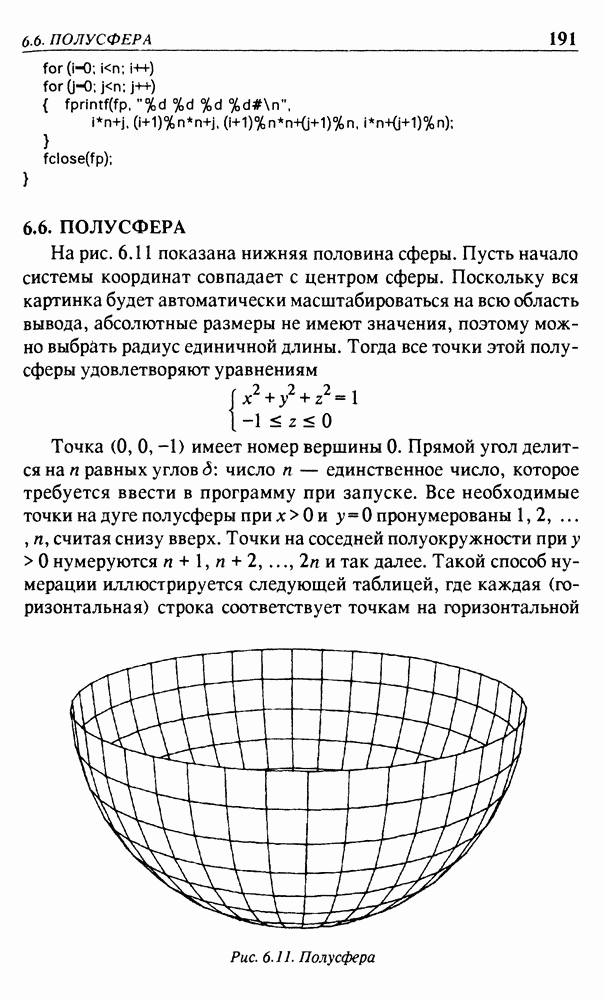
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА