| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
Векторное произведение двух векторов а и b обозначается

и равно вектору  который обладает следующими свойствами. Если
который обладает следующими свойствами. Если  для некоторого скаляра с, то
для некоторого скаляра с, то  В противном случае длина вектора
В противном случае длина вектора  равна
равна

где у — угол между векторами а и  а направление вектора
а направление вектора  перпендикулярно обоим векторам а и b и таково, что
перпендикулярно обоим векторам а и b и таково, что  именно в таком порядке, образуют правостороннюю тройку. По» следнее означает, что если вектор а поворачивается на угол
именно в таком порядке, образуют правостороннюю тройку. По» следнее означает, что если вектор а поворачивается на угол  в направлении к вектору
в направлении к вектору  то вектор
то вектор  имеет направление перемещения винта с правой резьбой, поворачиваемого в том же направлении. Из этого определения можно вывести следующие свойства векторного произведения:
имеет направление перемещения винта с правой резьбой, поворачиваемого в том же направлении. Из этого определения можно вывести следующие свойства векторного произведения:

В общем случае а 
Используя правую ортогональную систему координат, как и в параграфе 3.1, с единичными векторами  будем иметь
будем иметь

Используя эти значения векторных произведений в расширенной записи векторного произведения

получим

что может быть записано в виде

или в форме, более удобной для запоминания:


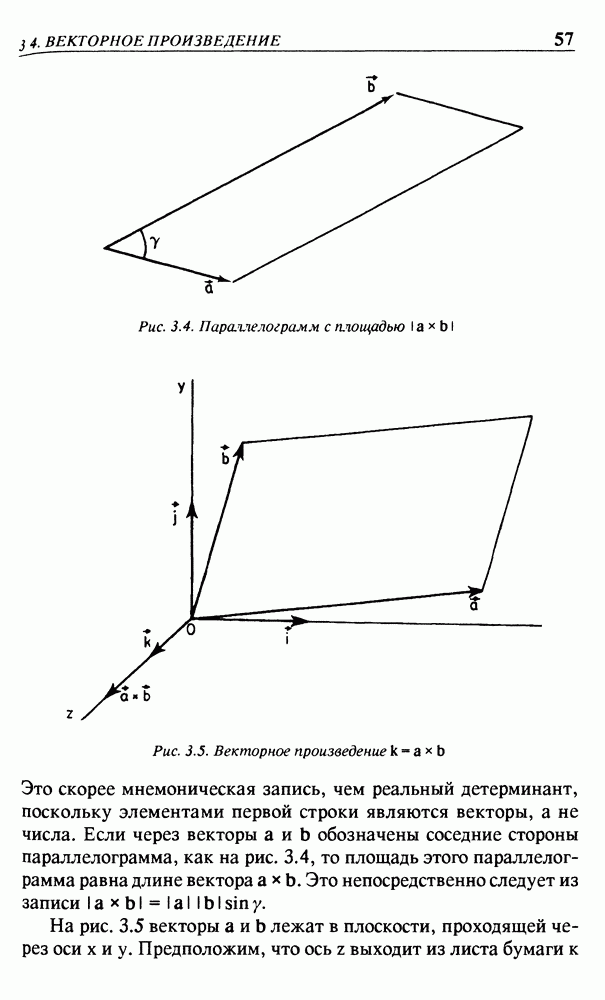
Рис. 3.4. Параллелограмм с площадью 

Рис. 3.5. Векторное произведение к 
Это скорее мнемоническая запись, чем реальный детерминант, поскольку элементами первой строки являются векторы, а не числа. Если через векторы а и b обозначены соседние стороны параллелограмма, как на рис. 3.4, то площадь этого параллелограмма равна длине вектора а  Это непосредственно следует из записи
Это непосредственно следует из записи 
На рис. 3.5 векторы а и b лежат в плоскости, проходящей через оси х и у. Предположим, что ось z выходит из листа бумаги к
читателю и соответствует правой координатной системе. Тогда для трехмерного пространства

Таким образом, вектор а  будет иметь то же направление, что и вектор к, но только в том случае, если детерминант
будет иметь то же направление, что и вектор к, но только в том случае, если детерминант

имеет положительный знак. Это налагает условие, что вектор а, поворачиваемый по направлению к вектору b на угол меньше 180°, вращается в положительном направлении (против часовой стрелки) тогда, и только тогда, когда  Этот способ будем ниже использовать для определения, обходятся ли вершины треугольника А, В, С в направлении против часовой стрелки при их перечислении именно в этом порядке.
Этот способ будем ниже использовать для определения, обходятся ли вершины треугольника А, В, С в направлении против часовой стрелки при их перечислении именно в этом порядке.
На рис. 3.6. имеем


Рис. 3.6. Точки А, В, С обходятся против часовой стрелки

Вершины А, В, С, именно в этом порядке, обходятся в направлении против часовой стрелки, если, и только если, вектор и поворачивается в сторону направления вектора  на угол
на угол  против часовой стрелки. Это означает, что направление обхода точек А, В, С может быть установлено на основе анализа детерминанта
против часовой стрелки. Это означает, что направление обхода точек А, В, С может быть установлено на основе анализа детерминанта

следующим образом:
 точки А, В, С обходятся против часовой стрелки;
точки А, В, С обходятся против часовой стрелки;
 точки А, В, С обходятся по часовой стрелке;
точки А, В, С обходятся по часовой стрелке;
 точки А, В, С лежат на одной прямой.
точки А, В, С лежат на одной прямой.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
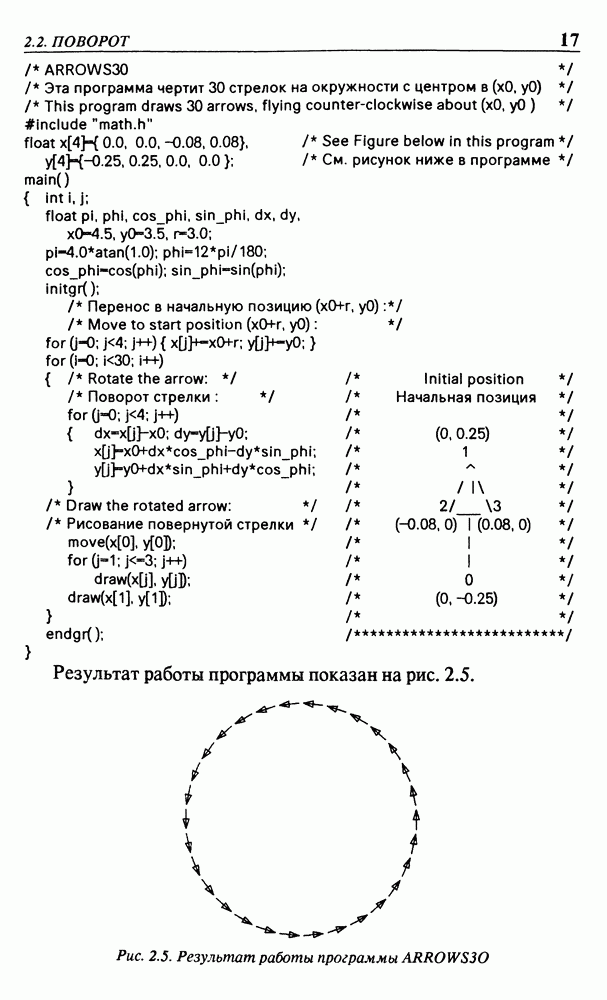
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
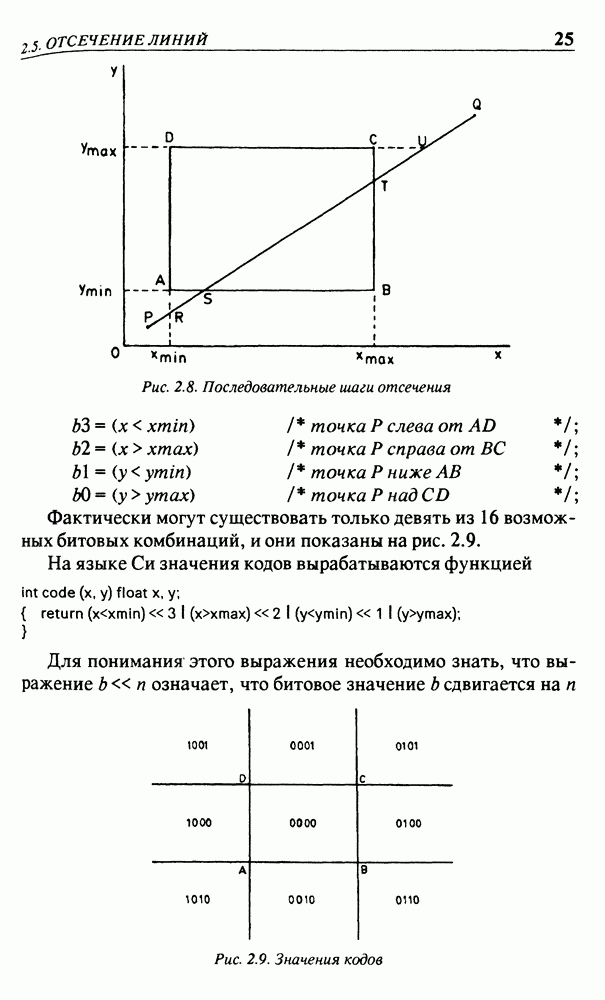
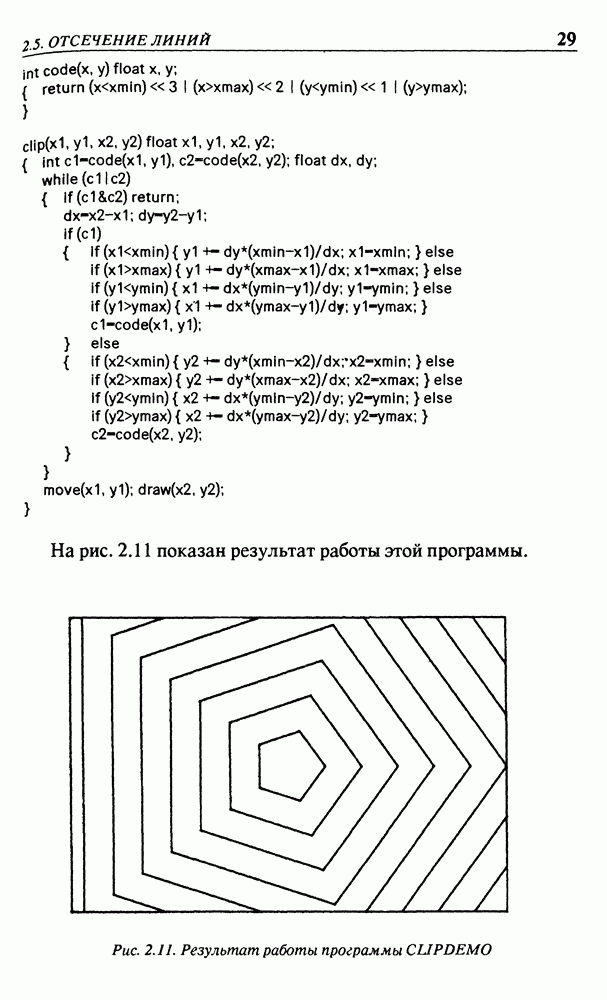
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
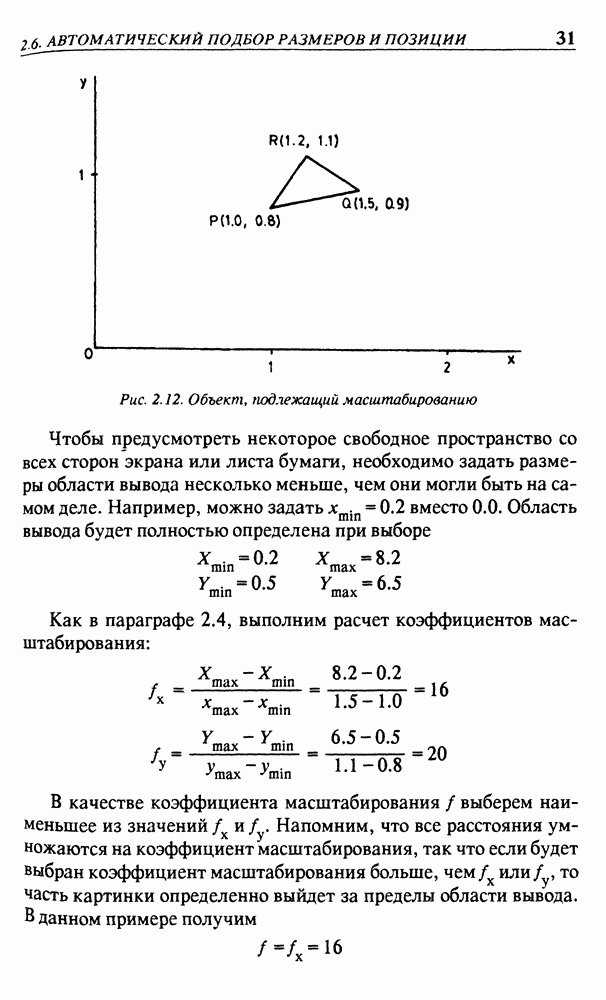
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
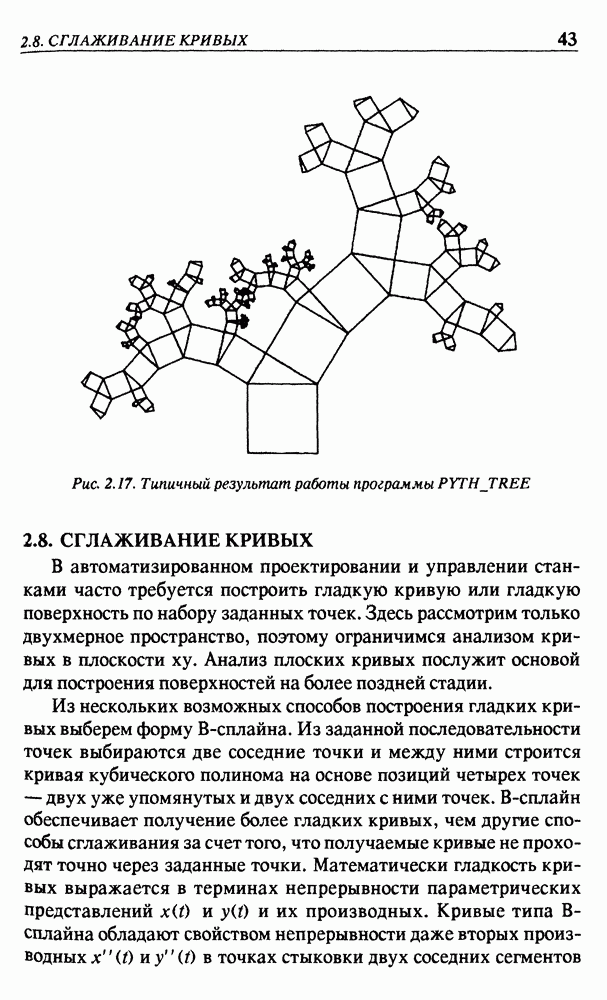
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
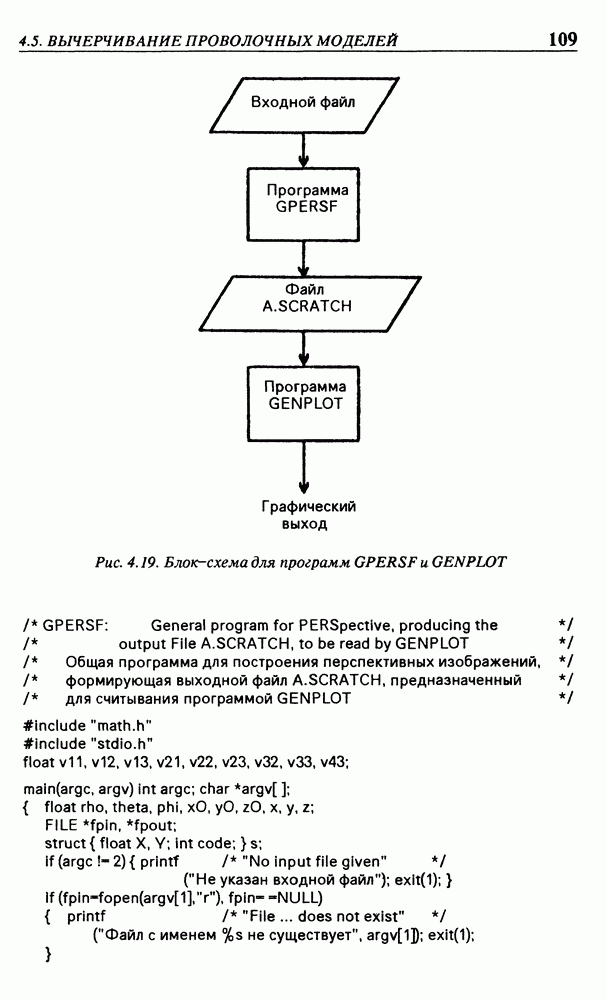
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
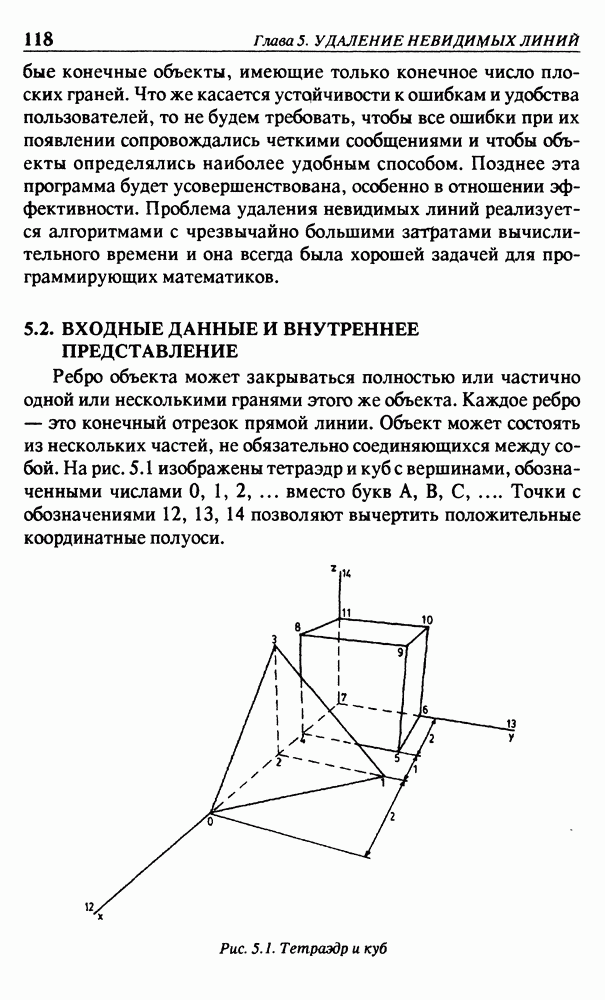
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
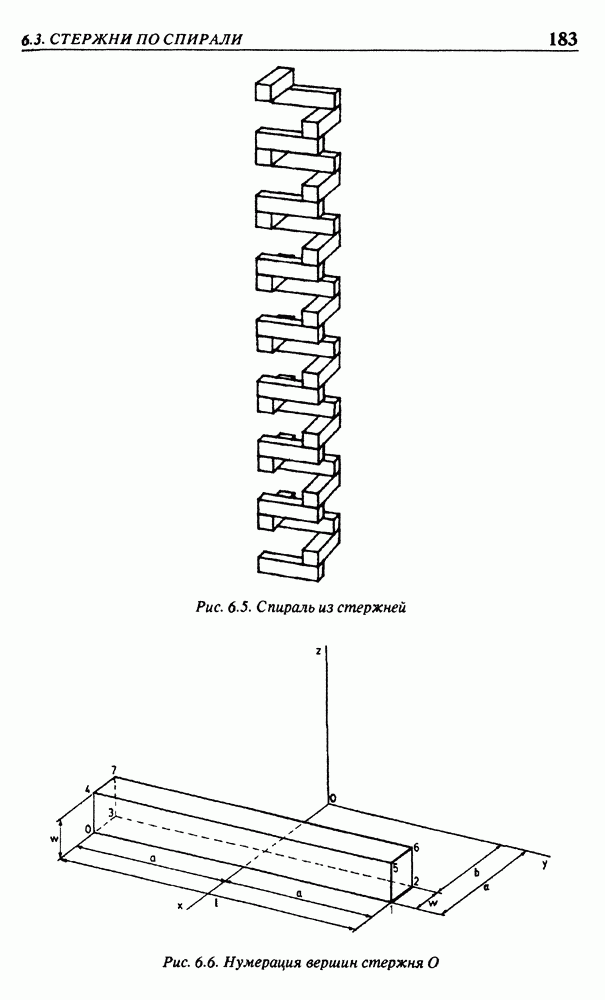
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
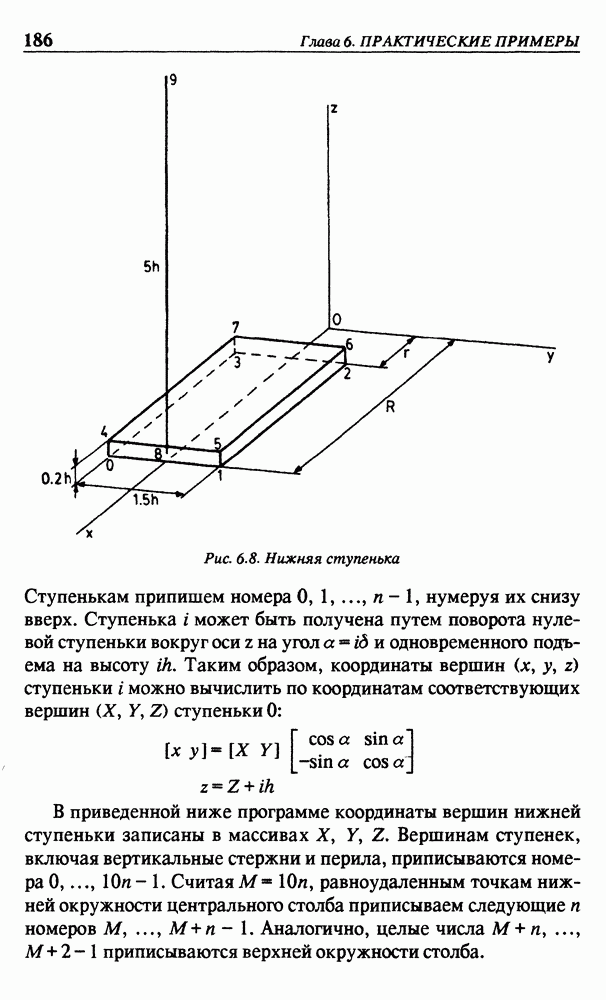
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
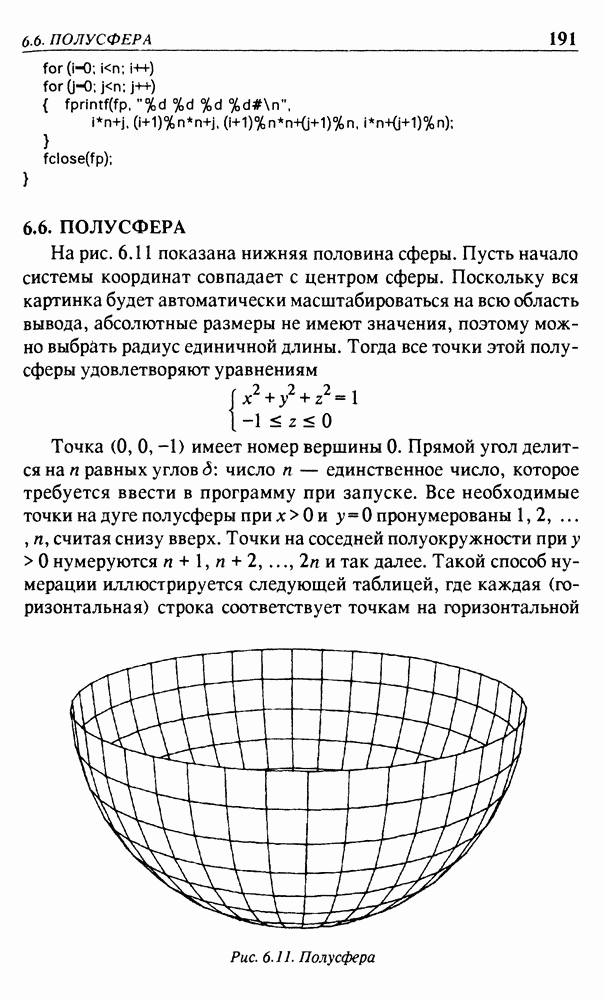
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА