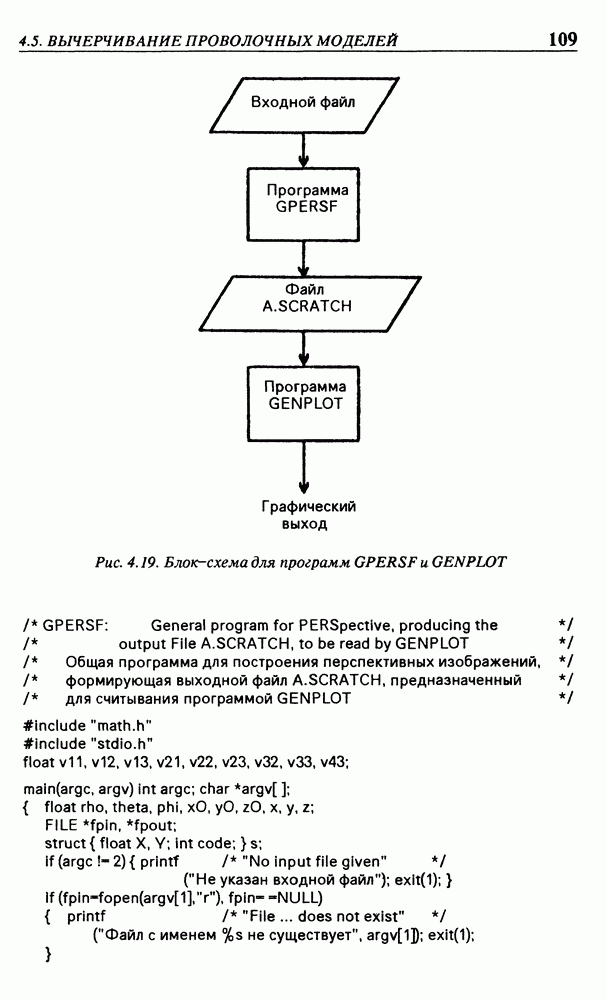
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
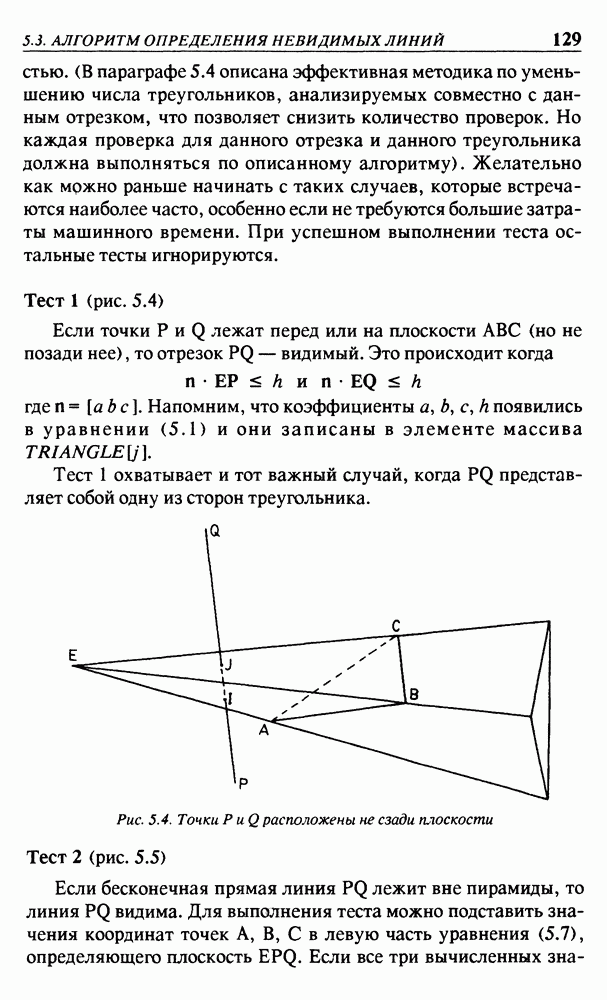
Ребро объекта может закрываться полностью или частично одной или несколькими гранями этого же объекта. Каждое ребро
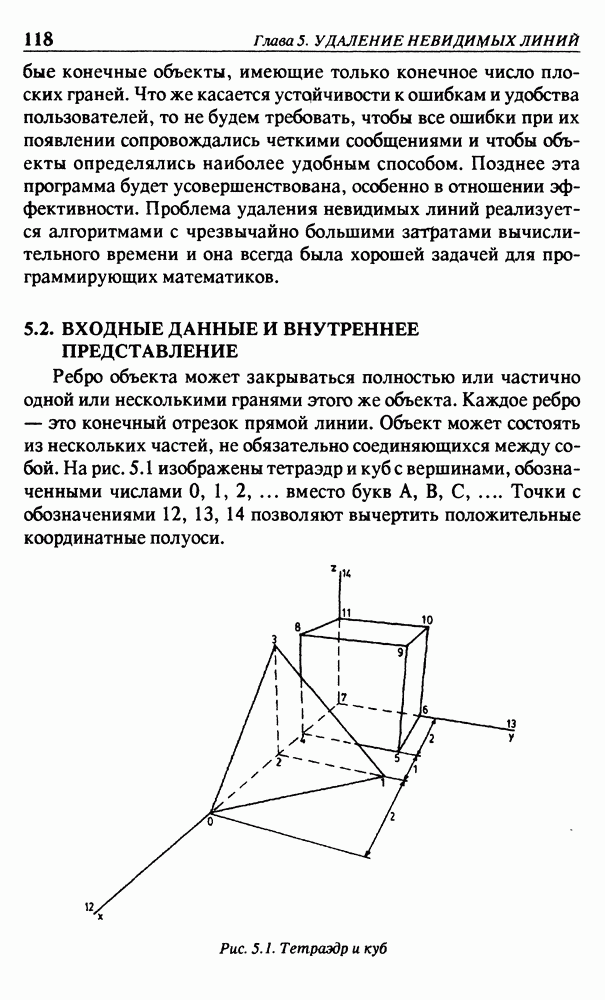
— это конечный отрезок прямой линии. Объект может состоять из нескольких частей, не обязательно соединяющихся между собой. На рис. 5.1 изображены тетраэдр и куб с вершинами, обозначенными числами  вместо букв
вместо букв  Точки с обозначениями 12, 13, 14 позволяют вычертить положительные координатные полуоси.
Точки с обозначениями 12, 13, 14 позволяют вычертить положительные координатные полуоси.

Рис. 5.1. Тетраэдр и куб
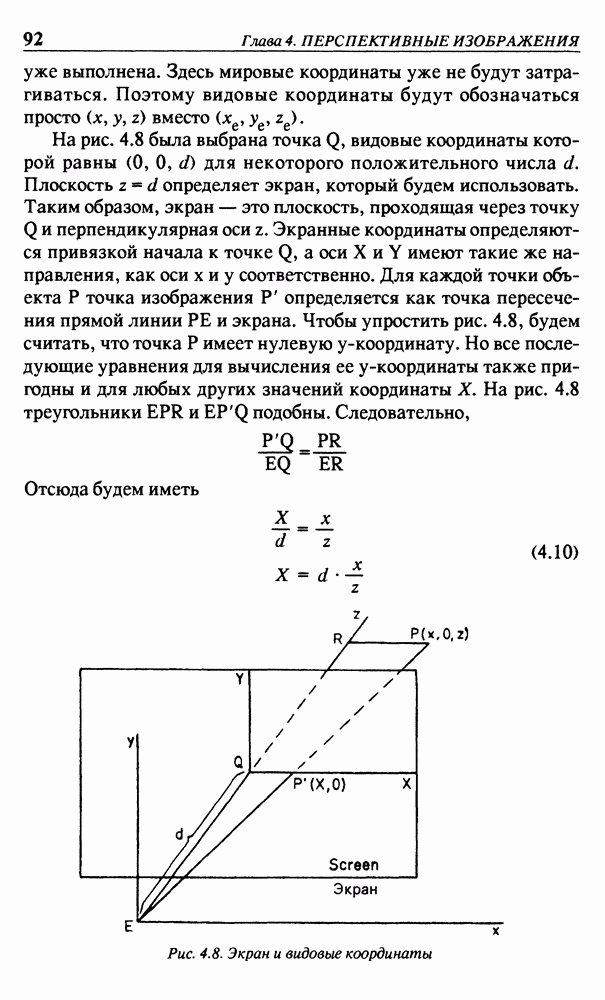
Составим такую программу, которая прочтет данные, описывающие точку наблюдения и объекты. Для любой (реальной) точки наблюдения графический вывод будет представлять собой изображение объекта. В противовес главе 4 будем считать объект непрозрачным. Как и в параграфе 4.5, пользователь должен задать две входные строки данных, определяющие точку О в прямоугольной системе координат и сферические координаты  для точки наблюдения. Для рис. 5.1 это будут следующие строки:
для точки наблюдения. Для рис. 5.1 это будут следующие строки:

Не будем здесь уделять много внимания удобству пользователя, а лучше введем концепцию кодирования вершин: поскольку каждая вершина потребуется несколько раз, то было бы очень нецелесообразно многократно задавать ее координаты. В данном примере для каждой вершины будем задавать ее номер от 0 до 11 вместе со значениями координат по осям  Конец этой части вводимой информации будет обозначаться отдельной строкой с символом
Конец этой части вводимой информации будет обозначаться отдельной строкой с символом  в первой позиции:
в первой позиции:

Как и в параграфе 4.5, точка О объекта является началом системы мировых координат, используемой в программе (обратите внимание на различие между буквой О и цифрой 0). Поскольку она имеет координаты (2.5, 1, 1), то внутри программы координаты точек с 0 по 14 будут уменьшены на эти значения. Так, например, точке 9 будут присвоены значения координат  вместо заданных (2, 2, 2).
вместо заданных (2, 2, 2).
Каждая грань объекта может быть описана в виде любой конечной области плоскости с границами в виде отрезков прямых линий. В качестве примера такой области можно назвать
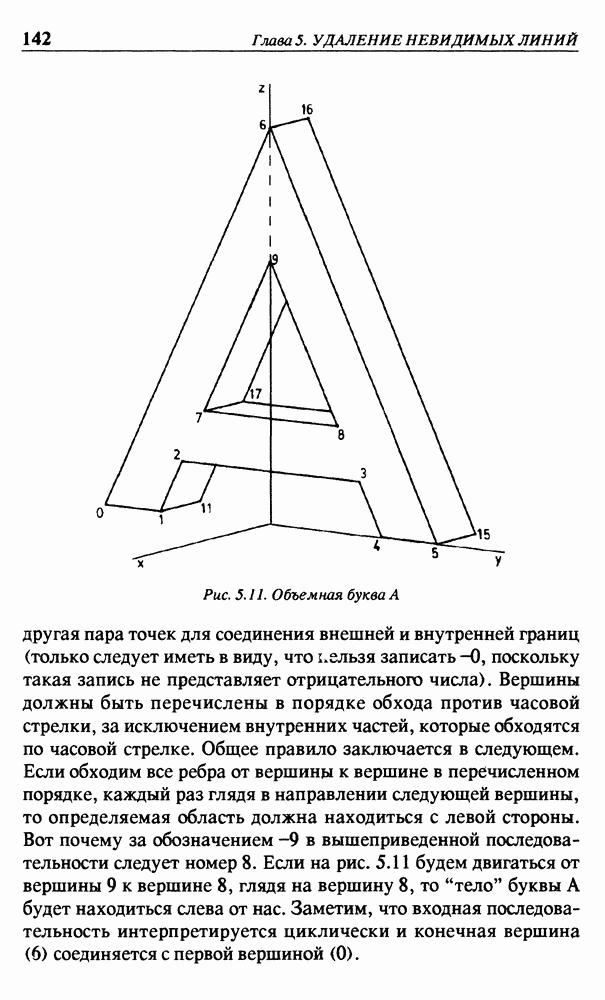
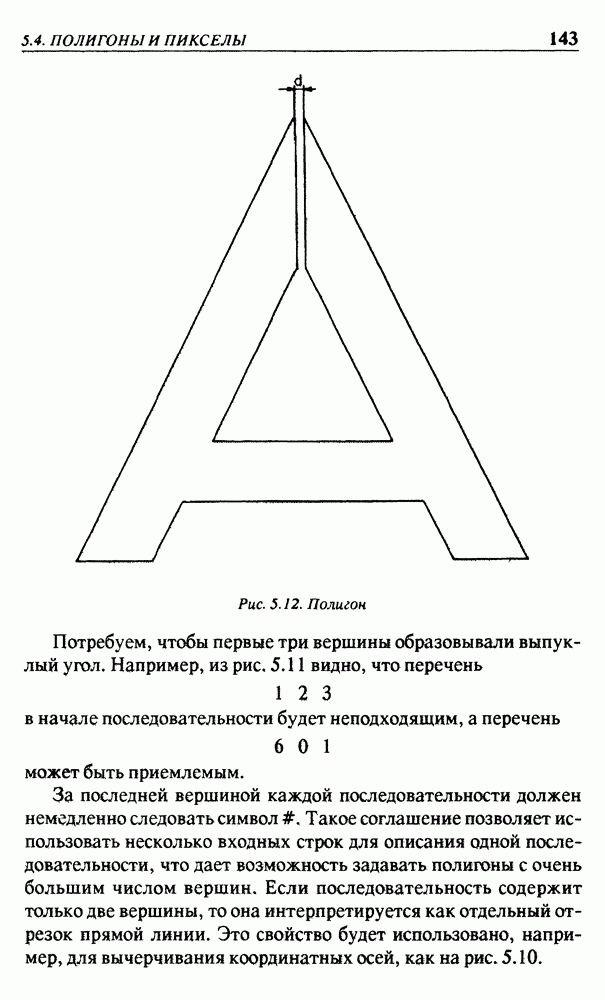
полигон, в котором допустимы также и отверстия. Чтобы программа была проще, пользователь должен сам разбить такие области на треугольники. Эти треугольники затем будут использоваться для определения, не закрывают ли они отрезки прямых линий. По причинам, которые поясним ниже, номера вершин в каждом треугольнике перечисляются в порядке обхода против часовой стрелки при рассматривании их с внешней стороны объекта. Каждая грань куба разбивается на два треугольника. Эту часть входных данных опять завершает символ  (на новой строке).
(на новой строке).

Теперь необходимо задать каждое ребро объекта. Хотя эти ребра уже известны как стороны треугольников, их следует описать снова. Во-первых, не все стороны треугольников являются ребрами объекта и, во-вторых, желательно иметь возможность вычерчивания дополнительных отрезков, не принадлежащих сплошному телу. Для иллюстрации вычертим части положительных координат полуосей, как показано на рис. 5.1. Как это ни курьезно, но в данном примере количество входных строк не увеличится, поскольку ребра объекта, лежащие на координатных осях, не нужно задавать повторно. Следовательно, имеем 17 входных строк:

Программа выполнит считывание всех входных данных из файла, имя которого передается в качестве аргументов программы  и
и  как описано в параграфе 4.5. Координаты каждой вершины сохраняются в массиве
как описано в параграфе 4.5. Координаты каждой вершины сохраняются в массиве  элементами которого являются структуры, содержащие три поля
элементами которого являются структуры, содержащие три поля  Заданные пользовательские координаты сначала переводятся в координаты системы, начало которой расположено в объектной точке О. Внутренние мировые координаты, в свою очередь, преобразуются в видовые координаты с помощью видовых преобразований (см. параграф 4.2). И именно эти видовые координаты записываются в массив
Заданные пользовательские координаты сначала переводятся в координаты системы, начало которой расположено в объектной точке О. Внутренние мировые координаты, в свою очередь, преобразуются в видовые координаты с помощью видовых преобразований (см. параграф 4.2). И именно эти видовые координаты записываются в массив 

Как мы уже знаем, точка Е — начало системы видовых координат, и направление наблюдения совпадает с направлением оси z. Следовательно, все значения  должны быть положительными. Это условие проверяется в программе, и выполнение программы прекращается, если оно не выполнено.
должны быть положительными. Это условие проверяется в программе, и выполнение программы прекращается, если оно не выполнено.
Список треугольников запоминается в массиве 

Вместе с номерами вершин для каждого треугольника записываются коэффициенты а, b, с, h уравнения плоскости

в которой расположен треугольник. Конечно, их можно было бы рассчитывать каждый раз, когда они оказываются необходимыми, но это означало бы напрасную трату времени, поскольку они требуются довольно часто. (Здесь четвертый коэффициент обозначен через  вместо
вместо  так как эта буква уже использована для обозначения расстояния до экрана.) Коэффициенты
так как эта буква уже использована для обозначения расстояния до экрана.) Коэффициенты  с выбираются такими, чтобы удовлетворялось условие
с выбираются такими, чтобы удовлетворялось условие

Тогда уравнение (5.1) можно записать в виде скалярного произведения

где

Так называемый вектор нормали  представляет собой вектор единичной длины, перпендикулярный плоскости треугольника. Для любой точки X в этой плоскости вектор
представляет собой вектор единичной длины, перпендикулярный плоскости треугольника. Для любой точки X в этой плоскости вектор  имеет такое свойство, что его скалярное произведение
имеет такое свойство, что его скалярное произведение  равно расстоянию между точкой Е и плоскостью.
равно расстоянию между точкой Е и плоскостью.
Скалярное произведение было введено в параграфе 3.2. Заметим, что здесь мы используем систему видовых координат с точкой Е в качестве начала системы координат и отрезок  определяет положительное направление оси z. Плоскость, параллельная экрану, описывается уравнением z в А, которое является вырожденным случаем общего уравнения (5.1) при
определяет положительное направление оси z. Плоскость, параллельная экрану, описывается уравнением z в А, которое является вырожденным случаем общего уравнения (5.1) при  В общем случае коэффициенты
В общем случае коэффициенты  вычисляются по координатам вершин треугольника А, В, С. В параграфе 3.3 мы видели, что плоскость, проходящая через эти точки, описывается уравнением
вычисляются по координатам вершин треугольника А, В, С. В параграфе 3.3 мы видели, что плоскость, проходящая через эти точки, описывается уравнением

Это уравнение можно переписать в виде

В программе коэффициенты а, А, с, А вычисляются по формулам:

Однократное вычисление коэффициентов а, 6, с, А, вместо их определения при каждой проверке отрезка на видимость, позволяет значительно сократить время вычислений.
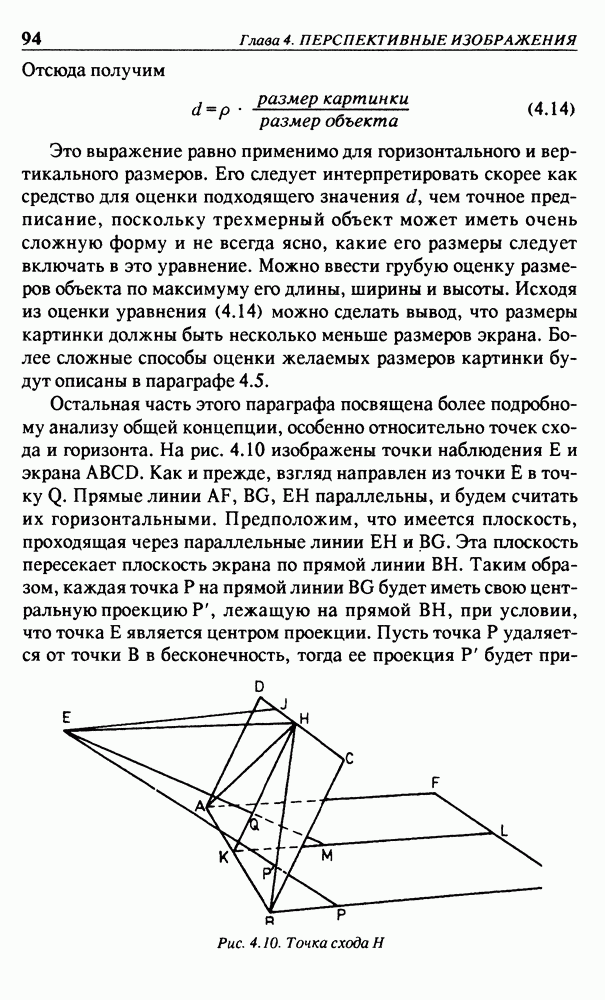
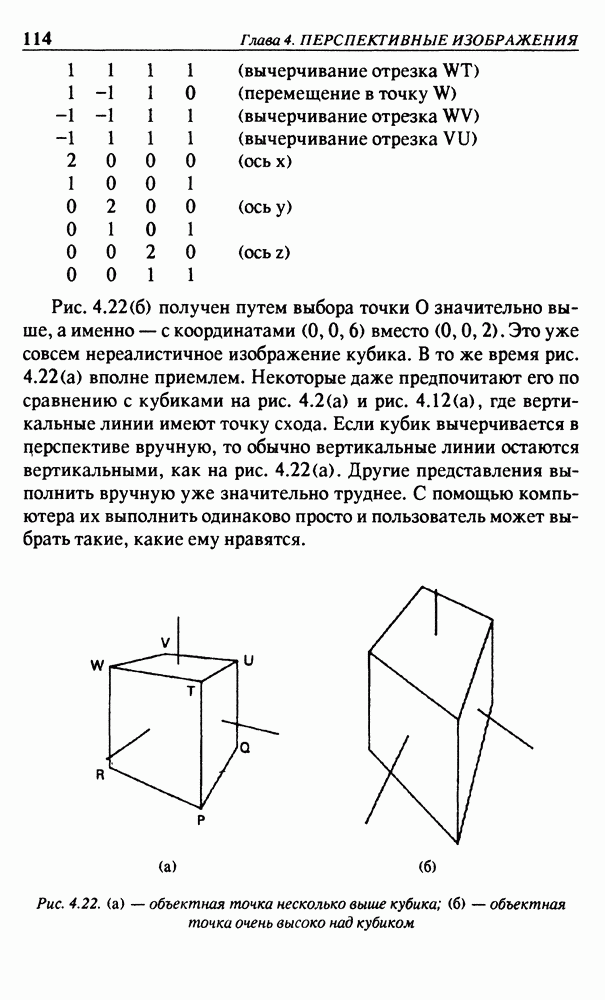
Если программа действительно должна быть по возможности проще, то необходимо было бы запоминать все треугольники по мере их ввода. Однако те треугольники, которые находятся сзади, сохранять не требуется и их можно проигнорировать. Рассмотрим треугольник 123 на рис. 5.1. На картинке он закрыт треугольником 130. Поскольку последний треугольник закрывает часть отрезка 45, то можно проигнорировать тот факт, что предыдущий треугольник делает то же самое. Задние грани закрываются видимыми гранями. Хотя задние грани могут закрывать от глаза некоторые точки, эти же точки закрываются и видимыми гранями. Бот почему задние грани можно проигнорировать. Самый простой способ идентификации задних граней основан на ориентации вершин.
Если мы посмотрим на грань 123 на рис. 5.1. в трехмерном пространстве извне (то есть со стороны отрицательной полуоси  то порядок обхода вершин 123 при вводе будет против часовой стрелки, поскольку такая ориентация требовалась при определе
то порядок обхода вершин 123 при вводе будет против часовой стрелки, поскольку такая ориентация требовалась при определе
определении входной последовательности. Однако на рис. 5.1 порядрк обхода 123 соответствует движению часовой стрелки. Это означает, что на картинке эта грань видна через тело объекта, а не извне. Таким образом, грань 123 — задняя. Применение этого способа определения положения граней для других треугольников на рис. 5.1 может послужить хорошим упражнением. Обращаясь к концу параграфа 3.4, можно обнаружить, что в этом случае требуется найти значение детерминанта

где  экранные координаты вершин А, В, С треугольника. Треугольник ABC будет задним, если
экранные координаты вершин А, В, С треугольника. Треугольник ABC будет задним, если  Но нет необходимости в действительном вычислении детерминанта, поскольку можно записать
Но нет необходимости в действительном вычислении детерминанта, поскольку можно записать

Так как значения  всегда положительны, то
всегда положительны, то  имеет тот же знак, что и величина
имеет тот же знак, что и величина  вычисленная в предыдущей программе. Если
вычисленная в предыдущей программе. Если  то плоскость ABC проходит через точку начала координат Е, совпадающей с точкой наблюдения. В этом случае треугольник ABC не будет закрывать никаких отрезков и его не надо запоминать в массиве
то плоскость ABC проходит через точку начала координат Е, совпадающей с точкой наблюдения. В этом случае треугольник ABC не будет закрывать никаких отрезков и его не надо запоминать в массиве  При
При  детерминант
детерминант  также имеет отрицательный знак и треугольник ABC является задним. Поэтому треугольник ABC будем записывать в массив только в том случае, если
также имеет отрицательный знак и треугольник ABC является задним. Поэтому треугольник ABC будем записывать в массив только в том случае, если  или, другими словами, если
или, другими словами, если 
С помощью векторного произведения можно убедиться, что треугольник ABC - задний, из условия  и без привлечения экранных координат. Но доказательство этого условия оставляем для упражнения читателям с хорошей математической подготовкой.
и без привлечения экранных координат. Но доказательство этого условия оставляем для упражнения читателям с хорошей математической подготовкой.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
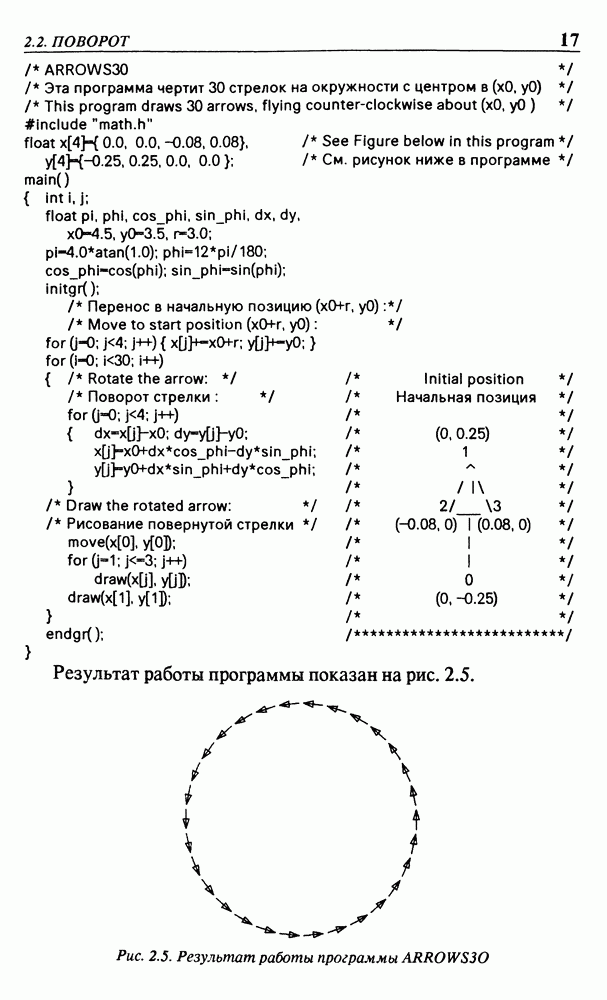
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
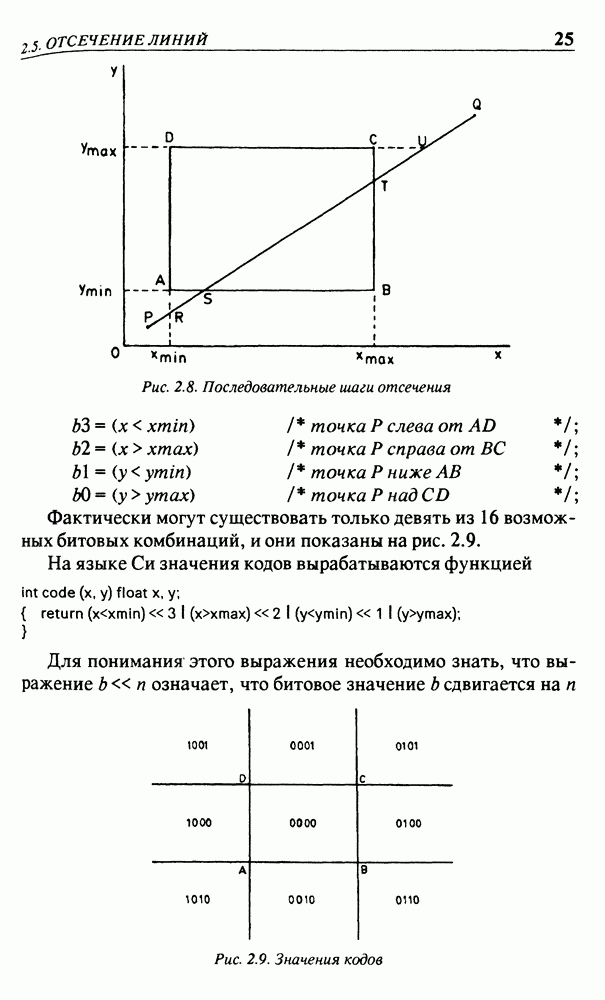
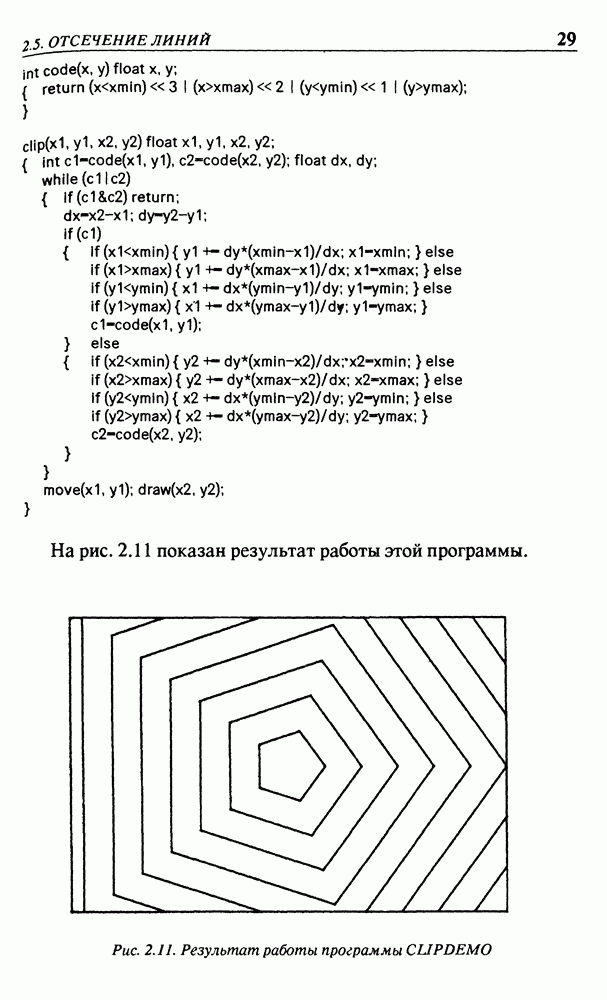
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
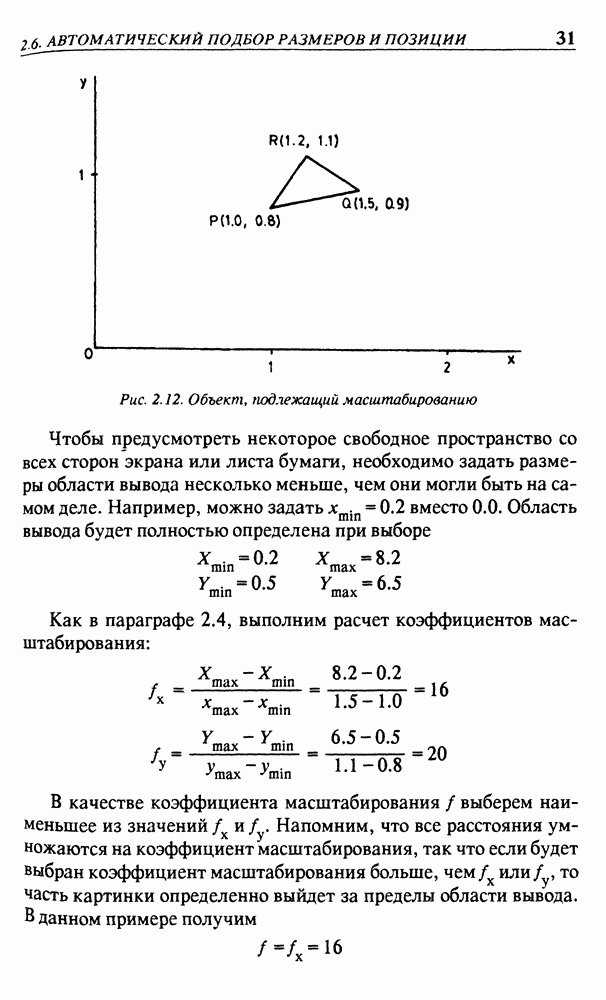
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
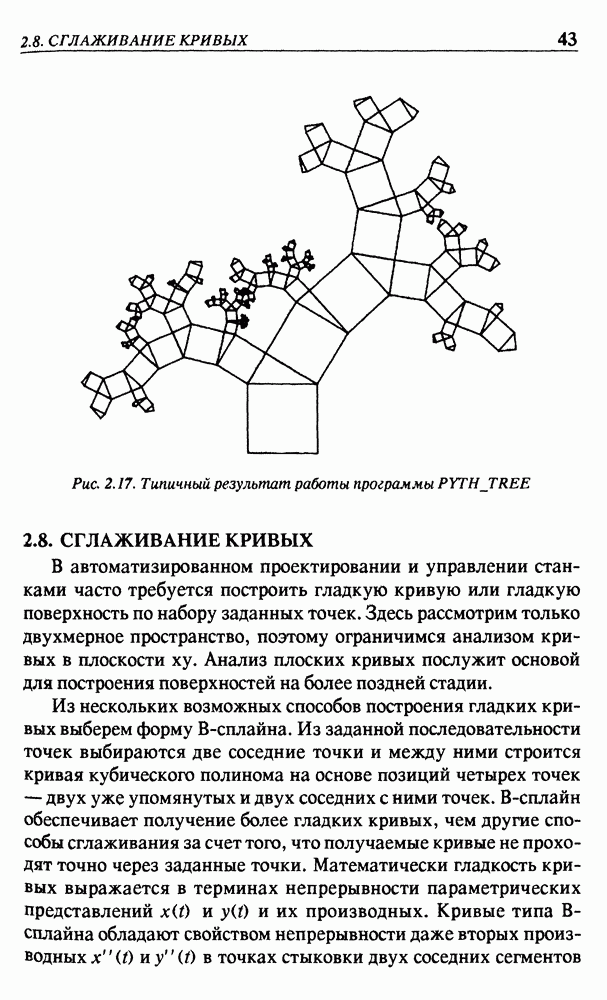
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
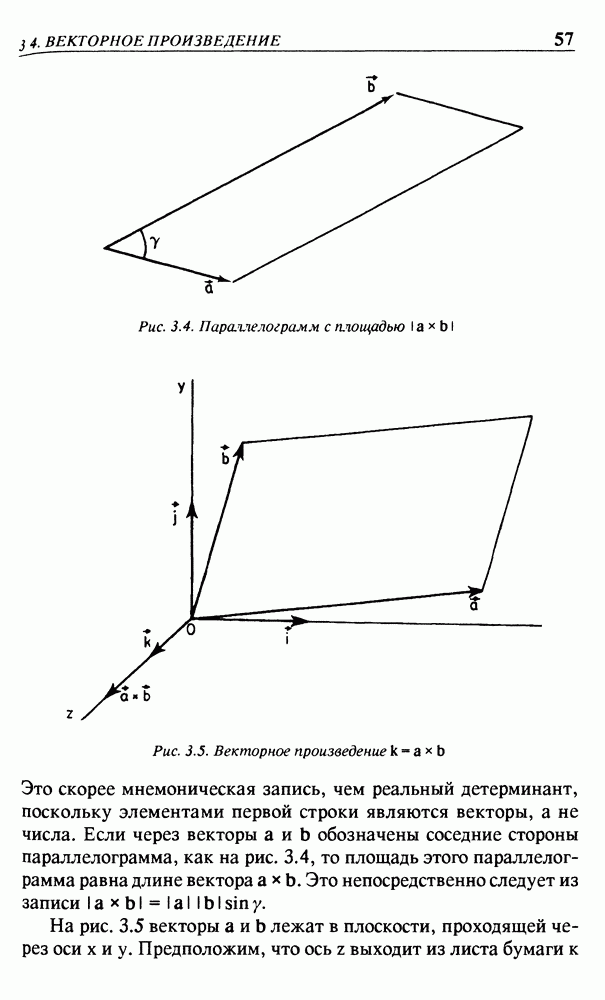
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
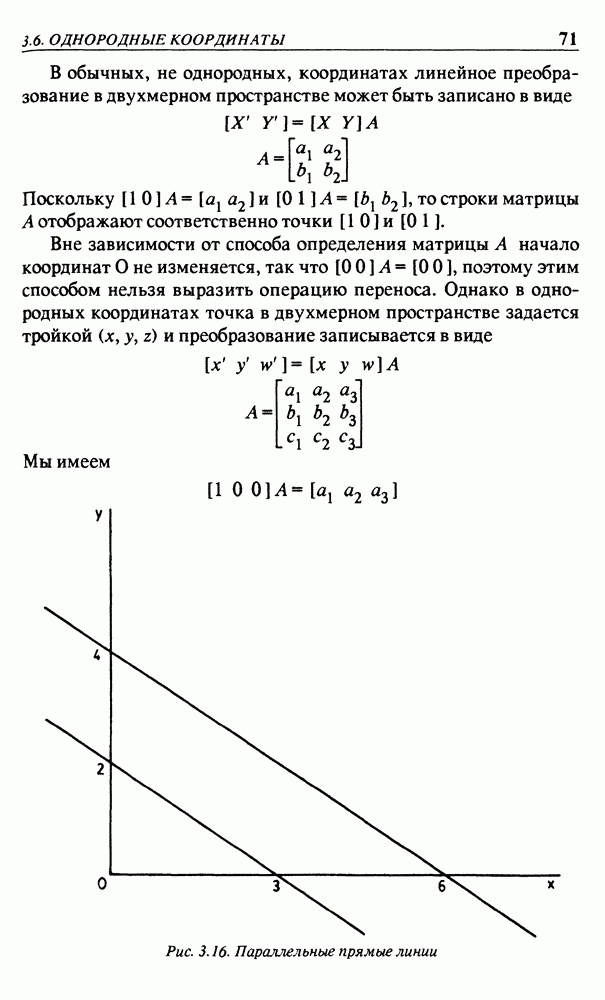
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
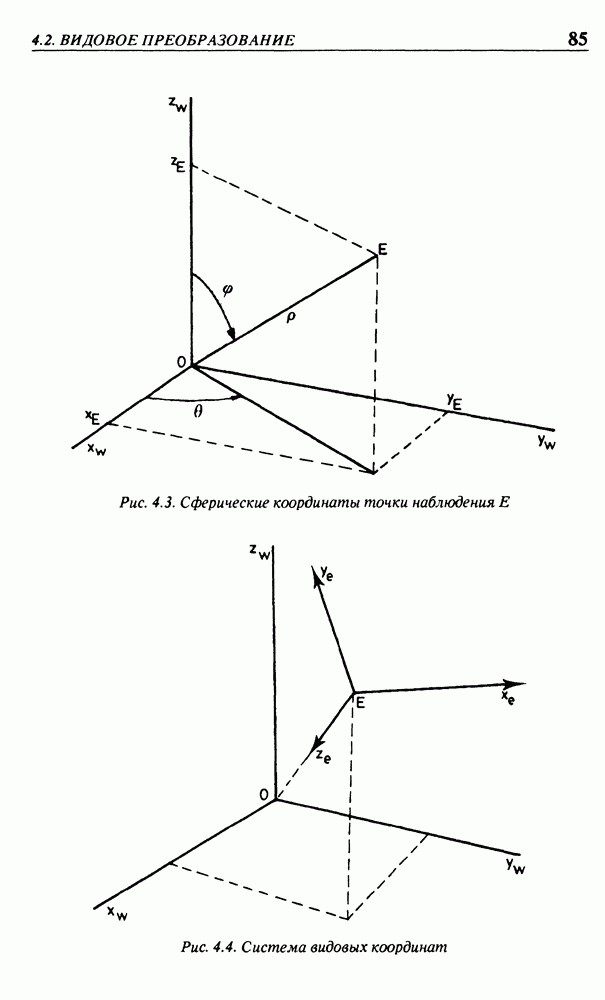
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
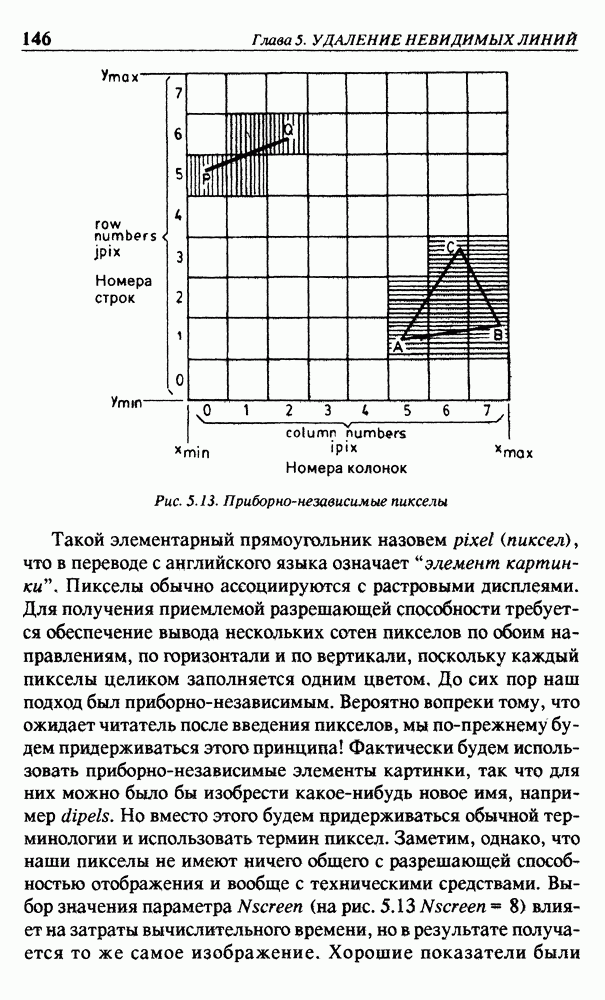
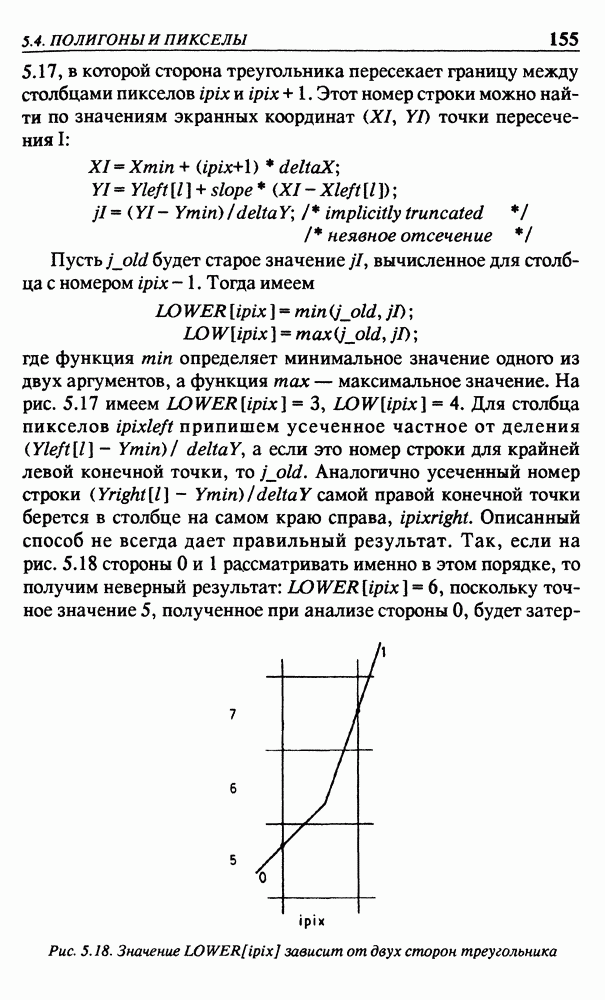
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
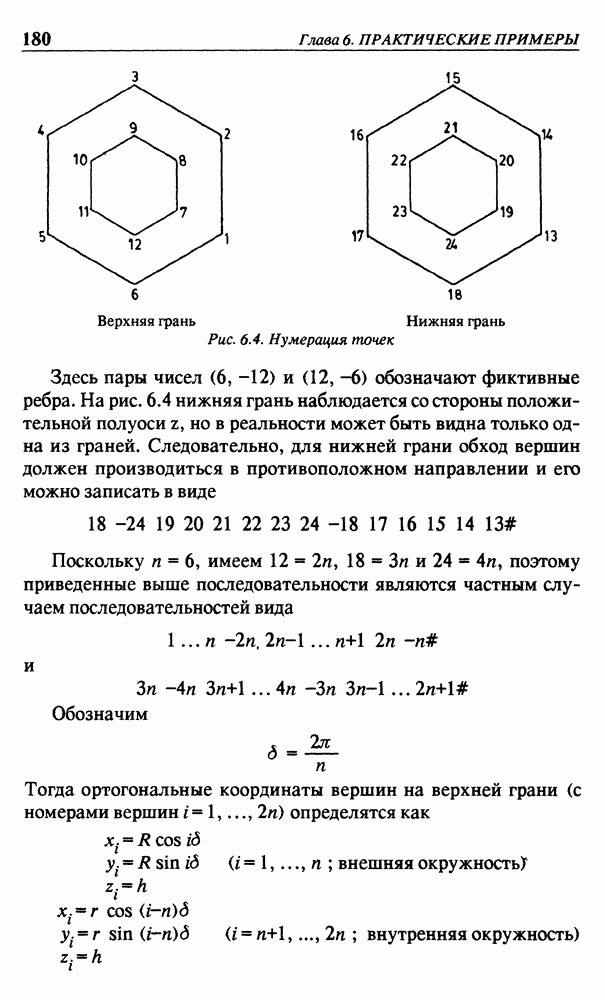
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
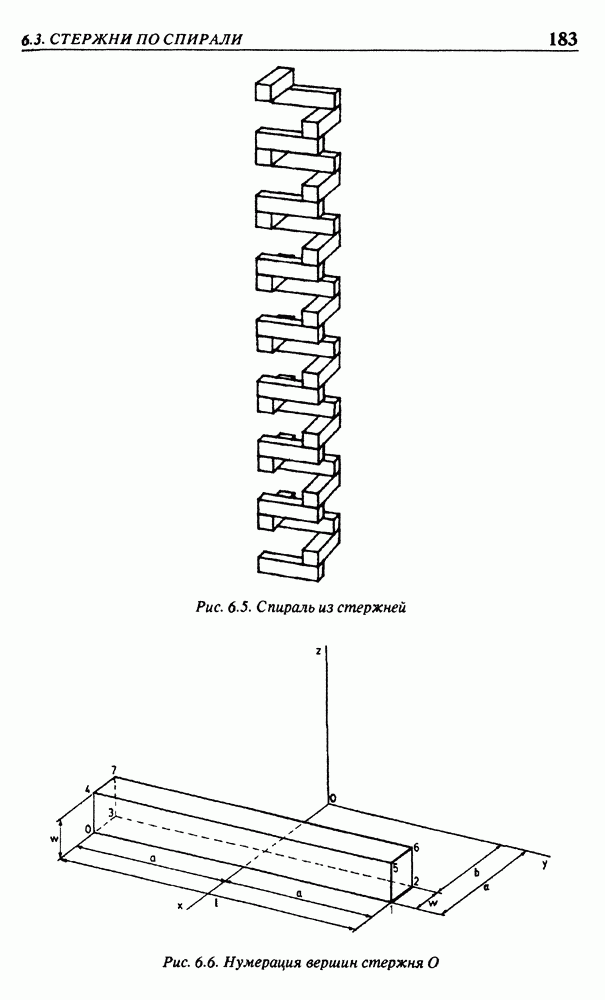
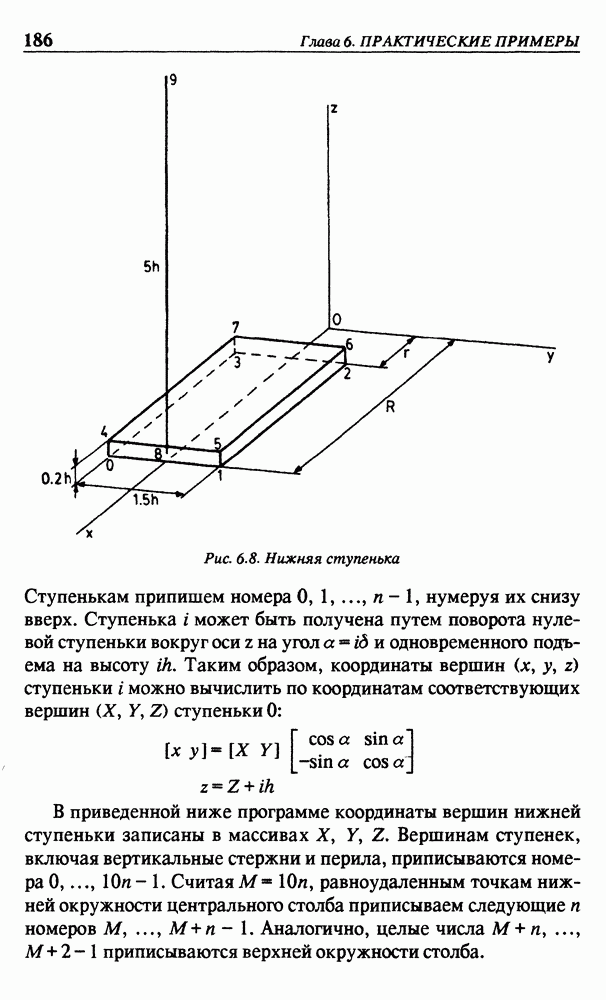
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
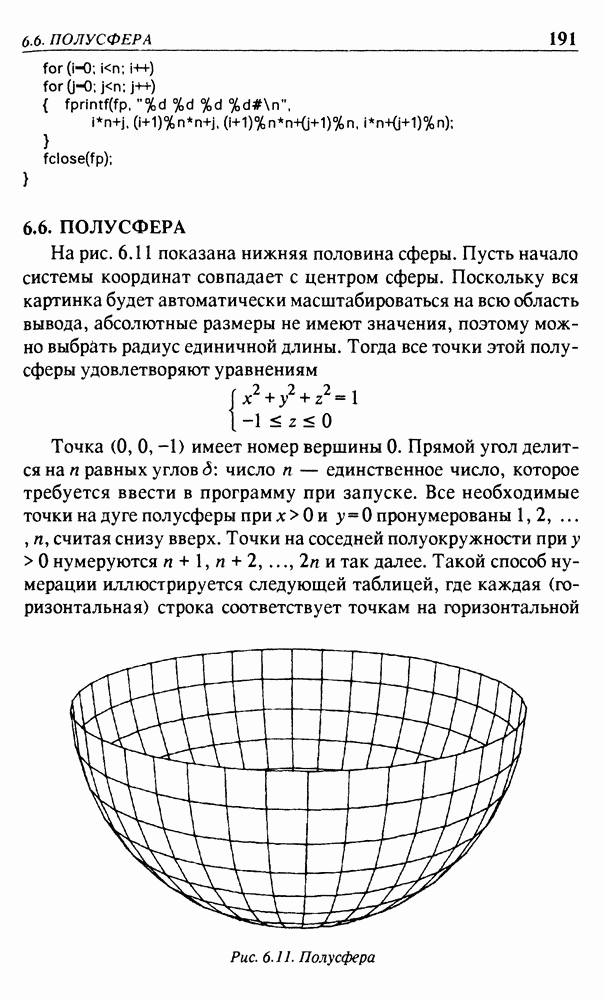
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА