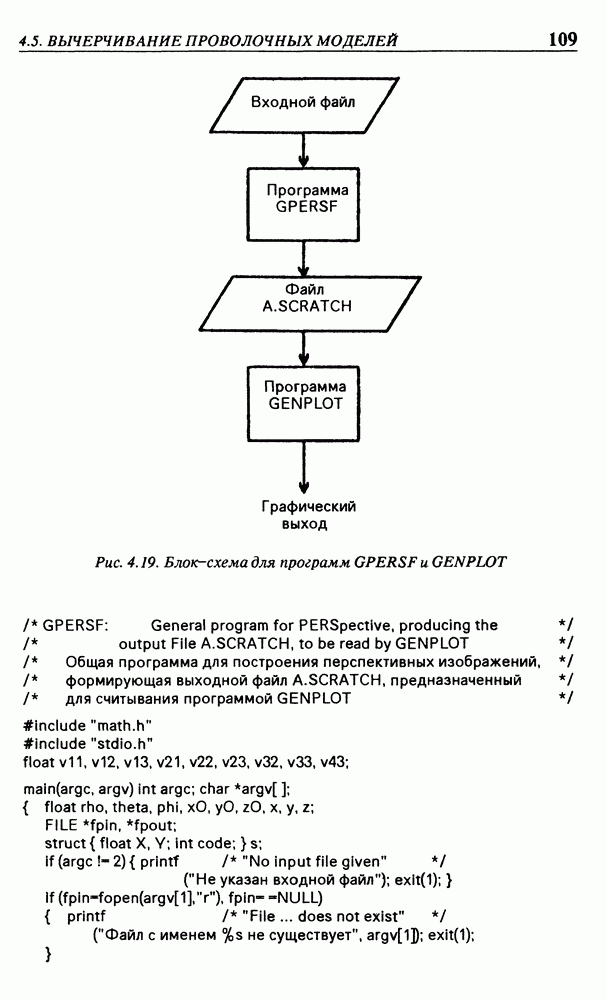
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
Читатель может вообразить, что мы находимся всего на пол-пути и что в этом параграфе будет не меньше математических выкладок, чем в параграфе 4.2. Однако большая часть работы
уже выполнена. Здесь мировые координаты уже не будут затрагиваться. Поэтому видовые координаты будут обозначаться просто  вместо
вместо 
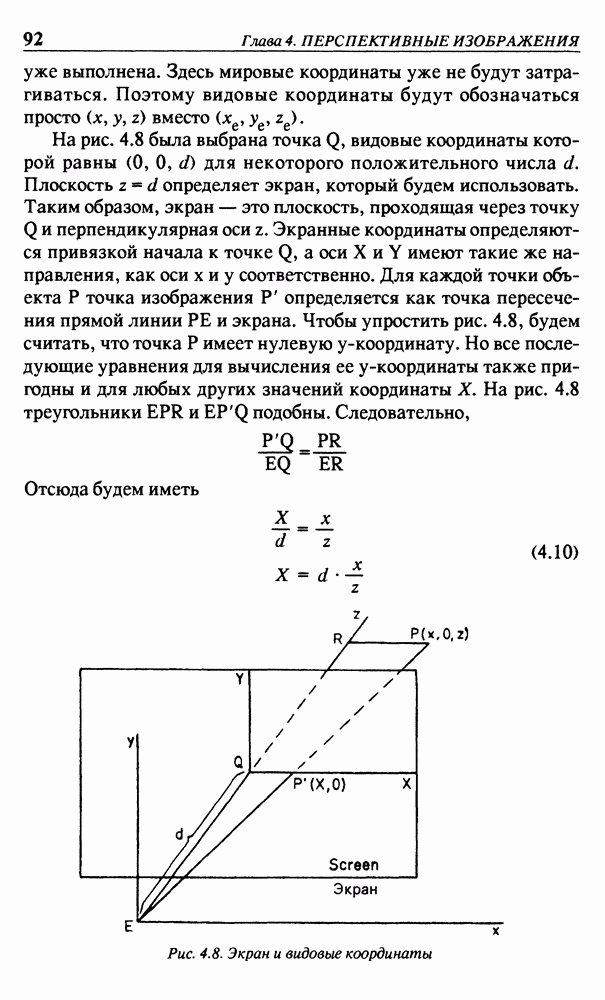
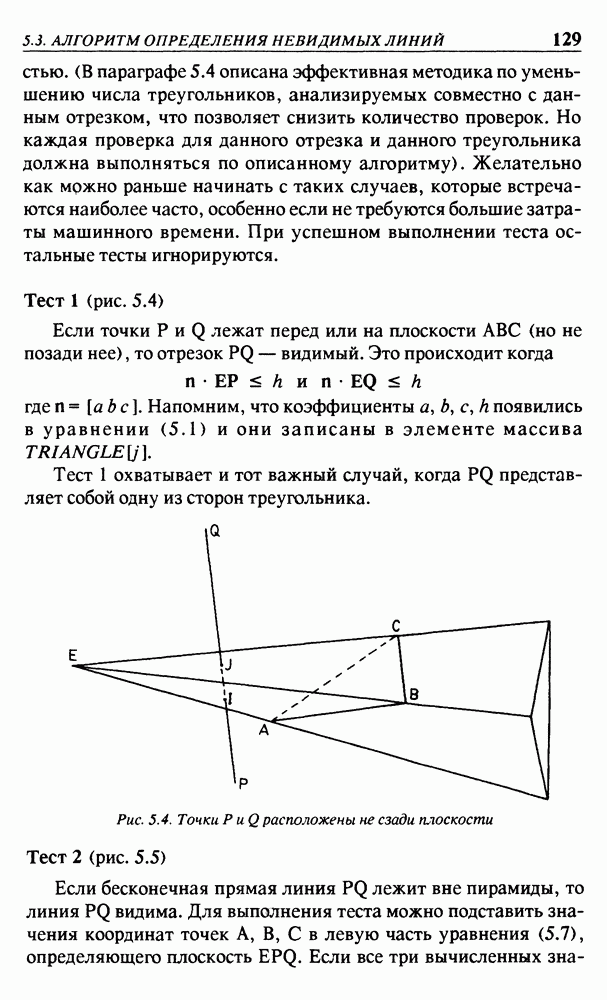
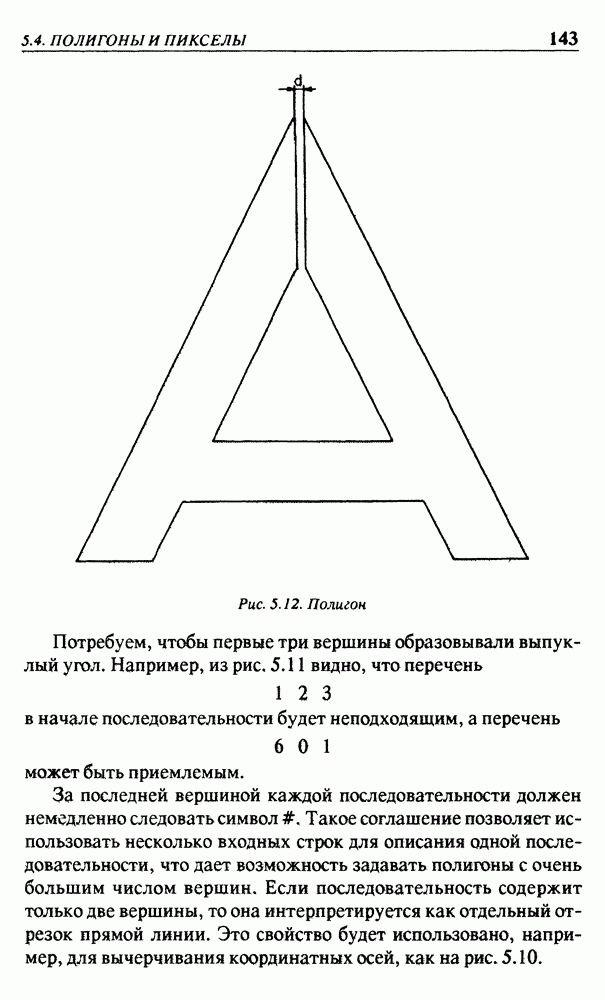
На рис. 4.8 была выбрана точка  видовые координаты которой равны
видовые координаты которой равны  для некоторого положительного числа
для некоторого положительного числа  Плоскость
Плоскость  определяет экран, который будем использовать. Таким образом, экран — это плоскость, проходящая через точку
определяет экран, который будем использовать. Таким образом, экран — это плоскость, проходящая через точку  и перпендикулярная оси z. Экранные координаты определяются привязкой начала к точке
и перпендикулярная оси z. Экранные координаты определяются привязкой начала к точке  а оси
а оси  имеют такие же направления, как оси х и у соответственно. Для каждой точки объекта Р точка изображения Р определяется как точка пересечения прямой линии
имеют такие же направления, как оси х и у соответственно. Для каждой точки объекта Р точка изображения Р определяется как точка пересечения прямой линии  и экрана. Чтобы упростить рис. 4.8, будем считать, что точка Р имеет нулевую у-координату. Но все последующие уравнения для вычисления ее у-координаты также пригодны и для любых других значений координаты
и экрана. Чтобы упростить рис. 4.8, будем считать, что точка Р имеет нулевую у-координату. Но все последующие уравнения для вычисления ее у-координаты также пригодны и для любых других значений координаты  На рис. 4.8 треугольники
На рис. 4.8 треугольники  и
и  подобны. Следовательно,
подобны. Следовательно,

Отсюда будем иметь


Рис. 4.8. Экран и видовые координаты
Аналогично можем получить

В параграфе 4.2 было введено предположение, что точка О начала системы мировых координат примерно совпадает с центром объекта. Поскольку ось z видовой системы координат совпадает с прямой линией  которая пересекает экран в точке
которая пересекает экран в точке  то начало
то начало  системы экранных координат будет находиться в центре изображения. Если бы мы потребовали, чтобы это начало координат располагалось в нижнем левом углу экрана, а размеры экрана составляли
системы экранных координат будет находиться в центре изображения. Если бы мы потребовали, чтобы это начало координат располагалось в нижнем левом углу экрана, а размеры экрана составляли  по горизонтали и
по горизонтали и  по вертикали, то можно заменить уравнения (4.10) и (4.11) на
по вертикали, то можно заменить уравнения (4.10) и (4.11) на

Нам еще требуется определить расстояние между точкой наблюдения Е и экраном. Грубо говоря, мы имеем соотношение:

что следует из подобия треугольников  и
и  на рис. 4.9.
на рис. 4.9.

Рис. 4.9. Размеры картинки и объекта
Отсюда получим

Это выражение равно применимо для горизонтального и вертикального размеров. Его следует интерпретировать скорее как средство для оценки подходящего значения  чем точное предписание, поскольку трехмерный объект может иметь очень сложную форму и не всегда ясно, какие его размеры следует включать в это уравнение. Можно ввести грубую оценку размеров объекта по максимуму его длины, ширины и высоты. Исходя из оценки уравнения (4.14) можно сделать вывод, что размеры картинки должны быть несколько меньше размеров экрана. Более сложные способы оценки желаемых размеров картинки будут описаны в параграфе 4.5.
чем точное предписание, поскольку трехмерный объект может иметь очень сложную форму и не всегда ясно, какие его размеры следует включать в это уравнение. Можно ввести грубую оценку размеров объекта по максимуму его длины, ширины и высоты. Исходя из оценки уравнения (4.14) можно сделать вывод, что размеры картинки должны быть несколько меньше размеров экрана. Более сложные способы оценки желаемых размеров картинки будут описаны в параграфе 4.5.
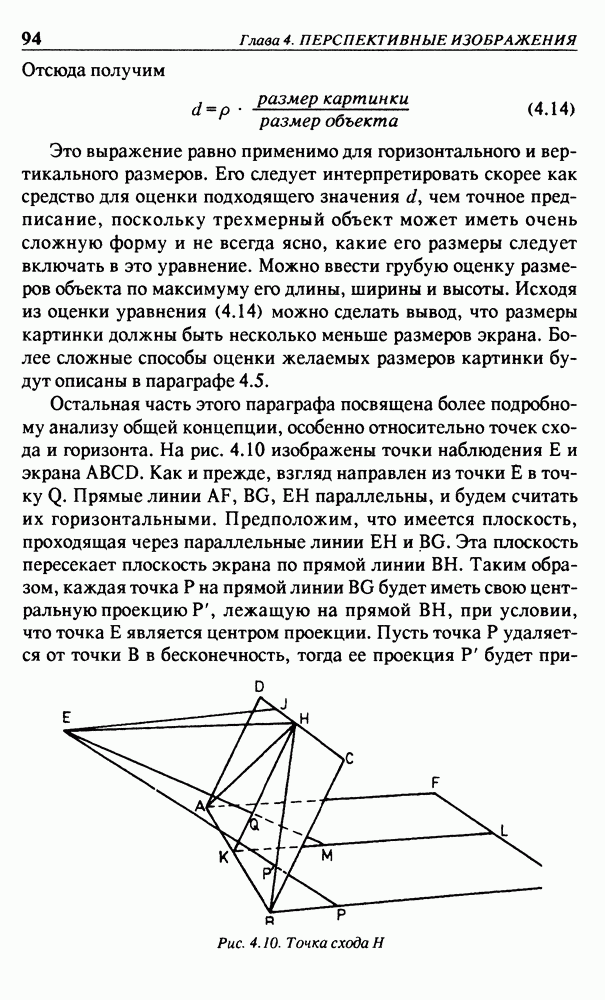
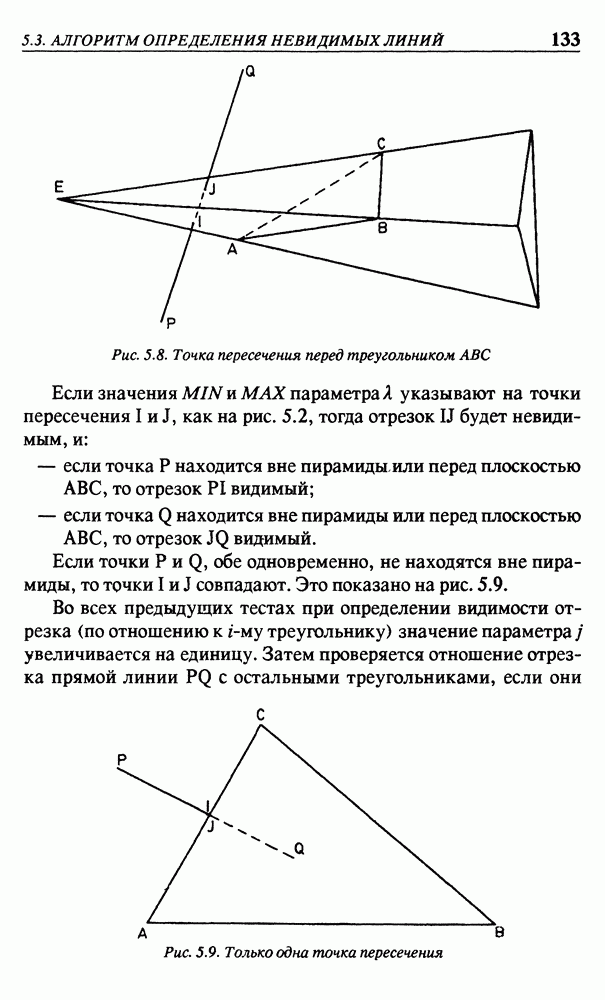
Остальная часть этого параграфа посвящена более подробному анализу общей концепции, особенно относительно точек схода и горизонта. На рис. 4.10 изображены точки наблюдения Е и экрана  Как и прежде, взгляд направлен из точки Е в точку
Как и прежде, взгляд направлен из точки Е в точку  Прямые линии
Прямые линии  параллельны, и будем считать их горизонтальными. Предположим, что имеется плоскость, проходящая через параллельные линии
параллельны, и будем считать их горизонтальными. Предположим, что имеется плоскость, проходящая через параллельные линии  и
и  Эта плоскость пересекает плоскость экрана по прямой линии
Эта плоскость пересекает плоскость экрана по прямой линии  Таким образом, каждая точка Р на прямой линии
Таким образом, каждая точка Р на прямой линии  будет иметь свою центральную проекцию
будет иметь свою центральную проекцию  лежащую на прямой
лежащую на прямой  при условии, что точка Е является центром проекции. Пусть точка Р удаляется от точки В в бесконечность, тогда ее проекция Р будет
при условии, что точка Е является центром проекции. Пусть точка Р удаляется от точки В в бесконечность, тогда ее проекция Р будет

Рис. 4.10. Точка схода Н
приближаться к точке Н. Это означает, что Н — точка схода для прямой линии, проходящей через точки  В терминах проективной геометрии точка Н представляет собой проекцию бесконечно удаленной точки, лежащей на прямой
В терминах проективной геометрии точка Н представляет собой проекцию бесконечно удаленной точки, лежащей на прямой  Как уже упоминалось в параграфе 3.6, параллельные линии пересекаются в бесконечно удаленной точке, так что точка Н будет также проекцией бесконечно удаленной точки, лежащей на прямой линии
Как уже упоминалось в параграфе 3.6, параллельные линии пересекаются в бесконечно удаленной точке, так что точка Н будет также проекцией бесконечно удаленной точки, лежащей на прямой линии  Если возьмем прямую линию с другим направлением, но также горизонтальную, например прямую линию
Если возьмем прямую линию с другим направлением, но также горизонтальную, например прямую линию  то такая
то такая
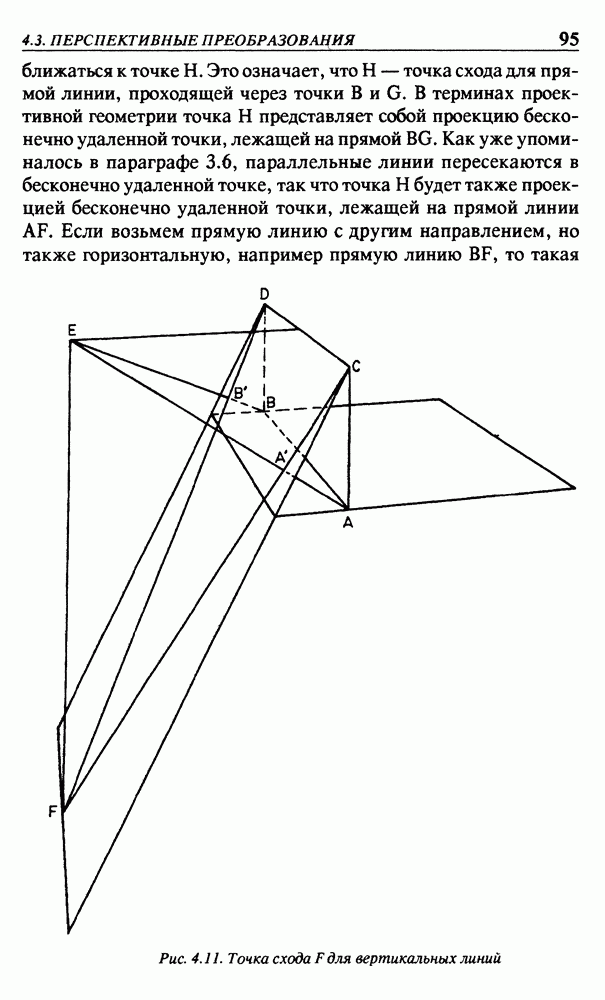
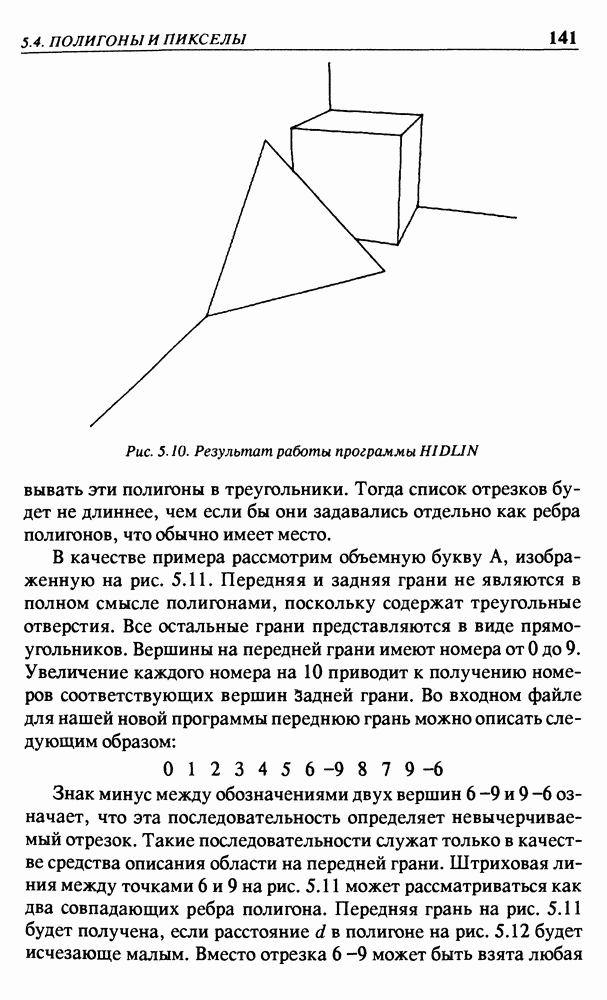
Рис. 4.11. (см. скан) Точка схода  для вертикальных линий
для вертикальных линий
линия также будет иметь точку схода, лежащую на прямой линии  Она находится как точка пересечения прямой линии
Она находится как точка пересечения прямой линии  и прямой линии, проходящей через точку Е и параллельной этой выбранной горизонтальной прямой линии. Прямая линия
и прямой линии, проходящей через точку Е и параллельной этой выбранной горизонтальной прямой линии. Прямая линия  это линия горизонта. Каждая точка
это линия горизонта. Каждая точка  на линии горизонта является точкой схода всех прямых линий, параллельных прямой линии
на линии горизонта является точкой схода всех прямых линий, параллельных прямой линии 
Точка схода есть не только у горизонтальных линий. На рис. 4.11 проведены вертикальные прямые линии  и
и  Точкой схода для них будет
Точкой схода для них будет  Это та точка, в которой вертикальная прямая линия, проходящая через точку Е, пересекает экран. Отрезки прямых линий
Это та точка, в которой вертикальная прямая линия, проходящая через точку Е, пересекает экран. Отрезки прямых линий  и
и  имеют проекции
имеют проекции  и
и  которые не параллельны.
которые не параллельны.
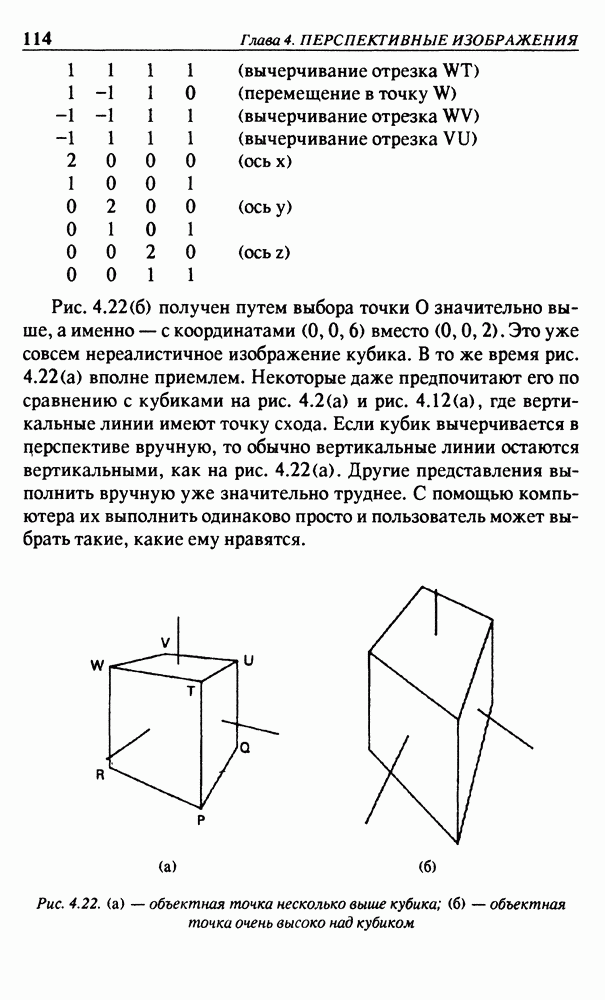
Строгий эффект перспективы для вертикальных прямых линий не всегда приемлем; часто предпочитают картинки, в которых вертикальные линии представляются почти вертикальными. Это происходит потому, что мы больше привыкли к горизонтальному, или почти горизонтальному, направлению взгляда. Некоторые чувствуют даже головокружение, если смотрят далеко вниз! Художники в своих картинах применяют “псевдоперспективу”, когда вертикальные линии рисуются точно вертикальными, даже если направление взгляда не горизонтально. В таком случае полученная картинка отличается от действительно видимой, но, несмотря на некоторую курьезность, выглядит достаточно правдоподобной. Примером может служить рис. 4.12(б). В параграфе 4.6 к этому явлению еще вернемся и покажем, что наша программа может формировать такие псевдоперспективные

Рис. 4.12. (а) - перспектива; (б) - псевдоперспектива

Рис. 4.13. Десять кубиков, параллельных экрану
картинки (см. рис. 4.22(a)). В общем, однако, рекомендуется выбирать точку наблюдения не очень близко к объекту, особенно в тех случаях, когда угол  показанный на рис. 4.3, примерно равен 90°. В этом заключается практический способ исключения сильного эффекта перспективы для вертикальных линий.
показанный на рис. 4.3, примерно равен 90°. В этом заключается практический способ исключения сильного эффекта перспективы для вертикальных линий.
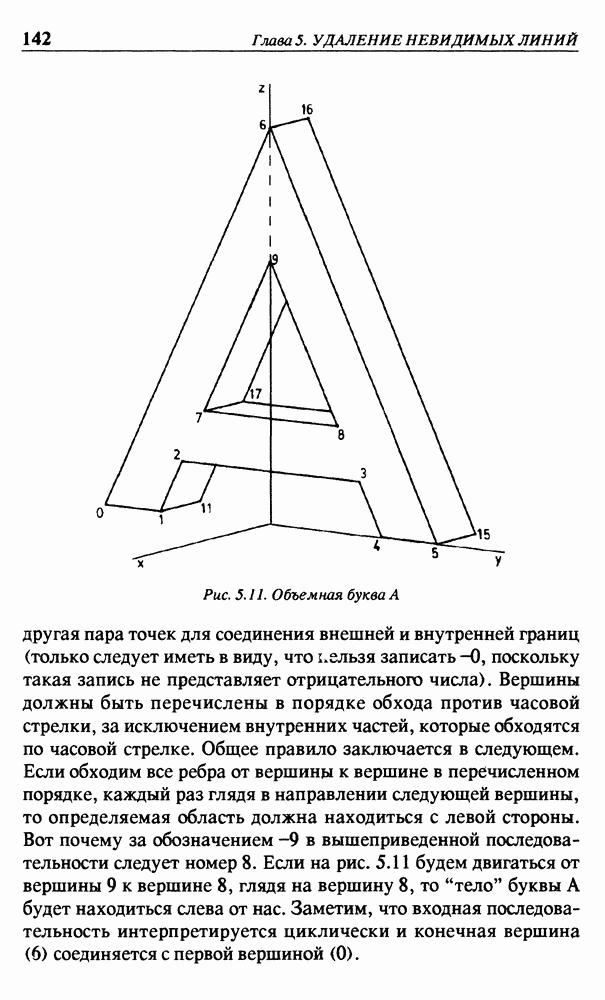
Другая несколько дискуссионная тема — представление линий, параллельных экрану. Они будут изображаться параллельными линиями на картинке. Рассмотрим, например, рис. 4.13 с изображениями десяти кубиков, расположенными в одну линию. Направление наблюдения — горизонтальное, то есть  . На этой картинке можно видеть парадоксальный эффект, относящийся к размерам кубиков. Кубик А удален значительно дальше, чем кубик Е, но на картинке оба этих кубика имеют одинаковые размеры. Кажется, что это неправильно, поскольку удаленные объекты должны иметь меньшие видимые размеры, чем более близкие. Однако это является результатом центрального проецирования, полученного по точным геометрическим правилам, выведенным на основе наших представлений. Изображение на рис. 4.13 практически нереально. Особенность нашего глаза такова, что мы можем видеть только точки, расположенные внутри определенного конуса, ось которого совпадает с направлением взгляда
. На этой картинке можно видеть парадоксальный эффект, относящийся к размерам кубиков. Кубик А удален значительно дальше, чем кубик Е, но на картинке оба этих кубика имеют одинаковые размеры. Кажется, что это неправильно, поскольку удаленные объекты должны иметь меньшие видимые размеры, чем более близкие. Однако это является результатом центрального проецирования, полученного по точным геометрическим правилам, выведенным на основе наших представлений. Изображение на рис. 4.13 практически нереально. Особенность нашего глаза такова, что мы можем видеть только точки, расположенные внутри определенного конуса, ось которого совпадает с направлением взгляда  Очень важный параметр этого конуса — угол
Очень важный параметр этого конуса — угол  отмеченный на рис. 4.14.
отмеченный на рис. 4.14.
Глаз, как и камера, допускает только такие значения угла а, которые не превышают некоторого максимального значения  При вычислениях лучше ограничивать не фактическое значение угла а, показанное на рис. 4.14, а примерно выдерживать отношение
При вычислениях лучше ограничивать не фактическое значение угла а, показанное на рис. 4.14, а примерно выдерживать отношение

откуда опять следует, что выбор слишком малого значения расстояния  , может быть источником затруднений. Если же значение
, может быть источником затруднений. Если же значение  будет выбрано сравнительно большим, то угол а может
будет выбрано сравнительно большим, то угол а может

Рис. 4.14. Конус наблюдения
оказаться малым, чтобы избежать обсуждаемых затруднений. Если все-таки это не годится, то может быть принято решение о замене плоского экрана частью сферической поверхности с центром в точке Е. Таким образом, можно допустить большие значения угла а, но при этом картинка не получится плоской. Сферическая картинка, в свою очередь, может быть спроецирована на плоскость. Читатели, интересующиеся такими необычными способами проецирования, могут обратиться к работе известного художника М. Эшера (1972). В данной работе ограничимся только плоскими картинками, которые получаются при сравнительно малых углах а.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
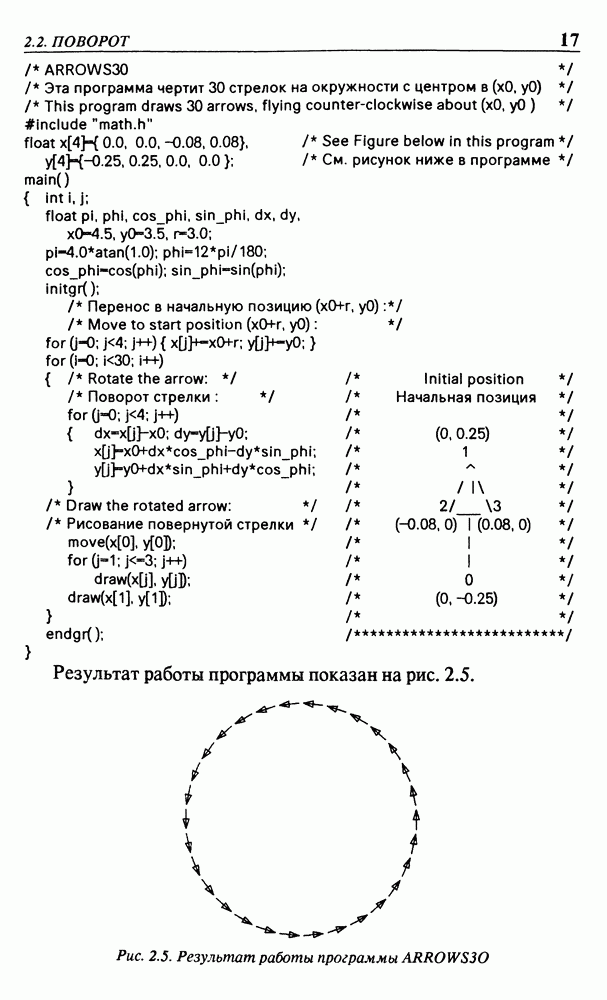
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
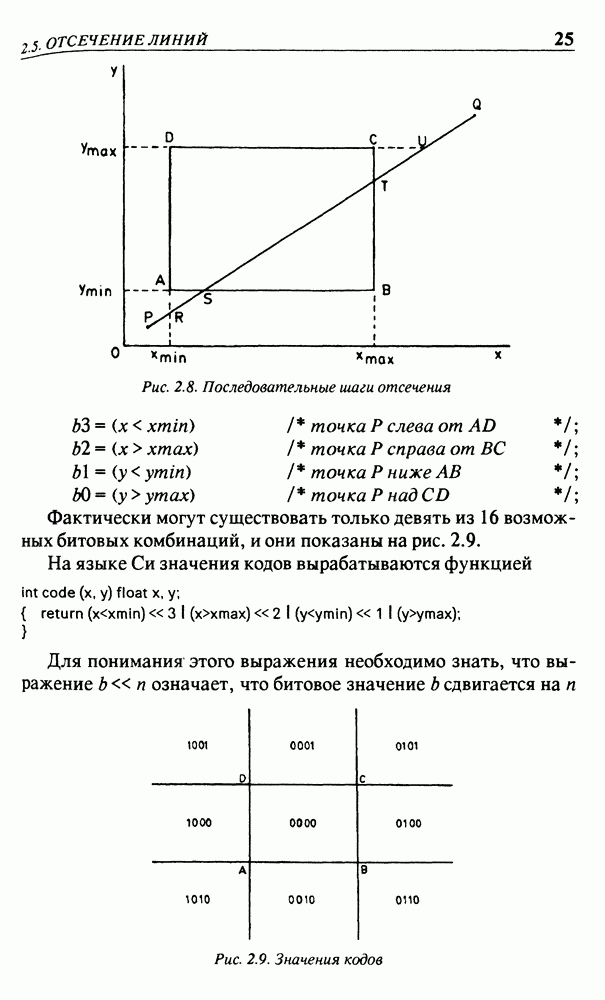
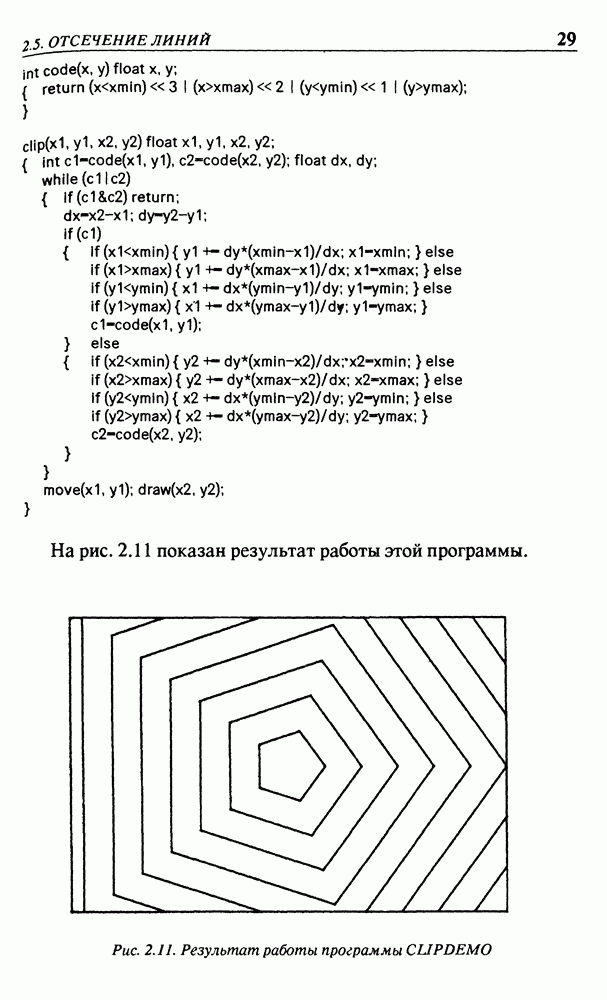
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
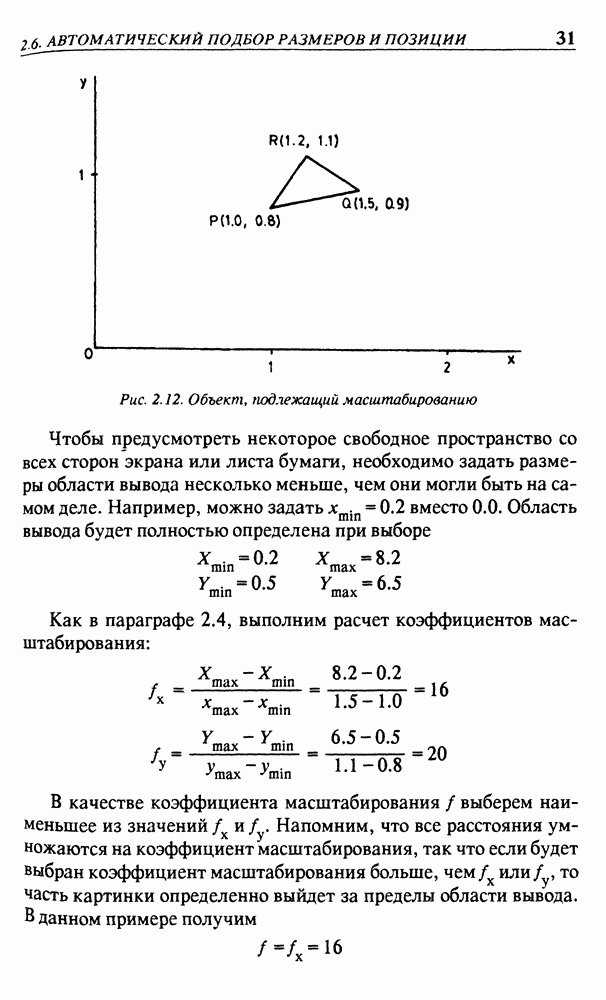
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
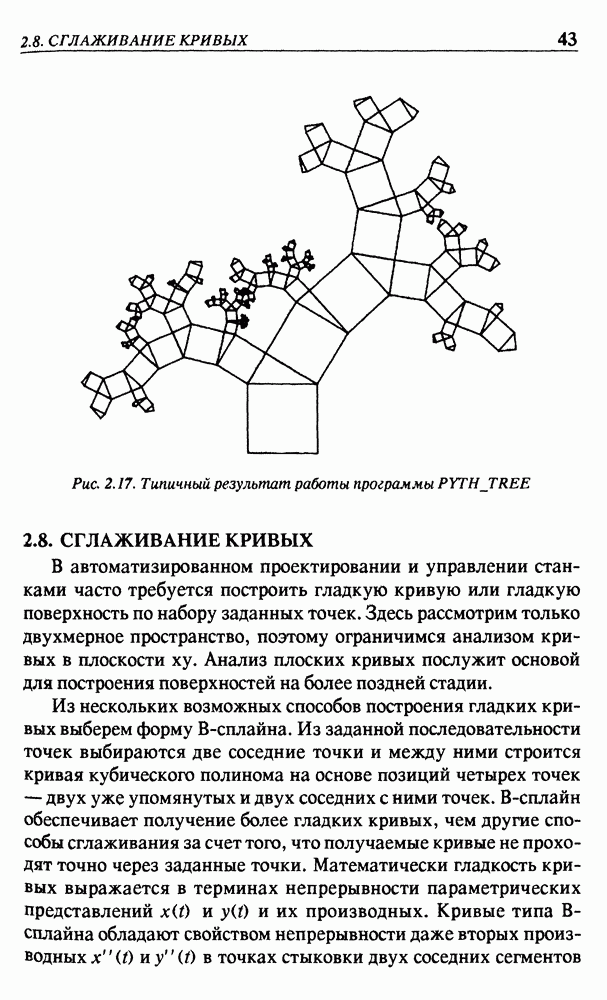
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
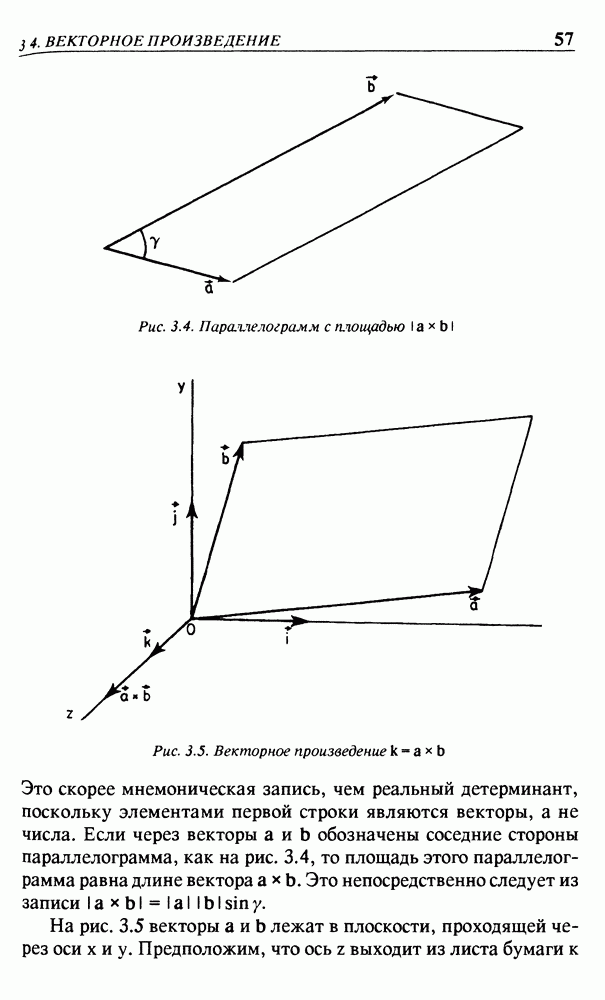
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
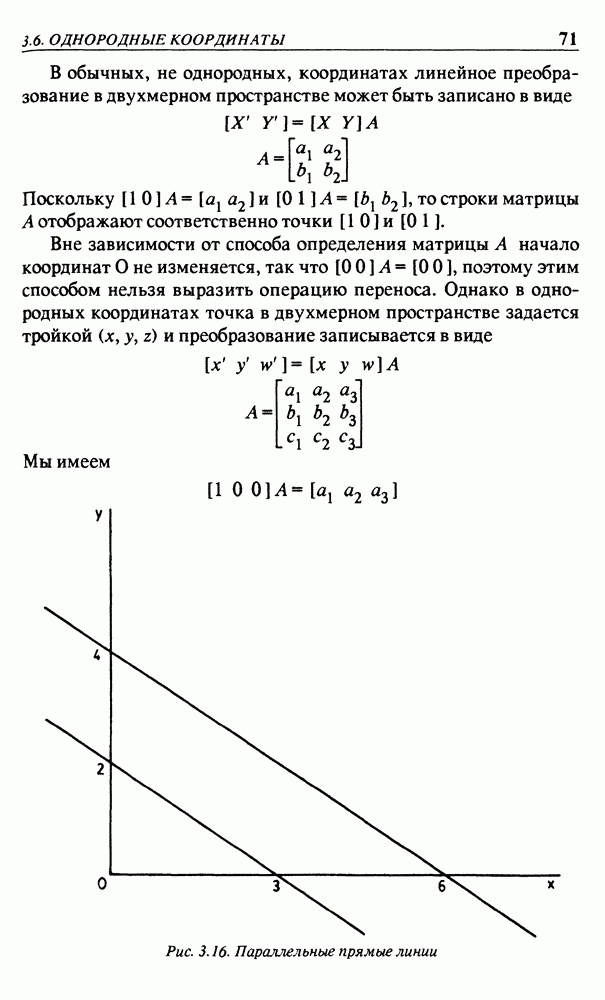
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
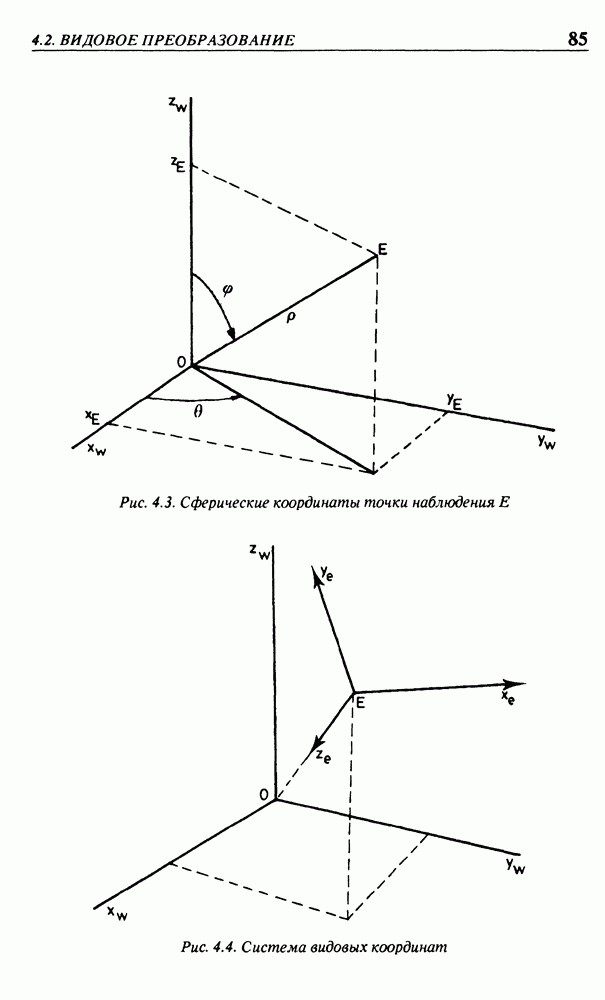
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
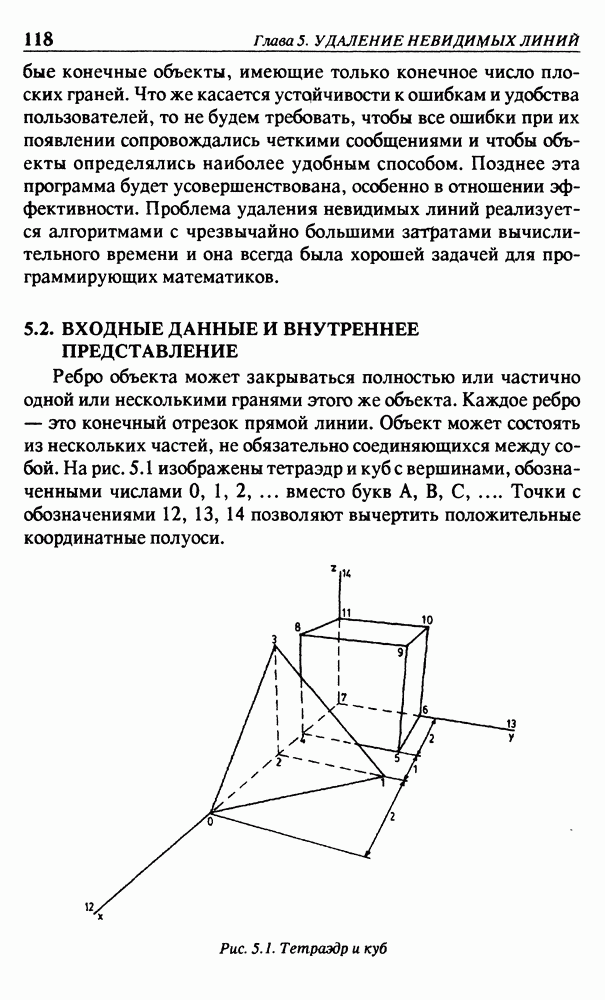
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
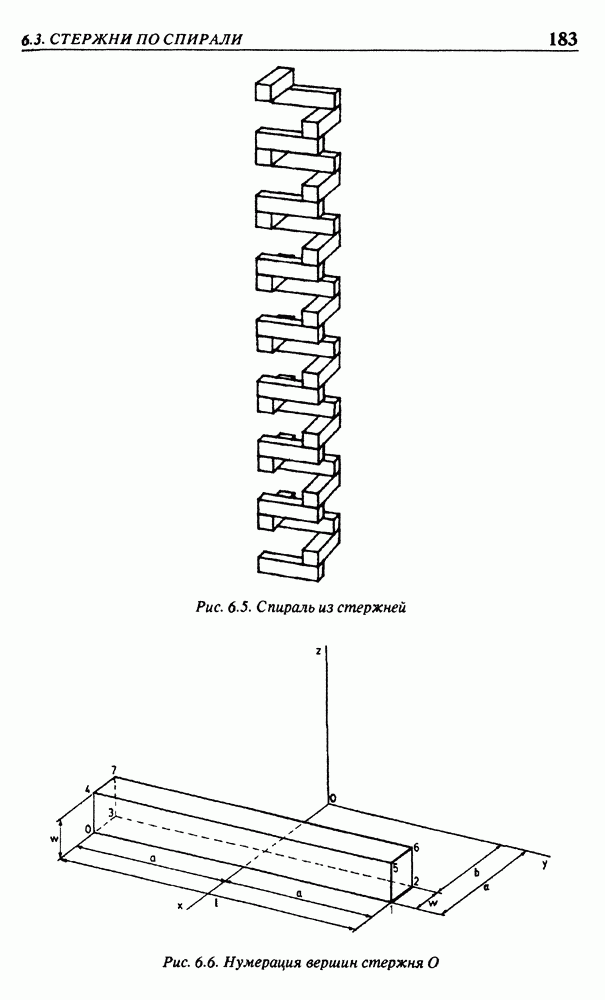
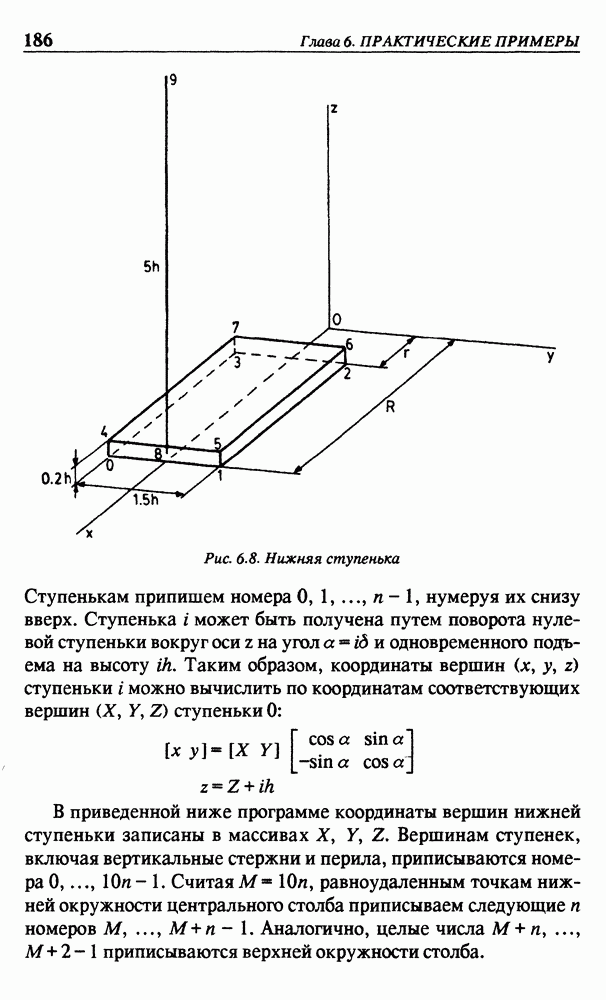
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
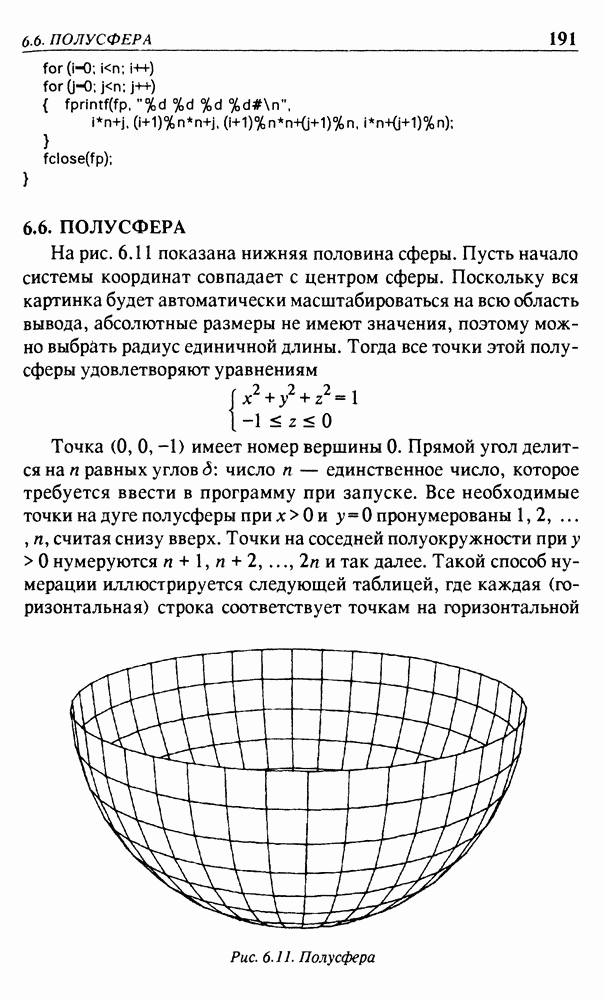
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА