| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ВЛИЯНИЕ РАСТВОРИТЕЛЯ НА ОТДЕЛЬНЫЕ СТАДИИ РАВНОВЕСИЯ В РАСТВОРАХ
В первом приближении
Эти три слова часто встречаются в научной литературе. Надобно признать, что это выражение служит одним из самых мощных источников, питающих реки научного фольклора. Но, право, иногда при рассмотрении проблемы в широком плане, первое, т. е. самое грубое, приближение оказывается весьма полезным.
Так вот, в первом приближении будем считать, что энергию любого взаимодействия в растворах определяют две составляющие — ковалентная и электростатическая:

Разновидности электростатических взаимодействий в растворах, определяющие величину энергии электростатических взаимодействий, уже, правда, мимоходом, перечислялись. Это прежде всего взаимодействие между двумя ионами, ион-ионное взаимодействие, энергию которого согласно закону Кулона
описывают выражением:

где  заряд иона;
заряд иона;  число Авогадро, следовательно, это уравнение передает энергию влазимодействия одного грамм-иоиа катионов с одним грамм-ионом анионов и, таким образом, относится к одному молю вещества;
число Авогадро, следовательно, это уравнение передает энергию влазимодействия одного грамм-иоиа катионов с одним грамм-ионом анионов и, таким образом, относится к одному молю вещества;  расстояние между ионами в ионном ассоциате, или сумма радиусов двух ионов;
расстояние между ионами в ионном ассоциате, или сумма радиусов двух ионов;  диэлектрическая проницаемость.
диэлектрическая проницаемость.
Знак «минус» в приведенном уравнении, появившийся потому, что 21 и 22 — заряды катиона и аниона разнозначны, указывает также и на то, что процесс взаимодействия двух разноименных зарядов энергетически выгоден, самопроизволен, так как любой самопроизвольный процесс ведет к уменьшению потенциальной энергии системы.
Все величины в уравнении для энергии ион-ионного взаимодействия, за исключением  постоянны, поэтому его можно переписать в форме:
постоянны, поэтому его можно переписать в форме:

Энергию ион-дипольного взаимодействия, например, сольватации иона калия молекулой метанола:  описывают уравнением:
описывают уравнением:

где  дипольный момент молекулы;
дипольный момент молекулы;  расстояние между центрами иона и дипольной молекулы.
расстояние между центрами иона и дипольной молекулы.
Так же, как и в случае предыдущего типа электростатического взаимодействия, постоянство ряда входящих в уравнение для ион-дипольного взаимодействия параметров позволяет представить его в форме:

Наконец, энергию взаимодействия двух дипольных молекул, например, уксусной кислоты и пиридина, описывают уравнением:

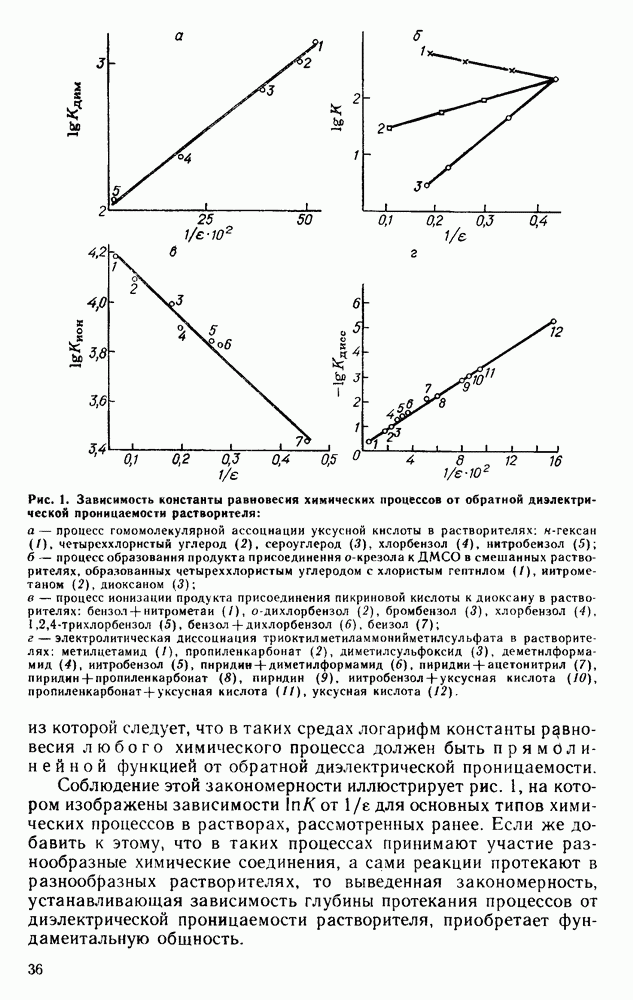
Общим для всех разновидностей электростатического взаимодействия является обратно пропорциональная зависимость от диэлектрической проницаемости. Если считать, что в первом приближении при каждом конкретном взаимодействии расстояния между взаимодействующими частицами в растворе постоянны, то энергия химической реакции в растворе в
соответствии со сказанным будет представлять собою сумму:

Подчеркнем, что это уравнение справедливо лишь для случая, когда  постоянно,
постоянно,  действительно константа, что возможно лишь в тех случаях, когда изменение диэлектрической проницаемости (а изменяться она может лишь с переменой растворителя) не приводит к изменению ковалентной составляющей
действительно константа, что возможно лишь в тех случаях, когда изменение диэлектрической проницаемости (а изменяться она может лишь с переменой растворителя) не приводит к изменению ковалентной составляющей  и не сказывается сколь-нибудь существенно на расстояниях, в пределах которых осуществляется взаимодействие. А это возможно лишь при...
и не сказывается сколь-нибудь существенно на расстояниях, в пределах которых осуществляется взаимодействие. А это возможно лишь при...
Еще одно отступление
В химической литературе часто можно встретить слова «индифферентный растворитель». Смысл, который вкладывается в этот термин, очевиден: растворитель, не взаимодействующий с растворенным веществом. Но ведь таких растворов, как мы видели, не бывает и быть не может. Выходит, химики, прибегающие к этой терминологии, не знают основополагающих положений современного учения о растворах?
Уже подчеркивалось, что в основе любого классификационного определения лежит договоренность, и классификационные понятия уже хотя бы поэтому относительны.
Да, компоненты любого раствора взаимодействуют. Но если энергия специфической сольватации намного меньше энергии универсальной сольватации, а следовательно, можно считать, что  то такой растворитель впервом приближении определяют как химически индифферентный. Тогда переход от одного растворителя к другому не ведет к изменению ковалентной составляющей, т. е.
то такой растворитель впервом приближении определяют как химически индифферентный. Тогда переход от одного растворителя к другому не ведет к изменению ковалентной составляющей, т. е.  и его называют условноиндифферентным (условно-универсальным).
и его называют условноиндифферентным (условно-универсальным).
Химические процессы именно в таких индифферентных либо условно-индифферентных растворителях описывают приведенным уравнением, выводы из которого сколь важны, столь и категоричны.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ЧТО ТАКОЕ КИСЛОТЫ И ОСНОВАНИЯ?
- Кислота — еще одно определение
- Без растворителя
- Отступление (нелирическое)
- «Ониевые соли»
- Отступление (нелирическое)
- Сольвосистемы
- Отступление очередное, почти лирическое
- Сановный протон
- Кислоты, основания, заряды…
- Теория ЖМКО
- Отступления, лирическое и нелирическое
- РАВНОВЕСИЯ В РАСТВОРАХ
- Распад и объединение молекул
- Продукты присоединения
- «Химические привидения»
- Дискуссии, споры…
- Посолить суп…
- Откуда берутся ионы?
- Общая схема равновесий в растворах
- ВЛИЯНИЕ РАСТВОРИТЕЛЯ НА ОТДЕЛЬНЫЕ СТАДИИ РАВНОВЕСИЯ В РАСТВОРАХ
- Константы равновесия
- КЛАССИФИКАЦИЯ РАСТВОРИТЕЛЕЙ
- Донорные и акцепторные числа растворителей
- Управлять растворителем…
- РАСТВОРИТЕЛЬ КАК СРЕДСТВО УПРАВЛЕНИЯ ХИМИЧЕСКИМИ ПРОЦЕССАМИ
- Управление молекулярным состоянием веществ в растворах
- Управление гетеромолекулярной ассоциацией
- И активисты, и лентяи
- Управление ионизацией
- Управление электролитической диссоциацией
- ДИФФЕРЕНЦИРУЮЩЕЕ И НИВЕЛИРУЮЩЕЕ ДЕЙСТВИЯ РАСТВОРИТЕЛЕЙ НА СИЛУ ЭЛЕКТРОЛИТОВ
- Дифференцирующее и нивелирующее
- Отступление — кислотно-основное
- И физика, и химия
- Небольшое отступление, или как следует сравнивать силу электролитов
- Кислотные растворители
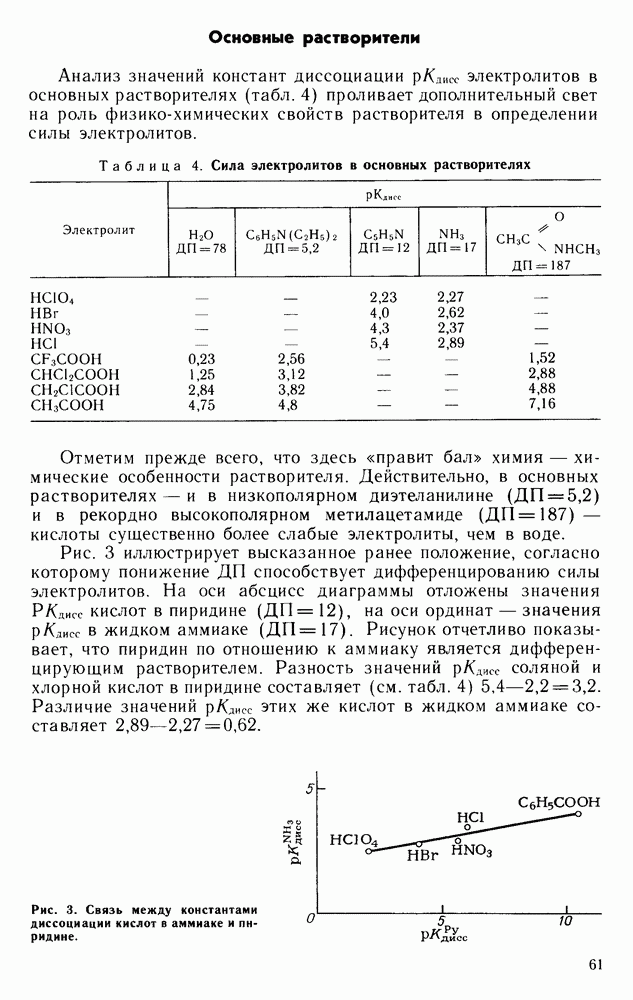
- Основные растворители
- Амфотерные растворители
- Отступление о достоинствах и недостатках объемного анализа
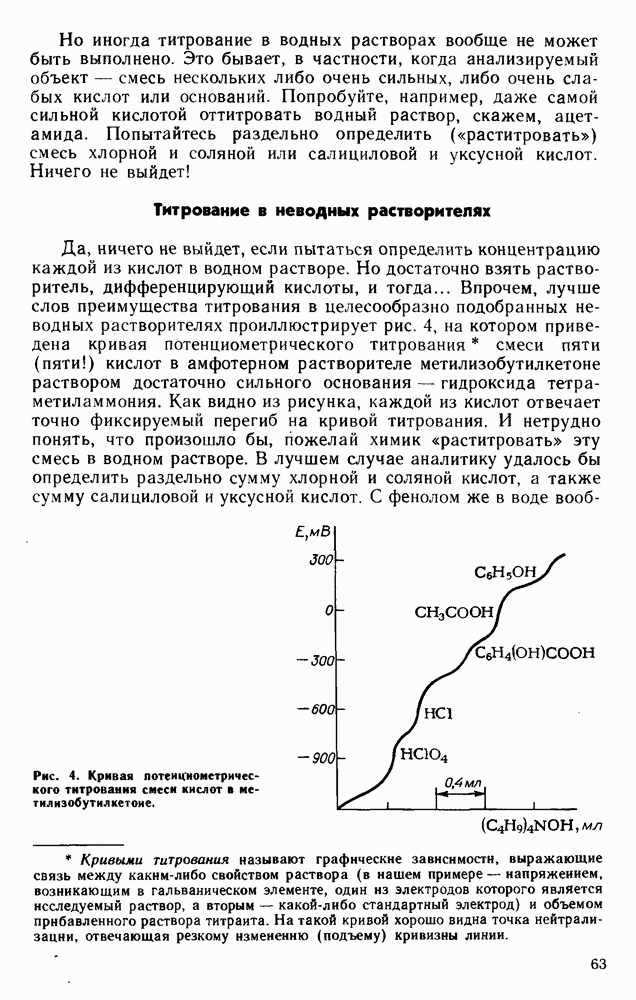
- Титрование в неводных растворителях
- РАСТВОРИМОСТЬ В НЕВОДНЫХ РАСТВОРИТЕЛЯХ
- Некоторые количественные закономерности
- О ХИМИЧЕСКИХ ФОРМАХ СУЩЕСТВОВАНИЯ ЖИВОГО ВЕЩЕСТВА ВО ВСЕЛЕННОЙ
- «Подходящий растворитель»
- ЭЛЕКТРОЛИЗ НЕВОДНЫХ РАСТВОРОВ
- Ряды напряжений в неводных растворах
- Только не из воды
- КИНЕТИКА РЕАКЦИЙ В НЕВОДНЫХ РАСТВОРИТЕЛЯХ
- Типы взаимодействий и их скорость в растворе
- СИНТЕЗЫ В НЕВОДНЫХ РАСТВОРАХ
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК РЕКОМЕНДАТЕЛЬНОЙ ЛИТЁРАТУРЫ