| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.4. Алгебры изображений отношений и их преобразование
В данном разделе мы изложим способ формализации среды наблюдателя с помощью структуры образа и рассмотрим операторы изображений, отображающие такую структуру в лингвистические структуры. Этот подход имеет самый предварительный характер и вне всякого сомнения требует значительных модификаций и поправок.
Первоначальная цель заключалась в том, чтобы структурировать входные данные для процессоров образов, таких, как абдукционные машины, рассматриваемые в гл. 7, или сети на формальных нейронах, рассматриваемые в гл. 6. Когда мы попытались это сделать, стало очевидно, что полученные в результате (входные) образы представляют самостоятельный интерес и заслуживают изучения, как таковые, чем мы и займемся здесь.
Допустим, что наблюдатель  может наблюдать среду, в которую он «погружен», и может с ней взаимодействовать. Получая сенсорные входные сигналы, профильтрованные средствами наблюдения, которыми он пользуется, наблюдатель пытается не только описывать, но также анализировать и понимать их, пытаясь сформировать логически связную систему. В дополнение к сенсорным входным сигналам — наблюдениям — наблюдатель может пользоваться определенными знаниями о среде, в которой он действует. Эти знания могут быть априорными или эмпирическими или комбинацией тех и других.
может наблюдать среду, в которую он «погружен», и может с ней взаимодействовать. Получая сенсорные входные сигналы, профильтрованные средствами наблюдения, которыми он пользуется, наблюдатель пытается не только описывать, но также анализировать и понимать их, пытаясь сформировать логически связную систему. В дополнение к сенсорным входным сигналам — наблюдениям — наблюдатель может пользоваться определенными знаниями о среде, в которой он действует. Эти знания могут быть априорными или эмпирическими или комбинацией тех и других.
Если наблюдатель  играет пассивную роль, то его не следует явно включать в изучаемый процесс, но это должно быть сделано
играет пассивную роль, то его не следует явно включать в изучаемый процесс, но это должно быть сделано  том случае, когда наблюдатель взаимодействует со средой.
том случае, когда наблюдатель взаимодействует со средой.
В данном контексте мы будем считать, что среда представляет собой некоторую часть пространственно-временного физического мира, состоящего из материальных объектов, которые обладают определенными свойствами. Какие именно свойства и отношения будет наблюдать наблюдатель  зависит, очевидно, от его «оборудования», а также от способа использования этого оборудования.
зависит, очевидно, от его «оборудования», а также от способа использования этого оборудования.
Традиционный научный подход, несомненно, предполагает, что наблюдатель будет концентрировать свое внимание на небольшом фрагменте окружающего его мира, наблюдать именно те явления.
которые относятся к этому фрагменту, и пытаться объединить свои наблюдения в некоторую осмысленную целостную картину. Окружающий нас мир весьма сильно структурирован; он построен из элементов, взаимодействующих между собой в соответствии с определенными правилами. Разумный наблюдатель пытается выявить отношения между элементами мира и обнаружить в них какие-то закономерности, или регулярности.
Допустим, что объекты наблюдения — это некоторая часть нашей планетной системы: Земля, Солнце, Луна. Каждый из трех этих объектов обладает наблюдаемыми признаками, к числу которых можно отнести координаты центра тяжести, представленные в некоторой системе координат, массы, может быть, скорости и угловые скорости, а также множество других. Любой признак такого рода эквивалентен некоторому утверждению об одном из элементов. Наблюдатель может также попытаться получить утверждения, касающиеся одновременно двух или трех объектов, т. е. бинарные или тернарные (тройные) отношения. Бинарным отношением может быть, например, результат измерения расстояния между Солнцем и Землей. Оно может быть вычислено непосредственно по уже упоминавшимся координатам центров тяжести. Еще одним отношением могло бы быть гипотетическое взаимодействие между Солнцем и Землей, например, то, что Солнце влияет на движение Земли, но не наоборот. В качестве примера тернарного отношения можно было бы взять отношение, которое представляет движение либо неподвижность центра тяжести системы и которое может быть установлено по координатам всех трех объектов.
Таким образом, мы приходим к рассмотрению множеств, сформированных из некоторых объектов, и отношений между ними, причем многие из этих отношений касаются исключительно отдельных признаков. Это означает, что в формализме для образов роль образующих играют объекты и отношения. Узлами графа, представляющего схему конфигурации, могут быть как объекты, так и отношения. Лишь в случае, когда задан только один тип (бинарных) отношений, из схемы можно исключить отношения, оставив в ней одни объекты. 
В этом смысле материал данного раздела отличается от разд. 6.1 - здесь мы включаем в рассмотрение также и отношения между образующими. Сейчас еще слишком рано судить о том, является ли такой подход более естественным, чем тот, которым мы пользовались в разд. 6.1.
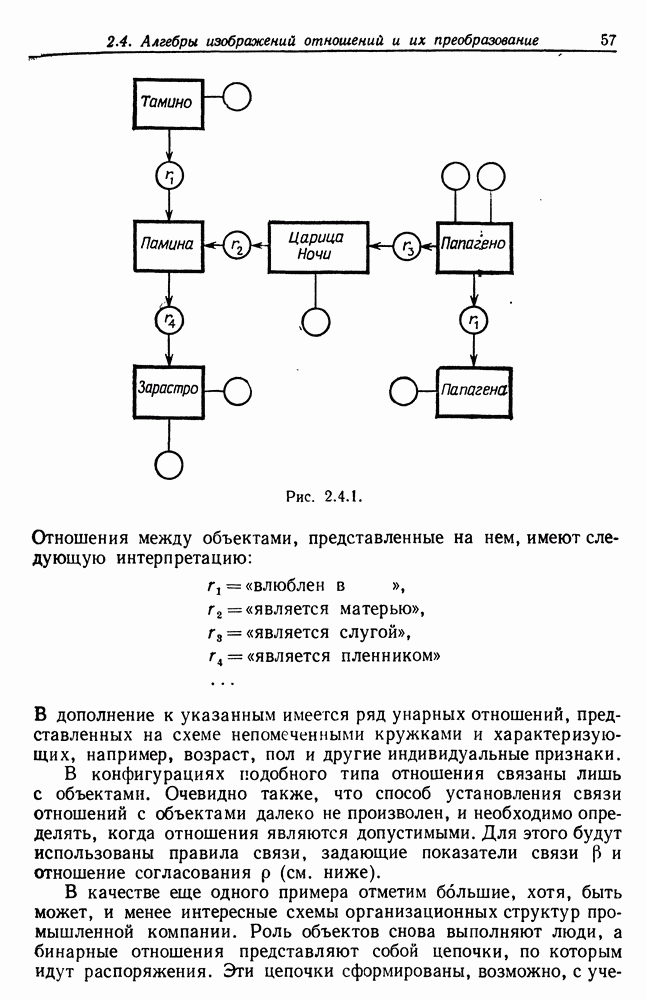
Естественные науки могли бы предоставить нам множество соответствующих примеров, но давайте вместо этого обратимся к примеру, где в качестве объектов выступают люди (см. рис. 2.4.1).

Рис. 2.4.1.
Отношения между объектами, представленные на нем, имеют следующую интерпретацию:

В дополнение к указанным имеется ряд унарных отношений, представленных на схеме непомеченными кружками и характеризующих, например, возраст, пол и другие индивидуальные признаки.
В конфигурациях подобного типа отношения связаны лишь с объектами. Очевидно также, что способ установления связи отношений с объектами далеко не произволен, и необходимо определять, когда отношения являются допустимыми. Для этого будут использованы правила связи, задающие показатели связи  и отношение согласования
и отношение согласования  (см. ниже).
(см. ниже).
В качестве еще одного примера отметим большие, хотя, быть может, и менее интересные схемы организационных структур промышленной компании. Роль объектов снова выполняют люди, а бинарные отношения представляют собой цепочки, по которым идут распоряжения. Эти цепочки сформированы, возможно, с учетом
ограничений, касающихся того, какая именно деятельность предусматривается отношениями управления. Естественно, в таких графах не должно быть циклов, что следует обеспечить, задав соответствующим образом тип соединения 2.
Чтобы рассмотреть конфигурации отношений в общем виде, введем наблюдаемую среду, заданную абстрактно. В рамках нашего формализма образов введем множество образующих  состоящее из объектов. Объект
состоящее из объектов. Объект  характеризуется индексом класса образующих
характеризуется индексом класса образующих  и в более полной степени — признаком а.
и в более полной степени — признаком а.
В число величин, представляемых  -вектором, могут быть включены пространственные координаты, характеризующие местоположение, ориентацию, а также и объем когда
-вектором, могут быть включены пространственные координаты, характеризующие местоположение, ориентацию, а также и объем когда  имеет стандартные положение и ориентацию. Если
имеет стандартные положение и ориентацию. Если  не есть сплошное твердое тело, то, кроме указанных, требуются также и внутренние пространственные координаты. Ими могли бы быть, например, некоторые углы, характеризующие взаимное расположение отдельных частей
не есть сплошное твердое тело, то, кроме указанных, требуются также и внутренние пространственные координаты. Ими могли бы быть, например, некоторые углы, характеризующие взаимное расположение отдельных частей  как у деревянных кукол, и даже координаты, характеризующие растяжение и сжатие частей, образующих объект. Более подробно этот вопрос будет рассмотрен в разд. 6.1.
как у деревянных кукол, и даже координаты, характеризующие растяжение и сжатие частей, образующих объект. Более подробно этот вопрос будет рассмотрен в разд. 6.1.
Внутренние координаты могут также характеризовать звуковые и световые эффекты, такие, как воспроизведение цвета и звука, но нам нужны также и признаки, представляющие менее «осязаемые» эффекты и виды деятельности, такие, как слушание, сон и т. п. постольку, поскольку они относятся к 
Эти признаки могут изменяться под воздействием  -преобра-зований. Положение и ориентация изменяются несомненно, и то же самое может происходить с другими внутренними координатами. Это относится не ко всем им, например, цвет будет трактоваться как постоянная; то же относится и к когда
-преобра-зований. Положение и ориентация изменяются несомненно, и то же самое может происходить с другими внутренними координатами. Это относится не ко всем им, например, цвет будет трактоваться как постоянная; то же относится и к когда  жесткое твердое тело.
жесткое твердое тело.
Индекс класса образующих а, с другой стороны, всегда будет оставаться фиксированным. Арность любого объекта — образующей — будет здесь произвольной, причем все показатели связей равны индексу класса образующей.
Индексы класса и объектов, и отношений будут формироваться на основе некоторого заданного множества А (его не следует путать с множеством  -значений). Мы будем полагать, что для
-значений). Мы будем полагать, что для  значения а принадлежат
значения а принадлежат  — совокупности подмножеств некоторого заданного множества А.
— совокупности подмножеств некоторого заданного множества А.
Поскольку все связи образующей  имеют один и тот же
имеют один и тот же  то нет существенной разницы в том, считаем ли мы, что
то нет существенной разницы в том, считаем ли мы, что  это
это  -мерный вектор, определенный на
-мерный вектор, определенный на  или отдельная точка в
или отдельная точка в  однако мы выбираем первый вариант.
однако мы выбираем первый вариант.
Для того чтобы придать рассмотрению конкретность, обратимся к примеру, для которого частичный список объектов, принадлежащих  приведен в табл. 2.4.1. Отметим, что образующая,
приведен в табл. 2.4.1. Отметим, что образующая,
Таблица 2.4.1 (см. скан)
скажем «мужчина», не есть слово «мужчина» английского или любого другого естественного языка. Эту образующую, так же как и другие элементы данной и следующей таблиц, следует рассматривать в качестве абстрактных понятий. Имеют место включения типа «человек» с «живое существо» и другие отношения множеств; индексом класса образующей служит какое-то подмножество некоторого множества А.
Чтобы упростить изложение, мы исключим время и будем работать в трехмерном пространстве, пренебрегая в результате весьма важным аспектом алгебр отношений.
Отправной точкой при построении конфигураций объектов-отношений служит некоторое множество объектов, причем единственное ограничение задается системой правил  типа «разделенные объемы» (см. случай 2.9.2, т. 1). Теперь за дело принимается наблюдатель
типа «разделенные объемы» (см. случай 2.9.2, т. 1). Теперь за дело принимается наблюдатель  и применяет свою «аппаратуру», представляемую некоторым множеством образующих-отношений
и применяет свою «аппаратуру», представляемую некоторым множеством образующих-отношений  . Всякая образующая такого рода
. Всякая образующая такого рода  располагает некоторой «необходимой» арностью
располагает некоторой «необходимой» арностью  а ее действительная арность удовлетворяет соотношению
а ее действительная арность удовлетворяет соотношению

Связи, соответствующие необходимой арности, перенумерованы как  сонбх
сонбх  причем нумерацией можно пренебречь, если сонбх
причем нумерацией можно пренебречь, если сонбх  Каждому значению
Каждому значению  соответствует связь с показателем связи
соответствует связь с показателем связи  который может принимать значения из множества
который может принимать значения из множества 
Остановимся снова вкратце на арности образующих. Мы допустили возможность переменной, но ограниченной снизу условием (2.4.1) арности. Строго говоря, это означает, что заданная образующая может иметь более чем одну арность. Последующее станет яснее, если значение арности будет введено в идентификатор образующей. Это означает, что каждая образующая имеет ровно одну арность. Если  конечна, то это означает существование максимальной арности.
конечна, то это означает существование максимальной арности.
Конфигурация, состоящая из объектов-образующих  , принадлежащих
, принадлежащих  и отношений
и отношений  принадлежащих
принадлежащих  считается регулярной, если
считается регулярной, если
(i) все  - удовлетворяют условию разделенных объемов;
- удовлетворяют условию разделенных объемов;
(ii) соединения устанавливаются только между  ,
,
(iii) все необходимые связи всех охвачены соединениями;
 если две связи соединены, то отношение связй «равенство» имеет место.
если две связи соединены, то отношение связй «равенство» имеет место.
Мы не будем вводить в конфигурации наблюдателя  за исключением тех случаев, когда он играет активную роль. Строго говоря, наблюдателя
за исключением тех случаев, когда он играет активную роль. Строго говоря, наблюдателя  следовало бы вводить в конфигурацию, так как он оказывается связанным с
следовало бы вводить в конфигурацию, так как он оказывается связанным с  хотя бы наблюдая, например, ее размер. Такое включение приведет к увеличению арностей на одну единицу. Мы опускаем наблюдателя, чтобы не захламлять схемы конфигураций.
хотя бы наблюдая, например, ее размер. Такое включение приведет к увеличению арностей на одну единицу. Мы опускаем наблюдателя, чтобы не захламлять схемы конфигураций.
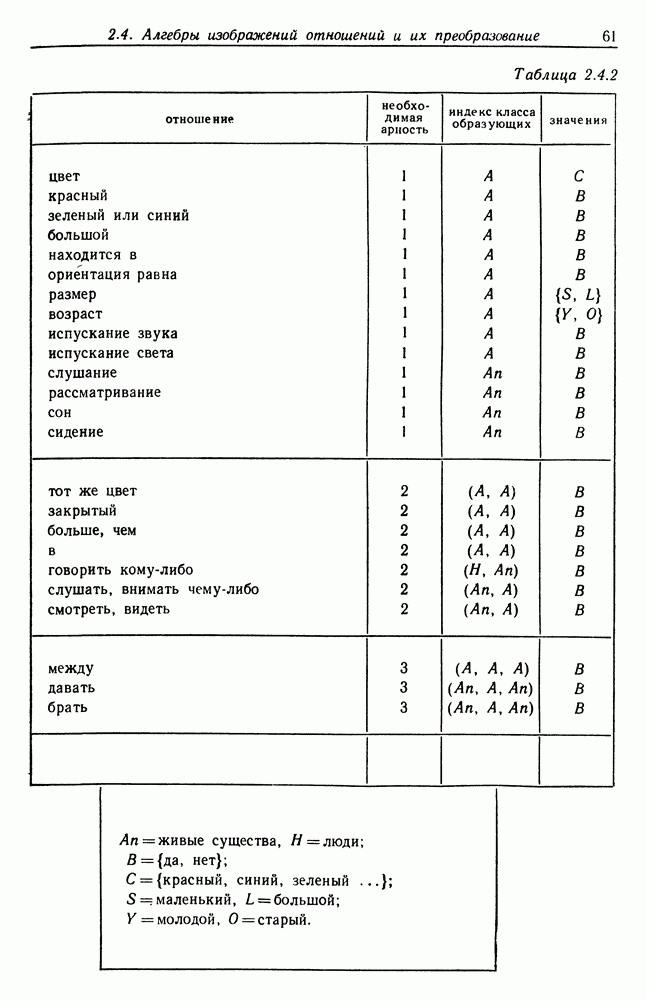
Как и выше, подчеркиваем, что описания, помещенные в левом столбце табл. 2.4.2, не следует рассматривать как слова естественного языка. Первое из них, например, следует трактовать не как английское слово «color» («цвет»), но как некоторую абстрактную операцию наблюдения цвета объекта. Трудно, естественно, освободиться от влияния языка, которым вы пользуетесь, а согласно гипотезе Уорфа, вообще невозможно. Как бы то ни было, вводя конфигурации, следует стараться делать это на абстрактном уровне.
Таблица 2.4.2 (см. скан)
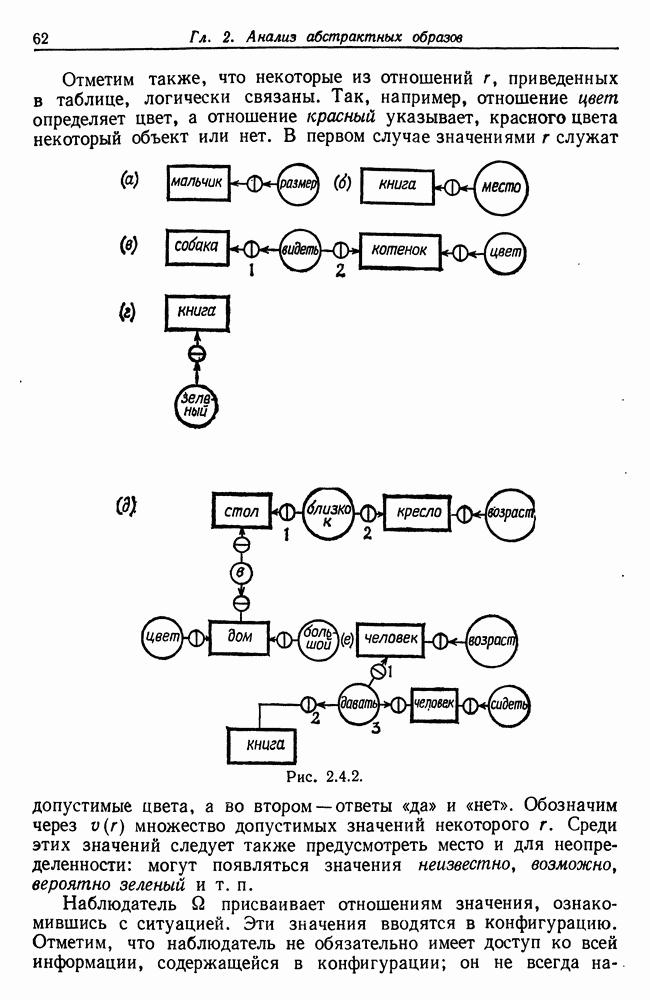
Отметим также, что некоторые из отношений  приведенных в таблице, логически связаны. Так, например, отношение цвет определяет цвет, а отношение красный указывает, красного цвета некоторый объект или нет. В первом случае значениями
приведенных в таблице, логически связаны. Так, например, отношение цвет определяет цвет, а отношение красный указывает, красного цвета некоторый объект или нет. В первом случае значениями  служат допустимые цвета, а во втором — ответы «да» и «нет». Обозначим через
служат допустимые цвета, а во втором — ответы «да» и «нет». Обозначим через  множество допустимых значений некоторого
множество допустимых значений некоторого  Среди этих значений следует также предусмотреть место и для неопределенности: могут появляться значения неизвестно, возможно, вероятно зеленый и т. п.
Среди этих значений следует также предусмотреть место и для неопределенности: могут появляться значения неизвестно, возможно, вероятно зеленый и т. п.
Рис. 2.4.2. (см. скан)
Наблюдатель  присваивает отношениям значения, ознакомившись с ситуацией. Эти значения вводятся в конфигурацию. Отметим, что наблюдатель не обязательно имеет доступ ко всей информации, содержащейся в конфигурации; он не всегда наблюдает
присваивает отношениям значения, ознакомившись с ситуацией. Эти значения вводятся в конфигурацию. Отметим, что наблюдатель не обязательно имеет доступ ко всей информации, содержащейся в конфигурации; он не всегда наблюдает
все признаки. Мы будем идентифицировать изображения, задавая соединения, индексы классов образующих  и значения
и значения  Никакой другой информации нет. В частности, мы не допускаем использования каких-либо дополнительных идентификаторов или нумераций объектов.
Никакой другой информации нет. В частности, мы не допускаем использования каких-либо дополнительных идентификаторов или нумераций объектов.
Строго говоря, мы работаем здесь только с полными конфигурациями, так как предполагается, что все необходимые связи соединены. Возможно, это условие следовало бы ослабить.
Отметим также, что эти (замкнутые) связи включены в информацию, которую содержит изображение.
Несколько примеров возможных конфигураций отношений и соответствующих им изображений приведены на рис. 2.4.2, где прямоугольники обозначают объекты, а кружки — отношения. Попытаемся теперь описать словами изображения: мы совершаем переход от предлингвистических образов к разговорной речи. Это отображение, конечно, будет многозначным, но мы попытаемся сделать так, чтобы оно имело единственное обращение. Естественный язык, конечно, может быть неоднозначным — лингвистическая литература изобилует примерами такого рода. Тем не менее сейчас мы хотим получить однозначное описание изучаемого изображения.
Таблица 2.4.3 (см. скан)
В первую очередь сделаем это неформально — так, как
показано в табл. 2.4.3. Многие другие лингвистические высказывания можно рассматривать как навеянные изображениями не только из-за различных значений содержащихся в них отношений, но также и в связи с изменчивостью; вызванной способом применения синтаксиса.
Это приводит нас к основной проблеме — как можно формализовать это многозначное отображение, если в явном виде заданы словарь и грамматика языка, которым мы будем пользоваться? Следовало бы попытаться понять интроспективно, как в действительности происходит отображение образов отношений в лексические цепочки, что продемонстрировано в табл. 2.4.3. Это нелегко выразить точно, на языке хорошо определенного алгоритма.
Поскольку, однако, конечным результатом служит линейная лексическая цепочка, определенная на некотором словаре  , то, чтобы задать топологию изображения, необходимо ввести в цепочку какую-то позиционную информацию. В конце концов именно поэтому нам и требуется грамматика: этого требует линейность лексической цепочки.
, то, чтобы задать топологию изображения, необходимо ввести в цепочку какую-то позиционную информацию. В конце концов именно поэтому нам и требуется грамматика: этого требует линейность лексической цепочки.
Один из способов заключается в использовании произвольных маркеров, как это принято в традиционной лингвистике, для указания синтаксических зависимостей, вносимых топологией. В строке (в) табл. 2.4.3 можно было бы, например, использовать маркеры, чтобы показать, что отношение, представляемое  связано с «dog» как с подлежащим и с «kitten» как с прямым дополнением, а прилагательное «red» относится к «kitten»:
связано с «dog» как с подлежащим и с «kitten» как с прямым дополнением, а прилагательное «red» относится к «kitten»:

Если семейство маркеров можно сделать достаточно богатым, то это позволяет сохранить топологическую информацию при отображении из  в лексические маркированные цепочки. Этот способ, однако, не вполне удовлетворителен. Во-первых, грамматика цепочек в явном виде не определяется. Не ясно даже, каковы терминальные символы. Ими не являются просто слова «the», «dog» и т. п., так как маркеры вводятся различными способами.
в лексические маркированные цепочки. Этот способ, однако, не вполне удовлетворителен. Во-первых, грамматика цепочек в явном виде не определяется. Не ясно даже, каковы терминальные символы. Ими не являются просто слова «the», «dog» и т. п., так как маркеры вводятся различными способами.
Во-вторых, не учитываются ограничения, свойственные говорящему человеку, в связи с особенностями его кратковременной памяти. В работе Кучеры и Каупера (1975) утверждается, что это ограничение следует вводить в любую реалистичную модель разговорной речи, в которой не встречаются предложения, вывод которых сопряжен с использованием большой кратковременной памяти для соблюдения сложных синтаксических зависимостей. Это не означает, что будут ограничены длина или количество
допустимых предложений, — ограничивается лишь объем необходимой временной памяти.
В качестве примера того, к чему мы стремимся, рассмотрим конкретное отображение в некоторое Это не слишком удачный пример, но основную идею он иллюстрирует достаточно хорошо.
Для формализации введем грамматику  следующего вида. Рассмотрим множество
следующего вида. Рассмотрим множество  всех
всех  -мерных векторов вида
-мерных векторов вида  где
где  — некоторое заданное фиксированное натуральное число. Размерность
— некоторое заданное фиксированное натуральное число. Размерность  следовательно, переменна, но ограничена.
следовательно, переменна, но ограничена.
Множество К состоит изо всех элементов вида  или
или  где
где  — верхние индексы, обозначающие «отношение» и «объект» соответственно, и
— верхние индексы, обозначающие «отношение» и «объект» соответственно, и  Оператор
Оператор  определим как
определим как  Множество
Множество  представляет состояния конечного автомата, и разумеется, оно конечно, так как А конечно, а
представляет состояния конечного автомата, и разумеется, оно конечно, так как А конечно, а  ограничена. В частности, пустым может быть как начальное состояние
ограничена. В частности, пустым может быть как начальное состояние  так и заключительное состояние
так и заключительное состояние 
Рассмотрим произвольную образующую причем если  то она является объектом, а если — отношением.
то она является объектом, а если — отношением.
В обоих случаях  вектор с
вектор с  компонентами. Введем множество
компонентами. Введем множество  терминальных символов
терминальных символов 

где  — векторы размерности самое большее
— векторы размерности самое большее  . Компоненты этих векторов принимают значения
. Компоненты этих векторов принимают значения  (см. выше), включая пустое множество
(см. выше), включая пустое множество  Обозначив
Обозначив  определим их размеры
определим их размеры

и будем считать, что  Номера
Номера  должны соответствовать упорядочению со связей образующей
должны соответствовать упорядочению со связей образующей  а значение
а значение  равно либо в, либо
равно либо в, либо  компоненте
компоненте  с верхним индексом
с верхним индексом  если
если  если
если  Аналогично дело обстоит для
Аналогично дело обстоит для 
Будем называть  префиксом и суффиксом образующей
префиксом и суффиксом образующей  соответственно, однако роли префиксов и суффиксов слов естественного языка они исполнять не будут.
соответственно, однако роли префиксов и суффиксов слов естественного языка они исполнять не будут.
Переходы  в конечном автомате будут иметь вид
в конечном автомате будут иметь вид

где

При удалении и добавлении в пункте  в первую очередь производится вычеркивание, затем переход к вектору меньшей размерности с тем же упорядочением и в заключение — присоединение (конкатенация) справа непустых элементов
в первую очередь производится вычеркивание, затем переход к вектору меньшей размерности с тем же упорядочением и в заключение — присоединение (конкатенация) справа непустых элементов  Таким способом позиционная информация сохраняется по отношению к нумерации различных связей.
Таким способом позиционная информация сохраняется по отношению к нумерации различных связей.
Целесообразно было бы обобщить рассмотренное выше с тем, чтобы заменить точное соответствие  и т.д. включениями
и т.д. включениями  и т. д. Здесь мы не будем заниматься этой задачей.
и т. д. Здесь мы не будем заниматься этой задачей.
Для того чтобы продемонстрировать, как такой автомат работает, положим  и
и  Тогда у нас есть три непустых подмножества
Тогда у нас есть три непустых подмножества

и следующие состояния:

и т. д. с другими комбинациями значений верхних индексов 
Если, например, арность образующей  равна двум
равна двум  то имеет место переход
то имеет место переход  где терминальный символ
где терминальный символ  определен, согласно (2.4.2), при
определен, согласно (2.4.2), при

Если же образующая  имеет арность, равную единице, и
имеет арность, равную единице, и  то переход принимает вид
то переход принимает вид  при
при


Рис. 2.4.3.
Обратимся к приведенной на рис. 2.4.3 конфигурации и преобразуем ее в предложение, принадлежащее  . В первую очередь упорядочим пять образующих по некоторому психологическому критерию, скажем в виде последовательности
. В первую очередь упорядочим пять образующих по некоторому психологическому критерию, скажем в виде последовательности 
Вопрос о выборе перестановки остается открытым, однако он вполне может нести определенную информацию, представлять соответствующие стилистические средства и выражать какие-то нюансы, отсутствующие на самом деле в заданном изображении.
Из начального состояния  переходим в состояние записав терминальный символ
переходим в состояние записав терминальный символ  Префикс Р равен просто
Префикс Р равен просто  вывод только начат, и
вывод только начат, и  . Но
. Но  и, следовательно, необходимо выбрать потребующуюся в будущем позиционную информацию
и, следовательно, необходимо выбрать потребующуюся в будущем позиционную информацию  что приводит к состоянию
что приводит к состоянию  Теперь появляется образующая
Теперь появляется образующая  и мы не можем исключить никакой информации. Здесь необходимо использовать три компонента, что нарушает условие
и мы не можем исключить никакой информации. Здесь необходимо использовать три компонента, что нарушает условие  . Итак, с помощью
. Итак, с помощью  данное йзображение отношений обработать нельзя.
данное йзображение отношений обработать нельзя.
Воспользуемся теперь перестановкой  Начав снова с состояния 1, мы сталкиваемся с
Начав снова с состояния 1, мы сталкиваемся с  что приводит к состоянию
что приводит к состоянию  и терминальному символу
и терминальному символу

Затем мы встречаемся с образующей  выбираем в связи с этим
выбираем в связи с этим  и записываем
и записываем

Происходит переход к состоянию  . Далее мы встречаемся с образующей
. Далее мы встречаемся с образующей  выбираем в связи с этим
выбираем в связи с этим  и записываем в результате терминальный символ
и записываем в результате терминальный символ

Происходит переход к состоянию  . Далее следует образующая
. Далее следует образующая  и записывается терминальный символ
и записывается терминальный символ

Происходит возврат к состоянию  . И наконец, образующая
. И наконец, образующая  и записываем терминальный символ
и записываем терминальный символ

Происходит переход к состоянию  что завершает вывод терминальной цепочки
что завершает вывод терминальной цепочки

Мы выявили синтаксические зависимости, представленные на рис. 2.4.4, а. Они, как это показано на рис. 2.4.4,б, представляют

Рис. 2.4.4.
текущее содержание кратковременной памяти: между  между
между  и т. д.
и т. д.
Оператор изображения  определен на некотором подмножестве и является многозначным. Многозначность связана с произвольностью выбора упорядочения образующих
определен на некотором подмножестве и является многозначным. Многозначность связана с произвольностью выбора упорядочения образующих  стратегией говорящего человека. От грамматики
стратегией говорящего человека. От грамматики  зависит объем лингвистических возможностей говорящего, т. е. насколько велико подмножество
зависит объем лингвистических возможностей говорящего, т. е. насколько велико подмножество
Свойства отображения  суммируются в следующем предложении;
суммируются в следующем предложении;
Предложение 2.4.1.
(i) Язык  задается конечным автоматом.
задается конечным автоматом.
(ii) Число состояний  автомата ограничено:
автомата ограничено:

число терминальных переменных  также ограничено:
также ограничено:

здесь  — число подмножеств А, фигурирующих в спецификациях связей правил
— число подмножеств А, фигурирующих в спецификациях связей правил  .
.
(iii) Отображение  обратимо: предложению, заданному в языке
обратимо: предложению, заданному в языке  соответствует точно одно идеальное изображение в
соответствует точно одно идеальное изображение в  .
.
Доказательство. Число состояний  так же, как и число терминальных символов
так же, как и число терминальных символов  (см. (2.4.2)), конечно. Текущее состояние
(см. (2.4.2)), конечно. Текущее состояние  содержит позиционную информацию, относящуюся к следующему такту. Она разделяет связи, присоединенные к объектам, и связи, присоединенные к отношениям, и, естественно, различные показатели связи из
содержит позиционную информацию, относящуюся к следующему такту. Она разделяет связи, присоединенные к объектам, и связи, присоединенные к отношениям, и, естественно, различные показатели связи из  При переходе из состояния
При переходе из состояния  в некоторое другое состояние
в некоторое другое состояние  терминальный символ
терминальный символ  указывает, как устранять позиционную информацию, используя Р для замыкания (и устранения) не соединенных к этому моменту связей, и какие новые связи должны быть открыты (исходя из 5). Правило (2.4.5 (в)) однозначно определяет
указывает, как устранять позиционную информацию, используя Р для замыкания (и устранения) не соединенных к этому моменту связей, и какие новые связи должны быть открыты (исходя из 5). Правило (2.4.5 (в)) однозначно определяет  по
по  следовательно, автомат детерминированный и утверждение
следовательно, автомат детерминированный и утверждение  доказано.
доказано.
Для того чтобы ограничить число состояний, заметим, что  где
где  — число элементов в
— число элементов в  и, следовательно,
и, следовательно,  Это обычно очень слабое ограничение, поскольку, как правило, разбиение
Это обычно очень слабое ограничение, поскольку, как правило, разбиение  содержит существенно меньшее число подмножеств. На самом деле следовало бы даже ожидать, что
содержит существенно меньшее число подмножеств. На самом деле следовало бы даже ожидать, что  Во всяком случае, для заданного
Во всяком случае, для заданного  справедливо соотношение
справедливо соотношение

Аналогично, чтобы ограничить число терминальных символов, замечаем, что векторы  самое большее размерности
самое большее размерности  и что если
и что если  компонент Р непустой, то
компонент Р непустой, то  компонент
компонент  должен быть пустым, и наоборот. Следовательно, при фиксированном
должен быть пустым, и наоборот. Следовательно, при фиксированном  либо
либо  либо
либо  принимает одно из
принимает одно из  непустых значений В. Для фиксированных
непустых значений В. Для фиксированных  однако, множество значений В детерминированно и изменяться может только их распределение
однако, множество значений В детерминированно и изменяться может только их распределение
на компонентах  . Итак, элементы
. Итак, элементы  распределяются по
распределяются по  с учетом указанного ограничения, так что существует самое большее
с учетом указанного ограничения, так что существует самое большее

возможностей. Если некоторые из значений В совпадают, то число вариантов может оказаться меньшим, чем в (2.4.13). Просуммировав, приходим к выражению (2.4.11).
Для доказательства утверждения  выпишем предложение
выпишем предложение  языка
языка  и просмотрим его слева направо. В процессе этого просмотра связи открываются и замыкаются в соответствии с
и просмотрим его слева направо. В процессе этого просмотра связи открываются и замыкаются в соответствии с  , а необходимые связи (и, быть может, некоторые другие) будут соединены. Следовательно,
, а необходимые связи (и, быть может, некоторые другие) будут соединены. Следовательно,  определяет изображение в так что, хотя отображение
определяет изображение в так что, хотя отображение  не обязательно должно быть задано на всей алгебре изображений и хотя оно не является однозначным, обратное отображение будет однозначным.
не обязательно должно быть задано на всей алгебре изображений и хотя оно не является однозначным, обратное отображение будет однозначным.
Замечание 1. Изображения представляют информацию, собранную наблюдателем  о тех материальных объектах, которые он может наблюдать. Это не семантика в подлинном смысле слова. Семантика, по крайней мере в понимании автора, связана с интерпретацией лингвистических высказываний и выяснением их значения. Алгебра изображений не имеет ничего общего с языком, как таковым, она связана с предлингвистикой. Элементы
о тех материальных объектах, которые он может наблюдать. Это не семантика в подлинном смысле слова. Семантика, по крайней мере в понимании автора, связана с интерпретацией лингвистических высказываний и выяснением их значения. Алгебра изображений не имеет ничего общего с языком, как таковым, она связана с предлингвистикой. Элементы  служат для говорящего человека мотивами и побуждают его порождать элементы
служат для говорящего человека мотивами и побуждают его порождать элементы  когда он в состоянии делать это. Преуспевает он в этом отношении или нет, зависит от ограничений на грамматику
когда он в состоянии делать это. Преуспевает он в этом отношении или нет, зависит от ограничений на грамматику  и выбираемой им стратегии. Лишь получив обратное отображение, можно говорить о подлинной семантике.
и выбираемой им стратегии. Лишь получив обратное отображение, можно говорить о подлинной семантике.
Замечание 2. На строение налагается ряд чрезвычайно жестких ограничений, одно из которых заключается в том, что мы имеем дело исключительно с «мгновенными» ситуациями. Время исключено из рассмотрения. При введении времени возникают также ограничения  , связывающие последовательные «моментальные фотографии»
, связывающие последовательные «моментальные фотографии»  Эти ограничения могут выражать, например, физическую непрерывность, неизменность материальных объектов и т. п. Следует изучить вопрос о том, как это можно реализовать.
Эти ограничения могут выражать, например, физическую непрерывность, неизменность материальных объектов и т. п. Следует изучить вопрос о том, как это можно реализовать.
Замечание 3. Мы полагаем, что конфигурации и изображения, выявленные наблюдателем  представляют физическую реальность. Вполне может случиться, что наблюдения противоречат друг другу и соответственно не отражают реальности. Другими словами, следует допустить существование механизма деформации <Г и исходить из того, что лингвистический анализатор работает не с
представляют физическую реальность. Вполне может случиться, что наблюдения противоречат друг другу и соответственно не отражают реальности. Другими словами, следует допустить существование механизма деформации <Г и исходить из того, что лингвистический анализатор работает не с 
Замечание 4. Некоторые конфигурации, принадлежащие множеству регулярных конфигураций  можно рассматривать как макрообразующие (см. гл. 2, т. 1) и использовать для пополнения алгебры изображений дополнительными правилами Я. Это приведет к алгебре изображений второго порядка, с которой можно работать аналогичным описанному выше образом. До сих пор подобные попытки в связи с нашими задачами не предпринимались.
можно рассматривать как макрообразующие (см. гл. 2, т. 1) и использовать для пополнения алгебры изображений дополнительными правилами Я. Это приведет к алгебре изображений второго порядка, с которой можно работать аналогичным описанному выше образом. До сих пор подобные попытки в связи с нашими задачами не предпринимались.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
- 4.2. Рентгенография кристаллов
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
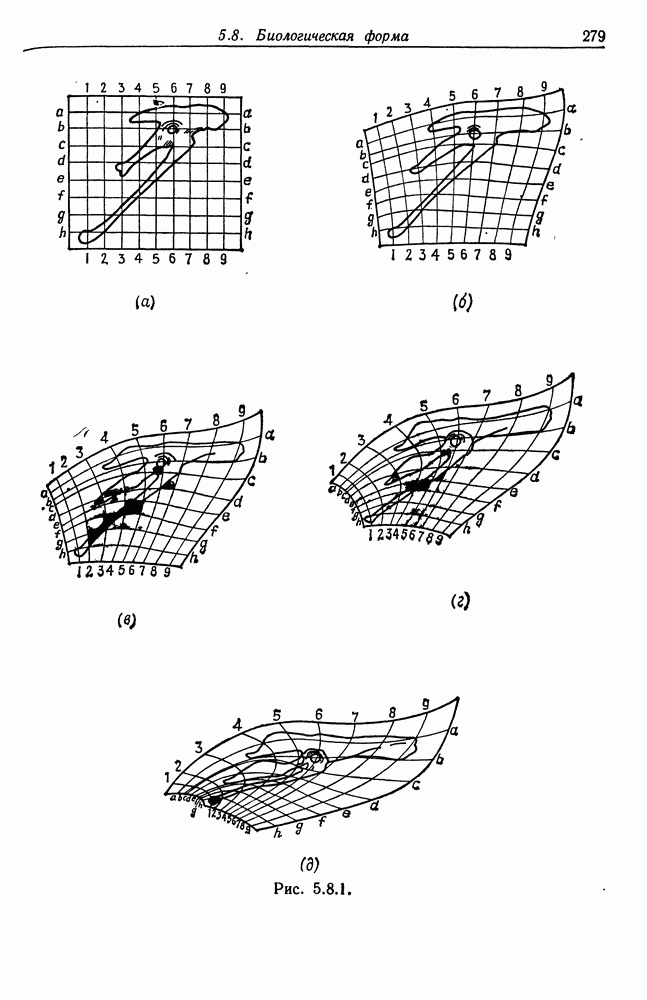
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы