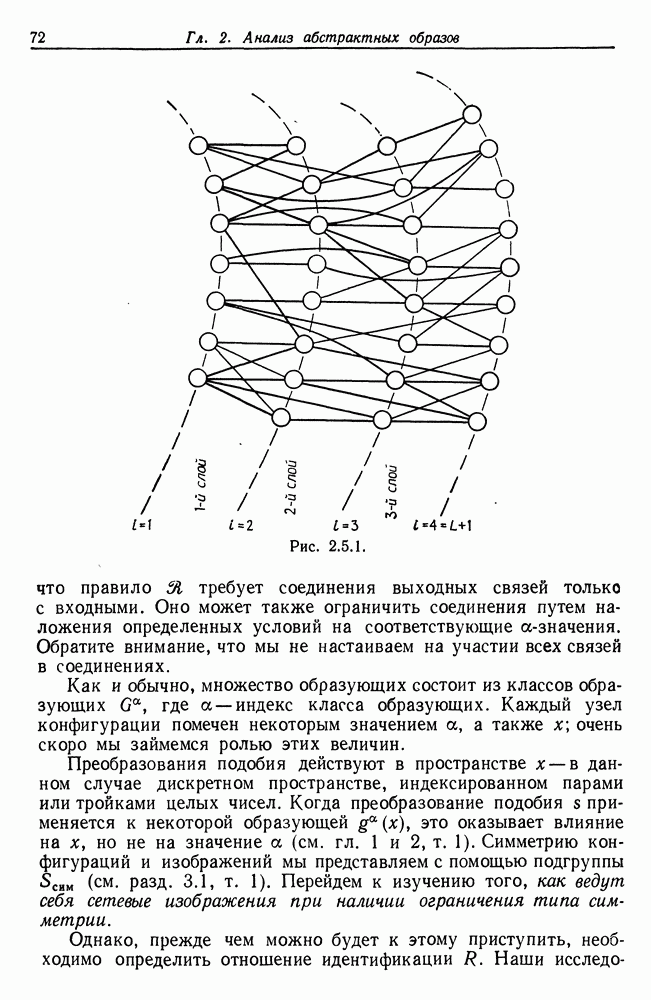
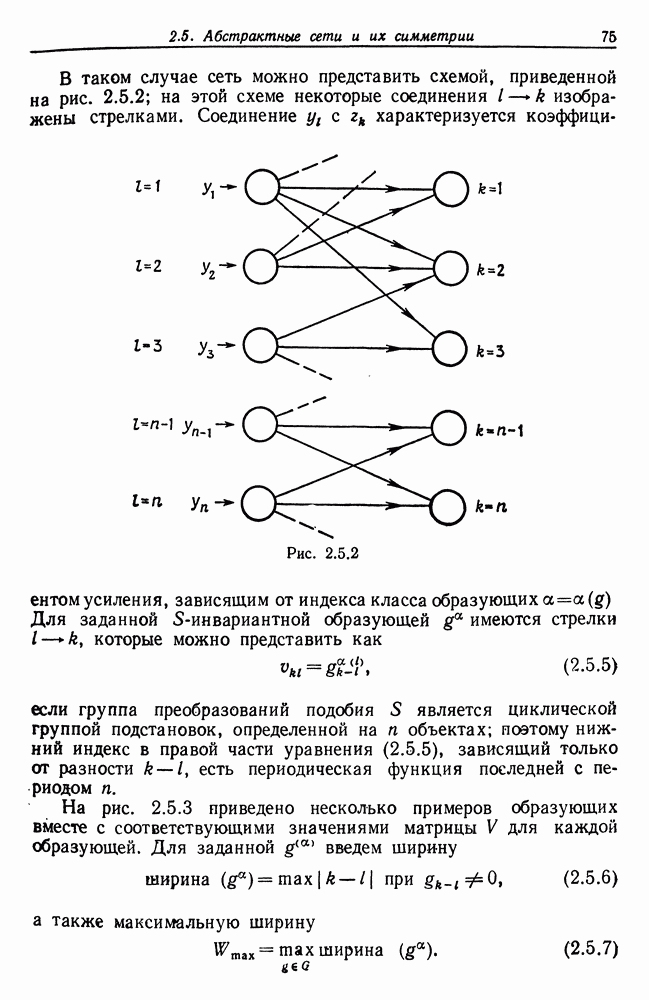
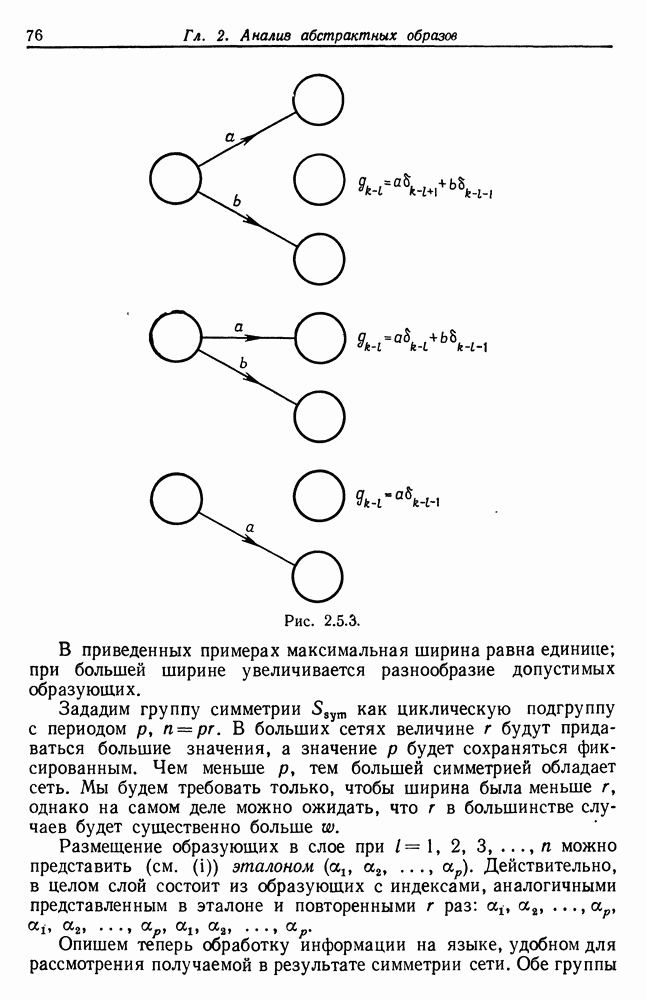
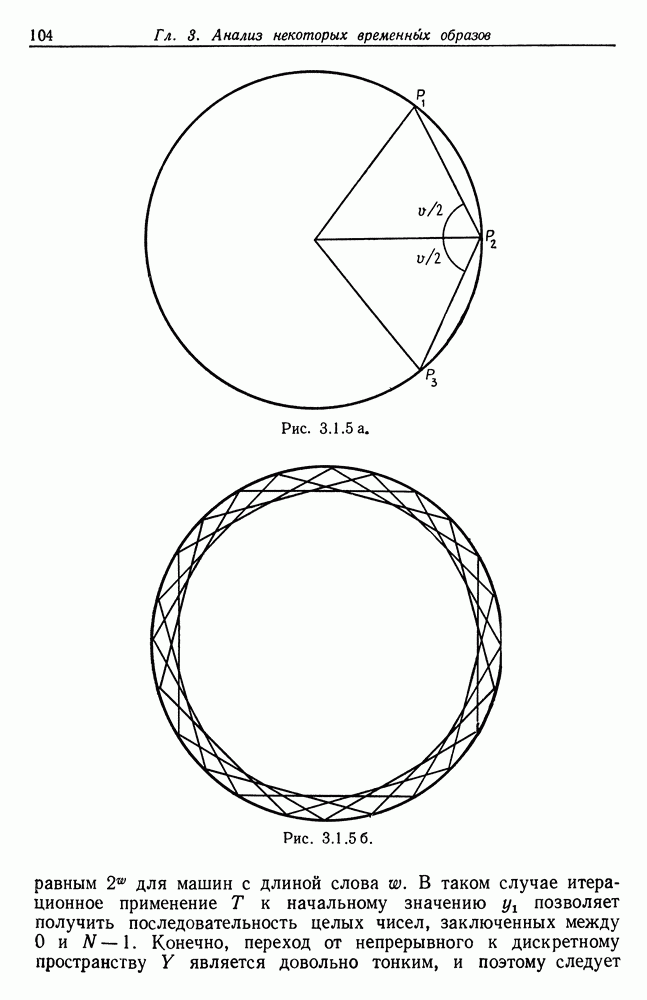
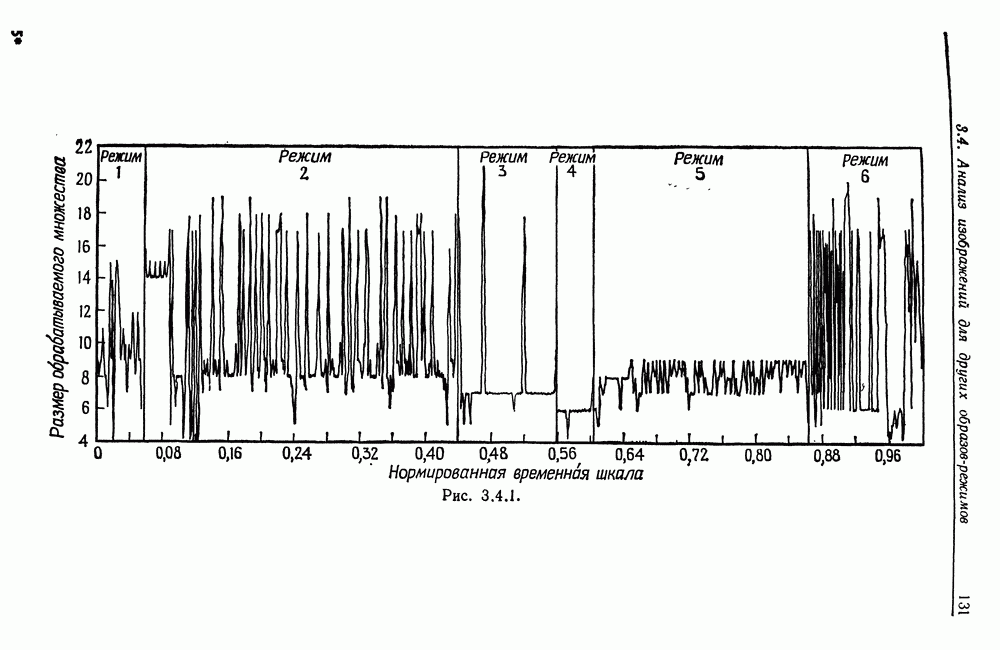
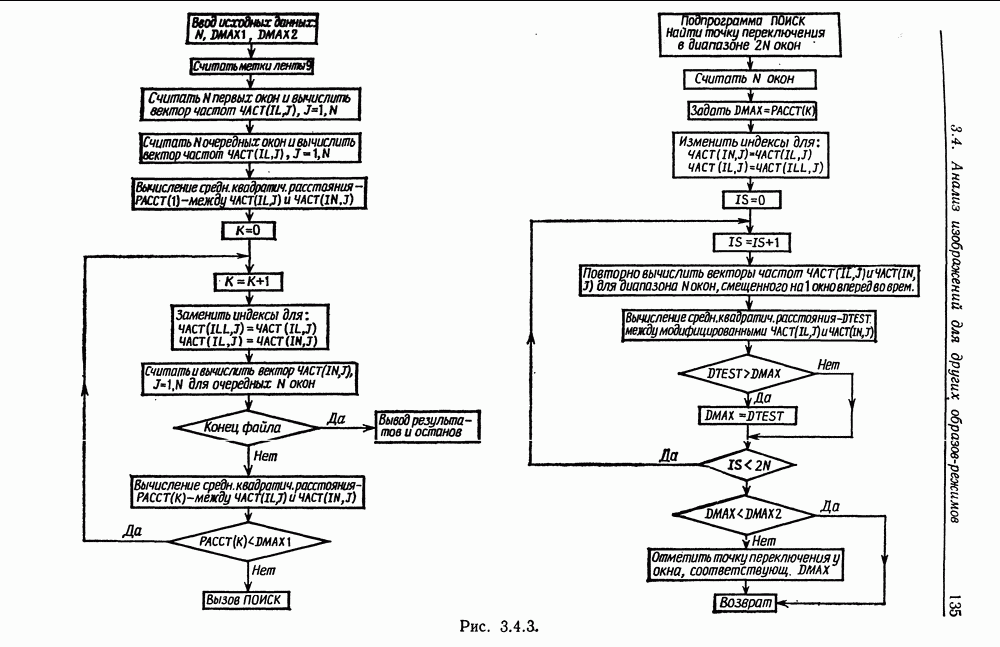
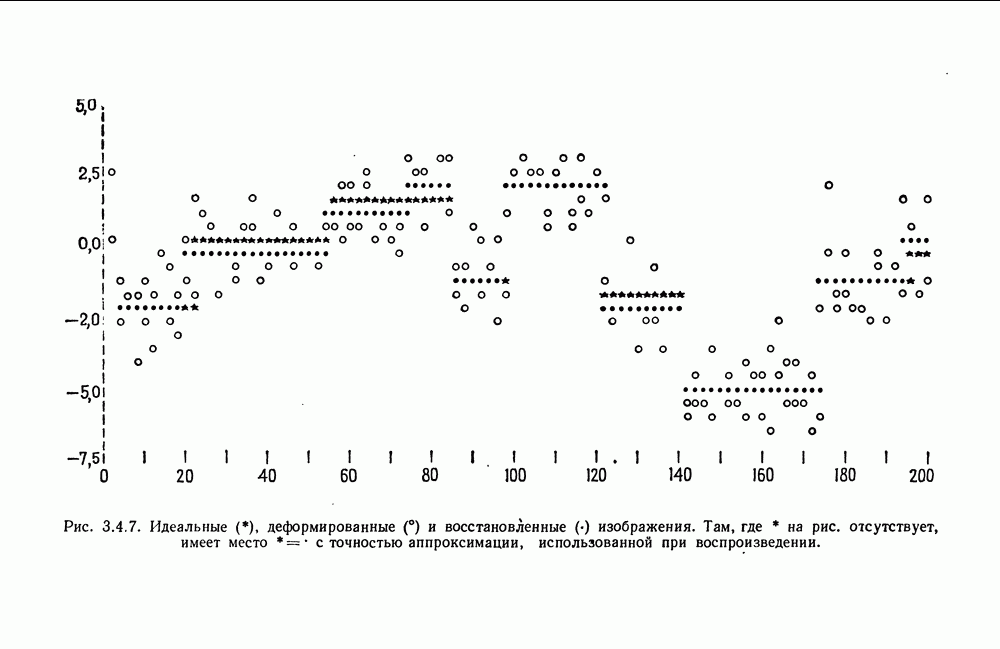
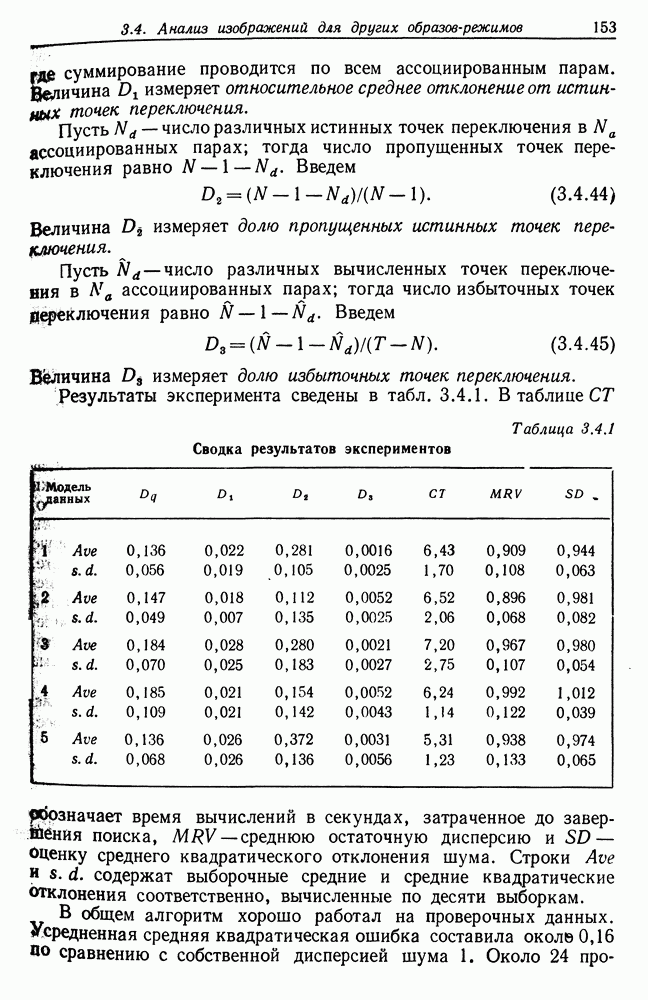
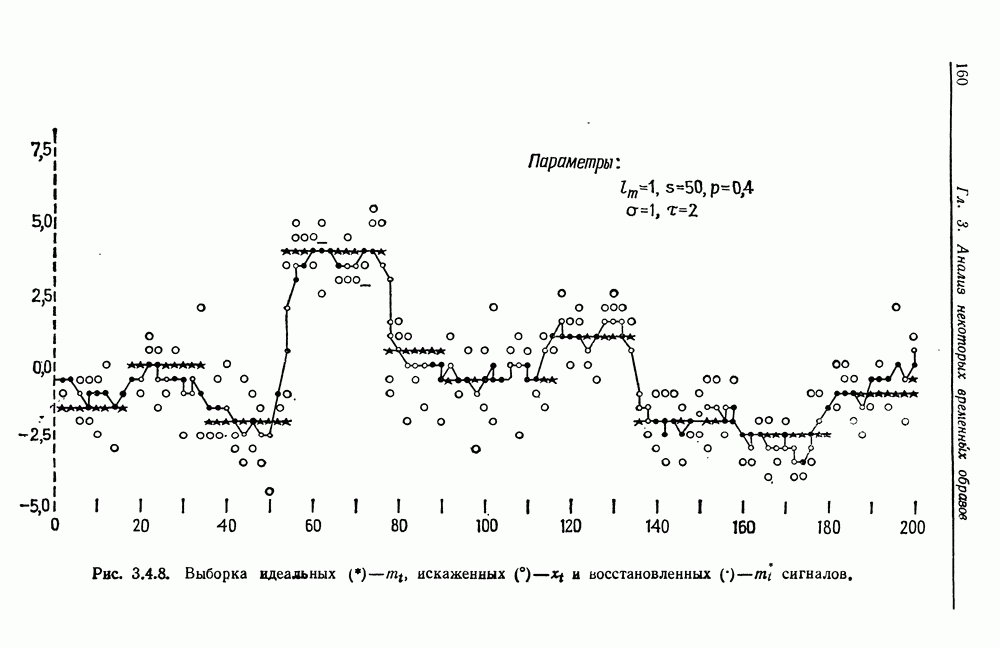
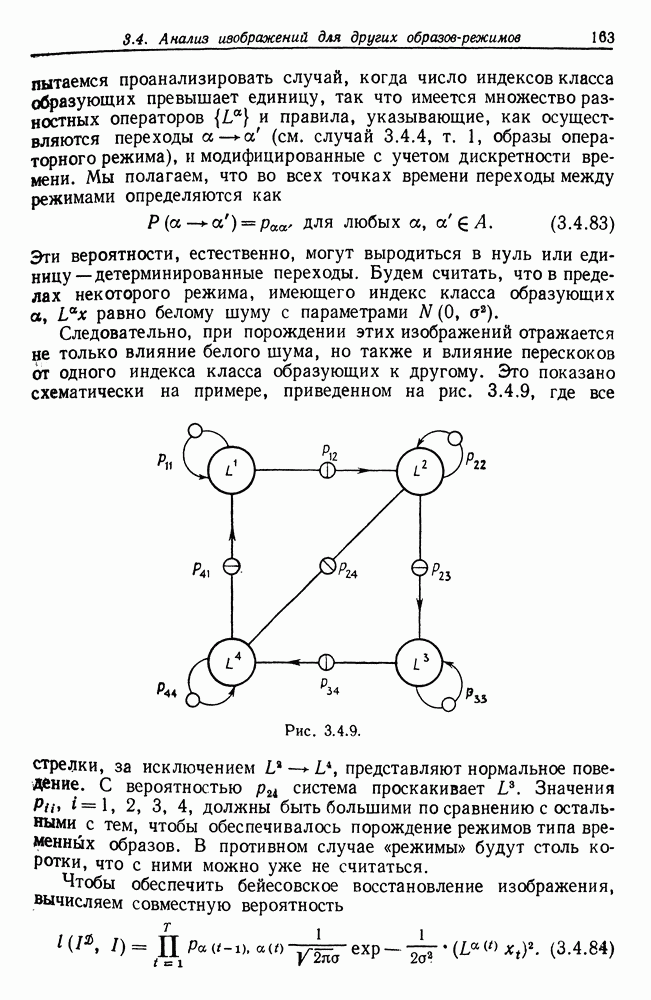
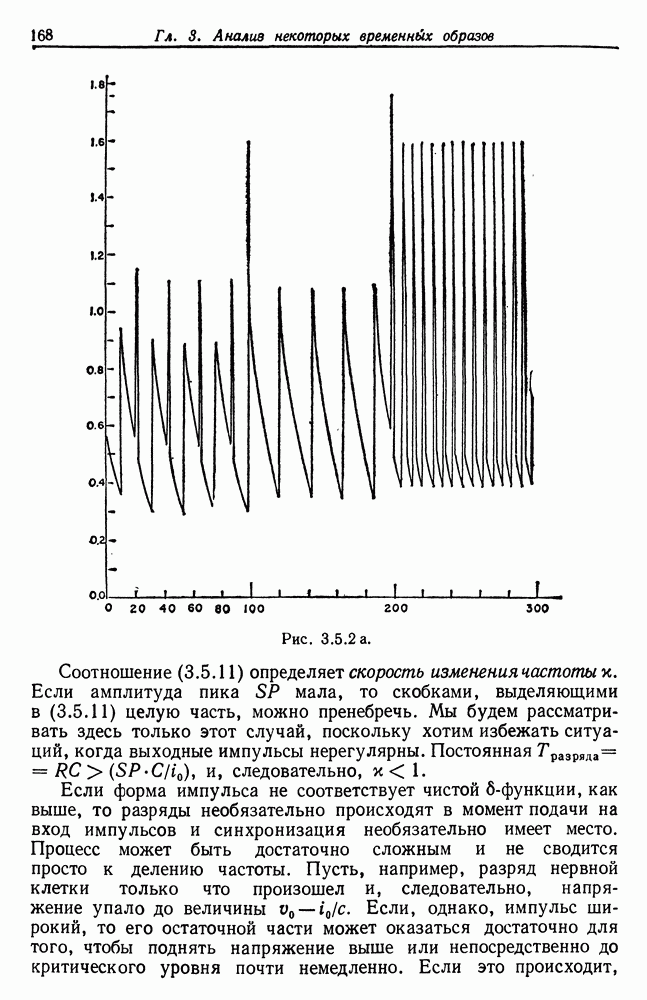
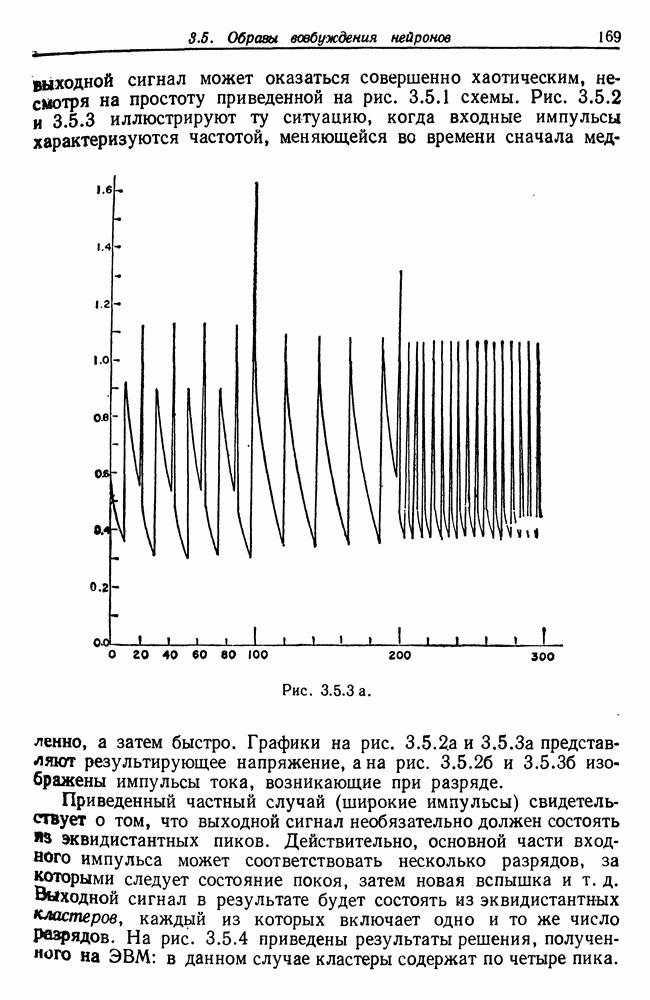
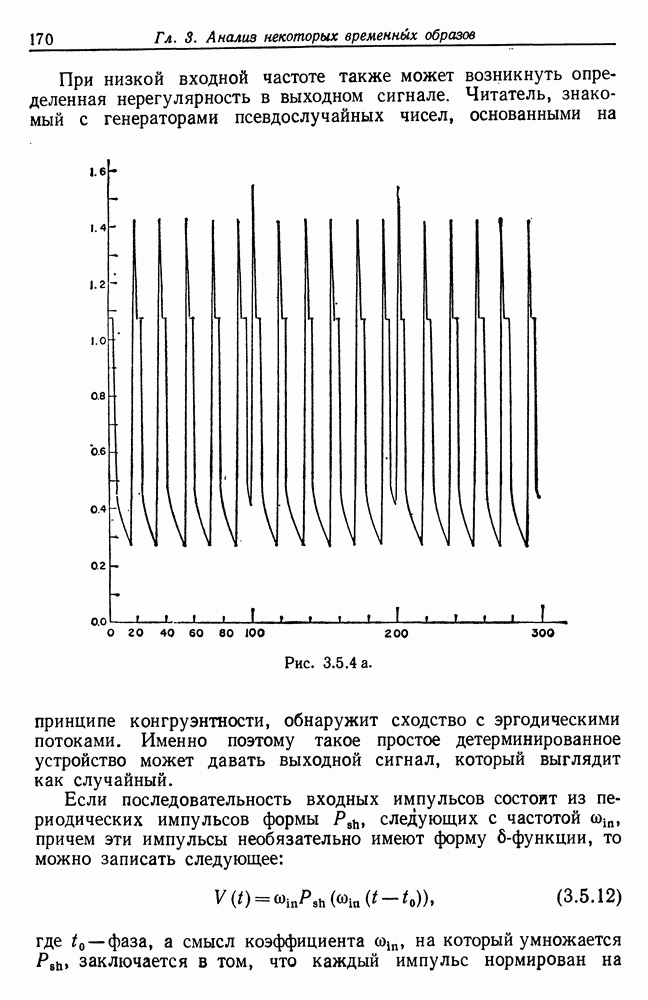
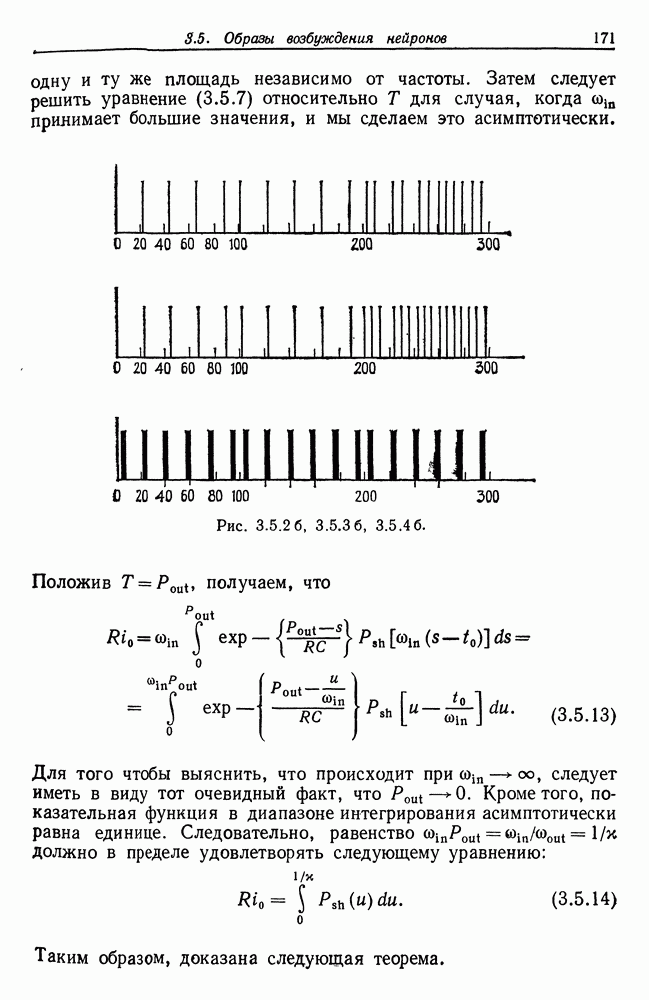
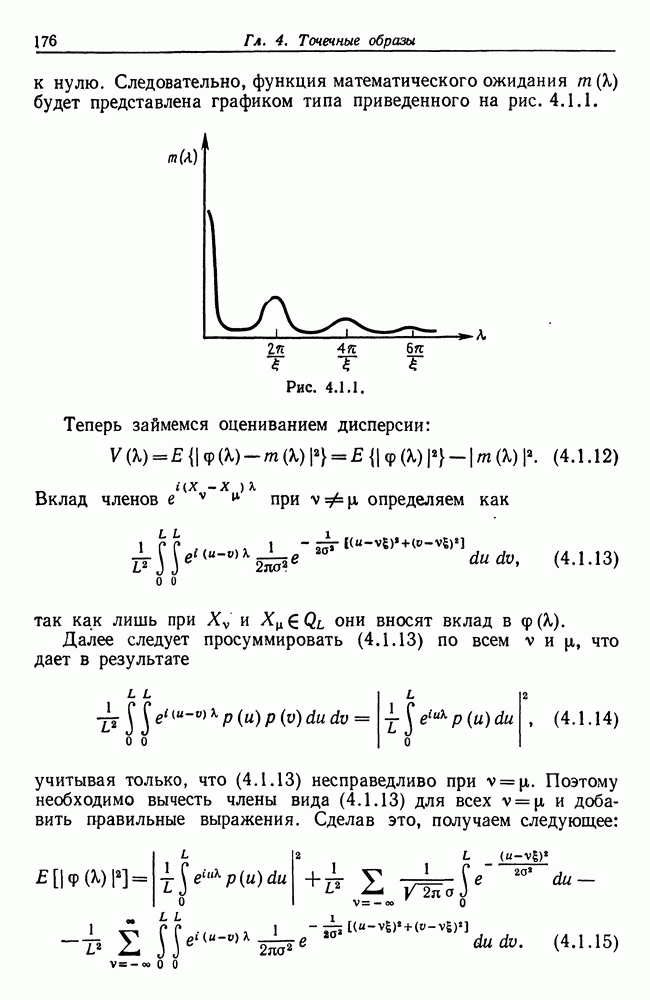
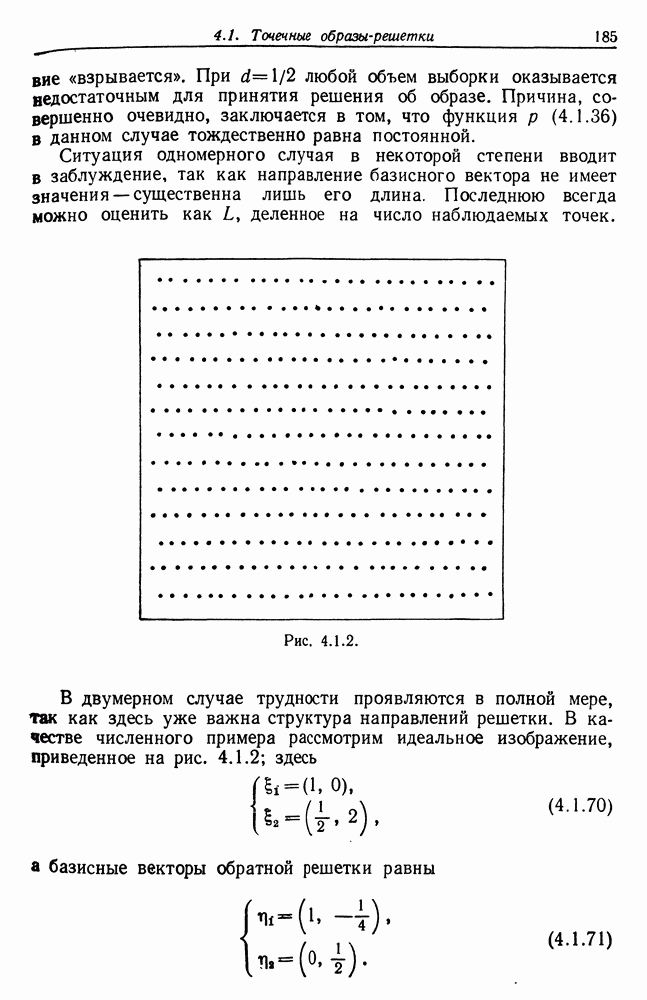
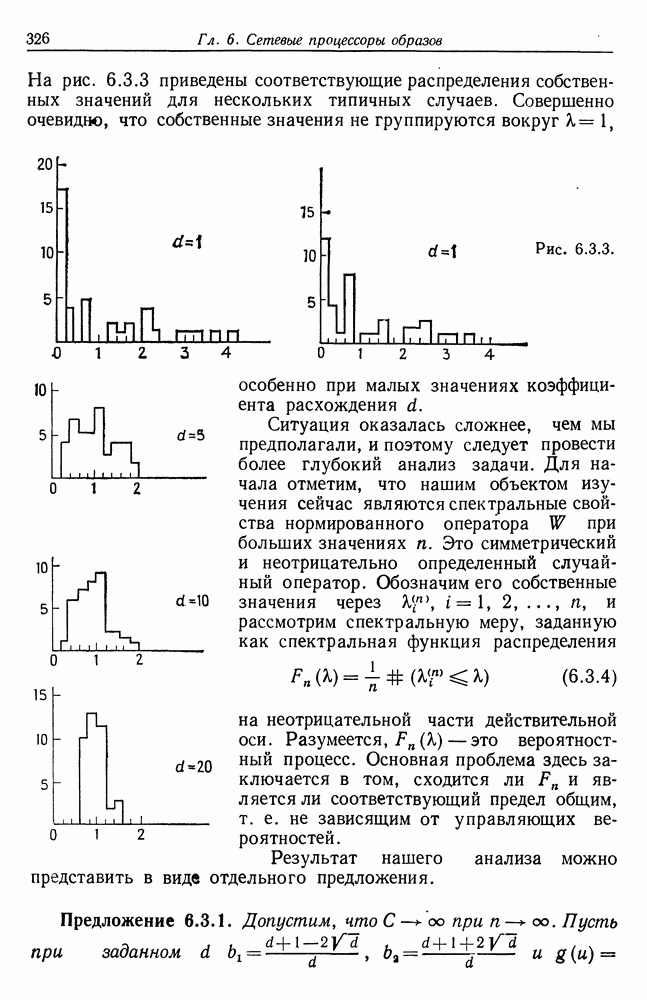
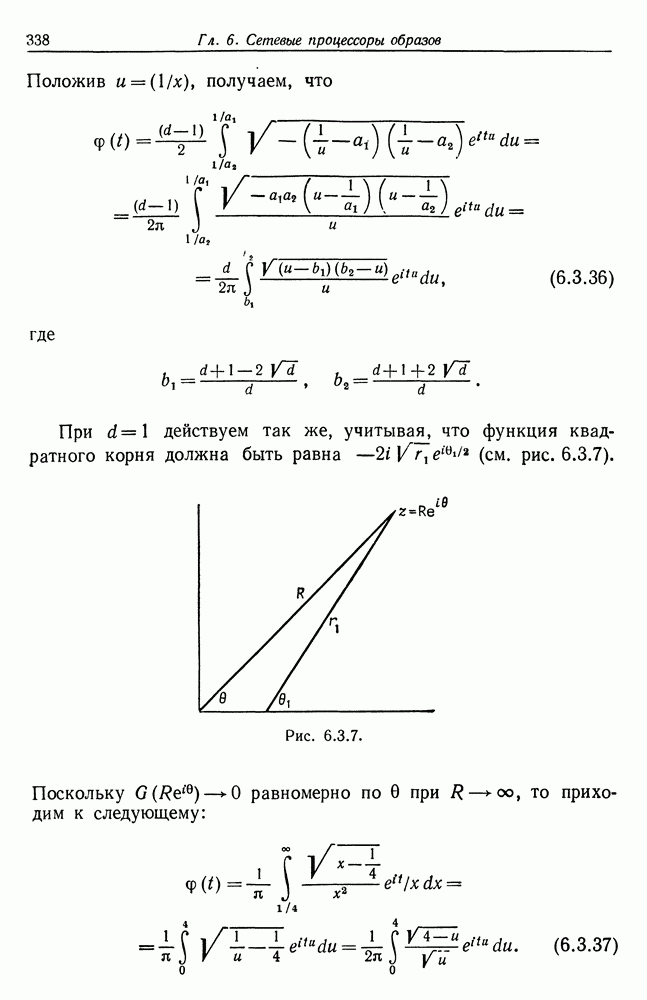
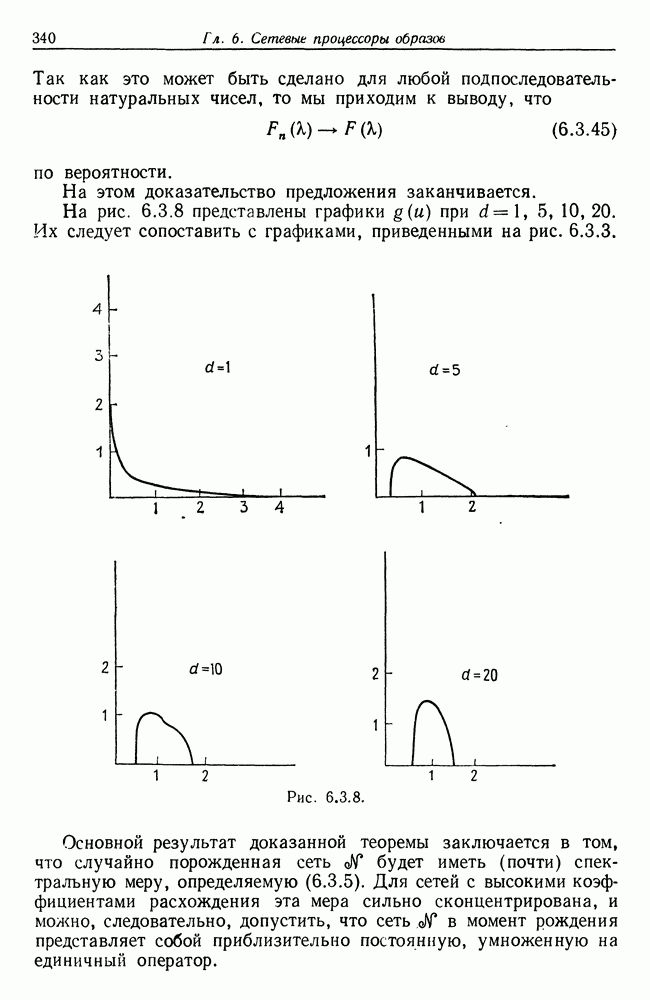
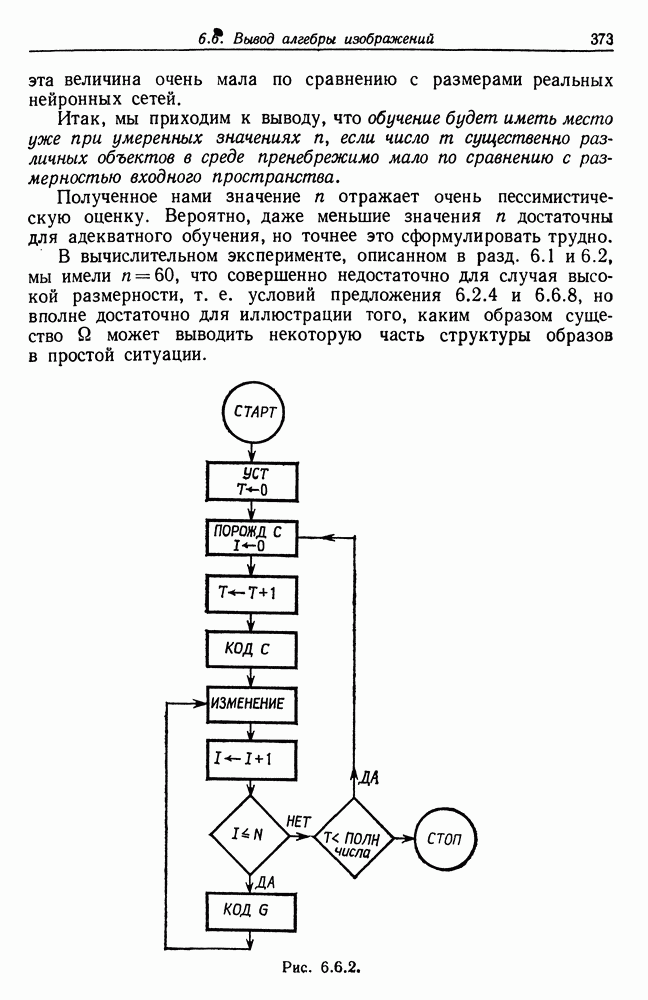
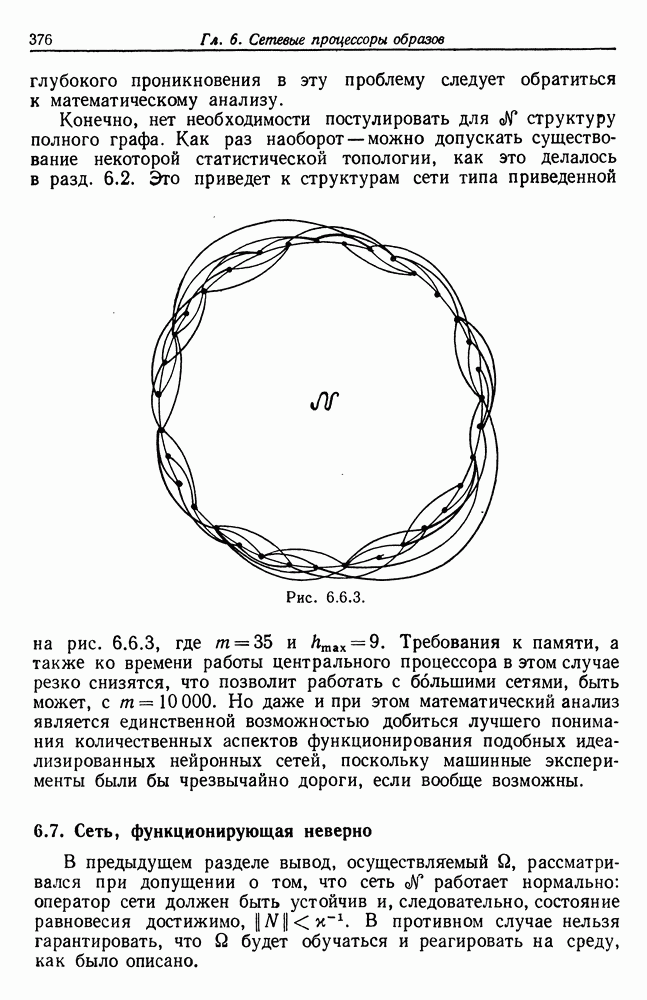
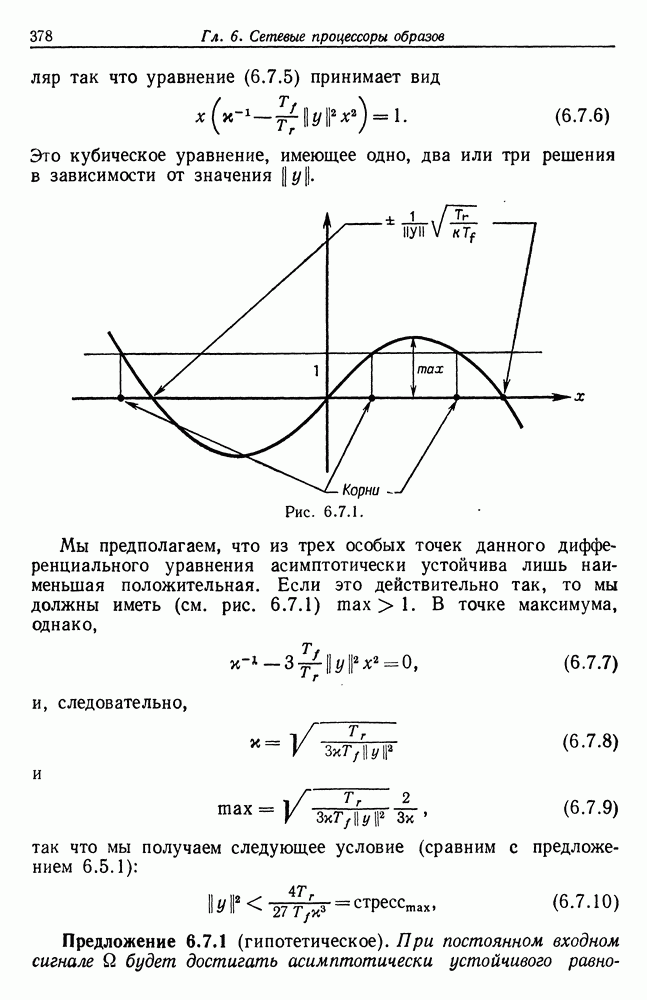
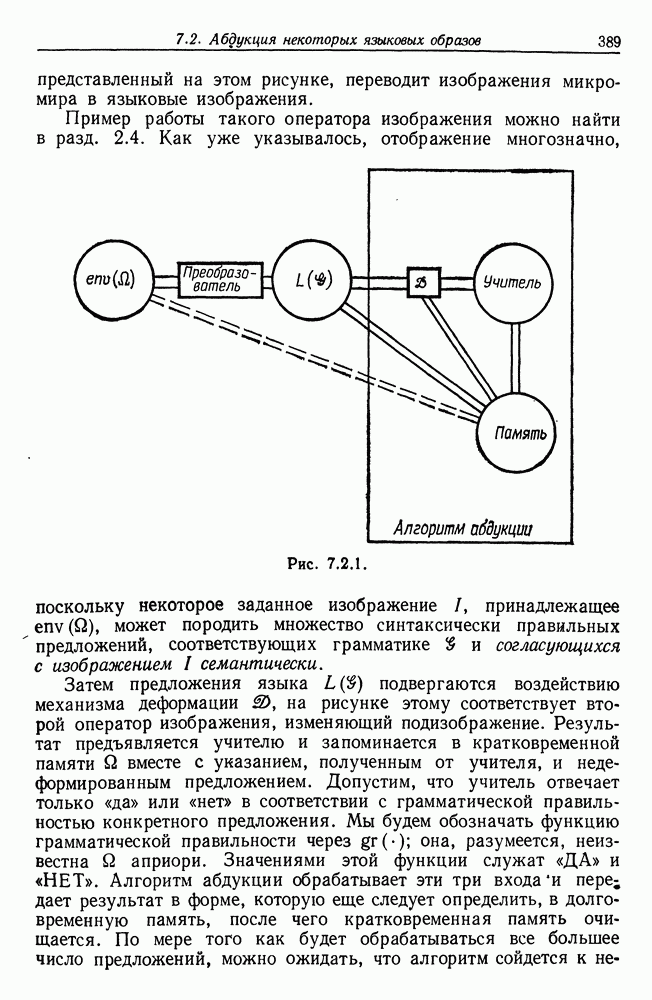
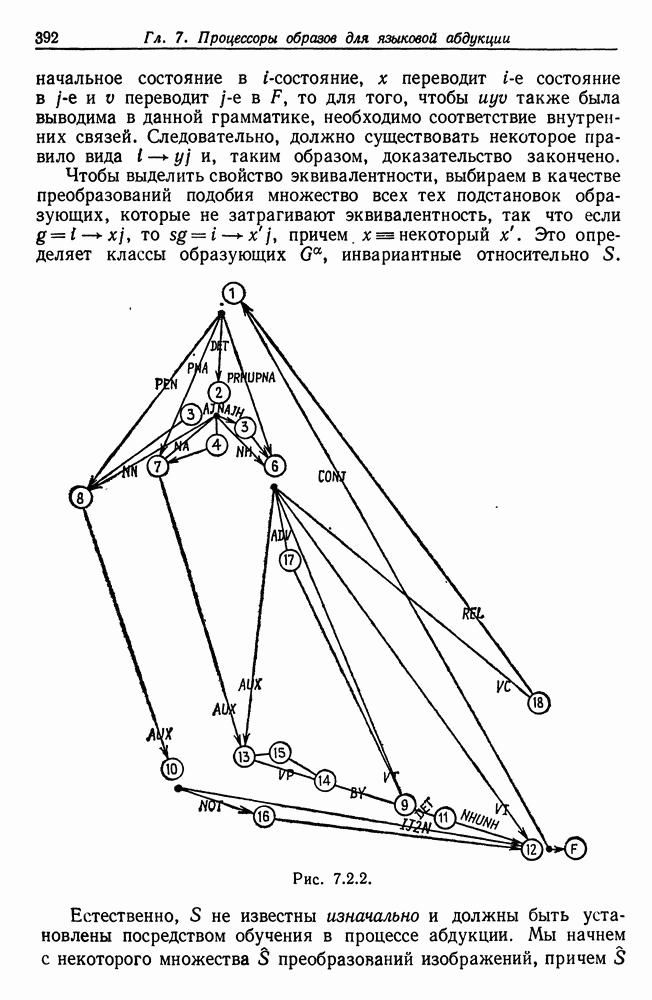
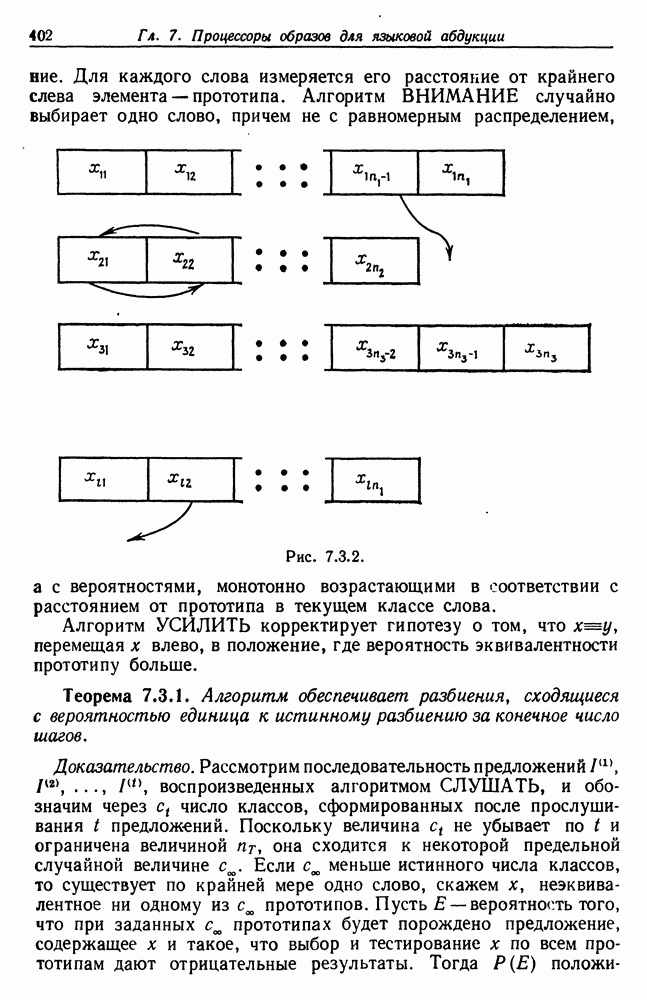
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.8. Биологическая форма
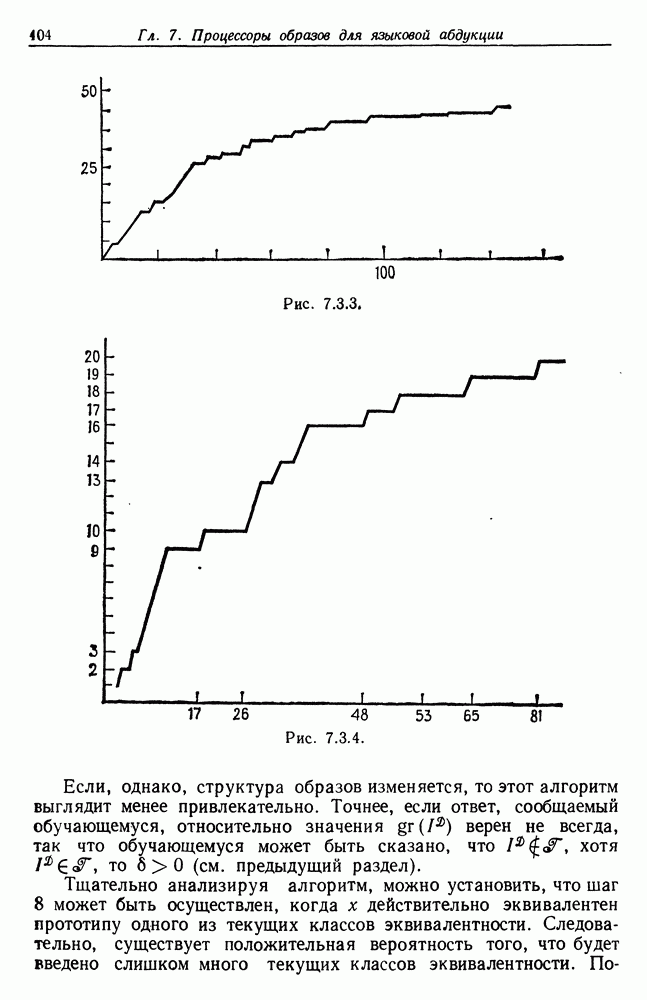
Математическое изучение биологической формы обычно проводится на языке процессов роста. Предложены динамические модели индивидуального развития отдельных особей и эволюции видов, приводящие к определенным формам, представляющим характеристики неустановившихся и/или предельных режимов решений соответствующих уравнений. В самом деле, трудно понять, как можно успешно исследовать задачи, связанные с биологической формой, кроме как во времени и в динамике.
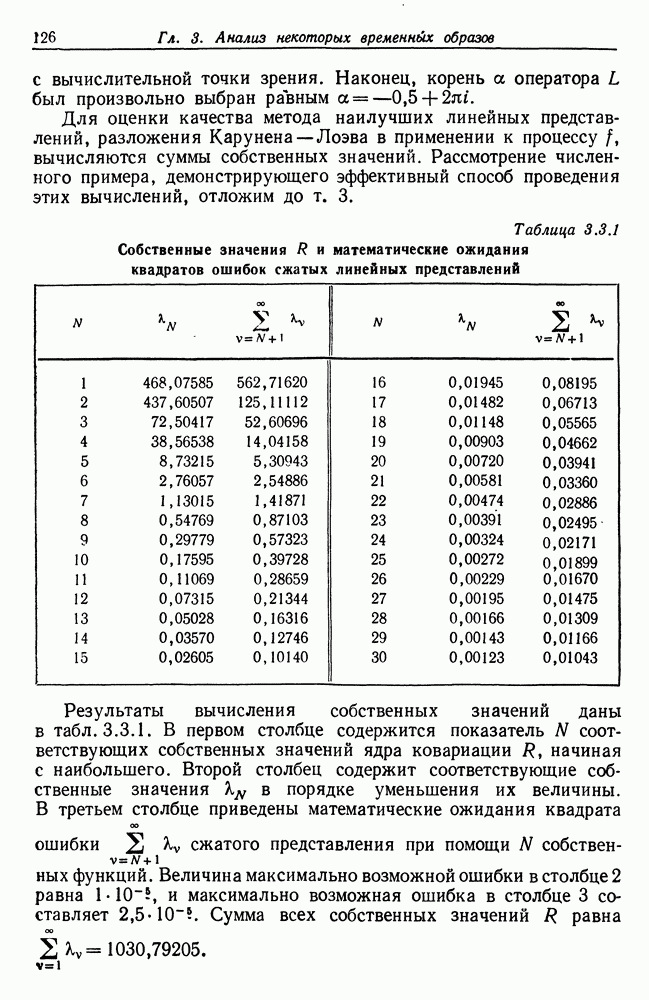
В третьем томе мы изучим ряд таких моделей роста и порождаемых ими форм. Здесь же мы сделаем лишь несколько предварительных замечаний относительно подхода, в котором время в явном виде не появляется вообще или по крайней мере играет вспомогательную роль.
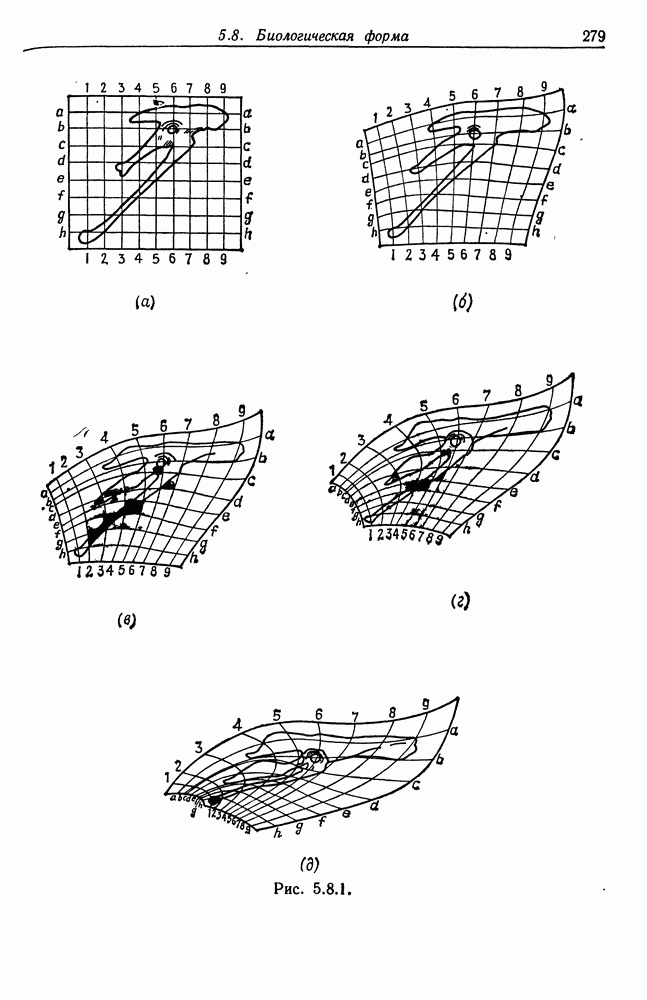
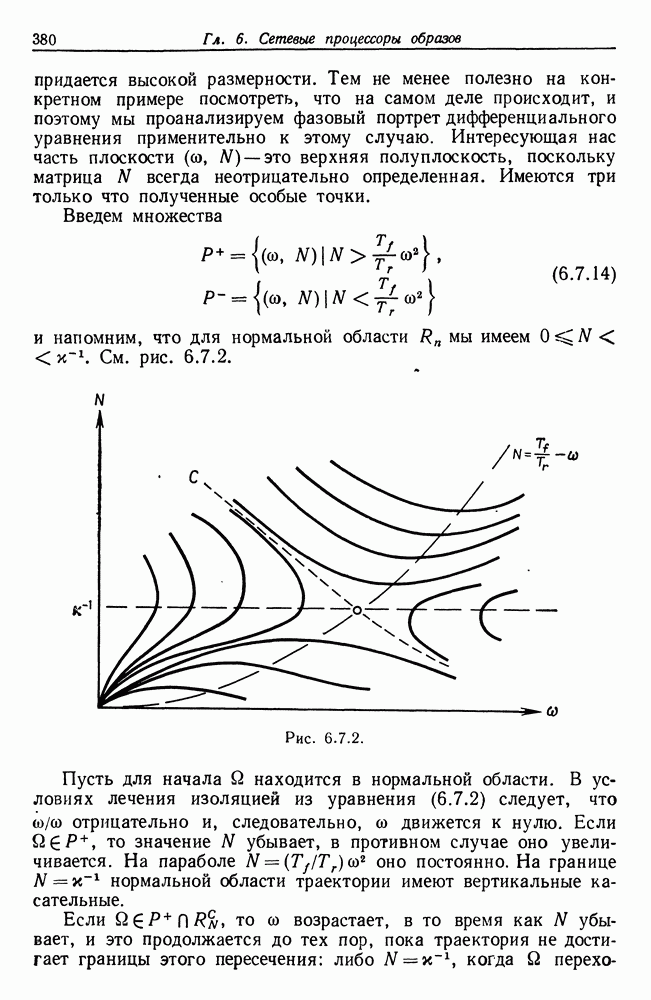
Мы имеем в виду именно то, что ДАрси Томпсон называет методом преобразований. В его знаменитой работе «Рост и форма» наиболее интересной является, вероятно, последняя глава, в которой речь идет о методе преобразований. В ней предпринята попытка связать форму различных, но не очень сильно отличающихся друг от друга видов посредством малых изменений — преобразований — системы координат. Там приводится множество примеров такого рода, один из них воспроизведен нами на рис. 5.8.1. На нем приведен таз археоптерикса  и его последовательные модификации
и его последовательные модификации  приводящие к тазу апаторниса
приводящие к тазу апаторниса  Подчеркивается, что этот метод следует применять для сопоставления только родственных форм: «Мы должны ограничиваться теми случаями, когда преобразования, необходимые для реализации сопоставления, просты, а преобразованные, так же как и исходные, координаты порождают гармоничную и более или менее симметричную систему. Мы неизбежно и вполне заслуженно запутаемся, если попытаемся посредством математического или любого иного метода сопоставлять организмы, далеко отстоящие друг от друга в Природе и в Зоологической классификации» (Томпсон (1961), с. 273).
Подчеркивается, что этот метод следует применять для сопоставления только родственных форм: «Мы должны ограничиваться теми случаями, когда преобразования, необходимые для реализации сопоставления, просты, а преобразованные, так же как и исходные, координаты порождают гармоничную и более или менее симметричную систему. Мы неизбежно и вполне заслуженно запутаемся, если попытаемся посредством математического или любого иного метода сопоставлять организмы, далеко отстоящие друг от друга в Природе и в Зоологической классификации» (Томпсон (1961), с. 273).

(кликните для просмотра скана)
Результаты часто оказываются поразительными и приводят к криволинейным системам координат, которые кажутся естественными для анализа заданных форм. ДАрси Томпсон не дает сколько-нибудь подробных объяснений по поводу того, каким образом он приходит к соответствующим системам координат, но при изучении множества приведенных им примеров создается впечатление, что в первую очередь он определяет отдельные точки на границе. Эти точки могут отличаться большими значениями кривизны или вообще какой-либо «особенностью». Затем он устанавливает соответствие между такими гомологичными точками двух форм и пытается экстраполировать это соответствие на форму в целом так, чтобы криволинейные координаты были как можно более гладкими. Делал он это, опираясь на свое искусство чертежника.
Одной из основных особенностей труда Д'Арси Томпсона является то, что математический анализ роста и формы не сводится просто к вычерчиванию кривых по точкам. Как раз наоборот, он пытается систематически формулировать процедуры анализа исходя из некоторых общих принципов, часто принимающих форму экстремальных принципов: используются изопериметрические представления, эффективность плана и т. д. Читатель может найти ясное и более современное изложение подобных идей в монографии Розена (1969), содержащей много материала, не известного во времена создания «Роста и формы».
Возвращаясь к методу преобразований, отметим, что неясно, какой именно экстремальный принцип (если вообще какой-нибудь) лежит в основе соответствующих геометрических построений. Заманчиво попытаться формализовать его, что мысейчас и сделаем, и реализовать формализованную процедуру на вычислительной машине, чего мы не сделали. Воспользуемся идеей, предложенной в работе Гренандера (1970), с. 200—204.
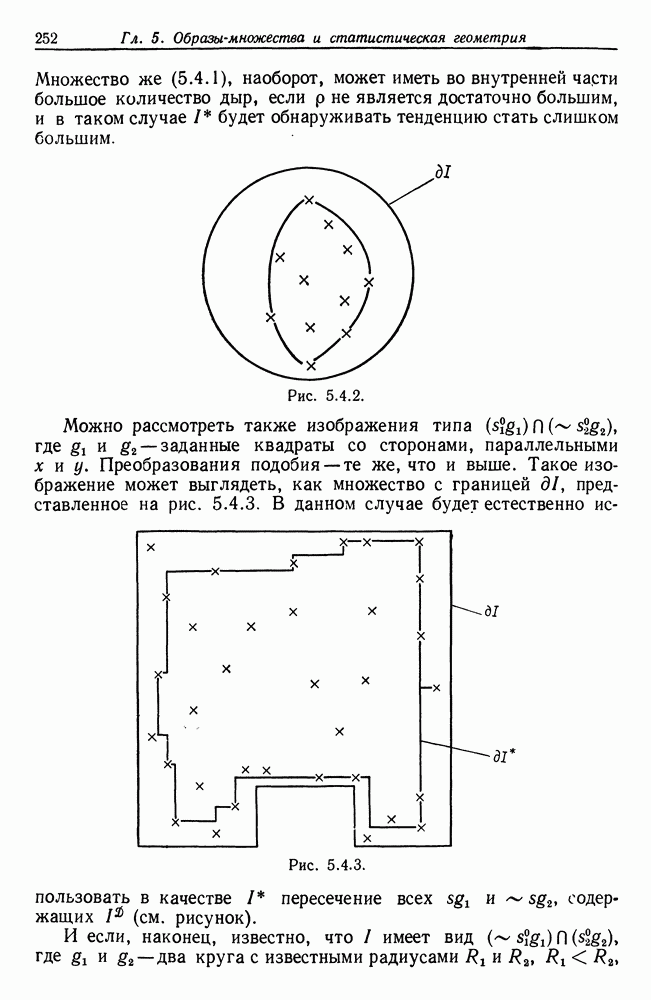
Для формализации понятия малых гладких деформаций в количественном смысле мы обратимся к языку теории упруго-изотропных материалов с малыми деформациями. Мы делаем это, конечно, не потому, что рассматриваем развитие биологических организмов как упругих тел, а потому, что, судя по всему, упругие деформации приводят к минимально сложному математическому аппарату, который позволяет нам получить желаемые результаты. Допустим, мы рассматриваем два изображения  из некоторой заданной алгебры изображений-множеств и отыскиваем «естественные» способы преобразования одного изображения в другое. На границе одного из изображений определяется функция гомологии
из некоторой заданной алгебры изображений-множеств и отыскиваем «естественные» способы преобразования одного изображения в другое. На границе одного из изображений определяется функция гомологии  задающая некоторый гомеоморфизм между
задающая некоторый гомеоморфизм между  и интервалом [0, 1). Для заданных изображений и
и интервалом [0, 1). Для заданных изображений и  будут отыскиваться отображения, сохраняющие гомологичные точки
будут отыскиваться отображения, сохраняющие гомологичные точки  так что
так что  на
на  Мы будем требовать, чтобы все используемые ниже отображения удовлетворяли этому условию.
Мы будем требовать, чтобы все используемые ниже отображения удовлетворяли этому условию.
Начиная с некоторого исходного множества  или исходного изображения рассмотрим все множества, полученные посредством упругих деформаций:
или исходного изображения рассмотрим все множества, полученные посредством упругих деформаций:

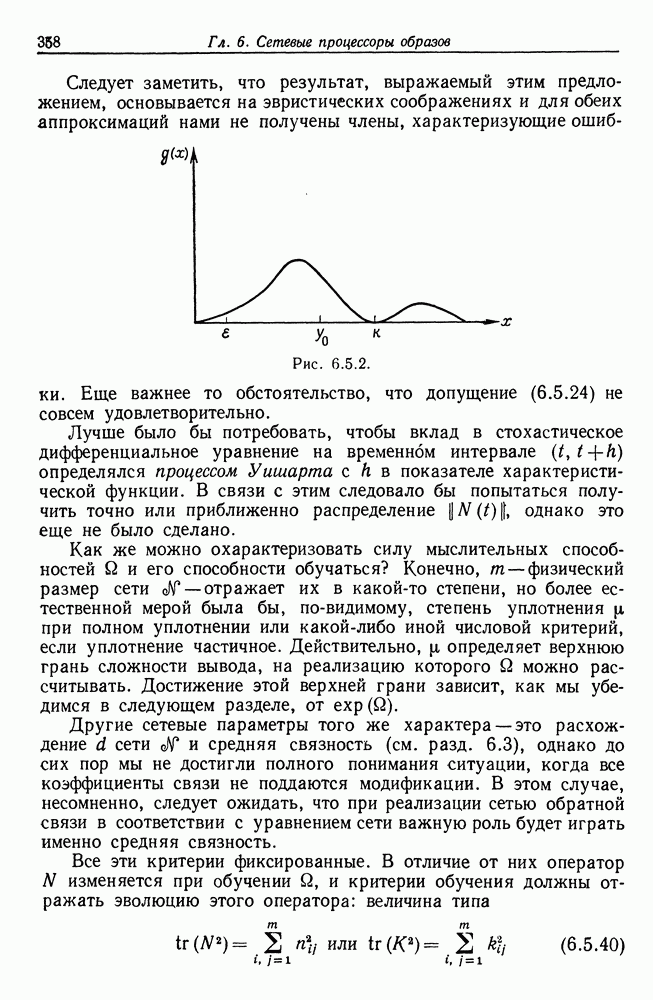
Тогда потенциальная энергия  деформированного множества равна (см., например, Мусхелишвили (1953))
деформированного множества равна (см., например, Мусхелишвили (1953))

где  — постоянные Ламе, характеризующие свойства материала. Если мы рассматриваем изображение
— постоянные Ламе, характеризующие свойства материала. Если мы рассматриваем изображение  в качестве ненапряженного, то работа, необходимая для получения из
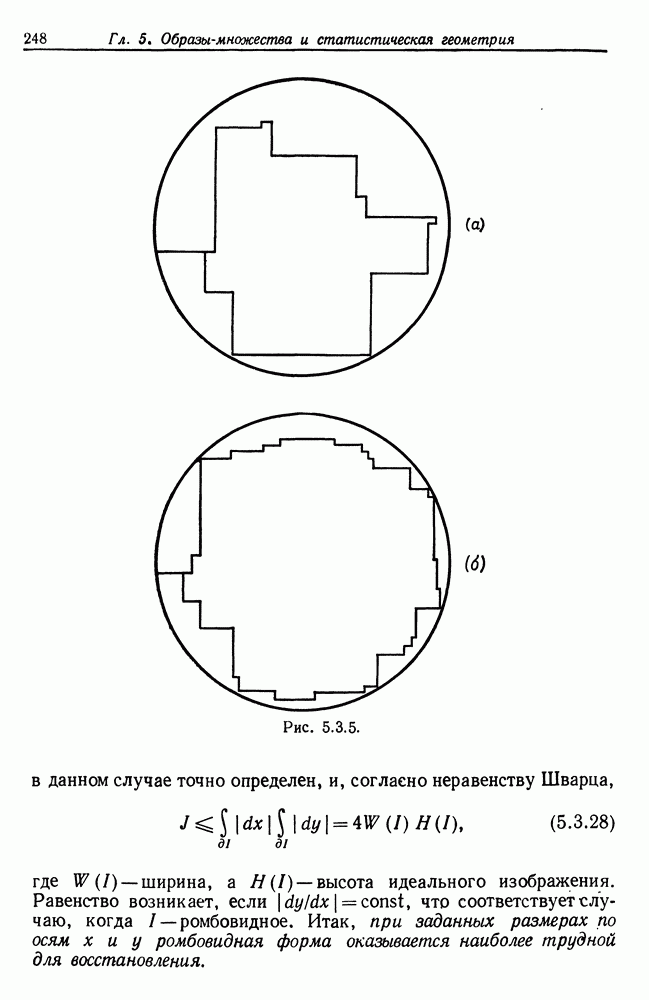
в качестве ненапряженного, то работа, необходимая для получения из  с помощью деформации, определяется выражением (5.8.2). Аналогично, если
с помощью деформации, определяется выражением (5.8.2). Аналогично, если  являются деформированными вариантами
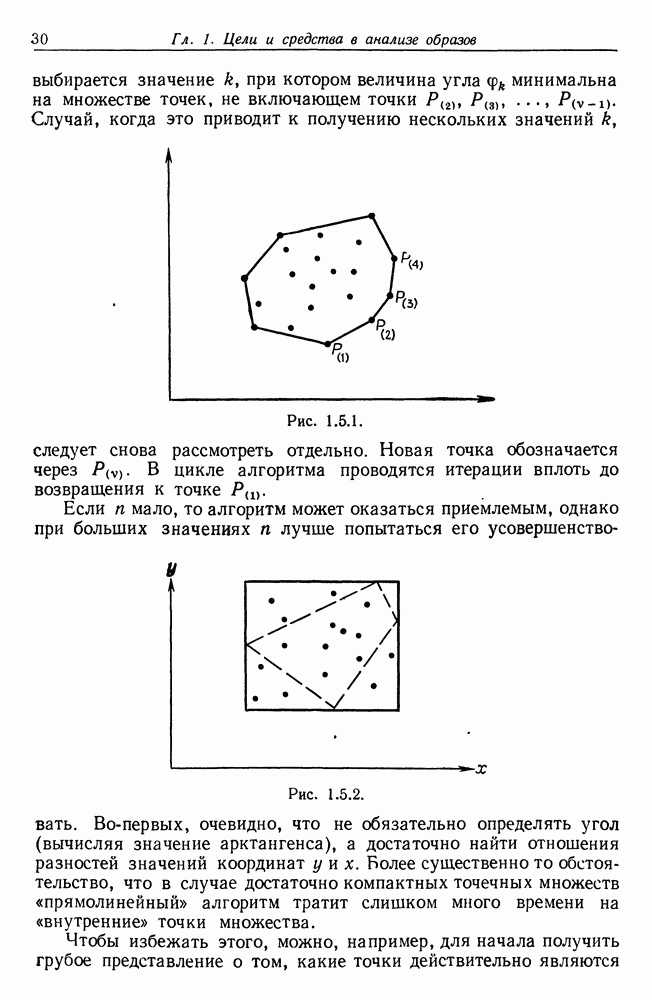
являются деформированными вариантами  то работа, необходимая для преобразования
то работа, необходимая для преобразования  определяется величиной
определяется величиной  и поэтому целесообразно ввести усилие деформации как
и поэтому целесообразно ввести усилие деформации как

Отметим, что деформации действуют на множества (напряженные), обладающие определенными заданными полями деформации, а не просто на множества как таковые.
Функция  определенная с помощью (5.8.3), удовлетворяет условию
определенная с помощью (5.8.3), удовлетворяет условию

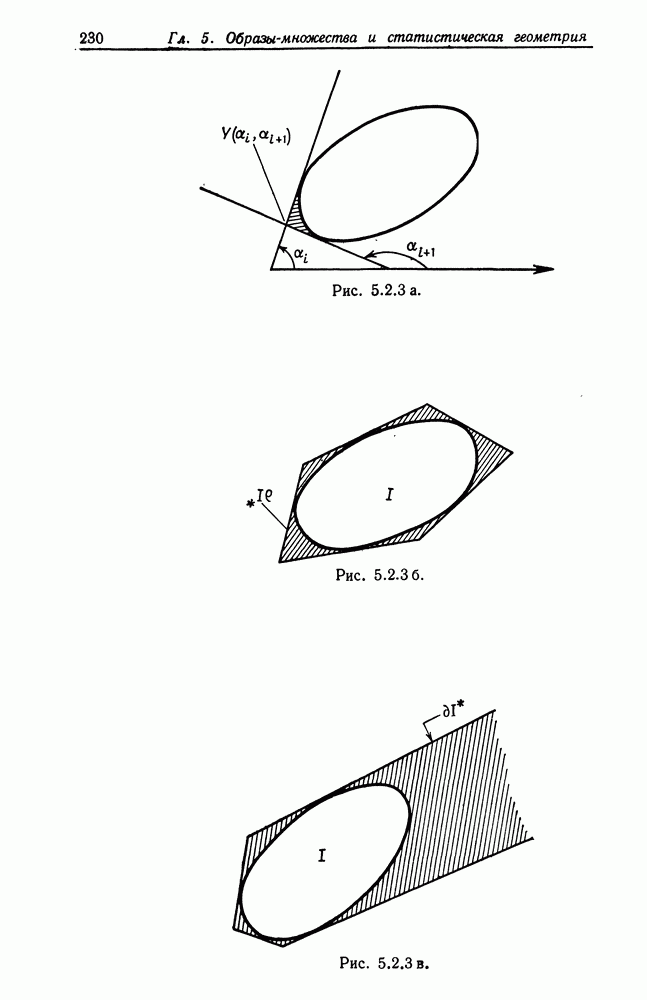
где  — деформации, обеспечивающие переход
— деформации, обеспечивающие переход  а — деформации, обеспечивающие переход
а — деформации, обеспечивающие переход  Очевидно, кроме того, что любое преобразование подобия
Очевидно, кроме того, что любое преобразование подобия  оставляет функцию
оставляет функцию  без изменений. Это очевидно с физической точки зрения, но можно дать и прямое доказательство. Следовательно,
без изменений. Это очевидно с физической точки зрения, но можно дать и прямое доказательство. Следовательно,  является полностью инвариантной функцией усилия (см. т. 1, с. 273).
является полностью инвариантной функцией усилия (см. т. 1, с. 273).
Теперь мы можем воспользоваться следующим экстремальным принципом для определения естественной координатной системы для деформированного изображения  Действительно, пусть (
Действительно, пусть ( определяется минимумом потенциальной энергии
определяется минимумом потенциальной энергии  с граничными условиями, заданными соотношением
с граничными условиями, заданными соотношением  на границах
на границах  Запишем
Запишем

что и определяет однозначно векторы смещения  на
на 
Эта задача минимизации приводит к уравнениям Навье

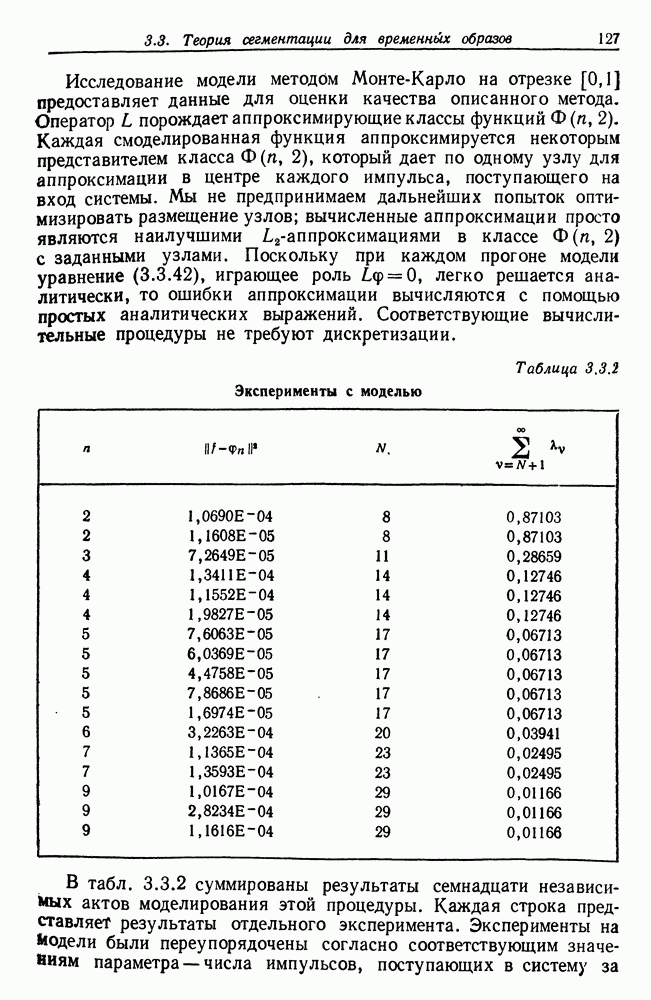
(см. Курант и Гильберт (1937)). При численном решении практичнее начинать непосредственно с задачи минимизации и определять решения  Следует, кроме того, отметить, что геометрия изображений может быть весьма сложной, скажем, они могут быть многосвязными, так что, очевидно, полезны методы конечных элементов, причем на этапе разбиения на элементы нужно применять методы сегментации, соответствующие заданной алгебре изображений.
Следует, кроме того, отметить, что геометрия изображений может быть весьма сложной, скажем, они могут быть многосвязными, так что, очевидно, полезны методы конечных элементов, причем на этапе разбиения на элементы нужно применять методы сегментации, соответствующие заданной алгебре изображений.
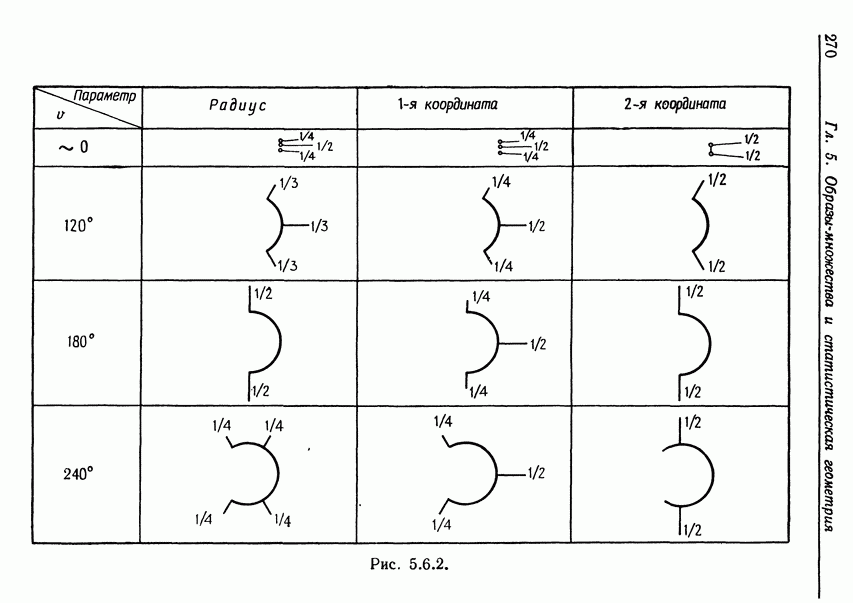
После того как решение  получено, естественная система координат изображения I определяется уравнениями
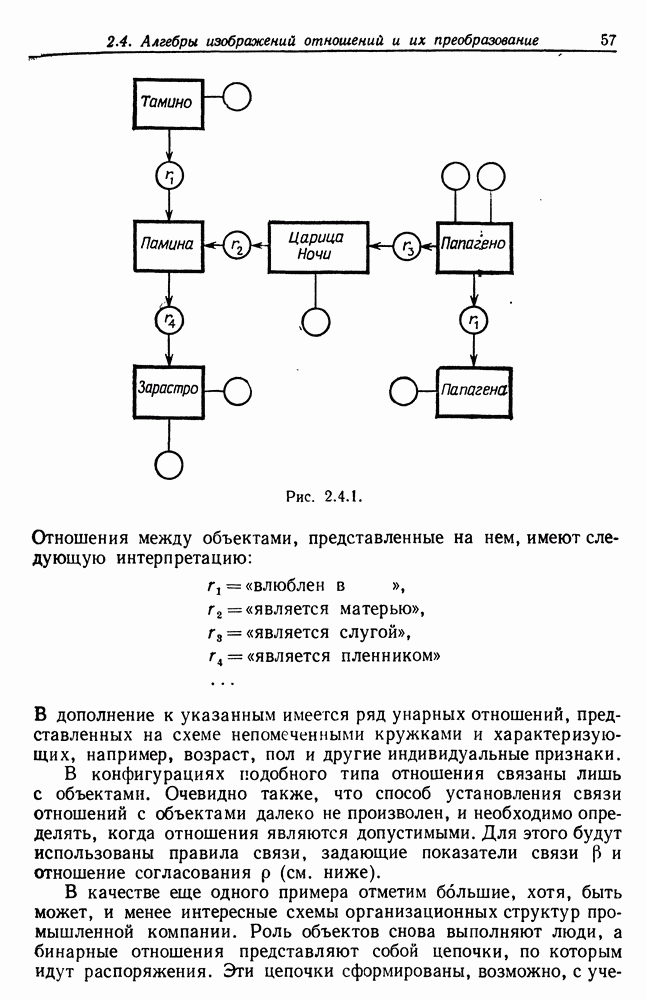
получено, естественная система координат изображения I определяется уравнениями

и на  можно построить криволинейные системы координат; последние можно сопоставить с системами координат, предложенными в «Росте и форме».
можно построить криволинейные системы координат; последние можно сопоставить с системами координат, предложенными в «Росте и форме».
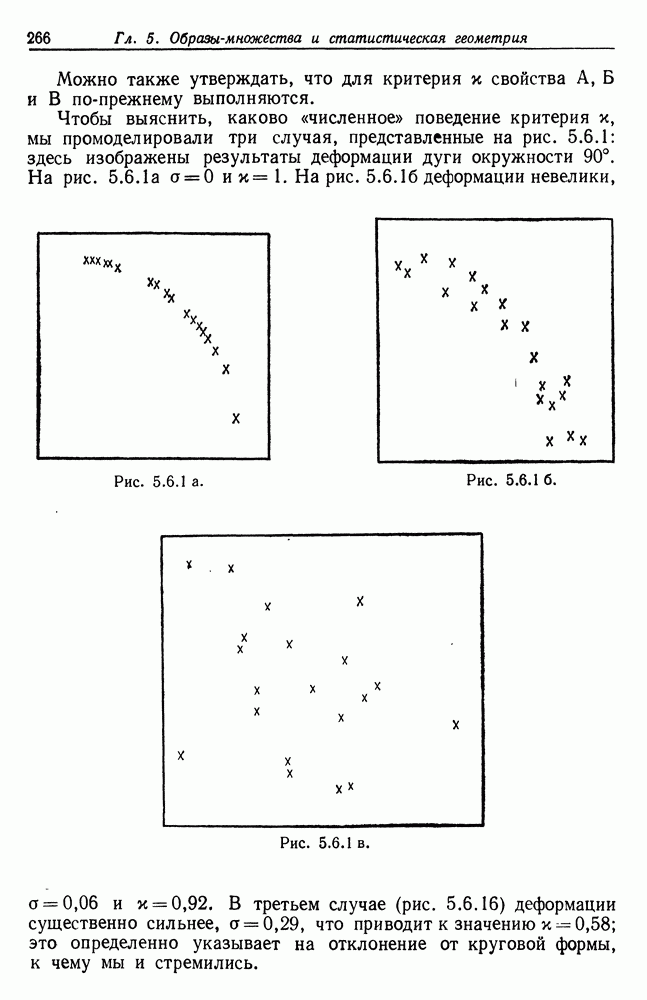
Численное изучение этой задачи до сих пор не было проведено.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
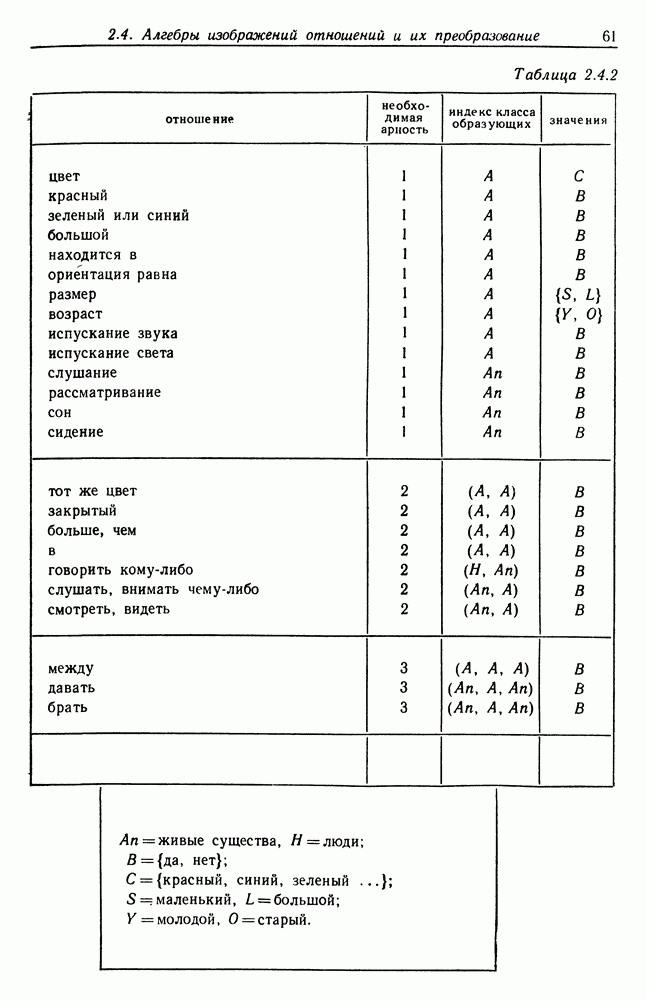
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
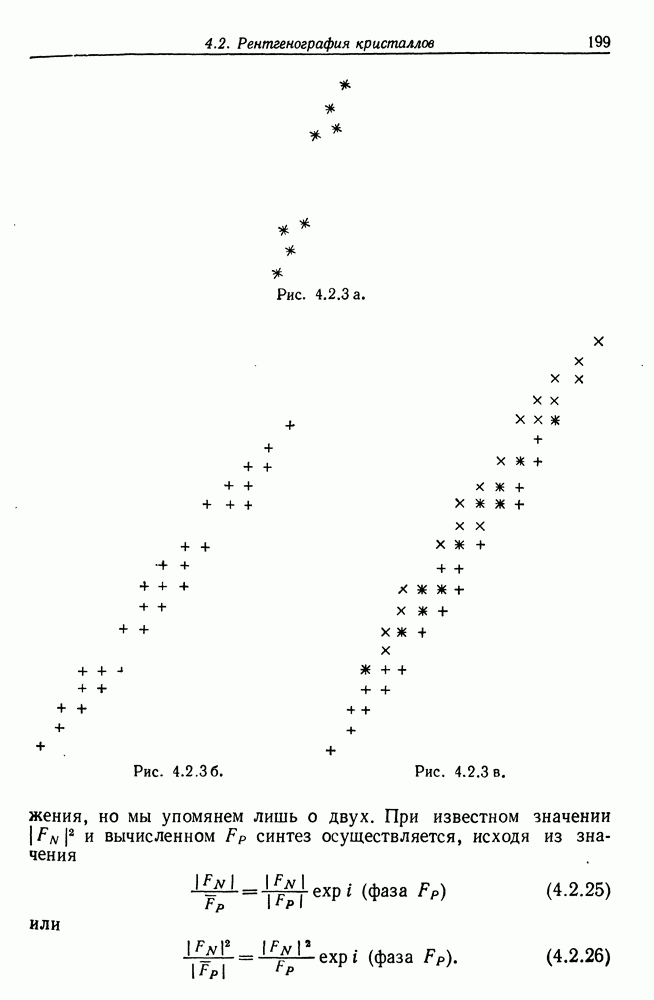
- 4.2. Рентгенография кристаллов
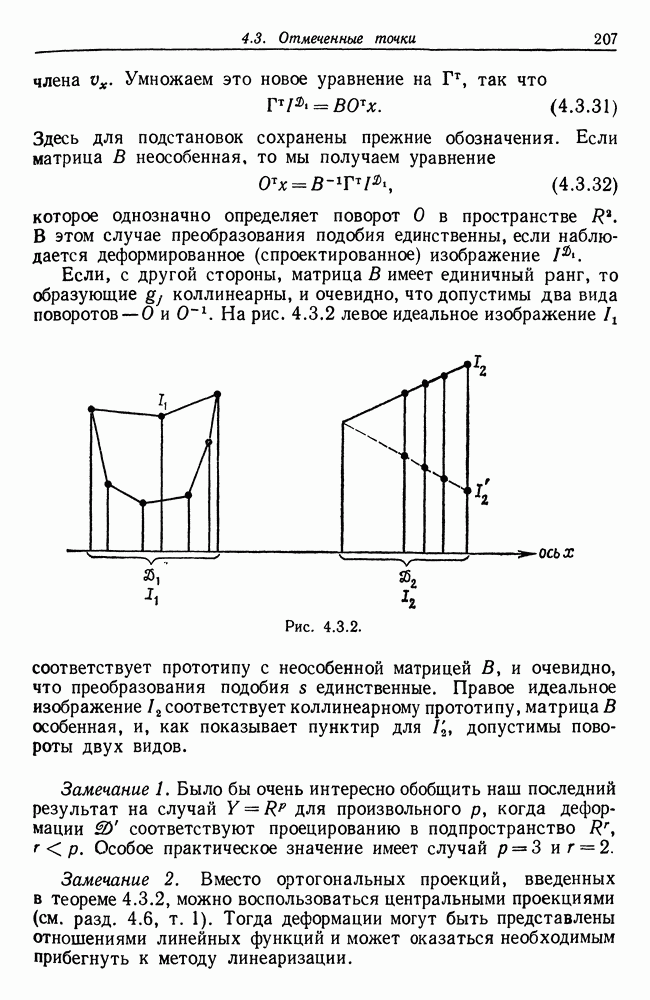
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
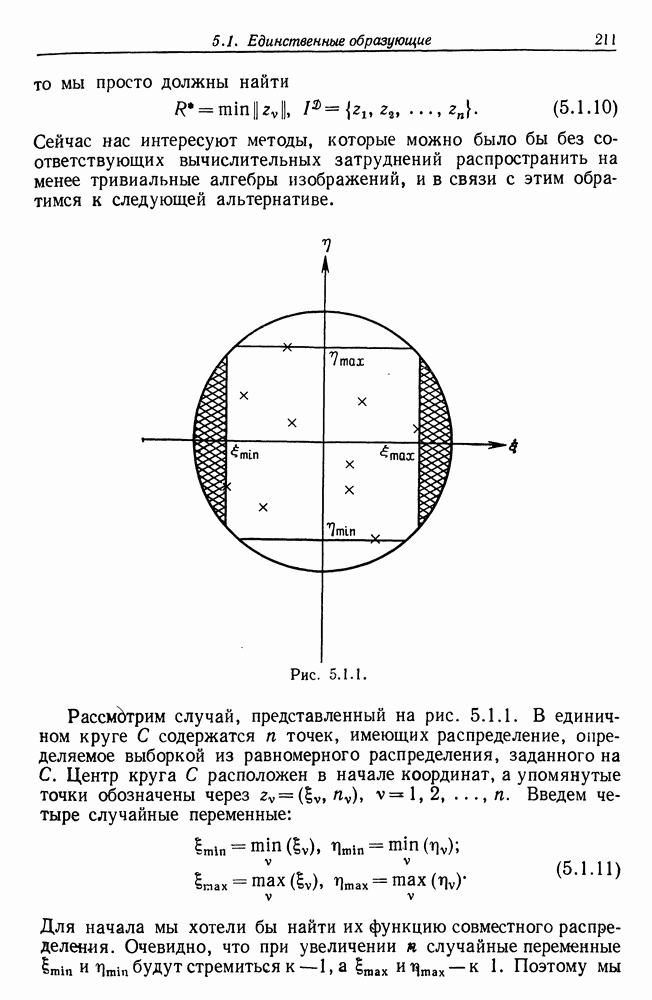
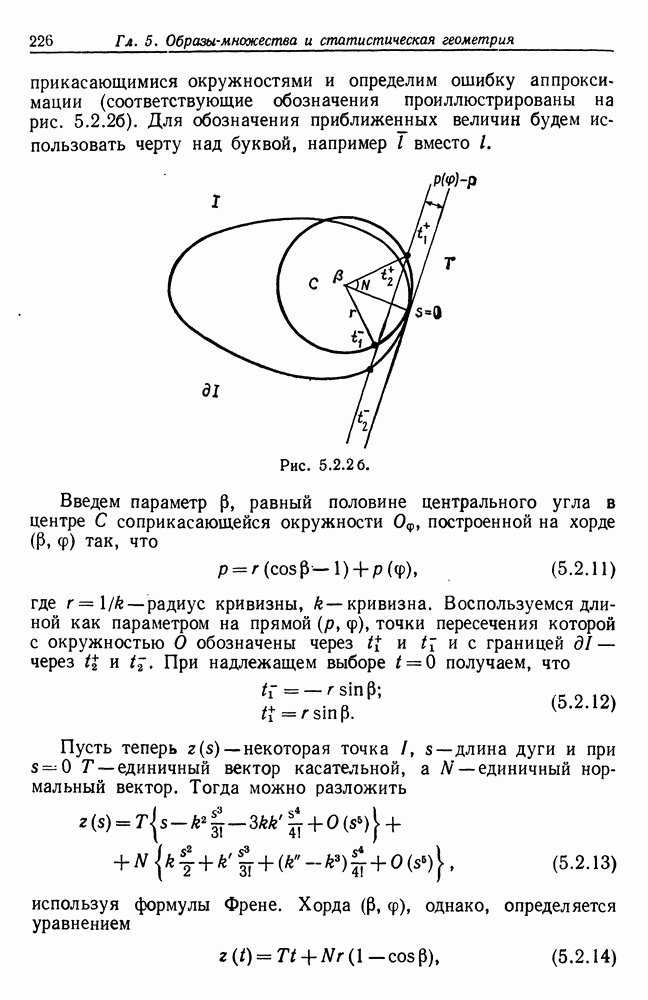
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
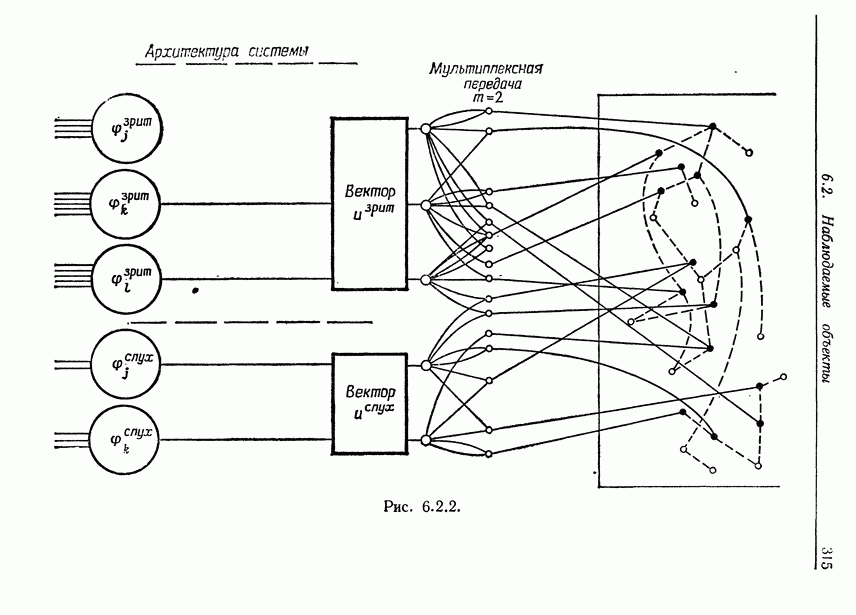
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы