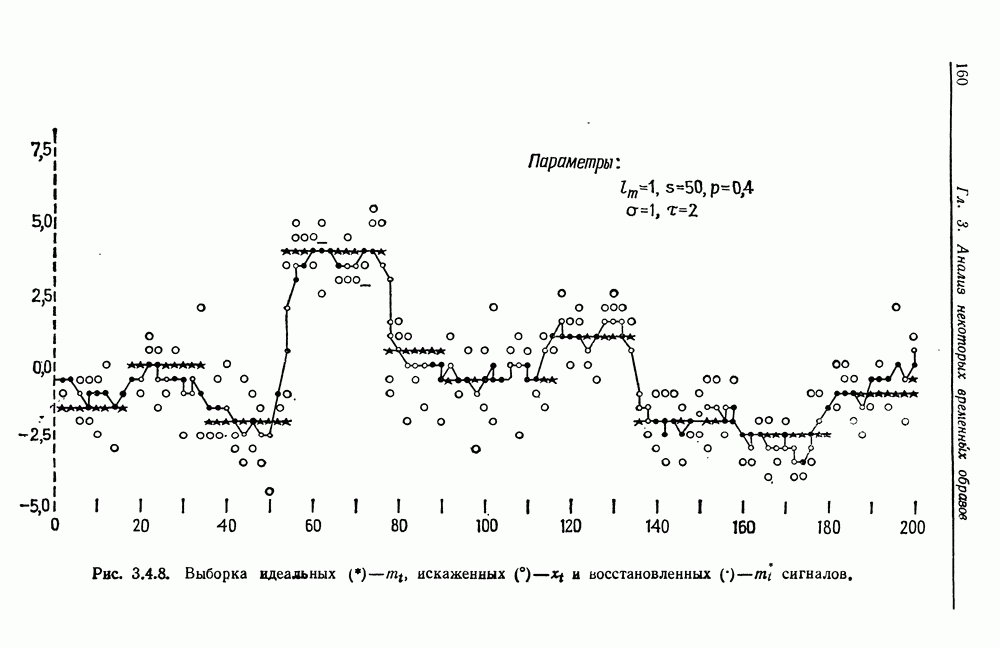
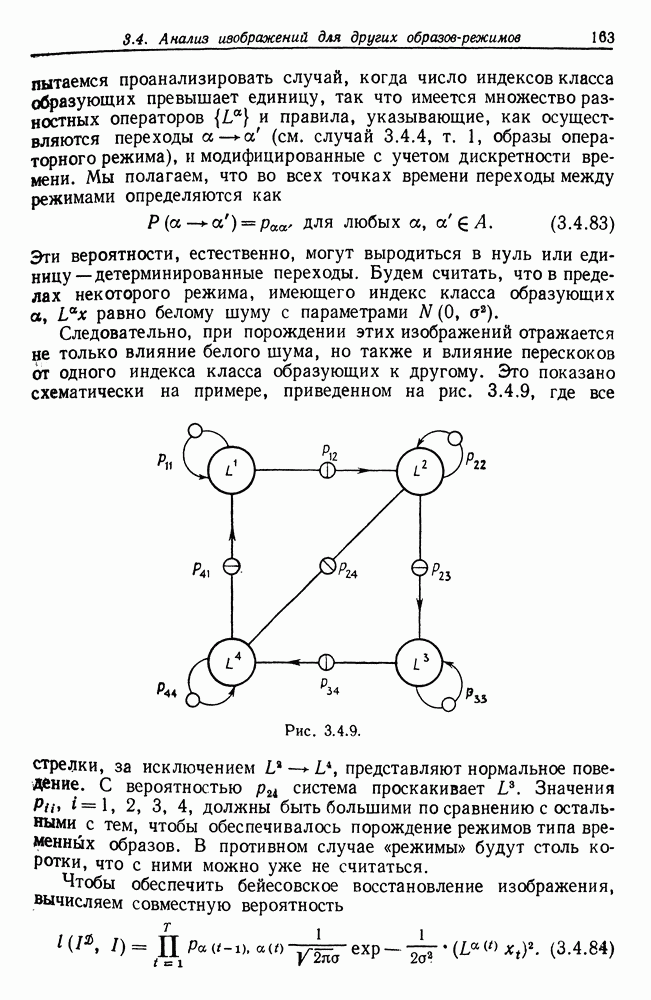
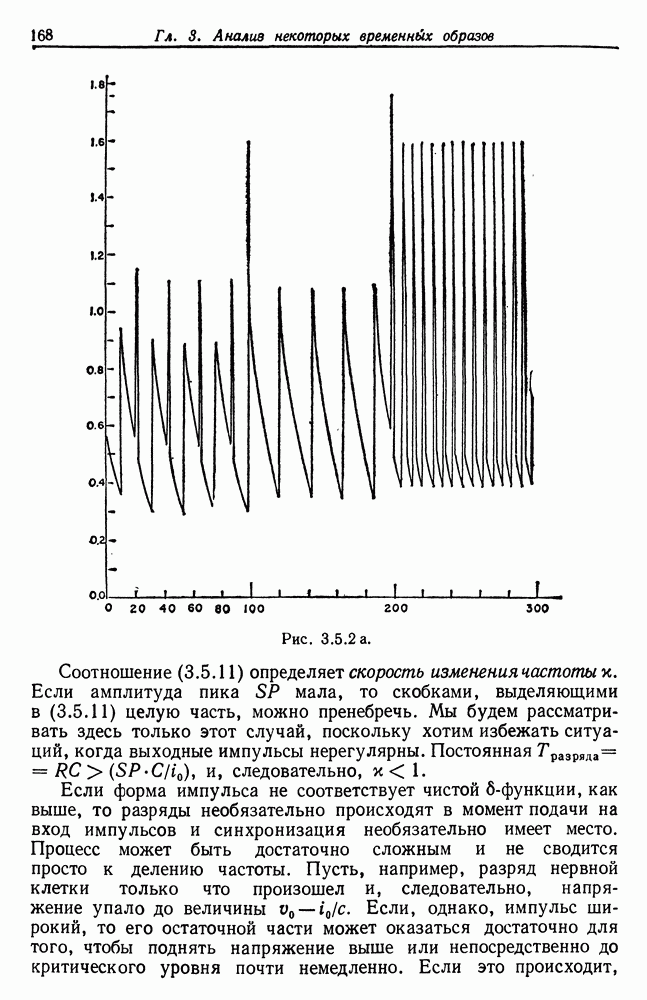
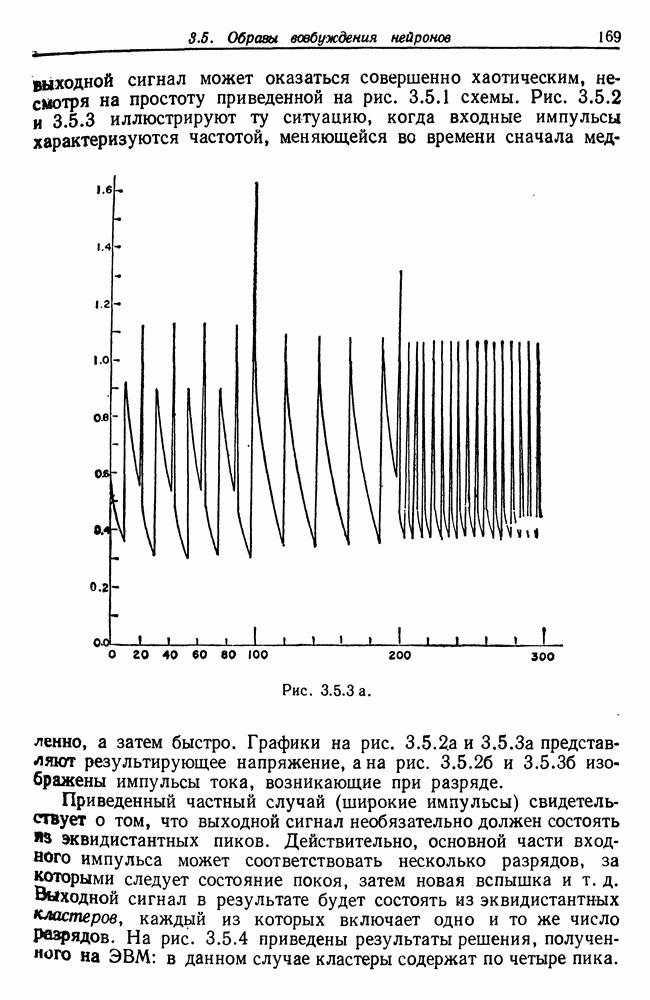
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.4. Разбиение на классы слов посредством сетей
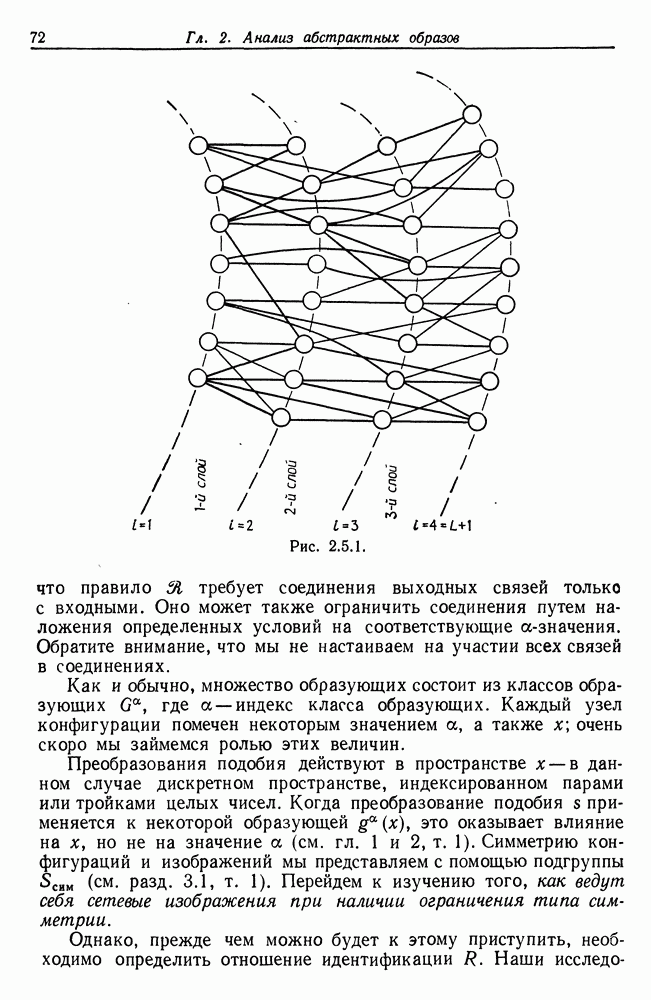
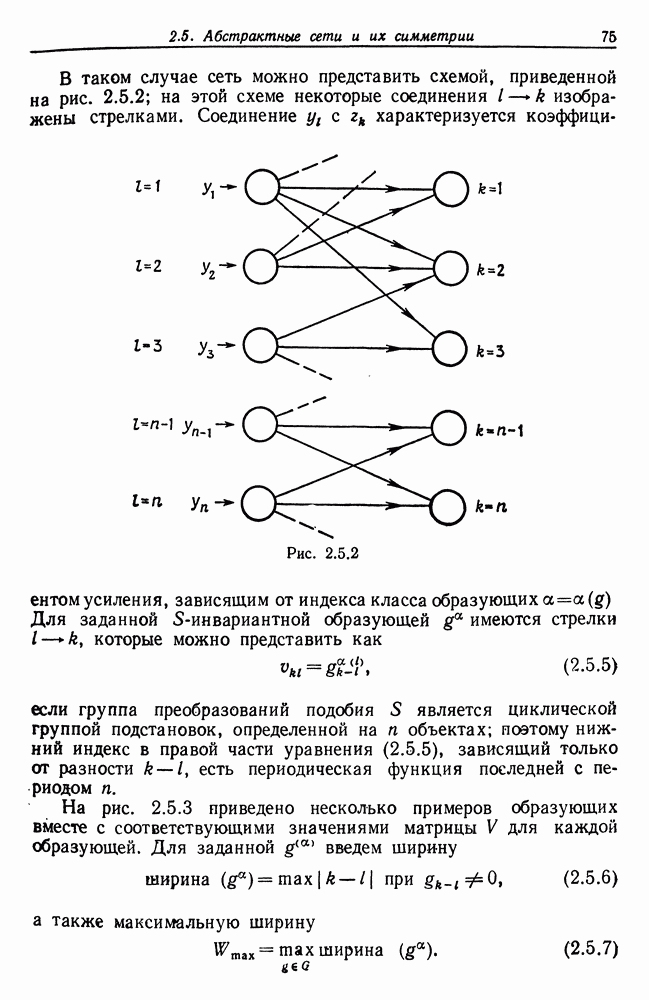
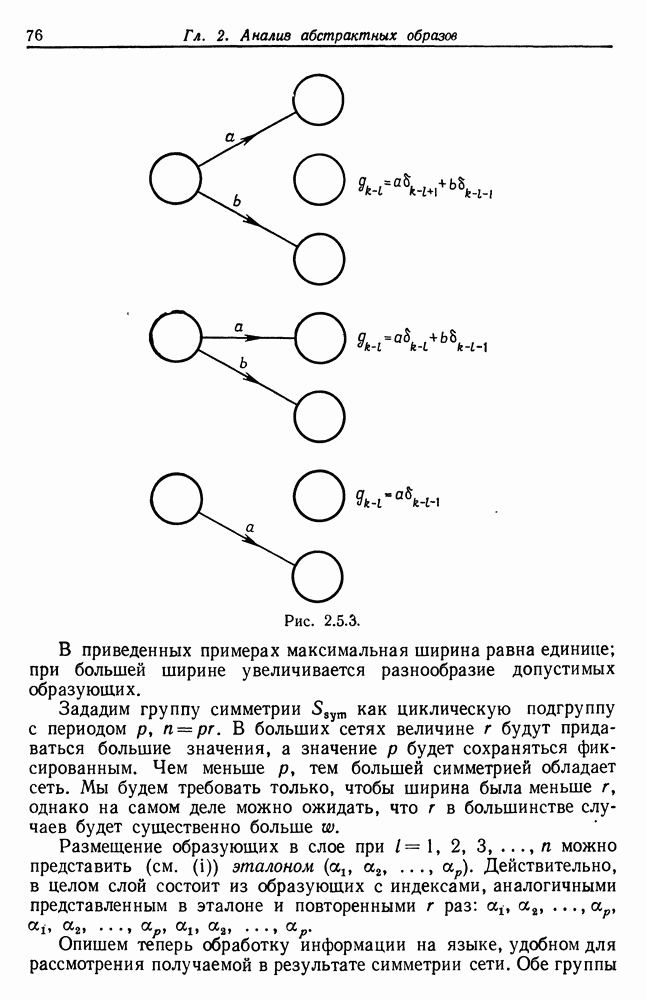
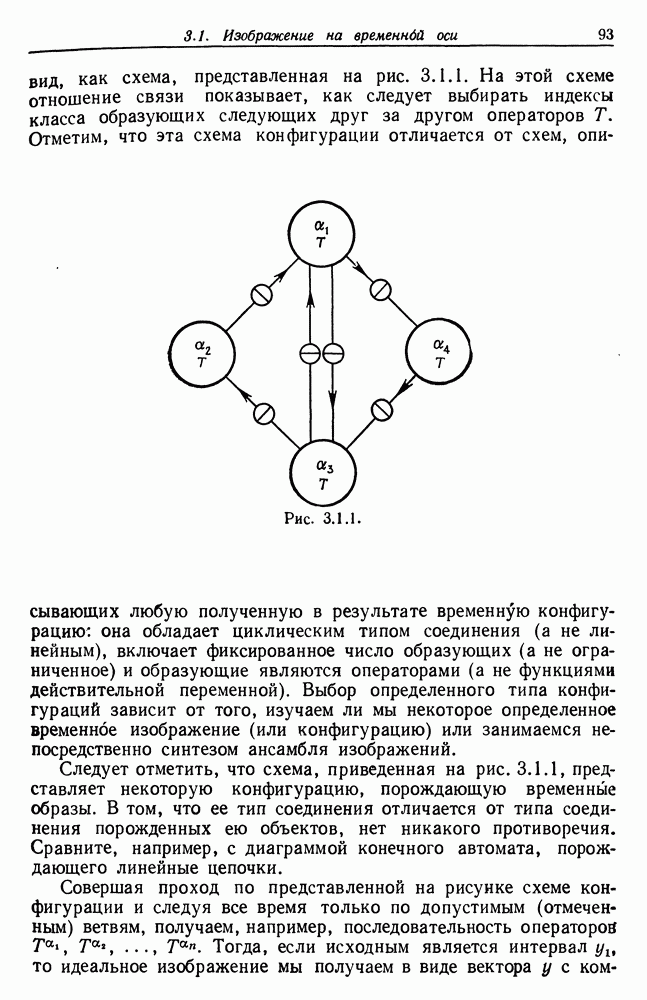
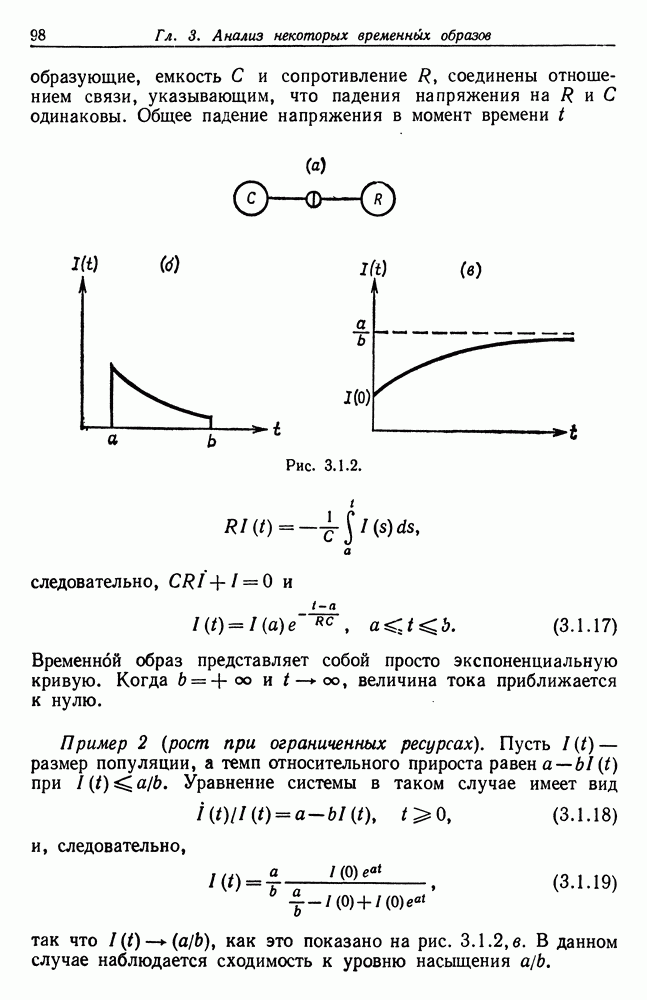
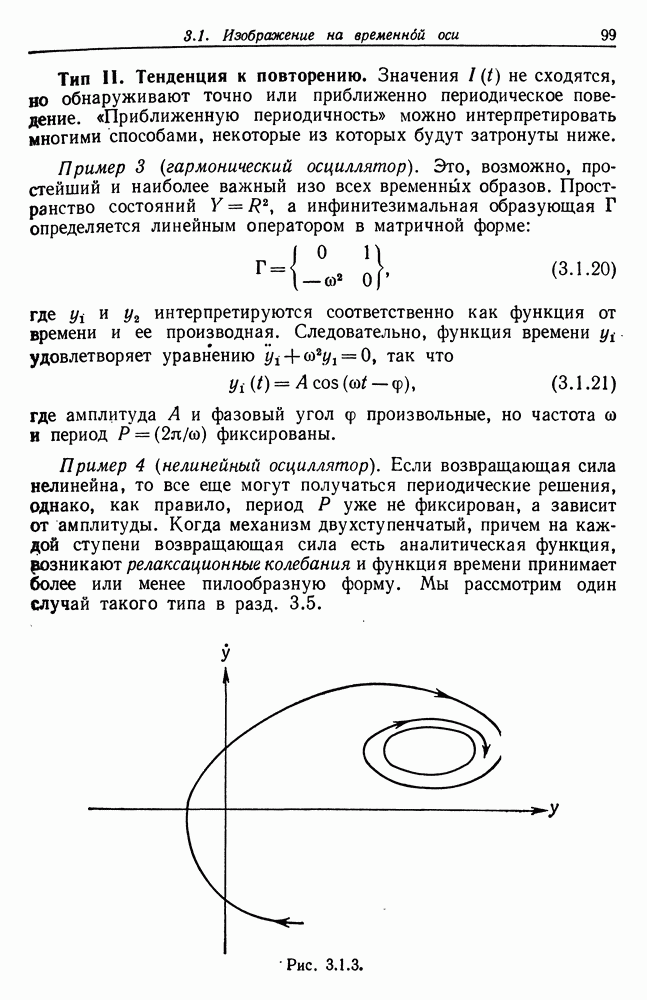
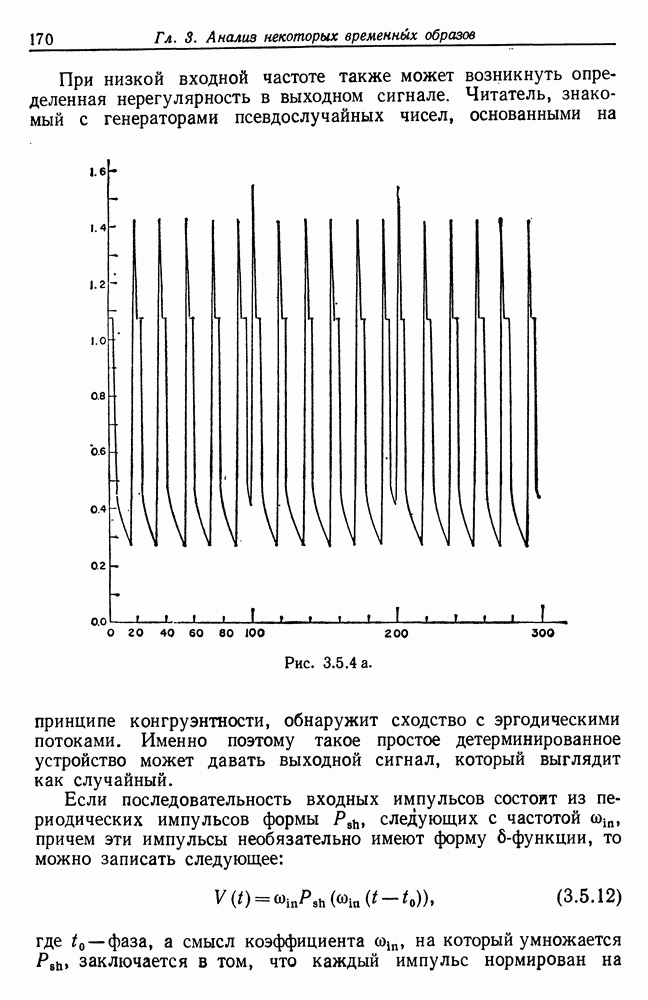
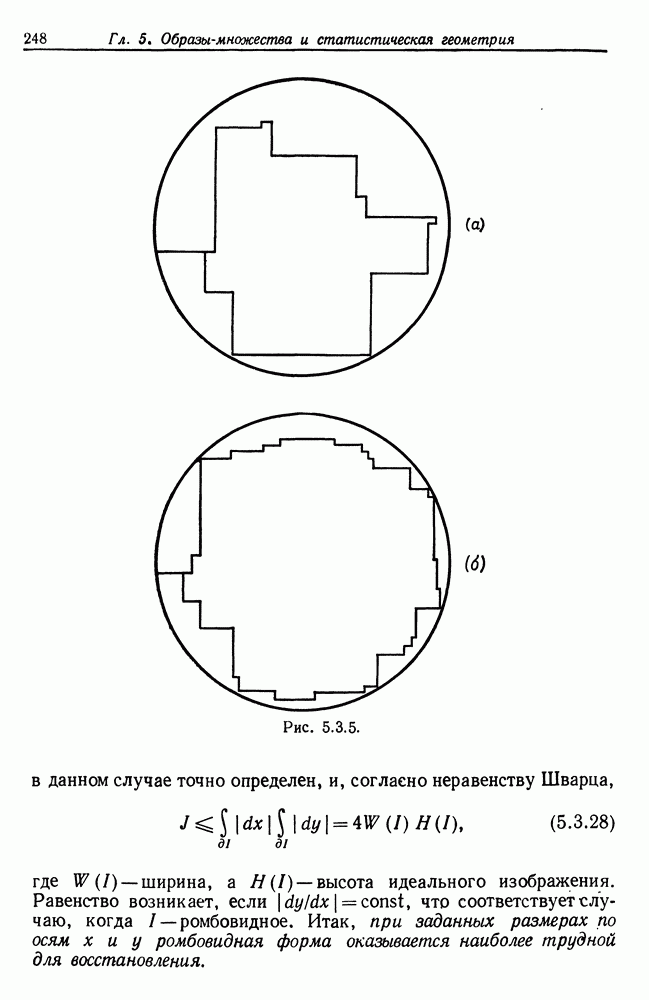
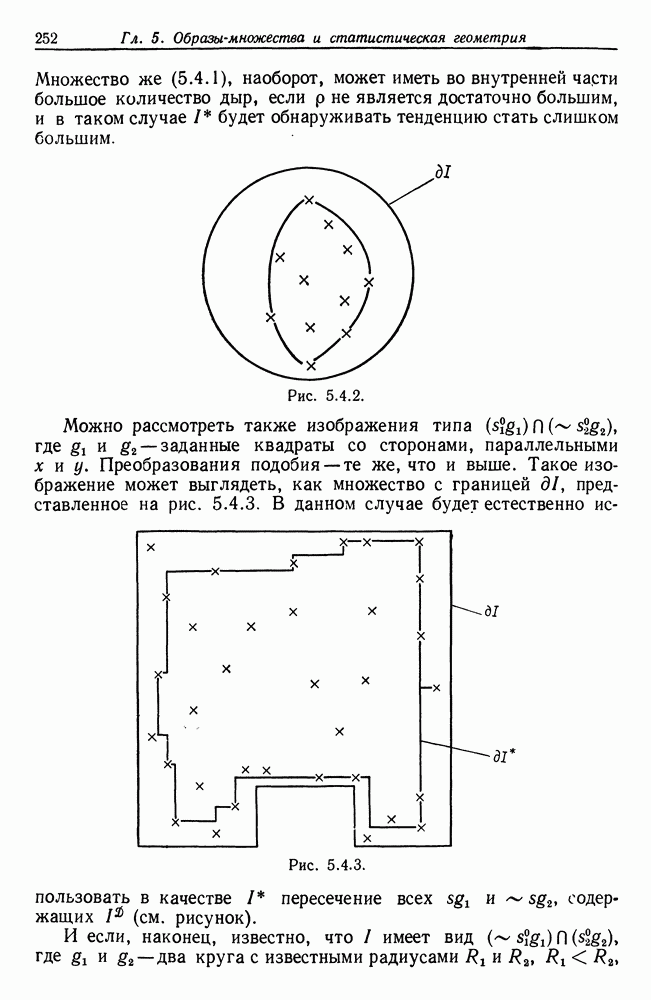
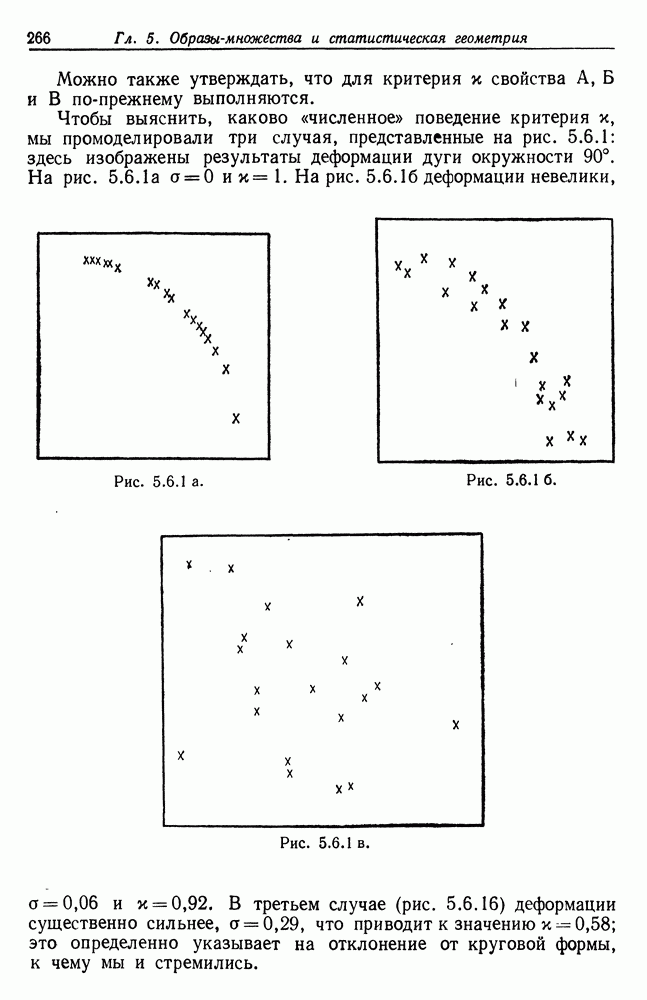
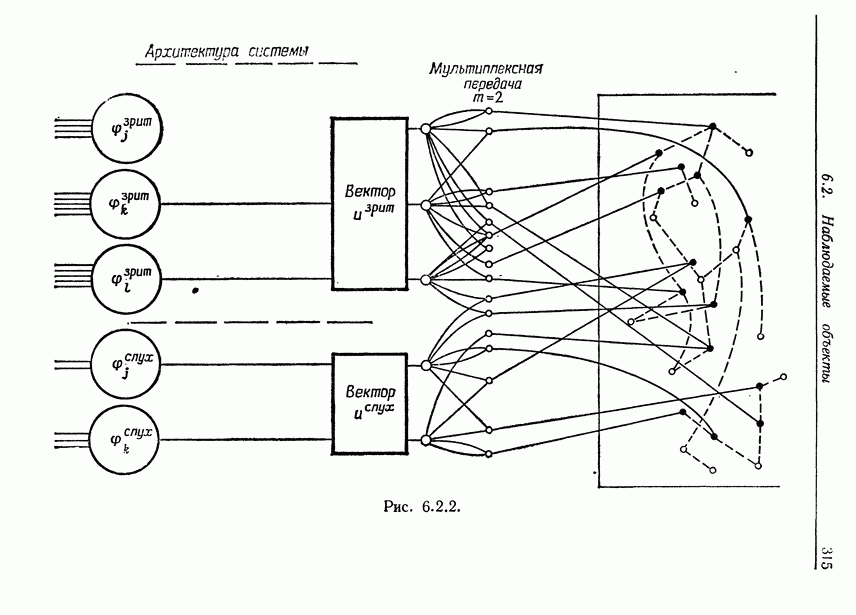
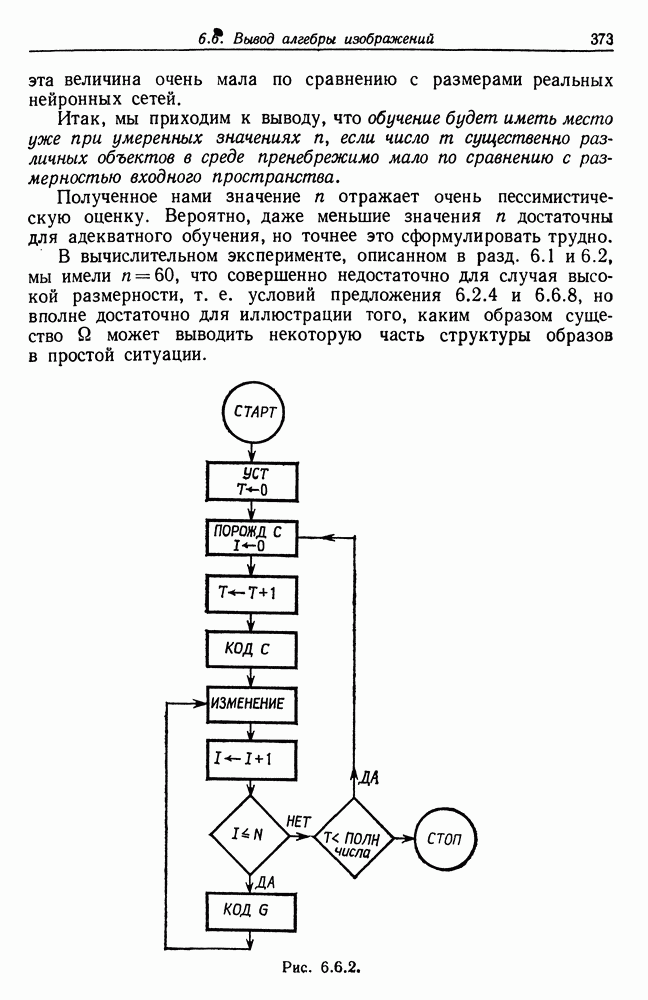
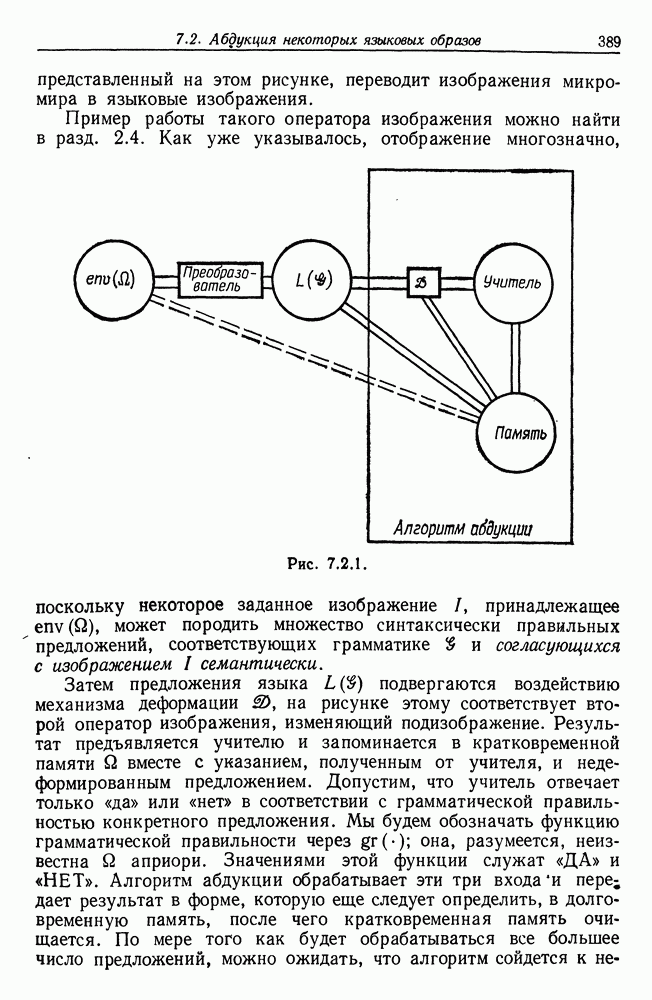
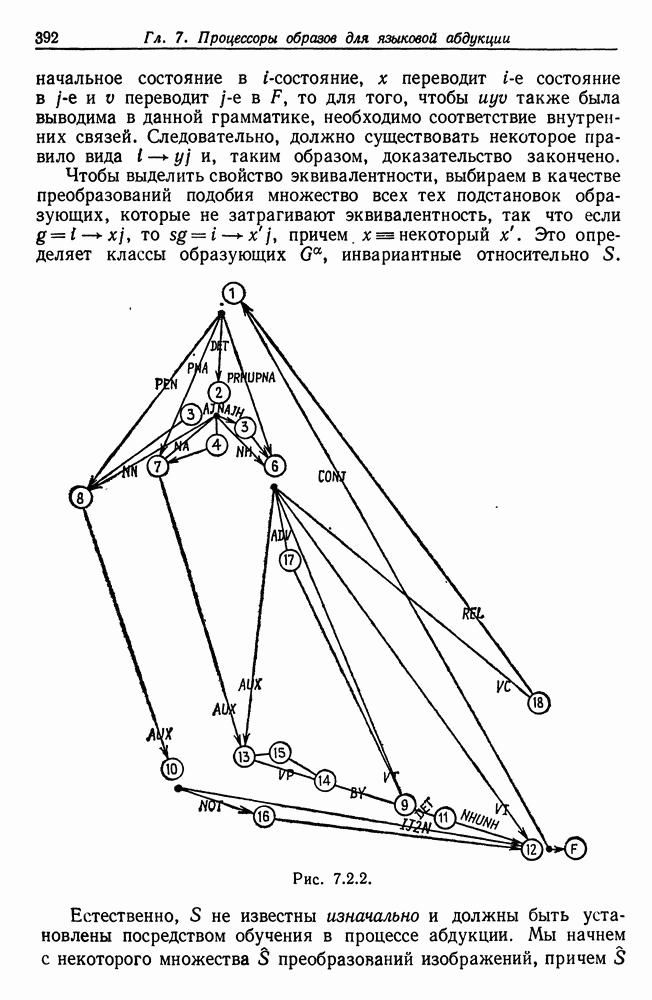
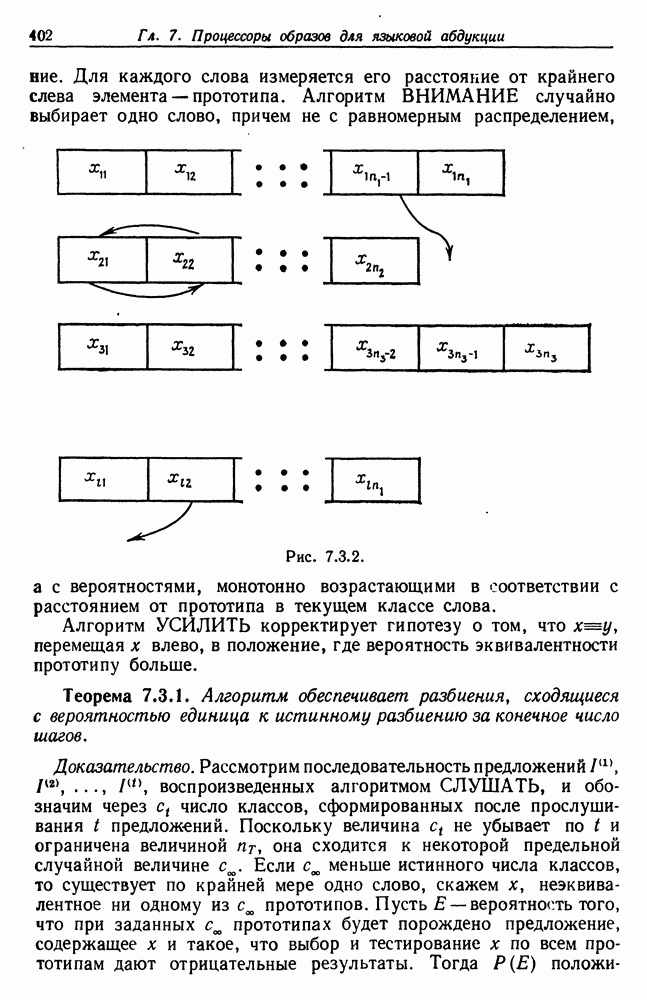
Сейчас мы рассмотрим альтернативный вариант процессора образов, предназначенный для обнаружения симметрий или  Другими словами, будет осуществлена абдукция разбиения на классы слов, но теперь на основе идей о выводе с помощью сети, изложенных в гл. 6.
Другими словами, будет осуществлена абдукция разбиения на классы слов, но теперь на основе идей о выводе с помощью сети, изложенных в гл. 6.
Допустим, что  слов,
слов,  представлены сенсорными векторами высокой размерности
представлены сенсорными векторами высокой размерности  Векторы у можно рассматривать как стандартизированную форму представления речевых сигналов. Следуя афоризму де Соссюра о «произвольности знака», будем допускать очень хаотичное кодирование, а именно: множество векторов у порождается как независимо тождественно распределенная выборка из некоторого многомерного нормального распределения
Векторы у можно рассматривать как стандартизированную форму представления речевых сигналов. Следуя афоризму де Соссюра о «произвольности знака», будем допускать очень хаотичное кодирование, а именно: множество векторов у порождается как независимо тождественно распределенная выборка из некоторого многомерного нормального распределения  с ограниченной общей мощностью, скажем,
с ограниченной общей мощностью, скажем, 
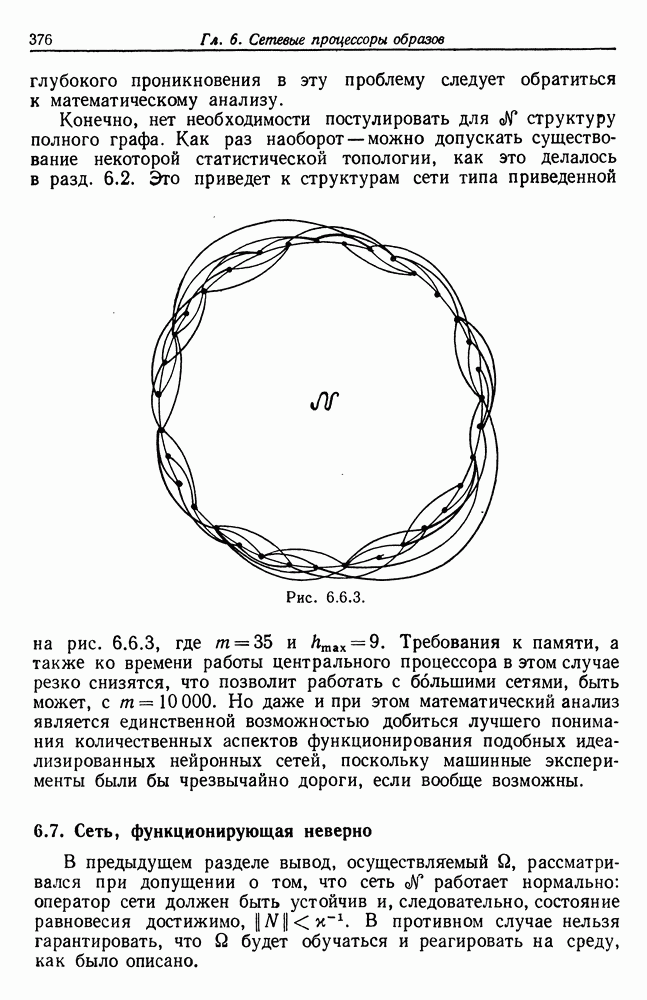
Только некоторая часть сети  будет использоваться при проведении языковой абдукции, и лишь некоторое подмножество этой части — для обнаружения класса слов. Вполне может оказаться, однако, что другим частям сети
будет использоваться при проведении языковой абдукции, и лишь некоторое подмножество этой части — для обнаружения класса слов. Вполне может оказаться, однако, что другим частям сети  должна быть придана та же самая логическая архитектура. Действительно, в значительной мере цель нижеследующего построения — определить классы эквивалентности объектов, что может потребоваться при решении многих задач нелингвистического характера.
должна быть придана та же самая логическая архитектура. Действительно, в значительной мере цель нижеследующего построения — определить классы эквивалентности объектов, что может потребоваться при решении многих задач нелингвистического характера.
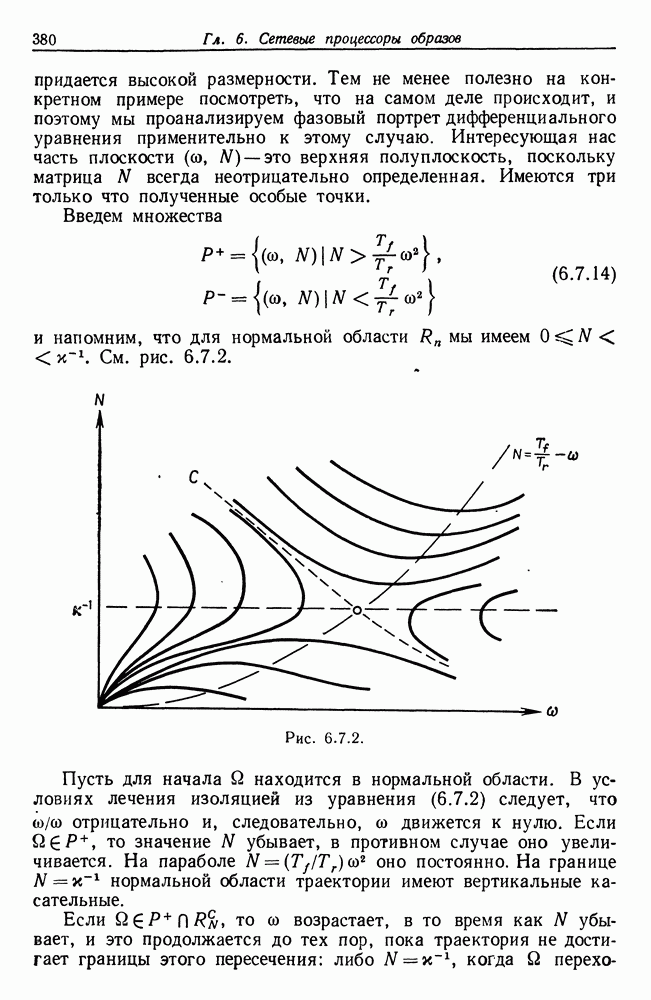
Результаты разд. 6.5 указывают, что при определенных условиях обучение будет иметь место и может быть описано с помощью некоторого оператора опыта Г. Конкретный вид оператора Г зависит от того, как представлены векторы  .
.
Слова встречаются в языке с вероятностями, которые мы вычислили в гл. 2, исходя из заданных параметров синтаксического поведения. Предполагается, что пары  слов порождаются в соответствии с этими вероятностями и одновременно предъявляются
слов порождаются в соответствии с этими вероятностями и одновременно предъявляются  только если они эквивалентны. Нам известно, что в случае
только если они эквивалентны. Нам известно, что в случае
когерентного кодирования и равного внимания к х и у это означает представление  причем
причем  если
если  и
и  в противном случае (см. предложение 6.2.10).
в противном случае (см. предложение 6.2.10).
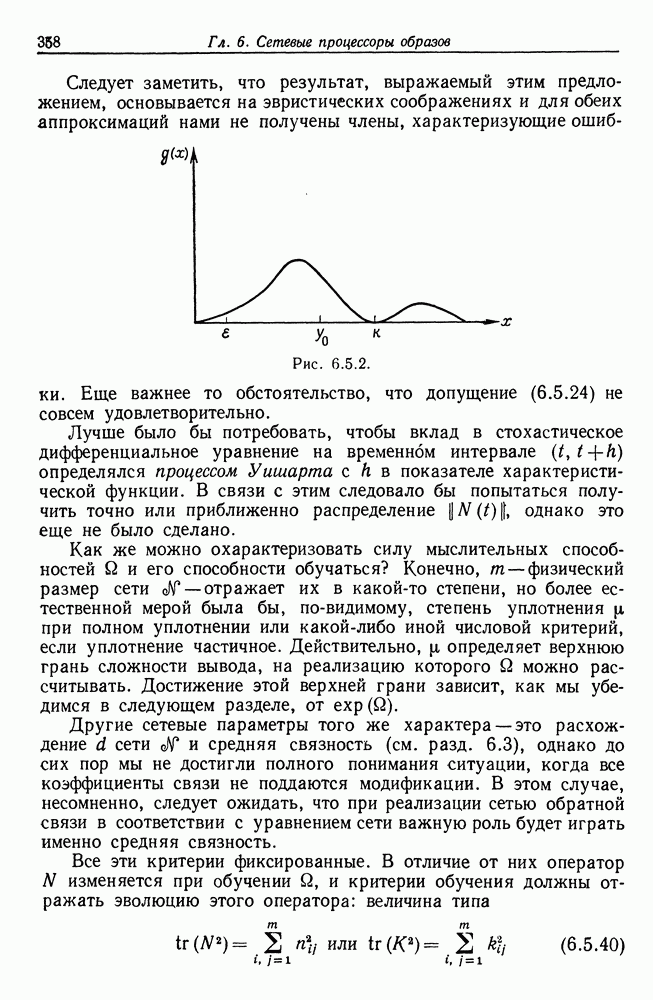
Это означает, что мы временно допускаем  т. е. временно пренебрегаем обеими ошибками; к важному случаю неравенства нулю обеих ошибок мы вернемся после доказательства следующей теоремы.
т. е. временно пренебрегаем обеими ошибками; к важному случаю неравенства нулю обеих ошибок мы вернемся после доказательства следующей теоремы.
В таком случае оператор опыта Г имеет вид (см. уравнение (6.2.44.))

Нам известно, что  проявляют тенденцию к взаимной ортогональности и приблизительно имеют единичную длину (см. предложение 6.6.5). Этим можно воспользоваться для того, чтобы получить некоторое представление о внутреннем произведении, которое индуцируется изменением геометрии в результате обучения:
проявляют тенденцию к взаимной ортогональности и приблизительно имеют единичную длину (см. предложение 6.6.5). Этим можно воспользоваться для того, чтобы получить некоторое представление о внутреннем произведении, которое индуцируется изменением геометрии в результате обучения:

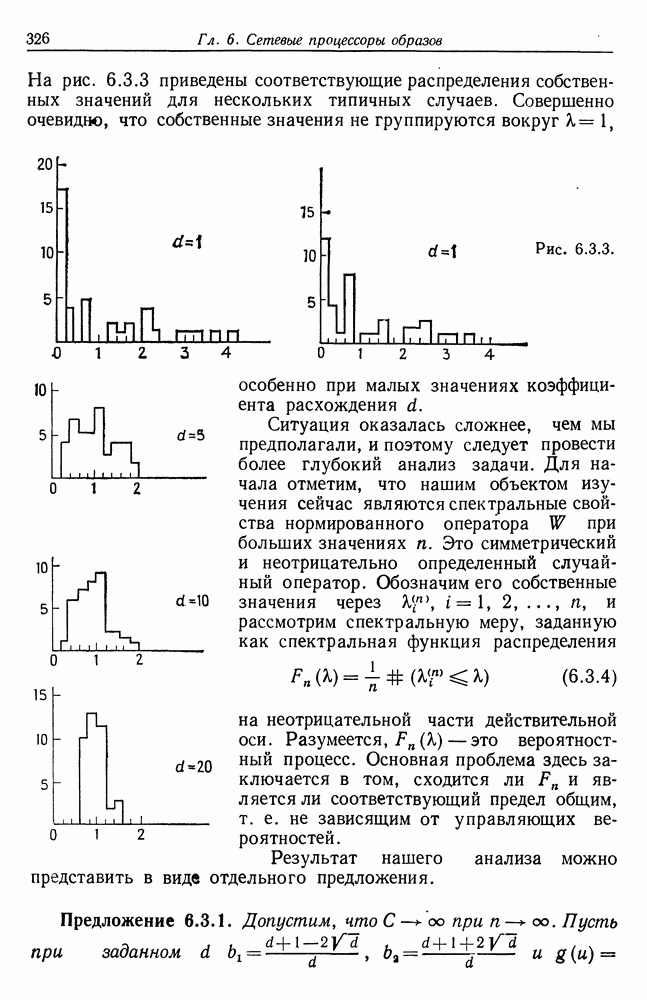
Строгий вывод с учетом характеризующих ошибку членов требует проведения более тщательного асимптотического анализа. Силверстайн (1976) проделал эту работу, и мы приведем его вывод.
Теорема 7.4.1. При любых  справедливо
справедливо

здесь при  имеет место сходимость по вероятности. Кроме того,
имеет место сходимость по вероятности. Кроме того,

и при

Здесь  — вероятность выбора слова из того же класса, что
— вероятность выбора слова из того же класса, что  :
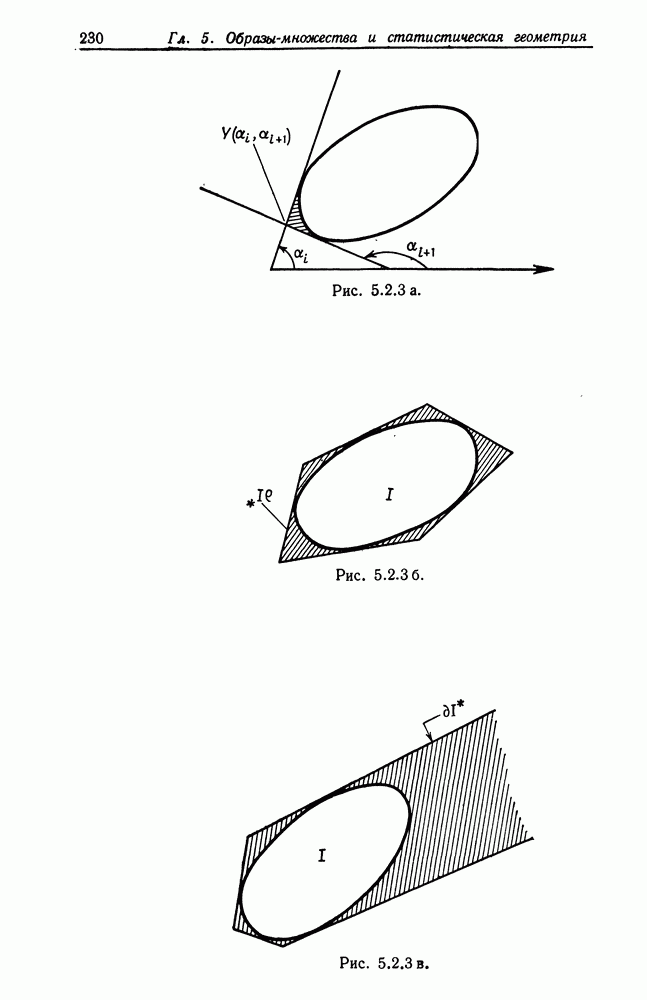
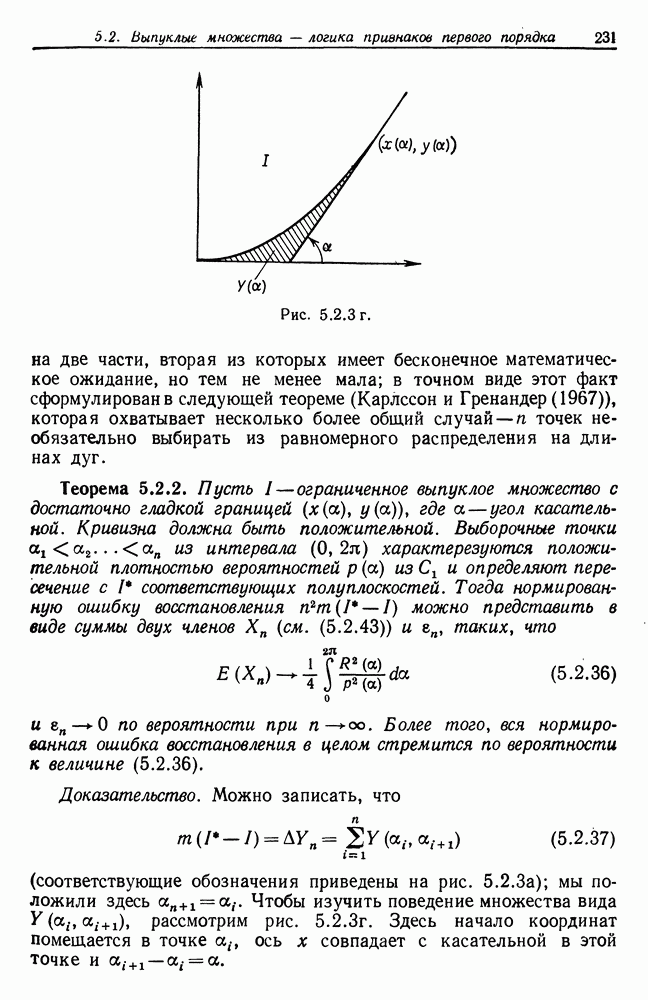
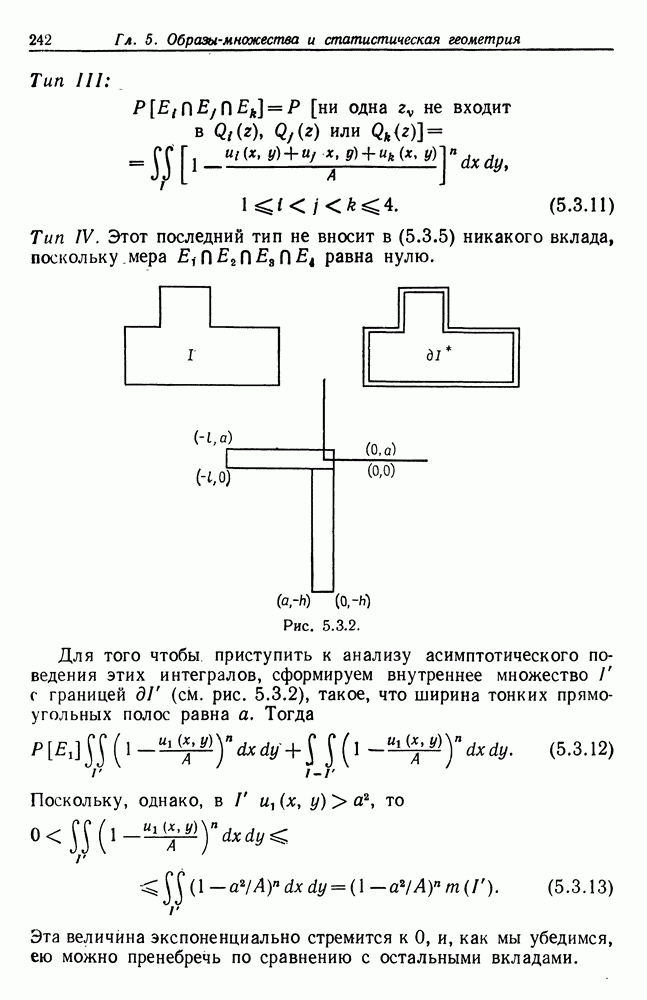
:

Доказательство. Нам потребуются математические ожидания внутренних произведений для измененной геометрии  и их квадраты. В связи с этим появятся произведения, включающие
и их квадраты. В связи с этим появятся произведения, включающие
два или четыре сомножителя. Непосредственное вычисление характеристической функции  (немодифицированная геометрия) дает
(немодифицированная геометрия) дает  при
при  Если
Если  то внутреннее произведение
то внутреннее произведение  представляет собой просто
представляет собой просто  умноженную на некоторую
умноженную на некоторую  -переменную с
-переменную с  степенями свободы. Это позволяет легко получить необходимые моменты, и при
степенями свободы. Это позволяет легко получить необходимые моменты, и при  мы имеем
мы имеем

С другой стороны, неравенство Шварца дает вполне очевидные границы:

Из (7.4.7) следует, что члены вида (7.4.8) будут стремиться к нулю при стремлении  к бесконечности, если одно из внутренних произведений связывает два различных вектора.
к бесконечности, если одно из внутренних произведений связывает два различных вектора.
При доказательстве теоремы ничто не мешает выбрать  Для
Для  введя новые индексы
введя новые индексы  при суммировании, получаем что
при суммировании, получаем что

Проводя дальнейшие упрощения, получаем следующее:

Кроме того,

Оба математических ожидания вторых сумм в (7.4.10) и (7.4.11) равны нулю, поскольку все члены этих сумм содержат нечетное число компонент одного вектора. Из (7.4.7) и (7.4.10) получаем следующее:

и, следовательно,

При  имеем
имеем

поскольку третий момент случайной  -переменной с
-переменной с  степенями свободы равен
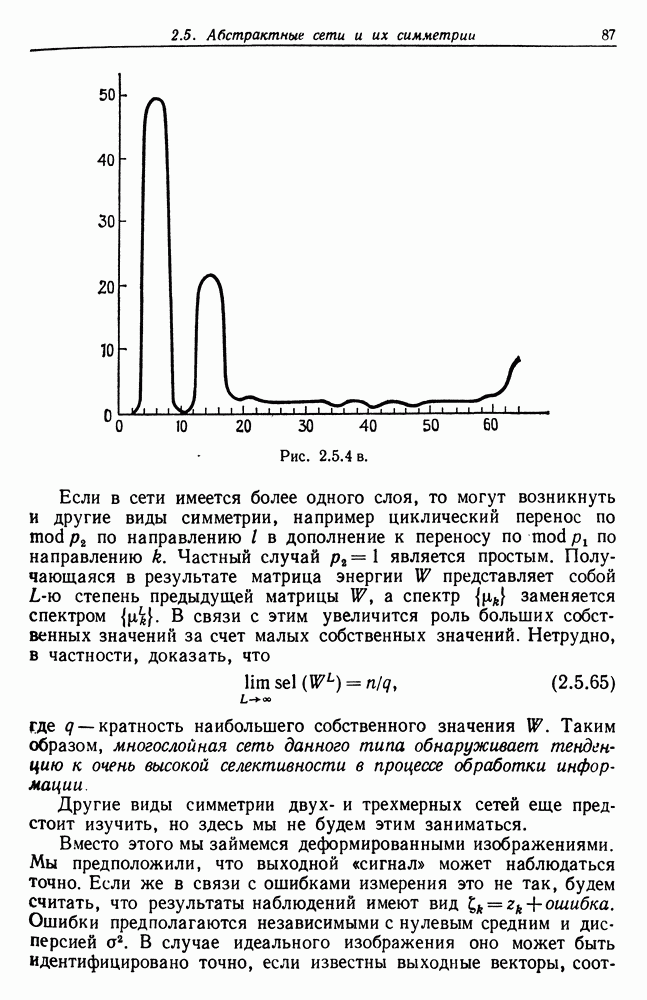
степенями свободы равен  .
.
На основании (7.4.7), (7.4.11) и (7.4.14) получаем, что

Из (7.4.13) и (7.4.15) следует, что  стремятся к конечным и равным пределам. Таким образом, дисперсия
стремятся к конечным и равным пределам. Таким образом, дисперсия  сходится к 0, что эквивалентно сходимости
сходится к 0, что эквивалентно сходимости  по вероятности. Кроме того,
по вероятности. Кроме того,

Для  мы аналогично получаем
мы аналогично получаем

Как и ранее, мы находим, что математические ожидания первой суммы в (7.4.17) и второй суммы в (7.4.18) равны нулю. На основании (7.4.7), (7.4.17) и того, что математическое ожидание величины, подчиняющейся распределению  степенями свободы, равно
степенями свободы, равно  получаем
получаем

и

Чтобы найти  , необходимо знать величину
, необходимо знать величину  Мы имеем
Мы имеем

здесь использовано (7.4.7) и то обстоятельство, что четвертый момент случайной переменной, подчиняющейся  равен
равен 
На основании (7.4.7), (7.4.8), (7.4.14) и (7.4.18), получаем, что 

Можно, следовательно, сделать вывод, что  сходятся к
сходятся к  по вероятности и
по вероятности и

Проводя дальнейшие упрощения, получаем, что при 

на чем доказательство заканчивается.
Из этой теоремы следует, что в результате обучение позволит существу  разделять слова
разделять слова  если
если  поскольку сеть дает отрицательную реакцию: в пределе
поскольку сеть дает отрицательную реакцию: в пределе  . Если
. Если  но
но  то в этом случае
то в этом случае  и, конечно, для идентичных слов
и, конечно, для идентичных слов 
Допустим теперь, что ошибки  пренебрежимо малы. Тогда мы не станем утверждать, что (7.4.3) справедливо, но будем вынуждены вновь обратиться к (7.4.1), где
пренебрежимо малы. Тогда мы не станем утверждать, что (7.4.3) справедливо, но будем вынуждены вновь обратиться к (7.4.1), где  следует теперь заменить на
следует теперь заменить на 

Рассматривая доказательство теоремы (7.4.1) с точки зрения непрерывности, можно убедиться, что (7.4.3) справедливо при небольших изменениях в правой части, если и  достаточно малы.
достаточно малы.
Сопоставим этот результат с обсуждением, проведенным в конце предыдущего раздела. Там устойчивость имела место относительно ошибки  но не
но не  Как только
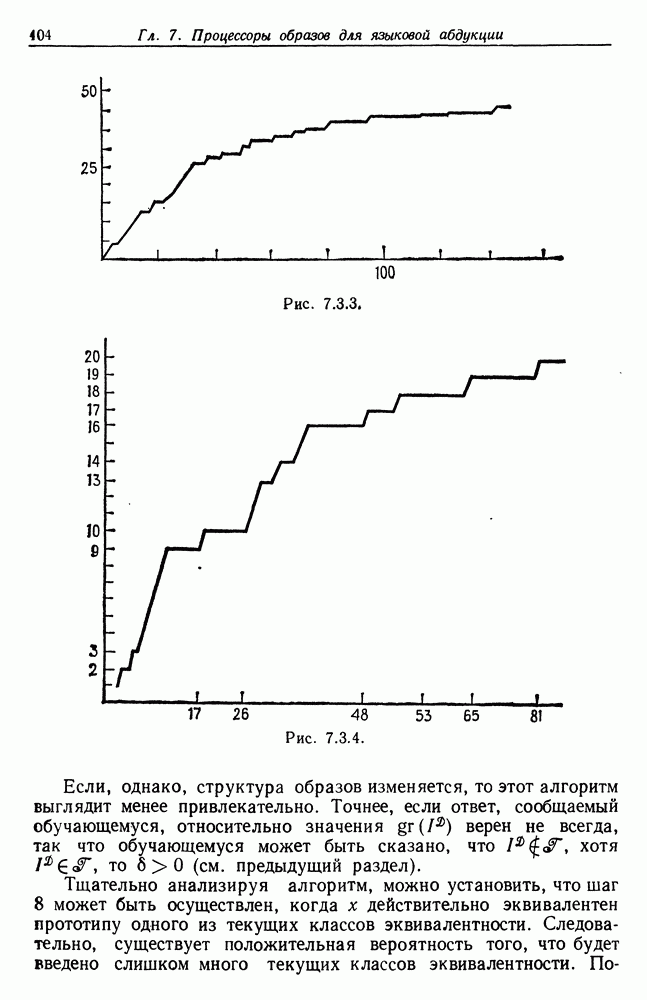
Как только  становится положительной независимо от того, насколько она мала, алгоритм «взрывается».
становится положительной независимо от того, насколько она мала, алгоритм «взрывается».
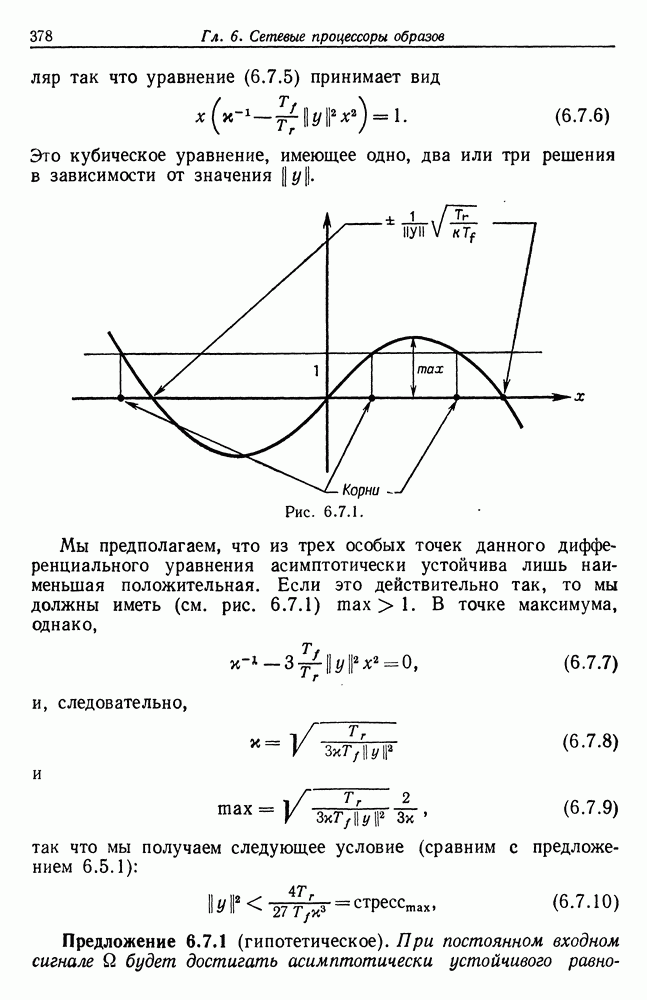
При алгоритме же, основанном на сети, малые ошибки не вызывают серьезных нарушений функций.
Итак, мы имеем возможность выбирать между довольно быстродействующим, но неустойчивым алгоритмом абдукции и устойчивым, но относительно медленным алгоритмом. Следует в то же время отметить, что второй алгоритм на самом деле окажется не медленнее первого, если при его реализации ориентироваться на параллельный режим работы, как это было бы в случае реальной «физической» сети.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
- Глава 3. Анализ некоторых временных образов
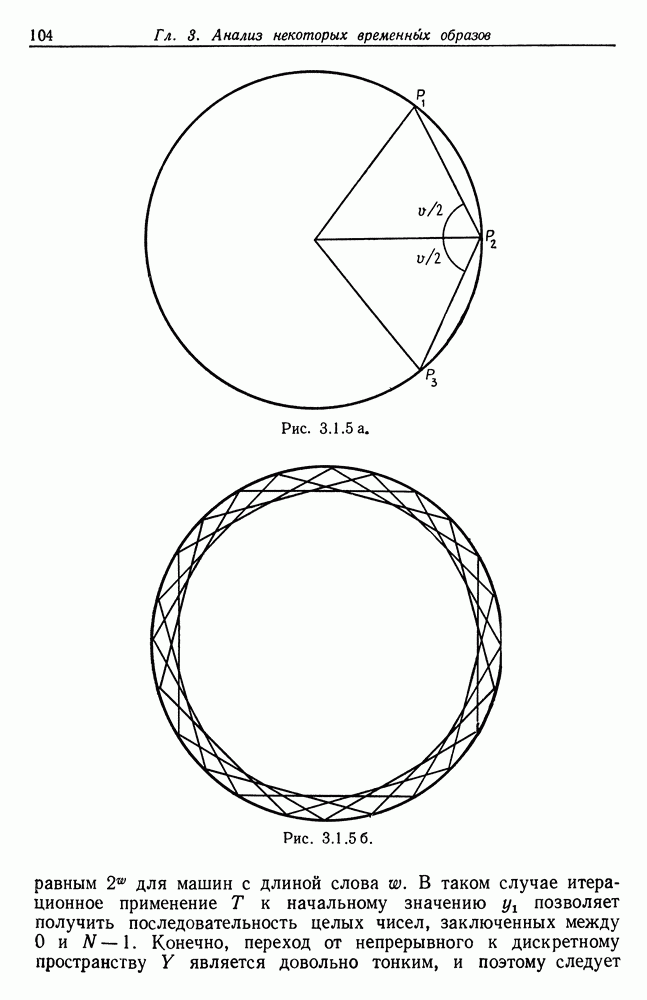
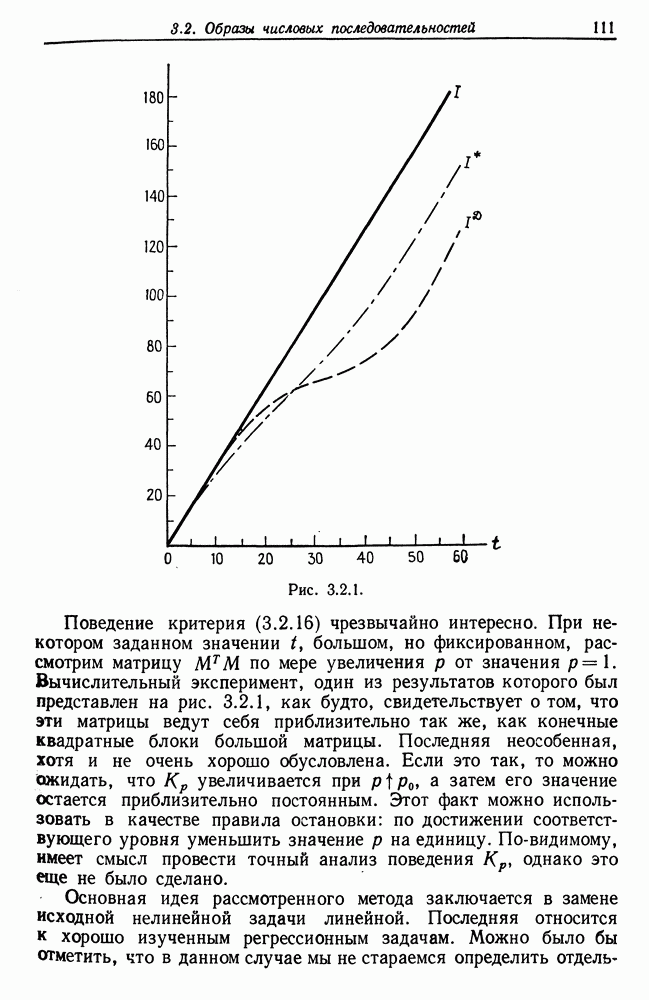
- 3.2. Образы числовых последовательностей
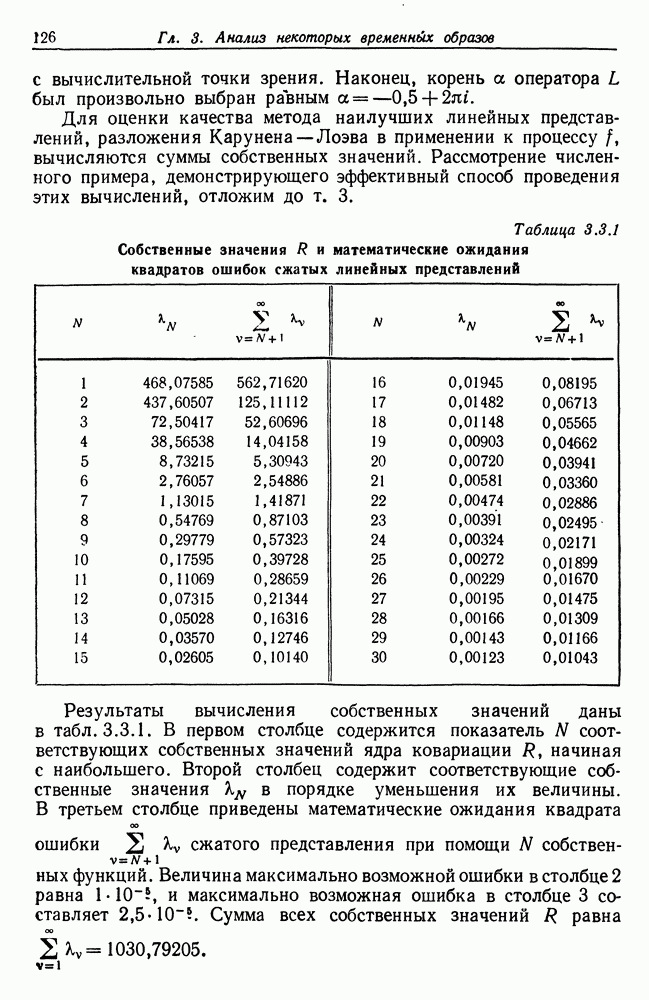
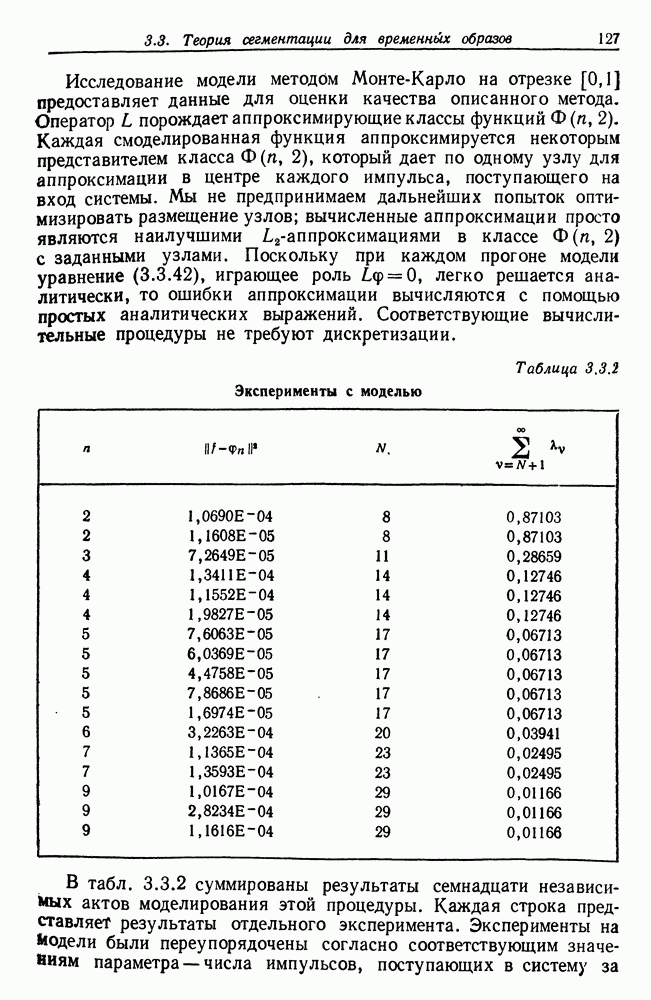
- 3.3. Теория сегментации для временных образов
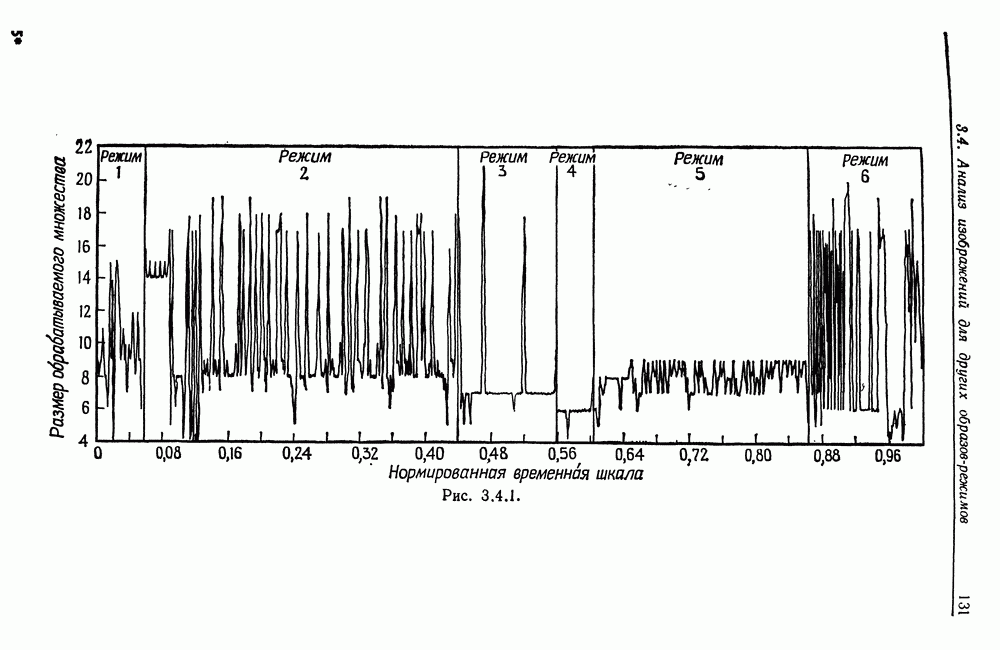
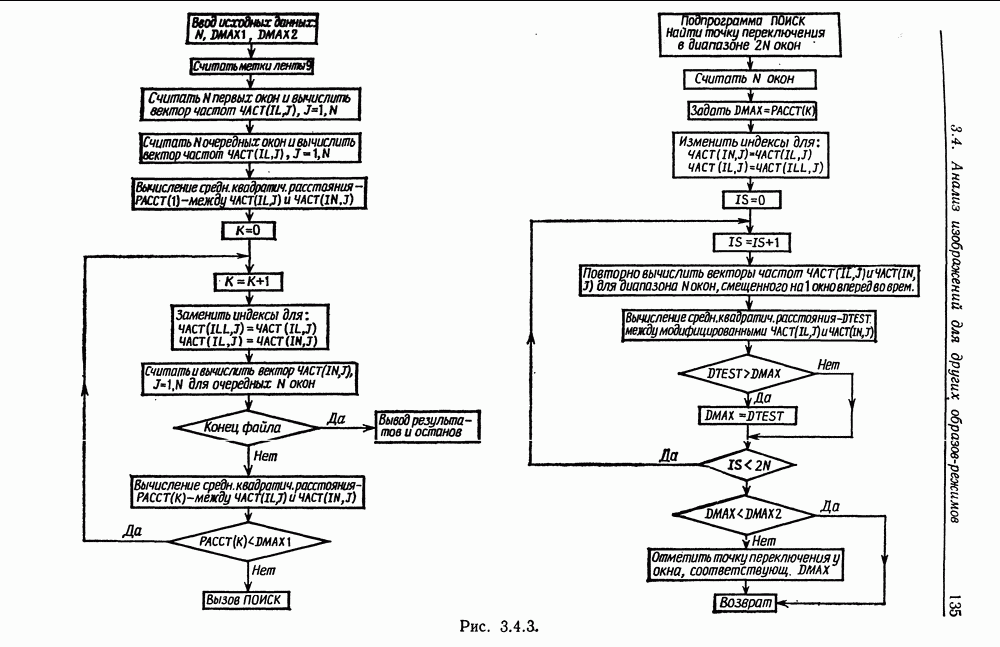
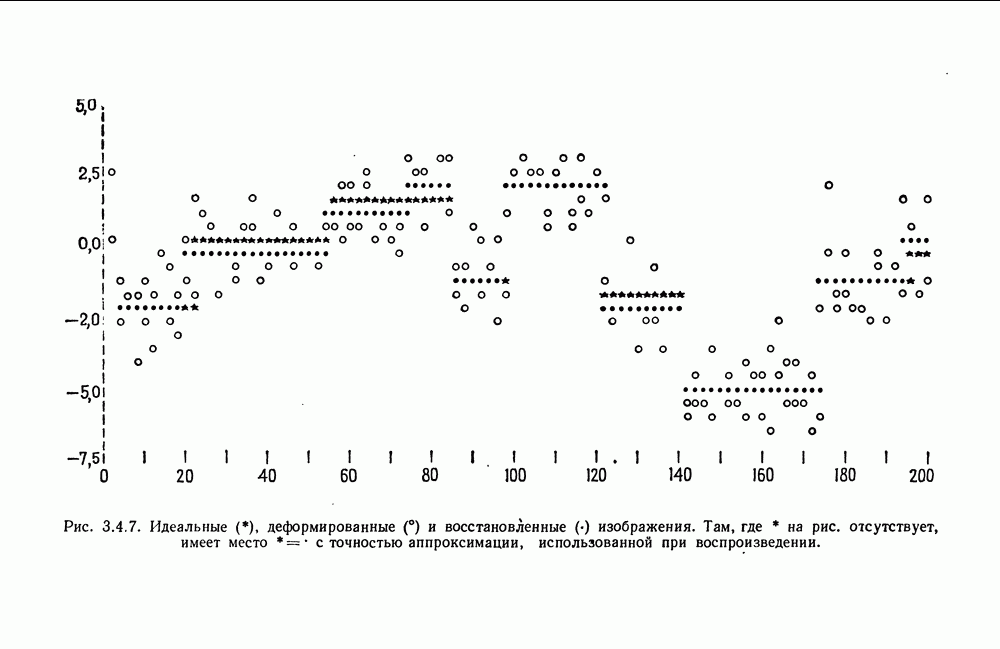
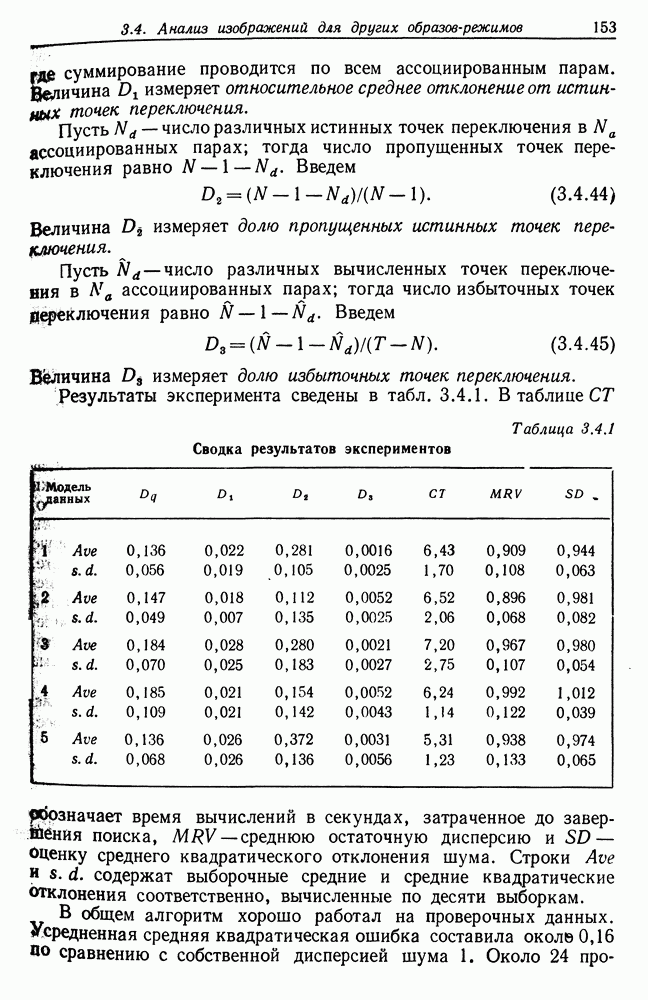
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
- 4.2. Рентгенография кристаллов
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
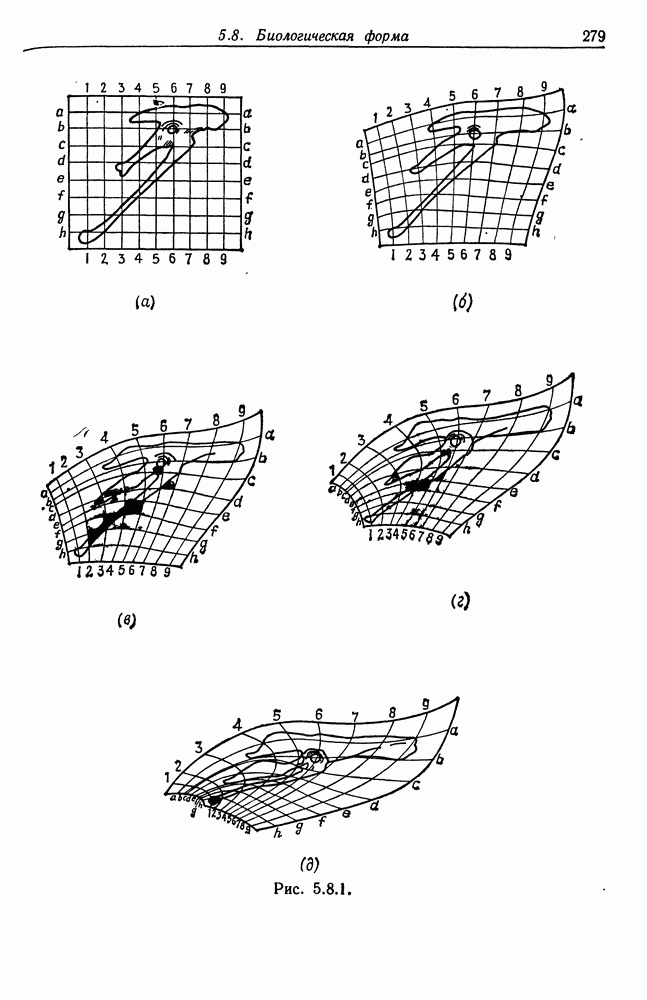
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы