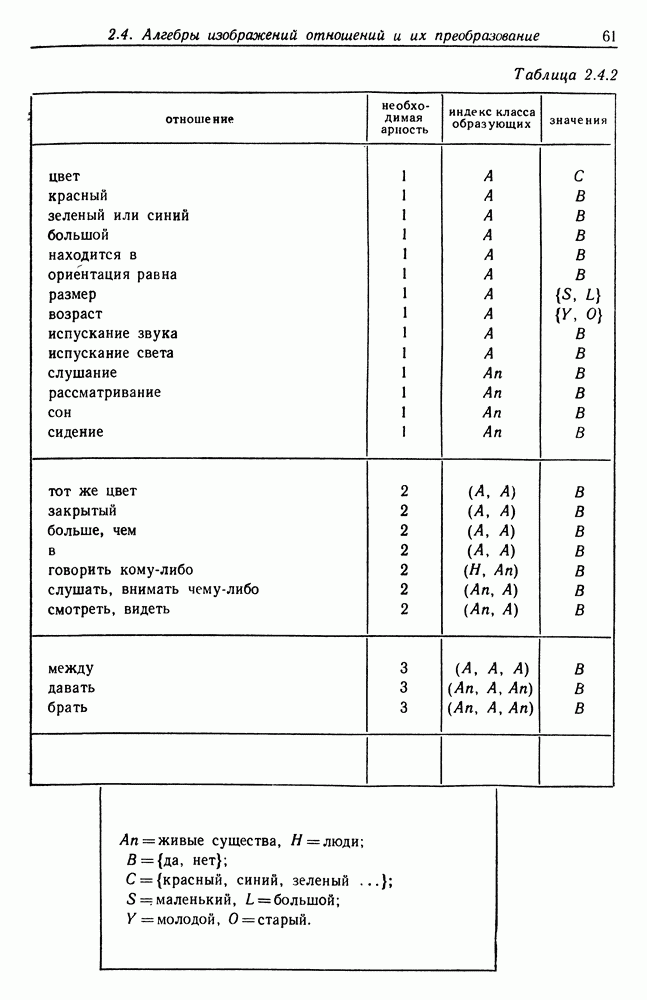
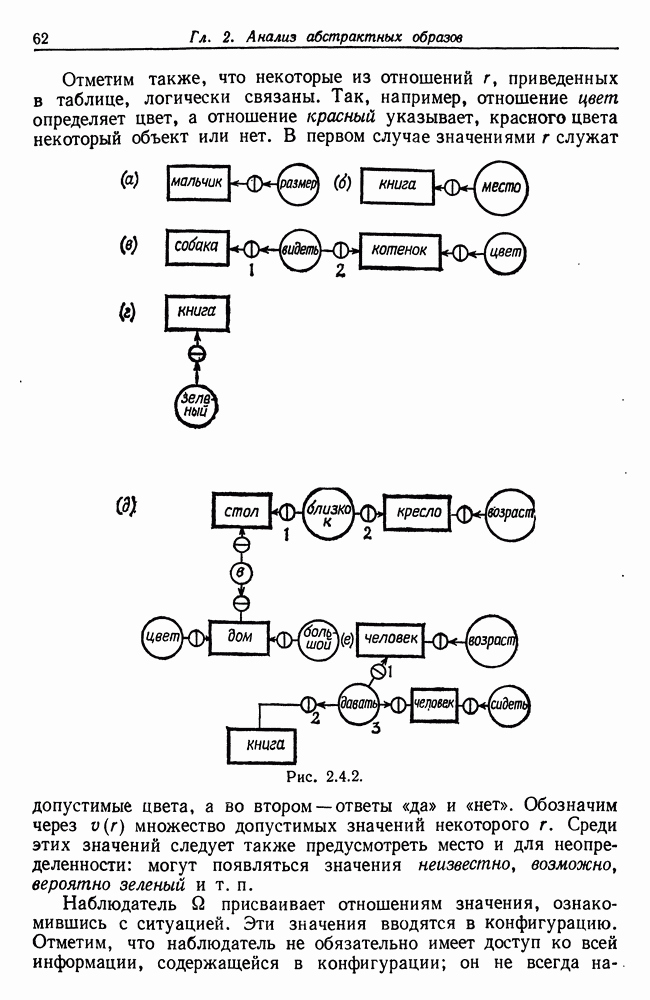
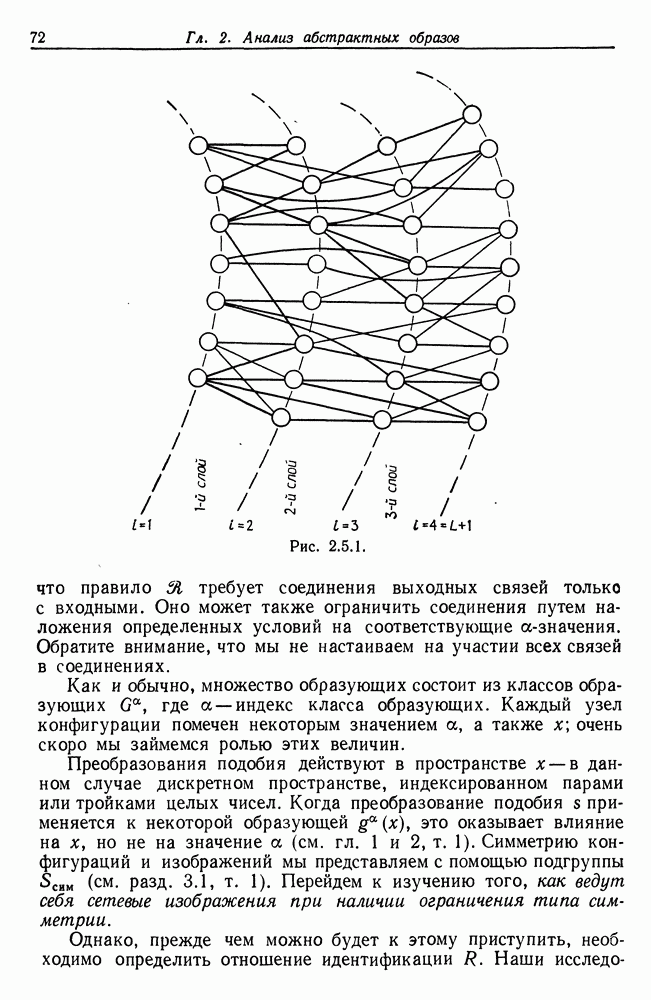
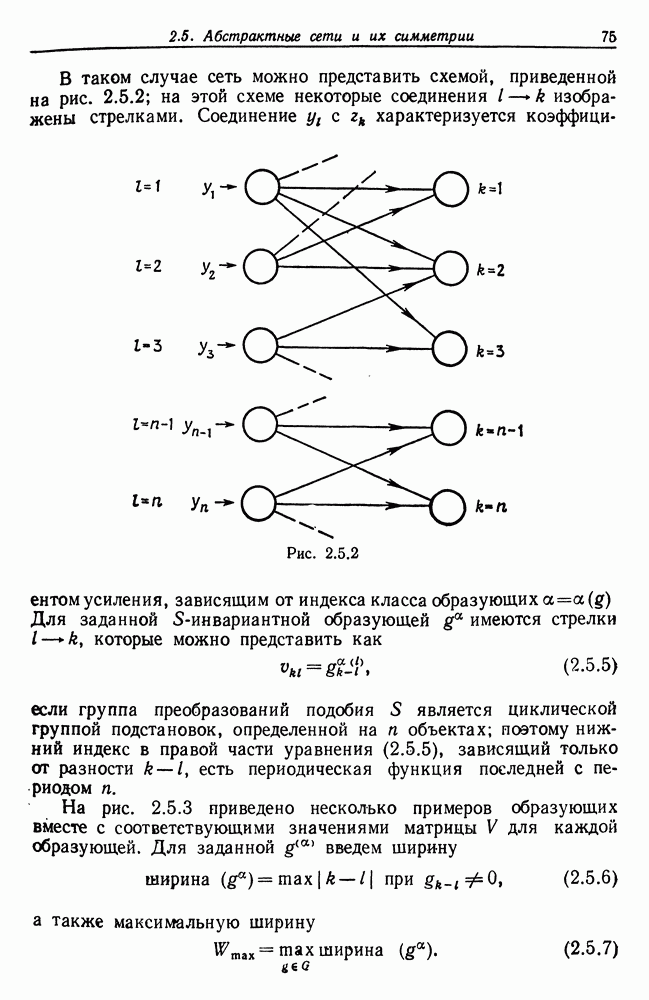
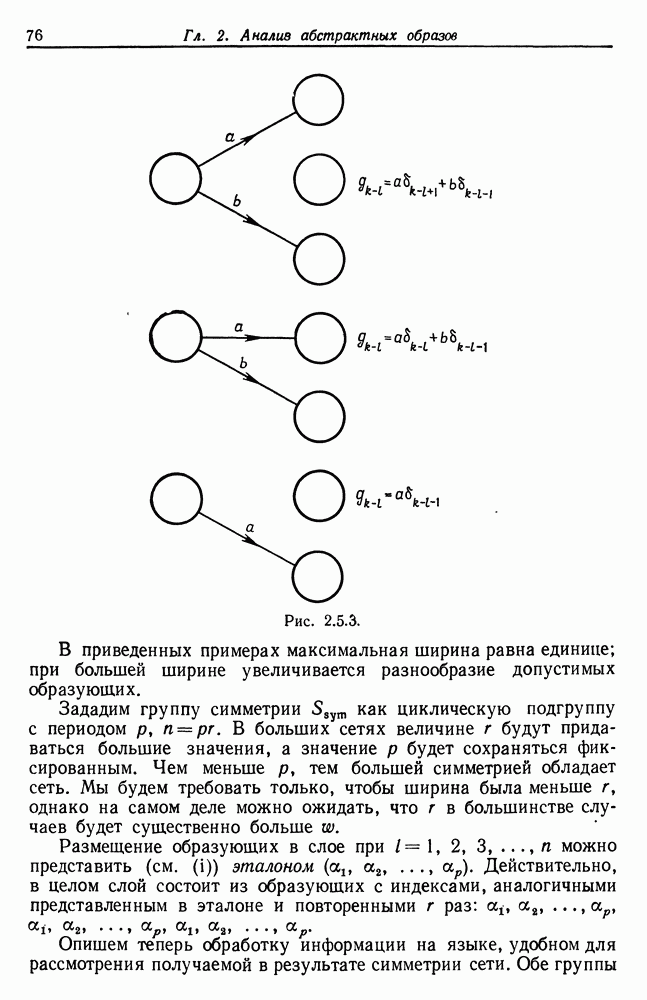
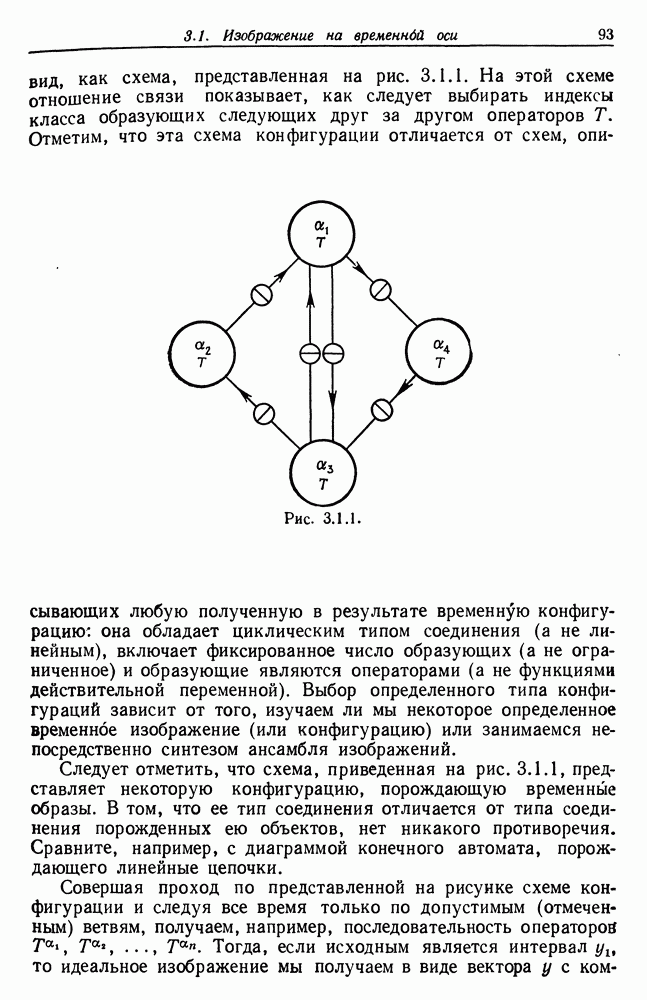
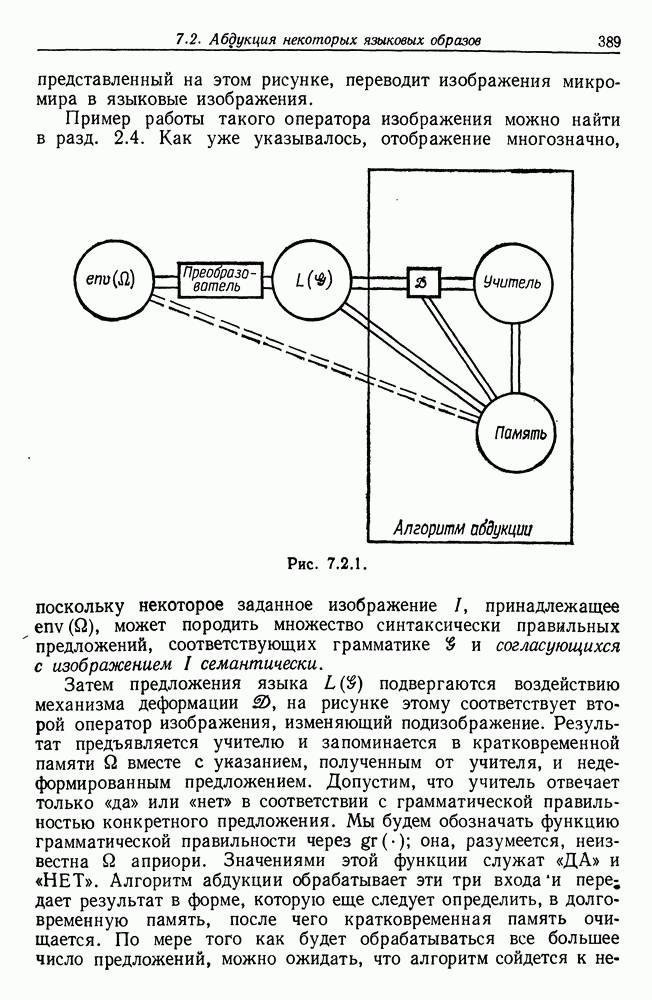
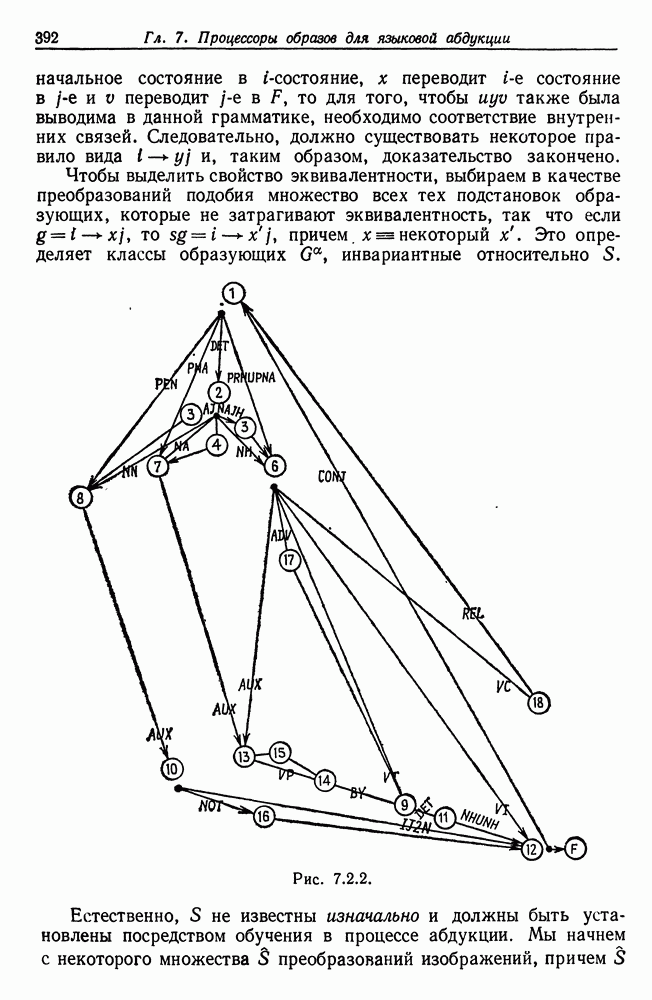
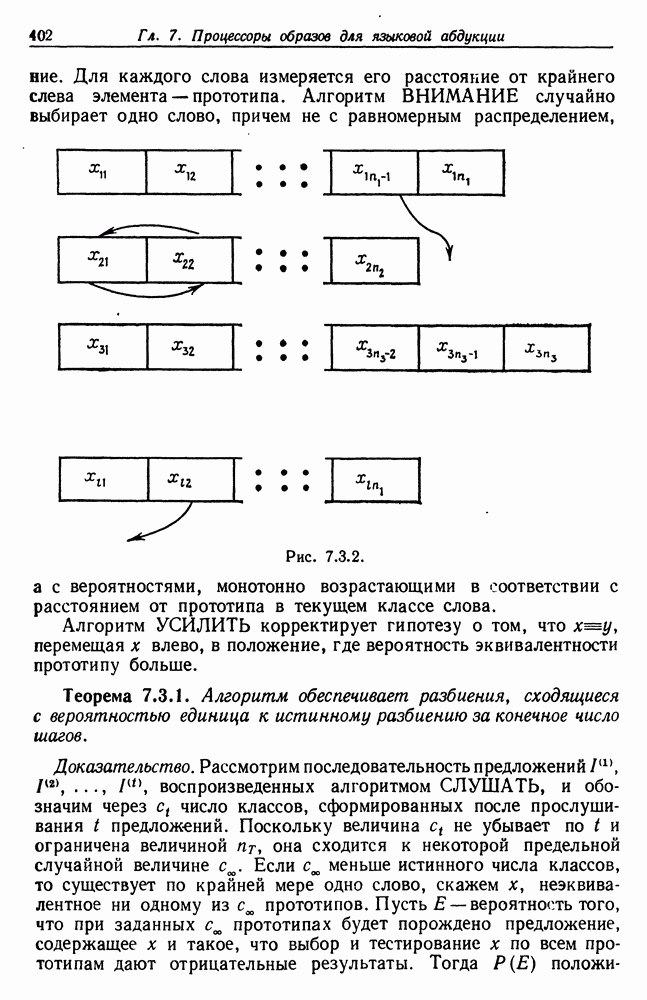
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2. Выпуклые множества — логика признаков первого порядка
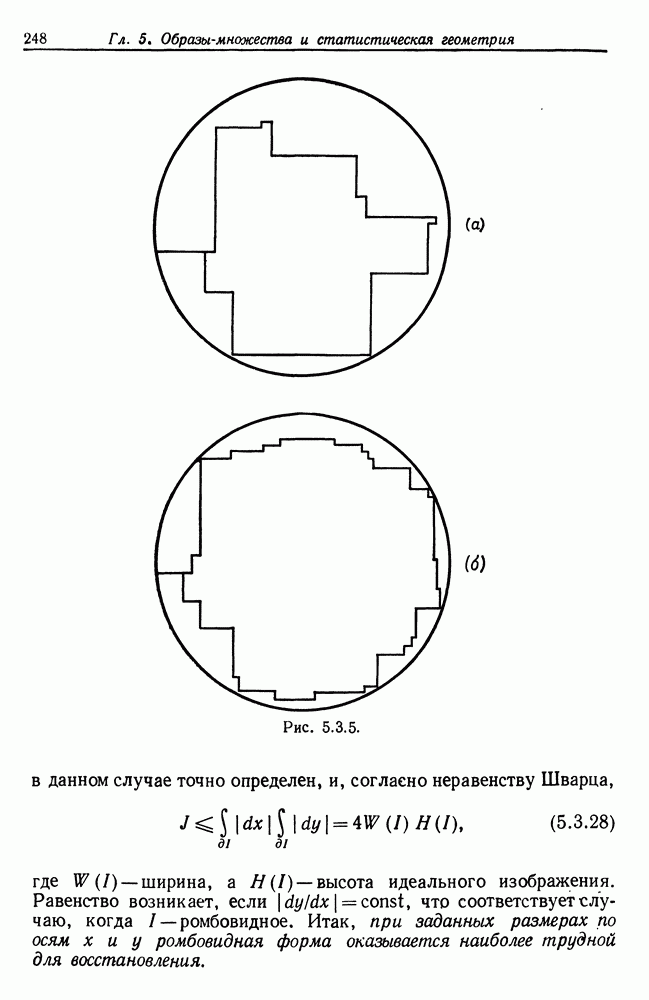
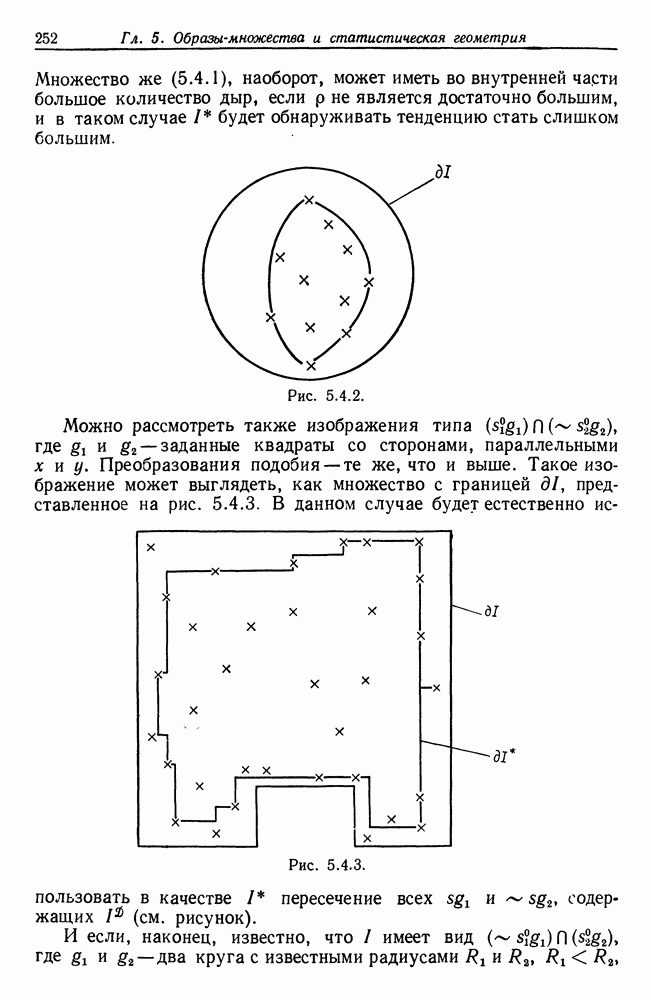
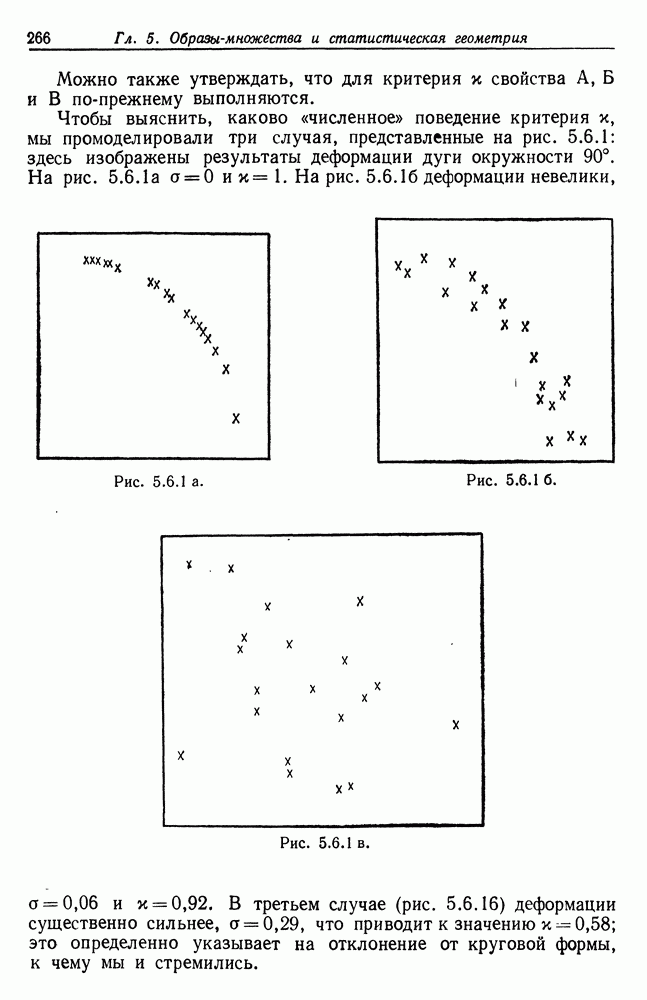
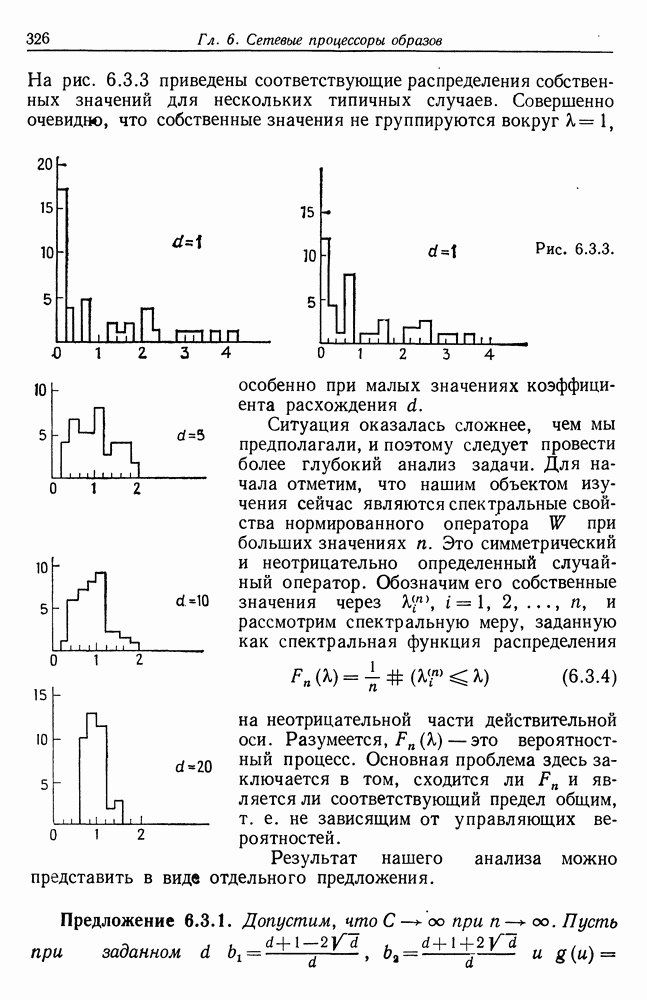
Алгебры изображений, рассматривавшиеся в предыдущем разделе, весьма жесткие: их можно параметризовать с помощью нескольких действительных параметров. Теперь мы переходим к более «свободным» алгебрам изображений,  ее. допускаем изображения с произвольной, даже бесконечной числовой сложностью (см. т. 1, с. 249). В данном разделе структурная сложность логики признаков равна единице, в разд. 5.3 она равна двум, а в разд. 5.4 - бесконечности; соответствующие множества лредполагаются компактными.
ее. допускаем изображения с произвольной, даже бесконечной числовой сложностью (см. т. 1, с. 249). В данном разделе структурная сложность логики признаков равна единице, в разд. 5.3 она равна двум, а в разд. 5.4 - бесконечности; соответствующие множества лредполагаются компактными.
Пусть в роли образующих выступают полуплоскости, а правило идентификации определяет пересечение образующих, так что мы приходим к идеальным изображениям, представляющим собой выпуклые множества на плоскости. Как же следует восстанавливать идеальное изображение, если  Совершенно очевидно, что утверждение, лежащее в основе соотношения (5.1.3), обеспечивает восстановление то принципу максимального правдоподобия выпуклой оболочки деформированного изображения Р:
Совершенно очевидно, что утверждение, лежащее в основе соотношения (5.1.3), обеспечивает восстановление то принципу максимального правдоподобия выпуклой оболочки деформированного изображения Р:

Разумеется, I будет стремиться к идеальному изображению  в том смысле, что
в том смысле, что

Доказательство соотношения (5.2.2) мы предоставляем выполнить читателю. Прежде чем перейти к обсуждению критической проблемы скорости сходимости в (5.2.2), остановимся крзатко на алгоритмических аспектах вычисления 
«Наивный» (и расточительный) алгоритм выглядит так:
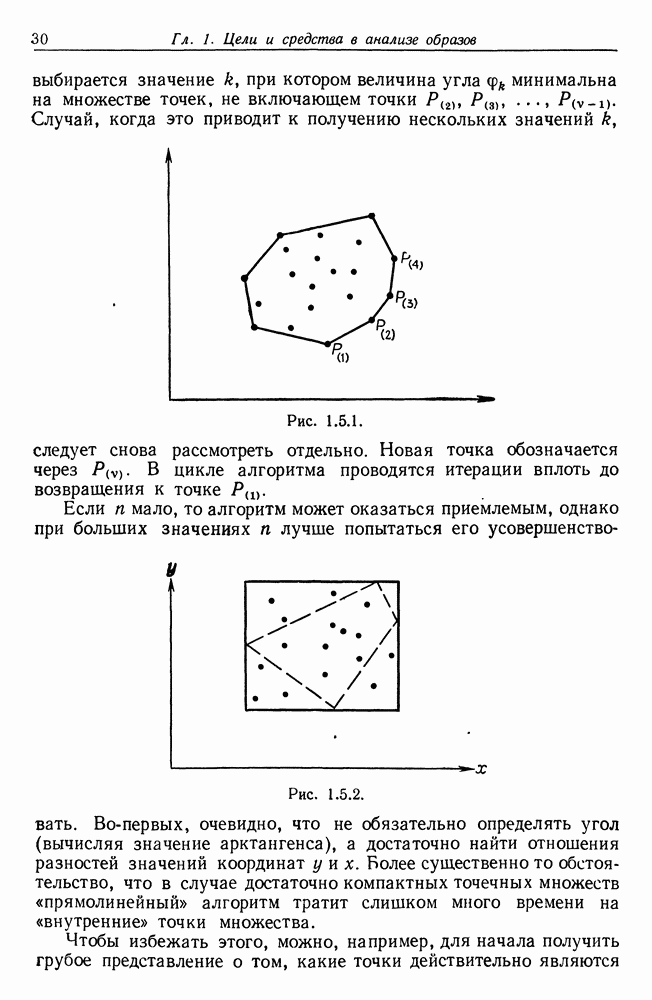
Шаг 1. Приближаемся к полуплоскостями снизу так, чтобы эти полуплоскости были ограничены горизонтальньпми прямыми. Выбирается первая встреченная точка Р. На рис. 5.2.1а — это точка  Если встречается не одна точка, то выбираем самую
Если встречается не одна точка, то выбираем самую

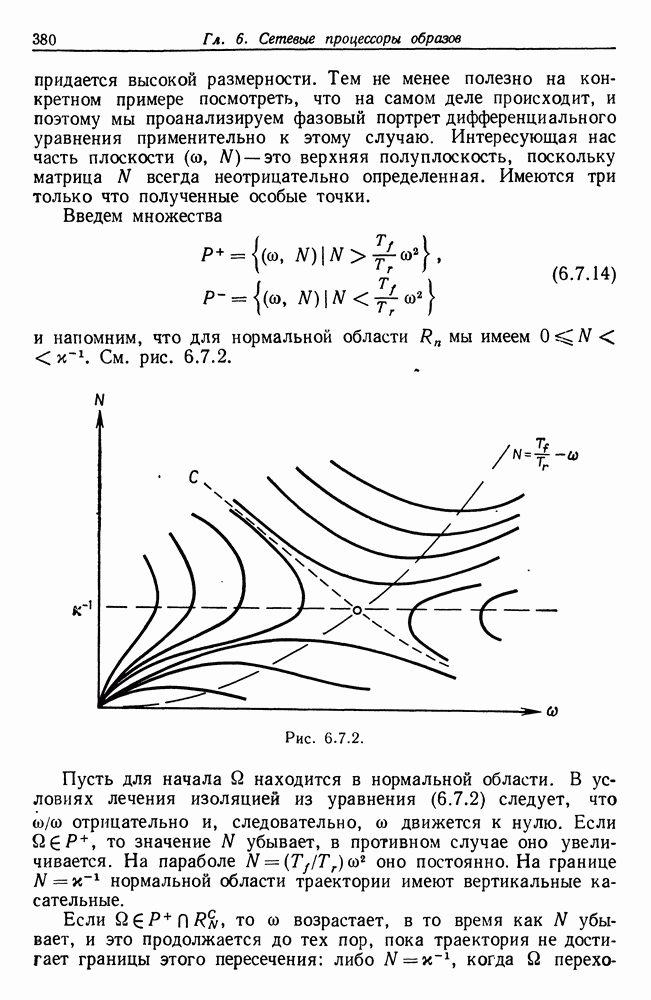
Рис. 5.2.1.а.
левую из них. Этот шаг связан с вычислением  после чего, возможно, потребуется определить минимальное значение
после чего, возможно, потребуется определить минимальное значение 
Шаг 2. После того как точки  определены, вычисляем углы между
определены, вычисляем углы между  к для всех точек Р в для которых еще не установчена принадлежность границе
к для всех точек Р в для которых еще не установчена принадлежность границе  за исключением
за исключением  Для этого необходимо многократное вычисление арктангенса. Выбираем точку Р, для которой указанный угол наименьший, или, если такая точка не единственная, выбираем ту точку на данном направлении, которая расположена на наибольшем расстоянии от
Для этого необходимо многократное вычисление арктангенса. Выбираем точку Р, для которой указанный угол наименьший, или, если такая точка не единственная, выбираем ту точку на данном направлении, которая расположена на наибольшем расстоянии от  . На рисунке, где
. На рисунке, где  мы имеем
мы имеем  .
.
Шаг 3. Возвращаемся к шагу 2 до тех пор, пока опять не встретится точка 
Сколько раз необходимо вычислять арктангенс в этом алгоритме, не зависит от количества экстремальных точек в деформированном изображении На самом деле нам, конечно, не нужна собственно величина угла— требуется лишь некоторая монотонная функция от него; поэтому от вычисления арктангенса можно отказаться, заменив его вычислением  Если
Если  имеет гладкую границу, то можно ожидать, что
имеет гладкую границу, то можно ожидать, что  содержит порядка
содержит порядка  экстремальных точек (см. примечания), и потому можно рассчитывать на то, что потребуется вычислить порядка
экстремальных точек (см. примечания), и потому можно рассчитывать на то, что потребуется вычислить порядка  значений. К этой величине следует добавить объем вычислений, необходимых для отыскания наименьшего угла в процессе каждого исполнения шага 2.
значений. К этой величине следует добавить объем вычислений, необходимых для отыскания наименьшего угла в процессе каждого исполнения шага 2.
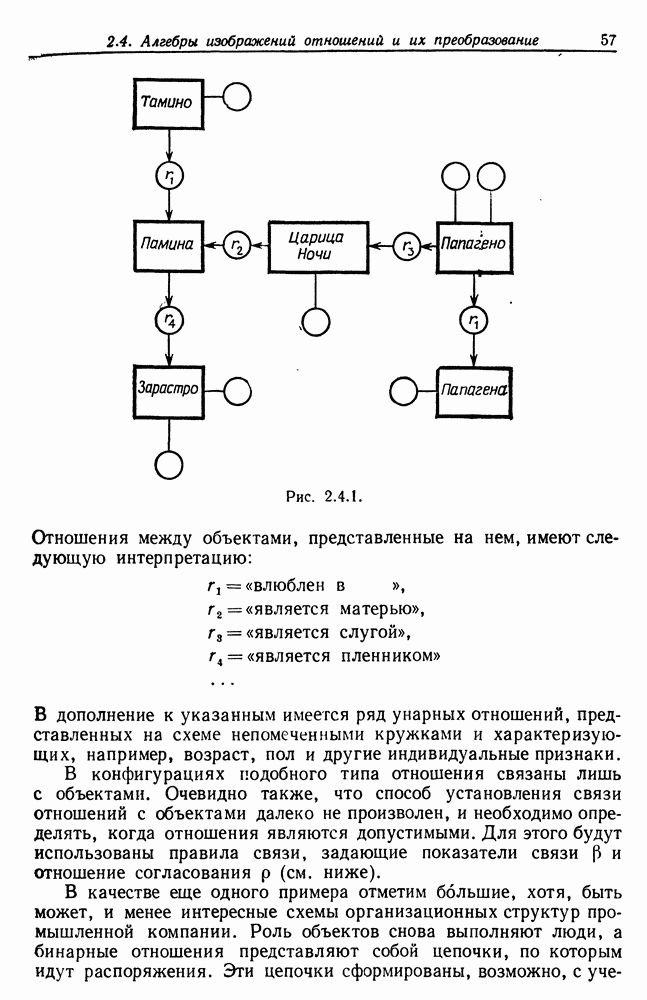
Довольно очевидно, что данный алгоритм слишком неэффективен для использования в случае любых, кроме небольших, значений  . В литературе можно встретить ряд попыток увеличить
. В литературе можно встретить ряд попыток увеличить
скорость за счет лучшей конструкции алгоритма, и мы рассмотрим алгоритм, предложенный Грэхемом (1972).
Шаг 1. В пространстве  отыскиваем некоторую точку Р, принадлежащую внутренности
отыскиваем некоторую точку Р, принадлежащую внутренности  например, путем проверки на коллинеарность трех точек
например, путем проверки на коллинеарность трех точек  вплоть до получения отрицательного результата; далее используем точку, расположенную внутри треугольника, построенного на этих трех точках. Если
вплоть до получения отрицательного результата; далее используем точку, расположенную внутри треугольника, построенного на этих трех точках. Если  — одна из точек
— одна из точек  то эта точка
то эта точка  исключается.
исключается.
Шаг 2. Определяем полярные координаты точек  деформированного изображения
деформированного изображения  относительно точки Р и некоторого фиксированного направления. Для этого необходимо
относительно точки Р и некоторого фиксированного направления. Для этого необходимо  раз вычислить арктангенс (см. замечание по этому поводу, сделанное выше), а также выполнить возведения в квадрат, сложения и извлечения корня, необходимые для определения радиусов.
раз вычислить арктангенс (см. замечание по этому поводу, сделанное выше), а также выполнить возведения в квадрат, сложения и извлечения корня, необходимые для определения радиусов.
Шаг 3. Элементы  упорядочиваем по возрастанию Для этого требуется порядка
упорядочиваем по возрастанию Для этого требуется порядка  операций (см., например, т. 3 монографии Кнута {1973)).
операций (см., например, т. 3 монографии Кнута {1973)).
Шаг 4. Если  удаляем точки
удаляем точки  для которых радиус наименьший.
для которых радиус наименьший.

Рис. 5.2.16.
Шаг 5. См. рис. 5.2.16. Вычисляем угол  причем вначале рассматриваем три последовательные точки:
причем вначале рассматриваем три последовательные точки:
(а) если  то среднюю точку исключаем;
то среднюю точку исключаем;
(б) если а  то возвращаемся к шагу 5, но при этом добавляем следующую точку.
то возвращаемся к шагу 5, но при этом добавляем следующую точку.
На шаге 5 мы либо уменьшаем временно множество точек, входящих в  на единицу, либо увеличиваем на единицу
на единицу, либо увеличиваем на единицу
общее число точек, которые в данный момент служат объектом анализа. Итак, алгоритм закончит работу самое большее за  итераций.
итераций.
Для оценки качества работы этого алгоритма необходимо знать время работы центрального процессора  потребное для выполнения операций алгоритма, например, соотношение числа арифметических операций и сравнений. Чему бы ни было равно это соотношение, при очень больших значениях
потребное для выполнения операций алгоритма, например, соотношение числа арифметических операций и сравнений. Чему бы ни было равно это соотношение, при очень больших значениях  основная составляющая общей потребности в машинном времени будет пропорциональна
основная составляющая общей потребности в машинном времени будет пропорциональна  Следовательно, этот алгоритм работает лучше, чем «наивный», и позволяет определять
Следовательно, этот алгоритм работает лучше, чем «наивный», и позволяет определять  даже при очень больших значениях
даже при очень больших значениях 
Однако скорость вычислений — это только одна из сторон проблемы. Необходимо оценить также скорость сходимости в (5.2.2), что существенно сложнее. Известно два результата: один из них относится к другой - к  . Их доказательство требует довольно подробного анализа, такого, который, вероятно, в будущем часто будет применяться в статистической геометрии.
. Их доказательство требует довольно подробного анализа, такого, который, вероятно, в будущем часто будет применяться в статистической геометрии.
Первый и весьма элегантный результат принадлежит Реньи и Сьюланке (1964); заключается он в следующем.
Теорема 5.2.1. Пусть I — ограниченное выпуклое множество, граница которого имеет достаточное число производных с положительной кривизной  где
где  -длина дуги. Тогда
-длина дуги. Тогда

где  определено в (5.2.33).
определено в (5.2.33).
Доказательство. Пусть  , если
, если  и
и  принадлежит границе
принадлежит границе  и пусть
и пусть  Тогда, если
Тогда, если  расстояние от начала координат, выбранного, скажем, внутри
расстояние от начала координат, выбранного, скажем, внутри  то можно записать, что
то можно записать, что

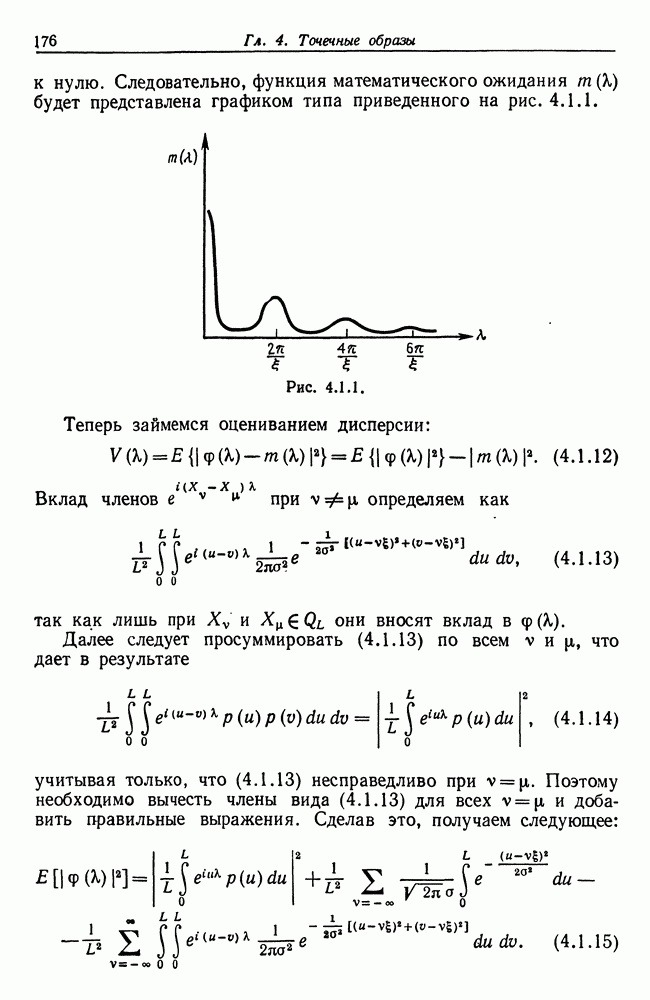
Взяв математическое ожидание от этой величины, получаем следующее:

где  мера Лебега. Интегрирование (5.2.5) по
мера Лебега. Интегрирование (5.2.5) по 
приводит к


Рис. 5.2.2 а.
где  наименьшая площадь, отсекаемая от
наименьшая площадь, отсекаемая от  (см. рис. 5.2.2а). Естественно,
(см. рис. 5.2.2а). Естественно,  и потому вторым членом подынтегрального выражения можно пренебречь. Следовательно,
и потому вторым членом подынтегрального выражения можно пренебречь. Следовательно,

Для того чтобы преобразовать это выражение, обратимся к одному классическому результату из интегральной геометрии (см. Бляшке (1949) с. 16):

где  — расстояние от прямой
— расстояние от прямой  до начала координат,
до начала координат,  — угол, образуемый этой прямой с некоторым фиксированным направлением, и
— угол, образуемый этой прямой с некоторым фиксированным направлением, и  — параметры точек и
— параметры точек и  этой прямой. Но
этой прямой. Но

где  - длина хорды, образованной пересечением
- длина хорды, образованной пересечением  с Подставляя в (5.2.7) выражения (5.2.8) и (5.2.9), получаем
с Подставляя в (5.2.7) выражения (5.2.8) и (5.2.9), получаем

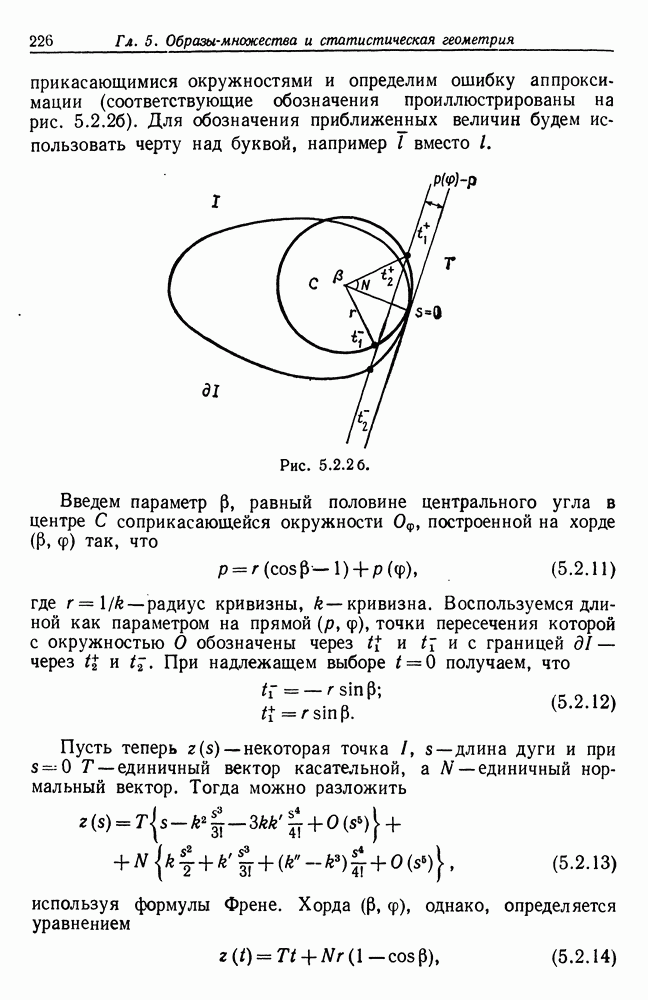
Основной вклад в правую часть выражения (5.2.10) определяется, несомненно, той частью области интегрирования, где  мала. Для определения этого вклада аппроксимируем
мала. Для определения этого вклада аппроксимируем  ее
ее
соприкасающимися окружностями и определим ошибку аппроксимации (соответствующие обозначения проиллюстрированы на рис. 5.2.26). Для обозначения приближенных величин будем использовать черту над буквой, например I вместо  .
.

Рис. 5.2.2 б.
Введем параметр  равный половине центрального угла в центре С соприкасающейся окружности
равный половине центрального угла в центре С соприкасающейся окружности  построенной на хорде
построенной на хорде  так, что
так, что

где  — радиус кривизны,
— радиус кривизны,  - кривизна. Воспользуемся длиной как параметром на прямой
- кривизна. Воспользуемся длиной как параметром на прямой  точки пересечения которой с окружностью О обозначены через
точки пересечения которой с окружностью О обозначены через  и с границей
и с границей  через
через  . При надлежащем выборе
. При надлежащем выборе  получаем, что
получаем, что

Пусть теперь  некоторая точка
некоторая точка  - длина дуги и при
- длина дуги и при  единичный вектор касательной,
единичный вектор касательной,  единичный нормальный вектор. Тогда можно разложить
единичный нормальный вектор. Тогда можно разложить

используя формулы Френе. Хорда  однако, определяется уравнением
однако, определяется уравнением

откуда следует, что

Из второго уравнения следует, что

а первое тогда превращается в следующее:

где  Учитывая этот результат и разлагая синусоидальную функцию в (5.2.12), получаем
Учитывая этот результат и разлагая синусоидальную функцию в (5.2.12), получаем

Если  как это имеет место на нашем рисунке, то соприкасающаяся окружность
как это имеет место на нашем рисунке, то соприкасающаяся окружность  пересекает
пересекает  и, следовательно,
и, следовательно,

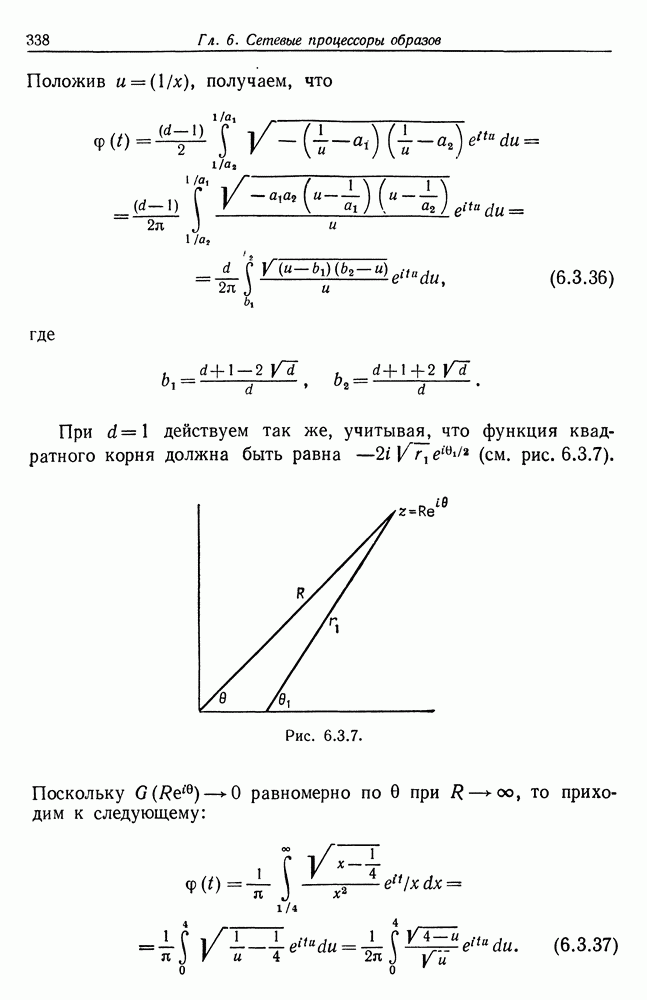
Если же  то уравнение (5.2.19) справедливо тем более, поскольку порядок касания равен трем или большей величине. И наконец, ошибка аппроксимации площадей равна
то уравнение (5.2.19) справедливо тем более, поскольку порядок касания равен трем или большей величине. И наконец, ошибка аппроксимации площадей равна

и теперь можно вернуться к уравнению (5.2.10). При этом мы будем отталкиваться от центрального угла  так что
так что

Кроме того,

В сочетании с (5.2.19) это приводит к следующему:

и аналогично

При этом интеграл (5.2.7) принимает вид

Теперь нам нужен интеграл

Подставим

и воспользуемся тем, что

где  Следовательно,
Следовательно,

причем интегрирование ведется в диапазоне от нуля до  Если же мы, однако, будем интегрировать вплоть до
Если же мы, однако, будем интегрировать вплоть до  то возникает ошибка экспоненциального порядка, которой можно пренебречь. Итак,
то возникает ошибка экспоненциального порядка, которой можно пренебречь. Итак,

Подставляя (5.2.30) в (5.2.25), получаем, наконец, что

где

При этом

Выражая последнее соотношение через производные по  (они обозначены точками), получаем
(они обозначены точками), получаем

или, дважды интегрируя по частям и используя соотношение  (см. т. 1, с. 156) получаем
(см. т. 1, с. 156) получаем

На этом доказательство теоремы заканчивается.
Второй результат, относящийся к скорости сходимости  при
при  связан с применением Выбор из ряда полуплоскостей именно тех, пересечение которых образует
связан с применением Выбор из ряда полуплоскостей именно тех, пересечение которых образует  производится следующим образом. Вдоль границы
производится следующим образом. Вдоль границы  случайным образом выбираем
случайным образом выбираем  точек с равномерным распределением относительно длины дуги. Пересечение соответствующих опорных полуплоскостей
точек с равномерным распределением относительно длины дуги. Пересечение соответствующих опорных полуплоскостей  в этих точках и составит
в этих точках и составит
Чтобы получить  восстановленное по принципу максимального правдоподобия, отметим, что увеличить правдоподобие можно не только как плотность распределения, но и как дискретную вероятность, допустив касание
восстановленное по принципу максимального правдоподобия, отметим, что увеличить правдоподобие можно не только как плотность распределения, но и как дискретную вероятность, допустив касание  со всеми полуплоскостями вдоль
со всеми полуплоскостями вдоль  сегментов положительной длины, скажем
сегментов положительной длины, скажем  Естественно, здесь где
Естественно, здесь где  длина границы
длина границы  Тогда правдоподобие будет пропорционально произведению
Тогда правдоподобие будет пропорционально произведению  и его можно максимизировать, выбирая
и его можно максимизировать, выбирая  для всех
для всех  что эквивалентно выбору
что эквивалентно выбору 
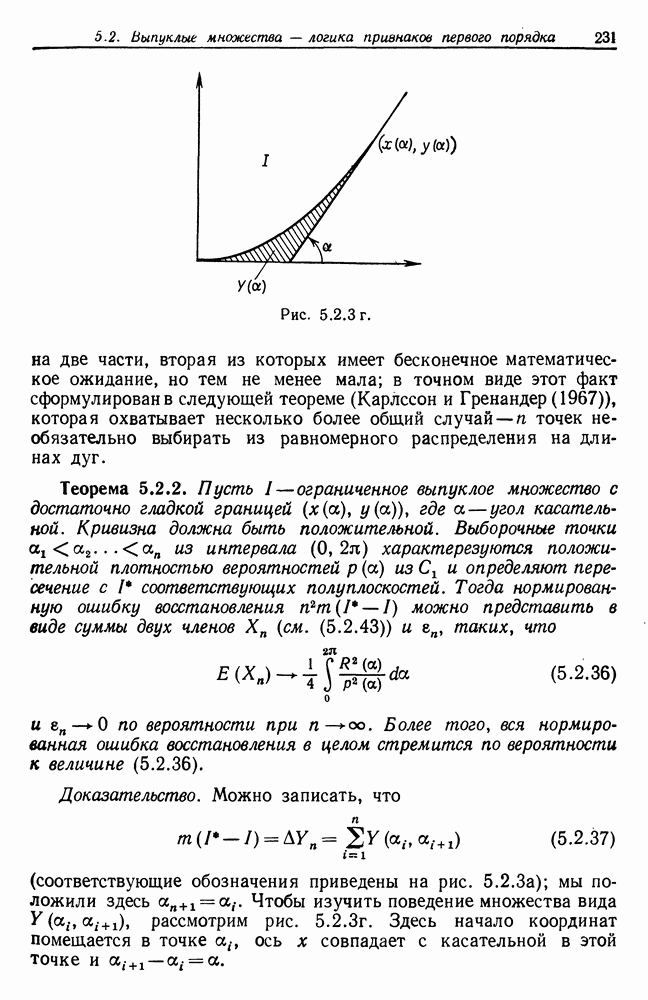
Теперь возникает одна дополнительная трудность, заключающаяся в том, что, строго говоря, величина  не имеет конечного математического ожидания. Напомним, что
не имеет конечного математического ожидания. Напомним, что  для
для  и что
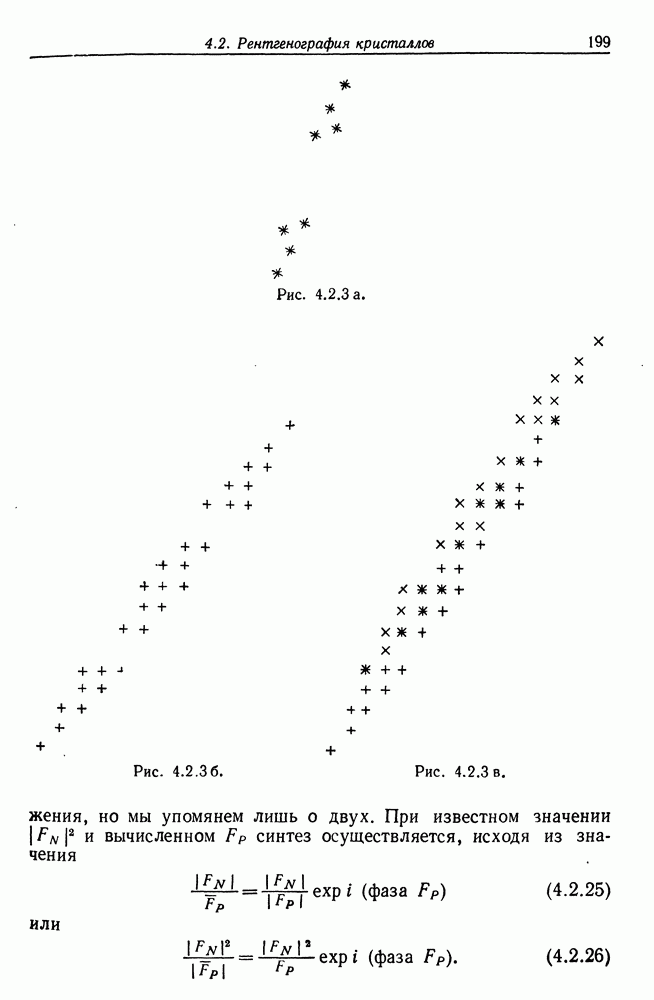
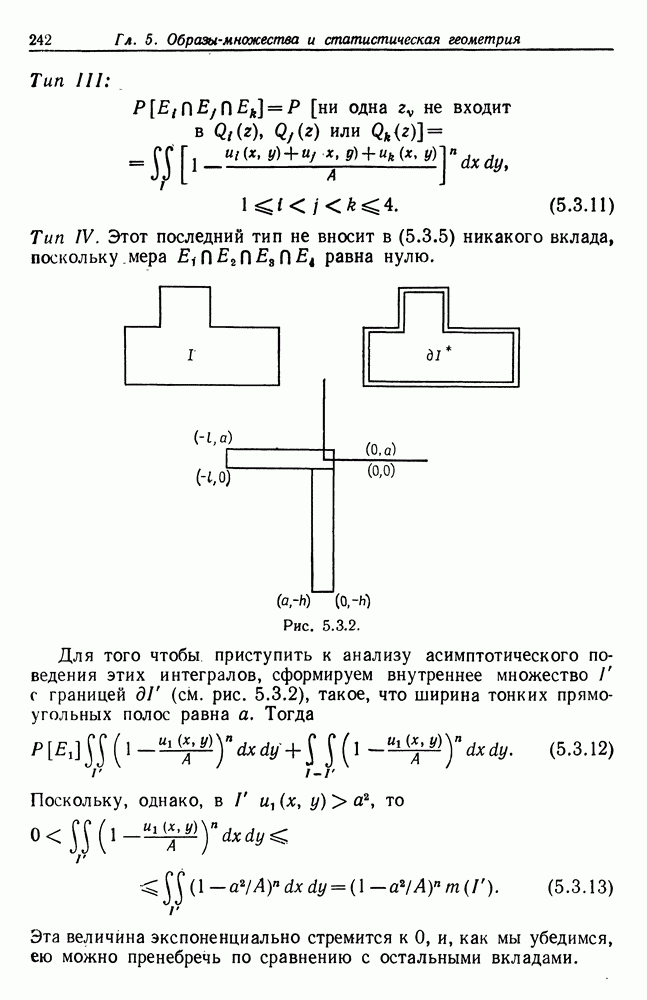
и что  может не быть ограниченной, как это показано на рис. 5.2.3в. Это происходит с вероятностью, стремящейся к нулю при больших
может не быть ограниченной, как это показано на рис. 5.2.3в. Это происходит с вероятностью, стремящейся к нулю при больших  но при всех конечных значениях
но при всех конечных значениях  эта вероятность положительна и, следовательно,
эта вероятность положительна и, следовательно,  Для того чтобы преодолеть это затруднение, величину
Для того чтобы преодолеть это затруднение, величину  разбиваем
разбиваем

(кликните для просмотра скана)

Рис. 5.2.3 г
на две части, вторая из которых имеет бесконечное математическое ожидание, но тем не менее мала; в точном виде этот факт сформулирован в следующей теореме (Карлссон и Гренандер (1967)), которая охватывает несколько более общий случай —  точек необязательно выбирать из равномерного распределения на длинах дуг.
точек необязательно выбирать из равномерного распределения на длинах дуг.
Теорема 5.2.2. Пусть I — ограниченное выпуклое множество с достаточно гладкой границей  где
где  -угол касательной. Кривизна должна быть положительной. Выборочные точки
-угол касательной. Кривизна должна быть положительной. Выборочные точки  из интервала
из интервала  характерезуются положительной плотностью вероятностей
характерезуются положительной плотностью вероятностей  из
из  и определяют пересечение с
и определяют пересечение с  соответствующих полуплоскостей. Тогда нормированную ошибку восстановления
соответствующих полуплоскостей. Тогда нормированную ошибку восстановления  можно представить в виде суммы двух членов
можно представить в виде суммы двух членов  (см. (5.2.43)) и еи, таких, что
(см. (5.2.43)) и еи, таких, что

и  по вероятности при
по вероятности при  Более того, вся нормированная ошибка восстановления в целом стремится по вероятности к величине (5.2.36).
Более того, вся нормированная ошибка восстановления в целом стремится по вероятности к величине (5.2.36).
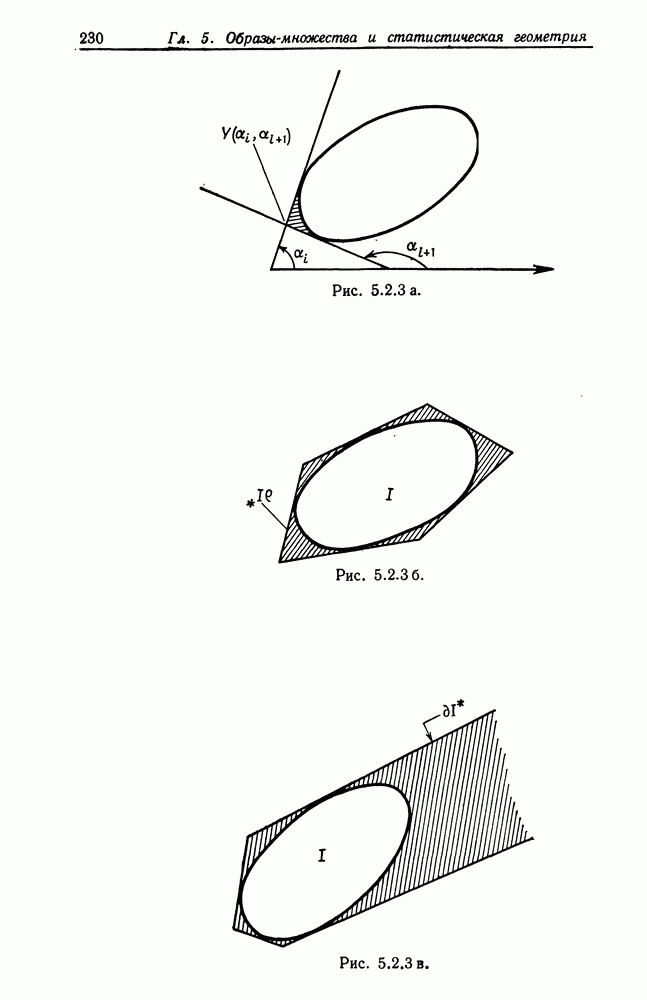
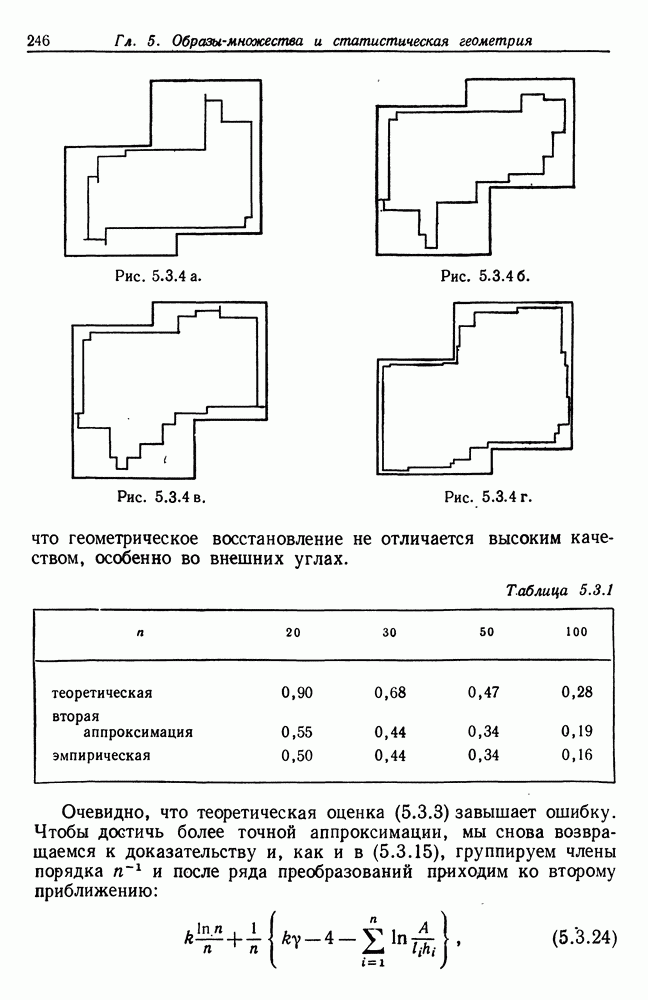
Доказательство. Можно записать, что

(соответствующие обозначения приведены на рис. 5.2.3а); мы положили здесь  Чтобы изучить поведение множества вида
Чтобы изучить поведение множества вида  рассмотрим рис. 5.2.3г. Здесь начало координат помещается в точке
рассмотрим рис. 5.2.3г. Здесь начало координат помещается в точке  ось
ось  совпадает с касательной в этой точке и
совпадает с касательной в этой точке и 
Рассмотрим площадь области  , расположенной под кривой
, расположенной под кривой  и обозначим радиус кривизны при
и обозначим радиус кривизны при  через
через  соответствует углу
соответствует углу  . В результате с помощью элементарных вычислений получаем, что
. В результате с помощью элементарных вычислений получаем, что

и, следовательно,

Далее, объединив (5.2.38) и (5.2.39), можно при малых а получить следующее разложение:

Отсюда следует, что

где

Покажем, что второй член  в (5.2.41) является асимптотически пренебрежимо малым. Введем
в (5.2.41) является асимптотически пренебрежимо малым. Введем

и, обратив внимание на то, что верхний предел суммирования равен  а не
а не  вычислим математическое ожидание этой величины. Для нашей упорядоченной выборки значений а приходим к обычному выражению для порядковых статистик
вычислим математическое ожидание этой величины. Для нашей упорядоченной выборки значений а приходим к обычному выражению для порядковых статистик

где интегрирование ведется в диапазоне  функция распределения, соответствующая плотности распределения р.
функция распределения, соответствующая плотности распределения р.
Воспользуемся подстановкой

которая является взаимно однозначной, поскольку функция распределения Р — строго возрастающая. Тогда имеем

где  это обратная функция
это обратная функция  Объединим последнее выражение с (5.2.43):
Объединим последнее выражение с (5.2.43):

Воспользуемся подстановкой

так что

здесь интегрирование ведется по области  . Разложим функцию
. Разложим функцию  в ряд Тейлора в окрестности
в ряд Тейлора в окрестности  Но так как
Но так как

ограниченны и непрерывны, то

откуда следует, что

Проинтегрируем выражение (5.2.52) сначала по 

Но поскольку 1

а  ограничено постоянными значениями времени, то
ограничено постоянными значениями времени, то

Проинтегрируем теперь выражение (5.2.52) по и. В результате получаем

и

Следовательно,

или, сделав обратные замены переменных,

Остается рассмотреть член

так как, определяя  с помощью (5.2.43), мы его не учитывали. Это не вызывает затруднений, поскольку
с помощью (5.2.43), мы его не учитывали. Это не вызывает затруднений, поскольку

где интегрирование ведется по  можно воспользоваться подстановкой
можно воспользоваться подстановкой

что приводит к следующему:

Выражение (5.2.62) можно мажорировать постоянными значениями времени:

Вид последнего выражения аналогичен (5.2.56), и, следовательно,  . На этом заканчивается первая часть доказательства:
. На этом заканчивается первая часть доказательства:

На следующем шаге предстоит усилить утверждение (5.2.64), показав, что не только математическое ожидание  но и сама величина стремится по вероятности к этому пределу. Чтобы сделать это, допустим, что
но и сама величина стремится по вероятности к этому пределу. Чтобы сделать это, допустим, что  малый интервал в интервале
малый интервал в интервале  , и рассмотрим выражение
, и рассмотрим выражение

где суммирование ведется по  или выражение
или выражение

где  Если разность
Если разность  достаточно мала и
достаточно мала и  достаточно велика, то при любом
достаточно велика, то при любом  величину
величину  можно заключить между двумя предельными значениями:
можно заключить между двумя предельными значениями:

Используя традиционное представление упорядоченной равномерной выборки в виде

где  тождественно независимо распределенные наблюдения, подчиняющиеся экспоненциальному распределению, можно записать следующее:
тождественно независимо распределенные наблюдения, подчиняющиеся экспоненциальному распределению, можно записать следующее:

где  индикаторная функция для интервала
индикаторная функция для интервала  Если
Если  достаточно велико, то выражение (5.2.69) с вероятностью, близкой единице, мажорируется сверху следующим выражением:
достаточно велико, то выражение (5.2.69) с вероятностью, близкой единице, мажорируется сверху следующим выражением:

здесь суммирование проводится в диапазоне от  до
до  снизу же оно ограничено выражением
снизу же оно ограничено выражением

здесь суммирование проводится в диапазоне от  до
до  Но
Но

по вероятности, так как  Кроме того,
Кроме того,  по вероятности, так что при
по вероятности, так что при 

по вероятности, откуда следует, что

по вероятности.
Третья, последняя часть доказательства должна показать, что величина  стремится к нулю по вероятности (см. уравнение (5.2.41)). Введем множество
стремится к нулю по вероятности (см. уравнение (5.2.41)). Введем множество

так что искомую вероятность можно представить как

где

Чтобы определить границы для входящих в (5.2.76) членов, прибегнем снова временно к равномерному распределению, обозначив  через
через  помощью порядковых статистик
помощью порядковых статистик  отождествляющих
отождествляющих  по модулю единица, и введем событие А, связанное с (5.2.75):
по модулю единица, и введем событие А, связанное с (5.2.75):

где  — положительная постоянная, и событие В:
— положительная постоянная, и событие В:

Известно (см., например, Уилкс (1962), с. 334), что все случайные величины  имеют плотность распределения вероятностей
имеют плотность распределения вероятностей  так что при
так что при 

Это приводит к следующему неравенству:

Здесь мы воспользовались тем обстоятельством, что  — обладают, как указывалось выше, одной и той же плотностью распределения вероятностей.
— обладают, как указывалось выше, одной и той же плотностью распределения вероятностей.
Используя (5.2.81), получаем, что

если  если
если  Для больших
Для больших  имеем
имеем

Из неравенства (5.2.81), однако, следует, что  для некоторых
для некоторых

и так как  то очевидно, что
то очевидно, что  .
.
Вернемся теперь к случаю, когда мы имели плотность распределения  и, как и выше, воспользуемся соотношением
и, как и выше, воспользуемся соотношением  Тогда
Тогда

где  Поскольку плотность
Поскольку плотность  положительна и непрерывна, то очевидно, что при некотором
положительна и непрерывна, то очевидно, что при некотором  справедливо
справедливо

и

Последнее неравенство с учетом полученных выше результатов приводит к тому, что

а для достаточно больших 

что стремится к 1.
Выбирая

на основе (5.2.88) и (5.2.89) получаем, что

и

Подстановка этих результатов в выражение (5.2.76) показывает, что  стремится по вероятности к нулю при
стремится по вероятности к нулю при  На этом доказательство теоремы 5.2.2 заканчивается.
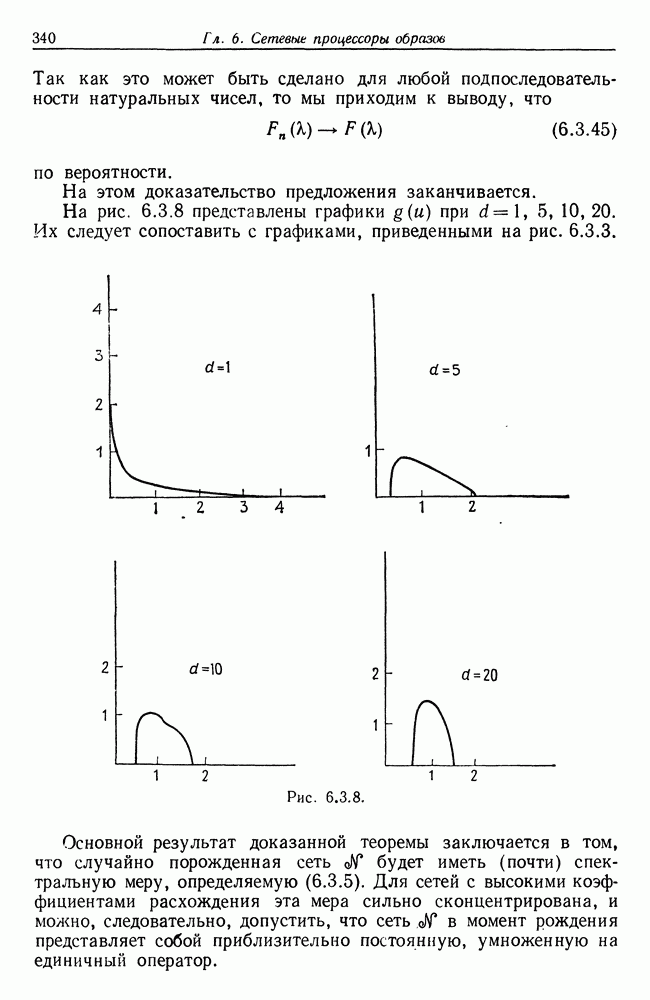
На этом доказательство теоремы 5.2.2 заканчивается.
Замечание. Следует отметить, что в отличие от теоремы 5.2.1 данный результат связан не только со сходимостью математического ожидания нормированной ошибки восстановления: он показывает, что сама нормированная ошибка восстановления сходится по вероятности. По-видимому теорема 5.2.1 не поддается подобному обобщению.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
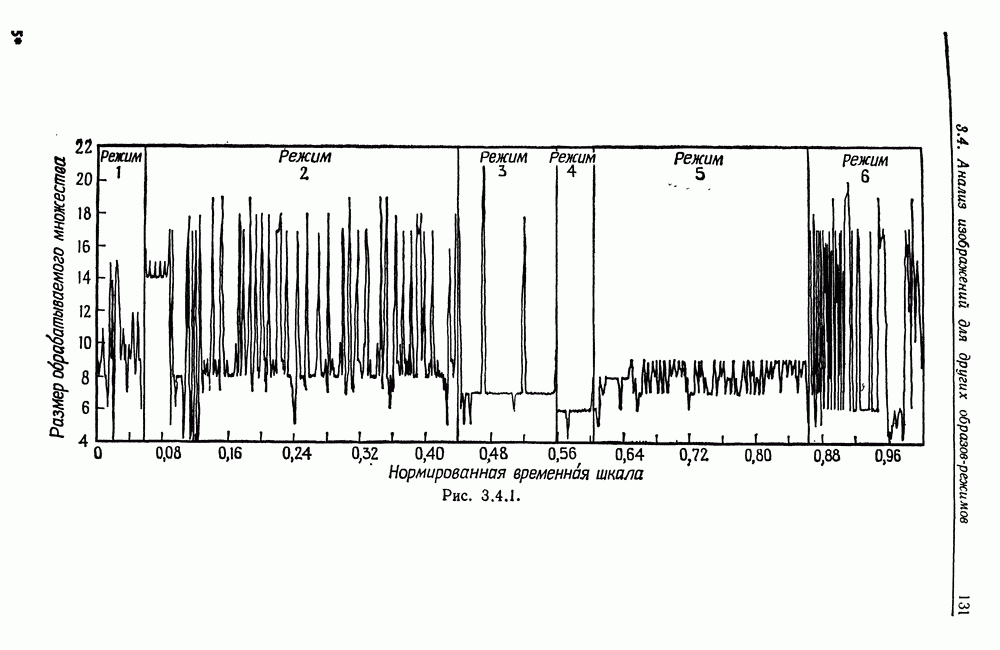
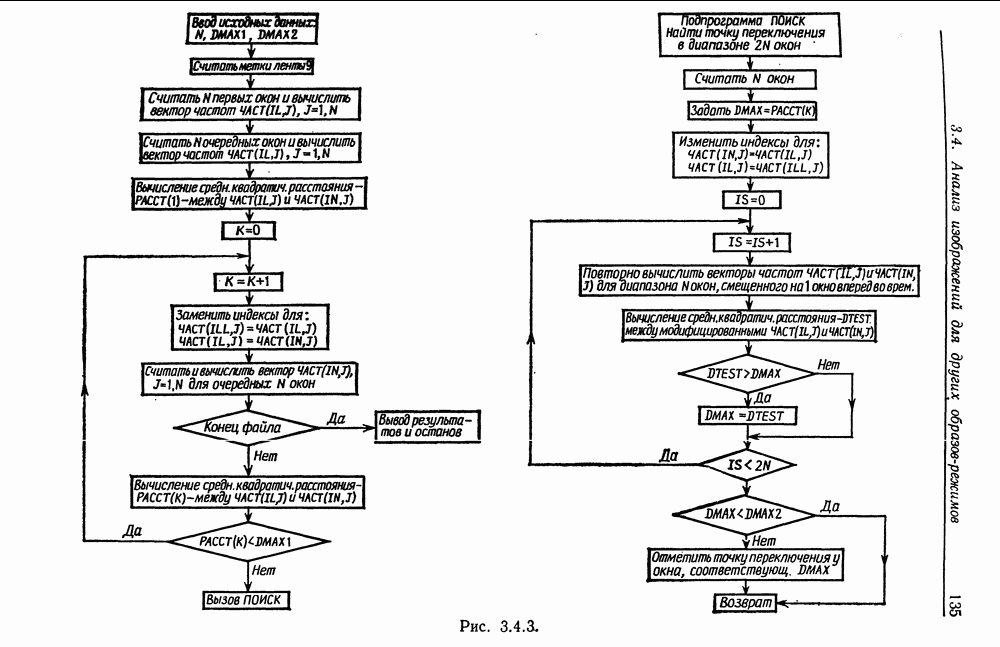
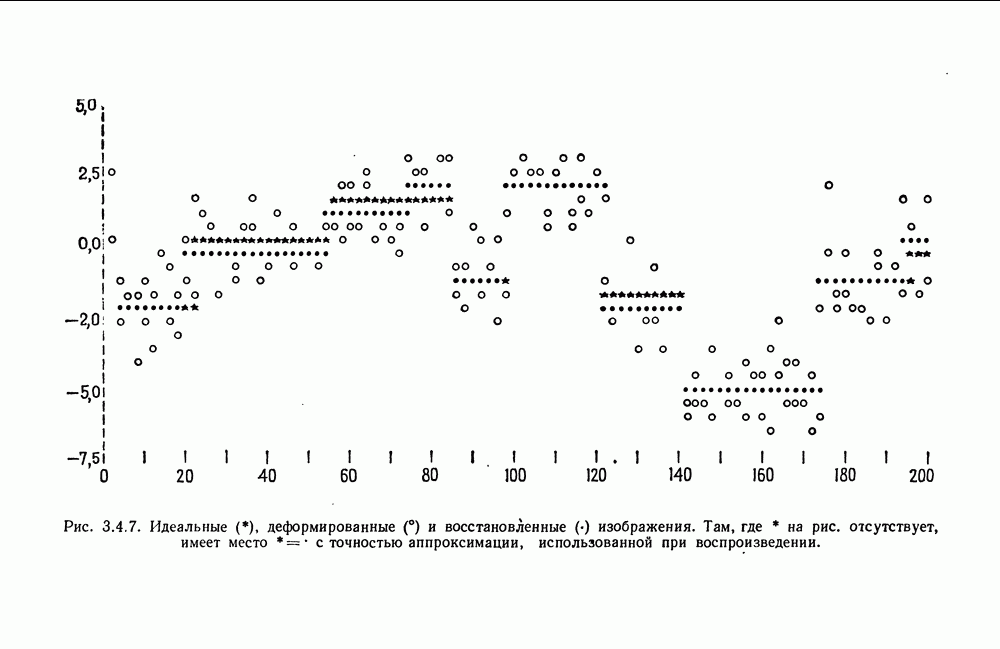
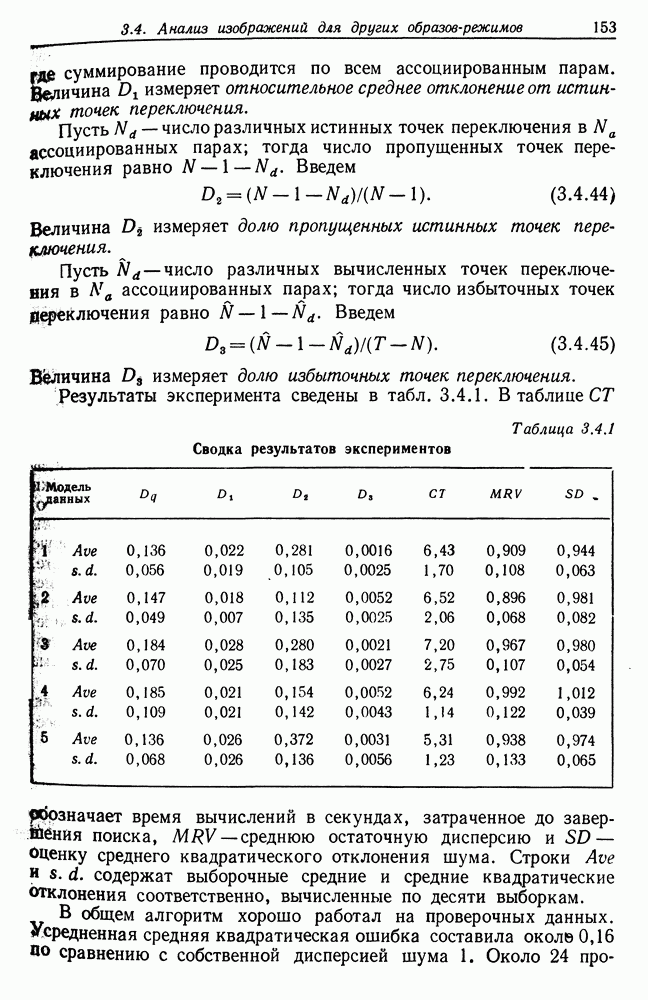
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
- 4.2. Рентгенография кристаллов
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
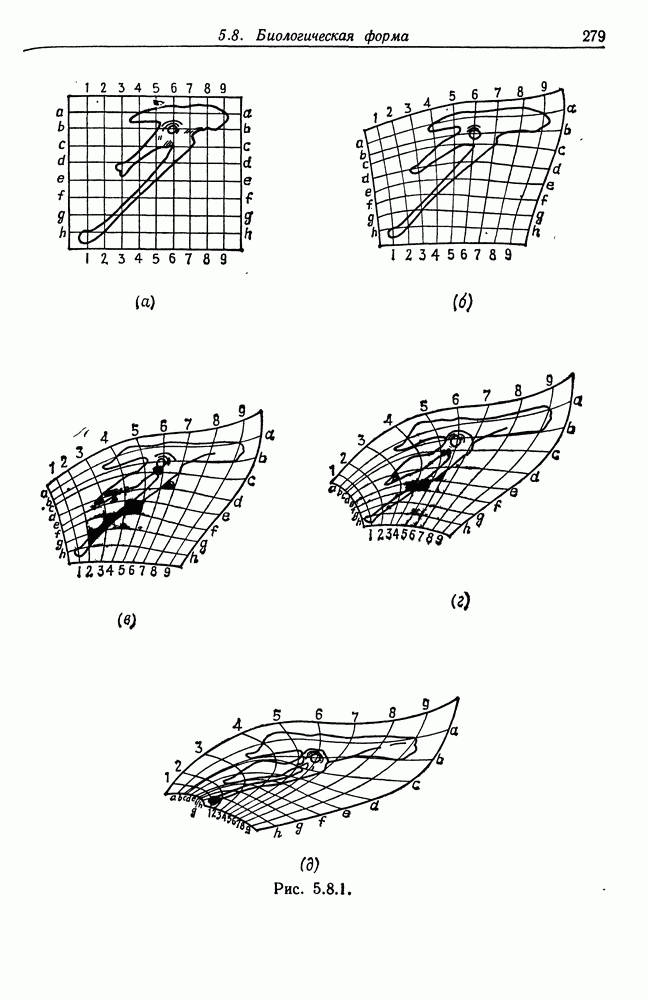
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
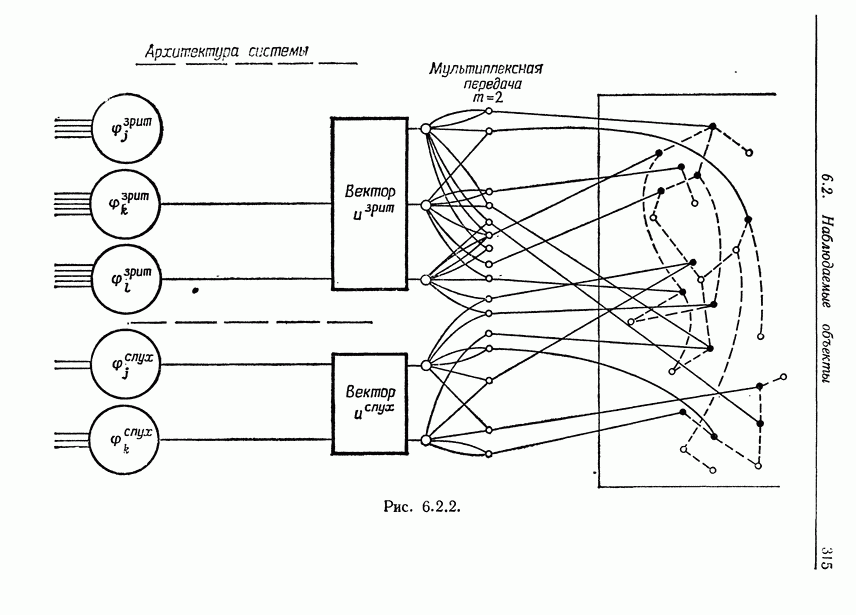
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы