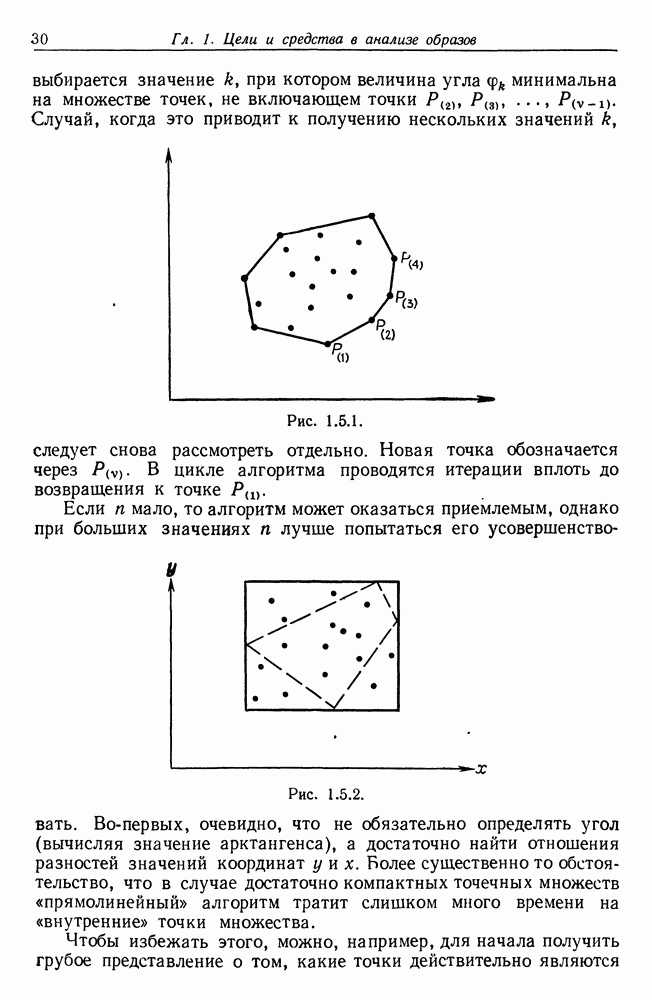
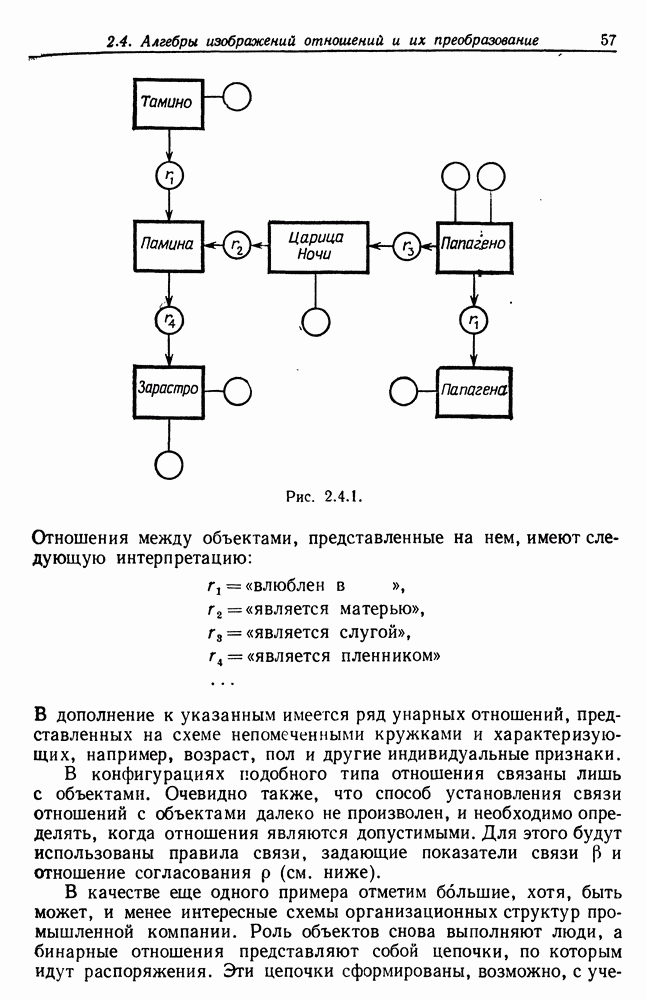
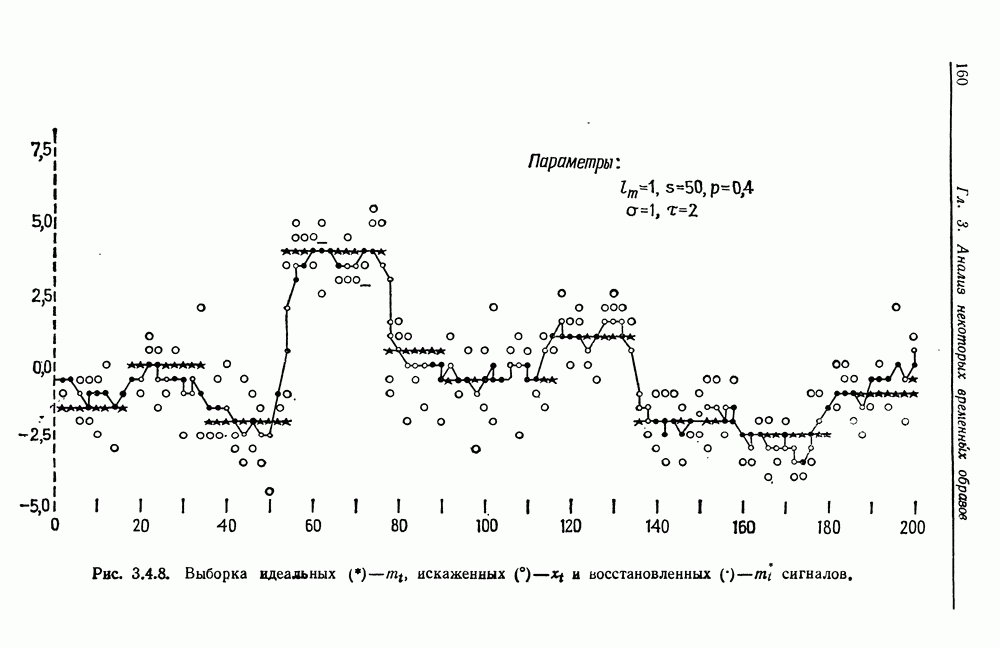
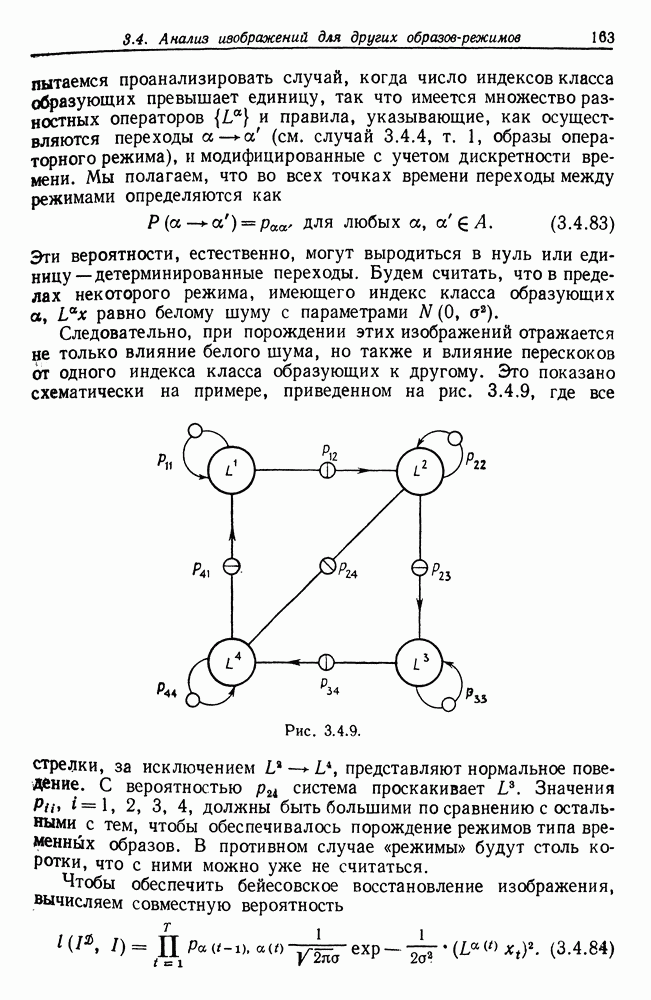
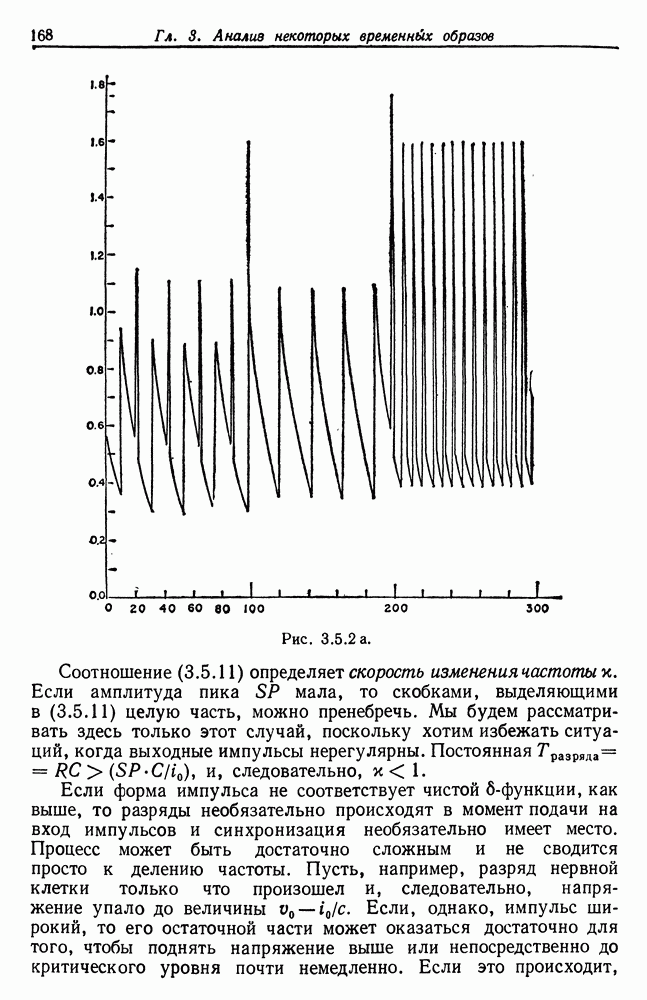
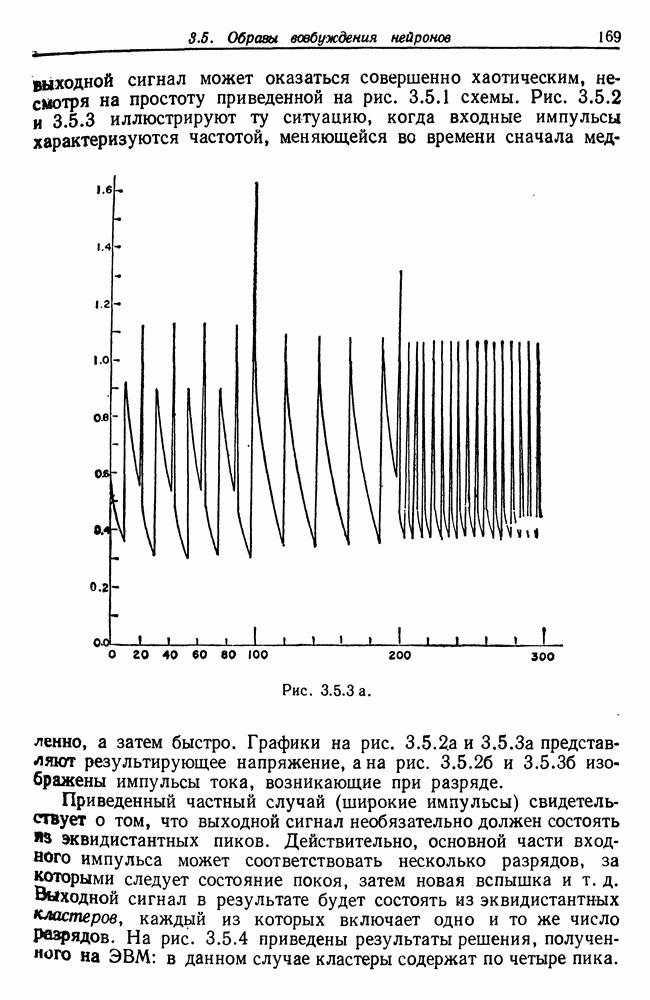
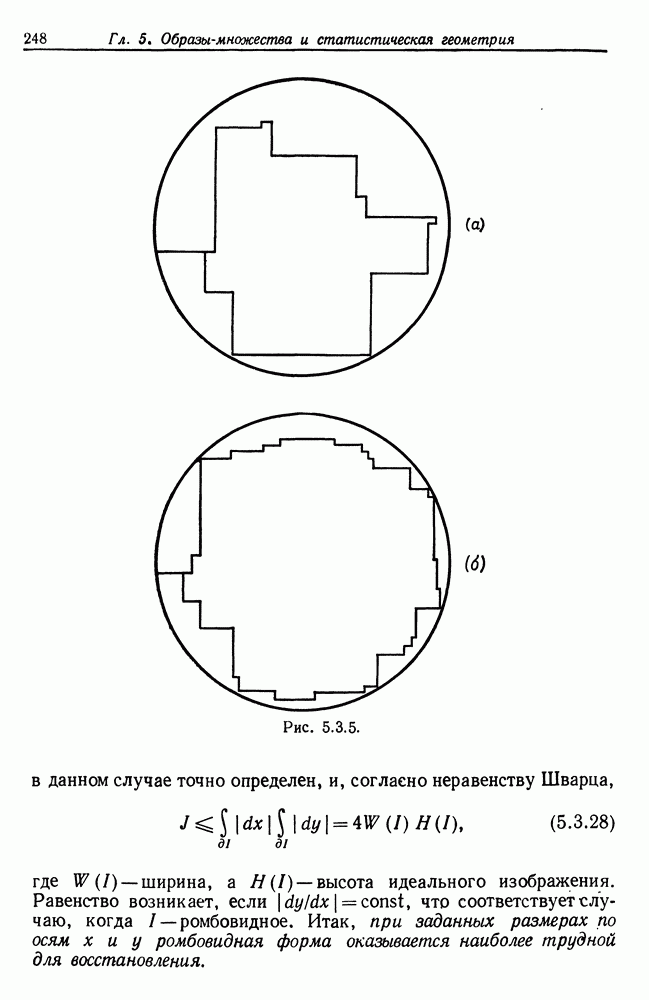
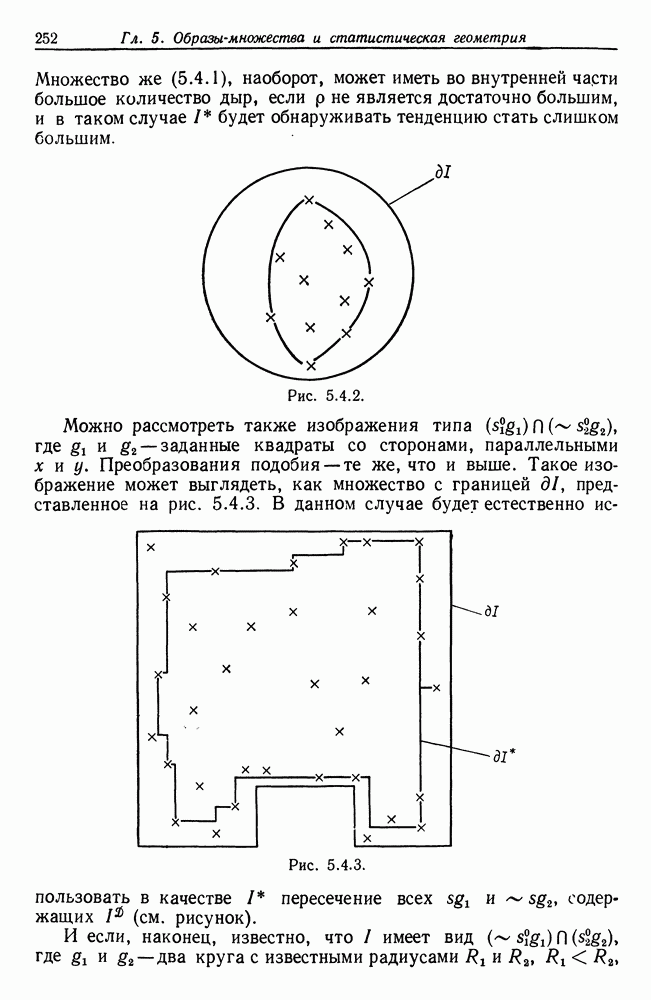
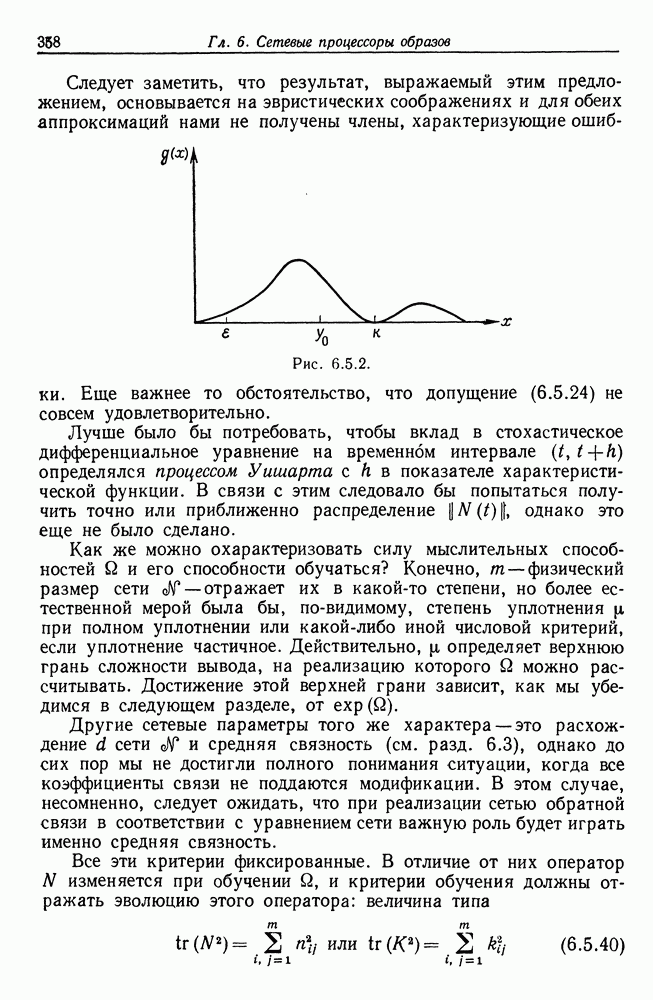
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5. Абстрактные сети и их симметрии
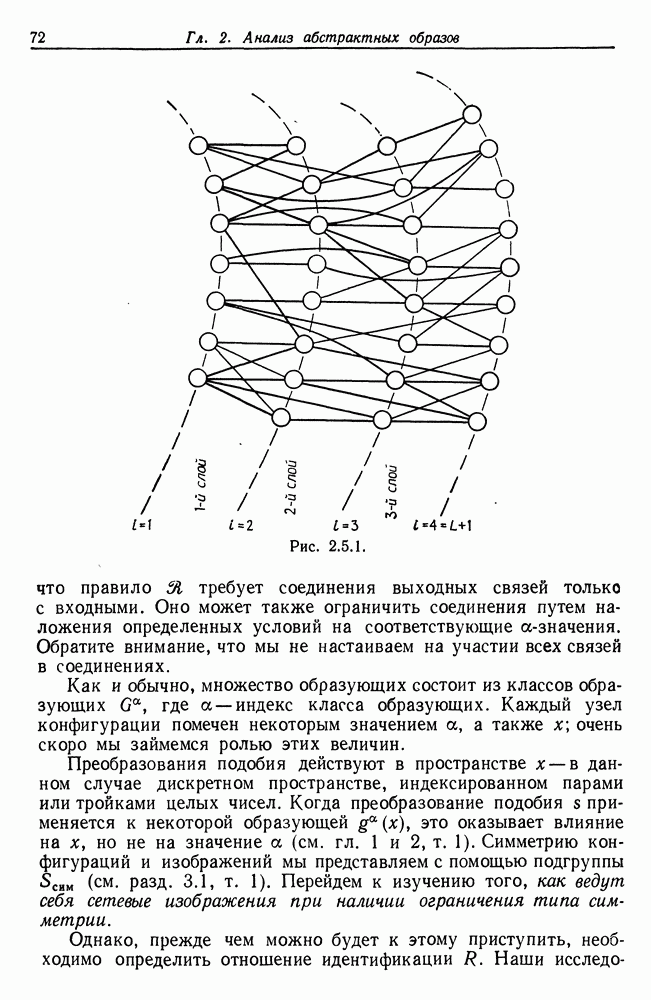
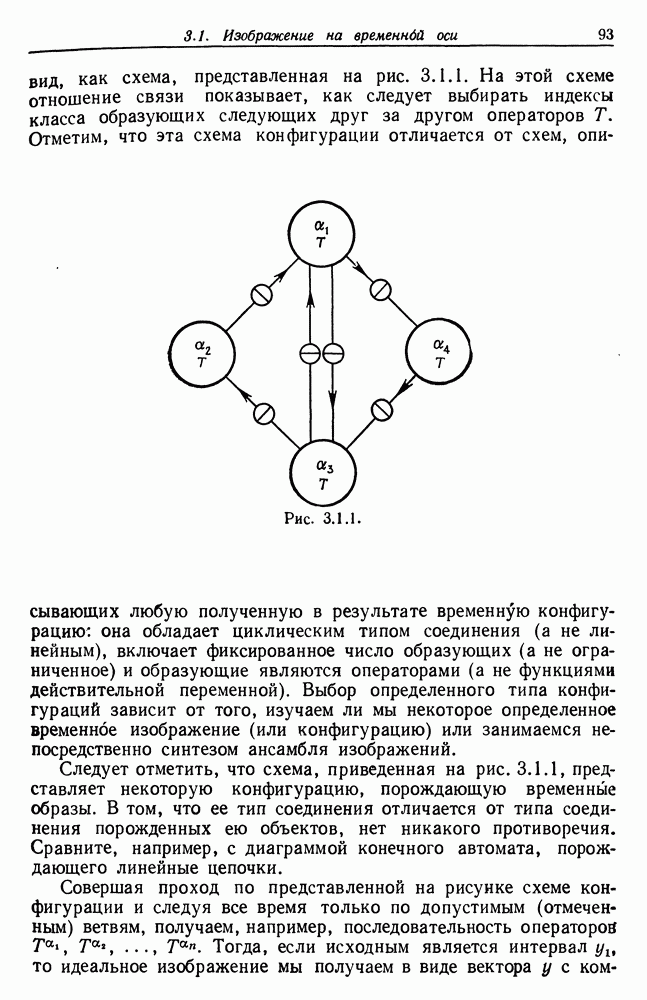
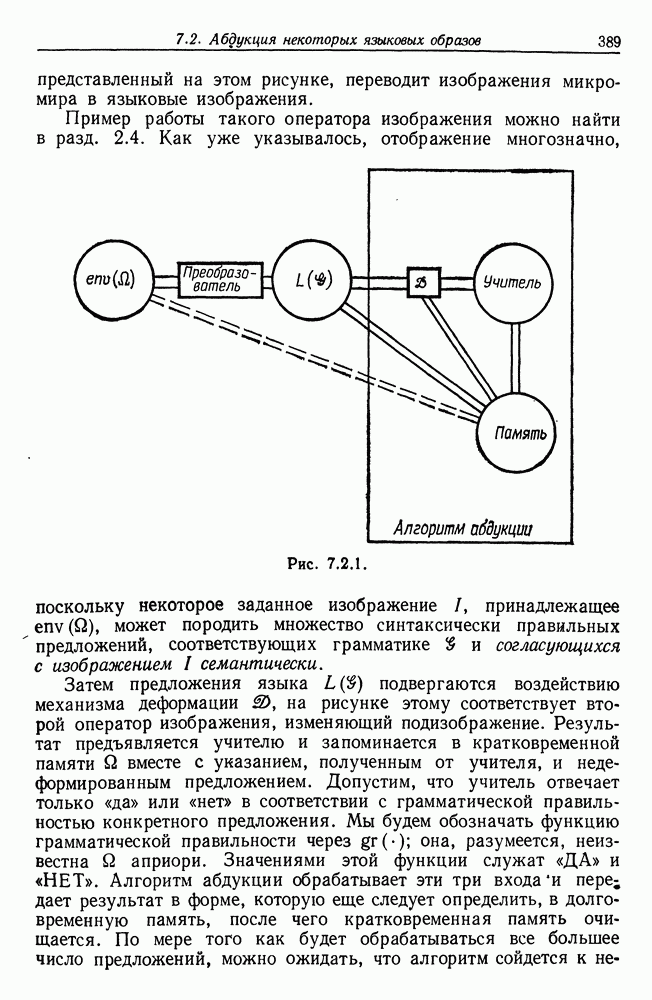
Образы, рассматривавшиеся в разд. 2.2-2.4, были сформированы из абстрактных образующих, объединявшихся при помощи линейного или древовидного типов соединения 2. Теперь мы обратимся к случаю, когда тип соединения 2 имеет слоистую организацию, и нас будут интересовать функциональные свойства конфигурации: мы будем изучать процессоры образов, имеющие регулярные структуры нескольких определенных типов. К этой же проблеме мы вернемся в гл. 6, где регулярность будет иметь лишь статистическую природу. Здесь же предполагается наличие детерминистской и очень жесткой регулярности.
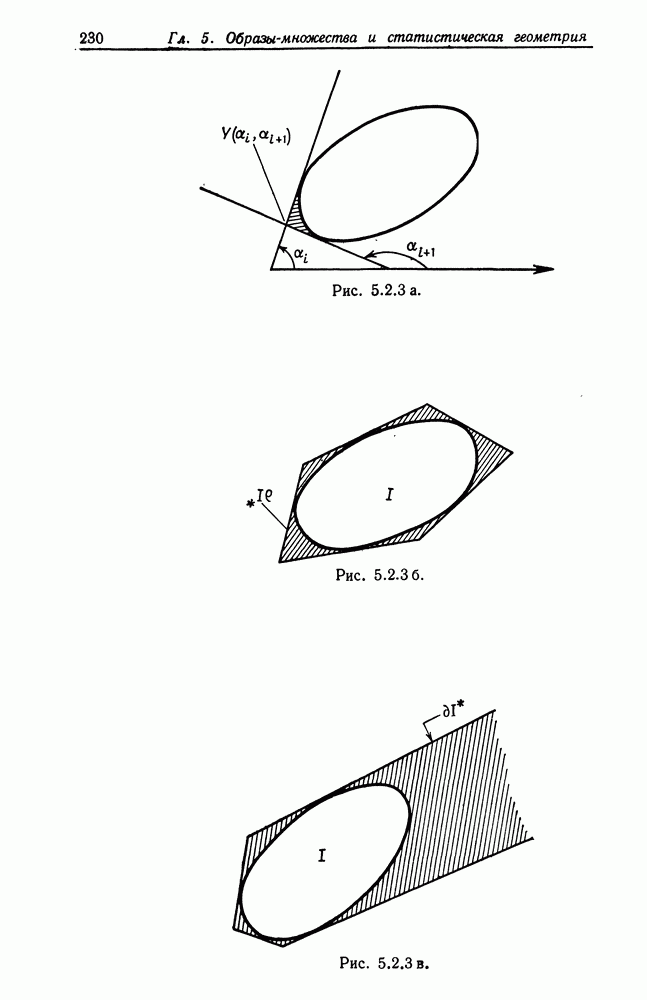
Случай 2.5.1 (слоистый тип соединения). Конфигурация с разделена на подконфигурации  где
где  номер слоя и
номер слоя и  -общее число слоев между образующими. Все выходные связи образующей, которая содержится в
-общее число слоев между образующими. Все выходные связи образующей, которая содержится в  соединены
соединены  входными связями образующих, которые содержатся в
входными связями образующих, которые содержатся в  . У подконфигурации
. У подконфигурации  однако, входные связи не соединены; так же обстоит дело с выходными связями подконфигурации
однако, входные связи не соединены; так же обстоит дело с выходными связями подконфигурации 
Подобная конфигурация может выглядеть, как на рис. 2.5.1, где для удобства чтения связи не показаны. Обработка информации осуществляется на  слоях
слоях  описания множества образующих, входящих в
описания множества образующих, входящих в  требуется какая-нибудь координата; обозначим ее, например, через
требуется какая-нибудь координата; обозначим ее, например, через  так произвольная образующая, принадлежащая с, снабжается индексом
так произвольная образующая, принадлежащая с, снабжается индексом 
Если I — целое число и  одно (двумерные сети) или пара Пхмерные сети) целых чисел, то множество значений
одно (двумерные сети) или пара Пхмерные сети) целых чисел, то множество значений  , естественно, дискретно. Формируя конкретную реализацию некоторой абстрактной сети, мы будем ставить в соответствие образующим двух- или трехмерные векторы и использовать непрерывное опорное пространство. Если мы имеем дело лишь с топологией конфигурации, как в данном разделе, и не обращаем внимание на
, естественно, дискретно. Формируя конкретную реализацию некоторой абстрактной сети, мы будем ставить в соответствие образующим двух- или трехмерные векторы и использовать непрерывное опорное пространство. Если мы имеем дело лишь с топологией конфигурации, как в данном разделе, и не обращаем внимание на  метрические свойства, то адекватным является первый вариант.
метрические свойства, то адекватным является первый вариант.
Чтобы определить допустимую конфигурацию, предположим.

Рис. 2.5.1.
что правило  требует соединения выходных связей только с входными. Оно может также ограничить соединения путем наложения определенных условий на соответствующие
требует соединения выходных связей только с входными. Оно может также ограничить соединения путем наложения определенных условий на соответствующие  -значения. Обратите внимание, что мы не настаиваем на участии всех связей в соединениях.
-значения. Обратите внимание, что мы не настаиваем на участии всех связей в соединениях.
Как и обычно, множество образующих состоит из классов образующих  где а — индекс класса образующих. Каждый узел конфигурации помечен некоторым значением а, а также
где а — индекс класса образующих. Каждый узел конфигурации помечен некоторым значением а, а также  очень скоро мы займемся ролью этих величин.
очень скоро мы займемся ролью этих величин.
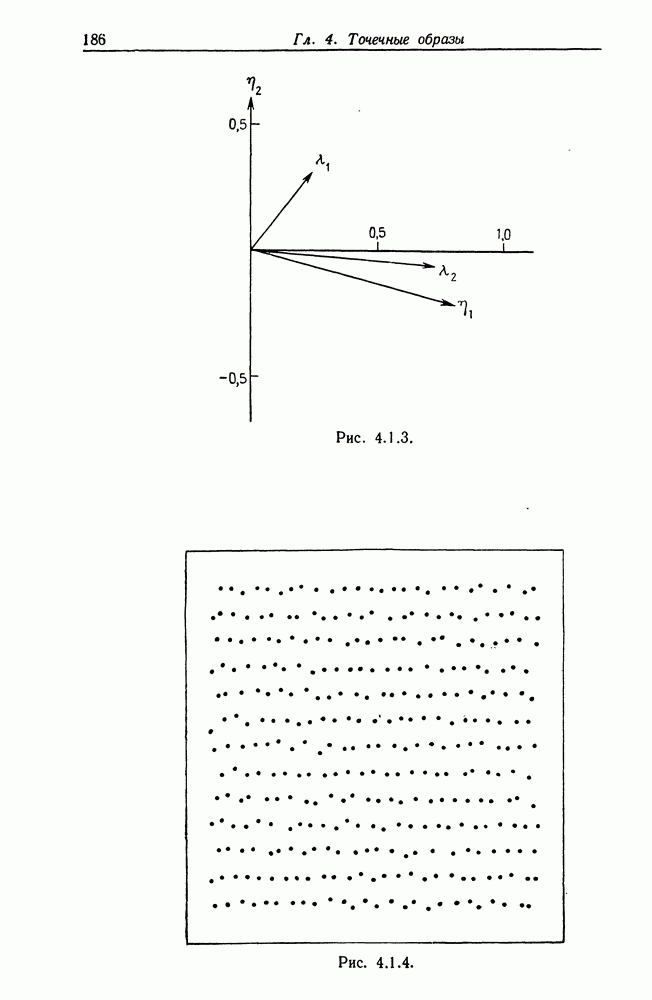
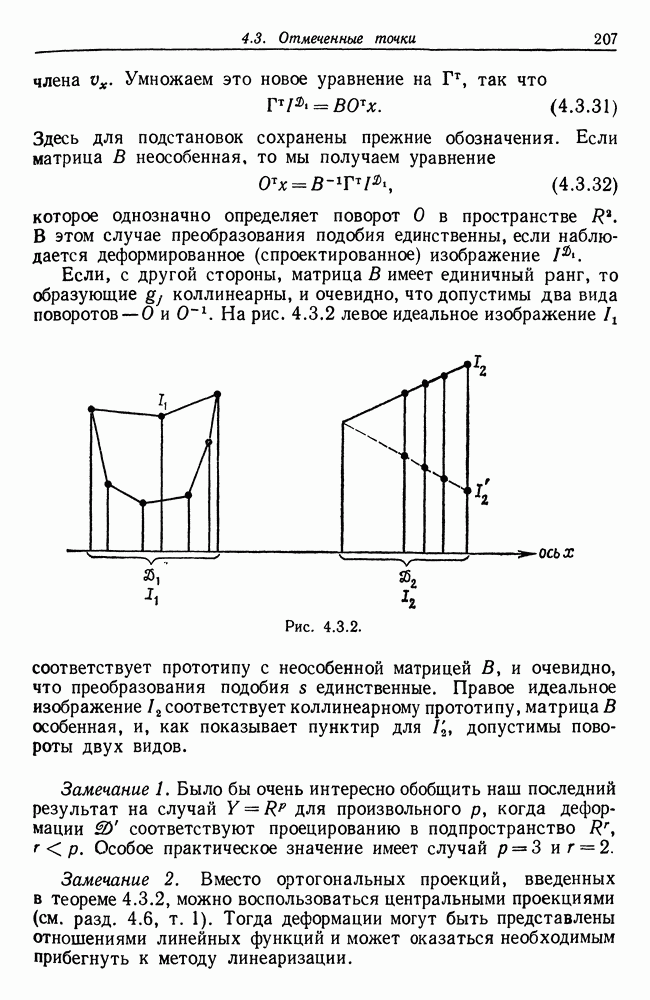
Преобразования подобия действуют в пространстве  в данном случае дискретном пространстве, индексированном парами или тройками целых чисел. Когда преобразование подобия
в данном случае дискретном пространстве, индексированном парами или тройками целых чисел. Когда преобразование подобия  применяется к некоторой образующей
применяется к некоторой образующей  это оказывает влияние на
это оказывает влияние на  но не на значение а (см. гл. 1 и 2, т. 1). Симметрию конфигураций и изображений мы представляем с помощью подгруппы
но не на значение а (см. гл. 1 и 2, т. 1). Симметрию конфигураций и изображений мы представляем с помощью подгруппы  (см. разд. 3.1, т. 1). Перейдем к изучению того, как ведут себя сетевые изображения при наличии ограничения типа симметрии.
(см. разд. 3.1, т. 1). Перейдем к изучению того, как ведут себя сетевые изображения при наличии ограничения типа симметрии.
Однако, прежде чем можно будет к этому приступить, необходимо определить отношение идентификации R. Наши исследования
были стимулированы работами, посвященными изучению формализованных нервных сетей математическими методами. Здесь мы воспользуемся грубой идеализацией, а в гл. 7 обратимся к описаниям, имеющим менее ограниченный характер.
Поведение нейронов описывается как непрерывными, так и дискретными моделями (см., в частности, обсуждение моделей Мак-Каллоха—Питтса в монографии Гриффита (1971, гл. 3)). Их реальное поведение на самом деле, по-видимому, представляет собой гибрид двух этих моделей. Здесь мы будем полагать, что нейрон действует как некоторый линейный оператор, т. е. соответствует непрерывной модели. Точнее, это означает, что образующая  имеющая входную арность
имеющая входную арность  и выходную арность
и выходную арность  может быть представлена матрицей
может быть представлена матрицей  связывающей
связывающей  -мерный входной вектор с
-мерный входной вектор с  -мерным выходным вектором. Обоснование этого допущения будет приведено в разд.
-мерным выходным вектором. Обоснование этого допущения будет приведено в разд. 
Обозначим множество открытых входных связей конфигураций через  и множество открытых выходных связей через
и множество открытых выходных связей через  Мы будем идентифицировать изображение, к которому принадлежит конфигурация, с помощью матрицы, связывающей входной вектор, определенный на
Мы будем идентифицировать изображение, к которому принадлежит конфигурация, с помощью матрицы, связывающей входной вектор, определенный на  с выходным вектором, определенным на
с выходным вектором, определенным на  Входные сигналы на входных связях складываются. Другими словами, входные сигналы у некоторой клетки
Входные сигналы на входных связях складываются. Другими словами, входные сигналы у некоторой клетки  суммируются, и эта сумма характеризует электрохимическую активность клеточного тела. Эта сумма, умноженная на коэффициенты усиления каждого из сочетаний входных и выходных связей, передается в следующий слой клеток.
суммируются, и эта сумма характеризует электрохимическую активность клеточного тела. Эта сумма, умноженная на коэффициенты усиления каждого из сочетаний входных и выходных связей, передается в следующий слой клеток.
В  раздражители вводятся в тела клеток, а в
раздражители вводятся в тела клеток, а в  наблюдается вызванная активность клетки.
наблюдается вызванная активность клетки.
В гл. 6 мы рассмотрим обучение в случае, когда клетка приобретает другие передаточные коэффициенты, соответствующие предыдущему предъявлению, однако в данном разделе мы займемся статическими сетями.
Если у — входной вектор размерности  — выходной вектор размерности
— выходной вектор размерности  то их можно связать соотношением
то их можно связать соотношением

где V — прямоугольная матрица, а все векторы здесь и ниже будут столбцами. Выходная  -энергия в таком случае определяется выражением
-энергия в таком случае определяется выражением

где  квадратная симметрическая и неотрицательно определенная матрица. Она представляет мощностные отношения в сети. Матрица энергии
квадратная симметрическая и неотрицательно определенная матрица. Она представляет мощностные отношения в сети. Матрица энергии  показывает, какую нервную активность
показывает, какую нервную активность  вызывают различные стимулы у.
вызывают различные стимулы у.
Введем собственные значения матрицы  где
где  Это действительные неотрицательные числа. Мы будем изучать спектр матрицы сети
Это действительные неотрицательные числа. Мы будем изучать спектр матрицы сети  — неупорядоченное множество значений
— неупорядоченное множество значений 
Допустим как крайний случай, что это множество кластеризуется и все  равны некоторому
равны некоторому  Последнее означает, что выходная энергия равна простой кратной входной мощности
Последнее означает, что выходная энергия равна простой кратной входной мощности  так что соответствующая обработка информации по существу тривиальна. Сеть обрабатывает информацию совершенно неселективно, относясь ко всем стимулам совершенно одинаково в том, что касается выходной энергии. Таким образом, селективность низка.
так что соответствующая обработка информации по существу тривиальна. Сеть обрабатывает информацию совершенно неселективно, относясь ко всем стимулам совершенно одинаково в том, что касается выходной энергии. Таким образом, селективность низка.
С другой стороны, если мы имеем достаточно сильно рознящиеся значения  то выделяются стимулы, обеспечивающие значительную выходную энергию, а именно собственные векторы матрицы
то выделяются стимулы, обеспечивающие значительную выходную энергию, а именно собственные векторы матрицы  соответствующие большим значениям
соответствующие большим значениям  Другие стимулы при малых значениях
Другие стимулы при малых значениях  вызывают слабую реакцию. Таким образом, селективность высока.
вызывают слабую реакцию. Таким образом, селективность высока.
Это свойство можно формализовать, введя отношение селективности

которое при выражении через отдельные собственные значения принимает вид

где

Если  велико, то вычислять значения
велико, то вычислять значения  непосредственно будет трудно. Попытаемся воспользоваться симметрией
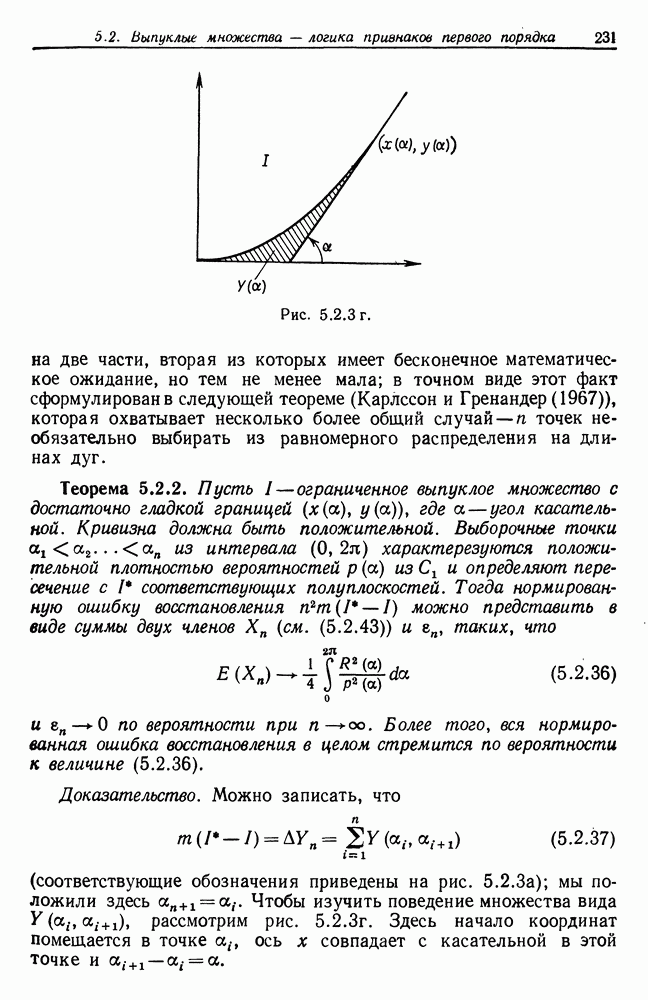
непосредственно будет трудно. Попытаемся воспользоваться симметрией  для того, чтобы установить энергетические свойства сети. Вывод довольно сложен, и для того, чтобы не затемнять идею рассуждения, рассмотрим следующий пример. Допустим, что (i) Для всех а отношения вход—выход полностью определены.
для того, чтобы установить энергетические свойства сети. Вывод довольно сложен, и для того, чтобы не затемнять идею рассуждения, рассмотрим следующий пример. Допустим, что (i) Для всех а отношения вход—выход полностью определены.
(ii)  — одиночный слой в каждой подконфигурации
— одиночный слой в каждой подконфигурации  образующих, причем каждый слой рассматривается как инвариантный относительно переносов, периодический с периодом
образующих, причем каждый слой рассматривается как инвариантный относительно переносов, периодический с периодом 

Рис. 2.5.2
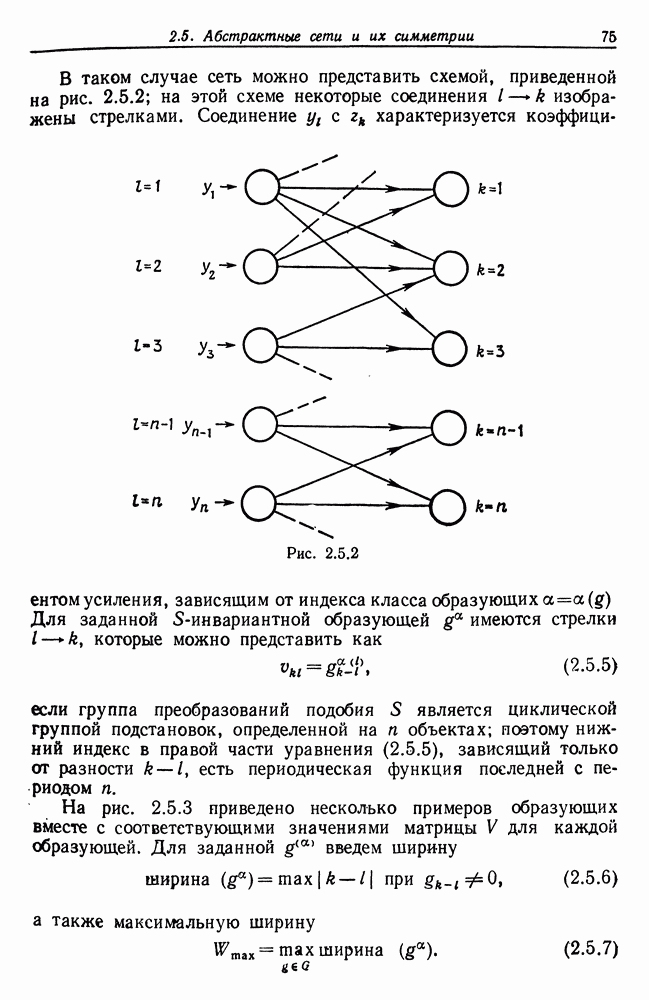
В таком случае сеть можно представить схемой, приведенной на рис. 2.5.2; на этой схеме некоторые соединения  изображены стрелками. Соединение
изображены стрелками. Соединение  характеризуется коэффициентом усиления, зависящим от индекса класса образующих
характеризуется коэффициентом усиления, зависящим от индекса класса образующих  Для заданной
Для заданной  -инвариантной образующей
-инвариантной образующей  имеются стрелки
имеются стрелки  которые можно представить как
которые можно представить как

если группа преобразований подобия  является циклической группой подстановок, определенной на
является циклической группой подстановок, определенной на  объектах; поэтому нижний индекс в правой части уравнения (2.5.5), зависящий только от разности
объектах; поэтому нижний индекс в правой части уравнения (2.5.5), зависящий только от разности  есть периодическая функция последней с периодом
есть периодическая функция последней с периодом 
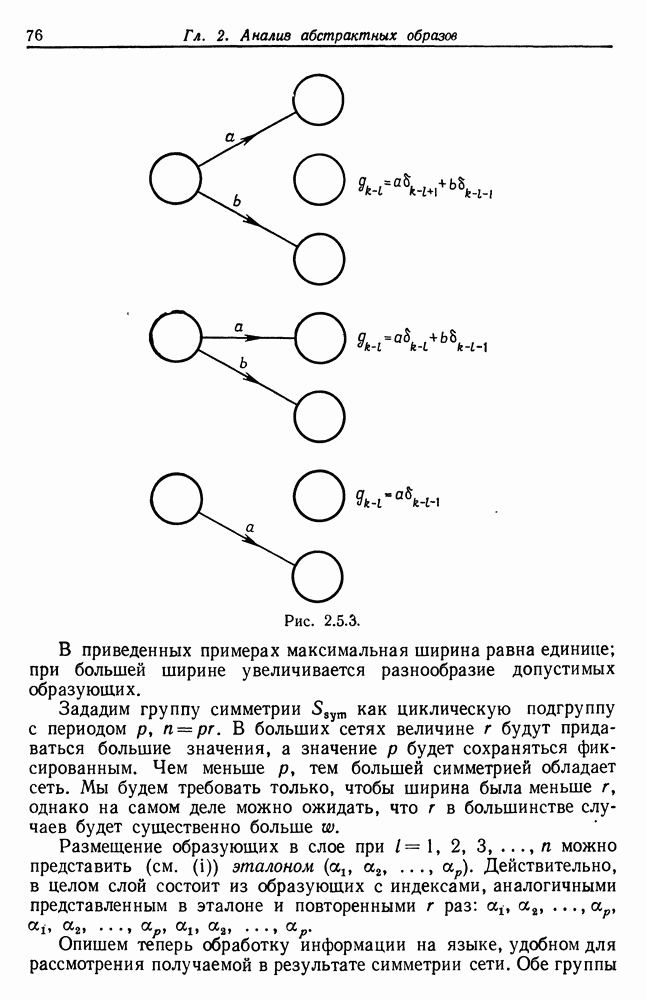
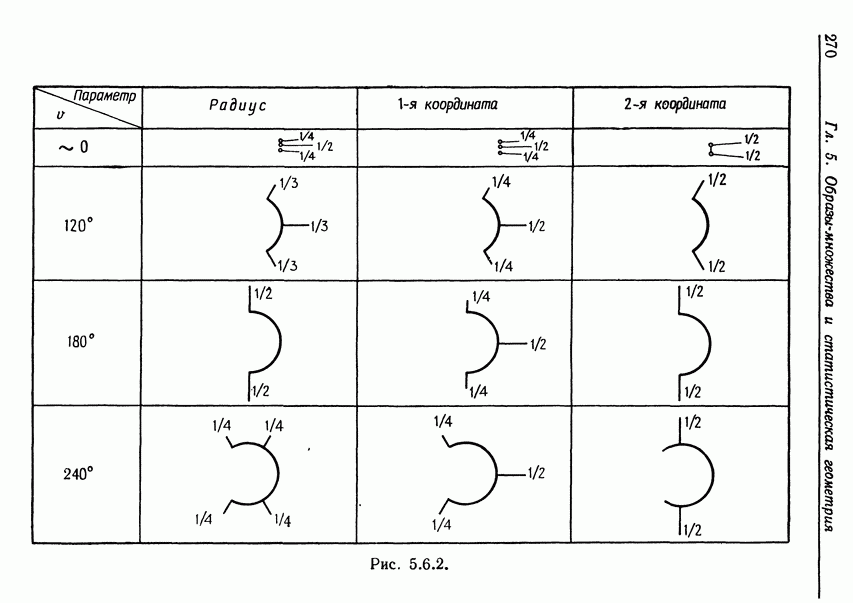
На рис. 2.5.3 приведено несколько примеров образующих вместе с соответствующими значениями матрицы V для каждой образующей. Для заданной  введем ширину
введем ширину

а также максимальную ширину


Рис. 2.5.3.
В приведенных примерах максимальная ширина равна единице; при большей ширине увеличивается разнообразие допустимых образующих.
Зададим группу симметрии  как циклическую подгруппу с периодом
как циклическую подгруппу с периодом  . В больших сетях величине
. В больших сетях величине  будут придаваться большие значения, а значение
будут придаваться большие значения, а значение  будет сохраняться фиксированным. Чем меньше
будет сохраняться фиксированным. Чем меньше  тем большей симметрией обладает сеть. Мы будем требовать только, чтобы ширина была меньше
тем большей симметрией обладает сеть. Мы будем требовать только, чтобы ширина была меньше  однако на самом деле можно ожидать, что
однако на самом деле можно ожидать, что  в большинстве случаев будет существенно больше
в большинстве случаев будет существенно больше 
Размещение образующих в слое при  можно представить (см. (i)) эталоном
можно представить (см. (i)) эталоном  . Действительно, в целом слой состоит из образующих с индексами, аналогичными представленным в эталоне и повторенными
. Действительно, в целом слой состоит из образующих с индексами, аналогичными представленным в эталоне и повторенными 
Опишем теперь обработку информации на языке, удобном для рассмотрения получаемой в результате симметрии сети. Обе группы
 циклические. Как можно ожидать, важную роль будет играть фактор-группа
циклические. Как можно ожидать, важную роль будет играть фактор-группа  Она также является циклической, но ее период равен
Она также является циклической, но ее период равен  Поэтому мы будет описывать образующие с помощью их преобразований Фурье относительно фурье-характеров фактор-группы
Поэтому мы будет описывать образующие с помощью их преобразований Фурье относительно фурье-характеров фактор-группы  Эти характеры представляют собой степени
Эти характеры представляют собой степени  и ниже они будут обозначаться через
и ниже они будут обозначаться через  .
.
Для заданной образующей  определим характеристический «многочлен» (с отрицательными и положительными показателями степени)
определим характеристический «многочлен» (с отрицательными и положительными показателями степени)

где  значение
значение  такое, что
такое, что

Если такое значение у существует, то оно должно быть единственным, поскольку при  справедливо соотношение
справедливо соотношение  Следовательно, мера определяется выражением
Следовательно, мера определяется выражением

При  (2.5.10) справедливо, когда
(2.5.10) справедливо, когда  . С другой стороны, для ненулевых членов, входящих в (2.5.8), при некотором
. С другой стороны, для ненулевых членов, входящих в (2.5.8), при некотором  должно выполняться
должно выполняться

Отсюда следует, что

или

Следовательно, требования определения  можно выполнить, выбирая
можно выполнить, выбирая

Характеристический многочлен, таким образом, определен. Отметим, что показатели входящих в него степенных выражений ограничены по абсолютной величине значением  независимо от того, сколь велико
независимо от того, сколь велико  Сеть может быть большой и пока
Сеть может быть большой и пока
период  остается фиксированным, порядок многочлена не превышает этой грани.
остается фиксированным, порядок многочлена не превышает этой грани.
Для  введем комплексные векторы
введем комплексные векторы 

Мы будем оперировать комплексными векторами  следующим образом: будем их суммировать, умножать на комплексный скаляр, перемножать, причем все эти операции будут выполняться покомпонентно. Подобный вектор а будет иметь обычную
следующим образом: будем их суммировать, умножать на комплексный скаляр, перемножать, причем все эти операции будут выполняться покомпонентно. Подобный вектор а будет иметь обычную  -норму
-норму

Сформируем для фиксированного  эрмитову матрицу
эрмитову матрицу 

и обозначим ее собственные значения через  Отметим, что эта матрица имеет малую размерность (по сравнению с
Отметим, что эта матрица имеет малую размерность (по сравнению с  ), и поэтому вычисления, необходимые для определения
), и поэтому вычисления, необходимые для определения  не слишком объемны. Эти величины дают полную информацию о спектре
не слишком объемны. Эти величины дают полную информацию о спектре  о чем свидетельствует следующая теорема.
о чем свидетельствует следующая теорема.
Теорема 2.5.1. При сформулированных условиях спектр матрицы энергии  состоит исключительно из чисел
состоит исключительно из чисел  включая кратности.
включая кратности.
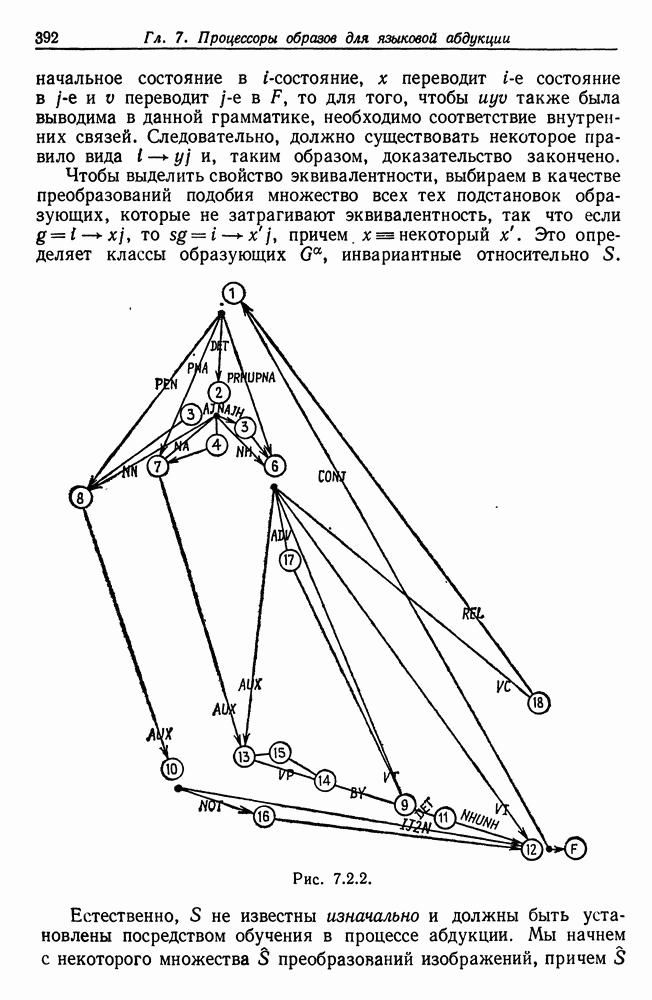
Доказательство. Оно состоит из двух частей. В первой мы рассматриваем задачу о собственных значениях для р-циклических матриц, а во второй оперируем этими матрицами.
Рассмотрим собственное значение X и соответствующий собственный вектор  удовлетворяющие уравнению
удовлетворяющие уравнению

Мы будем записывать  в виде, удобном для изучения симметрии образов:
в виде, удобном для изучения симметрии образов:

где  -векторы
-векторы

Наш эталон имеет вид  так что
так что  образующей соответствует индекс класса образующих
образующей соответствует индекс класса образующих  причем величина а — периодическая с периодом
причем величина а — периодическая с периодом  где
где  ,
,
Параметризуем нижние индексы  по модулю
по модулю  :
:

где  . Индексы
. Индексы  принимают все значения между
принимают все значения между  Воспользуемся записью
Воспользуемся записью  где
где  однозначно определяются заданными условиями.
однозначно определяются заданными условиями.
В системе уравнений (2.5.18) k-ю строку можно записать как

Введем матрицы  размера
размера  у которых
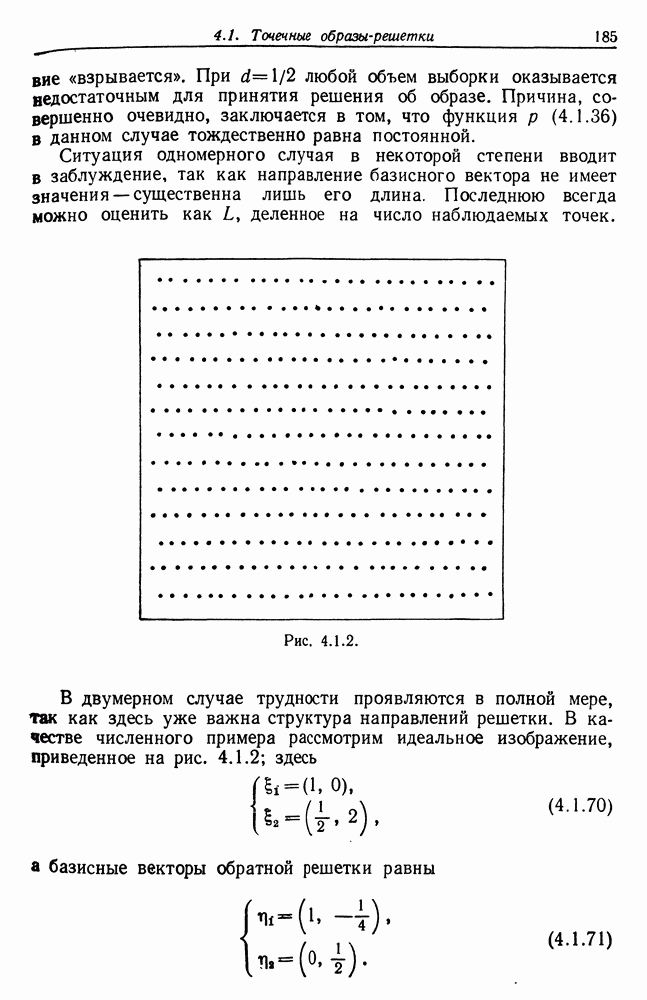
у которых

и

Тогда систему (2.5.22) можно представить в форме

Матрицы  циклические. Для того чтобы убедиться в том, что это действительно так, рассмотрим некоторый элемент
циклические. Для того чтобы убедиться в том, что это действительно так, рассмотрим некоторый элемент  (при фиксированных
(при фиксированных  ) (см. (2.5.5)) и воспользуемся соотношением
) (см. (2.5.5)) и воспользуемся соотношением  :
:

Однако  периодическая функция с периодом
периодическая функция с периодом  и если провести замену переменной суммирования
и если провести замену переменной суммирования  и воспользоваться круговой симметрией, то
и воспользоваться круговой симметрией, то

Это означает, что  Для произвольного целого
Для произвольного целого  и, следовательно, матрица
и, следовательно, матрица  -действительно циклическая.
-действительно циклическая.
Работать с циклическими матрицами удобнее всего, пользуясь их преобразованием Фурье относительно характеров их циклической группы. Если С — циклическая матрица

где  — периодическая величина с периодом
— периодическая величина с периодом  то фурье-преобразование С определяется как комплексный
то фурье-преобразование С определяется как комплексный  -вектор:
-вектор:

где  произвольное, а
произвольное, а  — корень степени
— корень степени  из единицы:
из единицы:

Если  — циклические матрицы размера
— циклические матрицы размера  имеющие преобразования Фурье соответственно
имеющие преобразования Фурье соответственно  , то
, то

где сложение, умножение на скаляр и умножение двух векторов понимаются как операции, осуществляемые покомпонентно, в чем можно убедиться с помощью (2.5.29). Множество циклических матриц замкнуто относительно сложения, умножения на скалярные. величины, перемножения и транспонирования.
Для того чтобы найти преобразование Фурье матрицы воспользуемся соотношением (2.5.24) и при фиксированных  получим
получим

Мы воспользовались здесь соотношением

Далее, используя, как и выше, индекс  получаем
получаем

или

где элементы матрицы  размера
размера  имеют вид
имеют вид

Следовательно, матрицу  можно записать в виде произведения двух матриц, элементы
можно записать в виде произведения двух матриц, элементы  которых равны соответственно
которых равны соответственно

Преобразование Фурье первой матрицы равно

Аналогично оно определяется и для второй матрицы. Если индекс  увеличить на величину
увеличить на величину  кратную
кратную  то это приведет лишь к изменению функции у благодаря умножению на
то это приведет лишь к изменению функции у благодаря умножению на  . С учетом (2.5.31) это дает
. С учетом (2.5.31) это дает

откуда непосредственно следует «эрмитовость» векторов 

При фиксированных  значение
значение  является комплексным числом. Сформируем аналогично (2.5.17) матрицу
является комплексным числом. Сформируем аналогично (2.5.17) матрицу  размера
размера  Множество чисел
Множество чисел  однозначно определяется значениями
однозначно определяется значениями

Этот факт следует из основных свойств симметрических многочленов (см., например, монографию Перрона (1932, 1, гл. 4-5)). Выразим теперь  через векторы
через векторы  что и составляет вторую часть доказательства теоремы.
что и составляет вторую часть доказательства теоремы.
Матрица энергии  эквивалентна матрице
эквивалентна матрице

поскольку матрица  может быть получена из (2.5.42) при помощи применения к строкам и столбцам одной и той же перестановки — ортогонального преобразования. Эти матрицы имеют одинаковые собственные значения, и, таким образом, степени матрицы
может быть получена из (2.5.42) при помощи применения к строкам и столбцам одной и той же перестановки — ортогонального преобразования. Эти матрицы имеют одинаковые собственные значения, и, таким образом, степени матрицы  имеют тот же след, что и степени матрицы
имеют тот же след, что и степени матрицы 
Матрицы  однако, являются циклическими, а с ними удобнее работать, оперируя их преобразованиями Фурье. В частности, след циклической матрицы представляет собой просто сумму компонентов вектора ее преобразования Фурье,
однако, являются циклическими, а с ними удобнее работать, оперируя их преобразованиями Фурье. В частности, след циклической матрицы представляет собой просто сумму компонентов вектора ее преобразования Фурье,  блок
блок  можно записать в виде
можно записать в виде

где суммирование ведется по  Следовательно,
Следовательно,

Поскольку, однако,  имеет собственные значения
имеет собственные значения  так что
так что

и поскольку эта сумма степеней берется по всем то отсюда следует, что множество  и этим завершается доказательство.
и этим завершается доказательство.
Непосредственное следствие этой теоремы относится к величинам и  которые нужны для вычисления селективности сети при помощи (2.5.2).
которые нужны для вычисления селективности сети при помощи (2.5.2).
Следствие 2.5.1. Значение селективности  можно определить при помощи величин
можно определить при помощи величин

и

Доказательство. Чтобы найти след матрицы  обратим внимание на ее связь с блочной матрицей
обратим внимание на ее связь с блочной матрицей  устанавливаемую изменением порядка строк и столбцов с помощью одной и той же перестановки. Поскольку эта процедура является ортогональным преобразованием, матрица
устанавливаемую изменением порядка строк и столбцов с помощью одной и той же перестановки. Поскольку эта процедура является ортогональным преобразованием, матрица  и блочная матрица имеют одинаковые собственные значения, в частности один и тот же след (при
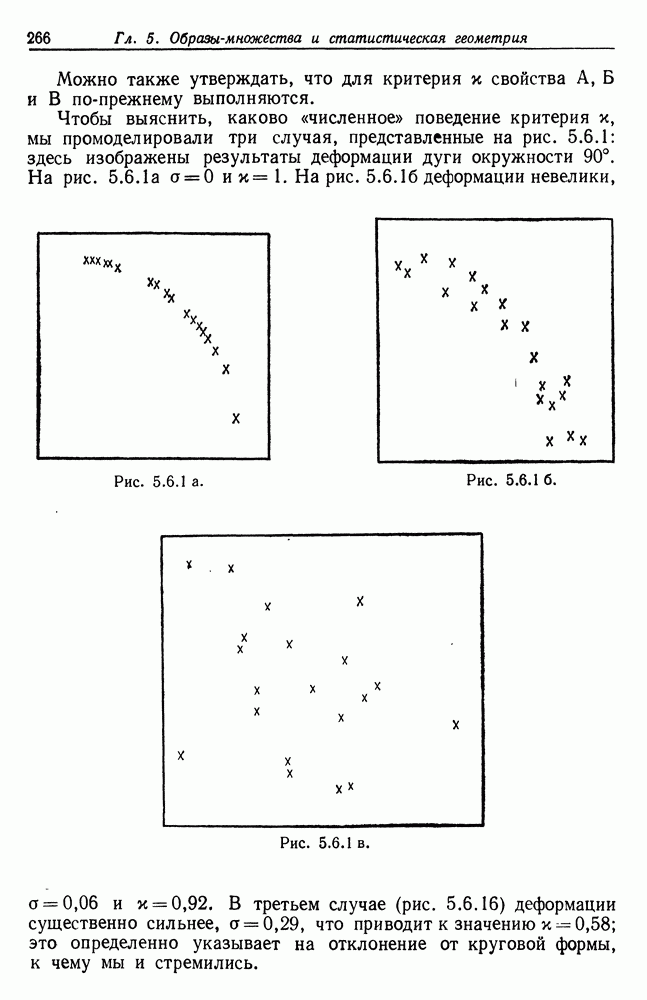
и блочная матрица имеют одинаковые собственные значения, в частности один и тот же след (при  ) равен следу
) равен следу  степени блочной матрицы.
степени блочной матрицы.
Но

так что

Последнее выражение эквивалентно (2.5.46) (см. (2.5.16)). Применяя ту же идею в случае  получаем
получаем

В этом выражении последнее суммирование проводится по  Изменяя порядок суммирования, приходим к
Изменяя порядок суммирования, приходим к

что и утверждалось.
Если устремить  к бесконечности, оставляя
к бесконечности, оставляя  и эталон
и эталон  фиксированными, то распределение собственных значений
фиксированными, то распределение собственных значений  становится более плотным на положительной полуоси. Они, однако, равномерно ограниченны, так как
становится более плотным на положительной полуоси. Они, однако, равномерно ограниченны, так как

и, следовательно, асимптотическое распределение собственных значений можно найти с помощью моментов  Отметим, что элементы матрицы
Отметим, что элементы матрицы  размера
размера  можно представить как полиномы относительно
можно представить как полиномы относительно  последние непрерывны и даже являются аналитическими при
последние непрерывны и даже являются аналитическими при  Обозначим
Обозначим  собственных значений
собственных значений  Через
Через  Эти функции алгебраические относительно
Эти функции алгебраические относительно  и аналитические на
и аналитические на  за исключением, быть может, точек разветвления, соответствующих кратным корням.
за исключением, быть может, точек разветвления, соответствующих кратным корням.
однако, следует заменить на  Используя то обстоятельство, что
Используя то обстоятельство, что  формируются как
формируются как  (см. теорему 2.5.1), получаем второе непосредственное следствие из этой теоремы.
(см. теорему 2.5.1), получаем второе непосредственное следствие из этой теоремы.
Следствие 2.5.2. Матрица энергии  имеет при
имеет при  фиксированном и
фиксированном и  стремящемся к бесконечности, асимптотическое распределение собственных значений
стремящемся к бесконечности, асимптотическое распределение собственных значений

где  — мера Лебега на интервале
— мера Лебега на интервале  .
.
Отсюда вытекают интересные следствия для плотности асимптотического распределения собственных значений  Пусть
Пусть  имеет локальный максимум в регулярной точке
имеет локальный максимум в регулярной точке  так что
так что

где натуральное число  характеризует «плоскость» максимума: малые значения
характеризует «плоскость» максимума: малые значения  означают, что при
означают, что при  функция плоская. Вклад в
функция плоская. Вклад в  член правой части (2.5.54), определяемый окрестностью
член правой части (2.5.54), определяемый окрестностью  можно, однако, представить как
можно, однако, представить как

плюс члены высшего порядка. Следовательно, равенство  устанавливает вклад, асимптотически равный
устанавливает вклад, асимптотически равный

Другими словами, плотность распределения  будет иметь особую точку при
будет иметь особую точку при  — локально максимальное значение
— локально максимальное значение 
В качестве примера применения этой теоремы рассмотрим случай наибольшей симметрии  т. е.
т. е.  При этом
При этом  просто циклические матрицы, что кардинально упрощает результаты. Выражение (2.5.15) нужно рассматривать лишь при
просто циклические матрицы, что кардинально упрощает результаты. Выражение (2.5.15) нужно рассматривать лишь при  причем только с индексами
причем только с индексами  Однако тогда выражение (2.5.8) для единственной образующей, которой мы располагаем,
Однако тогда выражение (2.5.8) для единственной образующей, которой мы располагаем,  принимает вид
принимает вид

 означает просто приведение к
означает просто приведение к  по модулю
по модулю  Следовательно,
Следовательно,

Теперь  просто скаляр, и поэтому собственные значения имеют вид (см. (2.5.39))
просто скаляр, и поэтому собственные значения имеют вид (см. (2.5.39))

где  или, в действительной форме,
или, в действительной форме,

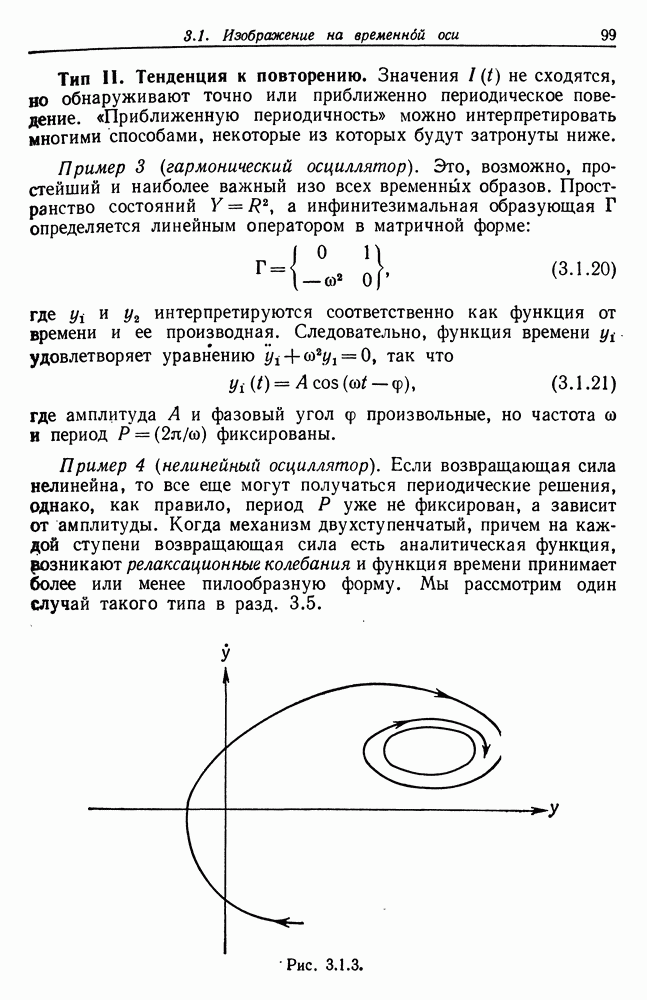
Случай  более информативен, поскольку он выявляет в общем виде важное свойство симметричных сетей, которое не удается обнаружить в предыдущем случае. Пусть ширина
более информативен, поскольку он выявляет в общем виде важное свойство симметричных сетей, которое не удается обнаружить в предыдущем случае. Пусть ширина  четная; вычислим характеристический многочлен (2.5.8) для
четная; вычислим характеристический многочлен (2.5.8) для
произвольной образующей:

Значения признаков образующей, представляющие собой коэффициенты в уравнениях (2.5.62), определяются из  соответственно, и в результате мы получаем четыре характеристических многочлена
соответственно, и в результате мы получаем четыре характеристических многочлена  Значения
Значения  для других
для других  необходимые для (2.5.39), можно найти при помощи умножения на соответствующую степень
необходимые для (2.5.39), можно найти при помощи умножения на соответствующую степень 
Используя (2.5.39), получаем следующее:

Множитель  асимптотически равен 1 для больших значений
асимптотически равен 1 для больших значений 
Отметим, что коэффициенты при  в (2.5.62) в случае нечетных аргументов обращаются в нуль; следовательно,
в (2.5.62) в случае нечетных аргументов обращаются в нуль; следовательно,  и
и

Собственные значения А представляют собой просто значения  Это, однако, возвращает нас к случаю
Это, однако, возвращает нас к случаю  (см. выражение (2.5.59)), и полный спектр
(см. выражение (2.5.59)), и полный спектр  оказывается просто смесью двух
оказывается просто смесью двух  -спектров. То, что это должно быть именно так, видно непосредственно, поскольку здесь две переменные подсети не взаимодействуют между собой вообше. В других случаях члены
-спектров. То, что это должно быть именно так, видно непосредственно, поскольку здесь две переменные подсети не взаимодействуют между собой вообше. В других случаях члены  характеризуют влияние взаимодействия между двумя периодическими подсетями на спектр матрицы энергии
характеризуют влияние взаимодействия между двумя периодическими подсетями на спектр матрицы энергии  в целом.
в целом.
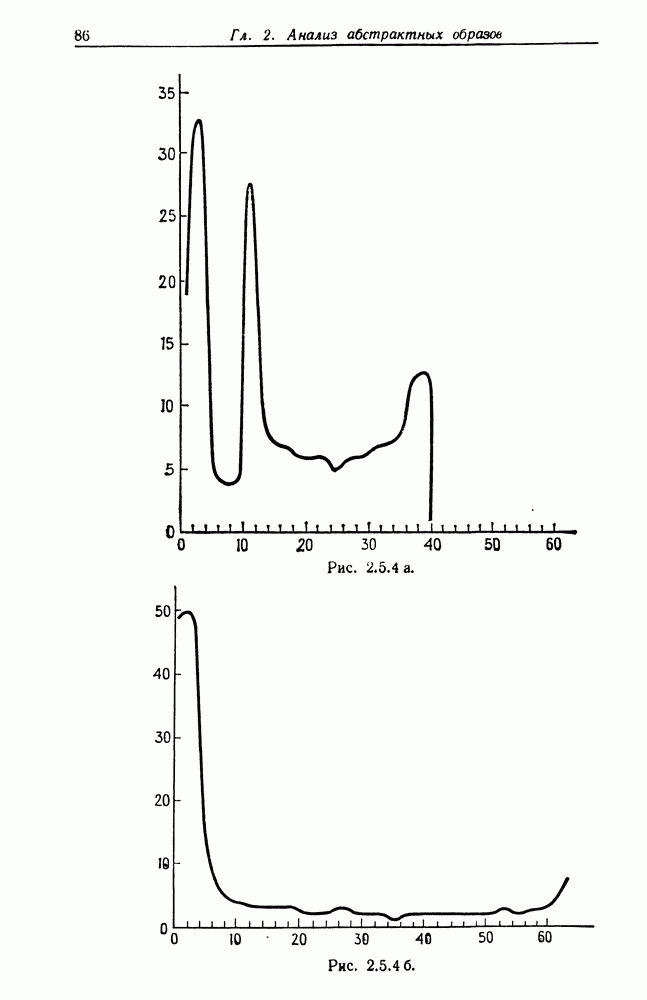
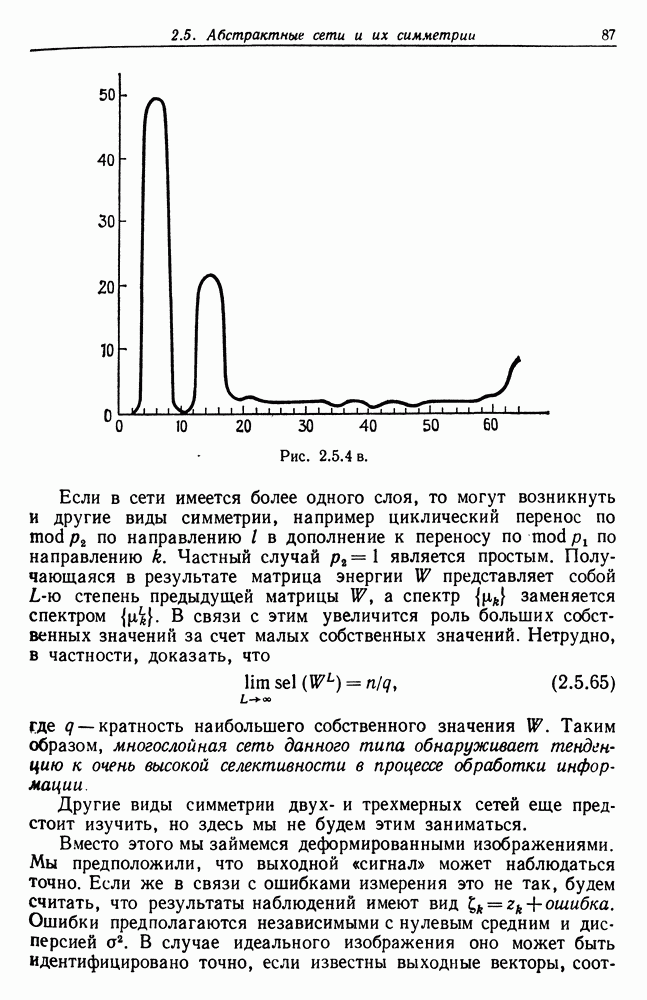
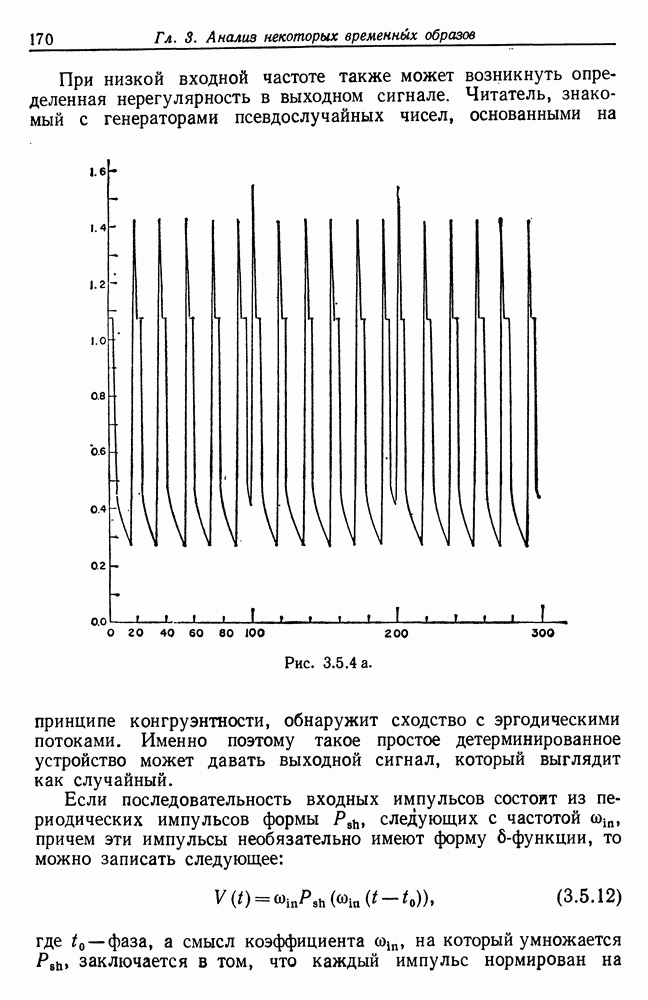
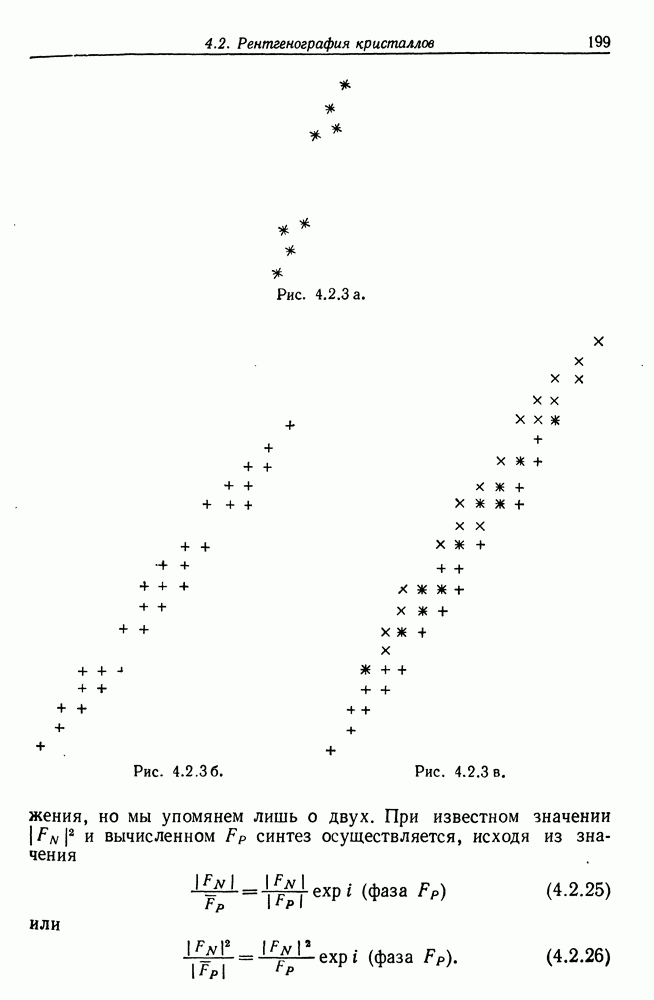
В качестве численного примера определим спектр матрицы для  и представим результат в виде непрерывного графика на рис. 2.5.4а. Обратим внимание на пики, соответствующие упоминавшимся выше особым точкам. В данном случае
и представим результат в виде непрерывного графика на рис. 2.5.4а. Обратим внимание на пики, соответствующие упоминавшимся выше особым точкам. В данном случае  , а значения
, а значения  равны 1, —1, 3, —2, 1 и 2, 3, 2, 0, 1 для
равны 1, —1, 3, —2, 1 и 2, 3, 2, 0, 1 для  соответственно.
соответственно.
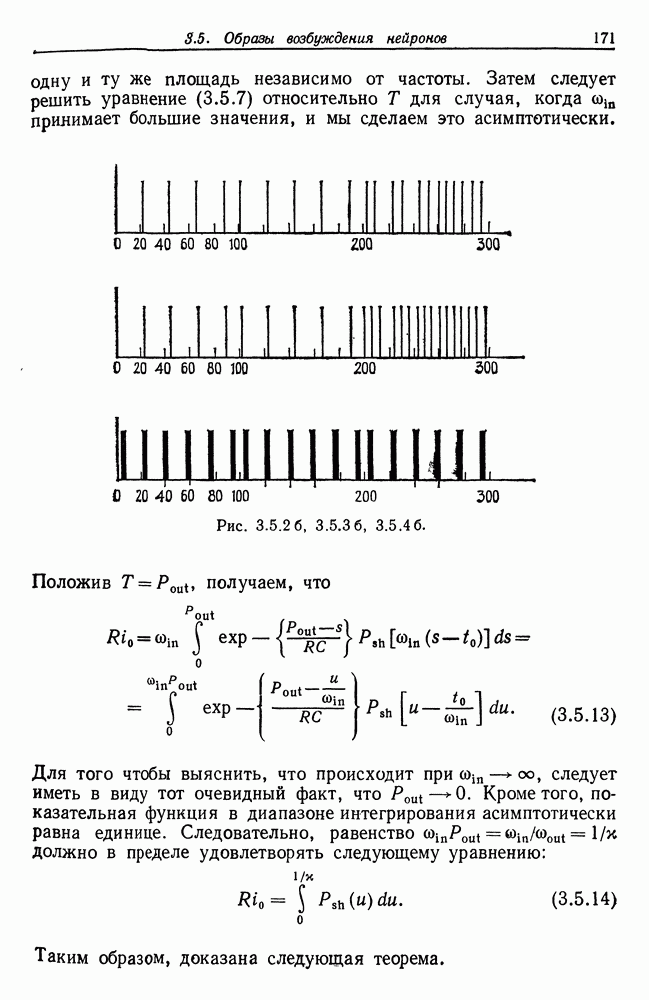
Мы определили также спектр сети того же размера, когда все образующие типа  (см. рис. 2.5.46) и типа
(см. рис. 2.5.46) и типа  (см. рис. 2.5.4в). Очевидно, что в этом случае два последних спектра не просто перемешиваются — их композиция оказывается сложнее из-за взаимодействия между двумя подсетями.
(см. рис. 2.5.4в). Очевидно, что в этом случае два последних спектра не просто перемешиваются — их композиция оказывается сложнее из-за взаимодействия между двумя подсетями.

(кликните для просмотра скана)
Рис. 2.5.4 b. (см. скан)
Если в сети имеется более одного слоя, то могут возникнуть и другие виды симметрии, например циклический перенос по  по направлению I в дополнение к переносу по
по направлению I в дополнение к переносу по  по направлению
по направлению  Частный случай
Частный случай  является простым. Получающаяся в результате матрица энергии
является простым. Получающаяся в результате матрица энергии  представляет собой
представляет собой  степень предыдущей матрицы
степень предыдущей матрицы  а спектр заменяется спектром В связи с этим увеличится роль больших собственных значений за счет малых собственных значений. Нетрудно, в частности, доказать, что
а спектр заменяется спектром В связи с этим увеличится роль больших собственных значений за счет малых собственных значений. Нетрудно, в частности, доказать, что

где  — кратность наибольшего собственного значения
— кратность наибольшего собственного значения  Таким образом, многослойная сеть данного типа обнаруживает тенденцию к очень высокой селективности в процессе обработки информации.
Таким образом, многослойная сеть данного типа обнаруживает тенденцию к очень высокой селективности в процессе обработки информации.
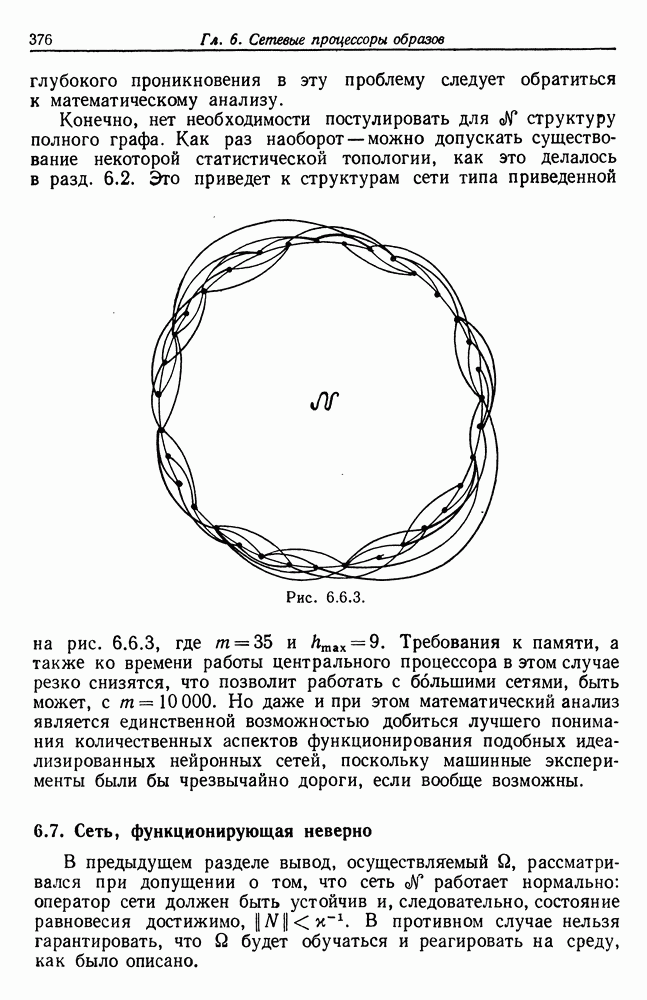
Другие виды симметрии двух- и трехмерных сетей еще предстоит изучить, но здесь мы не будем этим заниматься.
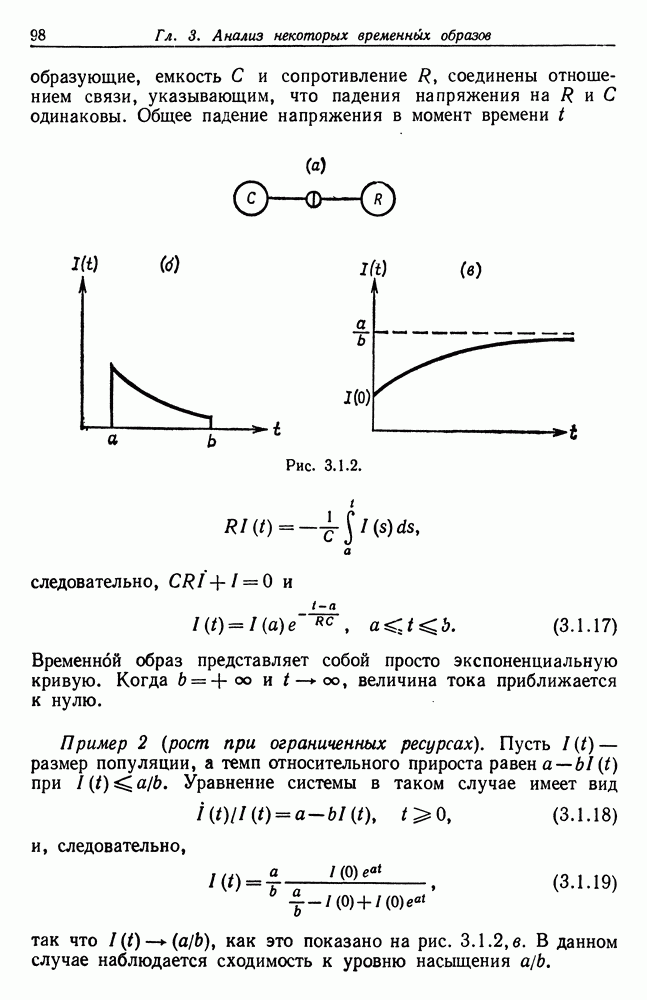
Вместо этого мы займемся деформированными изображениями. Мы предположили, что выходной «сигнал» может наблюдаться точно. Если же в связи с ошибками измерения это не так, будем считать, что результаты наблюдений имеют вид  Ошибки предполагаются независимыми с нулевым средним и дисперсией
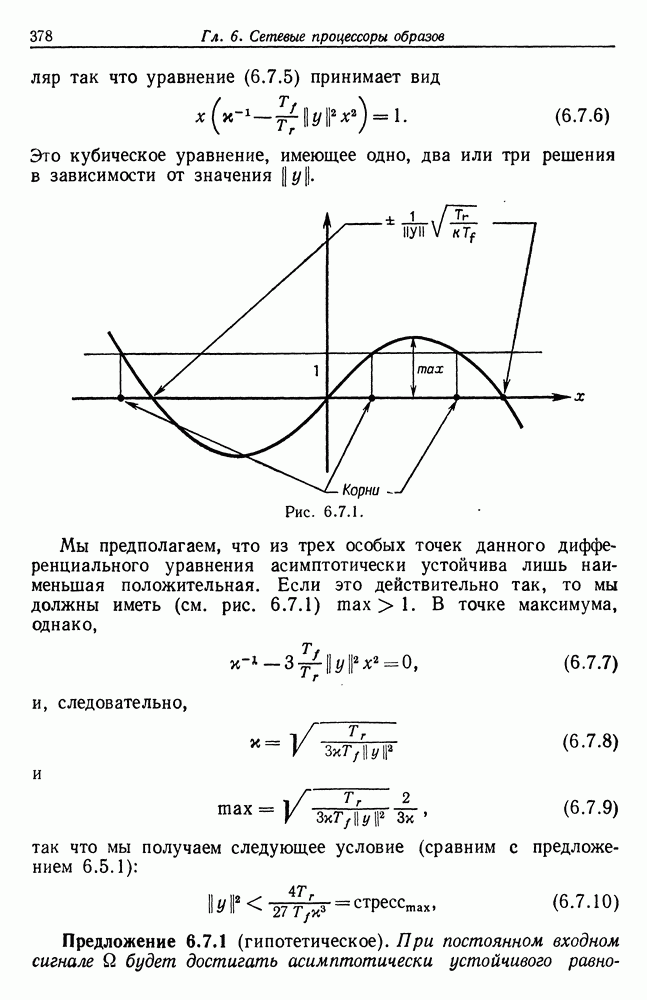
Ошибки предполагаются независимыми с нулевым средним и дисперсией  . В случае идеального изображения оно может быть идентифицировано точно, если известны выходные векторы, соответствующие
. В случае идеального изображения оно может быть идентифицировано точно, если известны выходные векторы, соответствующие
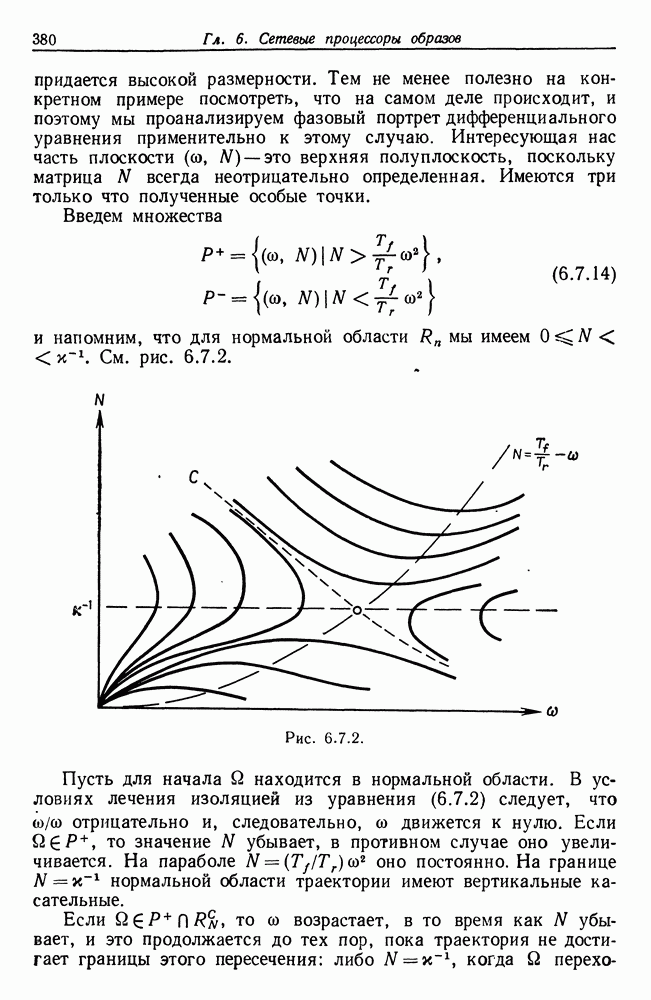
удачно подобранным входным векторам (см. ниже). В случае деформированного изображения этот прием уже не работает.
Рассмотрим в качестве примера случай  . С помощью (2.5.1) и (2.5.5) можно записать следующее:
. С помощью (2.5.1) и (2.5.5) можно записать следующее:

или в матричном виде как  где
где

и

Чтобы обеспечить восстановление по методу наименьших квадратов (см. гл. 1), мы применяем стандартную процедуру метода наименьших квадратов непосредственно к этим выражениям (см., например, монографию Крамера (1945), гл. 37). Для того чтобы обеспечить эту возможность, необходимо ввести условие линейной независимости шести столбцов матрицы (2.5.68). Тогда матрица  неособенная и восстановление по методу наименьших квадратов задается оценкой вектора
неособенная и восстановление по методу наименьших квадратов задается оценкой вектора

с ковариационной матрицей  . В частности, для идеальных изображений
. В частности, для идеальных изображений  обеспечивается полное восстановление, если столбцы матрицы (2.5.68) линейно-независимы. Для этого необходимо, чтобы
обеспечивается полное восстановление, если столбцы матрицы (2.5.68) линейно-независимы. Для этого необходимо, чтобы  или
или  . Тогда можно было бы выбрать, скажем,
. Тогда можно было бы выбрать, скажем,  когда векторы-столбцы становятся взаимно ортогональными. Отметим, что эти входные у обладают пространственной периодичностью с периодом
когда векторы-столбцы становятся взаимно ортогональными. Отметим, что эти входные у обладают пространственной периодичностью с периодом 
Вернемся к случаю общих  при рассмотрим
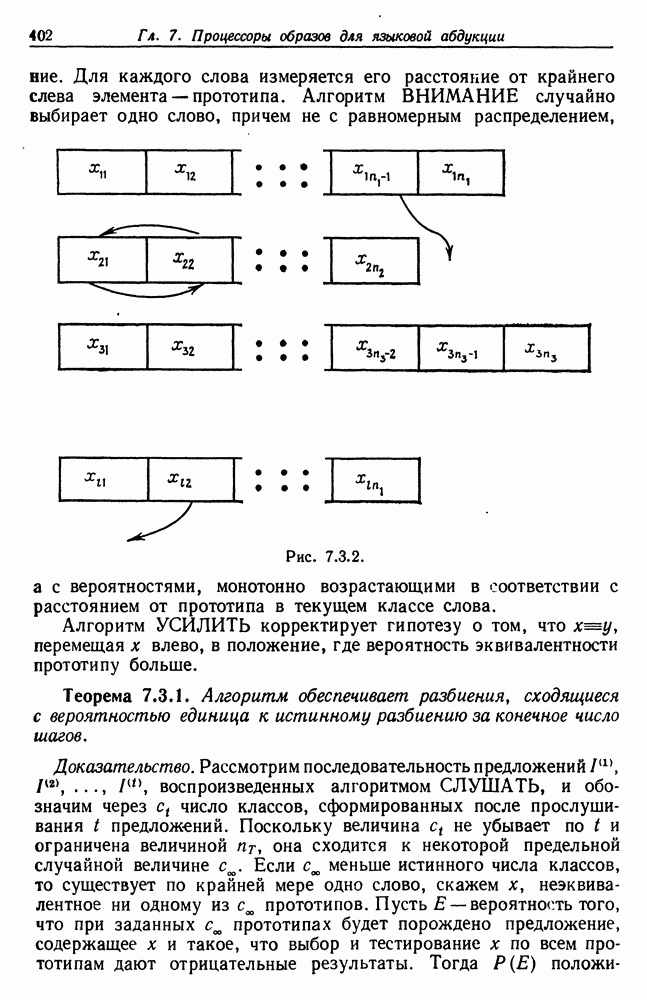
при рассмотрим  входных векторов
входных векторов

и обозначим соответствующие деформированные выходные векторы как  Здесь удобнее пользоваться комплексным представлением,
Здесь удобнее пользоваться комплексным представлением,
но можно, конечно, пользоваться и действительным. Запишем преобразование Фурье

Но так как

то

где первое суммирование проводится по тем  для которых выполняется
для которых выполняется  Это соответствует самое большее одному значению
Это соответствует самое большее одному значению  в носителе образующих, так как его длина
в носителе образующих, так как его длина  Дисперсия же второй суммы равна
Дисперсия же второй суммы равна  Следовательно, преобразование Фурье
Следовательно, преобразование Фурье

является несмещенной оценкой с дисперсией  Использование быстрого преобразования Фурье делает вычисления осуществимыми даже при больших значениях
Использование быстрого преобразования Фурье делает вычисления осуществимыми даже при больших значениях 
Спектральные свойства тех весьма «жестких» сетей, которые были рассмотрены в данном разделе, определены в терминах симметрии топологии сети. Если ансамбль потенциальных входных «сигналов» известен, то применительно к конкретной задаче можно синтезировать сеть данного типа, которая выполнит необходимую фильтрацию. Задача может заключаться в какой-либо разновидности предварительной обработки, например в определении ориентации края или увеличении контраста.
Для этого мы выбираем  настолько большим, насколько это необходимо для получения спектральных свойств, обеспечивающих достаточную степень аппроксимации. Значение
настолько большим, насколько это необходимо для получения спектральных свойств, обеспечивающих достаточную степень аппроксимации. Значение  с другой стороны, выбирается большим согласно теореме 2.5.1.
с другой стороны, выбирается большим согласно теореме 2.5.1.
Отметим, что подобные сети могут оказаться полезными для решения узкоспециализированных задач, если они определены заранее. Если задача не определена точно заранее, то эти сети становятся менее привлекательными; в таких случаях приходится вводить менее жесткие топологии, регулярность которых имеет лишь статистический характер. Мы займемся этим в гл. 6.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
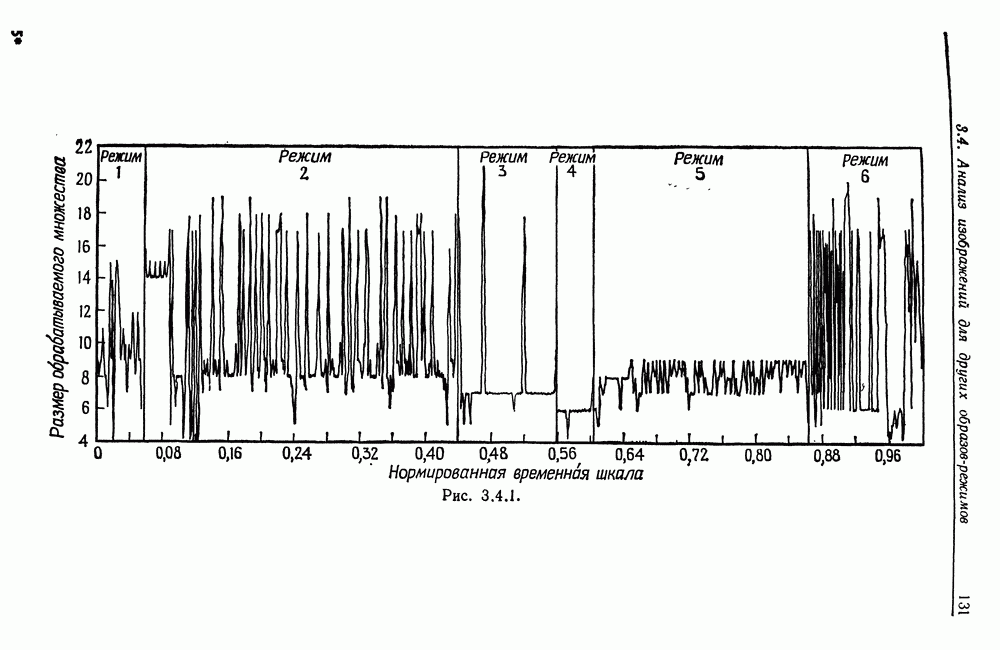
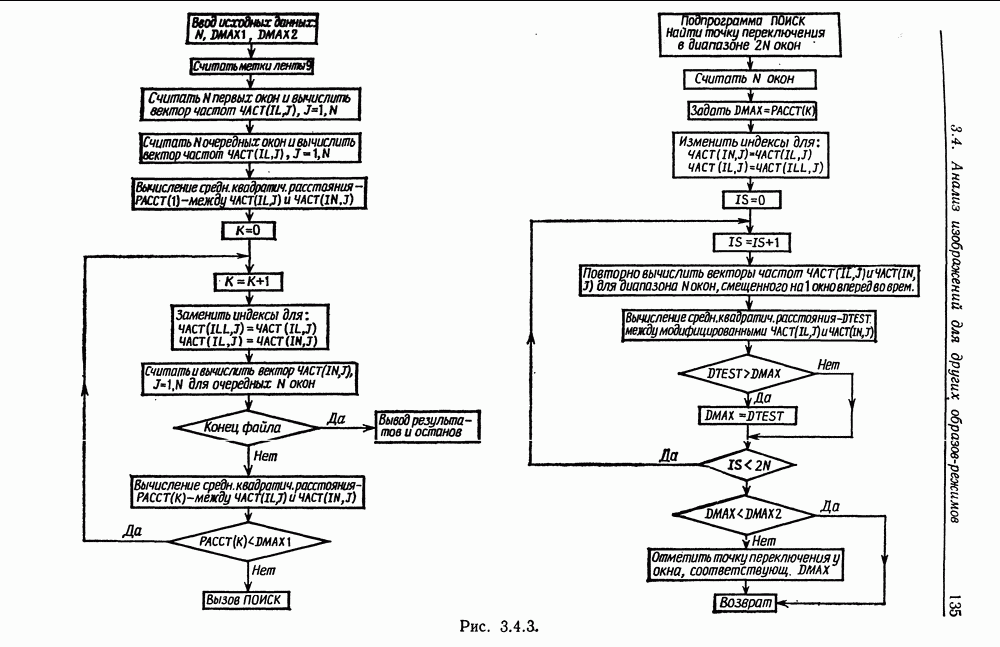
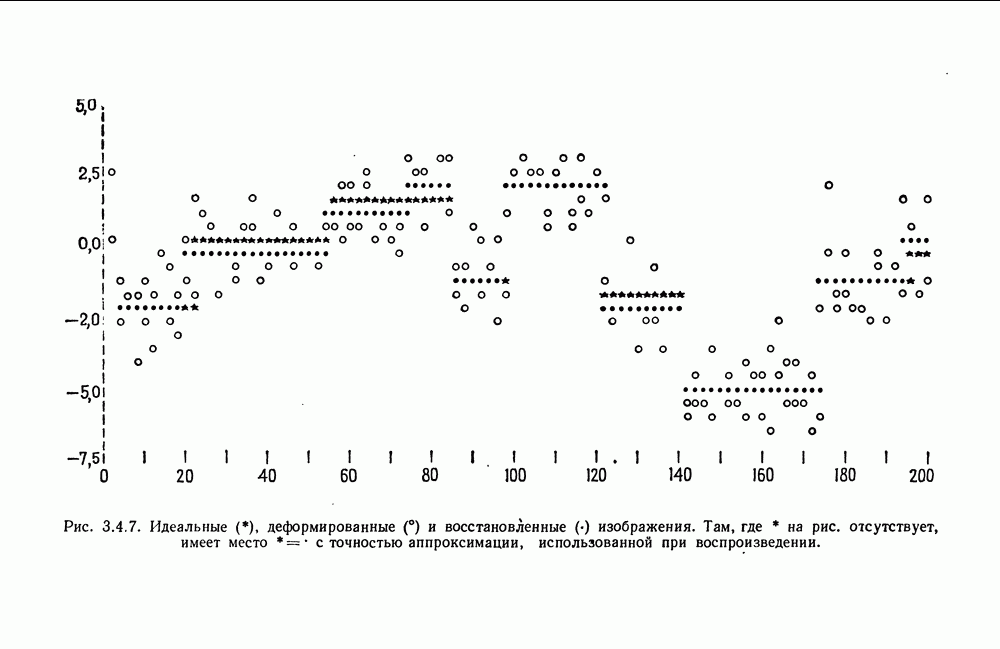
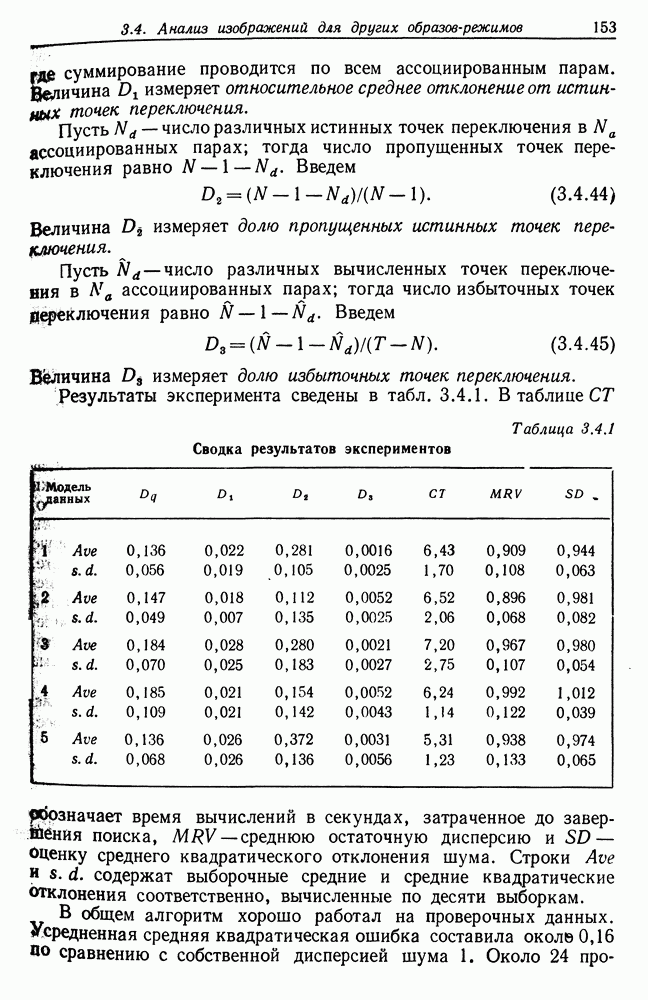
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
- 4.2. Рентгенография кристаллов
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
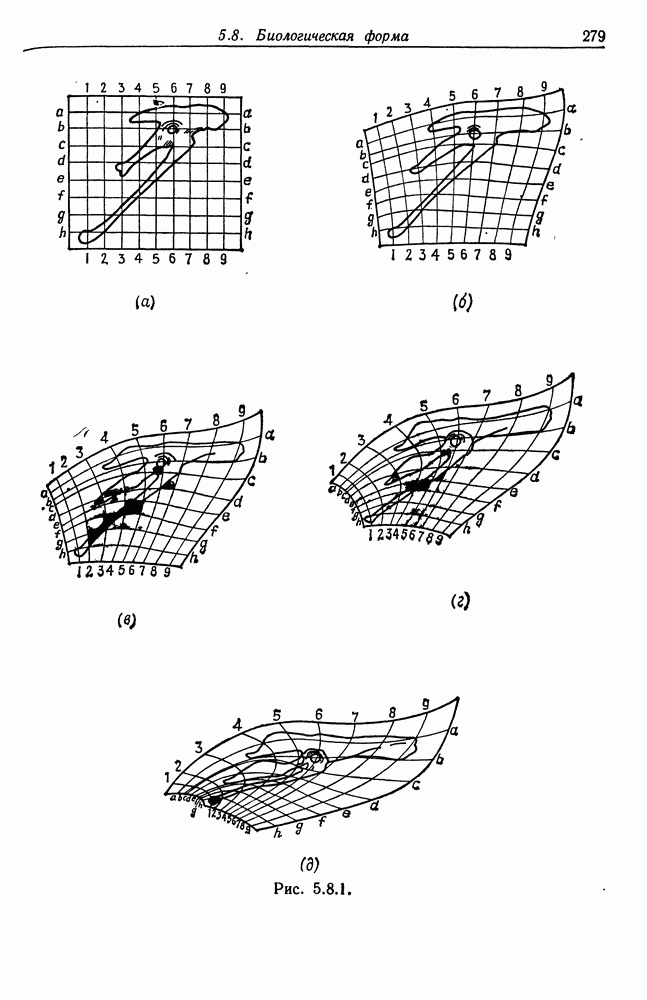
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы