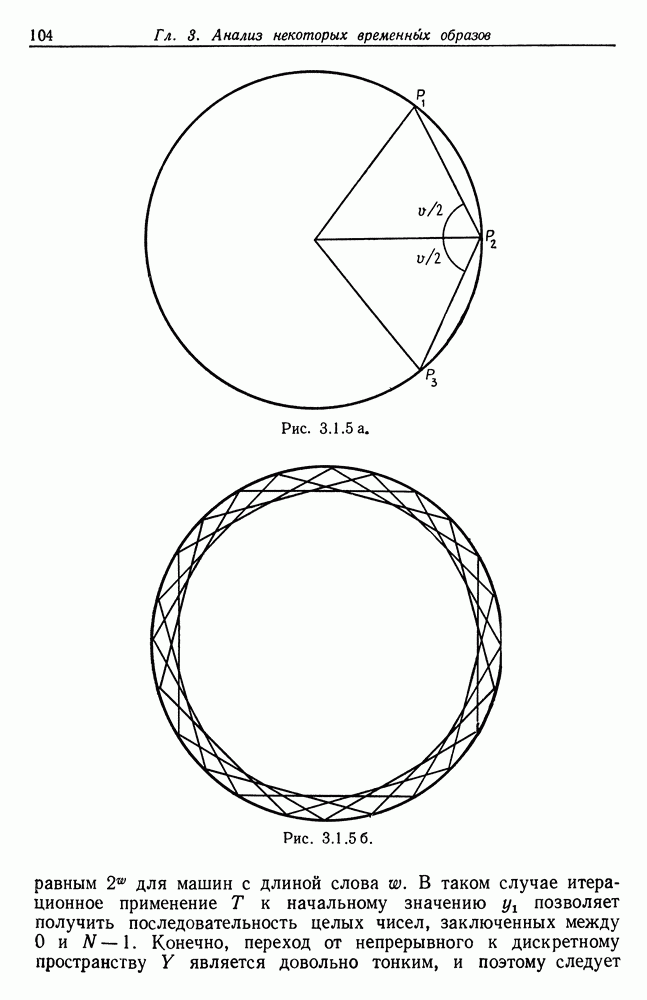
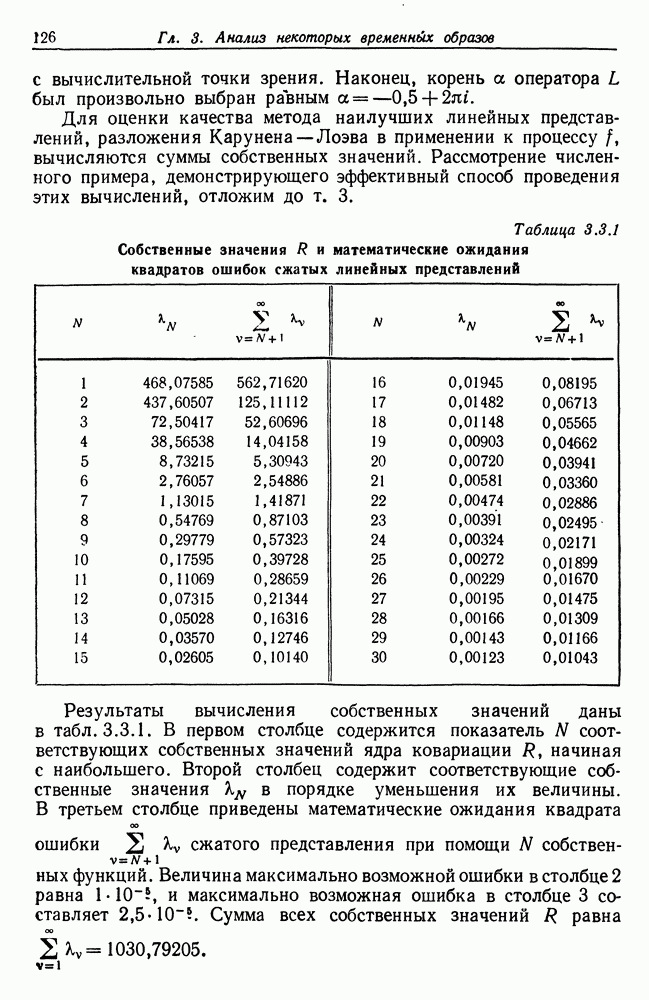
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.5. Алгоритмы анализа образов
Располагая осмысленным критерием качества, можно сопоставлять операторы изображения и в идеальном случае выбирать оптимальный оператор. Однако и при таких условиях решение может быть неполным: это зависит от того, можно ли осуществить соответствующий анализ образов с помощью алгоритма, поддающегося реализации посредством имеющихся вычислительных ресурсов. Последнее означает, что такой алгоритм не должен требовать нереальных затрат машинного времени и памяти.
В настоящем разделе мы обсудим эту проблему неформально с помощью нескольких примеров, которыми займемся более тщательно в следующих главах и томе 3.
При изучении изображений-сигналов мы рассмотрим вариант анализа образов, когда поиск решения связан с определением собственных значений симметрической матрицы М размера 
 численного анализа прекрасно известно, как это делается, и существует множество соответствующих алгоритмов (см., в частности, монографию Дальквиста и Бьёрка (1974;, гл. 5). Типичный алгоритм этого типа требует выполнения числа арифметических операций, асимптотически оцениваемого как
численного анализа прекрасно известно, как это делается, и существует множество соответствующих алгоритмов (см., в частности, монографию Дальквиста и Бьёрка (1974;, гл. 5). Типичный алгоритм этого типа требует выполнения числа арифметических операций, асимптотически оцениваемого как  .
.
Если  мало, то мы сразу примемся за дело, воспользовавшись одним из таких алгоритмов. Если же
мало, то мы сразу примемся за дело, воспользовавшись одним из таких алгоритмов. Если же  велико или предполагается многократное применение алгоритма, то необходимо уделить больше внимания вычислительной стороне дела. Более тщательное изучение задачи позволяет установить то обстоятельство, что матрица М обладает довольно специфической структурой: все элементы матрицы расположенные вдоль ее диагоналей, одинаковы и элементы матрицы зависят только от разности
велико или предполагается многократное применение алгоритма, то необходимо уделить больше внимания вычислительной стороне дела. Более тщательное изучение задачи позволяет установить то обстоятельство, что матрица М обладает довольно специфической структурой: все элементы матрицы расположенные вдоль ее диагоналей, одинаковы и элементы матрицы зависят только от разности  Матрицы такого вида называются теплицевыми, для них существует хорошо разработанная теория, описывающая асимптотическое поведение собственных значений. Заманчиво воспользоваться ею для ускорения вычислительного процесса. Это совсем не просто, но, как будет показано в т. 3, возможно. Итак, учтя специфику структуры задачи и проанализировав ее более досконально математически, можно существенно усовершенствовать вычислительный процесс.
Матрицы такого вида называются теплицевыми, для них существует хорошо разработанная теория, описывающая асимптотическое поведение собственных значений. Заманчиво воспользоваться ею для ускорения вычислительного процесса. Это совсем не просто, но, как будет показано в т. 3, возможно. Итак, учтя специфику структуры задачи и проанализировав ее более досконально математически, можно существенно усовершенствовать вычислительный процесс.
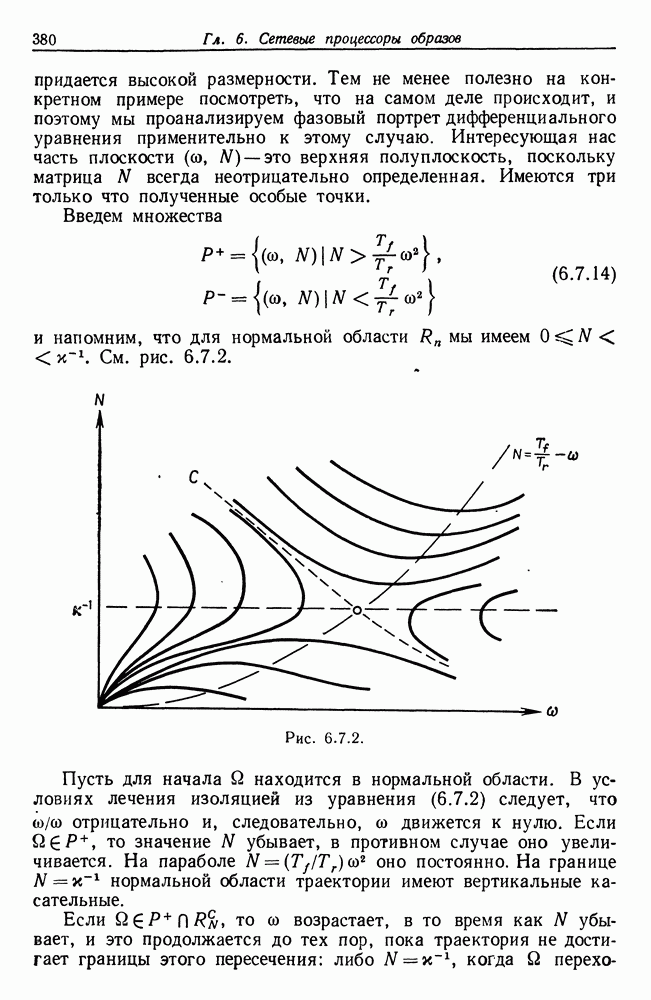
В данном случае мы, к счастью, располагали математической теорией, позволяющей усовершенствовать алгоритм. В иных случаях также можно достичь вычислительной эффективности, если отказаться от простодушного построения алгоритма, исходя из математического описания решения. Для некоторых вычислительных методов хорошо известно, каким образом можно добиваться Подобного усовершенствования; это относится, например, к вычислительным методам в линейной алгебре.
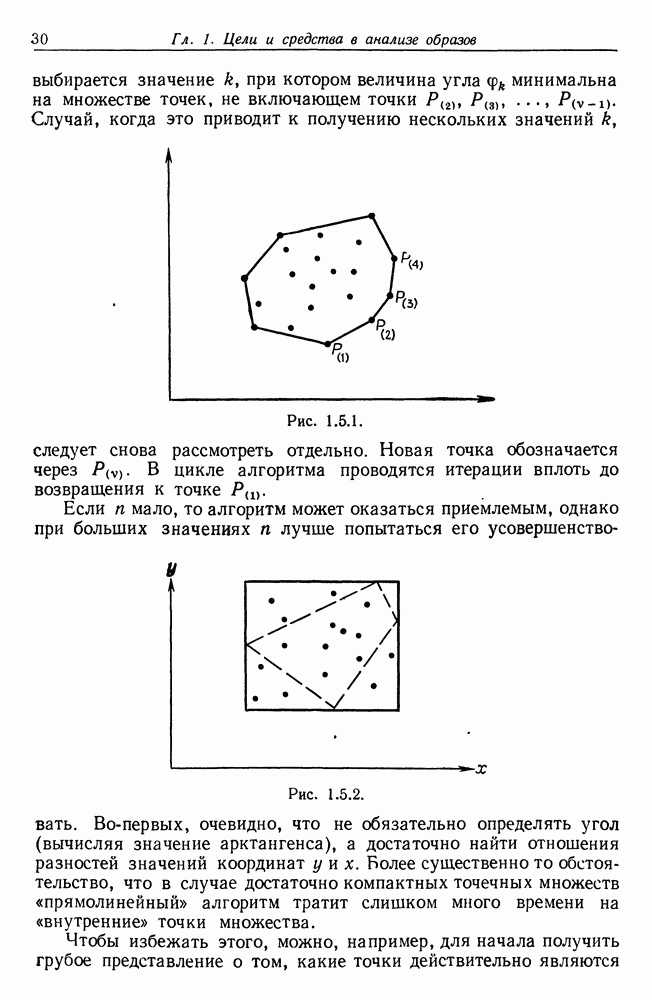
Если вычислительная задача относится к нестандартному типу, там придется отыскивать соответствующие частные алгоритмы, рассмотрим в качестве примера оператор изображения, заменяющий конечные точечные множества их выпуклой оболочкой (мы встретимся с таким случаем в гл. 5). Пусть координаты точек заданы как  Можно попытаться воспользоваться «прямолинейным» алгоритмом следующего вида. Выбивается точка с минимальным значением координаты у. Если таких очек несколько, то берется точка с максимальным значением координаты
Можно попытаться воспользоваться «прямолинейным» алгоритмом следующего вида. Выбивается точка с минимальным значением координаты у. Если таких очек несколько, то берется точка с максимальным значением координаты  Обозначим выбранную точку через
Обозначим выбранную точку через  рис. 1.5.1.
рис. 1.5.1.
В соответствующем цикле алгоритма определяется точка  после того, как найдены точки
после того, как найдены точки  . В диапазоне значений
. В диапазоне значений  определяются величины углов
определяются величины углов

выбирается значение  при котором величина угла
при котором величина угла  минимальна на множестве точек, не включающем точки
минимальна на множестве точек, не включающем точки  Случай, когда это приводит к получению нескольких значений
Случай, когда это приводит к получению нескольких значений  следует снова рассмотреть отдельно. Новая точка обозначается через
следует снова рассмотреть отдельно. Новая точка обозначается через  . В цикле алгоритма проводятся итерации вплоть до возвращения к точке
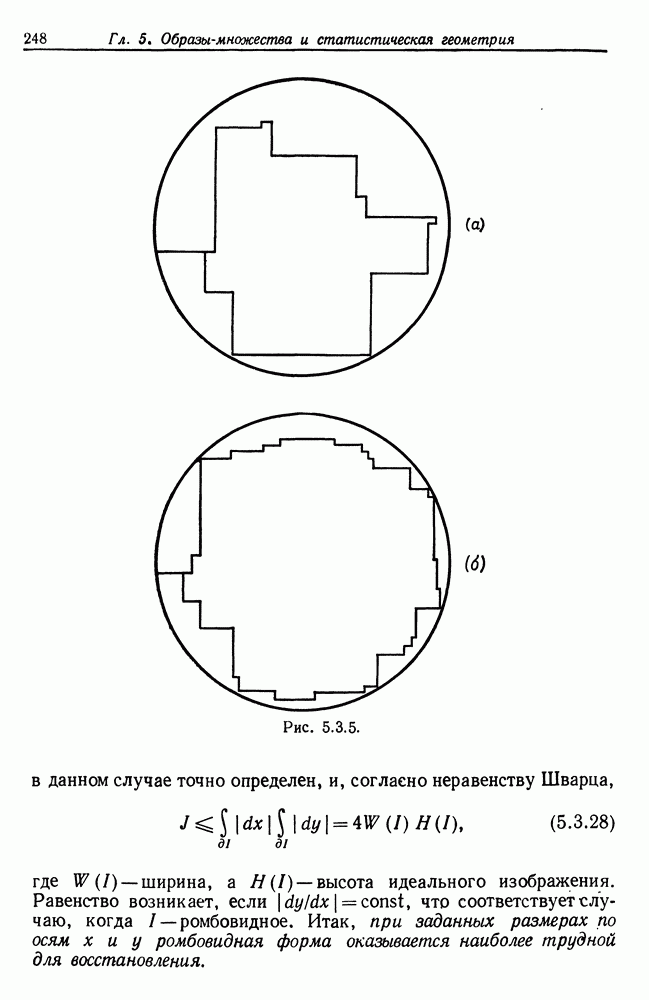
. В цикле алгоритма проводятся итерации вплоть до возвращения к точке  .
.

Рис. 1.5.1.

Рис. 1.5.2.
Если  мало, то алгоритм может оказаться приемлемым, однако при больших значениях
мало, то алгоритм может оказаться приемлемым, однако при больших значениях  лучше попытаться его усовершенствовать. Во-первых, очевидно, что не обязательно определять угол (вычисляя значение арктангенса), а достаточно найти отношения разностей значений координат у их. Более существенно то обстоятельство, что в случае достаточно компактных точечных множеств «прямолинейный» алгоритм тратит слишком много времени на «внутренние» точки множества.
лучше попытаться его усовершенствовать. Во-первых, очевидно, что не обязательно определять угол (вычисляя значение арктангенса), а достаточно найти отношения разностей значений координат у их. Более существенно то обстоятельство, что в случае достаточно компактных точечных множеств «прямолинейный» алгоритм тратит слишком много времени на «внутренние» точки множества.
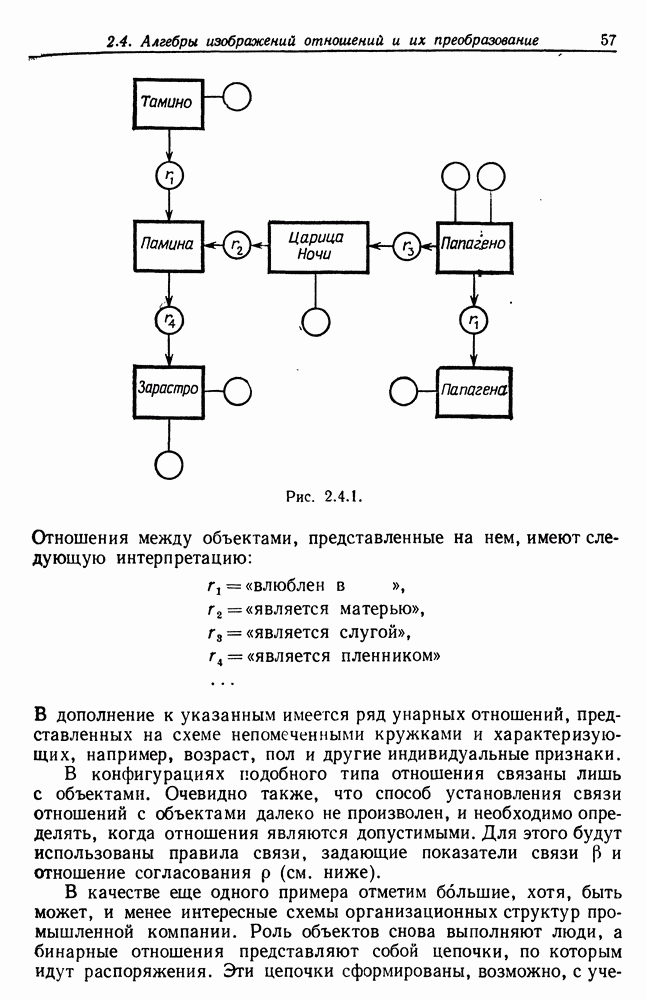
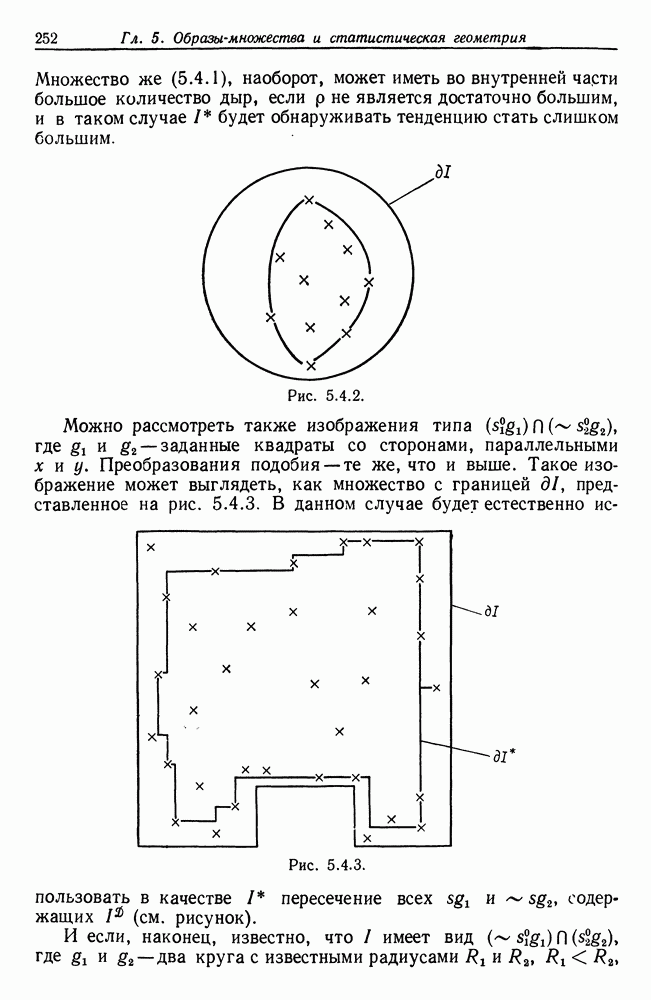
Чтобы избежать этого, можно, например, для начала получить грубое представление о том, какие точки действительно являются
«внутренними» и не входят в выпуклую оболочку. Эта идея возвращает нас к одному замечанию Р. Хемминга. Строится описанный квадрат со сторонами, параллельными осям координат, как на рис. 1.5.2, и выпуклая оболочка рассматриваемых точек заключена в границах квадрата. Эта оболочка будет четырехугольником, если на каждой стороне квадрата лежит по одной точке, в противном случае — многоугольником с большим числом сторон. Исключим из рассмотрения все точки, лежащие внутри многоугольника, и применим «прямолинейный» алгоритм к остальным точкам. Если множество точек достаточно компактно, то эта процедура принесет существенную экономию. Более подробное изучение этой алгоритмической задачи будет предпринято в гл. 6, где мы убедимся в том, что можно сделать много больше описанного здесь.
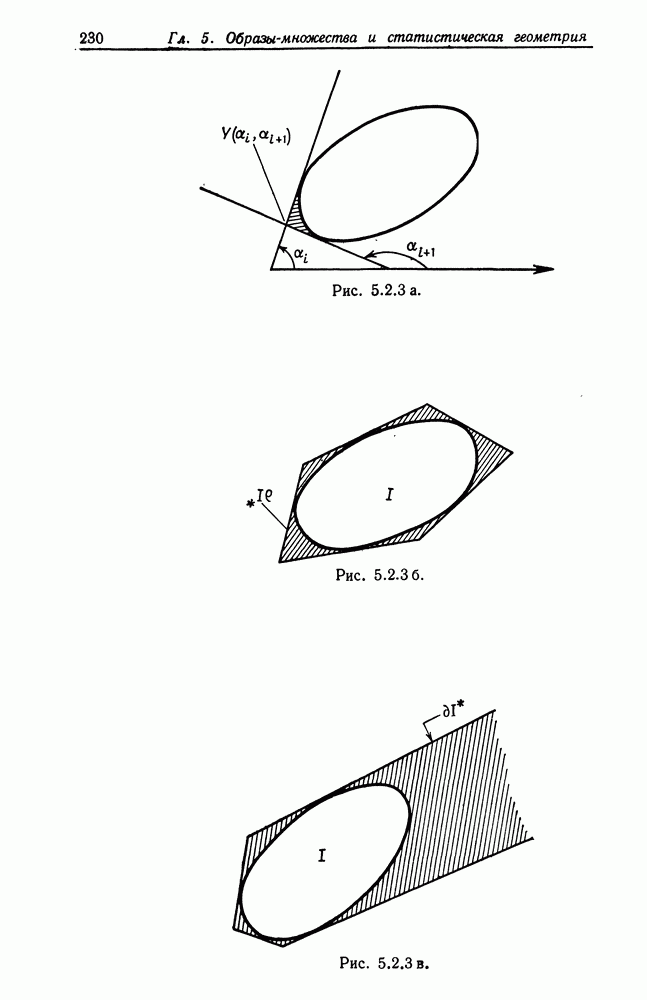
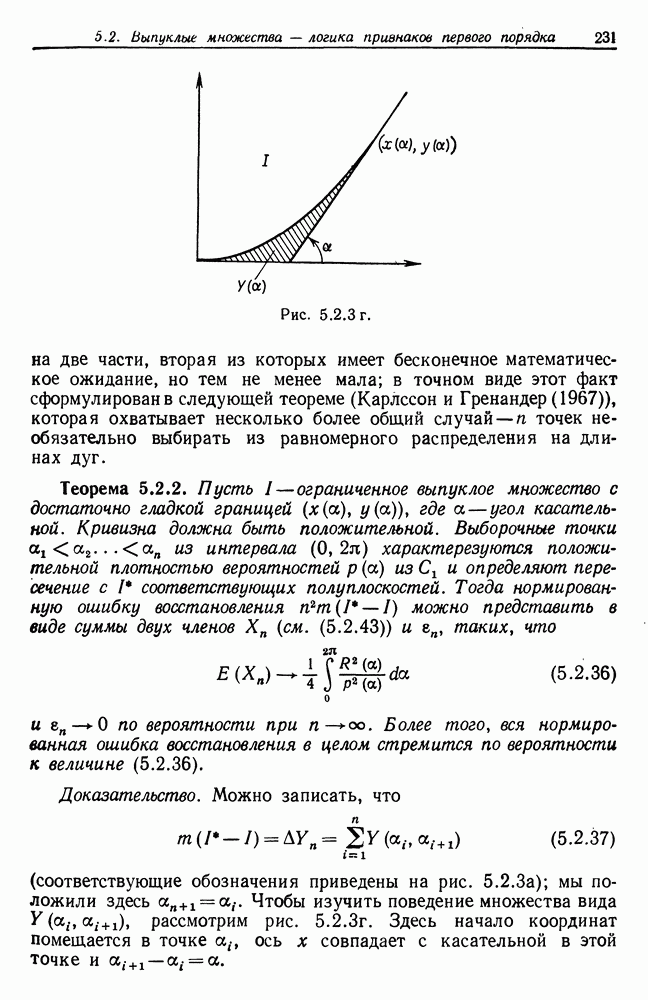
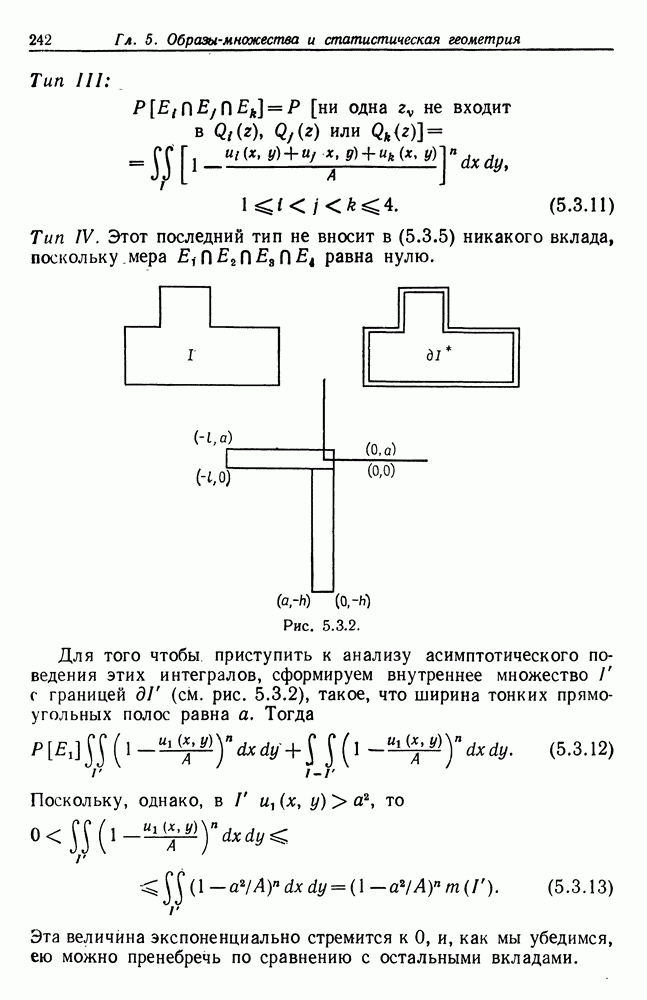
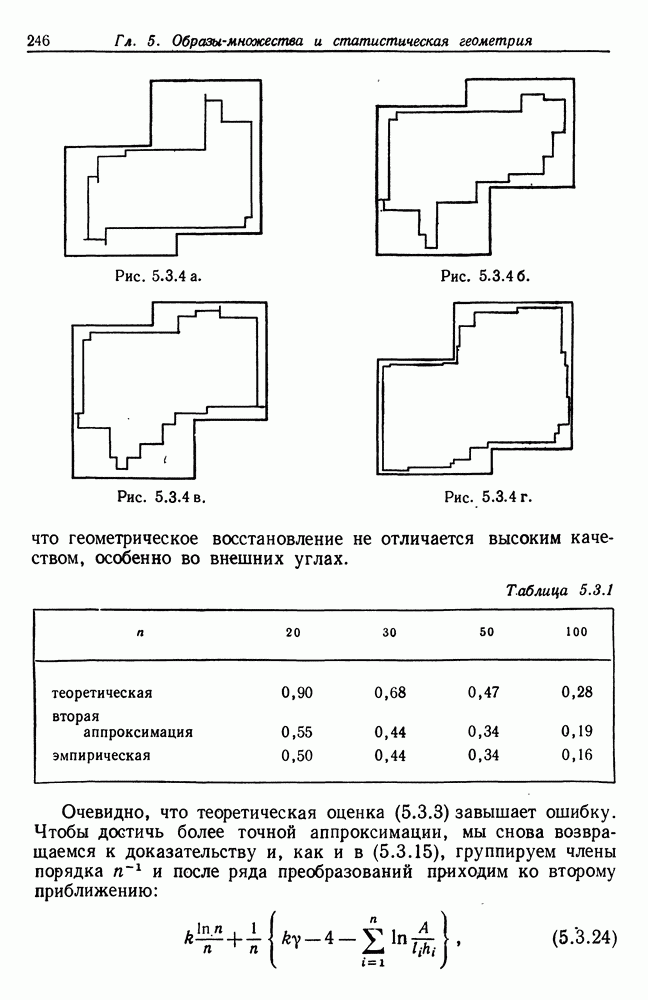
Очень часто определение оператора изображения будет связано с задачей отыскания максимума или минимума для  переменных. Если величина
переменных. Если величина  мала, например равна 1 или 2, то можно использовать стандартные процедуры численного анализа (см., скажем, монографию Дальквиста и Бьёрка (1974), гл. 10).
мала, например равна 1 или 2, то можно использовать стандартные процедуры численного анализа (см., скажем, монографию Дальквиста и Бьёрка (1974), гл. 10).
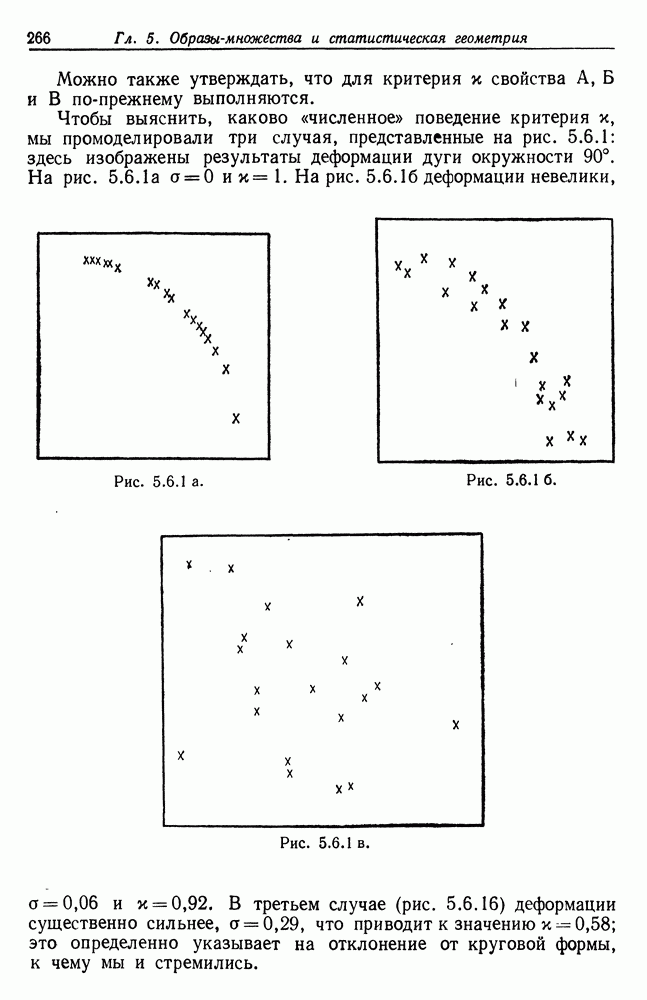
При больших размерностях мы сталкиваемся с обычными трудностями, возникающими при использовании методов спуска, эвристического поиска и т. п. Затруднения могут быть связаны с определением абсолютного, а не локального экстремума, сходимость может оказаться слабой и могут понадобиться значительные затраты вычислительных ресурсов. Следовательно, мы будем стараться избегать применения общих методов оптимизации. Одна из целей нашей теории образов заключается в структуризации задачи с помощью специфических алгебр изображений в максимально возможной степени с тем, чтобы уменьшить объем вычислений до осуществимых пределов, используя специальные структуры для получения преимуществ при вычислениях.
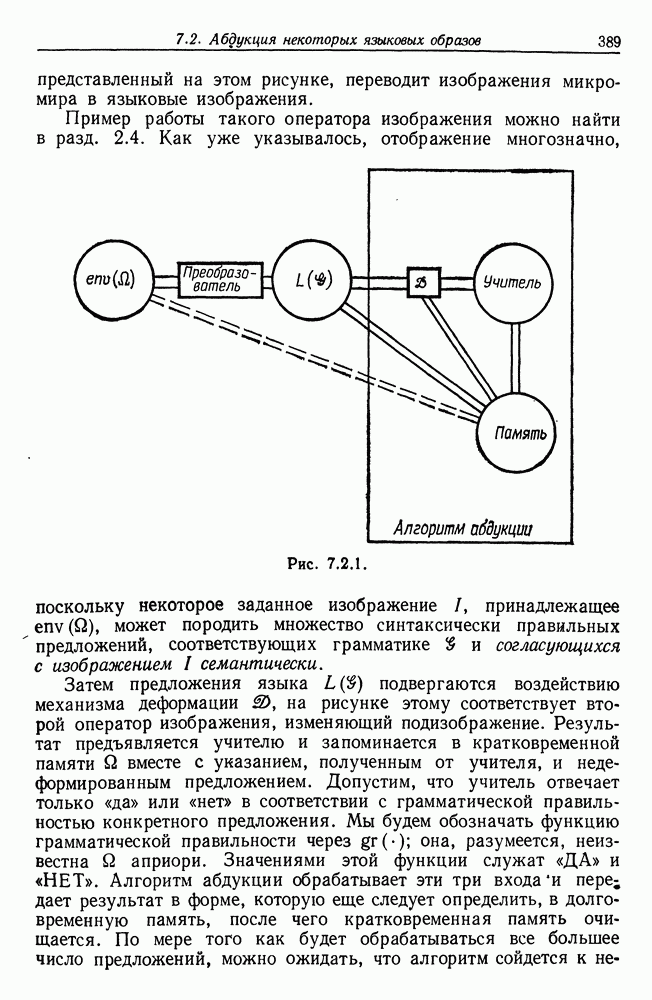
В настоящее время работа в области распознавания образов в значительной степени связана со стремлением получить более общие результаты в том, что касается алгоритмов обучения и тому подобного. Наш подход ориентирован на получение теоретических результатов применительно к специфическим видам образов. В то же время получаемые в результате алгоритмы должны быть эмпирически устойчивыми: ошибки наблюдения и другие ограничения, налагаемые на информацию и известные специалисту, выполняющему анализ данных, обязательно следует учитывать. Мы сделали это, включив в нашу теорию роль для деформаций.
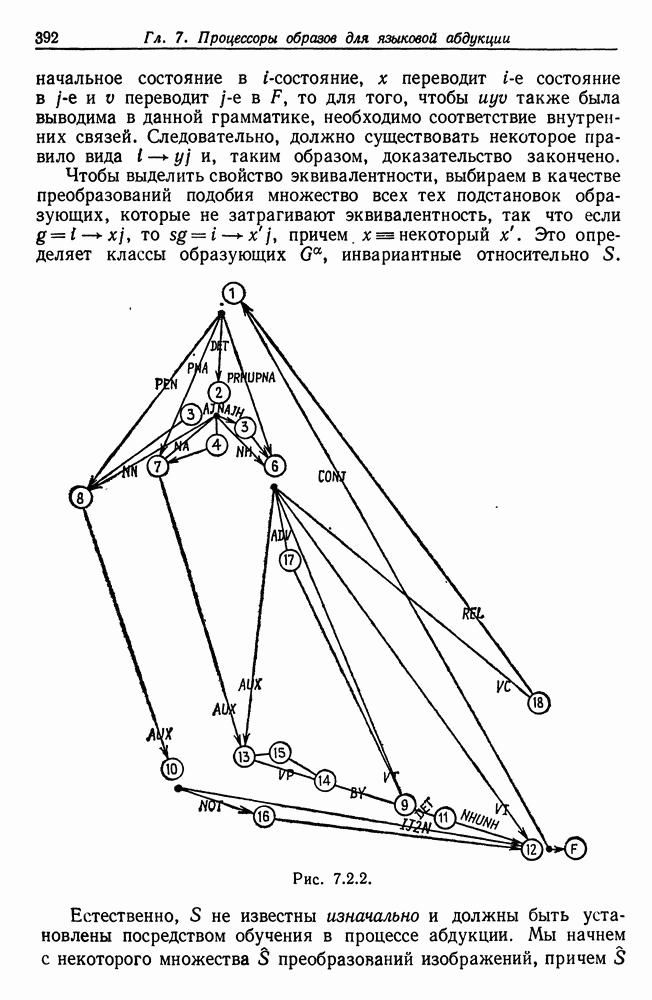
Материал в гл. 2—7 организован в соответствии с типом рассматриваемой структуры образа Мы будем пользоваться идеями, изложенными в томе 1, основывая анализ образов в каждом конкретном случае на определенной алгебре изображений и опираясь либо на структуры, введенные в томе 1, либо вводя новые.
Определив цепь синтеза образа во всей ее полноте, мы изучим задачи, относящиеся к восстановлению, аппроксимации и другим операциям над изображениями, с позиций, изложенных в предыдущих разделах. Начав с рассмотрения нескольких случаев, математическое содержание которых элементарно, мы перейдем к задачам, бросающим значительно более серьезный вызов. При этом неизбежно столкнемся с большими математическими трудностями, чем встречались нам в томе 1, где упор делался на концептуальный анализ.
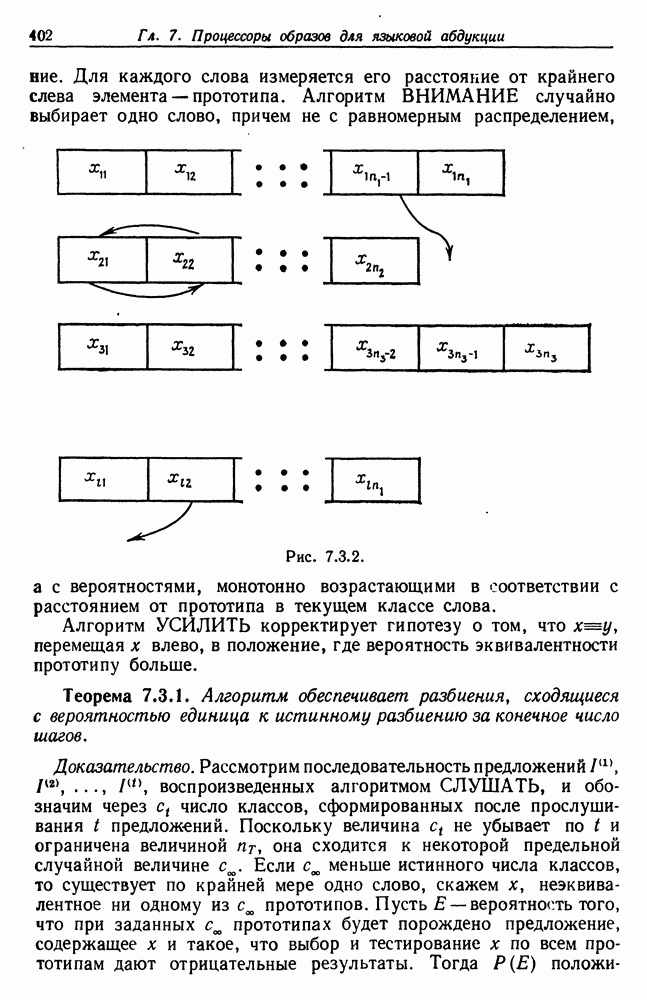
Математический анализ часто будет сопровождаться обсуждением алгоритмических проблем и вычислениями, как уже отмечалось в разд. 1.5. Вычислительные процедуры будут использоваться также и в другом качестве —не для получения результатов, а как средство, позволяющее нам глубже постичь задачу: они помогут нашей интуиции, позволят нам выдвигать гипотезы или прольют свет на уже полученные результаты.
Это будет достигнуто, если мы будем использовать вычислительные методы, так как описано в других наших публикациях (см., например, работы автора (1973)). Здесь речь не идет о вычислениях ради получения результатов, скорее мы имеем в виду экспериментальную математику. С помощью интерактивных вычислительных систем планируются и реализуются эксперименты, позволяющие при помощи обучения на индуктивной основе устанавливать принцип действия операторов изображения применительно к различным конкретным ситуациям. Для того чтобы делать это эффективно с точки зрения удобства для исследователя, а не затрат времени центрального процессора, необходимо располагать подходящими программными средствами. Большая часть программ была составлена на языке АПЛ, который, судя по всему, приводил к лучшим алгоритмам в том отношении, что алгоритмические трудности обнаруживались в явном виде, они не были затемнены несущественными деталями.
Проведение математического эксперимента на вычислительной машине требует, чтобы вычисления и анализ осуществлялись параллельно и быстро, причем таким способом, который может быть легко освоен исследователями. Очень важным подспорьем является доступ к устройствам вывода графической информации, непосредственно подключенным к ЭВМ: графопостроителям и дисплеям с телеэкраном. Не обязательно, чтобы это были устройства самых современных типов, и от них редко требуется высокая точность. В крайнем случае можно обратиться к автономным графопостроителям, таким, как CALCOMP, но это, конечно, замедлит выполнение экспериментов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
- 2.4. Алгебры изображений отношений и их преобразование
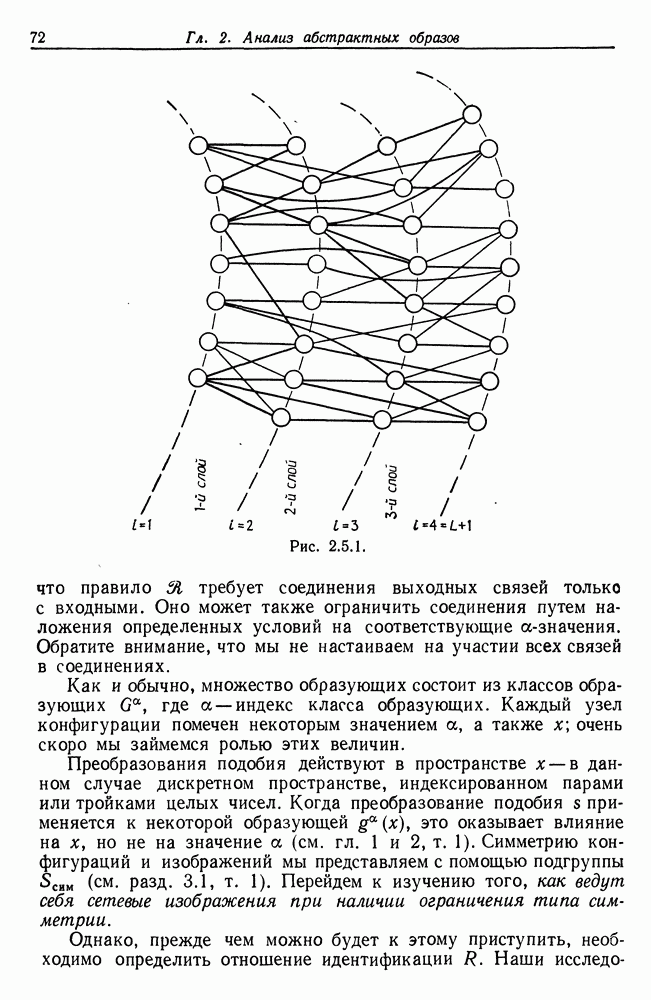
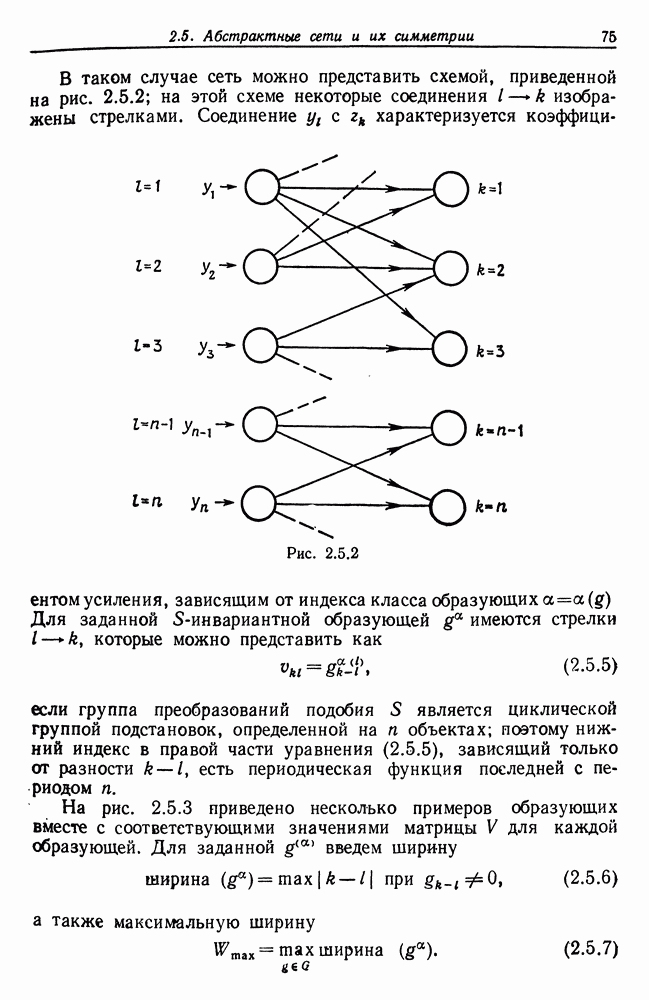
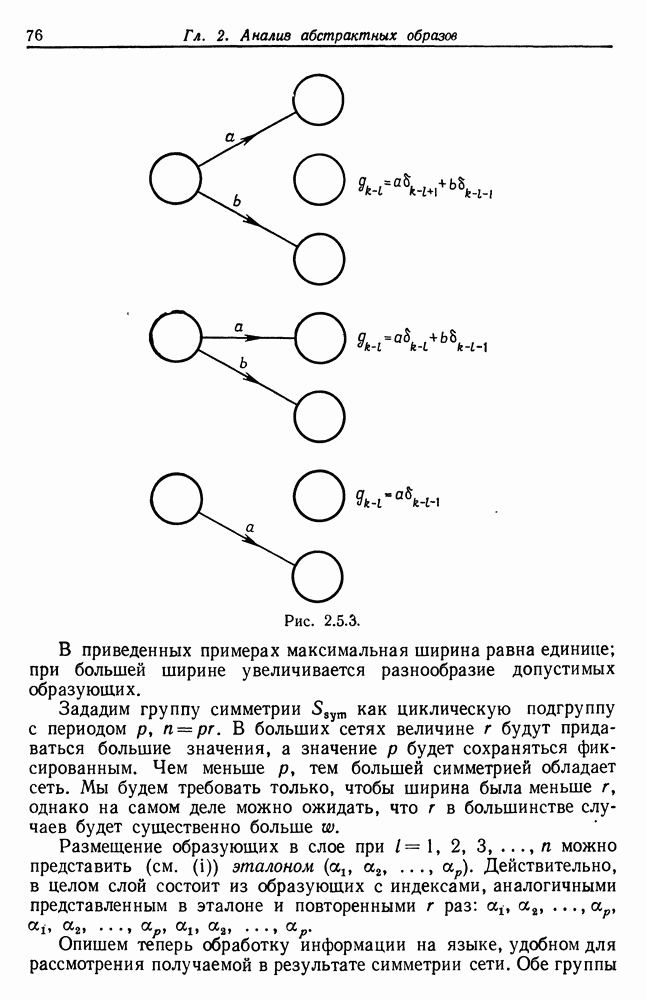
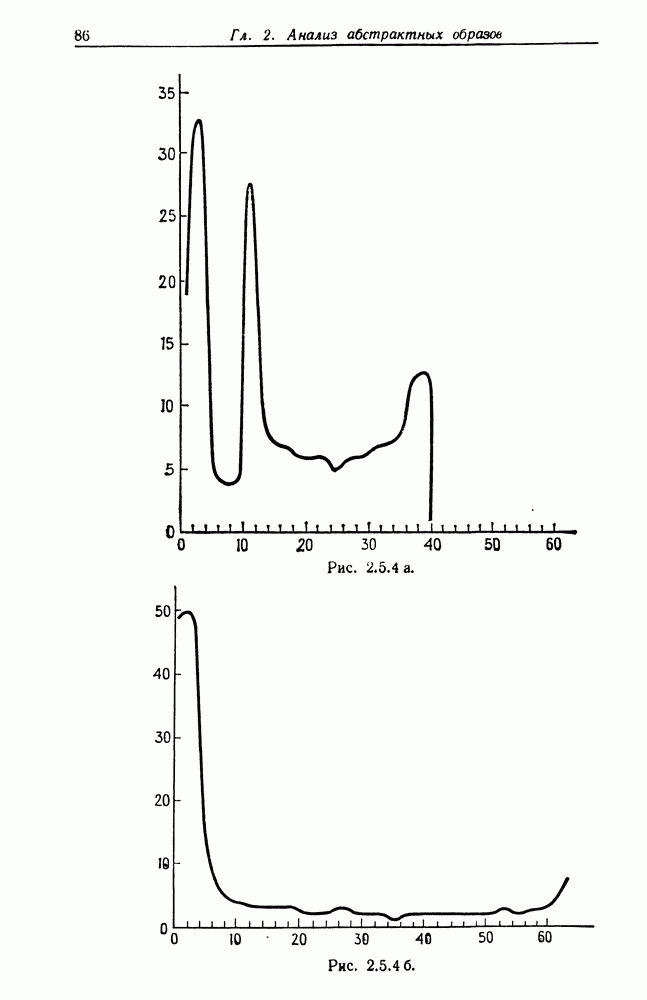
- 2.5. Абстрактные сети и их симметрии
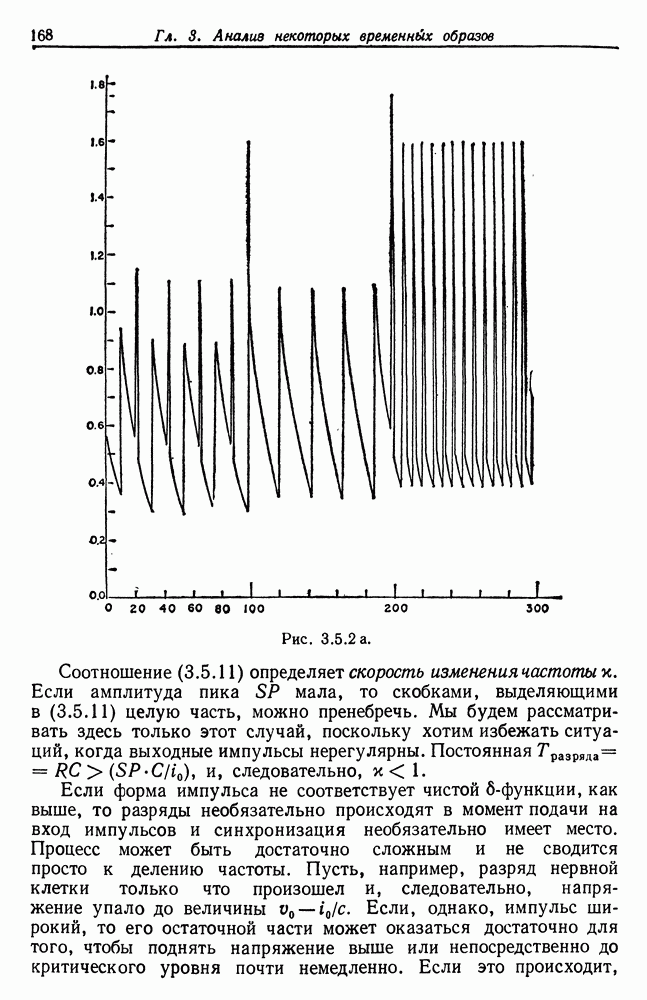
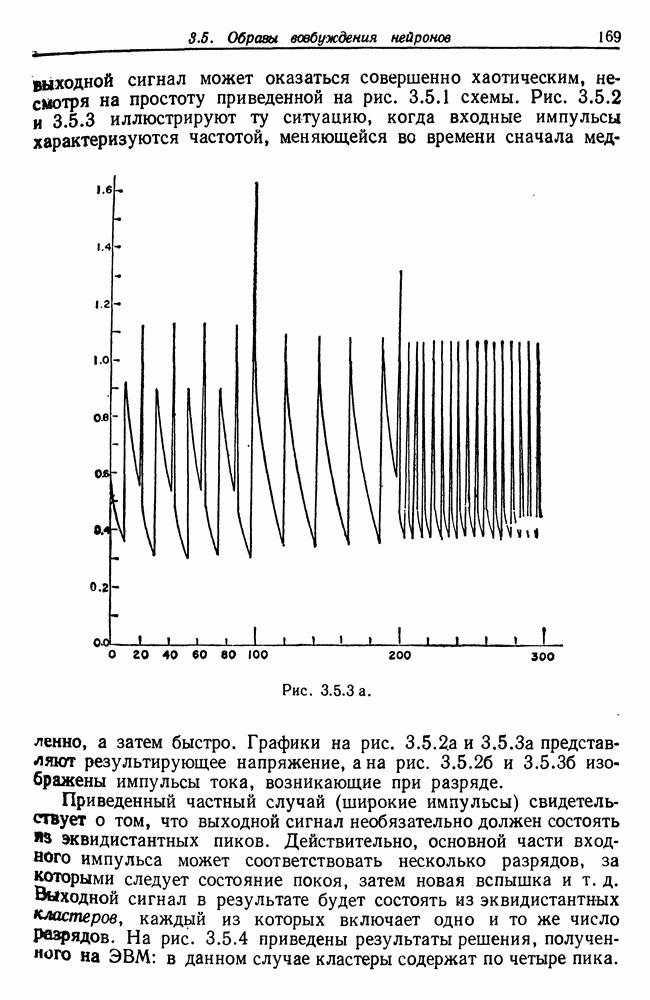
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
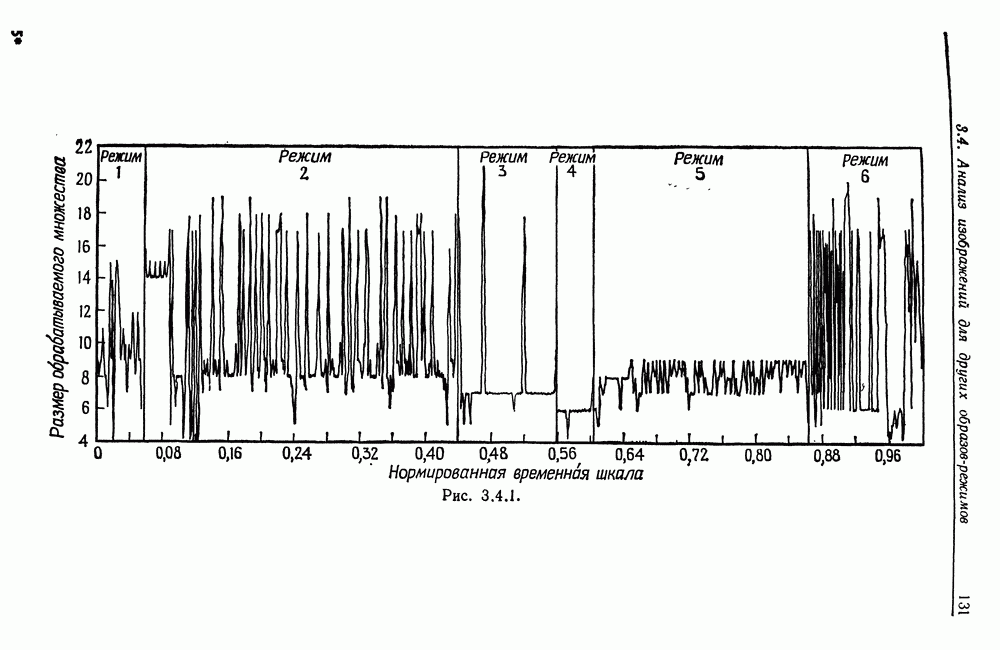
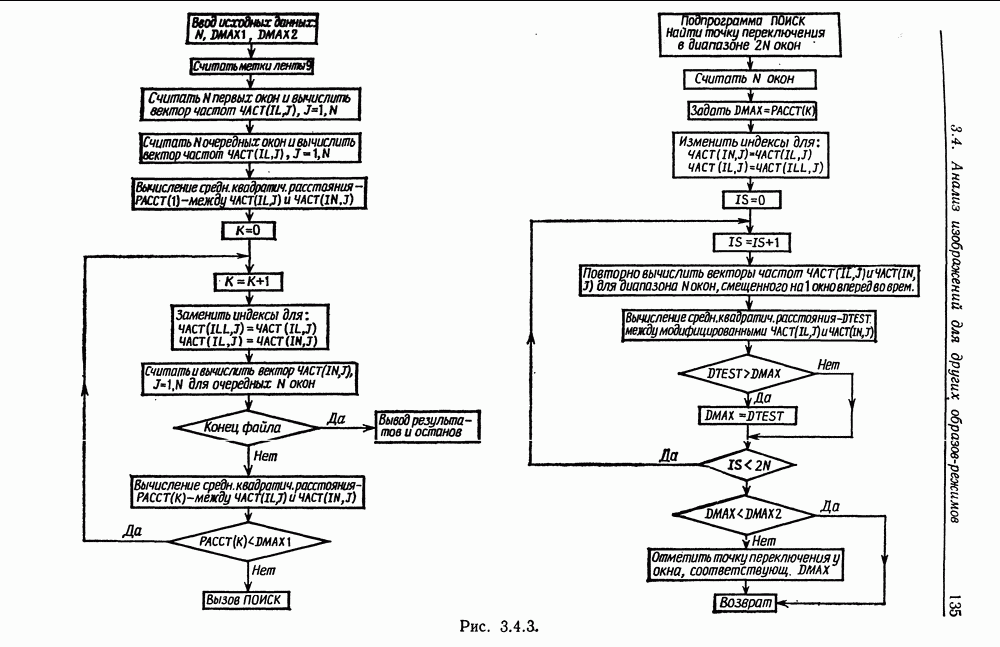
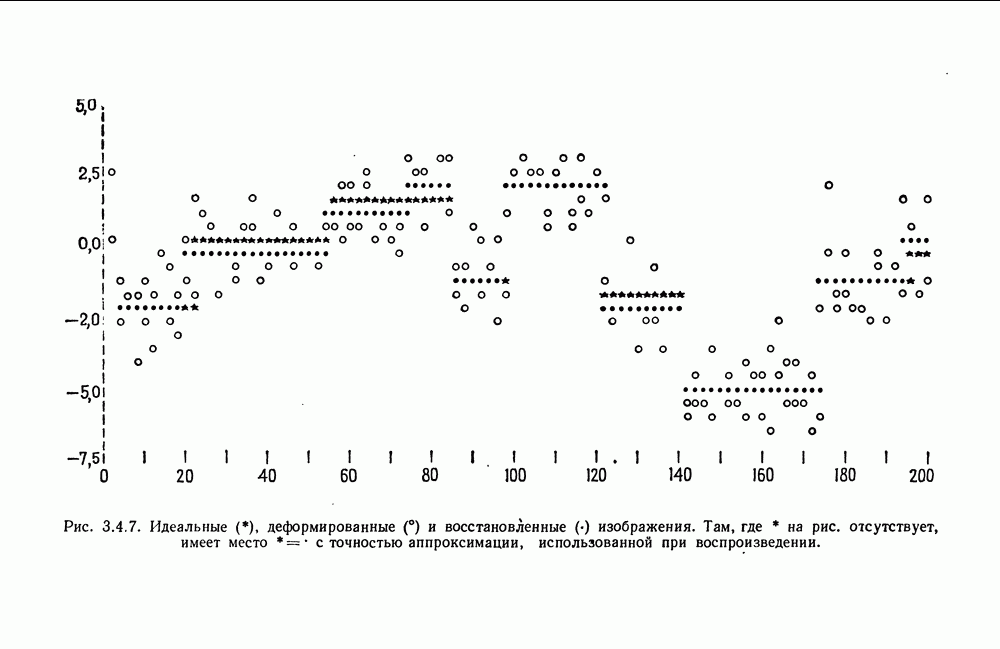
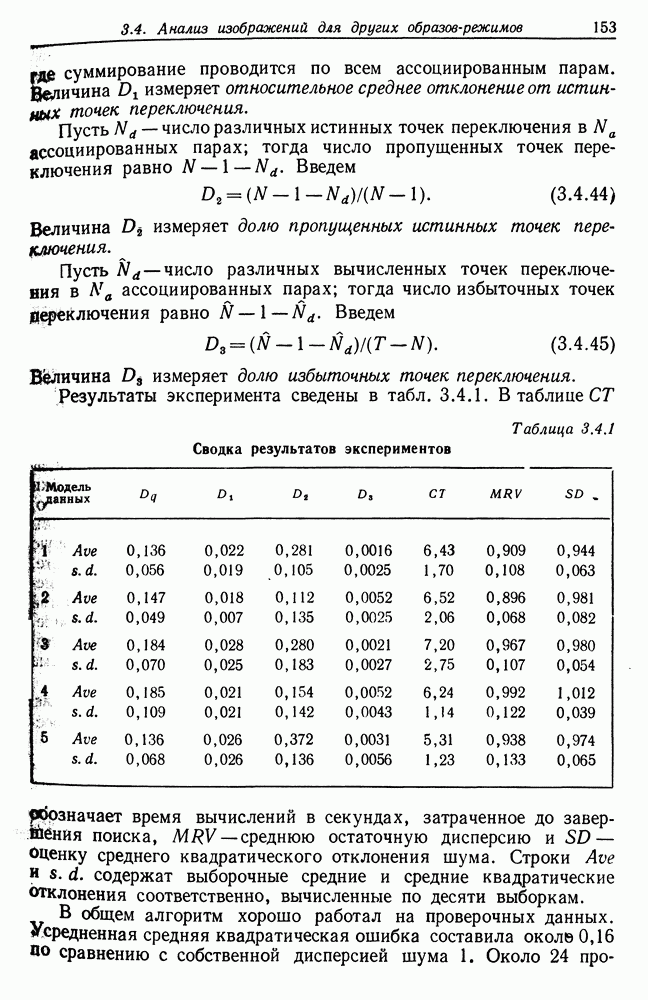
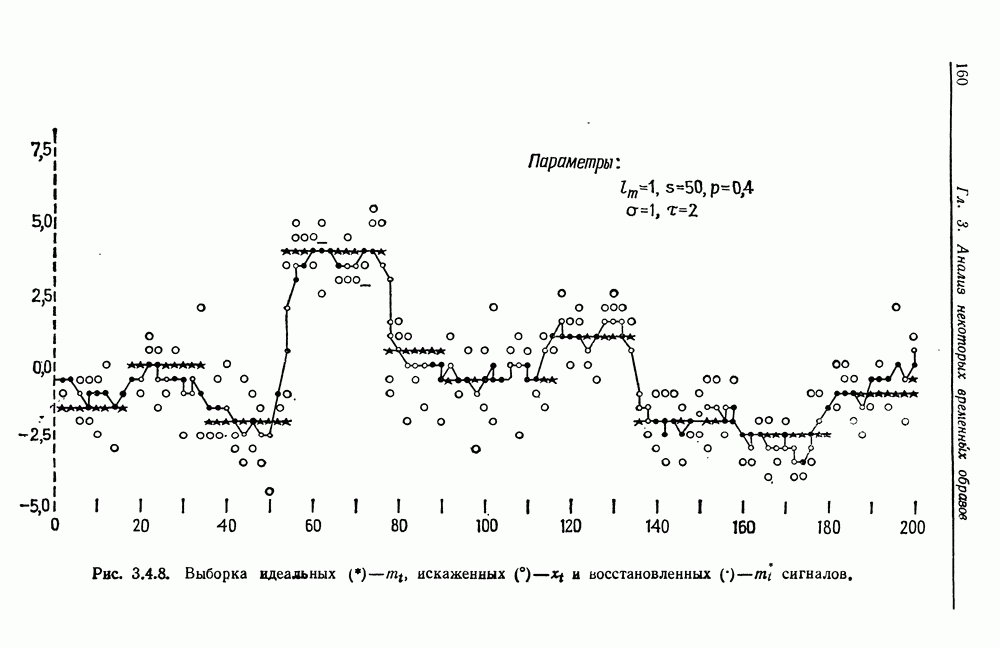
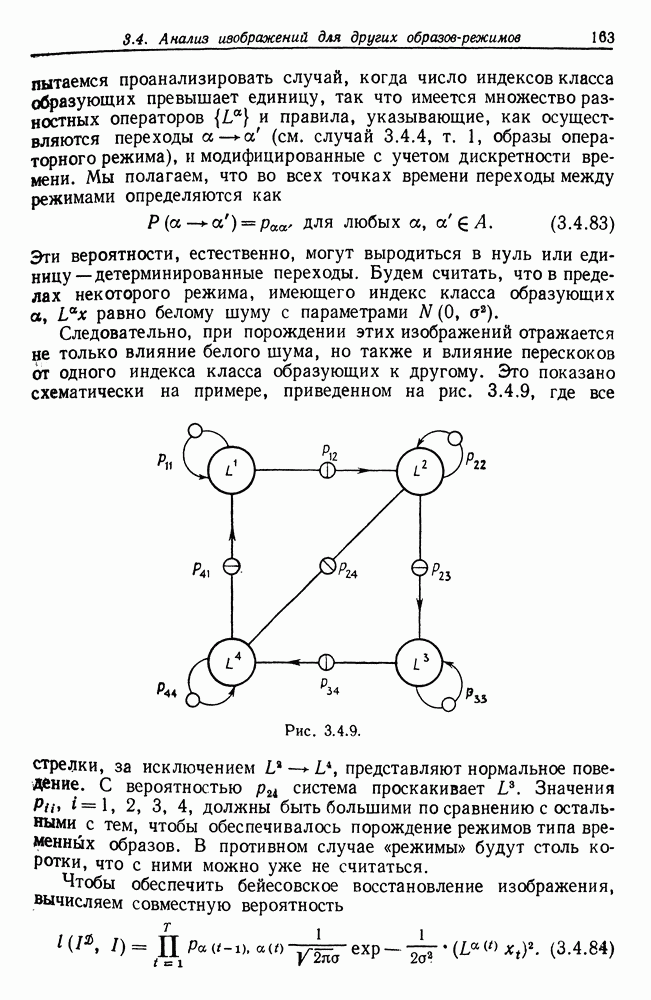
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
- 4.2. Рентгенография кристаллов
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
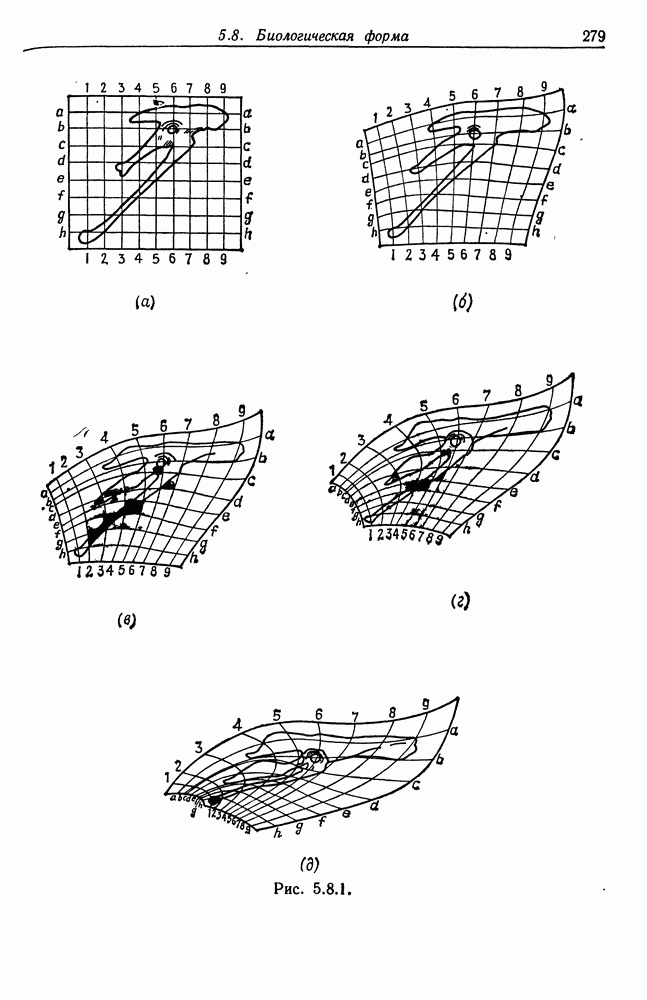
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
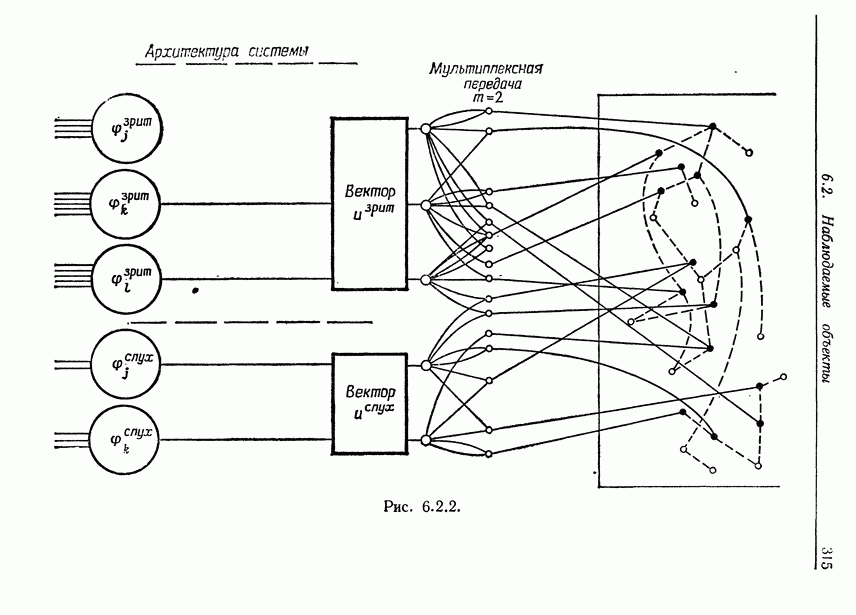
- 6.2. Наблюдаемые объекты
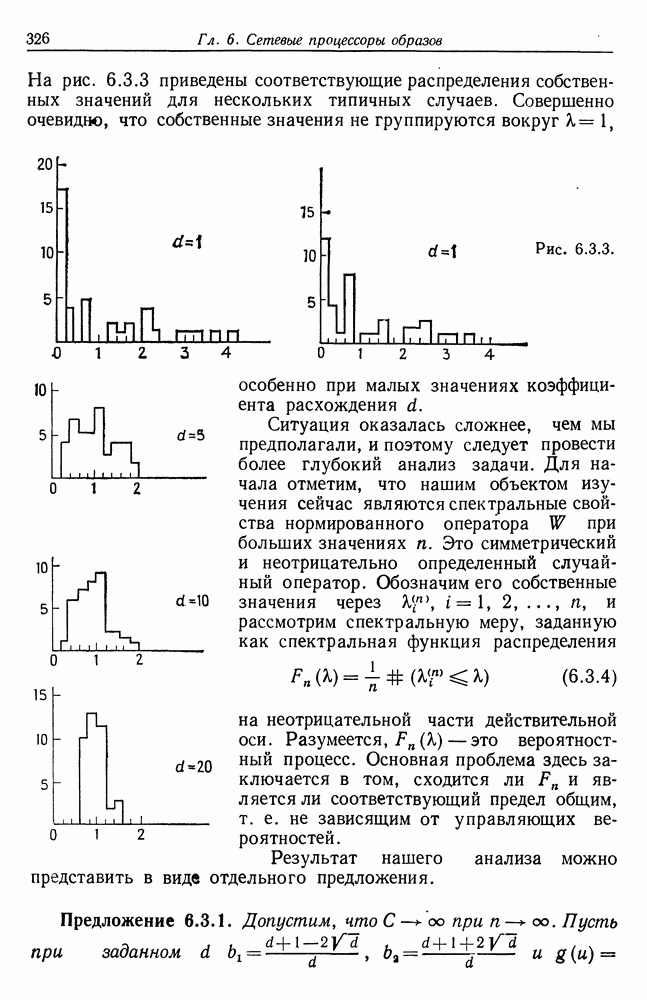
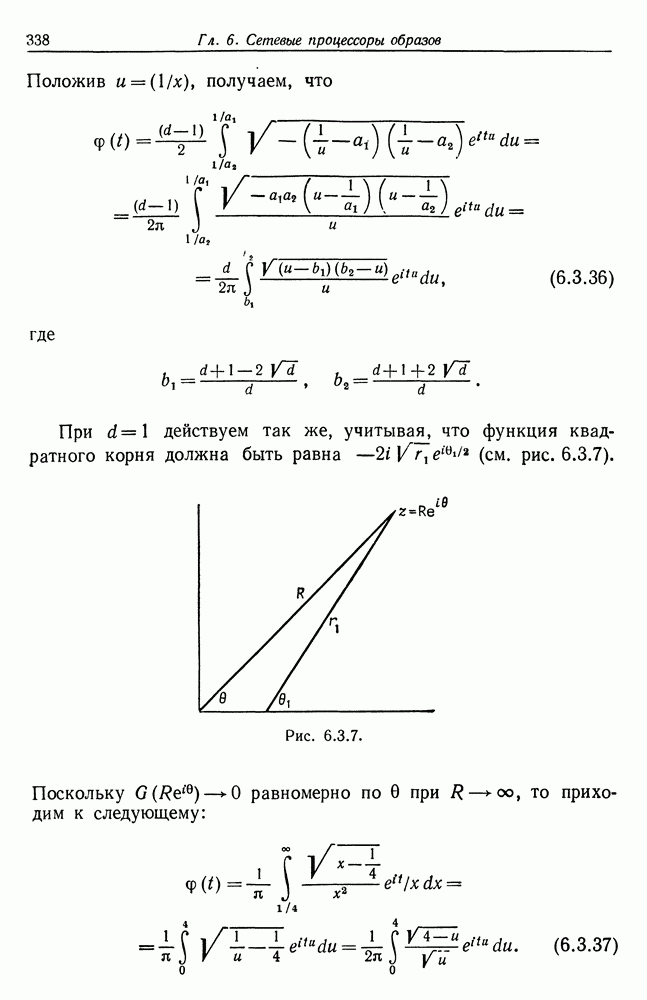
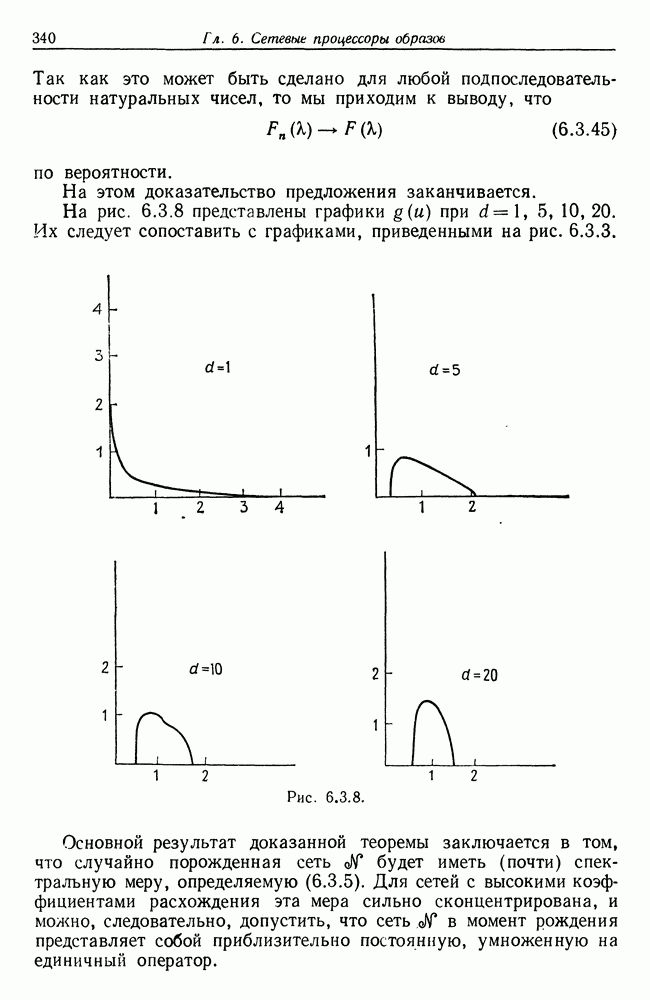
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы