| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 7. Процессоры образов для языковой абдукции
7.1. Абдукция регулярных структур
В гл. 6 мы изучали сеть  которая в состоянии изменять сама себя для того, чтобы обучиться по крайней мере некоторым из образов, встречающихся в ее среде. Достигается это при помощи изменения коэффициентов связи
которая в состоянии изменять сама себя для того, чтобы обучиться по крайней мере некоторым из образов, встречающихся в ее среде. Достигается это при помощи изменения коэффициентов связи  т. е. модификации процессора изображений, который представляет собой
т. е. модификации процессора изображений, который представляет собой  Осуществляемый в результате вывод образа относится к индуктивному типу: с помощью наблюдения, происходящего в среде, сеть
Осуществляемый в результате вывод образа относится к индуктивному типу: с помощью наблюдения, происходящего в среде, сеть  будет в состоянии все в большей и большей степени понимать окружающую ее структуру образов.
будет в состоянии все в большей и большей степени понимать окружающую ее структуру образов.
Теперь мы займемся процессорами образов, которые также выполняют вывод, связанный со структурой, но делают это способом, в котором во главу угла ставится явное порождение правдоподобных гипотез. Конечно, можно сказать, что и предыдущий процессор образов порождает гипотезы. В самом деле, изменения геометрии (см. разд. 6.6) можно интерпретировать как придание некоторым высказываниям (гипотезам) относительно алгебры изображений  большего правдоподобия, а другим — меньшего. Эта разновидность гипотез является, однако, неявной в отличие от тех, которые будут изучаться здесь.
большего правдоподобия, а другим — меньшего. Эта разновидность гипотез является, однако, неявной в отличие от тех, которые будут изучаться здесь.
Воспользовавшись термином, введенным К. С. Пирсом (см. Пирс (1955), с. 150—156), мы будем говорить об абдукции в случае, когда наш процессор применяется к изображениям, принадлежащим не полностью известной структуре образов, с тем, чтобы породить в качестве выходного результата правдоподобные гипотезы, касающиеся этой структуры. Быть может, этот процесс можно называть и «правдоподобными рассуждениями», следуя терминологии Пойа, но тогда лишь в ограниченном контексте, который будет описан в следующем разделе.
Обозначим входные изображения через  причем все они принадлежат некоторой алгебре изображений здесь эти изображения предполагаются идеальными. Модификации, необходимые, если они деформированы, сугубо нетривиальны, но обсуждение этого вопроса мы пока отложим.
причем все они принадлежат некоторой алгебре изображений здесь эти изображения предполагаются идеальными. Модификации, необходимые, если они деформированы, сугубо нетривиальны, но обсуждение этого вопроса мы пока отложим.
Следует подчеркнуть, что на выходе алгоритма абдукции (или абдукционной машины) должны воспроизводиться структуры образов, но не отдельные изображения для каждого входного изображения.
Другими словами, мы не ставим задачу отыскания некоторого одиночного оператора изображения, выполняющего определенную функцию, например восстановление изображения (см. разд. 1.1). Здесь мы работаем на следующем, более высоком уровне абстракции, и в данном случае отображение имеет вид

где П обозначает некоторую совокупность  структур образов скажем алгебр изображений. Естественно, П не должна быть абсолютно универсальной, выбор
структур образов скажем алгебр изображений. Естественно, П не должна быть абсолютно универсальной, выбор  лимитируется нашими априорными значениями об образующих, отношениях связи, типах соединения и т. п. Другой крайний случай, когда П включает всего две или несколько допустимых также представляет ограниченный интерес, и поэтому мы будем предполагать, что совокупность П включает большое или даже бесконечное множество структур образов.
лимитируется нашими априорными значениями об образующих, отношениях связи, типах соединения и т. п. Другой крайний случай, когда П включает всего две или несколько допустимых также представляет ограниченный интерес, и поэтому мы будем предполагать, что совокупность П включает большое или даже бесконечное множество структур образов.
Что касается числа множителей прямого произведения в левой части (7.1.1), то мы будем считать его конечным, но также будем считать, что и алгоритм абдукции должен быть последовательным в следующем смысле: при появлении очередного изображения для получения новой гипотезы требуется лишь умеренный объем дополнительных вычислений сверх того, что уже было вычислено, а не повторение всех расчетов с самого начала.
Еще важнее то, что мы будем стремиться к робастным (или устойчивым), нечувствительным к ошибкам и естественным процессорам образов. Устойчивость означает, что даже тогда, когда алгоритм рассчитан на хорошие результаты при работе с некоторым определенным типом структуры образов, он не окажется совершенно непригодным при предъявлении несколько иного типа структуры образов. Качество алгоритма может пострадать, но он не прекратит функционировать. Нечувствительность к ошибкам означает, что случайные ошибки вычислений или входных сигналов не должны приводить к каким-либо серьезным длительным последствиям — их влияние должно исчезать по мере роста числа обработанных изображений. Труднее уточнить понятие «естественности» - то, что одному исследователю кажется естественным алгоритмом, может показаться другому искусственным. Как бы то ни было, мы будем стараться выбирать алгоритмы так, чтобы была очевидной возможность их реализации в процессорах образов реального мира. Подробнее мы остановимся на этом вопросе позже.
Мы выделили именно эти три свойства вкупе с индуктивным (в противовес дедуктивному) типом логики потому, что нас интересуют модели, потенциально применимые к процессорам, которые встречаются в реальном мире, хотя в настоящее время их характеристики могут казаться нереалистичными (см. т. 1, с. 203).
С другой стороны, меньше внимания мы будем уделять прочим желательным качествам алгоритма, таким, как вычислительная эффективность, скорость сходимости и т. п.
Как же следует решать задачу вывода алгебры изображений  если задана последовательность изображений
если задана последовательность изображений  Если П — счетное и, следовательно, можно записать
Если П — счетное и, следовательно, можно записать

мы могли бы начать с изучения в качестве гипотетической структуры образов алгебры изображений  для
для  и, если продолжать эту процедуру для
и, если продолжать эту процедуру для  Как только встречается изображение
Как только встречается изображение  для которого и мы переходим к следующей алгебре изображений
для которого и мы переходим к следующей алгебре изображений  и снова проверяем, выполняется ли
и снова проверяем, выполняется ли  затем
затем  и т. д. Вся процедура заканчивается, когда мы получаем некоторую алгебру изображений
и т. д. Вся процедура заканчивается, когда мы получаем некоторую алгебру изображений  для которой все результаты проверки положительны, если такая ситуация вообще возникает.
для которой все результаты проверки положительны, если такая ситуация вообще возникает.
Чтобы гарантировать, что эта процедура приводит к правильной гипотезе  нам в принципе необходим доступ к неограниченной (потенциально бесконечной) последовательности изображений, а также надо иметь определенную уверенность, что эта последовательность «репрезентативна» для алгебры изображений
нам в принципе необходим доступ к неограниченной (потенциально бесконечной) последовательности изображений, а также надо иметь определенную уверенность, что эта последовательность «репрезентативна» для алгебры изображений  в целом. Ниже мы будем считать, что эта последовательность порождается простым случайным источником в соответствии с вероятностной мерой Р, заданной
в целом. Ниже мы будем считать, что эта последовательность порождается простым случайным источником в соответствии с вероятностной мерой Р, заданной  При этом, вообще говоря, необходимо, чтобы носителем меры Р служила вся алгебра изображений
При этом, вообще говоря, необходимо, чтобы носителем меры Р служила вся алгебра изображений 
Тогда можно попытаться доказать теоремы сходимости, указывающие, что алгоритм будет сходиться к  за конечное число шагов с вероятностью единица. Подобные результаты можно получить, допустив, например, что все алгебры изображений
за конечное число шагов с вероятностью единица. Подобные результаты можно получить, допустив, например, что все алгебры изображений  счетные, но мы не будем развивать эту идею.
счетные, но мы не будем развивать эту идею.
Действительно, такой алгоритм едва ли можно назвать естественным: по сути он представляет собой просто метод проб и ошибок. Более того, он не является абдукцией в указанном выше смысле, поскольку последовательные гипотезы не порождались как правдоподобные относительно наблюдавшейся последовательности — они просто заданы некоторой фиксированной последовательностью.
Для выбора правдоподобных гипотез переформулируем нашу задачу в соответствии с современной статистической доктриной. При заданной конечной части  последовательности изображений будем рассматривать алгебру истинных изображений
последовательности изображений будем рассматривать алгебру истинных изображений  как некоторый неизвестный «параметр», подлежащий оценке. Тогда можно поставить задачу определения «наилучшей» статистической оценки в соответствии с заданным критерием и обратиться
как некоторый неизвестный «параметр», подлежащий оценке. Тогда можно поставить задачу определения «наилучшей» статистической оценки в соответствии с заданным критерием и обратиться
к методам статистического оценивания. Естественно, наш «параметр»  может оказаться совсем не похожим на то, что считается параметром в стандартной теории статистического оценивания, это может быть нечто, значительно более сложное, но тем не менее мы в состоянии успешно решить подобную задачу оценивания.
может оказаться совсем не похожим на то, что считается параметром в стандартной теории статистического оценивания, это может быть нечто, значительно более сложное, но тем не менее мы в состоянии успешно решить подобную задачу оценивания.
Поэтому можно сказать, что полученная в результате оценка является правдоподобной, поскольку она в максимально возможной степени учитывает заданную информацию при выборе гипотезы. Однако подобные алгоритмы могут показаться не очень естественными. Соответствующие методы оценки могут основываться на методе максимального правдоподобия, бейесовском подходе, методе наименьших квадратов и т. д.; при нахождении максимума в них могут использоваться численные схемы типа метода Ньютона, обращение матриц или стратегии поиска. Идея о том, что разум человека будет при обучении определенному языку опираться на способность мозга, например, обращать матрицы, является не очень привлекательной. Необходимо поискать какие-то другие алгоритмы абдукции, которые покажутся более естественными.
При предъявлении последовательности изображений можно попытаться вывести если структура связей и отношения связей поддаются наблюдению, поскольку они дали бы информацию, по крайней мере частичную, о типе соединения 2 и отношении связи  Тогда можно было бы вывести некоторые комбинаторные правила
Тогда можно было бы вывести некоторые комбинаторные правила 
К сожалению, это редко оказывается возможным, поскольку внутренние связи обычно не поддаются непосредственному наблюдению; в гл. 3 т. 1 содержится много примеров. Чтобы обойти это затруднение, допустим, что обучающийся кроме последовательности идеальных изображений имеет доступ к учителю. Последний помогает обучающемуся, сообщая ему, принадлежат другие изображения  или нет. В таком случае в основу абдукции можно положить намеренные деформации
или нет. В таком случае в основу абдукции можно положить намеренные деформации  осуществляемые путем применения к каждому
осуществляемые путем применения к каждому  одного или нескольких механизмов деформации. Затем можно выяснить у учителя, принадлежит ли деформированное изображение
одного или нескольких механизмов деформации. Затем можно выяснить у учителя, принадлежит ли деформированное изображение  Ответы будут давать информацию о внутренних связях, хотя она и будет менее полной, чем в случае, когда наблюдению доступна вся конфигурация. Резюмируя изложенное, можно теперь сформулировать нашу задачу так:
Ответы будут давать информацию о внутренних связях, хотя она и будет менее полной, чем в случае, когда наблюдению доступна вся конфигурация. Резюмируя изложенное, можно теперь сформулировать нашу задачу так:
Случай 7.1.1 (вывод на основе деформаций). При заданных последовательности идеальных изображений  и некотором механизме деформации 3) используются сведения
и некотором механизме деформации 3) используются сведения
о справедливости или несправедливости включения исходя из чего порождаются гипотезы о структуре образов.
Эта постановка все еще слишком обща для того, чтобы быть практически полезной, поскольку она ничего не говорит о том, каким образом выбирать В гл. 4 т. 1 мы убедились, что существует богатое разнообразие механизмов деформации, и сейчас мы должны сузить выбор.
Учитывая, что нас интересует информация относительно  кажется естественным использовать некоторый механизм деформации
кажется естественным использовать некоторый механизм деформации  оставляющий без изменений большую часть изображения и модифицирующий лишь некоторое подизображение, с одной или несколькими связями, В случае если
оставляющий без изменений большую часть изображения и модифицирующий лишь некоторое подизображение, с одной или несколькими связями, В случае если  не принадлежит следует сконцентрировать внимание на указанном подизображении и его связи с остальной частью
не принадлежит следует сконцентрировать внимание на указанном подизображении и его связи с остальной частью  Более формально:
Более формально:
Случай 7.1.2 (деформация подизображении). Будем говорить, что механизм деформации  деформирует подизображении, если для любых
деформирует подизображении, если для любых  изображение разбивается на
изображение разбивается на

где  имеет ту же структуру внешних связей, что и
имеет ту же структуру внешних связей, что и 
Отметим, что в данном случае структура внешних связей остается без изменений, но не всегда это относится к показателям внешних связей. Читатель может обратить внимание, что мы уже сталкивались с вариантами, подобными случаю 7.1.2. Действительно, пульсирующие деформации (см. разд. 4.2, т. 1), суженные  при
при  деформируют только подизображение, которое содержит образующие
деформируют только подизображение, которое содержит образующие  Деформации, приводящие к исчезновению образующей (см. случай 4.2.9, т. 1), также относятся к этому типу: они уничтожают некоторое подизображение.
Деформации, приводящие к исчезновению образующей (см. случай 4.2.9, т. 1), также относятся к этому типу: они уничтожают некоторое подизображение.
Для того, чтобы обучиться чему-нибудь, наблюдая регулярность  необходимо ввести условие, в соответствии с которым деформированные изображения должны иногда оказываться вне
необходимо ввести условие, в соответствии с которым деформированные изображения должны иногда оказываться вне  т. е. деформации
т. е. деформации  должны быть гетероморфными. В противном случае при автоморфных деформациях мы не сможем отыскать истинные ограничения на комбинаторную структуру образов. Так, например, деформация сдвига (см. уравнение (4.2.1), разд. . 4.2, т. 1) не обладает достаточной мощностью. С другой стороны, случай 4.2.4 т. 1 дает деформации, которые кажутся многообещающими кандидатами в алгоритмы абдукции.
должны быть гетероморфными. В противном случае при автоморфных деформациях мы не сможем отыскать истинные ограничения на комбинаторную структуру образов. Так, например, деформация сдвига (см. уравнение (4.2.1), разд. . 4.2, т. 1) не обладает достаточной мощностью. С другой стороны, случай 4.2.4 т. 1 дает деформации, которые кажутся многообещающими кандидатами в алгоритмы абдукции.
Отношения изображений (7.1.3) и (7.1.4) можно рассматривать и по-другому, используя понятие конгруэнтности (см. т. 1, с. 32).
Если  конгруэнтно
конгруэнтно  то несомненно, будет регулярно в
то несомненно, будет регулярно в  Если же, однако, неконгруэнтно
Если же, однако, неконгруэнтно  то может оказаться нерегулярным, хотя и не всегда, но при некоторых
то может оказаться нерегулярным, хотя и не всегда, но при некоторых  Следовательно, ответ учителя на вопрос о том, выполняется ли сообщит нам определенные сведения об отношении конгруэнтности и тем самым о структуре образов. Благодаря тому что это «не всегда» так, мы не можем утверждать с определенностью, что получили правильную гипотезу. Мы имеем здесь дело с индукцией, а не с дедукцией.
Следовательно, ответ учителя на вопрос о том, выполняется ли сообщит нам определенные сведения об отношении конгруэнтности и тем самым о структуре образов. Благодаря тому что это «не всегда» так, мы не можем утверждать с определенностью, что получили правильную гипотезу. Мы имеем здесь дело с индукцией, а не с дедукцией.
Разовьем еще немного эту идею. Если бы мы попробовали применить пульсирующие деформации, то столкнулись бы с той трудностью, что группа преобразования подобия  может быть неизвестна нам полностью априори. Для того чтобы гарантировать достаточно резкие деформации, необходимо отыскать некоторое множество
может быть неизвестна нам полностью априори. Для того чтобы гарантировать достаточно резкие деформации, необходимо отыскать некоторое множество  отображений включающее
отображений включающее  но возможно большее, поскольку сдвигов может оказаться недостаточно. Тогда необходимо выбирать элементы
но возможно большее, поскольку сдвигов может оказаться недостаточно. Тогда необходимо выбирать элементы  применять их к некоторому подизображению и затем определять в процессе наблюдения, регулярно или нерегулярно деформированное изображение. Мы займемся этим вопросом более подробно в следующем разделе.
применять их к некоторому подизображению и затем определять в процессе наблюдения, регулярно или нерегулярно деформированное изображение. Мы займемся этим вопросом более подробно в следующем разделе.
После того как алгоритм абдукции построен, возникает вопрос, как реализовать его в виде работающего устройства. Так, например, сетевые процессоры, аналогичные рассматривавшимся в гл. 6, кажутся естественными кандидатами на роль абдукционных машин. Мы предпримем соответствующую попытку в разд. 7.4.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
- 4.2. Рентгенография кристаллов
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
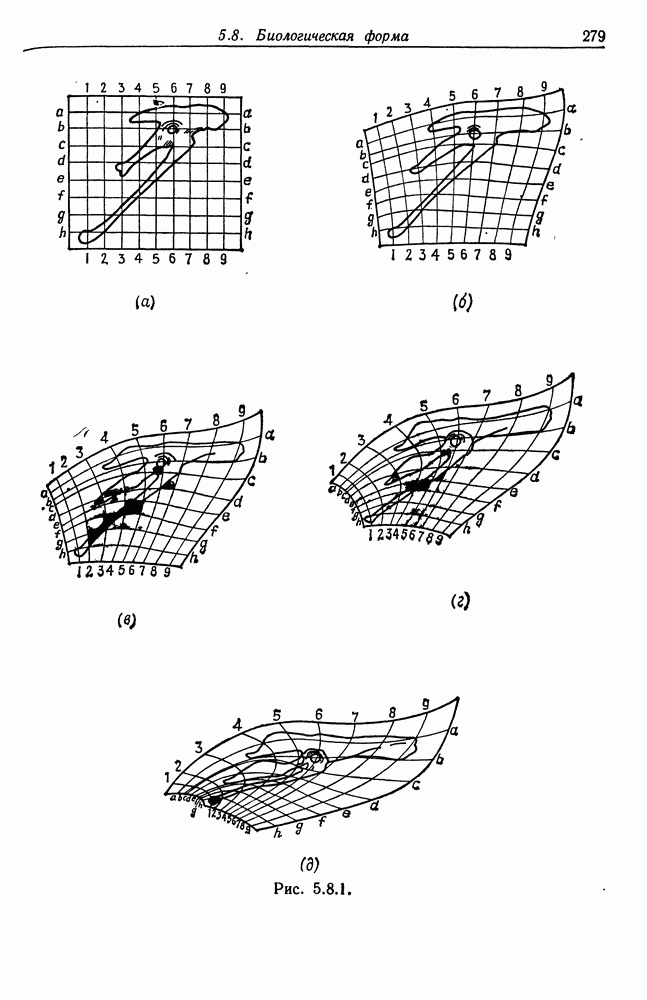
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
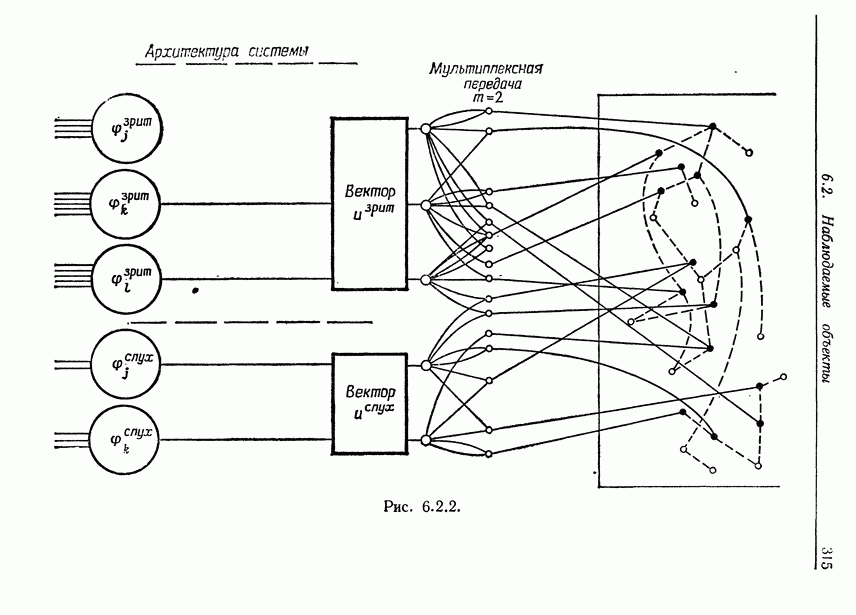
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы