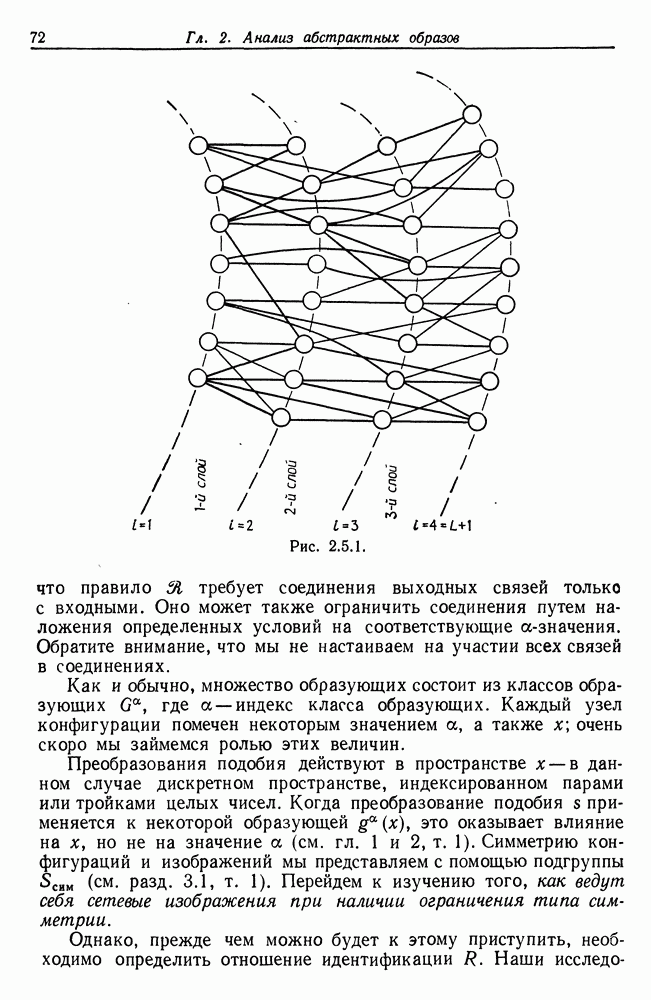
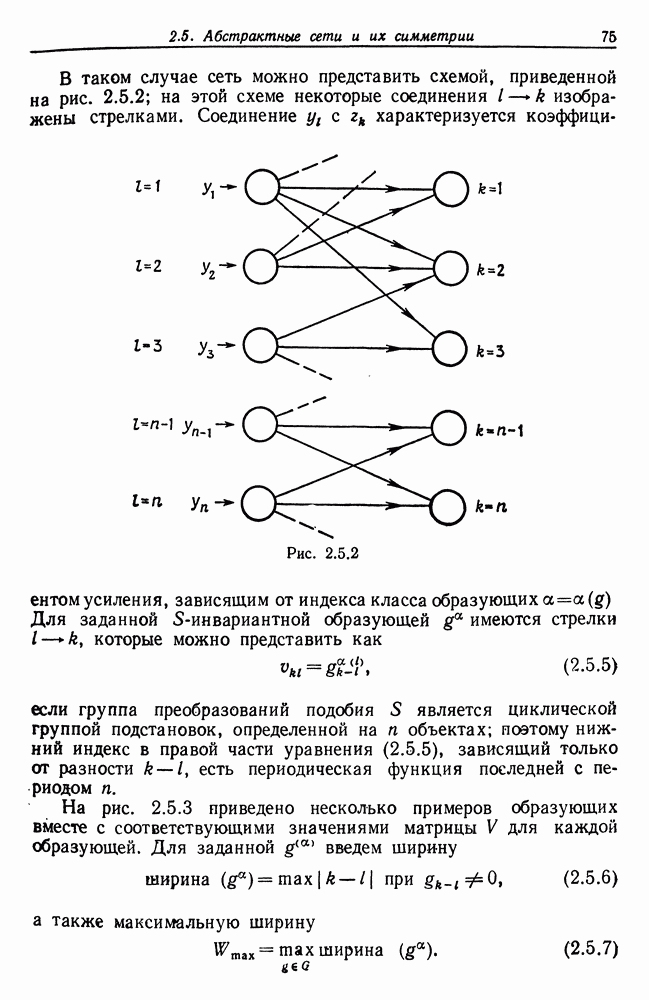
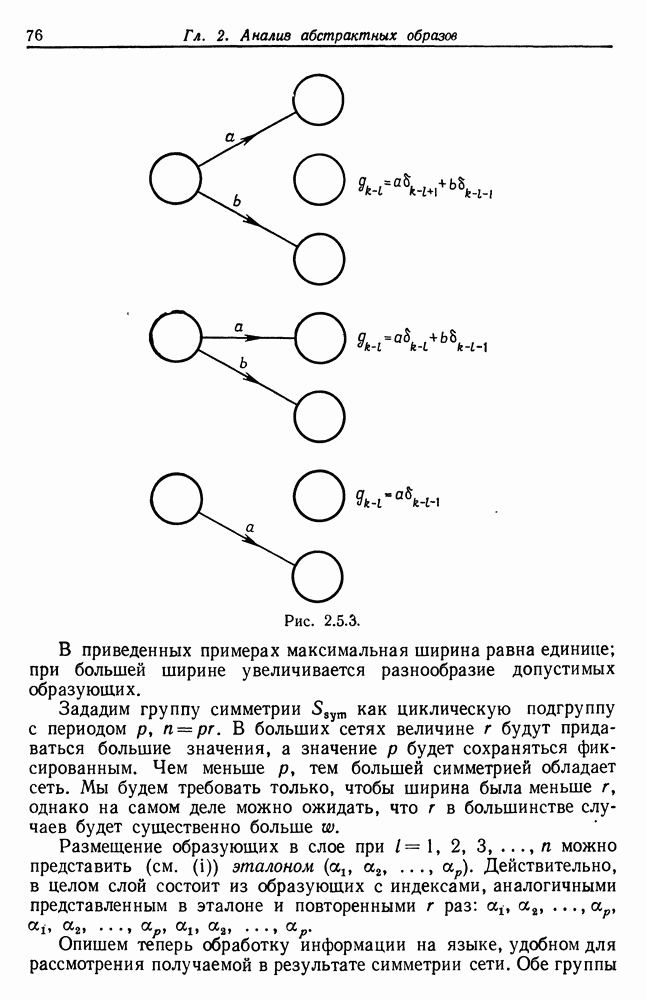
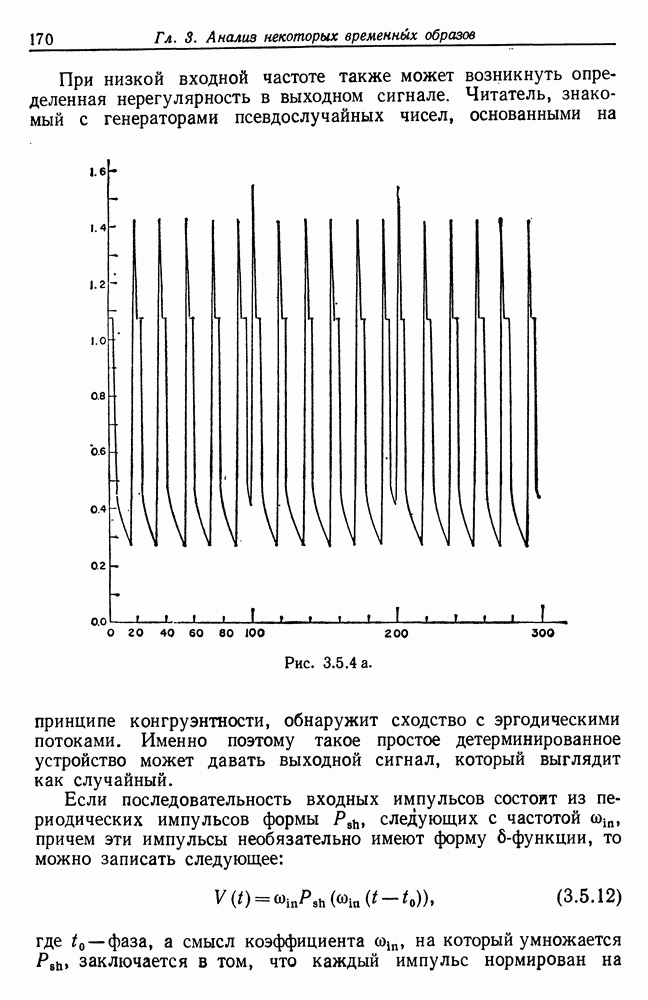
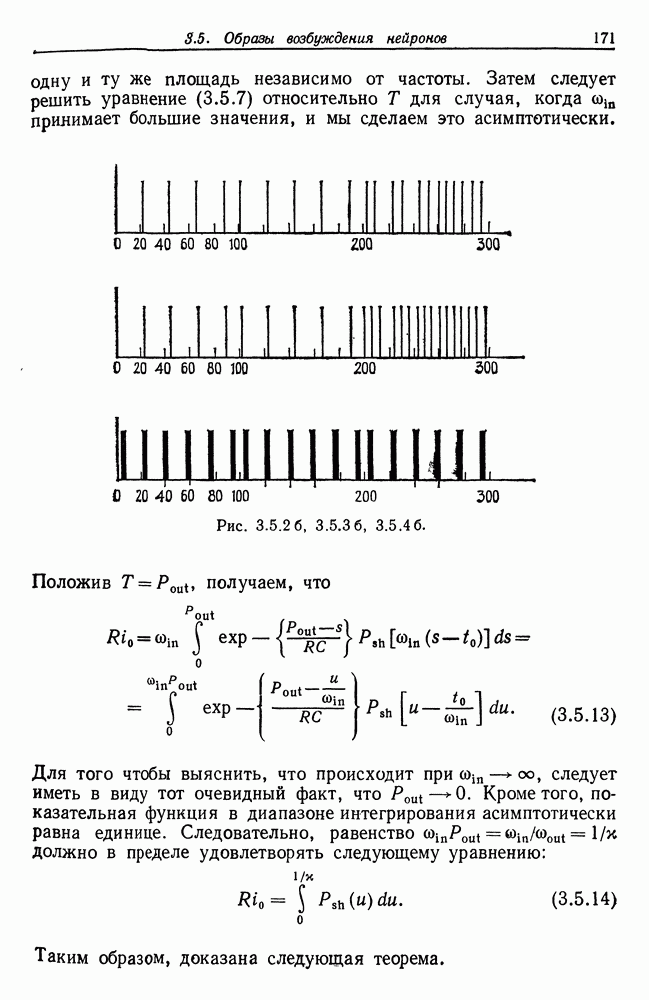
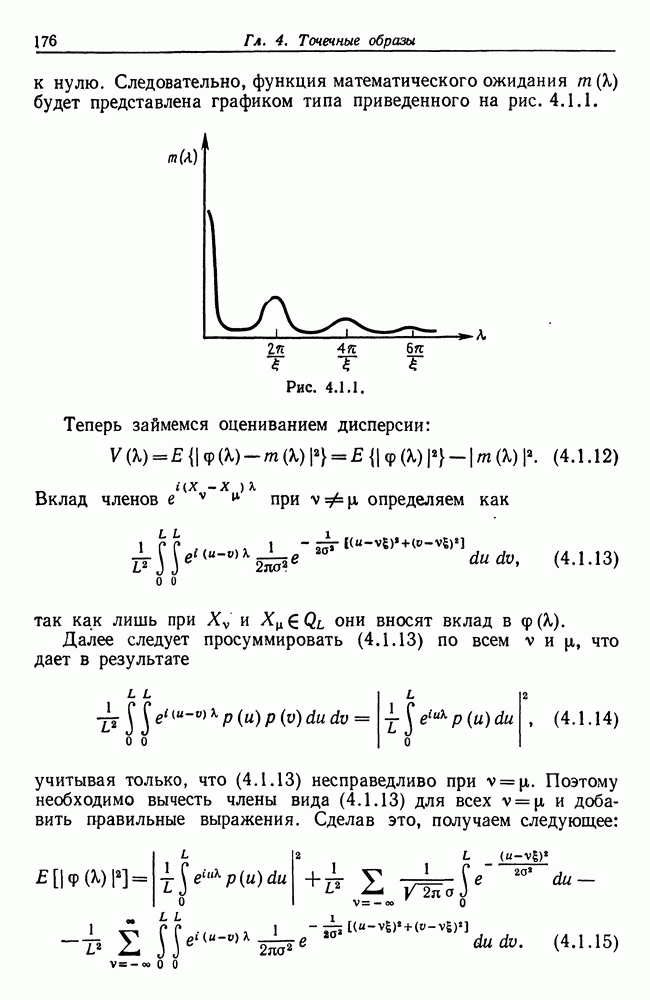
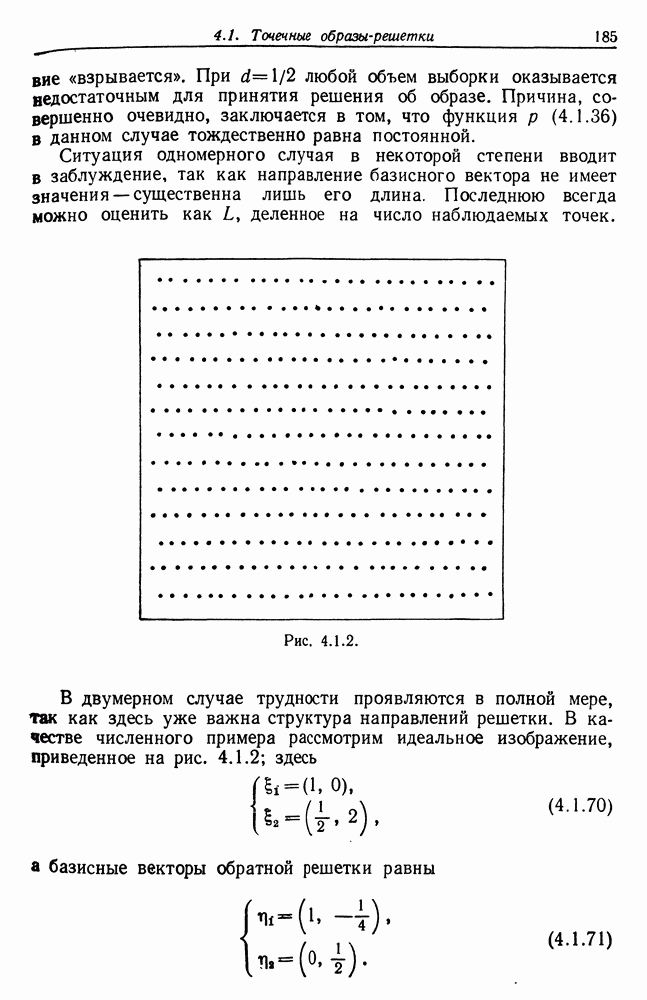
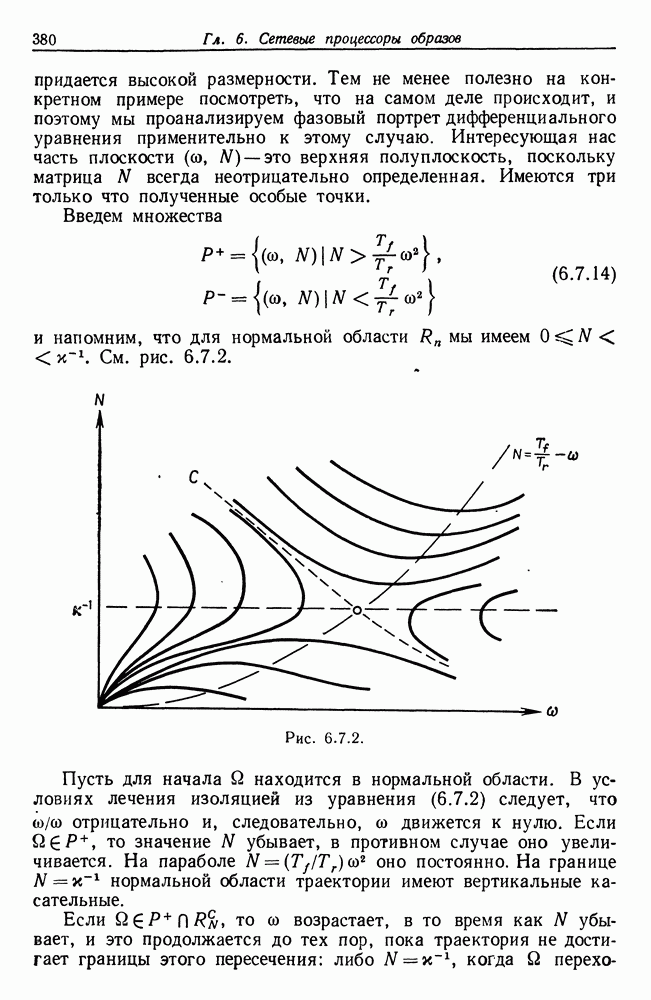
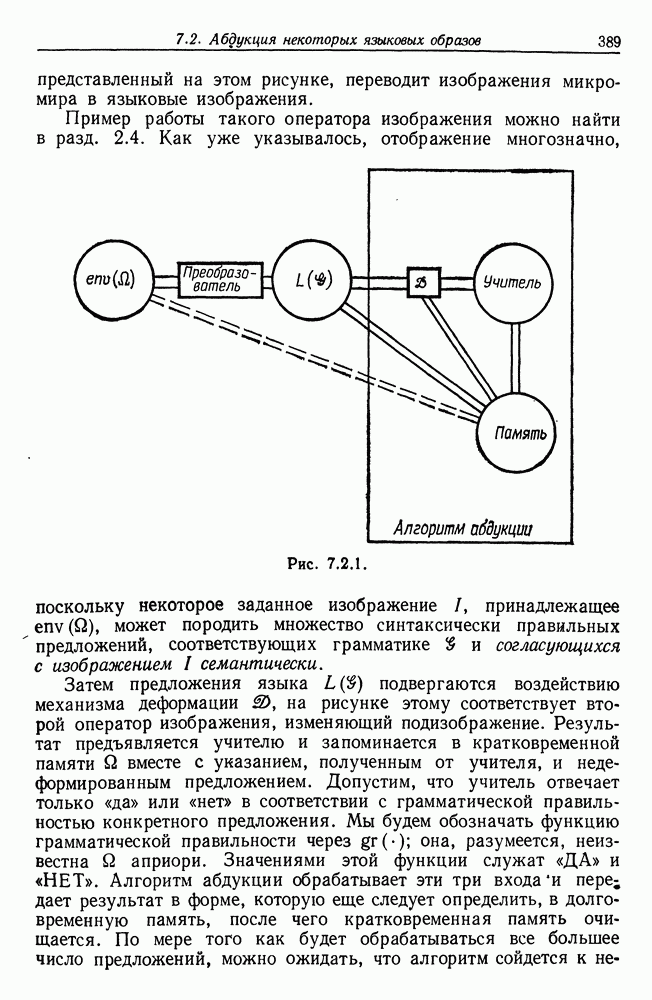
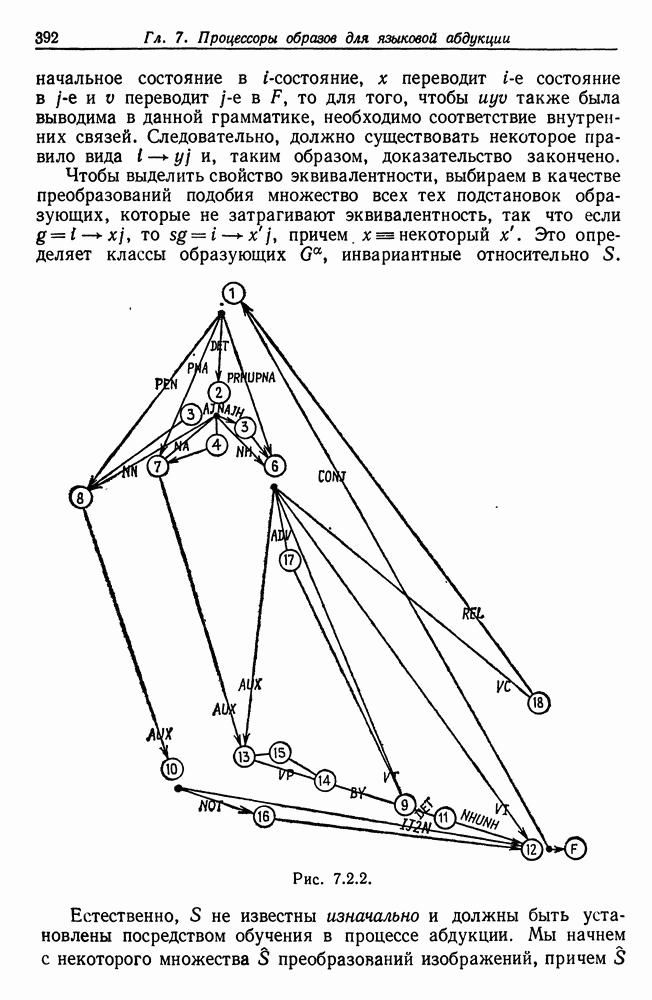
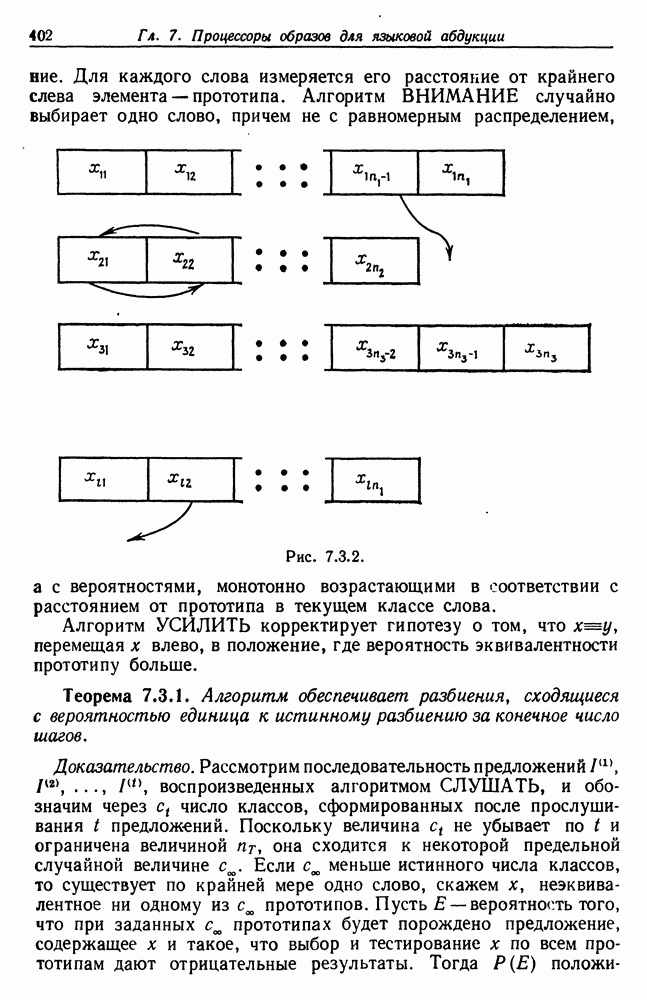
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
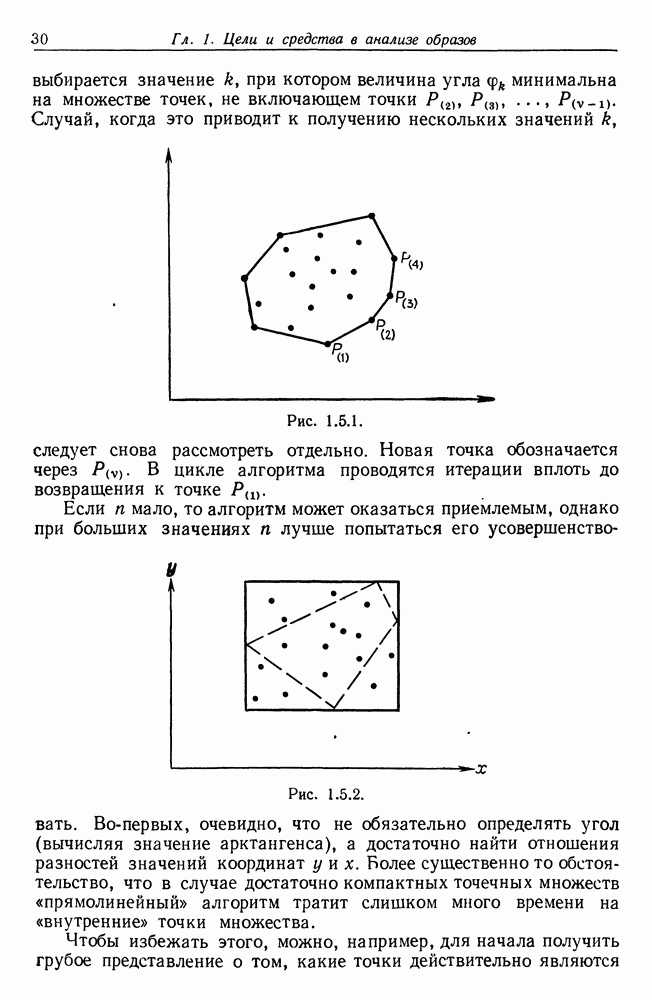
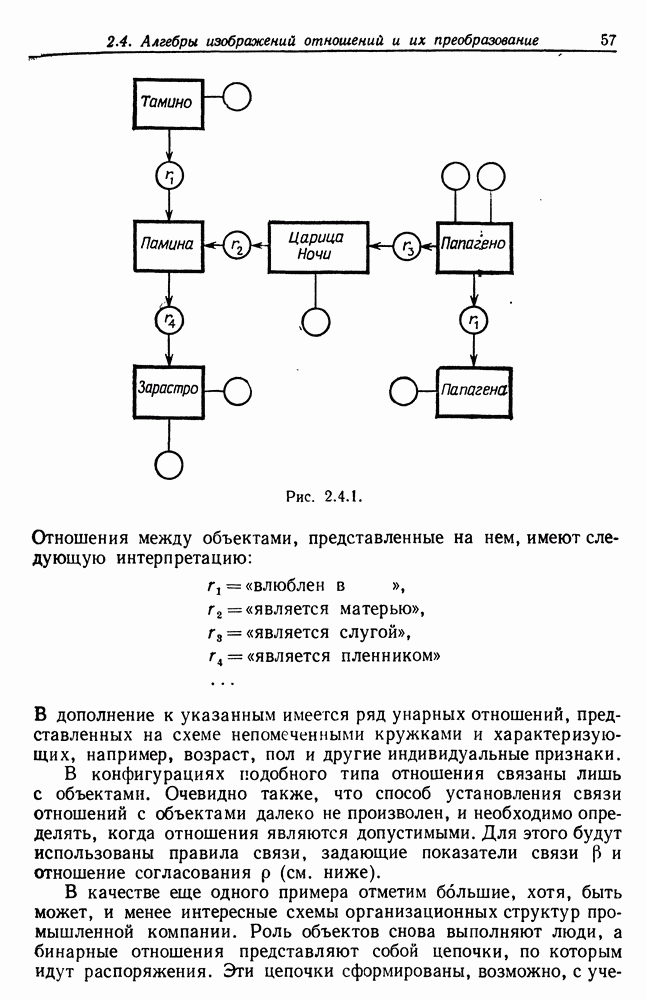
5.6. Зондирование границ
Современные измерительные устройства "не только исключительно точны, но также и в значительной степени автоматизированы. Оператор настраивает датчики системы на границу измеряемого объекта, нажимает кнопку, и полученные в результате этих манипуляций данные автоматически запоминаются и могут быть
сразу же обработаны на вычислительной машине или сохранены для дальнейшего использования.
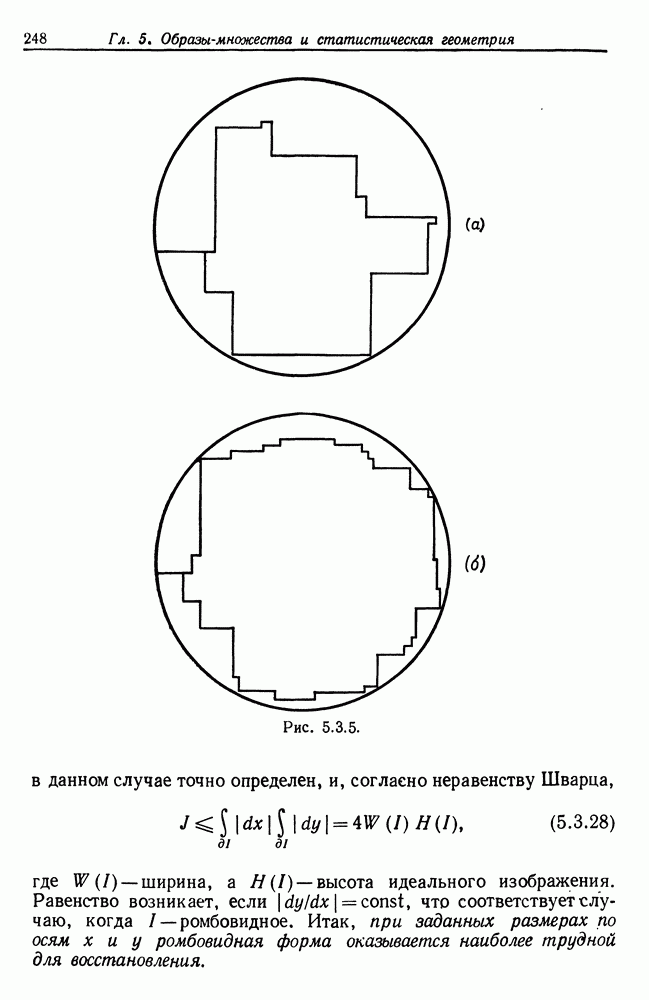
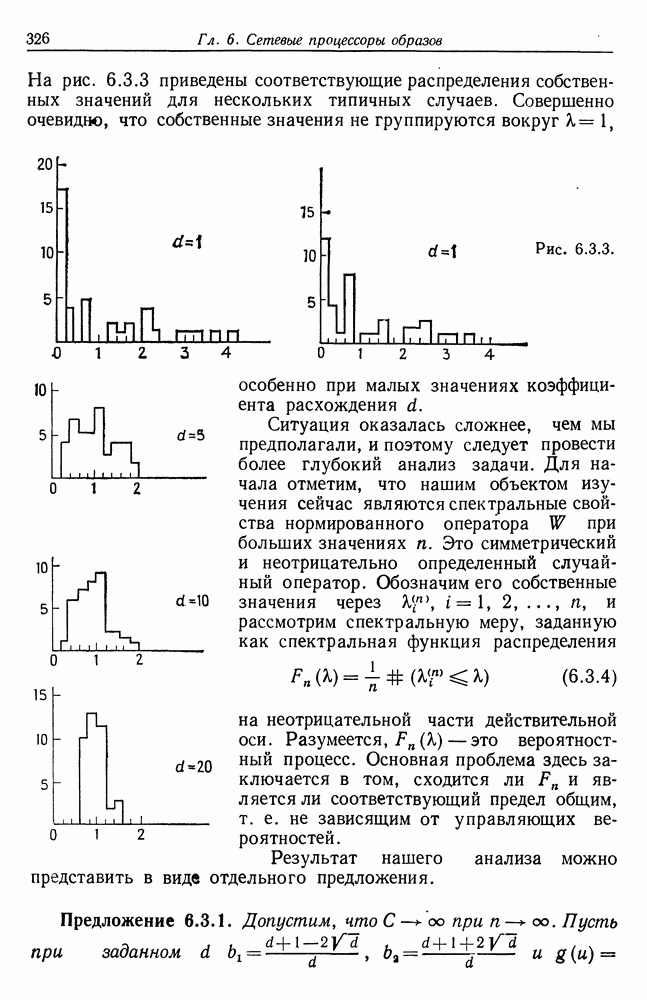
Несмотря на высокую точность, не следует пренебрегать ошибками измерения. Сейчас мы перейдем к изучению случая, когда при анализе изображений исходная конфигурация является одноатомной, а образующая есть некоторая область на плоскости, ограниченная гладкой кривой. Многоатомный случай, когда изображения имеют характер, описанный в разд. 5.4 перед теоремой 5.4.3, пока не изучен. Изображение  при этом может содержать углы, хотя все образующие имеют гладкую границу. Предполагается, что в этом случае точность восстановления изображений окажется выше.
при этом может содержать углы, хотя все образующие имеют гладкую границу. Предполагается, что в этом случае точность восстановления изображений окажется выше.
Пусть, например,  -мерная группа Ли, в которой введена локальная система координат с началом в единичном элементе группы:
-мерная группа Ли, в которой введена локальная система координат с началом в единичном элементе группы:  . Рассмотрим класс образов
. Рассмотрим класс образов  где
где  единственная образующая. Здесь предполагается, что образующая
единственная образующая. Здесь предполагается, что образующая  представляющая идеальное изображение
представляющая идеальное изображение  известна, и наша задача заключается в отыскании преобразования подобия
известна, и наша задача заключается в отыскании преобразования подобия  такого, что
такого, что  (см. разд. 5.1).
(см. разд. 5.1).
Границу прототипа будем записывать так:

здесь  принадлежит
принадлежит  вдоль
вдоль  При заданных
При заданных  точках
точках  мы будем наблюдать некоторое деформированное изображение
мы будем наблюдать некоторое деформированное изображение

где

и  подчиняется двумерному нормальному распределению с нулевым математическим ожиданием и ковариационной матрицей
подчиняется двумерному нормальному распределению с нулевым математическим ожиданием и ковариационной матрицей 
Учитывая, что мы имеем дело с измерительными устройствами высокой точности, можно рассчитывать на восстановление  с хорошим приближением — другими словами, получив точную оценку
с хорошим приближением — другими словами, получив точную оценку  для
для  можно ожидать, что
можно ожидать, что  будет близка к
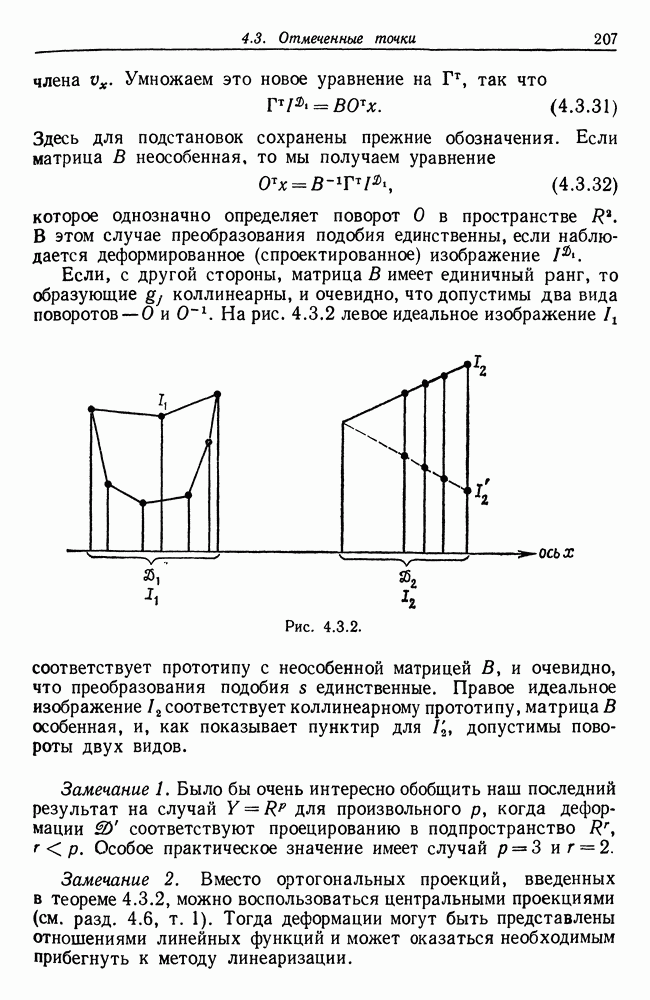
будет близка к 
Итак, весь механизм деформаций  можно рассматривать как произведение двух видов деформаций
можно рассматривать как произведение двух видов деформаций  Один из них определяется тем, что мы отыскиваем не всю границу
Один из них определяется тем, что мы отыскиваем не всю границу  а лишь
а лишь  ее точек (см. т. 1, с. 341). Второй механизм деформации
ее точек (см. т. 1, с. 341). Второй механизм деформации  это просто аддитивный шум, с которым справиться легче.
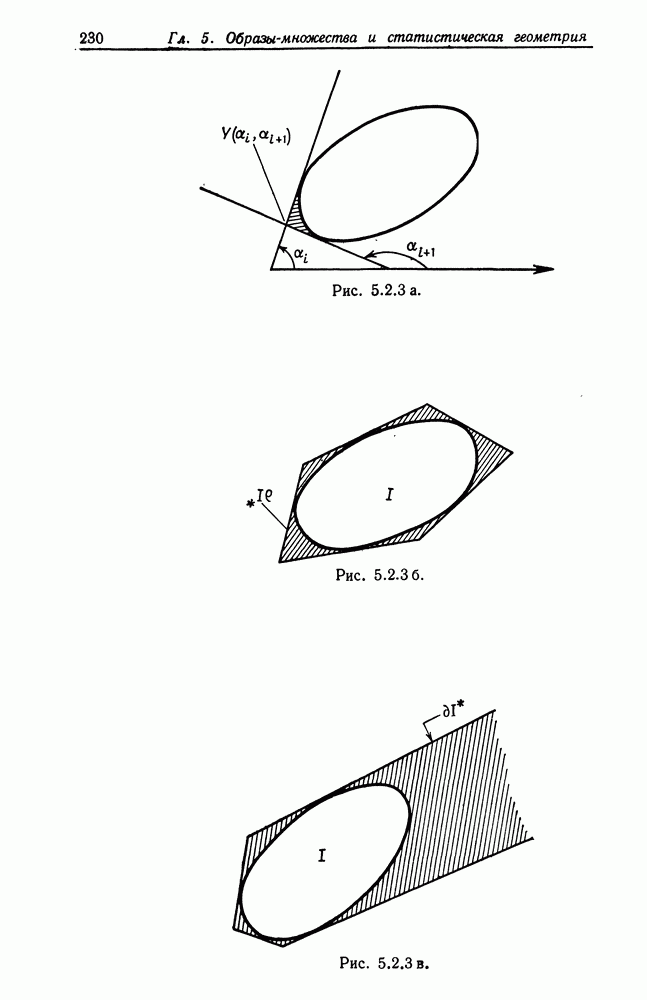
это просто аддитивный шум, с которым справиться легче.
При определении  может быть не вполне ясно, сколькими степенями свободы мы располагаем. Имеется
может быть не вполне ясно, сколькими степенями свободы мы располагаем. Имеется  наблюдений
наблюдений  неизвестных
неизвестных  Это, однако, не все. Следует, кроме того, рассматривать величины
Это, однако, не все. Следует, кроме того, рассматривать величины
 как неизвестные, на которые наложено лишь
как неизвестные, на которые наложено лишь  ограничений в виде соотношений
ограничений в виде соотношений  все
все  различные), и, следовательно, мы имеем
различные), и, следовательно, мы имеем  свободных параметров. Это означает, что общее число степеней свободы равно
свободных параметров. Это означает, что общее число степеней свободы равно  .
.
Начнем с того, что будем считать оценку  фиксированной и оценим
фиксированной и оценим  граничных точек
граничных точек  Оценка по методу максимального правдоподобия дает условие
Оценка по методу максимального правдоподобия дает условие

или с использованием множителей Лагранжа 

Отсюда непосредственно следует, что

где  следует выбирать так, чтобы выполнялось условие
следует выбирать так, чтобы выполнялось условие  Это дает нам приближение первого порядка (здесь мы всегда будем пользоваться именно таким порядком аппроксимации)
Это дает нам приближение первого порядка (здесь мы всегда будем пользоваться именно таким порядком аппроксимации)

где  означает градиент относительно вектора вычисленный в точке Следовательно,
означает градиент относительно вектора вычисленный в точке Следовательно,

Теперь переходим к определению  решая
решая

где запись  указывает на зависимость от неизвестного элемена группы
указывает на зависимость от неизвестного элемена группы 
И снова с помощью приближения первого порядка при  получаем
получаем

причем скалярные произведения — это внутренние произведения, первые в  вторые в
вторые в  Отметим, что
Отметим, что 
Таким образом, (5.6.9) приводит к системе уравнений относительно 

Зависимость членов  от
от  обозначена нижним индексом
обозначена нижним индексом  Разумеется, индекс суммирования
Разумеется, индекс суммирования  это просто немой символ, не имеющий никакой связи с элементом группы. Введем матрицу размера
это просто немой символ, не имеющий никакой связи с элементом группы. Введем матрицу размера 

и сформируем вектор-столбец с  компонентами, равный правой части (5.6.11), деленной на
компонентами, равный правой части (5.6.11), деленной на  Тогда
Тогда

очевидно, что  и ковариационная матрица равна
и ковариационная матрица равна

где

С помощью определения  (см. (5.6.8)) последнее выражение сводится к следующему:
(см. (5.6.8)) последнее выражение сводится к следующему:

В сочетании с (5.6.14) это определяет ковариационную матрицу  и, таким образом, получен следующий результат
и, таким образом, получен следующий результат  обозначает теперь произвольный элемент группы).
обозначает теперь произвольный элемент группы).
Теорема 5.6.1. При заданных условиях решение  (5.6.4) является при а
(5.6.4) является при а  асимптотически нормальной оценкой элемента группы
асимптотически нормальной оценкой элемента группы  для идеального изображения
для идеального изображения  с
с
распределением  :
:

матрица  определяется (5.6.12).
определяется (5.6.12).
Чтобы сделать этот результат более конкретным, рассмотрим пример, в котором  — прямое произведение переносов и изменений масштаба, а
— прямое произведение переносов и изменений масштаба, а  — единичный круг, так что
— единичный круг, так что

и

Следовательно,

и

для расположенных на границе  . В соответствии с (5.6.9) мы должны решить задачу
. В соответствии с (5.6.9) мы должны решить задачу

или, что то же самое,

Если ввести четыре вектора-столбца

то решение (5.6.23) можно свести к решению

здесь  матрица
матрица 

Если матрица М неособенная, то мы просто обращаем ее, чтобы получить  а затем и с из соотношения
а затем и с из соотношения  Матрица М, однако, является особенной в том и только в том случае, если векторы
Матрица М, однако, является особенной в том и только в том случае, если векторы  коллинеарны, и, следовательно, справедливо нетривиальное линейное соотношение
коллинеарны, и, следовательно, справедливо нетривиальное линейное соотношение

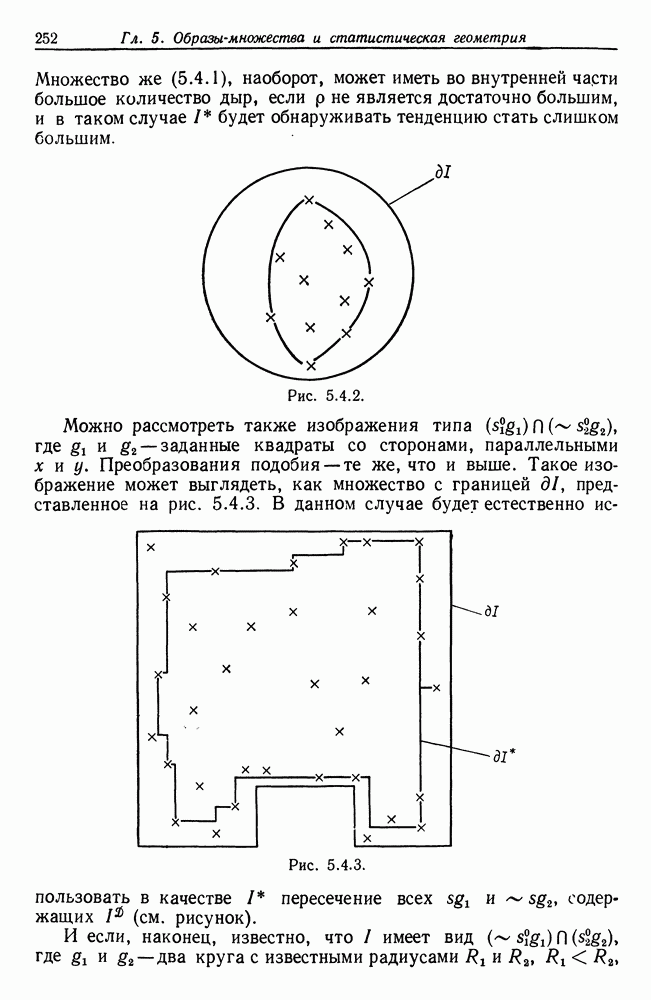
Эта возможность исключается, если не все точки деформированного изображения лежат на одной прямой. Практически это означает, что (1) радиус с не должен быть слишком большим и (2) точки  не должны лежать на круговой дуге с малым центральным углом. Отметим, что условие (2) связано с задачей планирования; ниже мы еще вернемся к этому.
не должны лежать на круговой дуге с малым центральным углом. Отметим, что условие (2) связано с задачей планирования; ниже мы еще вернемся к этому.
Радиус, в частности, можно аппроксимировать следующей функцией:

Она обладает такими свойствами:
A. R является однородной функцией первой степени, так что

Б. R определена, непрерывна и неотрицательна всюду, за исключением случая, когда точки  лежат на одной прямой.
лежат на одной прямой.
B. R инвариантна относительно евклидовой группы на плоскости и симметрической группы перестановок индексов точек 
Г. Если все точки  лежат на круговой дуге радиуса
лежат на круговой дуге радиуса  то
то 
Простейший способ проверить, выполнены ли условия  , это не пользоваться явным выражением (5.6.28), а опираться на тот факт, что мы минимизируем квадратичную форму (5.6.22).
, это не пользоваться явным выражением (5.6.28), а опираться на тот факт, что мы минимизируем квадратичную форму (5.6.22).
Таким образом, мы определили «радиус»  множеств типа «деформированные круговые дуги». Очевидно, что если
множеств типа «деформированные круговые дуги». Очевидно, что если  существенно отличается от круговой формы, то величина
существенно отличается от круговой формы, то величина  теряет смысл. Некоторую помощь в определении того, имеет ли это место, может принести вычисление величины
теряет смысл. Некоторую помощь в определении того, имеет ли это место, может принести вычисление величины

Отметим, что эта величина связана с минимальным значением квадратичной формы (5.6.22). В самом деле, это минимум есть
отношение двух определителей, и потому это отношение, деленное на  представляет собой нормированную остаточную сумму квадратов. Следовательно, близость
представляет собой нормированную остаточную сумму квадратов. Следовательно, близость  к единице означает, что деформированное изображение имеет очертания, близкие к круговой дуге, а малые значения
к единице означает, что деформированное изображение имеет очертания, близкие к круговой дуге, а малые значения  имеют прямо противоположный смысл.
имеют прямо противоположный смысл.
Критерий  обладает следующими свойствами:
обладает следующими свойствами:
A. Он инвариантен относительно евклидовой группы перестановки индексов наблюдаемых точек и изменения масштаба.
Б. Определен, непрерывен и принимает значения на отрезке  , за исключением случая, когда все точки лежат на одной прямой.
, за исключением случая, когда все точки лежат на одной прямой.
B. Если все точки лежат на круговой дуге, то 
В принципе все это выглядит прекрасно. Численные эксперименты показывают, однако, что критерий  не очень информативен: даже резкие отклонения от идеальной формы круговой дуги не приводят к существенно отличающимся от единицы значениям
не очень информативен: даже резкие отклонения от идеальной формы круговой дуги не приводят к существенно отличающимся от единицы значениям 
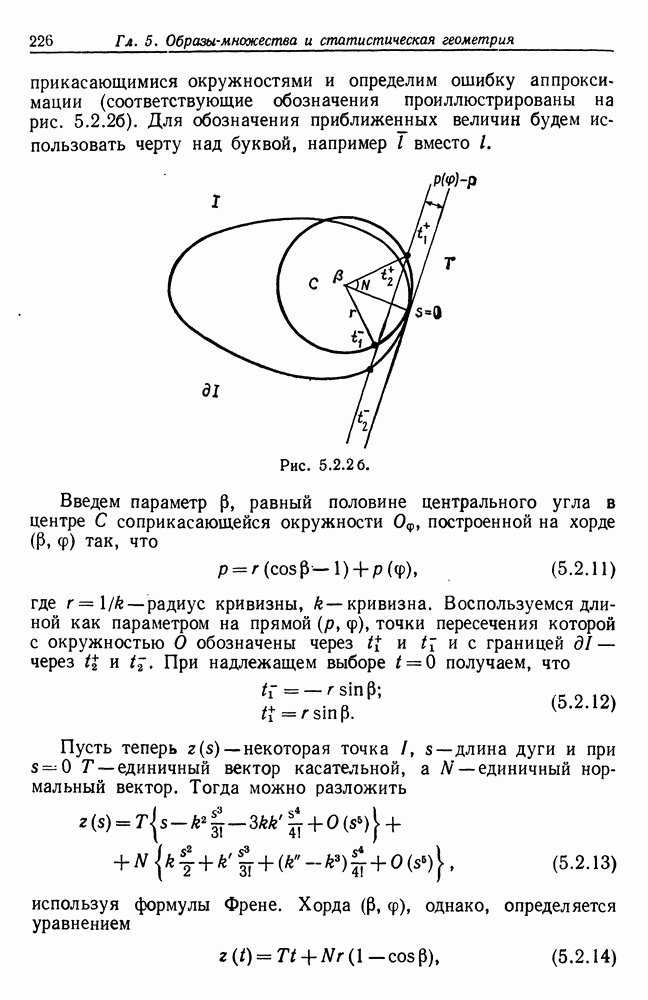
Для исправления этого недостатка предлагается следующая модификация критерия круглости. Определим, во-первых, оценки a, b и с. Для расстояний имеем

и для модифицированной оценки радиуса

Пусть

где


Можно рассчитывать, что модифицированная оценка радиуса с окажется лучше, чем с. Численные эксперименты показывают, что в практических случаях, связанных с работой измерительных устройств, если форма близка к круговой, улучшение оказывается совершенно несущественным. Тем не менее при значительных отклонениях от круговой формы разница становится ощутимой.
Можно также утверждать, что для критерия и свойства  по-прежнему выполняются.
по-прежнему выполняются.
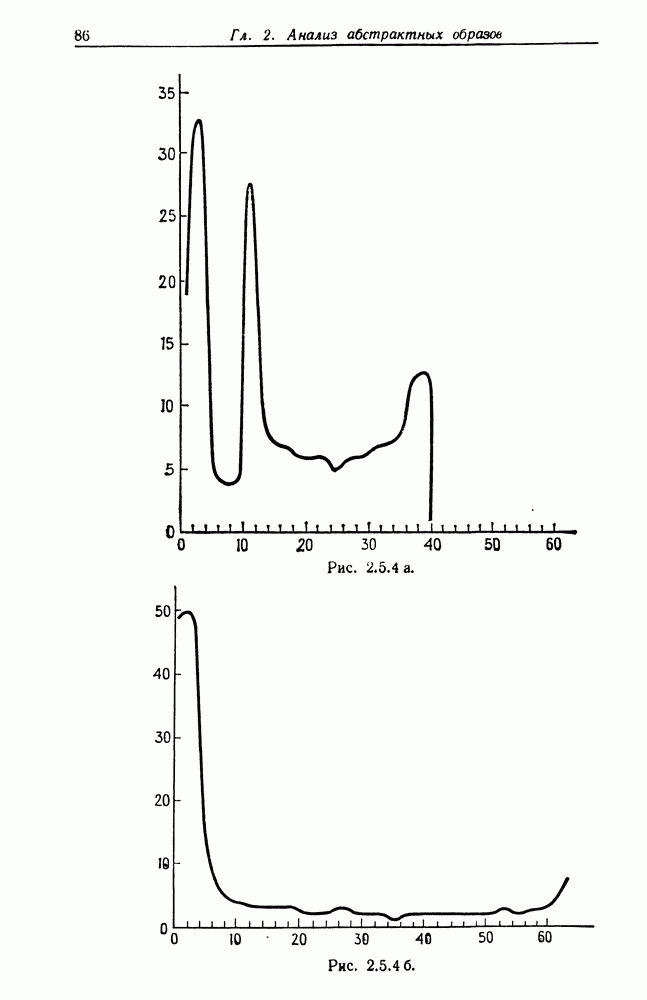
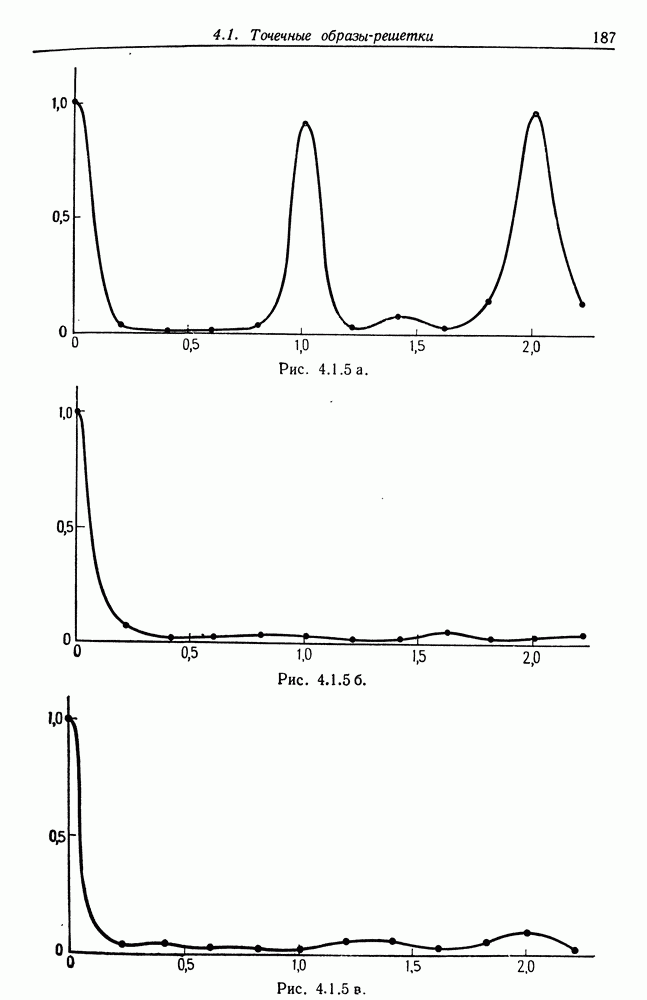
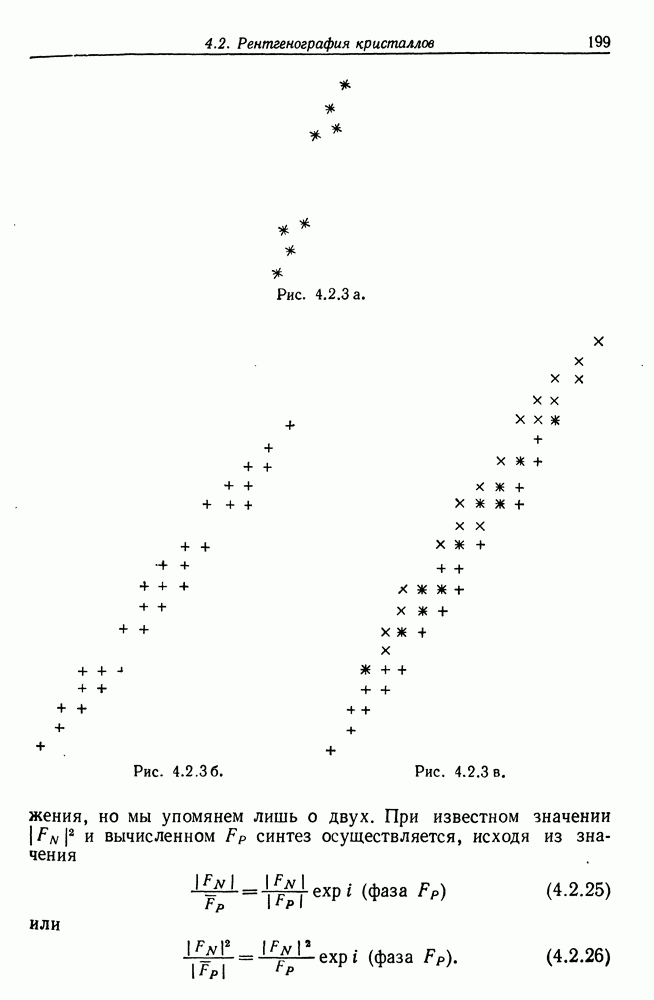
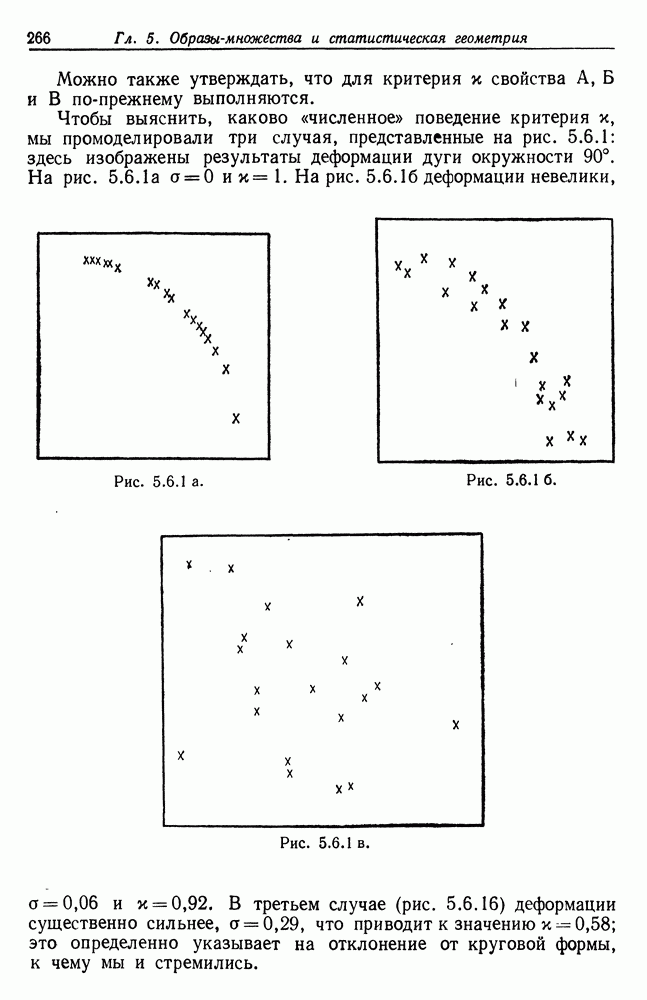
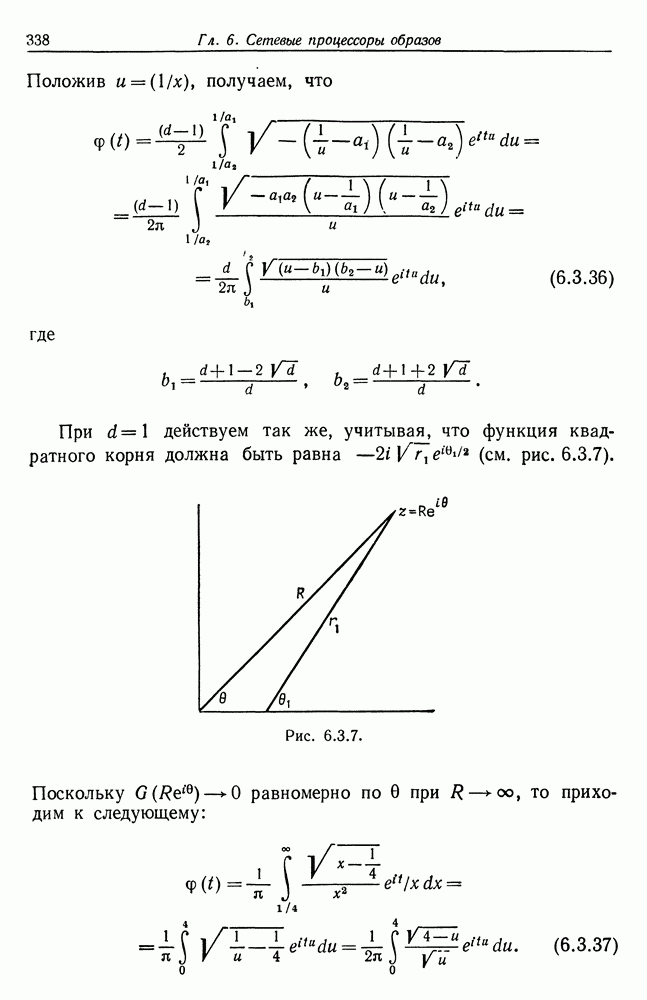
Чтобы выяснить, каково «численное» поведение критерия х, мы промоделировали три случая, представленные на рис. 5.6.1: здесь изображены результаты деформации дуги окружности 90°. На рис. 5.6.1а а = 0 и х = 1. На рис. 5.6.16 деформации невелики,  .
.

Рис. 5.6.1 в.
В третьем случае (рис. 5.6.16) деформации существенно сильнее,  , что приводит к значению
, что приводит к значению  ; это определенно указывает на отклонение от круговой формы, к чему мы и стремились.
; это определенно указывает на отклонение от круговой формы, к чему мы и стремились.
Для вычисления матрицы  с помощью (5.6.12) требуется
с помощью (5.6.12) требуется  . Но из (5.6.19) можно получить непосредственно
. Но из (5.6.19) можно получить непосредственно

причем третье уравнение не выполняется на  Если ввести матрицу
Если ввести матрицу

то мы получим

и

так что если  существует и матрица
существует и матрица  является неособенной, то
является неособенной, то

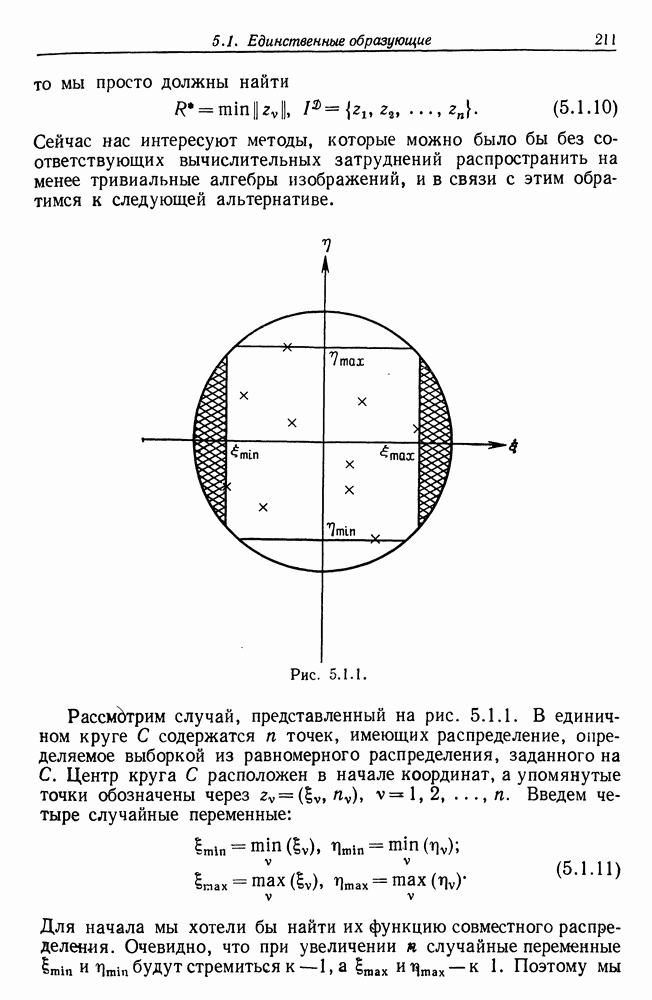
Здесь мы встречаемся с интересной задачей планирования: если число подлежащих проверке точек задано и имеется некоторое представление о том, как на плоскости расположено  то каким образом следует распределить пробные точки вдоль границы? Без ограничения общности йгожно допустить, что
то каким образом следует распределить пробные точки вдоль границы? Без ограничения общности йгожно допустить, что  . Допустим, что можно расположить точки зондирования на дуге с центральным углом
. Допустим, что можно расположить точки зондирования на дуге с центральным углом  Тогда
Тогда

Пусть распределены асимптотически в соответствии с функцией распределения Ф и симметричны относительно  Тогда
Тогда

где

здесь  же, что и Ф, за исключением точки
же, что и Ф, за исключением точки  где
где  имеет лишь половину (если она вообще там имеется) вероятностной меры Ф.
имеет лишь половину (если она вообще там имеется) вероятностной меры Ф.
Начнем с вопроса об оптимальном размещении точек зондирования в том случае, когда основной задачей является определение радиуса с с высокой точностью. Тогда в соответствии с (5.6.38) и (5.6.40) необходимо минимизировать:

Для максимизации  при заданном значении В обратим внимание на вид
при заданном значении В обратим внимание на вид  в (5.6.41) и воспользуемся тем же вариационным методом, к которому мы уже прибегали несколько раз раньше в этой работе (см., например, т. 1, с. 227). Пренебрегая подробностями, укажем, что должно выполняться нетривиальное линейное соотношение
в (5.6.41) и воспользуемся тем же вариационным методом, к которому мы уже прибегали несколько раз раньше в этой работе (см., например, т. 1, с. 227). Пренебрегая подробностями, укажем, что должно выполняться нетривиальное линейное соотношение

справедливое для всех  принадлежащих носителю
принадлежащих носителю  Поскольку мы рассматриваем только
Поскольку мы рассматриваем только  принадлежащие интервалу
принадлежащие интервалу  , носитель может содержать самое большее две точки
, носитель может содержать самое большее две точки  Пусть соответствующие вероятностные меры равны
Пусть соответствующие вероятностные меры равны  , так что
, так что

Можно записать, используя штрихи для обозначения дифференцирования по а, что

и

Рассмотрим сначала случай, когда и, следовательно,  и В больше нуля. Упорядочим углы так, чтобы выполнялись неравенства
и В больше нуля. Упорядочим углы так, чтобы выполнялись неравенства  непосредственная проверка (5.6.46) показывает, что минимум достигается при а, заключенном внутри отрезка [0, 1], причем
непосредственная проверка (5.6.46) показывает, что минимум достигается при а, заключенном внутри отрезка [0, 1], причем

Для минимизации необходимо сделать отношение  максимально возможным (напомним, что
максимально возможным (напомним, что  т. е.
т. е.

Непосредственная проверка показывает, что это справедливо и для предельного случая 
При обращении к случаю  ситуация в корне меняется. Положив
ситуация в корне меняется. Положив  и
и

получаем минимум, непосредственно равный нулю, поскольку  . Этот минимум не единственный.
. Этот минимум не единственный.
Допустим теперь, что наша основная цель заключается в том, чтобы отыскать первую координату центра а, и поэтому план зондирования должен обеспечить минимизацию

Максимизируя  поступаем, как и выше, и отыскиваем оптимальный план при
поступаем, как и выше, и отыскиваем оптимальный план при 

И наконец, чтобы получить  с максимально возможной точностью следует минимизировать
с максимально возможной точностью следует минимизировать


(кликните для просмотра скана)
Для этого достаточно разместить все точки на дуге центрального угла (повторные независимые измерения):

Объединим теперь результаты, учитывая соотношение между  (которое мы определили) и Ф (которое реально используется при построении плана).
(которое мы определили) и Ф (которое реально используется при построении плана).
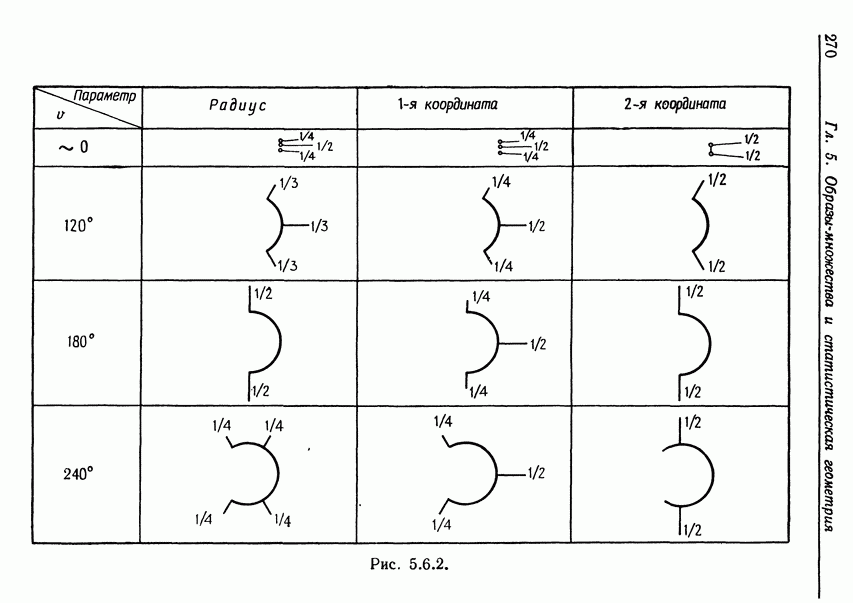
Теорема 5.6.2. Асимптотически оптимальный план строится так:
(i) Радиус. Если  то вычисляем отношение
то вычисляем отношение

и берем часть  при угле
при угле  и ±1/2 при каждом из углов
и ±1/2 при каждом из углов  Если
Если  долю 1/4 берем при каждом из четырех углов
долю 1/4 берем при каждом из четырех углов 
Первая координата центра. Долю 1/2 берем при угле  и доли
и доли  при углах
при углах 
Вторая координата центра. Если  часть точек зондирования берем при каждом из углов
часть точек зондирования берем при каждом из углов  Если
Если  часть точек зондирования берем при каждом из углов
часть точек зондирования берем при каждом из углов 
Соответствующие иллюстрации приведены на рис. 5.6.2, где оптимальные положения точек зондирования указаны для дуг с центральными углами 240, 180, 120° и углом, близким к нулю. Относительное число точек зондирования при различных углах обозначено направленными вовне отрезками прямых.
Пусть теперь форма будет произвольной при соблюдении заданных условий, и пусть  — переносы в
— переносы в  Тогда
Тогда

и

а также

Для того чтобы получить  с помощью (5.6.12), необходимо определить член
с помощью (5.6.12), необходимо определить член

где  Геометрический смысл этого члена становится понятен, если мы параметризуем
Геометрический смысл этого члена становится понятен, если мы параметризуем  с помощью дуги длины а, измеряемой от произвольной начальной точки, и угла, образуемого
с помощью дуги длины а, измеряемой от произвольной начальной точки, и угла, образуемого
касательной в точке о и измеренного в положительном направлении от оси  Вдоль границы
Вдоль границы  имеет место
имеет место

и

и т. д., что дает нам

С помощью функции распределения Ф вдоль границы  и выраженной через длину дуги а получаем удобное выражение для
и выраженной через длину дуги а получаем удобное выражение для 

где  — общая длина
— общая длина  Последнее в сочетании с теоремой 5.6.1 позволяет получить асимптотическую ковариационную матрицу для оценки
Последнее в сочетании с теоремой 5.6.1 позволяет получить асимптотическую ковариационную матрицу для оценки  двух элементоа группы и
двух элементоа группы и  которые в данном случае сводятся к параметрам переноса а и
которые в данном случае сводятся к параметрам переноса а и 
Кроме того, здесь естественно возникает задача построения плана оптимального определения двух параметров переноса. Эта задача пока не изучена.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
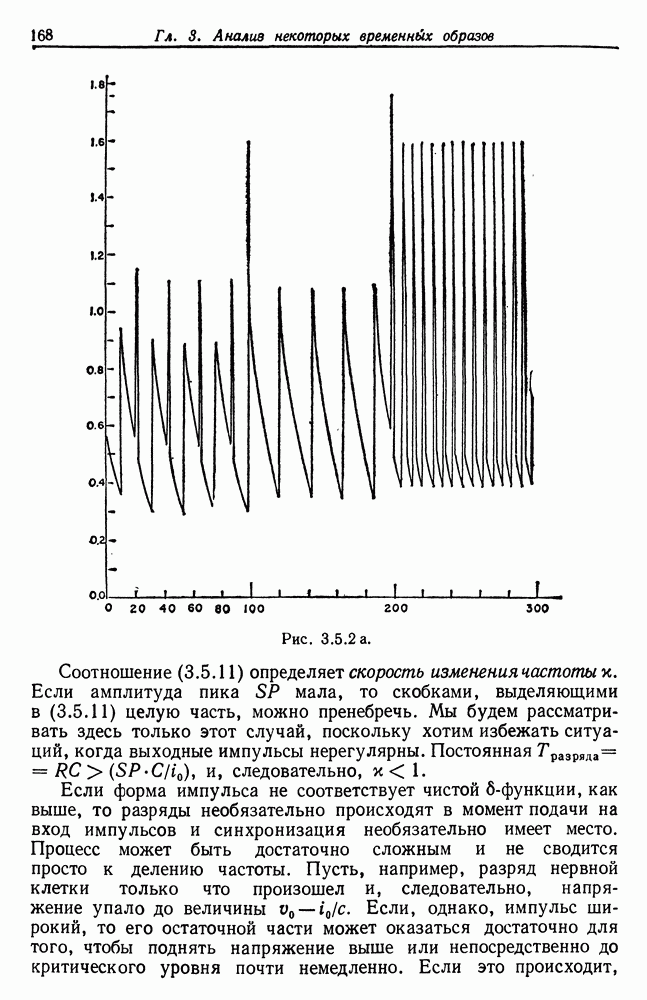
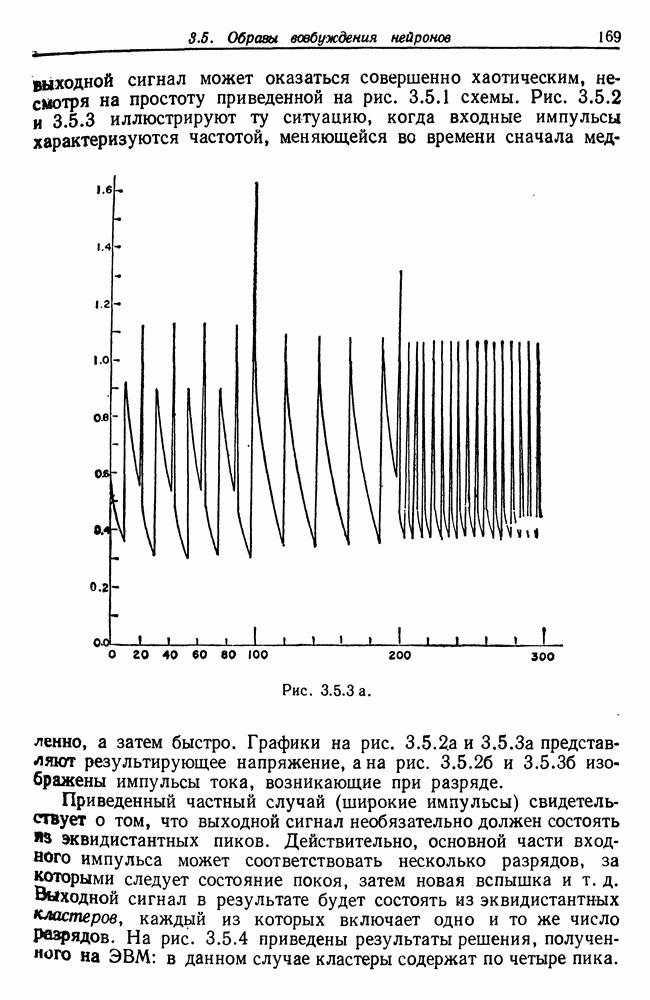
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
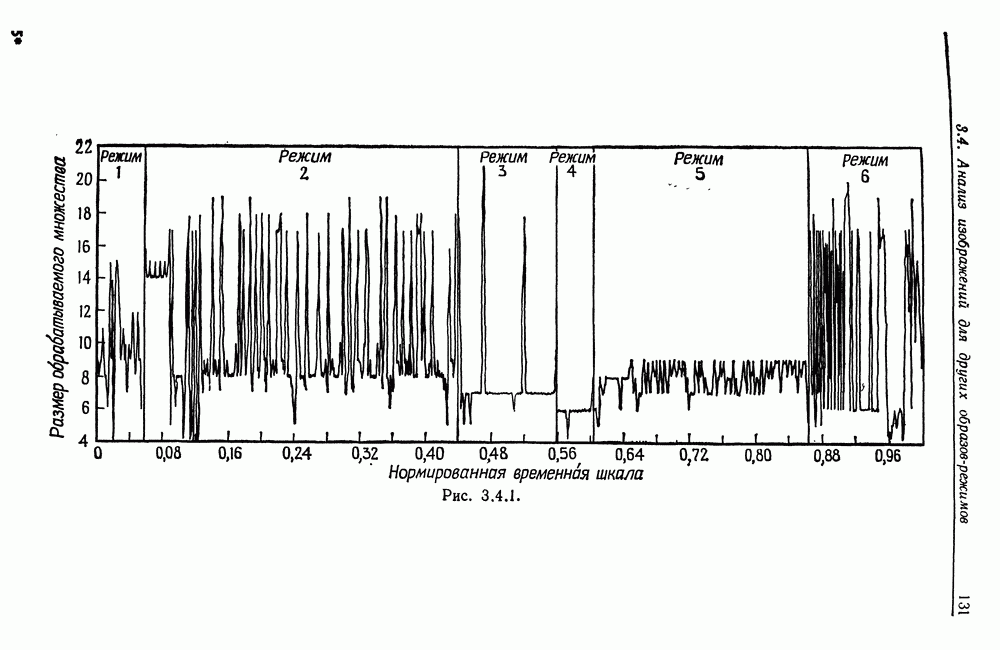
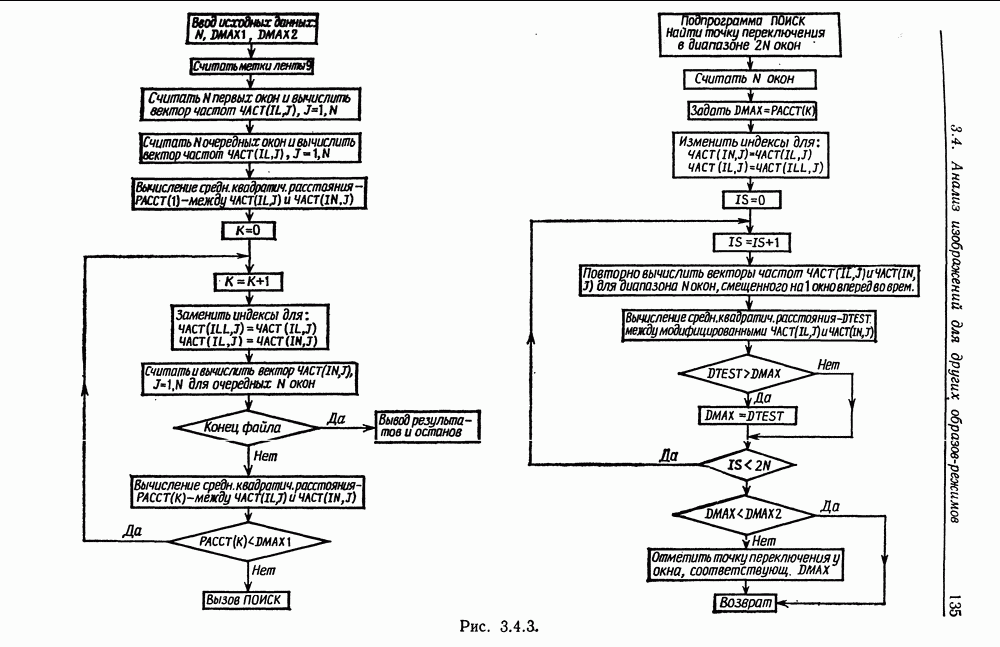
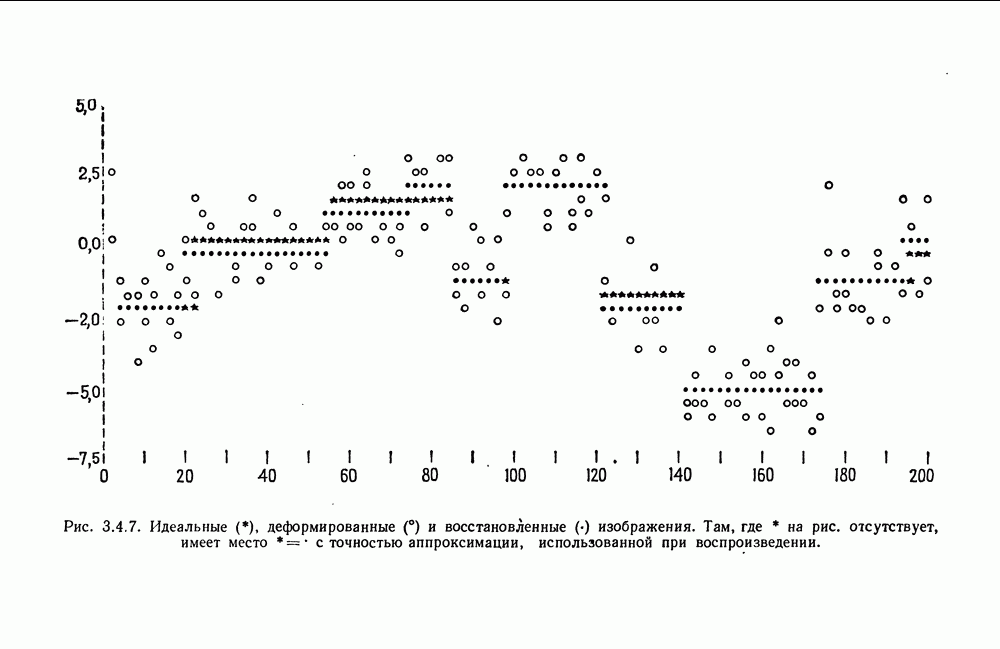
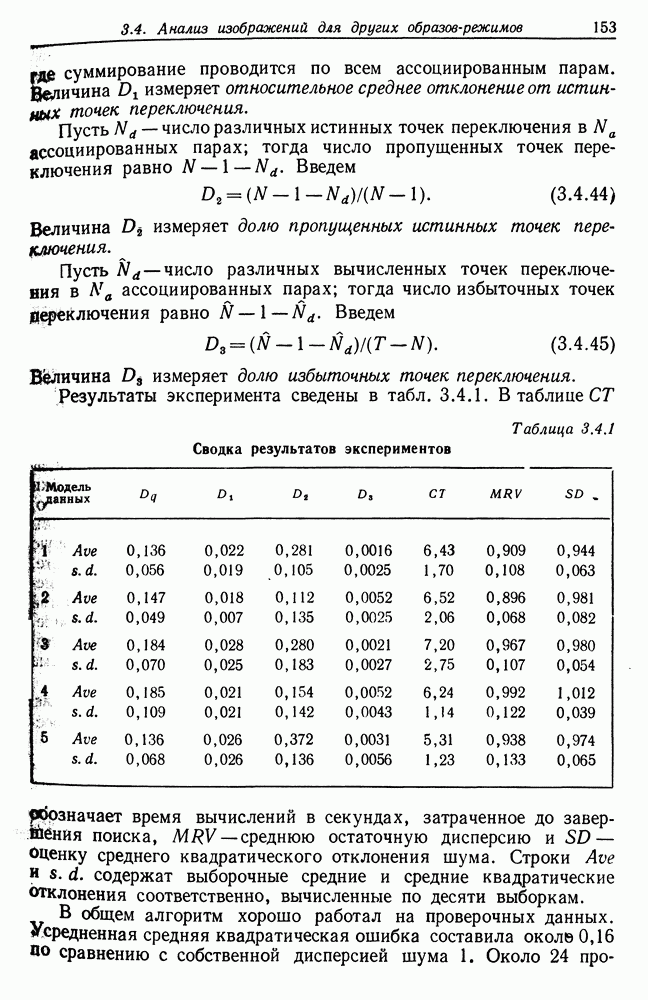
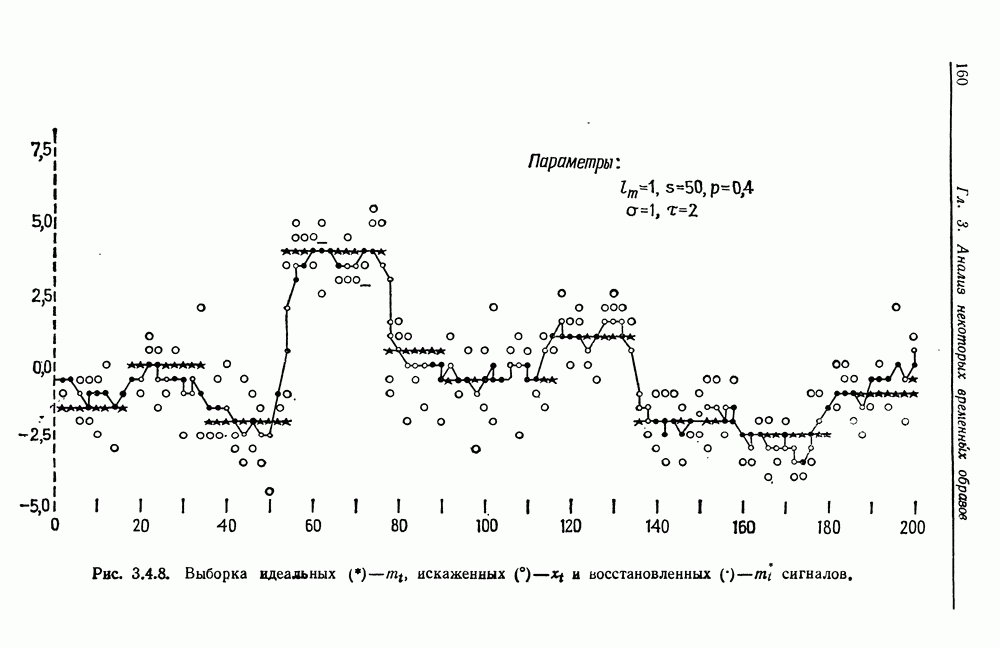
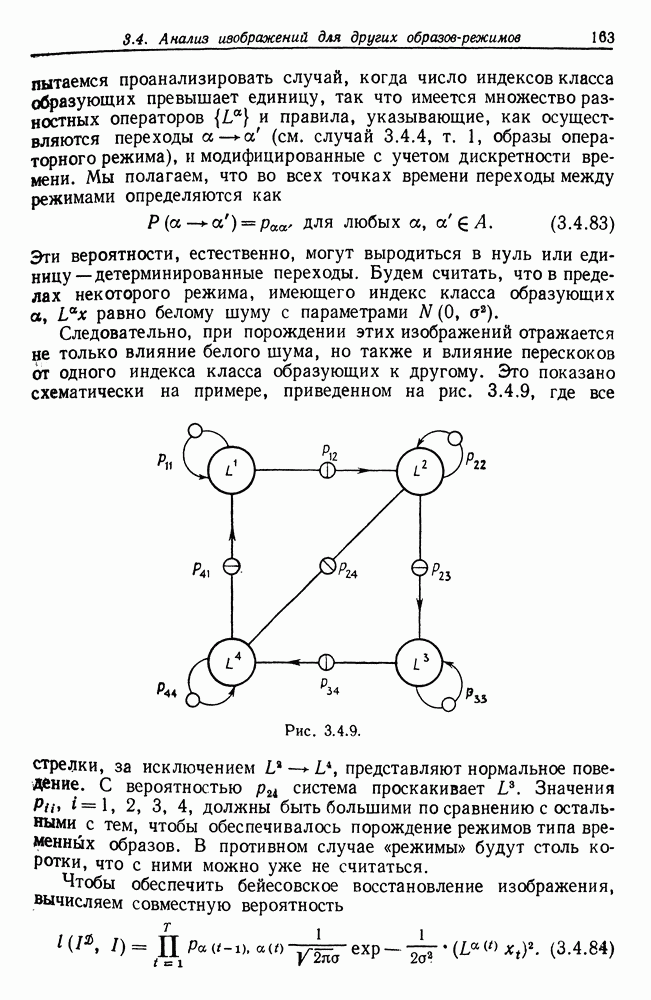
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
- 4.2. Рентгенография кристаллов
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
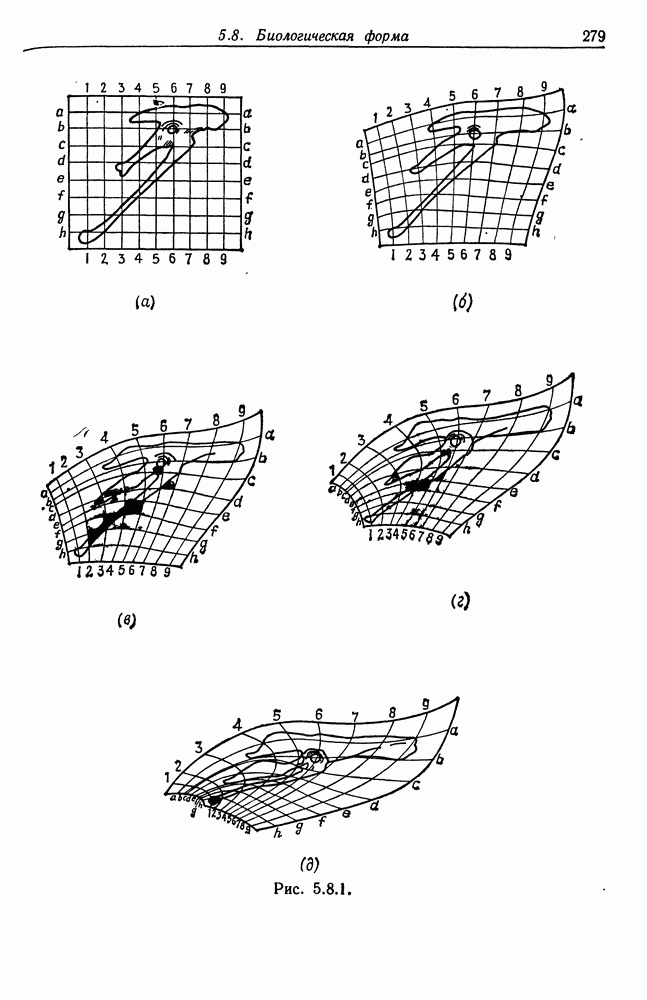
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
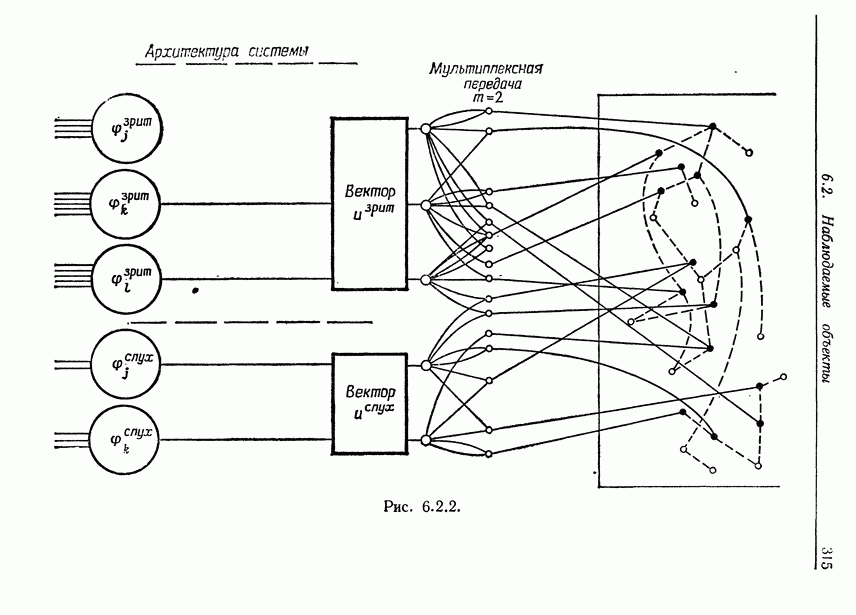
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы