| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.5. Один результат, относящийся к аппроксимации изображения
В тех случаях, когда изображения представлены конфигурациями высокой или бесконечной мощности, приходится задумываться о более экономных способах хранения содержащейся в них информации. Разумеется, это приводит к некоторой потере информации, и возникает проблема нахождения оптимального способа.
Один из способов заключается в том, чтобы искать изображения, аппроксимирующие заданное и имеющие в то же время простые описания. В качестве примера рассмотрим случай, когда
«свободные» и в качестве  используется по меньшей мере столь же грубое правило, как «идентификация множеств образующих» (см. т. 1, с. 81). Отметим, кстати, что может оказаться полезным ввести чуть более жесткое условие: два множества (конфигурации) образующих
используется по меньшей мере столь же грубое правило, как «идентификация множеств образующих» (см. т. 1, с. 81). Отметим, кстати, что может оказаться полезным ввести чуть более жесткое условие: два множества (конфигурации) образующих  отождествляются (по крайней мере), если совпадают их замыкания
отождествляются (по крайней мере), если совпадают их замыкания  Если множество
Если множество  конечно, то, естественно, ни к каким топологическим понятиям прибегать не следует.
конечно, то, естественно, ни к каким топологическим понятиям прибегать не следует.
Как бы то ни было, воспользуемся правилом идентификации, согласно которому из  и
и  (как множества) следует
(как множества) следует  кроме того, это
кроме того, это  отождествляет дополнения
отождествляет дополнения  где
где 
Пусть  — некоторое фиксированное инвариантное относительно
— некоторое фиксированное инвариантное относительно  подмножество образующих; определим отображение
подмножество образующих; определим отображение  как
как

Это непосредственно индуцирует отображение  как
как  изображение, принадлежащее и содержащее
изображение, принадлежащее и содержащее  (5.5.2) В самом деле, (5.5.2) приводит к однозначному результату, поскольку, если
(5.5.2) В самом деле, (5.5.2) приводит к однозначному результату, поскольку, если  принадлежат одному и тому же изображению, то
принадлежат одному и тому же изображению, то  и, учитывая дополнения, кроме того, естественно,
и, учитывая дополнения, кроме того, естественно,  так как
так как  рефлексивно. Следовательно, исходя из пункта
рефлексивно. Следовательно, исходя из пункта
(iii) определения 3.1.1 (т.1, гл. 3),

поскольку здесь соединение конфигураций означает просто объединение множеств образующих. Из (5.5.3) следует, однако, снова с учетом дополнений, что

Это доказывает, что отображение  определяется однозначно.
определяется однозначно.
Для доказательства свойства  определения 3.1.2 (т. 1, гл. 3) обратим внимание на то, что
определения 3.1.2 (т. 1, гл. 3) обратим внимание на то, что

Можно доказать также и свойство  этого определения, поскольку если
этого определения, поскольку если  то
то

Итак, мы доказали, что  представляет собой гомоморфное отображение
представляет собой гомоморфное отображение 
Если множество  достаточно плотно в
достаточно плотно в  то отображение
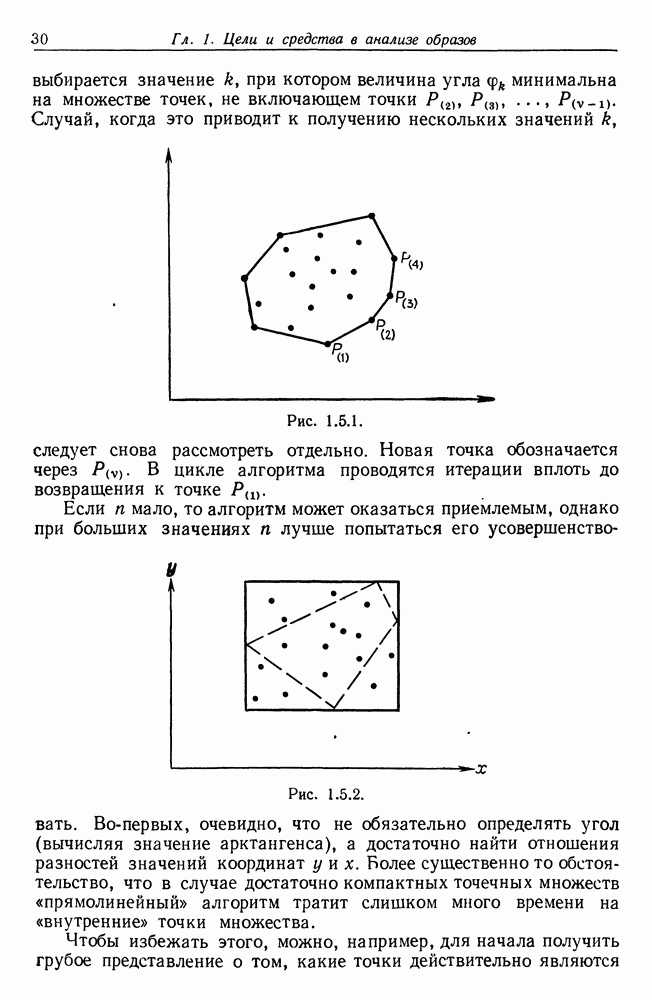
то отображение  можно рассматривать как некоторый оператор над изображениями, обеспечивающий аппроксимацию изображений более простыми изображениями. Рассмотрим один частный случай, связанный с предыдущим, но отличающийся от него: выпуклые множества изображений, которые нужно аппроксимировать выпуклыми многоугольниками, имеющими
можно рассматривать как некоторый оператор над изображениями, обеспечивающий аппроксимацию изображений более простыми изображениями. Рассмотрим один частный случай, связанный с предыдущим, но отличающийся от него: выпуклые множества изображений, которые нужно аппроксимировать выпуклыми многоугольниками, имеющими  сторон с направлениями
сторон с направлениями  Такая аппроксимация не гомоморфна, так как
Такая аппроксимация не гомоморфна, так как  не всегда равно
не всегда равно  Можно лишь утверждать, что первое множество заключено во втором.
Можно лишь утверждать, что первое множество заключено во втором.
В таком случае можно исследовать асимптотическое поведение ошибки аппроксимации и получить удобное выражение, представляющее ее через кривизну изображения  Однако вместо этого мы займемся более сложной задачей оптимального выбора
Однако вместо этого мы займемся более сложной задачей оптимального выбора  образующих из
образующих из  с тем, чтобы сделать ошибку аппроксимации возможно минимальной.
с тем, чтобы сделать ошибку аппроксимации возможно минимальной.
Эта задача отличается от рассматривавшейся в разд. 5.4 тем, что в ней отсутствует случайный механизм деформаций  вместо этого изображение I преднамеренно заменено некоторой его
вместо этого изображение I преднамеренно заменено некоторой его
аппроксимацией  Асимптотическая нижняя грань для ошибки аппроксимации была получена в работе Маклура и Вайтала (1975):
Асимптотическая нижняя грань для ошибки аппроксимации была получена в работе Маклура и Вайтала (1975):
Теорема 5.5.1. Если изображение  представляет собой компактное выпуклое множество в пространстве
представляет собой компактное выпуклое множество в пространстве  имеющее гладкую границу с непрерывным радиусом кривизны
имеющее гладкую границу с непрерывным радиусом кривизны  то
то

где  описанный многоугольник с
описанный многоугольник с  сторонами.
сторонами.
Известен также конструктивный способ достижения асимптотической нижней грани. Введем функцию распределения

Теорема 5.5.2. Пусть 12 представляет собой последовательность наилучших описанных многоугольников с  сторонами,
сторонами,  Определим функцию распределения
Определим функцию распределения

где  — направления нормалей к сторонам
— направления нормалей к сторонам  Тогда
Тогда

Более того, если  строго положительна, а
строго положительна, а  представляет собой последовательность описанных многоугольников с направлениями нормалей
представляет собой последовательность описанных многоугольников с направлениями нормалей  то
то  асимптотически оптимально.
асимптотически оптимально.
Читатель, интересующийся доказательствами этих теорем, может найти их в уже упоминавшейся статье Маклура и Вайтала. В разд. 3.3 мы уже описали этот метод.
Очень мало в настоящее время известно об аналогичной задаче аппроксимации изображения в случае логики признаков более высокого порядка или других образующих.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
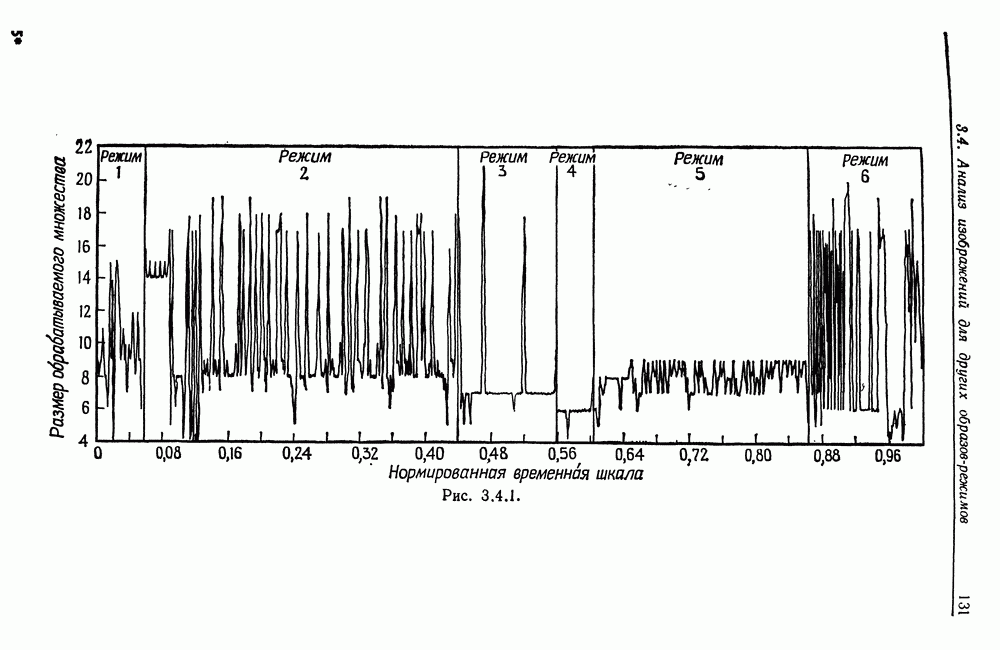
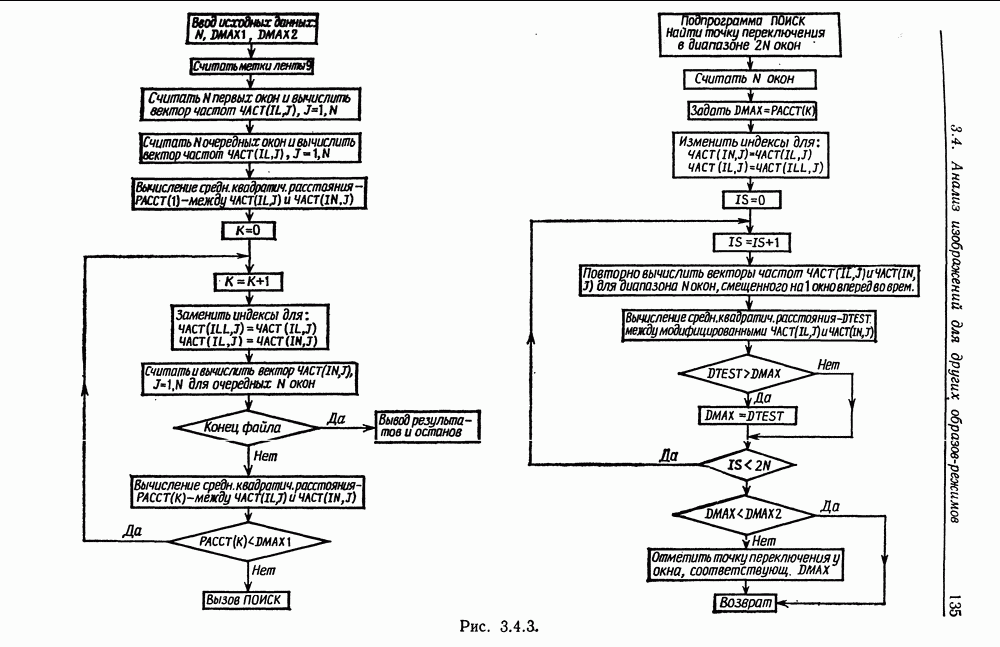
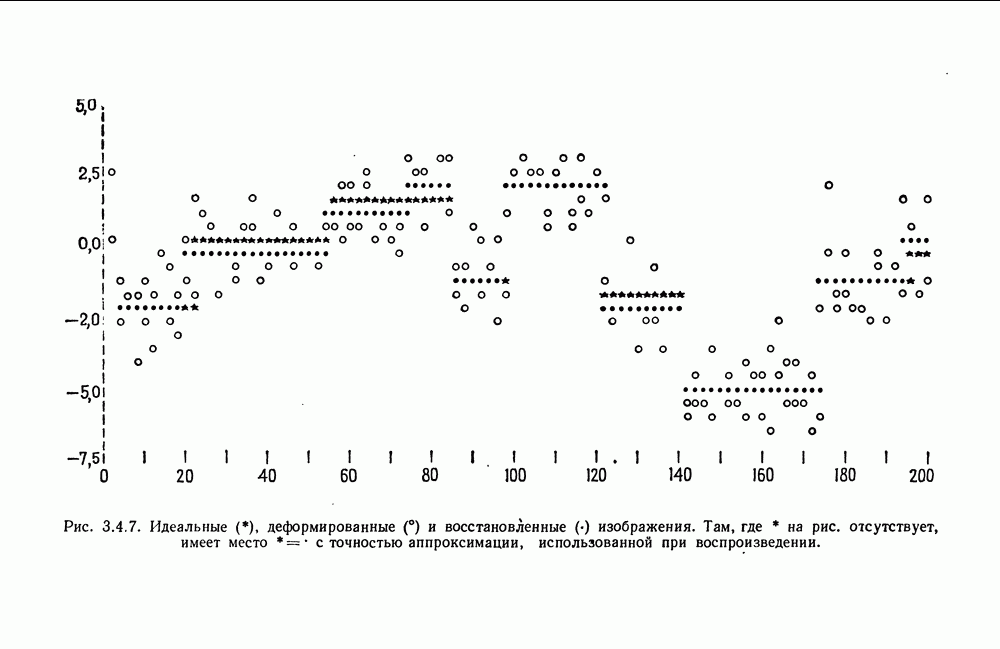
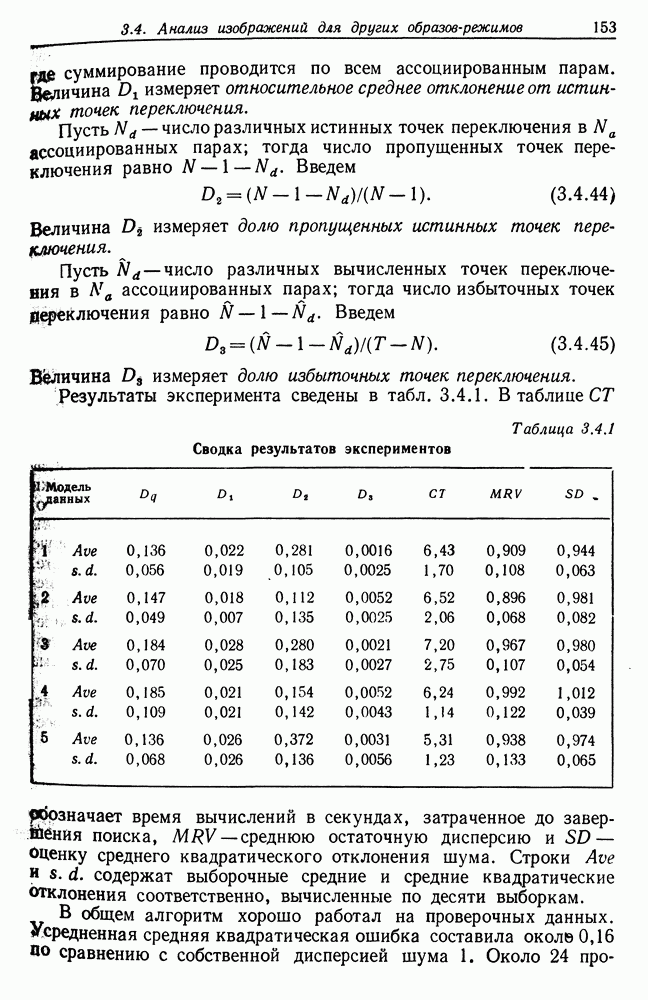
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
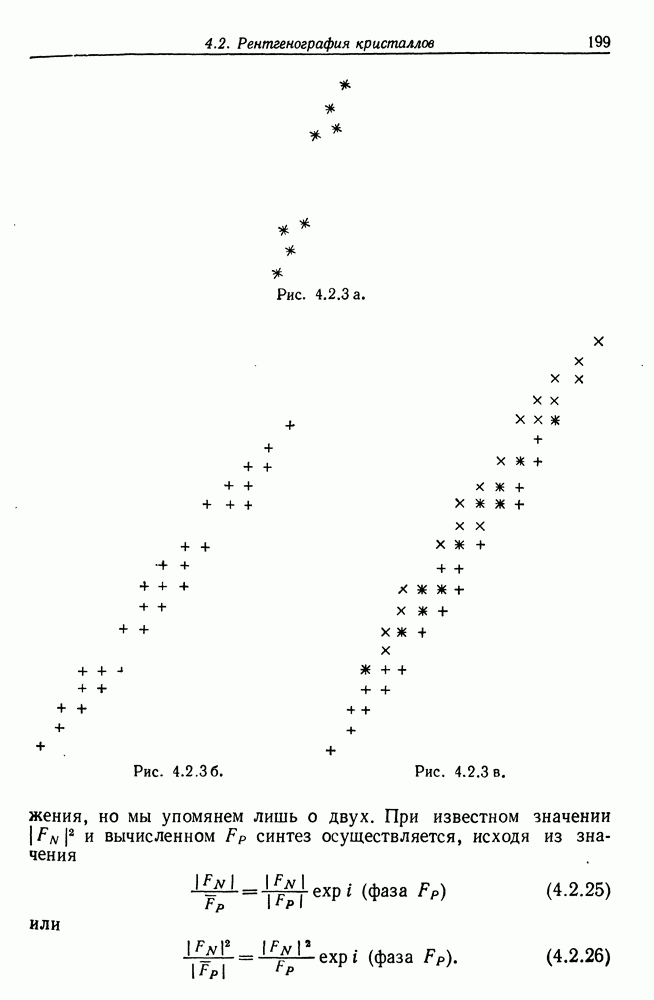
- 4.2. Рентгенография кристаллов
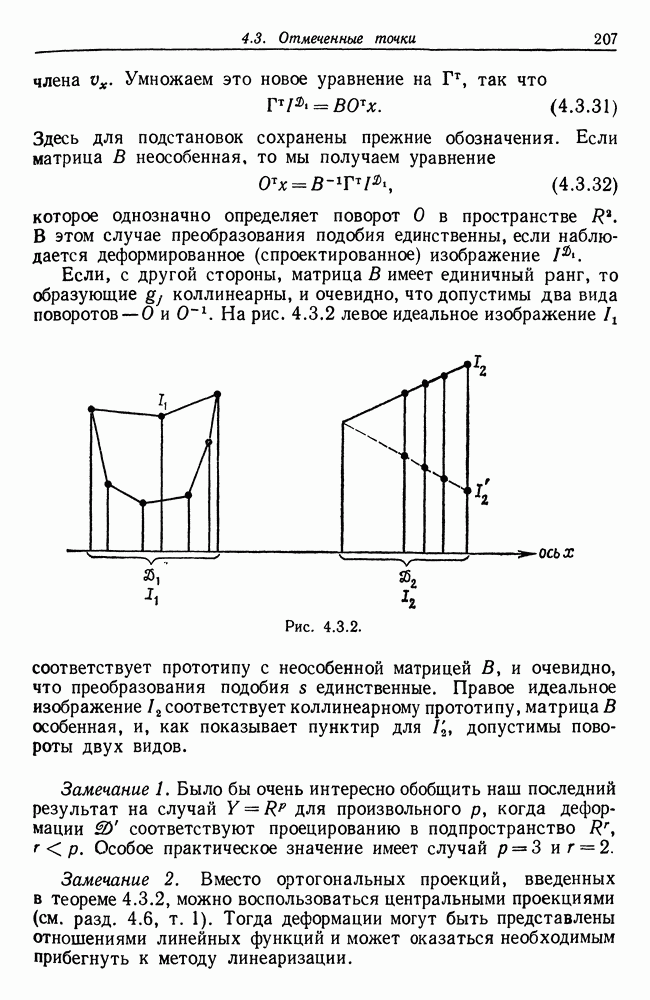
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
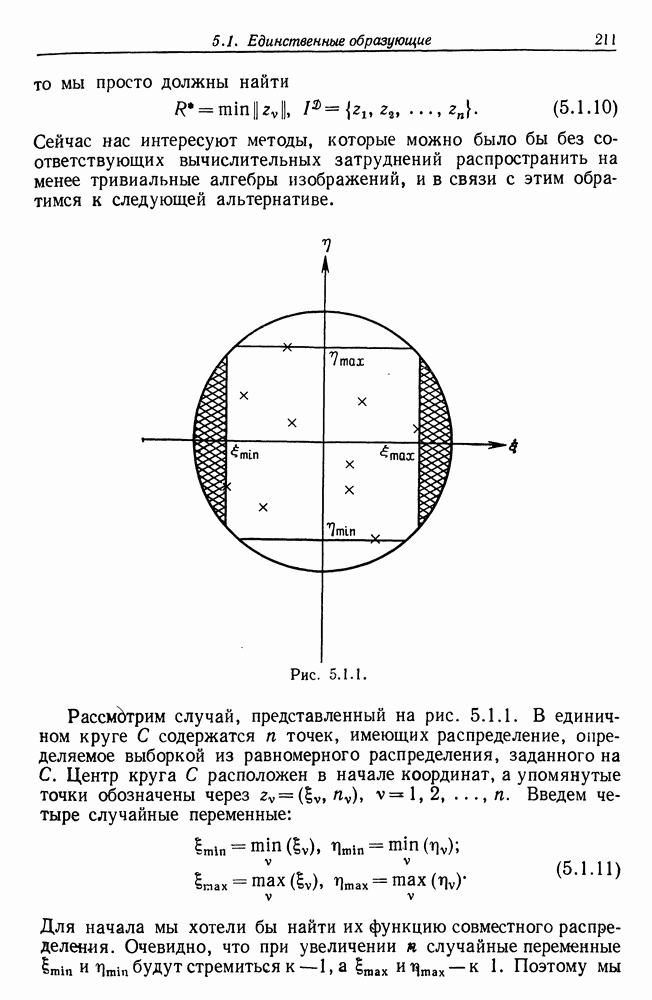
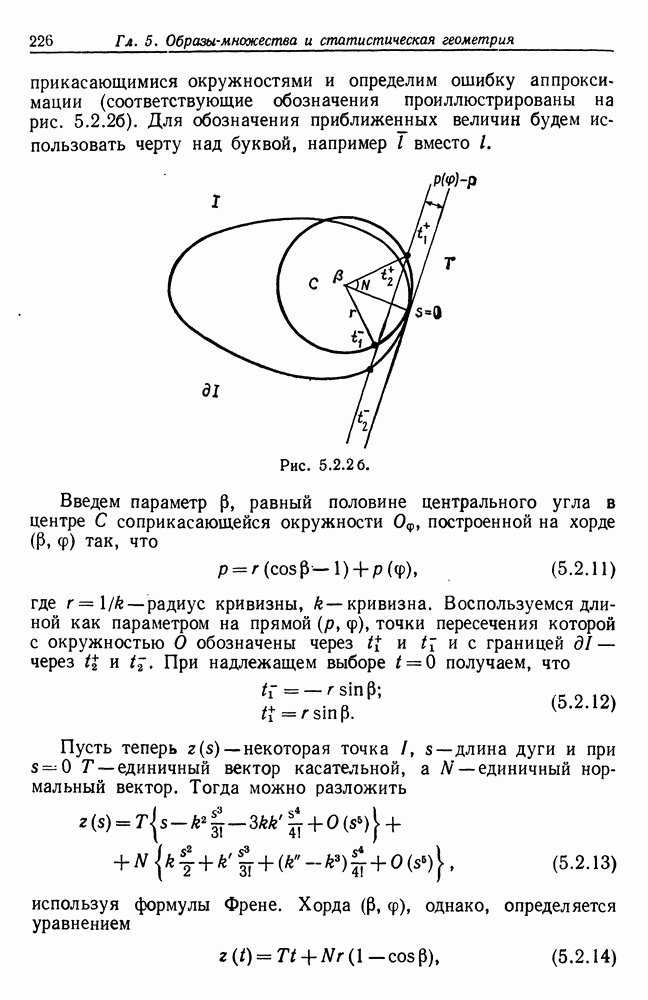
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
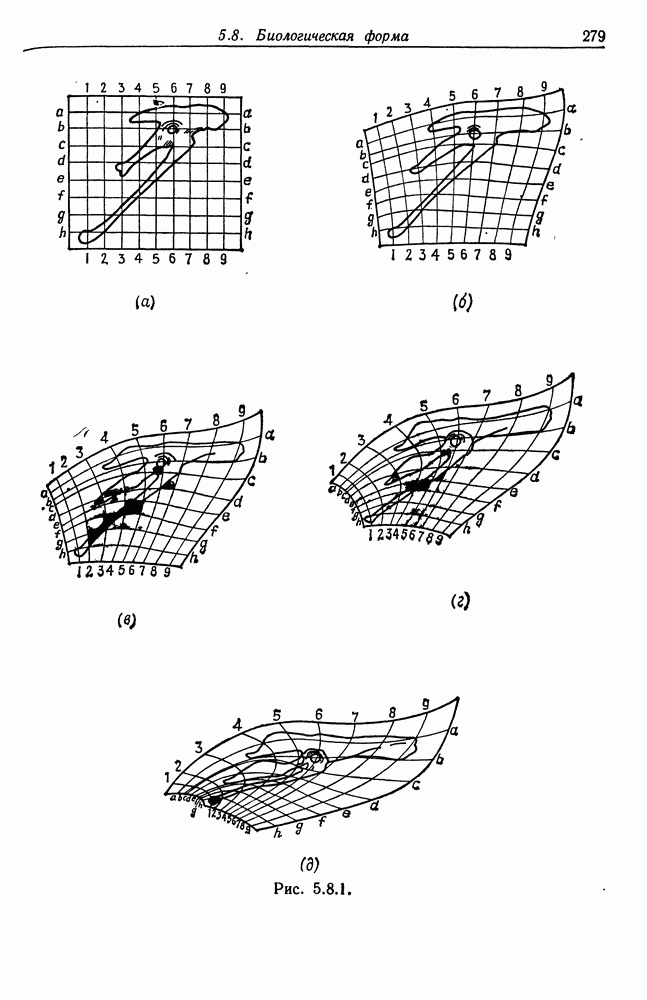
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
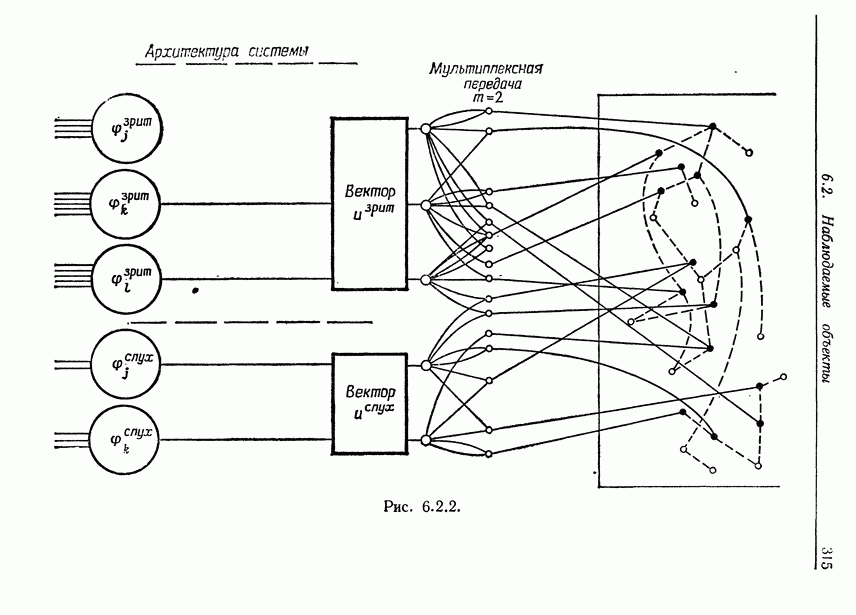
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы