| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4. Анализ изображений для других образов-режимов
Временные образы, рассмотренные в предыдущем разделе, теперь изучены достаточно хорошо. Менее ясной картина становится при переходе к временным образам более общего характера. Здесь возникают новые трудности.
(i) Режимы даны не в столь явном виде, как в случаях, когда они порождаются простыми образующими, например дифференциальными операторами с постоянными коэффициентами. Или же они могут быть простыми сами по себе, но требовать много больше информации на режим для того, чтобы оказалось возможным восстановление с хорошим качеством.
(ii) Индекс класса образующих а может иметь несколько значений, так что для каждого режима приходится определять также каким-либо способом соответствующее значение а. Последовательности значений а, допустимые для регулярных конфигураций, сами могут иметь структуру абстрактного образа.
(iii) Мы едва затронули задачу определения числа режимов. Если мы допустим, что оно может расти, то естественно ожидать лучшей аппроксимации, хотя численная сложность в конечном счете лишит результат привлекательности. Следовательно, необходимо тем или иным способом ввести в анализ изображений стремление к «простым» сегментациям.
В данном разделе мы проиллюстрируем осложнения, связанные с  и начнем со случая, когда структура образа довольно неопределенна и полученные результаты не столь полны, как того хотелось бы.
и начнем со случая, когда структура образа довольно неопределенна и полученные результаты не столь полны, как того хотелось бы.
Рассмотрим процесс выполнения программы ЭВМ при страничной организации памяти. Оперативная память разделяется на блоки, или страницы, имеющие обычно одинаковые размеры. В процессе выполнения программы происходят обращения к различным страницам оперативной памяти. Если перенумеровать страницы с помощью номеров  , то возникает
, то возникает
цепочка целых чисел — временной образ, если интерпретировать время как число выполненных команд. Если страница, к которой производится обращение, уже отсутствует в оперативной памяти, то ее следует туда загрузить. Если же, с другой стороны, места в памяти недостаточно, то сначала необходимо удалить какую-то другую страницу. Интенсивность такого страничного обмена может легко достичь недопустимого уровня, и следует принять меры, препятствующие этому (см. Деннинг (1970)).
Итак, если бы цепочка обращений к страницам была совершенно случайной, то очевидно, что дело было бы плохо, и было бы трудно предотвратить рост интенсивности страничного обмена до неприемлемого уровня. На самом деле это, однако, не так: программные обращения часто обнаруживают локальность, проявляющуюся в том, что соседние команды «склонны» обращаться к одной и той же странице, особенно если размер страницы велик (см. Деннинг (1968)).
К тому же программы в конце концов делаются людьми и программист, помня о проблеме страничного обмена, может намеренно придать своей программе в существенной мере локальный характер. В последние годы, особенно в связи с развитием структурного программирования, стало возможным требовать, чтобы при составлении программы учитывалось это обстоятельство.
Вычисления на имеющихся в настоящее время машинах выполняются в основном последовательно, а не параллельно. Если большую задачу необходимо обработать с помощью программы умеренного размера, то приходится всецело положиться на циклы. При этом, однако, в случае повторного обращения к циклу цепочка обращений к страницам оказывается более или менее периодической. Мало вероятно, что может возникнуть строгая периодичность, так как если цикл содержит большое число команд, то вполне могут появляться переходы через границы между страницами, но какой-то разновидности квазипериодического поведения ожидать следует.
Это одна из причин, по которым можно рассчитывать на возникновение временных образов-режимов в цепочках обращений. Точки переключения режимов характеризуют переход от одного цикла к другому, причем, естественно, могут встречаться циклы, вложенные в циклы, что порождает исключительно сложные временные образы.
В системах с мультипрограммированием можно ожидать также появления точек переключения и тогда, когда выполнение одной программы прерывается и начинается выполнение другой. Очевидно, что совместное влияние всех этих переключений может привести к внешне хаотической временной зависимости. Применение для ее анализа стандартных линейных и квадратичных методов анализа временных рядов не представляется продуктивным,

(кликните для просмотра скана)

(кликните для просмотра скана)
и мы полагаем, что более адекватный способ анализа может быть основан на структуре режима для временных образов.
Это предположение подкрепляется одним эмпирическим исследованием (см. статью Фрайбергера, Гренандера и Сампсона (1975)). Данные относятся к машине IBM 360/67 с операционной системой CMS. Размер страницы памяти — 4 килобайт, общее число страниц — 64. Программа-монитор собирает данные об обращениях и регистрирует число обращений к каждой странице в пределах временного окна, в нашем случае — это тысяча команд. Размер этого окна достаточно мал для того, чтобы можно было подробно изучить особенности обращений. На самом деле можно сделать его больше, так как практически масштаб времени скорее характеризуется числом команд порядка 10—20 тыс.
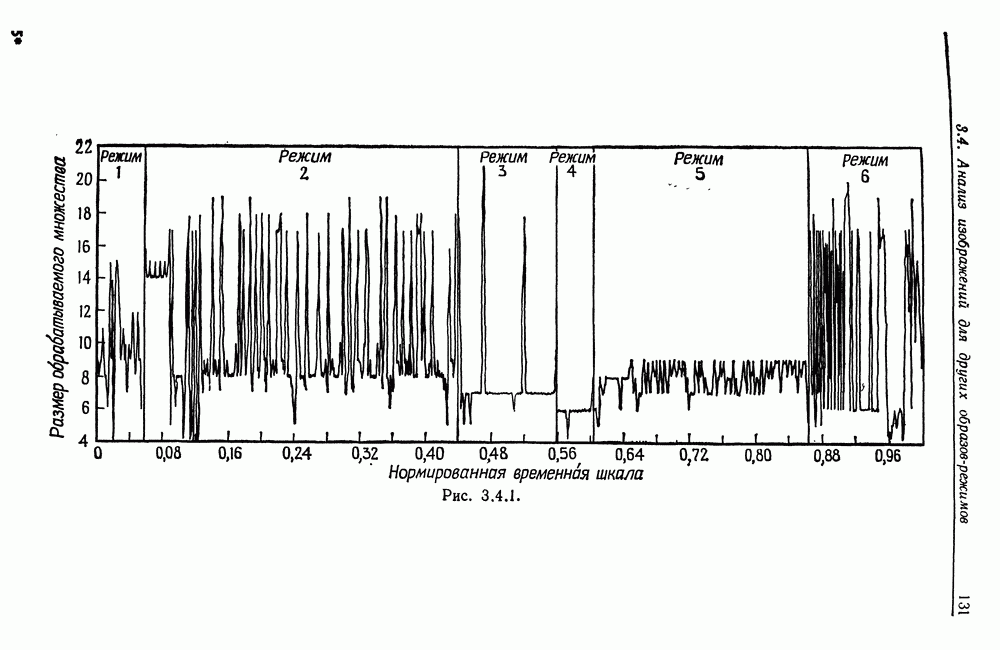
Вначале данные отображаются на дисплее с электронно-лучевой трубкой, и затем по ним строятся выборочные графики; на рис. 3.4.1 приведен пример возможной выдачи. По оси ординат откладывается размер обрабатываемого множества — число страниц, к которым производились обращения на протяжении одного временного окна. Ось абсцисс представляет нормированное время, причем за единицу времени принимается число команд, необходимых для выполнения всей программы.
Наибольший интерес для нас представляли большие программы, и мы остановились на компиляциях с Фортрана и ПЛ/1, а также на нескольких трансляциях с языка ассемблера. Данные записывались также на ленту для последующего анализа.
На рис. 3.4.1 представлены данные, характеризующие обращения к страницам памяти при компиляции программы с Фортрана. Более полно представляет картину рис. 3.4.2, на котором каждой горизонтальной линии соответствует одно временное окно. По горизонтали представлены различные страницы, которым в строке соответствует символ «х», если к данной странице в пределах данного окна производилось обращение. В противном случае соответствующий участок распечатки остается пустым. Отметим, что на рисунке представлена лишь часть процесса компиляции, а окна 63—260 исключены ради экономии места.
Уже беглое изучение этих рисунков дает представление о структуре режимов, хотя вопрос об их числе и разграничении остается открытым. Было изучено еще семь компиляций фортранных программ, и во всех случаях можно обнаружить по крайней мере шесть явно выраженных режимов.
Нетрудно установить, почему возникают эти режимы. Это является следствием конструкции компилятора с Фортрана, и режимы соответствуют шести этапам работы компилятора, а именно вызову процедуры, разбору, размещению, объединению, генерации кода и выводу (см. IBM System 360 Operating System, FORTRAN IV (G) Compiler, Program Logic Manual).
Хотя это и объясняет возникновение режимов, но не говорит ничего о том, как их можно выделять и анализировать в общем случае, когда мы не располагаем таким количеством априорных сведений и когда структура режима менее очевидна. Для того чтобы изучить эту важную проблему, рассмотрим вначале те же данные — обращения к страницам памяти, но теперь с тем, чтобы отыскать автономные алгоритмы, которые будут автоматически или полуавтоматически обнаруживать режимы при наличии небольших априорных сведений.
Занявшись этим, будем иметь в виду, что все временные образы, изучаемые в данном разделе, имеют линейный тип соединения, причем ось времени делится точками переключения на однородные режимы. Образующая, соответствующая такому интервалу, будет теперь представлять собой распределение вероятностей на множестве страниц памяти, из которого данные будут генерироваться при помощи обычной случайной выборки.
Это частный случай Случая 3.4.3, т. 1 (образы—стационарные режимы), и значения а представляют здесь различные распределения вероятностей на множестве страниц. Введем эмпирический аналог, 64-мерный вектор  где
где  относительная частота обращений к странице с номером
относительная частота обращений к странице с номером  на Протяжении окон
на Протяжении окон  Здесь N — малое ратуральное число, роль которого заключается в уменьшении влияния случайных вариаций.
Здесь N — малое ратуральное число, роль которого заключается в уменьшении влияния случайных вариаций.
Далее из эвристических соображений получаем, что если окна  приходятся на один и тот же режим, то норма
приходятся на один и тот же режим, то норма

должна быть малой. Если она велика, то следует предполагать, что точка переключения лежит на дискретном отрезке  .
.
В соответствии с этими замечаниями наша эвристическая процедура должна сводиться к выборочному вычислению векторов частоты обращения к страницам памяти на  последовательных окнах и отысканию точек времени, в которых среднее квадратическое расстояние
последовательных окнах и отысканию точек времени, в которых среднее квадратическое расстояние  между векторами частот принимает большие значения. Допустим теперь, что такое достаточно большое значение
между векторами частот принимает большие значения. Допустим теперь, что такое достаточно большое значение  ) обнаружено между векторами частот, вычисленными в окнах
) обнаружено между векторами частот, вычисленными в окнах  соответственно. Попытаемся затем максимизировать значение
соответственно. Попытаемся затем максимизировать значение  так как это должно позволить более точно определить положение точки, разделяющей стационарные режимы. Векторы частот корректируются
так как это должно позволить более точно определить положение точки, разделяющей стационарные режимы. Векторы частот корректируются  раз, так чтобы значение
раз, так чтобы значение  можно было вычислить между векторами с центром в каждом из
можно было вычислить между векторами с центром в каждом из  окон
окон  .
.

(кликните для просмотра скана)
Если максимальное значение  достаточно велико, то окно, которому соответствует этот максимум, отождествляется с точкой переключения. Другими словами, этот алгоритм предполагает, что если расстояние между векторами частот обращения, вычисленными в последовательных группах из
достаточно велико, то окно, которому соответствует этот максимум, отождествляется с точкой переключения. Другими словами, этот алгоритм предполагает, что если расстояние между векторами частот обращения, вычисленными в последовательных группах из  окон, принимает максимальное значение в окне
окон, принимает максимальное значение в окне  то окна
то окна  соответствуют совершенно различным режимам, имеющим различные векторы, характеризующие частоту обращения к страницам памяти. Это, однако, в определенном смысле идеализация, поскольку в принципе между режимами имеется переходный период, включающий по крайней мере несколько окон. Поэтому абсолютно точно локализовать точку переключения режимов невозможно.
соответствуют совершенно различным режимам, имеющим различные векторы, характеризующие частоту обращения к страницам памяти. Это, однако, в определенном смысле идеализация, поскольку в принципе между режимами имеется переходный период, включающий по крайней мере несколько окон. Поэтому абсолютно точно локализовать точку переключения режимов невозможно.
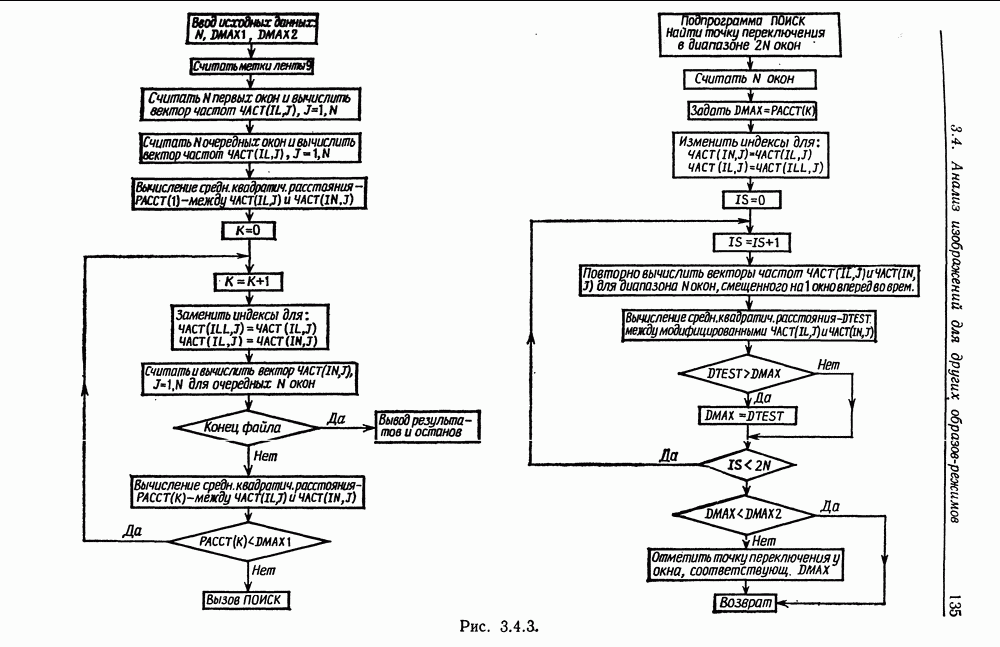
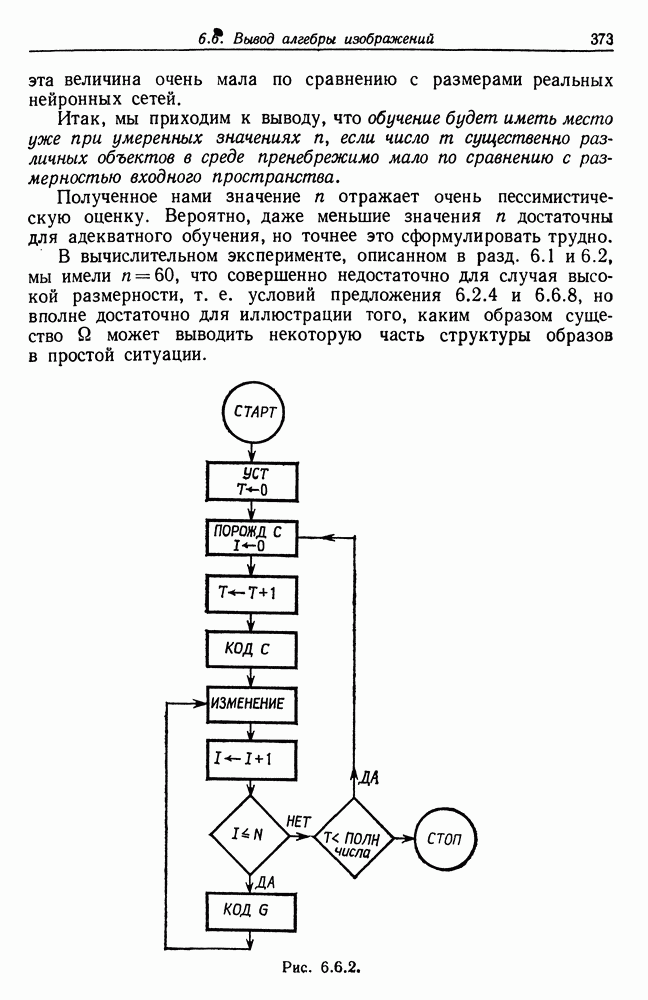
Описанный только что алгоритм весьма подробно представлен блок-схемой, приведенной на рис. 3.4.3. Алгоритм зампрограммирован на Фортране и реализован с помощью главной программы «РЕЖИМ» и подпрограммы «ПОИСК», которая вызывается для определения точки переключения путем максимизации расстояния D.
Очевидно, что выбор значения  -числа окон, на которых вычисляются векторы частоты, — имеет решающее значение для успешной работы алгоритма. Эта величина должна быть достаточно большой для того, чтобы могла быть получена хорошая оценка истинного характеристического вектора частот. С другой стороны, она должна быть меньше длины (выраженной в количестве окон) самого короткого стационарного режима из тех, что будут рассмотрены. Важен также и выбор значения расстояния
-числа окон, на которых вычисляются векторы частоты, — имеет решающее значение для успешной работы алгоритма. Эта величина должна быть достаточно большой для того, чтобы могла быть получена хорошая оценка истинного характеристического вектора частот. С другой стороны, она должна быть меньше длины (выраженной в количестве окон) самого короткого стационарного режима из тех, что будут рассмотрены. Важен также и выбор значения расстояния  которое считается «достаточно» большим. На самом деле таких значений два. Первое из них
которое считается «достаточно» большим. На самом деле таких значений два. Первое из них  это величина, значение которой должно быть превышено для того, чтобы найти точное положение точки переключения режимов в последовательности окон. Второе значение
это величина, значение которой должно быть превышено для того, чтобы найти точное положение точки переключения режимов в последовательности окон. Второе значение  -это величина, значение которой должно быть превышено максимальным значением
-это величина, значение которой должно быть превышено максимальным значением  при поиске по последовательности в диапазоне
при поиске по последовательности в диапазоне  окон (в подпрограмме «ПОИСК») окна, отождествляемого с точкой переключения режимов.
окон (в подпрограмме «ПОИСК») окна, отождествляемого с точкой переключения режимов.
Выбор параметров  зависит от характера конкретного исследуемого класса программ. Алгоритм успешно работал при выделении режимов обращений к страницам для компилятора Фортрана со следующими параметрами:
зависит от характера конкретного исследуемого класса программ. Алгоритм успешно работал при выделении режимов обращений к страницам для компилятора Фортрана со следующими параметрами:  . Подобный выбор
. Подобный выбор  означает, что никакой диапазон, меньший 20 окон, или 20000 команд, не может быть идентифицирован как стационарный режим. Очевидно, что более короткие временные отрезки не имеют существенного практического значения и меньшие значения
означает, что никакой диапазон, меньший 20 окон, или 20000 команд, не может быть идентифицирован как стационарный режим. Очевидно, что более короткие временные отрезки не имеют существенного практического значения и меньшие значения  затруднят точную оценку истинного характеристического вектора частот.
затруднят точную оценку истинного характеристического вектора частот.
В правой части машинной распечатки, приведенной на рис. 3.4.2,
указано значение расстояния  между последовательными векторами частот в диапазонах, включающих по 20 окон.
между последовательными векторами частот в диапазонах, включающих по 20 окон.
Точки переключения режимов для двух фортранных программ, определенные с помощью описанного алгоритма, показаны пунктирными линиями в тех случаях, когда эти точки не совпадают с точками переключений, определенными из интуитивных соображений (последние обозначены сплошными линиями). Максимумы функции расстояния, соответствующие этим разбиениям, указаны над или под пунктирными линиями. Минимальное значение  для любого окна, идентифицированного как точка переключения, равно 1,6771. Учитывая существование переходных периодов на стыках режимов, можно сказать, что данное разделение режимов, полученное с помощью описанного алгоритма, является настолько точным, насколько можно было рассчитывать. Отметим также, что для случаев компилирования программ с ПЛ/1 наилучшее
для любого окна, идентифицированного как точка переключения, равно 1,6771. Учитывая существование переходных периодов на стыках режимов, можно сказать, что данное разделение режимов, полученное с помощью описанного алгоритма, является настолько точным, насколько можно было рассчитывать. Отметим также, что для случаев компилирования программ с ПЛ/1 наилучшее  были получены при значениях
были получены при значениях  . Эти более высокие пороговые значения оказались йрббходимыми в связи с большими размерами обрабатываемых Множеств и значениями
. Эти более высокие пороговые значения оказались йрббходимыми в связи с большими размерами обрабатываемых Множеств и значениями 
Подробнее с изложенным материалом можно познакомиться  отчету Сампсона (1974), где, в частности, содержится критика выбора структуры образа.
отчету Сампсона (1974), где, в частности, содержится критика выбора структуры образа.
Описанная выше процедура носит слишком частный характер: она не основана на явных утверждениях относительно структуры идеального образа и не учитывает деформаций.  того чтобы устранить эти недостатки, мы провели еще одно исследование, с методологической точки зрения более общее, применительно к образам, похожим на рассмотренные в разд. 3.3.3, но деформированным из-за наличия шумов. Точнее, это означает, что данные
того чтобы устранить эти недостатки, мы провели еще одно исследование, с методологической точки зрения более общее, применительно к образам, похожим на рассмотренные в разд. 3.3.3, но деформированным из-за наличия шумов. Точнее, это означает, что данные  получаются из идеального изображения
получаются из идеального изображения  а время
а время  дискретное.
дискретное.

Правые концевые точки режимов  соответствуют разрывам режимов,
соответствуют разрывам режимов,  -длины режимов и — средние значения режимов. При непрерывном времени это соответствует случаю
-длины режимов и — средние значения режимов. При непрерывном времени это соответствует случаю  из предыдущего раздела.
из предыдущего раздела.
Рассматриваемый здесь механизм деформаций представляет собой деформации в результате воздействия аддитивного шума, т. е.  где
где

Если обратиться к восстановлению с помощью процедуры максимального правдоподобия, что при наличии условий (3.4.3) эквивалентно методу наименьших квадратов, то необходимо минимизировать

и

где  — длина режима
— длина режима  на множестве
на множестве  (множестве разбиений). Естественно, если разбиение
(множестве разбиений). Естественно, если разбиение  тоньше разбиения
тоньше разбиения  то
то  и, избегая чрезмерной вычислительной сложности, мы приходим к тривиальному разбиению, где
и, избегая чрезмерной вычислительной сложности, мы приходим к тривиальному разбиению, где  Если потребовать, чтобы то численное решение (3.4.4) при больших Т вызовет непреодолимые вычислительные затруднения.
Если потребовать, чтобы то численное решение (3.4.4) при больших Т вызовет непреодолимые вычислительные затруднения.
Альтернативный подход зиключается в том, чтобы, используя в качестве исходных диффузные временные образы, применить следующую бейесовскую процедуру. Допустим, что длины режимов  средние
средние  и шум
и шум  порождаются независимо, точки переключения образуют дискретный процесс восстановления и
порождаются независимо, точки переключения образуют дискретный процесс восстановления и  имеет распределение
имеет распределение  т. е.
т. е.

Средние значения режимов независимы и имеют одинаковые нормальные распределения

Без потери общности можно допустить, что 
Эту ситуацию можно считать разновидностью случая 3.4.3 т. 1 с той разницей, что появляется дополнительная структура, представляющая свойство восстановления в точках переключения последовательных режимов.
Вероятность разбиения  равна
равна

если считать, что  одна из точек восстановления.
одна из точек восстановления.
При заданном разбиении вектор  имеет нормальное условное распределение с нулевыми математическими
имеет нормальное условное распределение с нулевыми математическими
ожиданиями и ковариациями

Обозначим через  матрицу размера
матрицу размера  все элементы которой равны единице, и через
все элементы которой равны единице, и через  единичную матрицу размера
единичную матрицу размера  Тогда часть ковариационной матрицы, относящуюся к режиму длины
Тогда часть ковариационной матрицы, относящуюся к режиму длины  можно записать так:
можно записать так:

Отметим также, что полная ковариационная матрица  разделена на блоки, причем все блоки, находящиеся в окрестности главной диагонали, имеют вид (3.4.9). Из этого следует, что обратная матрица полной ковариационной матрицы точно так же разделена на блоки, причем блок (3.4.9) заменяется блоком следующего вида:
разделена на блоки, причем все блоки, находящиеся в окрестности главной диагонали, имеют вид (3.4.9). Из этого следует, что обратная матрица полной ковариационной матрицы точно так же разделена на блоки, причем блок (3.4.9) заменяется блоком следующего вида:

в последнем можно убедиться непосредственно, имея в виду, что  Обозначим определитель
Обозначим определитель  через
через  Вычислив его, получаем
Вычислив его, получаем

Тогда для функции условного распределения имеем

где  — часть данных, относящихся к режиму
— часть данных, относящихся к режиму 
Объединив (3.4.7) и (3.4.12), получаем функцию правдоподобия

Максимизация этого правдоподобия эквивалентна максимизации следующей величины:

Последнее эквивалентно максимизации величины

При таком подходе числовая сложность  вводится в целевую функцию, так что разбиение, обеспечивающее максимизацию, уже не является наиболее мелким. Численная максимизация (3.4.15) все еще может требовать нереальных вычислительных затрат.
вводится в целевую функцию, так что разбиение, обеспечивающее максимизацию, уже не является наиболее мелким. Численная максимизация (3.4.15) все еще может требовать нереальных вычислительных затрат.
Для того чтобы обойти это препятствие, попробуем обратиться к эвристическим алгоритмам, в которых используется адаптация. Рассмотрим некоторое множество В операторов О, преобразующих пару из обрабатываемого в данный момент изображения  в некоторое новое изображение
в некоторое новое изображение 

Каждый оператор должен быть устроен так (эвристически), чтобы  являлось в некотором смысле «лучшим» описанием
являлось в некотором смысле «лучшим» описанием  чем
чем  Множество В обычно конечное, хотя каждый оператор может быть параметризован с помощью некоторого множества управляющих параметров.
Множество В обычно конечное, хотя каждый оператор может быть параметризован с помощью некоторого множества управляющих параметров.
Процесс поиска заключается в применении к некоторой начальной структуре  последовательности преобразований
последовательности преобразований

причем выбирать  можно, исходя из любой смутной идеи, которая у нас появится относительно истинной природы данного изображения, либо совершенно произвольно (например, простейшая структура режима).
можно, исходя из любой смутной идеи, которая у нас появится относительно истинной природы данного изображения, либо совершенно произвольно (например, простейшая структура режима).
Тогда алгоритм восстановления  можно рассматривать просто как некоторую последовательность операторов из множества В, т. е.
можно рассматривать просто как некоторую последовательность операторов из множества В, т. е.

Определить такой алгоритм можно, задавая целиком последовательность или с помощью некоторой функции «преемника» У.
Желаемая степень автоматизации определяет до некоторой степени вид функции  Так, например, при «полуавтоматическом» анализе в режиме диалога функция
Так, например, при «полуавтоматическом» анализе в режиме диалога функция  может быть полностью определена человеком —на каждом этапе он выбирает тот оператор, который ему кажется подходящим. Предполагается, что он будет каким-то интуитивным образом оценивать использованные раньше операторы и полученные результаты с тем, чтобы выбрать очередной ход. Предопределить тип функции
может быть полностью определена человеком —на каждом этапе он выбирает тот оператор, который ему кажется подходящим. Предполагается, что он будет каким-то интуитивным образом оценивать использованные раньше операторы и полученные результаты с тем, чтобы выбрать очередной ход. Предопределить тип функции  это означает попытаться формализовать интуитивное поведение подобного рода.
это означает попытаться формализовать интуитивное поведение подобного рода.
Мы нуждаемся также в критерии остановки, указывающем, Квгда следует прекратить применять операторы изображения. Выбор фитерия остановки, как и операторов изображения, может производиться многими способами, и в качестве примера мы приведем следующий критерий, который был запрограммирован и проверен в численном эксперименте. Здесь выделяются только существенный режимы, длина которых превосходит некоторую величину  и используется пять операторов изображения:
и используется пять операторов изображения:
1. SDEV1- оператор оценивает дисперсию шума  и определяет возможные положения точек переключения.
и определяет возможные положения точек переключения.
2. STEST —оператор проверяет, насколько значительны обнаруженные точки переключения — принятие решения; COMBINE - оператор исключает точки переключения, которые оператор STEST  как незначительные—действие
как незначительные—действие
3. HTEST - оператор проверяет все режимы на однородность — принятие решения; DIVIDE — оператор разделяет режимы, неоднородность которых установлена оператором НTEST -действие.
4. ADJUST —оператор осуществляет локальную коррекцию точек переключения с тем, чтобы увеличить различия между соседними режимами.
5. GUESS —оператор предлагает предварительный вариант структуры режима.
Теперь рассмотрим каждый оператор по отдельности. 1. SDEVI.
Если получено разбиение  то для непосредственной оценки
то для непосредственной оценки  имеем
имеем

где  среднее по режиму
среднее по режиму  . Такая оценка приемлема только случаях, когда разбиение
. Такая оценка приемлема только случаях, когда разбиение  близко истинному разбиению,
близко истинному разбиению,  следовательно, ей нельзя пользоваться на ранних этапах процесса поиска. Кроме того, влияние неточной оценки
следовательно, ей нельзя пользоваться на ранних этапах процесса поиска. Кроме того, влияние неточной оценки  на оценку
на оценку  не совсем очевидно. Рассмотрим другую оценку:
не совсем очевидно. Рассмотрим другую оценку:

так что

здесь  истинное число режимов, а
истинное число режимов, а  математические ожидания режимов. Следовательно,
математические ожидания режимов. Следовательно,  дает отклоненную оценку
дает отклоненную оценку  отклонение положительно и увеличивается при росте числа режимов и увеличении различия между средними соседних режимов.
отклонение положительно и увеличивается при росте числа режимов и увеличении различия между средними соседних режимов.
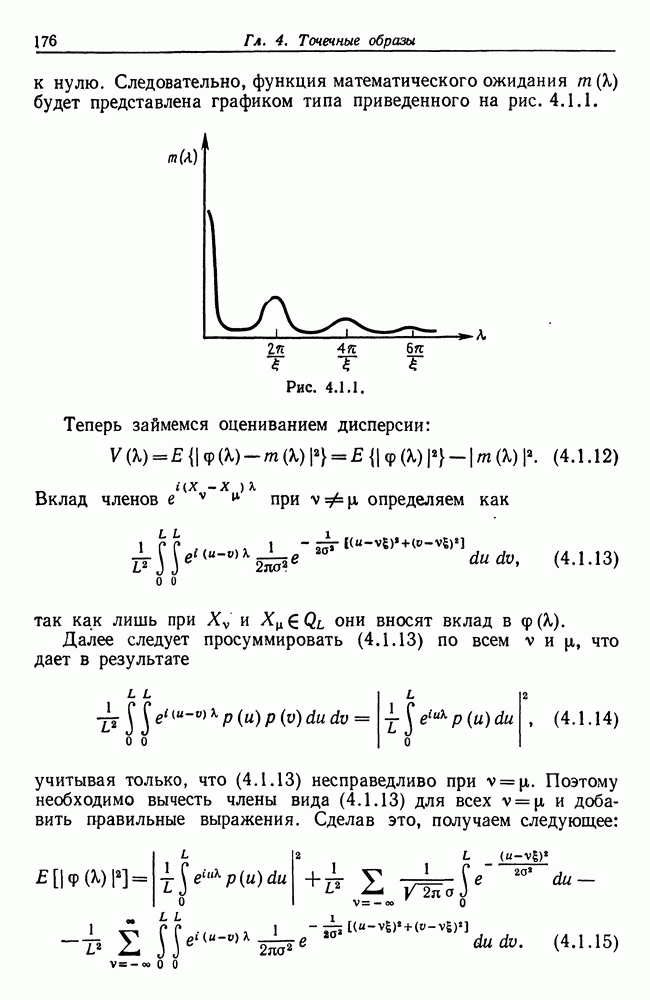
Это отклонение в оценке  объясняется членами
объясняется членами  где
где  истинные точки переключения; имеются возможности компенсировать это отклонение. Так, например, члены —
истинные точки переключения; имеются возможности компенсировать это отклонение. Так, например, члены —  имеющие чрезмерную величину, можно дезактивировать.
имеющие чрезмерную величину, можно дезактивировать.
Можно предложить различные способы дезактивации. Пусть

Можно исключать верхнюю  -часть
-часть  или те значения
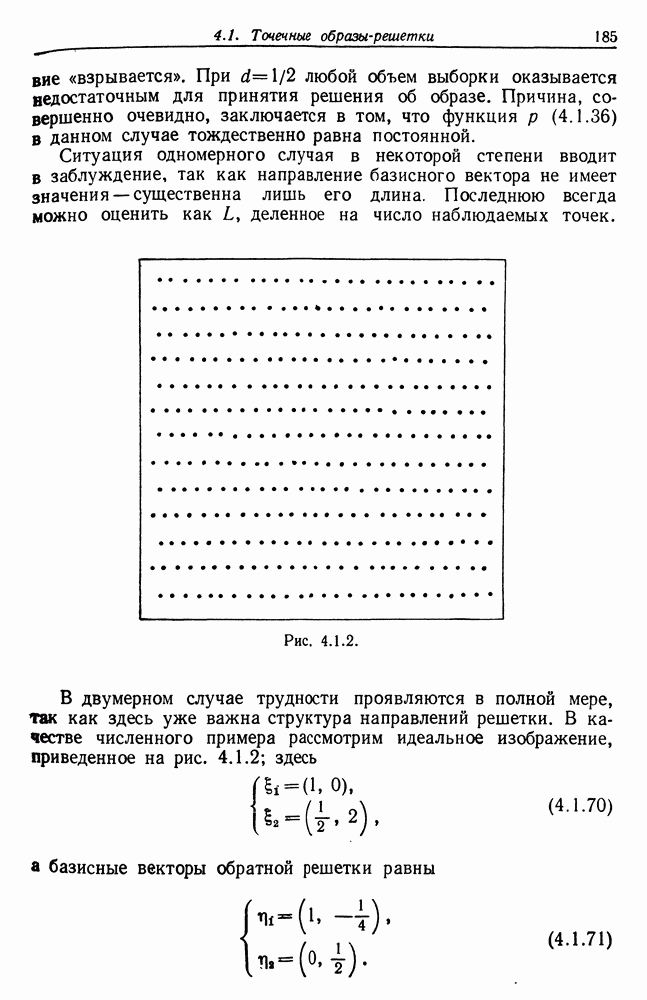
или те значения  которые превышают некоторый фиксированный уровень отсечения, определяемый имеющимися данными.
которые превышают некоторый фиксированный уровень отсечения, определяемый имеющимися данными.
Воспользуемся двухступенчатой процедурой. В первую очередь вычисляется среднее

затем те  значения которых превышают величину
значения которых превышают величину  исключаются, и среднее, вычисленное по оставленным значениям
исключаются, и среднее, вычисленное по оставленным значениям  используется в качестве оценки
используется в качестве оценки  т. е.
т. е.

где скобки  обозначают индикаторную функцию.
обозначают индикаторную функцию.
RLEVEL можно рассматривать как еще один эвристический параметр (подобно  который можно выбирать, исходя из характера распределения шума. Те точки (если они имеются), - в которых значения
который можно выбирать, исходя из характера распределения шума. Те точки (если они имеются), - в которых значения  исключаются, используются для формирования предварительного списка точек переключения.
исключаются, используются для формирования предварительного списка точек переключения.
Отметим, что  в нашей модели данных — глобальная постоянная и получение ее как совокупной оценки (на основе
в нашей модели данных — глобальная постоянная и получение ее как совокупной оценки (на основе  в противоположность
в противоположность  где используются локальные признаки) отличается тем дополнительным преимуществом, что последующая организация локальных поисков становится независимой от этой операции.
где используются локальные признаки) отличается тем дополнительным преимуществом, что последующая организация локальных поисков становится независимой от этой операции.

STEST. Для оценки каждого из обнаруженных к этому этапу концов режимов  мы пользуемся критерием разделения
мы пользуемся критерием разделения

где  (оценка
(оценка  ) — это рассмотренное выше среднее квадратическое отклонение
) — это рассмотренное выше среднее квадратическое отклонение  а
а  среднее по режиму
среднее по режиму  длины
длины  точка переключения
точка переключения  объявляется статистически значимой, если
объявляется статистически значимой, если  Это соответствует простому двухвыборочному критерию разности средних. Для совокупностей, имеющих нормальное распределение, целесообразно выбирать величину
Это соответствует простому двухвыборочному критерию разности средних. Для совокупностей, имеющих нормальное распределение, целесообразно выбирать величину  равную приблизительно 2.
равную приблизительно 2.
COMBINE. Оператор  применяется ко всем точкам переключения одновременно, что позволяет получить список статистически незначительных точек переключения. Затем эти точки исключаются. Отметим, что некоторые из остающихся после этого шага точек переключения могут быть незначительными, но они сохраняются в качестве рабочей гипотезы до тех пор, пока не будет проведена соответствующая проверка. Вся операция в целом нагана
применяется ко всем точкам переключения одновременно, что позволяет получить список статистически незначительных точек переключения. Затем эти точки исключаются. Отметим, что некоторые из остающихся после этого шага точек переключения могут быть незначительными, но они сохраняются в качестве рабочей гипотезы до тех пор, пока не будет проведена соответствующая проверка. Вся операция в целом нагана 

HTEST. Для проверки однородности каждого режима мы пользуемся простым критерием однородности  основанным на дисперсии, подсчитываемой для каждого режима.
основанным на дисперсии, подсчитываемой для каждого режима.
Пусть

Если режим  однороден, то при условии нормальности
однороден, то при условии нормальности

Таким образом,

режим  считается неоднородным, если
считается неоднородным, если

CV соответствует числу средних квадратических ошибок относительно  Для совокупностей, имеющих нормальное распределение, целесообразно выбирать величину
Для совокупностей, имеющих нормальное распределение, целесообразно выбирать величину  равную приблизительно 1,5.
равную приблизительно 1,5.
Отметим, что в предположении нормальности величина  действительно имеет
действительно имеет  -распределение с
-распределение с  степенями свободы при условии однородности. Можно было бы вычислять уровень отклонения
степенями свободы при условии однородности. Можно было бы вычислять уровень отклонения  или запоминать соответствующую таблицу (игнорируя влияние
или запоминать соответствующую таблицу (игнорируя влияние  но это было бы трудоемким, так как обычно такой тест приходится повторять многократно с различными
но это было бы трудоемким, так как обычно такой тест приходится повторять многократно с различными 
Для определения правильной точки разделения режима, когда использование оператора  позволило обнаружить неоднородность режима, мы выбираем подходящее число пробных точек разделения
позволило обнаружить неоднородность режима, мы выбираем подходящее число пробных точек разделения  скажем равномерно расположенных, вычисляем для каждой из этих точек величину «разности» между соответствующей левой и правой частями режима и выбираем в качестве новой точки переключения ту точку, в которой эта разность максимальна. Если длина рассматриваемого режима меньше, чем
скажем равномерно расположенных, вычисляем для каждой из этих точек величину «разности» между соответствующей левой и правой частями режима и выбираем в качестве новой точки переключения ту точку, в которой эта разность максимальна. Если длина рассматриваемого режима меньше, чем  , то используется максимально возможное число пробных точек.
, то используется максимально возможное число пробных точек.
Затем два полученных таким образом режима подвергаются изучению. Если длина левого режима  и длина правого режима то получаем новую точку переключения. Если
и длина правого режима то получаем новую точку переключения. Если  и или
и или  и
и  то соответствующая концевая точка переносится в новую точку разделения (поскольку неоднородность может объясняться тем обстоятельством, что истинная точка переключения, которую предположительно представляет концевая точка, на самом деле расположена где-то внутри режима). Если
то соответствующая концевая точка переносится в новую точку разделения (поскольку неоднородность может объясняться тем обстоятельством, что истинная точка переключения, которую предположительно представляет концевая точка, на самом деле расположена где-то внутри режима). Если  то обе концевые точки переносятся в новую точку разделения (случай, когда обе концевые точки кажутся ложными).
то обе концевые точки переносятся в новую точку разделения (случай, когда обе концевые точки кажутся ложными).
Если рассматриваемый режим оказывается первым или последним, то требуется несколько небольших модификаций.
Оператор HTEST применяется ко всем режимам, что позволяет получить список неоднородных режимов. Каждый из них затем делится или его концевая точка (точки) переносится, как было описано выше, причем все действия выполняются последовательно

Рис. 3.4.4. Пример применения оператора 
слева направо. Вся операция в целом определена как DIVIDE. Из рассмотренных до сих пор эта операция самая сложная.
На рис. 3.4.4 приведен пример применения операции DIVIDE при наличии сильной неоднородности. Оператор HTEST устанавливает однородность режима 4 и неоднородность девяти остальных режимов. Последующие действия включают следующие девять шагов:
1. Введение новой точки переключения в режим 1.
2. Перенос левой концевой точки режима 3 (первоначально режим 2).
3. Объединение обеих концевых точек режима 4 (первоначально режим 3).
4. Объединение обеих концевых точек режима 5 (первоначально режим 5).
5. Введение одной точки переключения в режим 5 (первоначально режим 6).
6. Перенос правой концевой точки режима 7 (первоначально  режим 7).
режим 7).
7. Перенос левой концевой точки режима 8 (первоначально режим 8).
8. Объединение обеих концевых точек режима 9 (первоначально режим 9).
9. Перенос левой концевой точки режима 9 (первоначально режим 10).

Локальная коррекция точки переключения заключается в рассмотрении точек, образующих окрестность корректируемой точки (расположенные слева и справа от нее точки АМАХ—точки,  которых максимум достигается без нарушения с обеих сторон условия минимальной длины режима), и выборе в качестве скорректированной точки переключения точки, обеспечивающей максимальное разделение.
которых максимум достигается без нарушения с обеих сторон условия минимальной длины режима), и выборе в качестве скорректированной точки переключения точки, обеспечивающей максимальное разделение.
Коррекции выполняются во всех точках переключения последовательно слева направо; в целом весь процесс определен как 

Чтобы ускорить процесс поиска оператор GUESS обращается к предварительному списку точек переключения (если они вообще  подготовленному оператором SDEVI, очищает его (слева вправо) так, чтобы оказались исключенными режимы длины. Меньшей L, и затем делит оставшиеся режимы на пробные режимы
подготовленному оператором SDEVI, очищает его (слева вправо) так, чтобы оказались исключенными режимы длины. Меньшей L, и затем делит оставшиеся режимы на пробные режимы
длины  каждый (если деление возможно, в противном случае в процедуру вносятся небольшие изменения). После этого вызывается оператор COMBINE для изучения полученной черновой структуры.
каждый (если деление возможно, в противном случае в процедуру вносятся небольшие изменения). После этого вызывается оператор COMBINE для изучения полученной черновой структуры.
Можно применить и более тщательно проработанные гипотезы. Введем, например, для  локальные средние
локальные средние

и нормированные разности

где  — оценка
— оценка  .
.
Предполагается, что  принимает большие значения, когда
принимает большие значения, когда  истинная точка переключения. Таким образом,
истинная точка переключения. Таким образом,

«правдоподобное» множество кандидатов в приближенные точки переключения. Поскольку вероятно, что  состоит из связных кластеров, следует выделить эти кластеры и составить предварительный список точек переключения (скажем, всех точек, имеющих в соответствующем кластере максимальное значение
состоит из связных кластеров, следует выделить эти кластеры и составить предварительный список точек переключения (скажем, всех точек, имеющих в соответствующем кластере максимальное значение 
Машинные эксперименты показали, что при удачном выборе  данный метод работает вполне удовлетворительно при выделении ярко выраженных точек переключения. Мы, однако, не
данный метод работает вполне удовлетворительно при выделении ярко выраженных точек переключения. Мы, однако, не  пользуемся им в наших дальнейших изысканиях, так как сознаем, что даже при очень «грубом» операторе GUESS, описанном выше, остальные адаптивные операторы, если применять их должным образом, обеспечат достаточно хорошие результаты.
пользуемся им в наших дальнейших изысканиях, так как сознаем, что даже при очень «грубом» операторе GUESS, описанном выше, остальные адаптивные операторы, если применять их должным образом, обеспечат достаточно хорошие результаты.
Здесь следует заметить, что выбор указанных операторов ни в коем случае не является «наилучшим» (если вообще можно установить, что есть наилучшее). Мы старались обосновать каждый оператор эвристически, учитывая различные факторы, в том числе точность получаемых результатов, простоту, объем необходимых вычислений, интуитивную привлекательность, устойчивость, чувствительность к выбору параметров и реализуемость. Кроме того, отдельные операторы сначала проверялись на модельных данных с тем, чтобы можно было получить какое-то представление об их применимости.
При построении алгоритма эти операторы можно объединять различными способами. Целесообразным представляется следующий. В качестве исходной выбирается простая структура «1 режим» и к ней применяется оператор  что обеспечивает оценку
что обеспечивает оценку  необходимую для применения остальных операторов и,
необходимую для применения остальных операторов и,
возможно, указывающую также на несколько точек переключения. Вторым, естественно, применяется оператор GUESS, а затем предварительное множество точек переключения корректируется. На этом предварительный этап обработки заканчивается. Дальнейшие усовершенствования заключаются в отыскании новых точек переключения или удалении явно ложных точек переключения с помощью оператора DIVIDE, коррекции новой структуры и последующей проверке точек переключения с помощью оператора СОМВINE. Этот алгоритм можно записать как

здесь использованы следующие обозначения 
Итак, функция «преемник У» задается как  Реально встречаются следующие сочетания операторов:
Реально встречаются следующие сочетания операторов:

Если рассматривать три последовательно применяемых оператора DIVIDE-ADJUST-COMBINE как один, то наш алгоритм можно представить в виде  где
где  (предварительная обработка),
(предварительная обработка),  (улучшение).
(улучшение).
Последовательное применение ряда статистических критериев к одному и тому же набору данных, как это делаем мы, противоречит общепринятой статистической доктрине. Следует, однако, иметь в виду, что мы занимаемся не статистическими выводами типа тех, которые обычно фигурируют при статистической проверке гипотез, а скорее используем критерии, аналогичные применяемым при проверке гипотез, в качестве эвристик при поиске в пространстве решений, но давая им иную интерпретацию.
При составлении программы структура режима представляется матрицей, состоящей из трех строк и столбцов, каждый из которых характеризует некоторый режим. Первая строка содержит точки переключения  вторая — сумму
вторая — сумму  по соответствующим режимам и третья — сумму квадратов
по соответствующим режимам и третья — сумму квадратов  . На основе этой матрицы нетрудно вычислить критерий разделения
. На основе этой матрицы нетрудно вычислить критерий разделения  и критерий однородности
и критерий однородности  функционирование алгоритма определяется заданием шести описанных выше параметров L, RLE-VEL, CS, CV, NTRYDIV и АМАХ.
функционирование алгоритма определяется заданием шести описанных выше параметров L, RLE-VEL, CS, CV, NTRYDIV и АМАХ.
Данные были получены из следующей модели:
(i) Точки переключения порождаются дискретным равновесным процессом восстановления, причем длины последовательных режимов определяются выражением  где В — биномиальная случайная переменная.
где В — биномиальная случайная переменная.

(кликните для просмотра скана)
(ii) Средние режимов порождаются независимо из распределения 
(iii) Шумы порождаются независимо из распределения  .
.
Распечатка, приведенная на рис. 3.4.5, иллюстрирует процесс поиска на данных длины 200 со следующими параметрами:  (математическое ожидание длины режима
(математическое ожидание длины режима  . Алгоритм имел следующие параметры:
. Алгоритм имел следующие параметры:  . Для контроля хода процесса восстановления величина средней остаточной дисперсии
. Для контроля хода процесса восстановления величина средней остаточной дисперсии

определялась после каждого применения оператора.
В распечатке истинная структура режима приведена под словом ДАННЫЕ: в первом столбце содержатся точки переключения, а во втором — соответствующие средние по режиму.
При поиске эвристические адаптивные операторы объединяются в два блока. Первый  применяется в начале и только один раз; второй
применяется в начале и только один раз; второй  применяется после блока
применяется после блока  многократно.
многократно.
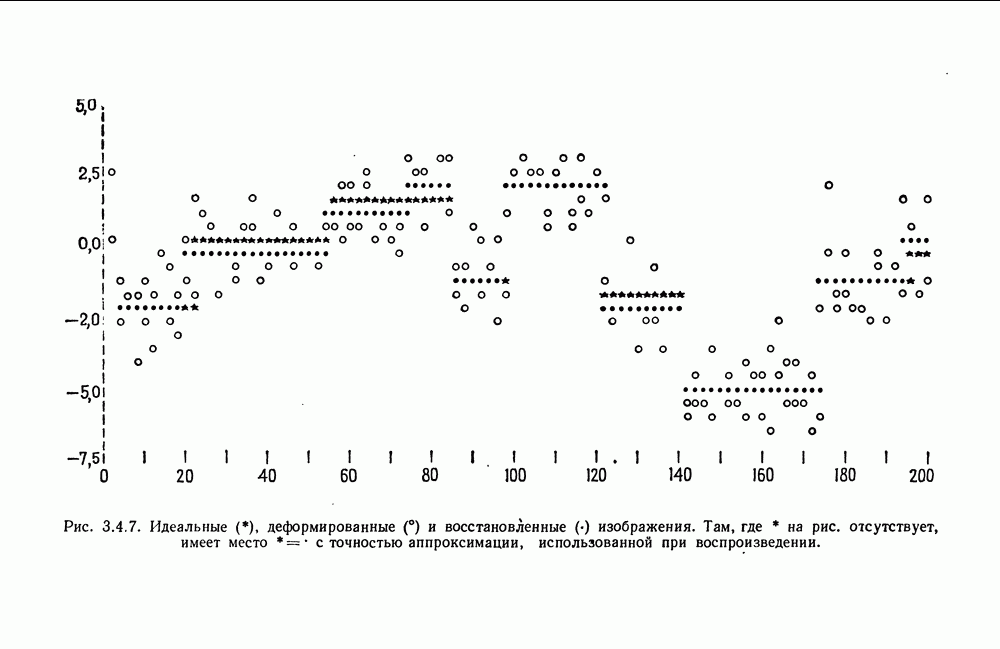
На рис. 3.4.6 приведен график изменения величины средней остаточной дисперсии во времени в процессе этого поиска, а на рис. 3.4.7 представлены идеальное, деформированное и окончательное восстановленное изображения. Можно отметить здесь, что алгоритм достигает стационарного состояния после небольшого числа шагов. В самом Деле, поскольку и множество разбиений, и множество адаптивных операторов конечны, поиск всегда должен приводить к циклу.

Рис. 3.4.6. Поведение средней остаточной дисперсии в процессе поиска.
Алгоритм прекращает поиск, обнаружив такой цикл. Результаты каждого прохода можно рассматривать как «приемлемые» решения, одно из которых — обладающее наименьшей средней остаточной дисперсией — принимается в качестве окончательного решения. Дальнейшие эксперименты показывают, что размер цикла обычно весьма мал и цикл может быть пройден за небольшое число шагов, по

(кликните для просмотра скана)
крайней мере при том типе данных и параметрах алгоритма, которые мы использовали в данном случае.
Практическая проверка описанного эвристического алгоритма Проводилась на нескольких моделях, сходных с моделью 1, но отличающихся от нее некоторыми деталями.
Модель данных 2. Шум, порожденный независимо источником с равномерным распределением.
Модель данных 3. Шум, порожденный независимо источником с двумерным экспоненциальным распределением.
Модель данных 4. Средние по режиму образуют стационарный процесс в узком смысле, причем любые  последовательных средних
последовательных средних  совместно нормально распределены с нулевыми средними и трехдиагональной ковариационной матрицей
совместно нормально распределены с нулевыми средними и трехдиагональной ковариационной матрицей

Модель данных 5. Распределение длин режимов определяется смесью двух биномиальных распределений:

параметры  можно выбрать так, чтобы получить смесь длинных и коротких режимов.
можно выбрать так, чтобы получить смесь длинных и коротких режимов.
Для каждой модели данных было сформировано по десять выборок, каждая длиной 200, однако в реальных условиях следует ожидать появления больших чисел. Во всех случаях соответствующие параметры выбирались так, чтобы математическое ожидание длины режима было равно 25, среднее квадратическое отклонение средних по режиму  и среднее квадратическое Отклонение шума
и среднее квадратическое Отклонение шума 
Для всех пяти моделей данных были приняты  , а значения
, а значения  и
и  выбирались, исходя из характера распределения шума. Для шума, распределенного нормально,
выбирались, исходя из характера распределения шума. Для шума, распределенного нормально,  Для равномерно распределенного шума при однородном режиме
Для равномерно распределенного шума при однородном режиме

Поскольку критерий однородности имеет вид

то для равномерно распределенного шума мы выбрали 

При однородном режиме и шуме с двумерным экспоненциальным распределением

так что мы задаем  .
.
Выбор величины  основывается на распределении
основывается на распределении

Мы задаем  так, чтобы выполнялось
так, чтобы выполнялось

Таким образом, для нормально распределенного шума  , для равномерно распределенного шума
, для равномерно распределенного шума  , для шума с двумерным экспоненциальным распределением
, для шума с двумерным экспоненциальным распределением 
Для сопоставления окончательного варианта восстановленной структуры режима с истинной использовалось несколько критериев отклонения. В частности, такой простой критерий, как средняя квадратическая ошибка

где  - математическое ожидание, а
- математическое ожидание, а  — оценка среднего значения.
— оценка среднего значения.
Может оказаться полезным и критерий, зависящий лишь от истинного разбиения и его оценки. Пусть  истинные точки переключения
истинные точки переключения  оценки точек переключения. Мы будем говорить, что оценивает
оценки точек переключения. Мы будем говорить, что оценивает  если
если  - ближайшая к
- ближайшая к  вычисленная точка, а
вычисленная точка, а  ближайшая к
ближайшая к  истинная точка переключения, т. е.
истинная точка переключения, т. е.

Пусть  общее число таких ассоциированных пар. Введем
общее число таких ассоциированных пар. Введем
где суммирование проводится по всем ассоциированным парам. Величина  измеряет относительное среднее отклонение от истинны точек переключения.
измеряет относительное среднее отклонение от истинны точек переключения.
Пусть  число различных истинных точек переключения в
число различных истинных точек переключения в  ассоциированных парах; тогда число пропущенных точек переключения равно
ассоциированных парах; тогда число пропущенных точек переключения равно  Введем
Введем

Величина измеряет долю пропущенных истинных точек переключения.
Пусть  число различных вычисленных точек переключения в
число различных вычисленных точек переключения в  ассоциированных парах; тогда число избыточных точек Переключения равно
ассоциированных парах; тогда число избыточных точек Переключения равно  Введем
Введем

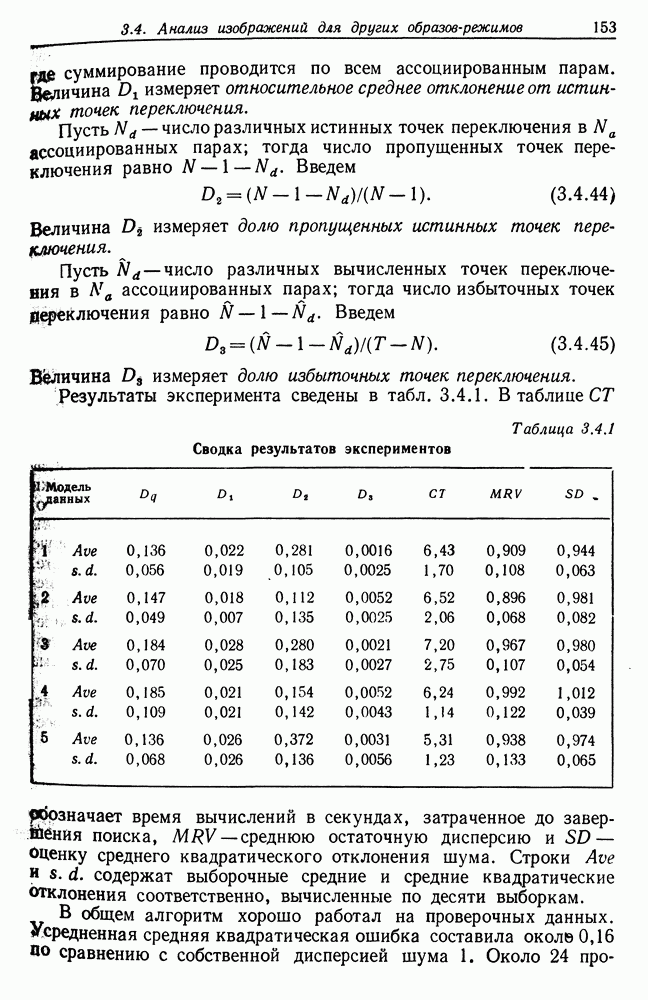
Таблица 3.4.1 (см. скан) Сводка результатов экспериментов
Величина  измеряет долю избыточных точек переключения. Результаты эксперимента сведены в табл. 3.4.1. В таблице
измеряет долю избыточных точек переключения. Результаты эксперимента сведены в табл. 3.4.1. В таблице  обозначает время вычислений в секундах, затраченное до завершения поиска,
обозначает время вычислений в секундах, затраченное до завершения поиска,  среднюю остаточную дисперсию и
среднюю остаточную дисперсию и  Оценку среднего квадратического отклонения шума. Строки
Оценку среднего квадратического отклонения шума. Строки  содержат выборочные средние и средние квадратические отклонения соответственно, вычисленные по десяти выборкам.
содержат выборочные средние и средние квадратические отклонения соответственно, вычисленные по десяти выборкам.
В общем алгоритм хорошо работал на проверочных данных. Усредненная средняя квадратическая ошибка составила околе 0,16 00 сравнению с собственной дисперсией шума 1. Около 24 процентов
истинных точек переключения оказались пропущенными, но по большей части они имели несущественный характер — небольшие различия средних у соседних режимов. Точность обнаруженных точек переключения составила около 2,3%, и, грубо говоря, на 200 точек данных приходилась одна избыточная точка переключения. Время вычислений составило около 6,4 с, что при работе с языком АПЛ приемлемо. Для практического использования этот алгоритм следует запрограммировать на более подходящем языке для того, чтобы уменьшить время работы центрального процессора. Окончательное значение средней остаточной дисперсии и оценка дисперсии шума очень близки к истинным величинам, как и следовало ожидать.
Из 50 рассмотренных выборок только в трех случаях поиск заканчивался циклами размера больше единицы (в двух случаях длина равна двум и в одном—трем).
Здесь следует заметить, что рассмотренные нами модели порождают стационарные случайные процессы  со спектральными плотностями, можно вывести не зависящий от времени линейный фильтр
со спектральными плотностями, можно вывести не зависящий от времени линейный фильтр  который, будучи примененным к
который, будучи примененным к  восстанавливает
восстанавливает  наилучшим возможным в смысле наименьших квадратов способом. Таким образом, можно найти
наилучшим возможным в смысле наименьших квадратов способом. Таким образом, можно найти  минимизирующий
минимизирующий  -ошибку, и вывести выражение для минимума ошибки при использовании линейно-квадратических методов. Для этого, естественно, необходимо знать параметры модели данных, и, таким образом, возникает новая задача, отличающаяся от той, которую мы рассматривали. Эту задачу мы изучаем в данном контексте, потому что она дает нам некий стандарт работоспособности, несмотря на то, что указанный метод требует наличия подробной априорной информации об образах в отличие от описанного выше.
-ошибку, и вывести выражение для минимума ошибки при использовании линейно-квадратических методов. Для этого, естественно, необходимо знать параметры модели данных, и, таким образом, возникает новая задача, отличающаяся от той, которую мы рассматривали. Эту задачу мы изучаем в данном контексте, потому что она дает нам некий стандарт работоспособности, несмотря на то, что указанный метод требует наличия подробной априорной информации об образах в отличие от описанного выше.
Перед тем как разрабатывать подобный метод фильтрации, обратим внимание на то, что точки переключения, средние режима и шумы порождаются тремя независимыми процессами.
(а) Точки переключения  образуют дискретный процесс восстановления следующего вида:
образуют дискретный процесс восстановления следующего вида:

Будем считать, что данный процесс начался достаточно давно и потому можно пользоваться соответствующими асимптотическими результатами, или, что то же самое, рассматривать соответствующий
равновесный процесс восстановления

здесь  предполагается конечным.
предполагается конечным.
(б) Средние режима  образуют белый шум с нулевым математическим ожиданием и дисперсией
образуют белый шум с нулевым математическим ожиданием и дисперсией 
(в) Шумы  образуют белый шум с нулевым математическим ожиданием и дисперсией
образуют белый шум с нулевым математическим ожиданием и дисперсией 
Как и выше,  если
если  Располагая выборкой
Располагая выборкой  мы хотим воспользоваться теорией линейной фильтрации для восстановления
мы хотим воспользоваться теорией линейной фильтрации для восстановления  Пусть
Пусть  реализация процесса переключения, тогда
реализация процесса переключения, тогда

и

На основании свойств равновесного процесса восстановления получаем, что

так что

Итак,  независимо от
независимо от 


(кликните для просмотра скана)
Чтобы построить не зависящий от времени линейный фильтр  который в применении к
который в применении к  восстанавливает
восстанавливает  наилучшим возможным в смысле наименьших квадратов способом, рассмотрим
наилучшим возможным в смысле наименьших квадратов способом, рассмотрим

где  -функция с комплексными значениями. В таком случае
-функция с комплексными значениями. В таком случае  -ошибка равна
-ошибка равна

Здесь  представлены в обычной символической записи.
представлены в обычной символической записи.
Предполагая, что спектральные плотности равны  соответственно, получаем
соответственно, получаем

Это выражение минимизируется при

(см. работу Гренандера (1950), разд. 6.5).
Чтобы проиллюстрировать, как применяется (3.4.62), конкретизируем рассматриваемый процесс восстановления, потребовав, чтобы

Тогда путем непосредственных вычислений получаем, что

и

Для того чтобы найти коэффициенты фильтра, представим функцию  ее разложением в ряд Фурье
ее разложением в ряд Фурье

следовательно,

и наконец,

где  отношение сигнал/шум. Поскольку
отношение сигнал/шум. Поскольку  и целесообразно выбирать симметрический фильтр, то пусть
и целесообразно выбирать симметрический фильтр, то пусть

где  и тогда
и тогда

и

Следовательно,  . Чтобы вычислить
. Чтобы вычислить  , сначала вычисляем
, сначала вычисляем 

здесь

В качестве численной иллюстрации примем, что  и вычислим
и вычислим  .
.
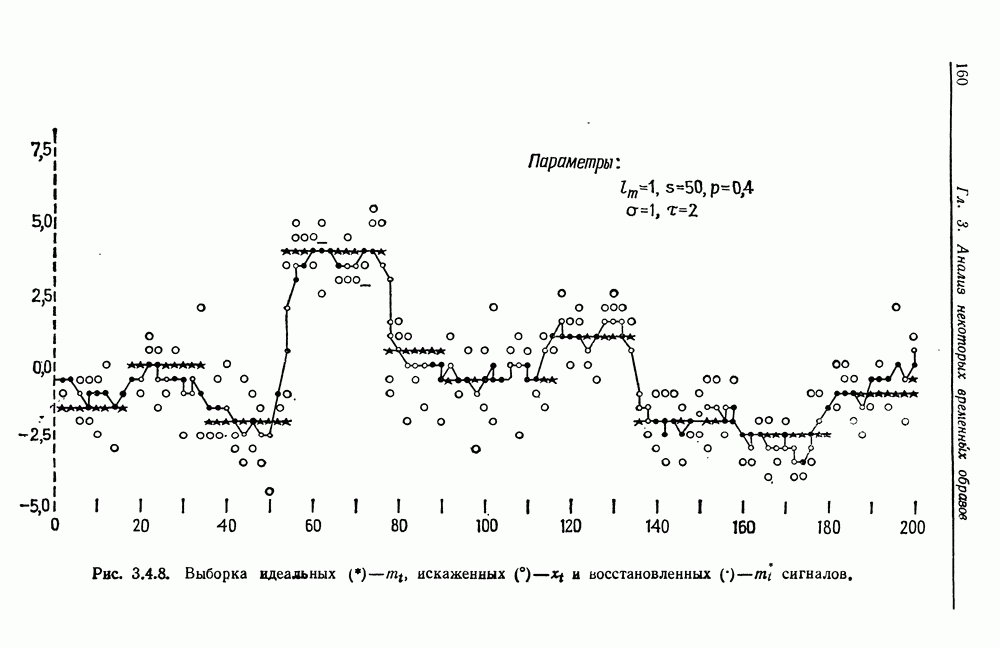
На рис. 3.4.8. приведены графики  восстановленного сигнала, который как будто хорошо оценивает
восстановленного сигнала, который как будто хорошо оценивает  так что естественно воспользоваться критериями вида
так что естественно воспользоваться критериями вида

и в тех случаях, когда  мы предполагаем наличие точки переключения на отрезке
мы предполагаем наличие точки переключения на отрезке 
Чтобы сопоставить качество работы эвристического адаптивного алгоритма и метода фильтрации, мы выбираем модель и параметры алгоритма в соответствии с центральным планом для 7 переменных с 22 центральными точками и 14 точками, расположенными на координатных осях; общее число наблюдений - 100. Недостаток места не позволяет нам здесь вдаваться в подробности этого довольно сложного вычислительного эксперимента; читатель, интересующийся этими вещами, может обратиться к отчету Анга, (1974), в котором обсуждается примененная нами методика поверхности отклика. Преимущество эвристического адаптивного метода заключается в том, что он требует лишь небольших априорных сведений о структуре области и его реализация связана с умеренными затратами машинного времени. Ограничения метода фильтрации связаны с необходимостью иметь большее количество априорной информации, а также с тем обстоятельством, что этот метод использует только линейные операции в чисто нелинейной ситуации.
Вывод состоит в том, что в любой ситуации, не структурированной с самого начала достаточно хорошо, следует предпочесть

(кликните для просмотра скана)
эвристический адаптивный метод. Отметим, однако, что это ведет лишь к догадкам о виде искомых режимов и не гарантирует статистической значимости. Эвристический метод предназначен лишь для предварительного анализа данных, но не для получения окончательного результата. Как только появляется определенная структура регулярности, ее следует использовать для увеличения точности, и эвристики уже становятся неадекватными.
Теперь мы снова обратимся к аналитическим методам и оставим эвристическое программирование. Если процессы-режимы в определенной степени структурированы, то должна быть возможность получить аналитические результаты, упрощающие машинную реализацию алгоритмов восстановления изображения. К настоящему времени мы получили таковые для двух достаточно частных случаев.
Первый аналогичен алгебре изображений, рассмотренной в разд. 3.3 (за исключением дискретности времени), но переход от одного режима к другому уже определяется процессом Бернулли; сравните также с допущением (3.4.63). Мы по-прежнему оперируем одним  -оператором, одним индексом класса образующих, и в каждой дискретной точке времени вероятность начала нового режима определяется некоторой величиной
-оператором, одним индексом класса образующих, и в каждой дискретной точке времени вероятность начала нового режима определяется некоторой величиной  Под новым режимом в данном случае понимается изменение функции времени посредством подачи существенного импульса, возмущающего уравнение
Под новым режимом в данном случае понимается изменение функции времени посредством подачи существенного импульса, возмущающего уравнение  Символ у представляет здесь импульсы, большая часть которых равна нулю при малых
Символ у представляет здесь импульсы, большая часть которых равна нулю при малых  гауссов белый шум. Тогда справедлив следующий результат.
гауссов белый шум. Тогда справедлив следующий результат.
Теорема 3.4.1. Пусть образ-режим  порождается как решение уравнения
порождается как решение уравнения

где  гауссов шум
гауссов шум  независимо тождественно распределены, причем
независимо тождественно распределены, причем  с вероятностью
с вероятностью  с вероятностью
с вероятностью  Восстановление режимов по методу правдоподобия достигается выбором в качестве точек переключения всех точек времени
Восстановление режимов по методу правдоподобия достигается выбором в качестве точек переключения всех точек времени  таких, что
таких, что

Замечание. Получающийся алгоритм очень прост. Нужно просто вычислить  при
при  и найти те значения
и найти те значения  для которых справедливо неравенство (3.4.76). Число таких точек указывает нам (ориентировочно) на число режимов, и, если это необходимо, можно оценить также размер импульсов (см. приведенное ниже уравнение (3.4.78)).
для которых справедливо неравенство (3.4.76). Число таких точек указывает нам (ориентировочно) на число режимов, и, если это необходимо, можно оценить также размер импульсов (см. приведенное ниже уравнение (3.4.78)).
Доказательство. Рассмотрим изображение, порожденное неизвестными режимами, на интервале  при
при  для
для
 . В каждой точке
. В каждой точке  разностное уравнение (3.4.75) подвергается некоторым воздействиям
разностное уравнение (3.4.75) подвергается некоторым воздействиям  Тогда функция совместного распределения для
Тогда функция совместного распределения для  принимает вид
принимает вид

здесь  образуется остальными целыми числами от 1 до
образуется остальными целыми числами от 1 до  Оценки импульсов
Оценки импульсов  по методу правдоподобия определяются с помощью следующего выражения:
по методу правдоподобия определяются с помощью следующего выражения:

Подставляя выражение (3.4.78) в (3.4.77), получаем 

Последнее выражение можно переписать в следующем виде:

или при 

Теперь остается лишь варьировать  оно может быть любым подмножеством множества
оно может быть любым подмножеством множества  Цель этих вариаций — увеличить
Цель этих вариаций — увеличить  или, что эквивалентно, сделать сумму в уравнении (3.4.81) по возможности минимальной. Очевидно, это можно обеспечить, проводя суммирование исключительно по отрицательным членам, и поэтому необходимо выбирать множество следующего вида:
или, что эквивалентно, сделать сумму в уравнении (3.4.81) по возможности минимальной. Очевидно, это можно обеспечить, проводя суммирование исключительно по отрицательным членам, и поэтому необходимо выбирать множество следующего вида:

На этом доказательство теоремы заканчивается.
Примечательно, насколько просто оказывается множество  при записи в такой форме с использованием оператора
при записи в такой форме с использованием оператора  Теперь попытаемся
Теперь попытаемся
проанализировать случай, когда число индексов класса образующих превышает единицу, так что имеется множество разностных операторов  и правила, указывающие, как осуществляются переходы
и правила, указывающие, как осуществляются переходы  (см. случай 3.4.4, т. 1, образы операторного режима), и модифицированные с учетом дискретности времени. Мы полагаем, что во всех точках времени переходы между режимами определяются как
(см. случай 3.4.4, т. 1, образы операторного режима), и модифицированные с учетом дискретности времени. Мы полагаем, что во всех точках времени переходы между режимами определяются как

Эти вероятности, естественно, могут выродиться в нуль или единицу — детерминированные переходы. Будем считать, что в пределах некоторого режима, имеющего индекс класса образующих  равно белому шуму с параметрами
равно белому шуму с параметрами  .
.
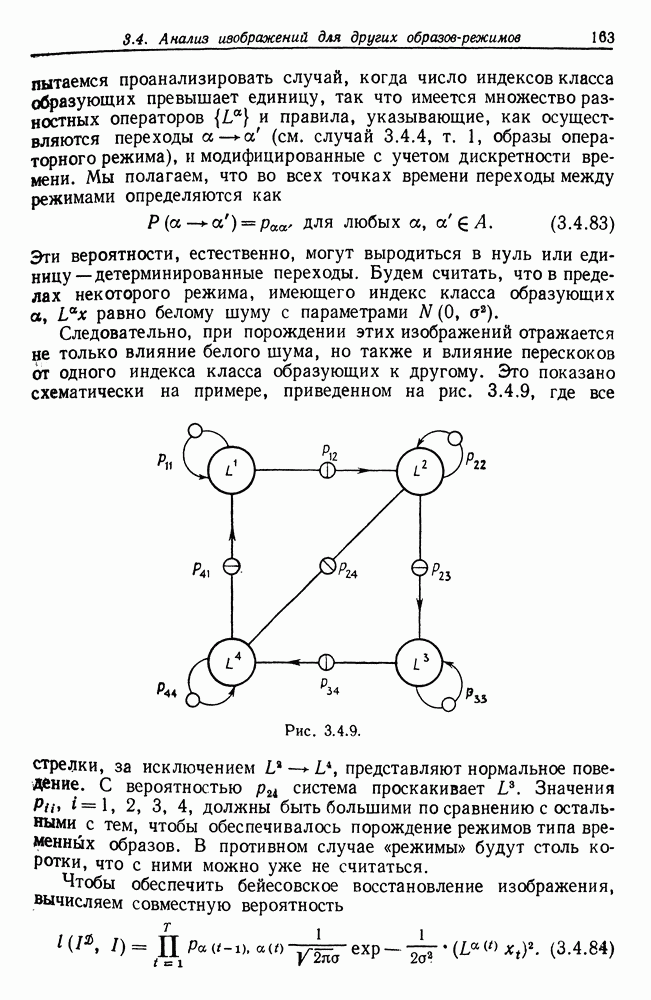
Следовательно, при порождении этих изображений отражается не только влияние белого шума, но также и влияние перескоков от одного индекса класса образующих к другому. Это показано схематически на примере, приведенном на рис. 3.4.9, где все стрелки, за исключением  представляют нормальное поведение. С вероятностью
представляют нормальное поведение. С вероятностью  система проскакивает
система проскакивает  Значения
Значения  , должны быть большими по сравнению с остальными с тем, чтобы обеспечивалось порождение режимов типа временных образов. В противном случае «режимы» будут столь коротки, что с ними можно уже не считаться.
, должны быть большими по сравнению с остальными с тем, чтобы обеспечивалось порождение режимов типа временных образов. В противном случае «режимы» будут столь коротки, что с ними можно уже не считаться.

Рис. 3.4.9.
Чтобы обеспечить бейесовское восстановление изображения, вычисляем совместную вероятность 

В уравнении (3.4.84) идеальное изображение  описывается с помощью
описывается с помощью  где
где  постоянна на интервалах, соответствующих
постоянна на интервалах, соответствующих  режимам
режимам  Как и прежде,
Как и прежде,  Решая задачи такого типа, мы сталкиваемся с обычными затруднениями — для вычисления (3.4.84) необходимо знать
Решая задачи такого типа, мы сталкиваемся с обычными затруднениями — для вычисления (3.4.84) необходимо знать  также ряд значений
также ряд значений  в зависимости от максимального порядка операторов
в зависимости от максимального порядка операторов  При больших Т знать некоторые начальные значения
При больших Т знать некоторые начальные значения  уже не так важно; это означает, что до начала анализа какая-то малая часть деформированного изображения исключается. Значение
уже не так важно; это означает, что до начала анализа какая-то малая часть деформированного изображения исключается. Значение  будет выбрано позже.
будет выбрано позже.
Перепишем уравнение (3.4.84) так, чтобы в более явном виде представить структуру режимов:

здесь  длина
длина  режима идеального изображения,
режима идеального изображения,  индекс класса образующих
индекс класса образующих  режима и
режима и

Следовательно, можно записать, что

 Уравнение (3.4.87) точно показывает вклад в
Уравнение (3.4.87) точно показывает вклад в  от каждого режима.
от каждого режима.
Чтобы максимизировать значение  по
по  необходимо отыскать некоторую функцию а
необходимо отыскать некоторую функцию а  удовлетворяющую условию
удовлетворяющую условию 

где

если  (см. уравнение (3.4.84)).
(см. уравнение (3.4.84)).
Теперь задача приведена к форме, удобной для применения динамического программирования. Действительно, введем

Эта сумма принимает минимальное значение, когда функции 
удовлетворяют условию  . Тогда, воспользовавшись выражением (3.4.88), можно получить следующую рекурсию:
. Тогда, воспользовавшись выражением (3.4.88), можно получить следующую рекурсию:

Это позволяет нам с помощью итерации дойти назад до значения  и получить последовательность
и получить последовательность  являющуюся решением уравнения (3.4.88).
являющуюся решением уравнения (3.4.88).
Теорема 3.4.2. Восстановление по методу правдоподобия для модели, предусматривающей перескоки с режима на режим, можно обеспечить при помощи последовательного решения методом динамического программирования уравнений (3.4.91) и (3.4.89).
Этот алгоритм еще не проверялся на числовых данных.
3.5. Образы возбуждения нейронов
Рассмотрим идеализированные нейроны, которые пораждают временные образы. Допустим, что электрические свойства нейрона представлены контуром  параллельно которому включено устройство мгновенного действия с релейной характеристикой (см. рис. 3.5.1; здесь
параллельно которому включено устройство мгновенного действия с релейной характеристикой (см. рис. 3.5.1; здесь  — входное напряжение).
— входное напряжение).

Рис. 3.5.1.
Точнее, это означает, что нервная клетка представлена контуром, в котором — это сопротивление и С — емкость. Ниже входное напряжение  всегда предполагается неотрицательным, а выходной ток обозначен как
всегда предполагается неотрицательным, а выходной ток обозначен как  Ток в первом контуре цепи обозначен через
Ток в первом контуре цепи обозначен через  а напряжение на конденсаторе — через
а напряжение на конденсаторе — через 
Нелинейное устройство будет иметь характеристику 

здесь  постоянная; устройство имеет только два состояния — выключено и включено.
постоянная; устройство имеет только два состояния — выключено и включено.
Тогда выходной сигнал проходит по линии передачи, действующей как фильтр LRC, до тех пор, пока он не достигает точек соединения с другими клетками. Присоединим пока к выходным концам цепи миллиамперметр, так что в сущности они окажутся закороченными, и посмотрим, как будет себя вести выходной сигнал.
Несмотря на простоту схемы, выходные характеристики оказываются интереснее, чем могло показаться с первого взгляда. Для их изучения воспользуемся просто законом Ома, получив в результате

и, исходя из определения емкости,

Исключая  и воспользовавшись условием (3.5.1), получаем
и воспользовавшись условием (3.5.1), получаем

В качестве начальных условий для (3.5.4) примем  Тогда получаем, что
Тогда получаем, что

до тех пор, пока  Если входной сигнал достаточно велик, то критический уровень
Если входной сигнал достаточно велик, то критический уровень  в конце концов будет достигнут. Когда это произойдет, скажем в момент времени Т (значение некоторого функционала
в конце концов будет достигнут. Когда это произойдет, скажем в момент времени Т (значение некоторого функционала  ), появляется мгновенный импульс тока. Затем напряжение на конденсаторе уменьшается на величину
), появляется мгновенный импульс тока. Затем напряжение на конденсаторе уменьшается на величину  и принимает новое значение
и принимает новое значение  Интегрирование уравнения (3.5.4) на малом временном интервале показывает, что сила импульса тока равна
Интегрирование уравнения (3.5.4) на малом временном интервале показывает, что сила импульса тока равна 
Другими словами, нервная клетка находится в состоянии покоя вплоть до момента времени  в этот момент она переходит в возбужденное состояние и напряжение мгновенно падает. Такое поведение имеет циклический характер, причем продолжительность цикла
в этот момент она переходит в возбужденное состояние и напряжение мгновенно падает. Такое поведение имеет циклический характер, причем продолжительность цикла  зависит от функции времени
зависит от функции времени  Можно, следовательно, ожидать, что продолжительность цикла будет флуктуировать.
Можно, следовательно, ожидать, что продолжительность цикла будет флуктуировать.
Чтобы лучше понять это явление, можно выразить входные потенциалы через критический уровень  , т. е. записав уравнение
, т. е. записав уравнение  Тогда уравнение (3.5.5), если принять в качестве начального значения
Тогда уравнение (3.5.5), если принять в качестве начального значения  приобретает вид
приобретает вид

и  решение уравнения
решение уравнения

Как же ведет себя величина  , если для того, чтобы получить
, если для того, чтобы получить  на вход подается периодическая последовательность импульсов? Какова, в частности, выходная характеристика для установившегося режима, наступающего по окончании переходного процесса? Пусть амплитуда импульса равна
на вход подается периодическая последовательность импульсов? Какова, в частности, выходная характеристика для установившегося режима, наступающего по окончании переходного процесса? Пусть амплитуда импульса равна  а период равен Р. Может оказаться, хотя этот случай и не представляет сейчас интереса, что порог
а период равен Р. Может оказаться, хотя этот случай и не представляет сейчас интереса, что порог  из уравнения (3.5.7) так и не будет достигнут, и клетка все время остается в невозбужденном состоянии. В противном случае она разряжается точно в момент появления какого-то импульса, так что обеспечивается синхронизация. При выборе этого момента в качестве начала отсчета времени величина правой части уравнения (3.5.7) при
из уравнения (3.5.7) так и не будет достигнут, и клетка все время остается в невозбужденном состоянии. В противном случае она разряжается точно в момент появления какого-то импульса, так что обеспечивается синхронизация. При выборе этого момента в качестве начала отсчета времени величина правой части уравнения (3.5.7) при  равна
равна

Следовательно, разряд будет возникать в этот момент времени в том и только том случае, если  наименьшее целое число, для которого справедливо следующее неравенство:
наименьшее целое число, для которого справедливо следующее неравенство:

Другими словами, разряд возникает при 
Теорема 3.5.1. Входная последовательность, состоящая из пиков величины  порождает периодический разряд с периодом
порождает периодический разряд с периодом

так что деление частоты происходит со скоростью 
Если, в частности, входные импульсы - «быстрые», т.е. подаются с высокой частотой  гц, то В в выражении (3.5.9) можно аппроксимировать и получить после некоторых преобразований непосредственное следствие.
гц, то В в выражении (3.5.9) можно аппроксимировать и получить после некоторых преобразований непосредственное следствие.
Следствие 3.5.1. Огтет будет иметь частоту  такую, что в пределе
такую, что в пределе

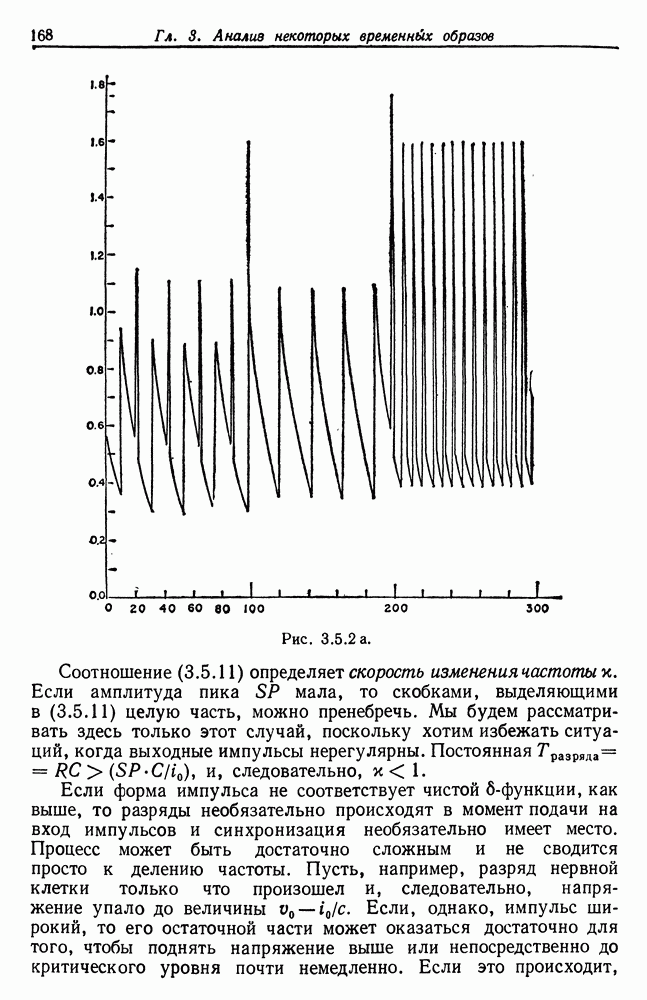
Рис. 3.5.2 а (см. скан)
Соотношение (3.5.11) определяет скорость изменения частоты  . Если амплитуда пика
. Если амплитуда пика  мала, то скобками, выделяющими в (3.5.11) целую часть, можно пренебречь. Мы будем рассматривать здесь только этот случай, поскольку хотим избежать ситуаций, когда выходные импульсы нерегулярны. Постоянная Тразряда
мала, то скобками, выделяющими в (3.5.11) целую часть, можно пренебречь. Мы будем рассматривать здесь только этот случай, поскольку хотим избежать ситуаций, когда выходные импульсы нерегулярны. Постоянная Тразряда  и, следовательно,
и, следовательно, 
Если форма импульса не соответствует чистой  -функции, как выше, то разряды необязательно происходят в момент подачи на вход импульсов и синхронизация необязательно имеет место. Процесс может быть достаточно сложным и не сводится просто к делению частоты. Пусть, например, разряд нервной клетки только что произошел и, следовательно, напряжение упало до величины
-функции, как выше, то разряды необязательно происходят в момент подачи на вход импульсов и синхронизация необязательно имеет место. Процесс может быть достаточно сложным и не сводится просто к делению частоты. Пусть, например, разряд нервной клетки только что произошел и, следовательно, напряжение упало до величины  Если, однако, импульс широкий, то его остаточной части может оказаться достаточно для того, чтобы поднять напряжение выше или непосредственно до критического уровня почти немедленно. Если это происходит,
Если, однако, импульс широкий, то его остаточной части может оказаться достаточно для того, чтобы поднять напряжение выше или непосредственно до критического уровня почти немедленно. Если это происходит,
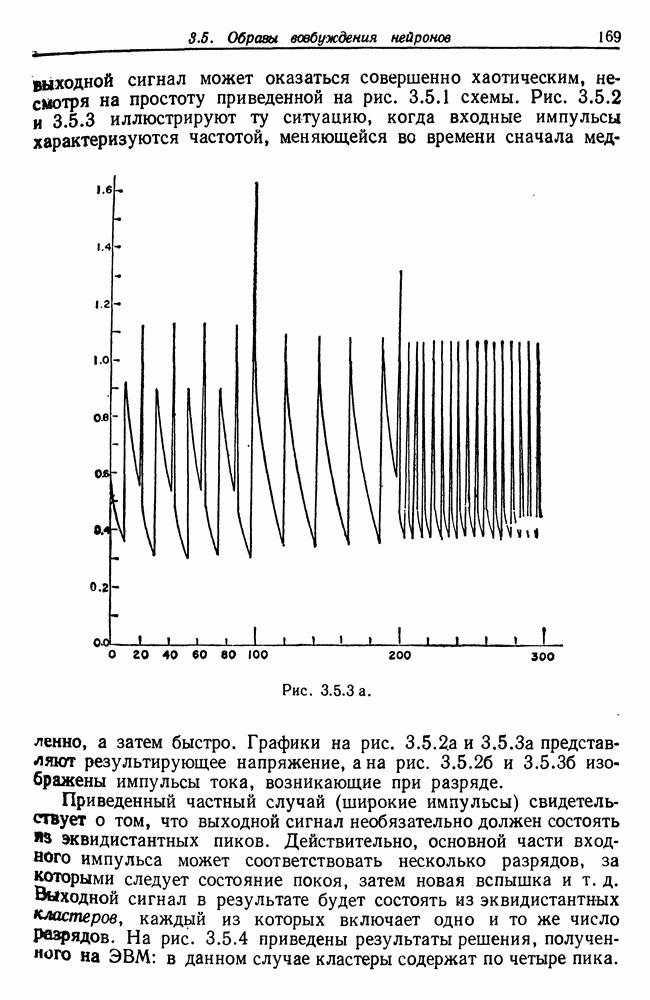
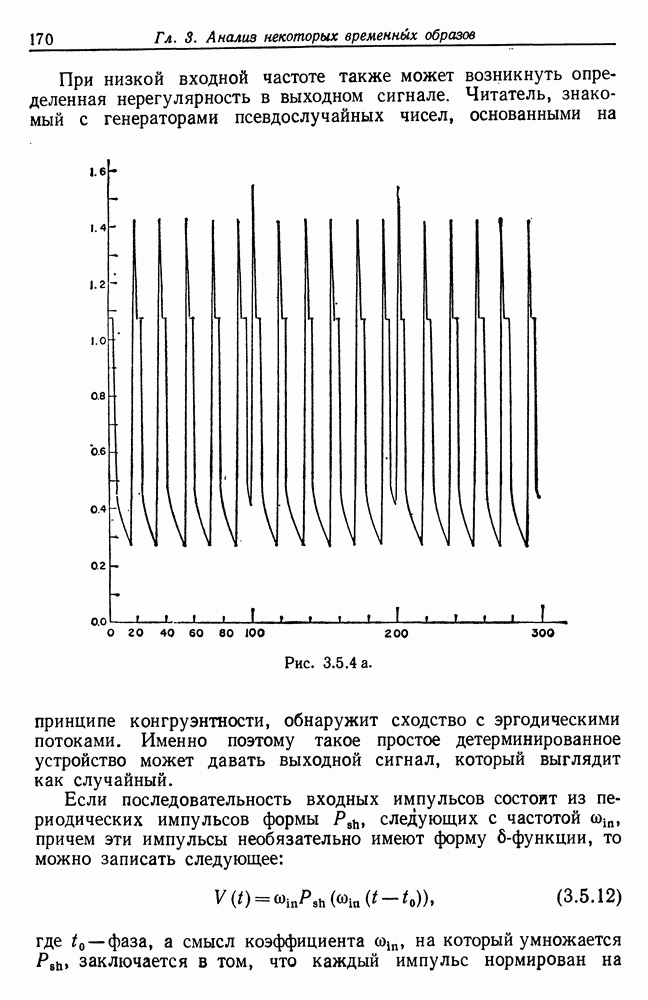
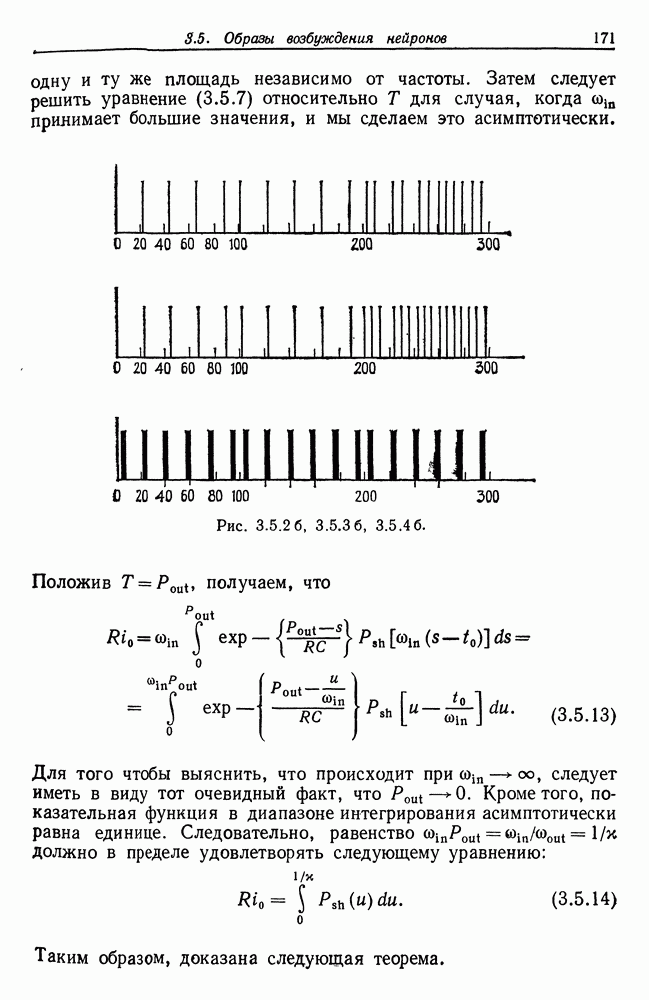
выходной сигнал может оказаться совершенно хаотическим, несмотря на простоту приведенной на рис. 3.5.1 схемы. Рис. 3.5.2 и 3.5.3 иллюстрируют ту ситуацию, когда входные импульсы характеризуются частотой, меняющейся во времени сначала медленно, а затем быстро. Графики на рис. 3.5.2.а и 3.5.3а представляют результирующее напряжение, а на рис. 3.5.26 и 3.5.36 изображены импульсы тока, возникающие при разряде.
Рис. 3.5.3 а. (см. скан)
Приведенный частный случай (широкие импульсы) свидетельствует о том, что выходной сигнал необязательно должен состоять эквидистантных пиков. Действительно, основной части входного импульса может соответствовать несколько разрядов, за которыми следует состояние покоя, затем новая вспышка и т. д. Выходной сигнал в результате будет состоять из эквидистантных кластеров, каждый из которых включает одно и то же число Разрядов. На рис. 3.5.4 приведены результаты решения, полученного на ЭВМ: в данном случае кластеры содержат по четыре пика.
При низкой входной частоте также может возникнуть определенная нерегулярность в выходном сигнале. Читатель, знакомый с генераторами псевдослучайных чисел, основанными на принципе конгруэнтности, обнаружит сходство с эргодическими потоками. Именно поэтому такое простое детерминированное устройство может давать выходной сигнал, который выглядит как случайный.
Рис. 3.5.4 а. (см. скан)
Если последовательность входных импульсов состоит из периодических импульсов формы  следующих с частотой
следующих с частотой  причем эти импульсы необязательно имеют форму
причем эти импульсы необязательно имеют форму  -функции, то можно записать следующее:
-функции, то можно записать следующее:

где  — фаза, а смысл коэффициента
— фаза, а смысл коэффициента  на который умножается
на который умножается  заключается в том, что каждый импульс нормирован на
заключается в том, что каждый импульс нормирован на
одну и ту же площадь независимо от частоты. Затем следует решить уравнение (3.5.7) относительно Т для случая, когда  принимает большие значения, и мы сделаем это асимптотически.
принимает большие значения, и мы сделаем это асимптотически.

Рис. 3.5.2 6, 3.5.3 6, 3.5.46.
Положив  получаем, что
получаем, что

Для того чтобы выяснить, что происходит при  следует иметь в виду тот очевидный факт, что
следует иметь в виду тот очевидный факт, что  Кроме того, показательная функция в диапазоне интегрирования асимптотически равна единице. Следовательно, равенство
Кроме того, показательная функция в диапазоне интегрирования асимптотически равна единице. Следовательно, равенство  должно в пределе удовлетворять следующему уравнению:
должно в пределе удовлетворять следующему уравнению:

Таким образом, доказана следующая теорема.
Теорема 3.5.2. Если  последовательность эквидистантных импульсов формы
последовательность эквидистантных импульсов формы  то предельная скорость изменения частоты
то предельная скорость изменения частоты

удовлетворяет уравнению (3.5.14).
Данное утверждение следует сопоставить с (3.5.11). В обоих случаях эту скорость можно выразить через физические постоянные. Мы не настаиваем на всех деталях допущений относительно цепи, приведенной на рис. 3.5.1, но здесь все же необходима нелинейность для того, чтобы получить эффект субгармонического резонанса.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
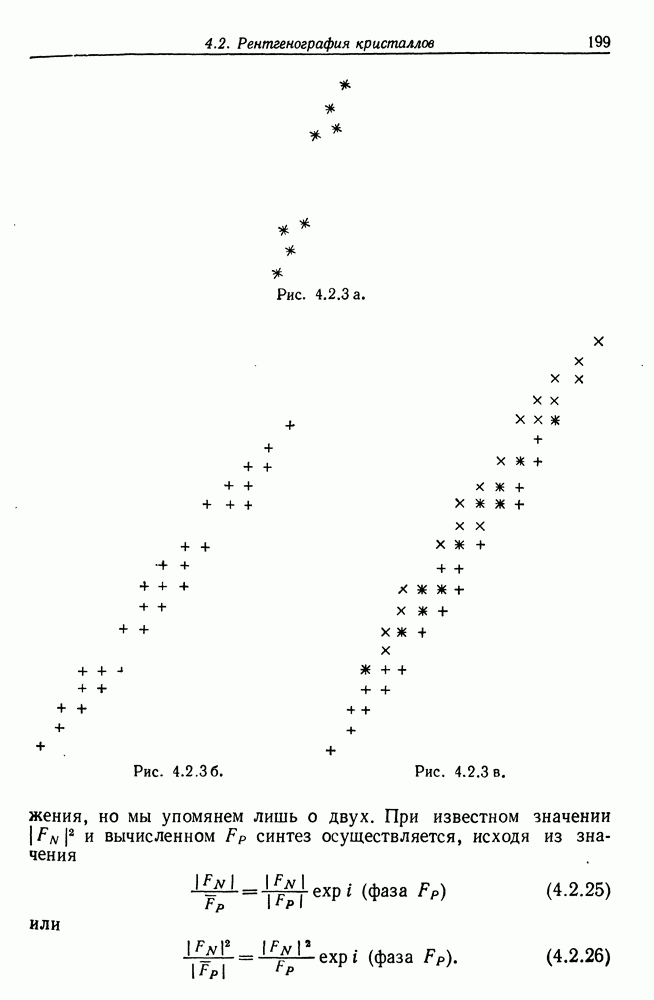
- 4.2. Рентгенография кристаллов
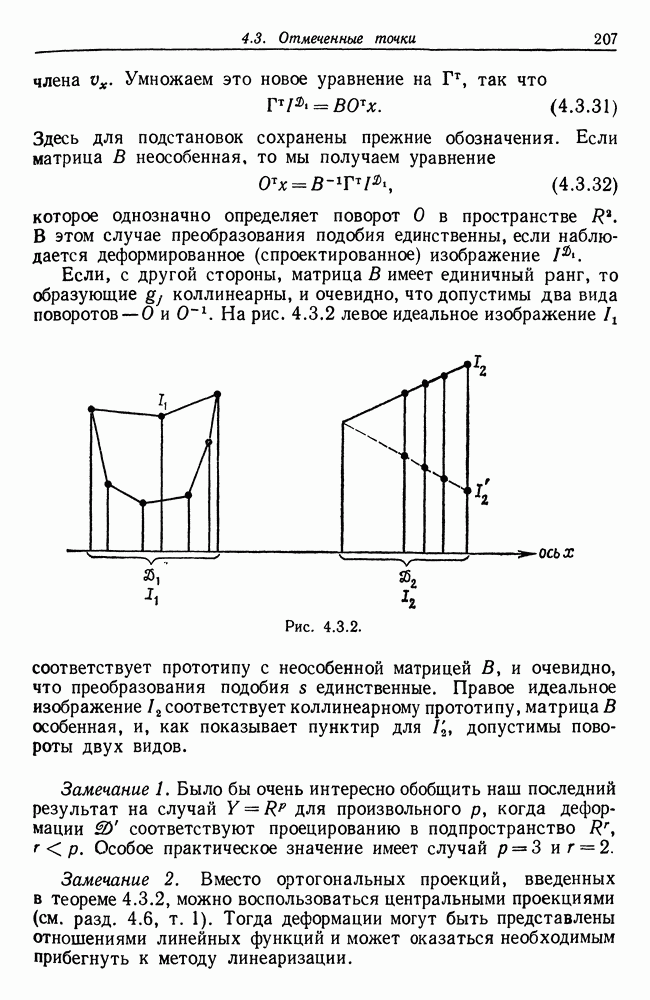
- 4.3. Отмеченные точки
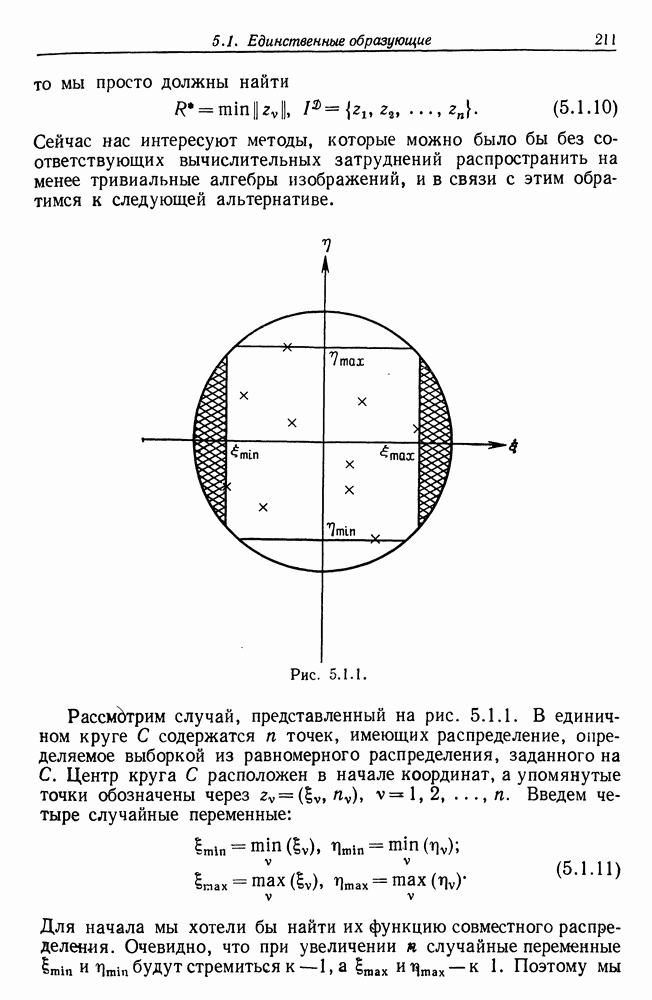
- Глава 5. Образы-множества и статистическая геометрия
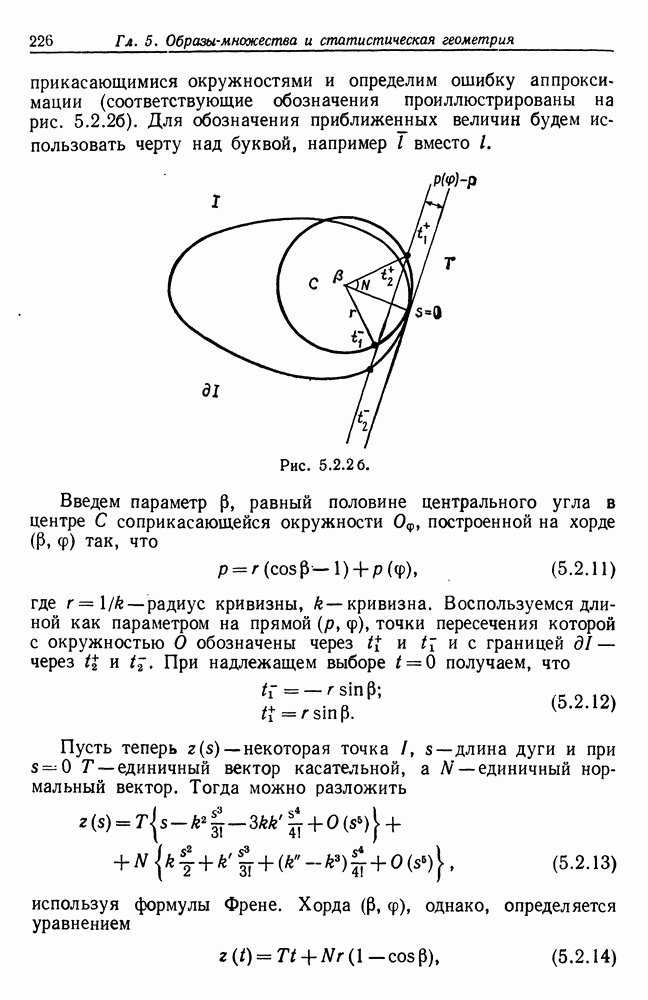
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы