| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3. Теория сегментации для временных образов
Рассмотрим образы-режимы у заданные на действительной оси и порожденные как решения уравнения  где
где  дифференциальный оператор порядка
дифференциальный оператор порядка  с постоянными коэффициентами. Уравнение должно быть справедливым в пределах каждого режима, и отношение связи гарантирует, что соответствующие граничные условия выполняются в тех точках времени, узлах, где два режима состыковываются. Сформулируем это точнее в виде следующего определения.
с постоянными коэффициентами. Уравнение должно быть справедливым в пределах каждого режима, и отношение связи гарантирует, что соответствующие граничные условия выполняются в тех точках времени, узлах, где два режима состыковываются. Сформулируем это точнее в виде следующего определения.
Определение 3.3.1. Фиксированному линейному дифференциальному оператору  порядка
порядка  с постоянными коэффициентами и целым числам
с постоянными коэффициентами и целым числам  и
и  поставлен в соответствие класс
поставлен в соответствие класс  функций
функций  на [0, 1], такой, что для каждой функции
на [0, 1], такой, что для каждой функции  существует ряд различных точек
существует ряд различных точек  удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
(i) функция  является решением в пространстве
является решением в пространстве  уравнения
уравнения  на каждом открытом подынтервале
на каждом открытом подынтервале 
(ii) функция  принадлежит
принадлежит  в окрестности всех
в окрестности всех 
Таким образом,  число внутренних узлов
число внутренних узлов  и
и  -число степеней свободы функции
-число степеней свободы функции  в каждом узле. Если
в каждом узле. Если  то условие (ii), очевидно, означает отсутствие ограничения непрерывности.
то условие (ii), очевидно, означает отсутствие ограничения непрерывности.
Рассмотрим в качестве примера случай, когда  и положим
и положим  Это значит, что функция
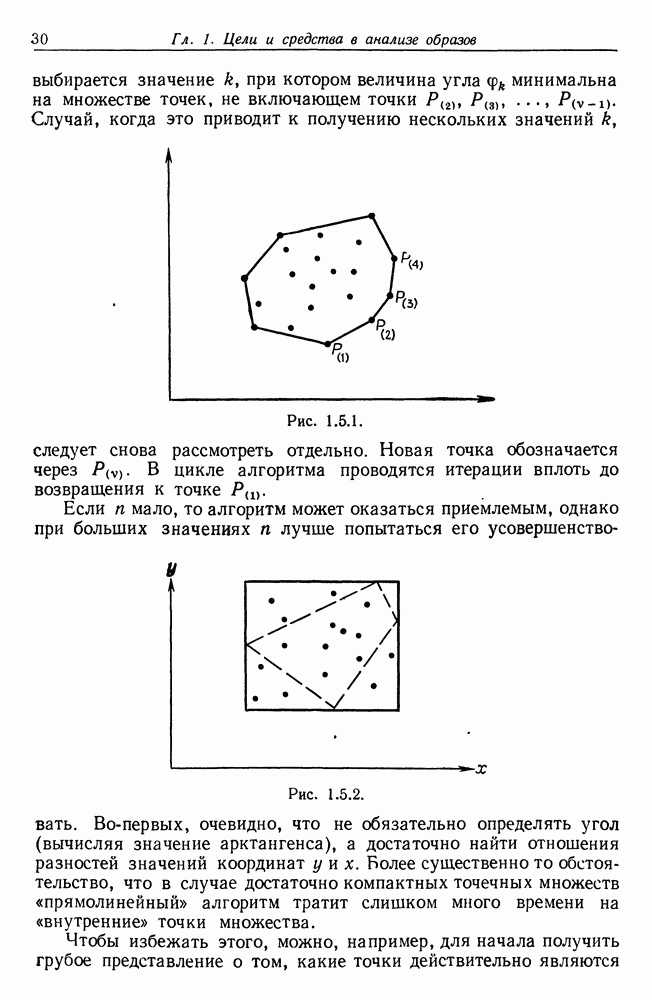
Это значит, что функция  непрерывна и кусочно-линейна, как это показано в левой части рис. 3.3.1, однако если
непрерывна и кусочно-линейна, как это показано в левой части рис. 3.3.1, однако если  то можно получить график типа представленного на рис. 3.3.1 справа. При других способах выбора
то можно получить график типа представленного на рис. 3.3.1 справа. При других способах выбора  возникает значительное разнообразие полиномиальных, экспоненциальных и тригонометрических сплайнов.
возникает значительное разнообразие полиномиальных, экспоненциальных и тригонометрических сплайнов.
В данном разделе мы в основном будем заниматься случаем, когда индекс класса образующих принимает только одно значение  так что мы будем работать ровно с одним дифференциальным оператором. Временные образующие определяются при этом отрезками режимов и соответствующими граничными значениями. Получающаяся в результате алгебра изображений имеет большое практическое значение; мы будем изучать ее применительно к аппроксимации изображений, а именно — насколько
так что мы будем работать ровно с одним дифференциальным оператором. Временные образующие определяются при этом отрезками режимов и соответствующими граничными значениями. Получающаяся в результате алгебра изображений имеет большое практическое значение; мы будем изучать ее применительно к аппроксимации изображений, а именно — насколько

Рис. 3.3.1.
хорошо можно аппроксимировать функциями класса Ф заданную функцию времени 
В настоящее время эта задача уже хорошо изучена, в основном, благодаря глубокому анализу, проведенному Д. Маклуром, чьи результаты и будут представлены в оставшейся части данного раздела. Дальнейшие подробности, а также многочисленные примеры читатель может найти в работе Маклура (1975). Кроме того, в работе Маклура—Вайтала (1975, разд. 4) можно познакомиться с другим способом вывода одного из результатов.
Основная задача заключается в отыскании аппроксимаций  обеспечивающих малое значение
обеспечивающих малое значение  -нормы
-нормы  и поддающихся вычислению при разумных затратах усилий. При минимизации этой нормы следует иметь в виду, что класс
и поддающихся вычислению при разумных затратах усилий. При минимизации этой нормы следует иметь в виду, что класс  не замкнут в
не замкнут в  . В самом деле, когда узлы являются переменными, следует допускать их объединение в кратные узлы и соответственное ослабление условий непрерывности в таких временных точках. Отсюда вытекает следующее определение.
. В самом деле, когда узлы являются переменными, следует допускать их объединение в кратные узлы и соответственное ослабление условий непрерывности в таких временных точках. Отсюда вытекает следующее определение.
Определение 3.3.2. Фиксированному линейному дифференциальному оператору  порядка
порядка  с постоянными коэффициентами и целым числам
с постоянными коэффициентами и целым числам  и
и  поставлен в соответствие класс
поставлен в соответствие класс  функций
функций  на [0, 1], такой, что для каждой функции
на [0, 1], такой, что для каждой функции  существует ряд различных точек
существует ряд различных точек  и соответствующие кратные целые
и соответствующие кратные целые  где
где  удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
(i) функция  является решением в пространстве
является решением в пространстве  уравнения
уравнения  на каждом открытом подынтервале
на каждом открытом подынтервале 
(ii) функция  принадлежит
принадлежит  в окрестности всех
в окрестности всех 
Это определение достаточно для того, чтобы гарантировать существование некоторой функции  обеспечивающей минимум
обеспечивающей минимум

Функция не должна быть, однако, однозначной. Доказательство этого факта см. в работе Маклура (1975), с. 13.
Задача отыскания минимума является нелинейной из-за влияния узлов  и на первый взгляд решить ее практически невозможно, особенно при больших
и на первый взгляд решить ее практически невозможно, особенно при больших  Воспользовавшись, однако, идеей, которая была высказана Далениусом и Ходжесом при изучении оптимальной стратификации (1957, 1959), можно получить удобные асимптотические результаты.
Воспользовавшись, однако, идеей, которая была высказана Далениусом и Ходжесом при изучении оптимальной стратификации (1957, 1959), можно получить удобные асимптотические результаты.
Рассмотрим для заданной функции  на [0, 1] и разбиения
на [0, 1] и разбиения  функционал вида
функционал вида

Отдельные члены (3.3.2) будут соответствовать ошибке аппроксимации на интервале  однако сейчас мы не будем останавливаться на этом. Вместо этого введем более общие допущения.
однако сейчас мы не будем останавливаться на этом. Вместо этого введем более общие допущения.
(А1) Для любых  удовлетворяющих условию
удовлетворяющих условию  а, Кроме того,
а, Кроме того,  субаддитивна на смежных
субаддитивна на смежных
подынтервалах [0, 1]; это означает, что если  то
то

(А2) Существуют некоторая соответствующая  функция
функция  , заданная на [0, 1], и постоянная
, заданная на [0, 1], и постоянная  , такие, что
, такие, что
(i) функция  неотрицательна и кусочно-непрерывна на [0,1] и имеет в худшем случае конечное число точек разрыва с конечным скачком;
неотрицательна и кусочно-непрерывна на [0,1] и имеет в худшем случае конечное число точек разрыва с конечным скачком;

Этот предел равномерный в том смысле, что разность  можно сделать равномерно малой, если
можно сделать равномерно малой, если  принадлежит интервалу, на котором функция
принадлежит интервалу, на котором функция  непрерывна.
непрерывна.

Допущение  предполагает, что
предполагает, что  неотрицательна. Допущение о субаддитивности эквивалентно предположению о том, что более мелкие разбиения [0,1] уменьшают
неотрицательна. Допущение о субаддитивности эквивалентно предположению о том, что более мелкие разбиения [0,1] уменьшают  .
.
Применяя эти общие результаты, чем мы займемся ниже, обычно нетрудно проверить выполнение допущений (А1) и (A3).
Более трудоемка проверка  так как вид
так как вид  и значение
и значение  должны определяться дедуктивно.
должны определяться дедуктивно.
Установим связь между отдельными результатами, характеризующими асимптотическое поведение

Лемма 3.3.1. Если для  выполняются допущения
выполняются допущения  то
то

Доказательство. Зафиксируем  и пусть
и пусть  представляет ее изображение в
представляет ее изображение в  (множество неотрицательных кусочно-непрерывных функций на [0,1]).
(множество неотрицательных кусочно-непрерывных функций на [0,1]).
Согласно допущению непрерывности, функционал  непрерывен по переменным
непрерывен по переменным  в компактной области
в компактной области  . Следовательно, функционал
. Следовательно, функционал  достигает минимума; существует оптимальное
достигает минимума; существует оптимальное  -точечное разбиение
-точечное разбиение  удовлетворяющее условию
удовлетворяющее условию

Обозначим  зависимость
зависимость  от
от  здесь
здесь  явном виде не указана, но ниже ее наличие будет подразумеваться.
явном виде не указана, но ниже ее наличие будет подразумеваться.
Докажем в первую очередь, что  имеет порядок
имеет порядок  ограничив его сверху определенным значением
ограничив его сверху определенным значением  этого порядка. Пусть
этого порядка. Пусть  фиксированные точки разрыва
фиксированные точки разрыва  Пусть также
Пусть также  обозначает равномерное разбиение [0,1] с
обозначает равномерное разбиение [0,1] с  внутренними точками
внутренними точками  при
при  Разбиение
Разбиение  содержит не более
содержит не более  внутренних точек [0,1]. Следовательно, благодаря оптимальности
внутренних точек [0,1]. Следовательно, благодаря оптимальности 

Непосредственное вычисление, основанное на допущении  доказывает, что
доказывает, что

и, таким образом,

Учитывая такой характер сходимости, можно считать, что некоторые подынтервалы разбиения  становятся произвольно малыми по мере роста
становятся произвольно малыми по мере роста  Введем обозначения
Введем обозначения

и

Пусть  длина интервала
длина интервала  содержащего
содержащего  Если
Если  то
то  Другими словами, существует некоторая положительная величина
Другими словами, существует некоторая положительная величина  такая, что для некоторого
такая, что для некоторого  непрерывна и положительна на
непрерывна и положительна на  и для последовательности разбиений
и для последовательности разбиений  имеет место
имеет место

Но из  следует, что
следует, что

Это в свою очередь означает, что

Правая часть этого неравенства расходится при увеличении  , что противоречит (3.3.10).
, что противоречит (3.3.10).
Теперь  можно разбить на части, в которых допущением
можно разбить на части, в которых допущением  можно или нельзя воспользоваться. Определим множество
можно или нельзя воспользоваться. Определим множество  соответствующее
соответствующее  как
как

По определению множества  асимптотическое выражение допущения
асимптотическое выражение допущения  можно использовать на подынтервалах Г, содержащих
можно использовать на подынтервалах Г, содержащих  На
На  определим теперь
определим теперь  -аппроксимацию
-аппроксимацию  ступенчатой функцией в виде
ступенчатой функцией в виде

и пусть  при
при  Из того что
Из того что  при
при  следует, что любое принадлежащее
следует, что любое принадлежащее  попадает в конечном счете в множество
попадает в конечном счете в множество  если
если  становится достаточно большим. Индикаторные функции
становится достаточно большим. Индикаторные функции  множества
множества  поточечно сходятся к
поточечно сходятся к  Кроме того, из
Кроме того, из  следует, что
следует, что  при
при  Так как
Так как  отличается от
отличается от  на множество меры нуль, то из этих двух замечаний, взятых вместе, следует, что
на множество меры нуль, то из этих двух замечаний, взятых вместе, следует, что

Кроме того, из допущения о равномерной сходимости в  следует, что функции
следует, что функции  равномерно ограничены на [0, 1].
равномерно ограничены на [0, 1].
Выделим теперь те члены суммы  для которых выполняется
для которых выполняется  Пусть символ суммирования 2 обозначает сумму, взятую по тем значениям
Пусть символ суммирования 2 обозначает сумму, взятую по тем значениям  для которых справедливо
для которых справедливо  . Согласно
. Согласно 

Применив допущение  можно получить следующее:
можно получить следующее:

здесь  Используя неравенство Гельдера, получаем
Используя неравенство Гельдера, получаем

Таким образом,

По теореоме о сходимости и учитывая (3.3.17), получаем, что

Доказательство леммы закончено.
Мы действительно можем считать, что

Один из способов прийти к этому заключению основан на построении  -точечного разбиения
-точечного разбиения  при котором
при котором  сходится к некоторому пределу, сколь угодно близкому к нижней грани. Подобные разбиения можно описать плотностями распределений на [0, 1].
сходится к некоторому пределу, сколь угодно близкому к нижней грани. Подобные разбиения можно описать плотностями распределений на [0, 1].
Пусть  строго положительная ограниченная кусочно-непрерывная функция на [0, 1], нормированная так, что
строго положительная ограниченная кусочно-непрерывная функция на [0, 1], нормированная так, что  Обозначим через
Обозначим через  интеграл
интеграл  Определим для произвольного
Определим для произвольного
целого числа  некоторое
некоторое  -точечное разбиение
-точечное разбиение  отрезка [0, 1] как
отрезка [0, 1] как

Точки  разбиения
разбиения  однозначно определены обращением функции распределения
однозначно определены обращением функции распределения 
Лемма 3.3.2. Предположим, что допущения  выполняются для
выполняются для  Пусть
Пусть  -точки разрыва
-точки разрыва  в интервале
в интервале  . Пусть
. Пусть  -положительная ограниченная кусочно-непрерывная плотность распределения на отрезке [0, 1], соответствующая распределению
-положительная ограниченная кусочно-непрерывная плотность распределения на отрезке [0, 1], соответствующая распределению  Для разбиений
Для разбиений  определенных согласно (3.3.25), имеет место
определенных согласно (3.3.25), имеет место

Доказательство. Допустим, во-первых, что  непрерывна. Точки
непрерывна. Точки  разбиения
разбиения  удовлетворяют условию
удовлетворяют условию  . Чтобы получить их границы, введем
. Чтобы получить их границы, введем 

Таким образом, обозначив

устанавливаем, что интервалы  строго положительны и стремятся к нулю при
строго положительны и стремятся к нулю при 
Применив допущение  получаем
получаем

Используя аналогично нижнюю грань  имеем
имеем

что доказывает утверждение (3.3.26). Когда  имеет конечное число
имеет конечное число  разрывов на отрезке [0, 1], разбиение
разрывов на отрезке [0, 1], разбиение  приводит к утверждению (3.3.26).
приводит к утверждению (3.3.26).
Учитывая это обстоятельство и применив к (3.3.26) простую вариацию, приходим к следующей теореме.
Теорема 3.3.1. Если допущения  выполняются для
выполняются для  то
то

Более того, если  строго положительна на отрезке [0, 1], вычисление значения функции
строго положительна на отрезке [0, 1], вычисление значения функции

дает асимптотически эффективные разбиения. Разбиения  асимптотически эффективны,
асимптотически эффективны, 

Доказательство. Требуемый результат можно получить при помощи подстановки  вместо
вместо  в выражение (3.3.26).
в выражение (3.3.26).
Необходимо вычислить локальные ошибки  воспользуемся теоремой Пойа о среднем значении (см. Пойа (1922)) и свойством
воспользуемся теоремой Пойа о среднем значении (см. Пойа (1922)) и свойством 
Определение 3.3.3. Оператор  имеет свойство
имеет свойство  на интервале
на интервале  , если на этом интервале существуют
, если на этом интервале существуют  решений уравнения
решений уравнения  таких, что все
таких, что все  определителей Вронского
определителей Вронского  строго положительны на интервале
строго положительны на интервале  .
.
Интервал, фигурирующий в данном определении, может быть как замкнутым, так и открытым, если производные функции  могут быть соответствующим образом определены в концевых точках или продолжены на них.
могут быть соответствующим образом определены в концевых точках или продолжены на них.
Любой линейный дифференциальный оператор с постоянными коэффициентами на достаточно малом интервале обладает свойством  Для того чтобы убедиться в этом, рассмотрим решения
Для того чтобы убедиться в этом, рассмотрим решения  уравнения
уравнения  при
при  . Действительная аналитическая функция обладает разложением в ряд вида
. Действительная аналитическая функция обладает разложением в ряд вида

где  Условие
Условие  выполняется, и
выполняется, и  если
если  заключено между
заключено между 
Так как все эти определители Вронского непрерывны и положительны в нуле, то все они строго положительны на достаточно коротком отрезке  Благодаря инвариантности решений однородного уравнения с постоянными коэффициентами относительно переносов наличие у оператора
Благодаря инвариантности решений однородного уравнения с постоянными коэффициентами относительно переносов наличие у оператора  свойства
свойства  на произвольном интервале определяется исключительно длиной, но не «абсолютным» расположением последнего. Следовательно, оператору
на произвольном интервале определяется исключительно длиной, но не «абсолютным» расположением последнего. Следовательно, оператору  соответствует некоторая постоянная
соответствует некоторая постоянная  такая, что если
такая, что если  то
то  имеет свойство
имеет свойство  на отрезке
на отрезке 
Исходя из этого, можно сформулировать следующий результат.
Теорема 3.3.2. Если оператор  имеет на отрезке
имеет на отрезке  свойство
свойство  и если
и если  принадлежит
принадлежит  то ошибка наилучшей
то ошибка наилучшей  -аппроксимации
-аппроксимации  на отрезке
на отрезке  решением уравнения
решением уравнения  равна
равна

для некоторой точки  отрезка
отрезка  от
от  не зависит и задается как
не зависит и задается как  где
где

Н — матрица Гильберта размера  с элементами
с элементами  вектор-столбец с компонентами
вектор-столбец с компонентами  .
.
Можно также записать  в виде
в виде

Доказательство теоремы 3.3.2 связано с установлением нескольких «вспомогательных» следствий из свойства  которые имеют и самостоятельный интерес.
которые имеют и самостоятельный интерес.
Лемма 3.3.3. Если оператор  имеет на отрезке
имеет на отрезке  свойство
свойство  и если
и если  — такие решения уравнения
— такие решения уравнения  для которых определители Вронского
для которых определители Вронского  строго положительны на отрезке
строго положительны на отрезке  при
при  то образуют на отрезке
то образуют на отрезке  полную чебышевскую систему: это означает, что всякая нетривиальная линейная комбинация имеет на отрезке
полную чебышевскую систему: это означает, что всякая нетривиальная линейная комбинация имеет на отрезке  самое большее
самое большее  ноль при
ноль при 
Доказательство. См. монографию Мейнардуса (1967), теорема 70, с. 88.
Исходя из того факта, что дифференциальный оператор  обладающий на некотором интервале свойством
обладающий на некотором интервале свойством  дает такое фундаментальное множество решений для однородного уравнения
дает такое фундаментальное множество решений для однородного уравнения  которое на этом интервале является полной чебышевской системой, можно показать, что наилучшие аппроксимации непрерывной функции
которое на этом интервале является полной чебышевской системой, можно показать, что наилучшие аппроксимации непрерывной функции  должны интерполировать
должны интерполировать  по меньшей мере в
по меньшей мере в  отдельных точках.
отдельных точках.
Лемма 3.3.4. Если оператор  имеет на отрезке
имеет на отрезке  свойство
свойство  и если
и если  наилучшая
наилучшая  -аппроксимация непрерывной функции
-аппроксимация непрерывной функции  на отрезке
на отрезке  с помощью решения уравнения
с помощью решения уравнения  при
при  то существуют
то существуют  различных точек
различных точек  удовлетворяющих условию
удовлетворяющих условию  в которых
в которых  при
при 
Доказательство. Филипс (1970) доказал этот результат для случая аппроксимации алгебраическими многочленами. Подробное доказательство леммы 3.3.4 приведено в работе Маклура (1975); ход рассуждений аналогичен доказательству Филипса.
И наконец, получим выражение для остаточного члена в случае интерполяции гладкой функции  с помощью решения уравнения
с помощью решения уравнения 
Лемма 3.3.5. Допустим, что оператор  имеет свойство
имеет свойство  на отрезке
на отрезке  принадлежит
принадлежит  удовлетворяет уравнению
удовлетворяет уравнению  на отрезке
на отрезке  различных точках
различных точках  интервала
интервала  Тогда
Тогда  для всех
для всех  принадлежащих отрезку
принадлежащих отрезку  где
где  единственное решение уравнения
единственное решение уравнения  на отрезке
на отрезке  удовлетворяющее условию
удовлетворяющее условию  при
при  некоторая промежуточная точка, такая, что
некоторая промежуточная точка, такая, что 
Доказательство. Это известная теорема Пойа о среднем значении (см. работу Пойа (1922)).
Доказательство теоремы 3.3.2. Первая часть этого доказательства следует за ходом рассуждений Филипса для случая аппроксимаций алгебраическими многочленами (см. монографию Филипса  Однако мы попытаемся здесь получить результат для общего случая аппроксимации.
Однако мы попытаемся здесь получить результат для общего случая аппроксимации.
Зафиксируем  таким образом, чтобы оператор
таким образом, чтобы оператор  имел на отрезке [0, Н] свойство
имел на отрезке [0, Н] свойство  пусть функция
пусть функция  принадлежит
принадлежит  и пусть
и пусть  — наилучшая
— наилучшая  аппроксимация
аппроксимация  на отрезке
на отрезке  с помощью решения уравнения
с помощью решения уравнения  Согласно лемме 3.3.4, существуют
Согласно лемме 3.3.4, существуют  различных точек
различных точек  интервала
интервала  в которых
в которых 
Построим на отрезке  следующие функции, связанные с
следующие функции, связанные с 
(i) — единственное решение уравнения  обращающееся в нуль в точках
обращающееся в нуль в точках 
(ii) — такое решение уравнения  которое имеет на
которое имеет на  минимальную среди всех решений этого уравнения
минимальную среди всех решений этого уравнения  норму. Таким образом,
норму. Таким образом,  является остаточным членом наилучшей аппроксимации
является остаточным членом наилучшей аппроксимации  с помощью решения уравнения
с помощью решения уравнения  согласно лемме 3.3.4, в интервале
согласно лемме 3.3.4, в интервале  существуют
существуют  различных точек
различных точек  в которых
в которых 
(iii) — единственное решение уравнения  обеспечивающее интерполяцию
обеспечивающее интерполяцию  в точках
в точках  т. е.
т. е.  Существование функций
Существование функций  обладающих указанными свойствами, гарантировано допущением о том, что оператор
обладающих указанными свойствами, гарантировано допущением о том, что оператор  имеет свойство
имеет свойство  на отрезке
на отрезке  .
.
Согласно лемме 3.3.5 об остаточном члене и определениям  Для любой точки
Для любой точки  отрезка
отрезка  и некоторой точки промежуточной для
и некоторой точки промежуточной для  Аналогичным образом
Аналогичным образом  Далее из этих выражений для остатка и свойств
Далее из этих выражений для остатка и свойств  следует, что
следует, что  обозначает обычную
обозначает обычную  норму на
норму на 

и

Кроме того, поскольку  непрерывна на
непрерывна на  , то для некоторой промежуточной точки
, то для некоторой промежуточной точки  отрезка
отрезка  из этих двух неравенств следует, что
из этих двух неравенств следует, что  Зафиксируем
Зафиксируем  и рассмотрим форму минимальной нормы
и рассмотрим форму минимальной нормы  на отрезке
на отрезке  Проведем замену переменной
Проведем замену переменной  и определим
и определим  при
при  Соответственно оператору
Соответственно оператору  имеющему характеристические корни
имеющему характеристические корни  определим оператор
определим оператор  где
где  обозначает дифференцирование по
обозначает дифференцирование по  Поскольку
Поскольку  удовлетворяет уравнению
удовлетворяет уравнению  на отрезке
на отрезке  то замена переменной
то замена переменной  обеспечивает выполнение
обеспечивает выполнение  на отрезке
на отрезке  .
.
Определим также алгебраический многочлен  где коэффициенты
где коэффициенты  выбираются так, чтобы
выбираются так, чтобы  -норма
-норма  на
на  была минимальной.
была минимальной.  удовлетворяет уравнению
удовлетворяет уравнению  на отрезке
на отрезке  Непрерывность и дифференцируемость решений уравнения
Непрерывность и дифференцируемость решений уравнения  по параметру
по параметру  в 0 означают, что
в 0 означают, что  для произвольной
для произвольной  -нормы,
-нормы,  на
на  . Из соотношения
. Из соотношения  получаем
получаем  где нормы берутся на отрезках
где нормы берутся на отрезках  соответственно. Учитывая также, что
соответственно. Учитывая также, что  , приходим к тому, что
, приходим к тому, что  .
.
Таким образом, норма  представлена как норма алгебраического многочлена
представлена как норма алгебраического многочлена  удовлетворяющего уравнению
удовлетворяющего уравнению  такого, что
такого, что  имеет минимальное
имеет минимальное  -отклонение от нуля на отрезке
-отклонение от нуля на отрезке  . В частном случае
. В частном случае  -аппроксимации
-аппроксимации  представляется многочленом Лежандра
представляется многочленом Лежандра  порядка
порядка  на
на 

(см. Девис (1963)). В данном случае  -норма
-норма  равна
равна

Вели возвести это выражение в квадрат, то из уравнения  получаются (3.3.35) и (3.3.33). Доказательство цоремы закончено.
получаются (3.3.35) и (3.3.33). Доказательство цоремы закончено.
Замечание. В силу общности проведенного доказательства можно получить также выражения и для других наилучших «аппроксимаций, которые совершенно аналогичны (3.3.33) для случая 
Задачу аппроксимации теперь можно свести к получению асимптотического решения путем применения теоремы 3.3.1 в сочетании с локальным результатом (3.3.33). Из последнего следует, что в данном случае функция  имеет вид
имеет вид  с показателем
с показателем  Это приводит к следующей теореме.
Это приводит к следующей теореме.
Теорема 3.3.3. Для любой функции  наилучшая
наилучшая  -аппроксимация
-аппроксимация  в классе
в классе  имеет норму ошибки
имеет норму ошибки  такую, что
такую, что

Теорема 3.3.3 указывает также, как можно получить асимптотически эффективное разбиение. Следует ввести функцию распределения

и использовать решения (3.3.25) в качестве узлов.
Данный результат удобен с вычислительной точки зрения. Чтобы оценить практические возможности метода, Маклур (1975) выполнил численное исследование, и ниже мы приводим некоторые из его результатов.
Однако, прежде чем заняться этим, хотелось бы подчеркнуть, что описанный метод не следует считать универсальным методом аппроксимации. Совсем наоборот, мы рекомендуем этот способ аппроксимации изображений только тогда, когда временные образы возникают в результате воздействия механизма деформации на идеальные изображения, относящиеся к классу режимов. Общая установка теории образов заключается в том, чтобы попытаться приспособить анализ к определенной алгебре изображений. В противном случае наша деятельность означала бы немногим более, чем изощренное вычерчивание кривых по точкам.
Итак, данный метод следует применять к временным образам класса режимов. Рассмотрим решения дифференциального уравнения второго порядка, исключая те моменты времени, в которых какой-либо импульс резко изменяет вторую производную. В качестве модели воспользуемся стохастическим дифференциальным уравнением

где случайный процесс  представляет флуктуационный шум на входе линейной системы, описываемой оператором
представляет флуктуационный шум на входе линейной системы, описываемой оператором

Моделируя чисто случайные импульсы, воздействующие на систему, определим

Точки представляющие моменты времени, когда в систему вводится импульс, воспроизводятся пуассоновским процессом восстановления. Интервалы  между последовательными моментами поступления импульса взаимно независимы и характеризуются одинаковыми экспоненциальными распределениями с плотностью
между последовательными моментами поступления импульса взаимно независимы и характеризуются одинаковыми экспоненциальными распределениями с плотностью

функция  описывающая вид входного импульса во всех точках
описывающая вид входного импульса во всех точках  выбирается таким образом, чтобы она аппроксимировала дельта-функцию; положим
выбирается таким образом, чтобы она аппроксимировала дельта-функцию; положим

Случайная величина  представляет амплитуду импульса, поступающего в систему в момент времени
представляет амплитуду импульса, поступающего в систему в момент времени  Мы полагаем, что
Мы полагаем, что  взаимно независимы и независимы относительно пуассоновского точечного процесса, а каждое
взаимно независимы и независимы относительно пуассоновского точечного процесса, а каждое  характеризуется нормальным распределением с нулевым математическим ожиданием и дисперсией
характеризуется нормальным распределением с нулевым математическим ожиданием и дисперсией 
Дифференциальный оператор  выбирается так, чтобы он моделировал гармонический осциллятор. Таким образом, характеристическое уравнение должно иметь комплексно-сопряженные корни
выбирается так, чтобы он моделировал гармонический осциллятор. Таким образом, характеристическое уравнение должно иметь комплексно-сопряженные корни  и
и

Действительная часть корня а отрицательна, следовательно, система устойчива и уравнение (3.3.42) имеет стационарное в узком смысле решение 
При подобном задании модели, порождающей временные образы, мы получаем возможность воспользоваться теорией, лежащей в основе ортогональных разложений стационарных в широком смысле процессов, для того чтобы вывести и реализовать наилучшие линейные представления образов в соответствии с процедурой, изложенной в разд.  . Эта линейная процедура зависит исключительно от свойств второго порядка процесса
. Эта линейная процедура зависит исключительно от свойств второго порядка процесса  . С другой стороны, можно воспользоваться более богатой структурой отдельных выборочных функций и отыскивать аппроксимации представления изображения как сегментированные решения уравнения
. С другой стороны, можно воспользоваться более богатой структурой отдельных выборочных функций и отыскивать аппроксимации представления изображения как сегментированные решения уравнения  Можно сравнить эти варианты.
Можно сравнить эти варианты.
Процесс  определяется заданием четырех параметров е-про-цесса и оператора
определяется заданием четырех параметров е-про-цесса и оператора  Зафиксируем
Зафиксируем  в плотности распределения (3.3.44); это означает, что средний интервал между моментами поступления импульсов равен 1/5 и математическое ожидание числа импульсов, приходящихся на единичный интервал, равно 5. Длительность каждого импульса фиксирована и равна
в плотности распределения (3.3.44); это означает, что средний интервал между моментами поступления импульсов равен 1/5 и математическое ожидание числа импульсов, приходящихся на единичный интервал, равно 5. Длительность каждого импульса фиксирована и равна  это достаточно малая величина, и, следовательно,
это достаточно малая величина, и, следовательно,  приемлемая аппроксимация дельта-функции, но она не настолько мала, чтобы процесс
приемлемая аппроксимация дельта-функции, но она не настолько мала, чтобы процесс  можно было точно описать сегментированными решениями уравнения
можно было точно описать сегментированными решениями уравнения  Среднее квадратичное отклонение величин
Среднее квадратичное отклонение величин  принимается равным
принимается равным  Соответствующие конечные результаты не зависят от этой величины; такой выбор удобен
Соответствующие конечные результаты не зависят от этой величины; такой выбор удобен
с вычислительной точки зрения. Наконец, корень а оператора  был произвольно выбран равным
был произвольно выбран равным 
Для оценки качества метода наилучших линейных представлений, разложения Карунена-Лоэва в применении к процессу  вычисляются суммы собственных значений. Рассмотрение численного примера, демонстрирующего эффективный способ проведения этих вычислений, отложим до
вычисляются суммы собственных значений. Рассмотрение численного примера, демонстрирующего эффективный способ проведения этих вычислений, отложим до  .
.
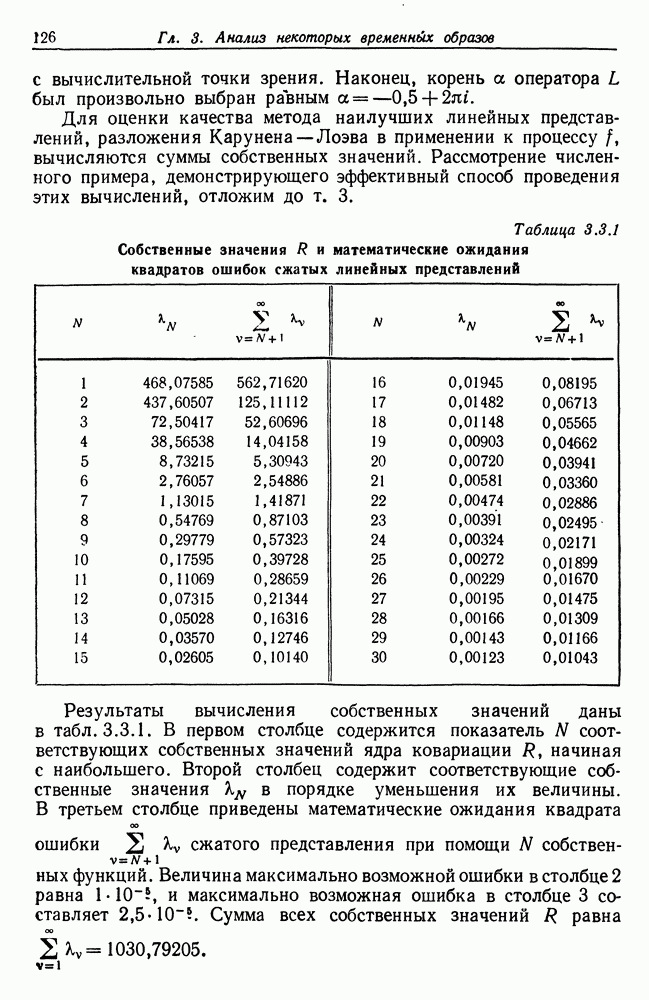
Таблица 3.3.1 (см. скан) Собственные значения  и математические ожидания квадратов ошибок сжатых линейных представлений
и математические ожидания квадратов ошибок сжатых линейных представлений
Результаты вычисления собственных значений даны в табл. 3.3.1. В первом столбце содержится показатель N соответствующих собственных значений ядра ковариации  начиная с наибольшего. Второй столбец содержит соответствующие собственные значения в порядке уменьшения их величины.
начиная с наибольшего. Второй столбец содержит соответствующие собственные значения в порядке уменьшения их величины.
В третьем столбце приведены математические ожидания квадрата ошибки  сжатого представления при помощи
сжатого представления при помощи  собственных функций. Величина максимально возможной ошибки в столбце 2 равна
собственных функций. Величина максимально возможной ошибки в столбце 2 равна  и максимально возможная ошибка в столбце 3 составляет
и максимально возможная ошибка в столбце 3 составляет  Сумма всех собственных значений
Сумма всех собственных значений  равна
равна  .
.
Исследование модели методом Монте-Карло на отрезке [0,1] предоставляет данные для оценки качества описанного метода. Оператор  порождает аппроксимирующие классы функций
порождает аппроксимирующие классы функций  Каждая смоделированная функция аппроксимируется некоторым представителем класса
Каждая смоделированная функция аппроксимируется некоторым представителем класса  который дает по одному узлу для аппроксимации в центре каждого импульса, поступающего на вход системы. Мы не предпринимаем дальнейших попыток оптимизировать размещение узлов; вычисленные аппроксимации просто являются наилучшими
который дает по одному узлу для аппроксимации в центре каждого импульса, поступающего на вход системы. Мы не предпринимаем дальнейших попыток оптимизировать размещение узлов; вычисленные аппроксимации просто являются наилучшими  -аппроксимациями в классе
-аппроксимациями в классе  с заданными узлами. Поскольку при каждом прогоне модели уравнение (3.3.42), играющее роль
с заданными узлами. Поскольку при каждом прогоне модели уравнение (3.3.42), играющее роль  легко решается аналитически, то ошибки аппроксимации вычисляются с помощью простых аналитических выражений. Соответствующие вычислительные процедуры не требуют дискретизации.
легко решается аналитически, то ошибки аппроксимации вычисляются с помощью простых аналитических выражений. Соответствующие вычислительные процедуры не требуют дискретизации.
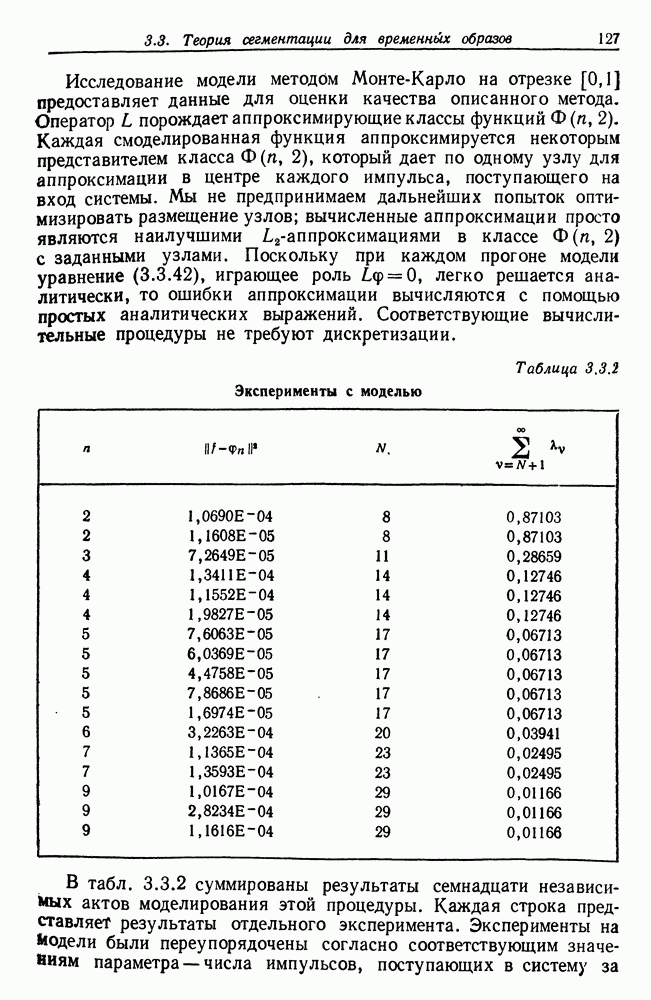
Таблица 3.3.2 (см. скан) Эксперименты с моделью
В табл. 3.3.2 суммированы результаты семнадцати независимых актов моделирования этой процедуры. Каждая строка представляет результаты отдельного эксперимента. Эксперименты на Модели были переупорядочены согласно соответствующим значениям параметра — числа импульсов, поступающих в систему за
единичный интервал, и соответственно числа узлов в полученном представлении. Первый столбец содержит значение этого параметра  при каждом прогоне модели. Во втором столбце дано значение квадрата ошибки
при каждом прогоне модели. Во втором столбце дано значение квадрата ошибки  аппроксимации
аппроксимации  функцией
функцией  класса
класса  , как это описано выше. Третий столбец содержит число
, как это описано выше. Третий столбец содержит число  параметров, полностью описывающих
параметров, полностью описывающих  так как оператор
так как оператор  второго порядка. Для сравнения со значениями, содержащимися в столбце 2, в последнем столбце приведены значения математических ожиданий квадрата ошибки
второго порядка. Для сравнения со значениями, содержащимися в столбце 2, в последнем столбце приведены значения математических ожиданий квадрата ошибки  наилучшего линейного представления
наилучшего линейного представления  с помощью
с помощью  главных собственных функций. Последние значения взяты из табл. 3.3.1.
главных собственных функций. Последние значения взяты из табл. 3.3.1.
Преимущества метода сегментированных аппроксимаций перед наилучшими линейными представлениями совершенно очевидны. Табл. 3.3.1 свидетельствует о том, что линейные представления хороши с точки зрения математического ожидания квадрата ошибки. Всего лишь при восьми аппроксимирующих собственных функциях математическое ожидание ошибки уже становится меньше единицы, в то время как дисперсия процесса  превышает 1000. Из табл. 3.3.2 следует, однако, что сегментированное представление существенно лучше, если в качестве критерия сравнения взять норму аппроксимации. Кроме того, поскольку сегментированное представление основывается на свойствах регулярности отдельных выборочных функций, то эти представления непосредственно отражают такие локальные свойства структуры образов, как расположение разрывов производных. Линейные представления не могут непосредственно воспроизводить такие структуры, поскольку собственные функции гладкие.
превышает 1000. Из табл. 3.3.2 следует, однако, что сегментированное представление существенно лучше, если в качестве критерия сравнения взять норму аппроксимации. Кроме того, поскольку сегментированное представление основывается на свойствах регулярности отдельных выборочных функций, то эти представления непосредственно отражают такие локальные свойства структуры образов, как расположение разрывов производных. Линейные представления не могут непосредственно воспроизводить такие структуры, поскольку собственные функции гладкие.
В дополнение к экспериментам, отраженным в табл. 3.3.2, при моделировании был рассмотрен подход к построению аппроксимаций, основанный на использовании плотности распределения. Можно прогнозировать качество этого подхода применительно к модели. Масса в плотности распределения узлов  концентрируется вокруг импульсов, подаваемых на вход системы. Поэтому в конечном счете разбиения, построенные из этой плотности, должны выделять все приложенные к системе импульсы. Поскольку, однако, абсолютная величина массы
концентрируется вокруг импульсов, подаваемых на вход системы. Поэтому в конечном счете разбиения, построенные из этой плотности, должны выделять все приложенные к системе импульсы. Поскольку, однако, абсолютная величина массы  сконцентрированной вокруг определенного импульса, зависит от амплитуды этого импульса, то вполне вероятно, что при построении, основанном на плотности распределения, мы пропустим какой-нибудь импульс и возникнут кратные узлы вблизи другого, если общее количество импульсов окажется большим. Это действительно наблюдается в экспериментах. Следовало бы также заметить, что в этих экспериментах количество импульсов легко определяется при помощи
сконцентрированной вокруг определенного импульса, зависит от амплитуды этого импульса, то вполне вероятно, что при построении, основанном на плотности распределения, мы пропустим какой-нибудь импульс и возникнут кратные узлы вблизи другого, если общее количество импульсов окажется большим. Это действительно наблюдается в экспериментах. Следовало бы также заметить, что в этих экспериментах количество импульсов легко определяется при помощи
варьирования числа узлов в последовательных аппроксимациях и наблюдения за поведением ошибки аппроксимации при различных количествах узлов. Когда все импульсы оказываются выделенными, ошибка аппроксимации резко падает до уровня, указанного в табл. 3.3.2.
Можно сделать вывод по крайней мере для данного случая, что аппроксимация, основанная на тщательном изучении структуры регулярности, имеет преимущества перед универсальным методом аппроксимации.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
- 4.2. Рентгенография кристаллов
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы